Rtreemix: an R package for estimating evolutionary pathways and genetic progression scores

Abstract

Summary: In genetics, many evolutionary pathways can be modeled by the ordered accumulation of permanent changes. Mixture models of mutagenetic trees have been used to describe disease progression in cancer and in HIV. In cancer, progression is modeled by the accumulation of chromosomal gains and losses in tumor cells; in HIV, the accumulation of drug resistance-associated mutations in the viral genome is known to be associated with disease progression. From such evolutionary models, genetic progression scores can be derived that assign measures for the disease state to single patients. Rtreemix is an R package for estimating mixture models of evolutionary pathways from observed cross-sectional data and for estimating associated genetic progression scores. The package also provides extended functionality for estimating confidence intervals for estimated model parameters and for evaluating the stability of the estimated evolutionary mixture models.

Availability: Rtreemix is an R package that is freely available from the Bioconductor project at http://www.bioconductor.org and runs on Linux and Windows.

Contact: jasmina@mpi-inf.mpg.de

1 INTRODUCTION

Many disease processes can be characterized on the molecular level by the ordered accumulation of genetic aberrations. Progression of a single patient along such a model is typically correlated with increasingly poor prognosis. Mixture models of mutagenetic trees provide a suitable statistical framework for describing these processes (Beerenwinkel et al., 2005a). For a given patient, the molecular disease state can be characterized by his/her genetic progression score that quantifies how many and which of the accumulating genetic events have already occurred (Rahnenführer et al., 2005).

This methodology has been successfully applied to describing both HIV progression and cancer progression. In HIV, the genetic events are mutations in the genome of the dominant strain in the infecting virus population that arise when a patient receives a specific medication. The respective analysis based on mutagenetic trees leads to the quantitative notion of a genetic barrier for the virus to escape from a given drug therapy to resistance (Beerenwinkel et al., 2005c). In cancer, the genetic events are lesions in the cancer cells such as chromosomal losses or gains. Higher genetic progression scores can be shown to be significantly associated with shorter expected survival times in glioblastoma patients (Rahnenführer et al., 2005) and times until recurrence in meningioma patients (Ketter et al., 2007).

We created the easy-to-use and efficient R package Rtreemix for (i) estimating mixtures of evolutionary models from cross-sectional data, (ii) deriving genetic progression scores from these models and (iii) performing stability analyses on different levels of the model.

2 IMPLEMENTATION

The Rtreemix package takes advantage of the high-level interface, the statistical tools and the large amount of data that R and Bioconductor projects provide. For estimating mixture models, the package builds up on efficient C/C++ code provided by a modified version of the Mtreemix software (Beerenwinkel et al., 2005b), which we made independent of the LEDA packageb in order to provide a free R package. It implements the main functionality of Mtreemix for model fitting and adds new functions for estimating genetic progression scores with corresponding confidence intervals and for performing model analysis. The R code makes use of the S4 class system which allows for high extensibility with user-defined functions.

The preprocessing of the input data is handled by the R language, giving the user easier access to a large amount of data. Model fitting and other time consuming operations are done by the C/C++code, using the R API. The fitted models are returned to R, and several methods are available for further analysis of the results. The package offers various diagnostic tools and functions for visualization, for example, plotting the estimated mixture models.

3 FUNCTIONALITY

Table 1 summarizes the main functions available from the R package Rtreemix. Note that as a special case of mixture models all functions can also be used for estimating and analyzing single evolutionary pathways. The functions fit and bootstrap estimate mixtures of evolutionary pathways from cross-sectional data, without and with bootstrap confidence intervals for model parameters, respectively. The estimation of the mixture model is improved in Rtreemix by specifying different starting solutions for mixture model fitting (Bogojeska et al., 2008). Computing the likelihoods of patterns of genetic events for a given model is done using the functions likelihoods and distribution. Simulation studies are performed with sim and generate. The functions gps and confIntGPS calculate, for sets of patients, the genetic progression scores with corresponding confidence intervals. Finally, various methods for comparing different mixture models (comp.models.levels) and for analyzing their stability on different levels (stability.sim) are available, see Bogojeska et al. (2008) and the vignette of the R package for details.

Table 1.

Functions provided by the Rtreemix package

Rtreemix	Description
fit	Fit mixture models of evolutionary pathways
bootstrap	Confidence intervals for mixture model
likelihoods	Compute likelihoods based on model
distribution	Calculate distribution induced by model
sim	Draw samples from mixture model
generate	Generate random mixture model
gps	Estimate genetic progression scores
confIntGPS	Confidence intervals for GPS
comp.models.levels	Compare topologies of two mixture models
comp.trees.levels	Compare topologies of model components
stability.sim	Perform stability analysis of mixture model

The novel functions are written in bold.

4 EXAMPLE

Datasets used for estimating mixture models consist of binary patterns that describe the occurrence of a set of genetic events in a group of patients. Each pattern corresponds to a single patient. The dataset from the Stanford HIV Drug Resistance Database (Rhee et al., 2003) comprises genetic measurements of 364 HIV patients treated only with the drug AZT. This dataset is loaded and a mixture model with K = 2 tree components is fit:

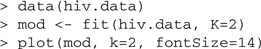
In the resulting plot, see Figure 1, an edge between two genetic events u and v is labeled with the conditional probability that the event v appears given that the event u has occurred. Confidence intervals both for the mixture parameters and for such conditional probabilities can be obtained with a bootstrap analysis, for B=100 bootstrap replicates with

Fig. 1.

Estimated model for the accumulation of drug resistance associated mutations in the HIV genome under AZT monotherapy. Nodes represent genetic events, and edge labels denote conditional probabilities between subsequent events. The columns next to the model are explained in the text.

The calculation of genetic progression scores and their corresponding confidence intervals for the given HIV dataset is straightforward

Figure 1 shows an evolutionary process for HIV evolution under pressure presented by the drug AZT, estimated from the HIV dataset. The model captures the two known major pathways of mutations 215F/Y−41L−210W (called TAM1 pathway) and 70R−219E/Q−67N (TAM2 pathway). Next to the three steps of the TAM1 pathway the corresponding genetic progression scores and their confidence intervals are plotted. Scores are normalized such that a value of 1 corresponds to a pattern with average progression across all samples. The two columns next toFigure 1 depict the scores, once conditioned on the occurrence of none (left) and once on the occurrence of all (right) of the three events of the TAM2 pathway.

As expected, estimated progression values increase along the model, with larger values in the case of known additional presence of the TAM2 pathway. In most cases, confidence intervals of progression scores of subsequent events are even non-overlapping, underlining the suitability of our modeling approach.