Predicting Dynamic Postural Instability Using Center of Mass Time-to-Contact Information

Abstract

Our purpose was to determine whether spatiotemporal measures of center of mass motion relative to the base of support boundary could predict stepping strategies after upper-body postural perturbations in humans. We expected that inclusion of center of mass acceleration in such time-to-contact (TtC) calculations would give better predictions and more advanced warning of perturbation severity. TtC measures were compared with traditional postural variables, which don’t consider support boundaries, and with an inverted pendulum model of dynamic stability developed by Hof et al. (2005). A pendulum was used to deliver sequentially increasing perturbations to 10 young adults, who were strapped to a wooden backboard that constrained motion to sagittal plane rotation about the ankle joint. Subjects were instructed to resist the perturbations, stepping only if necessary to prevent a fall. Peak center of mass and center of pressure velocity and acceleration demonstrated linear increases with postural challenge. In contrast, boundary relevant minimum TtC values decreased nonlinearly with postural challenge, enabling prediction of stepping responses using quadratic equations. When TtC calculations incorporated center of mass acceleration, the quadratic fits were better and gave more accurate predictions of the TtC values that would trigger stepping responses. In addition, TtC minima occurred earlier with acceleration inclusion, giving more advanced warning of perturbation severity. Our results were in agreement with TtC predictions based on Hof’s model, and suggest that TtC may function as a control parameter, influencing the postural control system’s decision to transition from a stationary base of support to a stepping strategy.

1. Introduction

The sensory systems provide a wealth of information related to the linear and angular kinematics of the body (Von Holst and Mittelstaedt 1950). A perturbation applied to the upper body will accelerate the body’s center of mass (CoM) towards the perimeter of the base of support. Here, the most important information may not be the current CoM position, but where it will be in the future. If CoM motion cannot be arrested before crossing the support boundary, a step must be taken to maintain stability. The decision to step must be made promptly because it takes time for muscles to generate force and initiate movement.

The central nervous system may use time-to-contact¹ (TtC) information to assess future postural stability (Carello et al. 1985; Riccio 1993). TtC is a boundary-relevant measure that combines information about the instantaneous kinematics of the CoM to predict a future time at which the CoM will contact the base of support boundary, akin to the “extrapolated CoM” described by Hof et al. (2005). TtC has been used to assess postural stability in quiet stance conditions involving relatively small CoM velocities and accelerations. Some calculate TtC as the distance to the base of support boundary divided by the velocity of the center of pressure (CoP) (Van Wegen et al. 2002; Hertel et al. 2006; Hertel and Olmsted-Kramer 2007) or CoM (Forth et al. 2007), while others also include CoP acceleration (Slobounov et al. 1997; Slobounov et al. 1998; Patton et al. 2000; Slobounov et al. 2006; Haibach et al. 2007). Comparison of these methods by Haddad et al. (2006) suggested that the addition of acceleration information might better represent static postural control. Of note is that the majority of these studies have used the TtC of the CoP rather than the CoM. In dynamic situations, in which there is a significant chance that the CoM will actually contact and go beyond the support boundary, TtC of the CoM may be a more informative measure because in practice the CoP can never reach the boundary. Moreover, unlike the CoM, the CoP is not a point associated with a specific mass and can therefore be moved instantaneously.

CoM TtC information could be important under dynamic postural conditions in helping to decide whether a step is needed to recover from a perturbation. Most studies evaluating stepping strategies use randomized platform (McIlroy and Maki 1996; Pai et al. 2000; Schulz et al. 2005) or waist-pull (Luchies et al. 1994; Pai et al. 1998; Mille et al. 2003) perturbations. Schulz et al. (2006) investigated the CoM TtC under such dynamic conditions, using the velocity-only TtC computation. Incorporation of acceleration information may allow earlier and more accurate assessment of perturbation severity, compared with velocity information alone. Further, sequentially increasing perturbation magnitudes might reveal different response patterns than randomized presentation, and test whether TtC operates as a control parameter as balance is gradually pushed towards and beyond the limit of dynamic stability. In that case, TtC should be closely associated with the scaling of postural responses and predictive of changes in postural states, such as the transition from a stationary base of support to a stepping strategy. Conceptually, this is similar to the abrupt transition from anti-phase to in-phase finger coordination that occurs when finger flexion/extension frequency (the control parameter) is gradually increased (Haken et al. 1985).

We hypothesized that boundary-relevant CoM TtC information would accurately predict the transition from a stationary base of support to a stepping strategy when sequentially increasing upper-body perturbations were applied to healthy young subjects. Further, we hypothesized that incorporation of CoM acceleration information in TtC computations would give more accurate predictions of the TtC values that would trigger stepping responses, and provide subjects with earlier warning of perturbation severity. TtC measures were compared with traditional measures of instability, including maximal CoM and CoP velocity and acceleration, and to variables arising from Hof et al.’s (2005) inverted pendulum model of dynamic stability.

2. Methods

2.1 Subjects

Ten healthy subjects (5 Male, 5 Female; 27±2.7 yrs; 71.0±14.3 kg; 1.72±0.10 m) without balance impairments participated in the experiment after completing an informed consent form approved by our Institutional Review Board.

2.2 Instrumentation

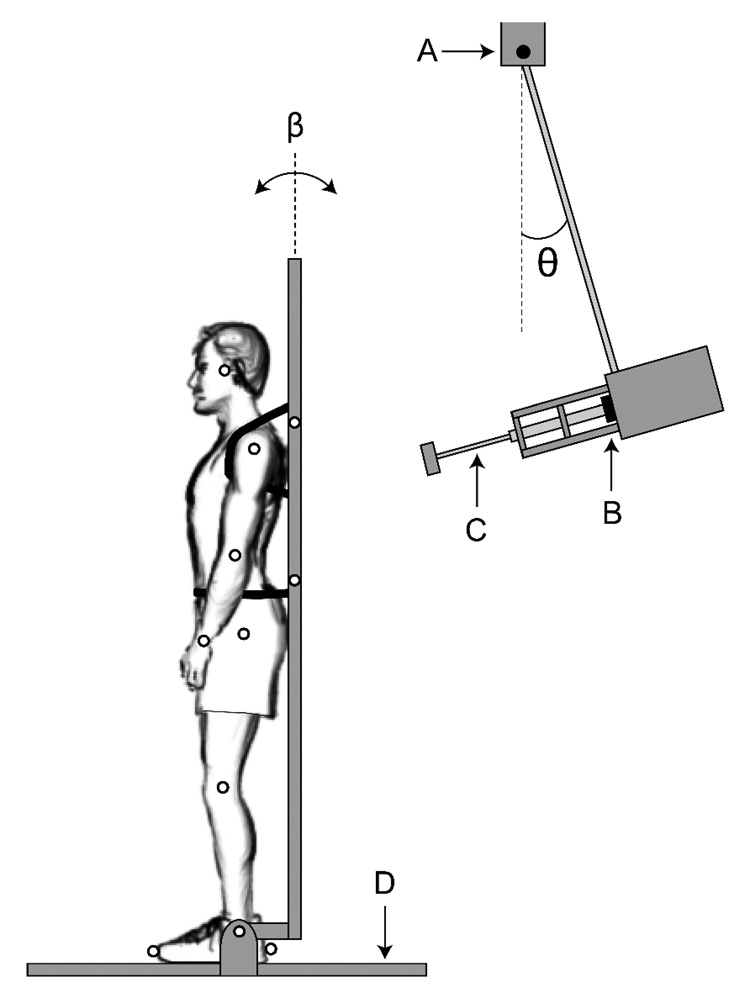
Forward sway was induced by bumping the subjects with a 15 kg pendulum (Figure 1). Pendulum angle was measured with a potentiometer (θ; Figure 1). A rope and pulley were used to position the pendulum at an initial angle displayed on an LCD. A lightweight wooden backboard with shoulder and waist straps constrained subject movement to the sagittal plane about the ankle joint, approximating an inverted pendulum (Peterka and Loughlin 2004). After release, the pendulum swung forward, striking the backboard at 78% of subjects’ standing height. Subjects listened to white noise through earphones to mask the sound of pendulum release. Perturbation force was measured with a uni-axial load cell (41/571-07, Honeywell International) in series with a shock absorber. Three-dimensional kinematics of passive reflective markers (Figure 1) were captured at 200 Hz (ProReflex MCU240, Qualysis). Ground reaction forces were measured with a force platform (BP6001200-2000, AMTI). Potentiometer and force data were sampled at 1000 Hz.

Figure 1.

Illustration of experimental setup showing backboard restraint and perturbation device (pendulum). Passive reflective marker locations are indicated by small open circles. Straps around the shoulders and waist were used to secure subjects to the backboard (shown) A: potentiometer; B: load cell; C: shock absorber; D: force platform; β: backboard angle; θ: pendulum angle. Angles are referenced to the vertical.

2.3 Protocol

Subjects’ upper bodies were strapped to the backboard, and their ankle joint axes were aligned with two support bearings. The feet were placed hip-width apart, parallel with the sagittal plane; arms were relaxed with hands clasped in front. Subjects were asked to fix their gaze on a mark on a wall at eye level 5 m away and to stand as still as possible. Subjects performed two 30 s quiet stance trials prior to the perturbation protocol. For each perturbation, the pendulum was held at a specified angle, a light signaled subjects to commence quiet stance, and after a random period of 2–6 s the pendulum was released to swing forward and strike the backboard. The pendulum was quickly withdrawn to prevent a second “rebound” perturbation. Subjects were told to resist the perturbation, resume quiet stance as quickly as possible, and only step if necessary to prevent a fall. The initial pendulum release angle was 10°, and was increased incrementally in subsequent trials by 5° (heavy subjects) or 2.5° (light subjects) until subjects stepped. Two sets of perturbations were performed; to minimize learning effects only the second set was analyzed.

2.4 Data Reduction

Quiet stance and perturbation data were filtered at 2 Hz and 10 Hz, respectively, using a low-pass fourth-order zero-lag Butterworth filter. Optimal filter cut-off frequencies were determined through power spectral analysis. Force and potentiometer data were downsampled to equal the kinematic data sampling rate (200 Hz), and the CoP was calculated from the ground reaction forces. Segment masses and CoM locations were estimated to determine the total body CoM position in the sagittal-plane (de Leva 1996). The anterior-posterior positions of the markers on the left toe and heel (Figure 1) were used to define the support boundaries; positional corrections were made to account for the radii of the markers. The initiation of the perturbation (marked by the abrupt rise in pendulum force) indicated time zero. To account for the differing inertias associated with varied subject masses, a postural “challenge” was computed by dividing the peak pendulum angular velocity at impact by the mass of each subject. For each subject the perturbation was applied at 78% of standing height, thereby controlling for effects of differing vertical CoM positions relative to the pendulum force application.

Based on Slobounov et al.’s (1997) formulation for calculating the TtC to a two-dimensional support boundary, which includes CoM acceleration information (TtC_ACC), the instantaneous CoM TtC_ACC for anterior-posterior motion towards the toe or heel boundary was calculated as

$$Tt{C}_{ACC}=\frac{-v\pm \sqrt{v^2-2a\left(p_{\text{max}}-p\right)}}{a}$$ (1)

where p, v, and a are the anterior-posterior positions, velocities, and accelerations of the CoM, respectively, and p_max is the anterior-posterior location of the toe (or heel) markers. The smallest positive real solution (i.e. the TtC to the first boundary crossed; toe or heel) was taken as the instantaneous TtC. The CoM TtC_VEL, which does not include acceleration (Riccio 1993), was calculated as

$$Tt{C}_{VEL}=\left|\frac{p_{\text{max}}-p}{v}\right|$$ (2)

Using an inverted pendulum model, Hof et al. (2005) computed the extrapolated position of the center of mass in the direction of the CoM velocity (XCoM)

$$XCoM=p+\frac{v}{{\omega }_0}$$ (3)

$${\omega }_0=\sqrt{\frac{g}{l}}$$ (4)

where ω₀ is the angular eigenfrequency of a non-inverted pendulum, g is gravitational acceleration, and l is the pendulum length, computed as the distance from the lateral malleolus to the CoM. The spatial margin of stability (MoS_XCoM) was then computed

$$Mo{S}_{XCoM}=p_{\text{max}}-XCoM$$ (5)

From this, the TtC of the XCoM (TtC_XCoM) was calculated

$$Tt{C}_{XCoM}=\left|\frac{p_{\text{max}}-XCoM}{v}\right|=\left|\frac{Mo{S}_{XCoM}}{v}\right|$$ (6)

Note that TtC_XCoM estimates the time it will take the extrapolated CoM (XCoM) to reach the support boundary if it continues with constant velocity, while TtC_VEL estimates the time it will take the actual CoM to contact the boundary with constant velocity. Therefore, TtC_XCoM will always be lower than TtC_VEL.

For non-stepping trials the global minima of the MoS_XCoM and each TtC time series were selected for further analysis. For stepping trials, TtC global minima would usually be zero due to boundary contact; therefore, the first local minimum after perturbation initiation was selected. The minimum MoS_XCoM value was set to zero if it crossed the support boundary (i.e. became negative). TtC latency (time after perturbation at which TtC minima occur) and CoM position at minimum TtC were computed and averaged across postural challenge levels for each subject. Ranges (maximum-minimum) across challenge levels for TtC latency, CoM position, and CoM velocity at minimum TtC were also computed for each subject individually and then averaged across subjects.

2.5 Statistical Analysis

Backboard angle prior to perturbation was compared to quiet stance angle using a paired t-test, to determine if subjects adjusted their postural orientation in anticipation of the perturbations. Subject-specific linear and nonlinear equations were used to characterize the relationships between postural challenge and traditional (peak forward CoM and CoP velocity and acceleration) and boundary-relevant (TtC_ACC, TtC_VEL, MoS_XCoM, and TtC_XCoM) measures of stability. Coefficients of determination (R²) were calculated to assess the strength of each relationship; paired t-tests were used to compare the R² values between the TtC_ACC, TtC_VEL, and TtC_XCoM calculations. Linear correlations were performed between the experimental and predicted stepping minimum values for TtC_ACC, TtC_VEL, and TtC_XCoM. Paired t-tests were used to compare the absolute differences between the experimental and predicted stepping minimum TtC values, average TtC latencies, CoM position values and ranges, and CoM velocity ranges using each of the three TtC calculation methods. The criterion for significance was p < .05.

3. Results

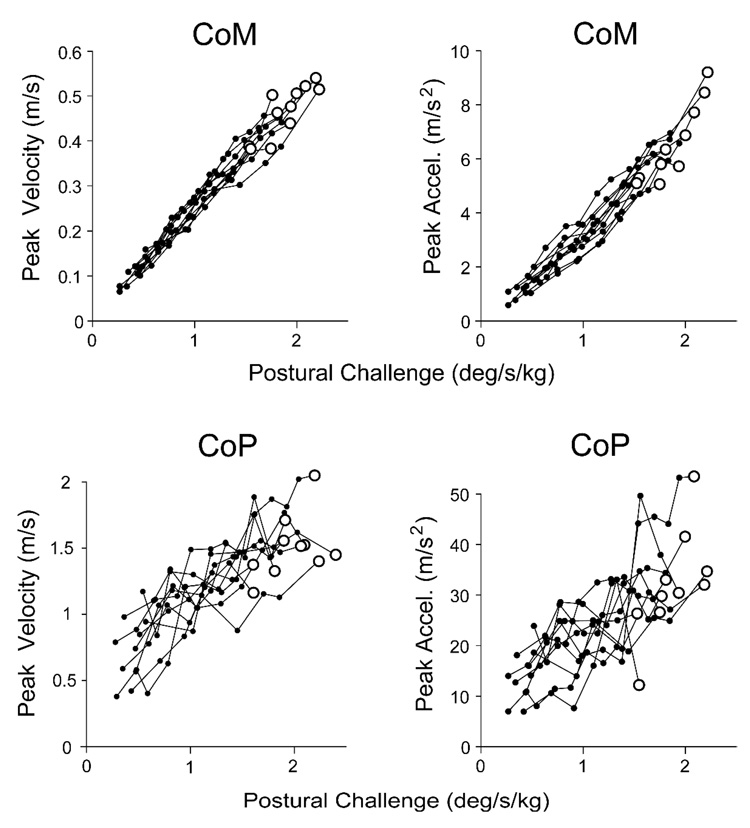
The mean backboard angle (β, Figure 1) was the same (p = .135) in quiet stance (0.45±0.87°; Mean ± Standard Deviation) as it was before the onset of perturbations (0.06±0.93°), indicating that subjects did not alter their postural orientation prior to pendulum impact. The relationships between postural challenge and peak forward CoM velocity and acceleration were well characterized by linear equations (R² = 0.98±0.02 and R² = 0.98±0.02, respectively; Figure 2). Linear relationships also represented peak forward CoP velocity and acceleration (Figure 2), but did not fit as well (R² = 0.75±0.15, R² = 0.68±0.21, respectively).

Figure 2.

Relationship between postural challenge and peak forward center of mass (CoM) velocity and acceleration (top), and peak forward center of pressure (CoP) velocity and acceleration (bottom). Each line represents data from one subject. Enlarged open circles represent stepping trials.

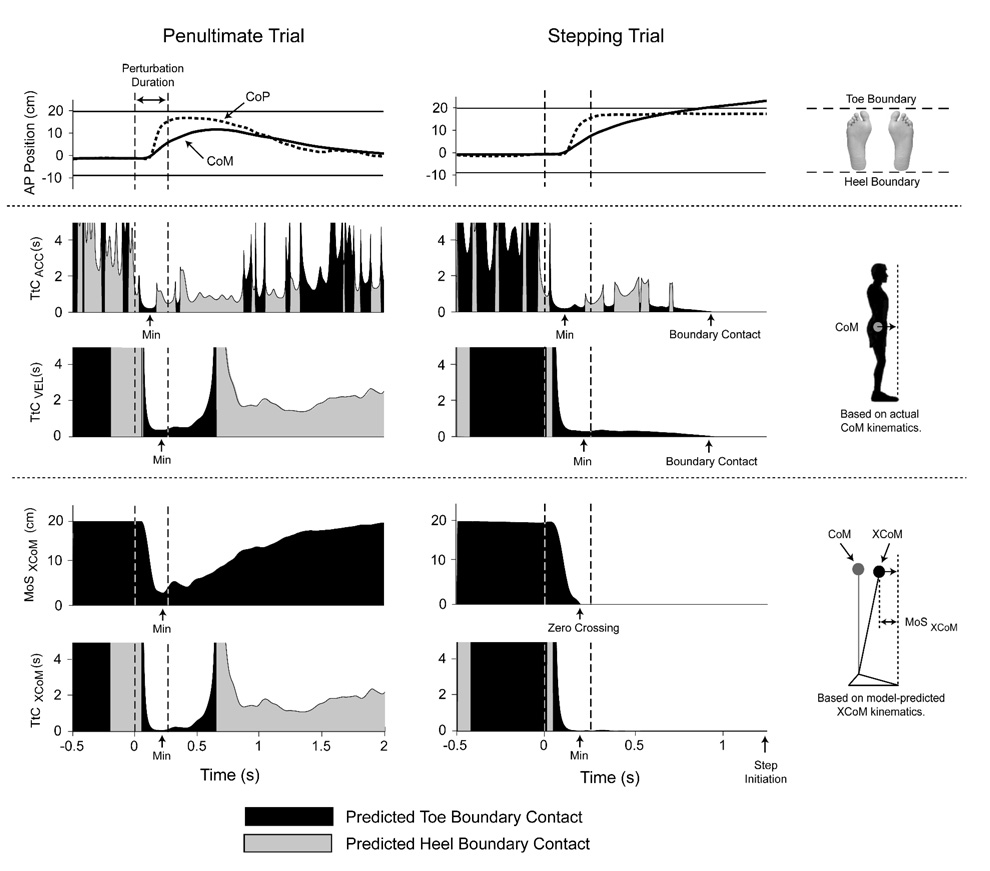
Typical CoM and CoP responses during the penultimate and stepping trials, and the selection of TtC_ACC, TtC_VEL, MoS_XCoM, and TtC_XCoM minima are illustrated in Figure 3. For all subjects, the MoS_XCoM demonstrated a strong inverse linear relationship with postural challenge level (R² = 0.94±0.03; Figure 4). The MoS_XCoM reached zero before the CoM contacted the support boundary for all subjects on the stepping trial, and reached zero during the penultimate trial for only one subject.

Figure 3.

Example of perturbation response for penultimate and stepping trials. Top graphs show center of mass (CoM) and center of pressure (CoP) kinematics, and toe and heel positions. Middle graphs show CoM time-to-contact (TtC) computed by including (TtC_ACC) and not including (TtC_VEL) acceleration information. Bottom graphs show the margin of stability (MoS_XCoM) and TtC (TtC_XCoM) of the extrapolated center of mass (XCoM) based on an inverted pendulum model (Hof et al. 2005).

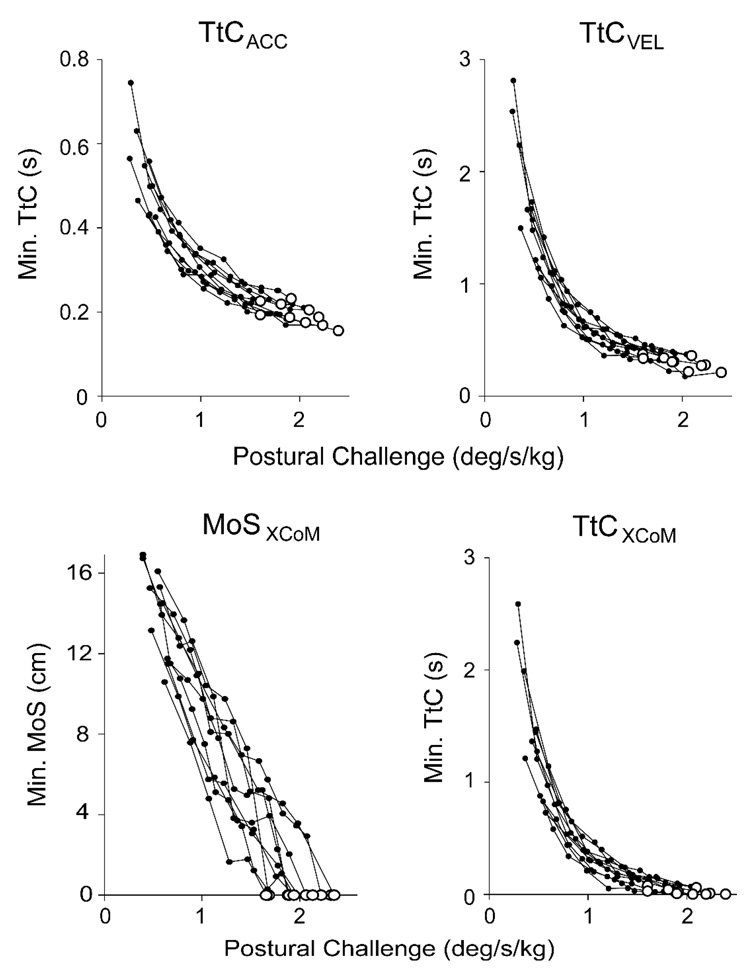
Figure 4.

Top: Minimum time-to-contact (TtC) based on the kinematics of the center of mass (CoM), computed with and without acceleration information (TtC_ACC and TtC_VEL, respectively), as a function of postural challenge level for all subjects. Bottom: Minimum margin of stability (MoS_XCoM) and TtC (TtC_XCoM) of the extrapolated center of mass, which are based on an inverted pendulum model. Enlarged open circles indicate stepping trials. Note that TtC_ACC vertical scaling is different from TtC_VEL and TtC_XCoM.

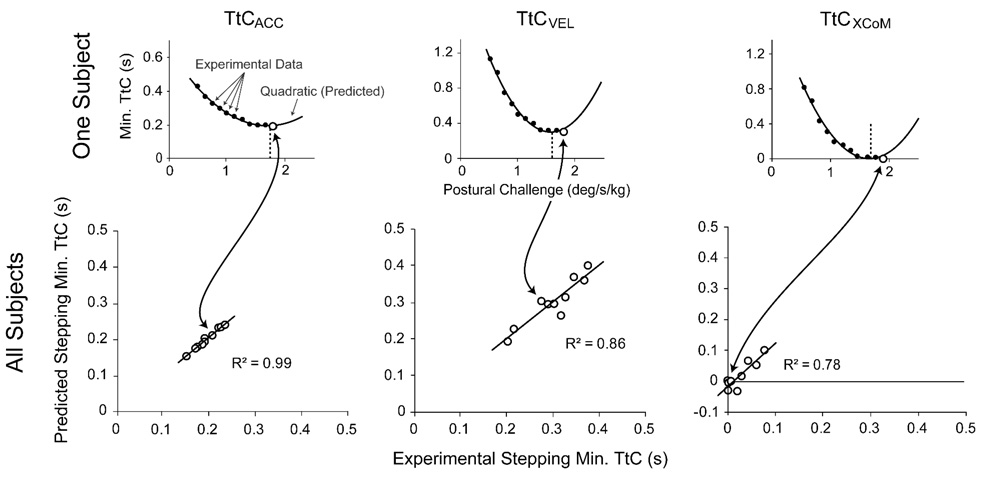
In contrast to the linear MoS_XCoM relation, the minimum TtC_ACC, TtC_VEL, and TtC_XCoM decreased nonlinearly with increasing postural challenge (Figure 4). Individual subject data were well fit by quadratic functions (TtC_ACC: R² = 0.96±0.03, TtC_VEL: R² = 0.94±0.04, and TtC_XCoM: R² = 0.94±0.04). Although the quadratic relations were strong for all three calculation methods, statistically the R² value for the TtC_ACC fit was higher than for either TtC_VEL (p = .023) or TtC_XCoM (p = .015).

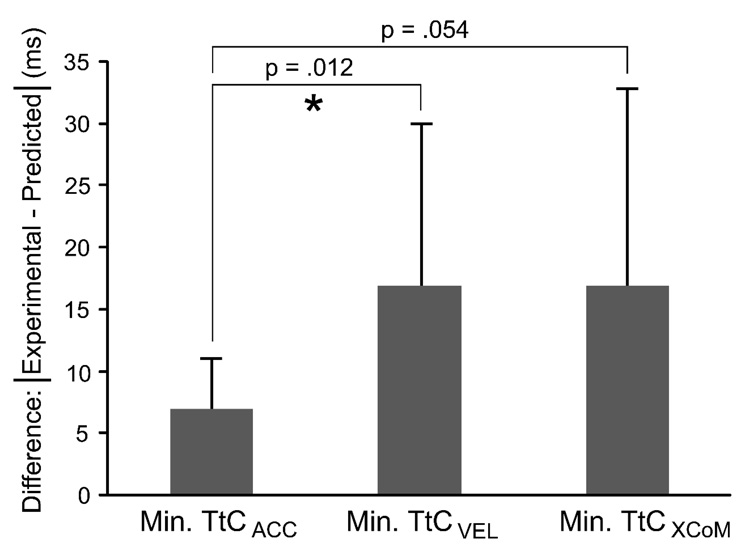
The vertex of each fitted quadratic function represents a prediction for the minimum TtC value that would elicit a stepping response (actual experimental stepping values: TtC_ACC = 195±27 ms; TtC_VEL = 301±56 ms; TtC_XCoM = 25±27 ms). Linear correlations between experimental and predicted stepping TtC values were strongest for TtC_ACC and weakest for TtC_XCoM (Figure 5). The absolute difference between experimental and predicted stepping TtC_ACC values was lower than for TtC_VEL values (Figure 6).

Figure 5.

Top Row: Experimental minimum time-to-contact (TtC) data and fitted quadratics for one subject when acceleration information is included (TtC_ACC, left), and not included (TtC_VEL, middle). The TtC of a model extrapolated center of mass (XCoM) is also shown (TtC_XCOM, right). Closed and open circles indicate non-stepping and stepping trials, respectively. Bottom Row: Linear correlations between the experimental and predicted (vertices of quadratic functions) minimum TtC values for stepping responses of all subjects using the different TtC calculation methods.

Figure 6.

Bar chart showing the means and standard deviations of the absolute differences between the experimental and predicted stepping TtC values for the different TtC calculation methods. Paired t-tests were performed to test for differences between calculation methods; prediction error for TtC_ACC was lower than for TtC_VEL and TtC_XCoM, but only the TtC_ACC vs. TtC_VEL comparison met our significance criterion (*p < .05).

The post-perturbation latencies were shorter and the CoM was farther from the toes at minimum TtC for TtC_ACC than for TtC_VEL and TtC_XCoM (Table 1). There were no clear relationships between increasing postural challenge and computed TtC latencies or their associated CoM positions. Across challenge levels, the range of TtC latencies, CoM positions, and CoM velocities at minimum TtC was smaller using the TtC_ACC calculation, compared to TtC_VEL and TtC_XCoM (Table 1).

Table 1.

Temporal and spatial variables at minimum center of mass (CoM) time-to-contact (TtC) using three different calculation methods (Mean ± Between Subjects Standard Deviation).

Variable	TtCACC	TtCVEL	TtCXCoM
Latency (ms)a	79 ± 5***	180 ± 23	180 ± 24
CoM Position (%)a,b	16.1 ± 8.2***	30.8 ± 8.6	29.3 ± 7.7
Latency Range (mm)c	16 ± 6**	67 ± 40	73 ± 49
CoM Position Range (mm)c	21 ± 7**	74 ± 43	66 ± 29
CoM Velocity Range (mm/s)c	251 ± 45*	324 ± 68	321 ± 75

^aLatency and CoM position data were first averaged across perturbations levels for each subject.

^bExpressed as a percentage of the distance from the ankle to the toe (0% = ankle; 100% = toe).

^cRange is first computed for each subject (maximum-minimum value occurring across perturbation levels).

^*TtC_ACC differs from TtC_VEL and TtC_XCoM at p < .05

^**p < .01

^***p < .001 in paired t-tests.

4. Discussion

Traditional postural control variables, including peak velocity and acceleration of the CoP and CoM, demonstrated linear increases with postural challenge. In contrast, minimum TtC measures were nonlinearly related to postural challenge, enabling prediction of stepping responses using quadratic equations, supporting our initial hypothesis. Such relationships were found when TtC was calculated with or without CoM acceleration information (TtC_ACC and TtC_VEL, respectively), and were in agreement with a model-based TtC of the extrapolated CoM (TtC_XCoM). The quadratic fits were more accurate and TtC minima occurred earlier with the inclusion of acceleration information, thus giving earlier warning of perturbation severity and supporting our second hypothesis.

It is unsurprising that the TtC_ACC relationship with postural challenge was well fit by a quadratic function, because of its computational formula. However, the TtC_VEL and TtC_XCoM relationships were also well fit by quadratics, even though they were calculated from linear formulae with no squared terms. The nonlinear nature of these two relations may be due to the statistical characteristics of CoM position and velocity at minimum TtC. Across challenge levels, the absolute range of CoM positions was much smaller than the range of CoM velocities at minimum TtC (averaging 21 mm vs. 251 mm/s for TtC_ACC, an order of magnitude difference, Table 1). In this case, dividing a narrowly changing position by a widely changing velocity produced ratios (i.e. TtC values) in a nonlinear pattern.

The average minimum TtC_VEL computed for stepping trials was 301 ms, which is shorter than those predicted by Schultz et al. (2006) for young females subjected to anterior-posterior waist-pulls (~575 ms). Our computed TtC_ACC values were even shorter, averaging 195 ms. These discrepancies are due to our protocol and selection of minimum TtC. Our subjects were gradually pushed towards the limit of their stability, and the minimum TtC following a transient impact was selected. In contrast, Schulz et al. used a series of randomized, continuously applied perturbations, and selected TtC values to optimize the percentage of correct stepping/non-stepping predictions.

The average post-perturbation latency of minimum TtC occurrence for TtC_VEL was 180 ms, meaning that information concerning the plausibility of arresting forward CoM motion without stepping was available to subjects very soon after (or during) the perturbation. Considering the substantial delay until the actual stepping response (> 1 s), one could argue the importance of such an early warning. This long “decision time” may be the result of the instructions to resist stepping, causing subjects to wait until the last possible moment to step. However, in more ecological situations, an early warning and early decision may be crucial. For example, complex terrain could impose a more lengthy preparation for the stepping response, and early warning would increase the probability of successful recovery.

The minimum TtC_ACC occurred at shorter latencies than minimum TtC_VEL (79 vs. 180 ms), giving even earlier warning of perturbation severity. The minimum TtC_ACC always occurred during the initial CoM acceleration, before the subjects could respond with CoP adjustments. Consequently, the minimum TtC_ACC was largely independent of subject responses, based solely on the dynamics of the perturbation. Schultz et al. (2006) reported a lengthening of the minimum TtC with age and impairment. However, they used the TtC_VEL calculation, for which minima occur later and thus may be influenced by the ability of the subjects to respond to the perturbation. One might expect that changes associated with aging or impairment would not have an effect on minimum TtC_ACC, because TtC_ACC is not affected by the capacity to respond to transient perturbations. Exceptions to this conjecture would include anticipatory postural adjustments, such as alterations in the amount of plantarflexor muscle activity prior to the perturbation, which could increase or decrease active musculotendinous stiffness at the time of perturbation onset.

The backboard constrained subjects to motion approximating an inverted pendulum and thus the use of an “ankle strategy”. This allows us to compare the TtC_XCoM of the extrapolated CoM model (Hof et al. 2005) with the TtC from the experimental subject CoM trajectories (TtC_ACC and TtC_VEL). Relationships between TtC_XCoM and postural challenge were very similar in shape to those of TtC_ACC and TtC_VEL (see Figure 4). Subjects should need to step if MoS_XCoM reaches zero, which was true in almost all cases. There was only one instance in which MoS_XCoM reached zero without a step, possibly due to small errors in CoM position estimation on the penultimate trial, when the CoM closely approaches the base of support boundary. Average TtC latencies and CoM positions at minimum TtC were not different between TtC_VEL and TtC_XCoM, supporting the inverted pendulum model. Differences between TtC_ACC and TtC_XCoM calculations were expected due to the inclusion of acceleration information in TtC_ACC calculations.

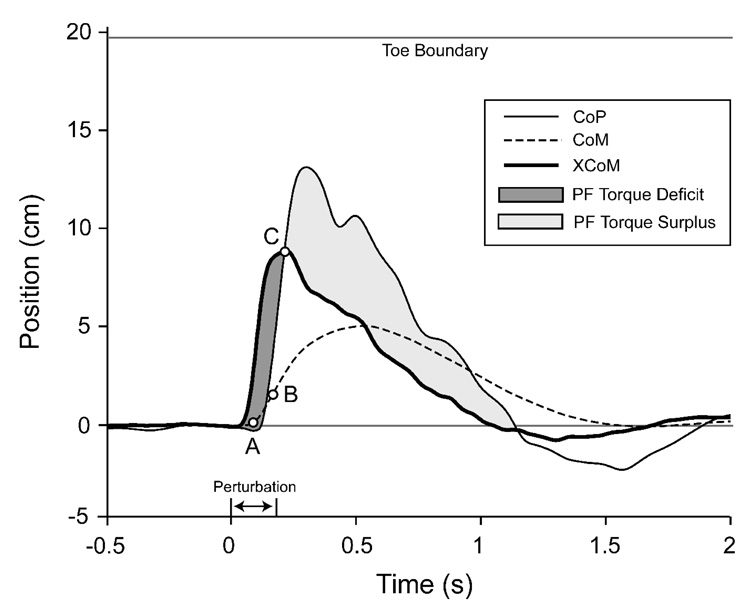
To aid in our comparison with the Hof et al. (2005) model, the CoP, CoM, and XCoM motions were plotted for a single, non-stepping trial (Figure 7). The model gives three possible states of dynamic posture, depending on relative XCoM and CoP positions. Initially, the perturbation induces potential instability, with the XCoM moving in front of the CoP. Without corrective action the CoM will eventually cross the support boundary. A “torque deficit” is apparent, as additional plantarflexor torque is needed to shift the CoP in front of the XCoM. When the CoP does move in front of the XCoM, a stable state is reached. As long as the CoP remains in front of the XCoM, the real CoM will be accelerated backward assuring stability (until the XCoM passes the ankle joint). In the stable state there is usually a “torque surplus”, with more plantarflexor torque than needed to arrest CoM motion before it reaches the base of support boundary (a “safety factor”). In stepping trials a third state occurs when the XCoM crosses the support boundary, with a loss of stability unless the base of support is changed.

Figure 7.

Time series data illustrating the responses of the center of mass (CoM; dashed line), center of pressure (CoP; thin black line), and extrapolated center of mass (XCoM; thick black line) during a non-stepping trial for one subject. The times at which the minimum time-to-contact (TtC) of the CoM occur (open circles) using different computation methods are shown: TtC_ACC (A), TtC_VEL (B), and TtC_XCoM (C). Regions of plantarflexor (PF) torque “deficit” and “surplus” are indicated by darker and light shading, respectively. Positions are given relative to the ankle joint center.

Finally, Tokuno et al. (2006) reported that perturbation responses were dependent on the direction and amplitude of “natural” body sway during quiet stance, with rearward platform translations evoking larger responses if the CoP was shifted forward at perturbation onset. Although the state of the postural system upon destabilization is certainly important, the position of the CoP (or CoM) at the onset of a perturbation alone is insufficient to predict the subsequent response. Our TtC results demonstrate the importance of CoM position, velocity, and acceleration with respect to the support boundary in assessing the magnitude of a postural threat. As shown in Figure 7, consideration of CoP position in conjunction with the extrapolated CoM (XCoM) can provide a continuous assessment of the “degree” of dynamic postural stability.

In summary, we found a quadratic relationship between the magnitude of upper body postural perturbations and the minimum CoM TtC; the vertex of the quadratic function predicted when subjects would transition from a stationary base of support to a stepping strategy. Predictions were more accurate and gave earlier warning of perturbation severity when CoM acceleration information was included, rather than with CoM velocity information alone. Our results agreed with TtC predictions based on an inverted pendulum model of postural control proposed by Hof et al. (2005), and suggest that the postural system could use TtC as a control parameter in evaluating perturbation severity and deciding whether to initiate a stepping response.