Abstract
The performance of high-sensitivity x-ray imagers may be limited by additive instrumentation noise rather than by quantum noise when operated at the low exposure rates used in fluoroscopic procedures. The equipment-invasive instrumentation noise measures (in terms of electrons) are generally difficult to make and are potentially not as helpful in clinical practice as would be a direct radiological representation of such noise that may be determined in the field. In this work, we define a clinically relevant representation for instrumentation noise in terms of noise-equivalent detector entrance exposure, termed the instrumentation noise-equivalent exposure (INEE), which can be determined through experimental measurements of noise-variance or signal-to-noise ratio (SNR). The INEE was measured for various detectors, thus demonstrating its usefulness in terms of providing information about the effective operating range of the various detectors. A simulation study is presented to demonstrate the robustness of this metric against post-processing, and its dependence on inherent detector blur. These studies suggest that the INEE may be a practical gauge to determine and compare the range of quantum-limited performance for clinical x-ray detectors of different design, with the implication that detector performance at exposures below the INEE will be instrumentation-noise limited rather than quantum-noise limited.
1. Introduction
Digital x-ray imaging has gained wide acceptance in diagnostic clinical practice because of its many useful features compared to screen–film systems, such as wide dynamic range, image processing through gray-scale manipulation, rapid sequence acquisitions and good image quality at reduced dose (Yaffe and Rowlands 1997, Nudelman 1982). Flat-panel detectors (FPD) based on thin-film transistor arrays are now considered as an alternative to conventional x-ray image intensifiers (XII) because they provide geometric distortion and veiling-glare-free images (Rowlands and Yorkston 2000). In addition to the conventional digital radiographic applications, these systems are also being used in low-dose, real-time, digital fluoroscopic imaging for navigation and localization of endovascular devices. The standard performance measure descriptors of such detectors are available in terms of Fourier-domain- and spatial-domain-based figures-of-merit (Cunningham 2000). The Fourier-domain linear-systems analysis considers the noise-equivalent quanta (NEQ) and the detective quantum efficiency (DQE) as a basis for figures-of-merit to evaluate detector performance (Metz et al 1995, Pineda and Barrett 2004a, 2004b, Siewerdsen and Jaffray 2000). The spatial domain signal-to-noise ratio (SNR) has been a simple, but most widely used, figure-of-merit for detector evaluation using the Rose model (Rose 1953, Burgess 1999). It has been well understood that the image SNR, and hence the image quality, is ultimately and ideally limited by the number of x-ray quanta used to create the digital image. The quantum-limited performance range could be defined as the exposure range wherein the minimum detectable signal is limited by quantum noise. The quantum-limited operating range of actual digital x-ray detectors is very much dependent on the system design, whereas additive instrumentation noise sources play a significant role in determining the exposure below which the minimum detectable signal is no longer determined by image quanta.
Fluoroscopic procedures require detectors with high sensitivity and high temporal resolution (readout time of about 1/30 s) for low exposure (0.1–10 μR or 0.026–0.26 nC kg−1 per frame), real-time imaging. XIIs have fulfilled these requirements over many decades of use. The system noise components in such units are due to digitization noise, TV system electronic noise and image intensifier input and output phosphor structure mottle (Kume et al 1986, Cowen and Workman 1992). Newer flat panels provide excellent undistorted, veiling-glare-free images at higher exposures, but have limitations with respect to SNR at low fluoroscopic x-ray exposures (Antonuk et al 1999). At such low exposures, both indirect and direct flat panels become instrumentation-noise rather than quantum-noise limited (Hunt et al 2004, Roos et al 2004). Key contributors of the instrumentation noise may be amplifier read-out noise or the switching and analog line-path noise due to capacitance coupling of adjacent lines encountered when taking the signal from the pixel to the amplifiers. In addition, the thermal noise generated in the pixel matrix could also be a potential source of instrumentation noise. Currently used protocols for both acceptance testing and routine quality assurance of digital fluoroscopic units lack convenient quantitative methodology to describe the range of exposure where a system becomes instrumentation-noise limited.
Considering the importance of low-dose fluoroscopy in interventional procedures, a clinically relevant, radiological noise representation in terms of the corresponding detector x-ray entrance exposure would be more easily implementable by medical physicists in the field, compared to the equipment-invasive measures of noise in terms of electrons per pixel. Furthermore, measurement of noise in terms of electrons does not readily allow for comparison of detectors of diverse design given differences in electrons to pixel gray value (in terms of arbitrary digital numbers) conversion factors, and is generally not useful without such information. Such a metric as defined here would also be able to identify the exposure range of quantum-noise-limited operation and instrumentation-noise-limited operation in routine quality assurance checks.
In an early effort to quantify these noise-limited ranges, Marshall et al (2001) suggested the use of the exposure at which system noise accounts for 50% of the total noise, i.e., where system noise is equal to the quantum mottle term. The results of their studies were dependent on the subjective performance of observers using a contrast-detail method to evaluate the relationship between contrast resolution and dose. Busse et al (2001) provided a quantitative discussion of various system noise sources in dynamic imaging detectors and developed metrics to compare detector technologies based on signal and electronic noise levels and their impact on DQE. In later years, studies on indirect flat-panel detectors (Roos et al 2004) have used the fact that the detector x-ray entrance exposure at which the instrumentation noise and the quantum noise are equal has an SNR that was reduced by a factor of due to the instrumentation noise. This was observed as a deviation from the ideal linear behavior of SNR versus detector entrance exposure at lower exposures such as those used in fluoroscopic procedures. Similar to Roos, several other authors have used an approach of plotting SNR versus exposure to determine an approximate threshold exposure (Suzuki et al 2002, Tousignant et al 2003). Various other methods have also been used in an attempt to determine the x-ray quantum-limited range of exposures including measuring the dark-field NPS to determine the electronic noise level and comparing this to the total noise at zero spatial frequency, with the anisotropic ASIC noise and the electronic noise subtracted as a function of exposure (Hunt et al 2004) and by examining the exposure at which the zero-frequency DQE drops to one-half its high dose value (Hunt et al 2003, Zhao et al 2003).
These works have been excellent sources for understanding the limitations due to instrumentation noise and illustrate the importance of knowing at what exposure the x-ray detector becomes instrumentation-noise limited. However, the above methods lack a simple connection between x-ray entrance exposure and the point below which such detectors are in the instrumentation-noise-limited regime.
The aim of this study is to build on these less formal descriptors and to develop a simple and practical metric that is easily implemented in the field and is based on the previously existing signal and noise descriptors for digital imaging systems in terms of the average signal and variance in pixel gray values. Additionally, this method should allow for the comparison of different detector technologies without requiring detailed knowledge of the various instrumentation noise sources and their differing sensitivities to x-rays. Thus for this metric, the instrumentation-noise-limited range of different detector technologies can be described in terms of the detector x-ray entrance exposure, allowing different detector technologies to be directly compared.
In this work, we report on the formulation of a metric, termed instrumentation noise-equivalent exposure (INEE), which represents the detector entrance exposure at which instrumentation noise and quantum noise become equal, and discuss the experimental results obtained from three different custom-designed CCD-based detectors with different x-ray sensitivities and a commercial x-ray image intensifier (XII). A simulation study is presented that demonstrates the effect of detector blur and image post-processing blur on INEE measurements. The purpose of the simulation study is to reveal the robustness of this metric against post-processing in digital images as well as its dependence on inherent detector blur. For comparison, the results for indirect commercial flat-panel detectors are taken from a previously mentioned study (Roos et al 2004) where the instrumentation noise was observed through a deviation from ideal linear behavior of the SNR versus exposure measurement.
2. Theory
In contrast to a system where the SNR is quantum-noise limited, the total noise in this formalism incorporates the quantum noise as well as the instrumentation noise added in quadrature (Rudin et al 2006). Therefore, the measured total noise (Nm) can be represented as
| (1) |
where E is the x-ray entrance exposure to the detector, INEE is the instrumentation noise-equivalent exposure (in units of entrance exposure) and k1 is a proportionality constant relating exposure to digital numbers. The first term within the parentheses on the right-hand side of equation (1) represents the quantum noise contribution, which is proportional to the x-ray entrance exposure (Poisson statistics). The second term on the right-hand side represents the constant instrumentation noise written in terms of its equivalent x-ray entrance exposure. Using the above equation, the measured SNR can be written as
| (2) |
where S represents the measured signal and k2 is the detector sensitivity in terms of pixel gray value per unit entrance exposure. The constant k1 is proportional to the constant k2 and their differences are unimportant for this analysis. Equation (2) can be re-written in the equivalent form as follows:
| (3) |
where A is a constant and represents the slope of a straight line expressing the relation between SNR2 and exposure (E) at sufficiently large values of E so that the term B/E ≪ 1; the term B represents the INEE. The INEE can be evaluated experimentally, when the measured SNR2 versus exposure data are fitted to equation (3) to determine the constant B. In other words, INEE is the detector entrance exposure at which instrumentation noise and quantum noise become equal (i.e., E = B in equation (3)) and SNR2 is half the value that would be obtained from quantum statistics alone. For exposures above the INEE, the detector performance would be more quantum limited, and for exposures below the INEE it would be more instrumentation-noise limited. It is to be noted that the INEE is not the actual electronic noise, but it is a relative term which relates the total instrumentation noise and the detector entrance exposure, and hence the INEE also depends on the properties of the imaging chain and its efficiency to transfer the image quanta. Therefore, the limits of a detector technology are readily identified with a clinically relevant measure—the detector entrance exposure. Furthermore, different detectors could be directly compared if one were to use a standardized spectrum, such as the RQA standards provided by the IEC 62220-1.
For digital imaging systems, we assume that the total quantum plus instrumentation noise may be represented in terms of the variance of pixel gray values in the offset- and gain-corrected flat-field images. Such a simple measured value of total noise could equivalently be expressed by equation (1), where the second term on the right-hand side corresponds to the instrumentation noise represented in units of practically measurable x-ray exposure. Therefore, a simple linear-regression fit of the measured data for variance versus x-ray entrance exposure to the detector would be sufficient for estimating the range of quantum-limited performance, and the INEE could then be calculated by dividing the intercept of the variance axis by the slope of the fitted curve. The resulting INEE from this measurement would be equivalent to the value of constant B determined using equation (3).
3. Methods and materials
In this paper, we will determine the INEE for several detectors from a plot of variance versus exposure using equation (1) and for one detector using a plot of signal-to-noise versus exposure using equation (3) and compare the results. A simulation study will be performed to determine the effect of detector and post-processing blur on the measured INEE value.
3.1. Experimental study
The sets of measurements presented in this paper were performed with four different detectors to demonstrate the usefulness of this metric. Three of these were custom-designed CCD-based detectors of different sensitivities, referred to as the micro-angiographic fluoroscopic detector (MAF), the high-sensitivity micro-angiographic fluoroscopic detector (HSMAF) and the micro-angiographic detector (MA). The key differences between the three detectors are in their CCD camera coupling arrangements (direct fiber-optic coupling in the MA and the HSMAF versus mirror-lens coupling in the MAF) and whether there is an additional gain stage (no additional gain in the MA versus an added variable-gain dual-stage micro-channel plate (MCP) light image intensifier (LII) in the MAF and the HSMAF). The detailed design and performance evaluation of the MA and the MAF detectors has been reported elsewhere (Rudin et al 2002, Ganguly et al 2003a, 2003b, Kyprianou et al 2005, Wu et al 2005). The HSMAF detector is a recent development from our group, and the detailed experimental performance evaluations of this detector are presented elsewhere (Yadava et al 2008). The fourth detector investigated was a standard commercial x-ray image intensifier (XII) unit with a CCD camera image sensor all mounted on a C-arm gantry. A comprehensive total-system performance evaluation of this XII system has been reported elsewhere (Yadava et al 2005).
Sequences of 60 flat-field images were acquired for each of the four detectors tested. A 60-frame-averaged flat-field image and dark image was used for offset and gain correction. The variance and SNR were determined from the 60 frames of corrected flat-field images. For image acquisition, the x-ray tube voltage was set to 72 kVp for each detector and, in order to achieve very low exposure to the detector (as required for the SNR method), the x-ray beam was attenuated by using combinations of filter materials such that the first half-value layers of the x-ray spectra used for the MA, the MAF, the HSMAF and the XII detectors were 8.2 mm Al, 10.2 mm Al, 10.1 mm Al and 10.3 mm Al, respectively. The LIIs in the MAF and the HSMAF were operated in a high sensitivity mode, with a high gain setting. Very low detector entrance exposures were measured using a combination of two ionization chambers. One ionization chamber (model 96035B, 15 cm3 ionization chamber with model 35617 electrometer; Keithley Instruments Inc., Cleveland, OH) was kept close to the x-ray source, and the other (model 96020A, 150 cm3 ionization chamber with model 35050A dosimeter; Keithley Instruments Inc.) close to the position of the detector input. The ratio of the readings between the ionization chambers at the higher exposures was used to determine the expected detector-chamber reading from the source-chamber reading for lower exposure measurements to overcome the limited sensitivity of the chamber nearest the detector. The variation in this ratio, representing the uncertainty in the exposure measurement, was found to be less than 1% and this uncertainty would have little effect on the uncertainty of the curve fit parameters. The uncertainty in exposure calibration or accuracy, which affects the absolute INEE determination, was 2.5% as quoted by the chamber calibration facility (Fluke Biomedical, Cleveland, OH). In these measurements, it was verified that the system output was linear with mAs from the low to high exposure ranges. For the relatively less sensitive micro-angiographic detector (MA), only one ionization chamber (model 96035B, 15 cm3 ionization chamber with 35050A dosimeter) was used to directly read the detector entrance exposure. The XII was used in the 7 inch magnification mode with an effective image pixel size of 150 μm. To eliminate grid lines, the antiscatter grid was removed from the XII input. Essentially, the same INEE value will be obtained with the grid in or out as long as exposure at the detector input is used for its determination. In order to calculate the variance and SNR, a small central ROI (50 pixels × 50 pixels) was selected in each of the 60 images. The mean pixel gray value within the ROI (signal) and its standard deviation (noise) were calculated for each of the 60 frames. The average of all the 60 variance and SNR values at each exposure were used for the INEE determination. The variability in the variance and the SNR over the sequence of 60 frame images at each exposure were described by calculating the standard deviation in their mean values. For the SNR-based INEE estimation, the squared value of the SNR versus exposure was fitted to equation (3) to determine the instrumentation noise-equivalent exposure (INEE), whereas for the variance-based estimation, a simple linear regression model was fitted over the variance versus exposure data and calculated from equation (1).
3.2. Simulation study
The measured values of output SNR and variance via the flat-field images from x-ray detectors may be affected by image post-process smoothing, detector blurring and other sources of blurring, such as correlation in image quanta detection across several pixels. Temporal correlations between images, resulting from potential lag and/or ghosting or through image post-processing (e.g., recursive filtering) may also have an effect as discussed further in the results and discussion section. Such smoothing and blurring may result in noise filtering that could lead to a higher SNR compared to that expected from an ideal Poisson-distributed x-ray image pattern. To determine the effect of detector blurring and image post-process smoothing on the measured INEE, Poisson-distributed random numbers representing the input x-ray quanta per pixel (Devroye 1986) were generated to simulate an ideal input x-ray image pattern. Different blurring or smoothing functions were simulated by Gaussian point spread functions (characterized by their full-width-at-half-maxima (FWHM)) defined in a 15 pixel × 15 pixel kernel. The reference pixel size and x-ray fluence were selected following measurements on the MA detector (43 μm square-image-pixels in a 1024 pixel × 1024 pixel matrix), but apply generally. A two-dimensional discrete convolution of the Poisson-distributed image with the Gaussian detector-blurring function results in an image with reduced noise, but without affecting the signal. The instrumentation noise was simulated using additive constant-variance and zero-mean noise. Addition of instrumentation noise after the blurring process simulates the detector-blurring case, whereas addition after detection but prior to the smoothing process represents the image post-processing case. For simplicity, the system was modeled to follow Poisson statistics throughout the imaging chain. The INEE was then determined by calculating the signal-to-noise ratio (SNR), and the variance over a range of input exposures for various Gaussian-width blur functions and additive noise levels.
4. Results and discussion
4.1. Experimental
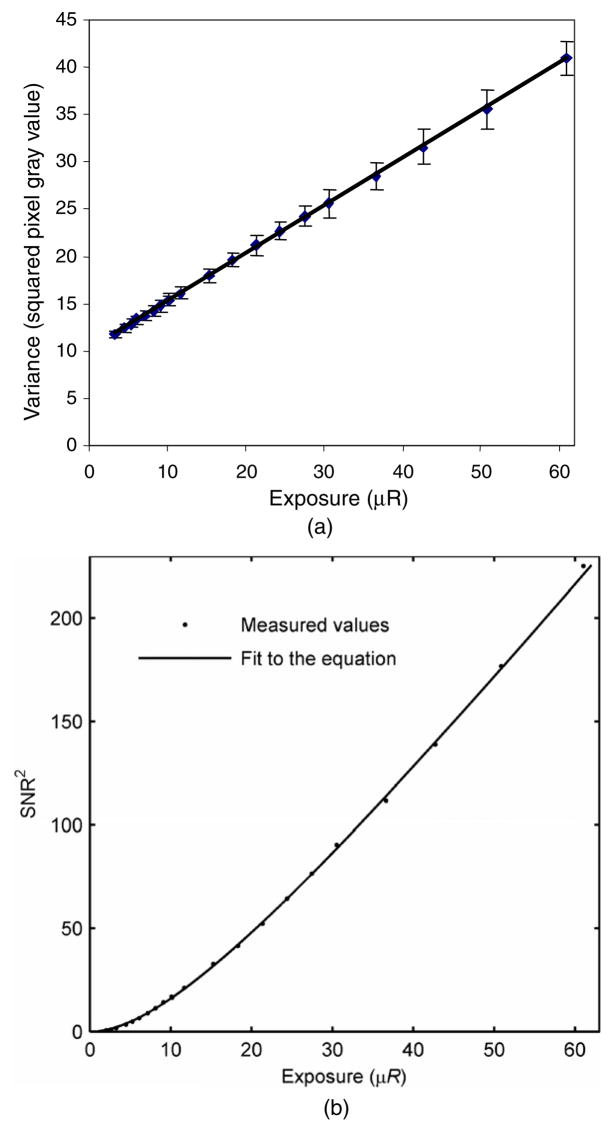
The measured data for variance versus exposure and the corresponding least-squares regression fits of equation (1) are presented in this section. For comparison between the variance-based and SNR-based estimation of the INEE, a set of data from the MA detector was fitted using both equations (1) and (3). The ratio of intercept (i.e., the variance at zero exposure or the instrumentation noise, in units of digital number) and slope (i.e., the conversion factor from digital number to equivalent exposure) determines the INEE in the linear fit to variance versus exposure data, whereas the fit parameter B represents the INEE in the SNR-based approach. Figures 1(a) and (b) show plots of the experimental data for the relatively less sensitive MA detector and corresponding least-squares fit to equations (1) and (3).
Figure 1.
(a) Variance-versus-exposure data and the least-squares regression fit of equation (1) for the determination of INEE for the MA detector. (b) SNR2-versus-exposure data and the least-squares regression fit of equation (3) for the determination of INEE for the MA detector.
The data points on each plot represent the experimentally measured values of variance and SNR2 as a function of the detector entrance exposure in μR, and the solid line represents the least-squares regression fit for each case.
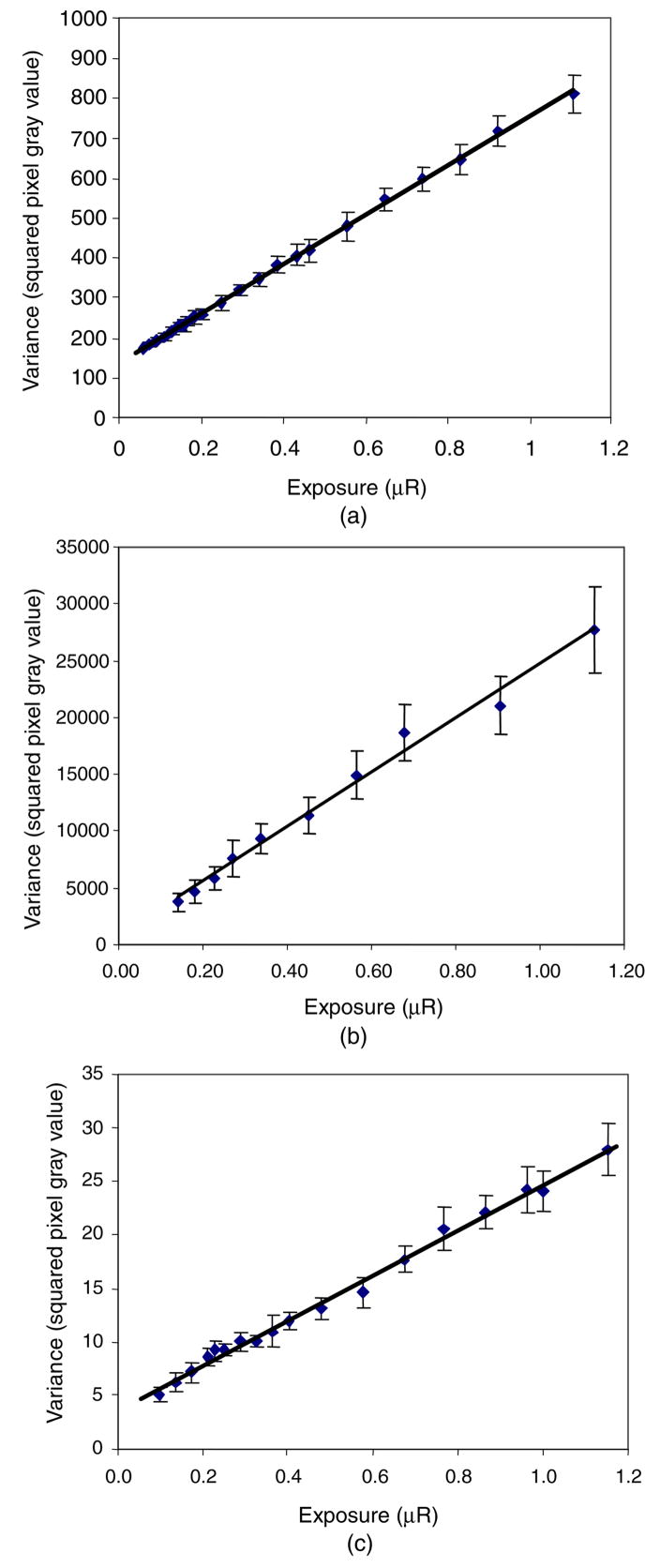
The resulting INEE from the variance-based and SNR-based approaches were found to be 20.4 ± 0.2 μR (5.26 ± 0.05 nC kg−1) and 20.1 ± 0.3 μR (5.19 ± 0.08 nC kg−1), respectively, which reflects good agreement between the two methods if the system has a linear response over the range of exposures. Figures 2(a)–(c) show the experimental data for variance versus detector entrance exposure and the corresponding least-squares fits to equation (1) for the other three detectors under study: the MAF, the HSMAF and the XII, respectively. It can be observed from the plots in figure 2 that the ranges of the variance axes differ greatly as a result of the differences in the operational gain settings and detector characteristics (i.e., the analog to digital conversion gain factor in the CCD) and indicate precisely why such a metric, as the INEE, is useful.
Figure 2.
Variance-versus-exposure data and the least-squares regression fit of equation (1) for the determination of INEE using the data for the (a) MAF, (b) HSMAF and (c) XII at low exposures.
From the fit, we found that the INEE for the MAF detector was 0.22 ± 0.01 μR (0.057 ± 0.003 nC kg−1): for the HSMAF detector it was 0.03 ± 0.02 μR (0.008 ± 0.005 nC kg−1), and for the XII detector it was 0.17 ± 0.01 μR (0.044 ± 0.003 nC kg−1). The plots of variance versus exposure, shown in figures 1(a) and 2(a)–(c), also show a noticeable difference in the scales of the exposure axes of the plots for the MAF, HSMAF and the XII compared to the MA. This is due to the difference in their sensitivity and performance objective as described in more detail below.
Table 1 gives a comparison of the measured INEE values for all four detectors with reference values for a flat-panel detector. Since the sensitivity of these detectors is directly influenced by the quanta collection in each pixel (and hence image pixel dimensions), a normalized INEE with reference to a 150 μm × 150 μm pixel area is also presented in table 1. The choice of this normalization factor is arbitrary, and in this case it was fixed to a reference pixel dimension of 150 μm2 that corresponds to approximately that of current state-of-the-art detectors. The use of the normalized INEE removes the effect of pixel dimensions on the calculated INEE and facilitates comparisons across detectors. This normalization does not affect the absolute measurements of the detector INEE which are related to the native pixel size of the detector. The X-ray spectrum may influence the measured INEE, just as it may affect DQE. This is to be expected, as the quantum detection efficiency and conversion gain of the phosphor are energy dependent. Further studies will be necessary to fully determine the spectral influence on measured INEE.
Table 1.
List of measured INEE values for various detector systems and the normalized INEE for 150 μm × 150 μm pixel area.
| Detector system | Pixel size (μm) | Measured INEE (μR) | Normalized INEE (μR) |
|---|---|---|---|
| MA | 43 | 20.4 | 1.68 |
| MAF | 82 | 0.22 | <0.1 |
| HSMAF | 35 | <0.1 | <0.1 |
| XII | 150 | 0.17 | 0.17 |
| Indirect CsI FPD | 194 | 2.75 | 4.60 |
The detector systems studied were assumed to have negligible temporal correlations between frames. For detectors where potential correlations may be significant (e.g., FPDs with lag and/or ghosting), a measurement may be made at various image acquisition rates to determine the effect of such correlations on the measured INEE. To minimize the effect of these correlations, the minimum frame rate should be utilized.
The MA detector reaches the range of instrumentation noise limits, where the instrumentation noise and the quantum noise become equal, at a relatively higher exposure of 20.4 μR (5.26 nC kg−1) with respect to common fluoroscopic exposures of 1.0–10 μR (0.26–2.6 nC kg−1), whereas the MAF, the HSMAF and the XII can operate without instrumentation noise limitations to well below exposure values required in interventional fluoroscopy. The measured value of INEE for the MA detector indicates that its intrinsic noise prevents it from operating in the quantum-noise-limited regime at low exposures reflecting the fact that the MA was not designed to be used in fluoroscopic applications. However, the INEE values for the MAF, the HSMAF and the XII imply that they can be employed in interventional fluoroscopy without being instrumentation-noise limited as expected from their higher system gain (higher sensitivity). Improvement in system gain tends to reduce the impact of instrumentation noise relative to quantum noise at lower exposures, resulting in improved INEE. In previous studies on the Varian 4030CB flat-panel detector (194 μm pixel), Roos et al (2004) have reported that the instrumentation noise and quantum noise are equal at 2.75 μR (0.71 nC kg−1), which corresponds to the INEE in this formulation. This reported value of INEE for this indirect flat-panel detector points out a significant inherent design limitation in such detector technology compared with XII and CCD-fiber-optic technology. The use of an additional amplifying stage in the CCD-based system (dual stage Gen2 MCP LII in the MAF and the HSMAF) reduces the INEE, indicating that such technology has the potential to provide an improved detector system for diagnostic and interventional applications where both high resolution as well as high sensitivity may be required. Similarly, the higher XII system gain leads to a reduced INEE value implying that XIIs may indeed provide improved image quality compared to flat-panel detectors for low-exposure fluoroscopy procedures.
4.2. Simulation
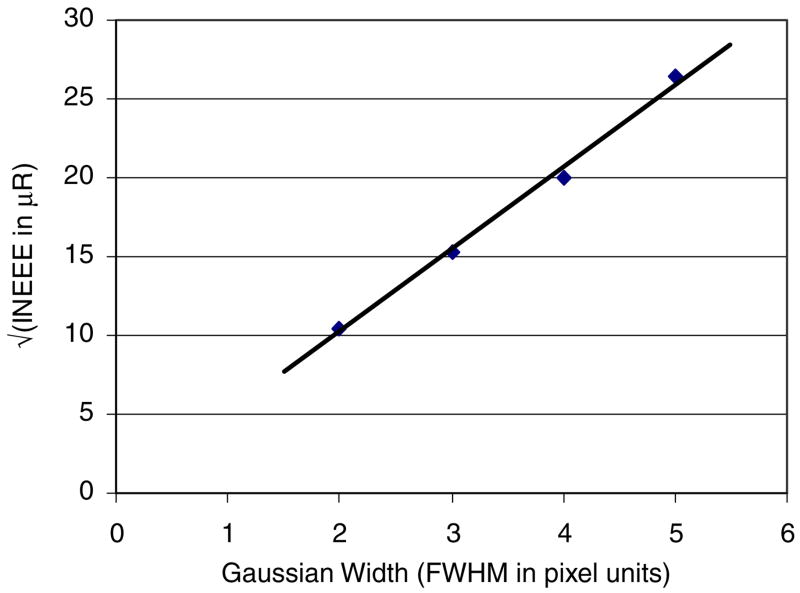
Figure 3 shows a plot of the square root of INEE versus FWHM of the Gaussian point spread function used to simulate the detector blur (where instrumentation noise was added after the filtering process). This plot shows a linear dependence of the square root of INEE on detector-blurring Gaussian width. The INEE increases with increasing detector blur, even when the instrumentation noise remains unchanged, because the detector blur reduces the quantum noise prior to the addition of instrumentation noise. Inherent detector temporal blur would have a similar effect, as increasing temporal correlations will also result in a reduction of quantum noise, with instrumentation noise remaining fixed. For simplicity, the blurring was assumed to be Gaussian. However, any blurring process (both stochastic and deterministic) occurring prior to the addition of instrumentation noise will result in a reduction of the quantum noise relative to the instrumentation noise, resulting in an increase in INEE with increasing detector blur.
Figure 3.
Square root of INEE versus FWHM of the Gaussian point spread function for the simulation case where constant additive noise was added after the filtering process (detector blurring).
Figure 4 shows a plot of the square root of INEE versus FWHM of the Gaussian point spread function used to simulate image post-process smoothing (where instrumentation noise was added prior to the filtering process). Such post-process smoothing reduces the quantum as well as the instrumentation noise simultaneously, as would similarly occur with recursive filtering. Therefore, the x-ray entrance exposure at which the two noise terms (quantum and instrumentation) become equal remains unaffected, which in turn implies that INEE does not change with the amount of filtering (both spatial and temporal) applied in the post-processing. Thus, a flat behavior over the range of Gaussian-widths reflects the independence of INEE from linear post-process-smoothing in digital x-ray images.
Figure 4.
Square root of INEE versus FWHM of the Gaussian point spread function for the simulation case where constant additive noise was added before the Gaussian filtering (postprocess-smoothing).
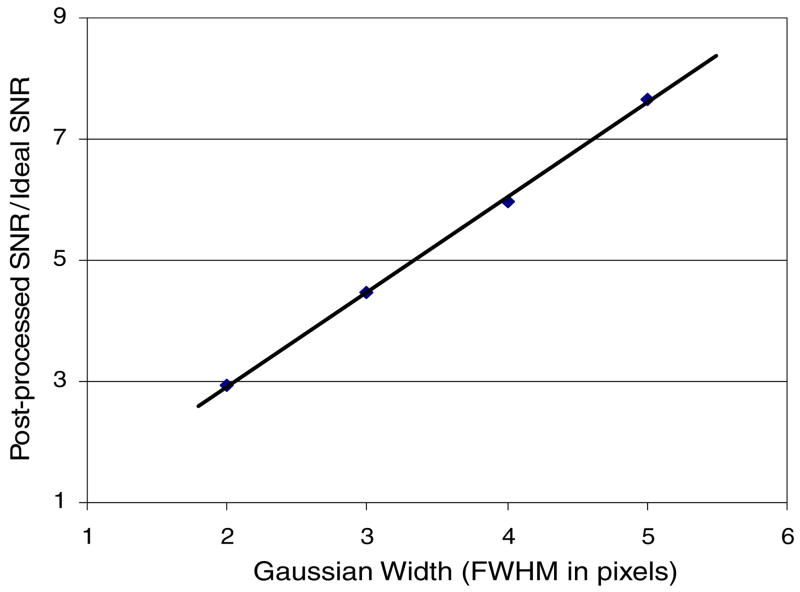
Figure 5 shows the change in SNR due to image post-process smoothing using Gaussian point spread functions of different FWHMs. Again, because the post-process smoothing reduces quantum and instrumentation noise simultaneously, while the zero-frequency signal remains constant, the SNR increases with the amount of filtering applied with a concomitant decrease of image spatial resolution. The linear increase in the SNR with Gaussian width of the post-process-smoothing function implies that such processing would leave the measured INEE unchanged regardless of the resulting SNR.
Figure 5.
Plot showing the increase in SNR due to image post-process-smoothing using Gaussian point spread functions of increasing FWHM in the simulation.
The results of the above simulation study demonstrated that INEE is dependent on detector blurring but independent of image post-process smoothing with linear filters. This study supports the practical implementation of INEE even if, in the current state-of-the-art digital imaging systems, the images are highly post-processed by smoothing filters and the quantitative measures of signal and noise are subject to these post-processing steps. This simulation study was limited to only linear filter post-process smoothing, but in practice there may be nonlinear smoothing of the images, which is not considered here.
This description does not consider any spatial frequency dependence but assumes that the measurements are zero-frequency signal versus total noise. The approach of using the total noise (i.e., the sum over all spatial frequencies) is expected to be more representative of the instrumentation noise than would be an investigation at one particular spatial frequency (i.e., zero).
Determining the relative contribution of the instrumentation noise at different spatial frequencies is beyond the scope of this paper and not considered in detail here; however, the frequency-dependent definition of INEE could be derived in a similar fashion using frequency-dependent signal (MTF) and noise power spectrum (NPS). Even though the frequency-dependent INEE would be a more complete descriptor to gauge the range of quantum-limited performance of various detector technologies, it may not be as easily implemented in the field as the frequency-independent INEE determined from the total noise and the zero-frequency signal. The limiting noise source in CCDs is the noise associated with the signal readout process (Janesick 2007). Charge in each pixel is converted separately into a change in analog voltage, which is then amplified prior to the ADC, resulting in random or white noise (Faraji and MacLean 2006). Similarly, the electronic noise of FPDs was shown to exhibit flat behavior after correction for the low-frequency (<0.2 cycles mm−1) effects of application-specific integrated circuits (Hunt et al. 2004). The spatial frequency dependence of the instrumentation noise is expected to largely result from the modulation of the signal as measured by the MTF. The signal at higher spatial frequencies is generally less than at low spatial frequencies. As a result, the INEE at higher spatial frequencies is expected to be proportionally greater as a result of requiring more exposure to get an equivalent amount of quantum noise.
5. Conclusion
A simple formal treatment of the instrumentation noise in terms of the detector entrance exposure was developed and applied to three custom-designed CCD-fiber-optic-based systems of different sensitivities and to a commercial x-ray image intensifier system, and was compared with values for a flat-panel detector system reported by other investigators. The instrumentation noise-equivalent exposure formalism provides a useful means of separating the system instrumentation noise and the photon-fluence-dependent quantum noise. This study demonstrates that the INEE is a practical way to gauge the range of quantum-limited performance for clinical x-ray imaging detectors such that exposure below the INEE will be instrumentation rather than quantum-noise limited. This method can be used to compare systems of differing designs and applied to quality assurance measurements of clinical digital detectors in the field for direct measure of the instrumentation noise limit in terms of equivalent x-ray exposure rather than relying on an equipment-invasive and less relevant measurement of electronic noise or other noise values provided by the vendor. The uncertainty in the INEE values obtained with the two methods used here are dependent on the uncertainty of signal and noise measurements specific to the detector system. By using the variance versus exposure data instead of SNR2 versus exposure, uncertainty in the INEE is minimized, as there is no additional error propagation from the uncertainty of signal measurements and the variance-based approach may be the preferred method to use. Also, the SNR-based approach is limited by the measurement of signal and noise at very low x-ray exposures that may be challenging in practical applications. The variance-only based approach should not be affected by the range of exposures used for determining the noise because the variance describes the total noise that includes the constant instrumentation noise irrespective of the input signal level. However, a larger range of exposures and a greater number of measurement points should increase the certainty in determining the fit parameters and thus the INEE.
The simulation study presented here has shown that smoothing (which is linear and performed on the acquired images as a post-processing step) does not change the measured value of the INEE. However, we find that the INEE increases with increasing detector blur even when the instrumentation noise is unchanged. This occurs because the detector blur reduces the quantum noise prior to the addition of instrumentation noise.
The scope of this paper was limited to zero-frequency signal and total noise, providing a simple and practical measure to gauge the instrumentation noise-equivalent exposure in high-sensitivity x-ray imaging detectors. Considering the fact that the signal and noise are spatial-frequency dependent, a more detailed description of frequency-dependent INEE is currently under investigation. Such an extended description of frequency-dependent INEE could be helpful in determining the extent of quantum-limited performance tailored to the imaging task, for example, applications specifically requiring high-resolution as well as high-sensitivity imaging capability. Finally, the simple additive noise model proposed in this work depends on obtaining detector signal and noise data which is not highly processed with nonlinear filters, the effect of which needs to be studied further.
In conclusion, the INEE metric provides the threshold exposure at which the detector instrumentation noise exceeds the quantum noise. Thus, the INEE can be used as a quantitative measure of the quantum-noise-limited exposure range and indicates the useful operational exposure range of the detector.
Acknowledgments
This work was supported in part by NIH Grants R01EB002873, R01NS43924 and equipment from Toshiba Medical Systems Corporation.
References
- Antonuk LE, Jee KW, El-Mohri Y, Maolinbay M, Nassif S, Rong X, Zhao Q, Siewerdsen JH, Street RA, Shah KS. Strategies to improve the signal and noise performance of active matrix, flat-panel imagers for diagnostic x-ray applications. Med Phys. 1999;27:289–306. doi: 10.1118/1.598831. [DOI] [PubMed] [Google Scholar]
- Borasi G, Nitrosi A, Ferrari P, Tassoni D. On site evaluation of three flat panel detectors for digital radiography. Med Phys. 2003;30:1719–31. doi: 10.1118/1.1569273. [DOI] [PubMed] [Google Scholar]
- Burgess AE. The Rose model, revisited. J Opt Soc Am. 1999;16:633–46. doi: 10.1364/josaa.16.000633. [DOI] [PubMed] [Google Scholar]
- Busse F, Rutten W, Wischmann HA, Geiger B, Spahn M, Bastiaens RJM, Ducourant T. Methodology to measure fundamental performance parameters of x-ray detectors. Proc SPIE. 2001;4320:287–98. [Google Scholar]
- Cowen AR, Workman A. A physical image quality evaluation of a digital spot fluorography system. Phys Med Biol. 1992;37:325–42. [Google Scholar]
- Cunningham IA. Applied linear-systems theory. In: Beutel J, Kundel HL, Van Metter RL, editors. Handbook of Medical Imaging. Bellingham, WA: SPIE Optical Engineering Press; 2000. [Google Scholar]
- Devroye L. Non-Uniform Random Variate Generation. Berlin: Springer; 1986. pp. 501–6.chapter 10 [Google Scholar]
- El-Mohri Y, Antonuk LE, Zhao Q, Wang Y, Li Y, Du H, Sawant A. Performance of a high fill factor, indirect detection prototype flat-panel imager for mammography. Med Phys. 2007;34:315–27. doi: 10.1118/1.2403967. [DOI] [PubMed] [Google Scholar]
- Faraji H, MacLean WJ. CCD noise removal in digital images. IEEE Trans Image Process. 2006;15:2676–85. doi: 10.1109/tip.2006.877363. [DOI] [PubMed] [Google Scholar]
- Ganguly A, Rudin S, Bednarek DR, Hoffmann KR, Kyprianou IS. Microangiographic detector for neuro-vascular imaging: I. Experimental measurements and feasibility. Med Phys. 2003a;30:3018–28. doi: 10.1118/1.1617549. [DOI] [PubMed] [Google Scholar]
- Ganguly A, Rudin S, Bednarek DR, Hoffmann KR, Kyprianou IS. Microangiographic detector for neuro-vascular imaging: II. Cascade model analysis. Med Phys. 2003b;30:3029–39. doi: 10.1118/1.1617550. [DOI] [PubMed] [Google Scholar]
- Hunt DC, Tousignant O, Demers Y, Laperriere L, Rowlands JA. Imaging performance of amorphous selenium flat-panel detector for digital fluoroscopy. Proc SPIE. 2003;5030:226–34. [Google Scholar]
- Hunt DC, Tousignant O, Rowlands JA. Evaluation of the imaging properties of an amorphous selenium-based flat panel detector for digital fluoroscopy. Med Phys. 2004;31:1166–75. doi: 10.1118/1.1707755. [DOI] [PubMed] [Google Scholar]
- Janesick JR. Photon Transfer: DN→[lambda] Bellingham, WA: SPIE Optical Engineering Press; 2007. [Google Scholar]
- Kume Y, Doi K, Ohara K, Giger M. Investigation of basic imaging properties in digital radiography: 10. Structure mottle of II-TV digital imaging systems. Med Phys. 1986;13:843–9. doi: 10.1118/1.595808. [DOI] [PubMed] [Google Scholar]
- Kyprianou IS, Rudin S, Bednarek DR, Hoffmann KR. Generalizing the MTF and DQE to include x-ray scatter and focal spot unsharpness: application to a new micro-angiographic system. Med Phys. 2005;32:613–26. doi: 10.1118/1.1844151. [DOI] [PubMed] [Google Scholar]
- Marshall NW, Kotre CJ, Robson KJ, Lecomber AR. Receptor dose in digital fluorography: a comparison between theory and practice. Phys Med Biol. 2001;46:1283–96. doi: 10.1088/0031-9155/46/4/325. [DOI] [PubMed] [Google Scholar]
- Metz CE, Wagner RF, Doi K, Brown DG, Nishikawa RM, Myers KJ. Towards consensus on quantitative assessment of medical imaging systems. Med Phys. 1995;22:1057–61. doi: 10.1118/1.597511. [DOI] [PubMed] [Google Scholar]
- Nudelman S. A study of photoelectronic-digital radiography: III. Image acquisition components and system design. Proc IEEE. 1982;70:715–27. [Google Scholar]
- Pineda AR, Barrett HH. Figures of merit for detectors in digital radiography: I. Flat background and deterministic blurring. Med Phys. 2004a:348–58. doi: 10.1118/1.1631426. [DOI] [PubMed] [Google Scholar]
- Pineda AR, Barrett HH. Figures of merit for detectors in digital radiography: II. Finite number of secondaries and structured backgrounds. Med Phys. 2004b:359–67. doi: 10.1118/1.1631427. [DOI] [PubMed] [Google Scholar]
- Rowlands JA, Yorkston J. Flat panel detectors for digital radiography. In: Beutel J, Kundel HL, Van Metter RL, editors. Handbook of Medical Imaging. Bellingham, WA: SPIE Optical Engineering Press; 2000. [Google Scholar]
- Roos PG, et al. Multiple gain ranging readout method to extend the dynamic range of amorphous silicon flat panel imagers. Proc SPIE. 2004;5368:139–49. [Google Scholar]
- Rose A. Quantum and noise limitations of the visual process. J Opt Soc Am. 1953;43:715–6. doi: 10.1364/josa.43.000715. [DOI] [PubMed] [Google Scholar]
- Rudin S, Kuhls AT, Yadava GK, Josan GC, Wu Y, Chityala RN, Rangwala HS, Ionita C, Hoffmann KR, Bednarek DR. New light-amplifier-based detector design for high spatial resolution and high sensitivity CBCT mammography. Proc SPIE. 2006;6142:624–34. doi: 10.1117/12.649501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudin S, Wu Y, Kyprianou IS, Ionita CN, Wang Z, Ganguly A, Bednarek DR. Micro-angiographic detector with fluoroscopic capability. Proc SPIE. 2002;4682:344–54. [Google Scholar]
- Saunders RS, Jr, Samei E, Jesneck JL, Lo JY. Physical characterization of a prototype selenium-based full field digital mammography detector. Med Phys. 2005;32:588–99. doi: 10.1118/1.1855033. [DOI] [PubMed] [Google Scholar]
- Siewerdsen JH, Jaffray JA. Optimization of x-ray imaging geometry (with specific application to flat-panel cone-beam computed tomography. Med Phys. 2000;27:1903–14. doi: 10.1118/1.1286590. [DOI] [PubMed] [Google Scholar]
- Suzuki K, Ikeda S, Ishikawa K, Iinuma G, Ogasawara S, Moriyama N, Konno Y. Development and evaluation of a digital radiography system using a large-area flat panel detector. Proc SPIE. 2002;4682:363–70. [Google Scholar]
- Tousignant O, Demers Y, Laperriere L, Nishiki M, Nagai S, Tomisaki T, Takahashi A, Aoki K. Clinical performances of a 14″ × 14″ real time amorphous selenium flat panel detector. Proc SPIE. 2003;5030:71–6. [Google Scholar]
- Wu Y, Rudin S, Bednarek DR. A prototype micro-angiographic fluoroscope and its application in animal studies. Proc SPIE. 2005;5745:1066–77. doi: 10.1117/12.589232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yadava GK, Kyprianou IS, Rudin S, Bednarek DR, Hoffmann KR. Generalized performance evaluation of x-ray image intensifier compared with a microangiographic detector. Proc SPIE. 2005;5745:419–29. doi: 10.1117/12.594593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yadava GK, Rudin S, Kuhls-Gilcrist AT, Bednarek DR. Generalized objective performance assessment of a new high-sensitivity micro-angiographic fluoroscopic (HSMAF) imaging system. Proc SPIE. 2008;6913:69130U-1–11. doi: 10.1117/12.769808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaffe MJ, Rowlands JA. X-ray detectors for digital radiology. Phys Med Biol. 1997;42:1–39. doi: 10.1088/0031-9155/42/1/001. [DOI] [PubMed] [Google Scholar]
- Zhao W, Blevis I, Germann S, Rowlands JA, Waechter D, Huang Z. Digital radiology using active matrix readout of amorphous selenium: construction and evaluation of a prototype real-time detector. Med Phys. 1997;24:1834–43. doi: 10.1118/1.598098. [DOI] [PubMed] [Google Scholar]
- Zhao W, Ji WG, Debrie A, Rowlands JA. Imaging performance of amorphous selenium based flat-panel detectors for digital mammography: characterization of a small area prototype detector. Med Phys. 2003;30:254–63. doi: 10.1118/1.1538233. [DOI] [PubMed] [Google Scholar]