Modelling studies to estimate the prevalence of foot-and-mouth disease carriers after reactive vaccination

Abstract

Foot-and-mouth disease (FMD) is a highly contagious and economically significant viral disease of cloven-hoofed animals. Vaccination can be used to help restrict the spread of the infection, but evidence must be provided to show that the infection has been eradicated in order to regain the FMD-free status. While serological tests have been developed, which can identify animals that have been infected regardless of vaccination status, it is vital to know the probable prevalence of herds with FMD carriers and the within-herd prevalence of those carriers in order to design efficient post-epidemic surveillance strategies that establish freedom from disease. Here, we present the results of a study to model the expected prevalence of carriers after application of emergency vaccination and the impact of this on the sensitivity of test systems for their detection. Results showed that the expected prevalence of carrier-containing herds after reactive vaccination is likely to be very low, approximately 0.2%, and there will only be a small number of carriers, most likely one, in the positive herds. Therefore, sensitivity for carrier detection can be optimized by adopting an individual-based testing regime in which all animals in all vaccinated herds are tested and positive animals rather than herds are culled.

1. Introduction

Foot-and-mouth disease (FMD) is a highly contagious and economically significant viral disease of cloven-hoofed animals (Thomson 1994). In endemically infected areas it constrains access of livestock and their products to export markets, and in the developed world where the disease has been eradicated measures are needed to prevent its introduction and control subsequent spread if this occurs. Outbreaks in formerly disease-free regions can be very costly due to eradication costs, loss of trade and wider economic impacts. The disease can be eradicated by restricting animal movements, culling infected and high-risk farms and backwards and forwards tracing of new infections from those already identified. Vaccination, using killed FMD virus vaccines, can also be used to help restrict the spread of the infection. Following the application of control measures, supporting evidence must be provided to show that the infection has been eradicated in order to regain the FMD-free status (OIE 2007). Although cattle, sheep, goats and pigs can all become infected with FMD, the most obvious clinical signs are seen in cattle and pigs and in highly productive breeds kept under intensive husbandry conditions. By contrast, sheep, especially if kept extensively and infected outside of the lambing season, may show few obvious signs of the disease. Another difference is that ruminants, but not pigs, can become persistently infected with FMD virus, carrying low levels of live FMD virus in the oropharynx beyond 28 days after initial infection. The epidemiological significance of these persistently infected animals, termed carriers, is highly controversial (Alexandersen et al. 2003). However, the fear that they may occasionally initiate new outbreaks has led to international trade rules requiring either long waiting periods for carriers to recover from infection or use of methods of carrier elimination before the FMD-free status can be restored to regions that suffer from outbreaks of the disease (OIE 2007).

FMD vaccination can reduce the susceptibility of animals to infection with FMD virus, protect from clinical illness and reduce shedding of virus and onward transmission. However, the protective effect takes time to develop and may be overwhelmed by a high level of challenge or a poor antigenic match between the vaccine strain and the challenge virus. Furthermore, animals that are clinically protected may still become infected and in the case of ruminants, go on to become subclinical carriers (Doel 2003). Consequently, when vaccination is used to help control infection in previously FMD-free regions that wish to rapidly regain the FMD-free status, vaccinated animals must either be slaughtered (vaccinate-to-kill) or must be tested to confirm that they do not harbour virus carriers (vaccinate-to-live). Serological tests can identify animals that have been infected regardless of vaccination status by detecting antibodies to the non-structural proteins (NSP) of FMD virus. These antibodies are elicited by replicating virus but not by vaccines that have been sufficiently purified from NSPs. Recent studies have characterized the sensitivity and specificity of available NSP antibody tests when used for carrier detection in cattle (Brocchi et al. 2006; Paton et al. 2006), but uncertainty over the prevalence of carriers after the use of a vaccinate-to-live policy hampers efforts to determine the effectiveness of testing regimes. The relatively low sensitivity of the testing regimes also adds complexity to such a task. Here, we present results of a study to model the expected prevalence of carriers after the application of emergency vaccination and the impact of this on the sensitivity of test systems for their detection.

There are two parts to the estimation of the prevalence of carriers post vaccination. Firstly, a stochastic simulation of FMD transmission determines the probable number of infected vaccinated herds for simulated outbreaks, taking into account vaccine efficacy according to the number of days post vaccination of each exposed herd. Secondly, the within-herd prevalence of carriers in each infected vaccinated herd that has at least one carrier is determined after estimating or making assumptions on the number of initial infecteds, the number of clinically affected cattle required for detection and the impact of vaccination on the appearance of clinical signs.

2. Material and methods

(a) Simulation of between-farm transmission

The probability of infection for each susceptible farm is calculated similarly to that of Keeling et al. (2001); that is, at each time step the probability that each uninfected farm becomes infected is calculated according to the formula

$$P_{\inf }(\text{farm}i)=1-\text{exp}\left(\sum _{j=1}^{\text{no}.\text{of infectious farms}}{\lambda }_0\eta (d_{ij})A_j{B}_i\right),$$ (2.1)

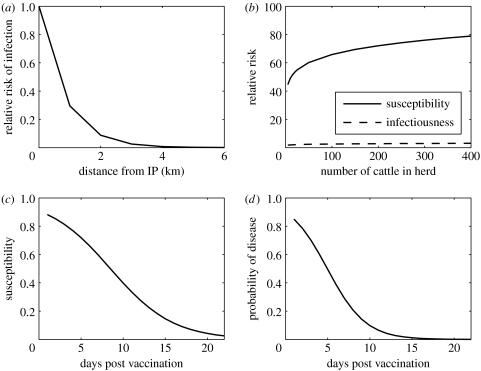
where η(d_ij) represents the probability of transmission from an infected to a susceptible farm at distance d_ij (where distance was determined by the Euclidean distance between the coordinates of each farm as given by the census data); A_j is a weighting factor that represents how the probability of an infected premises (IP) infecting other farms depends on the number of animals on the IP; similarly B_i represents how the probability of a susceptible farm becoming infected depends on the number of animals in the susceptible farm; and λ₀ is an arbitrary baseline hazard. Parameter estimates for each of these factors were taken from Diggle (2006), where a partial likelihood approach was applied to the 2001 epidemic data for Devon and Cumbria. Therefore, the relationship between the distance and the probability of infection is given by (figure 1a)

$$\eta (d)=\text{exp}\left\{-{\left(\frac{d}{0.41}\right)}^{0.5}\right\}+1.3\times {10}^{-4}$$

and the animal-number-dependent herd infectiousness and susceptibility are given by (figure 1b)

$$A_j=1.42N_{\text{cattle}}^{0.13}+N_{\text{sheep}}^{0.13}\text{and}{B}_i=36.2N_{\text{cattle}}^{0.13}+N_{\text{sheep}}^{0.13}.$$

The estimates for the herd infectiousness and susceptibility have a sub-linear dependence on the number of animals in the herd, and were shown by Diggle (2006) to provide a significantly better fit to the 2001 case data than a linear dependence, which has been adopted by Keeling et al. (2001) and Tildesley et al. (2006). Both Diggle (2006) and the estimates by Keeling et al. (2001) and Tildesley et al. (2006) show increased susceptibility and infectiousness as the number of cattle and sheep in the herd are increased, and both have greater per capita infectiousness and susceptibility for cattle compared with sheep. As proved by Keeling et al. (2001), infected herds are assumed to be infectious from 4 days after initial infection. This approximates to the inter-farm incubation period (Sellers & Forman 1973; Garland & Donaldson 1990) and the fact that peak shedding coincides with onset of clinical signs, although some shedding may precede this, especially in sheep (Alexandersen et al. 2003).

Figure 1.

Model assumptions regarding (a) the effect of distance on the probability of transmission between farms, (b) the effect on the number of cattle on the susceptibility and infectiousness of herds, (c) the reduction in the probability of infection of each vaccinated bovine with time after vaccination and (d) the reduction in the probability of a vaccinated bovine becoming clinical (as would be identified on a farm) with time after vaccination.

(i) Other assumptions

Time to detection for infected herds is derived from 2001 GB epidemic data. All animals in each IP are culled, with the time from confirmation to slaughter derived from the 2001 GB epidemic for Devon (for culling rates after 28 March 2001). Population at risk is the Devon farms from the 2004 census; the cattle population has been declining at approximately 2% per annum and so the 2004 census might be a small overestimate of the current population, but this difference will have an insignificant effect on the main output of this paper, the FMD carrier prevalence.

(b) Efficacy of and rates of vaccination

Both the probability of a vaccinated bovine animal becoming infected and the probability of it showing clinical signs recognizable on farm vary according to the number of days between vaccination and challenge and are shown in figure 1c,d. Estimates of these probabilities were derived from examination of published data in which cattle were challenged at various times after vaccination usually by contact with pig aerosols (Donaldson & Kitching 1989; Doel et al. 1994; Salt et al. 1995) or else by direct contact challenge from infected cattle (Cox et al. 2005, 2006).

The effect of vaccination on the probability of farm infection is included by reducing the per capita risk of infection for cattle in line with the estimate in figure 1c. The infectiousness of vaccinated herds as the number of days post vaccination increases is assumed to follow the relationship in figure 1d, i.e. it is assumed that clinical onset and infectiousness are correlated (Sellers et al. 1977).

Vaccination commences 7 days after the identification of the initial IP. There are 50 vaccination teams (in line with current contractual arrangements that Defra have made in the event of an outbreak), each of which can vaccinate 250 animals per day. They also inspect sheep and pigs for FMD, with this taking the same amount of time as vaccinating one bovine animal.

(c) Probability of becoming a carrier and within-herd prevalence

There are four steps in the calculation of whether an infected vaccinated farm has positive animals at post-epidemic surveillance (outlined in figure 2), and described in more detail below.

Figure 2.

Outline of the steps to calculate the probability that an infected vaccinated farm has carriers at post-epidemic surveillance (infs, infecteds).

(i) Calculate the number of initial infections within IPs

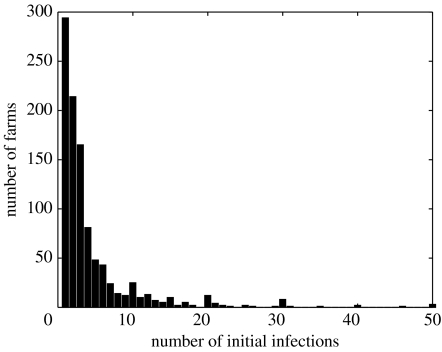
The number of animals found to be infected when IPs were discovered (‘initial infecteds’) was available from the 2001 epidemic data (figure 3). Linear regression showed a significant but small dependence on herd size, with the mean number of initial infections=4.1+0.0049 herd size; this gives a mean number of initial infections of approximately 4.2, 4.6 and 6.1 for herds of 25, 100 and 400 cattle, respectively. The majority of cases had a less number of estimated initial infections, with a few farms having relatively high estimates (up to 113 initial infections). For the estimation of the probability of becoming a carrier farm, it was assumed that the number of initial infections followed a Poisson distribution (the carrier probability was insensitive to the choice of sampling distribution) with mean depending on herd size according to the regression coefficients above, but reduced as the days after vaccination increases according to the reduction in susceptibility (figure 1c).

Figure 3.

Histogram of the estimated number of initial infections from the 2001 UK FMD epidemic.

(ii) Calculate clinically recognizable cases

The number of cattle with clinically recognizable disease is sampled from the binomial distribution with parameters n, the number of initial infecteds, and p, the probability of clinical onset given the number of days between infection and vaccination (figure 1d).

(iii) Determine if IP

Experimental data show that animals infected in the first few days post vaccination can develop clinical signs (Sellers et al. 1977; Donaldson & Kitching 1989), and that the presence of clinically affected animals shedding large amounts of virus will lead to further infections, regardless of vaccination status in contact animals (Cox et al. 2005, 2006). Therefore, it is assumed that if there are less than 5 days between infection and vaccination, then there will be further within-herd spread and there will be sufficient clinically recognizable cases for the herd to be detected as an IP. If there are 5 days or more, it is assumed that one clinical would be sufficient for a dairy herd to be detected as an IP, but two clinicals are required for a suckler herd, due to the cattle being observed less frequently. This assumption is based on professional full-time farmers monitoring their stock regularly and may not apply to recreational, semi-retired or hobby farmers.

(iv) Calculate number of carriers

This step is performed only if the premises have not been assigned as an IP. It is assumed that 50% of infected vaccinated cattle will become carriers of FMD (Kitching 2002). The number of carriers is sampled from the binomial distribution with n=number of infected cattle, p=0.5. If the number of carriers is greater than or equal to one, the farm is recorded as a carrier and the number of carriers gives the within-herd prevalence of positives at the time of post-epidemic surveillance.

(d) Scenarios considered for simulation modelling

The model was run with five initial IPs that had not yet been reported, a total of 200 times for each scenario.

There were three scenarios considered,

1. no vaccination,

2. vaccination of cattle on all farms that have more than 50 cattle and are within 10km of each IP, and

3. vaccination of cattle on all farms within 10km of each IP.

Farms were vaccinated in the order of distance from the IP, with the closest vaccinated first. They were also ordered by IP, with all the farms less than 10km from the first IP vaccinated before the farms from the second IP and so on. The model ran until 30 days after the date of last IP, at which point serosurveillance was initiated. Each vaccinated farm was tested using Cedi screen/Cedi retest/Svanova confirmation, the combination of which has a sensitivity of 67%, and specificity of 99.99% (Paton et al. 2006). The number of cattle tested on each farm was calculated according to the formula in Cannon & Roe (1982), based on the hypergeometric distribution, to detect a 5% prevalence with 95% confidence (taking into account the test sensitivity), or all the cattle on the farm if there were fewer cattle on the farm than given by the sample size calculation. The situation of all cattle in vaccinated farms being tested was also performed in the model. The number of farms that were false positive, true positive, false negative or true negative was recorded by the model for each run.

(e) Sensitivity analysis

The following parameters were those for which there were least data to derive values from and hence were regarded as the most uncertain; these were varied to determine the effect on the proportion of vaccinated farms that become carriers and the within-herd prevalence in carrier farms.

1. The number of initial infections was entirely dependent on herd size, assumed to follow a Poisson distribution with mean equal to 5% of the herd size.

2. The number of clinical cattle required for a herd to be identified as an IP in vaccinated herds was varied to equal 2 and 3 for all herd types.

3. The vaccine efficacy was varied so that the time taken for both 50% protection from infection and from showing clinical signs was increased by 50%, i.e. 50% protection from infection after approximately 12.5 days and 50% showing clinical signs after approximately 7.5 days.

4. The simulation model was also run for Cumbria and Cheshire, being two other regions with high cattle density.

5. Varying the proportion of infected cattle that become carriers to 25 and 75%.

In addition, in order to explore a scenario where the herd size and the probability of being a carrier farm would be highly correlated, the following was also considered:

1. Initial infections as in (i), 2% herd-level incidence of clinicals undetected.

All the above scenarios were applied to the vaccinate herds with more than 50 cattle strategy.

3. Results

(a) Effect of vaccination on epidemic size

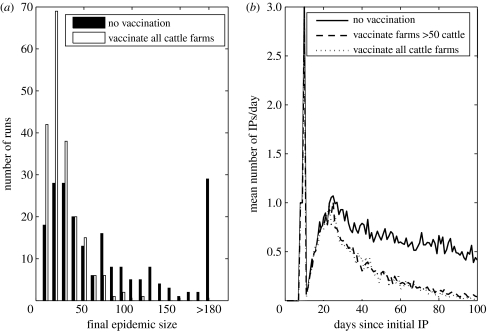
There was a highly variable distribution of epidemic sizes when no vaccination is carried out (figure 4a), with approximately 10% of the runs resulting in less than 10 IPs and approximately 15% resulting in more than 180. Vaccination resulted in a large reduction in the number of epidemics with more than 100 IPs, with 58 epidemics with more than 100 IPs for no vaccination compared with only 1 when all cattle farms less than 10km from each IP were vaccinated. This resulted in a lower average number of IPs per day from after the first three weeks or so from the first initial infected onwards for the vaccination strategies (figure 4b).

Figure 4.

Comparison of the effect of vaccinating cattle farms within 10k of each IP versus no vaccination on (a) the final epidemic size and (b) the mean number of IPs each day after 100 simulation model replicates.

The results showed a large reduction in the cases after vaccination, showing a 65 and 68% reduction in the average number of IPs for the two vaccination strategies compared with no vaccination. Vaccinating farms with less than 50 cattle produced marginally fewer cases than vaccinating only those farms with more than 50 cattle (figure 1b), but required an average of 2000 farms vaccinated (approx. 200 000 animals) when compared with approximately 1200 (approx. 160 000 animals) for vaccinating only those farms with more than 50 cattle.

(b) Population- and herd-level prevalence of carriers

There was a low probability of becoming a carrier in the first few days after vaccination, since the number of infecteds would always be large enough to produce sufficient infecteds for the farm to be identified as an IP. As time post vaccination increased, the probability of becoming a carrier increased due to the lower number of initial infecteds (as the protection level of the vaccine increased) and the lower probability of each of the infecteds showing identifiable clinical signs. Assuming one clinical was sufficient for the farm to be identified as an IP, the probability of becoming a carrier tended to 50% as the number of days post vaccination increases as there was then rarely more than one initial infected and that infected would be unlikely to show clinical signs, so that the probability of the farm becoming a carrier then depended solely on the probability that the single infected animal became a carrier, i.e. 50%.

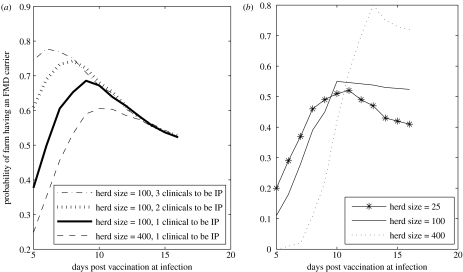
The number of clinical cattle required for the herd to be identified as an IP had a large impact on the carrier probability (figure 5a).

Figure 5.

The probability of an infected vaccinated farm becoming a carrier as the number of days between vaccination and infection increases for (a) the number of initial infections from the 2001 epidemic and (b) assuming the number of initial infections is Poisson distributed with a mean=5% of the herd, assuming one clinical to be an IP.

The probability of becoming a carrier with the initial infections as estimated from the 2001 epidemic (figure 3) showed little variation with herd size (figure 5a), due to the low dependence of the number of initial infecteds on herd size. If the number of initial infecteds depended solely on herd size, then the carrier probability would be highly dependent on the number of cattle in the herd (figure 5b), with the probability of having a carrier for larger farms (given infection) peaking later, as the larger number of initial infecteds results in a high probability of having at least one clinical in the first week or so.

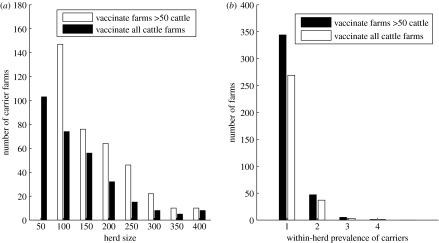
As farm size increased, there were fewer carrier farms in number (figure 6a), due to there being fewer larger farms in the population at risk. The vaccination of small farms led to fewer carrier farms (figure 6a). This occurred because in the vaccinate more than 50 strategy, the larger herds were vaccinated more rapidly (i.e. there was less of a queue for vaccination) and therefore had more exposure after being vaccinated than in the vaccinating all strategy, where it took longer before they were all vaccinated and more of the large herds became IPs.

Figure 6.

The results of 200 runs of the simulation model of (a) the total number of vaccinated herds with at least one carrier, grouped by herd size and (b) the within-herd prevalence of carriers in vaccinated herds.

The within-herd prevalence of carriers in infected vaccinated farms was low, with the majority of carrier farms having only one carrier (figure 6b). This was because farms with many initial infecteds were likely to be detected as an IP, and those farms infected more than 7 days after being vaccinated, where the probability of the vaccinated animals showing clear clinical signs was low, would have only a small number of initial infecteds.

The prevalence of vaccinated farms with carriers was very low, at 0.16% for the vaccinate more than 50 strategy (table 1) and 0.07% at the vaccinate all strategy. The mean within-herd number of carriers was 1.18 for the vaccinate more than 50 strategy and 1.2 for the vaccinate all strategy, the small difference arising due to the slight increase in the probability that vaccinated farms in the vaccinate more than 50 strategy will be infected at several days after vaccination compared with the vaccinate all strategy, and when this happens there is usually only one initial infected.

Table 1.

The results of changing key parameters on the prevalence of carriers and the specificity and sensitivity of post-epidemic testing of vaccinated farms.

parameter change	mean within-herd prevalence of carriers	percentage of vaccinated farms that are carriers	specificity of testing at herd level (%)	sensitivity of testing at herd level (%)
vaccinate herds with more than 50 cattle, Devon	1.18	0.16	99.3	39.6
mean initial infections=5% of herd size	1.30	0.14	99.5	49.5
two clinicals to be an IP	1.36	0.17	99.3	44.6
three clinicals to be an IP	1.42	0.19	99.3	46.0
vaccine effect 50% slower	1.28	0.11	99.3	43.5
Cumbria	1.21	0.13	99.3	44.8
Cheshire	1.26	0.17	99.3	42.6
25% of infected cattle →carriers	1.05	0.12	99.3	38.0
75% of infected cattle →carriers	1.33	0.18	99.3	50.2
mean initial infections=5% of herd size, 2% of herd clinical for detection	1.51	0.18	99.4	46.7

The herd-level testing, assuming a 5% design prevalence at 95% power, had low sensitivity; it identified 39% of carrier herds for the vaccinate more than 50 strategy, and 45% for the vaccinate all strategy. The higher rate of detection for the vaccinate all strategy was a result of the smaller herd size of vaccinated farms, as finding one or two positives in a small herd (where all the animals would be tested) has a greater chance of detection than one or two positives in a large herd, where only a proportion of the animals would be tested. If all animals were tested, the probability of detecting carrier herds was approximately 75%.The specificity of the herd-level testing was 99.3% for the vaccinate more than 50 strategy and 99.5% for the vaccinate all strategy, it being slightly higher when the average herd size of the vaccinated herds is smaller, since there would be a lower probability of false positives (at herd level) in this case.

(c) Sensitivity analysis

The prevalence of carriers and the predicted sensitivity and specificity of the herd-level testing, assuming a 5% design prevalence with 95% power are summarized in table 1.

The proportion of vaccinated farms that become carriers remained very low for all the parameter changes considered in the sensitivity analysis. Increasing the number of clinicals before being detected as an IP had the greatest impact, but even for this parameter the effect was relatively small.

Increasing the number of clinical cattle required to be detected as an IP had the greatest impact of the single parameters on the mean within-herd prevalence, but even with three clinicals before detection the mean within-herd prevalence of carriers was still low. Having a herd-size-dependent number of initial infections, increasing the proportion of infected cattle that become carriers and the time taken for the vaccine to take effect also increased the within-herd prevalence.

The sensitivity of testing (in terms of identifying herds with at least one carrier) depended on the within-herd prevalence, and so parameter changes that increased the within-herd prevalence also increased the herd-level sensitivity.

The scenario of a herd-size-dependent number of initial infections and a herd-size related number of clinicals required for detection resulted in the number of carriers in each herd being highly dependent on herd size, with herds of less than 100 cattle having only one carrier and a herd-size related increase of 0.0036 per capita in the mean number of carriers. This resulted in a slightly higher mean within-herd prevalence of carriers than the other scenarios, but this was mostly concentrated in the large herds and still resulted in a relatively low herd-level sensitivity.

The specificity of testing was affected only by the herd size of the true negative vaccinated farms, which varied little with the parameters for which sensitivity analysis was carried out. The parameter that had the largest effect on this was amending the number of initial infected cattle distribution, which increased specificity to 99.5% (compared with 99.3% for the default parameters).

There were small differences in the proportion of carrier farms and the within-herd prevalence between regions. There was also a difference in the efficacy of vaccination between regions, with a mean reduction of 35 and 33% of cases for vaccination in Cumbria and Cheshire, compared with 65% for Devon.

4. Discussion

This study has indicated that following emergency ring vaccination and slaughter of herds showing clinical FMD, the number of subclinically infected vaccinated herds is likely to be low and the number of carriers within such herds will in most cases be only one or at most two. Field studies to confirm or refute this are lacking since investigations of post-outbreak carrier rates have been carried out in areas where FMD is endemic and the circumstances of disease control (application of vaccine and recognition and removal of clinically affected herds) are very different, (e.g. Hedger (1970) for an early study and Sammin et al. (2007) for a recent study and Salt (2004) for a recent review). This low frequency of occurrence makes serological detection of carriers very difficult.

It has been proposed that the imperfect sensitivity of carrier detection can be improved by a herd-based testing strategy, which assumes that although some carriers that are tested may score false negative in tests, others will be detected leading to a correct herd-level classification. According to this philosophy, if any animals within a herd are scored as carriers, the whole herd should be culled (Anon. 2003). However, this necessitates the use of a combination of tests so as to maximize specificity and prevent unwarranted culling and this further reduces test system sensitivity (Paton et al. 2006). Our current results suggest that most carrier herds will contain only a single carrier animal and therefore a herd-based testing approach will not be helpful and neither will a design prevalence of 5%. It would be better simply to test all individuals and cull only those that are positive. Removing the need to cull entire herds whenever a single carrier is identified would allow the use of a test system in which more emphasis can be placed on sensitivity rather than specificity. For example, use of the scheme Ceditest screen with Ceditest confirmation of positives (Se, 0.86; Sp, 0.995) without final confirmation of positives by a second NSP test (Svanova test; Se, 0.67; Sp, 0.999). Effectively this would allow each carrier to be identified and removed with a confidence of 86%.

The results of this study also suggest that the vaccination of small herds does not result in the suggested ‘small-herd problem’ (Greiner & Dekker 2005); that is, there is no sample size problem for small herds not having sufficient animals to detect the design prevalence at the required statistical power. This is because our results show a lack of herd-size dependence on the number of carriers in the herd, which results in the carriers being easier to detect in small herds at a 5% prevalence/95% statistical power scenario because in small herds all the animals are sampled. A greater herd-size dependence on the within-herd prevalence occurs when there is a strong correlation between the herd size and the number of clinicals required for detection, although even in this case the sensitivity analysis showed that the overall prevalence of carrier herds and the mean within-herd prevalence in those herds were relatively low (table 1). The severity of clinical signs will also vary according to virus strain, but the variability of clinical signs in cattle is not wide and so strain dependence should not significantly affect the estimates in figure 1c,d. The relationship between challenge time post vaccination and clinical signs is more a function of vaccine quality and the degree to which the vaccine matches the virus strain. In the face of an outbreak, vaccine matching work is carried out to determine the optimum vaccine strain to use (Paton et al. 2005). Close matching should minimize variability in clinical signs due to this factor.

The results of this study suggest that the vaccination of small herds would have little benefit in terms of reducing the size of the epidemic. The focus of this study was not vaccination and there are several assumptions that could be studied in more detail in order to extend the work carried here. Firstly, it was assumed that the vaccine was administered to all animals, which might not be the case in an outbreak situation. Secondly, the order in which at-risk farms are vaccinated could influence the effectiveness of vaccination, although this was found to have only a minor effect (Tildesley et al. 2006). The choice of the vaccination radius could also influence the results; the study by Tildesley et al. (2006) found that the optimal vaccination ring, using the vaccination rates given in the present study, would be less than 6km. The effect of vaccination in this study appeared to be region dependent, with greater effect in Devon than Cumbria and Cheshire, and it would be interesting to explore further the variation in the impact of vaccination across different regions.

There is uncertainty in many of the parameters, especially those derived from experiments. The estimates used in this study for the incubation periods, the efficacy of vaccination and the rate at which infected cattle become carriers were based on a broad range of studies. Assembling the data from these studies in a rigorous way is problematic due to the different virus strains, different routes of inoculation and other potential confounding factors that will influence the outcome of the experiments. There are also difficulties in inferring field-level behaviour from experimental data due to the small number of animals usually involved in relevant experiments and the differences between the experimental and the field environment. The number of initial infecteds, estimated for each farm in the 2001 UK epidemic according to the number of initial clinical cattle in IP, is also highly uncertain. Nevertheless, the sensitivity analysis indicates that the main conclusions of low prevalence carriers in vaccinated herds after reactive vaccination were unaffected by varying the most uncertain individual parameter values.

In conclusion, this study has shown that the expected prevalence of carrier containing herds after reactive vaccination is likely to be very low, approximately 0.2%, and there will only be a small number of carriers, most likely one, in the positive herds. Therefore, sensitivity for carrier detection can be optimized by adopting an individual-based testing regime in which all animals in all vaccinated herds are tested and positive animals, rather than herds, are culled. As well as providing evidence that carriers are absent or can be removed, post-vaccination serosurveillance schemes to substantiate freedom from FMD infection must also provide evidence that virus is not circulating subclinically (OIE, Office International des Epizooties/World Organisation for Animal Health). As for carriers, there is great uncertainty over the extent to which such circulation is likely to occur and its consequences for risk of further spread of infection. The current modelling study suggests that about half of subclinically infected vaccinated herds are likely to contain carriers and the work might be extended to look at the likelihood of subsequent virus circulation. All schemes of serosurveillance should be seen as providing one element in the overall synthesis of evidence for freedom from infection (Martin et al. 2007). If a highly effective vaccine is applied rapidly and comprehensively and clinical surveillance is thorough, then the extent of subclinical infection is likely to be very low. Providing evidence that these requirements have been met is therefore at least, if not more, important than post-outbreak serosurveillance.