Effect of Pre-Impact Movement Strategies on the Impact Forces Resulting From a Lateral Fall

Abstract

Approximately 90% of hip fractures in older adults result from falls, mostly from landing on or near the hip. A three-dimensional, 11-segment, forward dynamic biomechanical model was developed to investigate whether segment movement strategies prior to impact can affect the impact forces resulting from a lateral fall. Four different pre-impact movement strategies, with and without using the ipsilateral arm to break the fall, were implemented using paired actuators representing the agonist and antagonist muscles acting about each joint. Proportional-derivative feedback controller controlled joint angles and velocities so as to minimize risk of fracture at any of the impact sites. It was hypothesized that (a) use of active knee, hip and arm joint torques during the pre-contact phase neither affects the whole body kinetic energy at impact nor the peak impact forces on the knee, hip, or shoulder; and (b) muscle strength and reaction time do not considerably affect peak impact forces. The results demonstrate that, compared with falling laterally as a rigid body, an arrest strategy that combines flexion of the lower extremities, combined with an axial rotation to progressively present the posterolateral aspects of the thigh, pelvis and then torso, can reduce the peak hip impact force by up to 56%. A 30% decline in muscle strength did not markedly affect the effectiveness of that fall strategy. However, a 300 ms delay in implementing the movement strategy inevitably caused hip impact forces consistent with fracture unless the arm was used to break the fall prior to the hip impact.

1. Introduction

Hip fractures, the most devastating and costly unintentional injuries in the elderly (Cummings, et al., 1985), are mostly associated with impact directly on the hip in lateral falls (Hayes, et al., 1993; Nevitt and Cummings, 1993). However, the age-related increase in hip fractures is not fully accounted for by the age-related increase in the number of falls or decrease in bone mass at the hip (Boonen, et al., 1993; Kannus, et al., 1996; Melton, et al., 1988a; Riggs, et al., 2006). So other factors, including the biomechanics of the actual fall, are thought to influence the likelihood of fracture (Cummings and Nevitt, 1989, DeGoede, et al., 2003).

Fall-related injury can either be reduced by decreasing the number of falls or by decreasing the severity of fall-related impacts, or both. Since the number of falls presumably cannot be reduced to zero, insights are needed to arrest a fall with the minimum risk of injury. Of the few biomechanical studies of lateral falls, both theoretical (van den Kroonenberg, et al., 1995) and experimental (Groen, et al., 2007; Robinovitch, et al., 1997; Sabick, et al., 1999) investigations have shown that active responses during a lateral fall can alter the resulting impact forces. However, the lateral falls simulated in those studies were either performed virtually in the frontal plane (Robinovitch, et al., 1997; Sabick, et al., 1999; van den Kroonenberg, et al., 1995), whereas real-life lateral falls often involve three-dimensional motions; or from a reduced fall height (i.e., falls from kneeling position in Groen, et al., 2007; Sabick, et al., 1999). It is not currently known whether coordinated knee, hip, and torso movements prior to hip impact can affect the severity of the hip impact resulting from a lateral fall from standing height.

Moreover, It has been shown that a squatting response reduced the impact velocity up to 18% in backward falls, but the effectiveness depends on the stage during descent when it is initiated (Robinovitch, et al., 2004) and on the available joint muscle strength (Sandler and Robinovitch, 2001). However, these effects on the impact severity in lateral falls are also not well understood.

The objective of this paper, therefore, was to investigate the effect of the pre-impact body segment movement strategies on the impact severity resulting from a lateral fall. Because experimental studies of repetitive falls from standing height are associated with a risk for injury, we instead used computer simulation to accomplish our goals. A three-dimensional, direct-dynamics model was therefore developed to test the hypotheses: (a), the use of knee, hip and arm joint rotations during the pre-contact phase neither affects the whole body kinetic energy at impact nor the peak impact forces on the knee, hip, or shoulder; and (b), reaction time and joint muscle strength do not affect the resulting peak impact forces.

2. Methods

A three-dimensional model, with 11 rigid segments (including shanks, thighs, pelvis, trunk, head, upper arms and forearms), was developed to simulate a lateral fall of a fifty-percentile young male (anthropometric data: Winter, 1990). The inertia of hands and feet were included in the shank and forearm segments, respectively. Segments were connected by frictionless hinge (knees, neck, and elbows), universal (waist and shoulder), and ball-and-socket (hips) joints, and their defined rotational degrees of freedom are listed in Table 2. The equations of motion were formulated numerically using the joint coordinate method (Nikravech, 1987).

Table 2.

The joint ranges of motion used in simulating lateral fall strategies

Normal Joint Range of Motion (NROM:°)		Joint Range of Motion (°) Used in Each Fall Strategy
Lower Extremity		Broomstick	Hip lat Flex	Spine & Hip	Free
Knee flex/ext	0~150	0° flex	0° flex	0~20° flex	NROM
Hip flex/ext	10° ext~130° flex	0° flex	0° flex	NROM	NROM
Hip add/abd	30° add~70°abd	0° abd	30° add	NROM	NROM
Hip rot	90° ir~60° er	0° ir	0° ir	NROM	NROM
Waist flex/ext (in sagittal plane)	30° ext~90° flex	0° flex	0° flex	NROM	NROM
Waist rot (in transverse plane)	−70~70	0°	0°	NROM	NROM
Upper Extremity		With Arm		Without Arm
Shoulder add/ abd	30° add~90° abd	NROM		0° abd
Shoulder flex	0~180	NROM		40° flex
Elbow fex	0~130	NROM		90° flex

Abbreviations: flex, ext, add, abd, rot, ir, er, and NROM represent ‘flexion’, ‘extension’, ‘adduction’, ‘abduction’, ‘rotation’, ‘internal rotation’, ‘external rotation’ ,and ‘Normal Joint Range of Motion’, respectively. The normal joint xranges of motion were derived from Luttgens and Hamilton, 1997.

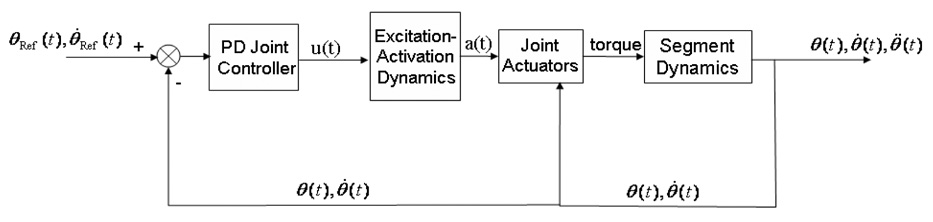
The structure of joint model is illustrated in Figure 1. Each rotational joint degree-of-freedom was driven by a pair of agonist and antagonist joint muscle torque actuators, which employed known torque-angle and torque-velocity relations (derived from Byrne, et al., 2001; Hoy, et al., 1990; Hughes, et al., 1999; Miyamoto and Oda, 2003; Pandy, et al., 1990; Winters and Kleweno, 1993). The fiftieth percentile young male’s maximum isometric muscle torque strength data was used for each joint actuator (derived from Hortobagyi and Katch, 1990; Schultz, 1992, see Table 1). The neuromuscular latency between incoming neural signal u(t) and muscle activation a(t) was modeled using a first-order system (derived from Thelen, et al., 2003). A pair of proportional-and-derivative (PD) joint controllers were incorporated at each joint to match actual and desired joint angles at each of the pre- and post-contact phases in an on-going lateral fall (the desired joint angles were determined via an optimization method, described later). A detailed formulation of the joint torque model is given by Lo (Lo, 2006).

Figure 1.

Block diagram showing interactions among the components of the muscle-joint model

Table 1.

Body weight, stature, and maximal unilateral isometric joint torque used in the simulation.

	Young Male
Body Weight (kg)	75
Stature (cm)	175
Maximal isometric joint torque (N-m)
Knee Flexion	175
Knee Extension	270
Hip Flexion	185
Hip Extension	220
Hip Adduction	80
Hip Abduction	108
Waist Flexion	100
Waist Extension	100
Waist Rotation	80
Shoulder Adduction	84
Shoulder Abduction	50
Shoulder Flexion	63
Shoulder Extension	87
Elbow Flexion	50
Elbow Extension	50

A nonlinear ground reaction force model was employed to calculate the impact forces according to the positions and velocities of the impact sites (DeGoede and Ashton-Miller, 2002; Gerristen, et al., 1995).

$$\begin{array}{ccc}f\hfill & =\{\begin{array}{cc}K|y{|}^3(1-B\dot{y}),\hfill & \hfill y<0\hfill \\ \hfill 0\hfill & \hfill y\ge 0\hfill \end{array}\hfill & \hfill \\ \hfill & \mathit{\text{where}}\hfill & \hfill \\ \hfill & \begin{array}{c}\begin{array}{cc}K=3.5(MN/m^3),\hfill & B=6{(m/s)}^{-1}\hfill \end{array}\hfill \end{array}\hfill & \begin{array}{l}\text{for soft tissue impact over the lateral and posterior surfaces of the}\hfill \\ \text{pelvis, anterior and posterior surfaces of the thorax, and shoulders}.\hfill \end{array}\hfill \\ \hfill & \begin{array}{cc}K=10.0(MN/m^3),\hfill & B=7{(m/s)}^{-1}\hfill \end{array}\hfill & \begin{array}{l}\text{for boney tissue impact at the heel, knee, greater trochanter,}\hfill \\ \text{elbow, wrist, and head}.\hfill \end{array}\hfill \end{array}$$

Impact forces were calculated for body parts that could potentially impact the ground including lateral aspects of heels, knees, greater trochanters, pelvis, and shoulders; the anterior and posterior surfaces of thorax, elbows (mid-point of humerus-transepicondylar line), wrists (mid-point of radius and ulna joints), and head (centers of nasal and occipital bones to represent anterior and posterior head impacts, respectively).

The impact severity of each fall was evaluated by calculating the impact injury risk factor, Φ (adapted from Hayes, et al., 1996). The ratio of the peak impact force to the fracture limit for each impact site was calculated, and the impact injury risk factor, Φ, was then defined as the maximum of all calculated ratios. A Φ greater than unity was presumably associated with fall-related fracture injury. We intentionally used older male fracture limits (derived from Frykman, 1967; King, 2000; 2001) to predict conservative fall strategies: 2 kN for wrist, elbow, and shoulder impacts; 5 kN for knee, hip and buttock impacts; 4 kN for thorax impact; and a low value of 20N for head impact (deliberately used to penalize the occurrence of the head impact).

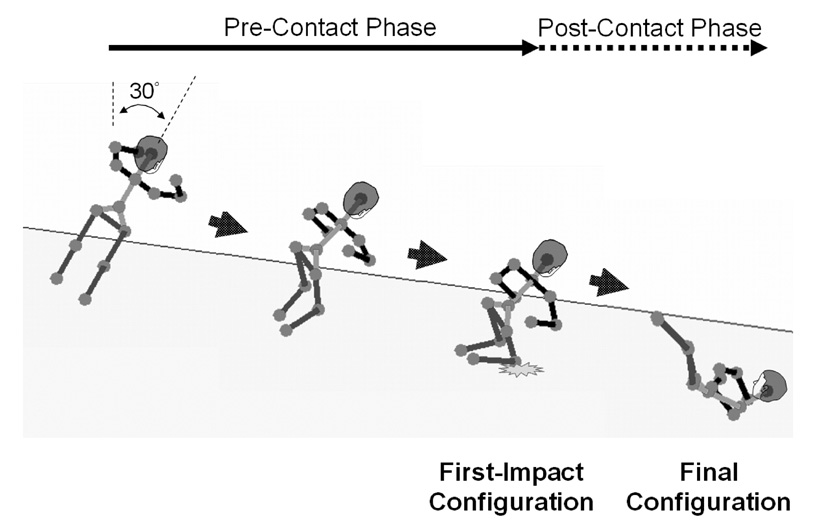
The initial condition for each fall was specified as a 30 degree lateral inclination to the right (see Figure 2) with each of the lower extremity and torso joint at its neutral position, similar to those of induced (Smeesters, et al., 2001) and simulated (Robinovitch, et al., 2003) lateral fall experiments. The initial shoulder position was 90° flexion and 30° abduction, and the initial elbow position was 70° flexion to represent a common involuntary arm elevation response to a slip (Marigold, et al., 2003).

Figure 2.

Right posterolateral view showing the two phases in a lateral fall to the model subject’s right. Secondary impacts (i.e., knee impact in this illustration) can occur during the post-contact phase.

To examine the effects of segment movements on the impact severity, different fall strategies were simulated and compared: In the ‘Broomstick’ fall strategy, the joint controllers attempted to maintain joint angles constant throughout the fall as though it was a single rigid body. This is an unlikely strategy, but acts as a control condition to which the results from other strategies may be compared. In the ‘Hip lateral flexion’ strategy, the right and left hip joints underwent 30° adduction and abduction, respectively, while other joints remained at their initial configurations. In the ‘Spine and Hip’ strategy, the ranges of motion of both knees were constrained between 0° to 20° flexion, while other joints were allowed to operate within their normal ranges of motion (derived from Luttgens and Hamilton, 1997). Finally, in the ‘Free’ strategy, all joints were allowed to operate within their normal ranges of motion. Each of these fall strategies were simulated both with and without the assistance of the right arm to break the fall.

When considering the assistance of the right arm in breaking the fall, the shoulder and elbow joints were allowed to move within their normal ranges of motion. Otherwise, the target angles of shoulder and elbow joints were defined to ensure that the arm was folded around the chest instead. The joint target angles of the eight strategies are summarized in Table 2.

The joint target angles of each strategy were determined via a deterministic, global optimization method (Holmstroem, 1999; Jones, 2001). Optimizations were conducted to minimize the impact injury risk, Φ, without exceeding maximal joint torques and joint ranges of motion specified in each strategy. Outcome variables, including the peak impact forces on each impact site, whole body kinetic energy at impact (defined as ${\displaystyle \sum _i(\frac{1}{2}{m}_i{v}_i^2+\frac{1}{2}}{I}_i{\omega }_i^2)$: where m_i and I_i are the inertia data; and v_i and ω_i are the linear and rotational speeds at each segment’s center of mass), and the instantaneous ‘pelvic roll angle’ (defined as the angle between the instantaneous medio-lateral axis of the pelvis and the starting segmental configuration in the frontal plane) were calculated and compared.

To simulate a neural latency following the loss of model static equilibrium, the joint controllers held each joint at its initial configuration for a prescribed time interval before starting to move to its target angles. To evaluate the sensitivity to this neural latency, minimal-impact falls with 100, 200, and 300 ms delays were found via optimization, and the resulting impact injury risks Φ were compared. Furthermore, to examine the sensitivity of the impact severity to the available joint strength, minimal-impact falls were obtained in the presence of 30% reduction (representing the effect of aging on muscle strength, i.e. Thelen, et al., 1996) in maximal joint torques. The dependency on joint muscle strength and decision making time will be analyzed only for those strategies with an injury risk below the fracture threshold.

3. Results

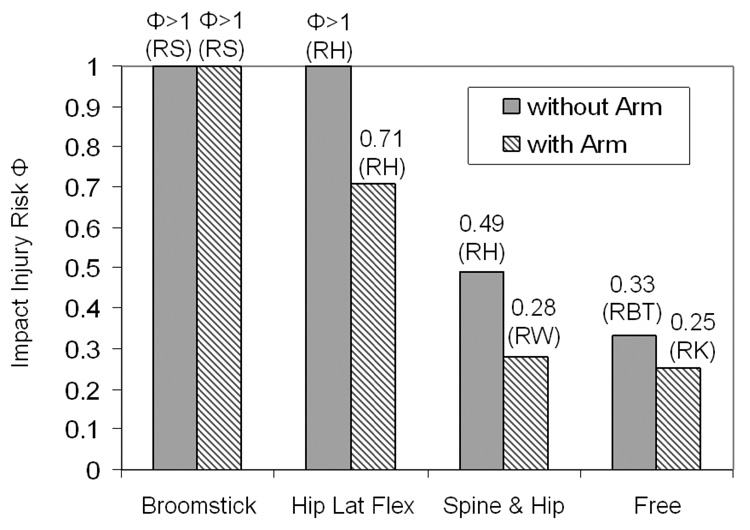
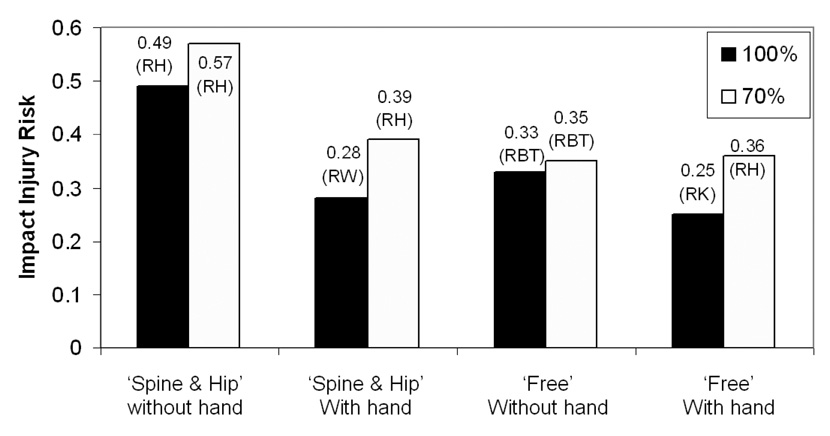
Without the assistance of the arm, each of the both the ‘Broomstick’ and ‘Hip lateral flexion’ strategies resulted in an injury risk Φ exceeding fracture threshold (Figure 3). The major impact sites of the ‘Broomstick’ and ‘Hip lateral flexion’ falls were the right shoulder (peak impact force: 7,858 N, see Table 3) and greater trochanter (peak impact force: 5,574 N, see Table 3), respectively. Use of an arm was not sufficient to avoid injury (Φ>1, see Figure 3) in the ‘Broomstick’ fall but reduced the peak hip impact force below the injury threshold (3,540 N, Φ=0.71) in the ‘Hip lateral flexion’ fall.

Figure 3.

Impact injury risk Φ for each of the four simulated lateral fall strategies with (shaded bars) and without (solid bars) the assistance of the arm. The letters in the brackets indicate the location of the major impact. RS, RE, RH, RW, RBT, and RK represent the right shoulder, elbow, hip, wrist, buttock, and knee, respectively.

Table 3.

Summary of the four simulated lateral fall strategies with and without the use of the right arm to break the fall

Movement Strategy	Φ	Leg Impact			Arm Impact
		Force (N)	Speed (m/s) (Hor., Ver.)	KE (J)	Force (N)	Speed (m/s) (Hor., Ver.)	KE (J)
Broomstick	3.93	GT: 3,533	(0.19, 2.36)	376	RE: 1,450 RS: 7,858	(0.24, 4.48) (0.42, 4.32)	382 325
Broomstick (with Arm)	1.01	GT: 2,975	(1.59, 1.87)	190	RW: 984 RE: 1,885 RS: 2,022	(0.12, 5.29) (1.43, 3.93) (1.54, 3.74)	300 277 87
Hip Lateral Flexion	1.11	GT: 5,574	(0.22, 2.45)	311	RS: 2,229	(0.54, 1.87)	115
Hip Lateral Flexion (with Arm)	0.71	GT: 3,540	(0.30, 2.15)	222	RW: 1,410 RE: 1,410	(0.40, 3.81) (0.35, 2.48)	264 158
Spine & Hip	0.49	GT: 2,452 P: 2,399 RBT: 2,335	(1.00, 2.73) (1.02, 2.97) (0.99, 3.45)	397 400 390	n/a	n/a	n/a
Spine & Hip (with Arm)	0.28	GT: 1,249 LGT: 1,077	(2.01, 1.34) (1.29, 2.14)	176 163	RW: 567 RE: 551	(0.45, 2.72) (0.68, 1.78)	179 184
Free	0.33	K: 512 GT: 1,585 P: 1,426 RBT: 1,635	(0.19, 1.01) (0.36, 1.81) (0.75, 2.42) (0.72, 2.41)	123 265 277 275	n/a	n/a	n/a
Free (with Arm)	0.25	K: 1,261 GT: 1,225 P: 836	(0.45, 2.05) (0.35, 1.16) (0.05, 0.94)	245 82 77	RW: 473 RE: 467	(5.27, 4.39) (1.75, 1.45)	230 73

Φ represents the calculated impact injury risk. GT represents the right greater trochanter; LGT, the left greater trochanter; P, lateral aspect of the right pelvis; RBT, posterior aspect of the right pelvis (Buttock); K, the right knee; RE, the right elbow; RW, the right wrist; and RS, the right shoulder. Hor. and Ver. indicate the horizontal and vertical speed, respectively. KE denotes Kinetic Energy.

The injury risk in the ‘Spine and Hip’ and ‘Free’ strategies were well below the calculated injury threshold (Φ=0.49 and 0.33, respectively, see Figure 3). Compared to a ‘Broomstick’ fall, 32% and 56% reductions in the peak hip impact forces (‘Broomstick’: 3,533 N; ‘Spine & Hip’: 2,399 N; ‘Free’: 1,585 N, see Table 3) were achieved with ‘Spine and Hip’ and ‘Free’ strategies, respectively. The use of the arm reduced impact injury risk by 42% and 24%, respectively, in ‘Spine and Hip’ and ‘Free’ fall strategies.

The impact forces and kinetic energies of sample fall strategies are illustrated in Figure 4~6. The differences in the energy histories among these sample fall strategies were compared to elucidate underlying mechanisms of impact force attenuation.

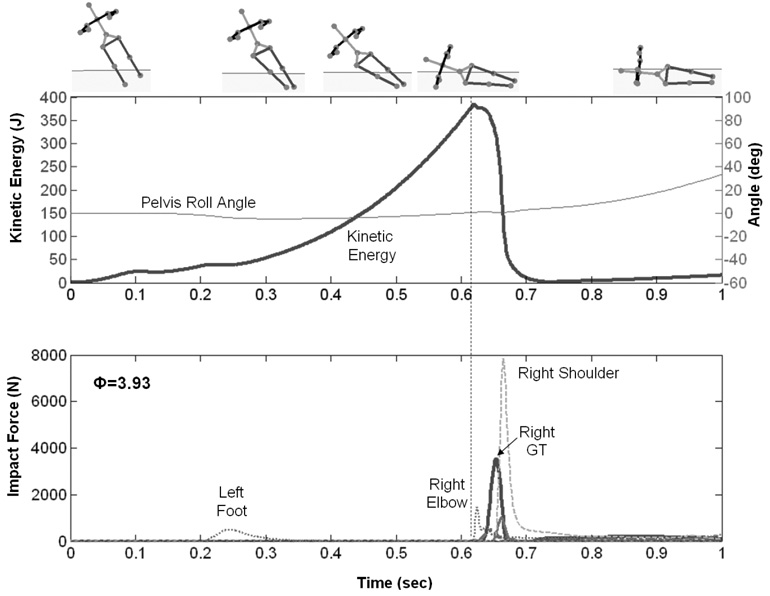
Figure 4.

Kinetic energy and impact force histories for the ‘Broomstick’ lateral fall strategy without the assistance of the arm. GT represents the greater trochanter.

Figure 4 shows that, in the ‘Broomstick’ fall, the whole body kinetic energy reached 385 J at the first impact, and the most of it was dissipated by impact forces within approximately 50 ms.

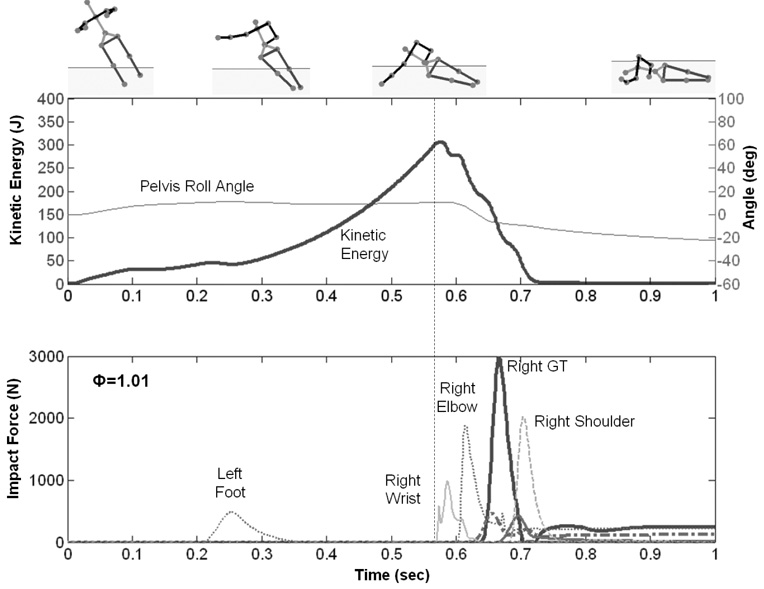
However, when arm movement was allowed in the ‘Broomstick’ fall strategy, the predicted optimal fall strategy is to use the arm to break the fall first (Figure 5). The whole body kinetic energy at first impact was 306 J and was dissipated by impact forces within approximately 150 ms, which is three times longer than that in the ‘Broomstick-without-arm’ fall arrest.

Figure 5.

Kinetic energy and impact force histories for the optimized ‘Broomstick’ lateral fall strategy with the assistance of arm. GT represents the greater trochanter.

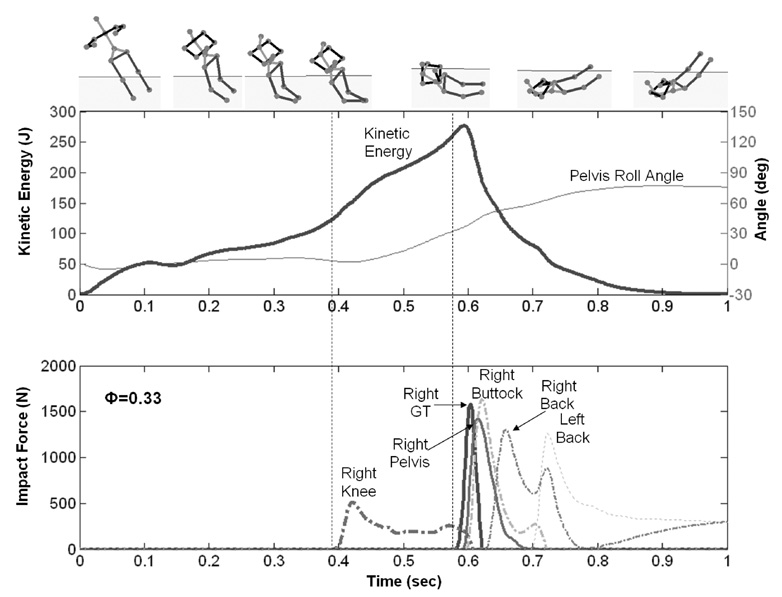
When all joints were allowed to move freely except for the arm, the optimized ‘Free’ strategy involved knee flexion, waist flexion, and axial trunk rotation to the left (Figure 6). The resulting impacts occurred across multiple sites, including the right greater trochanter (1,585 N), lateral pelvis (1,426 N), buttock (1,635 N), and back (1,303 N); and the injury risk factor for this fall was 0.33. The “pelvic roll angle” increased after the knee impact, and the whole-body kinetic energy was 265 J at greater trochanter contact. It took approximately 300 ms for the kinetic energy to be dissipated by all impacts.

Figure 6.

Kinetic energy and impact force histories for the optimized ‘Free’ lateral fall strategy without the assistance of arm. GT represents the greater trochanter.

Since the ‘Broomstick’ and ‘Hip Lateral Flexion’ fall strategies cause high impact forces close to or exceeded the ‘fracture threshold’ (Φ=1), we expected that performing these two injurious fall strategies with reduced joint muscle strength and longer decision-making time may result in even greater injury risk. Therefore, we excluded them in further sensitivity investigations.

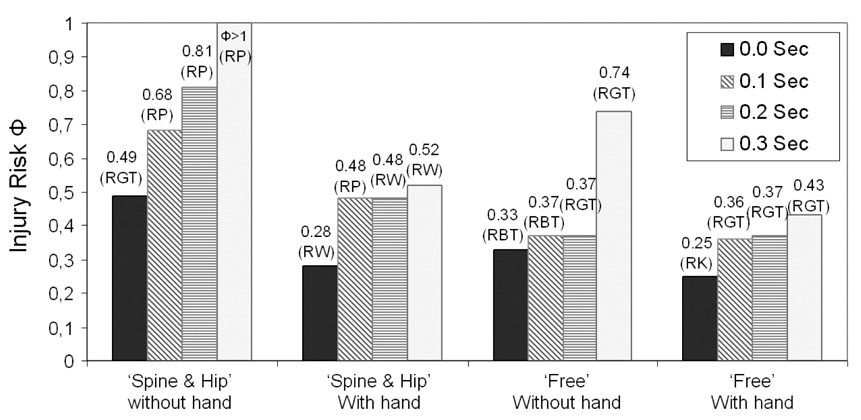
For the ‘Spine and Hip’ and ‘Free’ strategies, the presence of a simulated age-related 30% decline in maximum available joint strength increased the impact injury risk, Φ, regardless of whether the right arm was used (see Figure 7). However, the increase was not sufficient to cause injurious falls (Φ<1). Moreover, in the presence of more than a 200 ms delay in decision-making time, the predicted impact injury risk for both strategies involving hand use increased by at least 70%, whereas those of the strategies not involving the hand approximately doubled (Figure 8).

Figure 7.

The effect of available joint strength on the impact injury risk when performing ‘Spine & Hip’ and ‘Free’ fall strategies with or without the assistance of arm. The letters in the brackets indicate the location of the major impact. RH, RW, and RK denote the right hip, wrist, and knee. Dark and light bars indicate that the fall was simulated with 100% and 70% of available joint strength, respectively.

Figure 8.

The effect of decision-making time on the impact injury risk when performing ‘Spine & Hip’ and ‘Free’ fall strategies with the assistance of arm. The letters in the brackets indicate the location of the major impact. RGT, RP, RW, and RK denote the right greater trochanter, pelvis, wrist, and knee, respectively.

4. Discussion

The first hypothesis was refuted in that pre-impact control strategy had a pronounced effect on impact severity. For example, depending on the fall strategy, predicted vertical hip speed at impact ranged from 2.73 to 1.87 m/s, whole body kinetic energy at the hip impact varied from 398 to 176 J, and the resulting hip impact force could be reduced from 5,574 N, a force that would fracture a hip, to a force of 1,225 N, a value well below that required to fracture a hip. These predicted values corroborate and extend earlier experimental (Groen, et al., 2007; Robinovitch, et al., 1997) and modeling findings (van den Kroonenberg, et al., 1995). The large variation in the predicted impact severity caused by different fall strategies suggests that how a lateral fall is arrested may be an important factor in determining the likelihood of facture.

Another important finding is that a greater reduction in the hip impact severity can be achieved by using more of the available joint degrees of freedom during the fall. For example, compared to the ‘Broomstick’ lateral fall, allowing the use of knee, hip and spine rotations in a lateral fall (‘Free’ strategy) reduced the hip impact force by 56%. The mechanisms underlying this force reduction involve distributing the impact over a large body area and allowing more time for impact energy dissipation. In the ‘Broomstick’ strategy (Figure 4), the impact energy was dissipated by only two impact sites, the right hip and shoulder, within a short period of time (around 50 ms). On the other hand, in the ‘Free’ strategy (Figure 6), rolling the body about two major axes ensured that the momentum was not attenuated after any single impact. Consequently, each impact site was responsible for less impact energy dissipation and sustained less impact force.

We also found that using the lateral aspect of the knee as the first impact site in the ‘Free’ strategy, as is used by parachutists as the second of five impact sites (“feet”, “calves”, “thigh”, “buttock”, “diagonally across the back”) in the parachute landing fall (Marine-Corps-Field-Manual, 1996), can dissipate more energy via negative work at the knee during flexion and impact before the ipsilateral hip touches down (397 J and 376 J, respectively, for ‘Spine & Hip’ and ‘Broomstick’ vs. 265 J for ‘Free’). The finding of this ‘squatting’ energy dissipating mechanism corroborates the results of a backward fall experiment (Robinovitch, et al., 2004).

Our results in Figure 3 show that, while the use of the arm could reduce the impact force on the hip, trunk and knee movements were of even greater importance in determining whether the fall was injurious. This corroborates a recent experimental study that the use of the arm was not essential for reducing the hip impact force in a martial arts fall (Groen, et al., 2007).

The second hypothesis was also refuted in that slower decision-making time increased the fall-related injury risk. This result is in agreement with a previous epidemiology study (Nevitt, et al., 1991), in which the slower hand reaction time has been shown to be one of the risk factors for fall-related injuries. Based on the current simulation results, a delay exceeding 200 ms increased the predicted impact severity at least by 70% for the “Spine and Hip” and “Free” fall arrest strategies (see Figure 8). Since the selection of a response requires more time when there are a larger number of alternatives (Donders, 1969; Hick, 1952; Hyman, 1953), our results imply that knowing a priori the best protective maneuver before the fall, and triggering it in time, may be important for preventing injury. The impact injury risk increased in the presence of a 30% age-related decline in muscle strength, but the injury risk was still below the injury threshold (Φ=1). This implies people with weaker muscle strength, such as the elderly, may also be able to protect their hip and shoulder from severe impact by adjusting their knee, hip, and/or trunk movements.

Limitations of this study include the unproven assumption that the segmental movements are controlled by feedback PD controllers: the optimizer needed only to find the pre- and post-contact joint target angles instead of finding the neural input signals to the joint actuators at every instant of time. Such a position control scheme seems reasonable for comparing the effects of the grossly different segmental movement patterns that were studied. A second limitation is that we did not examine the sensitivity of the results to variations in the adiposity covering the hip or other body segments (Robinovitch, et al., 1995) or of the ground surface hardness characteristics (for example, Laing, et al., 2006). Nevertheless, none of these limitations void the main conclusions of the study.

In summary, the pre-impact segmental movement strategy was predicted to have a pronounced effect on the resulting impact injury risk. The predicted protective fall strategy includes early knee flexion and successive impacts on the lateral aspect of the flexed knee; and the posterolateral aspects of the hip, pelvis, and the torso. The predicted impact injury risk was below the injury threshold in the presence of a 30% age-related decline in muscle strength, a finding of benefit to the elderly. However, a 300 ms delay in the decision-making time approximately doubled the predicted fall injury risk, emphasizing the need to start the arrest early. Lower extremity movements were of greater importance than the use of arm in determining whether the fall was injurious. However, in the presence of a 300 ms decision-making delay, using the arm to break a lateral fall may reduce the fracture risk.