Abstract
The recent explosion in procurement and availability of high-dimensional gene- and protein-expression profile datasets for cancer diagnostics has necessitated the development of sophisticated machine learning tools with which to analyze them. While some investigators are focused on identifying informative genes and proteins that play a role in specific diseases, other researchers have attempted instead to use patients based on their expression profiles to prognosticate disease status. A major limitation in the ability to accurate classify these high-dimensional datasets stems from the ‘curse of dimensionality’, occurring in situations where the number of genes or peptides significantly exceeds the total number of patient samples. Previous attempts at dealing with this issue have mostly centered on the use of a dimensionality reduction (DR) scheme, Principal Component Analysis (PCA), to obtain a low-dimensional projection of the high-dimensional data. However, linear PCA and other linear DR methods, which rely on Euclidean distances to estimate object similarity, do not account for the inherent underlying nonlinear structure associated with most biomedical data. While some researchers have begun to explore nonlinear DR methods for computer vision problems such as face detection and recognition, to the best of our knowledge, few such attempts have been made for classification and visualization of high-dimensional biomedical data. The motivation behind this work is to identify the appropriate DR methods for analysis of high-dimensional gene- and protein-expression studies. Towards this end, we empirically and rigorously compare three nonlinear (Isomap, Locally Linear Embedding, Laplacian Eigenmaps) and three linear DR schemes (PCA, Linear Discriminant Analysis, Multidimensional Scaling) with the intent of determining a reduced subspace representation in which the individual object classes are more easily discriminable. Owing to the to the inherent nonlinear structure of gene- and protein-expression studies, our claim is that the nonlinear DR methods provide a more truthful low-dimensional representation of the data compared to the linear DR schemes. Evaluation of the DR schemes was done by (i) assessing the discriminability of two supervised classifiers (Support Vector Machine and C4.5 Decision Trees) in the different low-dimensional data embeddings and (ii) 5 cluster validity measures to evaluate the size, distance and tightness of object aggregates in the low-dimensional space. For each of the 7 evaluation measures considered, statistically significant improvement in the quality of the embeddings across 10 cancer datasets via the use of 3 nonlinear DR schemes over 3 linear DR techniques was observed. Similar trends were observed when linear and nonlinear DR was applied to the high-dimensional data following feature pruning to isolate the most informative features. Qualitative evaluation of the low-dimensional data embedding obtained via the 6 DR methods further suggests that the nonlinear schemes are better able to identify potential novel classes (e.g. cancer subtypes) within the data.
Index Terms: Dimensionality reduction, bioinformatics, data clustering, data visualization, machine learning, manifold learning, nonlinear dimensionality reduction, gene expression, proteomics, prostate cancer, lung cancer, ovarian cancer, principal component analysis, linear discriminant analysis, multidimensional scaling, Isomap, locally linear embedding, laplacian eigenmaps, classification, support vector machine, decision trees, LLE, PCA
I. Introduction
GENE- and protein-expression profiling have emerged as promising new methods for disease prognostication [1], [2], [3]. Attempts at analyzing several thousand dimensional gene- and protein- profiles have been primarily motivated by two factors; (a) identification of individual informative genes and proteins responsible for disease characterization [4], [5], [6], [7], and (b) to classify patients into different disease cohorts [8], [9], [10], [11], [12], [13], [14]. Several researchers involved in the latter area have attempted to use different classification methods to stratify patients based on their gene- and protein-expression profiles into different categories [8], [9], [10], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27]. While the availability of studies continues to grow, most protein- and gene-expression databases contain no more than a few thousand patient samples. Thus, the task of stratifying these patients based on the gene/protein profile is subject to the ‘curse of dimensionality’ problem [28], [29], owing to the relatively small number of patient samples compared to the size of the feature space. Classification of the new unseen test samples is thus poor due to the sparseness of data in the high-dimensional feature space. Additionally, many of the features within the expression profile may be non-informative or redundant, providing little additional class discriminatory information [11], [12] while increasing computing time and classifier complexity. In order to bridge the gap between the number of patient samples and gene/peptide features and overcome the curse of dimensionality problem, researchers have proposed (a) feature selection, and (b) dimensionality reduction to reduce the size of the feature space.
Feature selection refers to the identification of the most informative features and have been commonly utilized to precede classification in gene- and protein-expression studies [11], [14], [30]. However, since a typical gene or protein microarray records expressions from thousands of genes or proteins, the cost of finding an optimal informative subset from several million possible combinations becomes a near intractable problem. Further, genes or peptides that were pruned during the feature selection process may be significant in stratifying intra-class subtypes.
Dimensionality reduction (DR) refers to a class of methods that transforms the high-dimensional data into a reduced subspace to represent data in far fewer dimensions. In Principal Component Analysis (PCA), a linear DR method, the reduced dimensional data is arranged along the principal eigenvectors, which represent the direction along which the greatest variability of the data occurs [31]. Note that unlike with feature selection, the samples in the transformed embedding subspace no longer represent specific gene-and protein-expressions from the original high-dimensional space, but rather encapsulate data similarities in low-dimensional space. Even though the objects in the transformed embedding space are divorced from their original biological meaning, the organization and arrangement of the patient samples in low-dimensional embedding space lends itself to data visualization and classification. Thus, if two patient samples from a specific disease cohort are mapped adjacent to each other in an embedding space derived from their respective high-dimensional expression profiles, then it suggests that the two patients have a similar disease condition. By exploiting the entire high-dimensional space, DR methods, unlike feature selection, offer the opportunity to stratify the data into subclasses (e.g. novel cancer subtypes).
The most popular method for DR for bioinformatics related aplications has been PCA [3], [32], [33], [34], [35], [36], [37], [38]. Originally developed by Hotelling [39], PCA finds orthogonal eigenvectors along which the greatest amount of variability in the data lies. The underlying intuition behind PCA is that the data is linear and that the embedded eigenvectors represent low-dimensional projections of linear relationships between data points in high-dimensional space. Linear Discriminant Analysis (LDA) [31], also known as Fisher Discriminant Analysis, is another linear DR scheme which incorporates data label information to find data projections that separate the data into distinct clusters. Multidimensional Scaling (MDS) [40] reduces data dimensionality by preserving the least squares Euclidean distance in the low-dimensional space. Classifier performance with linear DR schemes for biomedical data has been a mixed bag. Dawson et al. [34] found that there were biologically significant elements of the gene expression profile that were not seen with linear MDS. Ye et al. [29] found that LDA gave poor results in distinguishing disease classes on a cohort of 9 gene expression studies. Truntzer et al. [35] also found limited use of LDA and PCA for classifying gene- and protein-expression profiles of a diffuse large b-cell lymphoma dataset since the classes appeared to be linearly inseparable. The afore-mentioned results appear to suggest that biomedical data has a nonlinear underlying structure [34], [35] and that DR methods that do not impose linear constraints in computing the data projection might be more appropriate compared to PCA, MDS, and LDA for classification and visualization of data classes in gene- and protein-expression profiles.
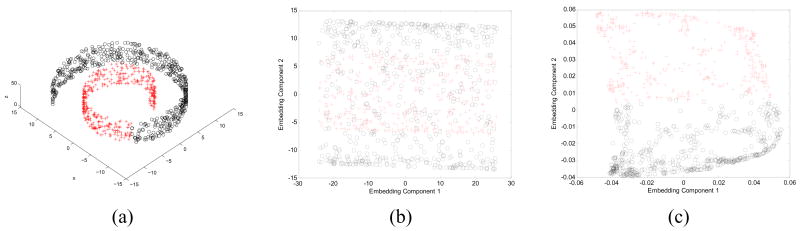
Recently, nonlinear DR methods such as Spectral Clustering [41], Isometric mapping (Isomap) [42], Locally Linear Embedding (LLE) [43], and Laplacian Eigenmaps (LEM) [44] have been developed to reduce data dimensionality without assuming a Euclidean relationship between data samples in the high-dimensional space. Shi and Malik’s Spectral Clustering algorithm (also known as Graph Embedding [41]) builds upon graph theory to partition the graph into clusters and separate accordingly. Madabhushi et al. [45] demonstrated the use of graph embedding to detect the presence of new tissue classes on high-dimensional prostate MRI studies. The utility of this scheme has also recently been demonstrated in distinguishing between cancerous and benign magnetic resonance spectra (MRS) in the prostate [46] and in discriminating between different cancer grades on digitized tissue histopathology [47], [48]. Tenenbaum (Isomap) [42] presented the Isomap algorithm for nonlinear DR and described the term ‘manifold’ for machine learning as a nonlinear surface embedded in high-dimensional space along which dissimilarities between data points are best represented. The Isomap algorithm estimates geodesic distances, defined as the distance between two points along the manifold, and preserves the nonlinear geodesic distances (as opposed to Euclidean distances used in linear methods) while projecting the data onto a low-dimensional space. Locally linear embedding proposed by Roweis and Saul [43] uses local weights to preserve local geometry in order to find the global nonlinear manifold structure of the data. The geodesic distance between data points is approximated by assuming that the data is locally linear. Recently, Belkin et al. presented the Laplacian Eigenmaps algorithm [44], which like Spectral Clustering, Isomap, and LLE, makes local connections, but uses the Laplacian to simplify determination of the locality preserving weights used to obtain the low-dimensional data embeddings. Graph Emedding, LLE, Isomaps, and LEM, all aim to nonlinearly project the high-dimensional data in such a way that 2 objects xa and xb that lie adjacent to each other on the manifold are adjacent to each other in the low-dimensional embedding space, and likewise, 2 objects that are distant from each other on the manifold are far apart in the low-dimensional embedding space. As previously demonstrated by Tenenbaum [42], Figure 1 reveals the limitations of using a linear DR for highly nonlinear data. Figure 1 shows the embedding of the swiss roll dataset shown in Figure 1(a) obtained by a linear DR method (MDS) in Figure 1(b) and a nonlinear DR scheme (LEM) in Figure 1(c). MDS, which preserves Euclidean distances, is unable to capture the non-linear manifold structure of the swiss roll, but LEM is capable of learning the shape of the manifold and representing points in the low-dimensional embedding by estimating geodesic distances. Thus, while MDS (Figure 1(b)) shows overlap between the two classes that lie along the swiss roll, LEM (Figure 1(c)) provides an unraveled swiss roll that separates the data classes in two-dimensional embedding space.
Fig. 1.
(a) Nonlinear manifold structure of the Swiss Roll dataset [42]. Labels from 2 classes (shown with black circles and red crosses) are provided to show the distribution of data along the manifold. (b) The low-dimensional embedding obtained via linear MDS on the Swiss Roll reveals a high degree of overlap between samples from the two classes due to the use of Euclidean distance as a dissimilarity metric. The embedding obtained via LEM on the other hand, is able to almost perfectly distinguish the two classes by projecting the data in terms of geodesic distance determined along the manifold.
While PCA remains the most popular DR method for bioinformatics related applications [32], [34], [35], [36], [37], [38], nonlinear DR methods have begun to gain popularity [3], [30], [45], [49]. Liu et al. [30] found high classification accuracy in the use of kernel PCA (non-linear variant of PCA) for gene expression datasets while Weng [49] recommended the use of Isomap for medical data analysis. Shi and Chen [3] found that LLE outperformed PCA in classifying 3 gene expression cancer studies. Dawson et al. [34] compared Isomap, PCA, and linear MDS for oligonucleotide datasets, and Nilsson et al. [50] compared Isomap with MDS in terms of their ability to reveal structures in microarray data. In these and other related studies [3], [34], [49], [50], the nonlinear methods were found to outperform linear DR schemes. While several researchers have performed comparative studies of classifier methods [51], [52], [53] to determine the optimal scheme for various applications, to the best of our knowledge, no comprehensive comparative study of different nonlinear and linear DR schemes in terms of their ability to discriminate between samples has been attempted thus far.
The primary motivation of this work is to systematically and quantitatively compare and evaluate the performance of 6 DR methods; three linear methods (PCA, LDA [31], linear MDS [40]) and three nonlinear DR methods (Isomap [42], LLE [43], and LEM [44]) in terms of their ability to faithfully represent the underlying structure of biomedical data. A total of 10 different binary-class gene- and protein-expression studies corresponding to prostate, lung, breast, gliomal and ovarian cancers, as well as leukemia and lymphoma are considered in this comparative study. Low-dimensional data embeddings of the cancer studies obtained from each of the 6 DR methods are evaluated in two ways. Firstly, the low-dimensional data embeddings for each dataset are compared in terms of classifier accuracy evaluated via a support vector machine (SVM) and a decision tree (C4.5) classifier. The intuition behind the use of classifiers is that if the embedding produced by a particular DR method accurately captures the structure of the data manifold, then xa, xb, belonging to different classes in the high-dimensional dataset D, will have low-dimensional embedding coordinates Gφ(xa), Gφ(xb) far apart from each other. Thus, if the underlying structure of the data has been faithfully reconstructed by the DR method, then the task of discriminating between objects from different classes becomes trivial (ie. a linear classifier would suffice). Note that a more complex classifier with a nonlinear separating hyperplane could potentially distinguish objects from different classes in an embedding space that does not represent a faithful reconstruction of the original multidimensional manifold. However, the emphasis in this work is not in identifying the optimal classification scheme, but rather to identify the DR method that can provide the optimal low-dimensional representations so that the task of discriminating different object classes becomes trivial. The role of classifiers in this work only serves to quantitatively evaluate the quality of the data embeddings. In addition to the use of 2 classifiers, we also consider 5 different cluster measures to evaluate the low-dimensional data representation. The intuition behind the use of the cluster validity measures is that in the optimal low-dimensional data representation, objects xa ∈ D with associated class label Y(xa) = +1 and all objects xb ∈ D, Y (xb) = −1 will form 2 distinct, tight, and well separated clusters.
The organization of the rest of this paper is as follows. In Section II is provided an overview of the 6 DR methods compared in this paper. In Section III the experimental setup for quantitatively comparing the linear and nonlinear DR schemes is described. Quantitative and qualitative results and accompanying discussion is presented in Section IV. Finally, concluding remarks are presented in Section V.
II. Overview of Dimensionality Reduction Methods
A. Terminology
A total of ten binary gene- and protein-expression and 1 multi-class dataset Dj, j ∈ {1, 2, …, 11}, were considered in this study. Each Dj = {x1, x2, …, xn} is represented by an n × M dimensional matrix of n samples xi, i ∈ {1, 2, …, n}. Each xi ∈ Dj has an associated class label Y (xi) ∈ {+1, −1} and an M-dimensional feature vector F(xi) = [fu(xi)|u ∈ {1, 2, …, M}], where fu(xi) represents the gene- or protein-expression values associated with xi. Following application of DR methods f, where φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM}, the individual data points xi ∈ D are represented by an m-dimensional embedding vector , where represents the embedding coordinate along the principal eigenvectors of xi in m-dimensional embedding space. Table I lists notation and symbols used frequently in this paper.
TABLE I.
List of frequently appearing symbols and notations in this paper.
| Symbol | Description |
|---|---|
| Dj | Dataset j arranged in a n × M dimensional matrix, where j denotes a specific dataset j ∈ {1, 2, …, 11} |
| xi | Patient samples xi ∈ Dj, where i ∈ {1, 2, …, n} |
| fu(xi) | Single feature associated with xi, where u ∈ {1, 2, …, M} |
| F(xi) | M-dimensional gene- or protein-expression feature vector describing xi |
| Transformed eigen feature obtained from F(xi), where υ denotes the index for the eigenvector, υ ∈ {1, 2, …, m} | |
| Gφ(xi) | m-dimensional feature (embedding) vector describing xi |
| φ | Denotes the DR method used to create Gφ(xi), where φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} |
| Y(xi) | Class label for observation xi, Y ∈ {+1, −1} |
| Classifier label determined via SVM applied to Gφ(xi) for all xi ∈ Dj | |
| Classifier label determined via C4.5 decision tree applied to Gφ(xi) for all xi ∈ Dj | |
| Inter-Centroid Distance between dominant data clusters | |
| Mean Cluster Tightness of object class +1 | |
| Mean Cluster Tightness of object class −1 | |
| Standard Deviation of Cluster Tightness of object class +1 | |
| Standard Deviation of Cluster Tightness of object class −1 |
B. Linear Dimensionality Reduction Methods
1) Principal Component Analysis (PCA)
PCA is widely used to visualize high-dimensional data and discern relationships by finding orthogonal axes that contain the greatest amount of variance in the data [39]. These orthogonal eigenvectors corresponding to the largest eigenvalues are called ‘principal components’ and are obtained in the following manner. Each data point xi ∈ D is first centered by subtracting the mean of all the features for each observation xi from its original feature value fu(xi) as shown in Equation 1.
| (1) |
for u ∈ {1, 2, …, M}. From feature values f̄u(xi) for each xi ∈ D, a new n × M matrix is constructed. The matrix is then decomposed into corresponding singular values as shown in Equation 2.
| (2) |
where via singular value decomposition, an n × n diagonal matrix λ containing the eigenvalues of the principal components and an m × n left singular matrix U and M × n matrix V are obtained. The eigenvalues in λ represent the amount of variance for each eigenvector in matrix VT and are used to rank the corresponding eigenvectors in the order of greatest variance. Thus, the first m eigenvectors are obtained, as they contain the most variance in the data while the remaining eigenvectors are discarded so each data sample xi ∈ D is now described by an m-dimensional embedding vector GPC A(xi).
2) Linear Discriminant Analysis (LDA)
LDA [31] takes into account class labels to find eigenvectors that can discriminate between two classes {+1, −1} in a dataset. The intra-class scatter matrix SW and inter-class scatter matrix SB [31] are computed from the sample means for data clusters +1 and −1, giving and respectively, where for xa ∈ D, Y (xa) = +1 and for xb ∈ D, Y(xb) = −1. Note that both μ + and μ− are m-dimensional vectors. From the sample means,
| (3) |
and
| (4) |
are calculated. SW and SB are then used to create the eigenvectors by singular value decomposition (Equation 5).
| (5) |
As with PCA, each data point xi ∈ D is now represented by a m-dimensional vector GLDA(xi) corresponding to the m largest eigenvalues in λ. While LDA has often been used as both a DR method and a classifier, it is limited in handling sparse data and for datasets where the Gaussian distribution assumption is not valid [29].
3) Classical Multidimensional Scaling (MDS)
MDS [40] is implemented as a linear method that preserves the Euclidean geometry between each pair of m-dimensional points xa, xb ∈ D, which is arranged into a symmetric n × n distance matrix Γ as shown in Equation 6.
| (6) |
where ||·||2 represents the Euclidean norm. MDS finds optimal positions for the data points xa, xb in m-dimensional space through minimization of the least squares error in the input pairwise Euclidean distances between xa and xb [40]. Note that classical MDS differs from nonlinear variants of MDS such as non-metric MDS [40], which do not preserve input Euclidean distances.
C. Nonlinear Dimensionality Reduction Methods
1) Isometric Mapping (Isomap (ISO))
The Isomap algorithm [42] modifies classical MDS to handle nonlinearities in the data through the use of a neighborhood mapping. By creating linear connections from each point xi ∈ D to its κ closest neighbors in Euclidean space, a manifold representation of the data is constructed, κ being a user-defined parameter. Nonlinear connections between points outside of the κ neighborhood are approximated by calculating the shortest distance between two points xa, xb ∈ D along the paths in the neighborhood map, where a, b ∈ {1, 2, …, n}. Thus, new geodesic distances (distances measured along the surface of the manifold) are calculated and arranged in an n × n pairwise distance matrix Δ, where Δ(xa, xb) contains the nonlinear geodesic distances between xa, xb ∈ D. The matrix Δ is then given as an input to the classical MDS algorithm from which each data point xi ∈ D, i ∈{1, 2, …, n}, is represented by its m-dimensional embedding vector GISO(xi).
2) Locally Linear Embedding (LLE)
LLE [43], like the Isomap algorithm [42] utilizes a neighborhood map connecting each data sample xi to its κ nearest neighbors in Euclidean space. However, instead of calculating manifold distances, LLE describes each xi in terms of its κ closest neighbors xa. Thus, for each xi, an M × κ matrix containing the centered features f̂u(xa) = fu(xa) − fu(xi) is obtained. To describe the local geometry for each xi, linear coefficients accounting for the location of xi relative to each xa can be optimized by solving for the κ dimensional weight vector w(xi, xa) via the linear system
| (7) |
where ℐ is a column vector of ones of length κ. From each of n weight matrices w, the n × n matrix, W, stores the linear coefficients of each xi and xa in W(xi, xa) and W(xi, xb) = 0, where xb are not among the κ nearest neighbors of xi ∈ D. A cost matrix χ is then computed from the weight matrix W as
| (8) |
where I is an n × n identity matrix. Singular value decomposition is used to obtain the m-dimensional embedding vector GLLE(xi) and for each xi ∈ D from cost matrix χ.
3) Laplacian Eigenmaps (LEM)
The Laplacian Eigenmaps [44] algorithm, similar to LLE and Isomap, establishes a locally linear mapping by connecting each point xi ∈ D to its κ nearest neighbors. Weights are assigned between each pair of points to form an n × n symmetrical weight matrix W̃, where weights W̃ (xi, xa) = 1, when xa is a κ nearest neighbor of each xi ∈ D, and W̃ (xi, xb) = 0, when xb represent is not a κ nearest neighbor of xi ∈ D. From weight matrix W̃ and a diagonal matrix of column sums , for all i∈{1, 2, …, n}, a symmetric, positive semi-definite matrix L called the Laplacian is calculated as
| (9) |
Singular value decomposition (Equation 2) is then used to obtain the m-dimensional embedding vector GLEM(xi) for each xi ∈D from the Laplacian L.
III. Experimental Design
The organization of this section is as follows. In Section III A, we provide a description of datasets followed by brief outline of methodology in Section III B. In Sections III C and III D, we briefly describe the different qualitative and quantitative evaluation measures we use for comparing the performance of the DR methods.
A. Description of Datasets
A total of ten publicly available binary-class [1], [7], [8], [16], [17], [19], [24], [25], [26], [54] and 1 multi-class dataset [32] corresponding to high-dimensional gene- and protein-expression studies1 were acquired for the purposes of this study. The two-class datasets correspond to gene- and protein-expression profiles of normal and cancerous samples for breast [7], colon [16], lung [26], ovarian [19], and prostate [17] cancer, leukemia [1], [32], lymphoma [8], [25], and glioma studies [24]. The multi-class dataset comprises 5 subtypes of leukemia. The size of the datasets range from 30 to 253 patient samples, with the number of corresponding features ranging from 791 to 54675 genes or peptides. Table II provides a description of all the datasets that we considered including a description of the data classes and the originating study for these datasets. Note that for each study, the number of patient samples is significantly smaller than the dimensionality of the feature space. No preprocessing or normalization of any kind was performed on the original feature space prior to dimensionality reduction. An experiment was however performed to compare DR performance with and without feature pruning on the original high-dimensional studies.
TABLE II.
Description of gene expression and proteomic spectra datasets considered in this study
| Dataset | Samples | Genes/Peptides | Class Description | Original Study |
|---|---|---|---|---|
| (1) ALL-AML Leukemia | 34 | 7129 | 20 ALL, 14 AML | Golub et al. [1] |
| (2) Breast Tumor | 30 | 54675 | 10 Tumor, 20 Normal | Turashvili et al. [7] |
| (3) Colon Cancer | 62 | 2000 | 40 Tumor, 22 Normal | Alon et al. [16] |
| (4) DLBCL-Harvard | 77 | 6817 | 58 DLBCL,19 FL | Shipp et al. [25] |
| (5) Glioma | 85 | 791 | 26 Grade III, 59 Grade IV | Freije et al. [24] |
| (6) Lung Cancer | 148 | 12533 | 15 MPM, 134 ADCA | Gordon et al. [54] |
| (7) Lung Cancer-Michigan | 96 | 7129 | 86 Tumor, 10 Normal | Beer et al. [26] |
| (8) Ovarian Cancer | 253 | 15154 | 162 Tumor, 91 Normal | Petricoin et al. [19] |
| (9) Prostate Cancer | 34 | 12600 | 25 Tumor, 9 Normal | Singh et al. [17] |
| (10) Types of DLBCL | 47 | 4026 | 24 Germinal, 23 Activated | Alizadeh et al. [8] |
| (11) Acute Lymphoblastic Leukemia | 58 | 12558 | 6 BCR-ABL, 9 E2A-PBX1, 6 MLL, 22 Hyperdiploid > 50, 15 T-ALL | Yeoh et al. [32] |
B. Brief Outline of Methodology
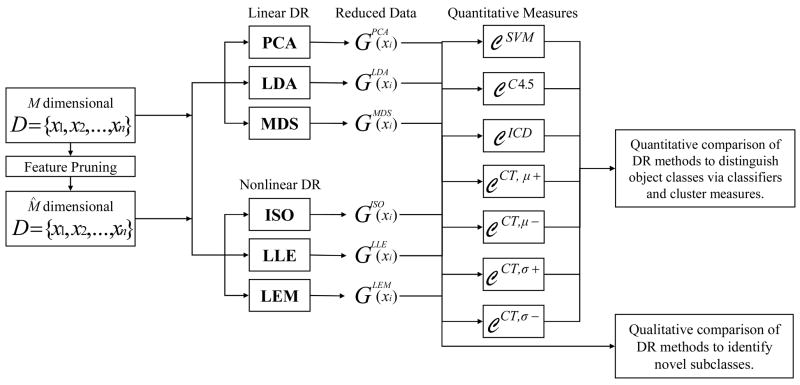
Our methodology for investigating the embedded data representation given by DR is comprised of 4 main steps described briefly below and illustrated in the flowchart in Figure 2.
Fig. 2.
Flowchart showing the overall organization and process flow of our experimental design.
Step 1) Dimensionality Reduction
To evaluate and compare the low-dimensional data embeddings, we reduced the dimensionality of M-dimensional xi ∈ Dj, j ∈ {1, 2, …, 11}, via 6 DR methods φ ∈{PCA, LDA, MDS, ISO, LLE, LEM}. The resulting m-dimensional embedding vectors Gφ(xi) now represent the low-dimensional signatures for each xi ∈ Dj and for each method φ. Additionally, we obtain m-dimensional embedding vectors for feature pruned samples xi ∈ Dj, j ∈ {1, 2, …, 11}, containing M̂ < M dimensional samples xi, for each method φ.
Step 2) Qualitative Evaluation for Novel Class Detection
In order to evaluate the presence of possible sub-clusters within the data, the dominant embedding coordinates , for each method φ, and xi ∈ D were plotted against each other. The graphical plots reveal the m-dimensional embedding representations of the high-dimensional data via each of the 6 DR methods. On the eigenplots obtained for each DR scheme, potential subclasses are visually identified.
Step 3) Quantitative Evaluation of DR performance via Classifier Accuracy
To evaluate the quality of the DR embeddings, two classifiers are trained using the low-dimensional embedding vector Gφ(xi), for φ ∈{PCA, LDA, MDS, ISO, LLE, LEM}, and xi ∈ D. For each D, the samples xi ∈ D are divided into a training set and a testing set . Samples will be used to train an SVM and decision tree (C4.5) classifier in the embedding space defined by embedding coordinates Gφ (xa), φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} to distinguish between the different classes. Once the classifiers have been trained, they will be applied to predict class labels , ∈ {+1, −1} for all for method φ. The classifier predictions , are compared against the true object label Y (xb) for xb ∈ D to estimate the classifier accuracy, recorded for each DR scheme. The same procedure is repeated using the feature pruned samples xi ∈ D with M̂ < M dimensionality, following DR.
Step 4) Quantitative Evaluation of DR performance via Cluster Validity Measures
To compare the size, tightness, and separation of class clusters from different DR methods, we first normalize the embedding space obtained via each of 6 DR methods φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM}. In this normalized embedding space, we calculate centroids G̃φ,+ and G̃φ,− corresponding to the +1 and −1 classes. From the centroids G̃φ,+ and G̃φ,−, we measure the separation between clusters as well as the tightness of each cluster by measuring the distances of each xi ∈ D to the corresponding class centroid. The same procedure is repeated following feature pruning.
C. Detailed Description of Experimental Design
1) Feature Pruning
A feature pruning step is employed to identify a set of informative features F̂(xi) = [fû(xi)|û ∈ {1, 2, …, M̂}] where M̂ < M for each xi ∈ D. The aim of feature pruning is to compare whether the trends in performance of the 6 DR methods considered in this study is similar when considering all features F(xi) and when considering only the most informative features F̂(xi). The feature pruning method based on t-statistics and described in [1], [15] was considered. For all xi ∈ D and for a specific gene- or protein-expression feature u ∈ {1, 2, …, M}, the mean and variance of the expression levels for the +1 or −1 class were computed. Hence
| (10) |
| (11) |
The values of were then used to calculate the information content of each gene or protein expression feature as
| (12) |
The different features are then ranked in descending order based on their information content . The top 10 percentile of most informative features fû, û ∈ {1,2,…,M̂}, where M̂ < M, are used to compute a second set of embeddings for each Dj, j ∈ {1,2,…, 11} and φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM}.
2) Qualitative Evaluation to Identify Novel Subclasses
The linear and nonlinear DR methods were evaluated in terms of their ability to identify new subclasses within the data. The 3 dominant eigenvalues , and are plotted against each other, for φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM}, and for all xi ∈ D. The 3D space of embedding coordinates Gφ (xi), for all xi ∈ D, were visually inspected for (a) distinct clusters within the dominant +1, −1 classes and (b) distinct clusters that appear to be far removed from the cluster centers Gφ,+ and Gφ,−. Since the ground truth for newly identified subclasses within the binary-class datasets was unavailable, we also compared the 6 DR schemes on a multi-class Acute Lymphoblastic Leukemia dataset [32], which is comprised of 5 known subclasses.
3) Quantitative Evaluation to Measure Class Discriminability
In this section, we describe in greater detail the different performance measures used for evaluating the efficacy of DR methods.
a) Dimensionality Reduction Comparison via Classifier Accuracy
The accuracy of 2 classifiers (Linear Support Vector Machines and C4.5 Decision Trees) was used to quantitatively evaluate G(xi), xi ∈ D on 11 datasets Dj, j ∈ {1,2,…,11}, using the class labels provided. Both classifiers considered, Support Vector Machines (SVMs) and C4.5 Decision Trees require the use of a training set to construct a prediction model for new data and a testing set . Each classifier was first trained by using labeled instances in , where for each , Y (xa) ∈ {+1,−1}. The classifier training is done separately for each DR method φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM}. To train the classifiers, we randomly set aside 1/3 of the samples in for training, and the remaining 2/3 samples in were used for testing. The 3-fold cross validation method was then used to determine the optimal classifier parameters. The classifier outputs , , where , was compared against the true object label Y (xb) ∈ {+1,−1}, Subsequently, accuracy, defined as the ratio of the number of objects , correctly labeled by the classifier to the total number of tested objects in each . Below we provide a brief description of the 2 classifiers considered in this study.
i. Support Vector Machines (SVMs)
Support vector machines (SVMs) were first introduced by Vladimir Vapnik [55] and are based on the structural risk minimization (SRM) principle from statistical learning theory. The SVM attempts to minimize a bound on the generalization error (error made on test data). SVM-based techniques focus on “borderline” training examples (or support vectors) that are most difficult to classify. The SVM projects the input training data Gφ(xi), for , onto a higher-dimensional space using the linear kernel defined in Equation 13 as
| (13) |
where b is the bias estimated on the training set . The general form of the SVM is given by
| (14) |
where xβ, for β ∈ {1, 2, …, ns} denotes the number of support vectors and the model parameter ξ is obtained by maximizing the following objective function.
| (15) |
subject to the constraint and 0 ≤ ξβ ≤ ω, where β, γ ∈ {1, 2, …, ns}, and where the parameter ω controls the trade-off between the empirical risk (training errors) and model complexity.
Additionally, a one-against-all SVM scheme was implemented for the multi-class case [14]. For this scheme, a binary classifier is built for each class to separate one class from all the other classes. Again, 1/3 of the samples from each class are randomly selected for training set and the predictions are made on the remaining 2/3 of the samples in . Each of the 5 binary classifiers make a prediction as to whether each xa ∈ Dj belongs to the target class. In the ideal case, only the binary classifier trained to identify Y (xa) as the target class should output a value of 1 and the other 4 classifiers would output 0. If so, xa is said to have been correctly classified. If not, xa is randomly assigned one of the 5 class labels. If the randomly assigned class label is not its true class label, xa is said to have been mis-classified. Otherwise, it is determined to have been correctly classified.
ii. C4.5 Decision Trees (C4.5)
A special type of classifier is the decision tree, which is trained using an iterative selection of individual features fu(xa) that are the most salient at the each node in the tree [56]. One of the most commonly used algorithms for generating decision trees is the C4.5 rules proposed by Quinlan [56]. The rules generated by this approach are in conjunctive form such as “if A and B then C” where both A and B are the rule antecedents, while C is the rule consequence. Every path from the root to the leaf is converted to an initial rule by regarding all the conditions appearing in the path as the conjunctive rule antecedents while regarding the class label Y (xa) xa ∈ D, held by the leaf as a rule consequence. Tree pruning is then done by using a greedy elimination rule which removes antecedents that are not sufficiently discriminatory. The rule set is then further refined by the way of the minimum description length (MDL) principle [57] to remove those rules that do not contribute to the accuracy of the tree. Hence for each φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM}, we obtain a separate decision tree classifier to classify every xi ∈ D as {+1, −1}. The C4.5 decision trees is extended for the multi-class case by simplying adding more output labels. Classifier evaluation is also similarly performed on Dj, j ∈ {1, 2, …, 11} following feature pruning.
b) Dimensionality Reduction Comparison via Cluster Validity Measures
The low-dimensional embeddings Gφ (xi), obtained for each φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM}, are also compared in terms of the 5 cluster validity measures. Prior to this however, the embedding coordinates Gφ (xi) for xi ∈ D need to be normalized within a unit hypercube ℋ in order to facilitate a quantitative comparison across the 6 DR schemes. The eigenvector , for each xi ∈ D and ν ∈ {1, 2, …, m}, is thus scaled between [0, 1] along each of m-dimensions via the formulation given by Equation 16.
| (16) |
where is the normalized embedding coordinate of xi along the νth dimension, where ν ∈ {1, 2, …, m}. For all xa ∈ Dj, such that Y (xa) = +1, the cluster center of the +1 class, G̃φ,+, is obtained by averaging the embedding coordinate locations along each dimension ν ∈ {1, 2, …, m} and for each φ. Formally, where n+ is the number of objects in the +1 class,
| (17) |
Thus the normalized cluster center for the +1 class is obtained as . Similarly we obtain the cluster center G̃φ,− for the −1 class. Having obtained G̃φ,+ and G̃φ,−we define 5 cluster validity measures as follows.
i) Inter-Centroid Distance (ICD)
is defined as the Euclidean distance between centroids G̃φ,+ and G̃φ,− [58]. is calculated for each Dj, j ∈ {1, 2, …, 10}, and for all φ.
ii) Cluster Tightness (CT)
To evaluate the tightness and distinctness of object clusters in the embedding space, we define and evaluate 4 cluster tightness measures: . is defined as the mean Euclidean distance of all objects xa ∈ Dj, Y (xa) = +1, from G̃φ,+. Formally, this is expressed as
| (18) |
We also similarly compute as the standard deviation of the Euclidean distances of all xa ∈ D from their corresponding cluster centroid G̃φ,+ [59]. Similarly, and are also defined for the −1 class. The calculation of the above cluster measures and normalization of the embedding coordinate system is repeated for all Dj, j ∈ {1, 2, …, 11} following feature pruning.
Following computation of the 7 quantitative performance measures (2 classifier, 5 cluster), a paired student t-test comparison is performed between the values for for each of the following 9 pairs of linear and nonlinear methods (PCA/ISO, LDA/ISO, MDS/ISO, PCA/LLE, LDA/LLE, MDS/LLE, PCA/LEM, LDA/LEM, MDS/LEM) across all datasets Dj, j ∈ {1,2,…,10}, under the null hypothesis that there is no difference in the 7 performance measures between each of the 9 pairs of linear/nonlinear DR methods. Thus, if p ≤ 0.05 for a pair of linear/nonlinear methods for a particular performance measure, the difference is assumed to be statistically significant. A similar t-test comparison is also performed using the embedding data obtained following feature pruning with the aim of showing similar trends across the 6 different DR methods applied to both the unpruned and the feature pruned datasets.
IV. RESULTS AND DISCUSSION
A. Qualitative Results
1) Class Separability in Embedding Space
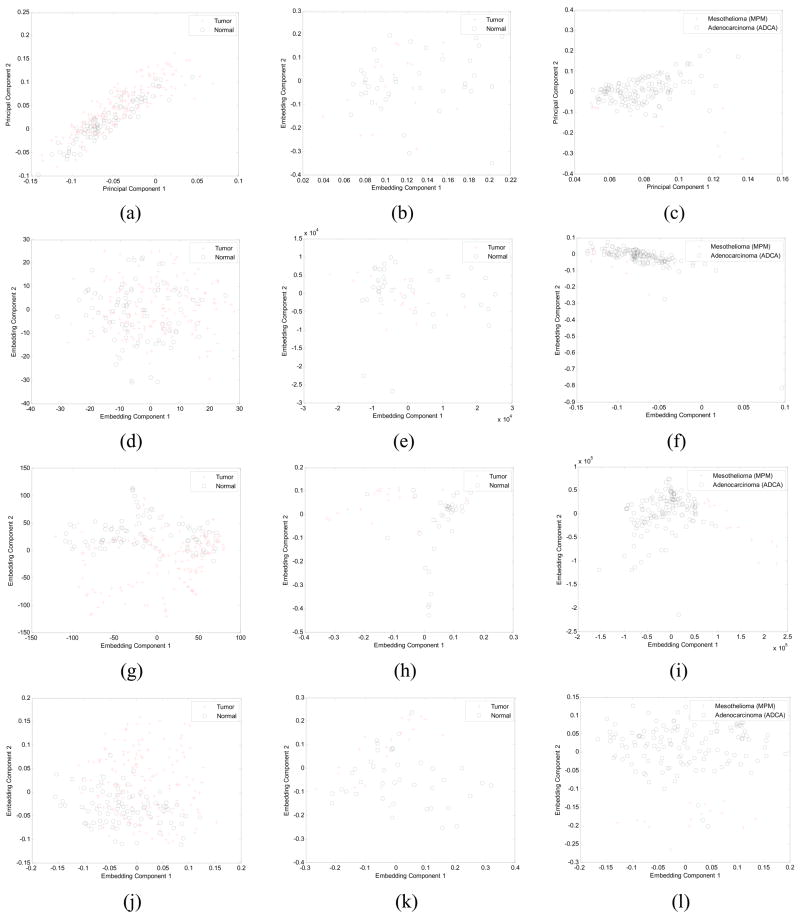
In Figure 3 are shown the 2 dimensional embedding plots of 6 different linear and nonlinear DR methods for 1 proteomic spectra (ovarian cancer [19]), and 2 gene expression (colon [16] and lung cancer [54]) datasets. Each of the plots in Figures 3(a)-(l) were generated by plotting the first dominant eigenvector versus the second dominant eigenvector of , for all xi ∈ Dj, and for a given DR method φ. The two object classes (+1) and (−1) are denoted with different symbols. Figures 3(a), (d) correspond to the embeddings generated by two of the linear DR methods (PCA, MDS) while Figures 3(g), (j) show the corresponding plots obtained from 2 of the nonlinear DR methods (ISO, LLE) on the ovarian cancer study. Note that in the embedding obtained with both Isomap and LLE (Figures 3(g), (j)), the 2 classes are clearly distinguishable while the corresponding embeddings obtained with PCA and MDS (Figures 3(a), (d)) reveal a significant degree of overlap between the +1 and −1 classes. A similar trend is seen with PCA and LDA (Figures 3(b), (e)) and LLE and LEM (Figures 3(h), (k)) on the colon cancer dataset [16]. Note that in spite of the presence of a couple of apparent outliers in the embeddings obtained by LLE and LEM, the nonlinear DR methods appear to perform much better compared to PCA and MDS (Figures 3(b), (e)). The difference is even more stark in the embeddings obtained with PCA (Figure 3(c)) and LDA (Figure 3(f)) compared to Isomap (Figure 3(i)) and LEM (Figure 3(l)) on the lung cancer [54] dataset in the right-most column.
Fig. 3.
Embedding plots were obtained by plotting dominant eigenvectors and against each other for ovarian cancer [19] ((a), (d), (g), (j)), colon cancer [16] ((b), (e), (h), (k)), and lung cancer [54] ((c), (f), (i), (l)) datasets for 6 different linear and nonlinear DR methods. Embedding plots for φ = (a) PCA (d) MDS, (g) ISO, and (j) LLE for the ovarian cancer dataset [19] are shown in the left column while in the middle column are shown embedding plots for colon cancer [16] obtained via φ = (b) LDA, (e) MDS, (h) LLE, and (k) LEM. Embedding plots for the lung cancer dataset [54] for φ = (c) PCA, (f) LDA, (i) ISO, and (l) LEM are shown in the right-most column.
2) Novel Class Detection in Embedding Space
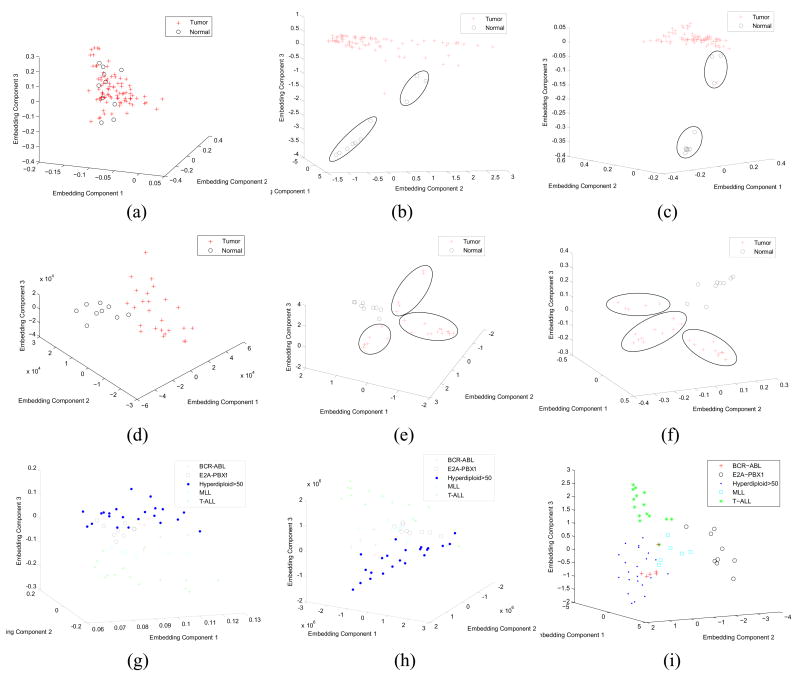
Figure 4 illustrates qualitatively the differences between the linear and nonlinear DR methods in capturing the true underlying low-dimensional structure of the data and highlights differences between the two types of methods in terms of their ability to identify subclasses in the data. In Figures 4(a)-(c) are shown the embedding plots obtained via LDA, LLE, and (c) LEM respectively for the lung cancer-Michigan dataset [26]. For LDA (Figure 4(a)), no meaningful clustering of samples was observable, while for both LLE and LEM, 2 distinct clusters of normal classes (denoted via superimposed ellipses) were identifiable. In Figure 4, sub-clusters (denoted in superimposed ellipses) in the prostate cancer dataset [17] for both LLE and LEM (Figures 4(e), (f)) were discernable but were occult in MDS (Figure 4(d)). Note the ellipses in Figures 4(b), (c), (e), and (f) are manually placed on the plots to highlight what appear to be possible new classes. Since 10 of the studies considered in this work were labeled as binary-class datasets, we were unable to evaluate the validity of newly detected subclasses. Note however that the 2 nonlinear methods for both the lung cancer [54] and leukemia datasets [1], [32] identify near identical sub-clusters, lending further credibility to the fact that the sub-clusters identified are genuine subclasses. To further test the ability of nonlinear DR schemes for novel class detection, a multi-class dataset comprising 5 known subtypes of acute lymphoblastic leukemia [32] was considered. As shown in Figure 4(g), PCA is unable to unravel the classes as discriminatingly as Isomap (Figure 4(h)) or LLE (Figure 4(i)). The 5 subclasses shown in Figures 4(g), (h), (i) are represented with different symbols.
Fig. 4.
Embedding graphs obtained by plotting the 3 most dominant embedding vectors and for xi ∈ Dj, for φ = (a) LDA, (b) LLE, and (c) LEM respectively on the lung cancer-Michigan dataset [26] in the top row. In the middle row the embedding results obtained on the prostate cancer study [17] for φ = (d) MDS, (e) LLE, and (f) LEM respectively. Finally the embedding plots obtained via (g) PCA, (h) ISO, and (i) LLE for the multi-class acute lymphoblastic leukemia dataset [32] are shown in the bottom row. Note that the ellipses in Figures 4(b), (c), (e), and (f) have been manually placed to highlight what appear to be potentially new classes.
B. Quantitative Results
1) Classifier Accuracy
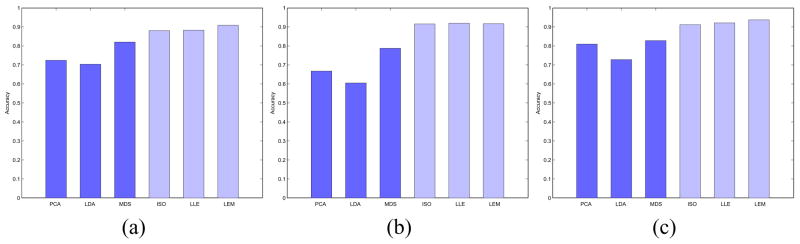
For each of the 10 binary- and 1 multi-class dataset, classifier accuracy ( , ) was assessed on the embeddings obtained via the 6 DR schemes on both unpruned (Figures 5(a), (b)) and feature pruned datasets (Figure 5(c)). It can be seen from Figure 5 that on the average, nonlinear DR methods (ISO, LLE, and LEM) perform better than their linear counterparts (PCA, LDA, and MDS) for both classifiers. In Tables III and IV are listed the accuracy results for the SVM and C4.5 classifiers respectively over the 10 binary-class datasets. Classifier accuracy comparing the performance of the 6 DR schemes via a SVM and C4.5 classifier on a multi-class dataset (Acute Lymphoblastic Leukemia [32]) are given in Table V. The results in Tables III-V clearly suggest that for both the binary- and multi-class case, the performance of the nonlinear DR schemes is superior compared to the linear DR schemes.
Fig. 5.
Average (a) and (b) for φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM}, for 10 binary-class datasets, before feature pruning. Additionally, average (c) is given for all φ, for 10 binary-class datasets, following feature pruning.
TABLE III.
Accuracy of for each of 10 binary-class datasets following DR for φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} without feature pruning.
| Dataset | Linear | Nonlinear | ||||
|---|---|---|---|---|---|---|
| PCA | LDA | MDS | ISO | LLE | LEM | |
| (1) ALL-AML Leukemia | 66.7 | 58.3 | 91.7 | 91.7 | 91.7 | 96.0 |
| (2) Breast Tumor | 66.7 | 66.7 | 71.4 | 81.0 | 76.2 | 89.2 |
| (3) Colon Cancer | 65.4 | 75.0 | 78.8 | 100.0 | 100.0 | 96.0 |
| (4) DLBCL-Harvard | 64.3 | 64.3 | 64.3 | 81.0 | 81.0 | 81.0 |
| (5) Glioma | 70.7 | 69.0 | 72.4 | 79.3 | 82.8 | 89.2 |
| (6) Lung Cancer | 92.0 | 91.0 | 91.0 | 96.0 | 94.0 | 97.0 |
| (7) Lung Cancer-Michigan | 89.2 | 89.2 | 98.5 | 98.5 | 100.0 | 100.0 |
| (8) Ovarian Cancer | 63.9 | 63.9 | 63.9 | 64.5 | 68.6 | 65.7 |
| (9) Prostate Cancer | 87.0 | 73.9 | 95.7 | 95.7 | 95.7 | 100.0 |
| (10) Types of DLBCL | 59.4 | 53.1 | 93.8 | 94.0 | 94.0 | 96.0 |
TABLE IV.
Accuracy of for each of 10 binary-class datasets following DR for φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} without feature pruning.
| Dataset | Linear | Nonlinear | ||||
|---|---|---|---|---|---|---|
| PCA | LDA | MDS | ISO | LLE | LEM | |
| (1) ALL-AML Leukemia | 70.8 | 41.7 | 87.5 | 96.0 | 96.0 | 96.0 |
| (2) Breast Tumor | 61.9 | 61.9 | 76.2 | 95.0 | 95.0 | 95.0 |
| (3) Colon Cancer | 65.4 | 42.3 | 71.2 | 95.0 | 95.0 | 95.0 |
| (4) DLBCL-Harvard | 52.4 | 61.9 | 64.3 | 87.0 | 81.0 | 83.3 |
| (5) Glioma | 60.3 | 60.3 | 69.0 | 95.0 | 95.0 | 95.0 |
| (6) Lung Cancer | 88.0 | 86.0 | 90.0 | 97.0 | 99.0 | 98.0 |
| (7) Lung Cancer-Michigan | 84.6 | 84.6 | 96.9 | 100.0 | 100.0 | 100.0 |
| (8) Ovarian Cancer | 56.8 | 59.8 | 46.2 | 56.8 | 65.1 | 60.9 |
| (9) Prostate Cancer | 100.0 | 47.8 | 100.0 | 100.0 | 100.0 | 100.0 |
| (10) Types of DLBCL | 28.1 | 59.4 | 87.5 | 95.0 | 95.0 | 95.0 |
TABLE V.
Accuracy of and in Distinguishing Subtypes of Acute Lymphoblastic Leukemia Dataset Following DR for φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} without feature pruning.
| Classifier | Linear | Nonlinear | ||||
|---|---|---|---|---|---|---|
| PCA | LDA | MDS | ISO | LLE | LEM | |
| SVM | 79.5 | 2.56 | 53.9 | 82.1 | 87.2 | 64.1 |
| C4.5 | 59.0 | 18.0 | 72.0 | 77.0 | 85.0 | 74.4 |
2) Cluster Metrics
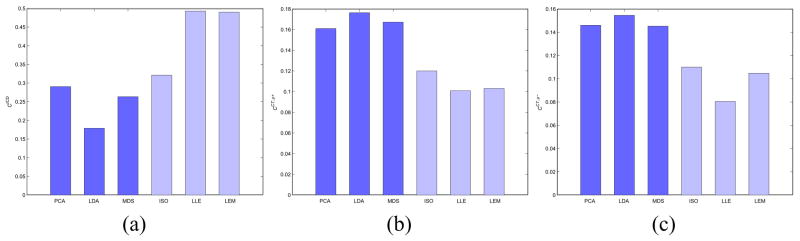
In Figure 6 and Tables VI–VIII are shown the results for the cluster validity measures for all φ. Figures 6(a), (b), and (c) correspond to average respectively across the 10 binary-class datasets after feature pruning. Tables VI–VIII show the average values for φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} over the 10 binary-class studies considered in this work without feature pruning. From Figure 6(a) and Table VI, we observe that the inter-centroid distance between the dominant clusters is on average greater for the nonlinear DR methods compared to the linear methods, in turn suggesting greater separation between the 2 classes. Similarly from Figures 6(b) and (c), we observe that the average values over all the 10 binary-class datasets are smaller for the nonlinear DR methods compared to the linear methods, suggesting the objects classes form more compact, tighter clusters in the embedding spaces generated via nonlinear DR schemes.
Fig. 6.
Average (a) , (b) values, and (c) values over 10 binary-class datasets for each φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} after feature pruning.
TABLE VI.
Values of for each of 10 binary-class datasets following DR for φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} without feature pruning.
| Dataset | Linear | Nonlinear | ||||
|---|---|---|---|---|---|---|
| PCA | LDA | MDS | ISO | LLE | LEM | |
| (1) ALL-AML Leukemia | 0.221 | 0.036 | 0.287 | 0.317 | 0.375 | 0.190 |
| (2) Breast Tumor | 0.143 | 0.149 | 0.213 | 0.236 | 0.241 | 0.243 |
| (3) Colon Cancer | 0.124 | 0.102 | 0.175 | 0.204 | 0.304 | 0.282 |
| (4) DLBCL-Harvard | 0.092 | 0.086 | 0.085 | 0.221 | 0.274 | 0.289 |
| (5) Glioma | 0.160 | 0.171 | 0.166 | 0.210 | 0.237 | 0.228 |
| (6) Lung Cancer | 0.170 | 0.057 | 0.235 | 0.282 | 0.332 | 0.352 |
| (7) Lung Cancer-Michigan | 0.058 | 0.070 | 0.371 | 0.371 | 0.795 | 0.623 |
| (8) Ovarian Cancer | 0.102 | 0.150 | 0.074 | 0.156 | 0.164 | 0.107 |
| (9) Prostate Cancer | 0.353 | 0.155 | 0.309 | 0.376 | 0.520 | 0.506 |
| (10) Types of DLBCL | 0.070 | 0.127 | 0.229 | 0.303 | 0.267 | 0.238 |
TABLE VIII.
Values of for each of 10 binary-class datasets following DR for φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} without feature pruning.
| Dataset | Linear | Nonlinear | ||||
|---|---|---|---|---|---|---|
| PCA | LDA | MDS | ISO | LLE | LEM | |
| (1) ALL-AML Leukemia | 0.099 | 0.131 | 0.090 | 0.071 | 0.085 | 0.073 |
| (2) Breast Tumor | 0.121 | 0.163 | 0.094 | 0.001 | 0.103 | 0.074 |
| (3) Colon Cancer | 0.096 | 0.115 | 0.105 | 0.074 | 0.101 | 0.080 |
| (4) DLBCL-Harvard | 0.082 | 0.098 | 0.081 | 0.001 | 0.069 | 0.067 |
| (5) Glioma | 0.104 | 0.115 | 0.094 | 0.090 | 0.075 | 0.048 |
| (6) Lung Cancer | 0.114 | 0.051 | 0.104 | 0.074 | 0.019 | 0.049 |
| (7) Lung Cancer-Michigan | 0.103 | 0.115 | 0.077 | 0.073 | 0.053 | 0.044 |
| (8) Ovarian Cancer | 0.101 | 0.079 | 0.086 | 0.077 | 0.073 | 0.057 |
| (9) Prostate Cancer | 0.090 | 0.151 | 0.100 | 0.092 | 0.071 | 0.059 |
| (10) Types of DLBCL | 0.126 | 0.107 | 0.103 | 0.076 | 0.106 | 0.070 |
In Table IX, p-values for the paired student t-tests obtained by comparing across the 10 binary-class datasets for each pair of linear and nonlinear DR methods (PCA/ISO, LDA/ISO, MDS/ISO, PCA/LLE, LDA/LLE, MDS/LLE, PCA/LEM, LDA/LEM, and MDS/LEM). Statistically significant differences were observed for all the performance measures considered for each pair of linear/nonlinear DR methods across all 10 binary-class datasets. Similar trends were observed for embeddings obtained from linear and nonlinear DR schemes following feature pruning. (Table X).
TABLE IX.
p-values obtained by a paired student t-test of across 10 datasets, comparing 9 pairs of linear/nonlinear DR methods without feature pruning.
| ISO/PCA | ISO/LDA | ISO/MDS | LLE/PCA | LLE/LDA | LLE/MDS | LEM/PCA | LEM/LDA | LEM/MDS | |
|---|---|---|---|---|---|---|---|---|---|
| 0.008 | 0.004 | 0.294 | 0.006 | 0.003 | 0.264 | 0.002 | 0.001 | 0.119 | |
| 0.004 | 1.0×10−4 | 0.069 | 0.003 | 4.6×10−5 | 0.049 | 0.004 | 7.0×10−5 | 0.059 | |
| 0.004 | 2.2×10−5 | 0.178 | 0.006 | 0.001 | 0.050 | 0.012 | 0.001 | 0.126 | |
| 0.006 | 0.003 | 0.006 | 0.003 | 0.001 | 0.003 | 0.001 | 4.6×10−4 | 0.001 | |
| 0.003 | 0.015 | 0.003 | 0.035 | 0.140 | 0.033 | 1.7×10−4 | 0.002 | 2.1×10−4 |
TABLE X.
p-values obtained by a paired student t-test of across 10 datasets, comparing 9 pairs of linear/nonlinear DR methods following feature pruning.
| ISO/PCA | ISO/LDA | ISO/MDS | LLE/PCA | LLE/LDA | LLE/MDS | LEM/PCA | LEM/LDA | LEM/MDS | |
|---|---|---|---|---|---|---|---|---|---|
| 0.041 | 0.001 | 0.100 | 0.019 | 3.9×10−4 | 0.056 | 0.010 | 2.1×10−4 | 0.029 | |
| 0.089 | 0.003 | 0.053 | 0.060 | 0.001 | 0.037 | 0.067 | 0.002 | 0.041 | |
| 0.488 | 0.001 | 0.213 | 0.005 | 5.3×10−4 | 0.002 | 0.009 | 1.4×10−4 | 0.004 | |
| 0.063 | 0.015 | 0.046 | 0.006 | 0.001 | 0.005 | 0.001 | 1.5×10−4 | 0.001 | |
| 0.045 | 0.017 | 0.046 | 0.067 | 0.035 | 0.069 | 0.008 | 0.002 | 0.009 |
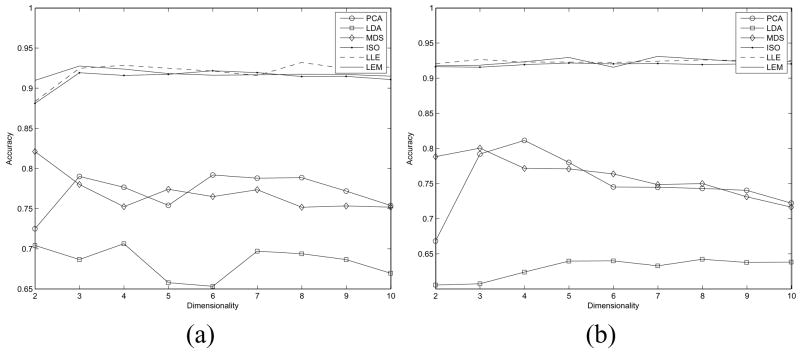
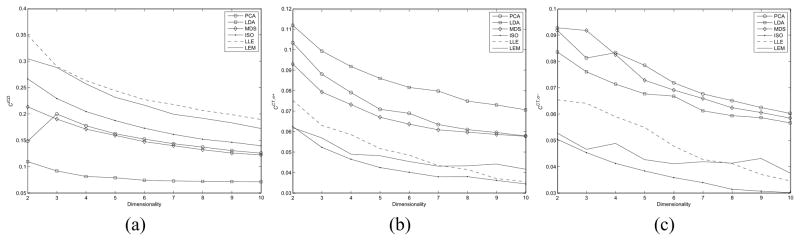
Additionally, we investigated the performance of each of the DR methods across the 10 binary-class studies as a function of the number of dimensions of the embedding space Gφ from a classification perspective. Figures 7(a), (b) show the average classification accuracy ( and ) respectively for each DR method, where the number of dimensions is being varied from 2 to 10 (υ ∈ {2, 3, …, 10}). Similarly, Figures 8(a), (b), and (c) show the cluster validity measures ( , and ) respectively for each DR method, where the number of dimensions is also being varied from 2 to 10 (υ ∈ {2, 3, …, 10}). For both the classifier and cluster validity measures, one can see similar trends across dimensions showing nonlinear DR methods outperforming linear methods (Figures 7, 8), thereby comprehensively demonstrating that the nonlinear DR schemes outperform the linear DR methods independent of the number of embedding dimensions considered.
Fig. 7.
Average classification accuracy for (a) and (b) over 10 binary-class datasets for φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} for υ ∈ {2, 3, …, 10}.
Fig. 8.
Average (a) (b) values, and (c) values over all 10 binary-class datasets for each φ, ∈ {PCA, LDA, MDS, ISO, LLE, LEM) for υ ∈ {2, 3, …, 10}.
V. Concluding Remarks
The primary objective of this paper was to identify appropriate dimensionality reduction methods to precede analysis and classification of high-dimensional gene- and protein-expression studies. This is especially important in applications where the goal is to identify two or more specific classes within the datasets. In this paper, we quantitatively compared the performance of 6 different DR methods, three linear (PCA, LDA, MDS) and three nonlinear (Isomap, LLE, Laplacian Eigenmaps) from the perspective of (a) distinguishing between cancer and non-cancer studies, and (b) identifying new object classes (cancer subtypes) from 10 binary high-dimensional gene- and protein-expression datasets for prostate, lung, breast, and ovarian cancers, as well as for leukemia, lymphomas, and gliomas. Additionally, a multi-class dataset comprising 5 distinct subtypes of lymphoblastic leukemia was also considered. The efficacy of the low-dimensional representations of the high-dimensional data obtained by the different DR methods was evaluated via 2 classifier schemes (SVM and C4.5) and 5 different cluster validity measures. The intuition behind the use of these evaluation measures was that if the low-dimensional embedding was indeed a faithful representation of the high-dimensional feature space, the 2 different data classes would be separable into distinct, tightly packed clusters. Embeddings were generated by the 6 different DR methods from the original high-dimensional data before and after feature pruning. Feature pruning was applied to identify only the top 10 percentile of most informative features in each dataset in order to reduce any possible nonlinearity in the data on account of redundant or uncorrelated features. The 3 different linear and 3 nonlinear methods were also compared pairwise via a paired student t-test in terms of the 7 performance measures and across all 10 datasets. In addition, 6 different DR methods were also qualitatively compared in terms of the ability of their respective embeddings to reveal the presence of new subclasses within the data. Our primary conclusions from this work are as follows,
The nonlinear methods significantly outperformed the linear methods over all the datasets in terms of all 7 performance measures, suggesting in turn the nonlinear underlying manifold structure of high-dimensional biomedical studies.
The differences between the linear and nonlinear methods were found to be statistically significant even after pruning the datasets by feature selection and were independent of the number of dimensions of the embedding space that were considered.
The nonlinear methods also appeared to be able to identify potential subclasses within the data better compared to the linear methods. The linear methods for the most part were unable to even discriminate between the 2 most dominant classes in each dataset.
In making our conclusions, we also acknowledge the following limitations of this study: 1) Our results are based on a relatively small database comprising 10 binary- and 1 multi-class gene- and protein-expression datasets. 2) Not all linear and nonlinear DR methods were considered in this study. 3) The performance of nonlinear methods are dependent on the size of the local neighborhood parameter κ within which data linearity is assumed.
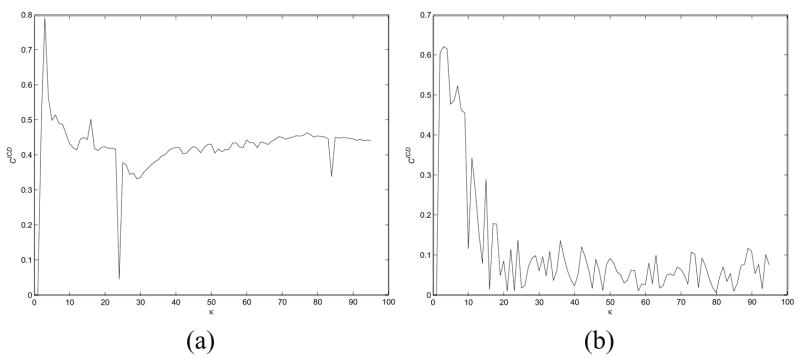
As the value of κ increases, the locally linear assumption is no longer valid and the nonlinear DR methods begin to resemble linear methods. The dependency of the nonlinear methods on the value of κ is reflected in the plots in Figure 9. For both φ = (a) LLE and (b) LEM, the corresponding cluster measures begin to decrease with increasing values of κ, suggesting the degeneracy of the non-linear schemes.
Fig. 9.
The degree to which nonlinearity in the data can be accurately approximated is dependent on the size of the local neighborhood κ within which linearity is assumed. As κ increases, the locally linear assumption is no longer valid. Figures 9(a) and (b) show and respectively plotted against increasing values of κ for the Lung Cancer-Michigan dataset. As κ increases, and both decrease, suggesting that the nonlinear DR schemes are effectively becoming linear.
In Table XI are listed the best and worst DR schemes based on each of the 7 performance criterion considered in this study. As can be surmised from Table XI, the nonlinear DR scheme LLE was the best dimensionality reduction method overall and the linear scheme LDA performed the worst.
TABLE XI.
Summary of the best and worst DR methods in terms of each of 7 performance measures.
| Best | Worst | |
|---|---|---|
| LEM | LDA | |
| LLE | LDA | |
| LLE | LDA | |
| LEM | LDA | |
| LLE | PCA | |
| LLE | LDA | |
| LEM | LDA |
Our results appear to suggest that if the objective is to distinguish multiple classes or identify sub-clusters within high-dimensional biomedical data, nonlinear dimensionality reduction methods such as LLE, Isomap, and Laplacian Eigenmaps may be a better choice compared to linear dimensionality reduction methods such as PCA. Preliminary results in an application involving prostate magnetic resonance spectroscopy [46] appear to confirm the conclusions presented in this work.
TABLE VII.
Values of for each of 10 binary-class datasets following DR for φ ∈ {PCA, LDA, MDS, ISO, LLE, LEM} without feature pruning.
| Dataset | Linear | Nonlinear | ||||
|---|---|---|---|---|---|---|
| PCA | LDA | MDS | ISO | LLE | LEM | |
| (1) ALL-AML Leukemia | 0.228 | 0.181 | 0.216 | 0.182 | 0.115 | 0.150 |
| (2) Breast Tumor | 0.187 | 0.107 | 0.193 | 0.001 | 0.195 | 0.138 |
| (3) Colon Cancer | 0.109 | 0.107 | 0.107 | 0.070 | 0.012 | 0.098 |
| (4) DLBCL-Harvard | 0.195 | 0.221 | 0.198 | 0.001 | 0.117 | 0.136 |
| (5) Glioma | 0.210 | 0.168 | 0.186 | 0.157 | 0.181 | 0.142 |
| (6) Lung Cancer | 0.117 | 0.080 | 0.095 | 0.081 | 0.057 | 0.107 |
| (7) Lung Cancer-Michigan | 0.155 | 0.111 | 0.139 | 0.057 | 0.131 | 0.081 |
| (8) Ovarian Cancer | 0.141 | 0.125 | 0.177 | 0.164 | 0.052 | 0.063 |
| (9) Prostate Cancer | 0.110 | 0.107 | 0.099 | 0.073 | 0.077 | 0.094 |
| (10) Types of DLBCL | 0.229 | 0.166 | 0.182 | 0.145 | 0.099 | 0.123 |
Acknowledgments
This work was supported by grants from the Coulter foundation, Busch Biomedical Award, Cancer Institute of New Jersey, New Jersey Commission on Cancer Research, Aresty Foundation, and the National Cancer Institute (R21CA127186-01, R03CA128081-01). We also thank Dr. Jianbo Shi and Dr. James Monaco for their advice and comments.
References
- 1.Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, Bloomeld CD, Lander ES. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286(531):531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
- 2.Peng Yonghong. A novel ensemble machine learning for robust microarray data classification. Computers in Biology and Medicine. 2006;36(6):553–573. doi: 10.1016/j.compbiomed.2005.04.001. [DOI] [PubMed] [Google Scholar]
- 3.Shi Chao, Chen Lihui. Feature dimension reduction for microarray data analysis using locally linear embedding. APBC. 2005:211–217. [Google Scholar]
- 4.Der SD, Zhou A, Williams BR, Silverman RH. Identification of genes differentially regulated by interferon alpha, beta, or gamma using oligonucleotide arrays. Proc Natl Acad Sci U S A. 1998 Dec;95(26):15623–15628. doi: 10.1073/pnas.95.26.15623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Maglietta Rosalia, D’Addabbo Annarita, Piepoli Ada, Perri Francesco, Sabino Liuni, Pesole Graziano, Ancona Nicola. Selection of relevant genes in cancer diagnosis based on their prediction accuracy. Artif Intell Med. 2007 May;40(1):29–44. doi: 10.1016/j.artmed.2006.06.002. [DOI] [PubMed] [Google Scholar]
- 6.Huang Te Ming, Kecman Vojislav. Gene extraction for cancer diagnosis by support vector machines–an improvement. Artif Intell Med. 2005;35(1–2):185–194. doi: 10.1016/j.artmed.2005.01.006. [DOI] [PubMed] [Google Scholar]
- 7.Turashvili Gulisa, Bouchal Jan, Baumforth Karl, Wei Wenbin, Dziechciarkova Marta, Ehrmann Jiri, Klein Jiri, Fridman Eduard, Skarda Jozef, Srovnal Josef, Hajduch Marian, Murray Paul, Kolar Zdenek. Novel markers for differentiation of lobular and ductal invasive breast carcinomas by laser microdissection and microarray analysis. BMC Cancer. 2007;7(55) doi: 10.1186/1471-2407-7-55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Alizadeh Ash A, Eisen Michael B, Davis R Eric, Ma Chi, Lossos Izidore S, Rosenwald Andeas, Boldrick Jennifer C, Sabet Hajeer, Tran Truc, Yu Xin, Powell John I, Yang Liming, Marti Gerald E, Moore Troy, Hudson James, Lu Lisheng, Lewis David B, Tibshirani Robert, Sherlock Gavin, Chan Wing C, Greiner Timothy C, Weisenburger Dennis D, Armitage James O, Warnke Roger, Levy Ronald, Wilson Wyndham, Grever Michael R, Byrd John C, Botstein David, Brown Patrick O, Staudt Louis M. Distinct types of diffuse large b-cell lymphoma identified by gene expression profiling. Nature. 2000;403(6769):503–511. doi: 10.1038/35000501. [DOI] [PubMed] [Google Scholar]
- 9.Ben-Dor A, Bruhn L, Friedman N, Nachman I, Schummer M, Yakhini Z. Tissue classification with gene expression profiles. J Comput Biol. 2000;7(3–4):559–583. doi: 10.1089/106652700750050943. [DOI] [PubMed] [Google Scholar]
- 10.Brown MP, Grundy WN, Lin D, Cristianini N, Sugnet CW, Furey TS, Ares M, Haussler D. Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc Natl Acad Sci U S A. 2000 Jan;97(1):262–267. doi: 10.1073/pnas.97.1.262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tan Aik Choon, Gilbert David. Ensemble machine learning on gene expression data for cancer classification. Applied Bioinformatics. 2003;2(3 Suppl):S75–83. [PubMed] [Google Scholar]
- 12.Song Le, Bedo Justin, Borgwardt Karsten M, Gretton Arthur, Smola Alex. Gene selection via the bahsic family of algorithms. Bioinformatics. 2007;23:490–498. doi: 10.1093/bioinformatics/btm216. [DOI] [PubMed] [Google Scholar]
- 13.Li Li, Jiang Wei, Li Xia, Moser Kathy L, Guo Zheng, Du Lei, Wang Qiuju, Topol Eric J, Wang Qing, Rao Shaoqi. A robust hybrid between genetic algorithm and support vector machine for extracting an optimal feature gene subset. Genomics. 1995;85:16–23. doi: 10.1016/j.ygeno.2004.09.007. [DOI] [PubMed] [Google Scholar]
- 14.Li Tao, Zhang Chengliang, Ogihara Mitsunori. A comparative study of feature selection and multiclass classification methods for tissue classification based on gene expression. Bioinformatics. 2004 Oct;20(15):2429–2437. doi: 10.1093/bioinformatics/bth267. [DOI] [PubMed] [Google Scholar]
- 15.Liu Huiqing, Li Jinyan, Wong Limsoon. A comparative study on feature selection and classification methods using gene expression profiles and proteomic patterns. Genome Inform. 2002;13:51–60. [PubMed] [Google Scholar]
- 16.Alon U, Barkai N, Notterman DA, Gish K, Ybarra S, Mack D, Levine AJ. Broad patterns of gene expression revealed by clustering of tumor and normal colon tissues probed by oligonucleotide arrays. Proc Natl Acad Sci. 1999;96(12):6745–6750. doi: 10.1073/pnas.96.12.6745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Singh Dinesh, Febbo Phillip G, Ross Kenneth, Jackson Donald G, Manola Judith, Ladd Christine, Tamayo Pablo, Renshaw Andrew A, D’Amico Anthony V, Richie Jerome P, Lander Eric S, Loda Massimo, Kantoff Philip W, Golub Todd R, Sellers William R. Gene expression correlates of clinical prostate cancer behavior. Cancer Cell. 2002;1(2):203–209. doi: 10.1016/s1535-6108(02)00030-2. [DOI] [PubMed] [Google Scholar]
- 18.Park Mira, Lee Jae Won, Lee Jung Bok, Song Sueuck Heun. Several biplot methods applied to gene expression data. Journal of Statistical Planning and Inferenece. 2007;138:500–515. [Google Scholar]
- 19.Petricoin Emanuel F, Ardekani Ali M, Hitt Ben A, Levine Peter J, Fusaro Vincent A, Steinberg Seth M, Mills Gordon B, Simone Charles, Fishman David A, Kohn Elise C, Liotta Lance A. Use of proteomic patterns in serum to identify ovarian cancer. The Lancet. 2002;359(9306):572–577. doi: 10.1016/S0140-6736(02)07746-2. [DOI] [PubMed] [Google Scholar]
- 20.Tamayo P, Slonim D, Mesirov J, Zhu Q, Kitareewan S, Dmitrovsky E, Lander ES, Golub TR. Interpreting patterns of gene expression with self-organizing maps: methods and application to hematopoietic differentiation. Proc Natl Acad Sci U S A. 1999 Mar;96(6):2907–2912. doi: 10.1073/pnas.96.6.2907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yang Sanghwa, Shin Jihye, Park Kyu Hyun, Jeung Hei-Cheul, Rha Sun Young, Noh Sung Hoon, Yang Woo Ick, Chung Hyun Cheol. Molecular basis of the differences between normal and tumor tissues of gastric cancer. Biochim Biophys Acta. 2007 doi: 10.1016/j.bbadis.2007.05.005. [DOI] [PubMed] [Google Scholar]
- 22.van ’tVeer1 Laura J, Dai Hongyue, van de Vijver Marc J, He Yudong D, Hart Augustinus AM, Mao Mao, Peterse Hans L, van der Kooy Karin, Marton Matthew J, Witteveen Anke T, Schreiber George J, Kerkhoven Ron M, Roberts Chris, Bernards Ren, Linsley Peter S, Friend Stephen H. Gene expression profiling predicts clinical outcome of breast cancer. Nature. 2002;415:430–536. doi: 10.1038/415530a. [DOI] [PubMed] [Google Scholar]
- 23.Pomeroy Scott L, Tamayo Pablo, Gaasenbeek Michelle, Sturla Lisa M, Angelo Michael, McLaughlin Margaret E, Kim John YH, Goumnerova Liliana C, Black Peter M, Lau Ching, Allen Jeffrey C, Zagzag David, Olson James M, Curran Tom, Wetmore Cynthia, Biegel Jaclyn A, Poggio Tomaso, Mukherjee Shayan, Rifkin Ryan, Califano Andrea, Stolovitzky Gustavo, Louis David N, Mesirov Jill P, Lander Eric S, Golub Todd R. Prediction of central nervous system embryonal tumour outcome based on gene expression. Nature. 2002;415:436–442. doi: 10.1038/415436a. [DOI] [PubMed] [Google Scholar]
- 24.Freije William A, Castro-Vargas F Edmundo, Fang Zixing, Horvath Steve, Cloughesy Timothy, Liau Linda M, Mischel Paul S, Nelson Stanley F. Gene expression profiling of gliomas strongly predicts survival. Cancer Research. 2004;64(18):6503–6510. doi: 10.1158/0008-5472.CAN-04-0452. [DOI] [PubMed] [Google Scholar]
- 25.Shipp Margaret A, Ross Ken N, Tamayo Pablo, Weng Andrew P, Kutok Jeffery L, Aguiar Ricardo CT, Gaasenbeek Michelle, Angelo Michael, Reich Michael, Pinkus Geraldine S, Ray Tane S, Koval1 Margaret A, Last Kim W, Norton Andrew, Lister T Andrew, Mesirov Jill, Neuberg Donna S, Lander Eric S, Aster Jon C, Golub Todd R. Diffuse large b-cell lymphoma outcome prediction by gene-expression profiling and supervised machine learning. Nature Medicine. 2002;8:68–74. doi: 10.1038/nm0102-68. [DOI] [PubMed] [Google Scholar]
- 26.Beer David G, Kardia Sharon LR, Huang Chiang-Ching, Giordano Thomas J, Levin Albert M, Misek David E, Lin Lin, Chen Guoan, Gharib Tarek G, Thomas Dafydd G, Lizyness Michelle L, Kuick Rork, Hayasaka Satoru, Taylor Jeremy MG, Iannettoni Mark D, Orringer Mark B, Hanash Samir. Gene-expression profiles predict survival of patients with lung adenocarcinoma. Nature Medicine. 2002;8:816–823. doi: 10.1038/nm733. [DOI] [PubMed] [Google Scholar]
- 27.Wigle Dennis A, Jurisica Igor, Radulovich Niki, Pintilie Melania, Rossant Janet, Liu Ni, Lu Chao, Woodgett James, Seiden Isolde, Johnston Michael, Keshavjee Shaf, Darling Gail, Winton Timothy, Breitkreutz Bobby-Joe, Jorgenson Paul, Tyers Mike, Shepherd Frances A, Tsao Ming Sound. Molecular profiling of non-small cell lung cancer and correlation with disease-free survival. Cancer Research. 2002;62:3005–3008. [PubMed] [Google Scholar]
- 28.Bellman RE. Adaptive Control Processes. Princeton University Press; 1961. [Google Scholar]
- 29.Ye Jieping, Li Tao, Xiong Tao, Janardan Ravi. Using uncorrelated discriminant analysis for tissue classification with gene expression data. IEEE/ACM Trans Comput Biology Bioinform. 2004;1(4):181–190. doi: 10.1109/TCBB.2004.45. [DOI] [PubMed] [Google Scholar]
- 30.Liu Zhenqiu, Chen Dechang, Bensmail Halima. Gene expression data classification with kernel principal component analysis. Journal of Biomedicine and Biotechnology. 2005;2:155–159. doi: 10.1155/JBB.2005.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Duda RO, Hart PE, Stork DG. Pattern Classification. 2. Wiley; 2000. [Google Scholar]
- 32.Yeoh Eng-Juh, Ross Mary E, Shurtleff Sheila A, Williams W Kent, Patel Divyen, Mahfouz Rami, Behm Fred G, Raimondi Susana C, Relling Mary V, Patel Anami, Cheng Cheng, Campana Dario, Wilkins Dawn, Zhou Xiaodong, Li Jinyan, Liu Huiqing, Pui Ching-Hon, Evans William E, Naeve Clayton, Wong Limsoon, Downing James R. Classification, subtype discovery, and prediction of outcome in pediatric acute lymphoblastic leukemia by gene expression profiling. Cancer Cell. 2002;1(2):133–143. doi: 10.1016/s1535-6108(02)00032-6. [DOI] [PubMed] [Google Scholar]
- 33.Dai Jian J, Lieu Linh, Rocke David. Dimension reduction for classification with gene expression microarray data. Statistical Applications in Genetics and Molecular Biology. 2006;5(1):1–15. doi: 10.2202/1544-6115.1147. [DOI] [PubMed] [Google Scholar]
- 34.Dawson Kevin, Rodriguez Raymond L, Malyj Wasyl. Sample phenotype clusters in high-density oligonucleotide microarray data sets are revealed using isomap, a nonlinear algorithm. BMC Bioinformatics. 2005;6:195. doi: 10.1186/1471-2105-6-195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Truntzer Caroline, Mercier Catherine, Estve Jacques, Gautier Christian, Roy Pascal. Importance of data structure in comparing two dimension reduction methods for classification of microarray gene expression data. BMC Bioinformatics. 8(90):2007. doi: 10.1186/1471-2105-8-90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Andersson Anna, Olofsson Tor, Lindgren David, Nilsson Bjorn, Ritz Cecilia, Eden Patrik, Lassen Carin, Rade Johan, Fontes Magnus, Morse Helena, Heldrup Jesper, Behrendtz Mikael, Mitelman Felix, Hoglund Mattias, Johansson Bertil, Fioretos Thoas. Molecular signatures in childhood acute leukemia and their correlations to expression patterns in normal hematopoietic subpopulations. PNAS. 2005;102(52):19069–19074. doi: 10.1073/pnas.0506637102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhu Yi, Wu Rong, Sangha Navneet, Yoo Chul, Cho Kathleen R, Shedden Kerby A, Katabuchi Hidetaka, Lubman David M. Classifications of ovarian cancer tissues by proteomic patterns. Proteomics. 2006;6:5846–5856. doi: 10.1002/pmic.200600165. [DOI] [PubMed] [Google Scholar]
- 38.Mendez Marco A, Hodar Christian, Vulpe Chris, Gonzalez Mauricio. Discriminant analysis to evaluate clustering of gene expression data. Federation of European Biochemical Societies. 2002;522:24–28. doi: 10.1016/s0014-5793(02)02873-9. [DOI] [PubMed] [Google Scholar]
- 39.Hotelling H. Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology. 1933;24:417–441. [Google Scholar]
- 40.Venna Jarkko, Kaski Samuel. Local multidimensional scaling. Neural Networks. 2006;19:889–899. doi: 10.1016/j.neunet.2006.05.014. [DOI] [PubMed] [Google Scholar]
- 41.Shi Jianbo, Malik Jitendra. Normalized cuts and image segmentation. IEEE Trans Pattern Analysis and Machine Intelligence. 2000;22(8):888–905. [Google Scholar]
- 42.Tenenbaum Joshua, de Silva Vin, Langford John C. A global geometric framework for nonlinear dimensionality reduction. Science. 2000;290(5500):2319–2322. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
- 43.Roweis Sam, Saul Lawrence. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290(5500):2323–2326. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- 44.Belkin Mikhail, Niyogi Partha. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Computation. 2003;15(6):1373–1396. [Google Scholar]
- 45.Madabhushi Anant, Shi Jianbo, Rosen Mark, Tomaszeweski John E, Feldman Michael D. Graph embedding to improve supervised classification and novel class detection: Application to prostate cancer. MICCAI. 2005:729–737. doi: 10.1007/11566465_90. [DOI] [PubMed] [Google Scholar]
- 46.Tiwari Pallavi, Madabhushi Anant, Rosen Mark. A hierarchical unsupervised spectral clustering scheme for detection of prostate cancer from magnetic resonance spectroscopy (mrs) MICCAI. 2007;2:278–286. doi: 10.1007/978-3-540-75759-7_34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Doyle S, Hwang M, Shah K, Madabhushi A, Feldman M, Tomaszeweski J. Automated grading of prostate cancer using architectural and textural image features. ISBI. 2007:1284–1287. [Google Scholar]
- 48.Doyle Scott, Hwang Mark, Naik Shivang, Feldman Michael, Tomaszeweski John, Madabhushi Anant. Using manifold learning for content-based image retrieval of prostate histopathology. MICCAI. 2007 [Google Scholar]
- 49.Weng S, Zhang C, Lin Z, Zhang X. Mining the structural knowledge of high-dimensional medical data using isomap. Med Biol Eng Comput. 2005;43:410–412. doi: 10.1007/BF02345820. [DOI] [PubMed] [Google Scholar]
- 50.Nilsson Jens, Fioretos Thoas, Hglund Mattias, Fontes Magnus. Approximate geodesic distances reveal biologically relevant structures in microarray data. Bioinformatics. 2004;20(6):874–880. doi: 10.1093/bioinformatics/btg496. [DOI] [PubMed] [Google Scholar]
- 51.Dietterich Thomas. Ensemble methods in machine learning. Workshop on Multiple Classifer Systems. 2000 [Google Scholar]
- 52.Madabhushi Anant, Shi Jianbo, Feldman Michael D, Rosen Mark, Tomaszewski John. Comparing ensembles of learners: Detecting prostate cancer from high resolution mri. CVAMIA. 2006:25–36. [Google Scholar]
- 53.Lim Tjen-Sien, Loh Wei-Yin, Shih Yu-Shan. A comparison of prediction accuracy, complexity, and training time of thirty-three old and new classification algorithms. Machine Learning. 2000;40:203–228. [Google Scholar]
- 54.Gordon Gavin J, Jensen Roderick V, Hsiao Li-Li, Gullans Steven R, Blumenstock Joshua E, Ramaswamy Sridhar, Richards William G, Sugarbaker David J, Bueno Raphael. Translation of microarray data into clinically relevant cancer diagnostic tests using gene expression ratios in lung cancer and mesothelioma. Cancer Research. 2002;62:4963–4967. [PubMed] [Google Scholar]
- 55.Cortes Corinna, Vapnik V. Support-vector networks. Machine Learning. 1995;20 [Google Scholar]
- 56.Quinlan JR. Bagging, boosting, and c4.5. AAAI/IAAI. 1996;1:725–730. [Google Scholar]
- 57.Quinlan JR, Rivest RL. Inferring decision trees using the minimum description length principle. Inform Comput. 1989;80(3):227–248. [Google Scholar]
- 58.Handl Julia, Knowles Joshua, Kell Douglas B. Computational cluster validation in post-genomic data analysis. Bioinformatics. 2005;21(15):3201–3212. doi: 10.1093/bioinformatics/bti517. [DOI] [PubMed] [Google Scholar]
- 59.Kovacs Ferenc, Legancy Csaba, Babos Attila. Cluster validity measurement techniques. 6th International Symposium of Hungarian Researchers on Computational Intelligence; 2005. [Google Scholar]