Response Processes in Information-Integration Category Learning

Abstract

Much recent evidence suggests that human category learning is mediated by multiple systems. Evidence suggests that at least one of these depends on procedural learning within the basal ganglia. Information-integration categorization tasks are thought to load heavily on this procedural learning system. The results of several previous studies were interpreted to suggest that response positions are learned in information-integration tasks. This hypothesis was tested in two experiments. Experiment 1 showed that information-integration category learning was slowed but not disrupted when the spatial location of the responses varied randomly across trials. Experiment 2 showed that information-integration learning was impaired if category membership was signaled by responding to a yes/no question and the category label had no consistent spatial location. These results suggest that information-integration category learning does not require consistent response locations. In these experiments, a consistent association between a category and a response feature was sufficient. The implication of these results for the neurobiology of information-integration category learning is discussed.

INTRODUCTION

Categorization is the act of responding differently to objects or events in separate classes or categories. It is a vitally important skill that allows us to find food and avoid toxins, and to approach friends and escape foes. During the past decade there has been a surge of interest in the neural basis of category learning. Perhaps the most important discovery to come from this research is that humans have multiple category-learning systems, which are each best suited for learning certain types of category structures, and are each mediated by different neural circuits (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Ashby & O’Brien, 2005; Erickson & Kruschke, 1998; Love, Medin, & Gureckis, 2004; Nosofsky, Palmeri, & McKinley, 1994; Reber, Gitelman, Parrish, & Mesulam, 2003).

In rule-based category-learning tasks the categories can be learned via some explicit reasoning process. Frequently, the rule that maximizes accuracy (i.e., the optimal strategy) is easy to describe verbally (Ashby et al., 1998). In the most common applications, only one stimulus dimension is relevant, and the subject’s task is to discover this relevant dimension and then to map the different dimensional values to the relevant categories. A variety of evidence implicates the prefrontal cortex (PFC), anterior cingulate, the head of the caudate nucleus, and medial temporal lobe structures in rule-based category learning (e.g., Brown & Marsden, 1988; Filoteo, Maddox, Ing, & Song, 2007; Muhammad, Wallis, & Miller, 2006; Seger & Cincotta, 2006).

In information-integration (II) category learning tasks, accuracy is maximized only if information from two or more stimulus components (or dimensions) is integrated at some pre-decisional stage (Ashby & Gott, 1988). In many cases the optimal strategy is difficult or impossible to describe verbally (Ashby et al., 1998). An example of an II task is shown in Figure 1. In this case the two categories are each composed of circular sine-wave gratings that vary in the width and orientation of the dark and light bars. The diagonal line denotes the category boundary. Note that no simple verbal rule correctly separates the disks into the two categories. Nevertheless, many studies have shown that people reliably learn such categories, provided they receive consistent and immediate feedback after each response (for a review, see Ashby & Maddox, 2005).

Figure 1.

Categories of circular sine-wave gratings that might be used in an information-integration category-learning task. The diagonal line is the category boundary.

The search for the neural locus of II category learning has focused on the basal ganglia, and more specifically on the striatum. For example, a number of studies have reported that patients with basal ganglia dysfunction are impaired in II tasks (Filoteo, Maddox, & Davis, 2001; Filoteo, Maddox, Salmon, & Song, 2005, 2007; Maddox & Filoteo, 2001) and neuroimaging studies of II learning have reported significant learning-related striatal activation (Cincotta & Seger, 2007; DeGutis & D’Esposito, 2007; Nomura et al., 2007; Seger & Cincotta, 2002). In addition, a large literature implicates the striatum in visual discrimination learning and category learning in nonhuman animals (for a review, see Ashby & Ennis, 2006). For example, single-cell recording studies in monkeys show that striatal medium spiny cells develop category-specific responses after categorization training (Merchant, Zainos, Hernandez, Salinas, & Romo, 1997; Romo, Merchant, Ruiz, Crespo, & Zainos, 1995; Romo, Merchant, Zainos, & Hernandez, 1997).

II category learning is also indirectly linked to the striatum via its similarities to the serial reaction time (SRT) task (Nissen & Bullemer, 1987), which is among the most widely studied procedural learning tasks. These similarities are important because there is much evidence that procedural learning is mediated largely within the striatum (e.g., Salmon & Butters, 1995; Willingham, 1998). One notable similarity concerns the learning of response positions, rather than abstract labels. Willingham, Wells, Farrell, and Stemwedel (2000) reported that switching hands on the response keys did not interfere with implicit SRT learning, but switching the location of the response keys caused significant interference. Ashby, Ell, and Waldron (2003) replicated this result with II category learning. More specifically, Ashby et al. (2003) reported that switching the location of the category response keys interfered with II performance, but not with rule-based performance. In this study, participants first learned either rule-based or II categories. Then one group switched the hands that they used to depress the response keys, and for another group the location of the response keys was switched (there was also a control group). Neither of these manipulations had any effect on the performance of participants in the rule-based conditions. In the II conditions however, switching hands had no effect on performance, but switching the response keys interfered significantly with response accuracy. The similarity of these II results to the results of Willingham et al. (2000), provide strong evidence for a procedural-learning contribution to II categorization.

Maddox, Bohil, and Ing (2004) reported the results of a related experiment. In A-B training conditions, the stimulus was displayed on each trial along with the query “Is this an A or B?” The observer pressed one key for category A and a separate key for category B, followed by corrective feedback. In the Yes-No training conditions, on half the trials the stimulus was displayed along with the query “Is this an A?” and on the other half of the trials the stimulus was displayed along with the query “Is this a B?” The observer pressed one key to respond “No”, and a separate key to respond “Yes”, and both keys had a fixed location. Thus, in A-B training each category was associated with a consistent response location, whereas in the Yes-No conditions there was no consistent mapping from category label to response location. For rule-based categories, there was no difference between these two training procedures, but with II categories, learning was significantly worse with Yes-No training.

Ashby et al. (2003) and Maddox et al. (2004) both interpreted their results as evidence that response locations are learned during II categorization. In the Ashby et al. (2003) study, switching the response keys changed the location of the two category responses and produced an interference. In the Yes-No training condition of the Maddox et al. (2004) study, participants sometimes pressed the Yes key to signal a category A response and sometimes they pressed the No key. The Yes and No keys had fixed locations, so the two category responses had no consistent locations, and impaired learning was observed.

The Ashby et al. (2003) study showed that changing the response locations after learning was essentially complete disrupted performance in II tasks, but it did not address the question of whether a consistent response location is needed during the initial learning. Maddox et al. (2004) partially addressed this issue, but participants in their Yes-No conditions made an extra logical decision that was not required during the more traditional A-B training. This is potentially problematic because it seems possible that working memory and executive attention are needed to answer the query “Is this an A?”. Several studies have shown that II category learning is not significantly affected when participants simultaneously perform a secondary task that requires working memory and executive attention (DeCaro, Thomas, & Beilock, 2008; Waldron & Ashby, 2001; Zeithamova & Maddox, 2006). One interpretation of this result is that executive processes and procedural-learning processes operate (largely) independently. If so, then any condition that requires their integration may be problematic for participants. For this reason, it is difficult to rule out the hypothesis that Maddox et al. (2004) observed an interference because the Yes-No condition required participants to integrate executive and procedural-learning processes, whereas the A-B condition did not.

This article presents a direct test of this response position hypothesis. Experiment 1 tests whether consistent response locations are required for initial II learning and Experiment 2 tests whether the Yes-No interference reported by Maddox et al. (2004) is because there was no consistent association between categories and response positions or because an extra logical decision was required.

EXPERIMENT 1

Experiment 1 tests whether consistent response locations are required for initial II learning. There is reason to believe that consistent response locations should not be required. Ashby, Ennis, and Spiering (2007) interpreted the results of Ashby et al. (2003) and Maddox et al. (2004) to mean that the most critical cortical projection of the II category learning system was somewhere in premotor cortex. Olson and Gettner (1999) reported that some cells in a prominent premotor area (i.e., supplementary eye fields, SEF) fired to a specific feature cue (e.g., a color) that signaled the animal where to move its eyes. In this study, a single color cue was always presented in one spatial location. When one color (e.g., red) appeared, the animals had to move their eyes to the right and when a different color appeared (e.g., blue) they moved their eyes to the left. The same cells gave similar responses when spatial cues were used rather than feature cues - that is, when the position of the cue signaled which eye movement to make, rather than the feature identity of the cue. Interestingly however, the SEF response was about 200 ms slower to the feature cues than to the spatial cues. Thus, it appears that, at least in SEF, some cells can learn to associate a feature identity with a response. To our knowledge, similar studies have not been conducted on cells in other premotor areas (e.g., supplementary motor area). Experiment 1 addresses the question of whether a similar association can be learned in II categorization.

In Experiment 1 each participant learned a pair of II categories like the ones shown in Figure 1. Also like Figure 1, the stimuli comprising each category were circular sine-wave gratings that varied in bar width and bar orientation. On each trial, a randomly selected exemplar from one of the two categories was shown to the participant, whose task was to assign it to one of the two categories by pressing an appropriate response key. Feedback about response accuracy was given after every response.

There were three conditions. In the Control condition, each category was identified by a color (blue or red). When a stimulus appeared, its presentation was accompanied by a blue circle in the lower left of the display and a red circle in the lower right. Participants could assign the stimulus to the blue category by pressing the response key directly beneath the blue circle and they could assign it to the red category by pressing the key beneath the red circle. The Random-Color condition was identical, except that the location of the blue and red circles varied randomly across trials. On half the trials (randomly determined), the blue circle appeared on the left and the red circle on the right, and on the other trials these assignments were reversed. Finally, the Random-Letter condition was identical to the Random-Color condition except the letters ‘A’ and ‘B’, which appeared in black, replaced the blue and red circles. The Random Color condition replicates exactly the response conditions of Olson and Gettner (1999). The Random Letter condition substitutes letters for the colors, since these are more common category labels in experiments with human participants.

Method

Participants

There were 20 participants in the Control condition, 51 participants in the Random-Color condition, and 18 participants in the Random-Letter condition. All participants received course credit from the University of California Santa Barbara for their participation in the experiment. All participants reported 20/20 vision or vision corrected to 20/20. The session was approximately 60 minutes in duration.

Stimuli and Stimulus Generation

Each stimulus was a circular sine-wave grating of constant size and contrast. Stimuli varied across trials in bar width (i.e., spatial frequency) and bar orientation. The categories were created using the randomization technique introduced by Ashby and Gott (1988). 300 Blue Category and 300 Red Category stimuli from II categories were generated by sampling randomly from two bivariate normal distributions (see Table 1). Each circular sine-grating was generated using Matlab routines from Brainard’s (1997) Psychophysics Toolbox and displayed on a 21-inch monitor with 1,280 × 1,024 resolution. The visual angle subtended by each circular sine-wav grating was approximately 3.3 degrees. Each random sample (x₁, x₂) was converted to a stimulus by deriving a frequency, f = .0013636x₂ -.014545, and an orientation, o = 1.45x₁-56. For example, the Red Category mean was converted to a Gabor pattern with f = .0013636(60) - .014545 = 0.067 cycles per degree and o = 1.45(45) - 56 = 9.25 degrees counterclockwise from horizational. The scaling factors were chosen in an attempt to equate the salience of frequency and orientation.

Table 1.

Category Distribution Parameters

Blue or “A” Category
μbw	μo	σ2bw	σ2o	covbw,o
45	60	35	35	33

Red or “B” Category
μbw	μo	σ2bw	σ2o	covbw,o
60	45	35	35	33

Note - cov, covariance; bw, bar width; o, orientation

Procedure

Each participant was tested individually in a dimly lit room. They were told to emphasize accuracy without worrying about speed of responding. On each trial, a stimulus and category membership color cues were presented on the screen until the participant responded. In the Control condition, the blue cue (a circle) always appeared on the left, and the red cue (a circle) always appeared on the right. In the Random-Color condition, the category membership cues were randomly assigned to the right or left side of the screen on each trial. On roughly half the trials, the red cue appeared on the left and the blue cue on the right, whereas on the other trials these assignments were reversed. The Random-Letter condition was identical to the Random-Color condition except the letters ‘A’ and ‘B’ denoted category membership, rather than the colors red and blue. Participants were given 5s to respond. If they did not respond within 5s a message appeared on the screen, “PLEASE RESPOND FASTER”, accompanied by a sawtooth tone (centered at 587 Hz). Immediately following the response, the stimulus and category membership cues disappeared, and corrective audio feedback was presented for 500 ms. Feedback was a pure tone (similar to the sound of a tuning fork) for a correct response (262 Hz) and a sawtooth tone (slightly harsher than a pure tone) for an incorrect response (centered at 440 Hz). These signals, which were presented at a comfortable loudness, were chosen because they are perceptually distinct. The feedback was followed by a pause of 1,500 ms. Each participant completed 600 trials. Self-paced breaks were provided every 50 trials.

Results

Accuracy-Based Analyses

The averaged accuracy rates are displayed in Figure 2. A visual inspection of Figure 2 indicates that accuracy was higher in the Control condition than in either the Random-Color or Random-Letter conditions. Both of these differences were significant by a sign test [Random-Color: 12/12, p < 0.001, g = .50 (large effect size, Cohen, 1988); Random-Letter, 11/12, p = 0.003, g = .42 (large effect size, Cohen, 1988)]. In contrast, there was no significant difference in accuracy between the Random-Color and Random-Letter conditions [sign test: 7/12, p > 0.2]. These results were partially supported by a 3 × 12 mixed design ANOVA [3 conditions (Control versus Random-Color versus Random-Letter) × 12 blocks]. The main effect of condition was not significant [F(2,86) = 0.688, p > 0.25], but there was a significant interaction [F(22, 946) = 1.67, p = .029]. There was also a less interesting main effect of block [F(11, 946) = 12.91, p < 0.001]. Post-hoc tests indicated that the interaction was driven by a significant difference among conditions during the first block [F(2, 86) = 4.78, p = 0.010, η² = .100 (medium effect size, Cohen, 1988)]. There were no significant differences among conditions in any other blocks [F(2, 86) < 2.186, p > 0.119].

Figure 2.

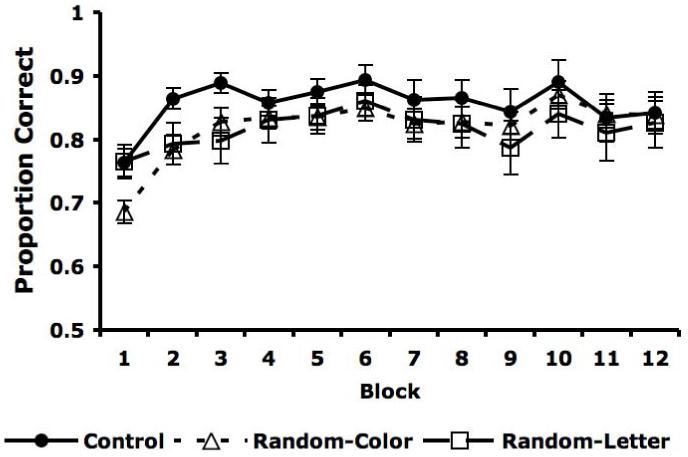
Proportion correct for Control (filled circles), Random-Color (empty triangles), and Random-Letter (empty squares) conditions for each of the twelve blocks with standard error bars.

Unlike ANOVA, the sign test ignores variance. Mean accuracy was consistently higher in the Control condition than in either the Random-Color or Random-Letter conditions, which caused large effect sizes in the sign test. Except for block 1, however, there was enough variability in these accuracies across participants to prevent significance via ANOVA. Thus, one interpretation of these analyses is that 1) there was a clear trend toward higher accuracy in the Control condition, 2) accuracy was significantly better during block 1 for the Control condition than for either Random condition, and 3) there were significant individual differences in later blocks.

To determine whether participants learned the categories, accuracy was computed within a 50-trial window starting at trial 1 and ending at trial 50. If the proportion correct within this window was greater than or equal to a criterion value then the participant was classified as a learner with a trials-to-criterion score of 50. If accuracy was less than the criterion then a new window was defined that included trials 2 to 51, and the analysis was repeated. The process was repeated until the last window was reached, which extended from trials 551 to 600. If the participant never reached criterion for any 50-trial window, he or she was classified as a non-learner.

This whole analysis was repeated for every participant with the following five different criterion values: .65, .70, .75, .80, and .85. Chi-squared tests revealed no significant differences among the conditions in the proportion of learners for any criterion level [all p > 0.10]. Similarly, among the learners (those participants who reached criterion), there were no significant differences among the conditions for any criterion level in the number of trials to criterion [all p > 0.208].

Model-Based Analyses

The accuracy-based analyses suggest that performance in the Random conditions was slightly impaired relative to the Control condition, especially during the early blocks. Even so, by the end of training there were no apparent differences among any conditions, in overall accuracy, percent of learners, or trials-to-criterion among learners. However, a variety of different decision strategies could all yield approximately equal accuracy, so it is difficult to draw strong conclusions from the accuracy-based analyses alone. For this reason, we also fit a number of different decision bound models (e.g., Ashby & Gott, 1988; Maddox & Ashby, 1993) to the data from each individual participant. Decision bound models assume that participants partition the perceptual space into response regions. On every trial, the participant determines which region the percept is in, and then emits the associated response.

Three different types of models were fit to each participant’s responses (see the Appendix for details): random response, rule-based, and II models. The random response models assume participants guess randomly on every trial. The rule-based and II models make no detailed process assumptions, in the sense that a number of different process accounts are compatible with each of the models (e.g., Ashby, 1992; Ashby & Waldron, 1999). For example, if an II model fits significantly better than a rule-based model, then we can be confident that participants did not use a rule-based strategy, but we cannot specify which specific II strategy was used (e.g., a weighted combination of the two dimensions versus more holistic processing).

The optimal strategy in Experiment 1 requires the integration of perceptual information across the bar width and bar orientation dimensions. For this reason, we are most interested in whether or not participants adopted an II strategy. Figure 3 shows the percentage of participants whose data were best fit by a model that assumed an II strategy in each block and condition of Experiment 1. Note first that in all three conditions, the percentage of participants using an II strategy gradually increased from the first block until a maximum was reached somewhere around the 7^th block. By the end of training, the percentage of participants using an II strategy is roughly the same in the three conditions.

Figure 3.

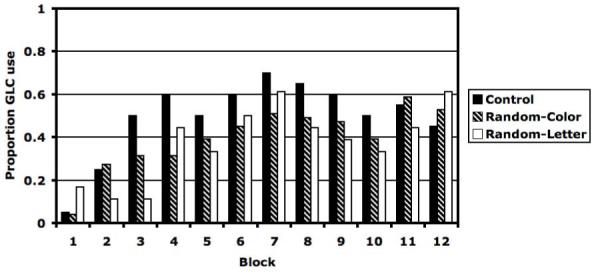
Proportion of participants best fit by information-integration strategy for Control, Random-Color, and Random-Letter conditions for each of the twelve blocks.

To test whether there was any difference in the eventual use of II strategies, we conducted binomial tests of the null hypothesis that participants were equally likely to use an II strategy in each pair of conditions for every block during the second half of the session (i.e., blocks 7 - 12). None of these tests were significant¹ [all p > 0.05]. Thus, these results suggest that participants in the Random Location and Control conditions all learned strategies of the same type.

Discussion

Initial learning was somewhat slower in the Random conditions, but asymptotic accuracy was no different than in the Control condition, and more importantly, the percentage of participants using an II decision strategy was also no different. Thus, our participants learned II categories when the response locations were inconsistent - a consistent feature identity was sufficient. Further, it did not seem to matter whether the feature that identified each category was a color, as in the Olson and Gettner (1999) single-unit recording study, or a letter, as is most common in human category learning research.

These results are consistent with the electrophysiological results of Olson and Gettner (1999), who described cells in SEF that could learn to associate an eye movement either with a spatial or a feature cue. In fact, the responses of these cells were similar to the two cue types, except they were approximately 200 ms slower to the feature cues. This suggests that both spatial and feature coding exist in SEF, but that spatial coding may be favored. This result also parallels our findings since participants in the Random conditions learned somewhat more slowly than participants in the Control condition. In other words, learning was faster when there was a consistent spatial and feature association than when only the feature association was consistent.

Our results suggest that the interference observed following a switch of the response keys in the Ashby et al. (2003) study may have been due to the blocked nature of the training. For the first 500 trials of that experiment, the response keys had consistent locations, which were reversed during the last 100 trials of the experiment. Note however, that the feature cues never changed - the ‘A’ category retained its same name throughout training and transfer. Thus, in the Ashby et al. (2003) study and in the Random conditions of our experiment, each category had a consistent feature cue and inconsistent response positions. The difference was that participants in our Random conditions could never use response location as a learning cue, whereas participants in the Ashby et al. (2003) study could (for the first 500 trials). If spatial cues dominate feature cues, as suggested by the results of Olson and Gettner (1999), then participants in the Ashby et al. (2003) study might have relied on spatial cues during initial training, thereby engendering an interference when they were required to rely on feature cues (or relearn a new spatial association).

EXPERIMENT 2

Experiment 1 showed that a consistent response location facilitated, but was not necessary for II learning. Experiment 2 tests whether the Yes-No interference reported by Maddox et al. (2004) occurred because there was no consistent association between categories and response positions or because an extra logical decision was required. Maddox et al. (2004) compared performance in the Yes-No condition to performance in a control condition in which the response positions were consistent throughout training. Experiment 1 suggests that our Random conditions would be a more appropriate control because in that case both the control and Yes-No conditions would have inconsistent response positions and would differ only in the extra logical decision required in the Yes-No condition.

Experiment 2 therefore included a single condition that was identical to the Control condition of Experiment 1, except the words ‘Yes’ and ‘No’ replaced the blue and red circles. In addition, a single red or blue circle (selected with equal probability) accompanied by a question mark was presented below each stimulus. The participant’s task was to press the key beneath the word ‘Yes’ if the stimulus was a member of the category associated with the color of the circle and to press the key beneath the word ‘No’ if it was not. Because the color of the circle varied randomly across trials, participants sometimes pressed the left (Yes) key if the stimulus belonged to the blue category and sometimes the right (No) key. The conditions of Experiment 2 were otherwise identical to the Experiment 1 conditions, and therefore the Control and Random conditions of Experiment 1 serve as appropriate controls for Experiment 2.

Method

Participants

There were 33 participants in the Yes-No condition. All participants received University of California Santa Barbara course credit for their participation in the experiment. All participants reported 20/20 vision or vision corrected to 20/20. The session was approximately 60 minutes in duration.

Stimuli and Stimulus Generation

The stimuli and stimulus generation procedures were identical to those outlined in Experiment 1.

Procedure

The general procedures were identical to those outlined in Experiment 1 except the participant was asked to make a Yes-No decision about category membership. On each trial, a categorization stimulus appeared in the center of the screen. A red or blue color cue (randomly selected with equal probability) accompanied by a question mark was displayed below the stimulus. In addition, the word ‘Yes’ appeared on the bottom left side of the screen and the word ‘No’ appeared on the bottom right side of the screen. Participants were instructed to press the response key under the word ‘Yes’ if the stimulus belonged to the cued category and to press the key under the word ‘No’ if it did not. The stimulus, color cue and question mark, and Yes-No response cues all disappeared after a response was made. Auditory feedback was provided after each response in the same manner as in Experiment 1.

Results

As mentioned above, the stimuli, category structures, and procedures were identical in Experiments 1 and 2 except for the response instructions. Thus, the Experiment 1 data can be used as controls in Experiment 2. In Experiment 1 however, there were no differences between the Random-Color and Random-Letter conditions, so when comparing to the Experiment 2 data we collapsed these two random-location conditions into one condition.

Accuracy-Based Analyses

The averaged accuracy rates are shown in Figure 4 together with the accuracy from the Experiment 1 Control condition. Also included is the average of the Experiment 1 Random-Color and Random-Letter conditions, which we hereafter denote as the Random-Location condition.

Figure 4.

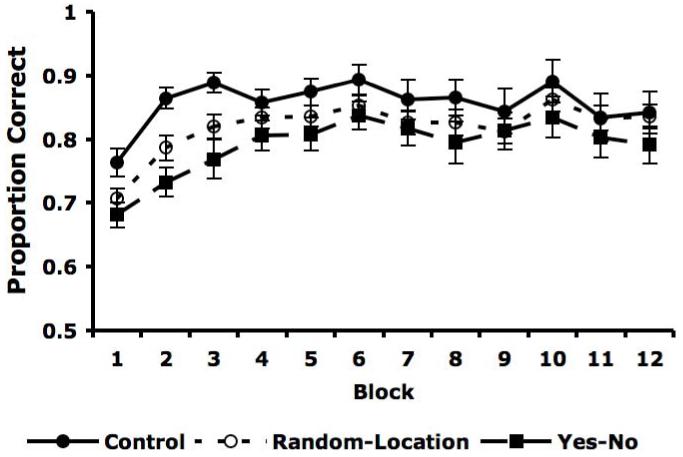
Proportion correct for Control (filled circles), Random-Location (empty circles), and Yes-No (filled squares) conditions for each of the twelve blocks with standard error bars.

Note that performance in the Yes-No condition is uniformly lower than in both the Control and Random-Location conditions. These differences are significant by a sign test [Yes-No worse than Control: 12/12, p < .001, g = .50 (large effect size, Cohen, 1988); Yes-No worse than Random-Location: 11/12, p = 0.003, g = .42 (large effect size, Cohen, 1988)]. We also tested whether these differences were significant by conducting a 3 × 12 mixed design ANOVA [3 conditions (Control, Random-Location, Yes-No) × 12 blocks]. There was a main effect of block [F(11, 1309) = 20.10, p < .001], but neither the main effect of condition [F(2, 119) = 1.692, p = 0.189] nor the interaction were significant [F(22, 1309) = 1.19, p > 0.2]. Thus, there was a clear trend for poorer performance in the Yes-No condition, but at the same time, there were considerable individual differences in block-by-block accuracy.

We also compared the proportion of learners in the three conditions and their trials-to-criterion using the same criteria and methods as in Experiment 1. Chi-squared tests revealed no significant differences among the conditions in the proportion of learners for any criterion level [all p > 0.11]. When the learning criterion was defined to be .80 or less, there were no significant differences among any of the conditions in trials-to-criterion [all p > 0.2]. However, when the learning criterion was defined to be .85, participants in the Yes-No condition required significantly more training to reach criterion than participants in either other condition [F(2, 109) = 3.50, p = 0.034, η² = .080 (medium effect size, Cohen, 1988)]. For example, on average, Yes-No participants reached this criterion in 132 trials, whereas Control participants required only 70 trials to reach the same criterion.

Model-Based Analyses

The same model-based analyses performed on the Experiment 1 data were repeated here. Figure 5 shows the percentage of participants in each of the three conditions whose data were best fit by an II model during each of the 12 experimental blocks. Note first that in every block the percentage of II users is lowest in the Yes-No condition. Thus, by a sign test, the probability a participant will learn to use an II strategy in the Yes-No condition is significantly lower than in either the Control or Random-Location conditions [12/12, p < .001, g = .50 in both cases (large effect size, Cohen, 1988)]. Follow-up binomial tests on proportions from pairs of conditions showed that participants in the Random-Location condition were significantly more likely than participants in the Yes-No condition to use II strategies in block 7 [t(102)= 2.21, p = 0.030], block 11 [t(102) = 2.64, p = 0.010], and block 12 [t(102) = 2.64, p = 0.010]. Participants in the Control condition were significantly more likely to use II strategies than participants in the Yes-No condition in all later blocks [all t(53) > 1.91, p < .06], except block 12 [t(53) = 1.32, p = 0.19].

Figure 5.

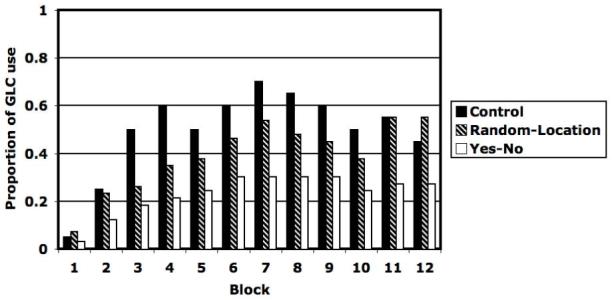
Proportion of participants best fit by information-integration strategy for Control, Random-Location, and Yes-No conditions for each of the twelve blocks.

Discussion

Compared to the Random-Location participants from Experiment 1, participants in the Yes-No condition of Experiment 2 had lower overall accuracy, required more training to reach a criterion accuracy level, and were less likely to use an II strategy. Thus, the Yes-No response decision appeared to interfere with II learning, but not because the response positions were inconsistent. Instead, the deficit must be because the Yes-No response required an extra logical decision compared to the random location conditions of Experiment 1.

Recall that Maddox et al. (2004) reported that with rule-based categories, Yes-No learning was no worse than learning under standard categorization training conditions (i.e., an ‘A’ or ‘B’ response with consistent response positions). This was true even when the rule-based condition required participants to learn a difficult conjunction rule that made it necessary for them to attend to both stimulus dimensions. Thus, it appears that the Yes-No decision, by itself, does not necessarily increase difficulty. Rather, it selectively increases difficulty in II tasks.

Why would a Yes-No decision interfere with II category learning, but not with an equally difficult² rule-based task? One possibility is that the extra logical decision required in Yes-No conditions recruits executive processes that are mediated primarily within PFC. For example, task-related activation in a variety of prefrontal regions has been reported in Yes-No categorization tasks (e.g., Reber, Stark, & Squire, 1999). If Yes-No categorization decisions require executive processes, then because rule-based categorization is an executive task, it may be straightforward for participants to integrate the Yes-No decision with the standard rule-based decision process. In other words, in rule-based tasks, no extra cognitive or neural processes should be needed in Yes-No conditions.

In contrast, II learning does not depend heavily on executive functions or the PFC, and if the motor learning component of II categorization is mediated in cortical areas that are poorly connected to PFC, then the extra logical decision required during Yes-No training would require recruiting a PFC network whose output may be difficult to integrate with default II decision processes. The inevitable result would be a learning deficit.

Note that reports that a working-memory dependent dual task interferes with rule-based learning (DeCaro et al., 2007; Waldron & Ashby, 2001; Zeithamova & Maddox, 2006) are not incompatible with this hypothesis. Presumably the interference occurs because rule-based categorization and the dual-task both depend on working memory and the combination of the two tasks exceeds available working memory capacity. The present results and those of Maddox et al. (2004) suggest that the extra logical decision required in Yes-No conditions loads on PFC based processes (e.g., working memory), but not enough to challenge capacity limits.

GENERAL DISCUSSION

Experiment 1 showed that consistent response positions are not required for effective II category learning. Instead, a consistent feature association is sufficient. Consistent response positions, in addition to a consistent feature association, appeared to speed early learning, but it did not lead to any asymptotic benefits, either in terms of overall accuracy or in the likelihood that an II strategy was used. These results suggest that the interference observed by Ashby et al. (2003) when they switched the location of the response keys may have been due to the blocked nature of training. One plausible hypothesis is that spatial associations are more effective than feature associations (e.g., Olson & Gettner, 1999), so that during training in the Ashby et al. (2003) study, when both spatial and feature associations were consistent, participants focused on the spatial associations (i.e., the location of the response). This caused an interference when the response keys were switched. In contrast, in Experiment 1, participants were forced to focus on the feature associations throughout the experiment (which they could do successfully).

Recall that Ashby et al. (2003) also reported that switching hands on the response keys did not interfere with II performance. In that condition, participants also had blocked training with consistent response locations before the hand-switch. However, note that switching hands on the keys does not change the response location, only the motor program used to execute the response. Thus, in the Ashby et al. (2003) hand-switch condition the response locations remained consistent throughout the experiment, so those results are not incompatible with our hypothesis that the button-switch interference was caused by the blocked nature of training.

In Experiment 2, participants who were required to make a Yes-No decision showed impaired II learning, relative to all three Experiment 1 conditions. The only difference between the Yes-No experimental conditions and the Random-Location condition was that the Yes-No response required an extra logical decision. Thus, the evidence supports the hypothesis that this extra decision caused the poorer performance. One plausible interpretation of this result is that the Yes-No decision depends on executive processes that are largely mediated within the PFC, and that the cortical targets of the striatal-based II learning system are poorly connected to the PFC.

As mentioned above, Ashby et al. (2007) proposed that the most critical cortical projection of the II category learning system was somewhere in premotor cortex. The present results do not contradict this hypothesis. The results of Olson and Gettner (1999) suggest that cells in one prominent premotor region (i.e., SEF) can learn to associate a motor action with either a spatial or a feature cue, but that spatial cues are more effective. This is exactly the result we obtained in Experiment 1. In Experiment 2, requiring an extra logical decision interfered with II learning. The same decision does not interfere with rule-based learning (Maddox et al., 2004), which is widely thought to depend on PFC. Thus, Experiment 2 is consistent with previous results suggesting that the cortical projection of the II system is probably not in the PFC.

Although much evidence implicates the striatum in II category learning, little is known about the relative contributions of the various striatal regions to this type of learning. A common neuroanatomical classification scheme partitions the striatum into three general regions: sensorimotor, associative, and limbic (e.g., Flaherty & Graybiel, 1993; Parent & Hazrati, 1995; Selemon & Goldman-Rakic, 1985; Yeterian & Pandya, 1995). Roughly speaking, the sensorimotor striatum includes most of the putamen, the associative striatum includes most of the caudate nucleus, and the limbic striatum includes the ventral striatum (e.g., nucleus accumbens). Of these, the category learning literature has focused on the associative striatum (e.g., for a review see Ashby & Ennis, 2006). For example, Ashby et al. (1998) hypothesized that with visual categories the critical striatal site should be within the tail of the caudate nucleus. At the time, this hypothesis was based almost entirely on the observation that all of extrastriate visual cortex projects directly to this striatal region. Even so, visual cortical areas also project to the putamen, so the relative contributions of the associative and sensorimotor regions to II category learning have never been clear.

This article investigated response processes in II category learning. Therefore, our results are presumably determined by the output or terminal projections of the cortical-striatal pathways that mediate II learning. The sensorimotor and associative regions of the striatum both project to cortex via the globus pallidus/substantia nigra pars reticulata and the thalamus. The sensorimotor striatum projects primarily into motor areas of cortex and SMA (or SMA-proper) via the ventral lateral (VL) nucleus of the thalamus (Matelli & Luppino, 1996). The SMA is densely interconnected with primary motor cortex and with other premotor areas (Dum & Strick, 2005). Furthermore, the SMA receives no direct projections from the PFC (Luppino, Matelli, Camarda, & Rizzolatti, 1993).

In contrast, the associative striatum projects to cortex primarily via the medial dorsal (MD) and ventral anterior (VA) thalamic nuclei. The MD nucleus projects widely into all areas of frontal cortex, including PFC, whereas VA projects most heavily into pre-SMA and SEF (Matelli & Luppino, 1996). The SEF project strongly to the frontal eye fields. However, SEF and pre-SMA are both densely interconnected with the PFC (Wang, Isoda, Matsuzaka, Shima, & Tanji, 2005), and neither area sends direct projections to any premotor or motor areas that mediate finger movements (Dum & Strick, 2005). As a result, a strong case can be made that pre-SMA is most properly classified as a prefrontal region (Akkal, Dum, & Strick, 2007). Thus, with the exception of the SEF, the associative regions of the striatum project primarily to prefrontal regions of cortex.

If the associative striatum was the only critical striatal region for II category learning then because of its prominent connections to PFC, one might expect that an extra Yes-No decision would not cause an interference. Because we did observe such an interference (as did Maddox et al., 2004), our results therefore suggest that the sensorimotor striatum may play a more prominent role in II category learning than previously assumed. This conclusion is consistent with single-unit recording results that show learning related changes in the firing of cells in SMA during a traditional procedural learning task (Lee & Quessy, 2003). In addition, several fMRI studies of II categorization have reported significant task-related activation in the putamen (e.g., Cincotta & Seger, 2007; Seger & Cincotta, 2002).

On the other hand, other results seem inconsistent with the hypothesis that the sensorimotor striatum is critical for II learning. First, a recent II neuroimaging study failed to report task-related activation in the putamen (Nomura et al., 2007). Instead, significant striatal activation was limited to the caudate nucleus. Second, Ell, Marchant, and Ivry (2006) reported that a group of patients with putamen lesions were impaired in rule-based category learning, but not in II learning. In addition, all known fMRI studies of II categorization have reported significant task-related activation in the caudate nucleus (Cincotta & Seger, 2007; Nomura et al., 2007; Seger & Cincotta, 2002). Thus, an important question for future research is to disentangle the relative contributions of the sensorimotor and associative regions of the striatum to II category learning.

APPENDIX

Three different rule-based decision bound models were fit to each participant’s data (2 Unidimensional models and the Conjunctive model), one information-integration model (General Linear Classifier), and two different random response models. For more details, see Ashby (1992) or Maddox and Ashby (1993).

Rule-Based Models

The One-Dimensional Classifier

This model assumes that participants set a decision criterion on a single stimulus dimension. For example, a participant might base his or her categorization decision on the following rule: “Respond blue if the bar width is small, otherwise respond red”. Two versions of the model were fit to the data. One version assumed a decision based on bar width, and the other version assumed a decision based on orientation. These models have two parameters: a decision criterion along the relevant perceptual dimension, and a perceptual noise variance.

The General Conjunctive Classifier

This model assumes that the rule used by participants is a conjunction of two one-dimensional classifiers (e.g., “Respond blue if the bar width is small AND the orientation is > 45°, otherwise respond red.”) Although several different versions of the model could be fit to the present data, only the version that seemed plausible based on a visual inspection of the response data was fit. The GCC has 3 parameters: one for the single decision criterion placed along each stimulus dimension (one for orientation and one for bar width), and a perceptual noise variance.

Information-Integration Models

The General Linear Classifier

The general linear classifier (GLC) assumes that participants divide the stimulus space using a linear decision bound. Categorization decisions are then based upon which region each stimulus is perceived to fall in. These decision bounds require linear integration of both stimulus dimensions, thereby producing an II decision strategy. The GLC has 3 parameters: the slope and intercept of the linear decision bound, and a perceptual noise variance.

Random Response Models

Fixed Random Responder Model

This model assumed that the participant responded randomly, essentially flipping an unbiased coin on each trial to determine the response. Thus, the predicted probability of responding “red” (and “blue”) was .5 for each stimulus. This model has no free parameters.

General Random Responder Model

This model assumed that the participant responded randomly essentially flipping a biased coin on each trial to determine the response. Thus, the predicted probability of responding “red” was a free parameter in the model that could take on any value between 0 and 1. This model is useful for identifying participants who are biased towards pressing one response key.

Goodness-of-Fit Measure

Model parameters were estimated using the method of maximum likelihood, and the statistic used for model selection was the Bayesian Information Criterion (BIC; Schwarz, 1978), which is defined as:

$$\mathrm{BIC}=r\ln N-2\ln L,$$

where r is the number of free parameters, N is the sample size, and L is the likelihood of the model given the data. The BIC statistic penalizes models for extra free parameters. To determine the best fitting model within a group of competing models, the BIC statistic is computed for each model, and the model with the smallest BIC value is the winning model.