Human vergence eye movements to oblique disparity stimuli: evidence for an anisotropy favoring horizontal disparities

Abstract

Binocular disparities applied to large-field patterns elicit vergence eye movements at ultra-short latencies. We used the electromagnetic search coil technique to record the horizontal and vertical positions of both eyes while subjects briefly viewed (150 ms) large patterns that were identical at the two eyes except for a difference in position (binocular disparity) that was varied in direction from trial to trial. For accurate alignment with the stimuli, the horizontal and vertical disparity vergence responses (HDVRs, VDVRs) should vary as the sine and cosine, respectively, of the direction of the disparity stimulus vector. In a first experiment, using random dots patterns (RDs) with a binocular disparity of 0.2°, this was indeed the case. In a second experiment, using 1-D sine-wave gratings with a binocular phase difference (disparity) of 1/4-wavelength, it was not the case: HDVRs were maximal when the grating was vertical and showed little decrement until the grating was oriented more than ~65° away from vertical, whereas VDVRs were maximal when the grating was horizontal and began to decrement roughly linearly when the grating was oriented away from the horizontal. We attribute these complex directional dependencies with gratings to the aperture problem, and the HDVR data strongly resemble the stereothresholds for 1-D gratings, which are minimal when the gratings are vertical and remain constant for orientations up to ~80° away from the vertical when expressed as spatial phase disparities [Morgan & Castet (1997) The aperture problem in stereopsis. Vision Research, 37, 2737–2744]. To explain this constancy of stereothresholds, Morgan & Castet (1997) postulated detectors sensitive to the phase disparity of the gratings seen by the two eyes (rather than their linear separation along some fixed axis, such as the horizontal). However, because 1) our VDVR data with gratings did not show this constancy and 2) the available evidence strongly suggests that there are no major differences in the disparity detectors mediating the initial HDVR and VDVR, we sought an alternative explanation for our data. We show that the dependence of the initial HDVR and VDVR on grating orientation can be successfully modeled by a bias in the number and/or efficacy of the detectors that favors horizontal disparities.

1. Introduction

When the images seen by the two eyes are slightly misaligned (binocular disparity) vergence eye movements are elicited at ultra-short latencies (Busettini, FitzGibbon & Miles, 2001; Busettini, Miles & Krauzlis, 1996; Masson, Busettini & Miles, 1997; Sheliga, FitzGibbon & Miles, 2006; 2007; Takemura, Inoue, Kawano, Quaia & Miles, 2001; Takemura, Inoue, Kawano, Quaia & Miles, 2002; Yang, Fitzgibbon & Miles, 2003). The direction of these disparity vergence responses (DVRs) is as expected of a negative feedback control system that uses binocular parallax to eliminate vergence errors: convergent with crossed disparities, divergent with uncrossed, left sursumvergent with left–hyper, and right sursumvergent with right–hyper (Busettini et al., 2001).

The initial DVRs are heavily dependent on the Fourier composition of the disparity stimulus (Sheliga et al., 2006), consistent with early spatial filtering of the monocular inputs prior to their binocular combination as in the disparity-energy model of complex cells in the striate cortex (Ohzawa, DeAngelis & Freeman, 1990). Significantly, DVRs can also be elicited at short latency by anticorrelated random-dot patterns in which the dots seen by the two eyes have opposite contrast (Masson et al., 1997; Takemura et al., 2001), even though these patterns are perceived as rivalrous and do not support depth perception (Cogan, Kontsevich, Lomakin, Halpern & Blake, 1995; Cogan, Lomakin & Rossi, 1993; Cumming & Parker, 1997; Masson et al., 1997). This is consistent with the idea that these initial vergence eye movements derive their visual inputs from early stages of cortical processing prior to the level at which depth percepts are elaborated (Masson et al., 1997). A key feature of these responses to anti-correlated patterns is that they are in the opposite direction to those elicited by correlated stimuli (Masson et al., 1997), consistent with the behavior of the disparity energy model and many disparity-selective neurons in striate cortex (Cumming & Parker, 1997; Fleet, Wagner & Heeger, 1996; Ohzawa et al., 1990; Qian, 1994; Read & Cumming, 2003; Read, Parker & Cumming, 2002). Recent studies have argued that many of the fundamental visual properties of the initial DVRs directly reflect disparity processing in the striate cortex and that these eye movements provide a powerful tool for probing the early cortical processing of disparity (Sheliga et al., 2006; 2007), though the medial superior temporal area of the cortex (MST) appears to play a critical role in the generation of these eye movements in monkeys: lesions of this area result in a major impairment of the initial DVRs (Takemura, Murata, Kawano & Miles, 2007) and single unit recordings in this area indicate that all of the major parameters of the initial DVRs are encoded in the population activity (Takemura et al., 2001; 2002). The MST area receives major projections from area MT (Desimone & Ungerleider, 1986; Ungerleider & Desimone, 1986), which receives direct projections from the striate cortex (Shipp & Zeki, 1989a), and this has generally been assumed to be the major route by which disparity signals reach MST. However, MT also receives an indirect input from V1 via V2 and V3 (Shipp & Zeki, 1989b; 1995) and very recent experiments indicate that cooling areas V2/V3 attenuates the initial HDVR as well as the responses of neurons in MT to disparity (Ponce, Lomber & Born, 2008). By concentrating on the initial DVRs it is possible to link the responses directly to the neural mechanisms decoding the binocular disparity and to avoid the many complex properties unrelated to the visual processing per se that can emerge at longer latencies, such as sensitivity to instruction (Stevenson, Lott & Yang, 1997) and perceived proximity (Enright, 1987a; 1987b; Ringach, Hawken & Shapley, 1996).

The initial HDVRs and VDRVs to cardinal stimuli (i.e., to pure horizontal and pure vertical disparities) share many basic characteristics, and the differences between them are often subtle, tending to be quantitative rather than qualitative. Thus, the initial HDVRs and VDVRs have very similar latency, contrast sensitivity, spatial frequency dependence, disparity tuning for broadband stimuli, sensitivity to orthogonal disparity offsets, and sensitivity to the relative contrasts of the competing harmonics in broadband stimuli (Busettini et al., 2001; 1996; Sheliga et al., 2006; 2007; Yang et al., 2003). This is consistent with the idea that the initial HDVRs and VDVRs are mediated by low-level disparity sensing mechanisms with very similar properties (Busettini et al., 2001).

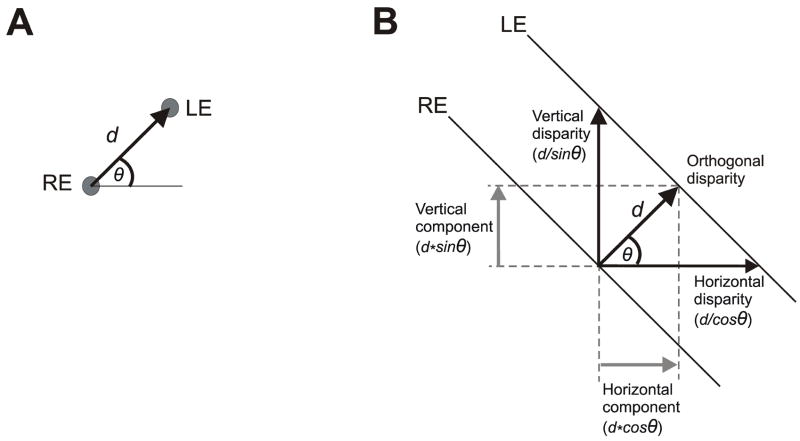
The present study used large-field visual stimuli and examined the initial HDVRs and VDVRs to disparities that always had the same magnitude but varied in direction. In Experiment 1 the visual stimuli were random-dot patterns (RDs) that were identical at the two eyes except for a position offset of 0.2° (disparity) that varied in direction from trial to trial. In Experiment 2 the stimuli were 1-D sine-wave gratings that were identical at the two eyes except for a ¼-wavelength phase difference (binocular disparity) and varied in orientation from trial to trial. When oblique disparities are applied to RDs the stimulus vector has a uniquely defined magnitude and direction, and in order to eliminate this misalignment of the two images the oculomotor system must generate a vergence response vector that has the same magnitude and direction (Fig. 1A). However, when oblique disparities are applied to large-field 1-D gratings, any component of the stimulus vector that lies parallel to the gratings will not be visible to the many small-field sensors that see only the central region of the gratings (e.g., Cumming & Parker, 2000). An observer who relies on such sensors cannot ascertain the true disparity vector applied to such grating stimuli, and this has been termed, “the aperture problem in stereopsis” (Morgan & Castet, 1997). In principle, the oculomotor system could realign the binocular images of the oblique gratings seen by such sensors by generating a vergence response vector in any one of many directions, e.g., pure horizontal, orthogonal to the gratings, pure vertical, and so forth (Fig. 1B). Clearly, the vergence response vector required for compensation here is not unique, and the observed response might be expected to depend on the algorithm that the sensors use to extract the disparity of the stimulus, which determines the individual sensor’s dependence on the direction of the disparity vector, but other factors—such as the distribution of preferred directions within the sensor population—must also be important. We now report that the initial DVRs with oblique 1-D grating stimuli had both horizontal and vertical components but often strongly favored the former, a bias not seen when oblique disparities were applied to RDs. We argue that these data reflect the aperture problem and we use simulations to indicate that a plausible explanation for them could be that the disparity detectors mediating the DVRs with oblique 1-D gratings have preferred directions covering all 360° but show a strong bias in favor of horizontal.

Figure 1.

Disparity stimulus vectors (definitions). (A) Two random dot patterns, identical except for a difference in position of 0.2°, were viewed dichoptically, but here we show only a single pair of corresponding dots; the disparity vector, given by the position of the dot seen by the left eye, LE, with respect to the position of the dot seen by the right eye, RE, had a magnitude of, d, that was fixed (0.2°), and a direction, θ°, measured counterclockwise from the horizontal, that varied from trial to trial. (B) Two 1-D sine-wave grating patterns, identical except for a phase difference of ¼-wavelength, were viewed dichoptically, but here we show only a single pair of corresponding iso-luminance lines; the disparity vector, given by the position of a point on the line seen by the left eye, LE, with respect to its nearest neighbor on the line seen by the right eye, RE, had a magnitude, d, that was fixed (¼-wavelength) and a direction, θ°, orthogonal to the grating and measured counterclockwise from the horizontal, that varied from trial to trial: termed “the orthogonal disparity”; the “horizontal disparity” (d/cosθ) and “vertical disparity” (d/sinθ) refer to the horizontal and vertical separations of the gratings seen by the two eyes; the “horizontal component disparity” (d*cosθ) and “vertical component disparity” (d*sinθ) refer to the horizontal and vertical components of the “orthogonal disparity vector”.

2. Experiment 1: Initial vergence responses when oblique disparities are applied to random dot patterns

This experiment used large RDs and recorded the HDVRs and VDVRs that were elicited when a binocular disparity of given amplitude was applied in various directions. A previous study indicated that the HDVRs to small horizontal disparities were compromised by vertical disparities of more than a few degrees and, likewise, the VDVRs to small vertical disparities were similarly compromised by horizontal disparities (Yang et al., 2003). In an attempt to minimize this disabling effect of orthogonal disparities, which was attributed to the small size of the receptive fields of the disparity detectors, we used stimuli with an absolute disparity of only 0.2°. If the vergence responses are to be aligned with the disparity stimuli then the HDVRs and VDVRs to these oblique disparities must show cosine and sine dependencies, respectively, on the direction of the disparity stimulus vector, and we report that this is indeed the case. We also report that the HDVRs and VDVRs to oblique disparities were similar in magnitude to those elicited by pure horizontal and pure vertical (i.e., cardinal) disparities whose amplitudes matched the horizontal and vertical components, respectively, of the oblique disparities.

2.1. Methods

Some of the techniques were very similar to those used previously (Sheliga et al., 2006; 2007; Yang et al., 2003) and these will be described only in brief here. Experimental protocols were approved by the NEI Institutional Review Board concerned with the use of human subjects.

2.1.1. Subjects

Four subjects participated in this study: two were the authors (HAR and FAM), the third was experienced in eye-movement recordings but uninformed about the purpose of the experiments (BMS), and the fourth was both inexperienced and uninformed (ST). All subjects had normal or corrected-to-normal vision.

2.1.2. Visual display and random dot stimulus

Dichoptic stimuli were presented using a Wheatstone mirror stereoscope (Sheliga et al., 2006; 2007). In an otherwise darkened room, each eye saw a computer monitor (Sony GDM-F520 21” CRT) through a 45° mirror, creating a binocular image straight ahead at a convergence distance of 530 mm from the eyes’ corneal vertices, which was also the optical distance to the images on the monitor screen. Monitor screens were 400 mm wide and 300 mm high (45.6° × 33.5°), with 1600 by 1200 pixels (i.e., 37 pixels/° directly ahead of each eye) and a refresh rate of 100 Hz. Each monitor was driven via an attenuator (Pelli, 1997a) by an independent PC. This arrangement allowed presentation of black and white images with 11-bit grayscale resolution. Two look-up tables (one for each monitor) each with 2048 equally spaced luminance levels from 0 cd/m² to 37.5 cd/m² were created.

The visual stimuli consisted of RDs that were identical at the two eyes except for a position difference of 0.20°, which specified the magnitude of the binocular disparity vector. The RDs were each presented inside a centered circular aperture (diameter, 33°) with a grey surround of luminance 18.8 cd/m². The individual dots were circular (diameter, 0.5°), occupied 10% of the pixels, and were either black or white (contrast 70%) on a grey background whose luminance matched that of the surround. The disparity stimulus vector was defined by the difference in the positions of the images seen by the two eyes (left minus right), with a direction, θ, measured counterclockwise from the horizontal: see Fig. 1A. In our sign convention, rightward and upward were positive so that the disparity was “crossed” when the vector was rightward (θ=0°), “left-hyper” when upward (θ=90°), “uncrossed” when leftward (θ=180°), and “right-hyper” when downward (θ=270°). We examined the dependence of the HDVR and VDVR on θ, which ranged from 0° to 337.5° in 22.5° intervals. Additional trials included pure horizontal and pure vertical disparities that matched the horizontal and vertical components, respectively, of the oblique disparities (magnitudes: 0.08°, 0.14°, 0.19°, and 0.20°). There were 20 different patterns of dots that were randomly selected from trial to trial.

2.1.3. Eye movement recordings

The horizontal and vertical positions of both eyes were recorded with the electromagnetic induction technique (CNC Engineering, Seattle, USA) using scleral search coils embedded in silastin rings (Skalar, Delft, The Netherlands), and the signals from each eye were sampled at 1KHz (Collewijn, van der Mark & Jansen, 1975; Robinson, 1963). At the beginning of each recording session a calibration procedure was performed for each of the two eyes independently with defined fixations targets as previously described (Sheliga et al., 2006; 2007).

2.1.4. Procedures

At the start of each trial, a central fixation cross (width 10°, height 5°, thickness 0.05°) appeared on both monitors. When the subject’s eyes had been positioned within 2° of the center of the crosses for 800 to 1100 ms (randomly varied), the crosses were replaced with the disparity stimuli (randomly chosen from a lookup table) for 150 ms, after which the screen changed to uniform grey (18.8 cd/m²) marking the end of the trial. After an inter-trial interval of 500 ms the fixation crosses reappeared signaling the start of another trial. The subjects were asked to fixate the center of the crosses and to refrain from blinking or making saccades except during the inter-trial interval. If no saccades were detected during the period of the trial the data were stored on a hard disk, otherwise the trial was aborted and repeated later. A complete block of trials had 29 stimulus conditions and was repeated at least 50 times.

The experimental paradigms were controlled by three PCs, which communicated via Ethernet using a TCP/UDP/IP protocol. One of the PCs was running the Real-time Experimentation software (REX) developed by Hays et al (1982), and provided the overall control of the experiment as well as acquiring, displaying, and storing the eye-movement data. The other two PCs were running a Matlab subroutine (MathWorks Inc., Natick, USA) utilizing the Psychophysics Toolbox extension (Brainard, 1997; Pelli, 1997b) and generated the binocular visual stimuli upon receiving a start signal from the REX machine (Sheliga et al., 2006; 2007).

2.1.5. Data analysis

The horizontal and vertical eye-position measures obtained during the calibration procedure were each fitted with second-order polynomials whose parameters were then used to linearize the corresponding eye-position data recorded during the experiment proper. The linearized eye-position measures were smoothed with a 6-pole Butterworth filter (3 dB at 45 Hz) and mean temporal profiles were computed for each stimulus condition. Trials with saccadic intrusions (that had failed to reach the eye-velocity threshold of 18°/s during the experiment) were deleted. The horizontal (vertical) vergence angle was computed by subtracting the horizontal (vertical) position of the right eye from the horizontal (vertical) position of the left eye. In our convention, rightward and upward eye movements were positive so that the DVRs were convergent when the vergence vector was rightward (0°), left sursumvergent (LSSV) when the vergence vector was upward (90°), divergent when the vergence vector was leftward (180°), and right sursumvergent (RSSV) when the vergence vector was downward (270°). The initial horizontal (HDVR) and vertical (VDVR) vergence responses for each stimulus condition were quantified by measuring the changes in the horizontal and vertical vergence positions over the 70-ms time periods commencing 70 ms after the onset of the disparity stimuli. The minimum latency of the DVRs was ~70 ms from the first appearance of the disparity stimuli so that these vergence-response measures were restricted to the initial open-loop period. These measures were also used to obtain an estimate of the initial direction of the DVRs, φ, given by arctan(VDVR / HDVR).

2.2. Results

2.2.1. Raw response measures

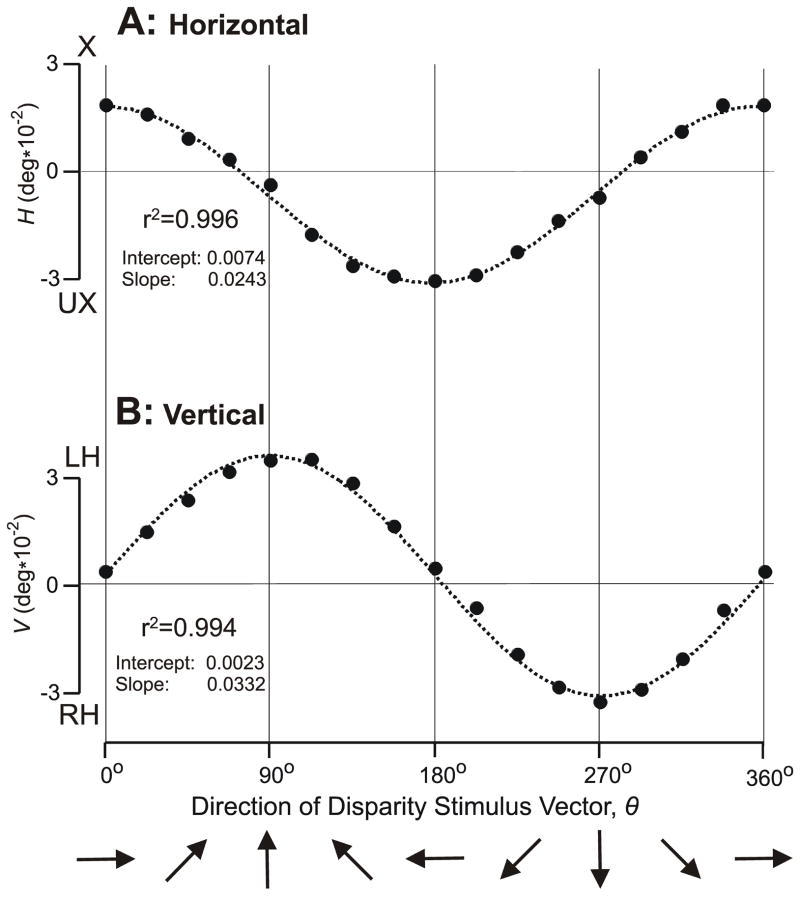
Figure 2 shows the dependence of the initial HDVR and VDVR measures on the direction of the disparity vector, θ, over the full 360° range for subject FAM: see the filled symbols. The curves in dotted line are the least-squares best-fit plots of a+(b*cosθ) in (A) and a+(b*sinθ) in (B), where a (offset) and b (gain) are free parameters. For both fits the r² values were 0.99.

Figure 2.

The initial vergence responses when a 0.2° disparity was applied to random dot patterns: dependence of response measures on the direction of the disparity vector, θ (subject FAM). (A) Mean changes in horizontal vergence, H, in filled symbols; convergent responses are positive; X, crossed disparity; UX, uncrossed disparity. (B) Mean changes in vertical vergence, V, in filled symbols; left-sursumvergent responses are positive; LH, left-hyper disparity; RH, right-hyper disparity. Dotted curves are least squares best-fit plots of a+(b*cosθ) in (A) and a+(b*sinθ) in (B), where a and b are free parameters. Each datum point is the mean response to 110–120 repetitions of the stimulus. Standard errors of the means were smaller than the symbols (range: 0.0008–0.0011°).

2.2.2. Folded response measures

Because the pattern of responses in each of the four quadrants of the disparity vector space (θ) were very similar, it was possible to improve the signal-to-noise ratio and simplify the subsequent analysis by folding the data into one quadrant using the following procedure. First, we calculated the mean HDVR measures for each of the pairs of oblique stimuli whose horizontal disparity components were the same but whose vertical components had opposite directions (e.g., θ=20° and 340°). Then, the mean HDVR responses to uncrossed disparities of a given magnitude were subtracted from the mean HDVR responses to crossed disparities of the same magnitude, yielding the “folded” response measures, H_F. Similarly, we calculated the mean VDVR measures for the pairs of oblique stimuli whose vertical disparity components were the same but whose horizontal components had opposite directions (e.g., θ=20° and 160°). Then, the mean VDVR responses to right-hyper disparities of a given magnitude were subtracted from those elicited by left-hyper disparities of the same magnitude, yielding the “folded” response measures, V_F. The filled circles in Fig. 3 show these folded vergence response measures for the complete data set obtained from subject FAM, with the H_F measures in (A) and the V_F measures in (B). Importantly, H_F and V_F were well predicted by H_F0cosθ_F and V_F90sinθ_F, respectively, where H_F0 was the magnitude of H_F when θ_F=0° and V_F90 was the magnitude of V_F when θ_F=90°: see the curves plotted in Fig. 3, for which the r² values were 0.999 (H_F) and 0.998 (V_F). The folded vergence response measures, H_F and V_F, of all 4 subjects were well described by this cosine (sine) scaling of the DVRs to pure horizontal (vertical) disparities: mean r² values (±SD) were 0.996±0.004 (H_F) and 0.997±0.002 (V_F).

Figure 3.

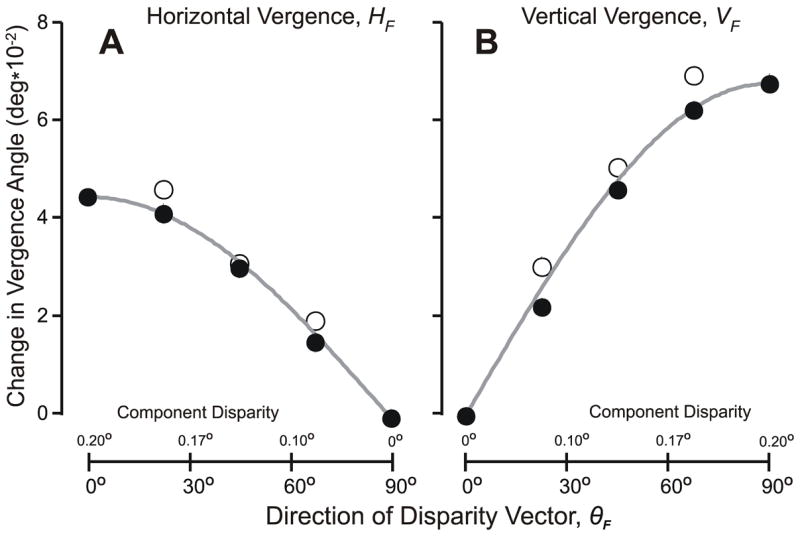
The initial vergence responses when oblique disparities were applied to random-dot patterns: dependence of the folded response measures on the direction of the folded disparity vector, θ_F (subject FAM). (A) Mean changes in horizontal vergence, H_F; data in filled symbols were obtained with oblique disparity vectors with a magnitude of 0.2°; data in open symbols were obtained with pure horizontal disparity vectors that matched the horizontal components of the oblique disparity vectors, and the magnitudes of their disparities, in degrees, are given on the abscissas above the axis (note: values increase to the left); grey curves are the values of H_F given by H_F0cosθ_F. (B) Mean changes in vertical vergence angle, V_F; data in filled symbols were obtained with oblique disparity vectors with a magnitude of 0.2°; data in open symbols were obtained with pure vertical disparity vectors that matched the vertical components of the oblique disparity vectors, and the magnitudes of their disparities, in degrees, are given on the abscissas above the axis; grey curves are the values of V_F given by V_F90sin θ_F.

The folded measures, H_F and V_F, with oblique disparities were also well correlated with the folded measures obtained when the RDs were subjected to cardinal disparities, i.e., pure horizontal and pure vertical disparities, that matched the horizontal and vertical components, respectively, of the oblique disparities: see the open circles in Fig. 3, for which the r² values were 0.992 (H_F) and 0.988 (V_F). This correlation was very good in all 4 subjects: mean r² values (±SD) were 0.993±0.005 (H_F) and 0.993±0.005 (V_F). However, in most instances, the responses to cardinal disparities were slightly greater than those to oblique disparities with matching cardinal components, especially near the optimal: On average, H_F was 13±14% greater with the cardinal stimuli than with the oblique stimuli, and for V_F this difference was 12±14%.

2.2.3. Directional errors

Deviations of H_F (and V_F) from cosine (and sine) dependencies on the direction of the disparity vector with oblique disparities—such as those seen in Fig. 3—will be referred to as “Directional Decoding Errors”. These errors were generally small when oblique disparities were applied to RDs but, nonetheless, the vergence response vectors were often not accurately aligned with the disparity stimulus vectors because of two additional sources of directional error. The first of these is evident in Fig. 2 from the orthogonal components with cardinal stimuli, i.e., the VDVRs with pure horizontal disparity stimuli and the HDVRs with pure vertical disparity stimuli. Note that these directional errors, which we will refer to as “Offset Errors”, were generally small (mean±SD: HDVR, 0.006±0.009°; VDVR, 0.002±0.004°) and are not apparent in the folded response measures in Fig. 3 because these measures are based on differences, i.e., the responses to crossed disparities have had the responses to the corresponding uncrossed disparities subtracted from them, and the responses to left-hyper disparities have had the responses to the corresponding right-hyper disparities subtracted from them. Another source of directional errors, which we will term “Gain Asymmetry Errors”, results from differences in the overall scaling of the HDVRs and VDVRs, which in Fig. 3 is evident from the difference in the peak H_F and V_F measures. Thus, these errors are apparent from the gain asymmetry given by H_F0/V_F90, which averaged 0.69±0.17 (range, 0.49–0.90) and accounted for most of the directional errors when oblique stimuli were applied to RDs.

2.3. Discussion of Experiment 1

We identified three potential sources of directional error with oblique disparity stimuli: 1) Offset Errors, which Busettini et al (2001) described in some detail (referring to them as “default responses”) and argued were a response to uncorrelation (i.e., the net response to the “false” matches); 2) Gain Asymmetry Errors, which we postulate are due to differences in the gains of the horizontal and vertical vergence controllers, and 3) Directional Coding Errors, which we now postulate reflect errors in the operation of the disparity sensing mechanism and so have the potential to provide insights into the low-level decoding of disparity. To examine the Directional Coding Errors more closely we first computed the “normalized folded vertical responses”, $V_F^{\prime }$ , using the known gain asymmetry, as follows:

$$V_F^{\prime }=V_F\text{g}\frac{H_{F0}}{V_{F90}}$$ (1)

It was then possible to compute the “directions of the normalized folded vergence response vectors”, ${\phi }_F^{\prime }$, given by arctan( $V_F^{\prime }/H_F$), and these values are plotted as a function of θ_F in Fig. 7, the data obtained with RDs being shown in open circles, with those for the subject FAM in (A) and the mean values for all subjects in (B). In this plot, the unity-slope (dashed) line indicates the data expected if the DVR mechanism were to decompose the oblique disparity vector into its sine (horizontal) and cosine (vertical) components so that the folded vergence response vector, ${\phi }_F^{\prime }$, was accurately aligned with the folded disparity stimulus vector, θ_F, i.e., no Directional Coding Errors. It is clear that the RD data in Fig. 7 are all very close to the unity-slope (dashed) line: for FAM, the fit to the unity-slope line had an r² value of 0.998, and for all subjects these fits had a mean r² (±SD) of 0.998±0.001. This suggests that the disparity sensing mechanism utilized by the DVR mechanism can accurately decode the disparity vector into its cosine and sine components when confronted with broadband RDs. However, we will see that there were appreciable deviations from this unity-slope line (i.e., Directional Coding Errors) in Experiment 2, which used oblique 1-D gratings, providing new insights into the disparity decoding mechanism mediating the DVRs to these stimuli.

Another interesting feature of the data obtained with RDs was that the folded HDVR and VDVR measures obtained with oblique disparities (closed circles in Fig. 3) usually fell slightly short of the measures obtained with pure cardinal disparities (open circles in Fig. 3). This shortfall probably reflects the disabling effect of adding an orthogonal component to the disparity, as described by Yang et al (2003), who attributed it to the limited extent of the receptive fields of the underlying disparity detectors.

3. Experiment 2: Initial vergence responses when disparities are applied to oriented 1-D gratings

The second Experiment recorded the initial HDVRs and VDVRs when binocular disparities were applied to 1-D sine-wave gratings and examined their dependence on the orientation of the grating. The gratings seen by the two eyes were identical in spatial frequency, contrast and orientation, and differed only in phase (by ¼-wavelength). Previous studies that recorded the initial vergence eye movements when disparities were applied to 1-D grating stimuli used only cardinal orientations, i.e., pure horizontal or pure vertical gratings (Sheliga et al., 2006; 2007). Grating stimuli are ambiguous insofar as a ¼-wavelength disparity can also be described as a ¾-wavelength disparity of opposite sign. However, the previous studies with gratings indicated that the direction of the associated vergence responses was always in accordance with a negative feedback mechanism that compensates for the ¼-wavelength phase difference, consistent with the idea that the underlying sensors give greatest weight to the nearest-neighbor matches. For a stereo pair of parallel gratings the nearest neighbor matches are those at right angles to the grating orientation (“orthogonal matches”), but it is possible that there are additional matching constraints that are not evident with cardinal gratings. For example, the matching algorithm could utilize “the nearest neighbor matches that are horizontally aligned”, yielding a disparity measure that would be sensitive to the orientation of the gratings. A further potential complication with sine-wave gratings is that the disparity detectors might sense the phase difference rather than the linear separation per se. Morgan & Castet (1997) showed that, when disparity was expressed in terms of the phase difference, the stereo acuity for 1-D gratings was little affected by tilting the grating up to 80° away from the optimal orientation (vertical). This led these workers to suggest that the underlying disparity detectors might be sensing the phase difference, although the orientation of the axis along which this operation was being performed—horizontal, orthogonal or some intermediate—was unclear because the phase difference is independent of orientation (except at, or near, the extremes, i.e., parallel with the grating). We now report that the initial HDVRs to oriented gratings show a very similar insensitivity to changes in the orientation of the grating away from the optimal (vertical). However, whereas the HDVR is least sensitive to changes in orientation near the optimal (vertical), the sensitivity of the VDVR to changes in orientation is almost at its greatest near the optimal (horizontal). Because the available evidence strongly suggests that HDVRs and VDVRS are mediated by disparity detectors with very similar properties (see Introduction), we argue that the insensitivity of the HDVR to orientation is unlikely to be explained by some property of the disparity sensing mechanism. Instead, we suggest that the dependence of the HDVR (and VDVR) on orientation results from an anisotropy in the efficacy/distribution of the disparity sensors that strongly favors the horizontal vector.

3.1. Methods

The subjects, eye-movement recording techniques, experimental procedures, and data analysis were identical to those in Experiment 1.

3.1.1. Visual display

The visual stimuli consisted of 1-D gratings with sinusoidal luminance profiles (Michelson contrast, 64%) presented inside a circular aperture (33° diameter) with a grey surround matching the mean luminance of the grating (18.8 cd/m²). On any given trial, the gratings seen by the two eyes were always identical in spatial frequency, contrast and orientation but differed in phase (disparity) by ¼-wavelength; no disparity was applied to the apertures. The orientation of the sine-wave gratings was defined by the axis of iso-luminance, measured counterclockwise from the horizontal. The magnitude, d, and direction, θ, of the associated disparity vector were measured orthogonal to the orientation of the grating (termed, “the orthogonal disparity”): see Fig. 1B. Note that the terms, “horizontal disparity” and “vertical disparity”, will be used to refer to the horizontal (d/cosθ) and vertical (d/sinθ) separations of the oblique gratings seen by the two eyes, whereas the “horizontal component disparity” and “vertical component disparity” will be used to refer to the horizontal (d*cosθ) and vertical (d*sinθ) components of the “orthogonal disparity vector”.

The sine-wave gratings were used in two separate paradigms. One paradigm examined the dependence of the HDVR and VDVR on spatial frequency (0.05–4.24 cycles/°) with disparity vectors in each of 16 directions (θ ranging from 0° to 337.5° in 22.5° intervals). In additional recording sessions, a second paradigm examined the dependence of the HDVR and VDVR on the direction of the disparity vector in more detail (θ ranging from 0° to 350° in 10° intervals) for each of four spatial frequencies (0.1, 0.25, 0.5, and 0.75 cycles/°). This last paradigm also included pure vertical and pure horizontal gratings (“cardinal stimuli”) whose spatial frequencies (and disparities) matched the horizontal and vertical spatial frequencies (and disparities), respectively, of the oblique gratings. The overall position of the gratings varied randomly from trial to trial in ⅛-wavelength steps.

3.2. Results

3.2.1. Raw response measures

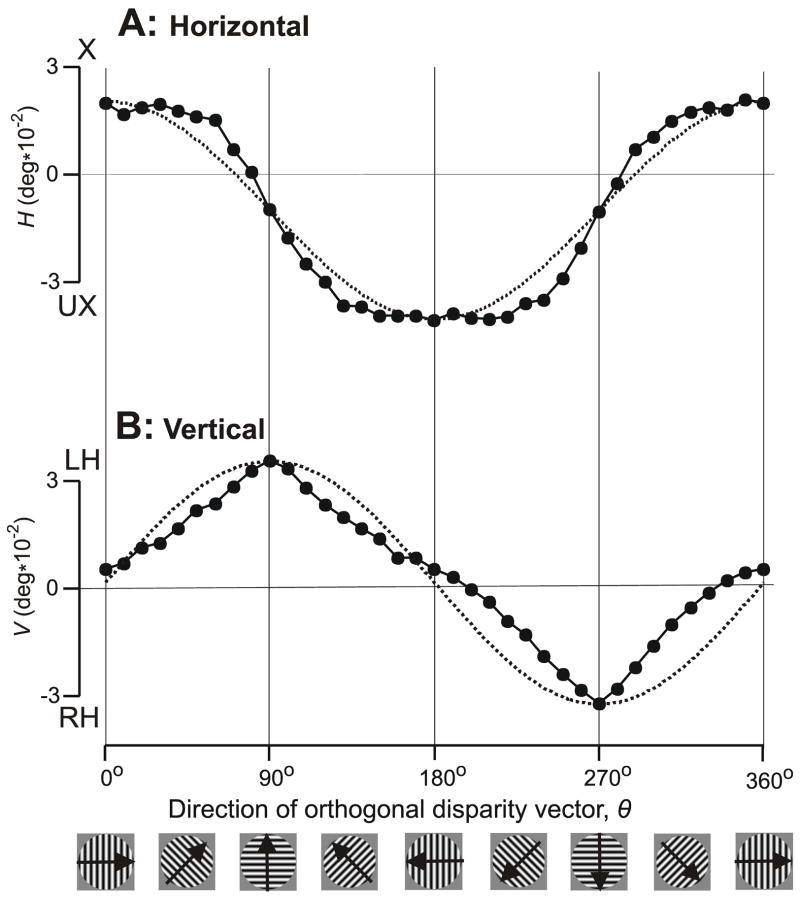
The filled symbols in Fig. 4 show the dependence of the initial HDVR (in A) and VDVR (in B) measures on the direction of the orthogonal disparity vector, θ, over the full 360° range for subject FAM with the 0.25 cycles/° grating stimulus. The organization of this figure is similar to that of Fig. 2, although here the curves in dotted line are plots of a+(b*cosθ) in (A) and a+(b*sinθ) in (B), where a (offset) and b (gain) are free parameters except that the functions are forced through the data peaks. It is clear that the peaks of the HDVR and VDVR measures are in phase with the peaks of the horizontal and vertical components, respectively, of the orthogonal disparity vector but the intermediate values deviate substantially from the cosine/sine dependencies on that were seen with RDs in Experiment 1: the HDVR measures show flattened peaks and have the appearance of a somewhat rounded square wave whereas the VDVR measures show sharpened peaks and have the appearance of a slightly distorted triangle wave.

Figure 4.

The initial vergence responses when 1-D sine-wave gratings (0.25 cycles/°) had a binocular disparity of 1/4–wavelength: dependence of response measures on the direction of the orthogonal disparity vector, θ (subject FAM). (A) Mean changes in horizontal vergence angle, H, in filled symbols; convergent responses are positive; X, crossed disparity; UX, uncrossed disparity. (B) Mean changes in vertical vergence angle, V, in filled symbols; left-sursumvergent responses are positive; LH, left-hyper disparity; RH, right-hyper disparity. Dotted curves are plots of a+(b*cosθ) in (A) and a+(b*sinθ) in (B), where a and b are free parameters and the functions are forced through the data peaks. Cartoons at bottom show sample grating patterns and the arrows indicate the directions of the orthogonal disparity vectors. Each datum point is the mean response to 203–304 repetitions of the stimulus. Standard errors of the means were smaller than the symbols (range: 0.0006–0.0015°).

3.2.2. Folded response measures

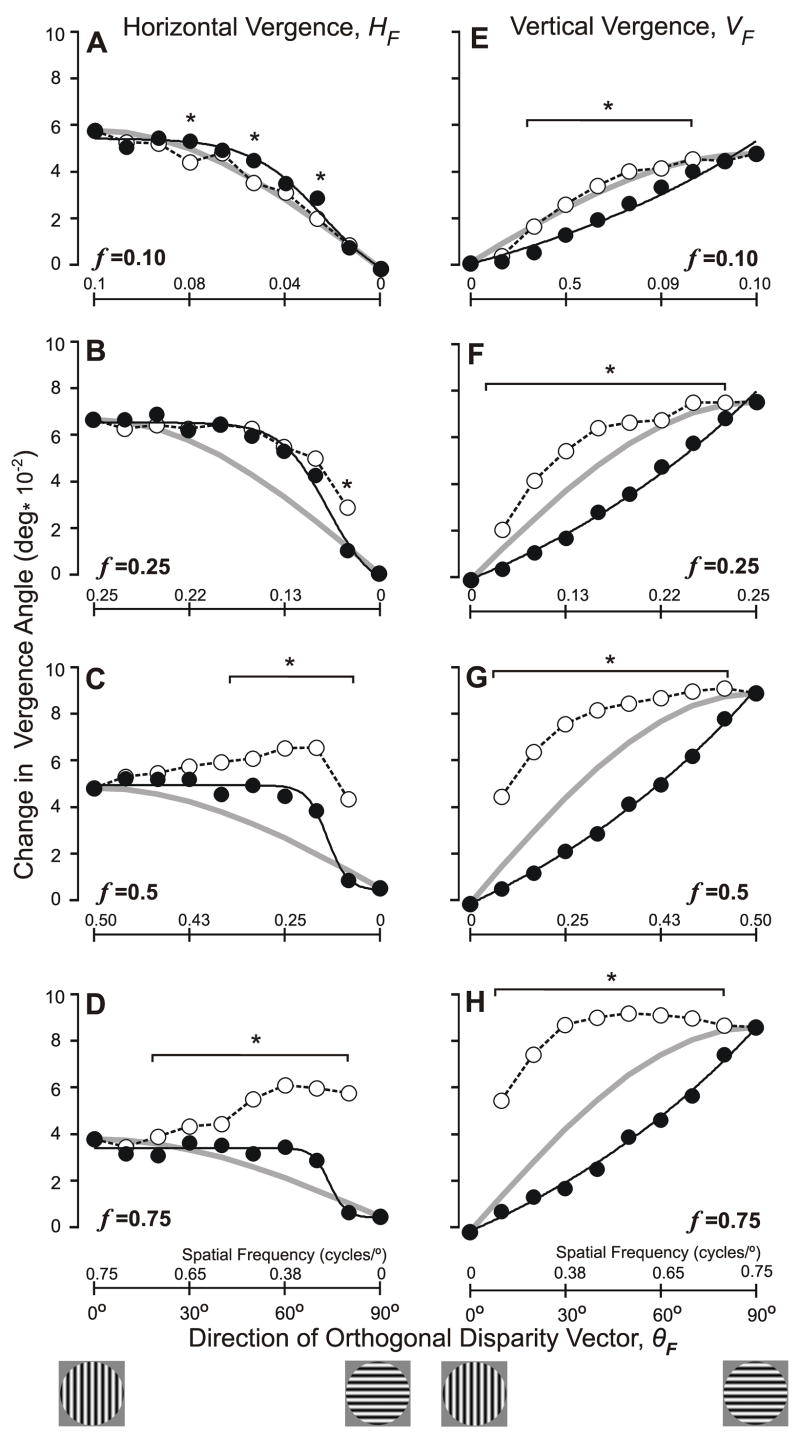
Because the pattern of responses in each of the four quadrants of the disparity vector space (θ) was essentially the same, we folded the data into one quadrant using the same procedure as in Experiment 1. The filled symbols in Fig. 5 show these folded vergence response measures for the complete data set obtained from subject FAM, with the H_F measures in the left column (A–D) and the V_F measures in the right column (E–H), while each row shows the data obtained with one of the 4 spatial frequencies: A, E (0.1 cycles/°); B, F (0.25 cycles/°); C, G (0.5 cycles/°); D, H (0.75 cycles/°). Note that the data in Fig. 4 were obtained with 0.25 cycles/° and are seen in Fig. 5B,F. The abscissas in Fig. 5, which specify the direction of the folded orthogonal disparity vector (θ_F), extend only from 0° to 90° —representing the shift from pure horizontal to pure vertical disparity vectors—and the small cartoons below the graphs indicate the orientations of sample (cardinal) grating patterns.

Figure 5.

The initial vergence responses when 1-D sine-wave gratings (0.25 cycles/°) had a binocular disparity of 1/4–wavelength: dependence of the folded response measures on the direction of the (folded) orthogonal disparity vector, θ_F (subject FAM). (A–D) Mean changes in horizontal vergence, H_F; data in filled symbols were obtained with obliquely oriented gratings with orthogonal spatial frequencies (f) of 0.1, 0.25, 0.5, and 0.75 cycles/°; the black lines show the least-squares best fits to these data obtained with Expression 1 (sigmoid function); data in open symbols linked by dashed lines were obtained with vertical gratings whose spatial frequencies matched the horizontal spatial frequencies of the oblique gratings (values, in cycles/°, are given on the abscissas above the axes, and increase in value to the left); grey curves are the values of H_F given by H_F0cos θ_F. (E–H) Mean changes in vertical vergence, V_F; data in filled symbols were obtained with obliquely oriented gratings with orthogonal spatial frequencies (f) of 0.1, 0.25, 0.5, and 0.75 cycles/°; the black lines show the least-squares best fits to these data obtained with Expression 2 (exponential function); data in open symbols linked by dashed lines were obtained with horizontal gratings whose spatial frequencies matched the vertical spatial frequencies of the oblique gratings (values, in cycles/°, are given on the abscissas above the axes); grey curves are the values of V_F given by V_F90sin θ_F. Asterisks indicate those data obtained with oblique gratings (closed symbols) that were significantly different (p<0.05, t-test) from the data obtained with matching cardinal gratings (open symbols). Cartoons at bottom show sample grating patterns. Standard errors of the means were smaller than the symbols (range: 0.0008–0.0034°).

It is now evident that, for subject FAM at least, as θ_F was shifted from horizontal to vertical (i.e., from 0° to 90° in Fig. 5), H_F always started out close to maximal and showed little change at first—especially with the gratings of higher spatial frequency, which showed a clear initial plateau—before declining towards zero as the disparity vector approached vertical, whereas V_F always started out close to zero and generally increased monotonically at a steadily increasing rate—especially with the gratings of higher spatial frequency—until reaching a peak when the disparity vector reached vertical. Thus, both H_F and V_F generally showed their lowest sensitivity to changes in θ_F when the latter was near horizontal (0°).

The dependence of H_F on θ_F deviated substantially from the cosine prediction (grey curves in Fig. 5A–D) and was examined quantitatively by fitting the values of H_F with a sigmoid function of the form:

$$B+\frac{A_{\mathit{max}}}{1+e^{\left(\frac{{\theta }_F-P_C}{K}\right)}}$$ (2)

where B is the offset, A_max is the maximum amplitude, and P_C is the center point of the curve (all in degrees), while K is the decay constant (in degrees⁻¹). The least squares best fits are shown in continuous black line in Fig. 5A–D and, on average, explained 97% of the variance of these data. The best-fit parameters for the data obtained from all subjects are listed in Table 1 and the mean r² value (±SD) for the entire data set was 0.974±0.057, indicating that this sigmoid function always provided a very good description of the H_F data. The values of θ_F at which these best-fit functions were 90% of their maximum value were calculated to provide estimates of the extent of the initial plateaux: for the four subjects, the mean (±SD) values were 65.6±8.9° at 0.1 cycles/°, 66.9±2.0° at 0.25 cycles/°, 66.4±7.8° at 0.5 cycles/°, and 66.1±3.9° at 0.75 cycles/°, i.e., the extent of the initial plateau generally showed only minor dependence on spatial frequency.

Table 1.

The dependence of H_F on θ_F: parameters of the best-fit sigmoid functions (given by Expression 2).

subject	f	B	Amax	Pc	K	r2	90%
FAM	0.10	−0.011	0.065	71.7	11.3	0.997	61.1
	0.25	−0.008	0.064	73.8	7.3	0.997	64.7
	0.50	0.004	0.044	73.5	3.2	0.997	57.7
	0.75	0.004	0.029	74.0	2.6	0.995	75.4
BMS	0.10	−0.016	0.087	74.8	10.8	0.995	79.3
	0.25	−0.007	0.077	76.6	5.7	1.000	68.5
	0.50	−0.001	0.045	78.5	2.9	0.987	72.7
	0.75	0.002	0.024	75.4	5.0	0.988	59.0
HAR	0.10	−0.016	0.085	73.1	11.3	0.997	63.2
	0.25	−0.004	0.056	75.8	5.3	0.996	67.5
	0.50	0.001	0.027	76.0	2.9	0.992	68.8
	0.75	0.005	0.008	71.9	8.4	0.900	62.4
ST	0.10	−0.001	0.137	68.6	4.8	0.995	58.7
	0.75	0.000	0.016	72.7	2.3	0.804	67.6

f, spatial frequency in cycles/°; B, offset in degrees; A_max, amplitude in degrees; P_c, center point of curve in degrees; K, decay constant in degrees⁻¹; r², coefficient of determination; 90%, value of θ_F at which H_F was 90%.

The dependence of V_F on θ_F deviated substantially from the sine prediction (grey curves in Fig. 5E–H) and was examined quantitatively by fitting the values of V_F with an exponential function of the form:

$$B+S\ast e^{\left(\frac{{\theta }_P}{\tau }\right)}$$ (3)

where B is the offset, S is the slope (both in degrees), and τ is a rate constant (in degrees⁻¹). The least squares best fits are shown in continuous black line in Fig. 5E–H and, on average, explained 99% of the variance of these data. The best-fit parameters for the data obtained from all subjects are listed in Table 2 and the mean r² value (±SD) for the entire data set was 0.992±0.008, indicating that this exponential function always provided a very good description of the V_F data. The rate constant, τ, showed little dependence on spatial frequency, with a mean±SD of 99.9±0.4/° for the entire data set.

Table 2.

The dependence of V_F on θ_F: parameters of the best-fit exponential functions (given by Expression 3).

subject	f	B	S	τ	r2
FAM	0.10	−0.035	0.035	100.0	0.991
	0.25	−0.055	0.055	100.5	0.997
	0.50	−0.063	0.062	100.0	0.999
	0.75	−0.060	0.059	100.0	0.998
BMS	0.10	−0.034	0.035	100.0	0.996
	0.25	−0.057	0.055	100.0	0.998
	0.50	−0.060	0.054	98.8	0.989
	0.75	−0.040	0.036	99.3	0.981
HAR	0.10	−0.018	0.019	100.0	0.989
	0.25	−0.026	0.027	100.0	0.997
	0.50	−0.030	0.029	100.0	0.997
	0.75	−0.028	0.025	100.0	0.987
ST	0.10	−0.040	0.040	100.0	0.994
	0.75	−0.035	0.032	99.5	0.971

f, spatial frequency in cycles/°; B, offset in degrees; S, slope in degrees; τ, decay constant in degrees⁻¹; r², coefficient of determination.

The open symbols linked by dashed lines in Fig. 5 show the folded DVR measures when ¼-wavelength disparities were applied to pure vertical (A–D) and pure horizontal (E–H) sine-wave gratings whose spatial frequencies matched the horizontal and vertical spatial frequencies, respectively, of the oblique gratings. The spatial frequencies of these “cardinal stimuli” are indicated above the horizontal axes in Fig. 5; of course, the scales on these abscissas are not linear—varying as the sine or cosine of θ_F—and, in the left column, the spatial frequencies increase in value to the left. With the lower spatial frequencies (0.1 and 0.25 cycles/°), the H_F measures obtained with the oblique and matching cardinal stimuli were generally similar—compare the closed and open circles in Fig. 5A, B—though there were a few differences that were statistically significant (p<0.05, t-test): see the asterisks. However, with the higher spatial frequencies (0.5 and 0.75 cycles/°), significant differences between the two H_F data sets were commonplace; in particular, the H_F data obtained with the cardinal stimuli did not show the initial plateau but rather a steady increase towards a peak: see the open circles in Fig. 5C, D. The V_F data obtained with oblique and matching cardinal stimuli were also dramatically different: the plots for the data obtained with oblique gratings (filled circles) are all concave upwards whereas the plots for the data obtained with matching cardinal stimuli (open circles) are all concave downwards (Fig. 5E–H).

These differences between the data obtained with oblique and matching-cardinal stimuli were typical of all subjects. In fact, the data plotted in open circles in Fig. 5 represent fragments of the spatial-frequency tuning curves, which are typically Gaussian when plotted on a log abscissa (Sheliga et al., 2006) and will be described in the next section.

3.2.3. Dependence on spatial frequency

Figure 6A,B shows the dependence of the folded vergence responses of subject FAM on spatial-frequency when the gratings had one of five orientations as θ_F ranged from 0° to 90° in 22.5° intervals, with the H_F data plotted in A and the V_F data plotted in B. When plotted on a logarithmic abscissa (as in Fig. 6A,B), the data set for a given grating orientation was always well fit by a Gaussian function (r²>0.99) with a standard deviation (σ) that showed only minor dependence on θ_F: see the parameters of the best-fit Gaussian functions in Table 3 (H_F) and Table 4 (V_F) listed under “orthogonal axis”. The data in Fig. 6 are in line with those in Fig. 5 insofar as the H_F curves all remain close to maximal amplitude when θ_F is ≤45° and show a clear reduction in amplitude only when θ_F is 67.5° (away from horizontal), whereas the V_F curves show progressive reductions in amplitude with each change in θ_F that shifts the (orthogonal) disparity vector further away from vertical. The spatial frequency at the peak of the Gaussian function (f_o) tended to increase slightly as θ_F shifted from horizontal to vertical for both the H_F and the V_F data: see the closed symbols linked by continuous lines in Fig. 6C (H_F) and Fig. 6D (V_F), which show the dependence of f_o on θ_F for each of the 4 subjects.

Figure 6.

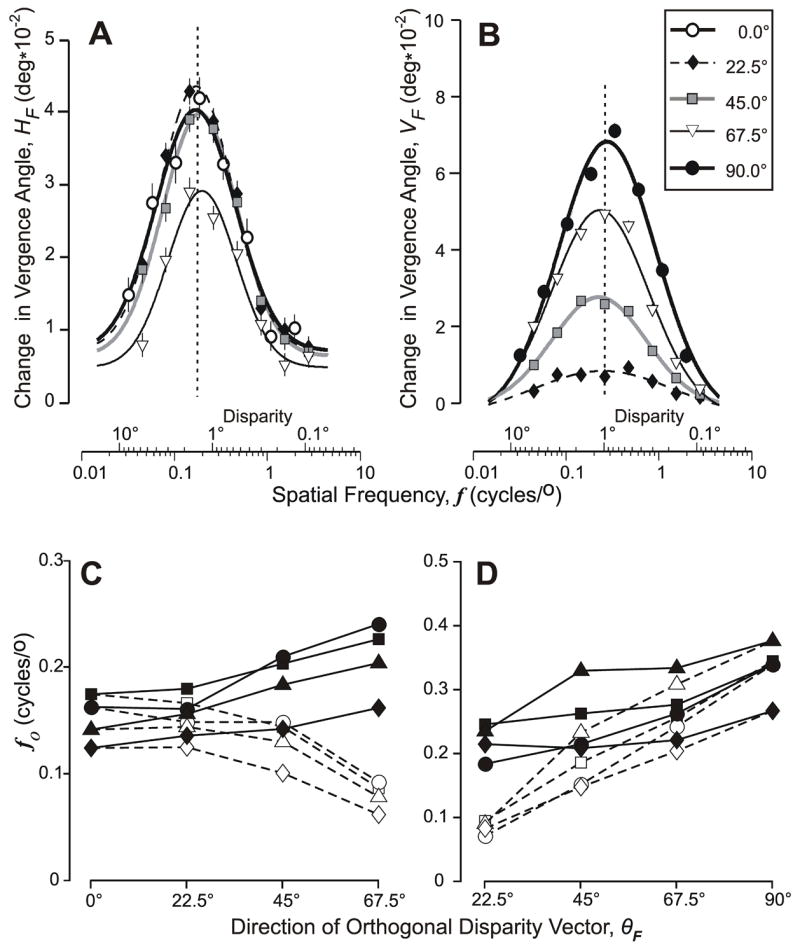
The initial vergence responses when 1-D sine-wave gratings had a binocular disparity of 1/4–wavelength: dependence of the folded response measures on the orthogonal spatial frequency of the grating (in cycles/°) when the orthogonal disparity vector (θ_F) had one of five (folded) directions. (A) Mean changes in horizontal vergence, H_F, as θ_F was fixed at 0°(open circles), 22.5°(diamonds), 45°(squares), and 67.5°(triangles); curves show the least-squares best fit Gaussian functions whose parameters are listed in Table 3; vertical dashed line is aligned on the peak of the Gaussian for which θ_F=0°; subject FAM. (B) Mean changes in vertical vergence, V_F, as θ_F was fixed at 22.5°(diamonds), 45°(squares), 67.5°(triangles), and 90°(closed circles); curves show the least-squares best fit Gaussian functions whose parameters are listed in Table 4; vertical dashed line is aligned on the peak of the Gaussian for which θ_F=90°; subject FAM. (C) Closed symbols show the spatial frequency at the peak of the best-fit Gaussian function (f_o)—based on fits like those in (A)—as a function of the direction of the (folded) orthogonal disparity vector, θ_F, for all four subjects: FAM (squares), BMS (circles), HAR (triangles), and ST (diamonds); open symbols as for the closed symbols except that spatial frequency was specified with respect to the horizontal axis. (D) As in (C) except based on V_F measures like those in (B), and open symbols show data when spatial frequency was specified with respect to the vertical axis.

Table 3.

The dependence of H_F on log spatial frequency for various values of θ_F: parameters of the best-fit Gaussian functions.

	Cardinal axis (horizontal)					Orthogonal axis
Subject	θF	Apeak	fo	σ	r2	Apeak	fo	σ	r2
FAM	0	0.054	0.17	0.43	0.991	0.054	0.17	0.43	0.991
	22.5	0.058	0.17	0.39	0.998	0.058	0.18	0.39	0.998
	45.0	0.056	0.14	0.40	0.997	0.056	0.20	0.40	0.997
	67.5	0.039	0.09	0.36	0.996	0.039	0.23	0.36	0.996
BMS	0	0.065	0.16	0.43	0.995	0.065	0.16	0.43	0.995
	22.5	0.067	0.15	0.53	1.000	0.067	0.16	0.53	1.000
	45.0	0.066	0.15	0.44	0.997	0.066	0.21	0.44	0.997
	67.5	0.056	0.09	0.53	0.997	0.056	0.24	0.53	0.997
HAR	0	0.053	0.14	0.45	0.998	0.053	0.14	0.45	0.998
	22.5	0.052	0.14	0.43	0.997	0.052	0.16	0.43	0.997
	45.0	0.058	0.13	0.44	0.994	0.058	0.18	0.44	0.994
	67.5	0.038	0.08	0.41	0.997	0.038	0.20	0.41	0.997
ST	0	0.120	0.12	0.32	0.996	0.120	0.12	0.32	0.996
	22.5	0.125	0.13	0.33	0.999	0.125	0.14	0.33	0.999
	45.0	0.132	0.10	0.38	0.996	0.132	0.14	0.38	0.996
	67.5	0.099	0.06	0.41	0.995	0.099	0.16	0.41	0.995

Cardinal axis (horizontal), indicates that spatial frequency is specified with respect to the horizontal; Orthogonal axis, indicates that spatial frequency is specified orthogonal to the orientation of the grating; θ_F, folded direction of the orthogonal disparity vector; A_peak, amplitude of the peak in degrees; f_o, spatial frequency of the peak in cycles/°; σ, standard deviation in °/cycle (log units to the base 10); r², coefficient of determination.

Table 4.

The dependence of V_F on log spatial frequency for various values of θ_F: parameters of the best-fit Gaussian functions.

		Cardinal axis (vertical)				Orthogonal axis
Subject	θF	Apeak	fo	σ	r2	Apeak	fo	σ	r2
FAM	22.5	0.008	0.09	0.54	0.994	0.008	0.25	0.54	0.994
	45	0.029	0.19	0.57	0.998	0.029	0.26	0.57	0.998
	67.5	0.055	0.26	0.57	0.999	0.055	0.28	0.57	0.999
	90	0.100	0.34	0.72	0.997	0.085	0.34	0.49	0.999
BMS	22.5	0.011	0.07	0.34	0.993	0.011	0.18	0.34	0.993
	45	0.030	0.15	0.53	0.999	0.030	0.21	0.53	0.999
	67.5	0.060	0.24	0.48	1.000	0.060	0.26	0.48	1.000
	90	0.085	0.34	0.49	0.999	0.085	0.34	0.49	0.999
HAR	22.5	0.006	0.09	0.68	0.968	0.006	0.23	0.68	0.968
	45	0.017	0.23	0.47	0.998	0.017	0.33	0.47	0.998
	67.5	0.031	0.31	0.51	0.995	0.031	0.33	0.51	0.995
	90	0.043	0.38	0.53	0.995	0.043	0.38	0.53	0.995
ST	22.5	0.010	0.08	0.33	0.950	0.010	0.21	0.33	0.950
	45	0.025	0.15	0.41	0.995	0.025	0.21	0.41	0.995
	67.5	0.050	0.20	0.39	0.998	0.050	0.22	0.39	0.998
	90	0.085	0.27	0.44	0.996	0.085	0.27	0.44	0.996

Cardinal axis (vertical), indicates that spatial frequency is specified with respect to the vertical. Other abbreviations as for Table 3.

For all of the above analyses, spatial frequencies were always specified along an axis orthogonal to the grating orientation—hence the listing of parameters under “orthogonal axis” in Tables 3 and 4—and we reanalyzed these tuning data by specifying the spatial frequency with respect to the horizontal and vertical (cardinal) axes. This shifted the tuning curves obtained with the oblique gratings to lower spatial frequencies: see the f_o entries in Tables 3 and 4 listed under “cardinal axis” and the open symbols linked by dashed lines in Fig. 6C, D. This realignment of the data had no influence on the goodness of fit of the Gaussian functions but reversed the tendency previously seen in the horizontal vergence data in Fig. 6C—so that f_o now decreases with increases in θ_F—and augmented the tendency previously seen in the vertical vergence data in Fig. 6D—so that f_o now shows clear decreases with decreases in θ_F. That f_o shows slightly less dependence on θ_F when spatial frequency is specified along the orthogonal provides support—admittedly only weak—for the idea that the orthogonal measure is the one with greater biologically relevance.

3.2.4 Directional “errors”

It is important to note that, in assessing the directional “errors” with 1-D grating stimuli, we defined the direction of the disparity stimulus vector as orthogonal to the orientation of the grating. As already pointed out earlier, with grating disparity stimuli the direction of the vergence response vector can range widely and still compensate for the binocular misalignment of the images. The most efficient vergence response would be in the direction of the nearest-neighbor matches, i.e., orthogonal to the gratings, so that deviations from this orthogonal might reflect inefficiency rather than errors per se. Despite this, for convenience we will refer to “misalignments” of the vergence response vector with the orthogonal disparity vector as directional “errors”. With grating stimuli, Offset “Errors” were larger and more variable than with random dot stimuli (mean±SD: HDVRs, 0.002±0.08°; VDVR, 0.033±0.14°). Gain Asymmetry “Errors” were generally larger and more variable than in Experiment 1: the gain asymmetry, given by H_F0/V_F90, averaged 0.989±0.725 (range, 0.27–2.72) and showed dependence on spatial frequency, with values greater than unity at the lowest spatial frequency and less than unity at the highest spatial frequency. That there were appreciable Directional Decoding “Errors” is evident from the folded response measures plotted in Fig. 5 (filled symbols), which often deviate substantially from the cosine/sine dependencies required to align the response vector with the stimulus vector (grey lines). These Directional Decoding “Errors” are further apparent from the “directions of the normalized folded vergence response vectors”, ${\phi }_F^{\prime }$ (computed as in Experiment 1), which are plotted as a function of θ_F in Fig. 7 in closed symbols, with the data for the subject FAM in (A) and the mean data for all subjects in (B). The values of ${\phi }_F^{\prime }$ for the data obtained with oblique gratings fall well short of the unity-slope (dashed) lines in Fig. 7, indicating a consistent bias in favor of the horizontal that tended to be greatest with the gratings of higher spatial frequency (0.5 and 0.75 cycles/°). The standard errors in Fig. 7B are generally small, indicating that inter-subject variability was usually modest. Note that the continuous lines plotted in Fig. 7 were generated by a model (see General Discussion later).

Figure 7.

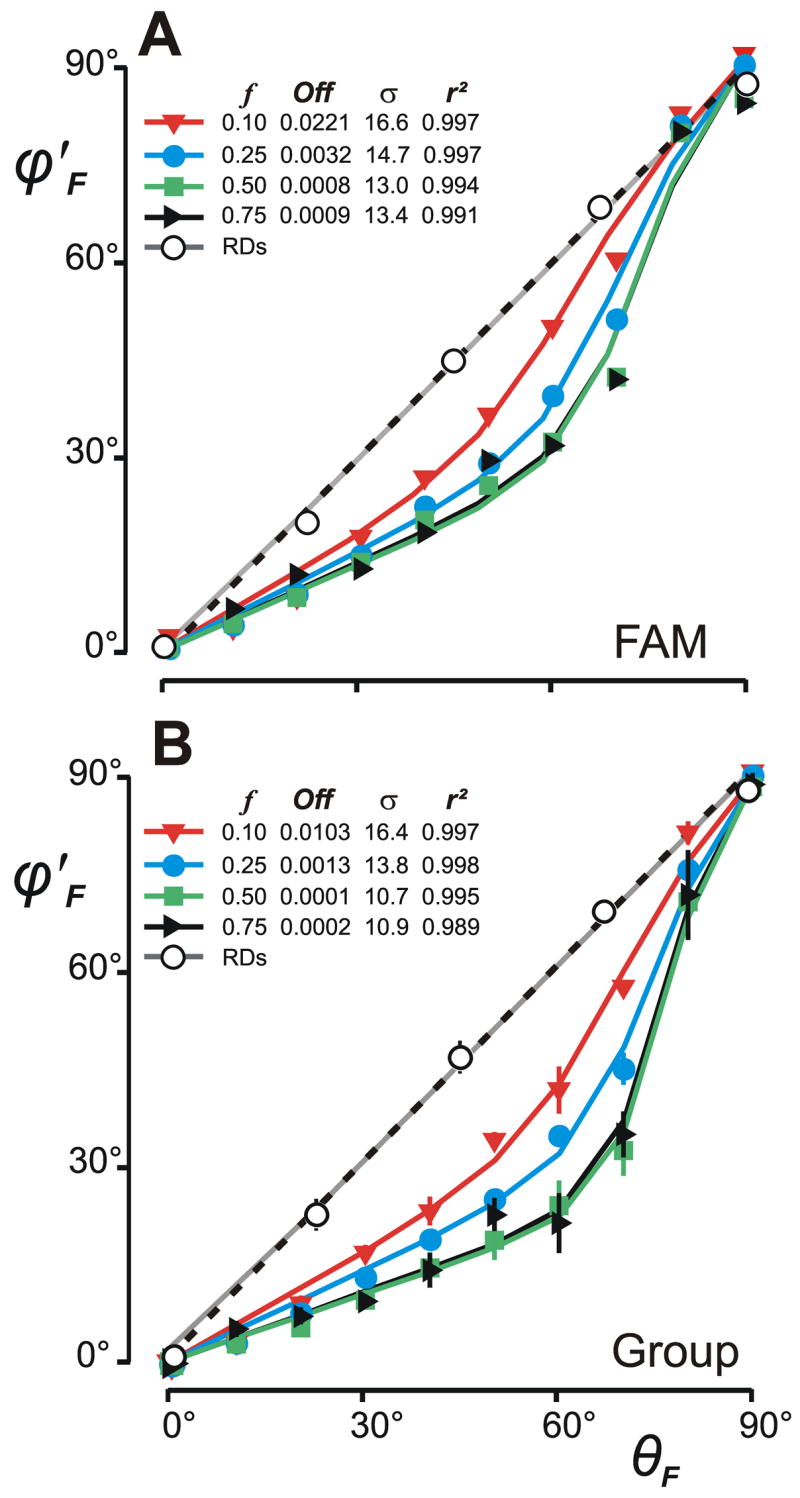
Directional Decoding “Errors”: dependence of the direction of the normalized folded vergence response vectors, φ′_F, on the direction of the (folded) disparity vector, θ_F. (A) Data for subject, FAM. (B) Mean data (±SD) for four subjects. Closed symbols show data obtained with sine-wave gratings using the orthogonal disparity vector (see key for spatial frequencies). Open circles show data obtained with random-dot patterns. Curves are least-squares best fits obtained with the anisotropy model; the parameters of the Gaussian functions specifying the distributions of the preferred directions of the disparity sensors in the model are listed together with the Coefficients of Determination (r²): f, spatial frequency; Off, vertical offset; σ, standard deviation. Dashed lines are the unity-slope lines.

3.3. Discussion of Experiment 2

Experiment 2 indicated that the Directional Decoding “Errors” with 1-D sine-wave grating stimuli were much greater than with RDs, an effect that we attribute to the aperture problem (Morgan & Castet, 1997). The HDVRs with 1-D grating stimuli were often strikingly insensitive to tilting of the grating away from the vertical optimum. Thus, based on best-fit sigmoid functions like those seen in Fig. 5A–D (continuous line), tilting the grating 66° away from vertical reduced the HDVR, on average, by only 10%. Interestingly, stereo thresholds for 1-D sine-wave gratings, when expressed in terms of the phase difference at the two eyes, are independent of orientation for tilts up to 80° away from the vertical optimum (Morgan & Castet, 1997). Further, these stereo thresholds are insensitive to spatial frequency, at least for gratings <2.4 cycles/° (Farell, 2003; Schor & Wood, 1983; Schor, Wood & Ogawa, 1984). Such observations have led to the suggestion that stereo acuity might rely upon detectors that sense the phase disparity rather than the linear separation per se (Morgan & Castet, 1997). The disparity detectors mediating the DVRs might indeed sense the phase disparity, but we think that this is an unlikely explanation for the insensitivity of the HDVR to changes in grating orientation. Thus, although the HDVR is minimally sensitive to changes in orientation near the optimal, the VDVR is almost maximally sensitive to such changes, and yet the available evidence strongly suggests that the disparity detectors mediating the initial HDVR and VDVR are very similar (see Introduction). One possible caveat here is that the horizontal vergence mechanism has a number of attributes that are not shared by the vertical vergence mechanism, including sensitivity to radial optic flow, accommodation, perspective, overlay, size-change, relative motion, perceived depth, and attention (Enright, 1987a; 1987b; Erkelens & Regan, 1986; Judge, 1996; Kodaka, Sheliga, Fitzgibbon & Miles, 2007; Ringach et al., 1996; Sheliga & Miles, 2003; Stevenson et al., 1997). However, many of these additional attributes exert their effects at much longer latencies than DVRs being considered here and those that do not—such as radial optic flow—are not operative in our experimental situation. In sum, even if the adequate stimulus for the disparity detectors is the phase difference between the images seen by the two eyes this is unlikely to be responsible for the insensitivity of the HDVR to grating orientation.

We defined the disparity stimulus vector as orthogonal to the orientation of the grating but, of course, the disparity detectors might actually sense the luminance matches along some other axis. Our finding that the folded measures (H_F, V_F) obtained with oblique gratings could deviate substantially from those obtained with cardinal gratings of matching horizontal (vertical) spatial frequency and disparity indicates that the underlying disparity detectors were not simply sensing the epipolar matches, i.e., not matching points of the same luminance along the horizontal meridian. The dependence of H_F and V_F on (log) spatial frequency was well represented by a Gaussian function whose width (σ) and peak frequency (f_o) showed relatively minor sensitivity to the grating orientation, i.e., the major effect of tilting the grating here was attenuation (rescaling). In fact, f_o was a little more sensitive to the spatial frequency when measured along the horizontal (vertical) axis than when measured orthogonal to the grating (Fig. 6C,D).

4. General discussion

4.1. Modeling the Directional Decoding “Errors” seen with oblique gratings

We sought to determine if the Directional Decoding “Errors” seen with oblique gratings could be explained by an anisotropy in the disparity sensing mechanism that favored horizontal vectors. Such a bias might arise if the vergence mechanism were to receive a disproportionately greater input from disparity detectors tuned to horizontal because 1) there is a greater preponderance of such detectors, and/or 2) a greater proportion of such detectors project to the vergence mechanism, and/or 3) such detectors exert a greater impact because they are more sensitive to disparity and/or have a greater efficacy. Unfortunately, supporting information is available only for the first of these various factors: A recent study that examined the responses of disparity selective cells in the monkey’s striate cortex to combined horizontal and vertical disparities reported a preponderance of cells with a preference for horizontal disparities, at least in the central visual field (Durand, Celebrini & Trotter, 2007).¹

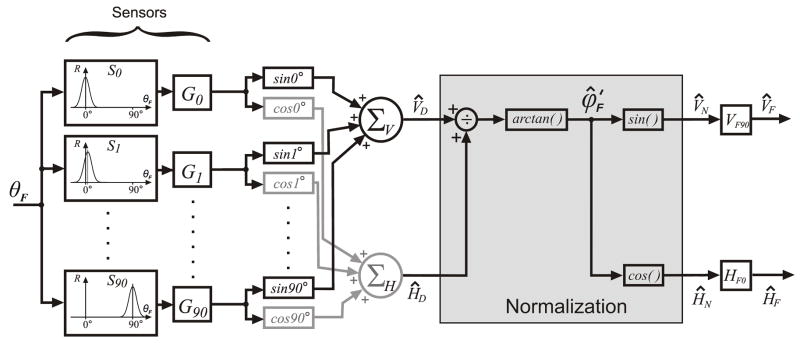
We tested the plausibility of this anisotropy hypothesis using a model shown in block diagram form in Fig. 8. The objective here was only to validate the concept and not to propose a detailed model of the disparity vergence mechanism. Further, we were concerned only with modeling the responses to our particular grating stimuli, specifically, the directional dependencies like those seen in Fig. 7. The model has 1) an input layer consisting of disparity sensors each with their own independent gain adjustment, 2) an intermediate layer that separately sums the weighted horizontal and weighted vertical components of the disparity signals and normalizes them, and 3) an output layer consisting of independent horizontal and vertical vergence controllers. A crucial part of the model is that the individual disparity sensors are direction selective, with preferred directions that extend over the full 360° but those near horizontal have higher gains, hence there is an anisotropy favoring horizontal disparities. The input to the model is the direction of the disparity stimulus vector, θ_F, and the outputs are the horizontal and vertical vergence responses, Ĥ_F and V̂_F.

Figure 8.

A block diagram of the anisotropy model. The individual disparity sensors have a Gaussian dependence on the direction of the disparity vector (measured orthogonal to the orientation of the stimulus grating) and all sensors have the same peak response amplitude and bandwidth. The preferred directions of these sensors are arranged in order at 1° intervals (S₀…S₉₀). The gains of the sensor outputs (G₀…G₉₀) have a Gaussian distribution centered on the G₀ element with a width and vertical offset that are free parameters. The outputs of the sensor gain elements, each weighted by the cosine (sine) of its preferred direction, are summed by the horizontal (vertical) vergence premotor controllers, Σ_H (Σ_V), to produce the horizontal (vertical) drive signals, Ĥ_D(V̂_D). A normalization stage then uses simple geometry, given by arctan (V̂_D/Ĥ_D), to derive a signal equivalent to the normalized folded response direction, ${\widehat{\phi }}_F^{\prime }$, which is then decomposed into cosine and sine components, Ĥ_N (V̂_N), that are scaled by the two measured parameters, H_F0 and V_F90, to produce outputs encoding the horizontal and vertical vergence responses: ${\widehat{H}}_F=H_{F0}cos{\widehat{\phi }}_F^{\prime }$ and ${\widehat{V}}_F=H_{F90}sin{\widehat{\phi }}_F^{\prime }$.

4.1.1. The disparity sensors

The sensors in the input layer of our anisotropy model were based on the disparity energy model of complex cells in striate cortex (Anzai, Ohzawa & Freeman, 1999; Fleet et al., 1996; Ohzawa et al., 1990), even though details of the model are still undergoing refinement (e.g., Haefner & Cumming, 2008; Read & Cumming, 2003; 2006; Read et al., 2002). It is known that the complex cells in the disparity energy model (and in striate cortex) show a Gaussian dependence on orientation when tested with monocular gratings (Bridge, Cumming & Parker, 2001; Read & Cumming, 2004), but no directional tuning data are available for either real or model neurons for oriented binocular disparity stimuli like those that we have used in the present study. It was therefore necessary to first determine the directional tuning functions for the disparity energy model using oriented binocular gratings with a constant ¼-wavelength phase difference (disparity).

For this we used the version of the disparity energy model originally described by Ohzawa et al., (1990) with monocular simple (MS) cells, binocular sub (BS) units and binocular complex (Cx) cells. The monocular receptive fields were described by 2-D Gabor functions, with isotropic Gaussian envelopes whose standard deviation was 0.2° and whose carrier frequency was 2.5 cycles/° (cf., Read & Cumming, 2004). The BS units sum inputs from right and left MS cells whose receptive fields have the same orientation but a fixed position disparity, and output the square of this sum after half-wave rectification. The BS units were arranged in “push-pull” pairs that were mutually inhibitory. Each Cx cell received two such pairs of BS units that had quadrature phase. The disparity stimulus consisted of right and left 1-D luminance modulated sine-wave gratings that had the same spatial frequency (2.5 cycles/°), contrast (64%), and orientation but differed in phase by ¼ wavelength. The orientation of the gratings was varied systematically from 0 to 180° in steps of 1°. The resolution of the simulation was 50 pixels/°. We determined the directional tuning of these model sensors by calculating the inner products of the retinal images with the receptive field functions. The Cx cell output showed a Gaussian dependence on grating orientation (r²: 0.999) with a half-height bandwidth (W_Cx) of 31° and a peak that coincided with the cell’s preferred orientation. This meant that the direction of the preferred disparity vector was always orthogonal to the grating orientation, consistent with recent recordings from disparity selective cells in the monkey’s striate cortex (Durand et al., 2007). The amplitude and bandwidth of this Gaussian function were strongly influenced by the spatial frequency of the grating, as well as by the location of the receptive field with respect to the center of rotation of the grating, but the direction of the preferred disparity vector was rather insensitive to these stimulus factors. Accordingly, all sensors in our anisotropy model had Gaussian directional tuning and were assigned the same bandwidth (W_Cx =35°) and the same peak amplitude (unity). The directions of the preferred disparity vectors of these sensors were distributed over the full 360° (though folded to 90° for the simulations), which is consistent with recent monkey neurophysiological data in visual cortex (Durand et al., 2007; Durand, Zhu, Celebrini & Trotter, 2002) and with human psychophysical data (Patel, Bedell & Sampat, 2006; Patel, Ukwade, Stevenson, Bedell, Sampath & Ogmen, 2003). There were 91 sensors, arranged in order of the directions of their preferred disparity vectors (i.e., counterclockwise with respect to horizontal) at 1° intervals (S₀, S₁…S₉₀), and each had its own gain adjustment (G₀, G₁…G₉₀). These gains had a Gaussian distribution that was centered on the S₀G₀ channel, whose preferred disparity vector was horizontal (0°), giving the model an anisotropy that favored horizontal disparities. The width (σ) and vertical offset of this Gaussian function were the only free parameters.²

4.1.2. Additional elements needed to run the simulations

Everything in the model that was beyond the sensors consisted only of the mathematical operations necessary to generate the biologically relevant vergence outputs and no attempt was made to simulate actual neural or mechanical mechanisms here. The outputs of the sensor gain elements (G₀, G₁…G₉₀), each weighted by the cosine (sine) of its preferred direction, were summed by the horizontal (vertical) vergence premotor controllers, Σ_H (Σ_V), to produce the horizontal (vertical) drive signals, Ĥ_D (V̂_D). A normalization stage then applied geometry, given by arctan (V̂_D/Ĥ_D), to derive a signal equivalent to the normalized folded response direction, ${\widehat{\phi }}_F^{\prime }$, which was then decomposed into cosine and sine components that were scaled by the two measured parameters, H_F0 and V_F90, to produce outputs encoding the horizontal and vertical vergence responses: ${\widehat{H}}_F=H_{F0}cos{\phi }_F^{\prime }$ and ${\widehat{V}}_F=H_{F90}sin{\phi }_F^{\prime }$. Of course, a physiologically more realistic model might employ some form of divisive normalization, such as that often described in striate cortex and MT (Carandini & Heeger, 1994; Carandini, Heeger & Movshon, 1997; e.g., Heeger, 1992; Heuer & Britten, 2002), before the summing junctions.

4.1.3. Results of the simulations

Figure 7 shows the least squares best fit of ${\widehat{\phi }}_F^{\prime }$ to ${\phi }_F^{\prime }$ for each spatial frequency (colored lines) together with a listing of the best-fit free parameters and the mean r² values. The latter averaged 0.995±0.003 (FAM data in Fig. 7A) and 0.996±0.003 (group data in Fig. 7B), indicating that the anisotropy model in Fig. 8 could reproduce the observed Directional Coding “Errors” very accurately. In addition, the simulated outputs, Ĥ_F and V̂_F, fitted the amplitude data, H_F and V_F, very well: mean r² values for the fits to the data of subject FAM plotted in Fig. 5 (based on the parameters listed in Fig. 7A) were 0.991±0.007 (H_F) and 0.995±0.002 (V_F), and for the fits to the group data (based on the parameters listed in Fig. 7B) were 0.962±0.059 (H_F) and 0.985±0.021 (V_F). Thus, on average, the anisotropy model could account for more than 99% of the variance in the Directional Decoding “Errors” and more than 96% of the variance in the response amplitude with oblique grating stimuli.

When we now ran the simulations with the directional bandwidth of the individual disparity sensors as an additional free parameter, the best-fit half-height bandwidths (W_Cx) ranged from 28° to 39° but did not improve the overall fits to the data significantly. However, it also became apparent that reducing W_Cx eliminated the impact of the anisotropy and made it possible to obtain excellent fits to the RD data. For example, the grey lines in Fig. 7, which fit the RD data with r² values of 0.999, were obtained when W_Cx=6°. Of course, we made no provision for the selective processing of the multiple spatial-frequency components of the RD patterns, nor the non-linear interactions that are known to occur with such broad-band stimuli (Sheliga et al., 2007).

4.2 Further biological implications

The insensitivity of stereo thresholds to the orientation of 1-D grating stimuli when based on phase disparity has been taken to suggest that the underlying disparity detectors might be sensing the phase difference between the two monocular images (Morgan & Castet, 1997). However, the present study suggests that the constancy of these stereo thresholds might instead reflect an anisotropy in the distribution of the directions of the preferred disparity vectors. Such an explanation does not exclude the possibility that the detectors responsible for the stereo thresholds sense phase differences. Indeed, the latter would be consistent with the relative insensitivity of stereo acuity to spatial frequency for gratings <2.4 cycles/° (Farell, 2003; Schor & Wood, 1983; Schor et al., 1984). Over this same range of spatial frequencies, however, our DVR data show a band-pass dependence (Fig. 6A,B), and there could be a number of reasons for this. For example, the vergence mechanism might receive inputs from disparity detectors responsive to only a restricted range of spatial frequencies. We did not attempt to model this feature.

The anisotropy that we have modeled as an array of disparity detectors with gains, G₀…G₉₀, whose values have a Gaussian distribution centered on the S₀G₀ (horizontal) channel, might arise at various points in the sensory pathways mediating the DVR and might also be instantiated in various ways, e.g., cells preferring horizontal disparities could be more numerous, carry more weight, or project more densely to the vergence motor controllers. The recent findings of Takemura et al (2001) strongly suggest that the sensory-motor interface for the initial DVR is in MST, where individual cells encode the sensory input (binocular disparity) and the summed population activity encodes the motor output (vergence eye movements). In this scheme, the vergence motor response is an emergent property of the population activity in MST (“population coding”), and lesions of this region are known to cause severe impairment of the initial DVR (Takemura et al., 2007). Area MT projects heavily to MST (Desimone & Ungerleider, 1986; Ungerleider & Desimone, 1986) and receives projections from striate cortex, both directly (Shipp & Zeki, 1989a) and via V2 and V3 (Shipp & Zeki, 1989b; 1995). Very recent findings indicate that cooling areas V2/V3 attenuates the initial HDVR and reduces the sensitivity of neurons in MT to disparity (Ponce et al., 2008). Other recent studies suggest that many of the fundamental characteristics of the DVR, such as dependence on contrast and spatial frequency, directly reflect the low-level properties of disparity selective neurons in the striate cortex (Sheliga et al., 2006; 2007). The clear suggestion is that the anisotropy in our model might occur as early as striate cortex, whose neurons have small receptive fields that depend on purely local disparity matches (Cumming & Parker, 2000) and so would be expected to display the aperture problem with extended grating patterns like those in the present study.

It was possible simulate the small Directional Decoding Errors seen with RDs by reducing the bandwidth of the orientation tuning functions in our model (W_Cx) to a few degrees, but disparity–selective neurons in the striate cortex have much greater bandwidths than this with RDs (mean±SD, 132±53°; range, 20–254°). ³ Based on studies of stereothresholds, Morgan & Castet (1997) suggested that the mechanisms that sense the binocular matches in patterns with 2-D features might be different from those that sense the matches in patterns with only 1-D features. Although many of the disparity-selective neurons in striate cortex respond well to the disparity of long lines that extend beyond the receptive field boundaries some—termed end-stopped cells—respond well only when the lines terminate within their receptive fields (Howe & Livingstone, 2006). Such end-stopped neurons might be expected to respond to the binocular matches in our RDs much better than to the binocular matches in our 1-D gratings. It would be interesting to know if the preferred directions of the disparity vectors that activate these end-stopped cells are uniformly distributed whereas those of other cells (that respond to extended lines) show the anisotropy favoring horizontal that we have postulated to explain the DVRs to oblique 1-D gratings.