Adaptive filtering enhances information transmission in visual cortex

Abstract

Sensory neuroscience seeks to understand how the brain encodes natural environments. However, neural coding has largely been studied using simplified stimuli. In order to assess whether the brain’s coding strategy depends on the stimulus ensemble, we apply a new information-theoretic method that allows unbiased calculation of neural filters (receptive fields) from responses to natural scenes or other complex signals with strong multipoint correlations. In the cat primary visual cortex we compare responses to natural inputs with those to noise inputs matched for luminance and contrast. We find that neural filters adaptively change with the input ensemble so as to increase the information carried by the neural response about the filtered stimulus. Adaptation affects the spatial frequency composition of the filter, enhancing sensitivity to under-represented frequencies in agreement with optimal encoding arguments. Adaptation occurs over 40 s to many minutes, longer than most previously reported forms of adaptation.

The neural circuits in the brain that underlie our behaviour are well suited for processing of real-world—or natural—stimuli. These neural circuits, especially at the higher stages of neural processing, may be largely or completely unresponsive to many artificial stimulus sets used to analyse the early stages of sensory processing and, more generally, for systems analysis. Thus, natural stimuli may be necessary to study higher-level neurons. Characterizing neural responses to natural stimuli at early or intermediate stages of neural processing, such as the primary visual cortex, is a necessary step for systematic studies of higher-level neurons. Neural responses are also known to be highly nonlinear^1–3 and adaptive^4–20, making them difficult to predict across different stimulus sets²¹. Therefore, even early in visual processing, characterizations based on simplified stimuli may not be adequate to understand responses to the natural environment.

For these reasons there has been a great deal of interest in studying neural responses to complex, natural stimuli (for example, see refs ^{1, 21–26}). However, the relationship between coding of natural and laboratory stimuli remains elusive due to the difficulty of characterizing neurons—assessing their receptive fields—from responses to natural stimuli, as we now describe.

A simple and commonly used model of neural responses is the linear–nonlinear model^27,28. In this model, the response of the neuron depends on linear filtering of the stimulus luminance values S by a receptive field L defined over some region of space and time. Mathematically, the filter output at time t is a sum over the spatial positions (x,y) and temporal delays t′to which the neuron’s response is sensitive: Σ_x,y,t′ L(x, y, t − t′)S(x, y, t′), which we abbreviate as L*S. The output of this filter is then passed through a nonlinear function f to yield the neuron’s response r: r(t) = f(L*S). The nonlinearity incorporates the fact that the firing rate cannot be negative and other aspects of neural response such as threshold, saturation and sensitivity or insensitivity to changes in stimulus polarity. We will use the terms neural filter or receptive field throughout this paper to mean the linear part L of the linear–nonlinear model.

Traditionally, neural receptive fields have been estimated as the spike-triggered average stimulus (STA; with appropriate correction for autocorrelation of the inputs)^{1,23–25,27,28} or by related methods^10,26,29. These methods give unbiased results for linear systems for any stimulus ensemble or for nonlinear systems if the ensemble is gaussian random noise. However, they produce systematic deviations from the true filter of nonlinear ‘linear–nonlinear’ neurons probed with natural stimuli (or other non-gaussian stimuli), even in situations where the only nonlinearity is due to a conversion of the output of a linear receptive field to firing rate^24,30. This happens because natural stimuli, unlike gaussian stimuli which may be completely described by pairwise correlations, have strong higher-order as well as pairwise correlations^31–33. The higher-order correlations may be viewed as what distinguishes natural from random gaussian stimuli. The bias in the filter estimate calculated using the gaussian or linear assumption increases with the strength of the nonlinearity and with the strength of stimulus correlations beyond second order^24,30, not vanishing even with infinite data.

Recently an information-theoretic method has been developed that correctly estimates receptive fields of nonlinear model neurons (with extensions to multiple linear filters) for arbitrary stimulus ensembles regardless of the strength of multi-point correlations, even in cases where the STA is zero³⁰. According to this method, one searches for the spatiotemporal filter L whose output, L*S, carries the most mutual information with the experimentally measured neuronal response r(t). In practice, this is done via a gradient ascent procedure, searching in the space of all possible spatiotemporal receptive fields or filters to find the most informative one (referred to as ‘the most informative dimension’, or MID). We can then calculate the nonlinearity associated with the MID from the data as the probability of a spike given the filter output; there is no need to make any assumption about the shape of the nonlinearity.

Similarly to other ‘spike-triggered’ methods, the MID method compares two probability distributions of outputs for a given filter: the distribution of outputs that occur before (or trigger) a spike, and the distribution of outputs over the entire stimulus ensemble regardless of neural response. If a filter represents a stimulus feature that affects neural responses, then certain values of its output will be more probable before a spike, and so the two distributions should differ from one another. The various methods all seek filters that maximize the difference between the two distributions, but differ in the measure of this difference. For the STA, the measure is the change in the mean of the two distributions; for the spike-triggered covariance method^10,26,29, it is the change in the variance; and for the MID, it is an information-theoretic measure (the Kullback–Leibler distance) that corresponds to the mutual information between the filter output and the spikes. The information-theoretic measure is more general than the mean or variance, because it is sensitive to correlations of all orders, which in part explains the success of the MID method in estimating neural filters from responses to natural stimuli. Here we apply this method to neural data, focusing on the single-filter model, to address the question of whether and how V1 receptive fields adapt to natural stimuli.

Receptive fields from noise versus natural scenes

We studied 40 simple cells (as characterized by responses to optimal moving gratings³⁴) in anaesthetized cat V1 (complex cells can also be characterized by the MID method³⁰ and will be considered in a future publication). We probed these neurons with natural and white noise inputs. These inputs differ in two important respects. First, they have very different pairwise correlations, which are described by the power spectra. The power spectrum of a white noise ensemble does not depend on either spatial or temporal frequency within a certain range, whereas the power spectrum of natural inputs depends on spatial frequency k as ~1/k² under a wide variety of conditions^31,33,35,36 (spatiotemporal statistics have similar structure³⁶). Second, natural scenes have strong statistical correlations beyond second order that cannot be described by the power spectrum, as evident in the much greater incidence of oriented edges in natural scenes than in gaussian noise with the same power spectrum^31,33.

To estimate spatiotemporal receptive fields or neural filters from responses to noise and natural stimuli, we applied both the linear systems and information-theoretic methods. The resulting estimated filters and STAs for two example cells are shown in Fig. 1. With respect to responses to the noise ensemble, we found the filter for each cell either as the traditional STA or as the MID³⁰. As expected for white noise stimuli, the two estimates do not differ significantly from each other for the illustrated cells or for most cells (P > 0.05 for 31 out of 40 cells, t-test, see Supplementary Methods); the remaining differences can be attributed to the residual spatial correlations in the white noise ensemble. This agreement illustrates the basic validity of the MID method under circumstances where the STA offers an independent unbiased estimate.

Figure 1. Filters and nonlinearities for two simple cells.

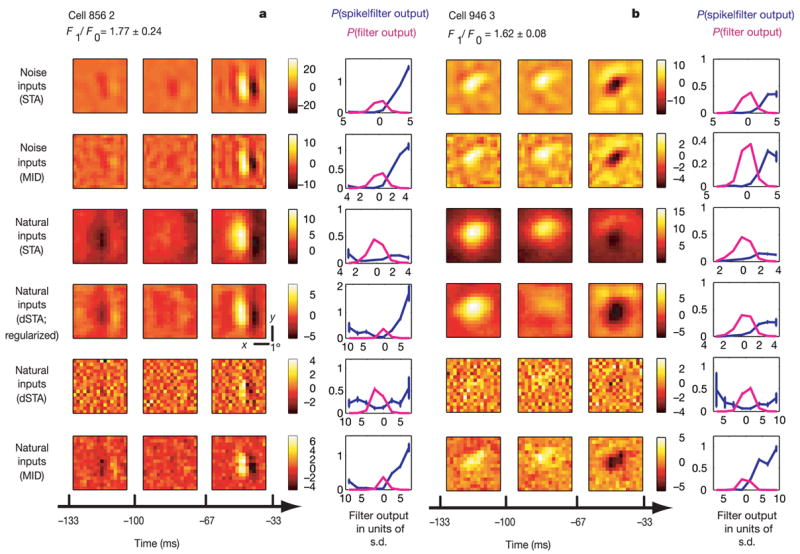
a, b, Top to bottom: STA and MID for noise ensemble; STA, dSTA, dSTA with regularization and MID for natural ensemble. Spatiotemporal receptive fields have three time frames covering the indicated time interval (− 133 to − 33 ms). In the right-most column for each filter we plot the probability distribution of filter outputs in the stimulus ensemble (magenta) and the spike probability given the filter output (blue; values on the y axis refer to these probabilities). The colour scale shows the filter in units of its average noise level (see Supplementary Methods). x–y scale bars: 18. Error bars show standard errors of the mean in all figures.

For responses to the natural stimulus ensemble, we calculated the STA and corrected it for second-order correlations present in the natural ensemble to obtain a decorrelated STA (dSTA). This would describe the neuron’s filter if the neuron were linear. Because this procedure of correcting for stimulus correlations tends to amplify noise, we also calculated the dSTA using regularization to prevent such amplification—such decorrelation with regularization has been used in most previous work estimating neural filters from responses to natural signals^1,21,24–26. Finally, we estimated the filter from natural inputs as the MID. As can be seen in Fig. 1, the MID produces an estimate of the filter for natural scenes that is much closer to the white noise filter than either the dSTA or the regularized dSTA. Across cells, the dSTA shows a greater difference from the white noise filter than does the natural ensemble MID, as judged by smaller correlation coefficients with either the noise ensemble STA or noise ensemble MID (40 out of 40 cells, P < 10^{− 6}). This demonstrates that some of the differences between the neural filters obtained from natural and noise stimulation in the linear model are due to biases in the estimation of the natural filter that can be removed once the linear–nonlinear model is considered and the MID is computed. In Fig. 1, we also plot the nonlinear functions that show spike probability as a function of filter output. They are similar in shape for the MIDs of the two ensembles, and this behaviour seems to be typical across cells.

We used the MIDs to estimate both the noise and natural filters in what follows. We studied all simple cells with a non-zero filter to both natural and noise inputs.

Despite the similarity of the filters obtained under the two conditions (see Fig. 1), a jackknife analysis of the errors in estimating the neural filters shows that the differences between the filters derived from noise and natural signals are statistically significant (P < 0.01) for all cells. To investigate the source of these differences and to make connections with classical studies on neural responses to moving periodic patterns (gratings) of certain orientations and spatial frequencies, we compute the spatiotemporal Fourier transform of the filter in the two spatial dimensions and time. The position of the maximum of the Fourier transform at the grating temporal frequency is our prediction for the optimal grating orientation and spatial frequency for a particular neuron. We did not detect any systematic shifts in optimal orientation and only a small shift in optimal spatial frequency as assayed from noise filters, natural signal filters and grating stimuli, in agreement with previous findings using the regularized dSTA^25,26 (see Supplementary Discussion).

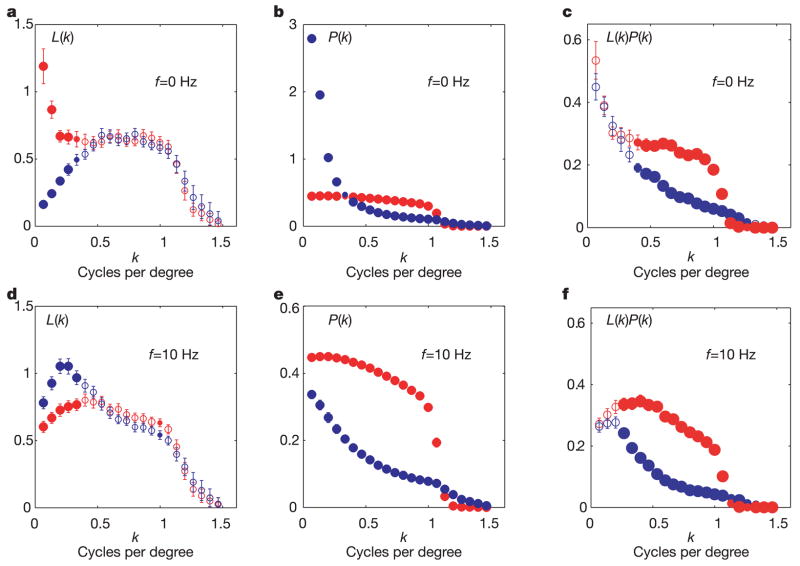
The most marked differences between the neural filters derived from natural versus noise stimulation are seen by considering the entire shape of the spatial frequency tuning curves (Fig. 2 and Supplementary Figs 1 and 2) and not just the location of the single best spatial frequency. For each cell and temporal frequency, we calculated the spatial frequency profile along the cell’s preferred stimulus orientation using interpolation of the filter’s two-dimensional discrete Fourier transform. Note that our temporal resolution allowed analysis only at two temporal frequencies (0 Hz and 10 Hz in each of two opposite directions of motion). Results at 10 Hz did not depend on direction of motion, so both directions were combined in Fig. 2, which shows the average tuning of the cells in our data set. For low spatial frequencies sensitivity decreased (increased) to common (rare) inputs, whereas at middle and high spatial frequencies the sensitivity did not change. For example, at zero temporal frequency, low spatial frequencies are more common in the natural than in the white noise stimulus ensemble (Fig. 2b). Correspondingly, neurons became less sensitive to those frequencies during stimulation with natural inputs than during stimulation with noise inputs (Fig. 2a). In the case of non-zero temporal frequencies the trend is reversed, because the noise stimulus ensemble has more power at nearly all spatial frequencies than the natural stimulus ensemble (Fig. 2d, e). These changes in filter can be observed in the majority of cells, and are not simply due to adaptation in a small subset of cells. This is shown in Supplementary Fig. 1, which illustrates the spatial frequency sensitivities of the two example cells for which the receptive fields are shown in Fig. 1, and Supplementary Fig. 2, which shows scatter plots of spatial frequency sensitivity of noise versus natural filters across all cells.

Figure 2. Neural filters compensate for changes in the input power spectrum.

Average amplitude spectra of neural filters (a, d) and input ensembles (b, e) corresponding to natural (blue circles) and white noise (red circles) stimulation for temporal frequencies of 0 and 10 Hz. The spectra were taken along the optimal orientation for each cell by interpolating the discrete two-dimensional Fourier transform. We use filled circles at frequencies where mean sensitivity was significantly different between the two ensembles (small circles for P < 0.05 and large circles for P < 0.01), and open circles otherwise. c, f, Plots of the product of the average neural filter and input ensemble amplitude spectra.

Optimal filtering in a nonlinear system

In retrospect, such shifts in spatial frequency sensitivity may be expected for neural coding to be optimal for both of two input ensembles (white noise and natural stimuli) that have such vastly different power spectra^31,33,35 (compare Fig. 2b, e). In general it is difficult to map optimal coding strategy from one ensemble to another; however, it could be done if both of the stimulus ensembles were gaussian so that they were entirely characterized by their power spectra. Suppose a neuron uses filter L_A and nonlinearity f_A to encode optimally gaussian stimulus ensemble A with spatiotemporal amplitude spectrum P_A(k,ω). What would then be an optimal strategy to encode gaussian ensemble B with amplitude spectrum P_B(k,ω)? One solution is to leave the nonlinearity unchanged and to compensate for differences in the input power spectra by changing neural filter properties so that:

$$L_{\text{A}}(k,\omega )P_{\text{A}}(k,\omega )=L_{\text{B}}(k,\omega )P_{\text{B}}(k,\omega )$$ (1)

This will leave unchanged all statistics of neuronal response, and so in particular will leave invariant any statistical measures of optimality. Alternative strategies involving a change in nonlinearity cannot be optimal unless there are multiple optima, because if ensemble A has a unique optimum, then the above strategy will give the unique optimum for ensemble B. (Note that, in response to an overall change in contrast, the nonlinearity can be rescaled^10,12, but this is equivalent to a rescaling of the filter according to equation (1) with no change in nonlinearity.)

These conclusions about the receptive field and nonlinearity apply only to gaussian stimuli. The higher-order correlations present in natural scenes may both lead to deviations from equation (1) in neural filters and cause changes in the shape of the nonlinearity. But in practice, the changes in the shape of the nonlinearity are small, and changes in neural filters that do take place act to compensate for changes in the input power spectrum as predicted from equation (1) (Fig. 2c, f). These changes in frequency sensitivity occur primarily at low spatial frequencies. No changes are observed at mid-to-high spatial frequencies, resulting in significant deviations from equation (1) in the middle range of frequencies. We can only speculate that other factors may limit the range of spatial frequencies over which adaptation can occur.

Adaptation increases information transmission

The above optimal coding argument provides at least a qualitative explanation of observed receptive field changes. Most theories of optimal coding define optimality in information-theoretic terms. To test directly whether the information maximization argument applies to our data, we calculated the average mutual information between the filter output and the neural response; the response at a given time is simply taken as the presence or absence of a single spike³⁰.

The changes in receptive fields act to increase the information after changes in stimulus ensemble, and this information would be substantially reduced if receptive fields did not change with the ensemble. That is, the natural filter carries more information about responses to the natural ensemble than to the noise ensemble (P < 10^{− 4}, paired Wilcoxon two-tailed test), whereas the noise filter carries more information about responses to the noise ensemble than to the natural ensemble (P = 0.03). The average information values across the population are shown in Fig. 3, and scatter plots on a cell-by-cell basis are provided in Supplementary Fig. 4. Each filter produces roughly equal information about responses to its own ensemble: the difference in information values achieved by applying the noise filter to the noise ensemble versus applying the natural filter to the natural ensemble is not significant (P = 0.18, paired Wilcoxon test). Each filter produces substantially less information about responses to the other ensemble (P < 10^{− 4} for natural or noise ensemble filtered with natural versus noise filter; paired Wilcoxon tests), and there is no significant difference between the swapped combinations (natural filter applied to noise ensemble or vice versa, P = 0.06, paired Wilcoxon test). We note that the changes in information are not due to overfitting or other computational artefacts, because information was calculated from responses to ensemble segments that were not used in calculating the filters, and the effects were not seen in data from a model linear–nonlinear cell with unchanging filter that was analysed similarly (see Supplementary Information).

Figure 3. Receptive field adaptation increases information transmission.

Bars show the mutual information between spikes and outputs of either the noise (blue, N) or natural scenes (red, S) filter applied to the natural scenes ensemble (solid) or noise ensemble (pixelated). NS, white noise filter applied to natural scenes ensemble; SS, natural scenes filter applied to natural scenes ensemble; NN, white noise filter applied to noise ensemble; SN, natural scenes filter applied to noise ensemble. The information values are given in bits (a) or in units of the total information carried by the arrival of a single spike I_spike³⁷ (b).

In addition to considering information I in bits (Fig. 3, top), we also measured information for each cell in units of I_spike³⁷, the information in the neuron’s response (as defined above) about the full, unfiltered stimulus (Fig. 3, bottom). I/I_spike measures the fraction of the total possible information that is captured by the single most informative filter (I_spike is a separate measurement that was available only for a subset of cells, making the data set smaller). As can be seen, the MID captures roughly 35% of the possible information for simple cells. Each filter provides a greater fraction of the overall information when applied to its own ensemble than the other (P ≤10^{− 4} for natural filter applied to natural versus noise ensemble and for either ensemble filtered with natural versus noise filter; P = 0.05 for noise filter applied to natural versus noise ensemble; paired Wilcoxon test).

Dynamics of receptive field adaptation

Even though the best linear–nonlinear model systematically changes with the stimulus ensemble, this does not establish that the neuron has changed its encoding strategy. The true encoding strategy may be complicated and nonlinear, so that even if it is static, the best linear–nonlinear estimate of it may change with the ensemble, much as the best linear approximation to a curve changes with position on the curve.

The most direct method to distinguish between an adaptive strategy and a complex but static coding strategy would be to estimate the filter as a function of time and see it change. This method yields very poor time resolution, because ~5 min of data are needed to estimate the filter, so adaptation that occurs on a faster timescale cannot be seen. Nonetheless we tried this method and saw appropriate, if weak, adaptation to noise stimuli even on this long timescale (see Supplementary Fig. 5). To achieve finer time resolution, we studied adaptation by measuring changes with time in the information carried by the output of a single, static filter; this information can be estimated from ~30 s of data. We used the following reasoning. If the coding is static, then the mutual information between this filter’s output and the neuron’s responses to a given ensemble should not systematically change in time. However, if the neuron’s receptive field adapts to the stimulus ensemble, then this information may systematically change in time. In particular, we take the static filter to be that characterizing a neuron when it is well adapted to a given ensemble—say the natural ensemble. When the neuron is newly exposed to a natural ensemble, the information carried by this filter should increase with increasing time of exposure to the natural ensemble, as the neuron adapts so that the filter that it actually uses to encode incoming stimuli into spikes becomes closer and closer to this static, fully adapted filter. Similarly, when the neuron is newly exposed to a noise ensemble, the information carried by this filter should decrease with increasing time of exposure to the noise ensemble, as the neuron’s own filter adapts to the noise and becomes less and less like the fully adapted natural scenes filter.

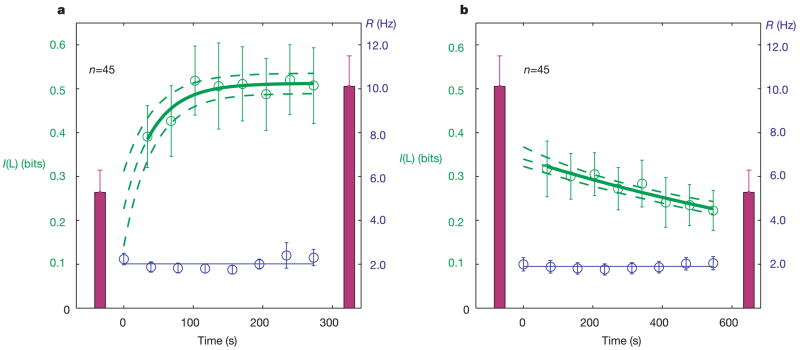
We derived filters from the last half of the 10-min presentations of each stimulus ensemble, when the neuron would be best adapted to the given ensemble if adaptation occurs. We then applied these static filters to both noise and natural stimuli, and measured information between spikes and filtered stimuli in successive 34-s periods during the first half of stimulus presentation (if the filter was derived from the second half of this stimulus) or in successive 68-s periods during all of the presentation of the opposite ensemble. Most cells did not show significant adaptation when considered individually, presumably due to the variability in measuring information over such brief time periods. However, averaging over the entire population of simple cells revealed clear adaptation over time, consistent with an adaptive coding strategy (Fig. 4). The information progressively increased with time when natural inputs were filtered with the neural filter derived from the natural stimulus ensemble (Fig. 4a; see also Supplementary Discussion and Supplementary Fig. 6), whereas the information decreased with time when that same filter was applied to noise inputs (Fig. 4b).

Figure 4. Adaptation dynamics.

a, b, The neural filter derived from the last half of natural stimulation is applied to the first half of natural (a) or to the noise (b) ensemble. Symbols show information (green, left y axis) and firing rate (blue, right y axis) averaged across cells, versus time. The solid line is an exponential fit; dashed lines show one standard deviation based on the jacobian of the fit (P = 0.01 in a and P = 0.003 in b using an F-test with null hypothesis of no time dependence). The taller (shorter) red bars show information for the natural filter applied to natural (noise) inputs (as in Fig. 3, but n = 45). The firing rates demonstrate that recordings are stable.

Fits of a single exponential to the average data demonstrate that there is a statistically significant monotonic change with time, with time constants τ = 42 ± 9 s for adaptation to the natural ensemble and τ = 22 ± 2 min for adaptation to the noise ensemble. These time constants are consistent with the fact that we could not detect adaptation to the natural ensemble with the 5-min timescale of direct filter measurements, but we could detect adaptation to the noise ensemble (Supplementary Fig. 5). Note, however, that the time constants are based on the assumption of exponential decay and do not exclude the possibility of multiple timescales, including scales faster than we were able to measure, or of alternative functional forms of decay.

We could not detect a significant trend with time in the information carried by the noise filter about either ensemble (see Supplementary Fig. 7). This is perhaps not surprising given that the average decrease in information for the noise filter applied to the noise versus natural ensembles was not significant (P = 0.14, unpaired t-test), and that the slow time course of adaptation to the noise ensemble suggests that the filter we tested was not fully adapted to it (see also the legend of Supplementary Fig. 7). Nonetheless, the presence of significant monotonic changes in the expected directions for the natural scenes filter applied to each ensemble demonstrates that the neuron’s coding strategy is adapting over time with exposure to a given ensemble.

Discussion

Adaptation is ubiquitous throughout the nervous system, and it occurs in many forms. In vision, adaptation to luminance mean and variance (contrast) has been observed in the retina^{5,6,9,13,14,17,18}, lateral geniculate nucleus¹⁶ and primary visual cortex^4,7,8,20, and related changes are observed in perception³⁸. In the framework of our model, adaptation may affect the neural gain (the nonlinear input–output function) or the spatiotemporal filter itself. Adaptation of the gain to the mean and variance of the stimulus ensemble (and perhaps to higher-order statistics³⁹) serves to fit a neuron’s dynamic range to the dynamic range of the stimulus^{5–7,9,10,12–14,16}. In addition, adaptation of the filter to the mean and variance of the stimulus^{2,3,5,6,14,17} has been observed, and it has been argued that such adaptation along with adaptation to the stimulus covariance can serve to maximize the information per spike in the neuron’s response^40,41. In general, filter adaptations are nearly instantaneous (<0.1 s), whereas changes in gain can be more gradual (time constants up to 10 s and perhaps longer for some components of adaptation to mean luminance)^{5,6,9,13,14,16,17}. Here we find an adaptive change in neural filters in response to stimulus statistics beyond the mean and variance, and one that occurs over much longer timescales than previously found even for contrast gain changes. This suggests that the observed adaptation represents a new mechanism for optimal coding.

Adaptation to the power spectrum could be considered a generalized form of contrast adaptation, in which different frequency channels providing input to cortical cells differentially adapt their gains so that channels with more stimulus power show greater adaptation. Indeed, variation of gain adaptation across different retinal pathways has been observed^9,13,16,18. However, these observations, and a recently reported pattern-specific component of retinal adaptation⁴², involved adaptation on significantly faster time-scales than observed here. Also, in the lateral geniculate nucleus, adaptive changes between white noise and natural stimulation were not observed in the temporal domain, at least for a majority of cells⁴³. This suggests that the adaptive changes reported here are of cortical origin. A pattern-specific component of cortical adaptation has been observed: for example, one that differentially affects responses according to the difference of the stimulus orientation, direction or spatial frequency from that of the adapting stimulus^{8,11,15,19,20}. At least in one case, this adaptation has been observed to have time constants on the order of a minute or longer¹¹. It is possible that the present observations may share some underlying mechanisms with such pattern-specific adaptation.

Many recent studies have used versions of the linear model or related models to estimate receptive fields from responses to natural stimuli^1,21,23–26. Some have reported that the estimates calculated from responses to natural stimuli differ from those calculated from responses to noise^1,21,23, whereas others^25,26 found no change in the major parameters of neural filters, such as optimal stimulus orientation and spatial frequency. It is not clear from these observations to what degree reported differences in neural filters are genuinely stimulus-induced or are due to biases in the estimation induced by the non-gaussian statistics of natural stimuli together with the nonlinearity of the input–output function. The fact that the receptive field obtained for a given ensemble from the linear model best predicted responses to other examples of its own ensemble^1,21,23 suggests at least partially genuine differences, which is also supported by our results on spatial frequency adaptation. However, the fact that we found larger differences between filters obtained in the linear approximation (dSTA for natural stimulus ensemble and STA for white noise ensemble) than between filters obtained in the linear–nonlinear model (MID for natural stimulus ensembles and STA or MID for white noise ensemble) suggests that biases also exist, and the new information maximization procedure used here removes these biases for real neurons, just as was demonstrated in numerical simulations³⁰.

We have found that V1 neurons adapt their filters to stimulus statistics beyond the mean and variance. This filter adaptation occurs over 40 s to many minutes, suggesting that it is not a consequence of previously described mechanisms of luminance or contrast adaptation. The adaptation serves to preserve information transmission and to reduce relative responses to stimulus components that are relatively more abundant in the stimulus ensemble, as predicted by optimal encoding arguments. It remains to be determined whether the neurons are adapting to changes in power spectra, in higher-order statistics, or both. The gradual nature of adaptive changes and their correspondence to optimization principles suggests that it might be possible to predict the direction and degree of adaptation to stimulus sets with statistics intermediate between those of white noise and natural stimuli. Thus, there is hope for creating a unified picture of neural responses across various input ensembles.

METHODS

All experimental recordings were conducted under a protocol approved by the University of California, San Francisco, Committee on Animal Research with procedures previously described⁴⁴. Spike trains were recorded using tetrode electrodes from the primary visual cortex of anaesthetized adult cats and manually sorted off-line. Visual stimulus ensembles of white noise and natural scenes were each 546 s long. After manually estimating the size and position of the receptive field, neurons were probed with full-field moving periodic patterns (gratings). Cells were selected as simple if, under stimulation by a moving sinusoidal grating with optimal parameters, the ratio of their response modulation (F₁; that is, amplitude of the Fourier transform of the response at the temporal frequency of the grating) to the mean response (F₀) was larger than one³⁴. The rest of the protocol typically consisted of an interlaced sequence consisting of three different noise input ensembles of identical statistical properties, and three different natural input ensembles. The interval between presentations varied in duration as necessary to provide adequate animal care. All natural input ensembles were recorded in a wooded environment with a hand-held digital video camera in similar conditions on the same day (see Supplementary Movie). The noise ensembles were white overall, but the spatial frequency spectrum was divided into eight circular bands, and each particular frame was limited to one band chosen at random; this white noise design was intended to increase the number of elicited spikes. The mean luminance and contrast of the noise ensembles were adjusted to match those of the natural ensembles. Both noise and natural inputs were shown at 128 × 128 pixel resolution, with angular resolution of approximately 0.12° per pixel. To calculate receptive fields, input ensembles were down-sampled to 32 × 32 pixels. The receptive field centre was determined from the maxima in the STAs for noise and natural ensembles and was set to the same position for analysis of both noise and natural inputs. A patch of 16 × 16 pixels was selected around the centre (angular resolution of 0.48° per pixel) to make analysis computationally feasible and to minimize effects due to undersampling (we strove to have the number of spikes greater than the dimensionality of the receptive fields³⁰). In all cases subsequent analysis of receptive fields verified that the selected patch fully contained the receptive field. These receptive fields were used in all quantitative analyses (Figs 2–4). Examples in Fig. 1 were computed at and are shown at twice the angular resolution to illustrate the finer structure of the receptive field, as well as differences in performance of the various methods.