Abstract
Distortion product otoacoustic emission suppression (quantified as decrements) was measured for f2=500 and 4000 Hz, for a range of primary levels (L2), suppressor frequencies (f3), and suppressor levels (L3) in 19 normal-hearing subjects. Slopes of decrement-versus-L3 functions were similar at both f2 frequencies, and decreased as f3 increased. Suppression tuning curves, constructed from decrement functions, were used to estimate (1) suppression for on- and low-frequency suppressors, (2) tip-to-tail differences, (3) QERB, and (4) best frequency. Compression, estimated from the slope of functions relating suppression “threshold” to L2 for off-frequency suppressors, was similar for 500 and 4000 Hz. Tip-to-tail differences, QERB, and best frequency decreased as L2 increased for both frequencies. However, tip-to-tail difference (an estimate of cochlear-amplifier gain) was 20 dB greater at 4000 Hz, compared to 500 Hz. QERB decreased to a greater extent with L2 when f2=4000 Hz, but, on an octave scale, best frequency shifted more with level when f2=500 Hz. These data indicate that, at both frequencies, cochlear processing is nonlinear. Response growth and compression are similar at the two frequencies, but gain is greater at 4000 Hz and spread of excitation is greater at 500 Hz.
INTRODUCTION
The purpose of this study was to compare low- and high-frequency cochlear processing in humans, using distortion product otoacoustic emission (DPOAE) measurements. Specifically, we were interested in evaluating response growth, compression, cochlear-amplifier gain, tuning and spread of excitation, based on measurements of DPOAE suppression, to determine if the human cochlea processes low- and high-frequency sounds differently.
DPOAEs typically are measured in response to two primary tones of slightly different frequency, with f2 representing the higher frequency in the primary-frequency pair and f1 representing the lower frequency in the pair. It is generally assumed that DPOAEs (at least initially) are generated at a location in the cochlea near the best place for f2, even though the response is typically measured at the 2f1–f2 frequency, which is about 1∕2 octave lower in frequency than f2. This fact has implications for DPOAE measurements as a function of frequency because noise in DPOAE measurements increases as frequency decreases. It is this interaction between frequency and noise level that is probably the most important factor contributing to the poorer test performance of DPOAE measurements in determining auditory status at lower frequencies in humans (e.g., Gorga et al., 1993, 1997). However, the difference in noise levels as a function of frequency potentially could have an impact on every OAE measurement in which low- and high-frequency cochlear processing are compared.
In a recent paper, low- and high-frequency cochlear nonlinearity was examined by measuring DPOAE input∕output (I∕O) functions for f2 frequencies of 500 and 4000 Hz (Gorga et al., 2007). Long averaging times were used in efforts to reduce the noise levels when f2=500 Hz. Behavioral thresholds were measured at both f2 frequencies for each subject, allowing us to set L2 (the level of f2) in sensation level (SL) relative to each subject’s threshold. To a first approximation, this approach provided a way to equate the representation of stimuli in the cochlea, both across frequency and subjects, and helped to account for differences in forward middle-ear transmission between 500 and 4000 Hz. For each subject, techniques were followed that allowed us to select the optimal L1 for each L2 for each subject individually (Neely et al., 2005; Gorga et al., 2007). Finally, the slopes of I∕O functions were evaluated as a way of comparing cochlear responses across frequency on the assumption that slope should be independent of reverse middle-ear transmission. While previous work has shown that reverse middle-ear transmission would be expected to affect the relative position of the DPOAE I∕O function along the y axis (Keefe, 2002), it would not be expected to influence the slope of that function. In total, these stimulus conditions and response measurements were selected in an effort to reduce noise to similar, low levels at both frequencies, account for forward middle-ear transmission, set optimal stimulus-level conditions individually, and provide a metric that was independent of reverse middle-ear transmission.
DPOAE I∕O functions at 500 and 4000 Hz differed at low levels of stimulation, with a maximum low-level slope of about 1 achieved at lower levels when f2=4000 Hz (Gorga et al., 2007). In contrast, the minimum slope in the I∕O functions was observed at similar stimulus levels of 40–50 dB SL for the two frequencies. When combined, these two observations provide support for the view that there was a wider dynamic range when f2=4000 Hz. These results also suggest that there may be greater cochlear-amplifier gain at 4000 Hz, compared to 500 Hz, to the extent that the observation of responses at lower levels reflects greater gain.
An important limitation of the previous study, however, was the differences in noise floor between 500 and 4000 Hz. Despite using long averaging times (as much as 210 s), residual noise floors were higher when f2=500 Hz. The influence of this difference in noise floor was greatest for low-level stimulus conditions, where differences in response properties at the two frequencies were observed. While the signal-to-noise ratio (SNR) was such that the responses at both frequencies exceeded the noise floor for the conditions in which the maximum slope was achieved, we were cautious in our interpretation of these data because we could not completely rule out the influence of differences in noise floor on the slope of the DPOAE I∕O functions at low levels of stimulation.
Our previous work, described earlier, was motivated by several observations, based on physiological and behavioral data, in which differences in cochlear processing for high and low frequencies have been evaluated. For example, frequency-threshold curves (FTCs) differ for auditory-nerve fibers innervating more basal, high-frequency cochlear regions, compared to fibers innervating lower frequency, apical regions (e.g., Kiang et al., 1965; Kiang and Maxon, 1974). In their normal state, fibers innervating the cochlear base are characterized by low thresholds and sharp tuning around their characteristic frequency (CF, the frequency to which the fiber has the lowest threshold), decreased sensitivity (higher thresholds) as frequency moves away from CF, and a low-frequency tail on which thresholds either increase slowly or remain relatively constant. In contrast, low-CF fibers have FTCs that are more symmetrical around their CF, and often lack the low-frequency, relatively constant-threshold tail that is evident in the responses of high-CF fibers.
Sewell (1984) provided data in which furosemide treatment resulted in greater changes in thresholds around the CF of high-frequency fibers, compared to fibers with low CFs. It has been argued that the low thresholds around fiber CF are a reflection of cochlear-amplifier gain at that frequency, and that the motile behavior of outer hair cells (OHC) is the source of this gain (Dallos et al., 1997; Hudspeth, 1997; Neely and Kim, 1983). Support for this view comes from lesion studies in which OHC damage resulted in threshold elevations near CF, with little or no change in thresholds on the low-frequency tail of the FTC (e.g., Dallos and Harris, 1978; Liberman and Dodds, 1984). The fact that thresholds change more for high-CF fibers following furosemide treatment may be interpreted to mean that there is more gain (that was affected by the treatment) for high-CF fibers. It is impossible to examine the responses of individual auditory neurons in humans; however, OAE responses are related to OHC function, and these responses can be measured in humans. For this reason, our efforts to compare low- and high-frequency cochlear responses in humans have focused on DPOAE I∕O measurements. We hope to exploit these features in further efforts, described in the following, to better understand cochlear function at high and low frequencies in humans.
The majority of data based on direct measurements of basilar-membrane responses comes from observations at the basal, high-frequency end of the cochlea of lower animals. Apparently, this is the case because access to the cochlear apex, even in experimental animals, is difficult, and the risk exists that the procedures that are used to gain access may cause damage to the cochlea. The OHCs are among the most vulnerable structures in the cochlea, and one would expect that their response properties would be altered if damage were to occur during the preparation. When OHC damage occurs, less nonlinearity is observed, regardless of frequency, because OHCs are the source of the nonlinear response. Thus, the experimental difficulty in obtaining access without causing damage has resulted in a situation in which fewer data are available that describe normal cochlear responses at the apex. There are, however, several studies that have directly assessed nonlinearity at the apical end of the cochlea (Cooper and Rhode, 1995, 1997, 1998; Rhode and Cooper, 1996). These studies suggest that nonlinearity is evident in both apical- and basal-region cochlear responses. However, differences were noted, in that the nonlinearity at the apical end of the cochlea exists for a wider range of frequencies and may be less in magnitude, compared to response properties at the cochlear base. In contrast to these findings, Zinn et al. (2000) did not observe compression at low and moderate stimulus levels for apical cochlear regions. Furthermore, they concluded that there was cochlear-amplifier gain at the base, but not at the apex. The apparent discrepancies may be due to factors associated with the relative inaccessibility of the cochlear apex.
With the exception of our recent paper (Gorga et al., 2007), the data related to this issue in humans comes mainly from studies in which behavioral-measurement techniques were used. Interestingly, early work on combination-tone generation indicated that nonlinear distortion was present in the human cochlea over a range of frequencies from below 500 to as high as 8000 Hz with no apparent trend in distortion level as a function of frequency (e.g., Plomp, 1965; Goldstein, 1967). More recently, Hicks and Bacon (1999) and Plack and Oxenham (1998) reported psychoacoustical data that suggest greater nonlinearity for high frequencies, whereas Plack and Drga (2003), Plack and O’Hanlon (2003), Lopez-Poveda et al. (2003), and Schairer et al. (private communication) observed no differences in nonlinearity between high and low frequencies in humans. The differences in results from the two groups of studies may be due, in part, to differences in measurement technique. In some of these studies, conclusions about cochlear nonlinearity were based on comparisons between response properties for on-frequency versus low-frequency stimuli (relative to the frequency of interest). In other studies, conclusions were based on measurements in which such on-frequency∕low-frequency comparisons were not used. The argument against the case in which on-frequency and low-frequency responses were compared is based on the view that the low-frequency stimulus (relative to the frequency of interest) may not have been sufficiently low enough to result in a linear response at the place where the frequency of interest is represented. Some support for this view is perhaps provided in the differences in FTCs for low-CF and high-CF fibers. Additional support may be provided by the work of Cooper and Rhode (1995), in which they noted that the nonlinearity at the apical end of the cochlea extends over a wider range of frequencies, compared to the extent of the nonlinear region at the cochlear base.
Sufficient uncertainty exists that further effort would be useful in evaluating cochlear nonlinearity in humans for high versus low frequencies. Our initial efforts suggested that differences do exist, based on an analysis of DPOAE I∕O functions. While evidence existed in those data for nonlinearity in response to both high- and low-frequency stimuli, the results would be consistent with the view that there is greater cochlear-amplifier gain for higher frequencies. Those data, however, were interpreted cautiously because the influence of differences in noise floor between low- and high-frequency measurements could not be completely controlled. The present study was designed to further explore cochlear nonlinearity in humans, using measurements of DPOAE suppression. These measurements were made for f2 frequencies of 500 and 4000 Hz, using a wide range of suppressor frequencies and levels for each f2. In addition, these measurements were made for a range of stimulus (probe) levels (L2). An advantage of the suppression measurements over I∕O functions is that they may be less affected by the noise floor. At both 500 and 4000 Hz, the response that was suppressed was above the noise during control conditions (the condition in which no suppressor was presented). Thus, the influence of noise is expected to be less in the present measurements.
METHODS
Subjects
Nineteen subjects participated in this study. These subjects were drawn from a larger sample of 103 subjects who participated in our previous studies in which DPOAE I∕O functions were measured (Gorga et al., 2007). In addition to inclusion criteria related to hearing sensitivity, which will be described in the following, these subjects were selected for two reasons. First, they indicated that they would be able to devote the amount of time that was required in order to complete data collection (about 40 h∕subject). An additional three subjects were enrolled in the study, but withdrew after several sessions because of difficulties meeting the time commitment. The data reported in the following came only from the 19 subjects who completed the study. In addition to the time-commitment inclusion criterion, subjects were selected because they produced DPOAEs above the noise floor for both 500 and 4000 Hz for a wide range of L2 levels. This determination was based on data that were obtained from the larger sample of subjects who participated in the I∕O study. Using the previous data to help in subject selection made it possible to describe suppression effects for both high- and low-level probes, which is important because previous data suggest that cochlear-amplifier gain is level dependent (Rhode, 1971; Ruggero and Rich, 1991), an effect that has been observed in data similar to those collected as part of this study (e.g., Gorga et al., 2002a, b, 2003).
Subjects ranged in age from 17 to 42 years, with a mean age of 24.8 years (s.d.=6.2). Each subject had audiometric thresholds of 15 dB HL or better (re: ANSI, 1996) for standard octave and interoctave audiometric frequencies from 250 to 8000 Hz. Additionally, subjects were required to have audiometric thresholds of 10 dB HL or better at 250, 500, 2000, 3000, and 4000 Hz, which included the primary (f2) frequencies (500 and 4000 Hz) that were the focus of the present measurements. These behavioral-threshold subject-inclusion data were collected using routine clinical procedures, to be contrasted with the procedures that were used later to determine the behavioral thresholds in order to set stimulus levels during DPOAE measurements (see the following). Each subject had a normal 226-Hz tympanogram on each day on which DPOAE measurements were made. Only one ear of each subject was tested, and was chosen as the ear with the lowest audiometric thresholds at 500 and 4000 Hz, in the hope that such a choice would result in the widest dynamic range of DPOAE measurements for individual subjects (e.g., Dorn et al., 1998). If the audiometric thresholds did not differ between ears, then the test ear was chosen at random.
Stimuli
DPOAEs were elicited in response to a pair of primary frequencies (f1 and f2), with f2=500 or 4000 Hz. These two frequencies were chosen because they represent distant locations in the cochlea, one closer to the base and the other closer to the apex. However, cochlear maps for humans suggest that these two frequencies are not represented at “extreme ends” of the cochlea, being approximately 71% and 33% from the base for 500 and 4000 Hz, respectively (Greenwood, 1990). Still, 500 Hz represents a lower practical limit for reliable DPOAE measurements. With an f2 of 500 Hz, the 2f1-f2 distortion product frequency (the frequency at which responses were measured) occurs at 320 Hz. At this measurement frequency, noise levels are high, making it difficult to measure responses. Reliable measurements are possible with an f2 of 500 Hz only if long averaging times are used. However, it would be even more difficult to obtain measurements for f2<500 Hz, because the further increase in noise with decreasing 2f1–f2 would require impracticably long averaging times. In a similar fashion, f2=4000 Hz was viewed as a practical high-frequency limit, but for different reasons. With the limitations of our current calibration approach (see the following), it was possible to avoid standing-wave problems for this frequency and its associated suppressor frequencies, something that would not have been possible if measurements included higher frequencies. In addition, the hardware used in the present study produced less output for higher frequencies, and would have reduced the range of primary and suppressor levels for which measurements could be made. The adequacy of these frequency limits is supported by recent data suggesting that cochleae in humans function differently for frequencies above 1000 Hz, compared to lower frequencies (Shera et al., 2007). Thus, the f2 frequencies used in the present study may provide insights from cochlear regions having different response properties. For both f2 frequencies, the ratio of f2 to f1 was constant at about 1.22. A larger ratio might have reduced the contributions from the DP place (the reflection source), although this is not always the case (Dhar et al., 2005). Even so, this would also have had the effect of reducing the overall level (and SNR) of the DPOAE (e.g., Dhar et al., 2005; Gaskill and Brown, 1990). Our interest in measuring suppression at low stimulus levels, where cochlear-amplifier gain is greatest, made the use of larger f2∕f1 undesirable.
The level of the higher frequency in the primary-frequency pair (L2) was set in dB sensation level (SL) relative to each subject’s behavioral threshold at f2. L2 varied from 20 to 50 dB SL when f2=500 Hz, and from 10 to 50 dB SL when f2=4000 Hz. These conditions were chosen because they resulted in at least a 10-dB SNR for conditions in which no suppressor was presented in the majority of subjects. The inclusion of the 10-dB SL condition at 4000 Hz reflects the fact that it was possible to achieve a positive SNR at lower L2 levels at 4000 Hz, compared to 500 Hz. The greater SNR at 4000 Hz is a consequence of the lower noise levels that are routinely observed at this frequency. Stimuli at 500 and 4000 Hz were presented relative to behavioral threshold in an effort to equate the “effective” representation of the two stimuli in the cochlea. In part, this approach should (to a first approximation) take into account differences in forward transmission through the middle ear at the two test frequencies. The “optimal” level of L1 (the level of f1, the lower frequency in the primary-frequency pair) was selected individually for each L2 and for each f2. By optimal level, we mean the L1 at each L2 for which the DPOAE level was largest in individual subjects. Different procedures were used to select these optimal conditions at 500 and 4000 Hz. At 4000 Hz, a procedure was used in which both L1 and L2 varied continuously (Neely et al., 2005), whereas the higher noise levels at 500 Hz required longer averaging times, which, in turn, required measurements at discrete combinations of L1 and L2 (Gorga et al., 2007). The procedures with which these levels were selected were described in detail previously (Neely et al., 2005; Gorga et al., 2007), and will not be repeated here. Although the procedures differed for each f2, in both cases, a range of L1 levels were tested for each L2 so that the L1 resulting in the largest DPOAE was identified and used in the main experiment. We elected to use this general approach because it took into account both subject and frequency differences in optimal-level conditions. While previous studies suggest that the decibel difference between L1 and L2 should increase as L2 decreases, the results from those studies are not entirely in agreement in the exact form of the primary-level relationship. For example, Kummer et al. (1998, 2000) presented data showing that a single equation (referred to as the scissor paradigm) is appropriate for setting optimal stimulus-level ratios independent of f2. In contrast, Neely et al. (2005) and Johnson et al. (2006) reported data in which the optimal level ratio varied across subjects and also depended on f2. The approach taken in the present study, which follows the procedures used by Neely et al., Johnson et al., and Gorga et al., makes no assumptions about the generalizability of the relationship between L1 and L2, either across subjects or across frequency. It results in optimal levels for each f2 and for each subject, thus assuring that stimulus conditions producing the largest DPOAE are used in every case.
Nine suppressor frequencies (f3) were used during suppression measurements when f2=500 Hz. They ranged from 129 to 750 Hz. When f2=4000 Hz, 14 f3 frequencies were used, ranging from 2064 to 5667 Hz. During DPOAE suppression measurements, it is not possible to select a suppressor whose frequency is identical to f2. A frequency slightly different from f2 must be used as the “on-frequency” condition. When f2=500 Hz, 515 Hz was used as the on-frequency suppressor, whereas when f2=4000 Hz, 4100 Hz served as the on-frequency suppressor. Suppressor level (L3) ranged from −20 to 85 dB SPL in 5-dB steps.
Procedures
Following obtaining informed consent, subjects were screened according to the above- described inclusion criteria. Once it was determined that the subject met inclusion criteria, behavioral thresholds were obtained with a more precise psychophysical procedure, compared to the routine clinical techniques that were used during the screening procedures associated with the inclusion criteria. Thresholds were measured with a two-interval, forced-choice, transformed up-down procedure that estimated the 71% correct point on the psychometric function (Levitt, 1971), using the same hardware that was used during DPOAE measurements. Averaged across subjects, the mean behavioral thresholds from these measurements were 11.9 dB SPL at 500 Hz (s.d.=3.2 dB) and 4.4 dB SPL at 4000 Hz (s.d.=4.8 dB). The individual thresholds for each subject were then used to set L2 in dB SL during the suppression measurements, which are the main focus of the study.
For all DPOAE measurements, approximately 1 s recorded waveforms were stored in alternating response buffers. The contents of the buffers were summed and the resulting level in the 2f1-f2 frequency bin was used to estimate DPOAE level. The contents of the two buffers were subtracted and the level in the 2f1-f2 frequency bin and the level in five frequency bins above and below 2f1-f2 were averaged to provide an estimate of noise level. During suppression measurements, L2 was set at one of four values (f2=500 Hz) or one of five values (f2=4000 Hz). This two-tone “probe” stimulus was presented as a control condition, in which there was no suppressor, and then presented with one of the suppressor frequencies, whose level was varied. Following the presentation of the highest L3, another control condition was included. This process was repeated for all of the suppressor frequencies, all L2 levels and both f2 frequencies for each subject.
Measurement-based stopping rules were used throughout data collection, but the rules differed for the two f2 frequencies. When f2=4000 Hz, measurements continued until the noise floor was ⩽−25 dB SPL, the SNR ⩾20 dB, or until 210 s of artifact-free averaging had taken place, whichever occurred first. In essentially every condition for this frequency, averaging stopped on the noise level and SNR rules, which were often met simultaneously. A compromise was needed, however, when f2=500 Hz, because the noise levels were higher at this frequency. At 500 Hz, averaging stopped when the noise floor was ⩽−25 dB SPL, the SNR was ⩾12 dB, or 210 s of artifact-free averaging had been completed. The only difference between this rule and the one used when f2=4000 Hz is the SNR stopping criterion. With this “compromise,” we were able to achieve reliable estimates of DPOAE level for a range of L2 conditions when f2=500 Hz (on the assumption that a SNR ⩾12 dB would result in a reliable estimate of DPOAE level), without averaging for the prohibitively long times that would be necessary to achieve the same low noise levels as were achieved routinely when f2=4000 Hz. For any conditions in which the presence of the suppressor reduced the SNR to less than 12 dB (by reducing DPOAE level), the effective stopping rules were the same at 500 and 4000 Hz. In general (depending on L2 and the extent to which the response was suppressed), measurements stopped either on the SNR criterion or the averaging-time criterion when f2=500 Hz, but almost never stopped on the noise-floor criterion. Differences in the conditions under which measurements stopped (and, therefore, the noise floor associated with measurements) was not considered a significant problem because the responses in the control conditions had positive SNRs at both f2 frequencies. Furthermore, a suppression threshold of 3 dB was used during the construction of DPOAE suppression tuning curves (STCs), from which main observations from the present study were made. This means that the SNR for the points on the STCs were positive. Even with differences in stopping rules designed to increase data-collection efficiency, each subject participated in about 40 h of data collection in order to complete measurements for all stimulus conditions. As expected from the previous description of stopping rules, the majority of the time was spent collecting data when f2=500 Hz.
Stimuli were produced by a 24 bit sound card (Digital Audio Labs, Card Deluxe) that drove a probe-microphone system (Etymotic, ER-10C). The “receiver equalization” of the ER-10C was bypassed to allow up to 20 dB higher level stimuli to be produced. Even so, there were conditions for which the maximum level produced by the hardware was insufficient to produce complete suppression. This occurred for f3 frequencies at the high- and low-frequency ends of the range of suppressors and for the higher L2 levels. Psychophysical thresholds were measured using custom-designed software that implemented the 2IFC procedure. Only one channel of the sound card and probe-microphone system were used for behavioral-threshold estimates. DPOAE data were collected with the same hardware that was used for the behavioral-threshold measurements, and were collected with custom-designed software (EMAV, Neely and Liu, 1994). Both channels of the sound card and probe-microphone system were used during DPOAE measurements, with f2 presented on one channel and f1 presented on the other. When a suppressor was included, it was presented on the same channel as f2. For both behavioral-threshold and DPOAE measurements, in-the-ear SPL calibration was used to determine stimulus levels. There are concerns regarding standing waves when this calibration approach is followed (e.g., Siegel and Hirohata, 1994; Siegel, 2007). In efforts to avoid these problems, the probe was repositioned more deeply whenever a notch in the calibration spectrum was observed in the vicinity of 4000 Hz. In this way, the notch (and presumably, the standing-wave problems producing it) was shifted toward higher frequencies outside the range of interest for the present study.
Figure 1 illustrates features of the procedures used in the present experiment. It provides examples of data that were collected during the suppression measurements, the conversion of these suppression data into decrements as a result of the presence of the suppressor, transformation of the data, and finally linear fits that were applied to the transformed data. The left column presents data when f2=500 Hz, while the right column shows data when f2=4000 Hz. For both f2 frequencies, L2 was presented at 40 dB SL. Results are shown for the on-frequency suppressor condition (f3=515 Hz for f2=500 Hz and f3=4100 Hz when f2=4000 Hz). Individual data points represent the means (±1 s.d.) based on data from all 19 subjects. In the top row, DPOAE and noise levels are plotted as a function of L3. An estimate of the DPOAE level for the control condition (when no suppressor was presented) is provided by the levels during the flat portion of the DPOAE level functions (i.e., when L3< about 40 dB SPL). The SNR can be estimated by comparing these values to the corresponding noise levels shown in Fig. 1. The differences in the results for 500 and 4000 Hz are due mainly to differences in noise floors, with smaller differences in DPOAE level. This is to be expected given the differences in noise for these two f2 frequencies, and occurred despite the measurement-based stopping rules and the long averaging times associated with them when f2=500 Hz. Still, suppressive effects were reliably measured for a range of L3 levels at both f2 frequencies. The data shown in the top row of Fig. 1 show that the suppressor had little or no effect on DPOAE level until L3 was about 40 dB SPL. As L3 increased above this level, DPOAE level was systematically reduced until it eventually equaled the noise floor, which occurred when L3≈75 dB SPL at both f2 frequencies.
Figure 1.
Top row: Mean DPOAE (squares) and noise (triangles) levels in dB SPL as a function of suppressor level, L3, in dB SPL. Bottom row: Mean DPOAE decrements (circles) in dB as a function of L3. Left column shows data when f2=500 Hz; right column shows data when f2=4000 Hz. In both cases, L2=40 dB SL, and an on-frequency suppressor (f3) was used (f3=515 and 4100 Hz for f2=500 and 4000 Hz, respectively). Closed symbols represent the transformed data points and the line represents a linear regression fit to the closed symbols. In all cases, error bars represent ±1 s.d. The short vertical dashed lines in the bottom row of panels are drawn at a decrement of 3 dB, which was used as suppression threshold for the construction of STCs.
The influence of differences in the stopping rules for the two frequencies also is evident in Fig. 1. Note that for all L3 levels, the mean noise floor at 4000 Hz is ⩽−25 dB SPL because this noise level was always achieved. In contrast, the noise floor is higher when f2=500 Hz for L3 levels <40 dB SPL, which represent conditions in which the SNR stopping rule (12 dB) at this frequency caused measurements to stop. For higher L3 levels, the mean noise floor for f2=500 Hz was lower because the DPOAE was reduced by suppression and the SNR criterion was not met, resulting in longer averaging times. However, even after the full 210 s of artifact-free averaging time, the noise floor was still higher at 500 Hz than it was at 4000 Hz.
Once the data were collected for both f2 frequencies, all L2 levels, and all f3 frequencies and L3 levels, the DPOAE levels in the presence of suppressors were converted into decrements. We have used decrements in DPOAE level in the past to represent the response to the suppressor for several reasons (Gorga et al., 2002a, b; 2003; Johnson et al., 2004). First, decrements describe the amount of suppression as a result of the presentation of the suppressor, which is the measure of interest. They also partially account for individual variability across subjects in DPOAE levels for control conditions. To convert the DPOAE data (as shown in the top row of Fig. 1) into decrements (as shown in the bottom row), the DPOAE levels for the control conditions at the beginning and the end of the L3 series for each f3 were averaged. To calculate the decrement, the DPOAE level in the presence of the suppressor was subtracted from the average level during the control conditions associated with each f3. The open circles in the bottom row of Fig. 1 show decrements (±1 s.d.) that were derived from the data shown in the top row of panels. A comparison of the error bars for DPOAE level in the top panel to the error bars for the decrements in the lower panel demonstrates the expected outcome in which the variability across subjects is reduced for some stimulus conditions by the conversion to decrements. In this representation, decrements of 0 dB indicate conditions for which there was no suppression. Conditions in which the response was suppressed into the noise floor are represented on the right-hand side of these functions, where an asymptotic maximum decrement was approximated. For these latter conditions, the SNR is approximately zero, as they correspond to the conditions in the top row of panels when DPOAE and noise levels were the same, meaning that the response was completely suppressed.
We were interested in linearizing the responsive portions of the decrement-versus-L3 functions because decrement curves typically have a shallower slope for small decrements. To meet this goal, the following rules were used before fitting the decrement functions: (1) only data points for which the SNR ⩾3 dB were included, (2) decrement-versus-L3 functions were fit only if at least one decrement was observed in the range from 3 to 15 dB, and (3) data points were included in the fits so long as the decrements increased monotonically with L3. The first inclusion criterion placed emphasis on data points for which the SNR was high, including those for which only a small amount of suppression (as little as 1 dB) was observed. The second criterion assured that only decrement-versus-L3 functions showing some suppression were fit. The third criterion was needed to assure that data points for which the reliability was low (i.e., those for which the SNR approached or equaled zero) were excluded; it also excluded those points for which no suppression was observed. The data points meeting the above-noted criteria on each decrement-versus-L3 function were transformed by
| (1) |
The points shown as closed circles in the bottom row of panels of Fig. 1 represent the transformed data for those conditions that met the inclusion criteria. The application of the transformation resulted in a linearization of the decrement-versus-L3 functions, in which the decrement is 3 dB when D=0. The solid line drawn in each panel represents the best linear fit to the decrement data, but only included those points shown as closed circles. The equations describing these fits for each combination of f2, L2, and f3 were used to estimate the slope of these functions (growth of suppression) and to determine the decrement “threshold” for construction of DPOAE STC. The short vertical dashed lines in Fig. 1 represent conditions for which the decrement=3 dB [D=0 in Eq. 1], which was used as suppression threshold for the purpose of constructing STCs.
RESULTS
Control conditions
Recall that measurements for every f3 were preceded and followed by a control condition in which no suppressor was presented. With 9 (500 Hz) or 14 (4000 Hz) f3 frequencies, there were either 18 (f2=500 Hz) or 28 (f2=4000 Hz) measurements of the control condition for each f2, L2 combination, which were averaged separately for every subject. Table 1 presents the means and standard deviations of these control conditions for each subject when f2=500 Hz, while similar data when f2=4000 Hz are provided in Table 2. Tables 1, 2 also provide grand means and standard deviations (averaged across subjects) of the individual mean DPOAE levels and individual standard deviations. Notably, for 2 of the 19 subjects at 20 dB SL when f2=500 Hz and for 1 of 19 subjects at 10 dB SL when f2=4000 Hz, the SNR was too low to permit reliable measurements of suppression. For all other conditions, reliable suppression measurements were possible because every subject produced responses that were above the noise floor for the control condition.
Table 1.
Means and standard deviations for the control condition in each of the 19 subjects at each of the four L2 levels when f2=500 Hz. Grand means and standard deviations are provided in the bottom two rows.
| Subject | L2=20 SL | L2=30 SL | L2=40 SL | L2=50 SL | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | s.d. | Mean | s.d. | Mean | s.d. | Mean | s.d. | |
| 01 | −7.544 | 2.785 | −0.362 | 1.931 | 5.813 | 1.761 | 8.039 | 1.355 |
| 02 | −1.887 | 1.909 | 0.985 | 2.474 | 3.857 | 2.675 | 7.114 | 1.703 |
| 03 | −7.266 | 2.920 | −0.484 | 3.359 | 6.836 | 2.035 | 6.958 | 2.268 |
| 05 | −0.099 | 2.159 | 7.001 | 1.322 | 8.838 | 1.555 | 9.976 | 1.594 |
| 06 | −7.065 | 3.509 | 0.643 | 2.123 | 2.571 | 1.900 | 2.294 | 1.889 |
| 07 | −1.990 | 2.287 | 4.844 | 1.909 | 7.904 | 2.222 | ||
| 08 | −9.527 | 2.713 | −7.854 | 2.070 | −2.401 | 2.158 | ||
| 09 | −7.958 | 3.606 | −3.509 | 2.128 | −0.952 | 1.442 | 1.402 | 1.683 |
| 10 | −8.043 | 4.419 | 1.558 | 2.230 | 6.427 | 2.312 | 9.447 | 2.304 |
| 11 | −7.077 | 2.984 | 0.339 | 2.405 | 5.503 | 1.633 | 7.235 | 1.879 |
| 12 | −9.031 | 3.747 | −1.047 | 1.861 | 5.727 | 1.820 | 6.071 | 1.462 |
| 15 | −2.414 | 3.860 | 3.333 | 2.094 | 6.070 | 2.706 | 7.756 | 2.653 |
| 16 | −0.318 | 1.582 | 4.507 | 2.133 | 7.670 | 1.154 | 8.673 | 1.429 |
| 17 | −1.481 | 2.535 | 5.941 | 1.432 | 7.179 | 2.093 | 4.990 | 1.450 |
| 18 | −6.453 | 2.135 | −1.001 | 1.488 | 2.351 | 2.376 | 1.090 | 2.867 |
| 19 | −7.396 | 1.631 | −1.164 | 2.310 | 4.859 | 2.424 | 8.509 | 2.648 |
| 20 | −6.037 | 2.185 | 0.494 | 2.466 | 4.730 | 3.307 | 5.726 | 5.022 |
| 21 | −9.774 | 2.415 | −2.056 | 1.847 | 1.979 | 1.890 | 5.102 | 1.459 |
| 22 | −15.044 | 2.817 | −5.969 | 2.069 | −0.441 | 2.545 | 2.092 | 3.449 |
| Mean | −6.171 | 2.776 | −0.121 | 2.141 | 4.000 | 2.085 | 5.683 | 2.184 |
| s.d. | 3.861 | 0.826 | 3.875 | 0.470 | 3.868 | 0.513 | 3.337 | 0.896 |
Table 2.
Means and standard deviations for the control condition in each of the 19 subjects at each of the five L2 levels when f2=4000 Hz. Grand means and standard deviations are provided in the bottom two rows.
| Subject | L2=10 SL | L2=20 SL | L2=30 SL | L2=40 SL | L2=50 SL | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | s.d. | Mean | s.d. | Mean | s.d. | Mean | s.d. | Mean | s.d. | |
| 01 | −15.609 | 3.379 | −5.626 | 1.350 | −1.263 | 1.789 | 4.853 | 1.172 | 8.733 | 1.529 |
| 02 | −3.733 | 2.473 | 2.483 | 3.057 | 7.419 | 2.484 | 11.247 | 2.556 | 13.500 | 2.792 |
| 03 | −2.394 | 1.423 | 0.425 | 2.546 | 2.695 | 2.562 | 2.648 | 3.615 | 6.148 | 2.538 |
| 05 | −8.408 | 1.424 | −2.240 | 1.070 | 1.974 | 0.695 | 6.268 | 0.830 | 8.565 | 1.764 |
| 06 | −3.299 | 2.779 | 4.655 | 1.577 | 10.679 | 0.964 | 14.080 | 0.875 | 16.571 | 1.012 |
| 07 | −16.459 | 1.926 | −14.510 | 3.722 | −8.206 | 4.655 | −5.113 | 4.588 | 0.444 | 4.237 |
| 08 | −16.455 | 2.089 | −11.472 | 3.572 | −5.444 | 3.171 | −1.295 | 2.410 | ||
| 09 | −14.122 | 1.564 | −6.770 | 1.427 | −3.153 | 0.927 | 1.192 | 1.672 | 6.566 | 1.700 |
| 10 | −0.130 | 2.177 | 1.011 | 2.238 | 2.593 | 3.043 | 7.847 | 1.385 | 11.911 | 0.951 |
| 11 | −2.104 | 1.786 | 1.847 | 1.366 | 4.842 | 1.301 | 8.267 | 1.120 | 10.312 | 2.321 |
| 12 | −6.853 | 2.900 | −2.063 | 2.116 | 1.059 | 1.406 | 4.813 | 1.041 | 7.637 | 0.853 |
| 15 | −7.970 | 1.230 | −5.003 | 1.759 | 0.021 | 1.821 | 4.164 | 2.228 | 7.958 | 1.086 |
| 16 | −11.720 | 3.076 | −3.560 | 2.376 | 2.051 | 3.591 | 8.264 | 3.051 | 11.399 | 4.277 |
| 17 | −7.731 | 1.265 | −1.651 | 2.733 | 5.422 | 1.082 | 10.508 | 0.678 | 13.702 | 0.345 |
| 18 | −2.412 | 3.847 | 4.516 | 1.263 | 7.065 | 1.258 | 8.623 | 1.597 | 10.561 | 1.494 |
| 19 | 2.269 | 1.314 | 5.551 | 0.910 | 9.004 | 1.424 | 13.324 | 1.389 | 16.224 | 1.020 |
| 20 | −11.011 | 2.654 | −0.641 | 1.612 | 5.505 | 0.921 | 9.644 | 0.697 | 12.507 | 0.614 |
| 21 | −8.916 | 1.126 | −4.524 | 0.839 | 1.112 | 0.802 | 4.992 | 0.534 | 8.688 | 0.447 |
| 22 | −4.387 | 2.944 | 1.128 | 1.894 | 4.805 | 1.747 | 7.660 | 2.206 | 9.817 | 2.402 |
| Mean | −6.944 | 2.183 | −2.181 | 1.892 | 2.218 | 1.897 | 6.202 | 1.811 | 9.471 | 1.779 |
| s.d. | 5.371 | 0.845 | 5.888 | 0.761 | 5.516 | 1.124 | 5.263 | 1.134 | 4.568 | 1.142 |
As expected, mean DPOAE levels varied across subjects. For example, the mean level varied from a low of −9.5 dB SPL in one subject (S#08) to a high of 7.0 dB SPL in another subject (S#05) when f2=500 Hz and L2=30 dB SPL. However, variability in the absolute DPOAE level across subjects is perhaps less important than the within-subject variability in the level produced for the control conditions. Within each subject, the level in the control condition had relatively small standard deviations, meaning that DPOAE level in the control condition was repeatable. In the two above-mentioned cases, the standard deviations for the control conditions were 2.7 and 1.3 dB, respectively, despite the large differences in mean absolute DPOAE level. The between-subject variability in DPOAE level always exceeded the within-subject variability, based on comparisons of the standard deviations for the control conditions. Averaged across all subjects and all f2, L2 combinations, the mean standard deviation for the control conditions was about 2.1 dB. Within-subject variability for the control conditions was only slightly greater at 500 Hz, compared to 4000 Hz. Thus, the control conditions were relatively stable within a subject at both f2 frequencies, despite the fact that subjects differed in the DPOAE level they produced for the same stimulus conditions.
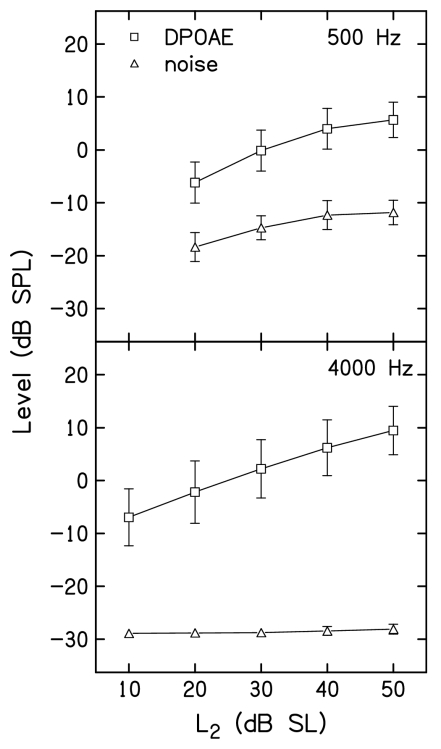
Figure 2 plots mean DPOAE and noise levels as a function of L2 at 500 Hz and 4000 Hz in top and bottom panels, respectively. These data were averaged across the 19 subjects, and provide a graphic representation of the mean DPOAE levels for the control conditions listed in Tables 1, 2, along with the corresponding mean noise levels, which were not provided in the tables. Error bars represent ±1 s.d. As expected, the SNR was always less at 500 Hz, compared to 4000 Hz, as seen in the differences between DPOAE and noise levels within each panel. The influence of the stopping-rule differences also is evident in Fig. 2. First, the noise floor was more variable at 500 Hz, compared to 4000 Hz. This occurred because measurements almost always stopped on the noise floor criterion when f2=4000 Hz, resulting in the same noise floor across subjects for all stimulus conditions, including the control conditions, for which data are shown in Fig. 2. In contrast, measurements stopped either on the SNR or test-time criterion (but almost never on the noise-floor rule), resulting in more variable noise levels across subjects and conditions. Also note that when f2=500 Hz, the noise floor increased as L2 increased. This is a consequence of including the 12 dB SNR stopping rule at this frequency. For higher L2 levels, the response was larger, causing the averaging to stop when the noise levels were higher, compared to the case for lower L2 levels. Even so, there was at least a 12-dB SNR in the mean control conditions, even when L2=20 dB SL and f2=500 Hz. In contrast, the mean noise floor always was less than −28 dB SPL and did not vary with L2 when f2=4000 Hz. Both of these observations reflect the fact that, at this frequency, averaging stopped when the noise-floor criterion was met. Despite the remaining differences in SNR between frequencies, even after allowing averaging to continue for up to 210 s of artifact-free averaging time, the mean differences between DPOAE and noise levels were large enough to permit reliable measurements for a wide range of L2 levels at both 500 and 4000 Hz.
Figure 2.
DPOAE and noise levels for the control conditions, in which there was no suppressor. Top: Mean DPOAE (squares) and noise (triangles) levels in dB SPL as a function of L2 in dB SL when f2=500 Hz. Bottom: Mean DPOAE (squares) and noise (triangles) levels in dB SPL as a function of L2 in dB SL when f2=4000 Hz. In both panels, error bars represent ±1 s.d.
Decrement-versus-suppressor level functions
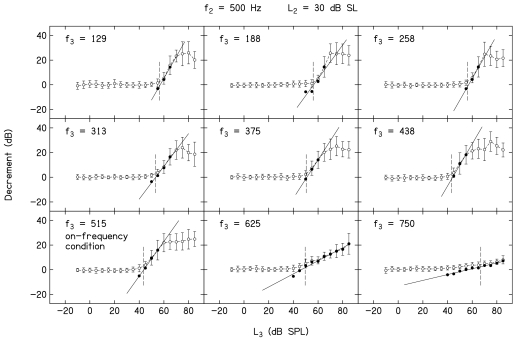
Figure 3 provides a family of decrement-versus-L3 functions when f2=500 Hz and L2=30 dB SL. Open symbols represent the decrement data, while closed symbols represent the transformed conditions meeting the inclusion criteria described earlier. The line in each panel represents the linear fit to the closed symbols. Mean decrements across all 19 subjects (±1 s.d.) are plotted. Data are shown for the nine f3 frequencies used when f2=500 Hz, and is indicated within each panel. An f3 of 515 Hz represents the on-frequency condition, in which f3≈f2. Several observations can be made based on an examination of these decrement functions. First, suppression is observed at the lowest L3 when f3≈f2. In this example, suppression is initially observed when L3=40 dB SPL, with the amount of suppression (decrement) increasing as L3 increases above this level until the response is completely suppressed, which occurs when L3=60 dB SPL. As one moves toward higher f3 frequencies, the L3 at which suppression first appears is similar to or slightly higher, compared to the case when f3≈f2. As one moves further away from f2 on the low-frequency side, the L3 at which suppression is first observed increases. For lower-frequency suppressors, complete suppression is observed, so long as sufficiently high suppressor levels can be presented. For f3>f2, complete suppression is not observed, even at the highest L3 of 85 dB SPL. This observation relates to an interaction between the L3 at which suppression first emerges, the way the decrement (suppression) grows with L3 for high f3 frequencies, and output limitations of our hardware. The slopes of the decrement-versus-L3 functions are frequency dependent, with a slope of approximately 1 for the on-frequency condition. As f3 decreases, the slope increases, with the steepest slope observed for suppressors 1 to 2 octaves below f2=500 Hz. In contrast, the slope decreases as f3 increases above the on-frequency condition, with the highest f3 (750 Hz) showing the shallowest slope. The combination of higher suppression thresholds and shallower slopes, when coupled with output limitations, makes it difficult to observe complete suppression when f3>f2, regardless of L2. The advantages of the transformation are particularly evident when f3=750 Hz. Despite the fact that decrement grows slowly with L3, the linearization of the function that resulted from the transformation allowed us to fit these data with a regression line that enabled us to estimate slope. The short vertical dashed lines in Fig. 3 (and in Fig. 4) are drawn at the same L3 levels as in Fig. 1, namely the L3 resulting in a decrement of 3 dB. These “thresholds” were used to construct STCs.
Figure 3.
Mean DPOAE decrements in dB as a function of L3 in dB SPL when f2=500 Hz and L2=30 dB SL. Error bars represent ±1 s.d. Suppressor frequency is indicated within each panel. Closed symbols represent the transformed data to which a linear regression, represented by the solid line, was fit. The short vertical dashed lines in each panel are drawn at a decrement of 3 dB, which was used as suppression threshold for the construction of STCs.
Figure 4.
Mean DPOAE decrements in dB as a function of L3 in dB SPL when f2=4000 Hz and L2=30 dB SL. Error bars represent ±1 s.d. Suppressor frequency is indicated within each panel. Closed symbols represent the transformed data to which a linear regression, represented by the solid line, was fit. The short vertical dashed lines in each panel are drawn at a decrement of 3 dB, which was used as suppression threshold for the construction of STCs.
Figure 4 presents decrement-versus-L3 functions when f2=4000 Hz and L2=30 dB SL, following the conventions that were used in Fig. 3. Data are shown for the 14 f3 frequencies that were used at 4000 Hz. As was the case when f2=500 Hz, suppression was observed at the lowest L3 when f3≈f2 (f3=4100 Hz). As f3 moved away from 4000 Hz in either direction, the level at which suppression was first observed increased. Complete suppression was observed for the on-frequency case and for low-frequency suppressors, but only within the range of f3 frequencies from 2667 to 4100 Hz (and perhaps 4333 Hz). For some f3 frequencies outside this range, the SNR for L3=85 dB SPL (the highest suppressor level used in the present study) approximates 0 dB, indicating that the response was completely suppressed. However, it is difficult to know from Fig. 4 whether complete suppression occurred for several f3 frequencies when f2=4000 Hz because higher suppressor levels could not be tested and, therefore, maximum asymptotic suppression was not evident. For f3 frequencies at and above 4667 Hz, the results summarized in Fig. 4 indicate that the response was not completely suppressed at the highest L3. The slope of the decrement function approximated 1 in the on-frequency condition, increased as f3 decreased below f2 (with the steepest slope when f3 was 1 octave below f2), and decreased as f3 increased above f2. These trends are the same as those observed when f2=500 Hz. The data shown in Figs. 34 were provided to illustrate general trends in the data and to provide a sense of the variability across subjects, at least as reflected in standard deviations. Decrement-versus-L3 functions will not be shown for other L2 levels because the results were similar to those shown in Figs. 34. Instead, the data for all values of L2 will be summarized in subsequent figures. Furthermore, our interest is to provide summary descriptions and comparisons of cochlear processing at low and high frequencies in humans. Relevant trends are best reflected in mean data, which will be presented in the figures to follow; however, the variability seen in Figs. 134 is representative of variability for other L2 conditions.
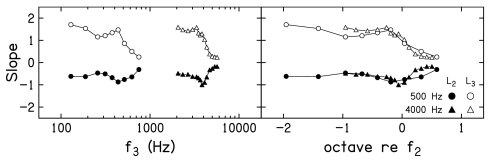
Figure 5 plots slope of decrement-versus-L3 functions as a function of f3. Each row provides data for a different L2. Only data for f2=4000 Hz are shown when L2=10 dB SL, because the control condition at this L2 when f2=500 Hz did not consistently result in a SNR ⩾10 dB. As a result, there was insufficient dynamic range to permit reliable suppression measurements when f2=500 Hz and L2=10 dB SL. Within each panel, slopes when f2=500 Hz are shown as circles, while similar slope estimates when f2=4000 Hz are shown as triangles. In the left column, a log-frequency scale is used, resulting in separation of the data for the two f2 frequencies. In the right column, the same data are replotted on a frequency scale in which octaves relative to f2 are used. In this latter representation, “0” represents the case when f2≈f3, and results in an overlap of the data at the two f2 frequencies. The impressions of the trends in slope related to f3, as seen in Figs. 34, are apparent here. In general, the steepest decrement-versus-L3 functions occur when f3 is an octave or more below f2. There is a transition f3 region, in which the slope decreases as f3 moves from just below f2 to above f2. The shallowest slopes are observed for the highest suppressor frequencies. Similarities and differences between the slopes are emphasized when slope is plotted on a relative scale. For example, it appears that similar slopes are achieved for f3 frequencies ⩾f2, whereas there is a tendency at most, but not all, L2 levels for the slope to be steeper for low-frequency suppressors when f2=4000 Hz, compared to when f2=500 Hz.
Figure 5.
Mean slopes of the decrement-vs-L3 functions as a function of f3 for f2=500 Hz (circles) and f2=4000 Hz (triangles). Data are plotted on a log frequency scale in the left column and a relative (octave) frequency scale in the right column.
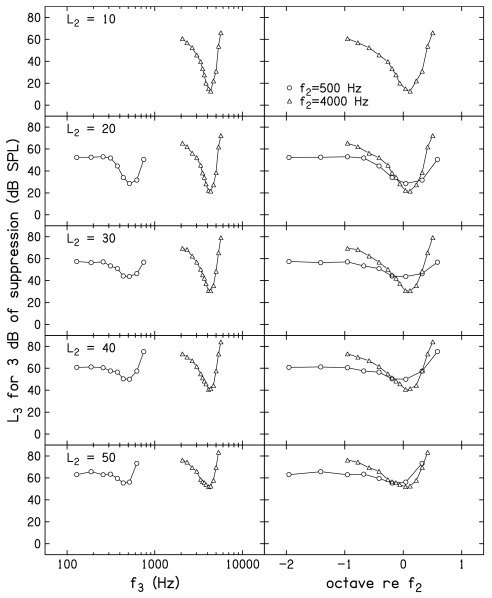
Suppression tuning curves
Figure 6 plots the L3 needed for 3 dB of suppression as a function of f3, following the same conventions as those used in Fig. 5. The value of L3 for 3 dB of suppression represents the D=0 intercept of the linear equations that were fit to the mean decrement-versus-L3 functions. A decrement of 3 dB was operationally defined as “suppression threshold” for this and other figures to follow. An advantage of using decrements of 3 dB as the criterion for constructing STCs is that it assures that positive SNRs (and, therefore, reliable estimates) existed for every point. Even when f2=500 Hz and L2=20 dB SL (the stimulus condition for which the response had the poorest SNR for the control condition), the SNRs when a 3 dB decrement occurred were typically ⩾7 dB. Higher SNRs were observed at the criterion decrement of 3 dB for all other f2 and L2 combinations. Defining STCs with conditions for which the SNR was high reduces the influence of noise level on differences between the results observed at 500 and 4000 Hz, despite the fact that the noise levels were not the same for the two f2 frequencies.
Figure 6.
Mean suppression tuning curves, in which the L3 for 3 dB of suppression is plotted as a function of f3, following the conventions used in Fig. 5.
There are many examples in the literature of DPOAE STCs when f2=4000 Hz, and there is nothing unusual about the ones presented in this paper. However, to our knowledge, this is the first time DPOAE STCs have been reported for an f2=500 Hz. We assume that part of the reason for the lack of data when f2=500 Hz relates to the difficulty in making reliable measurements at this frequency. This problem is a direct consequence of the higher noise levels around the 2f1–f2 distortion product when f2=500 Hz, and is why long averaging times were necessary in the present experiment in order to obtain reliable measurements.
The combination of increased averaging times and the criterion at which the DPOAE STCs were constructed resulted in reliable STC measurements for both 500 and 4000 Hz. The STCs at 500 Hz have properties that are similar in several ways to other more direct measures of tuning, such as FTCs. For example, the tuning curves have higher thresholds for suppression for the on-frequency condition, compared to 4000 Hz. This is not unlike the higher thresholds that are observed at CF for single auditory neurons with low-frequency CFs. Some of this effect can be attributed to the fact that the absolute level (in dB SPL) for the probe (L2) was higher at 500 Hz, compared to 4000 Hz, for equivalent SL. This occurred because the behavioral thresholds which served as the reference for L2 were, on average, 7.5 dB higher at 500 Hz. There is also less difference between the thresholds at the best frequency, compared to the thresholds on the low-frequency tail, although the more symmetrical pattern around CF that has been observed in the responses from individual auditory neurons is not as evident in the present DPOAE STCs at 500 Hz. This finding was not expected; we have no explanation for why low-frequency tails were evident in our DPOAE STCs, given that they often are not evident in FTCs from individual low-CF auditory neurons in lower animals.
Some of the above-mentioned observations may be more obvious in the right column of Fig. 6, where f3 is represented in octaves relative to f2. Notably, there appears to be a range of suppressor frequencies on the low-frequency side for which there is little or no threshold change as f3 decreases, a pattern that is more evident when f2=500 Hz. Recall that one concern in relation to some of the previously reported psychophysical estimates of cochlear nonlinearity at low frequencies was that the low-frequency masker was not sufficiently low to be outside of the compressive growth region at the place of the probe frequency. The data shown in both the left and right columns of Fig. 6 indicate that this is less of a concern in the present experiment. In fact, there is virtually no difference between the L3 for a decrement of 3 dB when f3=258 Hz (about 1 octave below f2), compared to when f3=129 Hz (nearly 2 octaves below f2). While we are surprised by the unexpected low-frequency tail when f2=500 Hz, we are confident that low-frequency suppressors 1 octave or more below f2 have relatively constant thresholds and, therefore, represent the frequency range of interest when f2=500 Hz. If anything, the results when f2=4000 Hz suggest that the inclusion of lower f3 frequencies would have been of value because it is difficult to determine if the lowest f3 used in the present study was sufficiently on the low-frequency tail of the response, where suppression thresholds might be expected to change slowly or remain relatively constant. Unfortunately, output limitations of our hardware in relation to the levels at which suppression first appears precluded measurements for lower suppressor frequencies when f2=4000 Hz. The implications of this observation, especially in relation to estimates of cochlear-amplifier gain, will be discussed subsequently.
Up to this point, decrement functions were fit with simple linear regressions (SLR), meaning that each f3, L2 combination was fit separately. The coefficients of these regressions are shown as slopes in Fig. 5 and the STCs derived from these fits are shown in Fig. 6. In Fig. 7, we summarize slopes from a multiple linear regression (MLR) in which both L3 and L2 were included in the analyses. In Fig. 7, the open symbols represent slopes of the decrement-versus-L3 functions as a function of frequency. The closed symbols represent the slopes of the decrement versus L2. Otherwise, the same conventions used in Fig. 5 are followed in Fig. 7. For both absolute and relative frequencies (left and right panels), the slopes of the L3 functions are positive and decrease as f3 increases. In contrast, the slopes of the L2 functions are negative for all f3, but are nonmonotonic, achieving a maximum negative slope when f3≈f2, with less negative slopes for both higher and lower f3 frequencies relative to f2. The representation of these slopes on a relative frequency scale emphasizes the similarities across frequency. Although variable, the slopes for f2=500 Hz and f2=4000 Hz are superimposed for many suppressor frequencies, especially for low frequencies relative to f2, suggesting that growth of response to the suppressor is similar at these two frequencies. Even so, there is a tendency for steeper slopes when f3<f2 for 4000 Hz, a trend that was also evident in some of the slope estimates from the SLRs, which were shown in Fig. 6. The SLR and MLR accounted for about 98% and 96% of the variance, respectively. Despite this fact, the two models differed significantly. However, the MLR may be preferable in that it required approximately 1∕3 of the variables, compared to what were used during SLR. In the interest of completeness, results based on both SLR and MLR will be provided in subsequent figures.
Figure 7.
Slopes of the decrement functions as a function of f3, based on multiple linear regression in which L2 and L3 were included in the regression analysis. Open symbols represent the slopes of the decrement-vs-L3 functions and closed symbols represent the slope of the decrements vs L2. Circles represent data when f2=500 Hz and triangles represent data when f2=4000 Hz.
The STCs shown in Fig. 6 are superimposed in the top panel of Fig. 8, with L2 as the parameter, which increases as the placement of the STC moves up in the figure (L2=50 dB SL shown as the top STC for both f2 frequencies). The “suppression thresholds” plotted in Fig. 6 and in the STCs shown in the top panel of Fig. 8 represent the D=0 intercept of the previously described SLRs that were fit to each mean decrement-versus-L3 function at each L2. Thus, the thresholds on the STC at one L2 were treated as if they were independent from those at other L2 levels. In the bottom panel of Fig. 8, MLRs, as described earlier, were fit to the decrement functions for each f3. The MLR forced the shift in suppression threshold with L2 to be uniform at each f3. This reduced inconsistencies in the STCs across L2 levels (but not across f3), which had the effect of smoothing the STCs. While the STCs derived from decrement functions fit with MLRs are more uniform across L2, the trends are essentially the same as those seen in the STCs that were obtained when SLRs were fit to the decrement-versus-L3 functions separately for each L2. Within both panels of Fig. 8, the closed symbols represent the mean behavioral thresholds for the 23 f3 frequencies and the two f2 frequencies. These thresholds confirm that the subjects who participated in this study had normal thresholds for a wide range of frequencies.
Figure 8.
Mean STCs for 500 and 4000 Hz. Top: STCs constructed using simple linear regressions that were fit to the decrement-vs-L3 functions. Bottom: STCs constructed using multiple linear regressions that were fit to the decrement-vs-L3 functions. Within each panel, L2 increases from the STC with the lowest suppression threshold to the highest. Superimposed in both panels are the mean behavioral thresholds (closed circles) for all the f2 and f3 frequencies used in the present study.
The representations shown in Fig. 8 emphasize the differences in changes in thresholds around the “tip” versus changes in threshold on the low-frequency tails of the STCs. For any L2, threshold differences between the tip and the tail are less when f2=500 Hz. At 4000 Hz, thresholds at the tip move about 10 dB for each 10 dB increase in L2, as expected. This trend is less evident when f2=500 Hz. For both f2 frequencies, smaller shifts in L3 with L2 are observed for low-frequency suppressors and larger shifts in L3 with L2 are seen for high-frequency suppressors relative to f2. The frequency at which the lowest suppression threshold occurred appears to migrate toward lower frequency as L2 increases. This latter trend is more evident when f2=500 Hz.
Quantitative descriptions of the DPOAE STCs
Figure 9 plots the level of the suppressor (L3) necessary to produce 3 dB of suppression as a function of L2. Data for f2=500 and 4000 Hz are shown in the left and right columns, respectively. The top row shows the results that were obtained when the SLRs were used to estimate the suppressor level, whereas the bottom row provides results when MLRs were used to derive the L3 that caused 3 dB of suppression. In each panel, open symbols represent the results when f3 was approximately 1 octave lower than f2 (which is being viewed as the low-frequency condition for which the response presumably is more linear at the f2 place). Closed symbols represent the results when f3≈f2 (the on-frequency condition for which we assume that the processing is similar and compressive for both f2 and f3 at or near the f2 place). The lines in each panel represent linear fits to the data, with the slopes of the lines provided within each panel adjacent to the set of data to which they apply. For both f2 frequencies, greater suppressor level was needed when f3 was 1 octave below f2, compared to when f3≈f2. The differences between L3 for low- and on-frequency suppressors were greatest for the lowest L2, and decreased as L2 increased. When f3≈f2, the L3 for 3 dB of suppression increased almost linearly with L2. At first glance, this may seem surprising, since cochlear responses for best-frequency tones are compressive; however, both f3 and f2 are being processed similarly by the compressive nonlinearity, resulting in a linear relationship between L3 and L2. An estimate of compression for f2 can be derived from the slope of the functions when f3=f2–1 octave on the assumption that the response to this suppressor is linear at or near the f2 place while the response to f2 is compressive at the same place. The reciprocal of the slopes for these conditions result in estimates of compression that range from 2.4 (f2=500 Hz, MLR) to 3.2 (f2=4000 Hz, MLR).
Figure 9.
L3 for 3 dB of suppression as a function of L2 (dB SL) for on-frequency (closed squares) and low-frequency (open squares) suppressors. The low-frequency suppressor was approximately 1 octave below f2. Top and bottom rows show results for simple and multiple linear regressions, respectively. Left and right columns show data for f2=500 Hz and f2=4000 Hz, respectively. The lines represent linear fits to each set of data. Slopes of these lines are provided as insets adjacent to the line to which they apply.
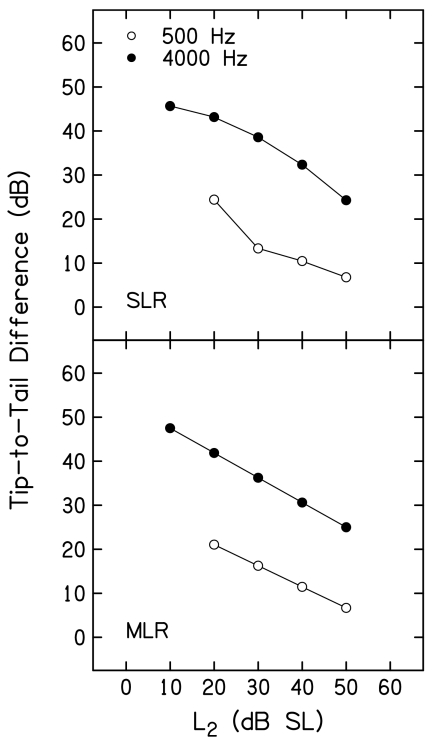
The data shown in Fig. 9 were converted into tip-to-tail differences by subtracting L3 when f3≈f2 from L3 when f3 was 1 octave below f2 at each L2. These tip-to-tail differences are plotted as a function of L2 in Fig. 10. Results based on SLR and MLR fits are shown in the top and bottom panels, respectively. Within each panel, open and closed symbols are used to represent results for f2=500 and 4000 Hz, respectively. Tip-to-tail differences decreased as L2 increased for both f2 frequencies. However, these differences were 15–25 dB greater when f2=4000 Hz, depending on L2. For example, the tip-to-tail differences at 4000 Hz were 49 and 43 dB for L2 levels of 10 and 20 dB SL (based on analyses in which MLRs were used). In contrast, the tip-to-tail difference at 500 Hz was about 20 dB when L2=20 dB SL. In fact, the smallest tip-to-tail difference at 4000 Hz (about 22 dB when L2=50 dB SL) was larger than the largest tip-to-tail difference observed at 500 Hz (about 20 dB when L2=20 dB SL). As a consequence of the MLR, the function relating tip-to-tail difference to L2 was a straight line for both f2 frequencies, as expected. While the functions relating tip-to-tail differences to L2 are less orderly when the results are based on the SLR, the overall pattern is the same.
Figure 10.
Tip-to-tail difference (in dB) as a function of L2 (dB SL) when f2=500 Hz (open circles) and when f2=4000 Hz (closed circles). Top and bottom panels show the results for simple and multiple linear regressions, respectively.
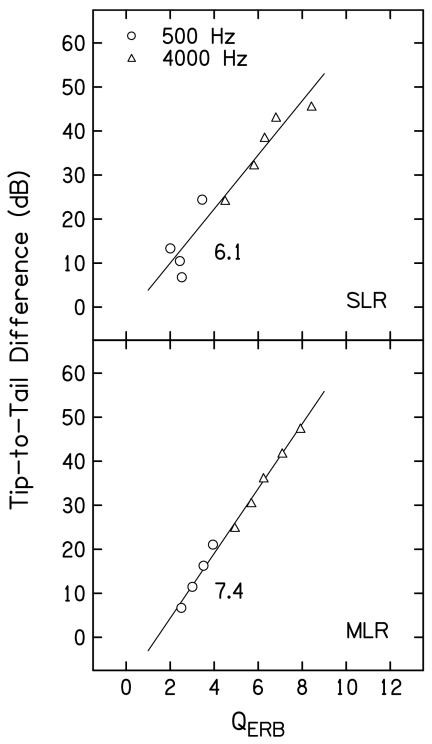
Figure 11 provides QERB estimates as a function of L2 for both primary frequencies, following the same conventions that were used in Fig. 10. QERB is calculated by dividing the characteristic or best frequency (f2) by the equivalent rectangular bandwidth (ERB), where ERB is defined as the bandwidth of a rectangular filter with the same best-frequency response that passes the same total power. While sharpness of tuning has frequently been estimated using Q10 in the single-unit literature [Q10=characteristic frequency (CF) divided by the bandwidth at 10 dB above the threshold at CF], QERB has been used recently to estimate sharpness of tuning for data obtained from humans (e.g., Shera et al., 2002; Gorga et al., 2003). It also has the advantage that it uses data from all points on the STC (appropriately weighted), as opposed to being limited to frequencies close to the tip frequency. Finally, it can be used in cases when a tip region is poorly defined, which was not the case in the present study. For both f2 frequencies, QERB decreased as L2 increased, more or less smoothly, depending on whether SLR or MLR was used. For both regressions, QERB was always larger when f2=4000 Hz, ranging from about 8 to 4. When f2=500 Hz, QERB ranged from less than 4 to about 2. Thus, this estimate of tuning was greater at 4000 Hz, compared to 500 Hz, and the smallest QERB at 4000 Hz (about 4.5 at L2=50 dB SL) was larger than the largest estimate at 500 Hz (about 4 at L2=20 dB SL). Larger changes in QERB with L2 were observed when f2=4000 Hz.
Figure 11.
QERB as a function of L2 (dB SL) following the conventions used in Fig. 10.
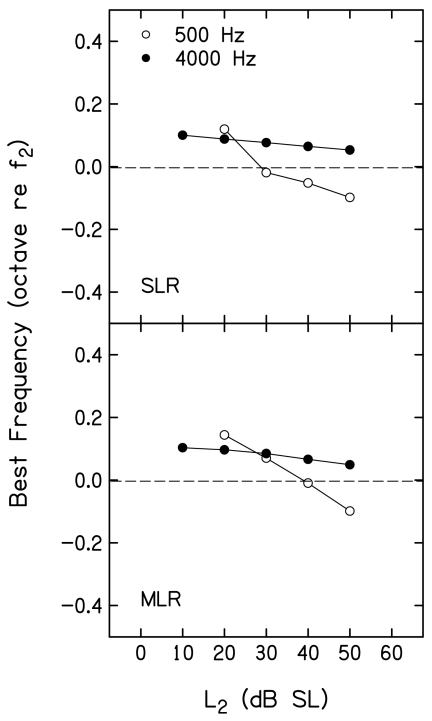
Figure 12 plots the best frequency [(BF), in octaves relative to f2] as a function of L2, following the conventions used in Figs. 1011. BF is the frequency for which the suppression threshold occurred at the lowest suppressor level. A cubic spline was used to interpolate to BF. The spline was sampled over a finer mesh based on mean L3 for 3 dB of suppression and corresponding f3 frequencies such that the resulting piecewise polynomial function is continuous and smooth between any two adjacent data points. As a result, BF defined from the spline did not necessarily occur at one of the suppressor frequencies used during measurements. The horizontal dashed line drawn at 0 octaves provides a point of reference. Values above this line represent cases in which BF was >f2, while values below represent cases when BF was <f2. Results for SLR and MLR are shown in the top and bottom panels, respectively. For both f2 frequencies, the best f3 was slightly higher in frequency than f2 at low L2 levels. This is to be expected because the suppressor frequency for the on-frequency condition was chosen intentionally to be slightly higher than f2. For both f2 frequencies, BF decreased as L2 increased, with larger changes (on a relative frequency scale, octaves) at 500 Hz, compared to 4000 Hz. When f2=4000 Hz, BF decreased as L2 increased, but always exceeded f2. In contrast, a larger decrease in BF was observed when f2=500 Hz, and, at L2 levels ⩾40 dB SL, BF was below f2.
Figure 12.
Best frequency in octaves (re: f2) as a function of L2 (dB SL), following the conventions used in Figs. 1011. The dashed line is drawn at 0 octaves relative to f2 and provides a point of reference.
DISCUSSION
A motivating factor for the present measurements was the observation from previous work, in which differences in dynamic range and perhaps cochlear-amplifier gain were observed for 500 and 4000 Hz, but concerns existed that differences in noise floor for these two frequencies might have influenced findings based on DPOAE I∕O functions (Gorga et al., 2007). High-level responses were similar at 500 and 4000 Hz, suggesting that there was little or no difference between the two frequencies in the amount of maximum compression (approximately 4:1 in both cases, based on the slopes of the I∕O functions). Differences in dynamic range were the result of differences in the low-level portion of the I∕O functions. The responses at low levels in many different measurements (e.g., behavioral threshold, thresholds at CF, or low-level portions of a DPOAE I∕O function) can be thought of as the result of gain produced by the cochlear amplifier. Thus, the suggestion of a wider dynamic range at 4000 Hz, compared to 500 Hz, in our previous data could be interpreted as an indication of greater cochlear-amplifier gain at the higher frequency. However, we were cautious in the interpretation of those data because the influences of differences in noise level were not completely controlled. Despite long averaging times, it was impossible to reduce the noise to the same low levels at both f2 frequencies. The effects of noise-floor differences would be manifest at low levels of the I∕O function, where the results at the two frequencies differed, affecting how confidently the previous results could be attributed to differences in cochlear processing for low- and high-frequency stimuli.
Like the previous study, measurement-based stopping rules including long averaging times were used in the present experiment in efforts to reduce the noise floor at both frequencies, and, like the previous study, the same noise floors were not achieved at 500 and 4000 Hz. However, unlike the previous study, the influence of differences in noise floor was reduced in the present experiment because the measurements of interest were made under conditions in which the SNR was favorable (although not the same) at both f2 frequencies. Figure 2 summarized the DPOAE and noise levels for the control conditions at the two frequencies. While the SNR always was greater at 4000 Hz, the SNR was never less than about 12 dB, and often exceeded that value at both 500 and 4000 Hz. STCs were constructed, using 3 dB decrements, meaning that the “suppression threshold” points on the STCs also represent conditions for which the SNR was positive. Thus, these curves presumably are based on reliable measurements where the influence of noise is less, and therefore, the major conclusions of this study, which are based on analyses of the STCs, also are assumed to be relatively unaffected by the noise.
The DPOAE levels measured in the control conditions differed across subjects and between frequencies. However, for a given subject and L2, the responses in the control conditions remained relatively stable (Tables 1, 2). This observation provides additional support relative to the reliability of the present measurements. Finally, the conversion of the data into decrements resulted in less variability across subjects for some stimulus conditions (Fig. 1), especially those surrounding the criterion used for constructing STCs. Converting DPOAE levels in the presence of the suppressor into decrements partially took into account differences in the absolute DPOAE levels produced by individual subjects.
The results described in Figs. 3456 are consistent with previous observations of DPOAE suppression, at least for the case when f2=4000 Hz (e.g., Abdala, 1998, 2001; Abdala et al., 1996; Gorga et al., 2002a, b, 2003; Kemp and Brown, 1983; Kummer et al., 1995). For example, decrements were observed at the lowest suppressor levels when f3≈f2. Higher suppressor levels were needed for both higher and lower f3 frequencies. The slopes of the decrement functions (which can be viewed as measures of the response to f3 at or near the f2 place) depended on frequency, with the steepest slopes for low frequencies, intermediate slopes for f3≈f2, and the shallowest slopes for f3>f2. To our knowledge, similar measurements at 500 Hz have not been reported, and thus, there are no data to which the present results can be directly compared. Even so, the results observed at 500 Hz are at least qualitatively similar to those observed at other, higher f2 frequencies. Suppression threshold and growth of suppression depended on the relationship between f3 and f2 in much the same way at 500 Hz as it did when f2=4000 Hz (compare decrement functions in Figs. 34, and the slopes of these functions at both frequencies, which were summarized in Fig. 5). The comparison of slopes for L2 and L3 provided in the right panel of Fig. 7 indicates that the rates of growth are nearly identical on a relative suppressor-frequency scale at 500 and 4000 Hz. In total, the results summarized in Tables 1, 2, Figs. 2345, and Fig. 7 provide evidence in support of both the validity and reliability of the present measurements.
Results suggesting that there may be differences in cochlear processing at 500 and 4000 Hz are provided in Figs. 68, where DPOAE STCs are presented for both frequencies. Differences in response properties are highlighted in the summaries of these STCs provided in Figs. 9101112. STCs are broader at 500 Hz, compared to 4000 Hz, which is an expected finding, given the known trends in tuning as a function of frequency, based on other physiological and behavioral measurements. Interestingly, there is more evidence of a low-frequency tail when f2=500 Hz, with less evidence of the tail at 4000 Hz. As stated earlier, we have no explanation for why low-frequency tails were observed in the present DPOAE STCs at 500 Hz, given previous physiological data from lower animals.
In any event, it is often assumed that the response to a low-frequency tone relative to BF (f2 in DPOAE suppression studies) is linear if the low-frequency tone is sufficiently low in frequency relative to BF. The fact that suppression thresholds were relatively constant for f3⩽258 Hz is taken as evidence in support of the view that measurements were made on the linear or, at least, asymptotic low-frequency tail of the response area when f2=500 Hz. In contrast, we are less convinced that an f3 was selected that was sufficiently low in frequency relative to 4000 Hz in order to be certain that the response to f3 is linear (or, at least asymptotic) at or near the f2 place.
Despite the observation that we may not be in the linear or asymptotic response region with the lowest f3 used in the present study when f2=4000 Hz, the differences in threshold between BF and a frequency one octave lower than BF are not the same at 500 and 4000 Hz. There is less threshold difference between on-frequency and low-frequency suppressors, but this cannot be attributed to problems associated with having an insufficiently low, low-frequency suppressor when f2=500 Hz because at least three suppressor frequencies had about the same thresholds on the tail of the 500 Hz STC. As expected, the slope of the functions relating L3 to L2 for on-frequency suppressors approaches 1 (i.e., between 0.87 and 0.93 at both 500 and 4000 Hz; see, for example, the closed symbols in the bottom row of Fig. 10). This is not a surprising outcome, because cochlear processing at or near the f2 place is nonlinear and compressive for both the signal eliciting the response and the suppressor reducing that response. As a result, the processing of both f2 and f3 is similarly nonlinear, resulting in a straight line with a slope approaching 1 when the probe and suppressor are approximately equal in frequency. It is unclear why the slope was not closer to 1. However, for both 500 and 4000 Hz, the “on-frequency” suppressor was slightly higher in frequency than f2. The observation of slopes less than 1 for f2≈f3 may be a consequence of the fact that the slope of the decrement-versus-L3 function decreases as f3 increases above f2, suggesting that the “growth of response” to f3 at or near the f2 place is more gradual, compared to the response to f2 at or near the same place.
An estimate of compression at f2 can be obtained by examining the slope of the functions relating L3 to L2 when f3 is 1 octave below f2 (open symbols, Fig. 9). Slopes for these conditions provide this estimate on the assumption that the response to f2 near the f2 place is compressive, while the response to f3 at or near the f2 place is more or less linear. Taking the reciprocal of the slope results in compression ratios that depend on whether the functions were derived from data which were fit with SLR versus MLR. More important, these reciprocals provide estimates of compression that range from about 2.4 to 3.2, and were similar for 500 and 4000 Hz, indicating that the responses were nonlinear at both frequencies. These estimates are less than those typically ascribed to cochlear compression, based on either behavioral data or direct measurements (e.g., Oxenham and Plack, 1997; Oxenham and Bacon, 2003; Robles and Ruggero, 2001; Rosengard et al., 2005). However, the present compression estimates are independent of stimulus level, so they are not directly comparable to estimates based on I∕O functions.
In similar fashion, the present estimates of compression also differ from the estimates for maximum compression that were derived from our previous measurements of DPOAE I∕O functions (Gorga et al., 2007). While estimates of the dynamic range differed at 500 and 4000 Hz (based on our previous data), the slopes of the functions for high-level inputs were about 0.25 or 0.20 at both frequencies, for a compression ratio of 4:1 or 5:1. In our previous work, we were concerned about the influence of differences in noise levels at the two frequencies. However, those concerns primarily related to measurements for low-level stimuli. Estimates of maximum compression in our previous data were made from high stimulus-level conditions. The influence of noise for high-level inputs is expected to be reduced because the SNR was large at both frequencies, increasing our confidence in the estimates of compression from the previously reported DPOAE I∕O functions. One interpretation of the apparent discrepancy between these different estimates of compression is that the slope of the function relating suppression threshold to L2 is not simply related to the slope of the corresponding I∕O function. While both depend upon the existence of a compressive nonlinearity, the transformation between slope of an I∕O function and slope of a function relating levels for on- and low-frequency suppressors is not simple.
Mills (1998) used tip-to-tail differences in DPOAE measurements in lower animals as an estimate of cochlear-amplifier gain. Pienkowski and Kunov (2001) and Gorga et al. (2002a, b; 2003) applied the same approach to DPOAE suppression data from humans. In general, the estimates of gain from these studies were within the range that would be expected, based on data from lower animals. Maximum observed gain was about 45 dB, and decreased as level (L2) increased. The results from the present study are similar to the previous findings, but only when f2=4000 Hz (Fig. 10). While the tip-to-tail difference (the estimate of cochlear-amplifier gain used in this and previous DPOAE studies) decreased as L2 increased for both f2 frequencies, smaller estimates of gain were observed at 500 Hz. Recently, Keefe et al. (2008) described comparable data based on suppression of stimulus frequency otoacoustic emissions (SFOAE). Tip-to-tail differences based on SFOAE STCs were roughly similar to those based on DPOAE STCs at both 500 and 4000 Hz.
In the present study, the smallest estimate of gain at 4000 Hz (22 dB when L2=50 dB SL) was greater than the largest estimate of gain at 500 Hz (20 dB when L2=20 dB SL). At L2=20 dB SL (the lowest level for which data were available at both f2 frequencies), the gain at 4000 Hz exceeded the gain at 500 Hz by more than 20 dB, or more than a factor of 10. These results suggest that cochlear-amplifier gain is present both at 500 and at 4000 Hz, but the gain is greater at 4000 Hz. Recall that tip-to-tail differences were based on a comparison of suppression threshold for cases in which f3≈f2 with the results when f3 was 1 octave below f2. At 500 Hz, the suppression threshold for the low-frequency f3 was similar and relatively constant for this and lower frequencies, suggesting that it represented a condition in which the response to f3 at or near the f2 place was perhaps linear (see the low-frequency tails of the STCs in Figs. 68). In contrast, it was less obvious that the suppression threshold for the lowest f3 at 4000 Hz was on an asymptotic portion of the STC, which might mean that we underestimated the gain at 4000 Hz. The differences in cochlear-amplifier gain between 500 and 4000 Hz, based on tip-to-tail differences, might be even greater if suppression measurements were made at a lower f3 when f2=4000 Hz. These gain differences indicate that cochlear processing in humans at these two frequencies is qualitatively similar, but quantitatively different.
The estimate of sharpness of tuning, QERB, decreased as L2 increased for both f2 frequencies (Fig. 11). No consistent dependence of QERB on level was observed in SFOAE STCs (Keefe et al., 2008), but was evident in similar estimates derived from SFOAE latencies (Schairer et al., 2006). These SFOAE data, as well as other QERB estimates based on SFOAE latency reported by Shera et al. (2002), revealed higher values of QERB than those observed in the present study at comparable levels. A possible reason for the smaller QERB in the present study is the presence of a second tone in the DPOAE stimulus. Suppression of the cochlear response to either tone is expected to reduce DPOAE level; thus, a wider range of f3 may be suppressive. In contrast, SFOAEs are elicited by a single tone; thus, the suppressive range of frequencies is expected to be narrower. This stimulus difference could explain why the QERB of DPOAE STCs is approximately 20% smaller than the QERB of SFOAE STCs (Keefe et al., 2008) or some of the latency-based estimates of SFOAE QERB (Schairer et al., 2006), but may be inadequate to explain the apparent discrepancy between our DPOAE QERB estimates and other latency-based SFOAE QERB estimates (Shera et al., 2002), which are as large as twice the present estimates.
The changes in our QERB estimates with level were greater at 4000 Hz, compared to 500 Hz. Part of this difference could relate to the fact that QERB was less at 500 Hz, even at the lowest L2 levels, so there was less “opportunity” for spread in the representation at this frequency with increased level. The analysis summarized in Fig. 11 represents a case in which the results derived from the MLR may have obscured an effect. Specifically, the results based on SLR showed discrete changes in QERB, which were smoothed by the MLR. In this case, it is unclear which analysis better describes the changes in QERB with level. Having said this, the smallest QERB at 4000 Hz (4.5 when L2=50 dB SL) was greater than the largest QERB at 500 Hz (4 when L2=20 dB SL). Sharper tuning at higher frequencies is the expected outcome, given previous physiological and psychophysical data from both humans and lower animals.
The systematic dependence of both tip-to-tail differences (Fig. 10) and QERB (Fig. 11) on L2 (especially evident in the results based on MLR) suggests a relationship between these two metrics. In Fig. 13, tip-to-tail difference is plotted as a function of QERB, following the convention used in previous figures, in that results based on SLR and MLR are shown in the top and bottom panels, respectively. The lines in these two panels represent linear fits to the data, combining the data from both 500 and 4000 Hz to generate the fits. We are unaware of other summaries in which these two variables were plotted against each other. Striking in Fig. 13 is the trade off between sharpness of tuning and cochlear-amplifier gain. As the tuning increases, so does the gain. Although purely speculative, one can imagine a situation in which sharpness of tuning is traded for gain in order to achieve some constant output. Also of interest is the observation that the data at 500 and 4000 Hz appear to fall on the same line. These results lead us to speculate that the nonlinearity at 500 Hz is the same as the nonlinearity at 4000 Hz, with the only difference being that we are operating at different points on the nonlinear function. An expression for “frequency-normalized gain-bandwidth product” (GBW) further emphasizes this point:
| (2) |
From SLR and MLR estimates of tip-to-tail and QERB, GBW=about 6 or 7 for every L2 level and for both f2 frequencies. The invariance of this relationship (across f2 and L2) supports the view that the nonlinear mechanism is similar at the 500 and 4000 Hz locations in the cochlea. It may be that different “set points” at these two locations cause the same nonlinear mechanism to operate within different ranges of gains, while consistently maintaining the same GBW at all levels at both locations.
Figure 13.
Tip-to-tail difference as a function of QERB, following the convention used in Figs. 101112. Circles represents data for 500 Hz and triangles represent data for 4000 Hz. For both frequencies, the point with the lowest tip-to-tail difference∕QERB represents results for the highest L2 level (50 dB SL at both frequencies) and the points with the largest QERB∕tip-to-tail difference represent results for the lowest L2 levels (20 dB SL at 500 Hz and 10 dB SL at 4000 Hz). Lines in each panel (SLR and MLR) represent linear fits to the data.
BF decreased as L2 increased for both f2 frequencies, although the changes were greater for 500 Hz (Fig. 12). This means that the location of the maximum nonlinear interaction between the primaries whose response was being suppressed shifted toward lower frequencies as level increased. This too is not a surprising observation, as evidence exists to suggest that the maximum representation for a given place occurs at lower frequencies for high levels of stimulation. The differences between frequency in the present study suggest that a greater apical shift occurred when f2=500 Hz.
In this study, we have not considered how a reflected contribution from the DPOAE place may have affected the present results. It is widely accepted that both a distortion and a reflection source may contribute to the DPOAE measured in the ear canal (e.g., Heitmann et al., 1998; Kalluri and Shera, 2001; Konrad-Martin et al., 2001; Shear and Guinan, 1999; Stover et al., 1996; Talmadge et al., 1999; Zweig and Shera, 1995). No effort was made in this study to eliminate reflection-source contribution. However, it is not apparent how reflection-source contribution could have affected the data we collected or alter our interpretation of the frequency effects observed in this study.
In summary, the present study provides estimates of cochlear-response properties for a high and a low frequency, based on measurements in which efforts were made to account for forward middle-ear transmission, individual differences in optimal primary-level ratios, and the influence of noise. Our results suggest that the responses from the 500 and 4000 Hz regions are similar, in that both show a frequency dependence in the rate at which suppression grows. In fact, the slopes of functions relating decrement to suppressor level are nearly identical at the two frequencies. Estimates of compression also were similar for 500 and 4000 Hz. Although evidence of tuning around the primary frequencies (f2), and level-dependent changes in cochlear-amplifier gain, tuning and best frequency was present, there were quantitative differences in these measures between the two f2 frequencies. These differences could not be attributed to differences in noise, which was a concern in our previous efforts to compare cochlear processing for low- and high-frequency stimuli. One of the clearest outcomes in the present study is evidence to suggest that cochlear-amplifier gain is greater at 4000 Hz, compared to 500 Hz. Assuming that cochlear-amplifier gain is maximal for low-level inputs, the difference in maximum gain was at least 20 dB, if not greater. Even so, it appears that the nonlinearity is similar at 500 and 4000 Hz, and that differences in QERB and tip-to-tail differences are the result of the fact that the nonlinear filter operates over different ranges of gain. In total, the results reported in the present study suggest that, in humans, there are both similarities and differences in cochlear processing at the base, compared to the apex, but the differences may represent simply a set-point variation of the same nonlinear mechanism.
ACKNOWLEDGMENTS
This work was supported by the NIH (NIDCD R01 DC002251 and P30 DC004662). We thank Sandy Estee for her assistance in subject recruitment, Sarah Michaels for help constructing some of the figures, and the subjects who made the time commitment that was necessary to complete their participation in the study. We also would like to thank Chris Shera and Andy Oxenham for constructive discussions of these data prior to submission, and two anonymous reviewers who provided helpful suggestions on a previous version of the manuscript.
References
- Abdala, C. (1998). “A developmental study of distortion product otoacoustic emission (2fl-f2) suppression in humans,” Hear. Res. 10.1016/S0378-5955(98)00073-2 21, 125–138. [DOI] [PubMed] [Google Scholar]
- Abdala, C. (2001). “Maturation of the human cochlear amplifier: Distortion product otoacoustic emission suppression tuning curves recorded at low and high primary levels,” J. Acoust. Soc. Am. 10.1121/1.1388018 110, 1465–1476. [DOI] [PubMed] [Google Scholar]
- Abdala, C., Sininger, Y. S., Ekelid, M., and Zeng, F.-G. (1996). “Distortion product otoacoustic emission suppression tuning curves in human adults and neonates,” Hear. Res. 10.1016/0378-5955(96)00056-1 98, 38–53. [DOI] [PubMed] [Google Scholar]
- American National Standards Institute (1996). “Specifications for audiometers,” ANSI S3.6-1996, New York.
- Cooper, N. P., and Rhode, W. S. (1995). “Nonlinear mechanics at the apex of the guinea-pig cochlea,” Hear. Res. 10.1016/0378-5955(94)00180-X 82, 225–243. [DOI] [PubMed] [Google Scholar]
- Cooper, N. P., and Rhode, W. S. (1997). “Mechanical responses to two-tone distortion products in the apical and basal turns of the mammalian cochlea,” J. Neurophysiol. 78, 261–270. [DOI] [PubMed] [Google Scholar]
- Cooper, N. P., and Rhode, W. S. (1998). “Apical cochlear mechanics: A review of recent observations,” in Proceedings of the International Symposium on Psychophysical and Physiological Advances in Hearing, edited by Palmer A. R., Rees A., Summerfield A. Q., and Meddis R. (Whurr, London), pp. 11–18.
- Dallos, P., He, D. Z., Lin, X., Sziklai, I., Mehta, S., and Evans, B. N. (1997). “Acetylcholine, outer hair cell electromotility, and the cochlear amplifier,” J. Neurosci. 17, 2212–2226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dallos, P. J., and Harris, D. M. (1978). “Properties of auditory-nerve responses in the absence of outer hair cells,” J. Neurophysiol. 41, 365–383. [DOI] [PubMed] [Google Scholar]
- Dhar, S., Long, G. R., and Talmadge, C. L. (2005). “The effect of stimulus-frequency ratio on distortion product otoacoustic emission components,” J. Acoust. Soc. Am. 10.1121/1.1903846 117, 3766–3776. [DOI] [PubMed] [Google Scholar]
- Dorn, P. A., Piskorski, P., Keefe, D. H., Neely, S. T., and Gorga, M. P. (1998). “On the existence of an age∕threshold∕frequency interaction in distortion product otoacoustic emissions,” J. Acoust. Soc. Am. 10.1121/1.423339 104, 964–971. [DOI] [PubMed] [Google Scholar]
- Gaskill, S. A., and Brown, A. M. (1990). “The behavior of the acoustic distortion product, 2f1–f2, from the human ear and its relation to auditory sensitivity,” J. Acoust. Soc. Am. 10.1121/1.399732 88, 821–839. [DOI] [PubMed] [Google Scholar]
- Goldstein, J. L. (1967). “Auditory nonlinearity,” J. Acoust. Soc. Am. 10.1121/1.1910396 41, 676–689. [DOI] [PubMed] [Google Scholar]
- Gorga, M. P., Neely, S. T., Bergman, B. M., Beauchaine, K. L., Kaminski, J. R., Peters, J., and Jesteadt, W. (1993). “Otoacoustic emissions in normal and hearing-impaired ears: Distortion product responses,” J. Acoust. Soc. Am. 10.1121/1.406691 93, 2050–2060. [DOI] [PubMed] [Google Scholar]
- Gorga, M. P., Neely, S. T., Dierking, D., Dorn, P. A., Hoover, B. M., and Fitzpatrick, D. (2003). “Distortion product otoacoustic emission tuning curves in normal-hearing and hearing-impaired human ears,” J. Acoust. Soc. Am. 10.1121/1.1575751 114, 263–278. [DOI] [PubMed] [Google Scholar]
- Gorga, M. P., Neely, S. T., Dorn, P. A., Dierking, D., and Cyr, E. (2002a). “Evidence of upward spread of suppression in DPOAE measurements,” J. Acoust. Soc. Am. 10.1121/1.1513366 112, 2910–2920. [DOI] [PubMed] [Google Scholar]
- Gorga, M. P., Neely, S. T., Dorn, P. A., and Konrad-Martin, D. (2002b). “The use of distortion product otoacoustic emission suppression as an estimate of response growth,” J. Acoust. Soc. Am. 10.1121/1.1426372 111, 271–284. [DOI] [PubMed] [Google Scholar]
- Gorga, M. P., Neely, S. T., Dierking, D., Kopun, J., Jolkowski, K., Groenenboom, K., Tan, H., and Stiegemann, B. (2007). “Low-frequency and high-frequency cochlear nonlinearity in humans,” J. Acoust. Soc. Am. 10.1121/1.2751265 122, 1671–1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorga, M. P., Neely, S. T., Starnes-Ohlrich, B., Hoover, B., Redner, J., and Peters, J. (1997). “From laboratory to clinic: A large scale study of distortion product otoacoustic emissions in ears with normal hearing and ears with hearing loss,” Ear Hear. 10.1097/00003446-199712000-00003 18, 440–455. [DOI] [PubMed] [Google Scholar]
- Greenwood, D. D. (1990). “A cochlear frequency-position function for several species-29 years later,” J. Acoust. Soc. Am. 10.1121/1.399052 87, 2592–2605. [DOI] [PubMed] [Google Scholar]
- Heitmann, J., Waldmann, B., Schnitzler, H.-U., Plinkert, P. K., and Zenner, H.-P. (1998). “Suppression of distortion product otoacoustic emissions (DPOAE) near 2f1–f2 removes DP-gram fine structure: Evidence for a secondary generator,” J. Acoust. Soc. Am. 10.1121/1.421290 103, 1527–1531. [DOI] [Google Scholar]
- Hicks, M. L., and Bacon, S. P. (1999). “Psychophysical measures of auditory nonlinearities as a function of frequency in individuals with normal hearing,” J. Acoust. Soc. Am. 10.1121/1.424526 105, 285–296. [DOI] [PubMed] [Google Scholar]
- Hudspeth, A. J. (1997). “Mechanical amplification of stimuli by hair cells,” Curr. Opin. Neurol. 7, 480–486. [DOI] [PubMed] [Google Scholar]
- Johnson, T. A., Neely, S. T., Dierking, D. M., Hoover, B. M., and Gorga, M. P. (2004). “An alternate approach to constructing distortion product otoacoustic emission (DPOAE) suppression tuning curves,” J. Acoust. Soc. Am. 10.1121/1.1815134 116, 3263–3266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, T. A., Neely, S. T., Garner, C. A., and Gorga, M. P. (2006). “Influence of primary-level and primary-frequency ratios on human distortion product otoacoustic emissions,” J. Acoust. Soc. Am. 10.1121/1.2133714 119, 418–428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalluri, R., and Shera, C. A. (2001). “Distortion-product source unmixing: A test of the two-mechanism model for DPOAE generation,” J. Acoust. Soc. Am. 10.1121/1.1334597 109, 622–637. [DOI] [PubMed] [Google Scholar]
- Keefe, D. H. (2002). “Spectral shapes of forward and reverse transfer functions between ear canal and cochlea estimated using DPOAE input∕output functions,” J. Acoust. Soc. Am. 10.1121/1.1423931 111, 249–260. [DOI] [PubMed] [Google Scholar]
- Keefe, D. H., Ellison, J. C., Fitzpatrick, D. F., and Gorga, M. P. (2008). “Two-tone suppression of stimulus frequency otoacoustic emissions,” J. Acoust. Soc. Am. (in press). [DOI] [PMC free article] [PubMed]
- Kemp, D. T. and Brown, A. M. (1983). “Suppressibility of the 2f1-2f2 stimulated acoustic emissions in gerbil and man,” Hear. Res. 10.1016/0378-5955(84)90092-3 13, 29–37. [DOI] [PubMed] [Google Scholar]
- Kiang, N. Y.-S., and Maxon, E. C. (1974). “Tails of tuning curves of auditory-nerve fibers,” J. Acoust. Soc. Am. 10.1121/1.1914572 55, 620–630. [DOI] [PubMed] [Google Scholar]
- Kiang, N. Y.-S., Watanabe, T., Thomas, E. C., and Clark, L. F. (1965). Discharge Patterns of Single Fibers in the Cat’s Auditory Nerve, MIT Research Monograph. No. 35 (MIT, Cambridge, MA). [Google Scholar]
- Konrad-Martin, D., Neely, S. T., Keefe, D. H., Dorn, P. A., and Gorga, M. P. (2001). “Sources of distortion product otoacoustic emissions revealed by suppression experiments and inverse fast Fourier transforms in normal ears,” J. Acoust. Soc. Am. 10.1121/1.1370356 109, 2862–2879. [DOI] [PubMed] [Google Scholar]
- Kummer, P., Janssen, T., and Arnold, W. (1995). “Suppression tuning curves of the 2f1-2f2 distortion-product otoacoustic emissions in humans,” J. Acoust. Soc. Am. 10.1121/1.413747 98, 197–210. [DOI] [PubMed] [Google Scholar]
- Kummer, P., Janssen, T., and Arnold, W. (1998). “The level and growth behavior of the 2f1-f2 distortion product otoacoustic emission and its relationship to auditory sensitivity in normal hearing and cochlear hearing loss,” J. Acoust. Soc. Am. 10.1121/1.423054 103, 3431–3444. [DOI] [PubMed] [Google Scholar]
- Kummer, P., Janssen, T., Hulin, P., and Arnold, W. (2000). “Optimal L1-L2 primary tone level separation remains independent of test frequency in humans,” Hear. Res. 10.1016/S0378-5955(00)00097-6 146, 47–56. [DOI] [PubMed] [Google Scholar]
- Levitt, H. (1971). “Transformed up-down methods in psychoacoustics,” J. Acoust. Soc. Am. 10.1121/1.1912375 49, 467–477. [DOI] [PubMed] [Google Scholar]
- Liberman, M. C. and Dodds, L. W. (1984). “Single-unit labeling and chronic cochlear pathology. III. Stereocilia damage and alterations of threshold tuning curves,” Hear. Res. 10.1016/0378-5955(84)90025-X 16, 55–74. [DOI] [PubMed] [Google Scholar]
- Lopez-Poveda, E. A., Plack, C. J., and Meddis, R. (2003). “Cochlear nonlinearity between 500 and 8000 Hz in listeners with normal hearing,” J. Acoust. Soc. Am. 10.1121/1.1534838 113, 951–960. [DOI] [PubMed] [Google Scholar]
- Mills, D. M. (1998). “Interpretation of distortion product otoacoustic emission measurements. II. Estimating tuning characteristics using three stimulus tones,” J. Acoust. Soc. Am. 10.1121/1.421101 103, 507–523. [DOI] [PubMed] [Google Scholar]
- Neely, S. T., Johnson, T. A., and Gorga, M. P. (2005). “Distortion-product otoacoustic emissions with continuously varying stimulus level,” J. Acoust. Soc. Am. 10.1121/1.1853253 117, 1248–1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neely, S. T., and Kim, D. O. (1983). “An active cochlear model showing sharp tuning and high sensitivity,” Hear. Res. 10.1016/0378-5955(83)90022-9 9, 123–130. [DOI] [PubMed] [Google Scholar]
- Neely, S. T. and Liu, Z. (1994). “EMAV: Otoacoustic emission averager,” Tech. Memo No. 17 (Boys Town National Research Hospital, Omaha, NE).
- Oxenham, A. J., and Bacon, S. P. (2003). “Cochlear compression: Perceptual measures and implications for normal and impaired hearing, Ear Hear. 10.1097/01.AUD.0000090470.73934.78 24, 352–366. [DOI] [PubMed] [Google Scholar]
- Oxenham, A. J., and Plack, C. J. (1997). “A behavioral measure of basilar-membrane nonlinearity in listeners with normal and impaired hearing,” J. Acoust. Soc. Am. 10.1121/1.418327 101, 3666–3675. [DOI] [PubMed] [Google Scholar]
- Pienkowski, M., and Kunov, H. (2001). “Suppression of distortion product otoacoustic emissions and hearing thresholds,” J. Acoust. Soc. Am. 10.1121/1.1538247 113, 1574–1586. [DOI] [PubMed] [Google Scholar]
- Plack, C. J., and Drga, V. (2003). “Psychophysical evidence for auditory compression at low characteristic frequencies,” J. Acoust. Soc. Am. 10.1121/1.1538247 113, 1574–1586. [DOI] [PubMed] [Google Scholar]
- Plack, C. J., and O’Hanlon, C. G. (2003). “Forward masking additivity and compression at low and high frequencies,” J. Assoc. Res. Otolaryngol. 4, 405–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plack, C. J., and Oxenham, A. J. (1998). “Basilar membrane nonlinearity and the growth of forward masking,” J. Acoust. Soc. Am. 10.1121/1.421294 103, 1598–1608. [DOI] [PubMed] [Google Scholar]
- Plomp, R. (1965). “Detectability threshold for combination tones,” J. Acoust. Soc. Am. 10.1121/1.1909532 37, 1110–1123. [DOI] [PubMed] [Google Scholar]
- Rhode, W. S. (1971). “Observations of the vibration of the basilar membrane in the squirrel monkey using the Mossbauer technique,” J. Acoust. Soc. Am. 10.1121/1.1912485 49, 1218–1231. [DOI] [PubMed] [Google Scholar]
- Rhode, W. S., and Cooper, N. P. (1996). “Nonlinear mechanics in the apical turn of the chinchilla cochlea in vivo,” Aud. Neurosci. 3, 101–121. [Google Scholar]
- Robles, L., and Ruggero, M. A. (2001). “Mechanics of the mammalian cochlea,” Physiol. Rev. 81, 1305–1352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosengard, P. S., Oxenham, A. J., and Braida, L. D. (2005). “Comparing different estimates of cochlear compression in listeners with a normal and impaired hearing,” J. Acoust. Soc. Am. 10.1121/1.1883367 117, 3028–3041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero, M. A., and Rich, N. C. (1991). “Furosemide alters organ of corti mechanics: Evidence for feedback of outer hair cells upon the basilar membrane,” J. Neurosci. 11, 1057–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schairer, K. S., Ellison, J. C., Fitzpatrick, D., and Keefe, D. H. (2006). “Use of stimulus-frequency otoacoustic emission latency and level to investigate cochlear mechanics in human ears,” J. Acoust. Soc. Am. 10.1121/1.2214147 120, 901–914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sewell, W. F. (1984). “The effects of furosemide on the endocochlear potential and auditory-nerve fiber tuning curves in cats,” Hear. Res. 10.1016/0378-5955(84)90057-1 14, 305–314. [DOI] [PubMed] [Google Scholar]
- Shera, C. A., and Guinan, J. J. (1999). “Evoked otoacoustic emission arise by two fundamentally different mechanisms: A taxonomy of mammalian OAEs,” J. Acoust. Soc. Am. 10.1121/1.426948 105, 782–798. [DOI] [PubMed] [Google Scholar]
- Shera, C. A., Guinan, J. J., and Oxenham, A. J. (2002). “Revised estimates of human cochlear tuning from otoacoustic and behavioral measurements,” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.032675099 9, 3318–3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A., Guinan, J. J., and Oxenham, A. J. (2007). “Otoacoustic estimates of cochlear tuning: Validation in the chinchilla,” 30th Midwinter Meeting of the Association for Research in Otolaryngology, Denver, CO. [DOI] [PMC free article] [PubMed]
- Siegel, J. H., and Hirohata, E. T. (1994). “Sound calibration and distortion product otoacoustic emissions at high frequencies,” Hear. Res. 10.1016/0378-5955(94)90106-6 80, 146–152. [DOI] [PubMed] [Google Scholar]
- Siegel, J. H. (2007). “Calibrating otoacoustic emission probes in Otoacoustic Emissions: Clinical Applications,” 3rd edition, edited by Robinette M. S. and Glattke T. J., Thieme Medical, New York, pp. 403–427.
- Stover, L. J., Neely, S. T., and Gorga, M. P. (1996). “Latency and multiple sources of distortion product otoacoustic emissions,” J. Acoust. Soc. Am. 10.1121/1.414630 99, 1016–1024. [DOI] [PubMed] [Google Scholar]
- Talmadge, C. L., Long, G. R., Tubis, A., and Dhar, S. (1999). “Experimental confirmation of the two-source interference model for the fine structure of distortion product otoacoustic emissions,” J. Acoust. Soc. Am. 10.1121/1.424584 105, 275–292. [DOI] [PubMed] [Google Scholar]
- Zinn, C., Maier, H., Zenner, H. P., and Gier, A. W. (2000). “Evidence for active, nonlinear, negative feedback in the vibration of the apical region of the in vivo guinea-pig cochlea,” Hear. Res. 10.1016/S0378-5955(00)00012-5 142, 159–183. [DOI] [PubMed] [Google Scholar]
- Zwieg, G., and Shera, C. A. (1995). “The origin of periodicity in the spectrum of evoked otoacoustic emissions,” J. Acoust. Soc. Am. 10.1121/1.413320 98, 2018–2047. [DOI] [PubMed] [Google Scholar]