A maximum likelihood latent variable regression model for multiple informants

SUMMARY

Studies pertaining to childhood psychopathology often incorporate information from multiple sources (or informants). For example, measurement of some factor of particular interest might be collected from parents, teachers as well as the children being studied. We propose a latent variable modeling framework to incorporate multiple informant predictor data. Several related models are presented, and likelihood ratio tests (LRT) are introduced to formally compare fit. The incorporation of partially observed subjects is addressed under a variety of missing data mechanisms. The methods are motivated by and applied to a study of the association of chronic exposure to violence on asthma in children.

1 Introduction

Use of surveys and questionnaires are a staple of many epidemiologic studies. Often these instruments may provide overlapping or parallel information regarding factors of particular interest. It is necessary to consolidate this information, particularly if it is collected on a construct that is difficult to measure accurately, precisely or directly. A variety of different consolidation approaches may be used, such as calculation of a weighted or unweighted score based on questionnaire items.^1,2 Studies involving children are often faced with the additional challenge of combining information obtained from multiple informants.^3–8 Because information obtained from young children may be unreliable, parents and/or teachers are frequently used as proxies. The use of additional informants varies according to the child’s age and the nature of the exposure and/or outcome under study. A common approach involves deriving separate analyses for each informant. Since there is often little agreement between the informants, results obtained from different models may yield dissimilar results and may be difficult to interpret. In addition, if there is a common association between the informants’ reports and the outcome then such approaches will be inefficient.

In this article, we consider maximum likelihood estimation of logistic regression models when there are multiple informants characterising a latent covariate and substantive interest focuses on the association of that latent variable with a univariate outcome. These methods are motivated by an epidemiologic study investigating the relationship between children’s exposure to violence (ETV) in the community, and the onset of asthma (as indicated by bronchodilator use). The study was based in a low income, racially diverse inner-city Boston neighborhood where community violence is prevalent.⁹ Mothers were administered a survey asking whether or not their child had witnessed any of several different violent events. Children over age 8 filled out the same survey themselves, while younger children were administered an age-appropriate survey based on cartoons and drawings. We assume that the questionnaire responses reflect an underlying, unobserved level of exposure to violence (ETV). We develop a likelihood-based latent variable model that uses data from multiple informants to estimate a child’s exposure to violence and then links this exposure with a health outcome. The proposed model differs from that of Horton and Laird,⁶ who assume that one informant (the mother) was used to provide auxiliary information, but was otherwise not of substantive interest. Our model provides a framework for utilizing the health outcome data even for children whose mothers did not allow them to complete the survey.

In the next section we define notation and develop a series of different multiple informant latent variable models. Section 3 addresses the behavior of these models in the presence of missing data under certain missing data assumptions. In section 4 we present an application based on the Boston Study. Section 5 presents some simulations and Section 6 concludes with a discussion of these methods.

2 Maximum likelihood (Rasch) regression models

Suppose that data collected on the vth of n children can be represented as X_v, an I × 1 vector consisting of responses to I survey items; Y_v, an outcome of interest and Z_v, a vector of potential confounders. We assume that all the survey responses X_v1,; …X_vI reflect a common, but unobservable true exposure variable, denoted θ_v, which in turn is related to the dichotomous outcome Y_v, after appropriate adjustment for confounders. Specifically, we assume:

$$f(Y_v=y_v\mid {\theta }_v;\mathit{\alpha },{\mathbf{Z}}_v)=\frac{exp[y_v({\alpha }_0+{\alpha }_1{\theta }_v+{\mathit{\alpha }}_2{\mathbf{Z}}_v)]}{1+exp({\alpha }_0+{\alpha }_1{\theta }_v+{\mathit{\alpha }}_2{\mathbf{Z}}_v)},$$ (1)

where α is a vector of parameters characterizing the relationship of θ_v and Z_v to Y_v. Because θ_v is not observed, the analysis must rely on data from the observed questionnaire responses which provide indirect information about θ.

The relationship between θ_v and the responses X_v to the survey can be naturally described using a Rasch model. Originally developed by Georg Rasch,^10,11 these models are commonly used in education and psychiatry to test constructs such as depression and intelligence, as well as to examine the reliability of test instruments. A special class of Item Response Theory (IRT) models, Rasch models characterize the probability of response for person v to a set of test or questionnaire items, denoted by X as a function of the person’s latent trait, θ, and a set of item parameters β₁…β_I that characterize the prevalence of each item via logistic regression:

$$P(X_{vi}=1\mid {\theta }_v,{\beta }_i)=\frac{exp({\theta }_v-{\beta }_i)}{[1+exp({\theta }_v-{\beta }_i)]}.$$ (2)

Note the assumption here that the distribution of X_vi does not depend on Z_v. The Rasch model assumes that given θ_v all items are independent. That is, given θ_v, the probability of a positive response to survey items i and j is the product of the individual probabilities. An important consequence of the conditional independence assumption is that conditional on the latent trait, θ_v, the joint distribution of the survey items and outcome can be factored as a product of univariate probabilities:

$$f({\mathit{X}}_v,Y_v\mid {\theta }_v,\mathit{v};\mathit{\beta },\mathit{\alpha })=f({\mathit{X}}_{\mathit{v}}\mid {\theta }_v;\mathit{\beta })f(Y_v\mid {\theta }_v;\mathit{\alpha })=\prod _{i=1}^{I}f(X_{vi}\mid {\theta }_v;\mathit{\beta })f(Y_v\mid {\theta }_v;\mathit{v};\mathit{\alpha }),$$ (3)

where f(X_vi|θ_v; β_i) is defined in (2), and f (Y_v|θ_v; Z_v; α) is the regression model of interest defined at (1).

In our motivating example, the outcome is a dichotomous indicator of bronchodilator use. Treating θ_v as random turns (3) into a type of random-intercept generalized linear (logistic regression) model for Y. To obtain estimates for α₁ (i.e., the effect of θ_v on Y_v), one can assume a distribution for θ_v, say G, then maximize the likelihood corresponding to the following marginal model:

$$f({\mathit{X}}_v\mid \mathit{\beta })f(Y_v\mid \mathit{\alpha })={\int }_{\theta }f({\mathit{X}}_v\mid {\theta }_v;\mathit{\beta })f(Y_v\mid {\theta }_v;\mathit{\alpha })dG({\theta }_v\mid \xi ),$$ (4)

where ξ is a set of parameters characterizing the distribution G. If θ_v is assumed to follow a normal distribution, then the model can be easily fit using SAS/NLMIXED. More generally, quadrature or other numerical approaches can be applied to maximize the marginal likelihood (4).

We consider the setting where there are multiple informants providing information that can be used to infer the latent exposure variable, θ_v and its relationship with Y. Specifically, suppose that the following random variables are observed for the vth subject: Y_v, the binary outcome (bronchodilator use); $X_{vi}^a$, the report of informant a on item i: $1,\dots ,I;X_{vi}^b$, the report of informant b on item i; and Z_v, an arbitrary covariate vector (e.g., age, sex of child). Given a latent predictor θ_v and the conditional independence assumption, the joint distribution of the observed data can be factored as:

$$f({\mathit{X}}_v^a,{\mathit{X}}_v^b,Y_v\mid {\theta }_v;\mathit{\beta },\mathit{\alpha },{\mathbf{Z}}_v)=f({\mathit{X}}_v^a,{\mathit{X}}_v^b\mid {\theta }_v;\mathit{\beta })f(Y_v\mid {\theta }_v;\mathit{\alpha },{\mathbf{Z}}_v)$$ (5)

where f(Y_v|θ_v; α, Z_v) is the outcome model defined at (1) and $f({\mathit{X}}_v^a,{\mathit{X}}_v^b\mid {\theta }_v;\mathit{\beta })$ is the model relating both a’s and b’s survey responses to the latent trait. The model is identifiable, even with only two informants, since there are I = 5 dichotomous indicators reported by each source.

Different factorizations of $f({\mathit{X}}_v^a,{\mathit{X}}_v^b\mid {\theta }_v;\mathit{\beta })$, reflecting various assumptions and simplifications of the association governing the joint distribution specified in equation (5) can be considered. Our proposed modeling framework is attractive because it allows the relaxation of assumptions that may be untenable in certain settings.

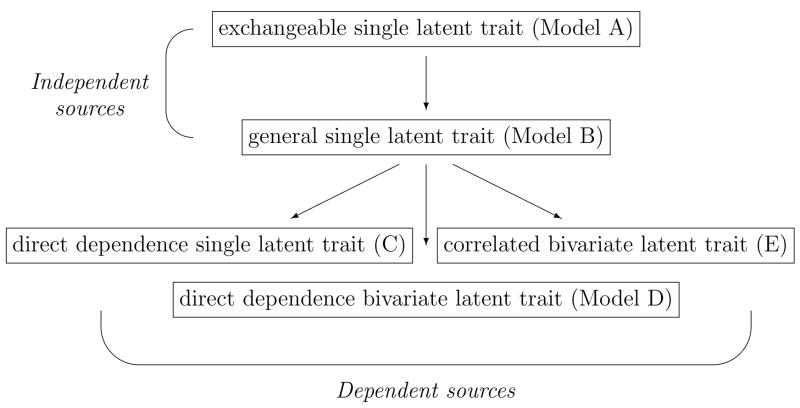
These models can be characterized in terms of estimating a single or multiple latent trait. The single latent trait models we describe include: Exchangeable (Model A), General (Model B) and Direct Dependence (Model C). We also consider two bivariate latent trait models: Direct dependence (Model D) and Correlated (Model E).

The first two models make strong assumptions (which may not be justified in terms of subject matter knowledge) regarding the independence of the informants, conditional on θ_v. The first model assumes that both informants respond to the same items at the same rate, while the second model assumes that both informants respond to the same items at different rates. The latter three models assume that data from source b contribute in some fashion to information in source a. Figure 1 describes the relationship of the five models. We assume that the informants are fully observed; we will relax this assumption in section 3.

Figure 1.

Nesting of models

Once the conditional joint distribution of ${\mathit{X}}_v^a$ and ${\mathit{X}}_v^b$ has been appropriately specified, one can obtain the marginal distribution of ${\mathit{X}}_v^a,{\mathit{X}}_v^b,Y_v$ conditional on Z_v, by assuming that the latent trait θ_v follows a distribution characterized by parameter ξ. It follows that

$$f({\mathit{X}}_v^a,{\mathit{X}}_v^b\mid \mathit{\beta })f(Y_v\mid \mathit{\alpha },{\mathbf{Z}}_v)={\int }_{\theta }f({\mathit{X}}_v^a\mid {\mathit{X}}_v^b\mid {\theta }_v;\mathit{\beta })f(Y_v\mid {\theta }_v;\mathit{\alpha },{\mathbf{Z}}_v)dG({\theta }_v\mid \mathit{\xi }).$$

While other distributional assumptions could be considered for θ_v, a normal assumption is computationally convenient since the resulting model is straightforward to fit using SAS/NLMIXED. Extensions to accommodate certain other distributions (e.g. lognormal) are straightforward.

2.1 Exchangeable single latent trait (Model A)

Model A assumes that X^a and X^b are independent conditional on θ and that informants a and b report the same events at the same rate. Heuristically, it assumes perfect agreement between informants at the macro level, though not necessarily perfect agreement within pairs, due simply to chance. This model essentially pools all of the information from both informants and considers the two informants to be independent replicates of each other:

$$\begin{array}{l}f({\mathit{X}}_v^a,{\mathit{X}}_v^b\mid {\theta }_v;\mathit{\beta })=f({\mathit{X}}_v^a\mid {\theta }_v;\mathit{\beta })f({\mathit{X}}_v^b\mid {\theta }_v;\mathit{\beta })\\ =\prod _{i=1}^I\frac{exp[x_{vi}^a({\theta }_v-{\beta }_i)]}{[1+exp({\theta }_v-{\beta }_i)]}\frac{exp[x_{vi}^b({\theta }_v-{\beta }_i)]}{[1+exp({\theta }_v-{\beta }_i)]}.\end{array}$$ (6)

Another way to think of this model is that informants a and b provide commensurate information. Their information could therefore be thought of as “exchangeable”: where one informant’s response has the same association with latent covariate and the outcome as the other informant. While model (6) is overly simplistic and unlikely to apply in practice, it provides a helpful basis for comparison with other models.

2.2 General single latent trait (Model B)

As in (6), Model B assumes that the two informants respond independently, conditional on the latent trait, but they report the various events at different frequencies. Defining β^a and β^b to be the item parameters for informants a and b, it follows that

$$\begin{array}{l}f({\mathit{X}}_v^a,{\mathit{X}}_v^b\mid {\theta }_v;\mathit{\beta })=f({\mathit{X}}_v^a\mid {\theta }_v;{\mathit{\beta }}^a)f({\mathit{X}}_v^b\mid {\theta }_v;{\mathit{\beta }}^b)\\ =\prod _{i=1}^I\frac{exp[x_{vi}^a({\theta }_v-{\beta }_i^a)]}{[1+exp({\theta }_v-{\beta }_i^a)]}\frac{exp[x_{vi}^b({\theta }_v-{\beta }_i^b)]}{[1+exp({\theta }_v-{\beta }_i^b)]}.\end{array}$$ (7)

2.3 Direct dependence single latent trait (Model C)

Model C relaxes the assumption that X^a and X^b are independent, by allowing the responses of respondent a to depend on those of respondent b and θ_v:

$$f({\mathit{X}}_v^a,{\mathit{X}}_v^b\mid {\theta }_v;\mathit{\beta },\tau )=f({\mathit{X}}_v^a\mid {\mathit{X}}_v^b\mid {\theta }_v;{\mathit{\beta }}^a,\tau )f({\mathit{X}}_v^b\mid {\theta }_v;{\mathit{\beta }}^b).$$

For example, we might assume

$$f({\mathit{X}}_v^a\mid {\mathit{X}}_v^b\mid {\theta }_v;{\mathit{\beta }}^a,\tau )f({\mathit{X}}_v^b\mid {\theta }_v;{\mathit{\beta }}^b)=\prod _{i=1}^I\frac{exp[x_{vi}^a({\theta }_v+\tau x_{vi}^b-{\beta }_i^a)]}{[1+exp({\theta }_v+\tau x_{vi}^b-{\beta }_i^a)]}\frac{exp[x_{vi}^b({\theta }_v-{\beta }_i^b)]}{[1+exp({\theta }_v-{\beta }_i^b)]}.$$ (8)

While the expression in (8) is mathematically convenient, results may be hard to interpret. An appropriate model for the relationship between informants may require that each informant have their own latent trait, an approach that we now consider.

2.4 Direct dependence bivariate latent trait (Model D)

The direct dependence Model D introduces two latent traits, ${\theta }_v^a$ and ${\theta }_v^b$, for informants a and b, respectively. In the case of the Boston study, for example, ${\theta }_v^a$ might represent the child’s exposure to violence, while ${\theta }_v^b$ represents the mother’s perception, which might be different. Of interest in this study is how θ^a (i.e., the child’s ETV) relates to Y_v. The model specification entails the following factorization:

$$f({\mathit{X}}_v^a,{\mathit{X}}_v^b,Y_v\mid {\theta }_v;\mathit{\beta },\mathit{\alpha },{\mathbf{Z}}_v,\tau )=f({\mathit{X}}_v^a\mid {\theta }_v^a,{\theta }_v;{\mathit{\beta }}^a,\tau )f({\mathit{X}}_v^b\mid {\theta }_v^b,{\mathit{\beta }}^b)f(Y_v\mid {\theta }_v^a;\mathit{\alpha },{\mathbf{Z}}_v),$$

so that the value of respondent b’s latent trait, ${\theta }_v^b$, influences how person a responds through the parameter τ. The model for $f({\mathit{X}}_v^a\mid {\theta }_v^b,{\theta }_v^a;{\mathit{\beta }}^a,\tau )f({\mathit{X}}_v^b\mid {\theta }_v^b,{\mathit{\beta }}^b)$, can be written as:

$$f({\mathit{X}}_v^a\mid {\theta }_v^b,{\theta }_v^a;{\mathit{\beta }}^a,\tau )f({\mathit{X}}_v^b\mid {\theta }_v^b;{\mathit{\beta }}^b)=\prod _{i=1}^I\frac{exp[x_{vi}^a({\theta }_v^a+\tau {\theta }_v^b-{\beta }_i^a)]}{[1+exp({\theta }_v^a+\tau {\theta }_v^b-{\beta }_i^a)]}\frac{exp[x_{vi}^b({\theta }_v^b-{\beta }_i^b)]}{[1+exp({\theta }_v^b-{\beta }_i^b)]},$$ (9)

where

$$\left[\begin{array}{c}{\theta }_v^a\\ {\theta }_v^b\end{array}\right]\sim N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}{\sigma }_a^2& 0\\ 0& {\sigma }_b^2\end{array}\right]\right).$$

Expression (9) differs from the direct dependence single latent trait model with respect to how informants a and b are related. The single trait model postulates that the response of informant a to item i is a function of the latent trait, the frequency of the item and the response of informant b to the same item. In contrast, model (9) implies that informant a’s response depends on their own latent trait, as well as that of informant b. While in abstract model (9) may sound complicated, it will often have an appealing practical interpretation. In the context of the Boston study, for example, ${\theta }_v^b$ is the mother’s perception of her child’s true ETV $({\theta }_v^a)$. The parameter τ describes the degree to which a child’s response $(x_v^a)$ is influenced by their mother’s perception. The SAS code used to fit Model D can be found in Appendix 1.

2.5 Correlated bivariate latent trait (Model E)

Model E also assumes that informants a and b each have their own latent traits, but characterizes the association between these latent traits through a covariance parameter σ_ab. This allows the distribution of X^a and X^b to follow separate Rasch models depending on θ^a and θ^b respectively. Consequently, $f({\mathit{X}}_v^a,{\mathit{X}}_v^b\mid {\theta }_v^a,{\theta }_v^b;\mathit{\beta })$ can be written as:

$$f({\mathit{X}}_v^a\mid {\theta }_v^a;{\mathit{\beta }}^a)f({\mathit{X}}_v^b\mid {\theta }_v^b;{\mathit{\beta }}^b)=\prod _{i=1}^I\frac{exp[x_{vi}^a({\theta }_v^a-{\beta }_i^a)]}{[1+exp({\theta }_v^a-{\beta }_i^a)]}\frac{exp[x_{vi}^b({\theta }_v^b-{\beta }_i^b)]}{[1+exp({\theta }_v^b-{\beta }_i^b)]}$$ (10)

where

$$\left[\begin{array}{c}{\theta }_v^a\\ {\theta }_v^b\end{array}\right]\sim N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}{\sigma }_a^2& 0\\ 0& {\sigma }_b^2\end{array}\right]\right).$$

For both correlated trait and direct dependence models the primary regression involves the relationship of ${\theta }_v^a$ and Z_v to Y_v; i.e.,

$$f(Y_v=y_v\mid {\theta }_v^a;\mathit{\alpha },{\mathbf{Z}}_v)=\frac{exp[y_u({\alpha }_0+{\alpha }_1{\theta }_v^a+{\mathit{\alpha }}_2{\mathbf{Z}}_v)]}{1+exp({\alpha }_0+{\alpha }_1{\theta }_v^a+{\mathit{\alpha }}_2{\mathbf{Z}}_v)}.$$

In the context of the Boston study this may be plausible, for the main hypothesis in this study is whether children’s exposure to violence ${\theta }_v^a$ has an association with the outcome. The SAS code used to fit Model E can be found in Appendix 1. These final two models (i.e., direct dependence and correlated trait) account for possible correlation between the latent traits.

2.6 Model comparison

Figure 1 displays the relationships between the various models. For example, the exchangeable model is obtained as a special case of the independence model by setting β^a = β^b. These models can thus be compared using a Likelihood Ratio Test (LRT) that follows a ${\chi }_I^2$ random variable with degrees of freedom equal to the number of survey items (I). Similarly, setting τ = 0 changes the non-independence model to the independence model, so these models can be compared using a LRT which is distributed as ${\chi }_1^2$. The exchangeable and general models are also nested within both bivariate trait models. However, because of boundary issues in the parameter space, special consideration for testing is required (see Appendix 2).

3 Missing Data

Data involving multiple informant reports are often incomplete, since by definition, more than one source needs to be contacted and interviewed. For example, in the Connecticut Child Surveys,^12,13 43% of teacher reports were missing, while only a small number of parents reports were unobserved. In the Boston Study, 54% of the children’s reports were missing, while all of the maternal reports were observed. The use of complete data methods (those which drop observations with any missing data) will lead to estimates that are ineffcient and, possibly, biased.

In the Boston Study, missingness can be described as monotone since questionnaire responses will always be available from mothers, but not always from children. Monotone missingness is common and an important special case. For example, missingness may be partly be design (e.g., a two stage study where complete data are only collected on a subset of subjects). When missingness is partly by design, assumptions about ignorable missingness (in the sense of Little and Rubin¹⁴), and conditional independence may be more plausible. If the assumption of ignorable missingness is not justifiable, then use of non-ignorable nonresponse models^14,15 will need to be explored. For the purposes of this paper, we assume that informant b has complete data across the I items and that n − m persons from informant a has complete data across the I items.

We define a missing data indicator, R:

$$R_v=\{\begin{array}{ll}0\hfill & {\mathit{X}}_v^a\text{ fully observed}\hfill \\ 1\hfill & {\mathit{X}}_v^a\text{ incomplete}\text{.}\hfill \end{array}$$

Analysis with incomplete data requires the consideration (implicitly or explicitly) of R into the joint distribution of the data.¹⁴ The joint model can be specified as

$$\begin{array}{l}f({\mathit{X}}_v^a,{\mathit{X}}_v^b,Y_v,R_v\mid {\theta }_v;\mathit{\beta },\mathit{\alpha },\psi ,{\mathbf{Z}}_v)=f({\mathit{X}}_v^a,{\mathit{X}}_v^b,Y_v\mid {\theta }_v;\mathit{\beta },\mathit{\alpha },{\mathbf{Z}}_v)\ast \\ f(R_v\mid {\mathit{X}}_v^a,{\mathit{X}}_v^b,Y_v,{\theta }_v,{\mathbf{Z}}_v;\psi ),\end{array}$$ (11)

where ψ is a parameter characterizing the missingness distribution.

If ${\mathit{X}}_v^a$ and ${\mathit{X}}_v^b$ are both observed, then the likelihood is based directly on expression (11), after integrating over the distribution of θ_v. If ${\mathit{X}}_v^a$ is missing, then the appropriate likelihood contribution needs to additionally integrate over ${\mathit{X}}_v^a$:

$$\begin{array}{l}\int f({\mathit{X}}_v^b,Y_v,R\mid {\theta }_v,\mathit{\beta },\mathit{\alpha },\psi ,{\mathbf{Z}}_v)dG({\theta }_v)=\int \int \{f({\mathit{X}}_v^a,{\mathit{X}}_v^b,Y_v\mid {\theta }_v,\mathit{\beta },\mathit{\alpha },{\mathbf{Z}}_v)\\ \ast f(R\mid {\mathit{X}}_v^a,{\mathit{X}}_v^b,Y_v,{\theta }_v,\mathit{\beta },\mathit{\alpha },{\mathbf{Z}}_v)d{\mathit{X}}_v^a\}dG({\theta }_v).\end{array}$$

Note that as long as the missingness mechanism is independent of ${\mathit{X}}_v^a$ and θ_v, it follows that

$$f(R\mid {\mathit{X}}_v^a,{\mathit{X}}_v^b,Y_v,{\theta }_v,\psi ,{\mathbf{Z}}_v)=f(R\mid {\mathit{X}}_v^b,Y_v,\psi ,{\mathbf{Z}}_v),$$

and this term will factor out of the likelihood, and its contribution can be ignored.

The contribution to the likelihood for person v, under the correlated trait model defined in (10) under ignorable missingness becomes:

$$l(\mathit{\beta },\mathit{\alpha })=\{\begin{array}{ll}\int f({\mathit{X}}_{v(\mathit{obs})}^a\mid {\theta }_v^a;{\mathit{\beta }}^a)f({\mathit{X}}_v^b\mid {\theta }_v^b;{\mathit{\beta }}^b)f(Y_v\mid {\theta }_v^a;\mathit{\alpha },{\mathbf{Z}}_v)dG({\theta }_v)\hfill & \text{if }{R}_v=0\hfill \\ \int f({\mathit{X}}_v^b\mid {\theta }_v^b;{\mathit{\beta }}^b)f(Y_v\mid {\theta }_v^a;\mathit{\alpha },{\mathbf{Z}}_v)dG({\theta }_v)\hfill & \text{if }{R}_v=1.\hfill \end{array}$$ (12)

4 Application: Asthma and exposure to violence

The Boston Study aimed to investigate associations between children’s exposure to violence (ETV) in their communities and the onset of childhood respiratory disease.^16,17 The items from the ETV questionnaire included I = 5 binary indicators of whether the child had witnessed someone being hit, shoved, or punched; whether he/she had witnessed a stabbing; whether he/she had heard gunshots; whether he/she had witnessed someone being shot; and whether he/she had witnessed emotional abuse.¹⁸ There are two sets of informants, mothers and children, both of whom were asked to complete a survey designed to indirectly characterize ETV. Children could only complete the survey if two conditions were met: the child was age 8 or older, and mothers gave permission for their children to answer the questionnaire. There were 188 mothers who answered the questionnaire, but refused permission for their children to take part in the survey (n = 15) or their children were too young to self-report ETV (n = 173). A total of 151 additional mother-child pairs completed the ETV survey.

Maternal report of child wheeze based on the child being prescribed a bronchodilator by a physician for wheezing or respiratory illness is also considered to be a covariate. The outcome is an indicator that takes the value 1 if the child has used a bronchodilator and 0 otherwise, as reported by the mother.

Table 1 describes demographics and summary statistics for children who completed the survey (2nd column) and those who did not (3rd column). There were about equal numbers of boys and girls, regardless of survey participation (p = 0.86, Fisher’s exact test). Hispanic mothers withheld permission for their children to participate in the ETV survey more than their White counterparts (p = 0.0002). Those women with some college experience were less likely to withhold permission than those with a high school degree or less (p = 0.05). Children who answered the survey were somewhat more likely to have a report of wheeze than children who did not (p = 0.10) though there were no significant differences in proportion of bronchodilator use (p = 0.64).

Table 1.

Demographic data on child survey participants and non-participants

Variable	Child survey complete (N = 151)	Child survey incomplete (N = 188)
Child’s Gender:
Female	77 (51%)	94 (50%)
Child’s Race/Ethnicity:
White	86 (57%)	66 (35%)
Hispanic	61 (40%)	115 (61%)
Other	4 (3%)	7 (4%)
Maternal Education:
< 12 years	53 (35%)	85 (45%)
12 years	61 (40%)	75 (40%)
> 12 years	37 (25%)	28 (15%)
Maternal report of child wheeze:
Yes	45 (30%)	41 (22%)
Bronchodilator:
Yes	52 (34%)	60 (32%)

Table 2 displays results from regression models for the probability of using a bronchodilator using the multiple informant models A{E discussed previously. The column labeled “Model” indicates the model used for the analysis, along with the corresponding number of parameters. The next three columns display estimated regression model parameters and their standard errors (intercept, the wheeze covariate and the latent ETV). The column labelled “−2LL” is −2 times the log-likelihood function of the model being fit. The first row of the table corresponds to the results of fitting the simple Model A (6), the second row corresponds to Model B (7) while the last three rows represent Models C (8), D (9) and E (10) that incorporate dependence between the informants. The “Δ” column contains the difference in −2LL column between any two nested models. The SAS code to fit models D and E can be found in Appendix 1.

Table 2.

Results for model for use of bronchodilator

Model (df)	Int. (α0) Est. (SE)	ETV (α1) Est. (SE)	Wheeze (α2) Est. (SE)	Association Est. (SE)	−2LL	Difference
A (9)	−0.799 (0.15)	0.424 (0.17)	0.204 (0.27)	NA	2161.4
B (14)	−0.800 (0.15)	0.392 (0.16)	0.213 (0.27)	NA	2084.1	77.3 (B vs. A)
C (15)	−0.800 (0.14)	0.385 (0.15)	0.213 (0.27)	τ = 0.124 (0.31)	2084.0	0.1 (C vs. B)
D (16)	−0.829 (0.16)	0.466 (0.26)	0.235 (0.28)	τ = 0.548 (0.19)	2076.2	7.9 (D vs. B)
E (16)	−0.834 (0.16)	0.419 (0.17)	0.236 (0.28)	ρ = 0.554 (0.14)	2071.7	12.4 (E vs. B)

Notes:

Model A (Exchangeable single latent trait)

Model B (General single latent trait)

Model C (Direct dependence single latent trait)

Model D (Direct dependence bivariate latent trait)

Model E (Correlated bivariate latent trait)

Application of an LRT test comparing the various models in Table 3 suggests clear evidence that the correlated bivariate latent trait model E provides the best fit to the data. Self and Liang¹⁹ showed that in cases such as these, in which interest focuses on testing whether a parameter is on the boundary of the parameter space, these statistics do not follow the standard chi-squared distribution, but rather a mixture of chi-squared distributions. In this case, because the test statistics are so large, even the least powerful approach that uses the usual chi-squared reference distribution would lead to the rejection of Model B in preference to Model E.

Table 3.

Simulations based on n = 1500 subjects, two informants based on a 5-item questionnaire with correlation of 0.4. Rows correspond to different patterns of missingness, with $\text{logit}(Pr(\text{missing}))={\gamma }_0+{\gamma }_1\sum X_{vi}^b+{\gamma }_{2}Y$. Table entries show the mean of the estimates of α₁ from 1000 simulated datasets fit using model (E), where the true value of α₁ is 2. Corresponding standard errors are given in parentheses.

γ0, γ1, γ2	Pr(missing)	Complete case only	All available cases
No missing data	0%	1.996 (0.263)	1.996 (0.263)
MCAR models
−1.735, 0, 0	15%	2.002 (0.287)	1.976 (0.274)
−1.098, 0, 0	25%	2.008 (0.306)	1.961 (0.282)
0, 0, 0	50%	2.024 (0.378)	1.900 (0.309)
MAR X models
−2.781, 0.5, 0	15%	2.003 (0.288)	1.979 (0.276)
−3.247, 1, 0	25%	2.002 (0.311)	1.963 (0.289)
−2.671, 1.5, 0	50%	1.801 (0.401)	1.907 (0.328)
MAR Y models
−1.931, 0, 0.5	15%	2.006 (0.289)	1.979 (0.276)
−1.506, 0, 1,	25%	2.018 (0.317)	1.963 (0.288)
−.509, 0, 1.5	50%	2.058 (0.443)	1.896 (0.326)

5 Missing Data Simulation

Table 3 reports the results of simulations based on 1500 subjects, where each subject is assumed to have two informants responses to a 5-item questionnaire, with a correlation of 0.4 between parent and child information. Missingness generated under MCAR was done through straight random number generation; under MAR, R was created using a logistic model in which the sum of the ETV survey items answered by adults $({\mathit{X}}_v^b)$ and use of bronchodilators (Y ) were used as covariates:

$$\text{logit}(P\{R_i=1\})={\gamma }_0+{\gamma }_1\sum X_{vi}^b+{\gamma }_{2}Y.$$ (13)

The parameters in (13) were chosen so that as γ₁ and γ₂ increase, the probability that R_i = 1 increases. A practical application, for example, is if the mother reports many witnessed events of violence against her child then her child may be less likely to complete the survey. The first column for Table 3 displays the percentage of children who were simulated as not answering the questionnaire.

For each row we generated 1000 datasets and fit the correlated bivariate latent trait complete case (CC) and available case (AC) models, where the true α₁ = 2. The second and third columns contains sample means and standard errors from the CC model. The fourth and fifth columns are the same information as the previous two columns using the correlated trait AC model. Maternal report of wheeze was not considered for this part of the analysis.

Overall, the correlated trait available case model performs well, recovering considerable information even as the numbers of non-participating children increases. There was little evidence for bias, which is not surprising given that all mechanisms were ignorable in the sense of Little and Rubin.¹⁴ An expected finding is that when there is complete data for child informants $({\mathit{X}}_v^a)$, there is little difference in variability in estimates between the methods and models shown.

6 Discussion

In this paper, we developed methods to incorporate information from two raters providing information on a latent trait of interest. These models characterize the relationship between informants and an outcome using a latent variable predictor model. This framework is likelihood-based and a variety of potential models are described (Figure 1). Because they are partially nested, the analyst may formally compare the fit of models describing the observed relationship between informants under a variety of conditional independence and latent variable assumptions. This methodology is particularly attractive because it is quite flexible and can be fit using existing statistical software.

Another advantage of these likelihood-based models relates to the incorporation of partially observed subjects with fully observed auxiliary (parent) information.⁶ For the correlated trait model under ignorable missingness assumptions, this model performed well as compared to the single informant model. When one set of raters are missing that covariance parameter can provide some information about the missing rater. This “borrowing” of mother’s survey data may mitigate the impact of the missing child’s response and therefore lead to more precise estimates compared to models that contain only child survey responses.

Appendix 1: SAS code to fit Models D and E

Appendix 2

To arrive at the general single latent trait model (B) from the direct dependence bivariate latent trait model (D), it is helpful to consider a reparameterization of the latent trait for informant a, specifically, ${\theta }_v^{\ast }\equiv {\theta }_v^a+\tau {\theta }_v^b$. Therefore, the model specified in equation (9) can be rewritten as $f(X_v^a\mid {\theta }_v^b,{\theta }_v^{\ast };{\mathit{\beta }}^a,\tau )f(X_a^b\mid {\theta }_v^b;{\mathit{\beta }}^b)$ where ${\theta }_v^{\theta }\sim N(0,{\sigma }_b^2)$ and ${\theta }_v^{\ast }\sim N(0,\mathit{Var}({\theta }_v^{\ast }))$, where

$$\begin{array}{l}\text{Var}({\theta }_v^{\ast })={\sigma }_a^2+{\tau }^2{\sigma }_b^2+\text{Cov}({\theta }_v,{\theta }_v^b)\\ ={\sigma }_a^2+{\tau }^2{\sigma }_b^2.\end{array}$$

The joint distribution of ${\theta }_v^{\ast }$ and ${\theta }_v^b$, is

$$\left[\begin{array}{c}{\theta }_v^{\ast }\\ {\theta }_v^b\end{array}\right]\sim N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}{\sigma }_a^2+{\tau }^2{\sigma }_b^2& \tau {\sigma }_b^2\\ \tau {\sigma }_b^2& {\sigma }_b^2\end{array}\right]\right).$$

Under this parameterization, when τ = 1 and ${\sigma }_a^2=0$, the covariance matrix for ${\theta }_v^{\ast }$ and ${\theta }_v^b$ is given by

$$\left[\begin{array}{ll}{\sigma }_b^2\hfill & {\sigma }_b^2\hfill \\ {\sigma }_b^2\hfill & {\sigma }_b^2\hfill \end{array}\right],$$

so that ${\theta }_v^{\ast }$ and ${\theta }_v^b$ have become, in actuality, the same latent trait. This is equivalent to the general independence model. However, since this scenario places ${\sigma }_a^2$ on the boundary of its parameter space, the LRT statistic does not have the usual asymptotic properties.¹⁹ A similar situation occurs when using the LRT to test general independence versus correlated trait models. Arriving at the independence model from the correlated trait model requires two steps: first, ${\sigma }_a^2={\sigma }_b^2$, which yields the following covariance matrix

$$\left[\begin{array}{ll}{\sigma }_a^2\hfill & \rho {\sigma }_a^2\hfill \\ \rho {\sigma }_a^2\hfill & {\sigma }_a^2\hfill \end{array}\right],$$

and then setting ρ = 1, with ρ on the boundary of its parameter space. Self and Liang¹⁹ describe the asymptotic distribution of a test situation similar to both correlated trait and direct dependence LRT as having 50: 50 mixture of a ${\chi }_1^2$ and ${\chi }_2^2$. While the resulting distribution is analytically more complicated, inference can proceed using numerical methods to describe the empirical sampling distribution of these likelihood ratio test statistics.