Solvation free energies of molecules. The most stable anionic tautomers of uracil

Abstract

Anionic states of nucleic acid bases are suspected to play a role in the radiation damage processes of DNA. Our recent studies suggested that the excess electron attachment to the nucleic acid bases can stabilize some rare tautomers, i.e. imine-enamine tautomers and other tautomers with a proton being transferred form nitrogen sites to carbon sites (with respect to the canonical tautomer). So far, these new anionic tautomers have been characterized by the gas phase electronic structure calculations and photoelectron spectroscopy experiments. In the current contribution we explore the effect of water solvation on the stability of the new anionic tautomers of uracil. The accurate free energies of solvation are calculated in a two step approach. The major contribution was calculated using the classical free energy perturbation adiabatic charging approach, where it is assumed that the solvated molecule has the charge distribution given by the polarizable continuum model. In the second step the free energy of solvation is refined by taking into account the real, average solvent charge distribution. This is done using our accelerated QM/MM simulations, where the QM energy of the solute is calculated in the mean potential averaged over many MD steps. We found that in water solution three of the recently identified anionic tautomers are 6.5 – 3.6 kcal/mol more stable than the anion of the canonical tautomer.

1. Introduction

The nucleic acid bases (NABs) are the basic elements of DNA and RNA, which are responsible for storing and translating genetic information. Their anions can be formed by trapping low-energy electrons produced in living cells by high-energy radiation. Recent experiments suggested that single and double strand breaks develop in DNA exposed to low-energy electrons.¹ Furthermore, charged nucleobases play a critical role in electron and hole transfer in DNA. ^{2 – 4} Therefore anionic states of nucleic acid bases have been intensively studied both experimentally and theoretically. ^5–14

For long the dominant opinion was that the most stable and adiabatically bound anions in the gas phase have a dipole-bound rather than valence character.¹⁵ The dipole-bound anions are, however, strongly perturbed by other atoms or molecules and their relevance in condensed phase environments is questionable. The majority of studies concentrated on the anions of canonical and amino-oxo and imino-hydroxy tautomers. In the latter a proton is transferred between electronegative atoms, N or O. Only recently we have demonstrated that the most stable valence anions of nucleic acid bases, such as uracil,¹⁶ thymine,¹⁷ 1-methylcytosine¹⁸, guanine¹⁹ and adenine²⁰ are related to tautomers that result from a proton transfer from a NH site to a carbon site. Moreover, some of these valence anions proved to be adiabatically bound with respect to the most stable tautomers of the neutral NABs and to be significantly more stable than dipole-bound anions based on the canonical NABs. The searches for the most stable tautomers and their later characterization were facilitated by the development of a hybrid combinatorial-computational approach²¹ and various chemoinformatics tools.²²

The most recent and accurate computational results for valence anions of uracil indicate that there are four important new tautomers, labeled U1–U4, in addition to the canonical tautomer, labeled U0 in Fig. 1.^16,17,23,24 The photoelectron spectrum of valence anions of U²⁵ remains in quantitative agreement with the computational predictions. Bachorz et al.^23,24 have recently employed state of the art electronic structure methods with focus on accurate predictions of the gas phase adiabatic electron affinity (AEA) for the U0–U4 tautomers and the electron vertical detachment energies (VDE) for the corresponding anions. They used explicitly-correlated second-order Moller–Plesset perturbation theory (RI-MP2-R12) in conjunction with conventional coupled cluster methods with single, double, and perturbative triple excitations (CCSD(T)) supplemented with basis set extrapolation techniques. The final energies were corrected for zero-point vibration energies, determined in harmonic approximation at the UHF-RI-MP2/aug-cc-pVTZ level of theory. The results are summarized in Table 1. At this refined level of theory the most stable valence anion is U1⁻, which is more stable than U0⁻ by ca. 2.5 kcal/mol. The latter is adiabatically bound with respect to the canonical neutral by ca. 0.5 kcal/mol. The valence anions of the remaining tautomers, i.e., U2⁻, U3⁻, U4⁻, are adiabatically unbound with respect to the canonical neutral by 2.0–8.5 kcal/mol, though they are characterized by significant values of VDE of 2.6–3.9 eV.

Figure 1.

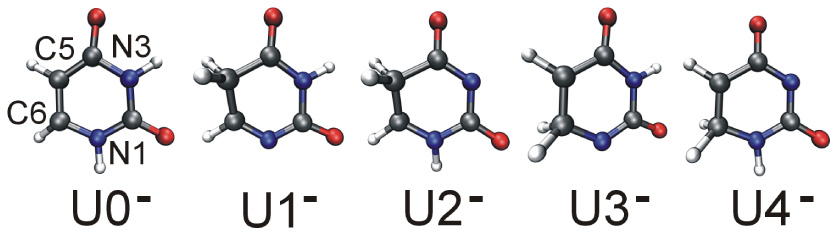
The most stable anionic tautomers of uracil identified by Bachorz et al.¹⁶,¹⁷

Table 1.

The relative energies (ΔE), energies corrected for zero point vibrations (Δ(E+ZPVE)) and free energies (ΔG) of the most important anionic tautomers of uracil reported in the previous studies and compared with the results obtained in the current study. The energies and free energies (in kcal/mol) are calculated with respect to the anion of the canonical tautomer (U0).

	Δ(E+ZPVE)*	ΔE**	ΔG***
Tautomer	Gas phase	Water	Gas phase	Water
U0−	0.00	0.00	0.00	0.00
U1−	−2.63	−0.88	−2.54	−3.64
U2−	2.81	−1.09	2.81	−6.49
U3−	7.66	6.12	7.31	1.29
U4−	9.02	1.54	8.16	−5.54

^*Ref. 24.

^**Ref. 17.

^***This study.

None of our studies presented so far focused on accurate predictions of the stability of important anionic tautomers of NABs in water solution. The relative stability of the most stable tautomers was only estimated at the DFT level with solvent effects simulated with continuum models. The effects of solvation on the relative energies of valence anions of U0–U4 were estimated¹⁷ at the B3LYP/6-31++G^** level using the PCM model,²⁶ and are summarized in Table 1. It was predicted that in water solution U1⁻ and U2⁻ are more stable by 0.9–1.1 kcal/mol than the anion of the canonical tautomer. U3⁻ and U4⁻ were found respectively, 6.1 and 1.5 kcal/mol less stable than the most stable tautomer - U1⁻. These PCM results differ quantitatively from the results of an initial study,¹⁶ where geometries were not optimized within the PCM model.¹⁶ It must be noted that none of the previous results were validated against other solvation models.

In the current contribution we revise our preliminary results^16,17 on the relative stability of anionic tautomers of uracil in water solution. For this purpose we supplement the best available relative electronic energies obtained recently by Bachorz et al. using the state-of-the-art electronic structure methods,²⁴ with accurate solvation free energies calculated with our recently presented approach.²⁷ The latter includes a solvating sphere of explicit water molecules. In this approach, the accurate free energies of solvation are calculated in two steps. The major contribution is calculated using classical MD simulations and the free energy perturbation (FEP) adiabatic charging (AC) approach, where it is assumed that the solvated tautomer has the charge distribution given by the polarizable continuum model (PCM). In the second step the classical free energy of solvation is refined to take into account the real, average charge distribution. This is done using our accelerated QM/MM simulations, where the QM energy of the solute is calculated in the mean solvent potential averaged over a number of MD steps. The calculated solvation free energies have been found to be the largest for the new anionic tautomers. In water solution, three of the new tautomers are more stable than the anion of the canonical tautomer.

2. Methods

2.1 The relative free energies of tautomers

In this study we consider five tautomers of anionic uracil that have been identified as the most stable in the gas phase.^16,17 These tautomers are named U0–U4 (Fig. 1), with U0 being the canonical tautomer, and U1–U4 are the remaining tautomers ordered according to their decreasing stability in the gas-phase. The relative energies of these tautomers were calculated by Bachorz et al.²⁴ at explicitly-correlated second-order Møller–Plesset perturbation theory (RI-MP2-R12) in conjunction with conventional coupled-cluster theory with single, double, and perturbative triple excitations (CCSD(T)). The Hartree-Fock and MP2 energies were extrapolated to the complete basis set limit. The final energies were corrected for the zero-point vibrational energies, determined in harmonic approximation at the UHF-RI-MP2/aug-cc-pVTZ level of theory. These results are summarized in Table 1.

In the current study we calculated thermal corrections to Gibbs free energies of the gas phase anionic tautomers. The geometries were optimized and harmonic frequencies calculated at the second order Moller-Plesset (MP2) level. The aug-cc-pVDZ basis set (APVDZ)²⁸ was used. The 1s orbitals of carbon, nitrogen and oxygen atoms were excluded from electron correlation treatments. Thermal and entropic corrections were calculated at the temperature of 300K. The final relative free energies calculated with respect to the anionic canonical structure are summarized in Table 1. The calculations were preformed using the Gaussian03 program package.²⁹

To calculate the relative free energies of two tautomers, Ux and Uy, in water solution, (ΔG_Ux−Uy)_sol we use a simple energy cycle of Figure 2:

$${\left(\mathrm{\Delta }{\mathrm{G}}_{\mathrm{U}\mathrm{x}-\mathrm{U}\mathrm{y}}\right)}_{\text{sol}}=-\mathrm{\Delta }{\mathrm{G}}_{\text{sol}}\mathrm{U}\mathrm{x}+{\left(\mathrm{\Delta }{\mathrm{G}}_{\mathrm{U}\mathrm{x}-\mathrm{U}\mathrm{y}}\right)}_{\text{gas}}+\mathrm{\Delta }{\mathrm{G}}_{\mathrm{\text{sol}}}\mathrm{U}\mathrm{y}$$ (1)

where (ΔG_Ux−Uy)_gas is the free energy difference between Ux and Uy in the gas phase and ΔG_solUx and ΔG_solUy are the free energies of solvation of Ux and Uy, respectively.

Figure 2.

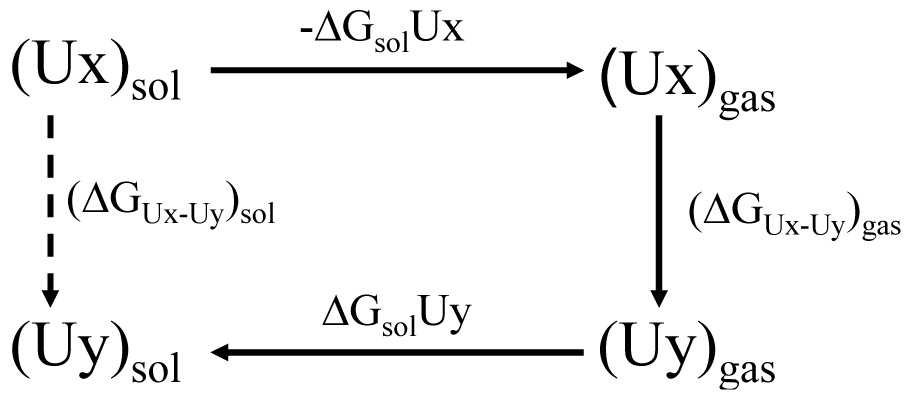
An energy cycle used to calculate relative free energies of tautomers in water solution.

2.2 The solvation free energies of tautomers

When considering the energies of tautomers in solution we will use a QM/MM approach where solute is treated at the quantum mechanical level and solvent is treated classically. The energy of such system is expressed as:

$$\begin{array}{c}{E}_{\mathit{\text{tot}}}=\langle {\varphi }_s{\psi }_S^{\mathit{\text{pol}}}|H_S^{\mathit{\text{gas}}}+V_{\mathit{\text{Ss}}}^{\mathit{\text{el}}}+V_{\mathit{\text{Ss}}}^{\mathit{\text{vdW}}}+H_{\mathit{\text{ss}}}|{\varphi }_s{\psi }_S^{\mathit{\text{pol}}}\rangle \cong \hfill \\ \cong E_{\mathit{\text{QM}}}^{\mathit{\text{pol}}}\left(\mathbf{R},\mathbf{Q}\left(U_s\right)\right)+E_{\mathit{\text{QM / MM}}}^{el}\left(\mathbf{R},\mathbf{r},\mathbf{Q}\left(U_s\right)\right)+E_{\mathit{\text{vdW}}}(\mathbf{R},\mathbf{r})+E_{\mathit{\text{MM}}}(\mathbf{r})\hfill \end{array}$$ (2)

where Ψ_S and ϕ_s are the wavefunctions of the solute (S) and solvent (s), the $H_S^{\mathit{\text{gas}}}$ and H_ss are the Hamiltonian operators describing the energy of the solute and solvent, respectively. The $V_{\mathit{\text{Ss}}}^{\mathit{\text{el}}}\text{and}{V}_{\mathit{\text{Ss}}}^{\mathit{\text{vdW}}}$ represent, respectively, the electrostatic and van der Waals solute-solvent potentials. The R and r are the solute and solvent coordinates, respectively, and Q is a vector of solute residual atomic charges obtained from ${\mathrm{\Psi }}_S^{\mathit{\text{pol}}}$ that depend on the potential U_s of the solvent. Here the first term, $E_{\mathit{\text{QM}}}^{\mathit{\text{pol}}}(\mathbf{R},\mathbf{Q}(U_s))=\langle {\mathrm{\Psi }}_S^{\mathit{\text{pol}}}|H_S^{\mathit{\text{gas}}}|{\mathrm{\Psi }}_S^{\mathit{\text{pol}}}\rangle ,$ is the energy of the gas phase Hamiltonian with a solute wavefunction polarized by the solvent. The second term, $(E_{\mathit{\text{QM / MM}}}^{\mathit{\text{el}}}(\mathbf{R},\mathbf{r},\mathbf{Q}(U_s))),$ is the solute-solvent electrostatic interaction, which is approximated with a classical expression:

$$E_{\mathit{\text{QM / MM}}}^{\mathit{\text{el}}}\equiv 332{\displaystyle \sum _{i(S)}{\displaystyle \sum _{j(s)}\frac{Q^i{q}^j}{r_{ij}}}}$$ (3)

where q are the solvent residual charges, whereas i and j are indexes of the solute and solvent atoms, respectively. The third term in Eq (2), E_vdW (R, r), is the solute-solvent van der Waals interaction and the last term, E_MM(r), is the solvent potential surface.

Such defined E_tot can be used to evaluate the solvation free energies using the following approach. The starting point is the free energy perturbation (FEP) adiabatic charging (AC) approach,^30,31,32 here we can use a potential in the form:

$$E_k=(\mathit{E\prime }(1-{\lambda }_k)+E_{\mathit{\text{MM}}})+(E_{\mathit{\text{tot}}}-E_{\mathit{\text{MM}}}){\lambda }_k(4)$$ (4)

where E’ denotes an energy of the system without electrostatic solute-solvent interaction$(\mathit{E\prime }=\langle {\mathrm{\Psi }}_S^{\mathit{\text{gas}}}|H_S^{\mathit{\text{gas}}}|{\mathrm{\Psi }}_S^{\mathit{\text{gas}}}\rangle +E_{\mathit{\text{vdW}}})$ and where λ_k changes from zero to one in n+1 steps. We can use the standard FEP equation: ^30,33,34

$$\begin{array}{c}\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\lambda }_k\to {\lambda }_{k+1})=-{\beta }^{-1}\text{ln}{\langle \text{exp}\{-(E_{k+1}-E_k)\beta \}\rangle }_{E_k}\hfill \\ \mathrm{\Delta }{G}_{\mathit{\text{sol}}}={\displaystyle \sum _{k=1}^{n+1}\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\lambda }_k\to {\lambda }_{k+1})}\hfill \end{array}$$ (5)

where β=1/(k_BT); k_B is the Boltzmann constant and T is the absolute temperature. Eq. (5) can be effectively approximated by using the linear response approximation (LRA) treatment³⁵:

$$\mathrm{\Delta }{G}_{\mathrm{\text{sol}}}\cong {\langle E_{\mathit{\text{tot}}}-(\mathit{E\prime }+E_{\mathit{\text{MM}}})\rangle }_{E_{\mathit{\text{tot}}}}+{\langle E_{\mathit{\text{tot}}}-(\mathit{E\prime }+E_{\mathit{\text{MM}}})\rangle }_{\mathit{E\prime }}+\mathrm{\Delta }{G}_{\mathit{\text{cav}}}$$ (6)

where ΔG_cav is the solvation free energy of the nonpolar neutral form of the solute (all solute residual atomic charges are zero). This term consists of two parts describing the hydrophobic and van der Waals free energies of cavity, which are not included in the first two terms of Eq. (6). They were described in Ref. 36. These terms do not represent the standard cavitation energy correction but the field dependant hydrophobic correction, which is more physically grounded.^36,37 The performance of this model has been established by careful systematic validation. This approach is quite reliable as can be judged from the extensive studies.^36,37,38

To calculate the solvation free energies of anionic tautomers of uracil we use a cycle illustrated in Figure 3, which makes use of both the FEP/AC and LRA approaches presented in Eq. (5) and Eq. (6), respectively. Here, we first polarize the solute molecule to a given charge distribution (e.g. partial charges obtained with the PCM solvation model ($\mathbf{Q}={\mathbf{Q}}_{\mathit{\text{PCM}}}^0,$ where “0” in a superscript designates a constant value), then we run a classical MM simulations and use the FEP/AC approach³⁰ to evaluate the free energy of solvation of such polarized solute. Then we evaluate a change in the free energy allowing the solute partial charges to “equilibrate” with the solvent potential. The vector of equilibrated QM/MM residual atomic charges is designed by Q_eq. Thus the QM/MM solvation free energy can also be written as:

$$\mathrm{\Delta }{G}_{\mathit{\text{sol}}}=\mathrm{\Delta }{E}_{\mathit{\text{QM}}}^{\mathit{\text{pol}}}({\mathbf{Q}}_{\mathit{\text{gas}}}^0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)+\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)+\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0\to {\mathbf{Q}}_{\mathit{\text{eq}}})$$ (7)

where the $\mathrm{\Delta }{E}_{\mathit{\text{QM}}}^{\mathit{\text{pol}}}$ term in Eq. (7) is the polarization energy, which is given by:

$$\mathrm{\Delta }{E}_{\mathit{\text{QM}}}^{\mathit{\text{pol}}}=\langle {\mathrm{\Psi }}_S^{\mathit{\text{sol}}}|H_S^{\mathit{\text{gas}}}|{\mathrm{\Psi }}_S^{\mathit{\text{sol}}}\rangle -\langle {\mathrm{\Psi }}_S^{\mathit{\text{gas}}}|H_S^{\mathit{\text{gas}}}|{\mathrm{\Psi }}_S^{\mathit{\text{gas}}}\rangle$$ (8)

where ${\mathrm{\Psi }}_S^{\mathit{\text{sol}}}\text{and}{\mathrm{\Psi }}_S^{\mathit{\text{gas}}}$ are the solute wave function in solution and in the gas-phase, respectively, and $H_S^{\mathit{\text{gas}}}$ is the gas-phase Hamiltonian. The $\mathrm{\Delta }{E}_{\mathit{\text{QM}}}^{\mathit{\text{pol}}}({\mathbf{Q}}_{\mathit{\text{gas}}}^0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$ represents the polarization energy of a molecule in the PCM solvation model and corresponds to energetic penalty of deforming the solute wavefunction in the presence of the solvent. The $\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$ term is the solvation free energy of the solute, the atomic charges of which have been obtained from the PCM model. The $\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$ can be obtained using the classical adiabatic charging approach based on FEP and therefore can be replaced by $\mathrm{\Delta }{G}_{\mathit{\text{sol}}}(\mathbf{Q}=0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)+\mathrm{\Delta }{G}_{cav}.$ The $\mathrm{\Delta }{G}_{\mathit{\text{sol}}}(\mathbf{Q}=0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$ is related with solute-solvent electrostatic interaction energy, which is not explicitly presented in this study. The last term of Eq. (7), namely $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0\to {\mathbf{Q}}_{\mathit{\text{eq}}})$, can be expressed using the LRA approach as:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0\to {\mathbf{Q}}_{\mathit{\text{eq}}})\cong \frac{1}{2}\left[{\langle E_{\mathit{\text{tot}}}(\mathbf{Q})-E_{\mathit{\text{tot}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)\rangle }_{E(\mathbf{Q})}+{\langle E_{\mathit{\text{tot}}}(\mathbf{Q})-E_{\mathit{\text{tot}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)\rangle }_{E({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)}\right]$$ (9)

where E_tot(Q) is the QM/MM surface with the fluctuating solute partial charges, which respond to changes in solvent configurations.

Figure 3.

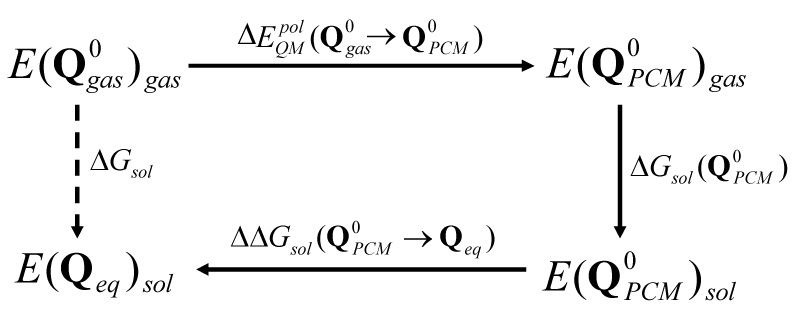
An energy scheme used in this study. $\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$ is calculated by the classical adiabatic charging approach and $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0\to {\mathbf{Q}}_{\mathit{\text{eq}}})$ is calculated using Eq. (9).

The main time consuming steps in the evaluation of Eq. (7) are evaluations of the LRA ${\langle \rangle }_{E(\mathbf{Q})}\text{and}{\langle \rangle }_{E({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)}$ terms expressed in Eq. (9). The main problem is the need for a very long computer time to evaluate the QM energy, which in turn makes it extremely challenging to perform proper configurational sampling. To make these calculations possible we employ our recently developed accelerated QM/MM approach²⁷ that introduces the average effect of the fluctuating solvent charges on the QM system by using equivalent charge distributions, which are updated every m steps of a MD simulation.

Our strategy for evaluating the average solvent potential, which is technically similar to the approach of Aguilar and coworkers,³⁹ is demonstrated schematically in Fig. 4. In this approach, we constrain the QM atoms (the solute atoms), evaluate the QM charges, Q⁽¹⁾, where (1) designates the first step and run m MM/MD steps allowing the solvent molecules to move in the potential $(E_{\mathit{\text{QM / MM}}}^{\mathit{\text{el}}}({\mathbf{Q}}^{(1)})+E_{\mathit{\text{vdW}}}).$ All m snapshots of solvent coordinates from m MD steps are stored. Then the charge of each solvent atom is scaled by 1/m and all m×N solvent atoms with the scaled solvent charges are sent to the QM program to reproduce an average solvent potential on the solute. The latter is used to obtain the corresponding solute polarization and a new set of solute charges Q⁽²⁾. The procedure is repeated until all terms contributing to Eq. (9) converge.

Figure 4.

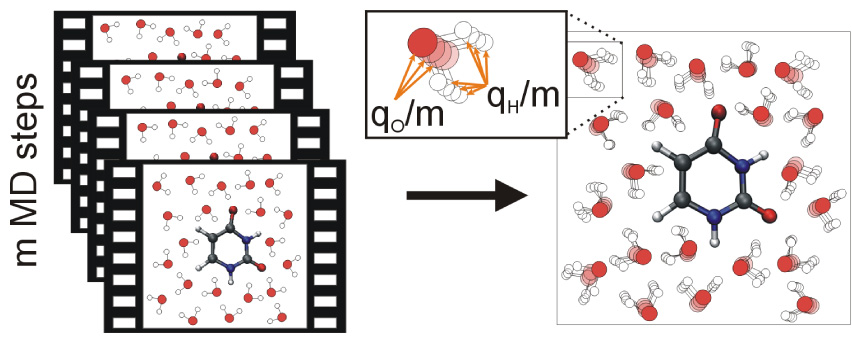
A schematic representation of the averaging of the solvent potential over m steps of a MD simulation.

The approach of representing an average solvent potential (Fig. 4) is simple to implement but unfortunately it generates m×N external charges to be included into the Hamiltonian within the QM program. This can be too expensive and inconvenient as shown in the previous study.²⁷ Thus, we introduce an approximation described in Fig. 5. In this treatment we divide the solvent into three regions. In the first region (region I), we convert the N_regI solvent atoms to m×N_regI external charges (scaled by 1/m). In the second region (region II) we represent each OH bond of N_regII water molecules with two charges representing average dipole of a moving OH bond, while in region III, we represent the average solvent field coming from N-N_regI-N_regII solvent molecules, by two point charges (q and −q) using:

$${\mathbf{E}}_O=\frac{2q}{{\left|{\mathbf{r}}_{\mathit{\text{OR}}}\right|}^3}{\mathbf{r}}_{\mathit{\text{OR}}}$$ (10)

where E_O is an electric field at point O (the geometrical center of the QM system) and r_OR is pointing along E_O to the charge q. The presented here three region solvent representation is the major improvement over the previously suggested approach,²⁷ where we used only two regions (of I and III type) to represent the solvent.

Figure 5.

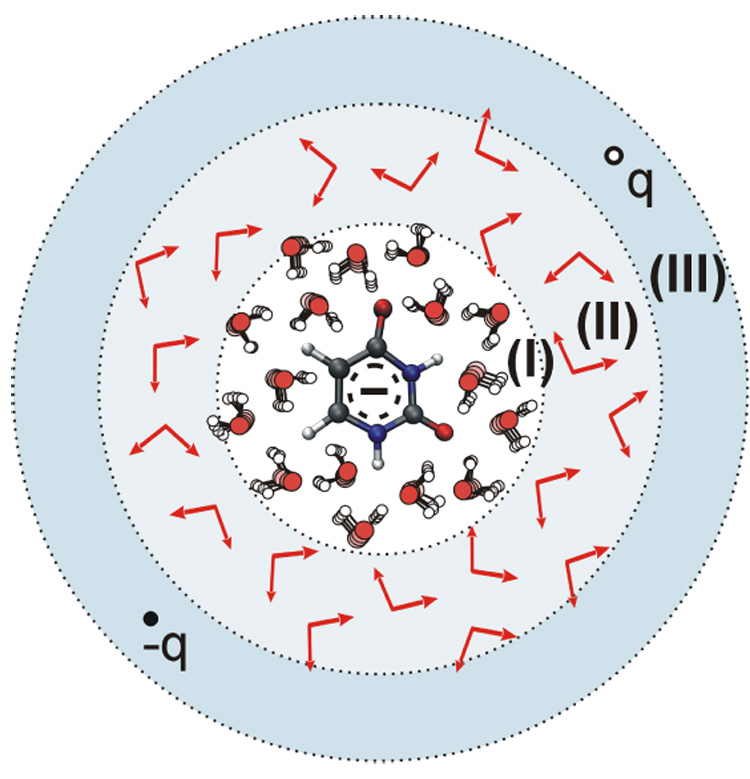
Model for the evaluation of the average solvent charges: average the explicit molecules in region (I), while representing the average potential of the molecules in regions (II) and (III) by average dipoles and two charges, respectively.

To perform the required calculation of Eq. (7), every considered anionic tautomer was hydrated in a sphere with a radius of 16Å, which contained 558–561 explicit water molecules depending on the tautomer. All solvent molecules are represented by the ENZYMIX force filed.⁴⁰ In the simulation model the sphere of explicit water molecules is surrounded by a surface region whose average polarization and radial distribution are determined by the surface constrained all-atom solvent (SCAAS) model.^32,41,42 The surface region is embedded in a bulk continuum region with a dielectric constant of 80. The long range interactions are treated by the local reaction field (LRF) approach.⁴³

The MD simulations presented here were performed using the MOLARIS package.⁴⁰ In every case we first relaxed the system in a 50 ps long simulation of 1 fs time steps. The classical adiabatic charging FEP calculations were preformed in 11 steps of 50ps each for both forward $(\mathrm{\Delta }{G}_{\mathit{\text{sol}}}(\mathbf{Q}=0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0))$ and backward $(\mathrm{\Delta }{G}_{\mathit{\text{sol}}}({\mathbf{Q}}_{\mathit{\text{PCM}}}^0\to \mathbf{Q}=0))$ processes. The results of both did not differ by more than 0.5 kcal/mol for the whole forward and backward charging processes. Their average is used as $\mathrm{\Delta }{G}_{\mathit{\text{sol}}}(\mathbf{Q}=0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$ and it is presented in Table 2.

Table 2.

The contributions to the free energy of solvation: polarization energy$\mathrm{\Delta }{E}_{\mathit{\text{QM}}}^{\mathit{\text{pol}}}({\mathbf{Q}}_{\mathit{\text{gas}}}^0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0),$ hydrophobic (Hdr) and van der Waals (vdW) contributions to ΔG_cav, classical AC solvation free energy $\mathrm{\Delta }{G}_{\mathit{\text{sol}}}(\mathbf{Q}=0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$ and the LRA terms of Eg. (9). The final solvation free energy ΔG_sol is calculated using Eq. (7). For comparison, the corresponding ΔG_sol values obtained with the PCM model are reported. All energies in kcal/mol.

			ΔGcav		Terms of Eq. (9)		ΔGsol
Tautomer	$\mathrm{\Delta }{E}_{\mathit{\text{QM}}}^{\mathit{\text{pol}}}({\mathbf{Q}}_{\mathit{\text{gas}}}^0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0),$	$\mathrm{\Delta }{G}_{\mathit{\text{sol}}}(\mathbf{Q}=0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$	Hdr	vdW	${\langle \rangle }_{E(\mathbf{Q})}$	${\langle \rangle }_{E({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)}$	This study	PCM
U0−	5.62	−71.59	6.30	−4.49	−2.12	−1.16	−65.80	−65.64
U1−	7.35	−73.29	6.35	−4.31	−3.43	−2.57	−66.90	−66.22
U2−	10.63	−84.76	6.33	−4.29	−3.44	−2.58	−75.10	−73.59
U3−	6.48	−79.75	6.31	−4.30	−0.90	−0.21	−71.81	−68.25
U4−	21.12	−93.03	6.35	−4.32	−0.03	−9.22	−79.50	−86.47

The combined QM/MM calculations were preformed to estimate the terms of Eq. 9. In each case we ran a 250 ps long simulation, which was sufficient to reach convergence of Eq. 9 (Fig. 6). When performing a QM calculation we used the mean solvent potential averaged over 200 MD steps (m=200). Within the QM calculation, the solvent was represented with our three layers model of Figure 4, with the radii of regions I, II and III being 10Å, 14 Å and 16 Å, respectively. All QM calculations were performed using the Gaussian03 package.²⁹ The B3LYP exchange-correlation potential was used with 6−31++G^** basis sets. The Merz-Kollman scheme⁴⁴ with default atom radii was used to determine charges on atoms to be later used in the MD simulations. The hydrophobic and van der Waals contributions to the free energy of solute cavity were calculated using the ChemSol 2.1 program.³⁶

Figure 6.

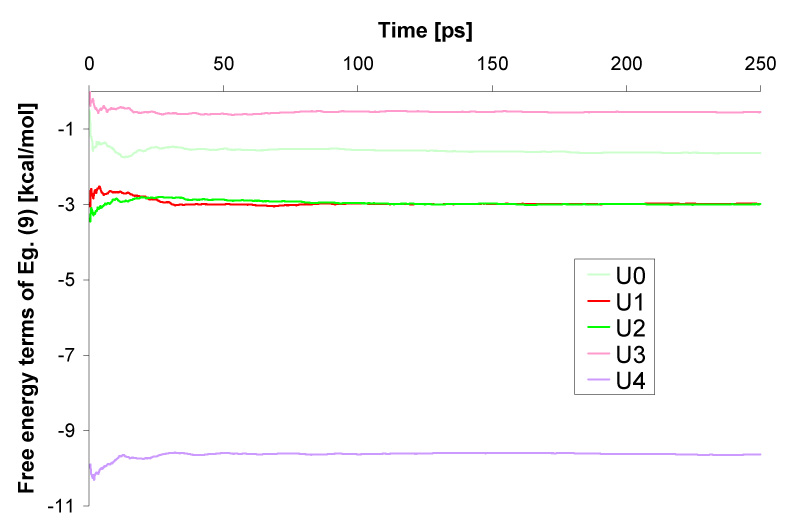
Convergence of the results given by Eq. (9) during 250ps simulations.

The accelerated QM/MM approach for performing calculations of solvation free energies introduces explicit water molecules. This model is more rigorous that PCM approaches, providing the electronic structure methods, force-fields and sampling are proper. We have made careful validation of the presented solvation model²⁷ on a model anionic system and we believe that the relative energies of anionic tautomers of uracil presented in the current study are more accurate than the PCM results presented in our initial studies.^16,17

The validation of the accelerated QM/MM approach has been conducted for model systems: a water molecule and a formate ion. The full study is presented in Ref. 27 and here we only highlight the most important findings. The calculations were conducted for different m’s (m=1…1000) and different solvent representation models (only region I, only region III or both). We found out that using different m’s leads to similar solvation free energies providing the convergence of the result has been reached. The solvation free energies do not depend strongly on the complexity of the solvent representation model employed. In the case of formate ion we were able to reproduce its experimental solvation energy within 1 kcal/mol error bars when using the model of combined region I and III and different m’s.

Since representing the effect of the fluctuating solvent charges by effective charges, and then updating the solute polarization by incorporating the effective charges in the solute Hamiltonian, slows down the QM calculation, there is a limiting m for which the accelerated approach is not efficient anymore. From our experience of the study²⁷ we conclude that m=200 is a good compromise and therefore it is used in the case of uracil anion. We found that in the case of m=200 the single QM calculation is 6.4 times longer then is the case on m=1, however the QM is executed only once per 200 MD steps. Therefore the overall speed up is of a factor of 31, that is, assuming that the time required to run m MD steps for MM subsystem is negligible comparing to QM.

3. Results

The calculated relative free energies of five anionic tautomers in the gas phase are presented in Table 1. They are compared with the gas phase electronic energies corrected for zero-point vibration energies. The discrepancies between these two thermodynamic characteristics are smaller than 0.9 kcal/mol. The U1⁻ is the most stable anionic tautomer on the gas phase free energy surface, and the canonical tautomer, U0⁻, is less stable by 2.54 kcal/mol. The remaining tautomers, U2⁻–U4⁻ are less stable than U1⁻ by, respectively, 5.35, 9.84 and 10.70 kcal/mol.

The calculation of solvation free energies of five anionic tautomers of uracil was done using Eq. (7), and all the contributing terms are shown in Table 2. We started by performing the PCM solvation model calculations. They provided an estimation of residual charges and polarization energies. The polarization energies, $\mathrm{\Delta }{E}_{\mathit{\text{QM}}}^{\mathit{\text{pol}}}({\mathbf{Q}}_{\mathit{\text{gas}}}^0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$, amount to 5.62–21.12 kcal/mol, with the largest value for U4⁻. The polarization of a molecule is typically correlated with the distribution of residual charges. The charges are used in the MD simulations and therefore they influence the values of classical solvation free energies obtained using the free energy perturbation adiabatic charging approach. Indeed, the largest absolute value of $\mathrm{\Delta }{G}_{\mathit{\text{sol}}}(\mathbf{Q}=0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$ of 93.03 kcal/mol is reported for U4⁻. The classical solvation energy, $\mathrm{\Delta }{G}_{\mathit{\text{sol}}}(\mathbf{Q}=0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$, amounts to −71.59 and −73.29 kcal for U0⁻ and U1⁻, respectively. Mid-range values of $\mathrm{\Delta }{G}_{\mathit{\text{sol}}}(\mathbf{Q}=0\to {\mathbf{Q}}_{\mathit{\text{PCM}}}^0)$ are reported for U2⁻ (−84.76 kcal/mol) and U3⁻ (−79.75 kcal/mol). The ΔG_cav terms for all U0⁻–U4⁻ tautomers are similar and amount to ca. 2 kcal/mol with the largest deviation of 0.2 kcal/mol reported for U0⁻.

The most challenging part in calculations of the free energy of solvation is the estimation of the terms contributing to Eq. (9). The sampling required to obtain the ${\langle \rangle }_{E(\mathbf{Q})}\text{and}{\langle \rangle }_{E({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)}$ terms of Eq. (9) was performed during a 250 ps MD simulation. We used our accelerated QM/MM approaches, where a calculation of the QM subsystem is performed in the mean field of the solvent averaged over 200 MD steps (Fig. 4). As demonstrated in Figure 6, the convergence of Eq. (9) was reached within ca. 150 ps of the MD simulation. The contributions resulting from Eq. (9) span a range from −0.21 to −3.44 kcal/mol for the U0⁻–U3⁻ tautomers. A much larger value of −9.63 kcal/mol is reported for U4⁻ and reflects a larger polarization of this tautomer. As expected,²⁷ the ${\langle \rangle }_{E(\mathbf{Q})}\text{and}{\langle \rangle }_{E({\mathbf{Q}}_{\mathit{\text{PCM}}}^0)}$ terms are quite similar as their difference does not exceed 1 kcal/mol.

The final free energies of solvation calculated using Eq. (7) are −65.80 and −66.90 kcal/mol for U0⁻ and U1⁻, respectively. Larger values of ΔG_sol are reported for the remaining tautomers, with the largest of −79.50 kcal/mol for U4⁻. In general, the strongest solvation develops for the tautomers with a proton transferred from N3 to a carbon atom (U2⁻ and U4⁻), which is consistent with the largest polarization of these molecules observed at the PCM model, and consistent with previously reported results.¹⁷

The solvation free energies obtained using Eq. (7) differ significantly from the PCM results obtained for the same molecular geometries. The difference is the largest, 7.0 kcal/mol, for the U4⁻ tautomer and smaller but still significant for U2⁻ and U3⁻ of 1.5 and 3.6 kcal/mol, respectively. In the case of U0⁻ and U1⁻ the solvation free energies obtained with Eq. (7) agree with the PCM results within 0.7 kcal/mol. The differences between results of Eq. (7) and the PCM solvation energies reflect two facts: (i) in our study we use explicit water molecules; (ii) in our method we allow the solute wavefunction to respond to the field of the explicit solvent molecules.

Big differences in the values of ΔG_sol among the considered anionic tautomers are reflected in the relative free energies of anionic tautomers in water. The latter are calculated using Eq. (1) and are summarized in Table 1. The most stable anionic tautomer in water solution is U2⁻, followed by U4⁻, which is less stable by 0.95 kcal/mol. The U1⁻ and U0⁻ are less stable than the most stable tautomer by 2.85 and 6.49 kcal/mol, respectively. The least stable from the set of five tautomers is U3⁻, being 7.78 kcal/mol less stable than U2⁻.

The current relative free energies differ significantly from the previously reported both the gas-phase and solution results. The most important finding is that U1⁻, U2⁻ and U4⁻ are more stable than U0⁻. In particular, the U4⁻ tautomer, which is unstable with respect to U0⁻ by 8.2 kcal/mol in the gas phase, becomes the second most stable tautomer in solution, more stable then U0⁻ by 5.5 kcal/mol. Our findings have some important consequences. Firstly, the evaluation of solvation energies for the anionic tautomers of nucleic acid bases should go beyond the initial screening at the PCM level. Secondly, some of the higher energy tautomers, like U4⁻ for uracil, could become very stable in water solution, even though they are not dominant in the gas phase. Therefore, one should consider repeating the screening for the most stable tautomers of the anionic nucleic acids bases²¹ in solution (e.g. using our hybrid combinatorial-computational approach combined with the PCM model), or include in the solvation studies a larger number of promising gas-phase tautomers identified at the level the energy-based screening.²¹

Finally, the fact that U2⁻ and U4⁻ are the most stable anionic tautomers in water solution might have important biological consequences. Both of these tautomers have hydrogen at the N1 atom where the sugar unit is connected in RNA. Therefore they can exist in the RNA environment and affect the structure of this nucleic acid. The consequences of these finding have been already discussed extensively in Ref. 16 and Ref. 17. It remains to be explored, which anionic tautomers of other NABs dominate in water solutions. These findings might become important for understanding of the effects of high energy radiation on DNA.

Another issue that should be explored is the chemical reactivity of these new anionic tautomers, both with the solvating water molecules and with the most common species in the RNA and DNA environments. For example, it is believed that anions of nucleic acid bases react with water forming hydrogenated nucleic acid bases and OH⁻ species.⁴⁵ The thermodynamics and kinetics of these processes will be studied in our future projects.

4. Summary

In this study we report the results of our calculations of the solvation free energies of the most stable anionic tautomers of uracil. These free energies were obtained using a two step approach. First the classical MD simulations were performed and the free energy perturbation adiabatic charging approach was employed to obtain classical solvation free energies. In this step it was assumed that the solvated molecules have the charge distributions given by the polarizable continuum model. In the second step the free energy of solvation was refined by taking into account the real, average solvent charge distribution that reflects polarization caused by explicit water molecules used in the solvation model. This was done using our accelerated QM/MM simulations, where the QM energy of the solute was calculated in the mean solvent potential averaged over 200 MD steps. The results suggest that in water solution three of the recently identified anionic tautomers, namely U2⁻, U4⁻ and U1⁻ (Fig. 1) are, respectively, 6.5, 5.5 and 3.6 kcal/mol more stable than the anion of the canonical tautomer. We also demonstrated that the solvation free energies of the most stable anionic tautomers obtained using our QM/MM approach are significantly different than the corresponding values obtained using the PCM model. In our opinion the PCM results can be successfully used for initial estimation of the solvation energies. We believe, however, that one would obtain more accurate results by full microscopic QM/MM calculations. Here we would like to emphasize that our conclusion is not completely trivial. It is obvious that microscopic models provide correct specific interactions with the solvent molecule. However, this does not guarantee better results since the use of the energy minimization or other poor sampling approaches would make the microscopic results completely unreliable. Similarly, the use of the semiempirical QM/MM (which would allow proper sampling as they are computational less expensive) might give poor results if the solute charges are not accurate. Only the use of ab initio QM/MM approaches with sufficient sampling leads to a stage where the QM/MM results start to be more reliable than those obtained by PCM or related approaches. Moreover, in contrast to the PCM model, the presented QM/MM approach can be employed to predict solvation free energies of charged nucleic acid bases incorporated into DNA. Such study will be performed in the future.