Just in time connectivity for large spiking networks

Abstract

The scale of large neuronal network simulations is memory-limited due to the need to store connectivity information: connectivity storage grows as the square of neuron number up to anatomically-relevant limits. Using the NEURON simulator as a discrete-event simulator (no integration), we explored the consequences of avoiding the space costs of connectivity through regenerating connectivity parameters when needed – just-in-time after a presynaptic cell fires. We explored various strategies for automated generation of one or more of the basic static connectivity parameters: delays, postsynaptic cell identities and weights, as well as run-time connectivity state: the event queue. Comparison of the JitCon implementation to NEURON’s standard NetCon connectivity method showed substantial space savings, with associated run-time penalty. Although JitCon saved space by eliminating connectivity parameters, larger simulations were still memory-limited due to growth of the synaptic event queue. We therefore designed a JitEvent algorithm that only added items to the queue when required: instead of alerting multiple postsynaptic cells, a spiking presynaptic cell posted a callback event at the shortest synaptic delay time. At the time of the callback, this same presynaptic cell directly notified the first postsynaptic cell and generated another self-callback for the next delay time. The JitEvent implementation yielded substantial additional time and space savings. We conclude that just-in-time strategies are necessary for very large network simulations but that a variety of alternative strategies should be considered whose optimality will depend on the characteristics of the simulation to be run.

Introduction

Memory storage remains a limitation when running very large neuronal networks (VLNNs). With number of neurons n, connectivity storage grows as n². With connectivity densities of 0.1–10%, 1 · 10⁶ neurons will require from 1 · 10⁹ to 1 · 10¹¹ synapses. A single connection requires at least an associated weight and delay as well as additional pointers or offsets to store the connectivity matrix. Conservatively, this will require 10 bytes (e.g., 2 floats and 2 chars) which will then bring the total synaptic memory load to 10 GB to 1 TB. The former value is currently executable on a large machine while the latter remains impossible without disk swapping on a single workstation, though it is possible by splitting the network across the nodes of a parallel supercomputer (Migliore et al. 2006).

Japanese industry pioneered just-in-time (JIT) technology and industrial organization. The idea was that supplies or intermediate assemblies would be brought to a factory as they were needed. This meant that primary or intermediate ingredients didn’t have to be stored on site: inventory is minimized by the addition of efficient, predictive scheduling and queuing systems to maintain work-flow. In the context of network simulations this means that a synaptic structure does not need to be set up until it is needed – that is, until a presynaptic cell fires or until an event needs to be delivered. We have exploited algorithmic space-time trade-offs to build large event-driven artificial-cell simulations in the NEURON simulator by utilizing just-in-time connections (JitCons) and just-in-time events (JitEvents) that are generated at the time of presynaptic cell spiking or postsynaptic cell notification respectively.

Although just-in-time techniques have been used by several modelers over the years, (e.g., Izhikevich and Edelman 2008), there has not been a published exploration of the consequences and limitations of the variety of possible alternative and complementary techniques. In the present paper, we explore several variations on the theme, noting a number of space-time trade-offs that should be considered.

Methods

The techniques and simulations described here are implemented in the NEURON simulator (www.neuron.yale.edu) (Hines & Carnevale 2001; Carnevale & Hines 2006). Although NEURON is a compartmental model simulator, it features an efficient event-queue utilizing either a generic splay-tree algorithm or a bin-queue (latter only used with a fixed step method) (Hines & Carnevale 2004; Lytton & Hines 2005). The NEURON integrator can be turned off during event-driven simulations so as to offer no time-overhead and minimal space-overhead. Individual neuron integrators can also be turned on to run hybrid networks with both compartmental and rule-based cells (Lytton & Hines 2004).

Simulations were run using a rule-based artificial cell unit design previously reported (Lytton & Stewart 2005; Lytton & Stewart 2006). In brief, this augmented integrate-and-fire cell is an event-driven unit that maintains 5 state variables associated with diffierent synaptic inputs (AMPA, NMDA, GABAA, GABAB – here denominating the kinetics of the respective associated receptors rather than the chemicals from which the acronyms are derived) as well as an afterhyperpolarization (AHP). These state variables are recalculated asynchronously as needed (another just-in-time feature) for handling an event. This is possible because each state variable follows a first order decay mechanism except when instantaneously displaced by an external or self-generated event. Additional verisimilitude is provided by incorporating a variety of rules governing refractory period, depolarization blockade, bursting, etc.

Use of the artificial cell allowed us to cleanly separate queuing and network organization issues from the space and time loads associated with numerical integration. However, for coding clarity, we also developed a free-standing JIT module (jitcon.mod) to be used with compartment models. This module separates the JIT machinery that was enmeshed with the cell machinery in the original implementation (enmeshed because both mechanisms are utilizing the same event queue). The compartment model simulation, available on ModelDB (http://senselab.med.yale.edu/senselab/ModelDB; Hines and Carnevale 2004), runs a simulation of 125 2-compartment Hodgkin-Huxley-based models using either JitCon or NetCon (selectable with a flag). This version was developed solely for distribution purposes and is not further discussed in the paper.

For our test models we used epileptiform simulations which provide ongoing activity without requiring repeated external stimulation or the use of constitutively active cells (i.e., current injection). The high activity levels in these simulations makes them particularly challenging to simulate. Simulations generally used 3 simulated cell classes – a small excitatory subset, a large excitatory subset and an inhibitory population. The 3 cell classes diffiered in terms of intrinsic parameterization and connectivity. Connectivity within and between classes was governed by connection densities (probabilities) of 5–20%. Connectivity was a directed random graph. Simulation size was generally varied from 1,000 to 320,000 cells with still larger simulations assessed on a limited basis. Simulations with this network design have been previously published (Lytton & Omurtag 2007). Comparisons were made to the standard NEURON synaptic data-structure, the NetCon (Lytton 1996).

All of the reported simulations were run under Redhat WS-64 Linux with kernel 2.6.18 on a 64-bit computer with dual AMD Opteron 250 processors and 12 GB of available memory. Simulations were run in a batch mode without graphics. Other users were logged off the machine and browsers and other intrusive programs were killed before profiling. Time was measured using the C clock() routine; memory usage was measured using the Unix pmap routine. All space measures are given as memory augmentations after program loading.

Results

The initial version of JitCon utilized on-demand generation of delays, connectivity and weights. Consistent regeneration of these values requires consistent use of seeds for the pseudo-random-number generators that are used. In order to do this, a unique identification number (ID, a serial number) was used for each cell. The IDs were scaled and combined for use as seeds (hashing). In the standard NetCon implementation, a presynaptic cell spike leads to the placement of an event on the event queue for later delivery to the postsynaptic cell. This event includes 4 fields: the synaptic weight (sometimes an array of weights); the destination; the delivery time; a flag. We use this flag to provide information about presynaptic identity that would otherwise be unavailable postsynaptically. The queue maintains delivery-time order.

Although detailed connectivity information is not stored in the JitCon network, the cells do have access to a basic network “sketch” from which the connectivity matrix can be calculated. This includes 1. a matrix of connection densities giving the average probability of finding a connection between two cells of given types; 2. a parallel matrix of mean connection strengths giving the mean weight for a connection between cells of those types; 3. a matrix of mean delays for a connection between cells of given type. The individual values to be placed on the queue are calculated using these matrices, a consistent seed, and a random number generator. Values are only calculated when they are needed. For example, the synaptic weight is not needed until the event is delivered and it is therefore calculated postsynaptically and not placed on the queue.

The diffierence between NetCon and JitCon implementation can best be illustrated by the pseudo-code algorithm. For the NetCon, a cell, here cell[53], spiking at t = t0 results in the following sequence:

cell[53].spike_event() // presynaptic mechanism activated

cell[53].lookup(projections) // find weight, destination and delay vectors

for i=1 to cell[53].divergence_size {

 wt=cell[53].weight[i]

 dest=cell[53].destination[i]

 del=cell[53].delay[i]

 new_event(wt,dest,t0+del,flag=0)

}

Note that the flag is not needed (it is set to 0) in this basic usage. The send_event() call places event Event on the queue with the listed information. (NB The ‘ ’ in e.g., cell[53].spike_event() is an operator used to access an object variable’s internal variables or functions.)

When t=Event.time, Event is delivered to e.g., synapse[5] of cell[78]. (For compartmental models the event goes to a particular synapse belonging to the cell. In the case of artificial cell models, the event goes directly to the cell itself.)

cell[78].synapse[5].read_Event()

cell[78].synapse[5].g +=Event.weight // augment conductance instantaneously

We have given here the simplest synaptic mechanism: augmenting the conductance directly. Typical synaptic algorithms will use a more complex algorithm.

The basic JitCon mechanism can be illustrated as follows. Here cell[53] is taken to be of type A.

cell[53].spike_event() // JitCon mechanism activated

seed_base=53 // cell[53].id= =53

// iterate through all discrete cell types, eg pyramidal, basket, stellate

for type=A, B, … {

 // divergence matrix precalculated from connection probabilities

 div=divergence[A][type] // cell[53] is of type A

 del=delay[A][type]

 for i=1 to div {

  seed=hash(seed_base,i)

  dest=random.integer(seed,min[type],max[type])

  delay=random.uniform(seed,(1−var)*del,(1+var)*del)

  new_event(0,dest,time+del,flag=53) // weight field empty

 }

}

Here random is an object that generates random values using a variety of distributions: random.integer(seed,min,max) generates integers in [min,max] and random.uniform(seed,min,max) produces a uniform deviate in [min,max]. Note that the cell IDs are generated in sequential order by type to facilitate retrieval by type. Note that the seed should be unique for each case. A hash function is used to produce the unique seed because e.g., a simple sum of ID+index would give the same seed for cell[53].id+2 as it would for cell[54].id+1. In practice, the algorithm is slightly more complicated in order to avoid double connects and self-connects.

Here again, after Event.delay time, Event is delivered.

cell[78].synapse[5].read_Event()

seed=hash(Event.flag,78,5) // unique seed for every connection

type=find_type(Event.flag) // generate presyn type from presyn ID

base_weight=weight[type][cell[78].type] // read weight[][] matrix

wt = random.uniform(seed,(1−wtvar)*base_weight,(1+wtvar)*base_weight)

cell[78].synapse[5].g +=wt

As with the delays and divergence matrices used presynaptically, the weight matrix is size N_type × N_type.

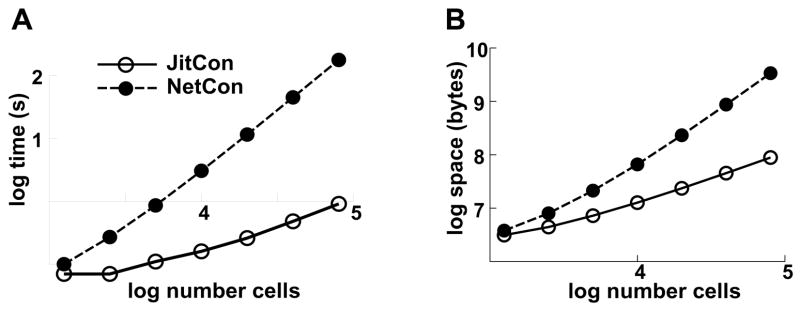
In the setup phase, JitCon provided substantial time and space savings relative to NEURON’s standard NetCon mechanism (Fig. 1). This is expected since JitCon need only set up cells (order n in time and space) and does not have to set up connections (order n² in time and space). The power-law scaling is evident in the linear regression for slopes of the lines on the log-log plot in Fig. 1B: 1.7 for NetCon and 0.8 for JitCon. Savings were particularly evident for larger simulations. With simulation size of 80,000 cells (10^4.9, rightmost point), setup time decreased 194-fold (176 s to 0.9 s) while job size at the end of setup was about 38-fold less (0.09 GB compared to 3.4 GB).

Fig. 1.

Time (A) and space (B) requirements for simulation setup are both significantly less for large network simulations. (All values are given as base 10 log.)

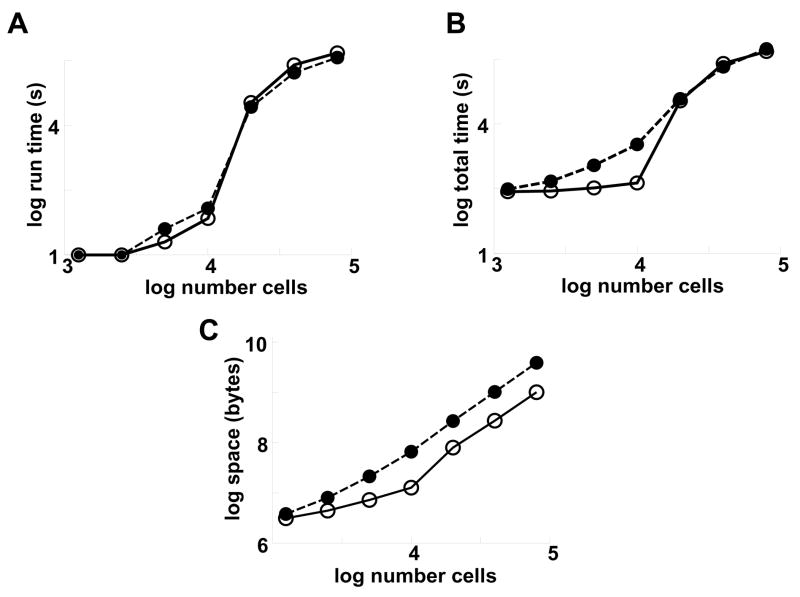
Setup speed-up was offset by runtime slow-down as the JitCon had to rely on the processor rather than on table look-up to find delays, weights and postsynaptic identifications during simulation (Fig. 2A). For these one-second simulations, setup time gain and run-time loss coincidentally balanced (Fig. 2B). With greater simulation-time, the NetCon simulation would show a total-time advantage. JitCon’s total space requirement was considerably less and scaled at a lower power: 1.7 for NetCon and 1.4 for JitCon (Fig. 2C). Looking only at the higher 3 scales, scaling was quite similar between the two methods: 1.9 for NetCon and 1.8 for JitCon. At the lower scales they differed substantially: 1.4 for NetCon and 0.7 for JitCon. The discontinuity between 10,000 and 20,000 cells seen here could also be seen in the run-times (Fig. 2A,B) and was due to activity dying out at the low scales but persisting at the high scales.

Fig. 2.

Changes in run and total time and space with JitCon. JitCon requires more run-time for large simulations (A). Changes in setup-time and run-time balance in these 1 s simulations, leading to comparable total times (B). Space saving increases with increased simulation size up to ~4-fold. (C). (NetCon: solid circles; JitCon: open circles)

With both NetCon and JitCon, memory grew with simulation size primarily because of queue growth, again particularly at the higher scales (Fig. 3). In addition to the queue, the JitCon case had some memory growth due to the transient creation of multiple divergence arrays as cells fired simultaneously. In the implementation tested, both NetCon and JitCon had the same queue storage requirements, although the JitCon queue item could be made slightly smaller since it need only hold an unsigned integer flag rather than floating-point weight pairs (for AMPA/NMDA or GABAA/GABAB). It should be noted that these epileptiform simulations have high rates of cell discharge (averaging 65 Hz in the 80,000 cell case). Such simulations feature large numbers of simultaneously firing cells that result in large numbers of events simultaneously placed on the queue, hence much higher queue demands than would be seen in simulations with lower firing rates. Although queue requirements are dependent on simulation pattern, they will be high for any simulation in which large numbers of cells spike together.

Fig. 3.

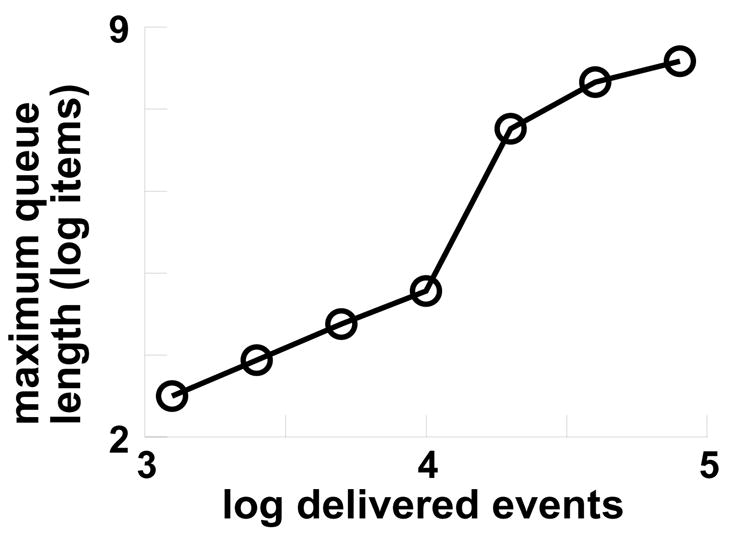
Large run-time space requirements are still a problem with JitCon due to large queue requirements.

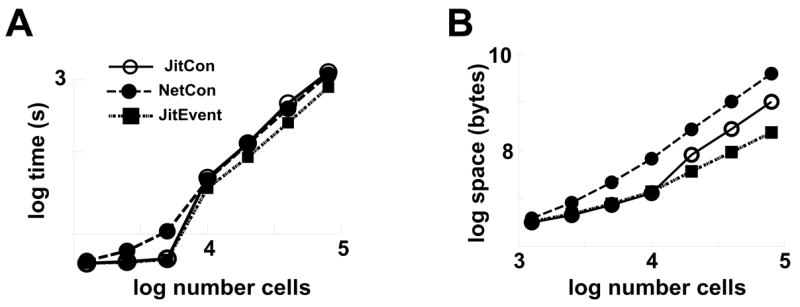
Queue-sparing simulations generally depend on restricting delay values (Makino 2003; Mattia & Del Giudice 2000; Watts 1994). NEURON already employs several queue sparing strategies (see Discussion). To reduce memory load in the present simulation, we implemented a JitEvent. This operated by always placing a single presynaptic cell callback event on the queue. When this event was delivered back to the presynaptic cell, the presynaptic cell directly called the postsynaptic cell with the event and placed another callback on the queue for delivery at t + (delay_n+1 − delay_n). This JitEvent system retained JIT weight calculation but dispensed with JIT postsynaptic identity determination and JIT delays. This compromise was made due to the computational intensity of the parallel sort on identities and delays by delay time required to provide the correct callback order.

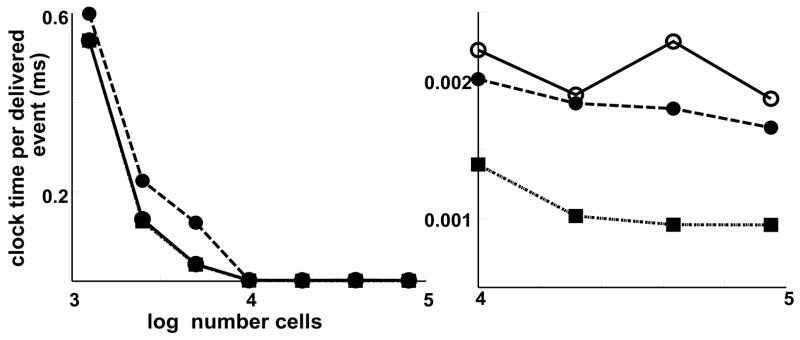
JitEvent was able to provide savings in both time and space compared to both NetCon and JitCon implementations (Fig. 4). At 80,000 cells, JitEvent produced a 40% speed-up (5.6 m vs. 9.1 m) and 17-fold space savings (0.23 GB vs. 3.9 GB) compared to NetCon. The excellent time profile of this implementation, even compared to the original NetCon system, was most apparent in the large-scale simulations (Fig. 5 right panel). The speed-up is likely secondary to maintaining a small queue, since a large queue cannot be kept in cache during insertion of new events.

Fig. 4.

JitEvent implementation (squares) produces total time (A) and space (B) savings compared to both NetCon (solid circles) and original JitCon (open circles). This simulation used only 3 delays per presynaptic cell – one for each type of postsynaptic cell.

Fig. 5.

Time per delivered event is much less using JitEvent (squares). (NetCon: solid circles; JitCon: open circles) Right panel shows high-scale detail.

Discussion

We have explored a variety of strategies to permit space savings in a large-scale event-driven network simulation. The central just-in-time strategy produced 3 types of values at run-time in lieu of storing them: synaptic delays, synaptic weights, postsynaptic target cell identifications. This JitCon implementation produced significant space savings. Although there was a run-time penalty, this was offset in our simulations by the savings in setup time. JitCon permitted us to run larger simulations than were otherwise feasible, but simulation size was still limited due to growth of the event queue. Therefore, a subsequent implementation utilized just-in-time generation of queued events (JitEvent). In this strategy, events were delivered back to the presynaptic cell instead of to the postsynaptic cell. The presynaptic cell was then responsible for postsynaptic cell activation and for placing another callback on the event queue. This implementation produced space and time savings compared to both JitCon and NetCon.

All simulations were implemented and run in NEURON. However, the implementation and run-time issues encountered will pertain to other event-driven simulators. Space-time trade-off is a general concept pertinent to all software, but particular issues come up in the context of neural simulation. There are static space requirements associated with connection storage (anatomical connection matrix) as well as dynamic space requirements associated with an event queue (dynamic connectivity). This dynamic connectivity means that simulation activity patterns will have a large influence on space and time requirements and thence on implementation choice.

In all types of simulation, there is a compromise made between level of simplification and computational tractability. In the present case, we avoided compartmental models and therefore avoided the overhead of numerical integration. These simulations used NEURON’s artificial cell event-driven mechanism. Such simulations can be embedded in or combined with detailed multi-compartment neuronal networks (Lytton & Hines 2004).

For the free-standing JitEvent implementation provided on ModelDB, the postsynaptic side uses the mechanism of NEURON’s ExpSyn, producing a conductance discontinuity with exponential conductance decay. Presynaptically, a ‘JitCon’ is inserted in the soma and receives spike input. It then places events on the queue via the callback mechanism described above.

In our final implementation, JitEvent, we stored identities of postsynaptic cells rather than regenerating these identities as needed. This retreat from the just-in-time strategy is part of a more general consideration: JIT identification of postsynaptic cells is reasonable as long as this identification is computationally cheap. In JitCon, identification was made cheap by use of an optimized routine to select random values from a uniform distribution (we used the MCell randomizer, one of those provided with the NEURON simulator; Bartol et al. 1991). In JitEvent, identification became expensive due to the need to sort postsynaptic cells by delay times. In general, identification will be expensive with any complex network connectivity: e.g., based on anatomical data, small-world designs or nested modules such as cortical columns. It is reasonable to assume that an algorithm which generates the full description of a network will occupy far less memory than the description itself: the Kolmogorov complexity of a network during a typical simulation is expected to be less than maximal. Hence the wider question is the extent to which the description can be compressed and the effects on performance of continual compression and decompression during a given simulation.

Queue design is central to any event-driven simulator. A variety of queue strategies can be utilized to saving time or space. NEURON itself utilizes several queue-sparing strategies. 1. If a presynaptic cell uses a single delay for projecting to n postsynaptic targets then only one event is placed on the queue instead of n events. This single event is then exploded into n events at the time of event delivery. 2. In NEURON’s parallel implementation, individual units have their own queues for self events (needed for artificial cells that must signal themselves for e.g., end of refractory period). This mechanism is being extended so that groups of cells, residing on a single CPU of a parallel supercomputer, will each have its own queue. 3. A binqueue is available when delays can all be expressed as integer multiples of one number, allowing them to be binned. Similarly, other simulators realize queue savings by restricting or discretizing delay values (Makino 2003; Mattia & Del Giudice 2000; Watts 1994). Other savings are possible when simulations are linear, allowing extrapolation of arbitrarily timed inputs to produce effects at fixed time steps (Morrison et al. 2007).

It is interesting to note how the space-time trade-off has shifted repeatedly over the years of computer history. Memory has always been the fixed constraint; one can always wait longer for the answer. A 1965 Digital Equipment Corporation PDP-8 had 4KB 12-bit words, requiring complex coding to fit in an operating system and an application program (see Lytton, 2002 for description of PDP-8 coding). By contrast, recent years have seen enormous expansion in both primary and secondary memory. This memory boon has encouraged the use of lookup tables, particularly for avoiding the slow calculation of transcendental values. In the present paper, we are shifting the space-time trade-off back towards time. This shift is likely to be a recurring feature as we move further into modeling systems that are hierarchically complex (Carlson & Doyle 2002; Csete & Doyle 2002).

In considering still larger networks, an additional dynamic that could be added would allow a set of neurons (a subnetwork corresponding to a brain area), to create and maintain its connectivity list in memory as long as that area is active and cede that memory when the subnetwork is less active. In this context, an additional direction for future development will be the incorporation of encapsulated artificial-cell networks as independent modules of compiled code (a mod file in NEURON). Such a network module could then be plugged in to other network modules or to a more detailed network that used compartmental models. Running such simulations on parallel supercomputers will permit ready execution of very-VLNNs of order 100 million neurons.