Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Oct 7.
Published in final edited form as: Ultrasound Med Biol. 2008 Mar 14;34(8):1317–1326. doi: 10.1016/j.ultrasmedbio.2008.01.006

ULTRASOUND SIMULATION IN THE DISTAL RADIUS USING CLINICAL HIGH-RESOLUTION PERIPHERAL-CT IMAGES

Vincent Le Floch *,†, Donald J McMahon ‡, Gangming Luo †,§,, Adi Cohen ‡, Jonathan J Kaufman †,∥, Elizabeth Shane ‡, Robert S Siffert ∥
PMCID: PMC2562908  NIHMSID: NIHMS48351  PMID: 18343017

Abstract

The overall objective of this research is to develop an ultrasonic method for noninvasive assessment of the distal radius. The specific objective of this study was to examine the propagation of ultrasound through the distal radius and determine the relationships between bone mass and architecture and ultrasound parameters. Twenty-six high-resolution peripheral-CT clinical images were obtained from a set of subjects that were part of a larger study on secondary osteoporosis. A single midsection binary slice from each image was selected and used in the two-dimensional (2D) simulation of an ultrasound wave propagating from the anterior to the posterior surfaces of each radius. Mass and architectural parameters associated with each radius, including total (trabecular and cortical) bone mass, trabecular volume fraction, trabecular number and trabecular thickness were computed. Ultrasound parameters, including net time delay (NTD), broadband ultrasound attenuation (BUA) and ultrasound velocity (UV) were also evaluated. Significant correlations were found between NTD and total bone mass (R2 = 0.92, p < 0.001), BUA and trabecular number (R2 = 0.78, p < 0.01) and UV and trabecular bone volume fraction (R2 = 0.82, p < 0.01). There was only weak, statistically insignificant correlation (R2 < 0.14, p = 0.21) found between trabecular thickness and any of the ultrasound parameters. The study shows that ultrasound measurements are correlated with bone mass and architecture at the distal radius and, thus, ultrasound may prove useful as a method for noninvasive assessment of osteoporosis and fracture risk.

Keywords: Osteoporosis, Ultrasound, Radius, Bone mass, Density, Net time delay, BUA, Peripheral-CT, Velocity

Osteoporosis is a significant health problem affecting more than 20 million people in the United States and more than 200 million worldwide (Anonymous 2001). Osteoporosis is defined as the loss of bone mass with a concomitant disruption in microarchitecture, leading to an increased risk of fracture (Kanis 2002). The most common osteoporotic fractures occur at the wrist, spine and hip. Hip fractures have a particularly negative impact on morbidity. Approximately 50% of those individuals suffering a hip fracture never live independently again (Miller 1978). Currently, there are about 200,000 hip fractures yearly in the U.S. and approximately one million worldwide (Anonymous 2001; Melton 1988). The aging of the worldwide population is expected to increase the incidence of hip and other fractures as well (Anonymous 2001).

The primary method for diagnosing osteoporosis and associated fracture risk relies on bone densitometry to measure bone mass (Kaufman and Siffert 2001). The use of bone mass is based on the well-established thesis that bone strength is strongly related to the amount of bone material present and that a stronger bone in a given individual is associated generally with a lower fracture risk (Johnell et al. 2005). Radiologic densitometry, which measures the (areal) bone mineral density (BMD) at a given site (e.g., hip, spine, forearm) is currently the accepted “gold standard” indicator of bone strength and fracture risk (Johnell et al. 2005; Blake and Fogelman 2003). Clinically, this is often done using dual energy X-ray absorptiometry (DXA), which measures the BMD in units of g/cm2 (Blake and Fogelman 2003). Recently, high resolution peripheral-CT imaging has become available for clinical research studies and has led to renewed interest in the distal radius for a better understanding of the relationship between bone structure and fracture risk.

Notwithstanding the fact that X-ray methods are useful in assessing bone mass and fracture risk, osteoporosis remains one of the largest undiagnosed and under-diagnosed diseases in the world today (Anonymous 2001). Among the reasons for this is that densitometry (i.e., DXA) is not a standard tool in a primary care physician's office. This is due to its expense and inconvenience, and reticence among patients concerning X-ray exposure, particularly in young adults and children.

Ultrasound has been proposed as an alternative to DXA for a number of reasons. These include the facts that it is nonionizing, relatively inexpensive and simple to use. Moreover, since ultrasound is a mechanical wave and interacts with bone in a fundamentally different manner than X-rays, it may be able to provide information on additional components of bone strength, notably its trabecular architecture (Siffert and Kaufman 2007; Kaufman and Einhorn 1993; Hosokawa 2005; Kaufman et al. 2008a).

The propagation of ultrasound through bone is a complex phenomenon, for which few analytic characterizations are available. In the past several years, computer simulation has emerged as an extremely useful tool (Kaufman et al. 2008a, 2008b; Haïat et al. 2007; Protopappas et al. 2006; Hosokawa 2005; Bossy et al. 2005; Luo et al. 1999). Simulation affords the user with the ability to address a whole host of questions which, as pointed out, have no analytic solution and for which the experimental setting may be very difficult to carry out.

The overall objective of this research is to develop an ultrasonic method for noninvasive assessment of the distal radius. The specific objective of this study was to examine the propagation of ultrasound through the distal radius and determine the relationships between bone mass and architecture on the one hand and ultrasound parameters on the other.

MATERIALS AND METHODS

Distal Radius Images

Twenty-six three-dimensional (3D) images of the distal radius were randomly selected from a larger set of studies on secondary osteoporosis. In this study, no clinical data were available on the subjects from which the set of images was obtained. The images were made with a high resolution peripheral-CT machine (XtremeCT, SCANCO Medical AG, Bassersdorf, Switzerland). The resolution is isotropic at 82 μm and the machine automatically thresholds the image into a binary (bone or soft tissue) structure. A single 2D slice from the center of the region-of-interest (ROI) of each of the 26 3D data sets was extracted. Figs. 1a, b and c, respectively, show a pilot view of the region of the radius imaged by the machine, a 2D transverse section showing the ulna and the radius and surrounding soft tissue and two typical 2D segmented (i.e., binary) slices used as models for simulating ultrasound propagation through the radius, as described in the next section. As may be seen in Fig. 1c, there are significant amounts of both cortical and trabecular bone in this portion of the distal radius. The ROI is located using the antero-posterior scout view (Fig. 1a). First, a reference line is manually placed at the endplate of the radius. The first CT slice (of the total of 110) is 9.5 mm proximal to the reference line (Boutroy et al. 2005). Thus, each central 2D slice of a given subject used in this study was 1.4 cm from the radius endplate.

Fig. 1.

Fig. 1

Open in a new tab

(a) Scanned region of the forearm showing the distal radius and ulna by the peripheral-CT machine. The region where the CT-slices are acquired is between the two dashed lines, the more distal one being 9.5 mm from the endplate of the radius (indicated by the solid line in the figure). The distance between the dashed lines is 9.020 mm. (Photograph courtesy of SCANCO Medical AG, Bassersdorf, Switzerland.) (b) Two-dimensional cross-section of a forearm showing an ulna and a radius. The thin curved grey line at the bottom of the image is a plastic holder into which the forearm is placed. (Photograph courtesy of SCANCO Medical AG, Bassersdorf, Switzerland.) (c) Binary slices of two distal radii used in the ultrasound simulations. The sample on the left (subject no. 654) has a total bone mass of 6.84 mm while the one on the right (subject no. 301) has a total bone mass of 3.10 mm. The overall size is a square 4 cm on a side.

Each 2D image was processed to obtain a set of mass and architectural features associated with each radius. To do this, a central location of 8 mm in width was analyzed corresponding to the region to be interrogated by the ultrasound wave (propagation from left to right) (Fig. 1c). The 8 mm size is chosen because it corresponds to the size of the source and receiver ultrasound transducers (discussed in the next section) and because the irregular geometry of the radius make “whole bone” interrogation problematic at least in part because of phase aberrations. Over this 8 mm wide section, the bone mass (characterized by an average thickness in millimeters and including both the cortical and trabecular portions), the average trabecular thickness, the average trabecular number, the anterior and posterior cortical thicknesses and the bone volume fraction (associated with the trabecular only portion) were all evaluated. The bone mass was computed by counting up the total number of bone pixels for each image line within the 8 mm region-of-interest, averaging the results for all (97) lines along the antero-posterior direction and finally multiplying by the resolution (0.82 mm/pixel) to obtain the bone mass in millimeters. Note that this representation of mass in terms of length can also be converted to an (areal) bone mineral density value as used in DXA by multiplying by the volumetric density value of fully mineralized cortical bone, given by ρc = 1.20 g/cm3 (Attix 1986). The trabecular thickness was computed by computing the set of trabecular thicknesses (defined as the number of bone pixels intercepted by each of the 97 image lines) and evaluating the mean. Trabecular number was computed by counting the number of trabeculae (defined as a region containing at least one bone pixel and surrounded by marrow on both sides) in each of the 97 image lines and evaluating the mean. The (anterior and posterior) cortical thickness parameters were computed by averaging the thickness of each of the 97 lines length of interception with the (anterior and posterior) cortical bone. Finally, the bone volume fraction of the trabecular portion was computed by adding up the total number of bone pixels with the ROI (excluding the cortical bone) and dividing by the total number of pixels within the same region. All of the 2D images were processed to obtain the set of associated bone parameters (Image Processing Toolbox, Matlab, The Mathworks, Inc., Natick, MA, USA). The summary statistics for the 26 slices are provided in Table 1. Note that the bone mass ranged from about 3.1 mm (0.37 g/cm2) to 6.8 mm (0.82 g/cm2), representing more than a 100% variation.

Table 1.

Characteristics of bone mass and architecture for the ultrasound simulation study

Characteristics Mean Standard deviation Range
Bone mass (mm) 5.06 1.33 3.10−6.83
Bone mass (g/cm2) 0.61 0.16 0.37−0.82
Anterior cortical thickness (mm) 1.17 0.33 0.74−1.66
Posterior cortical thickness (mm) 1.19 0.360 0.88−1.74
Bone volume fraction 0.24 0.066 0.12−0.32
Trabecular number 10.5 4.54 4.34−21.8
Trabecular thickness (mm) 0.27 0.072 0.16−0.34
Open in a new tab

Ultrasound simulations and parameters

The fundamental equation characterizing the 3D propagation of ultrasound in a medium comprised of isotropic materials having viscous loss is provided by the following viscoelastic wave equation (Auld 1990):

ρ∂2μ∂t2=(μ+η∂∂t)∇2μ+(λ+μ+ξ∂∂t+n∂3∂t)∇∇⋅μ (1)

In eqn 1, u = u (x, y, z, t) is the time-varying displacement vector which is a function of the Cartesian coordinates x, y and z, and has scalar components ux, uy and uz, respectively, ρ is the mass density, λ and μ are the first and second Lamé constants, respectively, η and ξ are the first and second viscosities, respectively and t is time. Equation 1 models only the linear propagation of ultrasound in a medium. Equation 1 must be solved with respect to the boundary conditions of a given model, which also include the input source(s) that have prescribed time-dependent displacements (or stresses) at a given location, as well as a set of initial conditions. For a heterogeneous propagation medium like bone, it should be noted that the material parameters (i.e., ρ, λ, μ, η and ξ) are implicit functions of the spatial coordinates x, y and z.

A finite difference time domain (FDTD) method was used to numerically solve the viscoelastic wave equation of eqn 1. A continuous stress and displacement formulation for the lossless case that imposes continuity of stresses and displacements across boundaries of the grid elements has previously been presented by (Delsanto et al. 1994) and (Schechter et al. 1994). This same formulation has been extended to the lossy case by (Luo et al. 1999; Kaufman et al. 2008a) and has also been implemented in commercial software (Wave 2000, CyberLogic, Inc., New York, NY, USA). This software was used to produce all of the simulations in this study. The material constants used for bone were ρb = 1850 kg/m3, λb = 9306 MPa, μb = 3127 MPa, η = 40 Pa · s and ξ = 0.1 Pa · s. This produced longitudinal and shear (phase) velocities at 1.5 MHz of 2901 m/s and 1307 m/s and differential specific attenuations of 6.09 dB cm−1 MHz−1 and 49.7 dB cm−1 MHz−1, respectively. The value of shear attenuation in bone has the most degree of uncertainty as reported in the literature; for example Goss et al. (1980) noted experimental values of 7.6 dB cm−1 MHz−1 while a more recent article by White et al. (2006) reported (at 0.84 MHz) that shear attenuation was 17 dBMHz−1, more than four times the value of longitudinal attenuation. Therefore, the higher value of shear attenuation used in this study is felt to be reasonable because of the higher center frequency (1.5 MHz) used. The material in the marrow spaces of the tissue was assumed to be fresh blood. For this case, ρm = 1055 kg/m3, λm = 2634 MPa, μm = 0 MPa, η = 0.1 Pa · s and ξ = 0 Pa · s. This produced longitudinal and shear (phase) velocities at 1.5 MHz of 1580 m/s and 42.3 m/s and differential specific attenuations of 0.16 dB cm−1 MHz−1 and 19367 dB cm−1 MHz−1, respectively (Goss et al. 1968, 1980; Selfridge 1985).

A set of 2D ultrasound simulations through each of the 26 bone slices was then carried out. Each simulation used the same 1.5 MHz Gaussian pulse source waveform, shown in Fig. 2. The 1.5 MHz frequency was chosen as a compromise for extracting as much information as possible (higher frequency and bandwidth) and having a low enough frequency to make propagation through trabecular bone in a clinical setting have sufficient signal-to-noise ratio without exceeding exposure safety levels. An 8 mm long transducer located on the anterior portion of the forearm image provided the input signal and an 8 mm long transducer in a through-transmission configuration at the posterior portion of the forearm image received the signal which had propagated through the radius. These are not “transducers” in the practical sense; rather the source is a time-dependent boundary condition on the displacement of the boundary over the 8 mm length, while the receiver is a “noncontact” measurement of the displacement of the boundary averaged over the 8 mm length. Figure 3 shows the configuration of the source, receiver and radius (surrounded by soft tissue) for a typical sample. A set of three images showing the propagating wave corresponding to three instants in time is shown in Fig. 4. The grey level displayed is proportional to the magnitude of the ultrasound-induced displacement at that location; also shown are the interfaces (as a bright grey level) between bone and soft tissue (or marrow).

Fig. 2.

Fig. 2

Open in a new tab

A 1.5 MHz Gaussian pulse source waveform used for all the ultrasound simulations.

Fig. 3.

Fig. 3

Open in a new tab

A schematic diagram showing the source, receiver, and bone slice in a through-transmission configuration. As may be seen, propagation of the wave travels from the source to the receiver, from left to right.

Fig. 4.

Fig. 4

Open in a new tab

Propagating wave through a slice from subject no. 132 (volume fraction = 0.17) showing snapshots of displacement magnitude at times (a) 10.51 μs; (b) 14.07 μs; and (c) 19.60 μs. In (a), the diffraction effect due to the finite size of the source can be seen by the trailing “edge wave.” In (b) and (c), in addition to the wavefront that propagates through the bone, there is also a large reflected component (from the near cortical surface) that is propagating from right to left and back to the source. This article does not examine this wave or its potential for containing useful information.

The simulated ultrasound waveforms were processed to compute a set of three ultrasound parameters associated with each 2D slice. The parameters are the net time delay (NTD), broadband ultrasound attenuation (BUA) and ultrasound velocity (UV). The latter two parameters have been well studied and reported in the literature; see for example (Langton et al. 1984; Kaufman and Einhorn 1993; Laugier 2008; Langton and Njeh 2008). In brief, the BUA was computed as the slope (estimated with a linear least squares curve fit) of the attenuation as a function of frequency, over the frequency range 600 kHz–1.2 MHz. The attenuation was obtained as the negative logarithm of the magnitude of the transfer function, which is the ratio of the Fourier transform of the received signal to the Fourier transform of the source waveform. The ultrasound velocity was computed by dividing the arrival time of the ultrasound waveform by the distance between the source and receiver. The arrival time (both for computing velocity and also for computing net time delay), of the ultrasound signal was defined as the time at which the first negative peak occurred. A less well-studied parameter is the NTD. The NTD is defined to be the difference in travel times of waveforms with and without the radius in the path, i.e., a soft tissue only path and a path that contains both soft tissue and the radius. The NTD has been shown analytically and experimentally to be a measure of the overall mass (i.e., including both cortical and trabecular contributions) of bone through which the ultrasound wave has propagated (Kaufman et al. 2007, 2008a).

RESULTS

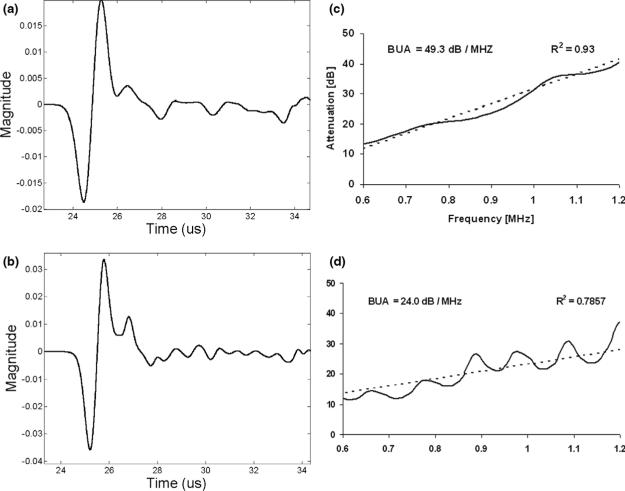
Two typical receiver waveforms associated with two subjects (no. 654 and no. 301) are shown in Fig. 5 (corresponding to the same subjects whose radial slices are shown in Fig. 1c). As may be seen, the signal for subject no. 654 (with volume fraction = 0.32) is much more attenuated than the signal for subject no. 301 (with volume fraction = 0.12). As may also be apparent, the latter signal has more high frequency content than the former; this is due to the higher degree of scattering present in the specimen with larger volume fraction which preferentially removes the higher frequency content of the propagating waveform (Serpe and Rho 1996; Hodgskinson et al. 1996; Bossy et al. 2005; Kaufman et al. 2008a). Also shown in Fig. 5c and d are the associated attenuation functions as a function of frequency, together with linear least squares curve fits (dashed lines), for subject radius no. 654 and no. 301, respectively. As may be seen, there is moderate degree of nonlinear behavior as manifested in the periodic-type interference. This is likely due to the presence of multi-path interference, as is apparent in the time domain signals of Fig. 5a and b. Nevertheless, the lowest R2 value for the least square curve fit for the 26 subjects was 0.74 and, therefore, good estimates of BUA were able to be obtained.

Fig. 5.

Fig. 5

Open in a new tab

Receiver signals for (a) radius no. 654 (volume fraction = 0.32) and (b) radius no. 301 (volume fraction = 0.12) and associated attenuation functions as a function of frequency (c) Broadband ultrasound attenuation (BUA) = 49.3 dB/MHz for radius no. 654 and (d) BUA = 24.0 dB/MHz for radius no. 301.

Table 2 displays the summary statistics for the ultrasound parameters. A plot of NTD versus total bone mass for the simulated data is shown in Fig. 6. As may be seen, there is a close linear correlation (R2 = 0.92) between the total bone mass and the NTD. Note that total bone mass is measured in terms of millimeters of bone; it could be equated to the more common expression of clinical bone mass by multiplying total bone mass in millimeters by volumetric density of cortical bone (nominally equal to 1.20 g/cm3) and expressing total bone mass in terms of areal bone mass in g/cm2. However, we prefer to express “total bone mass” in terms of “bone thickness.” Figure 7 shows the relationship between tra- becular number and BUA. The best fit was obtained with a quadratic relationship and produced an R2 value of 0.78. A plot of UV versus bone volume fraction is shown in Fig. 8; this produced an R2 value of 0.82.

Table 2.

Ultrasound parameters for the simulation study

Ultrasound parameters Mean Standard deviation Range
NTD (μs) 1.59 0.26 1.13−2.12
BUA (dB/MHz) 34.5 9.1 6.77−46.7
UV (m/s) 1688 51 1599−1803
Open in a new tab

NTD = net delay time; BUA = broadband ultrasound attenuation; UV = ultrasound velocity.

Fig. 6.

Fig. 6

Open in a new tab

Plot of net time delay (NTD) vs. total bone mass (R2 = 0.92, p < 0.001) for the 26 subjects.

Fig. 7.

Fig. 7

Open in a new tab

Plot of broadband ultrasound attenuation (BUA) vs. trabecular number (R2 = 0.78, p < 0.01) for the 26 subjects.

Fig. 8.

Fig. 8

Open in a new tab

Plot of ultrasound velocity (UV) vs. volume fraction (R2 = 0.82, p < 0.01) for the 26 subjects.

DISCUSSION AND CONCLUSION

The simulation results obtained here demonstrate that an ultrasound signal that has propagated through a distal radius contains significant information on its mass and architecture. In particular, the NTD, BUA and UV were shown to be correlated with bone mass, trabecular number and volume fraction, respectively. Of particular interest is the fact that the BUA was correlated with trabecular number. This may be significant since the strength of trabecular bone can be related to not only its mass (as represented through the volume fraction, for example) but to how that mass is organized. Thus, two structures with similar volume fraction but significantly distinct trabecular number may have very different mechanical behavior (Goulet et al. 1994; Siffert et al. 1996; Nazarian et al. 2006). In this context, it is interesting to see how trabecular number and volume fraction are related in the 26 radial slices of this study (Fig. 9). As may be seen, there are many subjects with similar volume fractions but with large variations in trabecular number. Conversely, there are many subjects with similar trabecular number but with large variations in volume fraction. In addition, since both cortical and trabecular bone contribute to the strength of the distal radius (Ashe et al. 2006), the three ultrasound parameters studied here may be able to estimate bone fragility better than a method which combines into a single measurement the cortical and trabecular masses (e.g., DXA). For example, Fig. 10 displays the amount of cortical bone as a percentage of total bone mass. As may be seen there is a significant variation (∼2x) in the percentage of cortical bone for the 26 subjects, ranging from about 35% to 70% of total bone mass. Therefore, ultrasound parameters—through their respective associations with total bone mass, trabecular number and trabecular volume fraction—may be able to identify those individuals at increased risk of fracture (Melton et al. 2007).

Fig. 9.

Fig. 9

Open in a new tab

Plot of trabecular number vs. volume fraction (R2 = 0.26, p = 0.3) for the 26 subjects.

Fig. 10.

Fig. 10

Open in a new tab

Plot of the amount of cortical bone as a percentage of total bone mass for the 26 subjects.

An interesting finding is the apparent nonlinear behavior of BUA with respect to trabecular number. BUA is also known to exhibit nonlinear behavior with respect to porosity variations over a sufficiently wide range (Serpe and Rho 1996; Hodgskinson et al. 1996). Whether these two findings are related remains to be elucidated. It will also be important to explore further the relationship of trabecular number to attenuation. The trabecular number as typically reported is normalized by length and so has units of 1/mm for example (Boutroy et al. 2005). Although we have not presented the data, the correlation of BUA to normalized trabecular number was much lower. This was true (that is, much lower correlations were observed) even when BUA was normalized by length (often denoted by nBUA). Indeed, the highest and most significant correlation was obtained between BUA and un-normalized trabecular number. It will be of interest to study this important aspect in future studies.

In this context, the utility of ultrasound simulation methods is clear. By linking them with clinical high resolution images of the distal radius (and this is, we believe, the first time such a study has been reported), it may be possible to identify those ultrasound parameters most correlated with osteoporotic fracture risk. This can be accomplished by using simulation to investigate a large number of signal processing methods, transducer configurations and a whole host of system parameters (e.g., frequency, focusing) that cannot be studied analytically or clinically (Kaufman et al. 2008a). It should also be noted that changes at the distal radius may be the first signs of osteoporosis, thus, increasing the value of assessment at this site (Mallmin and Ljunghall 1994; Cuddihy et al. 2002).

There are several limitations of this study that should be noted. First, the simulations were carried out in 2D and would eventually need to be validated by 3D simulations. However, another study (at the 1/3rd radius site) used 2D simulations that were validated through measurements on rods and tubes (Kaufman et al. 2008b) and, thus, it is expected that the simulations presented here would also prove to be valid as well. We have also used 2D assessment of trabecular structure; this is necessitated of course by the 2D slices utilized but it should be noted that these 2D histomorphometric features are well correlated to the 3D structure and properties of bone (Dalle Carbonare et al. 2005; Feldkamp et al. 1989).

An important consideration is that related to the artifact induced by volume averaging. The isotropic resolution of the CT device used in this study is 82 μm, which is slightly lower but of the order of magnitude of the typical size of a trabecula. This will inevitably lead to errors in the estimates of the bone parameters (i.e., bone mass, trabecular thickness, trabecular number, anterior and posterior cortical thicknesses and bone volume fraction). Further studies should be done to determine if other algorithms (e.g., a “thickness-independent algorithm (Boutroy et al. 2005)) for estimating the bone parameters would significantly change the results obtained. Even more importantly, the present study will need to be validated by in vitro and clinical studies as well.

In this regard, an in vitro study that compares actual measurements with that obtained with simulated data should be carried out in future studies. Although ultrasound simulations have been validated in terms of experimental measurements on trabecular bone specimens, this was done for much higher imaging resolutions (∼23 μm) where volume averaging was much less of an issue than it is in this study (Bossy et al. 2007). In addition, to translate this research into clinical practice there will be a number of practical issues to deal with, such as repositioning and reproducibility, acoustic coupling and soft tissue geometry. These and other experimental aspects will all have to be addressed to make the methods described here have clinical utility.

This study should also be extended to include clinical data, particularly data relating to the incidence of low-trauma fracture. As the present study is the first of its kind (namely the use of clinical high resolution peripheral-CT images as the basis for ultrasound simulations), its main purpose was to demonstrate feasibility of the proposed techniques and to determine if significant correlations exist between ultrasound parameters and mass and architecture of radial bones. Clearly, however, subsequent studies will need to incorporate clinical variates (e.g., age, sex, disease states, fracture history) into the analysis (Sornay-Rendu et al. 2007; Boutry et al. 2005; Melton et al. 2007). In addition, other architectural aspects such as connectivity and anisotropy should also be considered in future studies. Indeed the ability to carry out such studies is what makes the method potentially so useful: the ability to simulate ultrasound through clinical images and make side-by-side comparisons with clinical outcomes.

In conclusion, this simulation study has demonstrated the ability of ultrasound to noninvasively estimate the overall bone mass, trabecular number and trabecular bone volume fraction at the distal radius and with additional research may ultimately prove useful as a simple, noninvasive technique to estimate osteoporotic fracture risk.

Acknowledgments

The project described was supported by Grant Numbers R44AR054307 and R01AR049896 from the National Institute of Arthritis and Musculoskeletal and Skin Diseases and by The Carroll and Milton Petrie Foundation. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Arthritis and Musculoskeletal and Skin Diseases or the National Institutes of Health.

REFERENCES

  1. Anonymous Osteoporosis prevention, diagnosis, and therapy. JAMA. 2001;285:785–795. doi: 10.1001/jama.285.6.785. [DOI] [PubMed] [Google Scholar]
  2. Ashe MC, Khan KM, Kontulainen SA, Guy P, Liu D, Beck TJ, McKay HA. Accuracy of pQCT for evaluating the aged human radius: An ashing, histomorphometry and failure load investigation. Osteoporos Int. 2006;17:1241–1251. doi: 10.1007/s00198-006-0110-5. [DOI] [PubMed] [Google Scholar]
  3. Attix FH. Introduction to radiological physics and radiation dosimetry. Wiley-Interscience; New York, NY: 1986. p. 531. [Google Scholar]
  4. Auld BA. Acoustic fields and waves in solids. 2nd ed. Vol. 1. Krieger Publishing Company; Malabar, FL: 1990. 1990. [Google Scholar]
  5. Blake GM, Fogelman I. Review - DXA scanning and its interpretation in osteoporosis. Hosp Med. 2003;64:521–525. doi: 10.12968/hosp.2003.64.9.2243. [DOI] [PubMed] [Google Scholar]
  6. Bossy E, Laugier P, Peyrin F, Padilla F. Attenuation in trabecular bone: A comparison between numerical simulation and experimental results in human femur. J Acoust Soc Am. 2007;122:2469–2475. doi: 10.1121/1.2766779. [DOI] [PubMed] [Google Scholar]
  7. Bossy E, Padilla F, Peyrin F, Laugier P. Three-dimensional simulation of ultrasound propagation through trabecular bone structures measured by synchrotron microtomography. Phys Med Biol. 2005;50:5545–5556. doi: 10.1088/0031-9155/50/23/009. [DOI] [PubMed] [Google Scholar]
  8. Boutroy S, Bouxsein ML, Munoz F, Delmas PD. In vivo assessment of trabecular bone microarchitecture by high resolution peripheral quantitative computed tomography. J Clin Endocrin Metab. 2005;90:6508–6515. doi: 10.1210/jc.2005-1258. [DOI] [PubMed] [Google Scholar]
  9. Cuddihy M-T, Gabriel SE, Crowson CS, Atkinson EJ, Tabini C, O'Fallon WM, Melton LJ., III Osteoporosis intervention following distal forearm fractures: A missed opportunity? Arch Intern Med. 2002;162:421–426. doi: 10.1001/archinte.162.4.421. [DOI] [PubMed] [Google Scholar]
  10. Dalle Carbonare L, Valenti MT, Bertoldo F, Zanatta M, Zenari S, Realdi G, Lo Cascio V, Giannini S. Bone microarchitecture evaluated by histomorphometry. Micron. 2005;36:609–616. doi: 10.1016/j.micron.2005.07.007. [DOI] [PubMed] [Google Scholar]
  11. Delsanto PP, Schechter RS, Chaslekis HH, Mignogna RB, Kline R. Connection machine simulation of ultrasonic wave propagation in materials. II: The two-dimensional case. Wave Motion. 1994;20:295–314. [Google Scholar]
  12. Feldkamp LA, Goldstein SA, Parfitt AM, Jesion G, Kleerekoper M. The direct examination of three-dimensional bone architecture in vitro by computed tomography. J Bone Miner Res. 1989;4:3–11. doi: 10.1002/jbmr.5650040103. [DOI] [PubMed] [Google Scholar]
  13. Goss SA, Johnston RL, Dunn F. Comprehensive compilation of empirical ultrasonic properties of mammalian tissues. J Acoust Soc Am. 1968;64:423–457. doi: 10.1121/1.382016. [DOI] [PubMed] [Google Scholar]
  14. Goss SA, Johnston RL, Dunn F. Compilation of empirical ultrasonic properties of mammalian tissues. II. J Acoust Soc Am. 1980;68:93–108. doi: 10.1121/1.384509. [DOI] [PubMed] [Google Scholar]
  15. Goulet RW, Goldstein SA, Ciarelli MJ, Kuhn JL, Brown MB, Feldkamp LA. The relationship between the structural and orthogonal compressive properties of trabecular bone. J Biomech. 1994;21:375–389. doi: 10.1016/0021-9290(94)90014-0. [DOI] [PubMed] [Google Scholar]
  16. Haïat G, Padilla F, Peyrin F, Laugier P. Variation of ultrasonic properties with microstructure and material properties of trabecular bone: a 3D model simulation. J Bone Miner Res. 2007;22:665–674. doi: 10.1359/jbmr.070209. [DOI] [PubMed] [Google Scholar]
  17. Hodgskinson R, Njeh CF, Whitehead MA, Langton CM. The nonlinear relationship between BUA and porosity in cancellous bone. Phys Med Biol. 1996;41:2411–2420. doi: 10.1088/0031-9155/41/11/012. [DOI] [PubMed] [Google Scholar]
  18. Hosokawa A. Simulation of ultrasound propagation through bovine cancellous bone using elastic and Biot's finite-difference time-domain methods. J Acoust Soc Am. 2005;118:1782–1789. doi: 10.1121/1.2000767. [DOI] [PubMed] [Google Scholar]
  19. Johnell O, Kanis JA, Oden A, Johansson H, De Laet C, Delmas P, Eisman JA, Fujiwara S, Kroger H, Mellstrom D, Meunier PJ, Melton LJ, 3rd, O'Neill T, Pols H, Reeve J, Silman A, Tenenhouse A. Predictive value of BMD for hip and other fractures. J Bone Miner Res. 2005;20:1185–1194. doi: 10.1359/JBMR.050304. [DOI] [PubMed] [Google Scholar]
  20. Kanis J. Diagnosis of osteoporosis and assessment of fracture risk. Lancet. 2002;359:1929–1936. doi: 10.1016/S0140-6736(02)08761-5. [DOI] [PubMed] [Google Scholar]
  21. Kaufman JJ, Einhorn TE. Review - Ultrasound Assessment of Bone. J Bone Miner Res. 1993;8:517–525. doi: 10.1002/jbmr.5650080502. [DOI] [PubMed] [Google Scholar]
  22. Kaufman JJ, Siffert RS. Noninvasive assessment of bone integrity. In: Cowin S, editor. Bone mechanics handbook. Vol. 34. CRC Press; Boca Raton, FL: 2001. pp. 1–34.25. [Google Scholar]
  23. Kaufman JJ, Luo GM, Siffert RS. A portable real-time bone densitometer. Ultrasound Med Biol. 2007;33:1445–1452. doi: 10.1016/j.ultrasmedbio.2007.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kaufman JJ, Luo GM, Siffert RS. Ultrasound simulation in bone. IEEE Ultrason Ferroelectr Freq Control. 2008a doi: 10.1109/TUFFC.2008.784. in press. [DOI] [PubMed] [Google Scholar]
  25. Kaufman JJ, Luo GM, Blazy B, Siffert RS. Quantitative ultrasound assessment of tubes and rods: Comparison of empirical and computational results. In: Akiyama I, editor. Acoustical imaging. Vol. 29. Springer; New York, NY: 2008b. in press. [Google Scholar]
  26. Langton CM, Njeh CF. The measurement of broadband ultrasonic attenuation in cancellous bone: A review of the science and technology. IEEE Ultrason Ferroelectr Freq Control. 2008 doi: 10.1109/TUFFC.2008.831. in press. [DOI] [PubMed] [Google Scholar]
  27. Langton CM, Palmer SB, Porter RW. The measurement of broadband ultrasound attenuation in cancellous bone. Eng Med. 1984;13:89–91. doi: 10.1243/emed_jour_1984_013_022_02. [DOI] [PubMed] [Google Scholar]
  28. Laugier P. Instrumentation for in vivo ultrasonic characterization of bone strength. IEEE Ultrason Ferroelectr Freq Control. 2008 doi: 10.1109/TUFFC.2008.782. in press. [DOI] [PubMed] [Google Scholar]
  29. Luo G, Kaufman JJ, Chiabrera A, Bianco B, Kinney JH, Haupt D, Ryaby JT, Siffert RS. Computational methods for ultrasonic bone assessment. Ultrasound Med Biol. 1999;25:823–830. doi: 10.1016/s0301-5629(99)00026-5. [DOI] [PubMed] [Google Scholar]
  30. Mallmin H, Ljunghall S. Distal radius fracture is an early sign of general osteoporosis: Bone mass measurements in a population-based study. Osteoporosis Int. 1994;4:357–361. doi: 10.1007/BF01622198. [DOI] [PubMed] [Google Scholar]
  31. Melton LJ, III, Riggs BL, van Lenthe GH, Achenbach SJ, Müller R, Bouxsein ML, Amin S, Atkinson EJ, Khosla S. Contribution of in vivo structural measurements and load/strength ratios to the determination of forearm fracture risk in postmenopausal women. J Bone Miner Res. 2007;22:1442–1448. doi: 10.1359/jbmr.070514. [DOI] [PubMed] [Google Scholar]
  32. Melton LJ., III . Epidemiology of fractures. In: Riggs BL, Melton LJ III, editors. Osteoporosis: etiology, diagnosis, and management. Raven Press; New York, NY: 1988. pp. 133–154. [Google Scholar]
  33. Miller CW. Survival and ambulation following hip fracture. J Bone Joint Surg. 1978;60A:930–934. [PubMed] [Google Scholar]
  34. Nazarian A, Stauber M, Zurakowski D, Snyder BD, Müller R. The interaction of microstructure and volume fraction in predicting failure in cancellous bone. Bone. 2006;39:1196–1202. doi: 10.1016/j.bone.2006.06.013. [DOI] [PubMed] [Google Scholar]
  35. Protopappas VC, Fotiadis DI, Malizos KN. Guided ultrasound wave propagation in intact and healing long bones. Ultrasound Med Biol. 2006;32:693–708. doi: 10.1016/j.ultrasmedbio.2006.02.001. [DOI] [PubMed] [Google Scholar]
  36. Schechter RS, Chaslekis HH, Mignogna RB, Delsanto PP. Real-time parallel computation and visualization of ultrasonic pulses in solids. Science. 1994;265:1188–1190. doi: 10.1126/science.265.5176.1188. [DOI] [PubMed] [Google Scholar]
  37. Selfridge AR. Approximate material properties in isotropic materials. IEEE Trans Sonics Ultrason. 1985;SU-32:381–394. [Google Scholar]
  38. Serpe L, Rho JY. The nonlinear transition period of broadband ultrasound attenuation as bone density varies. J Biomech. 1996;29:963–966. doi: 10.1016/0021-9290(95)00146-8. [DOI] [PubMed] [Google Scholar]
  39. Siffert RS, Luo GM, Cowin SC, Kaufman JJ. Dynamical relationships of trabecular bone density, architecture and strength in a computational model of osteopenia. Bone. 1996;18:197–206. doi: 10.1016/8756-3282(95)00446-7. [DOI] [PubMed] [Google Scholar]
  40. Siffert RS, Kaufman JJ. Ultrasonic bone assessment: ‘The Time Has Come’ (Editorial). Bone. 2007;40:5–8.. doi: 10.1016/j.bone.2006.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Sornay-Rendu E, Boutroy S, Munoz F, Delmas PD. Alterations of cortical bone and trabecular architecture are associated with fractures in postmenopausal women, partially independent of decreased BMD measured by DEXA: The OFELY study. J Bone Miner Res. 2007;22:425–433. doi: 10.1359/jbmr.061206. [DOI] [PubMed] [Google Scholar]
  42. White PJ, Clement GT, Hynyen K. Longitudinal and shear mode ultrasound propagation in human skull bone. Ultrasound Med Biol. 2006;32:1085–1096. doi: 10.1016/j.ultrasmedbio.2006.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES