Multiple Diseases in Carrier Probability Estimation: Accounting for Surviving All Cancers Other than Breast and Ovary in BRCAPRO

SUMMARY

Mendelian models can predict who carries an inherited deleterious mutation of known disease genes based on family history. For example, the BRCAPRO model is commonly used to identify families who carry mutations of BRCA1 and BRCA2, based on familial breast and ovarian cancers. These models incorporate the age of diagnosis of diseases in relatives and current age or age of death. We develop a rigorous foundation for handling multiple diseases with censoring. We prove that any disease unrelated to mutations can be excluded from the model, unless it is sufficiently common and dependent on a mutation-related disease time. Furthermore, if a family member has a disease with higher probability density among mutation carriers, but the model does not account for it, then the carrier probability is deflated. However, even if a family only has diseases the model accounts for, if the model excludes a mutation-related disease, then the carrier probability will be inflated. In light of these results, we extend BRCAPRO to account for surviving all non-breast/ovary cancers as a single outcome. The extension also enables BRCAPRO to extract more useful information from male relatives. Using 1500 familes from the Cancer Genetics Network, accounting for surviving other cancers improves BRCAPRO’s concordance index from 0.758 to 0.762 (p = 0.046), improves its positive predictive value from 35% to 39% (p < 10⁻⁶) without impacting its negative predictive value, and improves its overall calibration, although calibration slightly worsens for those with carrier probability < 10%.

1. Introduction

People who are concerned that their family has a high prevalence of disease may seek genetic counseling to assess their probability of carrying inherited genetic mutations that cause the disease [1]. To aid such people (“consultands”), genetic counselors and other medical professionals (“genetic counselors”) employ statistical models to estimate the probability that the consultand carries deleterious inherited mutations by using the consultand’s reported family history of disease. For syndromes whose onset occurs over a lifetime (as is common in cancer), family history is the age at which each family member developed disease, or that member’s current age or age at death. The carrier probability is a crucial component in the consultand’s decision to take a genetic test (if a test exists), to undergo frequent disease screening, or to consider prophylactic options.

The two major types of models that have been used are empirical models and Mendelian models. Empirical models estimate the probability of testing positive on a genetic test, typically using regression, with features of the given family history as predictors. Instead, Mendelian models use Mendel’s laws and Bayes’s rule to combine family history information with each mutation’s known prevalence and penetrance (probability of disease at an age, given mutation status) to determine the probability that the consultand is a mutation carrier [2, 3, 4]. Mendelian models fully utilize biological laws of inheritance and use the complete family history from all relatives, and thus can offer better predictions than empirical models [5, 6]. This paper restricts itself to Mendelian models. An example of a Mendelian model is BRCAPRO, which estimates the probability that a consultand carries a deleterious mutation in the BRCA1 and BRCA2 genes, based on family history of breast and ovarian cancer [3, 7]. Another example is MMRpro, which computes the probability of carrying a mutation in the genes MLH1, MSH2, and MSH6, given family history of colorectal and endometrial cancer [33]. Recent methodologic advances for Mendelian models include incorporating multiple diseases and multiple mutations with incomplete penetrance [3], incorporating environmental risk factors [9, 10], accounting for genetic test imperfection [11], understanding the effects of misreported family history [12], and incorporating the effects of medical interventions [13]. This paper clarifies the independent and non-informative censoring assumptions and proves that such censoring remains ignorable even if people present for counseling because of a family history of disease. More importantly, this paper extends [3] by demonstrating the impact of dependent times to diseases, the effect of excluding diseases from the model, and that extending BRCAPRO to account for surviving all other cancers as a single outcome can improve BRCAPRO predictions.

Mutation prediction models must handle multiple diseases caused by mutations. We prove that any disease unrelated to mutations can be excluded from the model, unless that disease is both common enough and sufficiently dependent on a mutation-related disease time. However, if the model excludes a mutation-related disease, but the family has members who were diagnosed with it, then the carrier probability will be affected. Furthermore, we prove that even if a family has no members with a mutation-associated disease that is excluded from the model, then the carrier probability will be artificially inflated. Intuitively, a person surviving all mutation-related diseases contributes evidence against carrying a mutation that should be accounted.

We apply our results to BRCAPRO, which excludes non-breast/ovary cancers associated with BRCA mutations. For example, pancreatic and fallopian tube cancers are associated with BRCA mutations, and other sites may be associated as well, such as gastric, prostate, or colorectal [14]. BRCAPRO does not account for other cancers because of uncertainty in their association with BRCA caused by sparse data for each type of cancer. However, there is enough data to explore an alternative model that treats surviving all other cancers as a single outcome. This approach has the advantage of extracting information from the men in the family. We extend BRCAPRO to account for surviving other cancers and test if it improves BRCAPRO predictions based on 1500 families from the Cancer Genetics Network [15]. We also construct two examples to demonstrate how strong the dependence between a mutation-unrelated disease and breast/ovary cancer has to be so that BRCAPRO predictions are affected.

We begin by reviewing the notation, goals, and computation for Mendelian mutation prediction models. In section 2.3, we consider the potential for informative censoring caused by ignoring certain mutation-related diseases or by consultands seeking counseling at young ages due to their family history. In section 2.4 we present expressions describing the effects on the carrier probability of ignoring a disease independent of other mutation-related diseases, and, in section 2.5, for ignoring one dependent on other mutation-related diseases. In section 3, we apply these results by proposing a new BRCAPRO that accounts for all non-breast/ovary cancers, and show that this new BRCAPRO has improved discrimination and calibration. We finish in section 3.1 by presenting two examples using BRCAPRO of including mutation-unrelated diseases that are dependent on mutation-related diseases to illustrate the relationship between the informativeness of including such diseases versus its prevalence and dependence.

2. Methods

2.1. Computing the Carrier Probability

Mendelian models make predictions based on knowledge of which disease each relative developed and the age when it was diagnosed, as well as the age of censoring, that is, the age when he or she died or the age alive after which no information is known. For example, for BRCAPRO, the diseases are breast and ovarian cancer, and the censoring events are age at death or last contact. Note that, although this is rare, a woman can develop both breast and ovarian cancer in her lifetime. In this framework, everyone is eventually censored but disease history up to that age of censoring is observed. This section sets up the notation to handle diseases and censoring.

A Mendelian model considers D types of diseases and B causes of censoring that could occur for each family member i (i = 0 is the consultand). Each person has a binary vector indicating possible censoring events b_i = (b_i,₁, …, b_i,B) where b_i,j = 1 indicates that censoring cause j caused the censoring at age u_i. Also, each person has a binary vector indicating disease history c_i = (c_i,₁, …, c_i,D) where c_i,k = 1 indicates that disease k occurred at age y_i,k and let y_i = (y_i,₁, …, y_i,D) be the vector of all ages of disease occurrence. Denoting censoring information as U_i = {b_i, u_i} and disease information as T_i = {y_i, c_i}, each person’s history is the information H_i = {U_i, T_i} and the full family history for all n + 1 family members is the collection H = {H₀, H₁, …, H_n}.

Additionally, each person can have auxiliary variables x_i and let x = {x₀, x₁, …, x_n}. Auxiliaries can be any extra information known by the consultand, for example, environmental factors, genetic test results, or ethnicity. For example, in BRCAPRO, x₀ indicates if the consultand is of Ashkenazi Jewish ancestry, an ethnic group with increased prevalence of BRCA mutations. Implicitly, all probabilities in this paper will condition on x, so for simplicity we only explicitly show x in the conditioning when useful.

Mendelian models for autosomal genes assume that individuals independently inherit one allele from each parent at each autosomal locus and that the alleles are either normal or mutated. Let γ_i = 0, 1 indicate carrying the genotype(s) that confer(s) disease risk: for example, γ_i = 1 for a dominant trait when the member carries at least 1 mutant allele, but for a recessive trait γ_i = 1 implies that the relative carries two mutant alleles. We call γ_i the carrier status. The prevalence of γ_i = 1 amongst people with consultand-specific auxiliaries x₀ is π_x.

The aim of a Mendelian model is to compute the consultand’s carrier probability P(γ₀ = 1|H, x). By Bayes rule, the odds of the consultand being a carrier are a product of the carrier odds in the population and the Bayes Factor (BF):

$$\frac{P({\gamma }_0=1|H,x)}{P({\gamma }_0=0|H,x)}=\frac{{\pi }_x}{1-{\pi }_x}\times \mathit{\text{BF(H)}},\text{where}\mathit{\text{BF(H)}}=\frac{P(H|{\gamma }_0=1,x)}{P(H|{\gamma }_0=0,x)}.$$ (1)

The BF is a ratio of likelihoods. We compute the likelihood, assuming that each member’s phenotype H_i is independent of all other members’ phenotypes H_−i and auxiliaries x_−i given that member’s carrier status γ_i and auxiliary variables x_i:

$$P(H_i|{\gamma }_i,x_i,H_{-i})=P(H_i|{\gamma }_i,x_i).$$ (2)

Assumption (2) is a standard one for these types of calculations and has been discussed greatly in the literature with extensive simulations investigating departures from this assumption(c.f. [16]). The assumption is unrealistic if important risk factors are missing from x_i. The assumption could be made more realistic by including a frailty model into (3) to account for residual familial dependence [16] or by including all known genetic and environmental risk factors into the model [9]. However, Mendelian models are usually only employed when the mutation confers such high disease risk (as BRCA mutations tend to) that it overwhelms the effects of other, possibly unaccounted-for, risk factors. In this situation, departures from the assumption are less of a concern.

The likelihood P(H|γ₀, x) = P(H₀|γ₀, x₀)P(H₁, … H_n|γ₀, x) is

$$\begin{array}{ll}\hfill & P(H_0|{\gamma }_0,x_0){\displaystyle \sum _{{\gamma }_1=0}^1\dots }{\displaystyle \sum _{{\gamma }_n=0}^{1}P(H_1,\dots H_n|{\gamma }_0,\dots {\gamma }_n,x)P({\gamma }_1,\dots {\gamma }_n|{\gamma }_0,x)}\hfill \\ =\hfill & P(H_0|{\gamma }_0,x_0){\displaystyle \sum _{{\gamma }_1=0}^1\dots {\displaystyle \sum _{{\gamma }_n=0}^1\left({\displaystyle \prod _{i=1}^{n}P(H_i|{\gamma }_i,x_i)}\right)P({\gamma }_1,\dots {\gamma }_n|{\gamma }_0,x).}}\hfill \end{array}$$ (3)

Based on ((3)), the Bayes Factor in favor of γ₀ = 1 is

$$\frac{P(H_0|{\gamma }_0=1,x_0){\displaystyle {\sum }_{{\gamma }_{1,\dots ,{\gamma }_n=0}}^{1}P({\gamma }_1,\dots ,{\gamma }_n|{\gamma }_0=1,x){\displaystyle {\prod }_{i=1}^{n}P(H_i|{\gamma }_i,x_i)}}}{P(H_0|{\gamma }_0=0,x_0){\displaystyle {\sum }_{{\gamma }_{1,\dots ,{\gamma }_n=0}}^{1}P({\gamma }_1,\dots ,{\gamma }_n|{\gamma }_0=0,x){\displaystyle {\prod }_{i=1}^{n}P(H_i|{\gamma }_i,x_i)}}}.$$

Dividing top and bottom by ${\displaystyle {\prod }_{i=1}^{n}P(H_i|{\gamma }_i=0,x_i)}$, the above is

$$\frac{P(H_0|{\gamma }_0=1,x_0)}{P(H_0|{\gamma }_0=0,x_0)}\times \frac{{\displaystyle {\sum }_{\gamma 1,\dots ,\gamma n=0}^1\left({\displaystyle {\prod }_{i=1}^n\frac{P(H_i|{\gamma }_i,x_i)}{P(H_i|{\gamma }_i=0,x_i)}}\right)P({\gamma }_1,\dots ,{\gamma }_n|{\gamma }_0=1,x)}}{{\displaystyle {\sum }_{\gamma 1,\dots ,\gamma n=0}^1\left({\displaystyle {\prod }_{i=1}^n\frac{P(H_i|{\gamma }_i,x_i)}{P(H_i|{\gamma }_i=0,x_i)}}\right)P({\gamma }_1,\dots ,{\gamma }_n|{\gamma }_0=0,x)}}.$$

The factors with γ_i = 0 cancel out, leaving only factors with γ_i = 1, so that is each person’s contribution to the BF equals

$$\frac{P(H_i|{\gamma }_i=1,x_i)}{P(H_i|{\gamma }_i=0,x_i)}.$$ (4)

The BF contributions depend only on the likelihood contributions P(H_i|γ_i, x_i), so we next focus on computing these.

2.2. Computing the Likelihood Contributions: Diseases and Censoring Assumptions

For now, each person’s likelihood contribution P(H_i|γ_i, x_i) will be computed assuming that the times to each disease are independent given carrier status γ_i and auxiliaries x_i. This assumption is plausible for BRCAPRO because time to ovarian cancer and ipsi/contra-lateral breast cancers appear to be mutually independent in BRCA mutation carriers, except for dependence caused by medical interventions like oophorectomy [17, 18]. Interventions are explicitly handled in another paper [13]. Auxiliaries x_i can include all information necessary to make the assumption more plausible. In section 2.5, we consider dependent diseases. As it is possible to develop more than one cancer in a lifetime censored only by death or end of followup, our situation is most generally described as semi-competing risks [19]. However, developing multiple cancers is a rare occurance, even for BRCA mutation carriers.

To compute likelihood contributions, denote the density of getting each disease k at age y given carrier status γ as f_k(y|γ). This density is also known as the penetrance density. Under independent diseases, the probability of surviving disease k to age y, is

$$S_k(y|\gamma )=1-{\displaystyle {\int }_0^y{f}_k(u|\gamma )\mathit{\text{du}}.}$$ (5)

Each contribution P(H_i|γ_i) is the right-censored survival likelihood contribution:

$$P(H_i|{\gamma }_i)=P(U_i,T_i|{\gamma }_i)=P(U_i|T_i,{\gamma }_i)P(T_i|{\gamma }_i)$$

Under independent diseases, the second factor is the product of disease-specific densities for diseases that occurred and the disease-specific survivals for diseases that did not occur:

$$\begin{array}{lll}P(H_i,|{\gamma }_i)\hfill & =\hfill & P(U_i|T_i,{\gamma }_i){\displaystyle \prod _{k=1}^D{f}_k{(y_{i,k}|{\gamma }_i)}^{c_{i,k}}{S}_k{(u_i|{\gamma }_i)}^{1-c_{i,k}}}\hfill \\ \hfill & \propto \hfill & {\displaystyle \prod _{k=1}^D{f}_k{(y_{i,k}|{\gamma }_i)}^{c_{i,k}}{S}_k{(u_i|{\gamma }_i)}^{1-c_{i,k}}}\hfill \end{array}$$ (6)

if the censoring is ignorable, the topic of the next section.

2.3. Implications of Independent Non-Informative Censoring

For censoring to be ignorable, it must be independent and non-informative. Independent censoring means that all censoring events up to age t are independent of future events and so can depend only on past events T_i that occur before age t, denoted F(t−) (see [20, Chapter 6.2] for a formal treatment). Furthermore, under non-informative censoring, all censoring events are independent of carrier status γ_i. Under these assumptions, the probability of being censored in a small age interval [t, t + dt), given auxiliaries, is:

$$P(U_i\in [t,t+dt)|{\gamma }_i,T_i,x_i)=P(U_i\in [t,t+dt)|F(t-),x_i).$$ (7)

To see that these assumptions ensure that censoring is ignorable, note that in the Bayes Factor contributions 4, by using 7, the censoring term has no γ_i dependence and so cancels out.

Allowing U_i to depend on past events in T_i accounts for the fact that censoring may occur as the result of death from a mutation-related disease. If carriers and non-carriers have the same survival to death by mutation-related disease after getting that mutation-related disease, then equation (7) holds (where F(t−) contains the prior time to that mutation-related disease), so this is independent non-informative censoring.

However, if mutation carriers have different survival to a terminal event compared to non-carriers, then γ_i remains in equation (7), and the censoring is informative. For a BRCAPRO example, death by breast cancer would be informative of carrier status if mutation carriers benefited from therapy after breast or ovarian cancer differently from non-carriers. One small study suggests that women with BRCA mutations may have better survival from therapy for ovarian cancer than non-carriers [21]. If necessary, death by mutation-related disease can be accommodated into the likelihood contributions (6): denoting the mutation-related disease as D, let death by it be denoted D + 1, and plug into (6) the survival S_D+1(u_i|γ_i, y_i,D) and density f_D+1(u_i|γ_i, y_i,D) for death by disease D given age of diagnosis of disease D.

Informative censoring can also occur if the model does not include a mutation-related non-terminal disease. For example, since BRCAPRO does not currently account for incidence of pancreatic cancer (which is BRCA2 related), then censoring caused by subsequent death by pancreatic cancer is informative censoring because mutation carriers are more likely than non-carriers to develop pancreatic cancer and therefore to die from it (as long as pancreatic cancer treatments don’t benefit mutation carriers more than non-carriers; we know of no such evidence). This same problem arises when estimating penetrance [22]. This issue is avoided by including all mutation-related diseases into the model. If informative censoring is not addressed, the carrier probability estimate will be affected. Since pancreatic cancer is evidence in favor of carrying a BRCA2 mutation, then ignoring censoring by it causes underestimation of the carrier probability. However, if the unaccounted-for diseases are rare compared to other causes of censoring (as pancreatic cancer is) or are only weakly informative (as gastric, prostate, and colorectal cancers are likely to be), then non-informative censoring may be a reasonable approximation.

Another important censoring issue is that if consultands seek genetic counseling at a young age before disease occurs because they are aware of their family history, then being censored may contain information about carrier status because censoring depends on non-consultand family history H_−i. Superficially, the likelihood contributions P(H_i|γ_i, x_i) do not appear to condition on H_−i. However, by equation (2), they do, as H_−i only dropped out of the likelihood contributions because of the assumption that phenotypes are independent given carrier status and auxiliary variables (2). Under this assumption,

$$P(U_i|{\gamma }_i,T_i,x_i)=P(U_i|{\gamma }_i,T_i,x_i,H_{-i})=P(U_i|F(t-),x_i,H_{-i}).$$

Thus independent non-informative censoring accounts for consultands presenting based on their family history, as long as phenotypes are independent given carrier status.

2.4. Effect of Accounting for all Independent Diseases

By excluding a disease, we mean that the mutation prediction model does not account for it in the penetrances it uses and thus ignores that disease when it occurs in a family. Any independent diseases that do not depend on carrier status can be safely excluded, as such events cancel out of the Bayes Factor contributions (4) because they do not depend on γ_i. Any disease that causes independent non-informative censoring, such as deaths by mutation-unrelated causes, can be excluded for the same reason.

However, excluding a disease that does depend on carrier status affects the carrier probability predictions. To see why, exclude disease D and let f_D(y|γ = 1) > f_D(y|γ = 0). Combining equations (4) and (6), the BF contribution from disease D is a survival ratio if the person didn’t get disease D or a density ratio if the person did get disease D. If a person in the family is diagnosed with the excluded disease D, then the true density ratio is greater than 1, but by excluding D, a factor of 1 is substituted. Thus, the BF contribution will be underestimated, and thus so will the carrier probability estimate. Vice-versa, if the disease occurs less often in carriers, then the BF contribution will be overestimated. Since the BF is multiplicatively affected, so is the carrier odds and thus the carrier probability (for small carrier probabilities).

However, even if no one in the family gets disease D, the fact that the model excludes D will cause overestimation of the carrier probability. If f_D(y|γ = 1) > f_D(y|γ = 0), then S_D(y|γ = 1) < S_D(y|γ = 0), and the true survival ratio is less than 1, but by excluding D, a factor of 1 is substituted. Thus, in families where disease D does not occur, if the mutation prediction model excludes disease D, the carrier probability is overestimated when excluding a disease that occurs more often in carriers. Vice versa, if the disease occurs less often in carriers and the model excludes it, then the carrier probability will be underestimated in families where no one gets that disease. Again, since the BF is multiplicatively affected, so is the carrier odds and thus the carrier probability (for small carrier probabilities).

It is worth noting that the same results are obtained if we only consider the first cancer suffered by each relative (time-to-first-event pure competing risks) [23].

2.5. Dependent Diseases

Ignoring a disease that is dependent on other diseases has different effects than in the independence case. In particular, a mutation-unrelated disease that is dependent on other mutation-related diseases can still yield information about carrier status. By ’mutation-related’ we mean that the disease penetrance depends on carrier status. Intuitively, this happens because the mutation-unrelated disease yields information about the time to mutation-related disease which has direct information about carrier status.

For an example, consider the BRCAPRO example of breast cancer, ovarian cancer, and other cancers, denoted by subscripts br,ov,ot respectively. Under independence, the Bayes Factor contribution for surviving other cancers

$$\frac{S_{ot}(y|x,\gamma =1)}{S_{ot}(y|x,\gamma =0)}$$

is less than 1 since other cancers are positively-mutation-related with γ= 1. Under dependence the above factor becomes

$$\frac{S_{ot}(y|T_{br},T_{ov},x,\gamma =1)}{s_{ot}(y|T_{br},T_{ov},x,\gamma =0)}.$$

For further progress, we need a model for the dependence of the times to the three outcomes. One popular model is the positive-stable copula model [24], under which the multivariate survival is

$$P(T_{br}>t_{br},T_{ov}>t_{ov,}{T}_{ot}>t_{ot})=\mathit{\text{exp}}(-{\Lambda }_{.}^{\alpha }),$$ (8)

where each disease k has cumulative hazard ${\Lambda }_k^{\alpha },{\Lambda }_{.}={\displaystyle {\sum }_k{\Lambda }_k,}$and α ∈ (0, 1] represents the common dependence amongst the disease times with Kendall’s τ = 1 − α.

We compute the effect on the Bayes Factor of not including other cancers into the model when a person never develops cancer. The Bayes Factor considering only breast and ovarian cancers are

$$\frac{\mathit{\text{exp}}{\{-({\Lambda }_{br,1}+{\Lambda }_{ov,1})}^{\alpha }\}}{\mathit{\text{exp}}{\{-({\Lambda }_{br,0}+{\Lambda }_{ov,0})}^{\alpha }\}},$$

where ”1” means the cumulative hazard for carriers(γ = 1) and ”0” the cumulative hazard for non-carriers(γ = 0). The Bayes Factor including all other cancers is

$$\frac{\mathit{\text{exp}}{\{-({\Lambda }_{br,1}+{\Lambda }_{ov,1}+{\Lambda }_{ot,1})}^{\alpha }\}}{\mathit{\text{exp}}{\{-({\Lambda }_{br,0}+{\Lambda }_{ov,0}+{\Lambda }_{ot,0})}^{\alpha }\}},$$

assuming that the same dependence α holds for any pair of outcomes. The ratio of these two Bayes Factors is

$$R=\frac{\mathit{\text{exp}}{\{-({\Lambda }_{br,1}+{\Lambda }_{ov,1}+{\Lambda }_{ot,1})}^{\alpha }+{({\Lambda }_{br,1}+{\Lambda }_{ov,1})}^{\alpha }\}}{\mathit{\text{exp}}{\{-({\Lambda }_{br,0}+{\Lambda }_{ov,0}+{\Lambda }_{ot,0})}^{\alpha }+{({\Lambda }_{br,0}+{\Lambda }_{ov,0})}^{\alpha }\}}.$$

Note that even if Λ_ot,1 = Λ_ot,0, meaning that other cancers are mutation-unrelated, this ratio is not one. Thus a person surviving a mutation-unrelated disease can have information about carrier status, as long that disease is dependent on mutation-related diseases. To compute the ratio of Bayes Factors when a woman gets either breast or ovarian cancer and survives all other cancers, one can take a derivative of the multivariate survivor function (8) to get the expression for the density of breast or ovarian cancer jointly with surviving the other two diseases, then compute the Bayes Factors. The ratio of Bayes Factors in this case is

$$\frac{{({\Lambda }_{br,1}+{\Lambda }_{ov,1}+{\Lambda }_{ot,1})}^{\alpha -1}}{{({\Lambda }_{br,0}+{\Lambda }_{ov,0}+{\Lambda }_{ot,0})}^{\alpha -1}}\times R.$$

Again, even if other cancers were unrelated to mutation, this ratio is not one, implying that there can be information by surviving diseases unrelated to mutation that are dependent on mutation-related disease.

It is worth noting that the effect of dependency differs under different models of dependency. For example, if instead of the positive-stable family, we chose this model of dependence:

$$S_{ot}(y|T_{br},T_{ov},x,\gamma )=S_{ot}(y|x,\gamma )\times g(T_{br},T_{ov}),$$

for some function g independent of γ, then g cancels out of the Bayes Factor. Thus, under this model, dependency amongst diseases would not affect the Bayes Factor at all. We do not suggest that this model of dependence applies generally, but this example emphasizes that the effects of dependent diseases rely on the modeling of the dependency.

3. Results: Accounting for Surviving Other Cancers in BRCAPRO

As mentioned in the introduction, the current BRCAPRO does not account for surviving non-breast/ovary cancers, because of uncertainty in their association with BRCA due to sparse data for each cancer type. However, there is enough data to estimate the penetrance of surviving all other cancers as a single outcome independent of breast/ovary cancers in equation (6). This is useful as many families have only breast/ovary cancers. This outcome draws information from the men in the family, especially as prostate cancer is increasingly considered to be associated with BRCA2 [25]. To demonstrate the importance of including surviving all other cancers into BRCAPRO, we estimate its penetrance and then test if including it into BRCAPRO improves mutation prediction.

To account for surviving all other cancers, we need the penetrance curves for all other cancers. In equation (6), denote all other cancers as disease D. To estimate the penetrance density f_D(y|γ, x) at any age y by mutation status γ (0=no mutation, 1=BRCA1 mutation, 2=BRCA2 mutation) and sex (x = 0 is female, x = 1 is male), we fit a logistic curve through the age- and sex-specific penetrance densities given in [26, Table 3] for BRCA1 mutation carriers, and [27, Table 3] for BRCA2 mutation carriers. Using equation (5), the penetrance survivals S_D(y|γ, x) can be computed. In particular, the female penetrance survival for all other cancers amongst BRCA1 mutation carriers is 77% by age 70; for BRCA2 mutation carriers, it is 84%. The female non-carrier penetrance density f_D(y|γ = 0, x = 1) was calculated by first dividing the female BRCA1 carrier penetrance by the relative risk of 2.30 [26, Table 1] and the female BRCA2 carrier penetrance by 2.45 [27, Table 1], and since these are independent estimates of the female non-carrier penetrance, we then averaged the two (the two are not very different). To approximate the penetrance for a person carrying both BRCA1 and BRCA2 (an extremely rare situation), we treat their time to cancer as the minimum of the time to two independent events: cancer due to BRCA1 and cancer due to BRCA2 (results are not sensitive to this) [3]. For men, BRCA1 penetrances were computed using data from the same tables as above, for BRCA2 the data used is from [27, Table 3] summing over the prostate, pancreatic and other cancers columns, and computing the male non-carrier penetrances used relative risks of 1.34 [26, Table 1] and 2.45 [27, Table 1] for BRCA1 and BRCA2 respectively. In particular, prostate cancer plays a major role in the BRCA2 penetrance estimates, as it contributes a penetrance of 19.8% up to age 80 [27, Table 3] (recently, a specific BRCA2 mutation has been linked to prostate cancer [25]).

Table III.

Calibration of the BRCAPRO predictions that exclude surviving all non-breast/ovary cancers versus including surviving all non-breast/ovary cancers. The first two columns are for predicting BRCA1 or BRCA2 mutations, the second for predicting solely BRCA1 mutations, the third for predicting solely BRCA2 mutations. The rows are for all the data (overall), those with carrier probability < 10%, and with carrier probability > 10%, computing the ratio of observed to expected (O/E) and the left/right endpoints of its 95% confidence interval.

		Predicting		Predicting		Predicting
		BRCA1 or BRCA2		BRCA1		BRCA2
		Excluding	Including	Excluding	Including	Excluding	Including
Overall	O/E	0.87	1.01	0.95	1.04	0.72	0.94
	Left 95%	0.79	0.93	0.85	0.93	0.59	0.77
	Right 95%	0.95	1.10	1.06	1.16	0.86	1.12
< 10%	O/E	3.2	3.8	2.9	3.4	1.4	1.8
	Left 95%	2.6	3.0	2.2	2.7	1.0	1.4
	Right 95%	4.0	4.6	3.6	4.2	1.9	2.4
> 10%	O/E	0.72	0.80	0.75	0.78	0.52	0.62
	Left 95%	0.65	0.73	0.66	0.69	0.41	0.47
	Right 95%	0.79	0.88	0.84	0.88	0.65	0.78

Table I.

Effect on the BRCAPRO carrier probability of excluding vs. including all non-breast/ovary cancers into BRCAPRO for families based on figure 1. Non-breast/ovary cancers are included as per the methods of section 2.4.

Family	Excluding non-breast/ovary cancers	Including non-breast/ovary cancers
As in Figure 1	17%	7%
Mother has only ovarian cancer at 67	29%	17%
Mother has no cancer at 67	15%	6%
Sister has only ovarian cancer at 73	52%	32%
Sister has no cancer at 73	11%	5%
Father died at 67 instead of 87	17%	11%

Figure 1 compares the BRCAPRO BRCA2 Bayes Factor contribution (4) from a relative when the density f_D and survival S_D for all other cancers are included via equation (6) into BRCAPRO (solid lines) vs. excluded from BRCAPRO (dotted lines). Note that the dotted lines are the Bayes Factor contributions used by the current BRCAPRO, while the solid lines give us a sense of what the Bayes Factor contributions would be if BRCAPRO accounted for surviving all other cancers. Figure 1 plots the Bayes Factor contributions from three possible outcomes for a relative: breast cancer, ovarian cancer, or no cancer, with the age of those outcomes on the x-axis. Since the density of other cancers for carriers is always greater than that for non-carriers through age 90 (the relative risks are greater than 1), the figure confirms that all contributions are inflated whether the person got breast or ovarian cancer, or no cancer. The effect of excluding other cancers increases with age because its cumulative probability of occurring becomes appreciable. Intuitively, including all other cancers properly reduces the evidence for being a carrier by accounting for surviving all other cancers to reach old age. Although the dotted and solid lines don’t differ much until age 70, the worst overestimation in figure 1 is about 50% at the oldest ages. Thus excluding diseases could be a problem for families with many relatives who developed cancer at older ages.

Figure 1.

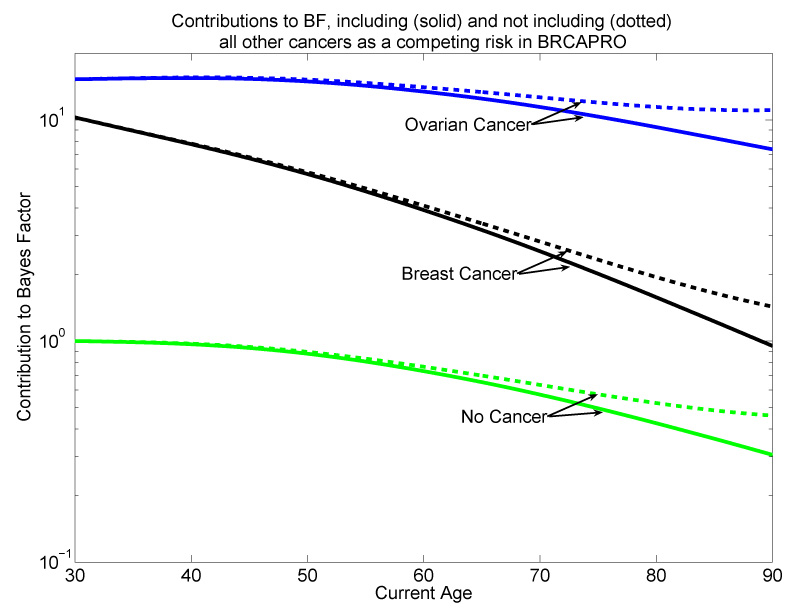
Effect of excluding and including all non-breast/ovary cancers as a competing risk on the contributions to the Bayes Factor in favor of carrying a BRCA2 mutation. The penetrance for all other cancers by BRCA2 carrier status is from The Breast Cancer Linkage Consortium, 1999. Dotted lines exclude all other cancers, solid lines include it.

To see the effect on the BRCAPRO carrier probability for a family with many older relatives, consider figure 2. This family has only breast and ovarian cancers and could have a BRCA mutation. If BRCAPRO excludes all other cancers, the consultand’s BRCA carrier probability is 17%. However, if BRCAPRO includes other cancers, the carrier probability falls to 7%. The discrepancy is large because the family’s cancers are at later ages, when the probability of suffering other diseases by that age is appreciable. This discrepancy is critical because many genetic counselors offer genetic testing to the consultand once the probability exceeds 10% [28]. Also, health insurers may not cover the expense of the test unless the probability is high enough [29].

Figure 2.

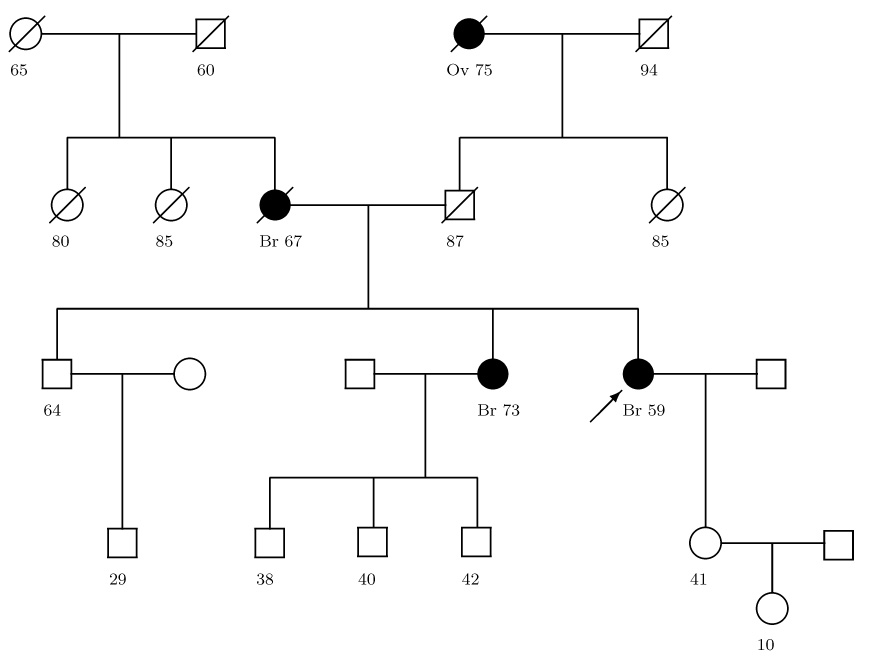
Family Tree with Breast (Br) and Ovarian (Ov) cancer history. The arrow points to the consultand. Circles are females, squares are males. Slash means the relative died, dark shape means the relative got cancer, light shape and no slash means the relative is alive with no cancer, and the age of those outcomes is below each member.

Table I shows how the BRCAPRO carrier probability changes when BRCAPRO accounts for all other cancers for different family histories based on figure 2. The largest discrepancies in table I occur for the two ovarian cancer scenarios, with probabilities decreasing from 52% to 32% and from 29% to 17%, although probably neither change would affect the decision to offer testing. Since the presence of ovarian cancer provides the most evidence in favor of a BRCA mutation [12], scenarios where a relative has ovarian cancer changes the carrier probability the most. The scenarios of the mother having no cancer at 67, or the sister having no cancer at 73, cross the 10% threshold, and so these change may well affect the decision to offer testing. The last scenario in table I has the father dying (not due to cancer) at 67 instead of 87. The carrier probability changes from 17% to 11%, because dying at 87 has the father survive an additional 20 years without developing cancer, and in particular, prostate cancer, which is the biggest contributor to the penetrance of all other cancers. This shows that accounting for surviving all other cancers helps extract information from the men in the family tree, who usually never develop breast cancer and thus normally contribute little, if any, information to BRCAPRO.

To see how clinically important it is to account for surviving other cancers, we calculated BRCAPRO carrier predictions for a subset of patients from participating centers in the Cancer Genetics Network (CGN), described elsewhere [15]. We used 1500 consultands with BRCA1 and BRCA2 mutation testing results and family history of breast and ovarian cancer diagnoses. 1166 consultands were not found to carry a mutation in either gene, 226 were BRCA1 carriers, 105 were BRCA2 carriers and 3 were carriers of mutations in both genes. For each consultand, we calculated the BRCAPRO probabilities of carrying a mutation in BRCA1, BRCA2 or either gene using v1.4-3 of the BayesMendel software [5]. This procedure was then repeated, accounting for surviving all other cancers as described in this section. We compared the discriminative abilities of BRCAPRO with and without surviving all other cancers by using the concordance index, defined as the percent of times, among all possible pairs of carriers and noncarriers, that an individual testing positive for deleterious mutations of either BRCA1 or BRCA2 has the higher carrier probability: a value of 0 represents perfect discordance in the model, 1 represents perfect prediction, and 0.5 represents chance prediction [30, 31].

The results are in table II. The concordance index for any BRCA mutation in the original BRCAPRO was estimated at 0.758, and for BRCAPRO accounting for surviving other cancers, 0.762 (p = 0.046). Thus there is a slight improvement by accounting for surviving other cancers. In particular, when restricting to BRCA1 mutations, the conconcordance index only goes from 0.7796 to 0.7798, but for BRCA2 mutations, it increases from 0.689 to 0.696. The improvement is greatest for predicting BRCA2 mutations, as may be expected since the most important other cancer taken into account is prostate cancer in BRCA2 carriers. We then use the standard 10% carrier probability threshold for making carrier status predictions. Since accounting for surviving other cancers can only decrease the carrier probability, the sensitivity decreases somewhat when accounting for surviving other cancers, but is offset by a greater increase in specificity (table II). Most importantly from the point of view of a consultand, table II shows that accounting for surviving other cancers does not affects the negative predictive value, yet increases the overall positive predictive value of BRCAPRO from 35% to 39% (p < 10⁻⁶).

Table II.

Characteristics of the BRCAPRO predictions that exclude surviving all non-breast/ovary cancers versus including surviving all non-breast/ovary cancers. The first three columns are for predicting BRCA1 or BRCA2 mutations, the second for predicting solely BRCA1 mutations, the third column for predicting solely BRCA2 mutations. The postive/negative predictive values (PPV,NPV), sensitivity, and specificity are all for a 10% carrier probability threshold. The p-value column tests if the difference between including and excluding is zero for each statistic.

	Predicting			Predicting			Predicting
	BRCA1 or BRCA2			BRCA1			BRCA2
	Excluding	Including	p	Excluding	Including	p	Excluding	Including	p
Concordance	0.758	0.762	0.046	0.7796	0.7798	0.90	0.689	0.696	0.18
PPV	35%	39%	< 10−6	41%	44%	< 10−6	38%	43%	< 10−6
NPV	90%	90%	0.86	88%	88%	0.94	85%	84%	0.91
Sensitivity	77%	74%	< 10−6	65%	62%	0.002	55%	46%	< 10−6
Specificity	58%	67%	< 10−6	73%	77%	< 10−6	74%	83%	< 10−6

The calibration of the models was checked by computing the ratio of the observed number of mutation carriers to the number of carriers expected under each model (O/E). An O/E = 1 implies that the model is well-calibrated; an O/E < 1 implies that the model over-predicts and vice-versa for O/E > 1. For the entire dataset, BRCAPRO excluding surviving all other cancers tends to over-predict, especially BRCA2 mutations (Table III). The BRCAPRO ncluding surviving all other cancers improves overall calibration. However, improvement is confined to those with carrier probabilities > 10%; for those < 10%, including all other cancers worsens calibration.

3.1. Dependent Diseases

As section 2.5 showed, mutation-unrelated diseases dependent on mutation-related diseases can carry information about carrier status. In this section, we present two examples to illustrate when it may be worthwhile to consider including such a disease in the model. The examples are based on BRCAPRO: in the first, let the disease be endometrial cancer (a rare disease that shares many of the same risk factors as breast and ovarian cancer), in the second, let the disease be diabetes (a common disease that shares far fewer risk factors with breast and ovarian cancer) [32]. Neither disease is related to BRCA mutations; endometrial cancer is rarer than diabetes, but likely to have a stronger dependence on breast/ovarian cancer than diabetes. The ratio of Bayes Factors in section 2.5 depends on both the prevalence of the disease and the strength of its association with mutation-related diseases. The age-specific risk for endometrial cancer is taken from the general population [8] and that for diabetes is taken from a logistic curves fit through table 1 and table 2 of [34].

We assume the positive-stable copula model for each of endometrial cancer and diabetes with breast and ovarian cancers, and try a few hypothetical but plausible choices of Kendall’s τ to illustrate how much dependence on breast/ovarian cancers is needed to affect the Bayes Factors of section 2.5 (figure 3). For endometrial cancer, if Kendall’s τ = 0.2, there is little change the to Bayes Factors depending on whether endometrial cancer is included (+17% maximum change) until τ increases to 0.5 (figure 3). Since the lifetime risk of endometrial cancer is only 3%, weak dependence does not importantly affect the Bayes Factors. For diabetes, if Kendall’s τ is 0.05, there is little effect on the Bayes Factors (+13% maximum change) until τ is increased to 0.2 (figure 3). Since the lifetime risk of diabetes is 30%, less dependence is needed affect the Bayes Factors. For both diseases, the amount of dependence necessary to change the Bayes Factors using a positive-stable copula is probably much larger than is realistic, and so does not warrant consideration for inclusion into BRCAPRO.

Figure 3.

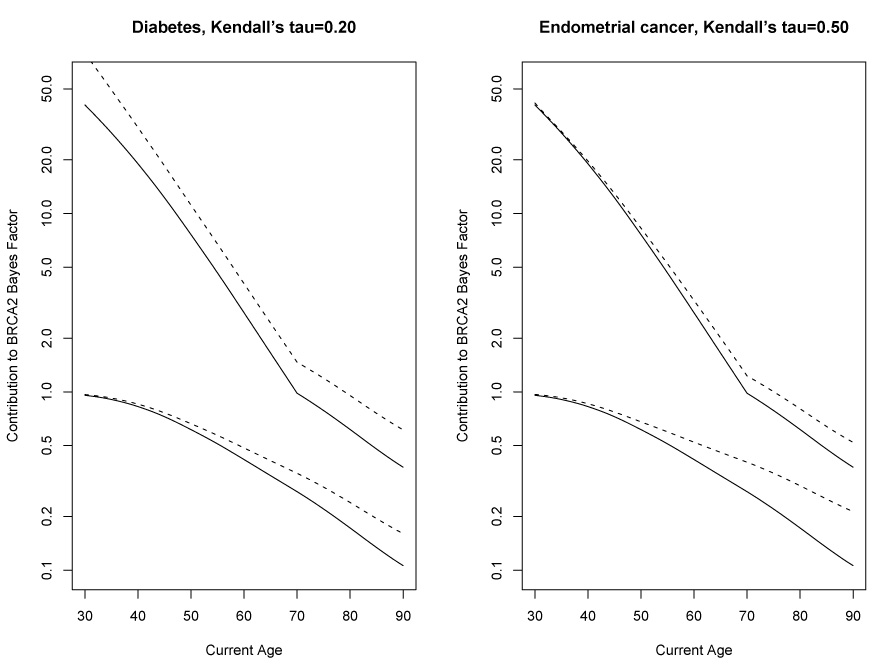
Effect of excluding and including diabetes (left panel) or endometrial cancer (right panel) as a disease on the contributions to the Bayes Factor in favor of carrying a BRCA1 mutation. Dotted lines exclude the disease for the panel, solid lines include it. For both panels, the upper pair of lines is for the relative getting breast cancer, the bottom pair is for surviving all diseases.

4. Discussion

This paper clarifies the role of the independent and non-informative censoring assumption in Mendelian modeling of carrier probabilities and proves that such censoring remains ignorable even if people present for counseling because of a family history of disease. More importantly, we extended [3] in three ways. We demonstrated that mutation-unrelated diseases dependent on mutation-related diseases can still provide information about mutation status, if the mutation-unrelated diseases are prevalent enough and have strong enough dependence on mutation-related diseases. We demonstrated that excluding mutation-related diseases from the model, when all family members survive all excluded diseases, deflates the carrier probability. We extended BRCAPRO to account for surviving all other cancers, combining these into a a single outcome and showed that this improves BRCAPRO’s concordance index and its positive predictive value with no impact on its negative predictive value. This extension also improves the over-prediction of BRCAPRO both overall and for those with carrier probability > 10%, although worsening the under-prediction seen at carrier probabilities < 10%.

The improvement in discriminatory power to BRCAPRO occurs for two reasons. One, incorporating surviving all other cancers helps extract information from the men in the family, who almost always survive breast cancers (even among carriers), and so usually contribute little, if any, information. The improvement is mostly for predicting BRCA2 mutations, for which surviving prostate cancer is important information. Second, surviving all other cancers appropriately discounts the carrier probability in families where many relatives survive to old ages, especially in families with many older relatives with cancer. Genetic counselors should be aware of this effect when considering such families.

Since including surviving all other cancers always decreases the carrier probability, it naturally corrects for over-prediction but exacerbates under-prediction. Thus BRCAPRO over-predicting both overall and for those with carrier probability > 10% is naturally mitigated, but the under-prediction for those with carrier probability < 10% can only be worsened. Again, the biggest effect is seen for predicting BRCA2 mutations.

Our results demonstrate that accounting for all other cancers improves the performance of BRCAPRO and points to the importance of extending BRCAPRO to account for each type of non-breast/ovary cancer. However, this extension at a level of accuracy adequate for clinical use is beyond the scope of this paper as it requires that the penetrance of each disease be reliably estimated. This estimation can be challenging when existing studies do not report a sufficient number of people with each disease. Although there are many studies looking for associations of BRCA mutations with other cancers [14], each study averages less than 5 cancers per site. A sensible option is to pool mutation-related diseases together to get a favorable bias-variance tradeoff, as the category of all other cancers tries to do. Ideally, all other cancers should include only mutation-related cancers, unless a mutation-unrelated disease is common enough and has strong enough dependence on a mutation-related disease (for BRCAPRO, we are not aware of any such disease). The next step is to try to account for all the above issues in a meta-analysis of all available data to produce reliable penetrance estimates for a carefully chosen set of other cancers likely to be associated with BRCA mutations.