Cell elongation is key to in silico replication of in vitro vasculogenesis and subsequent remodeling

Abstract

Vasculogenesis, the de novo growth of the primary vascular network from initially dispersed endothelial cells, is the first step in the development of the circulatory system in vertebrates. In the first stages of vasculogenesis, endothelial cells elongate and form a network-like structure, called the primary capillary plexus, which subsequently remodels, with the size of the vacancies between ribbons of endothelial cells coarsening over time. To isolate such intrinsic morphogenetic ability of endothelial cells from its regulation by long-range guidance cues and additional cell types, we use an in vitro model of human umbilical vein endothelial cells (HUVEC) in Matrigel. This quasi-two-dimensional endothelial cell culture model would most closely correspond to vasculogenesis in flat areas of the embryo like the yolk sac. Several studies have used continuum mathematical models to explore in vitro vasculogenesis: such models describe cell ensembles but ignore the endothelial cells’ shapes and active surface fluctuations. While these models initially reproduce vascular-like morphologies, they eventually stabilize into a disconnected pattern of vascular “islands.” Also, they fail to reproduce temporally correct network coarsening. Using a cell-centered computational model, we show that the endothelial cells’ elongated shape is key to correct spatiotemporal in silico replication of stable vascular network growth. We validate our simulation results against HUVEC cultures using time-resolved image analysis and find that our simulations quantitatively reproduce in vitro vasculogenesis and subsequent in vitro remodeling.

Introduction

Vasculogenesis—de novo formation of a primary vascular network from initially dispersed endothelial cells—is the first step in the development of the circulatory system in vertebrates. Under control of long-range guidance cues, including VEGFs and FGFs, the initial network, called the primary vascular plexus, expands through angiogenic sprouting. Later, association of the primary vascular plexus with additional cell types, including pericytes and smooth muscle cells, and regression of underused vessels transform the primary network into a vascular tree. Hence, vascular development results from the interplay between the endothelial cells’ intrinsic ability to self-organize and external regulation by guidance cues and additional cell types.

Here, we ask which aspects of vascular development result from such self-organization of endothelial cells and which aspects require additional cell types and guidance cues. Thus, experimentally, we must distinguish the endothelial cells’ intrinsic ability to form vascular-like patterns from those mechanisms requiring guidance and regulation by external tissues. To do so, we use a cell culture model, human umbilical vein endothelial cells (HUVEC) in Matrigel, which is a popular experimental model of capillary development (see, e.g., Chen et al., 2001; Kim et al., 2002; Mezentzev et al., 2005; Segura et al., 2002; Serini et al., 2003). Matrigel, which is obtained from mouse tumors, contains most of the growth factors the endothelial cells would normally encounter in vivo, while the cell culture model excludes interactions with additional cell types and the influence of remote guidance cues. The extracellular macromolecules and growth factors in the Matrigel stimulate HUVEC cells to elongate and form networks resembling vascular networks in vivo (Fig. 1), where cords of endothelial cells surround empty lacunae. The HUVEC cells do not penetrate into the Matrigel, forming instead a quasi-two-dimensional vascular-like pattern. Thus, our in vitro model compares best to in vivo quasi-two-dimensional vasculogenesis, e.g., in the avian or murine yolk sac (Gory-Fauré et al., 1999; LaRue et al., 2003).

Fig. 1.

Typical time sequence of in vitro vasculogenesis at 4 h (h), 9 h, 12 h, 24 h and 48 h after incubation. Scale bar is 500 μm.

Developmental biology classically aims to understand how gene regulation leads to the development and morphogenesis of multicellular organisms. Tissue mechanics is an essential intermediary between the genome and the organism: it translates patterned gene expression into three-dimensional shapes (Brouzés and Farge, 2004; Forgacs and Newman, 2005). We aim to understand how genetically controlled cell behaviors structure tissues. What cell behaviors are essential? How do cell shape changes structure the tissue? After identifying these key mechanical cell-level properties, we can separate genetic from mechanical questions. Which genes or gene modules influence the cells’ essential behaviors and shapes? How do genetic knock-outs modify cells’ behaviors? How do these modifications affect tissue mechanics, producing knock-out phenotypes?

Cell shape is an important determiner of tissue mechanics. Cells can change shape passively, due to mechanical strain, differential adhesion, or as a result of chemotactic migration by other cells, or actively by cytoskeletal remodeling. Such active, genetically controlled cell shape changes are ubiquitous in development, as Leptin and Wieschaus first demonstrated in the early nineties for Drosophila. Apical constriction of epithelial cells in early Drosophila embryos drives epithelial folding during ventral furrow formation. Numerous genes control these shape changes, including twist and snail (Leptin and Grunewald, 1990) and concertina (Parks and Wieschaus, 1991). In this example, active cell shape changes control morphogenesis by inducing stresses and strains in the ventral furrow. Cell shape can bias chemotactic cell migration by setting a preferred direction of motility. This synergy occurs, for example, during convergent extension in zebrafish, where slb/wnt11-controlled, oriented, bipolar shape changes aid persistent, directional cell migration (Ulrich et al., 2003).

Endothelial cells dramatically change shape during angiogenesis and vasculogenesis; in response to growth factors including VEGF-A and VEGF-C, intracellular-store-based calcium entry remodels the cells’ actin cytoskeletons, changing their shape from rounded to elongated and bipolar (Cao et al., 1998; Drake et al., 2000; Moore et al., 1998). These calcium-induced shape changes drive the formation of intracellular gaps in confluent rat pulmonary arterial endothelial cell (RPAEC) cultures (Moore et al., 1998), gaps which are similar to the lacunae in HUVEC cultures and in the yolk sac (Gory-Fauré et al., 1999; LaRue et al., 2003).

Computational models of cell aggregates provide important insights into the self-assembly of cells into tissues. They show how relatively simple cell-like behaviors, including cell shape changes, chemotaxis, haptotaxis, cell adhesion, differentiation or induction can produce biological patterns and shapes. Explanatory models of biological morphogenesis address situations ranging from the formation of bacterial (e.g., Budrene and Berg, 1995) and mesenchymal cell (Kiskowski et al., 2004) aggregation patterns and Dictyostelium morphogenesis (e.g., Vasiev and Weijer, 1999) to avascular tumor growth (Drasdo and Hohme, 2003), limb patterning (Hentschel et al., 2004) and gastrulation (Drasdo and Forgacs, 2000; Peirce et al., 2004). Many of these models treat cell aggregates as continua or treat cells as points or rigid spherical particles, thus ignoring the role of cell morphology in tissue shape changes. Glazier and Graner’s (1993) Cellular Potts Model (CPM) is a simulation technique which describes cell surfaces mesoscopically, allowing for detailed, yet computationally efficient tissue modeling. Glazier and Graner’s model has provided useful insights into a range of developmental mechanisms (reviewed in Merks and Glazier, 2005a), including Dictyostelium morphogenesis (Marée and Hogeweg, 2001), convergent extension during gastrulation (Zajac et al., 2003), epidermal patterning (Savill and Sherratt, 2003) and tumor invasion (Turner and Sherratt, 2002), but no studies have used the CPM explicitly to assess the role of cell shape changes in tissue morphogenesis. Ultimately, the utility of these models depends on their ability not only to reproduce but to predict experimental phenotypes, e.g., due to gene knock-outs.

Several in silico models have reproduced in vitro vessel-like patterns (Ambrosi et al., 2004; Gamba et al., 2003; Manoussaki et al., 1996; Murray, 2003; Namy et al., 2004; Serini et al., 2003). These models generate static patterns resembling those of the initial stages of the vascular network, but the papers did not compare the development of the in silico network to experimental results. Additionally, patterning in these models is transient: ultimately, the network patterns transform into “vascular island” patterns consisting of disconnected “tissue blobs” (Manoussaki, personal communication 2005; Preziosi, personal communication, 2005). All previous models have described endothelial cells in terms of densities (using partial differential equations), which makes the consideration of the role of endothelial cell properties such as cell shape and cell adhesion mathematically complicated. Continuum models are most suitable when the constituent agents are much smaller than the scale of interest, permitting the model to average out the behavior of individual particles (cf. hydrodynamics or hydrostatic pressure). Because the “vessels” of vascular networks often consist of only a few cells, explicitly considering individual cells, as we do, is essential.

We identify a small set of experimentally confirmed endothelial cell behaviors that suffices to quantitatively reproduce in vitro vascular network formation and subsequent remodeling by HUVEC in Matrigel. These behaviors are the constituents of a phenomenological model in which individual endothelial cells: (a) secrete a morphogen (Helmlinger et al., 2000) which extracellular matrix (ECM) inactivates, (b) preferentially extend filopodia up morphogen gradients (Gerhardt et al., 2003) and (c) rapidly elongate after contact with the ECM (Dye et al., 2004). Internal remodeling of the actin cytoskeleton drives this shape change (Moore et al., 1998). Releasing hundreds of such virtual endothelial cells into an “in silico Petri dish,” we study how cell-level phenomenology drives shape changes at the tissue scale.

Comparison of the dynamic evolution of our computational model to our in vitro experiments suggests that the endothelial cells’ bipolar, elongated shape is essential for blood-vessel development. We show how elongated cell morphology –causing anisotropic cell migration and cell alignment – produces a stable pattern resembling both in vitro and in vivo vascular networks. To distinguish between models, we consider the network’s time evolution as well as its final configuration. We present alternative models which produce the same end-result; only that including elongating endothelial cells correctly reproduces the dynamic evolution of in vitro vascular development. The biological output of these simulations is mechanical and dynamical understanding of how cell elongation and chemoattraction towards a growth factor, which endothelial cells secrete, produce the intrinsic patterning dynamics of endothelial cells.

Finally, we use our in silico model to infer the physicochemical properties of the molecular signals essential for vasculogenesis. We discuss the likely role of the ECM, and predict that the morphogen VEGF₁₆₅, an isoform of vascular endothelial growth factor (VEGF), which is usually identified as the main inter-endothelial signaling molecule, is likely too stable or too diffusive to be the main signaling molecule. We predict that a less mobile growth factor, e.g., one of the ECM-bound VEGF₁₈₉ or VEGF₂₀₆ isoforms, is the main signaling molecule.

Materials and methods

Cell cultures

We obtained passage 3–5 HUVECs from Clonetics Corporation and maintained them in EBM-2 medium (Clonetics, Maryland) at 37°C in an atmosphere of 95% air + 5% CO₂. In order to study angiogenesis, we filled each well of a 24-well plate with 200 μl of basement membrane matrix (Matrigel; Fisher Scientific, Pittsburgh, PA) diluted with EMB-2 (1:2) and allowed the gel to harden for 30 min at 37°C. We then added 50,000 HUVEC to each well (Kim et al., 2002), marked the wells on the bottom with a fine-point marker and used the marks to identify particular areas in the wells. We photographed the cells at 4, 9, 12, 24 and 48 h with a Nikon TE2000-U microscope equipped with a CCD camera (Diagnostic Instruments).

Morphometry

We measured the topology of the in vitro and in silico vascular-like networks using a method derived from Guidolin et al. (2004) (see Fig. 2). In order to transform the photographs to black-and-white, we first corrected for uneven back-lighting with a closing top-hat transform with a disk of radius 7 (Dougherty and Lotufo, 2003), followed by binary thresholding, with a threshold of min + (max − min)/10, with min and max denoting minimum and maximum grey values in the filtered image. We removed patches smaller than 50 pixels, then closed spurious gaps in the vascular cords with a morphological closing operation using a disk of radius 10 (Dougherty and Lotufo, 2003).

Fig. 2.

Morphometry of experimental photographs and simulation results (see Supplementary methods). Red: detected vessels. Green: detected branch points.

We constructed morphological skeletons and applied 30 (cell cultures) or 15 (simulations) pruning steps to remove artificial branches. We detected the nodes as pixels with three or more first-order neighbors. We removed spurious branch points by counting the number of branches which a small loop around a putative branch point crossed. We obtained the number of lacunae by counting the number of connected components in the inverted, skeletonized image.

Simulation model

Our simulation model, Glazier and Graner’s (1993) Cellular Potts Model represents endothelial cells on a rectangular, numerical grid, where a patch of identical non-zero values represents a cell and a value of 0 identifies the ECM. We describe chemoattractant diffusion macroscopically, in terms of concentrations. Grid points at patch interfaces represent cell surfaces. By repeatedly replacing a value at a cell interfaces by a neighboring grid point’s value, we mimic active, random extensions and retractions of filopodia and lamellipodia. Each cell (i.e., each “patch”) also has a set of attributes which describe its “target” state, including its length and area. An effective energy function describes the state of the cells and the tissue and their interactions. This effective energy is a convenient quantity to describe the cell phenomenology. The larger the energy, the more a cell deviates from its target state. For example, a simulated endothelial cell with a large target length would have a large effective energy if it rounded up, and two highly adhesive cells have high effective energy would reduce their effective energy by coming into contact. We iteratively attempt to carry out random cell extensions in the lattice and accept them if they reduce the cells’ effective energy. In our examples, the rounded simulated cell would elongate gradually, and the contact area between the two adhesive cells increase gradually. We also use effective energy terms, which may include both real and generalized energies, to describe our endothelial cells’ other properties. An “area constraint” ensures conservation of cell volume, and a chemotactic term reduces the effective energy whenever the cell protrudes into an area with a higher concentration of the chemoattractant.

We also accept some energetically unfavorable moves depending on an effective “temperature”, which corresponds to the rate of active, exploratory filopodial extensions and does not reflect conventional thermal temperature (the nomenclature derives from the physical origin of Glazier and Graner’s model). This explorative behavior drives the cells from locally favorable, but globally unfavorable positions, for example, in a somewhat noisy chemical gradient, a non-explorative cell would stop at a “bump” of chemoattractant, while an explorative cell would eventually drift away from it and find the gradient’s peak.

We use the CPM to study how the phenomenology of endothelial cells drives tissue-level dynamics. We make all of our biologically plausible model assumptions at the cell level, while we exclusively observe the model results at the level of the tissue. Thus, the resulting vascular morphologies result from cell behavior instead of from ad hoc global assumptions enforcing a vascular-like morphology.

Our model assumes that endothelial cells (a) assume an elongated shape (internally driven by cytoskeleton remodeling), (b) secrete a chemoattractant and (c) move up the chemoattractant. The chemoattractant (d) diffuses in the extracellular matrix and (e) slowly decays, producing chemoattractant gradients around endothelial cell clusters. The remainder of this section describes our algorithms for specifying cell behavior and chemoattractant dynamics in technical detail, including our specific extensions to Glazier and Graner’s model for simulating endothelial cell behavior.

Mesoscopic simulation of endothelial cell behavior

We have described CPM modeling of cell behavior previously (Glazier and Graner, 1993; Merks et al., 2004). The CPM represents biological cells as patches of lattice spins σ(x⃗) of identical state on a second-nearest-neighbor square lattice, where each state identifies, or “labels,” a single biological cell. Connections between neighboring lattice sites of unlike state σ(x⃗) ≠ σ(x⃗′) represent membrane bonds between cells, where J_{σ(x⃗), σ(x⃗′)} gives the bond energy, assuming that the types and numbers of cellular adhesion molecules determine J. An energy penalty increasing with the cell’s deviation from a designated target volume, A_σ, constrains the volume of the cells. To mimic cytoskeletally driven, active surface fluctuations, we randomly choose a lattice site, x⃗, and attempt to copy its spin σ(x⃗) into a randomly chosen neighboring lattice site x⃗′. This attempt represents a lamellipodial or filopodial protrusion of the first cell displacing the surface of the second cell. During a Monte Carlo Step (MCS), we attempt n copies, where n is the number of sites in the lattice. A further energy constraint favors protrusions in the direction of chemical gradients, thus mimicking chemotaxis (Savill and Hogeweg, 1997). We express the adhesion, target area deviations and chemotaxis in terms of the effective energy E,

$$E=\sum _{\overrightarrow{x},\overrightarrow{x^{\prime }}}{J}_{\sigma (\overrightarrow{x}),\sigma (\overrightarrow{x^{\prime }})}\left(1-{\delta }_{\sigma (\overrightarrow{x}),\sigma (\overrightarrow{x^{\prime }})}\right)+\lambda \sum _{\sigma }{(a_{\sigma }+A_{\sigma })}^2,$$ (1)

where x⃗′ represents the eight second-order neighbors of x⃗′; λ represents resistance to compression, and the Kronecker delta is δ_x,y = {1, x = y; 0, x ≠ y}. This energy is a convenient physical description of the cells’ deviation from their preferred phenomenological state; for example, an endothelial cell’s energy would be high when its elongation is hindered by surrounding cells.

We implement preferential extension of filopodia in the direction of chemoattractant gradients (Gerhardt et al., 2003) by including an extra reduction in energy at the time of copying (Savill and Hogeweg, 1997):

$$\mathrm{\Delta }{H}_{\text{chemotaxis}}=\gamma \left(c\left(\overrightarrow{x}\right)-c\left(\overrightarrow{x^{\prime }}\right)\right).$$ (2)

where x⃗′ is the neighbor into which site x⃗ copies its spin, c(x⃗) is the local concentration of chemoattractant, and γ is the strength of the chemotactic response, which we set to γ = 1000. The cells reside in an ECM which we model as a generalized CPM cell without a volume constraint and with σ = 0. We minimize E using standard Metropolis dynamics at a temperature, T = 50: we calculate how much the free energy E would change if we performed the copy, and accept the attempt with Boltzmann probability:

$$P(\mathrm{\Delta }E)=\left\{e^{\frac{-\mathrm{\Delta }E-E_0}{T}},\mathrm{\Delta }E\ge -E_0;1,\mathrm{\Delta }E<-E_0\right\},$$ (3)

where E₀ is an energy threshold which models viscous dissipation and energy loss during bond breakage and formation (Hogeweg, 2000). Each CPM cell i moves according to the effective-energy gradient around it, ν⃗_i ∝ ∇⃗ _i E, which mostly results from morphogen gradients in our vasculogenesis model. Thus, given an effective energy, we can calculate the resulting cell motion and the force required to create such motion. In the highly viscous environment of the ECM, the force F⃗_i exerted on a cell i is proportional to its velocity ν⃗_i, not its acceleration, i.e., F⃗_i ∝ ν⃗_i; a relation we call the overdamped force–velocity response. Thus, the force the generalized energy exerts on a cell is proportional to the local effective energy gradient F⃗_i∝ ∇⃗ _iE. We use neutral binding energy settings J_c,c = 40 between the endothelial cells, and J_c,M = 20 between the endothelial cells and the ECM. A high cell-border energy J_c,B = 100 prevents cells from adhering to the boundaries of the simulated area (which we define as frozen pixels of type B).

To mimic cell elongation due to cytoskeletal remodeling (Moore et al., 1998), we add a cell-length constraint to the free energy:

$$E^{\prime }=E+{\lambda }_{\text{L}}\sum _{\sigma }{(l_{\sigma }-L_{\sigma })}^2,$$ (4)

where l_σ is the length of cell σ along its longest axis, L_σ its target length, and λ_L the strength of the length constraint. Assuming that cells are ellipses, we can derive their length from their inertia tensor I (Zajac et al., 2003)—which mathematically represents the cell shape—as $l_{\sigma }=4\sqrt{{\lambda }_{b,\sigma }/a_{\sigma }}$, where λ_b,σ is the largest eigenvalue of I. Since both ends of the cells are slightly thicker than the middle, this relation overestimates the cell length by about 33%. We calculate a cell’s inertia tensor from the moments of the sites the cell occupies as:

$$I=\left[\begin{array}{cc}{\sum }_i{x}_i^2-\frac{1}{a}{\left({\sum }_i{x}_i\right)}^2& -{\sum }_i{x}_i{y}_i-\frac{1}{a}{\sum }_i{x}_i{\sum }_i{y}_i\\ -{\sum }_i{x}_i{y}_i-\frac{1}{a}{\sum }_i{x}_i{\sum }_i{y}_i& {\sum }_i{y}_i^2-\frac{1}{a}{\left({\sum }_i{y}_i\right)}^2\end{array}\right],$$ (5)

where a is the cell area. Updating the moments for each extension or retraction of a cell allows us to estimate l_σ without lengthy non-local calculations.

The length constraint could cause cells to split into disconnected patches. We prevent this artifact by introducing a connectivity constraint. This constraint reflects the physical continuity and cohesion of the actual cell. To check whether an index copy into site x⃗ will change local connectivity, we count how many of site x⃗’s neighbors x⃗′_i have the same index as x⃗ while the next location clockwise around x⃗ has an index different from that of x⃗ (see Fig. 3). If this quantity ${\sum }_i{\delta }_{\sigma (\overrightarrow{x}),\sigma (\overrightarrow{x^{\prime }{}_i})}\left(2-{\delta }_{\sigma (\overrightarrow{x}),\sigma (\overrightarrow{x^{\prime }{}_{i+1}})}-{\delta }_{\sigma (\overrightarrow{x}),\sigma (\overrightarrow{x^{\prime }{}_{i-1}})}\right)>2$, with the sum running in cyclic order and we have more than two (non-medium) cells in the local neighborhood, changing the site will destroy the local connectivity. This local test for connectivity loss may erroneously forbid a site update if its neighborhood connects via a non-local path (see, e.g., Fig. 3e). This approximation may result in “frozen” configurations, particularly after sudden domain extensions (e.g., during the initial phase of our simulation when the cells elongate rapidly). Instead of introducing a computationally very expensive (O(N²)) global connectivity test, we make cell fragmentation energetically costly by assigning a large energy penalty (we currently use E₀ > 2000) to updates that change local connectivity.

Fig. 3.

Connectivity constraint. Double arrows indicate “Collisions,” where the central site x⃗’s neighbors $\overrightarrow{{x^{\prime }}_i}$ have the same index as x⃗ while the next or previous location clockwise around x⃗ has an index different from that of x⃗ (i.e., site pairs for which ${\delta }_{{\sigma }_{\overrightarrow{x}},{\sigma }_{{\overrightarrow{x}}_i^{\prime }}}\left(1-{\delta }_{{\sigma }_{\overrightarrow{x}},{\sigma }_{{\overrightarrow{x}}_{i+1}^{\prime }}}\right)=1\text{or}{\delta }_{{\sigma }_{\overrightarrow{x}},{\sigma }_{{\overrightarrow{x}}_i^{\prime }}}\left(1-{\delta }_{{\sigma }_{\overrightarrow{x}},{\sigma }_{{\overrightarrow{x}}_{i-1}^{\prime }}}\right)=1$. (a) For precisely two collisions, we accept the proposed update. (b) For more than two collisions, we reject the proposed update, unless rule c applies. (c) For more than two collisions, with precisely two non-ECM cells involved, we accept the proposed update. (d) For more than two collisions with only one non-ECM cell involved, we reject the proposed update. (e) Incorrect rejection of a proposed update. The constraint detects a local connectivity violation for cell “b,” which actually would remain connected via the gray sites of “b”.

Continuum model of chemoattractant dynamics

Following a previous PDE model of in vitro vasculogenesis (Ambrosi et al., 2004; Gamba et al., 2003; Serini et al., 2003), we assume that endothelial cells secrete a chemoattractant, which gradually inactivates in the ECM. Thus, we set the diffusion and secretion of the chemoattractant to:

$$\frac{\partial c(\overrightarrow{x},t)}{\partial t}=\alpha {\delta }_{\sigma (\overrightarrow{x}),0}-\left(1-{\delta }_{\sigma (\overrightarrow{x}),0}\right)\epsilon c(\overrightarrow{x},t)+D^{2}c(\overrightarrow{x},t),$$ (6)

where δ_σ(x⃗),0 = 1 inside the cells, α is the rate at which the cells release chemoattractant, and ε is the decay rate of the chemoattractant. Every site within a cell secretes the chemoattractant, which only decays at sites within the ECM. We solve this PDE numerically using a finite-difference scheme on a lattice that matches the CPM lattice, using 15 diffusion steps per MCS with Δt = 2 s and Δx = 2 μm. For our parameter settings (D = 10⁻¹³ m² s⁻¹; α= ε = 1.8 × 10⁻⁴ s⁻¹) the chemoattractant diffuses much more rapidly than the cells move, enabling us to ignore any advection of the chemoattractant which may occur as the cells displace the ECM.

Results

Fig. 1 shows a time-sequence for in vitro vasculogenesis. The endothelial cells assemble into a structure resembling a capillary plexus: cords of cells enclose lacunae. Subsequent remodeling coarsens the pattern: smaller lacunae shrink and disappear, while larger lacunae grow in size.

Fig. 4 and the on-line Supplementary movie show a typical simulation of vasculogenesis. We randomly distributed 282 virtual endothelial cells over a simulated area of 666 μm × 666 μm to correspond to the in vitro cell density. Each CPM lattice site corresponds to a square of size 2 μm × 2 μm. We set the length of the simulated endothelial cells to about 100 μm, based on cell culture measurements. We assumed that the morphogen breaks down in the ECM at a rate of 1.8 × 10⁻⁴ s⁻¹ (Lauer et al., 2002; Serini et al., 2003) and diffuses slowly at about 10⁻¹³ m² s⁻¹. Each MCS corresponds to 30 s: for this choice of timescale, the mean and mode of the cell velocities is 5 μm/h with some cells moving up to 30 μm/h, agreeing well with in vivo observations of endothelial cell motility during vasculogenesis (Rupp et al., 2004).

Fig. 4.

Typical in silico vasculogenesis time sequence. Each lattice site represents an area of 2 μm × 2 μm. We randomly distributed 282 virtual endothelial cells over a 333 × 333 pixel area, which we positioned in a 500 × 500 lattice to minimize boundary effects. This cell density corresponds to that in the in vitro experiments. The total simulated area is 1000 μm × 1000 μm. Isolines (green) indicate ten chemoattractant levels relative to the maximum concentration in the simulation The grayscale indicates absolute concentration on a logarithmic scale.

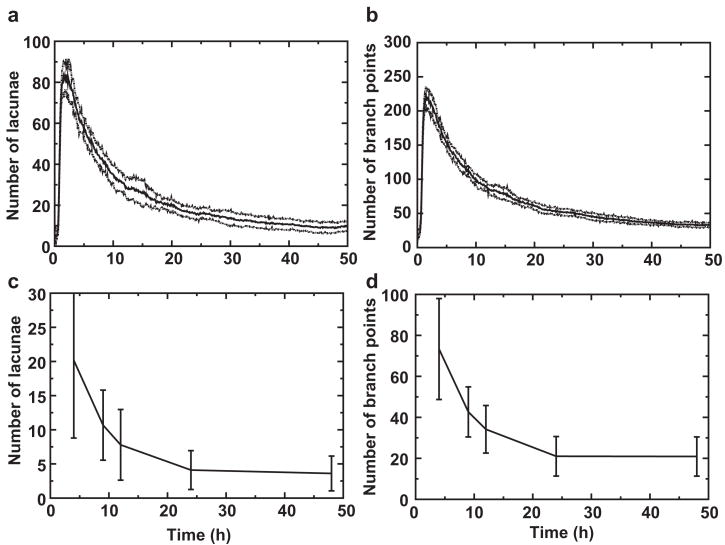
We characterize in vitro and in silico pattern coarsening using the image analysis algorithm we described above (Guidolin et al., 2004), counting the number of branch points and lacunae at different times. The kinetics of the in silico morphogenesis coincides with that of the cell cultures surprisingly well. Pattern coarsening in our in silico experiments (Figs. 5a, b) has the same temporal dynamics as in our in vitro experiments (Figs. 5c, d). The number of branch points and lacunae initially drops quickly, with non-exponential dynamics, then slowly stabilizes, resulting in a typical equilibrium size for the lacunae. In our in silico model, cell elongation is essential for vasculogenesis and remodeling. Reducing cell elongation below a critical cell length in our computer model eliminates vascular-like shapes (see Fig. 6).

Fig. 5.

Number of lacunae (a, c) and number of branch points (b, d) over time for in vitro (a, b) and in silico vascular-like morphogenesis (c, d). Error bars and stippled lines give standard deviations (n = 28 and n = 10 for in vitro and in silico experiments respectively).

Fig. 6.

Changes of patterns in in silico cell cultures with increasing endothelial cell length. (a) 20 μm, (b) 40 μm, (c) 60 μm, (d) 80 μm and (e) 100 μm. Isolines (green) indicate ten chemoattractant levels relative to the maximum concentration in the simulation. Greyscale indicates absolute concentration on a logarithmic scale.

Our standard model ignores cell adhesion in order to clarify the effects of cell elongation. However, endothelial cells do adhere strongly through adherens junctions (Gory-Fauré et al., 1999). In order to test whether cell adhesion affects our findings, we ran our simulation model with increasingly adhesive endothelial cells. Up to strongly adhesive settings of J_c,c = 5 and J_c,M = 20, cell adhesion did not change the vascular patterns; only for maximum cell adhesion of J_c,c = 1 and J_c,M = 20 did the lacunae become a little bit larger and more regular (Fig. 7). Also the size of the endothelial cells might affect morphogenesis, e.g., the size of the lacunae. In Fig. 8, we increase the length and surface area of the cells, simultaneously reducing the number of cells in order to keep the total area occupied by cells constant. Lacuna size does not depend on cell size, but on the width of the gradients instead (not shown), as in previous continuum models (Ambrosi et al., 2004; Gamba et al., 2003; Serini et al., 2003).

Fig. 7.

In silico vasculogenesis in simulations with increasing intercellular adhesion. (a) J_c,c = 20, (b) J_c,c = 15, (c) J_c,c = 10, (d) J_c,c = 5, (e) J_c,c = 1. Other settings as in standard model. Isolines (green) indicate ten chemoattractant levels relative to the maximum concentration in the simulation. Greyscale indicates absolute concentration on a logarithmic scale.

Fig. 8.

In silico vasculogenesis in simulations with increasing cell length and area; number of cells is adjusted to keep the total area covered by cells constant. (a) L = 200 μm, A = 800 μm², 141 cells; (b) L = 300 μm, A = 1200 μm², 94 cells; (c) L = 400 μm, A = 1600 μm², 70 cells; (d) L = 500 μm, A = 2000 μm², 56 cells. Other settings as in standard model. Isolines (green) indicate ten chemoattractant levels relative to the maximum concentration in the simulation. Grayscale indicates absolute concentration on a logarithmic scale.

To further study the robustness of the model and to identify its critical components, we attempted to reproduce vasculogenesis with different assumptions concerning its mechanisms. Variant models omitting the length constraint could produce patterns somewhat like those obtained in vitro if we assumed very strong intercellular adhesion (Merks et al., 2004) or chemoattractant gradients steep relative to cell size (Fig. 9). Both of these assumptions produce elongated cells without using a length constraint. Networks do not form if we prevent cell elongation using an energy constraint that enforces cell isotropy (not shown). These mechanisms very rapidly converge onto a (temporally stable) polygonal pattern but show practically no, or very rapid, coarsening (Figs. 10a–b), in contrast to the in vitro cultures and our simulations with elongated cells. Alternative cell polarization mechanisms can also form vascular-like morphologies: for example, contact inhibition of motility between endothelial cells, mediated e.g., by vascular endothelial cadherin-dependent VEGF signaling (Dejana, 2004) (Fig. 9) which we model by suppressing the chemotaxis energy term at endothelial cell interfaces (Merks and Glazier, 2005b). Again, this mechanism forms stable polygonal cell configurations, which do not reproduce the temporal behavior of in vitro cell cultures (Fig. 10c).

Fig. 9.

Alternative mechanisms of vasculogenesis which assume steep chemoattractant gradients (α = ε = 1.25 × 10⁻³ s⁻¹; λ_L = 0; 415 cells; other parameters as in main text). (a) Without shape constraints, steep gradients stretch the large (A = 100 pixel) cells, promoting the formation of stable, polygonal patterns resembling vascular networks. Enforcing round cells (L = 10, λ_L = 50) suppresses this mechanism. (b) Smaller cells (A = 50) do not stretch for these parameter values and do not form vascular networks. We have reported elsewhere (Merks et al., 2004) that cell adhesion (J_c,c = 1) can drive formation of vascular-like networks. Parameters are those in reference (Merks et al., 2004) (rescaled): 1000 cells, ε= 1.25 × 10⁻³ s⁻¹, α = 2.5 × 10⁻³ s⁻¹. Round cells (L = 0, λ_L = 50) suppress this mechanism. (c) Contact inhibition of motility drives in silico formation of polygonal patterns by round cells (L = 10, λ_L = 50). Here, we suppress formation of chemotactic filopodia and lamellipodia at endothelial cell contacts, e.g., through vascular endothelial cadherin-binding-dependent, conditional VEGF-A signaling (Dejana, 2004).

Fig. 10.

Alternative vascular development mechanisms do not show correct pattern coarsening (i.e., lacunar growth): (a) steep morphogen gradients (compare Fig. 7a), (b) adhesion (compare Fig. 7b) and (c) contact inhibition of motility (compare Fig. 7c). Mechanisms (a) and (b) depend on cell elongation; constraining cells to be round suppresses these mechanisms. Stippled lines indicate standard deviations over ten simulations.

Discussion

We have demonstrated that cell elongation, in conjunction with autocrine secretion of a chemoattractant, suffices to form vascular-like morphologies and subsequent remodeling by endothelial cells. Although other mechanisms, including contact inhibition of motility, can produce somewhat similar, stable network morphologies (Merks and Glazier, 2005b), an elongated cell shape is necessary for the spatiotemporal behavior of the model that corresponds with in vitro experiments. Our model suggests the following mechanism for in vitro vasculogenesis. The in silico cells migrate faster along their long axes than along their short axes (Fig. 11), simply because they need fewer surface protrusions and retractions to move normal to their short interface than to their long interface. For similar reasons, real elongated biological cells likely migrate faster along their long axes; moreover, they will more easily slide through the ECM along their long axes than sideways. Such anisotropic, cell-shape-dependent motility results in strong directional persistence because the cells must (slowly) reorient before moving into a new direction. Experimentally, elongated endothelial cells indeed have a longer movement persistence time than more rounded cells, including fibroblasts (Huang et al., 2005). Elongation of these cells appears to be an inherent, cytoskeletally dependent property, the basis of which is not considered in our model.

Fig. 11.

Random walks of round (solid line) and elongated (stippled line) virtual cells in the absence of chemotactic cues. Elongated cells migrate fastest along their long axis, while rounded cells undergo an isotropic random walk. Scale bar, 10 μm (5 lattice sites).

The anisotropic migration of elongated cells, which requires no extra assumptions in the CPM, produces a long persistence time in the presence of chemotactic cues because cells change direction slowly. The long persistence time introduces two timescales into vasculogenesis. Fast migration along the cells’ long axes produces rapidly interconnects the cells, producing fine vascular networks. Then slower, sideways migration coarsens the pattern as the cells align and close small lacunae. Round cells, which isotropically attract surrounding cells can only form rounded, disconnected “islands.” Thus, our simulations suggest why cell elongation is important in morphogenesis. We thus expect any other vasculogenesis model based on cell locomotion and morphogen gradients to find a similar role for cell elongation in pattern formation and pattern evolution. Our model also help explain why cell shape is essential for other developmental mechanisms, including gastrulation (see e.g., Gong et al., 2004).

Interestingly, the behavior of our model reproduces experiments by Drake et al. (2000), who found that VEGF-signaling induces an extended, bipolar shape in endothelial cells. Injecting chick embryos with dominant negative, soluble VEGFR-1, which competitively blocks VEGF signaling, causes endothelial cells to assume a round shape and aggregate into round islands (see Fig. 12) as in our model (Fig. 6), suggesting that dominant negative VEGFR-1 receptors affect endothelial cells’ shape, but not their ability to aggregate chemotactically.

Fig. 12.

Reproduced with permission of the authors from Drake et al. (2000). (a) Control, showing untreated endothelial cells’ formation of a normal capillary plexus. (c) Injecting soluble VEGFR-1 into chick embryos blocks VEGF-signaling, causing clusters of rounded, vascular progenitor cells to form. (b, d) Stained nuclei of vascular progenitor cells. Scale bar, 15 μm.

Other PDE models which assume that autocrine chemotaxis causes the initial stages of in vitro vasculogenesis (Ambrosi et al., 2004; Gamba et al., 2003; Serini et al., 2003) assume that cells accelerate in chemoattractant gradients rather than having the overdamped force–velocity response of experiments and the CPM. Our results indicate that isotropic chemoattraction with this biologically more realistic linear force–velocity relation (i.e. F = mv) does not suffice to form vascular networks: this mechanism forms disconnected, round “islands” instead; cell elongation is also required.

Above, we deliberately did not discuss the nature of the chemoattractant. Our model predicts its specific physicochemical properties. Previous chemotaxis models (Ambrosi et al., 2004; Gamba et al., 2003; Serini et al., 2003) and experiments (Helmlinger et al., 2000) assumed that the chemoattractant is vascular endothelial growth factor 165 (VEGF₁₆₅). Measured half-lives of VEGF₁₆₅ range from 30 to 60 min (Lauer et al., 2002; Serini et al., 2003), and its diffusion coefficient in agarose gels (Pluen et al., 1999) and tumor ECM (Netti et al., 2000) is about 10⁻¹¹ m² s⁻¹. For these parameters, our model also produces polygonal patterns resembling cell cultures. However, these patterns are not temporally stable: the final configuration is series of islands rather than a network (not shown). To reproduce network-like morphogenesis, the cells also must move extremely rapidly (about 100 times their velocity in culture), so that morphogenesis occurs when the gradients of the chemoattractant around the virtual cells are only partly established, and thus unusually short range and steep (not shown).

To produce stable vascular-like patterns over experimentally observed timescales, our model requires a slowly diffusing, quickly inactivated, chemoattractant. Gradients of the correct scale require a balance between diffusion and inactivation. The hypothetical chemoattractant must either diffuse approximately 100 times slower than VEGF₁₆₅ (D ≈ 1.0 × 10⁻¹³ m² s⁻¹) or have a half-life of a few minutes rather than 30 to 60 min. Intermediate combinations of parameters also work. VEGF₁₆₅ diffusion and decay produce gradients too shallow for the chemotaxis mechanism we have proposed to work. Instead, our model predicts that VEGF₁₆₅ is a long-range angiogenic stimulant, rather than a short-range morphogenetic signal. Indeed, recent experimental results suggest that endothelial cells do not produce VEGF₁₆₅ at early stages of vasculogenesis (Vokes et al., 2004), contrary to the assumptions of previous continuum models (Ambrosi et al., 2004; Gamba et al., 2003; Serini et al., 2003) and experiments on its exogenous effects (Helmlinger et al., 2000).

Several growth factors have both the small diffusion coefficient and short half-life that our model requires. Although D ≈ 1.0 × 10⁻¹³ m² s⁻¹ is unrealistically slow for free diffusion of VEGF₁₆₅ through the ECM, several other growth factors, including VEGF-A isoforms VEGF₁₈₉ and VEGF₂₀₆, bind tightly to ECM proteins (Distler et al., 2004), suggesting that their diffusion rates may correlate inversely with ECM protein concentrations. Hiratsuka et al. (1998) propose that the high-affinity VEGFR-1 receptor traps many VEGF molecules around endothelial cells. Such a mechanism might help generate short, steep VEGF gradients around endothelial cell aggregates.

Continuum, chemotaxis-based models (Ambrosi et al., 2004; Gamba et al., 2003; Serini et al., 2003) and our cell-oriented model (Merks et al., 2004) both show a positive correlation between the diffusion coefficient of the morphogen and the equilibrium lacunar size. Networks with smaller lacunae form in cell cultures in gels with higher ECM protein concentration (see, e.g., Vernon et al., 1992), in which chemoattractants may diffuse more slowly.

Several continuum models of vasculogenesis have shown that traction forces, which the endothelial cells exert on the extracellular matrix, can drive in silico, vascular-like morphogenesis (Manoussaki et al., 1996; Murray, 2003; Namy et al., 2004). These models suggest that the mechanical properties of the ECM, including its stiffness and elasticity, can explain the relation between gel concentration and the size of lacunae in the vascular network. We cannot rule out this possibility, but our hypothesis that ECM may trap autocrine growth factors to generate short, steep growth factor gradients around endothelial cell cords is also consistent with these experimental observations: dense protein matrices have more growth factor binding sites, slowing growth factor diffusion, which steepens gradients and, consequently, produces vascular networks with smaller lacunae. Further experiments may distinguish between these possibilities, e.g., by comparing morphologies in experiments using gels with similar stiffnesses and densities, but different densities of protein binding sites (Miura and Shiota, 2000).

Appendix A. Supplementary data

Supplementary data associated with this article can be found in the online version at doi: 10.1016/j.ydbio.2005.10.003.