Abstract
The delivery of oxygen to tissue by cell-free carriers eliminates intraluminal barriers associated with red blood cells. This is important in arterioles, since arteriolar tone controls capillary perfusion. We describe a mathematical model for O2 transport by hemoglobin solutions and red blood cells flowing through arteriolar-sized tubes to optimize values of p50, Hill number, hemoglobin molecular diffusivity and concentration. Oxygen release is evaluated by including an extra-luminal resistance term to reflect tissue oxygen consumption. For low consumption (i.e., high resistance to O2 release) a hemoglobin solution with p50=15 mmHg, Hill n=1, DHBO2=3×10−7 cm2/s delivers O2 at a rate similar to that of red blood cells. For high consumption, the p50 must be decreased to 5 mmHg. The model predicts that regardless of size, hemoglobin solutions with higher p50 will present excess O2 to arteriolar walls. Oversupply of O2 to arteriolar walls may cause constriction and paradoxically reduced capillary perfusion.
Keywords: Facilitated diffusion, O2 affinity, Transport simulation, Vasoconstriction, Blood Substitutes
1. Introduction
The purpose of this paper is to provide a quantitative framework for the design of acellular hemoglobins (Hb) to function as hemoglobin-based oxygen carriers (HBOCs), particularly O2 equilibrium binding properties and modified Hb molecular size. Numerical simulations of O2 transport from acellular Hb and RBCs in arteriolar-sized domains are calculated. The effects of variations of individual parameters on a generic Hb solution are considered. A range of extra-luminal transport resistances are used to understand the importance of intra-luminal O2 transport processes versus consumption rates for prospective HBOCs. In the context of this study, we use the terms O2 transport or O2 delivery to refer to the total amount of O2 transferred from a Hb solution flowing through a simplified, arteriolar-sized domain to the surrounding environment.
Scientists have been searching for a viable oxygen carrying resuscitation fluid to serve as a temporary surrogate to blood for the better part of the past century [1]. Hemoglobin is the obvious choice as the functional compound in such a fluid because of its high O2-carrying capacity [1]. HBOCs are composed of acellular Hbs chemically modified to decrease renal toxicity due to Hb dimerization and to provide O2 to hypoxic tissue. Modifications include cross-linking between Hb subunits, formation of Hb polymers, and surface conjugation of Hb molecules to poly(ethylene) glycol. Sites of modification are used to affect the O2-binding affinity of the HBOC. The resulting HBOCs display a wide variation in molecular size and O2 equilibrium binding characteristics [2].
The O2 affinities of HBOCs that have been developed and implemented in clinical trials may vary by as much as an order of magnitude. The p50s of a PEG-conjugated Hb product (MP4), 5 mmHg, and a polymerized bovine Hb product (PolyBvHb), 54 mmHg, represent this range. An extensive series of in vivo experiments with HBOCs of varied p50s have shown increased efficacy for HBOCs with high O2 affinities [3–5]; this data has led to the theory of autoregulatory vasoconstriction by arteriolar over supply of O2, which we discuss elsewhere [6,7]. More recently, there has been a general agreement that increasing the molecular size of Hb is advantageous; the estimated molecular weights of both MP4 (~95 kDa) [8] and PolyBvHb (~200 kDa) [9] are larger than unmodified or intramolecularly cross-linked Hbs (64 kDa) [10]. The increased molecular size limits the diffusion of acellular Hb within the lumen and potentially decreases extravasation of Hb into the vessel wall.
As a consequence of the particulate nature of blood, the O2 transport resistances associated with RBC suspensions are greater than those of acellular Hbs. The amount of O2 delivered from whole blood is limited by the diffusion kinetics of dissolved O2 (DO2 ~ 2 × 10−5 cm2/s [11]) and the relatively low solubility of O2 in plasma (~1.3μM mmHg−1 [12]). The presence of acellular Hbs is often linked to increased O2 fluxes as compared to RBCs for two main reasons: 1) The acellular location Hb within the cell-depleted layer near the vessel wall decreases the potential O2 diffusion distance and elevates the local O2 concentrations; 2) acellular HbO2 freely diffuses throughout the plasma space, providing an additional pathway for lateral O2 transport. An amended form of Fick’s law can be written as (1), with contributions to the total radial transport of O2 coming from the diffusion of dissolved O2 (JO2) and the “facilitated” diffusion of HbO2 (JHbO2).
| (1) |
The diffusivity of HbO2 (DHbO2) is in general 1–2 orders of magnitude smaller than the diffusivity of dissolved O2 (DO2), yet the concentration O2 bound to Hb ([HbO2]) is typically 1–2 orders magnitude larger than dissolved O2, ([O2]). For combinations of DHbO2 and [HbO2] on the high end of these ranges, the effect of JHbO2 is significant. This phenomenon has been thoroughly described in the literature [11]. Because of the difference in O2 transport kinetics between HBOCs and RBCs, the effects of HBOCs parameters must be considered under dynamic, flowing conditions.
Several mathematical models have been developed to describe the O2 transport from acellular Hb [13], RBCs [14], and RBC/acellular Hb mixtures [15] flowing through arteriolar-sized gas-permeable tubes. These models are well accepted, and have been extensively validated by gas-exchange experiments in arteriolar-sized conduits [14,16,17]. Such models provide O2 transport behavior to be quantified under dynamic flowing conditions in the absence of biological flow regulation, and these previous O2 transport experiments [7,14,16,17] and simulations [13–15] considered only small values of extra-luminal resistance. To increase the relevance of this type of mathematical modeling, we have applied additional extra-luminal boundary conditions to in vitro studies. We use the mass transfer Biot number (Bi) as a parameter to provide an estimate of the ratio of intra-luminal to extra-luminal O2 transport resistances. Although this parameter is a basic engineering construct that cannot describe the complexities of physiological O2 diffusion and consumption in tissue, the intention is to gain an understanding of the relative importance of HBOC design parameters when extra-luminal O2 processes are “fast”, i.e., low resistance, versus “slow”, i.e., high resistance. Increases in tissue O2 consumption rates correlate with decreased values of extra-luminal resistance [6]. For example, such differences could occur in tissues like brain compared to resting skeletal muscle, where O2 consumption is much larger (3.5 × 10−2 ml O2 min−1 g−1 [18] vs. 4.4 × 10−3 ml O2 min−1 g−1[19]), or skeletal muscle when it is contracting [20].
In vivo, processes that occur in the extra-luminal region are complex and somewhat controversial. For example, studies have indicated a large amount of O2 consumption within the microvascular wall, surrounded by a region of lower O2 consumption [21,22]. These findings are contrasted by a study that reveals the calculated vascular wall O2 consumption to be much larger than what has been observed in similar tissues [23]. There is no comprehensive model that describes the transport processes in this region. Thus, we have used diffusion-type boundary conditions with a variety of extra-luminal resistances. This works particularly well to reflect the increased in vivo O2 transport that was observed for higher O2 affinity Hbs [5,24], and provides an effect that cannot be captured using a constant O2 flux.
In this report, numerical simulations of O2 delivery are presented in 25-μm diameter domains for both pure acellular Hb and RBCs. Hb simulations are shown with variations of a single parameter (p50, n, [Hb], DHbO2), with other parameters held constant. RBC suspensions are simulated for comparison purposes. All simulations were performed for at least two values of extra-luminal resistance (Bi), intended to reflect the scope of potential O2 transport behavior for acellular Hb.
2. Methods
Hb Equilibrium Binding
Hemoglobin is a tetrameric protein composed of four subunits, each of which contains an iron-containing heme group capable of reversibly binding O2, represented by the generic reaction (2).
| (2) |
The parameters commonly used to describe O2 and Hb concentrations are the partial pressure of O2 (p) and Hb fractional saturation (Y). We follow the common physiological convention by referring to O2 tension (p) and O2 solubility (α) rather than [O2]. The values for α depend on hemoglobin concentration [25]; we use values interpolated between the properties of plasma and erythrocyte intra-cellular Hb [12,25]. The values of α and other parameters used in the simulation are given in Table 1. The fraction of total Hb which has O2 bound is given by Y (3).
Table 1.
Parameters used in the calculations
| Symbol | Description | Value | Source |
|---|---|---|---|
| r | radial coordinate | independent parameter | |
| z | axial coordinate | independent parameter | |
| R | tube radius | 12.5 μm | simulation parameter |
| Bi | mass transfer Biot number | 1, 3, or 10 | simulation parameter |
| αpl | O2 solubility coefficient, in plasma | 1.33 μM/mmHg | [12] |
| αrbc | O2 solubility coefficient, inside RBC | 1.47 μM/mmHg | [25] |
| DO2,pl | O2 diffusivity in plasma | 2.75 × 10−5 cm2/s | [11] |
| DO2,rbc | O2 diffusivity inside RBC | 1.48 × 10−5 cm2/s | [48] |
| [Hb]rbc | heme concentration inside RBC | 21.4 mM | [49] |
| α | O2 solubility coefficient | linearly interpolated between αpl and αrbc by [Hb] | |
| DO2 | O2 diffusivity | linearly interpolated between DO2,pl and DO2,rbc by [Hb] | |
| DHbO2 | HbO2 diffusivity | {1, 3, or 10} × 10−7 cm2/s | simulation parameter |
| [Hb]total | total [Hb] for RBC suspensions | 5, 10, or 15 g/dl | simulation parameter |
| λ | normalized radius of RBC rich core | 0.68, 0.74, or 0.90 | [33] |
| μc | core viscosity | 1.5, 2.5, or 3 cP | [35] |
| (3) |
The most common model used to describe this behavior is the Hill equation (4) [26].
| (4) |
The p50 is the p where Y = 0.5 and is a measure of the Hb-O2 binding affinity. The Hill number, n, is an empirical constant which gives Hb/O2 binding cooperativity. The major shortcoming of the Hill equation is the reduced accuracy at regions where Y < 0.1 and Y > 0.9. In the simulations we perform, Y values are always > 0.1, so this is not an issue.
The total O2 content of an Hb solution is the sum of the dissolved O2 and Hb-bound O2 (5).
| (5) |
We use mixed-mean or bulk concentrations, cb, (6) to describe the average value of p or Y at a given axial position [27], where u(r) is the flow profile, R is the tube radius, r is the radial position in the tube, and z is the axial position in the tube.
| (6) |
Several idealized Hbs with regular variations in p50, n, Hb diffusivity, and [Hb] are also simulated in this study to investigate effects of variations of individual parameters on O2 transport. The base molecule on which these variations are imposed has the properties p50 = 15 mmHg, n = 1, DHbO2 = 3 × 10−7 cm2/s, and [Hb] = 10 g/dl. The p50 was chosen because it is close to that of unmodified Hb. The values for n an DHbO2 are chosen because the most recently developed HBOCs have low cooperativity and increased molecular size (as compared to native Hb). The hemoglobin concentration is an intermediate value, although concentration effects are investigated.
Hb Reaction Kinetics
The rate of O2 liberation from Hb is related to HbO2, Hb, and O2 concentrations, as well as the association and disassociation rate coefficients k′ and k, respectively (7).
| (7) |
To reflect differences in k′ and k due to equilibrium binding effects, Moll developed a technique that holds the association coefficient constant and varies the dissociation coefficient in the Hill equation as a function of saturation, Y (8) [28].
| (8) |
The value for k′ is given by Gibson et al. as 3.5 × 106 M−1 s−1 for Hb at 37°C [29]. The use of constant association and variable disassociation coefficients to define activity for different Hbs is consistent with kinetic measurements for native and chemically-modified Hb [30,31]. The underlying assumption for this method is that the offloading of O2 from Hb is not a rate-limiting step and that intra-luminal O2 transport rates are primarily dependent on the speeds of lateral diffusive processes.
Acellular Hb Model
The coupled system of partial differential equations (PDEs) that describes transport of O2 from acellular HbO2 flowing through an arteriolar-sized, gas permeable tube is given in (9,10). The position variables r and z are given in the schematic in Fig. 1A.
Figure 1.
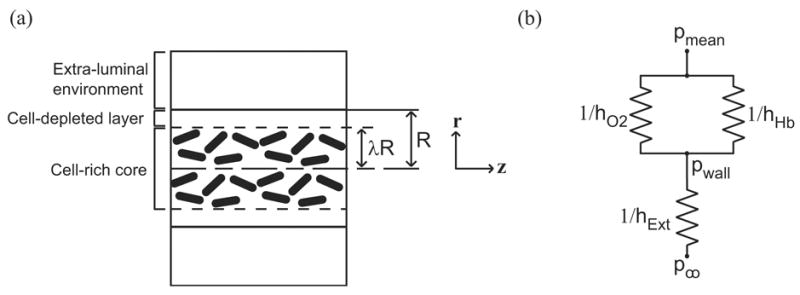
(a) Schematic of tube geometry and thickness of cell-depleted layer when red blood cells are present. (b) Oxygen transport resistance schematic. 1/hO2 and 1/hHb and are the resistances associated with dissolved O2 and Hb. 1/hExt is associated with the applied external resistance and is a function of the Biot number.
| (9) |
| (10) |
The related linear problem (i.e. with no reaction term) is known as the Graetz problem and has an analytical solution for the cases of simple boundary and entry conditions. Because of the tubular, constrained geometry, fluid flow is assumed to be axisymmetric and fully developed. A homogeneous Hb solution is Newtonian and will have a parabolic velocity profile, u(r). For high mass transfer Peclet numbers (Pe = Uavg R/D, PeO2 ≈ 10, PeHbO2 ≈ 102–103, Uavg = average velocity), axial diffusion may be neglected [32]. As a consequence, only axial convection and radial diffusion need be considered. The system in (9,10)was first given by Lemon et al. [13] and validated by experiments in 25-μm diameter artificial capillaries [16].
RBC Suspension Model
For RBC suspensions flowing through narrow tubes, shear-induced particle migrations create a RBC depleted layer near the tube wall (Fig. 1A). For arteriolar-sized domains, it is suitable to treat a region containing RBCs as a non-diffusing pseudo-continuum with average Hb concentrations at a given radial position. The transport equations must account for the differences between the cell-rich core region of radius λR and a concentric cell-depleted shell. The system of equations used to describe O2 transport within flowing RBC suspensions for the Hb-rich core region is given in (11,12).
| (11) |
| (12) |
The local hematocrit, h(r), is taken to be a constant value within the core region (0 ≤ r ≤ λR) and 0 in the shell (λR ≤ r ≤ R). The intracellular RBC Hb concentration, [Hb]rbc, is taken to be 21.4 mM (heme concentration). The average Hb concentration in the core regions depends on the local hematocrit and the velocity profile, which is discussed below.
In the shell region, the absence of Hb leads to pure dissolved O2 diffusion (13).
| (13) |
The velocity profile is blunted in the core region due to the presence of RBCs and is parabolic in the shell region. The profiles used in each region are (14) and (15).
| (14) |
| (15) |
The values for λ are taken from direct experimental measurements 25-μm diameter tubes by Tateishsi et al [33]. Because only values for 20%, 30%, and 40% hematocrits are available, the values for 15% hematocrit and 45% hematocrit are extrapolated linearly. The λ values used for 5, 10, 15 g/dl Hb (i.e. 15%, 30%, 45% hematocrit) are 0.68, 0.74, and 0.90, respectively. Velocity magnitudes in each region may be found from the two-phase flow model of Sharan et al [34]. The values for umax, upl, and B, given in (16), (17) and (18) below, are functions of the core viscosity (μc), plasma viscosity (μo), average flow speed (uavg), and λ.
| (16) |
| (17) |
| (18) |
Core viscosity values of 1.5 cP, 2.5 cP, and 3 cP are used for hematocrits 15%, 30%, and 45%, based on the work of Pries et al. [35], and a plasma viscosity of 1 cP is assumed.
The transport model has two major modifications compared to a version of that presented and validated in RBC artificial capillary experiments by Nair et al. [14]. Because it has been shown that < 5% of the O2 transport resistance is associated with diffusion in or near RBCs [14], we treat O2 tension and O2 solubility as constant inside and outside RBCs, rather than treating individual partitions of intra- and extra-cellular dissolved O2; this assumption has been validated elsewhere [36]. The thickness of the cell-depleted layer is taken directly from experimental observation instead of calculated from a set of algebraic equations which involve a number of hydrodynamic assumptions.
Boundary Conditions
The solution of (9, 10) and (11, 12) requires six boundary conditions to be specified: one each in p and Y at the tube entry, inner radial boundary, and outer radial boundary. The entry conditions are set to p = 100 mmHg (average p in the lungs) and Y of Hb is set to equilibrium with the p entry condition. The condition of axisymmetry requires that the radial partial derivatives of p and Y be set to zero at the centerline of the domain. The impermeability of the domain wall to the diffusion of Hb requires that the radial derivative of Y also be zero at r = R. The rate at which O2 leaks from the intra- to the extra-luminal environment is dictated by a boundary condition of the form (19).
| (19) |
Bi is the mass transfer Biot number, which is adjusted to control the rate at which O2 is transported into the extra-luminal environment. Bi is used as a standardized method to quantify processes, such as O2 diffusion and consumption, which occur outside of the lumen. Using this parameter, the rate at which O2 leaves the lumen is compared to an estimate of the intra-luminal diffusion rate. The formula for Bi is (hExt × L)/DO2, where hExt can be considered an extra-luminal mass transfer coefficient, L is a representative diffusion length, and DO2 is the diffusivity of O2 in solution. Thus, Bi provides an estimate of the ratios of intra-luminal to extra-luminal transport resistance (1/hExt to L/DO2). A circuit diagram schematic of intra- and extra-luminal mass transfer resistances is shown in Fig. 1B. The intra-luminal transport resistances can be represented as the contributions due to O2 diffusion (1/hO2), facilitated HbO2 diffusion (1/hHb), and extra-luminal processes (1/hExt). The value for hExt can be thought of as a function of the Biot number and hO2, where hExt ~ Bi × hO2. The Bi values primarily considered in this study are 1 and 10. All of the simulations performed assume p∞ = 0 mmHg.
Relevant time scales
The PDE formulations contain axial variations in only the first, convective term. This term may be normalized by relevant velocity and length scales [37] to show that considering variations along the length of a tube is analogous to considering the amount of time a parcel of fluid has been within the domain. We relate axial changes as a function of residence time, defined as z/uavg, where z is the axial position and uavg is the average flow velocity. Examples of physiologically relevant residence times can be determined from in vivo data of the hamster arteriolar network (Table 2). The average flow velocities are less than the displayed centerline RBC velocities by a factor of ~ 0.6, according to the analysis in Sharan et al. [34]. The average residence time for blood in a particular arteriolar segment is therefore given as Δt = L/(0.6 × vrbc), with residence times in each arteriolar segment < 0.5 seconds.
Table 2.
Description of Hamster retractor muscle arteriolar network. RBC velocities are taken at centerline. Data from [42].
| order | d, μm | Y | p, mmHg | vrbc, mm/s | length, mm | JO2, mlO2 cm−2 s−1 | Δt, sec |
|---|---|---|---|---|---|---|---|
| A1 | 55 | 0.67 | 39.7 | 15 | 3.67 | 4.0 × 10−5 | 0.41 |
| A2 | 45 | 0.63 | 36.9 | 11 | 1.78 | 4.2 × 10−5 | 0.27 |
| A3 | 34 | 0.61 | 35.8 | 5 | 0.48 | 6.5 × 10−5 | 0.16 |
| A4 | 22 | 0.55 | 32.3 | 2.5 | 0.31 | 4.8 × 10−5 | 0.21 |
Solution method
The system of coupled, nonlinear partial differential equations was solved with Comsol Multiphysics software (Comsol, Palo Alto, CA), a nonlinear, finite-element based solver that is commonly used for chemical/biological engineering applications. An automatic gridding function is used for the initial discretization of the domain, with subsequent grid resolutions applied manually in regions where high spatial resolution is necessary. This is particularly important near the radial boundary at the domain entry because of the occurrence of mass transfer boundary layer-type behavior. A typical grid using ~5000 elements causes the convergence of a Galerkin error monitor. Solutions are exported to Matlab (Mathworks, Natick, MA) for post-processing.
3. Results
Model validation
The model was validated by direct comparison of in vitro artificial capillary experiments performed in 27-μm diameter silicone tubes Page et al. [17] and in 57-μm diameter silicone tubes by McCarthy et al. [7]. The parameters used for the modeling are given in Table 3. Figure 2A shows the simulations replicating the Page deoxygenation experiments on RBCs, unmodified bovine Hb (BvHb), and polymerized bovine Hb (PolyBvHb). The simulation for each of these appears to be in good agreement with the experimental data. Figure 2B shows the data from the McCarthy experiments. The simulations for RBCs, PEG-conjugated Hb (PEGHb), and αα-cross-linked Hb (αα-Hb) are within reasonable agreement of the experimental data. A somewhat larger discrepancy between experiment and simulation is seen for unmodified, purified human Hb (HbA0), which may be due to dimer formation or other experimental problems that are not accounted for by this model.
Table 3.
Parameters used for validation simulations.
Figure 2.
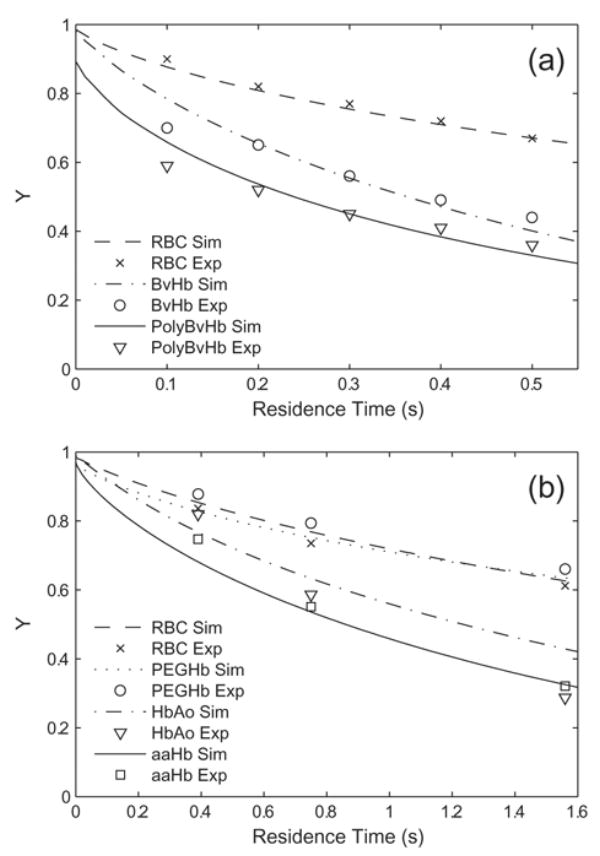
Results of simulations (Sim) compared to experiments (Exp) in (a) 27-μm diameter silicone tubes [Page, 1998a] and (b) 57-μm diameter silicone tubes [McCarthy, 2001]. Hb fractional saturation is plotted versus apparent residence time. The time scales are different because of the difference in tube diameters.
Extra-luminal Resistance Effects
Simulations were performed for a variety of Bi values, ranging from 0.1 to 103 on RBCs and generic acellular Hb. Increasing Bi > 100 yields negligible increases in total O2 transport, thus the case of Bi = 100 can be considered the maximum expected rate of O2 transport. This is comparable to the in vitro experiments of Page et al. [17] and McCarthy et al. [7]. The total O2 delivered versus apparent residence time is plotted in Fig. 3 for RBCs (p50 = 29 mmHg, [Hb] = 15 g/dl Hb). At 0.5 seconds, Bi = 1 gives 40% of the O2 delivered at the maximum rate (i.e. for Bi = 100), while Bi = 10 gives 90% of this amount. The O2 delivery for Bi = 3 is plotted to give an intermediate value between Bi = 1 and Bi = 10, and to show that variations of O2 transport in this region are not linear with Bi. The O2 delivered for Bi < 0.1 is small on the time scales we have considered and is not plotted.
Figure 3.
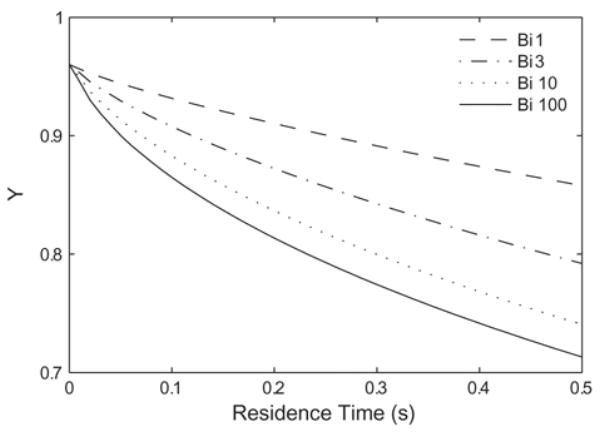
Effect of Biot number on the deoxygenation of a red blood cell suspension ([Hb] = 15 g/dl, p50 = 29 mmHg, n = 2.6). Increasing the extra-luminal O2 transport resistance (decreasing Bi) slows the rate of desaturation.
Effects of O2 binding kinetics and cooperativity
Rates of O2 dissociation may, theoretically, become rate limiting in this system. We performed simulations on very small diameter tubes, where the speeds of lateral O2 transport may be comparable to the rates at which O2 disassociates from Hb. If the dissociation of O2 from Hb is limiting to the amount of O2 released into the surrounding environment, the reaction kinetics must be modeled more carefully than the generalized treatment in (7) and (8). We performed simulations with several dissociation rate constants (k) to assess the magnitude at which the rate becomes limiting. Figure 4A shows the results of simulations carried out for Bi = 10 with a HBOC similar to tetramer hemoglobin, (p50 = 15 mmHg, n = 3, DHbO2 = 1 × 10−6 cm2/s, [Hb] = 10 g/dl). For clarity, we use the inverse of the expression in (8), so that a constant off-rate is applied and the on-rate is varied locally as a function of p, p50, and n, although the expression (8) gives equivalent results. Increases in k lead to progressively larger amounts of O2 transport, until the O2 transport approached some maximum value. This begins to occur above k = 10 s−1, where order of magnitude increases in k are required in order to raise the amount of O2 transport by similar, small amounts. The most common off rate used in Moll-type treatments (44 s−1) are in a range where O2 delivery is insensitive to small variations in k, and thus is adequate for the size scales we study. The off-rates reported in the literature are of a similar order [31]. However, significant limitations on O2 transport occur at either slower off-rates or smaller tube diameter than are considered here. For O2 dissociation kinetics to be a considerable limiting factor on the overall O2 transport behavior for our particular geometry, k must be reduced to on the order of ≤ 1 s−1.
Figure 4.

(a) Variations in Hb desaturation as a function of the off rate(k, s−1) when Bi = 10. The Hb has the properties p50 = 15 mmHg, n = 3, DHbO2 = 1 × 10−6 cm2/s, and [Hb] = 10 g/dl. (b) Effect of varied O2 binding cooperativity on O2 transport for generic Hb with p50 = 5 mmHg and p50 = 35 mmHg (DHbO2 = 3 × 10−7 cm2/s, [Hb] = 10 g/dl Hb) with Bi = 10. Cooperativity increases O2 delivery for high p50 Hbs and decrease O2 delivery for low p50 Hbs.
The effect of cooperative binding is dependent on both the p50 of the Hb solution and the extra-luminal resistance (the Biot number). Cooperative Hbs bind a greater fraction of O2 at p values near the p50 than non-cooperative Hb. For this reason, the amount of O2 available to be released tends to be greater for low n Hb, as long as p > p50. In cases where p50s are high, non-cooperative Hb is less saturated than cooperative Hb in the lungs. If the total O2 content is sufficiently reduced due to this, decreases in n may serve to reduce the amount of O2 released, although it also reduces the potential for O2 transport further downstream. An example of this behavior is given in Fig. 4B, which shows the O2 released from p50 = 5 mmHg and p50 = 35 mmHg Hb, each with n = 1 and n = 3 (DHbO2 = 3 × 10−7 cm2/s, [Hb] = 10 g/dl, Bi = 10). For p50 = 5 mmHg, increasing n from 1 to 3 decreases O2 transport by about 20%. Hb with n = 1 has only 4% less initial Hb saturation than Hb with n = 3, so the behavior is dominated by the differences in the available O2 when p > p50. For Hb with p50 = 35 mmHg, the Hb saturation at initial conditions is 22% less for n = 1 than n = 3. This leads to about a 40% increase in O2 transport for n = 3 Hb as compared to n = 1 Hb. At a p50 ~ 15 mmHg, the two trends exhibited roughly cancel each other out and there is no appreciable cooperativity effect. We will show later that for Bi = 10, Hbs with p50 ≤ 15 mmHg are of primary interest, and in such cases, increased cooperativity would decrease O2 transport. When the Biot number is decreased to 1, Hbs with p50s less than 35 mmHg show decreased O2 transport with increased n.
Facilitated Diffusion
The effect of modifying DHbO2 is only significant for lower values of extra-luminal resistance, such as when Bi = 10 (Fig 5). The additional O2 transport due to this effect is ~ 30% for simulations (DHbO2 = 1 × 10−6 cm2/s versus DHbO2 = 1 × 10−8 cm2/s). The effect of decreasing DHbO2 past 1 × 10−7 cm2/s is small. These facilitated-diffusion effects are not significant for Bi = 1, partly because of the decreased importance of intra-luminal diffusive processes when extra-luminal resistance is high, and partly due to the high degree of saturation of Hb. The values of DHbO2 we simulated are {10, 3, 1, 0.1} × 10−7 cm2/s. Assuming Hb as a spherical molecule in the Stokes-Einstein equation (20), DHbO2 values {10, 3, 1} × 10−7 cm2/s correspond to molecular radii of {2.3, 6.8, 23} nm.
Figure 5.
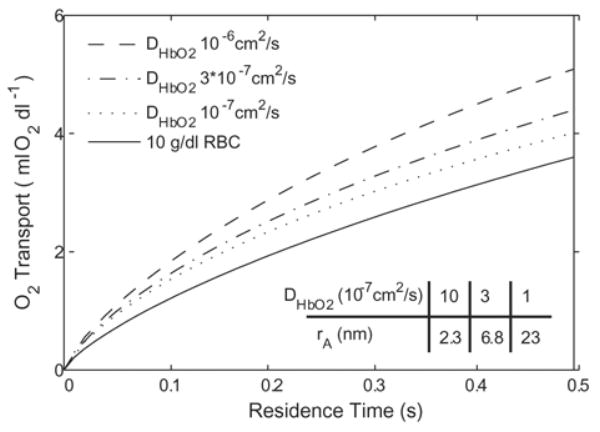
Effect of varied HbO2 diffusivity on O2 transport for generic Hb (p50 = 15 mmHg, n = 1, [Hb] = 10 g/dl) with Bi = 10. These effects are not seen to be significant at Bi = 1. Table gives equivalent molecular radii for each DHbO2 value, assuming a spherical Hb molecule diffusing through plasma.
| (20) |
Oxygen Affinity
Simulations were performed on a variety of idealized acellular Hbs with varying p50 (base molecule: n = 1, DHbO2 = 3 × 10−7 cm2/s, [Hb] = 10 g/dl) and are summarized in Fig. 6A and Fig. 6B. Regardless of the applied extra-luminal resistance, p50 has a significant effect on the amount of O2 transport. At the residence times that we study (0.5 seconds), ~1/10 of the total O2 content is delivered to the surrounding environment for Bi = 1 and ~ 1/3 of the total O2 content for Bi = 10. At either Bi number evaulated, increasing the p50 above 25 mmHg has a very small effect on the total O2 released. The largest variation in behavior is seen between p50 = 5 and p50 = 15 mmHg. For Bi = 1, RBC the total O2 transport is slightly less than Hb with p50 = 15 mmHg and n = 1, despite the much lower O2 affinity of RBCs (p50 = 29 mmHg). For Bi = 10, RBCs deliver similar amounts of O2 as Hb with p50 5 = mmHg. In this case, an increase in p50 from 5 to 25 mmHg has the potential to increase O2 transport by ~ 1/3 as compared to RBCs.
Figure 6.
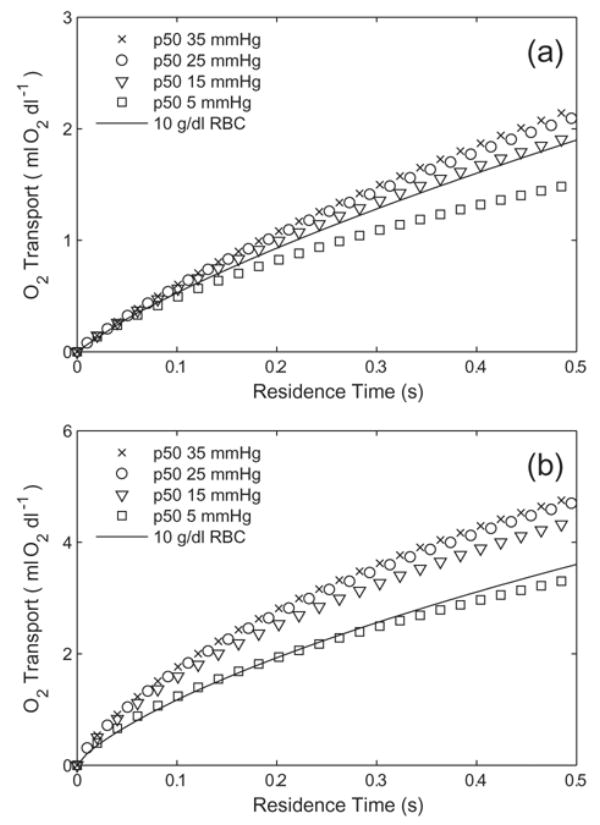
Oxygen transport by a generic Hb (n = 1, DHbO2 = 3 × 10−7 cm2/s, [Hb] = 10 g/dl Hb) with varied p50s for (a) Bi = 1 and (b) Bi = 10. RBCs (p50 = 29 mmHg, n = 2.6, [Hb] = 10 g/dl) are plotted for comparison.
Hb Concentration
The effect of Hb concentration is given in Fig. 7A and Fig. 7B. For Bi = 1, the O2 transported by Hb with p50 = 15 mmHg, n = 1, and DHbO2 = 3 × 10−7 cm2/s matches reasonably well with RBCs at 5, 10, and 15 g/dl (Fig. 7A). Tripling [Hb] from 5 g/dl to 15 g/dl increases the amount of O2 delivered by less than 50%. For Bi = 10, O2 transport from p50 = 15 mmHg is larger at every [Hb] matched with that for RBCs (Fig. 7B). The increases in total O2 transport by tripling [Hb] is about 80% for Hb and 60% for RBCs.
Figure 7.
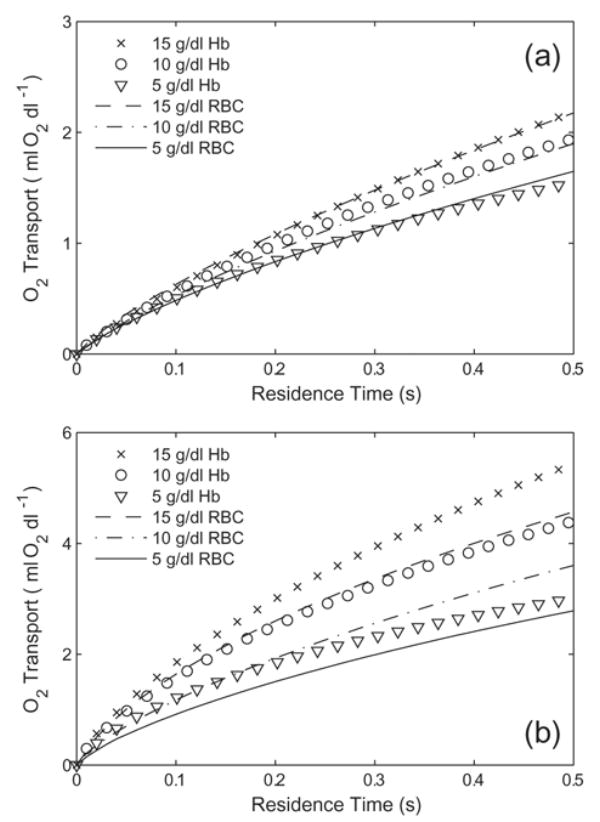
Oxygen transport by a generic Hb solution (p50 = 15 mmHg, n = 1, DHbO2 = 3 × 10−7 cm2/s) with varied Hb concentration for (a) Bi =1 and (b) Bi = 10. RBCs (p50 = 29 mmHg, [Hb] = 5–15 g/dl) are plotted for comparison.
Optimal Hb Properties to mimic RBCs on a heme-per-heme basis
The properties of an acellular Hb that match the O2 transport from RBCs at the same Hb concentration are a function of the applied boundary conditions, especially the Biot number. We have already shown that Hb with p50 = 15 mmHg and n = 1 is a good match for RBCs when Bi = 1, or Hb with p50 = 5 mmHg and n = 1 is a good match with Bi = 10 (Fig. 6A and Fig. 6B). Figure 8 shows the O2 transport from three acellular Hbs with significant binding cooperativity (n = 2.5) that supply comparable amounts of O2 to 10 g/dl RBCs. The results for RBCs should not be confused with the results in Fig. 3, which are for RBCs at 15 g/dl. Assuming n = 2.5 and DHbO2 = 3 × 10−7 cm2/s, the p50s that match Bi = 1, 3, and 10 are 20, 15, and 9 mmHg, respectively. For each of these cases, an increase in DHbO2 would necessitate a decrease in the p50 to provide the same amount of O2.
Figure 8.
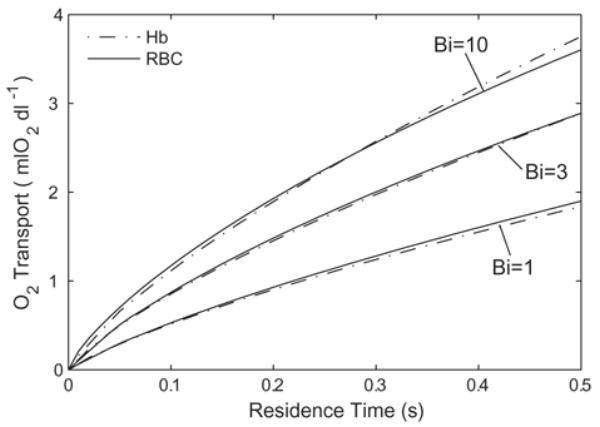
Oxygen transport from RBCs and from Hbs at various values of extra-luminal resistance that deliver similar amounts of O2. The Biot numbers for each grouping, starting from the bottom are 1, 3, and 10. The RBCs and Hb both have a [Hb] of 10 g/dl. The Hb has n = 2.5 and DHbO2 = 3 × 10−7 cm2/s. The p50s for Bi = 1, 3, and 10 are 20 mmHg, 15 mmHg, and 9 mmHg, respectively. Non-cooperative Hb choices can be seen in Fig. 6.
Lateral Oxygen Gradients
Thus far, we have reported simulated results for macroscopic transport of O2 from flowing Hb solutions into the surrounding environment, i.e., radial transport. Figure 9 shows the lateral intra-luminal O2 gradients for two of the Hb/RBC pairs plotted in Fig. 8, which give comparable O2 transport. These gradients are defined as the difference between p at the centerline and p at the radial lumen boundary. For each Bi number used in the simulations, the gradient for RBCs is larger than that for acellular Hb, an effect related to the reduction of intra-luminal O2 transport resistance for acellular Hb. For Bi = 1, the RBC lateral gradient is roughly twice as much as that for Hb; for Bi = 10 it is roughly three times that of Hb. Decreasing extra-luminal resistance (increasing Bi) increases the magnitude of lateral gradients.
Figure 9.
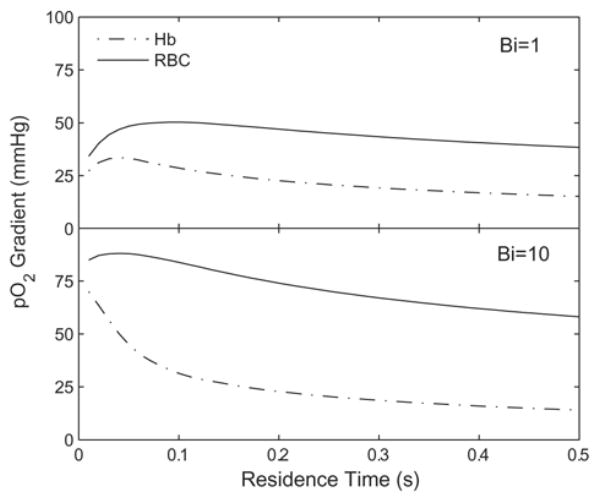
Lateral O2 gradients for Hb solutions and RBC suspensions which give equivalent O2 transport. The results are for the same simulations as shown in Fig. 8.
4. Discussion
Hemoglobin-based oxygen carriers can offload O2 more efficiently in arteriolar-sized vessels than red blood cells because they overcome transport barriers associated with low plasma O2 solubility, increased distance for O2 diffusion, and limited intracellular oxyHb diffusion (facilitated diffusion). Over supply of O2 can lead to two potentially undesirable consequences: 1) the onset of autoregulatory vasoconstriction and consequent reduced tissue oxygenation; 2) a decrease in Hb-bound O2 available for downstream O2 delivery in capillary beds. Oxygen delivery in arteriolar-sized tubes can be controlled by O2 equilibrium binding properties (p50 and n), diffusion kinetics (DHbO2), and Hb concentration.
Animal studies have shown that isolated decreases in p50 [24], increases in n [38], or increases in molecular size [39] all correlate with increased tissue perfusion. In vivo experiments have also shown that Hbs with a combination of high p50 and small molecular size cause vasoconstriction and hypertension [3,4]. Hemoglobin molecules that are small (i.e. near the size of unmodified Hb) may diffuse fast enough to augment O2 transport by carrying Hb-bound O2 from the center of a vessel towards the wall. Decreases in O2 affinity and increases in molecular size (i.e. DHb and consequently DHbO2) have been observed to accelerate O2 offloading for in vitro O2 transport models [7,13,15–17]. This combination of in vivo and in vitro observations has contributed to the theory that an over supply of O2 by acellular Hb in arterioles leads to autoregulatory vasoconstriction.
Here, we report mathematical modeling of O2 transport from Hb solutions in arteriolar-sized domains to assess the efficacy of prospective HBOCs. There are differences between these simulations and relevant in vivo conditions to be considered: the simulated extra-luminal boundary conditions are simpler, the domain is long and non-branching, and the acellular Hb solutions are not mixed with RBCs. However, the model provides a useful tool in understanding the relative importance of p50, n, [Hb], and DHbO2 for acellular Hbs.
To reduce the number of variables for HBOC design, we limited direct comparisons of acellular Hb and RBCs to those at the same Hb concentration. It should be noted that humans can survive with significantly reduced hematocrits [40], and with the added efficiency of O2 transport by acellular Hb solutions, it may not be necessary to create HBOCs that fully replace lost Hb content. The [Hb] for HBOCs that have been produced for clinical purposes vary from 4.2 g/dl to 13.1 g/dl, yet in vivo experiments have shown that low [Hb] HBOCs can provide adequate O2 for respiration [5].
We first tested the assumption that O2 dissociation kinetics do not limit overall O2 transport processes. We find the off rates used for the model Hbs, which were taken from measured values in the literature [31], to be within a range of values that total O2 transport is relatively insensitive.
Previous models of O2 transport in arteriolar-sized domains by acellular Hbs [13,15] have not considered extra-luminal processes that set the O2 gradient from intra- to extra-luminal space. At present there is no generally accepted model of arteriolar O2 consumption, but to take these overall processes into consideration mathematically, we lumped all extra-luminal processes into one parameter, the Biot number (Bi). Bi provides an inverse measure of extra-luminal resistance such that high resistance would reflect a relatively lower extra-luminal O2 consumption rate and vice versa. There is a balance between the amount of O2 available for transport, dictated by equilibrium binding effects (p50 and n) and the rate at which O2 diffuses laterally. This balance is dependent on the value of the extra-luminal resistance. When desaturation processes are fast (Bi small), the magnitudes of DO2 and DHbO2 do more to limit the total amount of O2 delivered than when desaturation processes are slower. Conversely, equilibrium binding effects are more important when the desaturation rates are slow. For 15 g/dl RBCs with Bi = 3, the average O2 flux at 0.5 seconds is 4.4 × 10−5 mlO2 cm−2 s−1 based on the results of the simulations shown in Fig. 3. The O2 flux, Javg, is calculated as (21) where Δ[O2]total is the change in total O2 content, R is the tube radius, and Δt is the elapsed residence time.
| (21) |
Physiological measurements, such as those given in Table 2 use (21) to determine Javg between two discrete points on a given arteriole. The value for Javg is specific to the position on an arteriole and the time increment, thus it is an estimate. The measured O2 fluxes for arterioles were tabulated for a large number of in vivo studies by Vadapalli et. al. [23]. The average O2 fluxes from 7 vessels with diameters between 19.5 μm to 35 μm (compiled in [23], original data from [41–44]) is 4.6 × 10−5 mlO2 cm−2 s−1. The Bi values we considered in this study (1 and 10) provide RBC fluxes which bracket this value, an attempt to describe a range of potential behavior.
Of the three design parameters we considered, the effect of DHbO2 is the most straight-forward. Facilitated diffusion is only significant for larger Biot numbers when the overall O2 transport is relatively fast. This is partially due to the emphasis on intra-luminal processes when extra-luminal resistance is small. This phenomenon may also be partly understood from a circuit representation of mass transfer processes (Fig. 1B). The intra-luminal transport resistances can be represented as the contributions due to O2 diffusion (1/hO2), facilitated HbO2 diffusion (1/hHb), and extra-luminal processes (1/hExt), where h is a generalized mass-transfer coefficient. The total resistance, Ω, between the lumen and the far field may be written as (22).
| (22) |
According to this, the value of hHb has the greatest proportionate effect on the value of Ω when extra-luminal resistance is small (i.e. hExt is large). The high degree of Hb saturation for the high extra-luminal resistance cases considered here also limit the potential gradients in Y. Decreasing DHbO2 by an order of magnitude from 10−6 cm2/s to 10−7 cm2/s suppresses most of the facilitated diffusion effect. If we consider a spherical molecule diffusing through water (according to the Stokes-Einstein equation), a molecular radius ~ 23 nm (i.e. DHbO2 = 10−7 cm2/s) would define the minimal size to eliminate additional transport due to facilitated diffusion. Hb polymers have been tested above this size range [45], with the intention of decreasing interactions of Hb with the endothelium; such modifications would not have an appreciable effect in reducing facilitated diffusion.
It may not be feasible to create PEG–Hb molecules that are large enough to completely eliminate facilitated diffusion, because PEG-Hb molecular size is enlarged by increasing the number and/or the length of attached PEG chains, which causes an increase in colloid osmotic pressure (COP) through hydraulic interactions with PEG. Increasing the molecular weight of native Hb by ~ 30 kDa due to PEGylation correlates to an increase in COP of 34 mmHg for 4.2 g/dl Hb solutions [46]. Such an increase in molecular weight leads to a 3-fold increase in molecular radius (to 9.3 nm). The amount of PEG required to increase the molecular size to 23 nm (i.e. increasing DHbO2 to 10−7 cm2/s) is likely to cause increases in COP > 100 mmHg. For such cases, it appears that the best strategy would be to further decrease p50. This model allows a quantitative estimation at how large such a reduction should be.
The effects of O2 affinity and binding cooperativity are inter-related and each is a function of the applied extra-luminal resistance. Regardless of the extra-luminal resistance value, varying the p50 has the potential to have a large effect on the amount of O2 released by Hb. The range of p50s for which O2 offloading is the most sensitive in our model (5–15 mmHg) is much lower than the p50 of RBCs (29 mmHg). In the context of this model, any increase in p50 above 25 mmHg does not serve a purpose. The p50 of an HBOC must be dropped by about 10 mmHg in order to see the same amount of O2 delivered relative to RBCs in the Bi = 10 case compared to the Bi = 1 case. The specific choices of p50 are also subject to the value of n, which is itself subject to extra-luminal conditions, and the value of p50. For the faster desaturation rate we studied, with p50 > 15 mmHg, increasing n increases O2 transport. For Hbs with high p50 and low cooperativity, a significant fraction of Hb will not bind O2 in the lungs; this Hb will be non-functional in terms of supplying O2 and may potentially participate in oxidative processes [47]. In either case, this leads to a flawed design. For p50s below 15 mmHg, cooperative binding decreases the amount of O2 supplied. This allows for the use of slightly higher p50 Hb to provide equivalent O2 transport as a lower cooperativity, lower p50 Hbs.
A brief investigation shows that the intra-luminal lateral p gradients required to deliver a given amount of O2 are much greater for RBCs than for acellular Hb. This is a consequence of the transport resistance associated with the cell-depleted layer (for RBCs) and the reduction in transport resistance due to facilitated diffusion (for acellular Hb).
The cell-depleted layer acts as an insulator to the cell-rich core region of RBCs, thus requiring larger gradients to drive O2 diffusion through the cell- depleted layer, and causing the total O2 delivery to be less sensitive to conditions at the vessel wall. The lack of a cell-depleted layer allows acellular Hb to have a lower p50, although it is more subject to extra-luminal conditions. As a consequence of this increased sensitivity, acellular Hb cannot be formulated to deliver O2 like RBCs for all potential extra-luminal environments. RBCs deliver O2 most like an acellular Hb with a p50 of 15 mmHg when Bi = 1 or 5 mmHg when Bi = 10. Therefore, low p50, increased n, and decreased DHbO2 are all strategies to artificially impose transport resistance onto acellular Hb and suppress O2 transport in the precapillary microcirculation.
Conclusion
If the goal of HBOC design is to limit precapillary O2 transport, this study provides some general guidelines for desired properties. High O2 binding affinity and cooperativity are desired, as well as an increase in molecular size and decreased diffusivity compared to native Hb. The p50 should be reduced to the p50 of unmodified Hb (15 mmHg) or less, depending of extra-vascular O2 consumption rates. For some classes of chemically modified Hbs, there are practical limitations on the ranges of design parameters available.
As we have shown, the problem with the design of HBOCs is not the difficulty of creating a molecule capable of carrying O2 to tissues; it is that the HBOCs tend to do their job too well, delivering O2 with higher efficiency than RBCs. An HBOC designed to transport O2 like RBCs must take into account the large scale reduction in intra-luminal transport resistance innate to acellular Hb solutions and find additional methods to limit O2 in the arterioles. The theory that HBOCs should be designed to target O2 release in specific, downstream sections of the vasculature has come about only after a large body of a research had been performed on early-generation HBOC products. In the context of this study, we can see that HBOCs that have p50s similar or greater than that of RBCs, tend to unload O2 faster than RBC suspensions. High O2 affinity HBOCs with decreased DHbO2 have shown increased efficacy as blood substitutes in animal models, as compared to the first-generation Hb products [3,5].
So far our studies have focused on the effects of HBOC design parameters on O2 delivery from solutions containing only RBCs or pure acellular Hb. Future studies will be aimed at more physiologically relevant conditions, such as Hb/RBC mixtures that would result from with the clinical use of HBOCs. An additional concern in the design of HBOCs is the uptake of nitric oxide from vessel walls by acellular Hb, another phenomenon that has been related to the onset of vasoconstriction. This removal of NO is thought to be accelerated in the presence of HBOCs due to the decreased diffusion distance and the high diffusivity of acellular Hb. Coupled O2 delivery and NO uptake simulations can be performed using a mathematical model with the same general form as the one presented here. Studies to investigate Hb-NO binding kinetics are planned for the future.
Acknowledgments
This work was supported by Grant R01 HL 076163 from the NIH, NHLBI. K.V., D.B., and R.W. are employees of Sangart, Inc. K.V., D.B., and R.C. hold stock options in the company. R.W. is the President, CEO and Chairman of the Board of Sangart.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Winslow RM. Blood Substitutes. In: Winslow RM, editor. Historical background. Elsevier; San Diego: 2006. p. 5. [Google Scholar]
- 2.Vandegriff KD. Blood Substitutes. In: Winslow RM, editor. The role of oxygen and hemoglobin diffusion in oxygen transport by cell-free hemoglobin. Elsevier; San Diego: 2006. p. 60. [Google Scholar]
- 3.Winslow RM, Gonzales A, Gonzales M, Magde MR, McCarthy M, Rohlfs RJ, Vandegriff KD. Vascular resistance and the efficacy of red cell substitutes in a rat hemorrhage model. J Appl Physiol. 1998;85:993–1003. doi: 10.1152/jappl.1998.85.3.993. [DOI] [PubMed] [Google Scholar]
- 4.Rohlfs RJ, Bruner E, Chiu A, Gonzales A, Gonzales M, Magde D, Magde MD, Vandegriff KD, Winslow RM. Arterial blood pressure responses to cell-free hemoglobin solutions and the reaction with nitric oxide. J Biol Chem. 1998;273:12128–12134. doi: 10.1074/jbc.273.20.12128. [DOI] [PubMed] [Google Scholar]
- 5.Tsai AG, Vandegriff KD, Intaglietta M, Winslow RM. Targeted O2 delivery by low-P50 hemoglobin: a new basis for O2 therapeutics. Am J Physiol Heart Circ Physiol. 2003;285:H1411–H1419. doi: 10.1152/ajpheart.00307.2003. [DOI] [PubMed] [Google Scholar]
- 6.Intaglietta M, Johnson P, Winslow RM. Microvascular and tissue oxygen distribution. Cardiovasc Res. 2000;32:632–643. [PubMed] [Google Scholar]
- 7.McCarthy M, Vandegriff KD, Winslow RM. The role of facilitated diffusion in oxygen transport by cell-free hemoglobins: implications for the design of hemoglobin-based oxygen carriers. Biophys Chem. 2001;92:103–117. doi: 10.1016/s0301-4622(01)00194-6. [DOI] [PubMed] [Google Scholar]
- 8.Vandegriff KD, Malavalli A, Wooldridge J, Lohman J, Winslow RM. MP4, a new nonvasoactive PEG-Hb conjugate. Transfusion. 2003;43:509–516. doi: 10.1046/j.1537-2995.2003.00341.x. [DOI] [PubMed] [Google Scholar]
- 9.Budhiraja V, Hellums JD. Effect of hemoglobin polymerization on oxygen transport in hemoglobin solutions. Microvasc Res. 2002;64:22–33. doi: 10.1006/mvre.2002.2418. [DOI] [PubMed] [Google Scholar]
- 10.Lehninger AL. Principles of Biochemistry. 2. Worth; New York: 1993. [Google Scholar]
- 11.Kreuzer F. Facilitated diffusion of oxygen and its possible significance; a review. Respir Physiol. 1970;9:1–30. doi: 10.1016/0034-5687(70)90002-2. [DOI] [PubMed] [Google Scholar]
- 12.Christofordes C, Laasberg L, Hedley-Whyte J. Effect of temperature and on solubility of O2 in human plasma. J App Phys. 1969;26:56–60. doi: 10.1152/jappl.1969.26.1.56. [DOI] [PubMed] [Google Scholar]
- 13.Lemon DD, Nair PK, Boland EJ, Olson JS, Hellums JD. Physiological factors affecting O2 transport by hemoglobin in an in vitro capillary system. J Appl Physiol. 1987;62:798–806. doi: 10.1152/jappl.1987.62.2.798. [DOI] [PubMed] [Google Scholar]
- 14.Nair PK, Hellums JD, Olson JS. Prediction of oxygen transport rates in blood flowing in large capillaries. Microvasc Res. 1989;38:269–285. doi: 10.1016/0026-2862(89)90005-8. [DOI] [PubMed] [Google Scholar]
- 15.Page TC, Light WR, Hellums JD. Prediction of microcirculatory oxygen transport by erythrocyte/hemoglobin solution mixtures. Microvasc Res. 1998;56:113–126. doi: 10.1006/mvre.1998.2088. [DOI] [PubMed] [Google Scholar]
- 16.Boland EJ, Nair PK, Lemon DD, Olson JS, Hellums JD. An in vitro capillary system for studies on microcirculatory O2 transport. J Appl Physiol. 1987;62:791–797. doi: 10.1152/jappl.1987.62.2.791. [DOI] [PubMed] [Google Scholar]
- 17.Page TC, Light WR, McKay CB, Hellums JD. Oxygen transport by erythrocyte/hemoglobin solution mixtures in an in vitro capillary as a model of hemoglobin-based oxygen carrier performance. Microvasc Res. 1998;55:54–64. doi: 10.1006/mvre.1997.2055. [DOI] [PubMed] [Google Scholar]
- 18.Altman PL, Ditter DS. Biology Data Book. III. FASEB; Bethesda: 1971. p. 1700. [Google Scholar]
- 19.Paul RJ. Vascular Smooth Muscle, Chemical energetics of vascular smooth muscle. chapt 9. sect. 2, vol. II. Am Physiol Soc; Bethesda: 1980. Handbook of Physiology. The Cardiovascular System; p. 201. [Google Scholar]
- 20.Lash JM, Bohlen HG. Perivascular and tissue PO2 in contracting rat spinotrapezius muscle. Am J Heart Circ Physiol. 1987;252:H1192–H1202. doi: 10.1152/ajpheart.1987.252.6.H1192. [DOI] [PubMed] [Google Scholar]
- 21.Tsai AG, Friesnecker B, Mazzoni MC, Kerger H, Buerk DG, Johnson PC, Intaglietta M. Microvascular and tissue oxygen gradients in the rat mesentery. Proc Natl Acad Sci USA. 1998;95:6590–6595. doi: 10.1073/pnas.95.12.6590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tsai AG, Friesnecker B, Cabrales P, Winslow RM, Intaglietta M. Microvascular oxygen distribution in an awake hamster window chamber model during hyperoxia. Am J Physiol Heart Circ Physiol. 2003;285:H1537–H1545. doi: 10.1152/ajpheart.00176.2003. [DOI] [PubMed] [Google Scholar]
- 23.Vadapalli A, Pittman RN, Popel AS. Estimating oxygen transport resistance of the microvascular wall. Am J Physiol Heart Circ Phyiol. 2000;279:H657–H671. doi: 10.1152/ajpheart.2000.279.2.H657. [DOI] [PubMed] [Google Scholar]
- 24.Sakai H, Tsai AG, Rohlfs RJ, Hara H, Takeoka S, Tsuchida E, Intaglietta M. Microvascular response to hemodilution with Hb vesicles as red blood cell substitutes: influence of O2 affinity. Am J Physiol Heart Circ Physiol. 1999;276:H553–H562. doi: 10.1152/ajpheart.1999.276.2.H553. [DOI] [PubMed] [Google Scholar]
- 25.Christofordes C, Hedley-Whyte J. Effect of temperature and hemoglobin concentration on solubility of O2 in blood. J App Phys. 1969;27:592–596. doi: 10.1152/jappl.1969.27.5.592. [DOI] [PubMed] [Google Scholar]
- 26.Hill AV. The combinations of haemoglobin with oxygen and with carbon dioxide. Biochem J. 1913;7:471–480. doi: 10.1042/bj0070471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rosner D. Transport processes in chemically reacting flow systems. Dover; New York: 1986. [Google Scholar]
- 28.Moll W. The influence of hemoglobin diffusion on oxygen uptake and release by red cells. Respir Physiol. 1968;6:1–15. doi: 10.1016/0034-5687(68)90014-5. [DOI] [PubMed] [Google Scholar]
- 29.Gibson QH, Kreuzer F, Meda E, Roughton FJW. The kinetics of human haemoglobin in solution and in the red cell at 37C. J Physiol (London) 1955;129:65–89. doi: 10.1113/jphysiol.1955.sp005339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Vandegriff KD, Le Tellier YC, Winslow RM, Rohlfs RJ, Olson JS. Determination of the rate and equilibrium constants for oxygen and carbon monoxide binding to R-state human hemoglobin cross-linked between the α subunits at lysine 99. J Biol Chem. 1991;266:17049–17059. [PubMed] [Google Scholar]
- 31.Vandegriff KD, Bellelli A, Samaja M, Malavalli A, Brunori M, Winslow RM. Kinetics of NO and O2 binding to a maleimide poly(ethylene glycol)-conjugated human haemoglobin. Biochem J. 2004;382:183–189. doi: 10.1042/BJ20040156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Papoutsakis E, Ramkrishna D, Lim HC. The extended Graetz problem with Dirichlet wall boundary-conditions. Appl Sci Res. 1980;36:13–34. [Google Scholar]
- 33.Tateishsi N, Suzuki Y, Cicha I, Maeda N. O2 release from erythrocytes flowing in a narrow O2 permeable tube: effects of erythrocyte aggregation. Am J Heart Circ Physiol. 2001;281:H448–H456. doi: 10.1152/ajpheart.2001.281.1.H448. [DOI] [PubMed] [Google Scholar]
- 34.Sharan M, Popel AS. A two-phase model for blood in narrow tubes with increased effective viscosity near the wall. Biorheology. 2001;38:415–428. [PubMed] [Google Scholar]
- 35.Pries AR, Niehaus D, Gaehtgens P. Blood viscosity in tube flow: dependence on diameter and hematocrit. Am J Physiol. 1992;263:H1770–H1778. doi: 10.1152/ajpheart.1992.263.6.H1770. [DOI] [PubMed] [Google Scholar]
- 36.Hellums JD, Nair PK, Huang NS, Ohshima N. Simulation of intra-luminal gas transport processes in the microcirculation. Ann Biomed Eng. 1996;24:1–24. doi: 10.1007/BF02770991. [DOI] [PubMed] [Google Scholar]
- 37.Incropera FP. Fundamentals of Heat and Mass Transfer. Wiley; Hoboken: 2002. [Google Scholar]
- 38.Cabrales P, Kanika ND, Manjula BN, Tsai AG, Acharya SA, Intaglietta M. Microvascular PO2 during extreme hemodilution with hemoglobin site specifically pegylated at cys-93(β) in hamster window chamber. Am J Physiol Hear Circ Physiol. 2004;287:H1609–1617. doi: 10.1152/ajpheart.00146.2004. [DOI] [PubMed] [Google Scholar]
- 39.Sakai H, Hara H, Yuasa M, Tsai AG, Takeoka S, Tsuchida E, Intaglietta M. Molecular dimensions of Hb-based O2 carriers determine constriction of resistance arteries and hypertension. Am J Physiol. 2000;279:H908–H915. doi: 10.1152/ajpheart.2000.279.3.H908. [DOI] [PubMed] [Google Scholar]
- 40.Winslow RM. Blood Substitutes. In: Winslow RM, editor. Clinical physiology: oxygen transport and the transfusion trigger. Elsevier; San Diego: 2006. p. 45. [Google Scholar]
- 41.Kuo L, Pittman RN. Effect of hemodilution on oxygen transport in arteriolar networks of hamster striated muscle. Am J Physiol Hear Circ Physiol. 1988;254:H331–H339. doi: 10.1152/ajpheart.1988.254.2.H331. [DOI] [PubMed] [Google Scholar]
- 42.Swain DP, Pittman RN. Oxygen exchange in the microcirculation of hamster retractor muscle. Am J Physiol. 1989;256:H247–H255. doi: 10.1152/ajpheart.1989.256.1.H247. [DOI] [PubMed] [Google Scholar]
- 43.Kuo L, Pittman RN. Influence of hemoconcentration on arteriolar oxygen transport in hamster striated muscle. Am J Physiol Hear Circ Physiol. 1990;259:H1694–H1702. doi: 10.1152/ajpheart.1990.259.6.H1694. [DOI] [PubMed] [Google Scholar]
- 44.Torres Filho IP, Kerger H, Intaglietta M. PO2 measurements in arteriolar networks. Microvasc Res. 1996;51:202–212. doi: 10.1006/mvre.1996.0021. [DOI] [PubMed] [Google Scholar]
- 45.Matheson B, Kwansa HE, Bucci E, Rebel A, Koehler RC. Vascular response to infusions of a non-extravasating hemoglobin polymer. J Appl Physiol. 2002;93:1479–1486. doi: 10.1152/japplphysiol.00191.2002. [DOI] [PubMed] [Google Scholar]
- 46.Winslow RM, Lohman J, Malavalli A, Vandegriff KD. Comparison of PEG-modified albumin and hemoglobin in extreme hemodilution in the rat. J Appl Physiol. 2004;97:1527–1534. doi: 10.1152/japplphysiol.00404.2004. [DOI] [PubMed] [Google Scholar]
- 47.Nagababu E, Ramasamy S, Rifkind JM. Site-specific cross-linking of human and bovine hemoglobins differentially alters oxygen binding and redox side reactions producing rhombic heme and heme degradation. Biochemistry. 2002;41:7407–7415. doi: 10.1021/bi0121048. [DOI] [PubMed] [Google Scholar]
- 48.Spaan JA, Kreuzer AE, Van Wely FK. Diffusion coefficients of oxygen and hemoglobin as obtained simultaneously from photometric determination of the oxygenation of layers of hemoglobin solutions. Pfluegers Arch. 1980;384:241–251. doi: 10.1007/BF00584558. [DOI] [PubMed] [Google Scholar]
- 49.Weibel ER. Structure and function in the mammalian respiratory system. Harvard University Press; Cambridge: 1984. The pathway for oxygen. [Google Scholar]


