Low-Dose-Radiation Stimulated Natural Chemical and Biological Protection Against Lung Cancer

Abstract

Research is being conducted world-wide related to chemoprevention of future lung cancer among smokers. The fact that low doses and dose rates of some sparsely ionizing forms of radiation (e.g., x rays, gamma rays, and beta radiation) stimulate transient natural chemical and biological protection against cancer in high-risk individuals is little known. The cancer preventative properties relate to radiation adaptive response (radiation hormesis) and involve stimulated protective biological signaling (a mild stress response). The biological processes associated with the protective signaling are now better understood and include: increased availability of efficient DNA double-strand break repair (p53-related and in competition with normal apoptosis), stimulated auxiliary apoptosis of aberrant cells (presumed p53-independent), and stimulated protective immune functions. This system of low-dose radiation activated natural protection (ANP) requires an individual-specific threshold level of mild stress and when invoked can efficiently prevent the occurrence of cancers as well as other genomic-instability-associated diseases. In this paper, low, essentially harmless doses of gamma rays spread over an extended period are shown via use of a biological-based, hormetic relative risk (HRR) model to be highly efficient in preventing lung cancer induction by alpha radiation from inhaled plutonium.

INTRODUCTION

Lung cancer is the leading cause of cancer death worldwide and cigarette smoking is considered the major risk factor. Tobacco smoke contains a complex of chemical carcinogens as well as the alpha-particle-emitter polonium-210 (²¹⁰Po). Because the population of smokers worldwide continues to be very large, effective lung cancer preventative modalities that can be implemented in a clinical setting for such high-risk individuals are needed. In this paper evidence is provided that low doses and dose rates of sparsely ionizing gamma radiation and extended exposure can efficiently prevent lung cancer among high-risk populations via stimulating and prolonging the body’s natural defenses (natural chemical and biological prevention).

Ionizing radiation has been present in the environment since the beginning of the universe. Radiation sources remain everywhere, including potassium-40 (⁴⁰K) in our bodies and in plants and animals we ingest; and ⁴⁰K and the uranium-238 (²³⁸U) decay chain in our homes, in the soil, and in the air we breathe. The sun we depend on for sustaining life on earth is also a source of ionizing radiation, as are other entities in space. Through evolution, mammalian life forms have developed natural cancer preventative processes (chemically and biologically regulated) that are stimulated by low doses and dose rates of sparsely ionizing forms of radiation (e.g., x rays, gamma rays, beta particles) (Parsons 2001, 2003; Sakai et al. 2003; Liu 2007). Low doses and dose rates of these radiations stimulate protective intercellular and intracellular signaling that leads to activated natural protection (ANP) against cancer and other genomic-instability-associated diseases (Olivieri et al. 1984; Mitchel et al. 1999; Sakai et al. 2006; Mitchel 2007; Scott 2007a). The protective signaling appears to be a generalized response to mild stress above an individual-specific threshold level (Scott 2005).

Radiation ANP, which provides a biological basis for radiation hormesis as now defined (Calabrese et al. 2007), appears to be an evolutionary benefit of the interaction of low-level ionizing radiation with mammalian life forms on earth. Thus, ANP is evolutionarily conserved (Mitchel 2006, 2007). High radiation doses and dose rates rather than preventing cancer, inhibit the protective processes that suppress cancer (Sakai et al. 2006; Liu 2007; Scott and Di Palma 2007).

Low-Dose Radiation ANP

Low-dose radiation ANP involves induced high-fidelity DNA repair in competition with normal apoptosis (presumably p53-dependent), activation of an auxiliary protective apoptosis-mediated (PAM) process that selectively removes precancerous (Scott et al. 2003; Scott 2004; Portess et al. 2007) and other aberrant cells, and also involves induced immune functions (Feinendegen et al. 2007; Liu 2007). However, the protective processes are transient over time intervals of hours or days, rather than permanent effects of an exposure (Feinendegen et al. 2007).

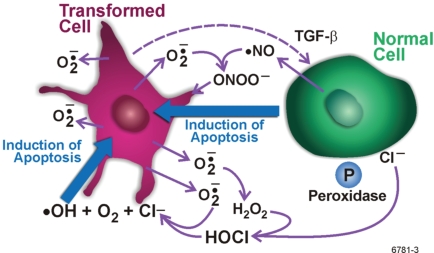
Bauer (1995, 1996, 2000) has described what is known about the PAM process among fibroblasts based on numerous signaling studies by his research group using that cell type. Figure 1 relates to the description. The protective process involves a sophisticated system of interdependencies and interactions of reactive oxygen and nitrogen species. The release of transforming growth factor beta (TGF-β1) by transformed cells is a key early event. Nontransformed cells, when activated, release a novel peroxidase (P) and nitric oxide (•NO). Superoxide anions ( $({\text{O}}_2^{\overline{•}})$) generated and released by transformed cells participate in the intercellular signaling and make transformed cells the selective target for intercellular induction of apoptosis (i.e., transformed cells are selectively removed via apoptosis). Chloride ions (Cl⁻) and hydrogen peroxide (H₂O₂) also participate in the intercellular signaling. The interactions of the indicated molecules result in two currently known major signaling pathways to protective apoptosis that are based on hypochlorous acid (HOCl)/hydroxyl radicals (•OH) and •NO/peroxynitrite (ONOO⁻). H₂O₂ plays a key role by fostering the HOCl/•OH pathway and inhibiting the •NO/ONOO⁻ pathway (Bauer 2000). Additional pathways to apoptosis are likely associated with the auxiliary PAM process (Bauer 2007), with the selected path possibly depending on the cell type to be eliminated via apoptosis (mutants, neoplastically transformed cells, micronucleated cells, etc.), the local cellular environment, the nature of the damage to DNA, and the stimulating agent (Scott and Di Palma 2007).

FIGURE 1.

Signaling pathways for the protective apoptosis mediated (PAM) process in fibroblast based on Bauer (1995, 1996, 2000), as redrawn by Scott and Di Palma (2007). See the main text for a detailed explanation of the findings of Bauer (1995, 1996, 2000). Different signaling pathways to apoptosis may apply for other cell types.

Stochastic threshold radiation doses (which are presumed to differ for each person and body organ/tissue) are required for ANP (Scott 2005). However, somewhat higher doses can inhibit protective signaling (e.g., signaling related the PAM process) and also suppress the immune system. This nonlinear continuum of dose-response is described by a J-shaped response curve (Calabrese and Baldwin 2001; Calabrese 2004, 2005; Calabrese et al. 2007).

Demonstrated Benefits of Radiation ANP

Low doses and dose rates of sparsely ionizing radiations have been found to:

• Protect against chromosomal damage from a subsequent high dose (Olivieri et al. 1984; Azzam et al. 1994).

• Protect against mutation induction by a high radiation dose if given before or after the high dose (Day et al. 2006, 2007).

• Eliminate precancerous (neoplastically transformed) cells (Azzam et al. 1996; Redpath et al. 2001).

• Prevent chemical-induced skin cancer (Sakai et al. 2003).

• Stimulate increased immune system functioning (Liu 2007; Ina and Sakai 2005).

• Suppress lung cancer induction by alpha radiation (Sanders 2007; Scott 2007b) and spontaneous cancers of all types (Chen et al. 2007).

• Suppress metastasis of existing cancer (Sakamoto et al. 1997; Sakamoto 2004).

• Protect against diseases other than cancer (Sakai et al. 2006).

Based on a number of years of adaptive-response research, we developed a biological-based, hormetic relative risk (HRR) model for cancer induction (Scott 2007b; Scott and Di Palma 2007) that accounts for radiation ANP. The current version of the model is discussed in the Methods section.

METHODS

Computational and Statistical Approaches

For fitting RR equations to lung cancer data for humans (Mayak plutonium [Pu] facility workers) exposed to alpha and gamma radiations, Bayesian inference methods (Gelman et al. 1995; Carlin and Louis 1996; Siva 1998) implemented via Markov chain Monte Carlo (MCMC) (Gilks et al. 1996; Gamerman 1997) were employed with WinBUGS software (Spiegelhalter et al. 2003), based on uniform priors for parameters to be estimated and a very long single chain as was previously done (Scott 2007b). However, in addition to fitting RR equations to the data, predictions were made for a different baseline cancer incidence to facilitate making comparisons to animal data. Predictions were also made for different irradiation scenarios. MCMC analyses were implemented with WinBUGS assuming tumor cases after a given radiation exposure to have a Poisson distribution. Radiation doses for a given dose group were assumed to be uniformly distributed over the group.

Judgments about convergence were based on comparing the Monte Carlo error and the posterior distribution’s standard deviation for each free parameter. The Monte Carlo error (computed in WinBUGS) represents an estimate of the difference between the mean of the sampled values (which are used as an estimate of the mean of the posterior distribution) and the true mean of the posterior distribution. Ratios of the Monte Carlo error for parameters to the posterior distribution standard deviation that were < 0.05 were considered consistent with convergence (Spiegelhalter et al. 2003). Autocorrelation were also monitored during the MCMC run to facilitate judging how long to run the chain. Where lung cancer RR data were compared for different species (dogs, rats, humans), they were adjusted to a common baseline incidence of 0.00095. Standard errors for cancer incidence were evaluated as recommended in Fleiss (1981) when evaluating the error for a proportion. Subjective (judgmental) upper bounds were used for reported zero cancer incidences. The bounds were set equal to one standard error for the cancer incidence, based on 1 assigned cancer case. A subjective upper bound of 1 was also assigned to RR estimates that were calculated to be < 1, but were not significantly different from 1.

Here, the focus is on application of the HRR model (Scott 2007b) to lung cancer data for protracted exposure to low doses of alpha radiation from inhaled plutonium in combination with very low doses of gamma rays to demonstrate the highly efficient prevention of alpha-radiation-induced lung cancer by gamma-ray ANP. Alpha radiation administered alone is a potent inducer of lung cancer. Small doses (close to natural background radiation levels) can cause a significant increased incidence (Sanders et al. 1976, 1977; Lundgren et al. 1991; Sanders 2007). However, for combined exposure to low-dose alpha and low-dose gamma rays, the gamma-ray ANP could possibly prevent cancer induction by alpha radiation. The level of protection can be quantified using the HRR model.

Hormetic Relative Risk Model

The HRR model was developed assuming proportionality between the RR for radiation-induced cancer and the RR for radiation-induced neoplastic transformation (Scott 2007b; Scott and Di Palma 2007). Thus, the model is empirical (although biological-based) and is not based on detailed mechanistic modeling of the underlying biological processes associated radiation-induced cancer. A fundamental assumption is that stochastic thresholds are associated with both activation and suppression of ANP-related signaling (Scott 2005). Protective thresholds associated with activation of protective signaling are assumed to be much lower than the deleterious thresholds associated with suppression of protective signaling (Scott 2005). Many other models of radiation-induced harm and a few for radiation-induced protection are also published but a survey of these models is beyond the intended scope of this paper.

With the current version of our HRR model, the irradiated population is separated into two dose- and dose-rate dependent parts: (1) a fraction F without ANP (unprotected fraction) and (2) a fraction (1−F) that has ANP (protected fraction). For persons with ANP, the average cancer relative risk is given by

$$R{R}_{\text{ANP}}= (1-\text{PROFAC}){\text{RR}}_{\text{LNT}}$$ (1)

where RR_ANP is the relative risk for persons with ANP (i.e., protected individuals) and RR_LNT is the relative risk for persons without ANP and is based on the linear-no-threshold (LNT) assumption. Risk is evaluated relative to an unirradiated population. Bayesian methods allow evaluating the expected proportion of the irradiated population that is protected for a given dose and dose rate and radiation combination when formally fitting the HRR model to data (Scott 2007b). These methods also allow predicting the expected impacts of different radiation exposure scenarios.

The protection factor (PROFAC) takes on values from 0 to 1 and here accounts for prevention of cancer among persons with gamma-ray ANP. The PROFAC estimates presented in this paper are evaluated relative to exposure to natural background radiation (conventional zero dose group). A value PROFAC = 0.25 would indicate that cancer would be expected to be prevented in 1 of every 4 individuals among those with radiation ANP. For a hypothetical population containing 1000 protected (by low-dose gamma-ray ANP) heavy cigarette smokers, if 100 were expected to develop lung cancer because of smoking, then with a gamma-ray PROFAC = 0.25, 25 of the 100 would be expected to be prevented from developing smoking-related lung cancer. Thus, not every protected person may escape lung cancer occurrence.

For alpha-radiation-induced lung cancer, relative risk can be evaluated based on a LNT function which includes the baseline cancer incidence (Scott 2007b):

$$R{R}_{\text{LNT}}=1+[(1-B)/B]K_{\alpha }{D}_{\alpha },$$ (2)

where B is the baseline (spontaneous) cancer incidence, K_α is the presumed always-positive slope parameter in the HRR model and D_α is the alpha radiation absorbed dose to the target organ. Equation 1 can be used for evaluating cancer RR for combined exposure to low-dose alpha and gamma rays when ANP is presumed to occur for everyone while Equation 2 can be used for exposure only to alpha radiation (no ANP presumed). Both equations are limited to doses below those that cause death from acute effects (Scott 2007b). The PROFAC relates only to low-dose gamma rays (or a radiation type of similar interaction characteristics such as x rays and beta radiation when used instead of gamma rays).

The population average RR can be evaluated as the weighted average:

$$\text{RR}=F*R{R}_{\text{LNT}}+(1-F) {\text{RR}}_{\text{ANP}}.$$ (3)

For low-dose-rate exposure and for lung cancer, Equation 3 is expected to apply for gamma-ray doses up to at least 2000 mGy, since gamma-ray doses in this range were not found to contribute to an increase in lung cancer risk under circumstances of combined exposure to alpha and gamma radiations (Tokarskaya et al. 2002). Equations 1−3 should not be used for the very large doses that cause death from acute effects. For moderate and high alpha radiation doses, RR_LNT can be calculated to be > 1. In such cases the results should be limited to the maximum absolute risk of 1. For a baseline (spontaneous) cancer incidence B, the RR therefore has the constraint RR ≤ 1/B.

For combined exposure to alpha and gamma rays and when RR_LNT = 1 and gamma-ray ANP occurs, Equation 3 yields the following useful relationship:

$$F+(1-F)(1-\text{PROFAC})=\text{RR}.$$ (4)

It follows from Equation 4 that if one has and estimate of both PRO-FAC and RR (e.g., an observed RR < 1), one can then estimate the fraction, F, of the irradiated population that is not protected (i.e., does not have ANP) and the corresponding fraction, 1 − F, that is protected (i.e., has ANP). This is demonstrated in the section entitled Predicting Cancer Incidences Assuming K_α to Be Evolutionarily Conserved.

In circumstances where one has an estimate of RR_ANP (based on exposure to alpha plus gamma radiation) when everyone is presumed protected and one for RR_LNT (for exposure only to alpha radiation) when no one is presumed protected, PROFAC for a given dose level D_α can be estimated using the relationship:

$$\text{PROFAC}=\text{1}-\text{{(observed} \text{RR} \text{under alpha plus gamma irradiation) / (observed or calculated} \text{RR} \text{under exposure only to alpha radiation)}.}$$

A large number of crude PROFAC estimates associated with low-LET radiation ANP against spontaneous lung cancer were recently published based on data from many epidemiological and ecological studies (Sanders and Scott 2007). Only limited epidemiological data are discussed in the sections that follow and do not include data related to radon exposure. Modeling radon-induced lung cancer was beyond the scope of this research, which has focused on exposures involving Pu isotopes alone or in combination with gamma rays (animal studies) or in combination with gamma rays and cigarette smoke (humans).

Lung cancer data from several animal studies that involved inhaling Pu isotopes (²³⁸Pu, ²³⁹Pu) alone or in combination with a ytterbium-169 (¹⁶⁹Yb) label are also discussed in the next section. The gamma-ray emitting ¹⁶⁹Yb label is widely used to facilitate monitoring how much Pu deposits in the respiratory track during inhalation exposures. Study designs have ensured that the gamma-ray doses from ¹⁶⁹Yb were too low to cause significant deleterious biological damage (Sanders et al. 1993; Lundgren et al. 1995; Muggenburg et al. 1996). In this paper the focus is on beneficial effects of such small gamma-ray exposures, i.e., gamma-ray ANP against lung cancer.

RESULTS AND DISCUSSION

Estimates of PROFAC and K_α for Different Species

Table 1 shows PROFAC estimates and subjective lower bounds for low-dose, low-dose-rate, gamma-ray prevention of lung cancer among alpha-radiation exposed female Wistar rats that either inhaled the alpha-emitter ²³⁹Pu alone (in dioxide form, i.e., ²³⁹PuO₂) or ²³⁹PuO₂ labeled with gamma-ray-emitter ¹⁶⁹Yb. The data are based on studies conducted earlier by Sanders et al. (1976, 1993) and recently re-evaluated in the context of gamma-ray ANP (Sanders 2007). Here, gamma-ray doses are presumed sufficient for ANP for every rat but not high enough for its inhibition. Also, alpha radiation doses in Table 1 are presumed not to be high enough to overwhelm or suppress gamma-ray-induced protective signaling. The gamma-ray doses in Table 1 are similar in magnitude to x-ray doses received from computed tomography (Thompson and Cullom 2006). However, for the data in Table 1, the gamma-ray exposure was protracted over several months (physical half-life for Yb-169 = 32 d). Extending the length of gamma-ray exposure is considered to prolong the time period over which protective signaling occurs. This increases the efficiency of protection as has been demonstrated for eliminating precancerous cells in vitro (Elmore et al. 2006) and was implicated for lung cancer in rats after combined alpha and gamma irradiation (Lundgren et al. 1995).

TABLE 1.

Lung cancer incidence among Wistar rats that inhaled Pu-239 + Yb-169 and associated expected (assuming no protection) and observed RR and related gamma-ray associated protection factor against cancer based on data from Sanders (2007)

Average Alpha Radiation Dose (mGy)	Average Gamma Radiation Dose (mGy)	Number of Animals	Lung Cancer Incidence	Expected Relative Risk Based on LNTa	Observed Relative Risk	PROFAC
0	0	1052	0.00095 ± 0.00095	1	1
56 ± 20	1	1389	0 (0.00072)b	20	0 [1]c	1.0 [0.95]d
190 ± 90	2	343	0 (0.0029)b	67	0 [1]c	1.0 [0.985]d
620 ± 160	1	145	0 (0.0069)b	216	0 [1]c	1.0 [0.995]d

^aBased on rats not exposed to gamma rays from a Yb-169 label and Equation 2 (filled circles in Figure 2) with RR evaluated based on B = 0.00095 rather than the value of 0.00150 reported by Sanders (2007) for rats exposed only to ²³⁹Pu alpha radiation; the calculated value for K_α is 3.3 × 10⁻⁴ mGy⁻¹.

^b

Binomial-distribution-associated standard error (SE) for frequency (Fleiss 1981) had exactly one rat developed lung cancer, given that no cancers were observed:

$$\text{SE}={[f(1-f)/N]}^{1/2}, \text{with} f=1/N, \text{where} N= \text{the number of animals exposed.}$$

^cSubjective upper bound (RR = 1).

^dSubjective lower bound on PROFAC based on a subjective upper bound of 1 for the observed RR; calculated using the expected RR (column 5) as a reference, i.e., PROFAC = 1 − (1/Expected RR). This equation is based on Equation 1.

Calculated values for RR_LNT based on fitting Equation 2 to lung cancer incidence data for rats exposed only to ²³⁹Pu (Sanders 2007) to estimate K_α (Table 2) are included in Table 1 and are based on the assumptions that no rats were protected (i.e., F = 1). The dose-group-specific excess absolute risk per unit dose was used to obtain three estimates (for group average doses not exceeding 780 mGy) of K_α that were then averaged to obtain K_α = 3.3 × 10⁻⁴ ± 9.5 × 10⁻⁴ mGy⁻¹ (Table 2). This estimate is reasonably close to the value of 1.2 × 10⁻⁴ ± 9.0 × 10⁻⁵ mGy⁻¹ previously reported for lung cancer in Mayak plutonium facility workers (Scott 2007b) based on Equation 1, which also includes the PROFAC. It is also close to the value of 1.0 × 10⁻⁴ ± 5.0 × 10⁻⁵ mGy⁻¹ previously reported for lung cancer in F344/Crl rats that inhaled the alpha emitting aerosol ²³⁹PuO₂ (Scott 2007b), based on studies conducted by Lundgren et al. (1991). Using the lowest two dose groups reported by Muggenburg et al. (1996) for ²³⁸PuO₂ alpha-particle-induced lung cancer in beagle dogs, a slope parameter of 1.7 × 10⁻⁴ ± 1.0 × 10⁻⁵ mGy⁻¹ was obtained and is consistent with the result obtained for rats and humans. Using the lowest four dose groups reported by Sanders et al. (1977) for ²³⁸PuO₂ alpha-particle-induced lung cancer in Wistar rats, a slope parameter of 1.5 × 10⁻⁴ ± 1.3 × 10⁻⁴ mGy⁻¹ was obtained and is consistent with other estimates summarized in Table 2. For the indicated exposure groups used by Sanders et al. (1976), group average alpha radiation doses to the lung range from 50 to 1530 mGy.

TABLE 2.

Evidence for slope parameter K_α for lung cancer induction being similar for different mammalian species and rodent strains.

Species or Strain	Radiation Types	Kα in mGy−1	Equation Used	Estimated or Implicated Value for PROFAC
Humans (Kokhryakov et al. 1996)	239Pu alpha + external gamma	1.2 × 10−4 ± 9.0 × 10−5	Equation 1	0.86 ± 0.07
F344/Crl rats (Lundgren et al. 1991)	239Pu alpha + 169Yb gamma	1.0 × 10−4 ± 5.0 × 10−5	Equation 2	0 (high dose data only)a
Wistar rats (Sanderset al. 1977)	238Pu alpha	1.5 × 10−4 ± 1.3 × 10−4	Equation 2	0
Wistar rats (Sanders 2007)	239Pu alpha	3.3 × 10−4 ± 9.5 × 10−5	Equation 2	0
Beagle dogs (Muggenburg et al. 1996)	238Pu alpha +169Yb gamma	1.7 × 10−4 ± 1.0 × 10−5	Equation 2	0 (high dose data only)a

^aThe protective signaling induced by low-dose gamma rays is assumed to be inhibited or overwhelmed by very high doses of alpha radiation.

The estimates for K_α in Table 2 for humans, rats, and dogs differ by less than a factor of 3.5. Their un-weighted average is 1.7 × 10⁻⁴ ± 9.1 × 10⁻⁵ mGy⁻¹, which could be presumed to apply to rats, dogs, and humans, and is later shown to appear to also apply to mice. Genetic polymorphisms that impact on DNA repair efficacy are expected to impact on the parameters K_α and B but not on the PROFAC (Scott 2007b). The similar results in Table 2 for K_α for the different genetic backgrounds suggest that genetic polymorphisms related to DNA repair may not, however, greatly impact K_α. For a point of reference, studies on relative susceptibility for lung cancer occurrence for pair-wise comparisons for different genetic polymorphisms that impact on DNA repair show relative susceptibility factors < 1.5 (Hu et al. 2004; Hung et al. 2005; Benhamou and Sarasin 2005; Schwartz et al. 2007). Genetic polymorphisms that impact on the PAM process and immune system functioning are expected to influence the PROFAC and B but not K_α (Scott and Di Palma 2007).

Note from Table 1 that the very small, essentially harmless protracted gamma-ray doses (1 to 2 mGy) appear to completely prevent (PROFAC = 1.0) the occurrence of lung cancer (spontaneous and alpha-radiation-induced) for alpha radiation doses up to several hundred mGy. However, subjective lower bounds on PROFAC presented in Table 1 would allow for a possible lower level of protection (PROFAC as low as 0.95).

While the RR was expected to be 216 in the absence of ANP (Table 1), based on data for exposure only to alpha radiation (presumably unprotected rats), adding an essentially harmless protracted gamma-ray dose (1 mGy) appears to have protected against 100 % of the expected lung cancers. Thus, all of the gamma-ray irradiated rats were apparently very well protected from lung cancer occurrence for the alpha radiation dose range indicated in Table 1.

Gamma-ray ANP against both alpha-radiation- and smoking-related lung cancers in humans is implicated by the RR data in Table 3 for Mayak plutonium facility workers chronically exposed at low rates to alpha and gamma radiations over many years. The data in Table 3 are based on Khokhryakov et al. (1996). The male and female workers inhaled the alpha-emitter ²³⁹Pu and were also exposed to external gamma-ray sources created as neutron-activation products in the workplace (Tokarskaya et al. 1997, 2002). Only alpha radiation doses were reported by Khokhryakov et al. (1996). Gamma-ray doses were presumed negligible. Many of the male workers were long-term heavy smokers. RR was evaluated relative to age-and gender-matched external controls, based on Russian national statistics. Variation in the baseline incidence in Table 3 relates to differences in the age/gender structure of the different dose groups (Khokhryakov et al. 1996).

TABLE 3.

Observed and expected dose-interval-averaged lung cancer RR for Mayak plutonium facility workers based on application of the HRR model to data from Khokhryakov et al. (1996)

Alpha Radiation Dose Range (mGy)	Mean Baseline Incidence per 100,000a	Observed Incidence per 100,000	Observed Unadjusted Average RR	Expected Unadjusted Average RR, HRR Modelb	Expected Adjusted Average RR, HRR Modelc
0–12	41 ± 25	16 ± 16	0.39 ± 0.46	0.36 ± 0.07	0.24 ± 0.07
12.1–50	57 ± 41	30 ± 30	0.53 ± 0.65	0.56 ± 0.09	0.40 ± 0.07
51–200	76 ± 55	120 ± 68	1.58 ± 1.45	1.59 ± 0.14	1.30 ± 0.12
201–800	86 ± 93	400 ± 200	4.65 ± 5.54	4.66 ± 0.23	4.24 ± 0.21
801–3200	99 ± 106	2780 ± 870	28.1 ± 31.3	28.1 ± 0.53	29.2 ± 0.55

^aBased on Russian national statistics (Khokhryakov et al. 1996)

^bBased on fitting the HRR model (Equation 1 used) to the data in column 4.

^cExpected (predicted) average RR based on the HRR model when the baseline B = 0.00095; results are averaged over each dose range indicated and have not previously been reported.

Equation 3 was fitted to the lung cancer group average RR data in column 4 of Table 3 using WinBUGS. The expected unadjusted and adjusted RR values obtained are presented in columns 5 and 6, respectively, of Table 3. The expected unadjusted RR values are based on the variable baseline incidences in column 2. The expected adjusted RR values are based on B = 0.00095. It was assumed that alpha radiation doses for each dose group were uniformly distributed over the group-specific dose intervals indicated and that gamma-ray doses were negligible, except for their stimulation of protective signaling (ANP). All exposed workers were assumed to be protected (i.e., F = 0 and PROFAC > 0) by gamma-ray ANP for the range of alpha radiation doses in Table 3. Thus, Equation 3 reduced to Equation 1, which was actually used. Being protected (i.e., having ANP), however, does not guarantee that cancer will be prevented for everyone. Note that the range of alpha radiation doses over which gamma-ray ANP is presumed to apply is up to 3200 mGy.

The MCMC analysis comprised 1 million iterations with the first 800,000 results discarded as burn-in as was previously done (Scott 2007a). However, this time predictions were also made during the MCMC run for a fixed baseline cancer incidence of B = 0.00095. For the variable baseline incidences, predictions were also made about the expected impact of excluding the alpha or the gamma radiation exposure. Predictions for the different dose groups were based on means of posterior distributions of the group average RR. This facilitates comparing results for humans to animal data discussed below. Means and standard deviations of the posterior distributions of model parameters obtained were K_α = 1.2 × 10⁻⁴ ±9.0 × 10⁻⁵ mGy⁻¹ and PROFAC = 0.86 ± 0.07 (Table 2). These estimates are identical to those previously reported (Scott 2007b).

For the lowest two dose groups in Table 3, the observed group average lung cancer RR values were not significantly > 0 (p > 0.05) nor were they significantly < 1. A subjective upper bound on these group average RR is 1 (corresponds to no change in the absolute risk), which would also be supportive of gamma-ray ANP against alpha-radiation-induced lung cancer, given that K_α was estimated to be 1.2 × 10⁻⁴ mGy⁻¹. A value for K_α > 0 implicates an increase in risk in the absence of gamma-ray ANP. The PROFAC estimate of 0.86 ± 0.07 was previously presumed to apply to both alpha radiation and cigarette smoke (Scott 2007b).

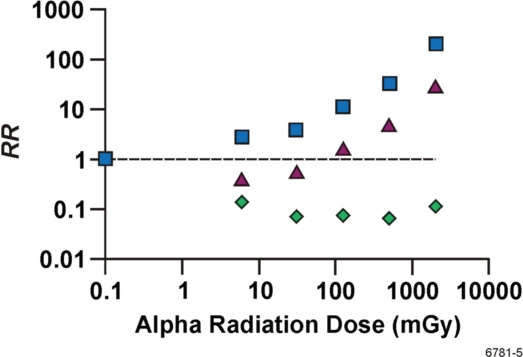
In the absence of gamma-ray ANP, the observed group average RR values in Table 3 would be expected to be approximately 7 times higher, as reflected by results in Figure 2. The figure presents the MCMC predicted dose group averages for RR_LNT (squares) which are estimates of the RR after exposure only to alpha radiation. The corresponding unadjusted RR values from Table 3 (column 5) for combined alpha + gamma irradiation are also presented in Figure 2 (triangles). In addition, the MCMC predicted dose group averages for RR when exposed only to gamma rays are also presented (diamonds). Data points are not connected with lines or curves because baselines differ for each dose group and results are based on averaging over wide alpha radiation dose intervals. The results in Figure 2 indicate that alpha-radiation-induced lung cancer can be prevented via gamma-ray ANP even in the dose range for which RR > 1.

FIGURE 2.

Expected dose-interval-averaged RR for lung cancer based on Mayak worker data (Table 3, column 4) and the HRR model. Data are plotted vs. the group-specific, midrange alpha radiation dose. Triangles, combined alpha + gamma irradiation (Table 3, column 5); squares, alpha radiation only as predicted with WinBUGS; diamonds, gamma radiation only as predicted with WinBUGS. The results for gamma radiation only were plotted vs. the corresponding alpha radiation midrange dose because gamma-ray doses were not reported by Khokhryakov et al. (1996). Logarithmic scales are used on both axes. The horizontal line is for RR = 1.

Lung Cancer Dose-Response Relationships for Different Species

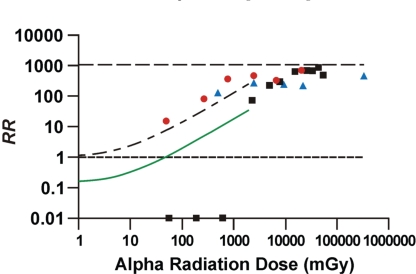
Figure 3 shows the lung cancer RR data for combined alpha and gamma-ray exposure of Wistar rats (Sanders 2007) and beagle dogs (Muggenburg et al. 1996). The Wistar rat data of Sanders (2007) for exposure only to alpha radiation are also included for comparison and to demonstrate the dramatic protection implicated to be associated with low-dose gamma-ray exposure when the alpha radiation dose is less than about 1000 mGy. For the data points and model prediction in Figure 3, RR is based on B = 0.00095. This places an upper limit of 1/0.00095 or 1053 on RR (upper horizontal line in Figure 3). It was assumed that the PROFAC = 0 for the alpha-irradiated dogs, because of the mainly very high radiation doses involved. Similarly PROFAC was assumed equal to zero for Wistar rats exposed only to alpha radiation.

FIGURE 3.

Lung cancer RR: unadjusted RR for Wistar rats that inhaled ²³⁹Pu + ¹⁶⁹Yb (squares) based on data from Sanders (2007); adjusted RR for Wistar rats for inhalation exposure to only ²³⁹Pu (circles) based on data from Sanders (2007); adjusted RR for Beagle dogs (triangles) that inhaled ²³⁸Pu based on data from Muggenburg et al. (1996); expected adjusted RR for protected adult humans (smooth curve) exposed via inhalation to ²³⁹Pu in combination with external gamma rays, based on Equation 3 with F = 0, PROFAC = 0.86, and K_α = 1.2 × 10⁻⁴ mGy⁻¹; expected adjusted RR for unprotected humans (rising dashed curve) based on Equation 3 with F = 1, PROFAC = 0, and K_α = 1.2 × 10⁻⁴. Logarithmic scales are used on both axes. Values for RR = 0 are plotted at RR = 0.01. The zero dose-group for which RR = 1 is excluded. The lower horizontal line is for RR = 1. The upper horizontal line is for RR = 1053. PuO₂ aerosols were used in all of the animal studies.

Note that the adjusted RR in Figure 3 seemed to converge for the different species and approach an asymptotic value below the upper limit of 1053 as the alpha radiation dose increased above 10,000 mGy. The mainly very high alpha radiation doses received by dogs (500 to 340,000 mGy) appear to have completely inhibited or overwhelmed protective signaling associated with gamma-ray ANP. The simulated smooth curve in Figure 3 is for protected adult humans and is based on Equation 3 with F = 0, K_α =1.2 × 10⁻⁴ mGy⁻¹ and PROFAC = 0.86. The upper dashed curve in Figure 3 is for exposure only to alpha radiation and applies to unprotected adult humans and was obtained by setting F = 1, K_α = 1.2 × 10⁻⁴ mGy⁻¹, and PRO-FAC = 0 in Equation 3. In this case, Equation 3 reduces to RR_LNT.

Alpha radiation doses > 2000 mGy appeared to have inhibited protective signaling (e.g., related to the PAM process) for rats and dogs based on the convergence of the dose-response data (for protected and unprotected groups) at high doses. Humans were presumed to be protected against alpha radiation doses up to 3200 mGy, based on results presented in Table 3.

Gamma-Ray ANP for Humans vs. Rats

Protection provided to humans and Wistar rats by low-dose/low-dose-rate gamma-ray ANP can be assessed relative to the rising dashed curve (humans) and filled circles (Wistar rats) in Figure 3 that relate to only alpha radiation exposure. Humans (smooth curve) appear to be somewhat less protected than were Wistar rats (filled squares). However, RR uncertainty for humans is quite large (Table 3, column 4) and the RR for humans cannot be stated with confidence to be different than from Wistar rats.

The data for Wistar rats exposed to both alpha and gamma rays in Figure 3 (filled squares) show a very steep increase in RR for doses above about 1000 mGy. This suggests that alpha radiation doses above about 1000 mGy may have suppressed or inhibited gamma-ray ANP in some of the rats. This dose zone of rapidly increasing RR has been called Transition Zone B (Scott 2007a,b). It is the dose zone where stochastic thresholds for inhibition/suppression of ANP occur. Transition Zone A occurs at very low doses and is the dose zone where stochastic thresholds for ANP occur. The dose zone that is between Transition Zone A and Transition Zone B is called the Zone of Maximal Protection. For the Zone of Maximal Protection, everyone is presumed to have ANP (i.e., F = 0). The boundaries for the indicated three zones are presumed to depend on dose-rate and the types of radiation involved (Scott 2005, 2007b).

The results in Figure 3 are consistent with the view that low doses and dose rates of gamma rays activate the body’s natural defenses (biological and chemical protection), which in turn can significantly reduce the risk of cancer from exposure to carcinogenic doses of other agents. Similar results have been demonstrated for suppression of chemically-induced cancer via low-dose-rate exposure to sparsely ionizing radiation (Mitchel et al. 1999; Sakai et al. 2003). For alpha radiation doses > 10,000 mGy in Figure 3, there is no evidence for gamma-ray ANP for rats and dogs. This suggests that deleterious biological signaling associated with very high alpha radiation doses may overwhelm or suppress protective signaling in rats, dogs, and humans that is associated with gamma-ray ANP.

Predicting Cancer Incidences Assuming K_α to Be Evolutionarily Conserved

The similar estimates in Table 2 for K_α for humans, rats, and dogs suggest that K_α may be evolutionarily conserved for mammals. If so, the average of the values in Table 2 (1.7 × 10⁻⁰⁴ mGy⁻¹) could then be used to predict the expected tumor incidence in other mammalian species (e.g., mice). To investigate this possibility, the indicated value for K_α and an observed spontaneous (baseline) lung cancer incidence of 0.0198 for 84-day old female C57BL/6J mice (Lundgren et al. 1987) has been used with Equation 1 (re-expressed as an absolute risk) to predict the expected lung cancer incidence in the mice after they were exposed to ²³⁹PuO₂ (with a ¹⁶⁹Yb label). Group-specific average alpha radiation doses to the lung were reported to be 1,200, 2,800, and 14,000 mGy for the three lowest exposed groups (Lundgren et al. 1987). Using PROFAC = 0.93 (average of estimates for Mayak workers [0.86] and Wistar rats [1.0]) led to predicted incidences of 0.016, 0.035, and 0.07 in comparison to the observed incidences of 0.029, 0.047, and 0.051, respectively. Predicted and observed values differed by less than a factor of 2. Thus, under the assumption that K_α is evolutionarily conserved for mammals, the predicted incidences are roughly consistent with those that were observed.

Using the same approach and the spontaneous lung cancer incidence of B = 0.00095 for the female Wistar rats in Table 1, one can predict the expected lung cancer incidence for the higher dose of 2,320 mGy that was used by Sanders (2007). The predicted incidence is (1−0.93)*(1) = 0.07. Here “(1)” is the maximum incidence possible under the LNT absolute risk function. The observed lung cancer incidence was 0.069 (Sanders 2007). The next higher dose used by Sanders was much higher (5,030 mGy). This dose appeared to suppress ANP in some of the Wistar rats in that the observed lung cancer incidence was 0.21 when the expected incidence based on PROFAC = 0.93 and K_α = 1.7 × 10⁻⁴ mGy⁻¹ was 0.07 using Equation 1 (i.e., assuming F = 0). With PROFAC = 0, the expected lung cancer incidence is 1.0 for the indicated dose. Thus, the data suggests that some but not all of the rats had gamma-ray ANP suppressed or that the high doses used may have caused significant life shortening due to acute effects. Assuming the fraction F of the rats had suppressed/inhibited gamma-ray ANP and no significant life shortening occurred, F is given by the solution to (see Equation 4)

$$F+(1-F)*(1-\text{PROFAC})=\mathrm{0.21.}$$

Substituting PROFAC = 0.93 and solving for F, one obtains F = 0.15 (i.e., 15% not having ANP). This implicates 85% of the irradiated group having a lung cancer frequency of 0.07 (= 1 − PROFAC) and the remaining 15% as having a frequency of 1.

The results obtained support the suggestion that K_α may be evolutionarily conserved for mammals. Many published radionuclide inhalation toxicity studies using alpha-emitting isotopes also used ¹⁶⁹Yb labels to monitor deposition of aerosol in the respiratory tract. Data from such studies should be re-examined for evidence for gamma-ray ANP. Further, absolute risk estimates for alpha-radiation-induced lung cancer based on such studies may be substantially underestimated for alpha radiation doses below about 100 mGy, when extrapolating from data for doses between 100 – 1,000 mGy using the LNT model.

Influence of Age at Exposure on Lung Cancer Risk

Lundgren et al. (1995) also examined the influence of age at exposure on the incidence of alpha-radiation-induced lung cancer among F344/Crl rats that inhaled ²³⁹PuO₂ along with a ¹⁶⁹Yb label. Interestingly, unlike for 84-day old rats whose cancer incidence increased as radiation dose increased, for 450-day old rats, a hormetic-type response was implicated for a group average alpha radiation dose of 880 mGy to the lung (Lundgren et al. 1995). Such observations are consistent with the view that PROFAC may increase with age (Scott and Di Palma 2007). If so, children may not benefit as much as adults from gamma-ray ANP.

Implications for Other Radiations

Because they are sparsely ionizing, gamma rays, x rays, and beta radiation have similar physical characteristics with respect to their interactions with biological tissue. Thus, extended exposures to essentially harmless low doses of any of these sparsely ionizing radiations would also be expected to efficiently stimulate protective signaling associated with ANP against lung cancer.

Possible Modalities for Lung Cancer Prevention

The PAM process when activated by sparsely ionizing radiation removes precancerous cells via selective apoptosis (Scott 2004; Bauer 2007; Portess et al. 2007). Cells transformed by a variety of carcinogens (including chemical carcinogens, UV light plus TGF-β, oncogenic retro-viruses, herpes simplex virus, or viral oncogenes such as ras and src) were found to be equally sensitive to the PAM process (Jürgensmeier et al. 1994; Bauer 1996). Low-dose-rate gamma irradiation has been demonstrated to suppress skin cancer induction by methylcholanthrene (Sakai et al. 2003) and lung cancer induction by alpha radiation (Figures 2 and 3). Methylcholanthrene and alpha radiation from ²¹⁰Po are known risk factors for lung cancer that are present in cigarette smoke.

What are the possible modalities of lung cancer prevention among high-risk smokers who have failed to heed smoking-cessation advice or other interventions such as exercise programs? Other than social and medical interventions to encourage smoking cessation, possible treatments would involve medically-supervised sparsely-ionizing radiation ANP. Repeated very small x-ray doses could be administered over and extended period from equipment in hospitals used for administering diagnostic x rays. Special radiation ANP rooms with elevated background gamma radiation could be used in medical facilities for implementing natural protection from a future lung cancer. Induced natural protection could also be provided against other types of cancer.

Most children are unlikely to be at high-risk for cancer. Thus, using low-dose-radiation ANP to prevent cancer among children may be inappropriate in most cases. Many other agents are also being studied related to possibly preventing lung and other cancers among high risk populations and individuals (Sporn and Suh 2000). It may be beneficial to consider combining low-rate, low-dose, low-LET radiation exposure with other cancer preventative agents or exercise-based induction of adaptive response (Ji et al. 2006; Sonneborn and Barbee 1998).

CONCLUSIONS

The results presented demonstrate that low doses of gamma rays when spread over time are a potent inducer of natural chemical and biological protection against lung cancer. Because gamma rays, x rays, and beta radiation have very similar physical characteristics related to their interaction with biological tissue, low x-ray and beta-radiation doses when spread over time (e.g., repeated very low doses of x rays, or continuous very-low levels of beta irradiation) are also expected to be potent inducers of natural chemical and biological protection against lung cancer.