Estimating Correlation with Multiply Censored Data Arising from the Adjustment of Singly Censored Data

Abstract

Environmental data frequently are left censored due to detection limits of laboratory assay procedures. Left censored means that some of the observations are known only to fall below a censoring point (detection limit). This presents difficulties in statistical analysis of the data. In this paper, we examine methods for estimating the correlation between variables each of which is censored at multiple points. Multiple censoring frequently arises due to adjustment of singly censored laboratory results for physical sample size. We discuss maximum likelihood (ML) estimation of the correlation and introduce a new method (cp.mle2) that, instead of using the multiply censored data directly, relies on ML estimates of the covariance of the singly censored laboratory data. We compare the ML methods with Kendall's tau-b (ck.taub) which is a modification Kendall's tau adjusted for ties, and several commonly used simple substitution methods: correlations estimated with non-detects set to the detection limit divided by two and correlations based on detects only (cs.det) with non-detects set to missing. The methods are compared based on simulations and real data. In the simulations, censoring levels are varied from 0 to 90%, ρ from -0.8 to 0.8 and ν (variance of physical sample size) is set to 0 and 0.5, for a total of 550 parameter combinations with 1000 replications at each combination. We find that with increasing levels of censoring most of the correlation methods are highly biased. The simple substitution methods in general tend toward zero if singly censored and one if multiply censored. ck.taub tends toward zero. Least biased is cp.mle2, however, it has higher variance than some of the other estimators. Overall, cs.det performs the worst and cp.mle2 the best.

Introduction

Environmental data frequently are left censored due to detection limits of laboratory assay procedures. Left censored means that some of the observations are known only to fall below a censoring point (detection limit) (1). This presents difficulties in statistical analysis of the data (2-4). Recent papers have discussed correlation estimation when only one of the variables is censored (5-7), and some attention has been given to the situation when both variables are censored (8,9). In addition, most work has focused on data that are singly censored (meaning there is only one censoring point). This paper examines methods for estimating the correlation between variables each of which is multiply censored, meaning that there are multiple censoring points.

Multiple censoring can arise if the laboratory detection limit varies from day to day or batch to batch. It can also result from the conversion of a laboratory result to a concentration. For instance, if the laboratory result is micrograms of a particular analyte and this is converted to a concentration by dividing by the physical sample size, for instance grams of dust, then the result will be multiply censored even if the original measurement was not.

Three measures of correlation commonly are used. The Pearson correlation coefficient, r_p, measures the strength of linear association between two variables, x and y. It is equal to the covariance of x and y divided by the product of the standard deviations of x and y.

$${\mathrm{r}}_{\mathrm{p}}=\frac{Cov(\mathrm{x},\mathrm{y})}{{\{Var\left(\mathrm{x}\right)Var\left(\mathrm{y}\right)\}}^{0.5}}$$ (1)

Inference about r_p, for small samples, is dependent on the assumption of normality of the data (10). When these assumptions are not met, nonparametric methods may be used. These measure the extent of monotone association between two variables.

Two non-parametric methods of measuring correlation are Spearman's rank correlation coefficient, r_s, and Kendall's correlation coefficient, tau. Spearman's r_s is simply the Pearson correlation of the ranks of the data. Kendall's tau is a measure of the concordance of x and y (11). Like Spearman's r_s, it is a correlation method based on ranks.

When the data are censored, a common practice is to set the non-detects to the detection limit (DL) divided by a constant, c, (frequently c = the square root of two or two) and estimate correlation by standard methods. Another approach has been to set censored values to missing so that correlation is estimated using only simultaneously detected values. This complete-case analysis is known to result in loss of accuracy and precision when the data are not missing completely at random (12).

A modification of Kendall's tau for estimating the Kendall correlation in the case of censored data has been suggested by several authors (4,13,14). Here, this method will be referred to as Kendall's tau-b. This is Kendall's tau adjusted for ties, with comparisons involving censored values considered ties under certain conditions. For more information see Helsel (4). An example is given in the Supporting Information.

Maximum likelihood (ML) has been advanced by several authors (6-8) as a method of estimating correlation as well as mean and variance when data are censored. The ML estimate (MLE) of a parameter vector θ is the value of θ that maximizes the likelihood function. In estimating the mean and standard deviation for a variable x, assumed normally distributed, the likelihood function for θ = (μ_x, σ_x) is:

$$\mathrm{L}(\mathrm{\theta })=\prod _{\mathrm{i}\in {\mathrm{I}}_{\mathrm{c}}}{F(\mathrm{Lx}}_{\mathrm{i}})\prod _{\mathrm{i}\in {\mathrm{I}}_{\mathrm{d}}}{f(\mathrm{x}}_{\mathrm{i}})$$ (2)

where F(Lx_i) is the normal cumulative distribution function (CDF) with parameter θ, f(x_i) is the normal probability density function (PDF) with parameter θ, I_c denotes the set of indices of the censored observations, x_i < Lx_i, and I_d denotes the set of indices of the detected observations.

In simultaneously estimating the means, standard deviations and correlation of two variables, x and y, assumed normally distributed, the likelihood function for θ = (μ_x, μ_y, σ_x, σ_y, ρ) is as follows. This equation has been adapted from Lyles et al. (8) for multiply censored data.

$$\begin{array}{l}\mathrm{L}(\mathrm{\theta })=\prod _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{G}}_{\mathrm{i}}{,\text{where G}}_{\mathrm{i}}\\ {=f(\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}})\text{if}{\mathrm{x}}_{\mathrm{i}}\text{and}{\mathrm{y}}_{\mathrm{i}}\text{are both detected}\\ {=f(\mathrm{x}}_{\mathrm{i}})F({\mathrm{Ly}}_{\mathrm{i}}|{\mathrm{x}}_{\mathrm{i}})\text{if}{\mathrm{x}}_{\mathrm{i}}{\text{is detected and y}}_{\mathrm{i}}{<\mathrm{Ly}}_{\mathrm{i}},\\ {=f(\mathrm{y}}_{\mathrm{i}})F({\mathrm{Lx}}_{\mathrm{i}}{|\mathrm{y}}_{\mathrm{i}})\text{if}{\mathrm{y}}_{\mathrm{i}}\text{is detected and}{\mathrm{x}}_{\mathrm{i}}{<\mathrm{Lx}}_{\mathrm{i}},\\ {=F(\mathrm{Lx}}_{\mathrm{i}}{,\mathrm{Ly}}_{\mathrm{i}})\text{if}{\mathrm{x}}_{\mathrm{i}}{<\mathrm{Lx}}_{\mathrm{i}}\text{and}{\mathrm{y}}_{\mathrm{i}}{<\mathrm{Ly}}_{\mathrm{i}},\\ \text{and}\\ {\mathrm{Lx}}_{\mathrm{i}}=\text{detection limit for}{\mathrm{x}}_{\mathrm{i}}\\ {\mathrm{Ly}}_{\mathrm{i}}=\text{detection limit for}{\mathrm{y}}_{\mathrm{i}}\\ f({\mathrm{x}}_{\mathrm{i}})=\text{normal PDF with parameter}{(\mathrm{\mu }}_{\mathrm{x}}{,\mathrm{\sigma }}_{\mathrm{x}}),\\ f({\mathrm{y}}_{\mathrm{i}})=\text{normal PDF with parameter}{(\mathrm{\mu }}_{\mathrm{y}}{,\mathrm{\sigma }}_{\mathrm{y}}),\\ F({\mathrm{Ly}}_{\mathrm{i}}{|\mathrm{x}}_{\mathrm{i}})=\text{normal CDF with parameter}{(\mathrm{\mu }}_{\mathrm{y}|\mathrm{x}\mathrm{i}}{,\mathrm{\sigma }}_{\mathrm{y}|\mathrm{x}}),\\ F({\mathrm{Lx}}_{\mathrm{i}}{|\mathrm{y}}_{\mathrm{i}})=\text{normal CDF with parameter}{(\mathrm{\mu }}_{\mathrm{x}|\mathrm{y}\mathrm{i}}{,\mathrm{\sigma }}_{\mathrm{x}|\mathrm{y}}),\\ f({\mathrm{x}}_{\mathrm{i}}{,\mathrm{y}}_{\mathrm{i}})=\text{bivariate normal PDF with parameter}\mathrm{\theta },\\ F({\mathrm{Lx}}_{\mathrm{i}}{,\mathrm{Ly}}_{\mathrm{i}})=\text{bivariate normal CDF with parameter}\mathrm{\theta },\\ {\mathrm{\mu }}_{\mathrm{y}|{\mathrm{x}}_{\mathrm{i}}}{=\mathrm{\mu }}_{\mathrm{y}}+({\mathrm{\rho }\mathrm{\sigma }}_{\mathrm{y}}/{\mathrm{\sigma }}_{\mathrm{x}}{\left)\right(\mathrm{x}}_{\mathrm{i}}-{\mathrm{\mu }}_{\mathrm{x}}),\\ {\mathrm{\mu }}_{{\mathrm{x}|\mathrm{y}}_{\mathrm{i}}}{=\mathrm{\mu }}_{\mathrm{x}}+({\mathrm{\rho }\mathrm{\sigma }}_{\mathrm{x}}/{\mathrm{\sigma }}_{\mathrm{y}}{\left)\right(\mathrm{y}}_{\mathrm{i}}-{\mathrm{\mu }}_{\mathrm{y}}),\\ {\mathrm{\sigma }}_{\mathrm{y}|\mathrm{x}}={\mathrm{\sigma }}_{\mathrm{y}}(1-{\mathrm{\rho }}^2{)}^{1/2},\\ {\mathrm{\sigma }}_{\mathrm{x}|\mathrm{y}}={\mathrm{\sigma }}_{\mathrm{x}}(1-{\mathrm{\rho }}^2{)}^{1/2}.\end{array}$$ (3)

Maximizing the likelihood function with respect to all five parameters can be problematic. Convergence may be slow or may fail to occur or may reach a local rather than a global maximum. In a preliminary set of investigations, comparable or superior performance was found when means and standard deviations were estimated separately from the correlation. Examples are shown in the Supporting Information (Figures S41-S42).

In this investigation, the performance of two ML estimators, denoted cp.mle and cp.mle2, is examined. With cp.mle, the mean and standard deviation of each of two multiply censored variables are estimated using equation 2. Then ρ is estimated using equation 3, with means and standard deviations held fixed. As discussed below, we found this estimator to be biased for multiply censored data.

In situations where the laboratory results (mass of analyte) is singly censored and physical sample size is fully detected, we propose an alternative estimator, cp.mle2. This estimator relies on the following identity (10):

$$\begin{array}{ll}cor(\mathrm{x}-\mathrm{z},\mathrm{y}-\mathrm{z})& =\frac{cov(\mathrm{x},\mathrm{y})-cov(\mathrm{x},\mathrm{z})-cov(\mathrm{y},\mathrm{z})+var\left(\mathrm{z}\right)}{{\{(var(\mathrm{x})+var(\mathrm{z})-2cov(\mathrm{x},\mathrm{z}))(var(\mathrm{y})+var(\mathrm{z})-2cov(\mathrm{y},\mathrm{z}))\}}^{0.5}}\\ & =\frac{{\mathrm{\sigma }}_{\mathrm{xy}}-{\mathrm{\sigma }}_{\mathrm{xz}}-{\mathrm{\sigma }}_{\mathrm{yz}}+{\mathrm{\sigma }}_{\mathrm{z}}^2}{{\{({\mathrm{\sigma }}_{\mathrm{x}}^2+{\mathrm{\sigma }}_{\mathrm{z}}^2-2{\mathrm{\sigma }}_{\mathrm{xz}})({\mathrm{\sigma }}_{\mathrm{y}}^2+{\mathrm{\sigma }}_{\mathrm{z}}^2-2{\mathrm{\sigma }}_{\mathrm{yz}})\}}^{0.5}}\end{array}$$ (4)

where x = log of laboratory results for one analyte, y=log of laboratory results for another analyte, and z=log of physical sample size. Here, x, y and z are assumed normally distributed.

With cp.mle2, ML estimates of σ_x, σ_y, σ_z are found separately for each variable using equation 2. ρ_xy, ρ_xz and ρ_yz are found using equation 3. Then σ_xy = ρ_xyσ_xσ_y, σ_xz = ρ_xzσ_xσ_z and σ_yz = ρ_yzσ_yσ_z.

We show results for simulated data and also for data from the Cape Cod Household Exposure Study. In the Cape Cod Household Exposure Study (CCHES), air, dust, and urine samples were collected from 120 study participants on Cape Cod, Massachusetts (15). Urine samples were analyzed for 21 pesticide and phthalate metabolites by the United States Centers for Disease Control using the methods described in (16). For the urine samples, the laboratory reported concentrations of the analytes and, in general, these were singly censored. However to adjust for dilution of the urine, these values were divided by the concentration of creatinine, resulting in multiply censored data. Our efforts to use these data to better understand major sources and pathways of chemical exposure led us to examine methods for estimating correlation between censored variables.

Methods

In order to compare the performance of correlation estimators, we conducted a simulation experiment and also examined their performance using variables in the CCHES data.

Simulations

Notation: Here x, y and z (with or without subscripts) are vectors of length n. ρ, ν, p and q are scalars. x-z is taken element-wise.

The following simulation procedure was repeated 1000 times for each set of parameter values. Data are assumed log normally distributed. Logs of laboratory data (for instance, micrograms of two different analytes, denoted x_lab and y_lab) are simulated as multivariate normal with mean 0, variance 1 and ρ varying from −0.8 to 0.8. Logs of physical sample sizes (e.g. air volume, dust weight, urine creatinine) denoted z, are simulated as normal, independent of x_lab and y_lab, with mean 0 and variance, v, set to either 0 or 0.5. (In the CCHES data, the correlations of laboratory data with physical sample sizes range approximately from -0.1 to 0.6. In this set of simulations, the correlation is assumed to be zero).

Logs of adjusted data (simulated concentrations), then, are x_adj = x_lab − z and y_adj = y_lab − z. The true Pearson, Spearman and Kendall correlations between x_adj and y_adj are computed. From equation 4, the theoretical Pearson correlation of x_adj and y_adj, ρ_adj= (ρ+ν)/(1+ν). The true Spearman correlation is close to this value and the true Kendall correlation is generally 60% to 80% of ρ_adj.

Next, x_lab and y_lab are censored. Censored proportions of x_lab, p_x, and y_lab, p_y, are varied from 0.0 to 0.9. For x_lab, the sample quantile, q_x, corresponding to p_x is found and regarded as the detection limit. Values of x_lab which are less than q_x are set equal to q_x and the singly censored result is denoted x_sc. y_lab is censored according to the same procedure as x_lab. Then the final multiply censored values are x_mc = x_sc - z and y_mc = y_sc − z.

Seven correlation estimates are computed at each iteration. These are (a) the Pearson correlation with non-detects set to DL/2 (cp.dl2), (b) the Pearson correlation estimated by maximum likelihood using the multiply censored data (cp.mle), (c) the Pearson correlation estimated by maximum likelihood using equation 4 (cp.mle2), (d) the Spearman correlation with non-detects set to DL/2 (cs.dl2), (e) the Spearman correlation based on detects only with non-detects set to missing (cs.det), (f) the Kendall correlation with non-detects set to DL/2 (ck.dl2), (g) Kendall's tau-b (ck.taub). Six of these methods are commonly used and cp.mle2 is proposed as an improved maximum likelihood estimator when unadjusted laboratory data are singly censored.

In the primary set of simulations, the value of the sample size, n, was set to 100. Values of ρ, (the correlation of the x_lab and y_lab) were varied from –0.8 to 0.8 in increments of 0.4. Values of the variance of the physical sample sizes (denoted v) were 0 and 0.5. Values of p_x were varied from 0.0 to 0.9, in increments of 0.1. Values of p_y were varied between p_x and 0.9 in increments of 0.1. Thus, the performance of the seven correlation estimates was examined under 5*2*55=550 parameter combinations. There were 1000 replications at each combination. Comparisons were made with sample sizes of 20, 50 and 1000, for a reduced set of parameter combinations.

Simulations and data analysis were carried out using S-Plus Version 7.0.4 for Windows (17) and R Version 2.2.0 for Windows (18). The computer programs are available on request.

CCHES data

We calculated the seven correlation estimates for all 210 pairs of 21 phthalate and pesticide metabolites measured in urine samples of 120 Cape Cod residents. Unlike the simulated data, we do not know the true correlation for these pairs, so our analysis is limited to consideration of (a) consistency among measures, (b) comparison with plotted data and (c) expected correlations based on knowledge about major sources of exposure.

Results and Discussion

Simulations

A good estimator should be both accurate (close to the true value) and precise (have low variability). One robust performance measure that combines these properties is the median absolute deviation (MAD) which here is defined as the median(absolute value(estimate-true value)). (For the Spearman and Kendall correlations, the true value is taken to be the mean of the correlations calculated for uncensored data). Many other performance measures exist and the apparent performance of an estimator will vary depending on the performance measure chosen. Performance of the estimators also varies with the parameter values including the correlation itself. In general, performance is worse with smaller sample sizes and, for multiply censored data, with negative correlations.

Figure 1 shows box plots for each of the estimators with parameter values n=100, ν=0.5 and ρ=0. The x axis shows the percent censored in x and y with 55 censoring combinations ranging from (0%,0%) to (90%,90%). The y axis ranges from -1.0 to 1.0 with the average true correlation indicated. Horizontal lines are drawn at this value +0.15 and -0.15. The complete set of box plots for all estimators and parameter combinations, with n=100, is available in the Supporting Information (Figures S1-S30). Additional box plots in the Supporting Information (Figures S31-S40) show the effect of setting the sample size, n, to 20, 50, 100 and 1000 with ρ=-0.8, ν=0, for a reduced set of censoring combinations. Here we can see that precision, but in general not accuracy, of the estimators improves with increasing values of n.

Figure 1.

Simulation Results. Box plots of estimates of correlation for parameter values: n = 100, ρ = 0, ν = 0.5, number of repetitions = 1000. Horizontal axis shows percent censored in x and y. (a) Pearson correlation for uncensored data (average is 0.33). (b) Estimator is cp.dl2. (c) Estimator is cp.mle. (d) Estimator is cp.mle2. (e) Estimator is cs.dl2 (average uncensored Spearman correlation is 0.32). (f) Estimator is cs.det. (g) Estimator is ck.dl2 (average uncensored Kendall correlation is 0.22). (h) Estimator is ck.taub.

In Figure 1, with average Pearson correlation=(ρ+ν)/(1+ν) = 0.5/1.5=0.33, Spearman correlation=0.32 and Kendall correlation=0.22, we see that the estimators cp.dl2 and cs.det tend away from the true correlation toward more positive values as censoring increases. ck.taub, on the other hand, tends toward zero as censoring increases. cs.det has very high variance with many extreme values. cp.mle2 has the least bias, but higher variance than cp.dl2 and ck.taub.

In general, the behavior of the estimators may be summarized as follows. We emphasize that these results are for simulated data assumed log-normally distributed.

Estimators with non-detects set to DL/2

When one of the variables, say x, is censored and the other is not, with increasing levels of censoring, x_mc tends toward a constant minus z (log of the physical sample size). The Pearson correlation tends toward cor(c-z,y_sc-z) = cor(-z, y_sc-z), where c is a constant vector. If v=0 (the physical sample size, z, is a constant) the correlation tends toward 0. If v=0.5, using equation 4 the Pearson correlation tends toward 0.5/sqrt(0.75) =0.577. The Spearman and Kendall correlations are similar in behavior.

With increasing levels of censoring in both variables, x_mc and y_mc both tend toward a constant minus z. If v=0 these estimators tend toward zero. On the other hand if v≠0, these estimators tend toward one.

cs.det

The behavior of cs.det follows that of cs.dl2, tending toward one if ν≠0 and zero if ν=0. However, the variance of the estimates is much higher. This is the most unreliable of the estimators discussed here and should not be used.

ck.taub

If ν=0 (data are singly censored) then ck.dl2 and ck.taub give identical results. Even if the data are multiply censored, as the levels of censoring increase, ck.taub, with so many ties in the comparisons, tends toward zero.

Maximum likelihood estimators

If ν=0 (data are singly censored) then cp.mle and cp.mle2 give the same results. However, if the data are multiply censored then cp.mle is negatively biased at high levels of censoring. cp.mle2, on the other hand, has little bias. The variance tends to be higher than that of many of the other methods, however.

The performance of these ML estimators could be improved if better estimates of the mean and standard deviation could be obtained. Preliminary work indicates that imputation methods discussed in (1) and Kaplan-Meier methods can achieve greater accuracy and precision than ML in estimating these parameters. This is an avenue for future research.

Median Absolute Deviation (MAD) Results

Table 1 shows the maximum levels of censoring (in both x and y) for each parameter combination investigated which result in MAD < 0.1. Here, we can see that cs.det performs the worst, seldom achieving MAD<0.1. For all sample sizes and correlation estimators, the worst performance is found for negatively correlated multiply censored data (ρ=-0.8, ν=0.5). Outside of this situation, for samples of size n=100, methods with non-detects set to DL/2 achieve MAD<0.1 with 40 to 80 or 90% censoring, Kendall's tau-b with 50 to 80% censoring and cp.mle2 with 70 to 90% censoring. For n=50, the Kendall correlations were the most consistent with MAD<0.1 for 50 to 70% censoring, cp.mle2 achieved MAD<0.1 with 20 to 90% censoring. For samples of size n=20, the estimators achieved MAD<0.1 only with highly positive correlations. For ρ=0.4, ν=0.5, only the Kendall correlations achieved MAD<0.1 for up to 40% censoring. It should be noted that, for the same dataset, Kendall correlations in general are smaller in magnitude than Spearman or Kendall so the criterion of MAD<0.1 actually favors the Kendall correlations slightly.

Table 1.

Simulation Results. Maximum levels of censoring (in both x and y) for each parameter combination which result in median absolute deviation <0.1.

	cp.dl2	cp.mle	cp.mle2	cs.dl2	cs.det	ck.dl2	ck.taub
n=100, ρ= 0.8, ν=0	70	90	90	60	10	80	80
n=100, ρ= 0.4, ν=0	60	70	70	60	10	80	80
n=100, ρ= 0.0, ν=0	90	70	70	80	20	80	80
n=100, ρ= -0.4, ν=0	50	60	60	50	0	80	80
n=100, ρ= -0.8, ν=0	30	60	60	40	0	50	50
n=100, ρ= 0.8, ν=0.5	90	90	90	90	80	70	80
n=100, ρ= 0.4, ν=0.5	70	60	90	60	50	60	60
n=100, ρ= 0.0, ν=0.5	50	60	70	50	10	50	60
n=100, ρ= -0.4, ν=0.5	40	30	70	40	0	40	50
n=100, ρ= -0.8, ν=0.5	30	20	60	40	0	40	30
n=20, ρ=0.8, ν =0.5	90	80	90	90	40	70	60
n=20, ρ=0.4, ν =0.5	0	0	0	0	0	40	40
n=20, ρ= 0, ν =0.5	0	0	0	0	0	0	0
n=20, ρ= -0.4, ν =0.5	0	0	0	0	0	0	0
n=20, ρ= -0.8, ν =0.5	0	0	0	0	0	0	0
n=50, ρ= 0.8, ν=0.5	90	90	90	90	70	70	70
n=50, ρ= 0.4, ν=0.5	70	60	70	60	30	60	60
n=50, ρ= 0, ν=0.5	40	20	30	40	0	50	50
n=50, ρ= -0.4, ν=0.5	30	0	20	10	0	40	50
n=50, ρ= -0.8, ν=0.5	30	10	30	30	0	40	30
n=1000, ρ= -0.8, ν=0.5	30	20	70*	40	0	40	30

^*70% censoring in both x and y was the maximum censoring level tested with samples of size n=1000.

Correlation estimates with CCHES urinary metabolites data

In the CCHES urine data, there are 21 different analytes and 21*20/2 = 210 pair wise relationships among them. We examined the distribution of each variable using normal probability plots and examined the relationships among them using scatter plots and then compared the performance of the seven estimates of correlation discussed above. Here we discuss four examples. All analyses were conducted using logs of the data.

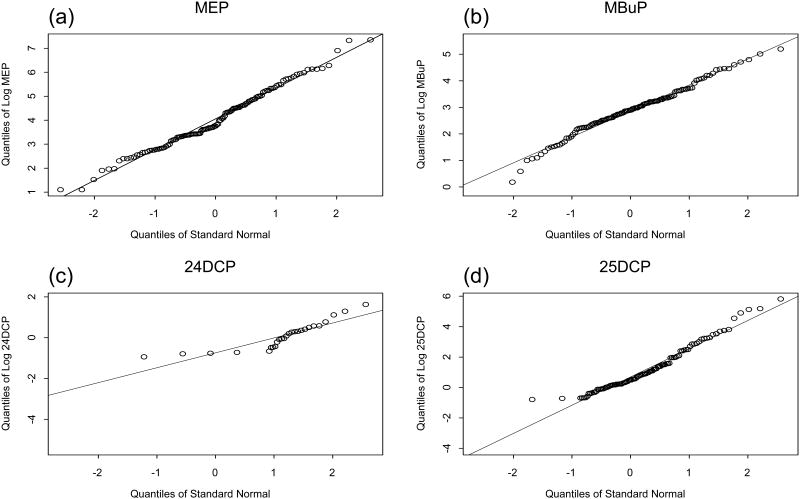
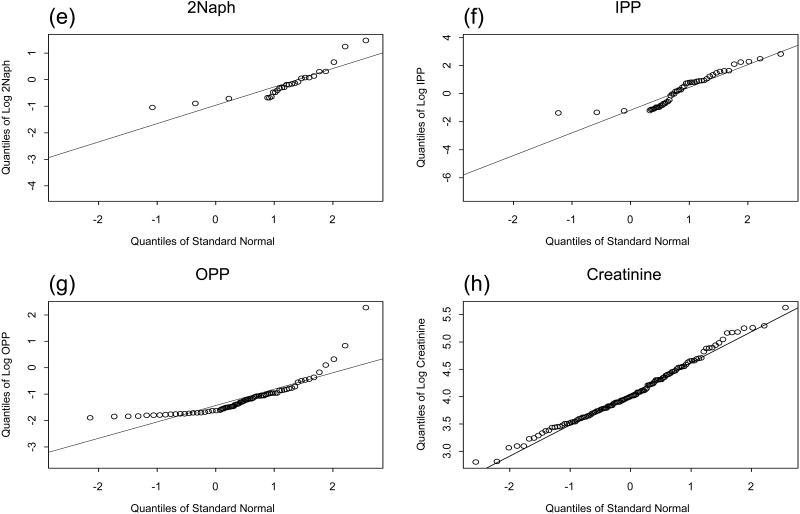
Figure 2 shows normal probability plots (QQ plots) for seven of the analytes and also for creatinine. Here the data are unadjusted and largely singly censored. Figure 3 shows scatter plots of the creatinine adjusted data for each of the selected pairs. Table 2a shows the numbers detected, censored and missing for each variable and Table 2b shows the seven correlation estimates for each relationship discussed.

Figure 2.

Normal probability plots of logs of selected CCHES variables. (a) MEP. (b) MBuP. (c) 24DCP. (d) 25DCP. (e) 2Naph. (f) IPP. (g) OPP. (h) Creatinine.

Figure 3.

Scatter plots of selected CCHES variables, non-detects are plotted at detection limit. For each observation, B indicates both variables are detected, x indicates x is detected, y indicates y is detected n indicates neither is detected. (a) x is log MEP, y is log MBuP. (b) x is log 24DCP, y is log 25DCP. (c) x is log 2Naph, y is log IPP. (d) x is log 24DCP, y is log OPP.

Table 2.

Table 2a. Numbers detected, censored and missing in selected CCHES variables.
X	Y	na	ndxb	ncxc	nmxd	pcxe	ndyf	ncyg	nmyh	pcyi	nsimdetj
MEP	MBuP	119	119	0	1	0.0	118	2	0	1.7	117
24DCP	25DCP	120	26	94	0	78.3	99	21	0	17.5	25
2Naph	IPP	120	26	94	0	78.3	48	72	0	60.0	10
24DCP	OPP	120	26	94	0	78.3	77	43	0	35.8	20
Table 2b. Correlation estimates for selected CCHES variables.
X	Y	cp.dl2	cp.mle	cp.mle2	cs.dl2	cs.det	ck.dl2	ck.taub
MEP	MBuP	0.25	0.25	0.24	0.23	0.21	0.16	0.16
24DCP	25DCP	0.34	0.01	0.46	0.21	0.24	0.15	0.25
2Naph	IPP	0.17	-0.01	0.00	0.32	0.46	0.28	-0.01
24DCP	OPP	0.32	0.02	0.07	0.45	0.45	0.35	0.05

^anumber not missing in x and y

^bnumber detected in x

^cnumber censored in x

^dnumber missing in x

^epercent censored in x

^fnumber detected in y

^gnumber censored in y

^hnumber missing in y

ⁱpercent censored in y

^jnumber simultaneously detected in x and y

The normal probability plots in Figure 2 were created using the S-Plus Environmental Statistics function qqplot.censored. The logs of the ordered data (empirical quantiles) are plotted on the vertical axis and the corresponding theoretical quantiles from the assumed normal distribution are plotted on the horizontal axis. This is described further in Millard (1). Here we can see that the variables appear to satisfy the assumption of a normal distribution with the possible exception of 2Naph and OPP.

In the scatter plots, non-detects are plotted at the detection limit. Each point is represented by a letter. “B” indicates that both are detected, “x” that x is detected, “y” that y is detected and “n” that neither is detected. Hence, for a point represented by an x, if the true value were known, the plotting position would be somewhere on a vertical line extending below the x. For a point represented by a y, if the true value were known, the plotting position would be somewhere on a horizontal line extending to the left of the y. For a point represented by an n, if the true value were known, the plotting position would be somewhere below and to the left of the n.

Figure 3a shows the relationship between monoethyl phthalate (MEP) and monobutyl phthalate (MBuP), which are urinary monoester metabolites of diethyl phthalate and di-n-butyl phthalate.

We expect these two phthalates to be positively correlated because the parent compounds are used in personal care products such as fragrances and cosmetics (19). With one missing and no censored values in MEP and only two censored values in MBuP there are 117 simultaneous detects. As might be expected, the correlation estimates are consistent (Pearson estimates 0.25, cs.dl2 0.23, Kendall estimates 0.16). cs.det (0.21) is lower than cs.dl2 because it does not take into account the influence of the two points in the lower left of the plot that are censored for MBuP.

Figure 3b shows the relationship between 2,4-dichlorophenol (24DCP) and 2,5-dichlorophenol (25DCP). We expect these urinary metabolites to be positively correlated because they are both derived from exposure to chlorinated benzenes and chlorinated phenols. 94 values (78%) are censored in 24DCP and 21 values (18%) are censored in 25DCP resulting in only 25 simultaneous detects and 20 simultaneous non-detects. As might be expected the correlation estimates vary widely. Based on the simulation results, we expect that ck.taub (0.25) underestimates the true Kendall correlation at this level of censoring. Here cp.mle2 is 0.46.

Next we discuss two pairs of urinary metabolites that are not expected to be highly correlated based on major sources of exposure. Figure 2c shows a plot of 2-naphthol (2Naph), a metabolite of the polyaromatic hydrocarbon naphthalene, and isopropoxyphenol (IPP), a metabolite of the pesticide propoxur. 2Naph has 78% censored values and IPP has 60% censored values resulting in only 10 simultaneous detects and 56 simultaneous non-detects. The plot shows a diagonal line of n's where neither compound was detected. (Just as a reminder, these are plots of the creatinine adjusted data and simultaneous non-detects are plotted as “n” at the detection limit divided by the concentration of creatinine). Correlation methods based on setting censored values to the DL/2 thus can be artificially inflated. (This artifact is shown also in plots of simulated data in the Supporting Information, Figure S43). Kendall's tau-b and the ML estimates are not vulnerable to this error and are close to zero. The estimate based on detects only (0.46) is high because of the small number of detects and the strong influence of the single point in the upper right corner.

Figure 2d shows a plot of the pesticide metabolite 2,4-dichlorophenol (24DCP) and the disinfectant o-phenyl phenol (OPP). 24DCP has 78% censored values and OPP has 36% censored values resulting in 20 simultaneous detects and 37 simultaneous non-detects. Again, the correlation estimates based on setting the non-detects to DL/2 and cs.det are high. The ML methods and ck.taub give much lower estimates (0.05 or less).

Summary and Recommendations

Always plot the data. QQ plots investigate the distribution of the data. Scatter plots show relationships between variables and can reveal outliers and influential points.

Correlations using detects only never should be used.

For samples of size 20, the correlation estimators achieve MAD<0.1, only for highly positive correlations.

For samples of size 50, ck.taub gives the most consistent results, achieving MAD<0.1 with 50 to 70% censoring in most cases.

For samples of size 100 or more, cp.mle2 gives the best results and can be used with 60 to 90% censoring, depending, unfortunately, on the correlation.

Because the behavior of the estimators is complicated and depends on the parameter being estimated, we suggest comparing estimates of correlation and not relying too heavily on any single estimate for highly censored data.

Future Work

In future work, we will examine the impact of departures from the assumptions employed in the simulations, in particular, the assumption that the data are log normally distributed. We also would like to look more closely at the effect of sample size.

Here we have focused on point estimates of correlation. Future work will examine interval estimates.

As mentioned above, the performance of maximum likelihood estimators of correlation would be enhanced if better estimates of the mean and variance could be obtained. Future work will investigate parametric and nonparametric (for instance Kaplan-Meier) methods for improving estimates of mean and variance.

Statistical methods must be developed that explicitly incorporate the variability of all observations and not simply that of the censored values. The analysis of duplicate samples can help to assess the variability of the laboratory methods.

Supplementary Material

1si20060921_08. Supporting Information Available.

The Supporting Information is available at http://pubs.acs.org. It provides box plots of simulation results for all parameter values considered, including results with different sample sizes and results with simultaneous estimation of all five parameters for cp.mle. Also shown are scatter plots of simulated data and an example of the computation of Kendall's tau-b.