Caffeine Reduces the Activation Extent and Contrast-to-Noise Ratio of the Functional Cerebral Blood Flow Response but not the BOLD Response

Abstract

Measures of the spatial extent of functional activation are important for a number of functional magnetic resonance imaging (fMRI) applications, such as pre-surgical planning and longitudinal tracking of changes in brain activation with disease progression and drug treatment. The interpretation of the data from these applications can be complicated by inter-subject or inter-session variability in the measured fMRI signals. Prior studies have shown that modulation of baseline cerebral blood flow (CBF) can directly alter the functional CBF and blood oxygenation level dependent (BOLD) responses, suggesting that the spatial extents of functional activation maps based on these signals may also depend on baseline CBF. In this study, we used a caffeine dose (200 mg) to decrease baseline CBF and found significant (p<0.05) reductions in both the CBF activation extent and contrast-to-noise ratio (CNR) but no significant changes in the BOLD activation extent and CNR. In contrast, caffeine significantly changed the temporal dynamics of the BOLD response but not the CBF response. The decreases in the CBF activation extent and CNR were consistent with a significant caffeine-induced decrease in the absolute CBF change accompanied by no significant change in the residual noise. Measures of baseline CBF also accounted for a significant portion of the inter-subject variability in the CBF activation map area and CNR. Factors that can modulate baseline CBF, such as age, medication, and disease, should therefore be carefully considered in the interpretation of studies that use functional CBF activation maps.

Introduction

Measures of the spatial extent of functional activation are important for a number of clinical functional MRI (fMRI) applications, such as longitudinal tracking of changes in brain activation with disease progression and medical treatment (Davis et al. 2005) and pre-surgical planning (Haberg et al. 2004). However, interpretation of activation maps based on the blood oxygenation level dependent (BOLD) signal can be complicated by the BOLD signal’s complex dependence on a number of physiological variables. Furthermore, the BOLD signal has been found to vary significantly across subjects and imaging sessions (Aguirre et al. 1998).

As an alternative, functional perfusion or CBF activation maps obtained with arterial spin labeling (ASL) reflect the response of a single physiological variable. Because ASL CBF measures reflect delivery of blood to the capillary bed, it has been suggested that these measures may be better localized to the sites of neural activity than the BOLD signal, which is biased toward large draining veins (Luh et al. 2000). Also, studies have suggested that CBF measurements may be less susceptible to intra-subject and inter-subject variability as compared to BOLD (Aguirre et al. 2002; Tjandra et al. 2005) and have more robust behavior in the presence of baseline signal drifts (Wang et al. 2003; Olson et al. 2006).

These potential advantages of ASL CBF over BOLD fMRI make CBF activation maps a desirable candidate for clinical fMRI applications. However, it is also important to consider how differences in baseline CBF may affect CBF and BOLD activation maps since baseline CBF can be significantly altered by age, disease, and medical treatment (Lassen 1959; Melamed et al. 1980). Prior studies have shown that the BOLD signal amplitude may be inversely proportional to baseline CBF (Cohen et al. 2002), while the functional absolute CBF change may be either directly proportional to (Shimosegawa et al. 1995) or independent of (Kastrup et al. 1999) baseline CBF. These prior findings suggest that modulation of the baseline CBF may alter the spatial extents of functional activation maps. In this study, we directly assess the dependence of both functional CBF and BOLD activation maps on baseline CBF.

Theory

In this section we review the general linear model that is used to generate statistical measures for both CBF and BOLD contrast from ASL data. We also present expressions that are useful for understanding the factors that can affect the contrast-to-noise ratio.

General Linear Model

The general linear model (GLM) for ASL data can be written as:

$$\mathbf{p}=\kappa (\mathbf{X}{\mathbf{h}}_{\mathbf{\text{BOLD}}}+\mathbf{M}(\mathbf{X}{\mathbf{h}}_{\mathbf{\text{CBF}}}+{\mathbf{1}}_N\mathrm{b})+\mathbf{S}\mathbf{d}+\mathbf{P}\mathbf{c}+\mathbf{n})$$ [1]

where p is a N × 1 vector that represents the raw measured data consisting of alternating tag and control images (Mumford et al. 2006; Restom et al. 2006) and κ is a scaling term that is described in more detail below. In general, X is an N × k design matrix, h_BOLD is a k × 1 vector of BOLD hemodynamic parameters, M is a N × N diagonal matrix consisting of alternating −1s and 1s for the tag and control images, respectively, h_CBF is a k × 1 vector of CBF hemodynamic parameters, 1_N is a N × 1 column vector of 1s, and b is a scalar representing the baseline CBF value. In this paper, we construct X as the N × 1 vector obtained from the convolution of a block design stimulus pattern with a gamma density function (Boynton et al. 1996). The peak-to-peak amplitude of X is normalized to unity, so that the parameter weights h_BOLD and h_CBF represent the amplitudes of the BOLD and CBF responses, respectively. The term Sd represents nuisance components, where S is a N × 2 matrix composed of constant and linear terms, and d is a 2 × 1 vector of scalar weights. The constant term is a vector of 1’s so that the first element of d represents the amplitude of the constant component. The term Pc represents physiological noise components, where P is a N × m matrix of physiological noise regressors and c is a m × 1 vector of regressor weights. Finally, n is a N × 1 vector that represents additive Gaussian noise with covariance matrix σ²C.

In this paper, we define the scaling term as $\kappa ={\mathbf{M}}_{0B}(T{I}_1)e^{-T{I}_2/T_{1B}}{e}^{-T{E}_1/T_{2B}^{*}},$ where M_0B is the equilibrium magnetization of the arterial blood, TI₁ is the specified bolus width of the tag, TI₂ is the inversion time, T_1B denotes the longitudinal relaxation time constant of arterial blood, TE₁ is the echo time of the first echo (see Methods), and $T_{2B}^{*}$ is the transverse relaxation time constant of arterial blood. An estimate of M_0B in measured signal units can be obtained with the use of additional calibration scans (Wang et al. 2005), as described in the Methods section. We assume that T_1B and $T_{2B}^{*}$ are equal to 1664 and 106 ms, respectively (Lu et al. 2004; St Lawrence and Wang 2005) . Note that because of the short echo time used in this study (2.9ms, see Methods), the definition of the scaling constant is fairly insensitive to variations in $T_{2B}^{*}.$ With the scaling term defined as above, the CBF response amplitude h_CBF and the baseline CBF value b are in physiological units of mL/(100g-min) (Wong et al. 1998). Furthermore, the use of the estimate of M_0B accounts for differences in scanner gains between scan sessions, facilitating the inter-session comparison of the BOLD amplitude h_BOLD and the constant term.

Since test statistics formed from the GLM are invariant with respect to κ, it is convenient to define a normalized GLM of the form:

$$\tilde{\mathbf{p}}=\mathbf{X}{\mathbf{h}}_{\mathbf{\text{BOLD}}}+\mathbf{M}(\mathbf{X}{\mathbf{h}}_{\mathbf{\text{CBF}}}+{\mathbf{1}}_N\mathrm{b})+\mathbf{S}\mathbf{d}+\mathbf{P}\mathbf{c}+\mathbf{n}$$ [2]

where p˜ = p/κ. We use this normalized GLM for the remainder of the paper.

For statistical tests, it is helpful to rewrite the GLM in the following form:

$$\tilde{\mathbf{p}}=\mathbf{Z}\beta +\mathbf{n}$$ [3]

where Z = [X MX M1_N S P] and $\beta ={\left[{\mathbf{h}}_{\mathbf{\text{BOLD}}}^T{\mathbf{h}}_{\mathbf{\text{CBF}}}^T{\mathrm{b}}^T{\mathbf{d}}^T{\mathbf{c}}^T\right]}^T.$ The F-statistic to test the contrast Aβ̂ = 0 can be written as

$$F=\frac{N-r}{s}\frac{{\left(\mathbf{A}\widehat{\mathit{\beta }}\right)}^T{\left[\mathbf{A}{({\mathbf{Z}}^T\mathbf{Z})}^{-1}{\mathbf{A}}^T\right]}^{-1}\left(\mathbf{A}\widehat{\beta }\right)}{RSS}$$ [4]

where A is a s×r contrast matrix, β̂=(Z^TZ)⁻¹Z^Tp̂, RSS is the residual sum of squares, r is the total number of regressors, and s is the number of tested contrasts (Seber and Lee 2003). As described in further detail under Methods, the current study employs a dual echo acquisition sequence in which the first and second echoes are used for the estimation of CBF and BOLD activation, respectively. Since the data acquired in each echo exhibits both CBF and BOLD-weighted components, the form of the GLM presented above applies to both sets of data. To assess the significance of the CBF activation we compute the F-statistic with A = [0 1 0] where 0 is a 1×(r−2)row vector of zeros. Similarly, we test the significance of the BOLD activation by defining A = [1 0 0].

Expressions for Contrast-to-Noise Ratio

The F-statistic has the form of a squared contrast-to-noise ratio in which the numerator is an estimate of the energy in the contrast of interest (after nuisance terms have been removed) and the denominator is the estimate of the noise variance (Liu et al. 2001). The square root of the F-statistic thus has the form of a contrast-to-noise ratio. Indeed, in the absence of nuisance terms and with the assumption of uncorrelated noise, the square root of the F-statistic for the BOLD contrast can be written as $\sqrt{F_{\mathit{\text{BOLD}}}}={\Vert \mathbf{X}\Vert }_2\frac{{\widehat{h}}_{\mathit{\text{BOLD}}}}{{\widehat{\sigma }}_{n,\mathit{\text{BOLD}}}}\text{where}{\widehat{h}}_{\mathit{\text{BOLD}}}$ is the estimate of the BOLD response amplitude (normalized as described above to account for differences in inter-session gains), ${\widehat{\sigma }}_{n,\mathit{\text{BOLD}}}$ is the estimate of the noise standard deviation for the BOLD-weighted data, and ‖X‖₂ denotes the norm of the design matrix, which for this paper is simply a vector norm. When nuisance terms and correlated noise are considered, the general form of the statistic is

$$\sqrt{F_{\mathit{\text{BOLD}}}}={\eta }_{\mathit{\text{BOLD}}}\frac{{\widehat{h}}_{\mathit{\text{BOLD}}}}{{\widehat{\sigma }}_{n,\mathit{\text{BOLD}}}}$$ [5]

where ${\eta }_{\mathit{\text{BOLD}}}=\sqrt{{\mathbf{X}}^T{({\mathbf{C}}^{-1/2})}^T(\mathbf{I}-{\mathbf{P}}_{NW}){\mathbf{C}}^{-1/2}\mathbf{X}}$, and P_NW = C^−1/2N(N^TC⁻¹N)⁻¹N^T (C^−1/2)^T is a projection matrix that projects onto the subspace spanned by the whitened nuisance regressors (Liu et al. 2001), where N = [MX M1_N S P]are the nuisance regressors for the BOLD-weighted data. Note that the square root operation is well-defined because we have assumed that X is a vector. Also, since the peak-to-peak amplitude of X is normalized to unity in this study, η_BOLD is greater than one (mean = 4.2, standard deviation = 0.65, with the actual value depending on the subspace spanned by the whitened nuisance regressors), making $\sqrt{F_{\mathit{\text{BOLD}}}}\text{larger than}\left({\widehat{h}}_{\mathit{\text{BOLD}}}/{\widehat{\sigma }}_{n,\mathit{\text{BOLD}}}\right)$ by a factor of η_BOLD. Equation 5 indicates that, to first order, changes in $\sqrt{F_{\mathit{\text{BOLD}}}}$ across conditions can be attributed to changes in ${\widehat{h}}_{\mathit{\text{BOLD}}}\text{and}{\widehat{\sigma }}_{n,\mathit{\text{BOLD}}}.$ In addition, there will be a second order effect on the magnitude of ${\eta }_{\mathit{\text{BOLD}}}$ due to inter-session differences in the structure of the covariance matrix and the space spanned by the physiological noise regressors that make up a portion of the nuisance subspace. Since the BOLD signal is typically expressed in terms of percent change, it is helpful to rewrite Equation 5 as

$$\begin{array}{ll}\sqrt{F_{\mathit{\text{BOLD}}}}& ={\eta }_{\mathit{\text{BOLD}}}\frac{{\widehat{h}}_{\mathit{\text{BOLD}}}}{{\mathit{\text{BOLD}}}_0}\frac{{\mathit{\text{BOLD}}}_0}{{\widehat{\sigma }}_{n,\mathit{\text{BOLD}}}}\hfill \\ \hfill & ={\eta }_{\mathit{\text{BOLD}}}·\frac{\%\mathrm{\Delta }\mathit{\text{BOLD}}}{100}·{\mathit{\text{SNR}}}_{\mathit{\text{BOLD}}}\hfill \end{array}$$ [6]

where %ΔBOLD denotes the percent change in the BOLD signal, BOLD₀ = c^Td̂ denotes the baseline BOLD signal (i.e constant term) with c^T =[1 0], and the signal-to-noise ratio SNR_BOLD is the baseline signal divided by the standard deviation of the noise.

Similar to the expressions presented above for the BOLD estimates, the square-root of the F-statistic for the CBF estimate has the form

$$\sqrt{F_{\mathit{\text{CBF}}}}={\eta }_{\mathit{\text{CBF}}}\frac{{\widehat{h}}_{\mathit{\text{CBF}}}}{{\widehat{\sigma }}_{n,\mathit{\text{CBF}}}}$$ [7]

where ${\widehat{h}}_{\mathit{\text{CBF}}}$ denotes the estimate of the CBF response amplitude, ${\widehat{\sigma }}_{n,\mathit{\text{CBF}}}$ is the estimate of the noise standard deviation, both in physiological units of mL/(100g-min), and ${\eta }_{\mathit{\text{CBF}}}=\sqrt{{\mathbf{X}}^T{\mathbf{M}}^T{({\mathbf{C}}^{-1/2})}^T(\mathbf{I}-{\mathbf{P}}_{NW}){\mathbf{C}}^{-1/2}\mathbf{M}\mathbf{X}}$ where P_NW is the previously defined projection matrix with N = [X M1_N S P] as the nuisance regressors for the CBF-weighted data. Equation 7 can be rewritten as

$$\begin{array}{ll}\sqrt{F_{\mathit{\text{CBF}}}}& ={\eta }_{\mathit{\text{CBF}}}\frac{{\widehat{h}}_{\mathit{\text{CBF}}}}{\widehat{b}}\frac{\widehat{b}}{{\widehat{\sigma }}_{n,\mathit{\text{CBF}}}}\hfill \\ \hfill & ={\eta }_{\mathit{\text{CBF}}}·\frac{\%\mathrm{\Delta }\mathit{\text{CBF}}}{100}·{\mathit{\text{SNR}}}_{\mathit{\text{CBF}}}\hfill \end{array}$$ [8]

where %ΔCBF denotes the percent change in the CBF signal, b̂ is the estimate of the baseline CBF signal in physiological units, and SNR_CBF is the baseline CBF signal divided by the standard deviation of the noise.

In the Methods and Results sections, we make use of Equations 5 through 8 to better understand how changes in $\sqrt{F_{\mathit{\text{CBF}}}}$ depend on changes in ${\widehat{h}}_{\mathit{\text{CBF}}},{\widehat{\sigma }}_{n,\mathit{\text{CBF}}},$ %ΔCBF, and SNR_CBF; and similarly, how changes in $\sqrt{F_{\mathit{\text{BOLD}}}}$ depend on changes in ${\widehat{h}}_{\mathit{\text{BOLD}}},{\widehat{\sigma }}_{n,\mathit{\text{BOLD}}},$ %ΔCBF, and SNR_CBF.

Methods

Experimental Protocol

Data presented here were also used for a separate analysis examining the metabolic effects of a caffeine dose (Perthen et al. 2008), and the experimental protocol is repeated here for convenience. Ten healthy adult subjects (5 males, mean age 33 years, standard deviation 7 years) participated in the study after giving informed consent. Subjects were instructed to refrain from ingesting caffeine for twelve hours prior to the study. The estimated daily caffeine usage of each subject based on self-report of coffee, tea, and caffeinated soda consumption is shown in Table 1. Each experiment consisted of a pre-dose and a post-dose imaging session. In between the sessions, the subjects ingested a 200 mg caffeine pill and rested outside of the magnet for 30 minutes, similar to previous protocols using caffeine (Liu et al. 2004; Behzadi and Liu 2006). A total of 45 minutes elapsed between ingestion of the caffeine pill and the first functional scan in the post-dose session to allow for proper absorption of caffeine from the gastrointestinal tract (Fredholm et al. 1999).

Table 1.

Per subject and average values of the estimated daily caffeine usage, number of active voxels in CBF activation maps, and CBF data metrics in the CBF intersection ROI.

Subject	Estimated daily caffeine usage (mg/d)	CBF # active voxels		$\sqrt{F_{\mathit{\text{CBF}}}}$		${\widehat{h}}_{\mathit{\text{CBF}}}$ (mL/(100g-min))		${\widehat{\sigma }}_{\mathit{\text{CBF}}}$		b̂;Baseline CBF (mL/(100g-min))		%ΔCBF		SNRCBF
		Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post
1	187.5	503	326	5.07	3.81	36.2	30.6	28.1	32.1	84.6	72.2	44.0	44.4	3.15	2.35
2	250.0	313	188	3.70	3.37	44.6	47.0	55.8	64.6	56.2	30.6	92.1	192.9	1.08	0.59
3	175.0	185	115	3.50	2.87	40.8	32.1	43.2	40.9	59.7	25.7	75.3	163.4	1.39	0.66
4	180.0	262	221	2.98	3.44	39.3	37.7	51.7	49.4	56.0	43.7	98.0	111.9	1.20	0.98
5	140.0	512	368	5.18	3.71	49.9	34.5	36.4	36.2	72.6	41.8	109.6	86.6	2.13	1.20
6	150.0	544	448	3.94	4.29	38.2	34.8	45.0	36.3	92.3	57.4	42.7	64.8	2.22	1.71
7	145.0	323	270	3.98	4.03	54.9	40.5	54.4	37.3	87.8	50.4	66.0	93.5	1.75	1.40
8	113.0	385	430	4.80	4.08	48.0	33.6	38.8	34.0	88.1	46.5	57.1	81.2	2.54	1.50
9	138.0	294	250	4.07	3.34	39.1	30.3	35.9	37.8	81.8	59.7	49.6	57.1	2.35	1.69
10	85.0	549	371	5.45	4.09	41.8	31.9	31.3	29.7	83.2	47.8	52.3	93.5	2.87	1.68
mean	156.4	387.0	298.7	4.27	3.70	43.3	35.3	42.1	39.8	76.2	47.6	68.7	98.9	2.07	1.38
std	42.9	124.4	102.7	0.77	0.42	5.7	4.9	9.1	9.7	13.3	12.9	22.8	44.2	0.67	0.51
t-test		0.003;		0.030;		0.002;		0.347;		<0.001;		0.033;		<0.001;
(p;t)	-	−3.99		−2.58		−4.24		−0.99		−8.85		2.51		−7.10

Each imaging session consisted of the following resting-state and functional scans: 1) a resting-state scan (8 min 20s of the off condition) and 2) two block design scans (6 min 50s each scan, consisting of 60s initial off period, 4 cycles of 20s on/60s off, then 30s final off period). The on periods of the functional task consisted of a full-contrast full-field black and white checkerboard pattern flashing at 8 Hz. In the center of the screen was a small white square with the numbers (2-4-3-5) appearing sequentially at 2 Hz. The off periods were of equal luminance to the on periods and consisted of a gray background with a white square in the middle. Subjects were instructed to fixate on the center white square at all times and press buttons on a 4-button response box in accordance to the numbers, where each number corresponded to the index through pinky fingers of the right hand. The flashing checkerboard was intended to activate the visual cortex while the motor task maintained subject attention. In the pre-dose session only, subjects had two hypercapnia scans at the end of the study where they received a 5% CO₂ gas mixture through a non-rebreathing mask. The hypercapnia and the resting state scans were used for a related study (Perthen et al. 2008).

A high-resolution anatomical scan was done at the beginning of each session to facilitate the alignment of post-dose and pre-dose data. Also, after the resting-state scan, minimum contrast and cerebrospinal fluid (CSF) scans were acquired to facilitate quantification of CBF.

Image Acquisition

Imaging data were acquired on a GE Signa Excite 3 Tesla whole body system with a body transmit coil and an eight channel receive head coil. Laser alignment was used to landmark the subjects and minimize differences in head position between pre-dose and post-dose sessions.

The resting-state and functional scans were acquired with a PICORE QUIPSS II (Wong et al. 1998) ASL sequence (TR = 2.5 s, TI1/TI2 = 600/1500 ms) with a dual echo spiral readout (TE1/TE2 = 2.9/24 ms, FOV = 24 cm, 64 × 64 matrix, and a flip angle of 90°). Six oblique axial 5-mm slices were prescribed about the calcarine sulcus for all functional runs.

The calibration scans for CBF quantification used the same in-plane parameters as the functional scans, but the number of slices was increased to ensure coverage of the lateral ventricles. The CSF reference scan consisted of a single-echo, single repetition scan acquired at full relaxation at an echo time of 2.9 ms, while the minimum contrast scan was acquired with TR = 2 s and TE = 11 ms. The high-resolution anatomical scan was acquired with a magnetization prepared 3D fast spoiled gradient echo (FSPGR) sequence (TI = 450 ms, TR = 7.9 ms, TE = 3.1 ms, 12° flip angle, FOV 25 cm, matrix 256 × 256 × 256).

Cardiac pulse and respiratory effort data were monitored using a pulse oximeter (InVivo) and a respiratory effort transducer (BIOPAC), respectively. The pulse oximeter was placed on the subject’s left index finger, and the respiratory effort belt was placed around the subject’s abdomen. Physiological data were sampled at 40 samples per second using a multi-channel data acquisition board (National Instruments).

Data Preprocessing and General Linear Model Analysis

All images were coregistered using AFNI software (Cox 1996). The structural scan from each post-dose session was aligned to the structural scan of its respective pre-dose session, and the rotation and shift matrix used for this alignment was then applied to the post-dose images (Liu et al. 2004). Data from the first ten seconds of each functional scan were discarded to allow magnetization to reach a steady state.

A general linear model (GLM) analysis (see Theory) was performed on the block design functional runs to determine statistical significance of the responses. For each scanner session, data from the two functional runs were concatenated for GLM analysis (Restom et al. 2006). Pre-whitening was performed using an autoregressive AR(1) model (Woolrich et al. 2001). The measured cardiac and respiratory data were included as regressors in the GLM to account for the influence of physiological fluctuations on the measurements (Restom et al. 2006). F statistic and p value maps indicating significance of CBF functional activation were obtained from the GLM analysis of the first echo data. Analysis of the second echo data yielded similar maps for the BOLD functional activation.

For each voxel, values of $\sqrt{F_{\mathit{\text{CBF}}}},{\widehat{h}}_{\mathit{\text{CBF}}},{\widehat{\sigma }}_{n,\mathit{\text{CBF}}},\text{and}\widehat{b}$ were calculated directly from the GLM analysis of the first echo data. Per voxel values of %ΔCBF and SNR_CBF were calculated from the per voxel ${\widehat{h}}_{\mathit{\text{CBF}}},{\widehat{\sigma }}_{n,\mathit{\text{CBF}}},\text{and}\widehat{b}$ values using Equation 8. Also for each voxel, a CBF time series was computed from the running subtraction of the first echo data after detrending and removal of BOLD-weighted components (Liu and Wong 2005). Similarly, per voxel values of $\sqrt{F_{\mathit{\text{BOLD}}}},{\widehat{h}}_{\mathit{\text{BOLD}}},{\widehat{\sigma }}_{n,\mathit{\text{BOLD}}},$ and BOLD₀ were calculated from the GLM analysis of the second echo data, and per-voxel values of %ΔBOLD, and SNR_BOLD were obtained using Equation 6. The per voxel BOLD time series were obtained from the running average of the second echo data after detrending and removal of CBF-weighted components.

Defining Regions-of-Interest, Average Parameter Values, and Average Time Series

Figure 1 shows an example of region-of-interest (ROI) formation for the most inferior functional slice from Subject 8. ROIs were defined using a combination of the following masks: 1) a visual cortex anatomical mask, 2) a volume overlap mask, and 3) a mask based on functional activation. The visual cortex anatomical mask was defined as the posterior third of the brain in each functional slice to include visual areas while excluding motor areas. With the slice coverage used in this protocol, the acquired slices did not include visual areas of the temporal lobe. After registration of the post-dose functional volume to the pre-dose volume, some voxels (especially those in the outer two slices) had only minimal overlap between the two sessions. To identify areas with sufficient overlap between the pre-dose and post-dose sessions, a volume overlap mask was defined to include voxels in the brain with over 90% volume overlap between the pre-dose and post-dose sessions. Initial CBF functional activation maps were defined from voxels that exhibited functional CBF activation at an overall significance level of p<0.05, with correction for multiple comparisons using the AFNI AlphaSim program (Cox 1996). The intersection of the visual cortex anatomical mask, the volume overlap mask, and the initial CBF functional activation maps from the pre-dose and post sessions defined the pre-dose and post-dose CBF activation maps, respectively. The binary version of these maps (e.g 1 assigned to non-zero values of the maps) constituted the CBF activation masks. For each subject, a CBF intersection ROI was formed from the intersection of the pre-dose and post-dose CBF activation masks to select the same volume of activation between sessions for pairwise comparison. In addition, a CBF union ROI was also formed for each subject by taking the union of the pre-dose and post-dose CBF activation masks. This process was repeated with the BOLD data (overall significance level p<0.05) to create pre-dose and post-dose BOLD functional activation maps, and BOLD intersection and union ROIs.

Figure 1.

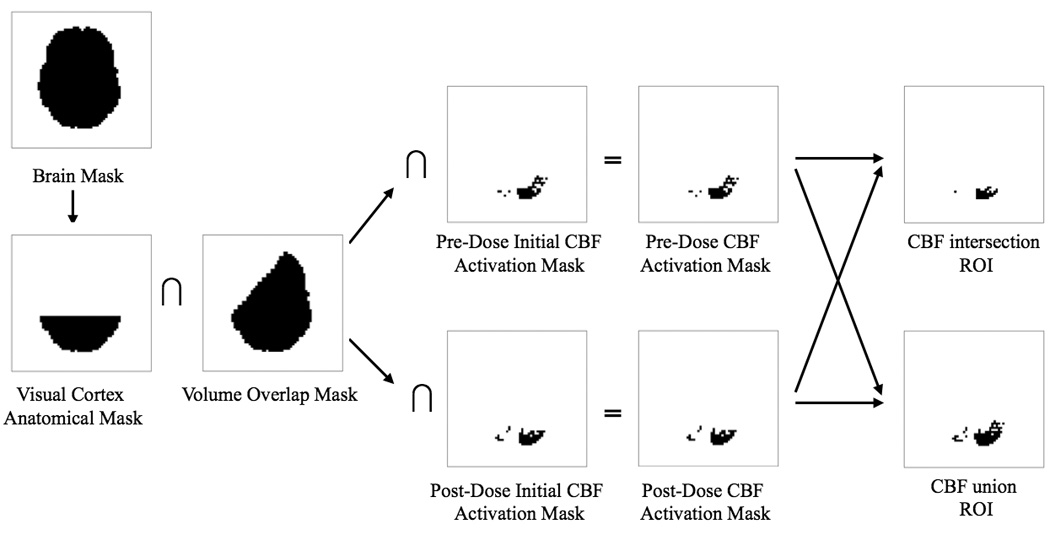
Example of region-of-interest (ROI) formation for the most inferior functional slice from subject 8. As seen in the volume overlap mask, the left anterior portion of the brain in this slice had less than 90% volume overlap between the pre-dose and post-dose sessions. For this example, the initial CBF activation masks are identical to the CBF activation masks because this slice did not include areas of motor activity.

For each metric and ROI, a per-subject average value was obtained by averaging the metric across all voxels within the ROI. The per voxel ΔCBF time series were defined as the per voxel CBF time series after subtraction of the per voxel baseline CBF (b̂). Division of the per voxel ΔCBF time series by b̂ produced the per voxel %ΔCBF time series. The per voxel ΔCBF and %ΔCBF time series were averaged over voxels within each ROI to form the per subject ΔCBF and %ΔCBF time series. The per subject ΔCBF and %ΔCBF time series were averaged over cycles to form the per subject ΔCBF and %ΔCBF block responses, which were then averaged over subjects to form the group average ΔCBF and %ΔCBF block responses, respectively. Similarly, per voxel %ΔBOLD time series, per subject %ΔBOLD time series, and the per subject and group average %ΔBOLD block responses were computed.

To assess the temporal dynamics of the CBF and BOLD responses, we interpolated each subject’s ΔCBF and %ΔBOLD block responses to a time resolution of 0.25s and computed the following timing parameters: 1) time to reach 50% of the peak response (T₅₀), 2) time after the peak to return to 50% of the peak response (TA₅₀), and 3) the full-width half-maximum (FWHM = TA₅₀ − T₅₀).

Statistical Tests

We used two-tailed paired t-tests to compare pre-dose and post-dose parameter estimates. For both the CBF and BOLD data, we compared the pre-dose and post-dose values of the number of functionally active voxels (using the pre-dose and post-dose activation maps) and the contrast-to-noise ratio estimates $\sqrt{F_{\mathit{\text{CBF}}}}\text{and}\sqrt{F_{\mathit{\text{BOLD}}}}$ (with separate tests for the intersection and union ROIs). In addition, to better understand the factors that alter the contrast-to-noise ratio, we also performed pre-dose versus post-dose comparisons of the amplitude estimates ${\widehat{h}}_{\mathit{\text{CBF}}}\text{and}{\widehat{h}}_{\mathit{\text{BOLD}}},$ the noise estimates ${\widehat{\sigma }}_{n,\mathit{\text{CBF}}}\text{and}{\widehat{\sigma }}_{n,\mathit{\text{BOLD}}},$ the baseline estimates b̂ and BOLD₀, the percent change estimates %ΔCBF and %ΔBOLD, and the signal-to-noise ratio estimates SNR_CBF and SNR_BOLD.

To further assess the dependence of the number of active voxels, the contrast-to-noise ratio, and the functional response amplitude on baseline CBF, we computed the correlation between the number of active voxels (CBF or BOLD) and the per subject baseline CBF estimate b̂, the correlation between the CNR estimates $(\sqrt{F_{\mathit{\text{CBF}}}}\text{or}\sqrt{F_{\mathit{\text{BOLD}}}})$ and b̂, and also the correlation between the absolute functional amplitudes $({\widehat{h}}_{\mathit{\text{CBF}}}\text{and}{\widehat{h}}_{\mathit{\text{BOLD}}}),$ and b̂. To account for the effect of activation extent size on the measurement of response amplitude (Laurienti et al. 2002), we also computed the correlation between b̂ and the CBF total response magnitude (defined as the product of ${\widehat{h}}_{\mathit{\text{CBF}}}$ and the number of active CBF voxels) and the correlation between b̂ and the BOLD total response magnitude (defined as the product of ${\widehat{h}}_{\mathit{\text{BOLD}}}$ and the number of active BOLD voxels). These correlations were computed using data from the pre-dose session only, the post-dose session only, and the union of the pre-dose and post-dose sessions.

To assess caffeine’s effect on CBF and BOLD temporal dynamics, we used paired two-tailed t-tests to compare the pre-dose and post-dose timing parameters (T₅₀, TA₅₀, and FWHM) across subjects. In addition, to examine whether possible changes in the shape of the curve affected correlation of the responses with the GLM reference function (X), we computed the correlation between the reference function and the per subject ΔCBF and %ΔBOLD time series. Paired two-tailed t-tests were then used to compare the pre-dose and post-dose correlation values across subjects.

Results

Figure 2 shows example pre-dose and post-dose activation maps from Subject 1 for the CBF data (top two rows) and BOLD data (bottom two rows). The post-dose CBF activation map (second row) exhibits fewer active voxels than the pre-dose CBF activation map (top row). In contrast, there is not a clear difference between the number of active voxels in the pre-dose (third row) and post-dose (last row) BOLD activation maps. Figure 3 shows example pre-dose and post-dose activation maps for the third or fourth most inferior slice from each subject for the CBF data (top two rows) and BOLD data (bottom two rows). Consistent with the trend found in Subject 1’s data in Figure 2, the post-dose CBF activation maps (second row) exhibit fewer active voxels than the pre-dose CBF activation maps (top row) for all subjects. Also in agreement with Figure 2, the number of active voxels in the pre-dose (third row) and the post-dose (last row) BOLD activation maps appear to be similar. For the CBF data, Table 1 shows per subject and average metric values and two-tailed paired t-test results for comparisons of: 1) the number of active voxels in the pre-dose versus post-dose activation maps, and 2) the metrics in the intersection ROI. Table 2 shows the same information for the BOLD data. In agreement with the results of Figure 2 and Figure 3, we found that the caffeine dose significantly reduced the number of voxels across subjects in the post-dose as compared to the pre-dose CBF activation maps (22.8% reduction, p = 0.0031, t = −3.99), but did not find a significant difference in the number of voxels in the pre-dose versus post-dose BOLD activation maps (p = 0.69, t = 0.41).

Figure 2.

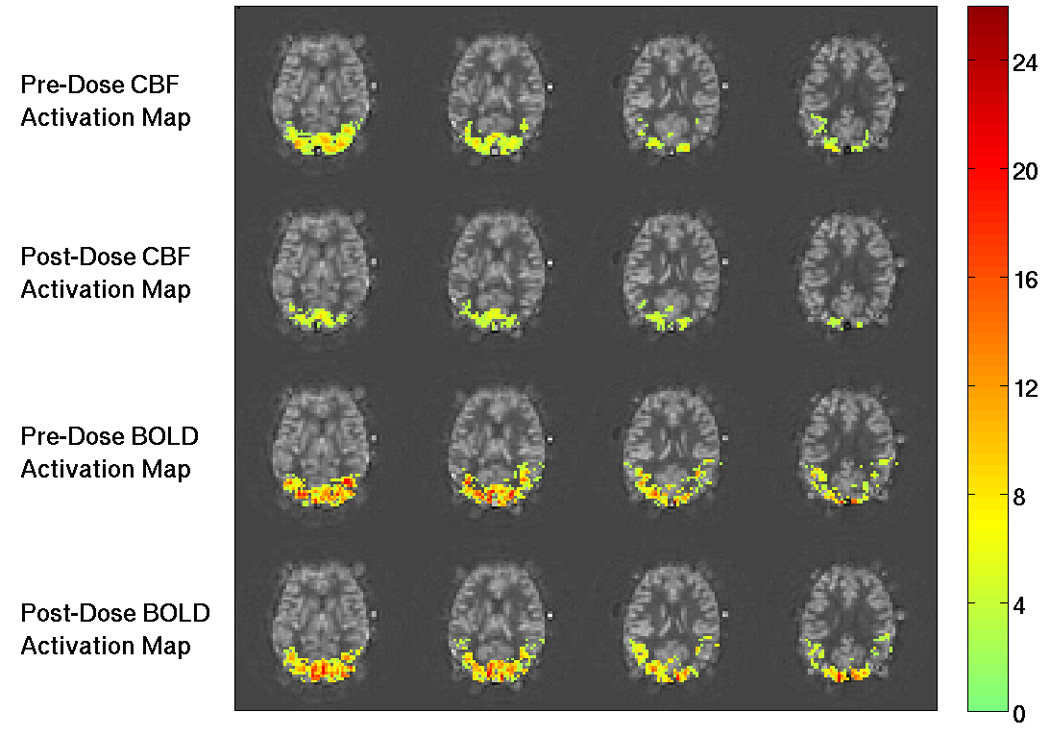
Example functional activation maps from Subject 1. The CNR values for activated regions are overlaid on baseline CBF maps. Top and second rows show the pre-dose and post-dose CBF activation maps, respectively. The number of voxels is visibly decreased from the pre-dose to the post-dose conditions. The third and fourth rows show the pre-dose and post-dose BOLD activation maps, respectively. There is no apparent difference in the number of active BOLD voxels between the two conditions. The colorbar shows CNR $(\sqrt{F_{\mathit{\text{CBF}}}}\text{and}\sqrt{F_{BOLD}})$ values.

Figure 3.

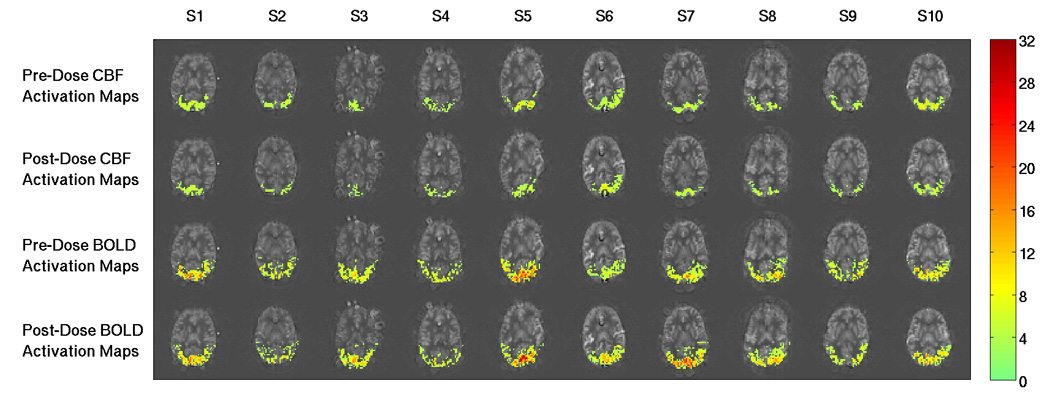
Example functional activation maps for the third or fourth most inferior slice from each subject. Each column shows data from a single subject (denoted S1 to S10), and CNR values for activated regions are overlaid on baseline CBF maps. Top and second rows show the pre-dose and post-dose CBF activation maps, respectively. The number of active CBF voxels is visibly decreased from the pre-dose to the post-dose conditions for all subjects. The third and fourth rows show the pre-dose and post-dose BOLD activation maps, respectively. The number of active BOLD voxels in the two conditions appear to be similar. The colorbar shows CNR $(\sqrt{F_{\mathit{\text{CBF}}}}\text{and}\sqrt{F_{BOLD}})$ values.

Table 2.

Per subject and average values of the number of active voxels in BOLD activation maps and BOLD data metrics in the BOLD intersection ROI.

Subject	BOLD # active voxels		$\sqrt{F_{BOLD}}$		${\widehat{h}}_{BOLD}$		${\widehat{\sigma }}_{n,BOLD}$		BOLD0		%ΔBOLD		SNRBOLD
	Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post
1	735	726	7.95	7.20	61.3	66.7	32.7	36.1	5864.8	5853.0	1.07	1.21	200.1	178.4
2	780	924	5.58	4.92	77.0	68.0	49.8	52.8	5508.6	5605.4	1.47	1.26	123.0	116.9
3	982	911	5.93	6.16	61.0	55.9	44.1	40.2	5643.6	5161.1	1.11	1.13	135.2	136.7
4	832	658	5.62	4.84	76.3	64.4	51.9	48.6	5387.3	5482.8	1.50	1.24	121.3	128.7
5	1399	1273	8.32	7.95	76.5	67.4	38.7	35.5	6150.9	5561.1	1.34	1.35	182.2	173.9
6	865	981	4.18	6.11	64.5	72.0	52.7	39.1	5865.2	5822.8	1.17	1.32	136.3	171.5
7	689	953	5.78	9.19	70.4	70.7	47.6	34.3	6247.2	5678.7	1.16	1.28	143.0	174.0
8	1035	1084	5.94	6.82	64.2	66.3	43.5	39.2	6154.5	5637.4	1.09	1.24	164.0	159.8
9	734	665	6.27	5.75	53.6	53.3	37.2	36.8	5746.9	5545.3	0.98	1.03	164.4	162.5
10	763	811	7.07	6.88	52.9	50.7	31.5	31.0	6054.3	5878.9	0.90	0.89	207.7	207.5
mean	881.4	898.6	6.26	6.58	65.8	63.5	43.0	39.4	5862.3	5622.7	1.18	1.20	157.7	161.0
std	202.2	183.0	1.16	1.27	8.6	7.1	7.3	6.3	276.7	201.2	0.19	0.13	29.5	25.5
t-test	0.694;		0.484;		0.301;		0.083;		0.023;		0.734;		0.570;
(p;t)	0.41		0.73		−1.10		−1.95		−2.74		0.35		0.59

Consistent with the observed reduction in the number of functionally active CBF voxels, the caffeine dose significantly reduced $\sqrt{F_{\mathit{\text{CBF}}}}$ in the CBF intersection ROI (13.4% reduction, p = 0.030, t = −2.58). The reduction in $\sqrt{F_{\mathit{\text{CBF}}}}$ was consistent with a significant decrease in ${\widehat{h}}_{\mathit{\text{CBF}}}$ (18.4% reduction, p = 0.002, t = −4.24) and a lack of a significant change in ${\widehat{\sigma }}_{n,\mathit{\text{CBF}}}$ (p = 0.35, t = −0.99) (see also Equation 7). The caffeine dose significantly increased %ΔCBF (43.5% increase, p = 0.033, t = 2.51) and significantly reduced SNR_CBF (33.3% decrease, p < 0.001, t = −7.10). Note that the product of these average relative changes (1.435 0.667 = 0.957) shows an overall decrease roughly consistent with the reduction in $\sqrt{F_{\mathit{\text{CBF}}}}$ (see Equation 8). There is not exact agreement because the per subject average $\sqrt{F_{\mathit{\text{CBF}}}}$ does not equal the product of the per subject average values of %ΔCBF and SNR_CBF, reflecting the fact that the product of two average quantities does not in general equal the average of the product. In agreement with the findings of our previous studies (Liu et al. 2004; Behzadi and Liu 2006), the caffeine dose significantly reduced the baseline CBF estimate b̂ across subjects (37.6% reduction, p < 0.001, t = −8.85). When considered together with the lack of a significant change in ${\widehat{\sigma }}_{n,\mathit{\text{CBF}}}$ the decrease in b̂ is consistent with the observed decrease in SNR_CBF . Consistent with the results obtained with the CBF intersection ROI, the caffeine dose significantly decreased $\sqrt{F_{\mathit{\text{CBF}}}}$ (p=0.008, t=−3.43), ${\widehat{h}}_{\mathit{\text{CBF}}}$ (p<0.001 t=−6.80), SNR_CBF (p<0.001, t=−6.89), and b̂ (p<0.001, t=−8.94), significantly increased %ΔCBF (p=0.01, t=3.24), and did not significantly change ${\widehat{\sigma }}_{n,\mathit{\text{CBF}}}$ (p=0.18, t=−1.47) in the CBF union ROI.

In agreement with the lack of a significant difference in the number of functionally active BOLD voxels between the pre-dose and post-dose conditions, the caffeine dose did not significantly change $\sqrt{F_{\mathit{\text{BOLD}}}}$ (p = 0.48, t = 0.73) for the intersection ROI. Consistent with the lack of a significant change in $\sqrt{F_{\mathit{\text{BOLD}}}},$ we found that the caffeine dose did not have a significant effect on either ${\widehat{h}}_{\mathit{\text{BOLD}}}$ (p = 0.30, t = −1.10) or ${\widehat{\sigma }}_{n,\mathit{\text{BOLD}}}$ (p = 0.083, t = −1.95) (see Equation 5). In addition caffeine did not lead to a significant change in either SNR_BOLD (p = 0.57, t = 0.59) or %ΔBOLD (p = 0.73, t = 0.35) (see Equation 6). We found that the caffeine dose significantly decreased BOLD₀ (4.0% reduction, p = 0.023, t = −2.74). Although there were not significant changes in either SNR_BOLD or ${\widehat{\sigma }}_{n,\mathit{\text{BOLD}}},$ the average percent changes in these quantities (2.1% increase and 8.4% decrease, respectively), are roughly consistent with the observed decrease in BOLD₀. Consistent with the results obtained with the BOLD intersection ROI, the caffeine dose did not significantly change $\sqrt{F_{\mathit{\text{BOLD}}}}$ (p=0.44, t=0.81), ${\widehat{h}}_{\mathit{\text{BOLD}}}$ (p=0.74, t=−0.34), ${\widehat{\sigma }}_{n,\mathit{\text{BOLD}}}$ (p=0.08, t=−1.96), SNR_BOLD (p=0.50, t=0.70), or %ΔBOLD (p=0.51, t=0.68), but significantly decreased BOLD₀ (p=0.02, t=−2.92) in the BOLD union ROI. The similarity of the paired t-test results of metrics in the intersection and union ROIs for both the CBF and BOLD data indicate that pairwise comparisons of pre-dose and post-dose data were not sensitive to the choice of ROI.

Figure 4 shows scatter plots of (a) the number of functionally active CBF voxels versus the baseline CBF estimate b̂ and (b) $\sqrt{F_{\mathit{\text{CBF}}}}$ versus b̂ across subjects for data from both the pre-dose (blue solid circles) and post-dose (red crosses) sessions. We found that b̂ was significantly correlated to the number of active CBF voxels in the pre-dose condition (r = 0.76, p = 0.011), the post-dose condition (r = 0.65, p = 0.042), and the union of the pre-dose and post-dose conditions (r = 0.72, p <0.001). Similarly, b̂ was significantly correlated with $\sqrt{F_{\mathit{\text{CBF}}}}$ in the pre-dose condition (r = 0.65, p = 0.043), the post-dose condition (r = 0.71, p = 0.022) and the union of the pre-dose and post-dose conditions (r = 0.66, p = 0.0014). Although b̂ was not significantly correlated with ${\widehat{h}}_{\mathit{\text{CBF}}}$ (pre-dose only: p = 0.97; post-dose only: p = 0.09; pre-dose and post-dose: p = 0.99), it was significantly correlated with the CBF total response magnitude in the pre-dose condition (r = 0.71, p = 0.023) and the union of the pre-dose and post-dose conditions (r = 0.73, p < 0.001) but not the post-dose condition (r = 0.56, p = 0.096). In contrast, b̂ was not significantly correlated with the number of active BOLD voxels (pre-dose only: p = 0.610; post-dose only: p = 0.452; pre-dose and post-dose: p = 0.439) or $\sqrt{F_{\mathit{\text{BOLD}}}}$ (pre-dose only: p = 0.497; post-dose only: p = 0.359; pre-dose and post-dose: p = 0.702). Also, b̂ was not significantly correlated with either ${\widehat{h}}_{\mathit{\text{BOLD}}}$ (pre-dose only: p = 0.49; post-dose only: p = 0.33; pre-dose and post-dose: p = 0.35) or the BOLD total response magnitude (pre-dose only: p = 0.56; post-dose only: p = 0.82; pre-dose and post-dose: p = 0.95).

Figure 4.

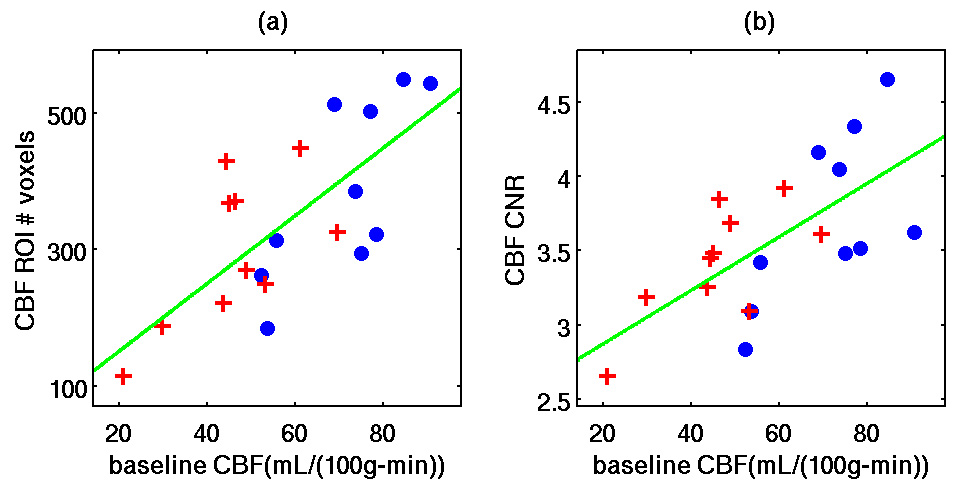
Scatter plots of (a) the number of voxels in the CBF activation maps versus baseline CBF (pre-dose only: r = 0.76, p = 0.011; post-dose only: r = 0.65, p = 0.042; pre-dose and post-dose: r = 0.72, p <0.001) and (b) CBF CNR versus baseline CBF (pre-dose only: r = 0.65, p = 0.043; post-dose only: r = 0.71, p = 0.022; pre-dose and post-dose: r = 0.66, p = 0.0014). Data are from the pre-dose (blue solid circles) and post-dose (red crosses) sessions. As discussed in the text, no significant correlations were found with similar analyses of baseline CBF versus the number of voxels in the BOLD activation maps, the BOLD CNR, ${\widehat{h}}_{BOLD},\text{or}{\widehat{h}}_{\mathit{\text{CBF}}}$ (p>0.09).

Figure 5 shows the pre-dose (blue lines) and post-dose (red lines) group average (a) %ΔBOLD, (b) %ΔCBF, and (c) ΔCBF block responses. Consistent with previous findings from our group (Liu et al. 2004), the caffeine dose visibly accelerated the temporal dynamics of the BOLD block response and significantly decreased T₅₀ (22.5% decrease, p<0.001, t=−4.87) and TA₅₀ (6.4% decrease, p=0.002, t=−4.31) but did not change the FWHM (p=0.81, t=−0.24). Caffeine had a less visible effect on the CBF block response, with no significant effect on T₅₀ (p=0.23, t=−1.28) or FWHM (p=0.22, t=−1.32) and an almost significant reduction in TA₅₀ (p=0.07, t=−2.09). The correlations between the reference function and the per subject %ΔBOLD time series were not significantly changed by caffeine (p=0.49, t=−0.73). Consistent with the relative lack of caffeine-induced change in the temporal dynamics of the CBF response, we also found no significant caffeine-induced change in the correlations between the reference function and the per subject ΔCBF time series (p=0.30, t=1.09).

Figure 5.

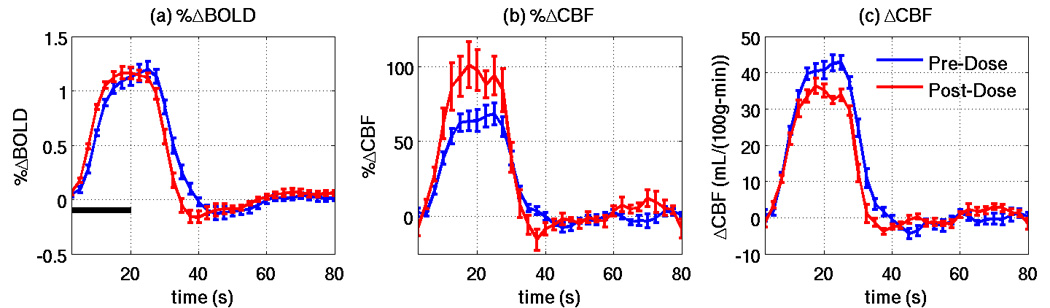
Pre-dose (blue lines) and post-dose (red lines) group average responses for (a) %ΔBOLD, (b) %ΔCBF, and (c) ΔCBF. Vertical bars show standard error, and the horizontal black bar indicates the visual stimulus.

Discussion

The caffeine dose significantly decreased the number of functionally active voxels in the CBF activation maps but not the BOLD activation maps. The decrease in the number of active CBF voxels was consistent with a significant decrease in $\sqrt{F_{\mathit{\text{CBF}}}}.$ This reduction was in turn found to reflect a reduction in the functional response amplitude ${\widehat{h}}_{\mathit{\text{CBF}}}$ without a concomitant drop in the noise standard deviation ${\widehat{\sigma }}_{n,\mathit{\text{CBF}}}.$ Alternatively, we could also view the drop in $\sqrt{F_{\mathit{\text{CBF}}}}$ as due to a significant drop in SNR_CBF that is partially offset by an increase in %ΔCBF . Note that the decrease in SNR_CBF is a direct consequence of the caffeine-induced reduction of baseline CBF coupled with a lack of change in the noise term ${\widehat{\sigma }}_{n,\mathit{\text{CBF}}}$ (see Equation 8).

Several prior studies have provided support for two competing models describing the dependence of the functional CBF response on baseline CBF: an additive model and a proportional model. In the additive model, %ΔCBF is inversely related to baseline CBF while the absolute functional CBF change (${\widehat{h}}_{\mathit{\text{CBF}}}$ in this study) is constant. This model is supported by two arterial spin labeling studies, one with subjects breathing room air (Kastrup et al. 1999), and another using breathhold-induced hypercapnia to increase baseline CBF (Li et al. 2000). In the proportional model, ${\widehat{h}}_{\mathit{\text{CBF}}}$ is proportional to baseline CBF, and %ΔCBF is constant, as supported by the results of a PET study using hypercapnia and hypocapnia to modulate baseline CBF (Shimosegawa et al. 1995). However, there is also evidence indicating that neither model provides an adequate description. In a PET study that controlled end-tidal CO₂ levels (Kemna et al. 2001) and a pulsed arterial spin labeling study that used indomethacin to reduce baseline CBF (St Lawrence et al. 2003), decreases in baseline CBF produced reductions in both %ΔCBF and the absolute functional CBF change. In this work, we found a significant caffeine-induced reduction in ${\widehat{h}}_{\mathit{\text{CBF}}}$ and a significant increase in %ΔCBF, which is not consistent with either the additive or the proportional model. Discrepancies between study findings may be related to the different measurement techniques and methods of baseline CBF manipulation. Further work is clearly needed to elucidate the neurovascular mechanisms relating changes in both %ΔCBF and ${\widehat{h}}_{\mathit{\text{CBF}}}$ to changes in baseline CBF.

The dependence of functional CBF contrast on baseline CBF was further demonstrated by the correlation analyses presented in Figure 4, where it was shown that both $\sqrt{F_{\mathit{\text{CBF}}}}$ and the number of activated voxels in the CBF activation maps were significantly correlated with baseline CBF. The observed correlations were significant whether considering the pre-dose data only, the post-dose data only, or the union of the pre-dose and post-dose data. This finding indicates that the effect of baseline CBF on functional CBF contrast is a critical factor that should be considered in the analysis of functional CBF maps. In agreement with (Kastrup et al. 1999), we did not find a significant correlation between ${\widehat{h}}_{\mathit{\text{CBF}}}$ and baseline CBF. Note that the observed decrease in ${\widehat{h}}_{\mathit{\text{CBF}}}$ with the caffeine-related decrease in baseline CBF might have suggested the presence of a positive correlation between ${\widehat{h}}_{\mathit{\text{CBF}}}$ and baseline CBF. However, the decreases in ${\widehat{h}}_{\mathit{\text{CBF}}}$ were observed by comparing each subject’s pre-dose and post-dose values across a common region-of-interest, which was specific to each subject. In examining the correlation of ${\widehat{h}}_{\mathit{\text{CBF}}}$ and baseline CBF across subjects, we computed these metrics using all voxels showing significant functional CBF activation. As shown in Figure 4a, the number of activated voxels varied across subjects and showed a positive correlation with baseline CBF. The increase in the number of voxels in subjects with higher baseline CBF values tended to lower the average ${\widehat{h}}_{\mathit{\text{CBF}}}$ measured across the activated region, offseting any trend towards an increase in ${\widehat{h}}_{\mathit{\text{CBF}}}$ and contributing to a lack of correlation between ${\widehat{h}}_{\mathit{\text{CBF}}}$ and baseline CBF. The correlation between the CBF activation extent and baseline CBF and the lack of correlation between ${\widehat{h}}_{\mathit{\text{CBF}}}$ and baseline CBF suggests that the product of ${\widehat{h}}_{\mathit{\text{CBF}}}$ and the number of active CBF voxels should be correlated with baseline CBF. Indeed, we found significant positive correlations between the CBF total response magnitude and baseline CBF for the pre-dose data and for the union of the pre-dose and post-dose data.

In agreement with the findings of the current study, previous studies have shown that caffeine reduces the baseline BOLD-weighted signal BOLD₀ (Haacke et al. 2003; Perthen et al. 2008), most likely reflecting an increase in deoxyhemoglobin content that accompanies the caffeine-induced reduction in baseline CBF. Our finding that %ΔBOLD was not significantly affected by caffeine agrees with the findings of our previous studies (Liu et al. 2004; Behzadi and Liu 2006) but not others (Mulderink et al. 2002; Chen and Parrish 2007). As noted by (Laurienti et al. 2002), differences in chronic caffeine usage and the duration of withdrawal between these studies may account for the differences in the modulation of the BOLD signal amplitude. In their study, (Laurienti et al. 2002) found that a caffeine dose tended to increase BOLD magnitude in high (>300mg/day) caffeine users and decrease BOLD magnitude in low (<120mg/day) caffeine users when both groups began from a withdrawal state. A more recent study by the same group found that a caffeine dose tended to decrease BOLD magnitude in both high (>600mg/day) and low (<200mg/day) caffeine users when both groups began from a native state (Yang et al. 2007). The results in the withdrawal state (30 hours) of caffeine were consistent with their previous study, with an increase in the BOLD signal in the high users and a decrease in the low users.

Consistent with previous results from our group (Liu et al. 2004), we found that the caffeine dose accelerated the temporal dynamics of the BOLD response. However, we also found that the caffeine dose did not significantly change the temporal dynamics of the CBF response. The difference in the temporal dynamics of the CBF and BOLD responses may reflect the different physiological origins of the two responses, where the CBF response reflects the change in a single physiological variable while the BOLD response exhibits a complex dependence on changes in cerebral blood flow, cerebral blood volume and oxygen metabolism (Buxton et al. 2004). An additional potential factor is the relative difference in the dynamics of the vasculature associated with the two responses, with the CBF response depending primarily on the dynamics of the arterioles and capillaries and the BOLD response being weighted towards the dynamics of the venules and veins (Luh et al. 2000). The different vascular weighting of the CBF and BOLD responses is also reflected in differences in the spatial patterns of activation shown in Figure 2 and Figure 3.

In this study, we used a fixed caffeine dose to decrease baseline CBF in a group of subjects that had similar self-reported daily caffeine usage levels. However, it is important to note that differences in daily caffeine usage level and subject-dependent changes in blood caffeine concentration levels from the pre-dose to post-dose sessions may also affect functional CBF and BOLD responses. For future studies, accounting for these factors by inclusion of plasma or saliva caffeine concentration measurements would help to further our understanding of the correlation between baseline CBF and the CNR and activation extent of the CBF response.

A key assumption in this study is that the performance of the motor and visual tasks are equivalent in the pre-dose and post-dose sessions. While the presented stimuli are identical between sessions, it is possible that subjects became more vigilant to the motor task after a caffeine dose, reducing attention to the visual stimulus. However, the relatively undemanding task of pressing buttons with one hand at 2 Hz was easily performed by our subjects, so was unlikely to require disporportionate amounts of attention in the pre-dose and post-dose sessions. In addition, our findings of a significant caffeine-induced increase in %ΔCBF and no significant change in %ΔBOLD do not appear to be consistent with decreased visual activity after caffeine. Furthermore, a previous study by our group (Liu et al. 2004) that used only a visual stimulus also found no change in %ΔBOLD with a caffeine dose, further suggesting that performance on the motor task had a negligible effect on the visual response in the present study.

We also consider whether the results of this study are due to brain physiology or technical limitations in measurement methods. The caffeine-induced reduction of CBF CNR and activation extent appears to be a product of both factors. Use of arterial spin labeling to measure baseline CBF produced a caffeine-induced decrease in SNR from reduction of the perfusion signal. Also, the caffeine-induced physiological reduction in the absolute functional CBF response $({\widehat{h}}_{\mathit{\text{CBF}}})$ prevented %ΔCBF from compensating for the SNR reduction, leading to the overall CNR decrease. In contrast, we found the BOLD response is less sensitive to caffeine-induced reductions in baseline CBF. It is possible that the observed lack of change in the BOLD response may be due to BOLD SNR limitations at 3 Tesla. A previous study at 7 Tesla found an increase in %ΔBOLD with a hypocapnia-induced decrease in baseline CBF (Cohen et al. 2002). However, one study at 1.5 Tesla found a general caffeine-related increase in the BOLD response (Mulderink et al. 2002), while two other studies at 1.5 Tesla found that caffeine’s effect on the BOLD response depended on the daily caffeine usage levels of the subject groups (Laurienti et al. 2002; Yang et al. 2007). These findings suggest that BOLD SNR limitations at 3T are not a main factor in the observed lack of a caffeine-induced change in the BOLD response and that the discrepancy between our findings and those of (Cohen et al. 2002) is most likely due to other differences in the experimental protocols.

A possible confound in this study was the use of hypercapnia at the end of the pre-dose session. BOLD and CBF signals are expected to be close to a physiological steady-state 30 to 60 seconds after a hypercapnic stimulus (Stefanovic et al. 2006). As the first functional scan of the post-dose session took place at least 45 minutes after the last hypercapnia run, confounds due to the hypercapnia are expected to be negligible.

In summary, our results show that caffeine significantly reduces the CNR and activation extent of the functional CBF response. Furthermore, we found that measures of baseline CBF could explain a significant portion of the inter-subject variability in the number of activated CBF voxels and the CNR of the CBF data. Taken together, these observations suggest that additional factors that can modulate baseline CBF, such as disease, normal aging, and the use of vasoactive medications, such as statins, are also likely to have an effect on functional CBF maps. Consideration of these factors and measures of baseline CBF should therefore be integrated into the analysis and interpretation of studies that utilize functional CBF maps obtained with arterial spin labeling.