LOT: a tool for linkage analysis of ordinal traits for pedigree data

Abstract

Summary: Existing linkage-analysis methods address binary or quantitative traits. However, many complex diseases and human conditions, particularly behavioral disorders, are rated on ordinal scales. Herein, we introduce, LOT, a tool that performs linkage analysis of ordinal traits for pedigree data. It implements a latent-variable proportional-odds logistic model that relates inheritance patterns to the distribution of the ordinal trait. The likelihood-ratio test is used for testing evidence of linkage.

Availability: The LOT program is available for download at http://c2s2.yale.edu/software/LOT/

Contact: heping.zhang@yale.edu

1 INTRODUCTION

Linkage analysis has been proven useful in mapping genes for human diseases, such as breast cancer (Claus et al., 1990; Easton et al., 1993; Hall et al., 1990). Many human disease phenotypes are rated on discrete, ordinal scales. Typically the ordinal phenotypes are dichotomized into binary traits before such data can be analyzed using standard linkage-analysis programs such as GENEHUNTER (Kruglyak et al., 1996). Loss of power for linkage analysis due to dichotomization of ordinal traits has been reported (Corbett et al., 2004; Feng et al., 2004). Although association studies have gained momentum in genetic analysis, numerous valuable datasets such as COGA and Framingham Heart Study (Atwood et al., 2002) have been cumulated from linkage studies and hence it remains very important to develop effective methods and software to analyze data from linkage studies.

We have developed a tool, LOT, for linkage analysis of ordinal trait for pedigree data based on the work of Feng et al., (2004) with some modifications and improvements. LOT detects linkage between a marker to an ordinal trait locus by examining whether the inheritance pattern of the marker, which can be inferred from the pedigree data, is associated with the trait using a latent-variable proportional-odds logistic model.

2 METHODS AND IMPLEMENTATION

2.1 Model

LOT first infers the inheritance pattern of a pedigree by means of inheritance vectors, v. The derivation of the inheritance vectors is independent of the type (continuous or categorical) of the trait. LOT implements the same method used in Kruglyak et al., (1996). In the next step, LOT uses a proportional-odds logistic model, with the addition of two types of latent random variables, to detect association between a marker and a disease locus. The two types of latent variables, U₁ and U₂, represent: (1) the common genetic or environmental factors in a family that are not observed through the covariates and (2) the genetic susceptibility introduced by the family founders and transmitted to their offspring, respectively. Conditional on all of the latent variables and inheritance vectors, within the i-th family, the traits of all non-founders are independent. Let superscript i index families and subscript j index non-founders in a family. Given a trait Y taking an ordinal value from k=0, 1,…, K(K≥1), the trait of the j-th non-founder in the i-th family follows the distribution:

where x is the vector of covariates that is available for each study subject, vⁱ is the inheritance vector at the disease gene locus for the i-th family, β is the vector of parameters reflecting the covariate effects on the trait, α_k is the trait-level-dependent intercept and γ=(γ₁,γ₂)′ indicates the familial and genetic contributions to the trait. We refer to Feng et al., (2004) for more details. The EM algorithm (Dempster et al., 1977) is used to find the maximum-likelihood estimation (MLE) of the parameters. After obtaining the MLEs of the parameters, a likelihood-ratio test (LRT) is used for determining the significance level of linkage. The null hypothesis is that a disease gene is not in linkage with the marker, i.e. H₀: γ₂=0. Thus, the numerator and denominator of LRT are the maximum likelihood in the presence of a major disease gene linked to the current marker or intermarker locus and the maximum likelihood in the absence of linkage, respectively.

2.2 LOT and GENEHUNTER

LOT and GENEHUNTER (parametric analysis) have equivalent parametrizations when the trait is binary. For clarity, let us assume no residual familial and genetic effects and no covariates (i.e. no U₁ and x). For the parametric analysis in GENEHUNTER, the likelihood at a location t can be written as

where N is the number of families, Vⁱ is the set of all possible inheritance vectors for the i-th family, f=(f₀, f₁, f₂) denotes the fixed penetrance parameters that must be specified beforehand,

and D_jⁱ is the number of disease alleles for the j-th individual in the i-th family. θ₂ corresponds to the disease allele frequency. In LOT, for any given θ₂, α and γ₂ that control the penetrance of the binary trait as follows,

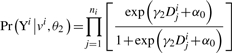where n_i is the number of non-founders in the i-th family. Thus, exp (α₀)/1+exp (α₀), exp (γ₁+α₀)/1+exp (γ₁+α₀) and exp (2γ₁+α₀)/ 1+exp (2γ₁+α₀) represent the equivalent parameterization of the pene-trance in the model used in LOT to that in GENEHUNTER.

2.3 Ascertainment

Families are not always ascertained at random, and often through members who have certain health conditions. For example, in the hoarding study presented below, all families included at least two siblings with Gilles de la Tourette syndrome. A non-random ascertainment may result in over-sampling subjects affected with diseases from the original population. Parameter estimation may be biased and proper adjustment for ascertainment should be considered in this circumstance, as discussed in Wang and Zhang (2007). Because there are so many schemes of ascertainment and in many cases, the relationship between the ascertainment scheme and the trait of interest may be poorly characterized. For these and other reasons, like other linkage analysis programs, LOT does not correct for ascertainment, although in theory a well-characterized ascertainment scheme can be incorporated in the likelihood and hence accommodated in LOT. Users are advised to make a serious effort to document the ascertainment scheme and scrutinize their analysis, for example, by simulation. We refer to Feng and Zhang (2006) for details.

2.4 Implementation

LOT, implemented in C and Java, comes with a user-friendly graphic user interface (GUI) on Windows and Linux. It can be executed from command line on Windows, Linux and Mac OS X.

3 EXAMPLE USAGE

LOT supports input files in a format similar to the standard GENEHUNTER format. Two input files are required: a locus data file and a pedigree file. The locus file contains information on genetic distances between markers, number of alleles at each locus and their frequencies. The pedigree file provides information about the structure of each pedigree, the values of the ordinal trait, the genotype of each marker for each individual and the value of the covariates, if any. For formats and detailed instruction please refer to the Supplementary information website.

LOT produces two types of output: a table and a diagram. The first two columns in the table contain the names of the markers and the map position of the markers and intermarker locations, respectively. The next three columns contain the complete (natural) log-likelihood without considering the latent variables (‘Without Us’), the log-likelihood considering only U₁ (‘With U1’) and the log-likelihood considering both U₁ and U₂ (‘With U1 & U2’), computed for each marker and intermarker location. This tabulated output is automatically saved as a tab delimited plain-text file. The graphic output displays the significance level of linkage of each location based on the result of the likelihood estimation. Users have the option to save the diagram as a PNG image. Currently, the graphical output is only available for versions of LOT with GUI. In addition to the final output, LOT interactively prints onto the main window the progress of the computation.

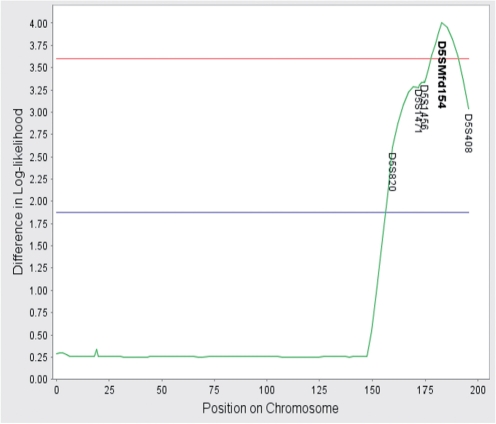
Figure 1 displays the graphical output produced by LOT for a hoarding study dataset (Feng et al., 2004). The response in this study is an ordinal trait that takes the value of 0, 1 and 2 based on the hoarding symptoms of a patient. Zero was recorded if both of the hoarding items on the Yale–Brown Obsessive-Compulsive Scale symptom checklist were rated as present for the patient, one if only one item was present and two if both items were absent. Shown in the figure is the result from the markers on chromosome 5. The horizontal axis indicates map locations on the chromosome and the vertical axis stands for the difference in log-likelihood between the model considering only U₁ and the model considering both U₁ and U₂. The green curve denotes the gain in log-likelihood when both latent variables are included in the computation compared to when only the familial and genetic factors (U₁) are considered. The blue line and red line indicates the thresholds for suggestively significant linkage and significant linkage, respectively. The thresholds are calculated following the definition of suggestive linkage and significant linkage suggested by Lander and Kruglyak (1995) based on the assumption that the total number of markers in a genome-wide linkage scan is about 400. This is usually the case for microsatellite markers. These thresholds provide a reference for the users. Users are encouraged to recalculate the thresholds according their study settings. As shown in Figure 1, at any position where the green curve exceeds the threshold for suggestive linkage the name of the marker is printed on the graph in black; if the green curve exceeds the threshold for significant linkage, the marker name is printed in bold letters.

Fig. 1.

Graphical output from LOT for a hoarding study dataset. The blue and red lines indicate, respectively, the thresholds of significant and suggestive evidence for linkage between a marker and the trait locus. The thresholds were computed empirically by generating data under the null hypothesis using permutation and 370 microsatellite markers from the hoarding study.

The computational time of LOT grows linearly in the number of markers. The computational time for computing the inheritance vectors grows exponentially in the number of non-founders within a pedigree and linearly in the number of pedigrees when all pedigrees have the same structure. The computational time of the remaining part of the program grows quadratically in the number of samples. While running the LOT program, the bottleneck in computational time is the remaining part. Thus, practically, the estimated running time of the LOT program grows quadratically with the number of samples. In the above example, 223 samples and 24 markers were analyzed on a desktop workstation with Intel Pentium D CPU 3.20 GHz processor and 3.50 GB of RAM. The computation was completed in 211 s. In another analysis with 3074 samples and 32 markers, it took 49 357 s to complete on the same machine.

4 SIGNIFICANCE AND CONCLUSION

LOT provides a new means to perform linkage analysis of pedigree data when the target phenotype is ordinal. The severity of many diseases is rated on ordinal scales. LOT can be employed to study the genetic basis of such complex traits. It implements a latent-variable proportional-odds logistic model that allows analyzing the ordinal traits directly as opposed to dichotomizing the ordinal traits into binary traits and analyzing them using standard linkage analysis software. Analyzing ordinal traits directly circumvents loss of information and consequent loss of power caused by dichotomization. When applied to a binary trait, LOT produces results that are comparable to GENEHUNTER. LOT provides intuitive results by visualizing the significance level of linkage between the markers and the disease trait.