Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Oct 10.
Published in final edited form as: Biochemistry. 2005 Dec 20;44(50):16513–16523. doi: 10.1021/bi051020m

Computational Studies of the Farnesyltransferase Ternary Complex Part I: Substrate Binding†

Guanglei Cui 1, Bing Wang 1, Kenneth M Merz Jr 1,*
PMCID: PMC2566548  NIHMSID: NIHMS60850  PMID: 16342942

Abstract

Farnesyltransferase (FTase) catalyzes the transfer of farnesyl from farnesyldiphosphate (FPP) to cysteine residues at or near the C-terminal of protein acceptors with a CaaX motif (a, aliphatic; X, Met). Farnesylation is a critical modification to many switch proteins involved in extracellular signal transduction pathway, which facilitates their fixation on the cell membrane where the extracellular signal is processed. The malfunction caused by mutations in these proteins often causes uncontrolled cell reproduction and leads to tumor formation. FTase inhibitors have been extensively studied as potential anticancer agents in recent years, several of which have advanced to different phases of clinical trials. However, the mechanism of this biologically important enzyme has not been firmly established. Understanding how FTase recruits the FPP substrate is the first and foremost step towards further mechanistic investigations and the design of effective FTase inhibitors. Molecular dynamic simulations were carried out on the ternary structure of FTase complexed with the FPP substrate and an acetyl-capped tetrapeptide (acetyl-CVIM), which revealed that the FPP substrate maintains an inactive conformation and the binding of the diphosphate group can be largely attributed to residues R291β, K164α, K294β, and H248β. The FPP substrate assumes an extended conformation in the binding site with restricted rotation of the backbone dihedral angles; however, it does not have a well defined conformation when unbound in solution. This is evident from multinanosecond MD simulations of the FPP substrate in vacuum and solution. Our conclusion is further supported by theoretical j-coupling calculations. Our results on the FPP binding are in good agreement with previous experimental kinetic studies on FTase mutants. The hypothetical conformational activation of the FPP substrate is currently under investigation.

Introduction

Farnesyltransferase (FTase) is a zinc metalloenzyme that removes the diphosphate group from the farnesyldiphosphate (FPP) substrate and connects the resulting farnesyl moiety, a 15-carbon isoprenoid, to the cysteine at or near the C-terminus of protein acceptors (Figure 1) (1). This posttranslational modification is important for many GTP-binding switch proteins on RTK (receptor tyrosine kinase) signal transduction pathways, facilitating their attachment and localization to the inner side of the plasma membrane (2-7). These proteins function as molecular switches, regulating cell proliferation and differentiation, promoting cell survival, and modulating cellular metabolism. Their malfunction is often associated with uncontrolled cell growth that may lead to tumor and cancer formation. As a member of the GTPase switch protein superfamily, Ras is found to be related to roughly 30% of human cancers as a single mutation traps it in the GTP-bound activated state, signaling cell growth even in the absence of growth factors. Interference of the association of these proteins to the plasma membrane through FTase inhibition nearly reduces or terminates the growth of cancer cells, which identifies farnesyltransferase as a viable therapeutic target (8-12). Several FTase inhibitors (FTIs) have entered different clinical trial phases along the drug discovery pipeline, showing promises in the clinical treatment of human cancers (13-18).

Figure 1.

Figure 1

Open in a new tab

The farnesylation reaction.

Through an elucidation of the exact mechanism of farnesylation by FTase the rational design of small molecule therapeutics can be significantly accelerated. Given the importance of FTase it is not surprising that this protein has been extensively studied by X-ray crystallography (19-25), steady-state kinetics (26, 27), transient kinetics (28), and site-directed mutagenesis (27) over the past ten years. From these studies an overall mechanistic “picture” has been established. Four distinct stages have been identified (Figure 2), including the orderly binding of the FPP substrate and protein targets, the activation of the initial ternary complex that features a 7 Å gap between the two reacting species, the zinc-catalyzed chemical reaction step, which can be accelerated by 700-fold if magnesium ion is present in the binding site, and the rate-limiting product release step. Although the understanding of farnesylation mechanism has been significantly advanced, many key questions remain unanswered (29), most notably the conformational activation of the bound FPP substrate, the binding of a co-catalytic magnesium ion and its function, and the release of farnesylated protein substrates and the biological role of an “exit groove” found in a recently published X-ray structure (19). We have embarked on a series of computational studies with the intention of providing valuable insights into these critical issues, starting with the investigation of the FPP substrate binding in the reactive FTase ternary complex.

Figure 2.

Figure 2

Open in a new tab

Structural evidence that highlights the key waypoints on the farnesylation reaction pathway (from left to right, apo-Ftase, 1FT1; the binary complex of FTase and FPP, 1FT2; the ternary complex of FTase, HFP and actyl-CVIM, 1QBQ; product complexes of FTase with the farnesylated peptide, 1KZP and 1KZO).

The binding of the FPP substrate takes place first, followed by the binding of the protein target (30, 31). Studies on FTase mutants suggest that several polar amino acid side chains (K164α, H248β, R291β, K294β, and Y300β) contribute to the binding of the FPP substrate, however, the specific interaction between these side chains and the two phosphate groups and the exact location where the interaction is made can only be speculated owing to the lack of structural information of reactive FTase ternary complexes. Several crystal structures of FTase ternary complexes have been solved so far with either FPP analogs or slow peptide substrates or peptide-like inhibitors, and none assumes the postulated active FPP conformation that features a reduced distance between the two reacting species. The crystal structure (PDB code: 1QBQ) of the ternary complex of FTase and α-hydroxyfarnesylphosphonic acid (HFP) and a tetrapeptide (ACE1-CYS2-VAL3-ILE4-MSE5) indicates that the farnesyl moiety and the tetrapeptide share the same binding site surrounded with hydrophobic residues. Moreover, the side chain of ILE4 forms close van der Waals contacts with the second isoprene of the farnesyl group. The phosphonic acid moiety of HFP is tightly bound to a highly positively charged pocket, comprising K164α, R291β, and K294β. In the crystal structure of FTase and FPP binary complex (PDB code: 1FT2), H248β and Y300β are also involved in FPP binding by hydrogen bonding to the β-phosphate. Mutations of these amino acid side chains cause the decrease in the rate of chemistry (kchem) measured from steady-state kinetics experiments, which leads to the proposal of a general acid-base mechanism with Y300β and K164α serving as the catalytic residues (27, 32). However, the functions of these conserved amino acid residues in the enzymatic reaction were reexamined in a recent transient kinetics study (28), which argued that Y300β, H248β and K164α mainly stabilize and position the diphosphate moiety into a “pose” that is suitable for the following chemical reaction. To design effective FTase inhibitors that compete with FPP binding, accurate and consistent structural and dynamic information of the FPP binding site is of great value.

Obtaining this information based solely on X-ray crystallography and biochemical/biophysical assays can be difficult, but they offer an excellent starting point for theoretical studies. Here we provide insights into FPP binding, particularly the functions of residues K162α, R291β, K294β, H248β and Y300β, with detailed structural and dynamic information of the FTase ternary complex with FPP and a reactive tetrapeptide substrate (acetyl-CVIM) from a 5.8 nanosecond molecular dynamics (MD) simulation. To our knowledge, this is the first MD simulation of FTase and substrate complexes reported so far. Previously, only the zinc-bound FTase was studied with a one-nanosecond molecular dynamics simulation (33), in which the zinc site was modeled with the cationic dummy atom approach, suggesting relatively large conformational flexibility of nine conserved residues in the FTase active site. In our study, we focus on the specific binding of the FPP diphosphate group and the conformational preference of the bound farnesyl group. The bonded approach of Hoops et al was used (34), in which harmonic covalent bonds were placed between the bound zinc and the 4 surrounding first-shell amino acid side chains.

Molecular dynamics simulation has the advantage of studying largely experimentally inaccessible states, giving us the opportunity to directly examine the key elements in FPP binding. Farnesyldiphosphate is tightly bound in the hydrogen bond network formed by residues K164α, R291β, K294β, and H248β. The interactions of these residues with the two phosphate units are analyzed in detail below. Qualitatively, our findings from the 5.8 nanosecond MD simulation, particularly the specific interactions between the two phosphate groups and FPP binding residues, are in excellent agreement with what have been reported from transient kinetics studies (28). The FTase ternary complex remains in the inactive conformation with the two participating “reactive” atoms of farnesylation remaining separated by over 7 Å. Our analysis demonstrates that Y300β is too distant to make significant contribution to the binding of FPP substrate. It is known that the mutation of residue Y300β decreases the reaction rate by almost 500 fold. We speculate that it may promote the reaction rate by assisting FPP in its approach towards the nucleophile or by stabilizing the leaving diphosphate group. The definitive role of residue Y300β will be left for future work. In the following sections, we focus on the description of our simulation methods of the FTase ternary complex and present a detailed analysis of our results.

Methods

The model structure of FTase and the substrates forming the ternary complex were built from two crystal structures (PDB code: 1FT2 and 1QBQ). 1FT2 is the binary complex of FTase and FPP, while 1QBQ is the ternary complex of FTase, the peptide substrate (Acetyl-CVIM), and HFP. Both structures were solved at resolutions of above 2Å (23). The backbone conformations defined by the atoms C, CA, N, and O were almost unaltered upon the binding of the peptide substrate (root mean square deviation is 0.8Å). The two superimposed structures were then merged to give the structure of the reactive FTase ternary complex with HFP replaced by FPP from X-ray structure 1FT2. The FPP binding site is sandwiched between two FTase subunits, fully accessible to solvent. Ten crystal water molecules were found within 5Å of HFP in the X-ray structure 1QBQ. Ionizable amino acid side chains (Asp, Glu, Arg, and Lys) in the FPP binding site were modeled in their usual protonation states corresponding to physiological pH, and FPP was fully deprotonated, bearing three negative charges. The twenty-five (25) histidine residues found in 1QBQ were all treated as neutral. Moreover, via visual inspection, the protonation pattern was selected based on the formation of reasonable hydrogen bonding networks between the His residues and its surrounding environment. The cysteine of the zinc-bound peptide was modeled as a thiolate, which is the more widely accepted protonation state for this residue, although the possibility of having a zinc-bound thiol form of the peptide cannot be ruled out entirely (29). 284 crystallographically determined solvent molecules from 1QBQ were carried into the final structure. All molecular mechanics (MM) and dynamics simulations were conducted with the sander module in the AMBER8 modeling suite (35). Cornell's ff94 force field for proteins (36) and Wang's gaff force field for small organic compounds (37) were used in the simulation with missing force field parameters developed using protocols described below. Quantum mechanics (QM) calculations needed during the parameterization process were carried out with Gaussian'98 (38) and Gaussian'03 (39). In general, missing partial charges were derived following a two-stage restrained electrostatic potential (RESP) fitting procedure (40, 41) after geometry optimization at HF/6-31G*. The energy profiles for unknown dihedral angle types were obtained by taking the difference of computed quantum mechanics and molecular mechanics energies (EQM-EMM) of a set of QM optimized conformations with pre-assigned dihedral angles (36). This energy profile was then least-square fitted with a sum of cosine terms by varying the magnitude, phase, and multiplicity of each term.

Parameterization of the Zinc Environment

The bonded approach was employed to model the zinc-ligand interactions in the molecular mechanics treatment (34, 42). It has been shown in our previous studies (43-45) that the bonded approach is a straightforward and effective way to retain the tetrahedral geometry of the zinc-ligand coordination environment and the electrostatic characteristics of the zinc-ligand interactions. The force field parameters needed to model the zinc environment in the protein were derived from a truncated cluster model, in which each ligating amino acid was represented only by its side chain atoms. The zinc ion in the FTase ternary complex is coordinated by 4 amino acids - Asp297β, Cys299β, His362β and Cys1p from the peptide substrate, which was then represented as [Zn-(methylthiolate)2(methylimidazole)(acetate)]−1 in our cluster model.

Starting with the geometry in the crystal structure, this cluster model was optimized with QM in vacuum using B3LYP/6-31+G*. The zinc-ligand covalent bond parameters and atomic charges were then derived using the optimized geometry following protocols described in detail elsewhere (43-45). The new atomic charges were then incorporated with the atomic charges in ff94 while keeping the atomic charges of the backbone atoms intact. The equilibrium values for the added bond lengths and bond angles were taken from the X-ray crystal conformation. All the parameters used to represent the zinc environment in the FTase ternary complex are included in the supplementary material.

Parameterization of Farnesyldiphosphate

Farnesyldiphosphate is a 49-atom molecule that can be divided into 3 isoprenoid and one diphosphate groups. Crystallographic evidence reveals that FPP is initially locked in an inactive conformation by FPP binding residues (possibly a combination of K164α, R291β, K294β, H248β and Y300β), which creates a 7.2Å gap between the two reacting centers. Based on the comparison of the FPP conformations in 1QBQ and the FTase product complex (PDB code: 1KZP), it has been hypothesized that rotation of the diphosphate-connecting isoprenoid group eliminates the gap so that the following chemical events can be carried out (19). So, it is important to accurately model the conformational preferences of the isoprenoid groups by our classical force field for any of the following simulations to be meaningful. We systematically derived missing force field parameters from quantum mechanical calculations on small fragments (Figure 3). This divide-and-conquer strategy should offer better transferability and less conformational dependency of the derived parameters (36).

Figure 3.

Figure 3

Open in a new tab

Farnesyldiphosphate and model compounds used in force field parameter development.

gaff, a generic AMBER-compatible force field for small organic compounds, was used as the starting point for the model building process. Proper atom types were conveniently assigned using the antechamber module included in the AMBER8 suite of programs. sp3 and sp2 carbon atoms were assigned atom type c3 and c2 respectively. Each unique dihedral angle type in the farnesyl group was closely examined to ensure a close agreement between QM and MM calculated torsion profiles evaluated at 36 rotational conformers optimized at the HF/6-31G* level of theory. Energy profiles evaluated with MP2/6-31G* on calculated minima along the rotational angles are in agreement with those calculated with HF/6-31G* (data not shown). Therefore, HF/6-31G* calculated profiles were used to reduce the computational cost. Two new torsion terms for dihedral type c3-c3-c2-c2 and c3-c3-c2-c3 were necessary from the superposition of the QM and MM calculated torsion profiles (see Figures 4-6). The energy minima found on the torsion profiles were also used in multi-conformer RESP charge calculations, during which neutrality constraints were applied on capping methyl groups (41). Therefore, the net -3 charge of FPP was assigned completely to the diphosphate group. The derived atomic charges and augmented torsion terms can be found in the supplementary material.

Figure 4.

Figure 4

Open in a new tab

Torsion profile for the dihedral of type c2-c2-c3-c3.

Figure 6.

Figure 6

Open in a new tab

Torsion profile for the dihedral of type c2-c3-c3-c2.

QM J Coupling Calculation of Farnesyldiphosphate

In order to determine the conformational preference of FPP, we have carried out J coupling constants calculations on the model molecule 1,5-hexadiene. Conformers were generated by the variation of the ϕ2 dihedral angle from −180° to 0° in 10° intervals. Geometries of these conformers were optimized at the Hartree-Fock (HF) /6-31G* level. Indirect spin-spin coupling constants were determined at the B3LYP/6-311G** level of theory. All four contributions (Fermi contact, diamagnetic spin-orbital, paramagnetic spin-orbital, spin-dipole) were included in the coupling constants calculations, although the Fermi contact terms were generally found to be dominant.

MD Simulation of the Farnesyltransferase Ternary Complex

The MD simulation of the FTase ternary complex was conducted at 300K and 1 atm (NPT ensemble). The particle mesh Ewald (PME (46)) method was used in the explicit solvent MD simulation of the FTase ternary complex. The default PME parameter values in AMBER were used (8Å cutoff for the real-space non-bonded interactions and a reciprocal space grid spacing of approximately 1Å). The net charge of the entire system was −23 and was neutralized by applying a uniform neutralizing plasma (47, 48), which raised every point charge in the system by 0.0003. A net neutral system is a requirement of the Ewald summation method, and can also be achieved by adding explicit cations, such as Na+. Including explicit ions during MD simulations is important in cases where ions are involved in specific interactions with the solute, such as DNA; however, it increases the computational cost due to the relatively long relaxation time of explicit ions. The ternary complex was solvated in an octahedral periodic box with each side at least 8Å from the closest solute atoms. The 3-site constrained water model TIP3P (49) was used in the simulation. SHAKE was used to fix the length of covalent bonds in which hydrogen atoms were involved (50). Rigid body motion of the system as a whole was removed (51). The whole system (67,342 atoms) was first relaxed to remove possible steric clashes with several short, weakly restrained, energy minimizations, and then the system temperature was slowly brought up to 300K over 50 picoseconds of MD simulation with a 1-femtosecond timestep. Concomitantly, the restraining force was gradually removed. The whole system was coupled to a temperature bath (coupling strength 1.0 picosecond) controlled by Berendsen's weak coupling method (52). At the end of the relaxation process, various mechanical properties of the system (density, potential energy, and volume) had reached stable values. The production portion of the MD simulation was then carried out for 5.8 nanoseconds with a 2-femtosecond time step. During the simulation, snapshots were saved every 2 picoseconds.

Potential of Mean Force Calculations

The conformational preference of the φ2 dihedral angle (defined by C3-C4-C5-C6) of FPP was determined by potential of mean force (PMF) calculations both in vacuum and in aqueous solution (53). The rotation of φ2 was sampled via 36 MD simulations using umbrella biasing potentials, which were harmonic functions whose centers were uniformly distributed between -180 and 180 degrees. The same biasing strength (32.4 kcal /mol·rad2) was used for all biased MD simulations, each of which was equilibrated for one nanosecond followed by another nanosecond of data collection. The dihedral values sampled were saved every 20 picoseconds, which resulted 50,000 data points for each MD simulation. The weighted histogram method (WHAM) (54) was used to reconstruct the unbiased dihedral distribution from the 50,000×36 dihedral values sampled and to calculate the free energy profile for the rotation around φ2. The convergence criterion of the WHAM analysis was 0.001 kcal. A few extra biased MD simulations were carried out to increase the sampling at select points in order to yield smooth free energy profiles. The statistical uncertainty of the calculated free energy profiles was estimated by a Monte Carlo bootstrap analysis.

Results and Discussion

Conformational Preference of Farnesyldiphosphate

Previously, both chemical reactivity studies and structural studies suggested that farnesyldiphosphate prefers a self-coiled or folded conformation especially in hydrophilic solvents (55-58). However, a recent NMR spectroscopic study (59) argued, based on the measured J-coupling constants, that a more extended conformation is dominant regardless of the nature of the surrounding environment, characterized by the trans conformation of the two isoprenoid groups (torsion angles defined by C3-C4-C5-C6, φ2 and C7-C8-C9-C10, φ4). Our QM calculated torsion profile for dihedral type c2-c3-c3-c2 indicated that both trans and gauche conformations correspond to energy minima with almost equal probability (transis only favored over gauche by 0.2 kcal/mol, Figure 6). The gauche and trans conformations are predicted to be separated by an energy barrier of 3.5 kcal/mol. Hence, the transition between trans and gauche conformers at room temperature is unlikely to be significantly hindered. We carried out MD simulations of free FPP both in the gas-phase and in solution (10 nanoseconds each). It is clear from Figure 7 that both trans and gauche conformations were significantly populated in the gas phase. The free energy profiles of the rotation of φ2 in the gas phase and the aqueous phase were calculated with umbrella sampling techniques combined with WHAM (Figure 8). The transpopulations of φ2 calculated from the WHAM analysis in the gas phase and solution were 52.6%, and 59.9% respectively, which were calculated by integrating the trans and gauche density distributions. The overall characteristics of the calculated free energy profiles closely resembles the potential energy profile calculated by QM. The solvation effect on the rotation of φ2 was not substantial. However, solvation did affect the barrier height near 0 degrees and perhaps, more importantly, the population of gauche conformers was reduced by 7.3%. This indicates that a slightly more compact FPP structure was found in the gas phase, which was further confirmed by the radius of gyration (Rg) of FPP in two different environments. On average, FPP is 0.7Å smaller in the gas phase than in solution. Although somewhat counter-intuitive since we expected hydrophobicity-induced intramolecular self-packing in aqueous solution, the favorable electrostatic attraction between the β-phosphate and the sp2 hydrogen atom in the first isoprenoid group is a major contributor to a more compact structure in gas phase. In a high dielectric solvent, this electrostatic contact is greatly weakened due to the strong solvation of the diphosphate group.

Figure 7.

Figure 7

Open in a new tab

FPP backbone dihedral angle distributions in the gas-phase MD simulation (φ1, φ2, φ3, φ4, from top to bottom).

Figure 8.

Figure 8

Open in a new tab

The free energy profiles of φ2 (top, kcal/mol vs. degrees) in gas phase (solid line) and solution (dash line). The corresponding dihedral probability densites were shown at the bottom. The errors in the calculated free energy profiles were not plotted for clarity; in general, the statistic uncertainty at any given point is within ±0.02 kcal/mol.

The J-coupling constants for φ2 were calculated using the model compound 1,5-hexadiene, in the gas-phase, at 18 discrete dihedral angles (Figure 10) and was interpolated with cubic spline. The ensemble averaged J-coupling constants of φ2 in the gas and aqueous phase was found to be 3.6±0.1 and 3.9±0.1 respectively. The gas-phase result is in excellent agreement with the measured J coupling constant (3.6±0.2) for [3,6-bis-13C]-farnesol in CDCl3 (60), while the solution result is higher than that measured (3.5±0.2) for [3,6-bis-13C]-FPP in D2O. Nonetheless, we note that both trans and gauche conformations are readily accessible at room temperature and the dominant conformation of unbound FPP is unlikely to be extended based on our MD simulation results and the calculated ensemble-averaged J coupling constants. On the other hand, the transition between trans and gauche is nearly prohibited when FPP is bound (Figure 9). As a matter of fact, the rotations of other farnesyl dihedral angles are frozen as well (data not shown). The extensive van der Waals contacts formed between the farnesyl group and the surrounding FTase and peptide residues, particularly Y166α, R202β, G250β, Y251β, and W303β, make other conformations less accessible.

Figure 10.

Figure 10

Open in a new tab

J-coupling constants of dihedral type c2-c3-c3-c2 calculated at 18 discrete dihedral angle values using B3LYP 6-31G* optimized geometries of 1,5-hexadiene.

Figure 9.

Figure 9

Open in a new tab

FPP backbone dihedral angle distribution in the MD simulation of the FTase ternary complex (φ1, φ2, φ3, φ4, from top to bottom).

Farnesyltransferase Ternary Complex

The simulated FTase solution structure closely resembles the X-ray crystal structure. The backbone RMSD is around 1.3Å, and the overall heavy-atom RMSD is 1.8Å (Figure 11). The crystal geometry of the zinc-ligand coordination environment was well reproduced (Table 1). Although we have not addressed whether the peptide substrate is bound as a thiol or thiolate (an unsolved issue raised in reference (29)), what we were most interested in understanding was the interaction of the FPP diphosphate moiety with its surroundings. Our choice of the protonation state only reflects the tight-binding form (32, 61, 62) in the most accepted interpretation on this issue, which pictures that the peptide substrate enters the binding site in its thiol form and is subsequently deprotonated by a nearby residue, possibly K164α (28).

Figure 11.

Figure 11

Open in a new tab

Root mean square deviation (in angstrom) of the 5.8 ns MD simulation of FTase ternary complex (black, backbone atoms only; red, all heavy atoms).

Table 1.

Geometry of the Zinc-Ligand Coordination

Crystal Value Average from MD
Zn-His362β 2.24 2.22
Zn-Cys299β 2.21 2.20
Zn-Cys1p 2.48 2.46
Zn-Asp297β (OD2) 1.90 1.85
His362β-Zn-Cys299β 121 128
His362β-Zn-Cy1p 97 99
His362β-Zn-Asp297β (OD2) 132 138
Cys299β-Zn-Cys1p 111 96
Cys1p-Zn-Asp297β (OD2) 91 86
Cys299β-Zn-Asp297β (OD2) 100 93
Open in a new tab

The two phosphate units of FPP interact mostly with 5 amino acid side chains, H248β, K164α, R291β, K294β, and Y300β, which have been recently probed with transient kinetics experiments (28). We have examined the distances of these residues to each individual phosphate unit (Pα and Pβ), which qualitatively addresses the strength of the individual interactions. K294β is almost equally distant to the two phosphorous atoms (Pα and Pβ, Figure 12). The average distance of 3.5Å suggests strong multiple hydrogen bond interactions with the oxygen atoms on the phosphorous atoms (the average bond length between the phosphorous and non-bridging oxygen atoms was ∼1.48Å). R291β, 5.5 Å from the β-phosphate, primarily interacts with the α-phosphate through bidentate hydrogen bonds involving atom NE and NH2 (Figure 13). The exact hydrogen bond patterns of R291β and K294β slightly differ from what was observed in the FTase ternary complex with FPP and a slow peptide substrate (PDB code: 1JCQ) (20), in which the R291βNE hydrogen-bonds to an oxygen atom on the β-phosphate and K294β only interacts with a terminal oxygen atom on the β-phosphate. However, there is little doubt that these two positive residues are deeply involved in FPP binding (Figure 14).

Figure 12.

Figure 12

Open in a new tab

Distances from K294NZ to the two diphosphate phosphorous atoms (black, Pα; red, Pβ). The distances were averaged every 20 picoseconds.

Figure 13.

Figure 13

Open in a new tab

Distances from R291βNH2 (top) and R291βNE (bottom) to the two diphosphate phosphorous atoms (black, Pα; red, Pβ). The distances were averaged every 20 picoseconds.

Figure 14.

Figure 14

Open in a new tab

The hydrogen bond pattern observed in a snapshot taken at the end of the MD simulation. The highlighted residues are shown as sticks colored by atom names. The rest of the protein is shown as a semitransparent surface colored in grey. The hydrogen bonds that the FPP substrate formed are shown as dotted line. The residues on the left are K294β, R291β, and H248β. The FPP substrate is overlaid on top of Y300β.

On the other hand, the exact binding pattern of K164α, H248β, and Y300β have not been unambiguously identified experimentally, except that it has been shown in site-specific mutagenesis experiments that they make different contributions to FPP binding (26, 27). Removing the hydroxyl group from Y300β decreases the rate of chemistry (kchem) by 500-fold while changing H248β and K164α to Ala reduces kchem by 50-fold. Using farnesylmonophosphate (FMP) as substrate, Pickett et al. (28) measured the effects of these three mutations on the reactivity of FTase. When compared to what they found when using FPP as substrate led them to conclude that Y300β energetically stabilizes the “reaction-ready” FPP conformation through hydrogen bonds with the α-phosphate. Their experiments also offered “compelling” evidence that K164α does not interact with the α-phosphate, and H248β interacts weakly with the α-phosphate. Our MD simulation shows that H248β is further away from the β-phosphate (Figure 15 and Figure 19). The distance between His248βNE2 and the α-phosphate is on average 4.2Å, 0.7Å further than what was found for R291β and K294β. At this distance, it may form transient hydrogen bonds with the bridging oxygen atom O1 between the farnesyl group and the α-phosphate. K164α, on the other hand, binds preferably with the β-phosphate (Figure 16 and Figure 19). Additionally, it forms stable hydrogen bonds with the capping acetyl of the peptide substrate, which is consistent with previous studies that K194α is important for peptide binding (26). The close contact of K164α with the backbone carbonyl oxygen of the peptide substrate is also seen in the crystal structure of the FTase ternary complex with the isoprenoid analogue I2 and a K-Ras peptide (21). Our simulation suggests and this hydrogen bonding interaction may not require a protonated peptide substrate, but it could be sequence-dependent.

Figure 15.

Figure 15

Open in a new tab

Distances from H248β to the two diphosphate phosphorous atoms and the bridging oxygen atom O1 between the farnesyl group and the diphosphate (black, Pα; red, Pβ; green, O1). The distances were average every 20 picoseconds.

Figure 19.

Figure 19

Open in a new tab

The hydrogen bond pattern observed in the same MD snapshot as in Figure 14. R291β and H248β are shown on the right as references points. On the top K164α forms a hydrogen bond with the β-phosphate of the FPP substrate. The tetrapeptide substrate is shown on the left. The hydrogen bond between K164α and the acetyl-O was transiently broken near the end of the MD simulation. Y300β is shown at the bottom.

Figure 16.

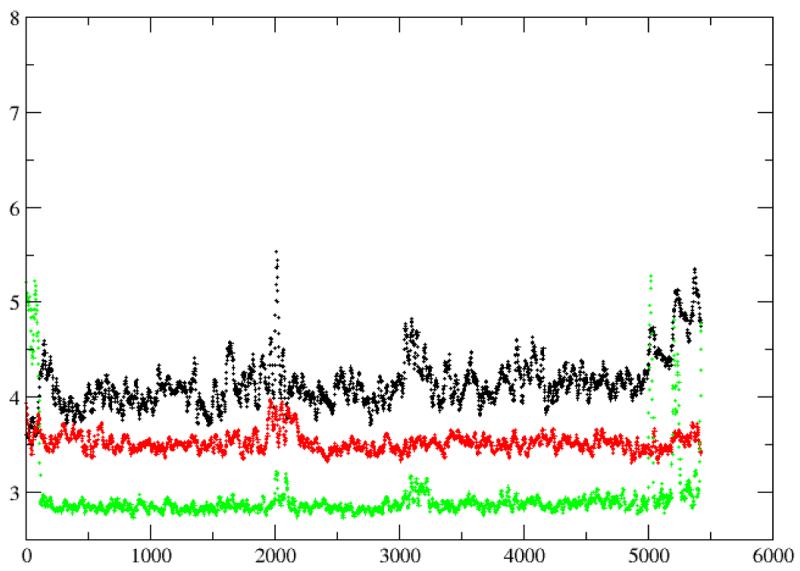
Figure 16

Open in a new tab

Distances from K164β to the two diphosphate phosphorous atoms and the carbonyl oxygen atom (O) at the N-terminal of the peptide substrate (black, Pα; red, Pβ; green, O). The distances were average every 20 picoseconds.

Mutagenesis experiments established that Y300β is important to farnesylation. Nevertheless, we do not observe Y300β forming any substantial interactions with either of the phosphates (Figure 17 and Figure 19), judging from the distance to either of the diphosphate oxygen atoms. Throughout the 5.8-nanosecond MD simulation, FPP was locked in the “inactive” conformation featuring a large gap between the two reacting centers (Figure 18). The time scale of the transition from the “inactive” conformation to the “reaction-ready” conformation is likely beyond the reach of standard MD simulation techniques. Although identifying the exact role or roles that Y300β plays requires reaction profile calculations, we agree with the suggestion that Y300β may boost the reaction rate by stabilizing a transitional diphosphate conformation.

Figure 17.

Figure 17

Open in a new tab

Distances from Y300β to the two diphosphate phosphorous atoms (black, Pα; red, Pβ). The distances were average every 20 picoseconds.

Figure 18.

Figure 18

Open in a new tab

The distance between the two reacting centers (C1 of FPP and SG of the peptidic thiolate), averaged every 20 picoseconds.

Conclusions

We have carried out the first molecular dynamics simulation of the farnesyltransferase ternary complex with the two reactive substrates, allowing us to investigate in detail the individual interactions that are crucial to the binding of farnesyldiphosphate. The conformational preference of farnesyldiphosphate was discussed and compared with previous experimental findings. The unbound substrate may adopt either trans or gauche conformations in aqueous solution, but neither appears to be “dominant”. The population analysis of multi-nanosecond MD simulations of the unbound FPP and J coupling calculations indicate that FPP is intrinsically flexible and can undergo conformation changes easily in different media. The conformational space of the farnesyl group is significantly reduced upon binding to FTase. The lost of conformational entropy must be compensated by optimal contacts with the hydrophobic residues or side chains in the binding site. The highly negative diphosphate moiety of the FPP substrate is tied to a location that is roughly 8Å from the peptide binding site. The contribution to binding of the α- and β-phosphate from K164α, R291β, K294β, H248β, and Y300β was qualitatively analyzed and was in good agreement with previous transient kinetics studies. The direct simulation of the conformational activation of FPP is computationally difficult owing to the intricate hydrogen bond network, electrostatic and hydrophobic interactions. Moreover, we found a number of long-lived water molecules sandwiched between FPP and the peptide substrates throughout the entire MD trajectory. In the crystal structure of 1QBQ, three well-defined solvent molecules were found in the same location. Therefore, the FPP diphosphate group is at least partially solvated, which makes the FPP conformational activation process even more interesting.

Supplementary Material

si20050530_051

Figure 5.

Figure 5

Open in a new tab

Torsion profile for the dihedral of type c3-c3-c2-c3.

Acknowledgements

We thank the NIH for support through grant GM44974.

Footnotes

†

This work was supported by a NIH grant (GM44974) to K.M.M., Jr.

Supporting information Available

Force field parameters for the zinc coordination sphere in FTase and the FPP substrate are included in the separate supplementary material, which is available free of charge via the Internet at http://pubs.acs.org.

Reference

  • 1.Zhang FL, Casey PJ. Annu. Rev. Biochem. 1996;65:241–269. doi: 10.1146/annurev.bi.65.070196.001325. [DOI] [PubMed] [Google Scholar]
  • 2.Adjei AA. Blocking oncogenic Ras signaling for cancer therapy. Journal of the National Cancer Institute. 2001;93:1062–1074. doi: 10.1093/jnci/93.14.1062. [DOI] [PubMed] [Google Scholar]
  • 3.Resh M. Regulation of cellular signalling by fatty acid acylation and prenylation of signal transduction proteins. Cell. Signalling. 1996;8:403–412. doi: 10.1016/s0898-6568(96)00088-5. [DOI] [PubMed] [Google Scholar]
  • 4.Seabra M. Membrane association and targeting of prenylated Ras-like GTPases. Cell. Signalling. 1998;10:167–172. doi: 10.1016/s0898-6568(97)00120-4. [DOI] [PubMed] [Google Scholar]
  • 5.Sinensky M. Recent advances in the study of prenylated proteins. Biochimica Et Biophysica Acta-Molecular and Cell Biology of Lipids. 2000;1484:93–106. doi: 10.1016/s1388-1981(00)00009-3. [DOI] [PubMed] [Google Scholar]
  • 6.Sinensky M. Functional aspects of polyisoprenoid protein substituents: roles in protein-protein interaction and trafficking. Biochim. Biophys. Acta. 2000;1529:203–209. doi: 10.1016/s1388-1981(00)00149-9. [DOI] [PubMed] [Google Scholar]
  • 7.Roskoski R. Protein prenylation: a pivotal posttranslational process. Biochemical and Biophysical Research Communications. 2003;303:1–7. doi: 10.1016/s0006-291x(03)00323-1. [DOI] [PubMed] [Google Scholar]
  • 8.Rowinsky EK, Windle JJ, Von Hoff DD. Ras protein farnesyltransferase: A strategic target for anticancer therapeutic development. Journal of Clinical Oncology. 1999;17:3631–3652. doi: 10.1200/JCO.1999.17.11.3631. [DOI] [PubMed] [Google Scholar]
  • 9.Head J, Johnston SRD. New targets for therapy in breast cancer -Farnesyltransferase inhibitors. Breast Cancer Research. 2004;6:262–268. doi: 10.1186/bcr947. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Bell IM. Inhibitors of farnesyltransferase: A rational approach to cancer chemotherapy? Journal of Medicinal Chemistry. 2004;47:1869–1878. doi: 10.1021/jm0305467. [DOI] [PubMed] [Google Scholar]
  • 11.Sausville EA, Elsayed Y, Monga M, Kim G. Signal transduction-directed cancer treatments. Annual Review of Pharmacology and Toxicology. 2003;43:199–231. doi: 10.1146/annurev.pharmtox.43.100901.135813. [DOI] [PubMed] [Google Scholar]
  • 12.Nam NH, Parang K. Current targets for anticancer drug discovery. Current Drug Targets. 2003;4:159–179. doi: 10.2174/1389450033346966. [DOI] [PubMed] [Google Scholar]
  • 13.Khuri FR, Glisson BS, Kim ES, Statkevich P, Thall PF, Meyers ML, Herbst RS, Munden RF, Tendler C, Zhu YL, Bangert S, Thompson E, Lu C, Wang XM, Shin DM, Kies MS, Papadimitrakopoulou V, Fossella FV, Kirschmeier P, Bishop WR, Hong WK. Phase I study of the farnesyltransferase inhibitor lonafarnib with paclitaxel in solid tumors. Clinical Cancer Research. 2004;10:2968–2976. doi: 10.1158/1078-0432.ccr-03-0412. [DOI] [PubMed] [Google Scholar]
  • 14.Rao S, Cunningham D, de Gramont A, Scheithauer W, Smakal M, Humblet Y, Kourteva G, Iveson T, Andre T, Dostalova J, Illes A, Belly R, Perez-Ruixo JJ, Park YC, Palmer PA. Phase III double-blind placebo-controlled study of farnesyl transferase inhibitor R115777 in patients with refractory advanced colorectal cancer. Journal of Clinical Oncology. 2004;22:3950–3957. doi: 10.1200/JCO.2004.10.037. [DOI] [PubMed] [Google Scholar]
  • 15.Doll RJ, Kirschmeier P, Bishop WR. Farnesyltransferase inhibitors as anticancer agents: Critical crossroads. Current Opinion in Drug Discovery & Development. 2004;7:478–486. [PubMed] [Google Scholar]
  • 16.Taveras a. G., Kirschmeier P, Baum CM. Sch-66336 (Sarasar (R)) and other benzocycloheptapyridyl farnesyl protein transferase inhibitors: Discovery, biology and clinical observations. Current Topics in Medicinal Chemistry. 2003;3:1103–1114. doi: 10.2174/1568026033452104. [DOI] [PubMed] [Google Scholar]
  • 17.Caponigro F, Casale M, Bryce J. Farnesyl transferase inhibitors in clinical development. Expert Opinion on Investigational Drugs. 2003;12:943–954. doi: 10.1517/13543784.12.6.943. [DOI] [PubMed] [Google Scholar]
  • 18.Huang CY, Rokosz L. Farnesyltransferase inhibitors: recent advances. Expert Opinion on Therapeutic Patents. 2004;14:175–186. [Google Scholar]
  • 19.Long SB, Casey PJ, Beese LS. Reaction path of protein farnesyltransferase at atomic resolution. Nature. 2002;419:645–650. doi: 10.1038/nature00986. [DOI] [PubMed] [Google Scholar]
  • 20.Long SB, Hancock PJ, Kral AM, Hellinga HW, Beese LS. The crystal structure of human protein farnesyltransferase reveals the basis for inhibition by CaaX tetrapeptides and their mimetics. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:12948–12953. doi: 10.1073/pnas.241407898. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Long SB, Casey PJ, Beese LS. The basis for K-Ras4B binding specificity to protein farnesyl-transferase revealed by 2 angstrom resolution ternary complex structures. Structure. 2000;8:209–222. doi: 10.1016/s0969-2126(00)00096-4. [DOI] [PubMed] [Google Scholar]
  • 22.Strickland CL, Windsor WT, Syto R, Wang L, Bond R, Wu Z, Schwartz J, Le HV, Beese LS, Weber PC. Crystal structure of farnesyl protein transferase complexed with a CaaX peptide and farnesyl diphosphate analogue. Biochemistry. 1998;37:16601–16611. doi: 10.1021/bi981197z. [DOI] [PubMed] [Google Scholar]
  • 23.Long SB, Casey PJ, Beese LS. Cocrystal structure of protein farnesyltransferase complexed with a farnesyl diphosphate substrate. Biochemistry. 1998;37:9612–9618. doi: 10.1021/bi980708e. [DOI] [PubMed] [Google Scholar]
  • 24.Dunten P, Kammlott U, Crowther R, Weber D, Palermo R, Birktoft J. Protein farnesyltransferase: Structure and implications for substrate binding. Biochemistry. 1998;37:7907–7912. doi: 10.1021/bi980531o. [DOI] [PubMed] [Google Scholar]
  • 25.Park HW, Boduluri SR, Moomaw JF, Casey PJ, Beese LS. Crystal structure of protein farnesyltransferase at 2.25 angstrom resolution. Science. 1997;275:1800–1804. doi: 10.1126/science.275.5307.1800. [DOI] [PubMed] [Google Scholar]
  • 26.Hightower KE, De S, Weinbaum C, Spence RA, Casey PJ. Lysine(164)alpha of protein farnesyltransferase is important for both CaaX substrate binding and catalysis. Biochemical Journal. 2001;360:625–631. doi: 10.1042/0264-6021:3600625. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Wu Z, Demma M, Strickland CL, Radisky ES, Poulter CD, Le HV, Windsor WT. Farnesyl protein transferase: Identification of K164 alpha and Y300 beta as catalytic residues by mutagenesis and kinetic studies. Biochemistry. 1999;38:11239–11249. doi: 10.1021/bi990583t. [DOI] [PubMed] [Google Scholar]
  • 28.Pickett JS, Bowers KE, Hartman HL, Fu HW, Embry AC, Casey PJ, Fierke CA. Kinetic studies of protein farnesyltransferase mutants establish active substrate conformation. Biochemistry. 2003;42:9741–9748. doi: 10.1021/bi0346852. [DOI] [PubMed] [Google Scholar]
  • 29.Sousa S, Fernandes P, Ramos M. Unraveling the mechanism of the farnesyltransferase enzyme. JOURNAL OF BIOLOGICAL INORGANIC CHEMISTRY. 2005;10:3–10. doi: 10.1007/s00775-004-0612-6. [DOI] [PubMed] [Google Scholar]
  • 30.Huang CC, Hightower KE, Fierke CA. Mechanistic studies of rat protein farnesyltransferase indicate an associative transition state. Biochemistry. 2000;39:2593–2602. doi: 10.1021/bi992356x. [DOI] [PubMed] [Google Scholar]
  • 31.Furfine ES, Leban JJ, Landavazo A, Moomaw JF, Casey PJ. Protein Farnesyltransferase - Kinetics of Farnesyl Pyrophosphate Binding and Product Release. Biochemistry. 1995;34:6857–6862. doi: 10.1021/bi00020a032. [DOI] [PubMed] [Google Scholar]
  • 32.Rozema DB, Poulter CD. Yeast protein farnesyltransferase. pK(a)s of peptide substrates bound as zinc thiolates. Biochemistry. 1999;38:13138–13146. doi: 10.1021/bi990794y. [DOI] [PubMed] [Google Scholar]
  • 33.Pang YP, Xu K, El Yazal J, Prendergast FG. Successful molecular dynamics simulation of the zinc-bound farnesyltransferase using the cationic dummy atom approach. Protein Science. 2000;9:1857–1865. [PMC free article] [PubMed] [Google Scholar]
  • 34.Hoops SC, Anderson KW, Merz KM. Force-Field Design For Metalloproteins. Journal Of The American Chemical Society. 1991;113:8262–8270. [Google Scholar]
  • 35.Case DA, Darden TA, Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Merz KM, Wang B, Pearlman DA, Crowley M, Brozell S, Tsui V, Gohlke H, Mongan J, Hornak V, Cui G, Beroza P, Schafmeister C, Caldwell JW, Ross WS, Kollman PA. University of California; San Francisco: 2004. [Google Scholar]
  • 36.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A 2nd Generation Force-Field for the Simulation of Proteins, Nucleic-Acids, and Organic-Molecules. Journal of the American Chemical Society. 1995;117:5179–5197. [Google Scholar]
  • 37.Wang J, Wolf RM, Caldwell JW, Kollman PA, Case DA. Development and testing of a general AMBER force field. J. Comput. Chem. 2004;25:1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  • 38.Frisch MJ, T. GW, Schlegel HB, Scuseria GE, Robb MA, C. JR, Zakrzewski VG, Montgomery JA, Jr., Stratmann RE, B. JC, Dapprich S, Millam JM, Daniels AD, K. KN, Strain MC, Farkas O, Tomasi J, Barone V, C. M, Cammi R, Mennucci B, Pomelli C, Adamo C, Clifford S, O. J, Petersson GA, Ayala PY, Cui Q, Morokuma K, M. DK, Rabuck AD, Raghavachari K, Foresman JB, C. J, Ortiz JV, Baboul AG, Stefanov BB, L. G, Liashenko A, Piskorz P, Komaromi I, Gomperts R, M. RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, N. A, Gonzalez C, Challacombe M, Gill PMW, J. B, Chen W, Wong MW, Andres JL, Gonzalez C, H.-G. M, Replogle ES, Pople JA. Gaussian, Inc.; Pittsburgh, PA: 1998. [Google Scholar]
  • 39.Frisch MJ, T. GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr., Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, AlLaham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian, Inc.; Pittsburgh PA: 2003. [Google Scholar]
  • 40.Bayly CI, Cieplak P, Cornell WD, Kollman PA. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges - the Resp Model. Journal of Physical Chemistry. 1993;97:10269–10280. [Google Scholar]
  • 41.Cieplak P, Cornell WD, Bayly C, Kollman PA. Application of the Multimolecule and Multiconformational Resp Methodology to Biopolymers - Charge Derivation for DNA, Rna, and Proteins. Journal of Computational Chemistry. 1995;16:1357–1377. [Google Scholar]
  • 42.Ryde U. Molecular-Dynamics Simulations Of Alcohol-Dehydrogenase With A 4-Coordinate Or 5-Coordinate Catalytic Zinc Ion. Proteins-Structure Function And Genetics. 1995;21:40–56. doi: 10.1002/prot.340210106. [DOI] [PubMed] [Google Scholar]
  • 43.Suarez D, Diaz N, Merz KM. Molecular dynamics simulations of the dinuclear zinc-beta-lactamase from bacteroides fragilis complexed with imipenem. Journal Of Computational Chemistry. 2002;23:1587–1600. doi: 10.1002/jcc.10157. [DOI] [PubMed] [Google Scholar]
  • 44.Suarez D, Merz KM. Molecular dynamics simulations of the mononuclear zinc-beta-lactamase from Bacillus cereus. Journal Of The American Chemical Society. 2001;123:3759–3770. doi: 10.1021/ja003796a. [DOI] [PubMed] [Google Scholar]
  • 45.Diaz N, Suarez D, Merz KM. Molecular dynamics simulations of the mononuclear zinc-beta-lactamase from Bacillus cereus complexed with benzylpenicillin and a quantum chemical study of the reaction mechanism. Journal Of The American Chemical Society. 2001;123:9867–9879. doi: 10.1021/ja0113246. [DOI] [PubMed] [Google Scholar]
  • 46.Darden T, York D, Pedersen L. Particle Mesh Ewald - an N.Log(N) Method for Ewald Sums in Large Systems. Journal of Chemical Physics. 1993;98:10089–10092. [Google Scholar]
  • 47.Nijboer BRA, Ruijgrok TW. On The Energy Per Particle In 3-Dimensional And Two-Dimensional Wigner Lattices. Journal Of Statistical Physics. 1988;53:361–382. [Google Scholar]
  • 48.Darden T, Pearlman D, Pedersen LG. Ionic charging free energies: Spherical versus periodic boundary conditions. Journal Of Chemical Physics. 1998;109:10921–10935. [Google Scholar]
  • 49.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Journal Of Chemical Physics. 1983;79:926–935. [Google Scholar]
  • 50.Allen MP, Tildesley DJ. Computer Simulation of Liquids. Clarendon Press; Oxford: 1987. [Google Scholar]
  • 51.Harvey SC, Tan RKZ, Cheatham TE. The flying ice cube: Velocity rescaling in molecular dynamics leads to violation of energy equipartition. Journal of Computational Chemistry. 1998;19:726–740. [Google Scholar]
  • 52.Berendsen HJC, Postma JPM, Vangunsteren WF, Dinola A, Haak JR. Molecular-Dynamics with Coupling to an External Bath. Journal of Chemical Physics. 1984;81:3684–3690. [Google Scholar]
  • 53.Daan Frenkel BS. Understanding Molecular Simulation: From Algorithms to Applications. 2 ed. Vol. 1. Academic Press; 2002. [Google Scholar]
  • 54.Kumar S, Bouzida D, Swendsen R, Kollman P, Rosenberg J. The Weighted Histogram Analysis Method For Free-Energy Calculations On Biomolecules.1. The Method. Journal of Computational Chemistry. 1992;13:1011–1021. [Google Scholar]
  • 55.Breslow RM, M. L. Tetrahedron Lett. 1978:887–890. [Google Scholar]
  • 56.van Tamelen EE. Acc. Chem. Res. 1968;1:111–120. [Google Scholar]
  • 57.Murgolo N, Patel A, Stivala S, Wong T. The Conformation Of Dolichol. Biochemistry. 1989;28:253–260. doi: 10.1021/bi00427a035. [DOI] [PubMed] [Google Scholar]
  • 58.Di Bernardo S, Fato R, Casadio R, Fariselli P, Lenaz G. A high diffusion coefficient for coenzyme Q(10) might be related to a folded structure. FEBS Letters. 1998;426:77–80. doi: 10.1016/s0014-5793(98)00313-5. [DOI] [PubMed] [Google Scholar]
  • 59.Zahn T, Eilers M, Guo Z, Ksebati M, Simon M, Scholten J, Smith S, Gibbs R. Evaluation of isoprenoid conformation in solution and in the active site of protein-farnesyl transferase using carbon-13 labeling in conjunction with solution- and solid-state NMR. Journal Of The American Chemical Society. 2000;122:7153–7164. [Google Scholar]
  • 60.Zahn TJ, Eilers M, Guo ZM, Ksebati MB, Simon M, Scholten JD, Smith SO, Gibbs RA. Evaluation of isoprenoid conformation in solution and in the active site of protein-farnesyl transferase using carbon-13 labeling in conjunction with solution- and solid-state NMR. Journal of the American Chemical Society. 2000;122:7153–7164. [Google Scholar]
  • 61.Hightower KE, Huang CC, Casey PJ, Fierke CA. H-Ras peptide and protein substrates bind protein farnesyltransferase as an ionized thiolate. Biochemistry. 1998;37:15555–15562. doi: 10.1021/bi981525v. [DOI] [PubMed] [Google Scholar]
  • 62.Saderholm MJ, Hightower KE, Fierke CA. Role of metals in the reaction catalyzed by protein farnesyltransferase. Biochemistry. 2000;39:12398–12405. doi: 10.1021/bi0011781. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

si20050530_051
NIHMS60850-supplement-si20050530_051.pdf (21.8KB, pdf)

RESOURCES