Application of Principal Component Analysis to Distinguish Patients with Schizophrenia from Healthy Controls Based on Fractional Anisotropy Measurements

Abstract

Principal component analysis (PCA) is often used to reduce the dimension of data before applying more sophisticated data analysis methods such as non-linear classification algorithms or independent component analysis. This practice is based on selecting components corresponding to the largest eigenvalues. If the ultimate goal is separation of data in two groups, then these set of components need not have the most discriminatory power. We measured the distance between two such populations using Mahalanobis distance and chose the eigenvectors to maximize it, a modified PCA method, which we call the discriminant PCA (DPCA). DPCA was applied to diffusion tensor based fractional anisotropy images to distinguish age-matched schizophrenia subjects from healthy controls. The performance of the proposed method was evaluated by the one-leave-out method. We show that for this fractional anisotropy data-set, the classification error with 60 components was close to the minimum error and that the Mahalanobis distance was twice as large with DPCA, than with PCA. Finally, by masking the discriminant function with the white matter tracts of the John Hopkins University atlas, we identified left superior longitudinal fasciculus as the tract which gave the least classification error. In addition, with six optimally chosen tracts the classification error was zero.

Introduction

Neuroimaging studies typically collect data from different modalities, such as MRI, EEG, and MEG, with common parameters across subjects with the goal of extracting useful information from these large data sets. Even within one modality of MRI, one could collect T1 and diffusion tensor imaging (DTI) data for mapping anatomic structure, fMRI for functional imaging, perfusion maps for blood flow distributions, and spectroscopy for metabolite mapping. Multivariate statistical methods have proved to be useful in order to systematically find relationships between these different neuroimaging measurements and clinical or cognitive test results.

The first step in group analysis of subjects typically consists of aligning the images of different subject to a common template based on the principles of voxel-based morphometery (Ashburner and Friston, 2000), followed by smoothing to compensate for accuracy of image registration and normalization. Then a number of statistical methods can be applied to ask specific questions of this aligned data set. These methods can be based on the framework of multivariate linear models (Worsley et al., 1997) with the significance of hypothesis being based on t- or F-distributions or alternatively based on non-parametric statistical methods using permutation tests (Nichols and Holmes, 2002). A number of multivariate statistical methods in context of brain imaging have been discussed (Kherif et al., 2002; Kherif et al., 2003). An alternative method based on independent component analysis (ICA, (Comon, 1994)) was applied to study group differences in fMRI data (Calhoun et al., 2001).

When data from multiple modalities is collected it is important to do a co-analysis or a joint-analysis of data. The importance of performing joint analysis of structural gray matter based on a T1-image and auditory odd-ball fMRI data with ICA was demonstrated by Calhoun et al., (2006). Non-parametric methods have been used to jointly analyze gray matter and perfusion maps of subjects with Alzheimer’s disease (Hayasaka et al., 2006). One problem with joint multi-modal analysis of neuroimaging data is its high dimensionality. In order to reduce the computation time and the need of large amounts of computer memory, principal component analysis (PCA) has been widely used in exploratory data analysis to reduce data dimensionality. This is case for us, where PCA is routinely used before ICA analysis (Calhoun et al., 2006). The use of a related method based on singular value decomposition for multivariate analysis was discussed in Kherif et al. (2002). PCA is considered to be a form of exploratory data analysis, when we want to reduce data dimensionality without throwing out the essential features of the data set. The important features depend on the questions being asked of the data set. If the goal of a given study is to discriminate between two or more groups, then applying standard PCA for feature reduction can undesirably eliminate features that discriminate and primarily keep features that best represent both groups (Chang, 1983; Jollife, 2002; Jollife et al., 1996; McLachlan, 2004). An alternative method for selecting features has been proposed by Chang (1983), which maximizes the Mahalanobis distance between two groups. This method is not well known in the medical literature and has the interesting property that eigenvectors are the same as in conventional PCA but are ordered differently to maximize the Mahalanobis distance. An optimization step is not required as the optimal ordering of eigenvectors is known analytically. We call this method discriminatory PCA (DPCA) to contrast it with the standard PCA, which orders eigenvectors to maximally explain the variance of the data set.

It should be pointed that DPCA as a method of selecting the basis functions of the reduced dimension subspace has been discussed previously (Jollife, 2002; McLachlan, 2004). The general solution for dimensionality reduction is posed as that of finding an appropriate projection matrix P, such that after the data is projected onto a lower dimensional subspace the distance between the groups is maximum (McLachlan, 2004). The optimization procedure and the projection matrix depend on the choice of the distance measure. Among other distance measures this method has been applied with Bhattacharyya (Jimenez and Landgrebe, 1999) and Kullback-Leibler (Duda et al., 2001) distances. In this paper we restrict ourselves to the eigenvectors corresponding to standard PCA but order them differently to maximize discrimination.

There are two parts to this paper. In the first part we discuss the alternative method for ordering the eigenvectors of the covariance matrix (DPCA) to maximize the Mahalanobis distance. A toy example to compare this method with standard PCA and with Fisher’s linear discriminant function (FLD) (Duda et al., 2001) for separating two classes is given. In the second part we apply this method to a fractional anisotropy (FA) data set to distinguish subjects with schizophrenia and healthy controls.

Schizophrenia is characterized by disruption of cognitive functions which among other brain abnormalities seen in the disorder, may be related to impairment of white matter integrity (Kubicki et al., 2007; Kubicki et al., 2002; Kubicki et al., 2003; Lim et al., 1999). DTI is a macroscopic measurement technique that allows the study of white matter microstructure based on anisotropic diffusion of water in white matter bundles. DTI measurements of FA, axial diffusivity, and radial diffusivity are considered to be measures of white matter fiber bundle coherence, organization and density. The current status of DTI imaging in schizophrenia, including DTI based tractography (Mori et al., 2005) has been reviewed in Kanaan et al. (2005) and Kubicki et al. (2007). There is no current consensus on which fiber tracts are consistently involved in schizophrenia. Abnormalities in uncinate fasciculus, cingulum bundle, and superior longitudinal fasciculus are the most common positive findings in DTI studies. There have not been voxel-based morphometry studies which have tried to identify fiber tracts useful for distiguishing schizophrenia subjects from healthy controls.

We apply DPCA to an FA data set from 45 schizophrenia subjects and 45 age-matched healthy controls. This part of the study is similar to the work done by Skelly et al. (2008). The emphasis in this study is on finding white matter tracts that are important in discriminating schizophrenia subjects from healthy controls. In Skelley’s study white matter regions that were significantly different between schizophrenia subjects and healthy controls were found. Skelly also found for the patient group, white matter regions that correlated with Positive and Negative Symptoms Scales (PANSS) (Kay et al., 1987). Skelley did not test these white matter regions for classification of the subjects in the two groups.

We begin with exploratory, voxel-based strategy, and identify white matter regions based on FLD function which distinguish subjects with schizophrenia from healthy controls. The spatial maps identified by this method are not specific to major white matter structures. In order to seek out relevant white matter structures we performed a correlation of the FLD function with the white matter tract atlas from Johns Hopkins University (Hua et al., 2008; Mori et al.), which is now part of the FSL software package (http://www.fmrib.ox.ac.uk/fsl/).

This paper demonstrates that conventional PCA as an exploratory data processing step for dimensionality reduction in classification studies may not be optimal. An alternate method for ordering the PCA eigenvectors is proposed which has better discriminatory characteristics. This method is applied to an FA data set from schizophrenia subjects and healthy controls, followed by further analysis to identify white matter tracts for discriminating these two groups.

Theory

Chang (1983) presented his theory in terms of population statistics. Here we express it in terms of sample statistics (Jollife et al., 1996). Suppose we have n₁ samples from one class and n₂ samples from another class, with n = n₁ + n₂, being the total number of samples. Each sample consists of an image of the subject, spatially normalized and registered to each other. The image is then written as an m dimensional column vector x_jk, k = 1,…, n_j, and j = 1,2 for the two classes. The samples from each class can be grouped together as X_j = (x_j1, x_{j 2},…, x_jnj), j = 1,2 and written as

$$X=(X_1,X_2).$$ [1]

X is a m×n matrix with each column being the image of a different subject. Here we have m features and n subjects. The feature dimensionality reduction consists of finding a projection matrix P_q with q orthonormal columns of dimension m, such that q < min(m, n). Then

$$Y_q=P_q^{T}X,$$ [2]

is the reduced q×n dimensional data set and

$$\widehat{X}=P_q{P}_q^{T}X$$ [3]

is the back-projected approximation to X. Similarly for the two classes we can define

$$Y_{qj}=P_q^T{X}_j,j=1,2.$$ [4]

In order to retain the maximum discrimination in the reduced subspace we want to maximize the distance D(Y_q1,Y_q2). A number of different distant measures have been used. These include Mahalanobis distance (McLachlan, 2004), which is also part of this study, the Bhattacharyya distance (Jimenez and Landgrebe, 1999), and the Kullback-Leibler divergence (Hastie et al., 2003). In addition a projection pursuit algorithm closely coupled to classification error minimization based on an appropriate optimization algorithm can be devised (Demirci et al., 2008). As mentioned before here we focus on Chang’s method.

Let the sample means be ${\mu }_j=\frac{1}{n_j}{\displaystyle \sum _{k=1}^{n_j}}{x}_{jk}$, j = 1,2 and the group mean is then given by $\mu =\frac{n_1{\mu }_1+n_2{\mu }_2}{n}$. The total sum of squares matrix about the group mean μ is defined by

$$T=\sum _{j=1}^2\sum _{k=1}^{n_j}(x_{jk}-\mu ){(x_{jk}-\mu )}^T$$ [5]

The matrix T can be written in terms of within- and between-group sums of squares matrices. We have

$$T=W+B,$$ [6]

where $W={\displaystyle \sum _{j=1}^2}{\displaystyle \sum _{k=1}^{n_j}}(x_{jk}-{\mu }_j){(x_{jk}-{\mu }_j)}^T$ and $B={\displaystyle \sum _{j=1}^2}{n}_j({\mu }_j-\mu ){({\mu }_j-\mu )}^T=\frac{n_1{n}_2}{n}d{d}^T$, with d = μ₁ − μ₂. The Mahalanobis distance Δ in terms of sample statistics is given by

$${\mathrm{\Delta }}^2=d^T{(\frac{W}{n})}^{-1}d.$$ [7]

In the one-dimensional case, with sample means μ₁ and μ₂ and $s^2=\frac{W}{n}$, an estimate of the common variance, the Mahalanobis distance (Eq. [7]) is ${\mathrm{\Delta }}^2=\frac{{({\mu }_1-{\mu }_2)}^2}{s^2}$, which is proportional to the square of the t-statistic when testing the difference between the means. Similarly, the Mahalanobis distance is a measure of the difference between means in a higher dimensional space. It was originally defined for equal covariance matrices for the two classes (McLachlan, 2004). In Eq. [7] we define it in terms of sample statistics and allow for different covariance matrices for the two groups by defining it in terms of the mean covariance matrix.

The approximation problem consists of finding the optimal α, {β_jk }, and P_q which minimizes $\mathit{Err}={\displaystyle \sum _{j=1}^2}{\displaystyle \sum _{k=1}^n}{\Vert x_{jk}-\alpha -P_q{\beta }_{jk}\Vert }^2$. The answer is given by α = μ, ${\beta }_{jk}=P_q^T(x_{jk}-\mu )$ and P_q is given by PCA. We are approximating after centering the data. In the following we assume n<m, because the image data has a much higher dimension than the number of subjects. The matrix T has rank n−1 because the mean has been subtracted. This implies that T has at the most n−1 non-zero eigenvalues. The eigenvalue decomposition of T is given by,

$${Tf}_k={\lambda }_k^2{f}_k,k=1,\mathrm{.....},n-1,$$ [8]

where f_k are the orthonormal eigenvectors and ${\lambda }_k^2$ the corresponding eigenvalues arranged in decreasing magnitude order. Then

$$P_q=F_q=[f_1,f_2,\mathrm{....},f_q],$$ [9]

and the minimum approximation error is given by $\mathit{Err}={\displaystyle \sum _{k=q+1}^{n-1}}{\lambda }_k^2$, which can be normalized to ${\mathit{Err}}_n={\displaystyle \sum _{k=q+1}^{n-1}}{\lambda }_k^2/{\displaystyle \sum _{k=1}^{n-1}}{\lambda }_k^2$. This normalized approximation error is the ratio of variance of the data set not accounted by the principal components to the total variance. Chang (1983) has shown that Mahalanobis distance for this approximation is given by

$${\mathrm{\Delta }}_q^2=\frac{{\displaystyle \sum _{k=1}^q}\frac{{(f_k^{T}d)}^2}{{\lambda }_k^2}}{1-\frac{n_1{n}_2}{n^2}{\displaystyle \sum _{k=1}^q}\frac{{(f_k^{T}d)}^2}{{\lambda }_k^2}}.$$ [10]

This expression does not depend on any ordering of the eigenvalues and is clearly not maximum for the choice suggested by PCA for selecting {f_k } corresponding to the largest eigenvalues. In fact Eq. [10] suggests that in order to maximize ${\mathrm{\Delta }}_q^2$, we should order the vectors in decreasing order of $\frac{{(f_k^{T}d)}^2}{{\lambda }_k^2}$. If F_q = (f₁, f₂,…, f_q) is defined with this ordering, then the lower dimensional data set is given by $Y_q=F_q^{T}X$.

What we have shown here is that if we want to use principal components for dimensionality reduction before other more detailed analysis, then keeping the principal components according to the usual criteria of corresponding to the largest eigenvalues is not optimal for purposes of discrimination. The ordering of eigenvectors in the decreasing order of $\frac{{(f_k^{T}d)}^2}{{\lambda }_k^2}$ will give better results. This does not mean that our projection matrix F_q is the best for classification because a result like that depends on the classification algorithm used and also there are other ways of obtaining F_q as suggested earlier by directly maximizing some distance measure.

In order to see the difference between the two different ordering of the eigenvectors we test their classification performance by the FLD function as the classification rule. In a manner similar to the definitions of W and B, we can define the within- (W_q) and between-group (B_q) sums of squares matrices for Y_q in the lower dimensional space. The FLD function is obtained by finding a w, which maximizes w^T B_qw/w^TW_qw. This gives

$$w=W_q^{-1}d.$$ [11]

The data is projected on w and one-dimensional classification done. The predictive performance of the features selected was validated by the leave-one-out method (Hastie et al., 2003).

In our data set and for a number of imaging studies the data points in a image (m) are typically much greater than the number of subjects (n). After the common mean is removed the data can be represented by a (n−1)×n matrix without any loss of information. This is represented by projecting the data with matrix F of Eq. [8]. There is no loss of information because the original data can be exactly back calculated from the reduced data set. In other words any further analysis can be effectively carried based on this (n−1)×n matrix. In this paper we discuss the consequences of PCA to reduce this matrix size further to a q×n matrix, where q<n−1.

Method

Data from 45 schizophrenia subjects (mean age 39.3 (sd=12.0, range = 19–59, 12 females, 9 non-right handed) and 45 age-matched healthy controls (mean age 38.3 (sd=11/8, range = 19–60, 26 females, 8 non-right handed) were obtained on a 3.0T Siemens Allegra scanner at the Olin Center, Institute of Living. All subjects provided written informed consent to participate after the procedures were explained to them. These procedures were approved by Yale University and Hartford hospital institutional review boards. The schizophrenia subject’s symptoms were rated using the PANSS interview (Kay et al., 1987). PANSS scores were not available for 4 subjects. For others, the mean of the positive PANSS scale was 15.6 (sd=5.3, range = 7–28), the mean of the negative PANSS was 15.7 (sd=6.0, range = 7–31), and the mean of the general PANSS scale was 31.8 (sd=9.1, range=18–57). 25 patients had chronic schizophrenia, 14 had relapse, and 6 were first-break schizophrenia subjects. Among the schizophrenia subjects, 10 were taking first-generation antipsychotics, 31 were taking second-generation antipsychotics, 8 were taking mood stabilizers or antidepressants, and 5 were taking no medications or we did not have any information.

The DTI image was obtained with a 12 direction standard Siemens sequence with b=1000 s/mm². Other parameters were: FOV=200mm, slice thickness =3mm, 45 slices, TE=83 ms, and TR=5900 ms. Data processing consisted of eddy current correction (FSL), calculating FA (dtifit, FSL), registering the images to a FA template (tbss, FSL). The spatially normalized output was masked such that FA > 0.05 across all subjects for each voxel to include only voxels with non-zero anisotropy, and written out as a 149206×90 matrix, where each column is the image. The eigenvectors were calculated for the sample covariance matrix T, then ordered according to the standard PCA, and the proposed method. The error for approximating to a lower dimension subspace and Mahalanobis distance Δ was calculated.

We tested the predictive capability of FA to distinguish the two groups for the reduced data sets by the leave-one-out and FLD classification method. The discriminant function is given by Eq. [11]. We sequentially left one of the subjects out of processing, selected a certain number of components and classified the subject as with schizophrenia or healthy controls and counted the errors. In order to reduce the effect of subject variability and registration errors on classification we smoothed the data by Gaussian filters of widths 4mm, 6mm, and 8mm and the performance evaluated by the leave-one out method. Finally, to identify anatomic regions contributing more towards discrimination, we used the Johns Hopkins University (JHU) white matter tract atlas (Mori et al.), now also part of FSL. A subset of the FLD function was selected by masking with the 20 tracts in the JHU atlas and the probability of classification error was calculated for that portion of the FLD function corresponding to each tract.

Results

A comparison between the results obtained with PCA, DPCA, and FLD for a two dimensional simulation example with different separation of the groups as measured by the ratio of difference in the means to the standard deviation for the two groups is shown in Figure 1. The objective is to select a one-dimensional subspace. Figure 1A is the case when the two groups are close together. We see that projecting the data on PCA (solid) line only merges the two classes. Projecting on DPCA (dash-dot-dash) and on FLD (Dash-dash) would separate the two groups. The results of DPCA and FLD are similar. In Figure 1B the groups are a little further apart and as before projecting on PCA won’t work while DPCA result is good for separation but it is now inferior to the FLD result for purposes of separation. Finally in Fig. 1C the groups are far apart and the PCA result overlaps with those of DPCA, while the two are also similar to the FLD result. This example points out a situation when conventional PCA fails. It points out that when groups are far apart the three methods are similar. In the intermediate case the FLD method was the best while DPCA was better than the PCA method. This leads us to conclude that PCA can give poor results for discrimination and the DPCA method (Chang, 1983) is simple because it has the same eigenvectors as those of PCA, but other optimization procedures can give better results. We are proposing DPCA as an exploratory data reduction technique with its selection not tightly tied to a classification algorithm and which can be followed by a more complex analysis as ICA or classification with support-vector-machines.

Figure 1.

A comparison between the results obtained with PCA, DPCA, and FLD for a two dimensional simulation example. The results with different separation between the two groups are shown. Figure 1A: When the means of the two groups are close together, then projecting the data on PCA (solid) line would only merge the two classes. Projecting on DPCA (dash-dot-dash) and on FLD (Dash-dash) would separate the two groups. Figure 1B: Here projecting on PCA won’t work while DPCA result is good for separation but it is inferior to the FLD result for purposes of separation. Figure 1C: When the means are far apart then PCA result overlaps with DPCA choice and the two are similar to the FLD result.

Initial analysis of the FA data from human subjects showed that smoothing with 6mm width Gaussian filter resulted in the least classification error and the following results are shown for this case. The classification error with leave-one-out method was 0.27 with no smoothing and with 4mm FWHM Gaussian smoothing, 0.2 with 6mm smoothing, and 0.22 with 8mm smoothing.

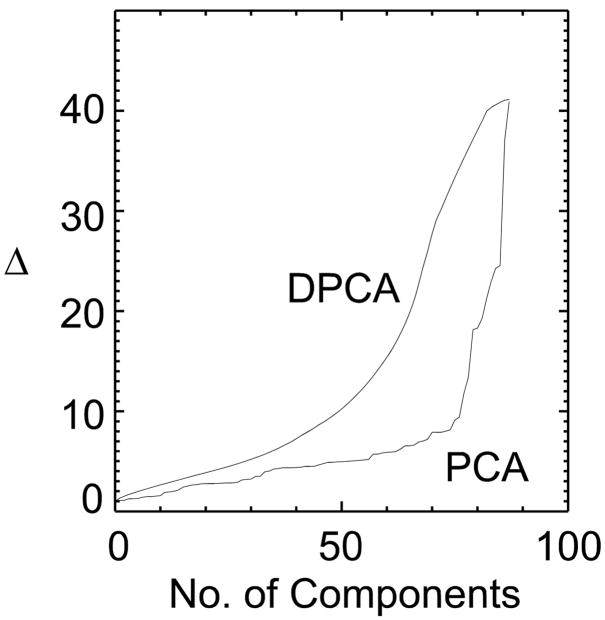
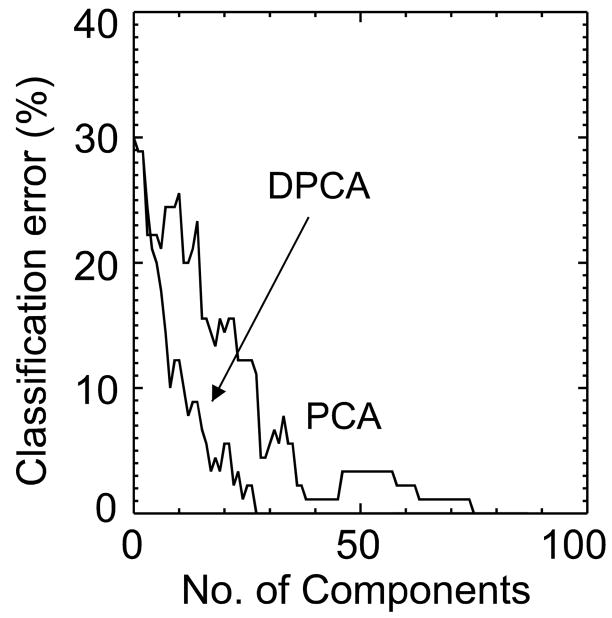
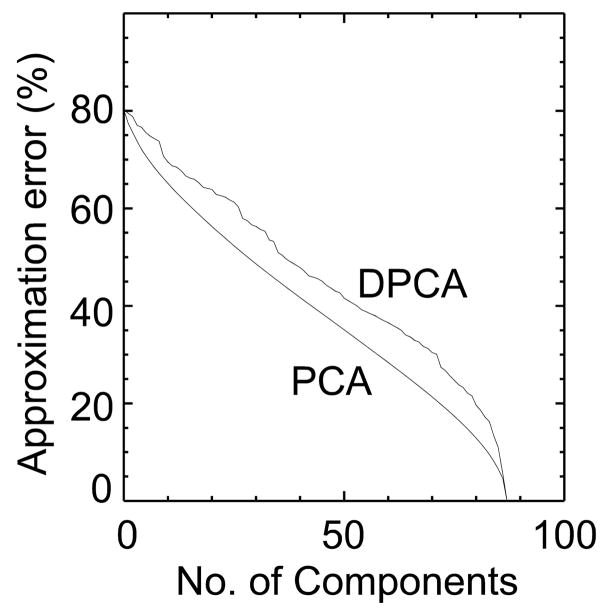
Figure 2 compares the Mahalanobis distance, Fig. 3 the classification error and Fig. 4 the approximation error between standard PCA and DPCA. As expected, when all components are chosen both methods are equivalent and by chance the first component is the same for both methods. With 50 components the distance between the two groups is twice as large with DPCA then with PCA. The classification error (Fig. 3) follows the trend predicted by the Mahalanobis distance plot. The error function in Figure 3 is not monotonic as the distance function in Figure 2 because it is based on actual results of classifying the 90 subjects. The classification error is lower for DPCA, being zero after 30 components have been selected. On the other hand, the classification error for PCA was zero after 75 (more than twice) components were selected. This is also compatible with Figure 2, where the Mahalanobis distance for PCA rapidly increases after 75 components. If the FLD function is calculated from all the samples then the two groups can be perfectly separated with only 30 DPCA components. Figure 4 shows the increase in the approximation error for DPCA as compared to PCA.

Figure 2.

The Mahalanobis distance is compared for ordering of components according to DPCA and by PCA. The Mahalanobis distance is greater for the DPCA method for all selected dimensionalities with being twice as great for 50 components.

Figure 3.

The classification error with DPCA and with PCA as a function of number of components is compared. The classification error for DPCA is lower than that for PCA. In the case of DPCA the classification error is zero after 30 components while for PCA the error is zero after more than twice the number of components.

Figure 4.

The approximation error for dimensionality reduction is compared for the principal components ordered by DPCA and PCA. As expected the error with PCA is smaller than DPCA for all dimensions.

The results of the predictive performance of FLD classification tested by the leave-one-out method are shown in Fig. 5 for DPCA and PCA. The error with DPCA is smaller than PCA, although with only a small number of subjects. Even with all the components selected we have 20% error, rising to 30% when only one component is chosen. In this example after 60 DPCA components are selected there is no further reduction in error for DPCA and the error with PCA is greater by one subject. We reduced a 149206×90 matrix to a 60×90 matrix while maintaining similar classification error as the total data set. The fact that if all the subjects are used for defining the FLD function we get perfect separation, while if we leave-one-out then we get 20% error, indicates that the sample statistics are not representative of the population statistics for our data set. Further work is needed to identify robust classification boundaries in applications with relatively a small number of subjects.

Figure 5.

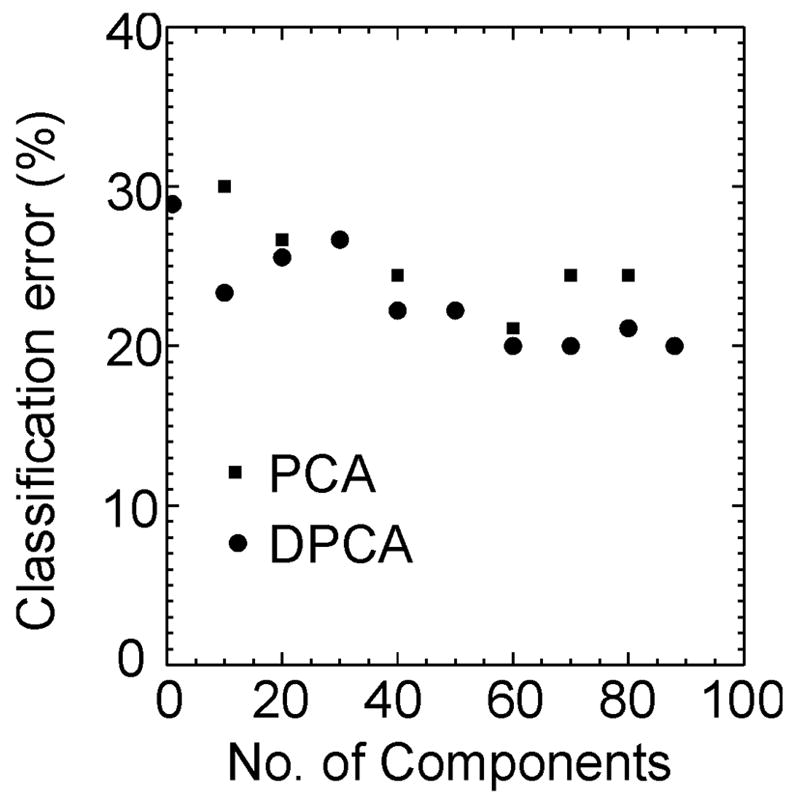
The results of the FLD classification algorithm performance by the leave-one-out method with the components selected by the DPCA and the PCA methods. The classification error for DPCA is lower than that for PCA. The classification error does not substantially reduce after 60 dimensions have been selected and there is difference of only one subject between the two methods.

On examining which subjects gave us classification errors, 8 subjects were consistently misclassified both by DPCA and PCA, independently of the number of components selected. These subjects were not distinguished either by their schizophrenia diagnosis (e.g. first break, relapse, or chronic), by their PANSS scores, or by their ages.

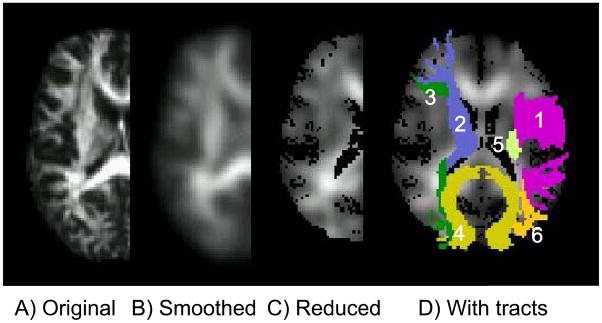
Figure 6 shows the results of data processing pipeline. It gives a visual idea of the effects of smoothing and dimensionality reduction. The back-projection of the 60 component image is shown in Fig. 6C. There is zero classification error with FLD calculated from these images. In order to find out which anatomic region contributed more significantly towards classification we masked the FLD with each of the 20 white matter tracts of the JHU atlas and classified the 90 subjects. The results are shown in Table 1 with the tracts listed in increasing order of classification error. The left superior longitudinal fasciculus gave the least error followed by the right superior longitudinal fasciculus.

Figure 6.

The processing pipeline is shown: A) the original FA image, B) after smoothing by a 6mm FWHM Gaussian filter, C) the reduced 60 dimensional image, and D) the reduced image superimposed with the six tracts which gave zero classification error. The tracts can be identified with reference to Table 2.

Table 1.

The probability of error corresponding to the Fisher’s linear discriminant function masked individually by the 20 white matter tracts. The notation and a pictorial representation of the fiber tracts are given in Hua et al. (2008).

Tract	Probability of error
(SLF) Superior longitudinal fasciculus (Left)	0.144
(SLF) Superior longitudinal fasciculus (Right)	0.156
(tSLF) Superior longitudinal fasciculus temporal part (Left)	0.256
(CgC) Cingulum of the cingulate cortex part (Left)	0.256
(UnC) Uncinate fasciculus (Left)	0.267
(tSLF) Superior longitudinal fasciculus temporal part (Right)	0.289
(UnC) Uncinate fasciculus (Right)	0.300
(CST) Corticospinal tract (Left)	0.311
(ILF) Inferior longitudinal fasciculus (Left)	0.389
(CgC) Cingulum of the cingulate cortex part (Right)	0.400
(ATR) Anterior thalamic radiation (Right)	0.411
(IFO) Inferior fronto-occipital fasciculus (Left)	0.422
(CgH) Cingulum of the hippocampus part (Right)	0.433
(CST) Corticospinal tract (Right)	0.433
(ILF) Inferior longitudinal fasciculus (Right)	0.456
(CgH) Cingulum of the hippocampus part (Left)	0.456
(IFO) Inferior fronto-occipital fasciculus (Right)	0.456
(ATR) Anterior thalamic radiation (Left)	0.489
(FMi) Forceps minor	0.500
(FMa) Forceps major	0.544

Next we performed a sequential analysis to identify the best two tracts, the best three tracts, and so on, until we got zero error. At each stage we added the best possible tract to minimize the classification error. These results are indicated in Table 2. After six tracts are chosen we obtained zero classification error. The six tracts in decreasing order of contribution to classification error were: 1) Superior longitudinal fasciculus (left), 2) Anterior thalamic radiation (right), 3) Inferior fronto-occipital fasciculus (right), 4) Forceps major, 5) Corticospinal tract (left), and 6) Inferior longitudinal fasciculus (left). The previous selection of tracts is not unique and other combinations are possible which give zero classification error. Further work is required to select among these different choices which give similar performance relative to classification error.

Table 2.

The minimum classification error with tracts added sequentially to mask the Fisher’s linear discriminant function.

	Tract	Probability of error
1	Superior longitudinal fasciculus (Left)	0.144
2	Anterior thalamic radiation (Right)	0.1
3	Inferior fronto-occipital fasciculus (Right)	0.044
4	Forceps major	0.022
5	Corticospinal tract (Left)	0.011
6	Inferior longitudinal fasciculus (Left)	0.0

When we compared each tract separately the two tracts which resulted in the least classification error were the left superior longitudinal fasciculus and the right superior longitudinal fasciculus. Interestingly, these two tracts were not the best when used together. The two tracts that jointly gave the least classification error were the left superior longitudinal fasciculus and the right anterior thalamic radiation. This implies that the information for separating the two groups was correlated in the superior longitudinal fasciculus on the two sides of the brain, and together they do not provide the best information for separation. Thus tracts which individually did not give good group separation were useful when used in combination with other tracts.

Discussion

We have shown that the DPCA method of ordering the eigenvectors is useful when dimensionality reduction is done before classification in two groups. This method is computationally as fast as conventional PCA. This is because the main computational effort in PCA is in finding the eigenvectors of a covariance matrix and for DPCA the same eigenvectors are used, but ordered differently. The rule for the new ordering is analytical and not based on some search. Thus the ordering is fast. If a problem can be solved without dimension reduction, then the discussion of this paper is not relevant. In fact for the FA data sets analyzed in this paper dimension reduction was not necessary. FA data set served as an example to understand the DPCA method. The proposed method will be useful when data sets from different modalities are combined or if the subsequent analysis is sufficiently complex that there is a need for dimension reduction. An example of the later is ICA, where PCA is used for dimensionality reduction before ICA is done.

An interesting finding of this paper was that the DPCA method had very good performance when the full data set was used for finding the FLD but had considerably larger errors with the leave-one-out method. The performance of the PCA method was equally bad. This is a problem of using the sample statistics for estimating the classification rule and later discovering that it does not quite represent the population statistics. One reason for this is that our image dimension is much larger then the number of subjects (sample size) making it very difficult to correctly capture the statistical properties of the full image dimension. Although not demonstrated in this paper, it is entirely possible that once we identify sub-structures based on some data driven approach (such as presented here) then subsequent analysis with a reduced set of features (region-of-interests) will give more robust results.

The analysis used in this paper is based on voxel-based strategy, where the images from different subjects are aligned to a common template, then smoothed and followed by some statistical analysis. The method for finding the differences between the two groups is multivariate. The classification rule linearly combines the FA values from different regions, which is more general then just taking an overall mean from some region-of-interest and comparing it to a threshold. The results of this method will be better than or equivalent to the results obtained from some predefined regions-of-interest.

This study has similarities with a previous DTI study on schizophrenia (Skelly et al., 2008). The prominent fibers tracts for classification in this study were superior longitudinal fasciculus, anterior thalamic radiation, inferior fronto-occipital fasciculus, forceps major, cortico spinal tract, and inferior longitudinal fasciculus. The previous study (Skelly et al., 2008) showed FA deficits in white matter consisting of projection fibers (posterior limb of internal capsule), association fibers in the cingulum, the inferior longitudinal fasciculus, anterior thalamic radiation, and commissural fibers of the forceps minor. The superior longitudinal fasciculus was significant in its correlation to the PANSS scores. These results of the two studies are not identical but do have a pattern. In our study superior longitudinal fasciculus was prominent for distinguishing patients from health controls while this was not the case with Skelly et al. (2008) study, but it did have significant correlation with PANSS scores. Some of the association fibers were common to both the studies and support the theory that there is greater probability of disconnection between different brain regions in schizophrenia. The involvement of projection fibers and commissural fibers was found in both the studies. Although in our study forceps major was more useful for classification then the forceps minor found in the previous study. These results show the need for larger data sets and further comparisons among different data analysis methods to isolate their effect of on final results. Larger data sets will also allow us to separate the patient data into sub-groups and give us a better understanding of the differences we observe after analysis.

There have been other studies where size and the shape of corpus callosum has been different in patients with schizophrenia (Downhill et al., 2000; Rotarska-Jagiela et al., 2008). In our method of analysis changes in size and shape of white matter structures is difficult to evaluate because images have been normalized to a common template which modifies the volumes of structures to be compared.

The long term goal is to identify white matter tracts involved in schizophrenia and related to the symptoms (PANSS scores). In this paper, we begin with a data driven method, and use it to identify white matter regions useful in classification based on a predefined white matter atlas. Ultimately we do not want the classification rule to be data dependent. We want to identify significant white matter regions in schizophrenia and test their validity across data from larger schizophrenia populations and from different sites. The results of this paper give additional support to the theory that there will not be a single white matter tract associated with schizophrenia and in different people with schizophrenia there will be different tracts affected.

Conclusions

In this paper we showed that the DPCA method of ordering eigenvectors is superior to the conventional PCA ordering, when the primary purpose of a study is classification of subjects in two groups. In the example of the DTI data set DPCA was considerably better than PCA when the full data set was used for purposes of classification and only marginally better for the leave-one-out method of evaluating the classification performance. The proposed method should be considered as an alternative to standard PCA when analyzing high dimensionality data sets it is important to retain group differences in the exploratory dimensionality reduction step. In our example data set, we were able to reduce the image dimension to 60 while maintaining classification performance comparable to that of the full data set. The left superior longitudinal fasciculus yielded the maximum discrimination between schizophrenia subjects and healthy controls for a single tract. When combining multiple tracks the classification error was further improved (especially when combining tracks for which the discrimination information was not correlated).