Cryosurgery Planning Using Bubble Packing in 3D

Abstract

As part of an ongoing project to develop automated tools for cryosurgery planning, the current study focuses on the development of a 3D bubble packing method. A proof-of-concept for the new method is demonstrated on five prostate models, reconstructed from ultrasound images. The new method is a modification of an established method in 2D. Ellipsoidal bubbles are packed in the volume of the prostate in the current study; such bubbles can be viewed as a first-order approximation of a frozen region around a single cryoprobe. When all cryoprobes are inserted to the same depth, optimum planning was found to occur at about 60% of the length of the prostate (measured from its apex), which leads to cooling of approximately 75% of the prostate volume below a specific temperature threshold of −22°C. Bubble packing has the potential to dramatically reduce the run time for automated planning.

Introduction

Cryosurgery is the destruction of undesired biological tissues by freezing; it has been used to treat cancerous tissue in a large variety of clinical applications, such as skin, hemorrhoids, brain, bone, kidney, liver, breast, and prostate cancers [1]. Prostate cryosurgery was the first minimally invasive cryosurgical procedure to advance from the experimental stage to routine surgical treatment [2]. However, the minimally-invasive approach has created a new level of difficulty for cryosurgery planning, in which a pre-defined 3D region must be treated while preserving the surrounding tissues.

A dozen or more cryoprobes may be used simultaneously in modern prostate cryoprocedures. If effectively localized, one of the potential benefits of a large number of cryoprobes is superior control over the freezing process. Naturally, the application of a large number of cryoprobes is a cause for debate regarding cost-effectiveness. Furthermore, inserting a large number of cryoprobes into a small target region (i.e., a small organ) may cause additional injury to surrounding healthy tissue. The clinical and technological complications of a cryoprocedure using such a large number of cryoprobes may not yet be fully appreciated.

Not only cooling probes must be considered for cryosurgical planning, but also a heating device, known as the “urethral warmer” (the urethra extends near the center of the prostate). The urethral warmer is embodied in a standard catheter, providing a close-to-core body temperature of 37°C along its outer surface. It has been demonstrated that the urethral warmer can potentially minimize post-cryosurgical complications associated with damage to the urethra [3].

To date, cryoprobe localization is an art held by the cryosurgeon, based on the surgeon's own experience and accepted practices. Currently, the means for determining optimal location, or optimal thermal history for the cryoprobes, are limited. Cryoprobes are typically operated intuitively, until the target area is believed to be frozen. Towards the end of the freezing process, cryoprobes are usually turned on and off in a trial-and-error fashion, in order to achieve desired coverage of the target region. The need in this process is associated with suboptimal cryoprobe placement, whereas optimal placement may lead to simultaneous operation of all cryoprobes, thereby reducing the duration of the operation. Suboptimal cryoprobe localization may lead to one or more of the following deficiencies: areas in the target region may be left untreated; healthy surrounding tissue may experience cryoinjury; an unnecessary number of cryoprobes may be used; the duration of the surgical procedure may become excessive; and post-cryosurgery complications may occur--all of which affect the quality and cost of medical treatment. Computerized planning tools would help to alleviate these deficiencies, which is the subject of the current report.

The difficulties in planning a minimally invasive cryoprocedure have been widely acknowledged by other researchers, and efforts to develop computerized means for facilitating planning are reported in the literature [4--6]. These previous studies suggested various parameters to be optimized, combining geometrical consideration with thermal history in the target region; they did not, however, offer an efficient means for cryosurgical planning that could be utilized in practice.

In efforts to develop clinically relevant tools for cryosurgery planning, this research group has recently presented a computerized tool for cryoprobe placement [7]. This tool operates iteratively, and relies on a series of bioheat transfer simulations of the cryosurgical procedure. At the end of each simulation, defective regions are identified; a defect is defined as either tissue outside the target area that was simulated to be cryoinjured, or tissue inside the target area that was not simulated to be cryoinjured. Using a force-field analogy technique, defective regions apply forces to the cryoprobes and displace them prior to the next bioheat transfer simulation. This process of simulation and cryoprobe displacement repeats until no additional improvement can be achieved.

Two challenges are yet to be met before the prototype tool can be reduced to clinical practice: accelerating the bioheat transfer simulations, and selecting an efficient initial condition for automated planning. Accelerating bioheat transfer simulation is a goal which has been approached through parallel efforts [8]. A technique for selecting an initial condition for force-field analogy has also been presented recently [9] in 2D, termed “bubble packing.” The bubble packing technique has been demonstrated as an effective tool for generating a high quality initial condition--prior to the more computationally expensive force field optimization method. The subject matter of the current paper is the migration of the bubble packing method to 3D.

In this paper, the mathematical formulation used for bioheat transfer simulations in cryosurgical planning is reviewed first. Next, the mathematical formulation of bubble packing in 3D is presented, including the principles of anisotropic bubbles and their application to cryosurgery planning. Bubble packing is demonstrated on five 3D models of the prostate, reconstructed from ultrasound images; the reconstruction technique is also presented in this paper. Finally, the discussion section focuses on evaluating the quality of bubble packing by means of bioheat transfer simulations.

Mathematical Formulation of Bioheat Transfer

The quality of bubble packing (formulated in the next section), is evaluated from numerical simulations of bioheat transfer, combined with the application of the concept of defective region. The classical bioheat equation is used to model bioheat transfer in the prostate [10]:

$$C\frac{\partial T}{\partial t}=\nabla (k\nabla T)+{\stackrel{.}{w}}_b{C}_b(T_b-T)$$ (1)

where C is the volumetric specific heat of the tissue, T is the temperature, t is the time, k is the thermal conductivity of the tissue, ẇ_b is the blood perfusion rate, C_b is the volumetric specific heat of the blood, and T_b is the blood temperature entering the thermally treated area (core body temperature). Table 1 lists typical model properties, which were used in the current study. The metabolic heat generation can be neglected [11] during cryosurgery, and therefore it is omitted from Eq. (1).

Table 1.

Representative thermophysical properties of biological tissues used in the current study (T in degree K) [17-19]

Thermophysical Property	Value
Thermal conductivity, k, W/m-K	0.5 15.98−0.0567×T 1005×T−1.15	273 <T 251 < T < 273 T < 251
Volumetric specific heat, C, MJ/m3-K	3.6 880 − 3.21×T 2.017×T − 505.3 0.00415×T	273 < T 265 < T < 273 251 < T < 265 T < 251
Latent heat, L, MJ/m3	300
Blood perfusion heating effect, wbCb, kW/m3-K	40

The numerical scheme applied in the current study has been recently developed to meet the specific requirement for short run time for clinical applications [8], and is presented here in brief:

$$T_{i,j,k}^{p+1}=\frac{\Delta t}{\Delta V_{i,j,k}[C_{i,j,k}+{\left({\stackrel{.}{w}}_b{C}_b\right)}_{i,j,k}\Delta t]}\underset{l,m,n}{\Sigma }\frac{T_{l,m,n}^p-T_{i,j,k}^p}{R_{l,m,n-i,j,k}}+\frac{\Delta t{\left({\stackrel{.}{w}}_b{C}_b\right)}_{i,j,k}{T}_b+C_{i,j,k}{T}_{i,j,k}^p}{C_{i,j,k}+{\left({\stackrel{.}{w}}_b{C}_b\right)}_{i,j,k}\Delta t}$$ (2)

where i,j,k and l,m,n are space indices, p is a time index, ΔV is the volume associated with a numerical grid point, Δt is a time interval, and R is the thermal resistance to heat transfer between numerical grid points. Implementation of Eq. (2) is performed with variable grid regions and variable time steps, which are the main contributors to the decrease in runtime [8].

The objective for the development of the current planning tool is to maximize freezing damage internal to the target region, while minimizing freezing damage external to the target region--all for a given number of cryoprobes selected by the cryosurgeon. The outer surface of the target region in this study is defined as the outer contour of the prostate, but excluding the boundary between the prostate and the urethra. Consistent with clinical practice, it is further assumed that cryoinjury is directly related to the thermal history of the tissue. While the concept of the so-called “lethal temperature” is widely accepted by clinicians, as the threshold temperature below which maximum cryoinjury is achieved, the monitored parameter during cryosurgery is the freezing front via ultrasound imaging, which is likely to be associated with the isotherm of 0°C (i.e., the onset of crystal formation). Since currently accepted values for the lethal temperature are in the range of −50°C to −40°C [1, 12], and since cryoinjury is assumed to progress gradually between the onset of crystal formation and the lethal temperature threshold, the isotherm of −22°C has been selected for planning in the current study. The optimal match of the latter isotherm with the contour of the target region is the objective of the current planning, splitting the undesired effects of excessive cryoinjury external to the target region and insignificant cryoinjury internal to the target region. Nevertheless, the isotherm value of −22°C is selected here for demonstration purposes only, while its actual value is left for the cryosurgeon to decide. The objective function for planning can be formulated as:

$$G=\frac{1}{V_t}{\int }_{V_s}w{\mathit{dV}}_s;w=\{\begin{array}{ccc}\hfill 1\hfill & \hfill -22°C<T\hfill & \hfill \text{interior to the target region}\hfill \\ \hfill 0\hfill & \hfill T\le -22°C\hfill & \hfill \text{interior to the target region}\hfill \\ \hfill 1\hfill & \hfill T\le -22°C\hfill & \hfill \text{exterior to the target region}\hfill \\ \hfill 0\hfill & \hfill -22°C<T\hfill & \hfill \text{exterior to the target region}\hfill \end{array}\phantom{\}}$$ (3)

where V_s is the volume of the entire simulated domain (including both the target and external regions), V_t is the volume of the target region, and w is a spatial weight defect function, determined by the local temperature distribution. The tool developed in this study is based on the underlying assumption that displacement of a cryoprobe is considered to be an improvement if the value of the objective function, G, decreases.

Mathematical Formulation of Bubble Packing in 3D

When the thermophysical properties and blood perfusion rate are assumed to be uniform throughout the simulated domain, the shape of the target tissues becomes the most critical factor for planning. It may be assumed that an evenly spaced layout of cryoprobes would result in a better plan, potentially leading to the optimum layout with the incorporation of the force-field technique. The current study is aimed at evenly distributing cryoprobes by using the bubble packing method, in which the center of each bubble represents a cryoprobe location. While the concept of bubble packing is well established [13-15], and the application of bubble packing to cryosurgery has recently been demonstrated in 2D [9], the current study focuses on two new aspects of the bubble packing method: the application in 3D for cryosurgical planning, and the usage of anisotropic or, ellipsoidal, bubbles.

Principles of Bubble Packing

Bubble packing is a physically based approach that efficiently finds the even distribution of an arbitrary number of points inside a given geometric domain. The method first generates spherical elements--bubbles--inside that domain. Next, van der Waals-like forces are assumed to drive bubbles, until a minimum energy configuration of bubbles is reached. In broad terms, the van der Waals model represents proximity-based forces between every two elements in the domain. An attraction force is applied when the two elements are too distant from one another, while a repulsion force is applied when they are too close. Only one distance exists where these forces equilibrate. Once bubbles are seeded, or mathematically defined in the domain, their motion is simulated until all inter-bubble forces equilibrate. In the current study, the van der Waals-like forces are defined as:

$$f\left(l\right)=\{\begin{array}{cc}\alpha l^3+\beta l^2+\gamma l+\epsilon \hfill & 0\le l\le 1.5l_0\hfill \\ 0\hfill & 1.5l_0<l\hfill \end{array}\phantom{\}}$$ (4)

subject to the boundary conditions of:

$$f\left(l_0\right)=f\left(1.5l_0\right)=0,f^{\prime }\left(0\right)=0,f^{\prime }\left(l_0\right)={\kappa }_0$$ (5)

where l is the distance between the two bubbles, l₀ is the distance of force equilibrium between two isolated bubbles, κ₀ is the approximated linear spring constant at a distance l₀; α, β, γ, and ε are force constants.

The motion of bubbles towards equilibrium is simulated as a force relaxation process:

$$m_i\frac{d^2{x}_i\left(t\right)}{{\mathit{dt}}^2}+c_i\frac{{\mathit{dx}}_i\left(t\right)}{\mathit{dt}}=f_i\left(t\right),i=1\dots n$$ (6)

where x_i is the location of the i^th bubble, while m_i and c_i denote the mass and damping coefficient of the i^th bubble, respectively; m_i, and c_i are assumed from computational convergence consideration, but their actual values have no physical meaning in the context of cryosurgery. Note that f_i(t) is the sum of all inter-bubble forces working on the i^th bubble. Equation (6) is numerically integrated using the fourth-order Runge-Kutta method [16]. Finally, the volume of the bubbles is adjusted to both minimize the gap between bubbles and prevent bubble overlapping when force relaxation progresses with the change in bubble size [9].

Anisotropic Bubbles

The developing frozen region in a single cryoprobe operation has an elongated egg shape, which can be first-order approximated as an ellipsoid. Consistent with this observation, ellipsoidal bubbles are assumed for bubble packing. The ratio of the principal radii of the ellipsoidal bubble was found from a heat transfer simulation around a single cryoprobe. The principal radii ratio was taken as the location of the −22°C isotherm (the target isotherm for planning) after 500 seconds of simulation; the developing frozen region size approached its steady-state value at that time. Comparable radius values for a wide selection of freezing conditions have been presented by Rabin and Shitzer [11]. It is acknowledged that in a multi-cryoprobe operation, the isolate frozen regions around cryoprobes eventually fuse to form a large unified frozen region, which cannot be represented with bubble packing. Therefore, the ellipsoidal bubble packing can only be regarded as a first-order approximation of the early stage of the procedure. The quality of this approach is evaluated in the Results and Discussion section, below.

In a context other than cryosurgery, Yamakawa and Shimada [15] proposed a technique for ellipsoidal bubble packing termed “anisotropic bubble packing”. In anisotropic bubble packing, the distance between two bubbles depends not only on the positions of the bubble centers, but also on the relative orientation of bubbles. Anisotropy in the current study is defined by three orthogonal principal directions and three radii. The principal directions are defined with unit vectors u, v, and w, where each bubble is stretched by a ratio of λ_u, λ_v, and λ_w in those directions, respectively:

$$R=\left(\begin{array}{ccc}\hfill u_x\hfill & \hfill v_x\hfill & \hfill w_x\hfill \\ \hfill u_y\hfill & \hfill v_y\hfill & \hfill w_y\hfill \\ \hfill u_z\hfill & \hfill v_z\hfill & \hfill w_z\hfill \end{array}\right);S=\left(\begin{array}{ccc}\hfill {\lambda }_u\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\lambda }_v\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_w\hfill \end{array}\right)$$ (7)

and where R and S are the rotation and scaling matrices, respectively. The 3×3 matrix describing the 3D anisotropy is given by [15]:

$$M={\mathit{RSR}}^T$$ (8)

Since matrix M is a positive definite matrix, it can be decomposed into two matrices Q and Q^T:

$$M=Q^{T}Q$$ (9)

where

$$Q=\left(\begin{array}{ccc}\hfill \sqrt{{\lambda }_u}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{{\lambda }_v}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \sqrt{{\lambda }_w}\hfill \end{array}\right)R^T$$ (10)

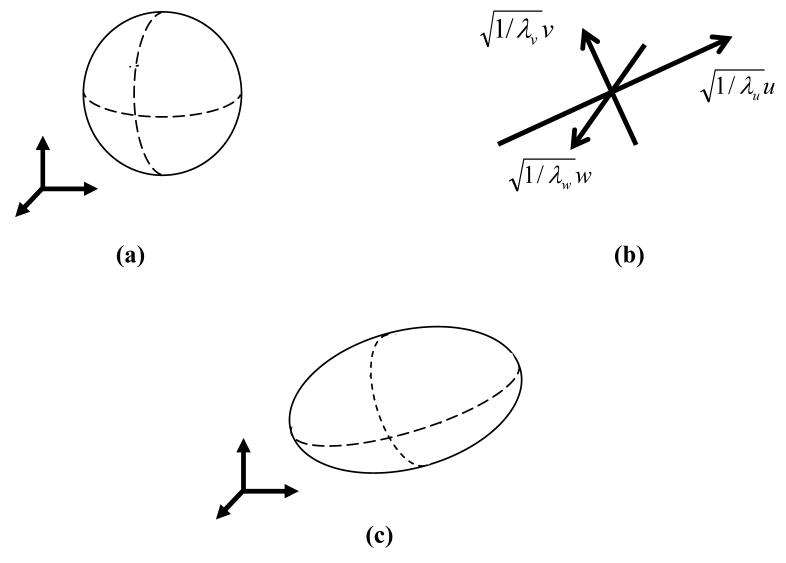
Figure 1 illustrates the transition from an isotropic bubble into an anisotropic bubble. Based on the analysis of the developing temperature field around a single cryoprobe, as discussed above, aspect ratios of λ_u=0.43, λ_v=0.43, and λ_w=1.0 were selected in the current study to best-fit the target region with ellipsoidal bubbles.

Figure 1.

Schematic illustration of (a) a spherical (isotropic) bubbles, (b) principle axes and ratios of the deformation, and (c) an anisotropic bubble after the deformation.

In the case of isotropic bubbles, the distance of force equilibrium between adjacent bubbles is the sum of the bubbles' radii, Eqs. (4) and (5). In the case of anisotropic bubble packing, the distance between the center of the ith bubble and its surface, along the straight line connecting the centers of adjacent bubbles i and j, r_i', is given by:

$$r_i^{\prime }=r_i{M}_i{d}_{\mathit{ij}};d_{\mathit{ij}}=\frac{(x_j-x_i)}{\Vert (x_j-x_i)\Vert };i,j\in n$$ (11)

where r_i is the radius of bubble i before deformation, x_i and x_j are the position vectors of bubbles i and j, respectively, and d_ij is a unit vector directing from x_i to x_j; the use of the symbol prime in r' is to indicate the direction of d_ij. It follows that for the anisotropic case:

$$l_0=r_i^{\prime }+r_j^{\prime }$$ (12)

as illustrated in Fig. 2. As in the case of isotropic bubbles, system relaxation towards force equilibrium follows the model of motion described in Eq. (6). Once relaxed, the center point of each bubble defines the medial point of the active surface of the cryoprobe. Note that all bubbles are forced to have the same orientation, which conforms to the direction of cryoprobe insertion.

Figure 2.

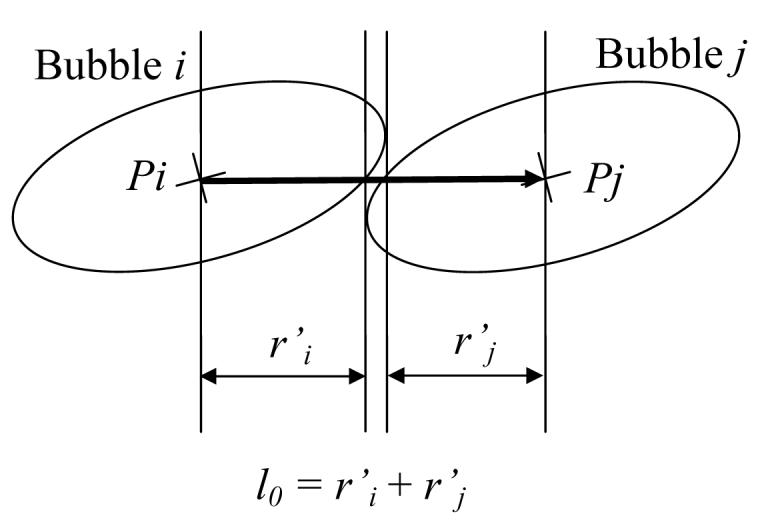
Schematic illustration of the equilibrium distance between two anisotropic bubbles.

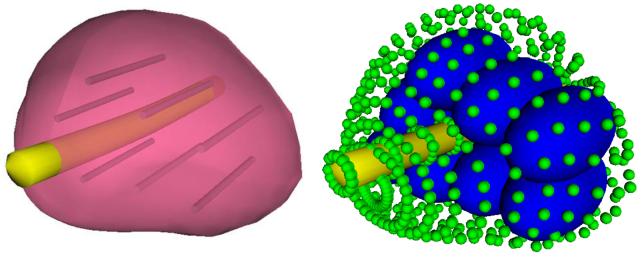
In order to keep the bubbles inside the prostate domain, boundary bubbles are defined on the outer surface of the prostate, as well as along the urethral warmer, as illustrated in Fig. 3. Conceptually, a boundary bubble is similar to a regular bubble only in its repelling force; a boundary bubble has an infinitesimal radius, a zero attractive force, and a fixed position. (Note that the infinitesimal boundary bubbles are enlarged in Fig. 3 for illustration purposes only.) It follows that regular bubbles are repulsed from the boundary with an ideal equilibrium distance equal to the radius of the regular bubble.

Figure 3.

Illustration of boundary representation for bubble packing: the contour of the reconstructed prostate model (left) is replaced with boundary bubbles (small bubbles on the right), and cryoprobe representing bubbles (large bubbles on the right) are packed in the domain; the size of the infinitesimal boundary bubbles is enlarged for illustration purposes. Also illustrated on the left are the active surfaces of cryoprobes, based on the bubble-packing results.

Cryoprobe Insertion Depth

If cryoprobes could be placed anywhere in the target region, the anisotropic bubble packing problem would be well defined, and a solution could be found. However, clinical practices pose additional constraints on this problem. One constraint is that the insertion direction of all cryoprobes must be identical, which restricts the longer dimension of all ellipsoidal bubbles to the same direction--roughly parallel to the urethral warmer (Figs. 3 and 4). Another constraint is that the tip of all cryoprobes must be placed on the same plane--perpendicular to the direction of cryoprobe insertion; while this represents a severe constraint, it can be relaxed in future studies. It follows that the insertion depth of cryoprobes becomes a major factor which can potentially affect the quality of planning.

Figure 4.

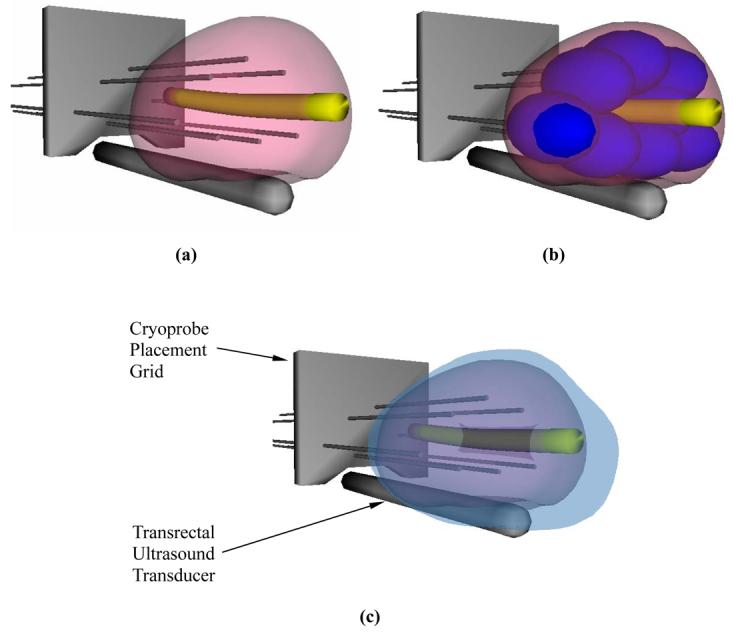
Schematic illustration of cryosurgery planning: (a) the prostate and urethral warmer are modeled based on ultrasound images, (b) bubble packing generates a recommended cryoprobe layout, and (c) the quality of planning is evaluated from a simulated temperature distribution at the point of minimum defect; the blue region represents area with temperatures below −22°C, the target isotherm for planning in the current study.

To overcome the difficulty associated with the latter constraint, an analysis of the optimal insertion depth has been performed. Here, the bubble packing method was sequentially executed on a series of prostate cross-sections, all perpendicular to the direction of cryoprobe insertion. In each run, bubbles are allowed to move in the cross-sectional plane only. Note that the ellipsoidal bubbles are still interacting with the boundary bubbles, lying on the surface of the prostate, which potentially create forces on each bubble from all direction. Extra-bubble volume is calculated at the end of that run, which is defined as the difference between the volume of the target region and the combined volume of all packed bubbles. An optimum insertion depth is assumed when the extra-bubble volume reaches a minimum. In this study, a bioheat transfer simulation is executed only for the case of minimum extra-bubble volume. Results and discussion about the effect of the insertion depth are provided below, in comparison to geometrical parameters of the target region.

Target Region Reconstruction from Ultrasound Images

The target region was reconstructed from ultrasound images of the prostate of five individuals; ultrasound data was made available by Aaron Fenster, Robarts Imaging Institute, London, Ontario, Canada. From ultrasound data, 3D prostate models were created as follows. First, the operator selected 8 to 11 better-quality images, representing axial cross-sections of the prostate (in practice, data for generation of up to 800 cross-sections was available for each individual). Next, the operator identified 10 to 15 points on the prostate contour, in each selected image. A group of third-order Bezier curves was obtained by interpolation between the selected points on each cross-section. Prostate contours in the sagittal section were further interpolated between axial cross-sectional contours. Since a urethral warmer was not present during imaging of any of the prostates, modeling of the urethral warmer was added as a 6 mm in diameter tube, in which the center line coincides with the center of the urethra, as identified from imaging. Finally, boundary bubbles were placed on the interpolated target region surface with a desired resolution.

For visualization purposes, the 3D reconstructed model was smoothed using a third-order Bezier surface interpolation, as illustrated for example in Fig. 4(a). The reconstruction procedure took about 10 minutes for each prostate.

Results and Discussion

Bubble packing was studied on the five prostate models, having an average volume of 49.3±19.5 ml and an average length of 46.3±6.0 mm, as listed in Table 2. Geometrical parameters for the bioheat transfer simulations were selected to be consistent with Rossi et al. [8] and are presented here in brief. The cross-sectional area in the simulated domain is 3.5 times larger than the cross-sectional area in the prostate model; the simulated domain is 1.5 times as long as the prostate model. These dimensions satisfy the thermal assumption that the body can be modeled as an infinite domain, when compared with the prostate size. The simulated domain was discretized with variable axial grid intervals. A 3 mm × 3 mm grid was used throughout the majority of the domain, while finer grids of 1 mm × 1 mm were used in the vicinity of cryoprobes and the urethral warmer, where temperature gradients are steeper.

Table 2.

Reconstructed prostate dimensions from five individuals and results of anisotropic bubble packing evaluated with bioheat transfer simulation, where V_P is the prostate volume, L_P is the prostate length, L_V2 is the distance from the apex of the prostate to a plane splitting the volume of the prostate into two segments having identical volumes, L_S is the optimal insertion depth of cryoprobes, and the defect is presented in comparison with the overall prostate volume.

Patient	Prostate Dimensions	# of Probes	Insertion Depth, LS, mm (LS/LP)	Defect %	Bubble Packing Runtime, sec	Bioheat Simulation Runtime, sec
A	VP = 44.4 ml LP = 44.5 LV2 = 26 ml	4	26 (0.59)	40.6	19	174
		6	24 (0.54)	35.1	22	77
		8	26 (0.59)	29.5	27	60
		10	27 (0.61)	23.8	34	54
		12	26 (0.59)	26.6	10	53
		14	27 (0.61)	26.5	8	51
B	VP = 62.8 ml LP = 49.9 LV2 = 28 mm	4	33 (0.66)	49.5	17	401
		6	33 (0.66)	34.7	25	188
		8	31 (0.62)	28.4	31	117
		10	28 (0.56)	24.7	35	106
		12	29 (0.58)	26.0	43	90
		14	29 (0.58)	26.5	7	86
C	VP = 23.0 ml LP = 37.2 LV2 = 23 mm	4	24 (0.65)	49.0	24	61
		6	24 (0.65)	32.7	25	38
		8	24 (0.65)	30.7	29	30
		10	25 (0.68)	31.0	5	26
		12	25 (0.68)	33.7	5	24
		14	25 (0.68)	34.5	6	25
D	VP = 73.6 ml LP = 52.9 mm LV2 = 27 mm	4	29 (0.56)	55.7	19	513
		6	29 (0.56)	30.3	23	367
		8	27 (0.52)	26.2	26	172
		10	27 (0.52)	27.2	31	130
		12	28 (0.54)	26.4	34	112
		14	28 (0.54)	28.4	7	120
E	VP = 42.8 ml LP = 47.0 mm LV2 = 28 mm	4	29 (0.63)	43.2	19	197
		6	28 (0.61)	33.7	24	88
		8	27 (0.58)	27.3	26	66
		10	27 (0.58)	27.2	30	52
		12	29 (0.63)	28.8	43	53
		14	27 (0.58)	31.0	6	46

For cryosurgery simulations, the temperature of each cryoprobe was assumed to decrease linearly from 37°C down to −145°C over 30 seconds, and to stay constant thereafter (typical parameters for a Joule-Thomson based cryoprobe using Argon). Case studies included 6 to 14 cryoprobes, in which all cryoprobes are operated simultaneously. A diameter of 1.3 mm (represented by a 1 mm × 1 mm square, which has the same surface area for heat conduction as a 1.3 mm cylinder), and an active length of 25 mm were assumed for each cryoprobe. While the active length can play a significant role in planning of cryosurgery, further studies on its effect are deemed unnecessary for the current proof-of-concept report. At the beginning of the bubble packing process, bubbles were seeded at the boundary between the urethral warmer and the prostate, at its mid-length and at equiangular intervals.

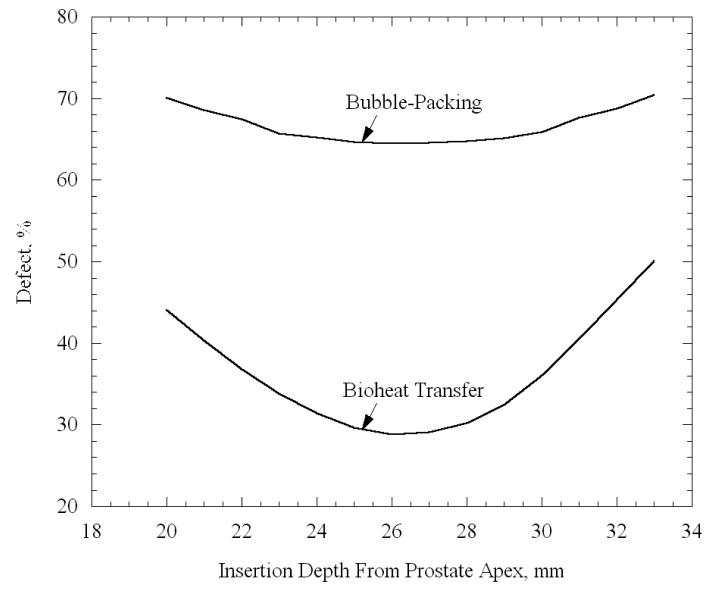
Typical results for the dependency of the total defect volume upon the insertion depth, for one prostate model with 8 cryoprobes, are displayed in Fig. 5. The insertion depth is measured from the apex of the prostate to the center of the active surface of the cryoprobe (12.5 mm from the cryoprobe tip for the current study), and a sequence of bubble packing routines was performed in insertion depth intervals of 1 mm. Figure 5 displays both the defect volume calculated from bubble packing, i.e., the extra-bubble volume within the target region, and the defect volume calculated from bioheat transfer simulations, Eq. (3). While the definition of defect based on bubble packing has no physical meaning, resulting in significantly higher values than the defect calculated from bioheat transfer simulations, it can be seen from Fig. 5 that both defect volume curves have only one minimum, at almost exactly the same insertion depth value (close to 26 mm). Similar studies on the other prostate models listed in Table 2 yielded disagreement in the range of up to ±2 mm, between these two methods of evaluating the optimum insertion depth for minimum defect volume. It can be concluded that bioheat transfer simulations are not critical in seeking the optimum insertion depth. Note that in 2D, bubble packing has been demonstrated to be faster by an order of magnitude than the force-field optimization, where the objective of the bubble packing stage is to reduce the run time of the force-field stage. Run time studies in this report are based on an AMD Athlon (TM) XP 3000+computer, 2.10 GHz processor, 400 MHz front side bus, and 1 GB of PC3200 DDR memory. The software was implemented with Visual C++ .NET and executed using Windows XP Professional.

Figure 5.

The dependence of the total defect volume on insertion depth, measured from the apex of the prostate to the center of the active surface of the cryoprobes; the total defect volume is normalized with respect to the prostate volume (Patient A with 8 cryoprobes, Table 2).

It may be assumed that the optimum insertion depth is derived from prostate geometrical considerations, bearing in mind that all reconstructed prostate models are fairly similar in shape. With this observation in mind, the distance from the apex of the prostate to a plane splitting the volume of the prostate into two segments with identical volumes, L_v2, has been calculated for all cases (see Table 2). It can be seen from Table 2 that the ratio of optimum insertion depth is always significantly smaller than L_v2. It can further be seen from Table 2 that the ratio of optimum insertion depth to prostate length, L_S/L_P, is 0.60±0.05, and it is only slightly affected by the number of cryoprobes (though not with a specific trend). This observation suggests that a value of 0.6 can be taken as a rule-of-thumb for an initial placement depth, to further accelerate cryosurgical planning. Note that a ratio of ±0.05 represents an uncertainty in insertion depth of about ±2.5 mm.

Prior work on 2D models suggested that increasing the number of cryoprobes decreases the overall defect area [7, 9]. In the current study however, when 3D models are under consideration, a different trend arises, when the number of cryoprobes ranges from 4 to 14. It can be seen from Table 2 that a minimum defect volume is found for ten cryoprobes in three prostate models, and for eight cryoprobes in two other prostate models. Based on bubble packing alone, the commonly accepted rule-of-thumb--that the defect volume should decrease with the increasing number of cryoprobes--does not hold. However, the current study presents proof-of-concept for bubble packing in 3D only, where a second phase of optimization is planned in the grand scheme, using the force-field method. It is expected that the force-field method will further decrease the overall defect volume, and may demonstrate further advantages to the increasing number of cryoprobes; this is the subject matter of the next stage of this ongoing research.

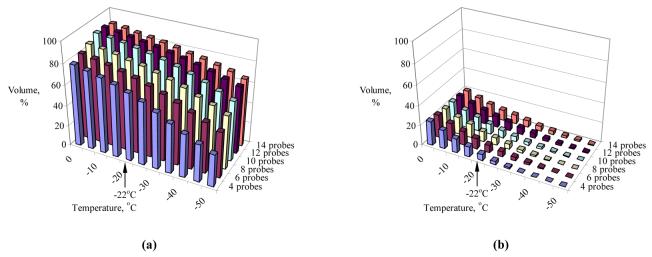
Figure 6 displays representative temperature volume histograms (TVH) of Patient A (Table 2) in the target region and in the external region, normalized with respect to volume of the target region. It can be seen from Fig. 6 that more than 75% of the target volume is simulated to have temperatures below the isotherm for planning, −22°C, while an external defect volume of less than 10% is found at the same point in time. Comparable results were obtained from all other cases in this study. The actual isotherm value for planning is likely to remain a point for viable debate in years to come, as it always represents a compromise between insufficient internal cryoinjury and excessive external injury. Furthermore, the weight function w in Eq. (3) can be modified to take into account additional parameters of optimization, in order to give different weight to external versus internal defects, or to represent a higher risk of freezing to the rectum, for example. Either way, the concept of bubble packing in 3D in combination with bioheat transfer simulations has been proven, and modification of the weight function must incorporate future clinical data.

Figure 6.

Temperature volume histogram of the target region (a) and the external region (b), where the volume is normalized with respect to the prostate volume (Patient A, Table 2).

It can be seen from Table 2 that the bubble-packing procedure is always shorter than a bioheat transfer simulation, for the same prostate model and conditions; in more than half of all cases, it is shorter by an order of magnitude. Furthermore, the parameters of bubble packing can be optimized for run time, however, this stage of software optimization is deemed unnecessary for the current proof-of-concept report. Finally, bubble packing has the potential to dramatically reducing the number of iterations for the process of force-field optimization, where each iteration is based on a bioheat transfer simulation [9]. Upgrading of force-field optimization to 3D is currently underway.

Summary and Conclusions

In efforts to develop clinically relevant tools for cryosurgery planning, this research group has recently presented a computerized planning tool for cryoprobe placement, based on the force-field analogy technique. Two challenges are yet to be met before the prototype tool can be applied to clinical practice: accelerating the bioheat transfer simulations, and selecting an efficient initial condition for the automated process of planning. While accelerating bioheat transfer simulations is a subject matter in a parallel study, the current study focuses on a technique for selecting a good initial condition. More specifically, the current study concerns the migration of the bubble packing method from 2D to 3D, with an increased level of complexity associated with anisotropic bubbles.

Bubble packing was studied on five reconstructed prostate models from ultrasound images, and the quality of planning was evaluated based on bioheat transfer simulations. An optimum cryoprobe insertion depth was found at about 0.6 of the prostate length, when measured from the apex. Once the insertion depth was established, a cryoprobe layout was found, leading to cooling of about 75% of the prostate volume below a specific temperature threshold of −22°C. This temperature threshold is used in the current study for demonstration purposes only, while its actual value for planning is likely to remain a point for viable debate in years to come.

While bubble packing is presented in this study as proof-of-concept only, its parameters could be further optimized to decrease run time. Even in its present form, a bubble packing procedure is significantly shorter than a single bioheat transfer simulation. Furthermore, bubble packing has the potential to dramatically reduce the number of iterations in the process of force-field optimization, in which each iteration is based on a bioheat transfer simulation. Upgrading the two-phase optimization technique from 2D to 3D, using bubble packing followed by force-field analogy, represents the next phase of this ongoing research.