Abstract
We developed a computationally efficient algorithm AMBIENCE, for identifying the informative variables involved in gene–gene (GGI) and gene–environment interactions (GEI) that are associated with disease phenotypes. The AMBIENCE algorithm uses a novel information theoretic metric called phenotype-associated information (PAI) to search for combinations of genetic variants and environmental variables associated with the disease phenotype. The PAI-based AMBIENCE algorithm effectively and efficiently detected GEI in simulated data sets of varying size and complexity, including the 10K simulated rheumatoid arthritis data set from Genetic Analysis Workshop 15. The method was also successfully used to detect GGI in a Crohn's disease data set. The performance of the AMBIENCE algorithm was compared to the multifactor dimensionality reduction (MDR), generalized MDR (GMDR), and pedigree disequilibrium test (PDT) methods. Furthermore, we assessed the computational speed of AMBIENCE for detecting GGI and GEI for data sets varying in size from 100 to 105 variables. Our results demonstrate that the AMBIENCE information theoretic algorithm is useful for analyzing a diverse range of epidemiologic data sets containing evidence for GGI and GEI.
THE risk of developing many chronic diseases such as cancer, cardiovascular diseases, autoimmune diseases, and mental disorders may involve interactions among a number of genetic, endogenous, and exogenous environmental factors (Shields and Harris 2000; Talmud and Stephens 2004; Caspi and Moffitt 2006; Ambrosone et al. 2007; Arason et al. 2007). The successful identification of critical gene–environment interactions (GEI) may provide the scientific basis for preventative public health measures to help individuals with particular genetic susceptibilities reduce their exposure to disease risk-increasing environmental variables. Better analytical methods for detecting GEI can facilitate identification of environmental factors capable of modifying the effects of genetic risk factors on disease outcome.
Advances in high-throughput genotyping methods have made generating dense genetic maps of the human genome for epidemiological studies feasible. The additional information from these methods improves the prospects for uncovering the interactions underlying genetic etiology of multifactorial diseases. With respect to study design, identification of gene–gene interactions (GGI) is important for follow-up sequencing studies and results from GEI analyses can help in reducing confounding in replication studies by ensuring relevant informative environmental variables are collected. Statistical GGI and GEI analyses can also provide evidence in support of specific disease mechanisms. Unfortunately, there is a paucity of comprehensive approaches that can conduct higher-order GGI and GEI analyses on a genomewide scale (Purcell et al. 2007).
Although there is considerable need for GGI and GEI analyses to understand the genetics of many diseases, there are unique scientific challenges attributable to the potential involvement of multiple genetic and environmental factors in the etiology of the disease, the high dimensionality of the data sets from genomewide studies, and combinatorial explosion. As the number of ways of selecting a subset of K genetic or environmental variables for assessing interactions from N such variables is equal to  , the binomial coefficient or N-choose-K function, the number of interactions increases with extraordinary rapidity. This combinatorial growth makes it computationally difficult, if not impossible, to exhaustively assess the full range of genetic and environment variables for potential interactions associated with diseases in epidemiologic studies. As an example, there are 1.67 × 1011 possible three-way GGIs for a data set with 10,000 SNPs. If the calculations for each GGI could be accomplished in 1 msec, the computation time required would be >5 years.
, the binomial coefficient or N-choose-K function, the number of interactions increases with extraordinary rapidity. This combinatorial growth makes it computationally difficult, if not impossible, to exhaustively assess the full range of genetic and environment variables for potential interactions associated with diseases in epidemiologic studies. As an example, there are 1.67 × 1011 possible three-way GGIs for a data set with 10,000 SNPs. If the calculations for each GGI could be accomplished in 1 msec, the computation time required would be >5 years.
The multifactor dimensionality reduction (MDR) technique (and software) for identifying and analyzing GEI was developed by Ritchie and colleagues (Ritchie et al. 2001; Hahn et al. 2003; Moore et al. 2006). MDR is based on nonparametric multifactor models and allows statistical and cross-validation analysis of GGI and GEI for balanced case–control and discordant sib-pair designs (Ritchie et al. 2001, 2003; Hahn et al. 2003; Bush et al. 2006). MDR uses constructive induction wherein the dimensionality of the multilocus genotype is systematically reduced by pooling into high and low risk groups (Moore et al. 2006). The MDR method has been extended to unbalanced data sets (Velez et al. 2007) and a theoretical analysis of MDR has shown the similarity of the MDR classifier to the naive Bayes classifier (Hahn and Moore 2004). The MDR approach has been used to study GEI in atrial fibrillation, autism, and diabetes mellitus (Cho et al. 2004; Tsai et al. 2004; Ma et al. 2005; Motsinger et al. 2006). The recently proposed generalized MDR (GMDR) method employs the generalized linear model (GLM) framework for scoring in conjunction with MDR for dimensionality reduction (Lou et al. 2007). GMDR enables inclusion of covariates and handles both discrete and continuous traits in population-based study designs. GMDR employs the same risk-pooling, dimensionality reduction strategy as MDR and yields the original MDR as a special case when covariates are not present and the trait under investigation is binary (Lou et al. 2007). However, despite availability of a more efficient parallel computing implementation (Bush et al. 2006), MDR and its variants, including GMDR, are computationally intensive, especially when >10 polymorphisms need to be evaluated (Ritchie et al. 2001).
One approach that allows hypotheses of specific types of GGI and GEI to be tested is the pedigree disequilibrium test (PDT) (Martin et al. 2000) as implemented in the software program UNPHASED (v3.10) (Dudbridge 2003). Although designed for family-based studies (including case–parent trios and affected sibling pairs study designs), the PDT approach is flexible enough for the analysis of associations in case–control study designs. Likelihood-ratio tests (LRT) can be built to test synergistic epistasis, i.e., when the effect of the combination of two alleles at two different diallelic loci is greater than the additive effects of the loci alone. The LRT can also be built to test for effect measure modification, which occurs when varying levels of an environmental risk factor modify the risk ratio of the genotype. The PDT has the appeal of a formal statistical framework: the hypothesis tests for synergistic epistasis and effect measure modification are statistical tests of interaction. It is flexible with regard to study design and can accommodate missing data. The PDT approach has been used to extend the MDR to allow analysis of families (Martin et al. 2006). However, the computational challenges remain.
The available methods are computationally prohibitive for analyzing interactions in genomewide data and there is a need for novel methodology. Information theoretic methods are among the most promising approaches for enhancing single-nucleotide polymorphism (SNP) analysis, GGI and GEI analysis, and visualization (Liu and Lin 2005; Bhasi et al. 2006a,b; Moore et al. 2006). Information-theoretic approaches have well-developed theory and are versatile and genetic model independent but only limited research on leveraging these strengths into analytical strategies for GGI and GEI has been done. Several reports have used the Kullback–Leibler divergence (KLD) for genetic analysis (Smith et al. 2001; Anderson and Thompson 2002; Rosenberg et al. 2003; Liu and Lin 2005). The KLD is a measure of the “distance” between two distributions because it measures the inefficiency of assuming that the distribution is q when the true distribution is p. In genetic analyses, the most frequent application of the KLD has been for two-group comparisons such as those used to evaluate ancestry informative markers (Smith et al. 2001; Anderson and Thompson 2002; Rosenberg et al. 2003). However, the KLD has also been proposed as a multilocus linkage disequilibrium (LD) measure to enable identification of TagSNPs (Liu and Lin 2005) and our group has adapted the KLD for analytical visualization (Bhasi et al. 2006a,b). Information theory statistics employing entropy-based statistics have been proposed for genomewide data analysis to test for allelic association with a phenotype (Zhao et al. 2005, 2007; Li et al. 2007). Entropy-based methods for two-locus interactions have also been proposed recently and were found to confirm the negative epistasis between sickle cell anemia and α-thalassemia genetic variations against malaria (Dong et al. 2007).
Information theoretic approaches offer many potent capabilities and advantages for GGI and GEI analyses. These approaches utilize extensions of the KLD to measure complex multivariate dependencies among genetic variations and environmental factors without complex modeling. In our previous report, we developed an approach for GGI and GEI visualization and identification that utilizes two established and complementary information-theoretic metrics, the K-way interaction information (KWII) and the total correlation information (TCI) for GEI and GGI analyses (Chanda et al. 2007). We demonstrated that the KWII spectra of a data set are capable of identifying critical interactions and contain information that can be utilized to infer the biological mechanisms generating the interactions.
The goals for this research were to substantively extend the concepts and methods developed in our earlier report (Chanda et al. 2007) by (i) developing a novel metric, the phenotype-associated information (PAI) that is robust to the confounding effects of factors such as pairwise and higher-order LD and correlations between environmental variables, (ii) demonstrating that the PAI is a useful information theoretic metric for effectively screening GGI and GEI, and (iii) developing an algorithm AMBIENCE that employs the PAI metric to efficiently search the combinatorial space to identify the variables involved in the strongest interactions. The results from this work will enable the development of better methods for efficient, large-scale interaction analysis.
MATERIALS AND METHODS
Terminology and representation:
The methods in this article are applicable to both GEI and GGI analyses and henceforth we simply use the term GEI to refer to both. The term GGI is used only when environmental variables are not present in a data set.
Definition of interaction:
The KWII is a parsimonious, multivariate measure of information gain, which is defined and described in detail below (Jakulin and Bratko 2004; Jakulin 2005). In our information theoretic framework, we use the KWII as the measure of interaction information for each variable combination. We operationally define that a positive KWII value for a variable combination indicates the presence of an interaction, negative values of KWII indicate the presence of redundancy, and a KWII value of zero denotes the absence of K-way interactions.
This operational definition based on the KWII corresponds closely to but is not exactly the same as the formulation of statistical interactions in the context of logistic regression. For a succinct discussion of the concordance and differences with other definitions see Jakulin (2005).
Entropy:
The entropy, H(X), of a discrete random variable X can be computed from the probabilities of p(x) using the formula
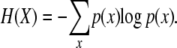 |
K-way interaction information (KWII):
For the three-variable case, the KWII is defined in terms of entropies of the individual variables, H(A), H(B), and H(C) and the entropies, H(AB), H(AC), H(BC), and H(ABC), of the combinations of the variables:
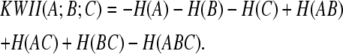 |
For the K-variable case on the set 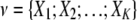 , the KWII can be written succinctly as an alternating sum over all possible subsets
, the KWII can be written succinctly as an alternating sum over all possible subsets 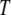 of
of 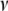 using the difference operator notation of Han (1980):
using the difference operator notation of Han (1980):
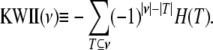 |
The number of variables K in a combination is called the order of the combination. The KWII represents the gain or loss of information due to the inclusion of additional variables in the model. It quantifies interactions by representing the information that cannot be obtained without observing all K variables at the same time (McGill 1954; Fano 1961; Jakulin and Bratko 2004; Jakulin 2005). The KWII of a given combination of variables is a parsimonious interaction metric. It does not contain contributions arising from the KWII of other lower-order combinations of these variables.
In the bivariate case, the KWII is always nonnegative but in the multivariate case, KWII can be positive or negative. The interpretation of KWII values is intuitive because positive values indicate synergy between the variables, negative values indicate redundancy between variables, and a value of zero indicates the absence of K-way interactions.
TCI:
For the three-variable case, the TCI (Watanabe 1960) is defined in terms of entropies of the individual variables H(A), H(B), and H(C) and the entropy of the joint distribution H(ABC):
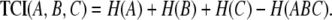 |
For the K-variable case on the set 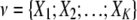 , the TCI can be expressed as the difference between the entropies of the individual variables H(Xi) and the entropy of the joint distribution H(X1 X2 … XK):
, the TCI can be expressed as the difference between the entropies of the individual variables H(Xi) and the entropy of the joint distribution H(X1 X2 … XK):
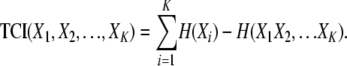 |
The TCI is the amount of information shared among the variables in the set; equivalently, it can be viewed a general measure of dependency. A TCI value that is zero indicates that knowing the value of one variable tells you nothing about the others, i.e., that the variables are independent. The maximal value of TCI occurs when one variable is completely redundant with the others; i.e., knowing one variable provides complete knowledge regarding all the others.
Phenotype-associated information:
The PAI is obtained from the TCI, which represents the overall dependency among the genetic and environmental variables and the phenotype variable by removing the TCI contributions representing the interdependencies among the genetic and environmental variables. The interdependencies among variables can be caused by factors such as LD or by a common source for multiple pollutant exposures. Accordingly, PAI is defined by
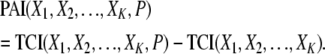 |
In the above equation, the genetic and environmental variables are denoted by the X1, X2, … , XK, and the phenotype variable is denoted by P. In the PAI definition, the TCI(X1, X2, … , XK, P) term represents the overall dependency among the genetic and environmental variables and the phenotype whereas the TCI(X1, X2, … , XK) term represents the interdependencies among the genetic and environmental variables in the absence of the phenotype variable.
Rationale for the PAI in GEI analysis:
The PAI is a measure of the interdependencies that affect the phenotype and is robust to interdependencies among the variables. Information and dependencies among genetic and environmental variables can be distributed in complicated ways; e.g., there may be complete interredundancy among some variables whereas others may be independent. Furthermore, there may be interdependencies of various degrees; e.g., variables without direct associations could have higher-order interdependencies. In the genetic epidemiology context, the presence of factors such as LD indicates that many disease-uninformative genetic variants are not independent of each other. Other biological factors such as admixture can also confound the differences between diseased and nondiseased groups because of differences among various racial groups.
The KWII is the more valuable information metric because it is a parsimonious measure of interaction for the variable combination of interest alone and does not contain contributions from lower-order interactions. However, KWII computations on the entire combinatorial space are computationally intractable because they require the entropies of all subsets. In addition, the KWII cannot be used for hill-climbing algorithms because it takes on both positive and negative values. Thus, it is necessary to concomitantly address the biological complexities and computational efficiency in GEI analysis.
Only individual and joint entropies are needed for TCI calculations, making it computationally far more tractable than the KWII. TCI (and PAI) on the other hand, is always greater than or equal to zero and increases monotonically with increased combination size [i.e., TCI(A, B, C, D) ≥ TCI(A, B,C)], making it potentially suitable for hill-climbing algorithms. Unfortunately because the TCI is a general measure of dependency, it is sensitive to factors that cause correlations and interredundancies among variables such as LD.
The PAI is an effective approach to overcoming these GEI-associated biological and computational issues.
Properties of the PAI:
We developed the PAI to obtain a TCI-based measure that is robust to the confounding effects of biological dependencies such as LD.
PAI, TCI, and KWII are each equal to mutual information for single variable associations with the phenotype. However, for higher-order combinations, the PAI definition removes the TCI for pairwise and multimarker LD among the genetic variables and similar uninformative dependencies among environmental variables from the overall TCI. As a consequence, the PAI does not have the biological drawbacks such as sensitivity to LD and to correlations among environmental variables that limit the usefulness of the TCI.
The PAI also offers the computational efficiency associated with TCI calculations. The PAI is always greater than or equal to zero (see appendix) and increases monotonically with increased combination size (see appendix), making it very suitable as the basis for hill-climbing algorithm design.
The PAI contains useful information regarding the KWII of the genetic and environmental variables and the phenotype. By derivation (see appendix), it can be shown that
 |
This equation demonstrates that the PAI is the cumulative phenotype-associated synergy present in all subset combinations of the variables X1, X2, … , XK and P. It is important to note that each component of the KWII is free of the confounding effects of other combinations.
We use the PAI to identify the interesting regions in the combinatorial space and then compute the KWII for the reduced combinatorial space. This is a “greedy search” strategy that avoids combinatorial explosion because it does not conduct GEI analysis for every possible combination.
The AMBIENCE algorithm:
The AMBIENCE algorithm is computationally much more efficient than the exhaustive search (EXS) approach used in our earlier report (Chanda et al. 2007) to compute KWII for all possible SNP combinations, which requires exponential time. The pseudocode for AMBIENCE is shown in Figure 1.
Figure 1.—
Pseudocode for the AMBIENCE search algorithm.
The AMBIENCE algorithm employs the PAI to search for combinations of genetic variations and environmental variables related to the disease phenotype. Let 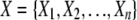 be the set of all genetic/environmental variables and P be the disease phenotype variable. The inputs to the AMBIENCE algorithm are X, P, and algorithm parameters θ and τ, which represent the number of combinations retained in the iterations of the search and the number of iterations, respectively. The parameter τ determines the highest order of variable combination detected.
be the set of all genetic/environmental variables and P be the disease phenotype variable. The inputs to the AMBIENCE algorithm are X, P, and algorithm parameters θ and τ, which represent the number of combinations retained in the iterations of the search and the number of iterations, respectively. The parameter τ determines the highest order of variable combination detected.
We start by calculating 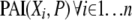 . We retain the top θ combinations with the highest values of PAI. Let this set of variables be denoted by S1. In the next step, we calculate
. We retain the top θ combinations with the highest values of PAI. Let this set of variables be denoted by S1. In the next step, we calculate 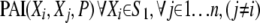 . We again retain the top θ combinations with the highest values of
. We again retain the top θ combinations with the highest values of 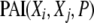 in set S2. The above steps are repeated τ times. Thus, we greedily search for combinations containing up to τ variables that have higher values of PAI. These combinations identify regions in the combinatorial space that have combinations with strongly interacting variables. Finally, for each combination C identified by the above search steps, we calculate the
in set S2. The above steps are repeated τ times. Thus, we greedily search for combinations containing up to τ variables that have higher values of PAI. These combinations identify regions in the combinatorial space that have combinations with strongly interacting variables. Finally, for each combination C identified by the above search steps, we calculate the 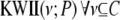 to identify the most parsimonious strongly interacting combinations
to identify the most parsimonious strongly interacting combinations 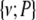 .
.
Additional analyses of time complexity and evaluations of computational speed for AMBIENCE are presented in results.
Simulations for case studies:
Simulated data sets were used to critically assess the effectiveness of the PAI metric to correctly identify the interacting variables. We selected the interaction model for case study 1 from our earlier article (Chanda et al. 2007) because it had necessary levels of complexity and also contained nuanced GEI patterns that could provide a challenging test for evaluating the PAI. The model for case study 2 was constructed to be more complex than case study 1 and was motivated by genetic, environmental, and biomarker variables implicated in congestive heart disease. The simulations assumed complete penetrance.
A population of 50,000 individuals with randomly varying genotypes and environmental exposures consistent with the underlying GEI models was generated for each of the case studies. The case–control study design was assumed. From the population of 50,000 individual genotypes, a sample of 500 cases and 500 controls was randomly selected. The value 1 was used to represent cases and 0 was used for controls. The standard deviations due to sampling were calculated from 100 independent repetitions of this procedure.
Case studies 1A and 1B:
The underlying GEI model for case studies 1A and 1B is summarized in Figure 2A. The simulated data for case studies 1A and 1B consisted of four environmental variables, E1–E4, and six SNP variables, SNP 1–SNP 6. The environmental variables E1 and E2 were assumed associated with the disease phenotype whereas E3 and E4 were assumed to be uninformative. The environmental variables E1 and E3 were assumed to have two states, low exposure (assigned value = L) and high exposure (assigned value = H) that were treated as categorical. The environmental variables E2 and E4 were assumed to have three states, low exposure (assigned value = L), medium exposure (assigned value = M), and high exposure (assigned value = H) that were also treated as categorical. The percentages of subjects in low- and high-exposure groups of E1 and E3 were each 50%; the percentages of subjects in low-, intermediate-, and high-exposure groups of E2 and E4 were 33.33% each, respectively. The disease was modeled to occur for various combinations of exposure to the environmental variables E1 and E2 via interactions with alleles for two SNPs, SNP 1 and SNP 2. To mimic an additive genetic model, the values 1, 2, and 3 were used to represent the homozygous state for the major allele, the heterozygous genotype, and the homozygous state for the minor allele, respectively, for all six SNP variables. The more common and less common (disease) alleles of SNP 1 and SNP 2 were assigned allele frequencies of 0.9 and 0.1, respectively. The other SNP variables, SNP 3–SNP 6, were uninformative and had allele frequencies of 0.5. All SNPs were assumed to be diallelic with the three possible genotypes in Hardy–Weinberg equilibrium. A binary phenotype variable, C, representing case (assigned value = 1) or control (assigned value = 0) was used.
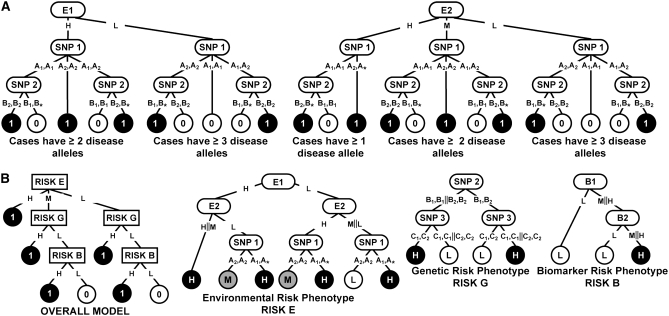
Figure 2.—
(A) The interaction model used to generate the data for case studies 1A and 1B. (B) The interaction model used to generate the data for case study 2. In A, the environmental variables E1 (with states H, L) and E2 (with states H, M, and L) independently interact with two SNP variables, SNP 1 (with alleles A1 and A2) and SNP 2 (with alleles B1 and B2) to determine the disease status (controls are indicated by 0 and cases are indicated by 1). In B, the disease occurs due to exposure to the environmental variables E1 and E2 via interactions with the biomarker variables B1 and B2 and alleles for three SNPs, SNP 1, SNP 2, and SNP 3. The environmental, genetic, and biomarker risks are denoted by E, G, and B, respectively. The asterisk in a genotype represents a “wild card” indicating that either allele is allowable. The uninformative variables are not shown.
In both case studies 1A and 1B, the E1 and E2 variables were assumed to act independently of each other and the case phenotype value was assigned when combinations of the SNP genotypes and either environmental variable resulted in a case.
In case study 1A, absence of LD among the SNP variables was assumed. In contrast, for case study 1B, the SNP variables SNP 3 and SNP 4 were assumed to be in LD (R2 = 0.9) with each other.
Case study 2:
This case study is summarized in Figure 2B and contains a complex combination of environmental variables, SNP variables, and biomarker variables that determine the disease phenotype.
The model for case study 2 consisted of four environmental variables, E1–E4, four SNP variables, SNP 1–SNP 4, and two biomarker variables B1 and B2. The overall risk of developing the disease phenotype was determined by contributions from three components termed (i) environmental risk component (risk E), (ii) the genetic risk component (risk G), and (iii) the biomarker risk component (risk B). The risk E component was assumed to have three states (H, high; M, medium; and L, low) whereas risk G and risk B were assumed to have two states (H and L). The SNP 1 variable interacted with the E1 and E2 environmental variables to determine the environmental risk component (risk E) of disease risk in Figure 2B. The gene–gene interactions between SNP 2 and SNP 3 variables determined the genetic risk component (risk G) of disease risk whereas interactions between the two biomarker variables, B1 and B2, determined risk B.
The environmental variables, E1 and E2, were disease associated whereas E3 and E4 were assumed to be uninformative. The environmental variables E1 and E3 were each assumed to have two states, low exposure (assigned value = L) and high exposure (assigned value = H); the remaining environmental variables E2 and E4 each had an additional state of medium exposure (assigned value = M). The percentages of subjects in low- and high-exposure groups of E1 and E3 were each 50%; the percentages of subjects in low-, medium-, and high-exposure groups of E2 and E4 were each 33.33%, respectively.
Both biomarker variables, B1 and B2 were assumed associated with the disease phenotype and were each assumed to have three states, low exposure (assigned value = L), medium exposure (assigned value = M), and high exposure (assigned value = H). The percentages of subjects in the low-, medium-, and high-exposure groups of B1 and B2 were 33.33% each, respectively.
All four SNP variables were assumed to be diallelic with the three possible genotypes in Hardy–Weinberg equilibrium. The values 1, 2, and 3 were used to represent the homozygous state for the major allele, the heterozygous genotype, and the homozygous state for the minor allele, respectively, for all four SNP variables. The more common and less common (“disease”) alleles of SNP 1, SNP 2, and SNP 3 were assigned allele frequencies of 0.9 and 0.1, respectively. The remaining SNP variable SNP 4 was uninformative and had allele frequencies of 0.5.
A binary phenotype variable, C, representing case (assigned value = 1) or control (assigned value = 0) was used. The disease was modeled to occur for various combinations of exposure to the environmental variables E1 and E2 via interactions with the biomarker variables B1 and B2 and alleles for three SNPs, SNP 1, SNP 2, and SNP 3. Variables E1, E2, and SNP 1 interact to affect the environmental risk E of the disease. Variables SNP 2 and SNP 3 interact to affect the genetic risk G of the disease. Variables B1 and B2 interact to affect the biomarker risk B of the disease.
Examples of prototypical environmental variables in congestive heart disease are inflammation and smoking. Biomarkers that are predictive of congestive heart disease risk include factors such as C-reactive peptide and blood cholesterol levels in serum.
Visualization of GEI:
Results are summarized graphically as KWII, TCI, and PAI “spectra” as previously described (Chanda et al. 2007). These spectra are bar plots with KWII, TCI, or PAI on the x-axis and the corresponding variable combinations on the y-axis. The variable combinations on the y-axis were grouped according to the number of variables involved in the combinations; i.e., the one-variable-containing combinations, two-variable-containing combinations, and three-variable-containing combinations were each placed in separate groups. Within each group, the combinations were arranged in ascending order so that specific variable combinations of interest could be easily found.
Analysis of public domain data sets:
GEI analysis of Genetic Analysis Workshop 15 data:
The data corresponding to problem 3 of Genetic Analysis Workshop 15 (GAW15) were obtained from the GAW site (http://www.gaworkshop.org/gaw15data.htm) and used with permission.
These data consist of 100 replicates of simulated data that are modeled after the rheumatoid arthritis (RA) data. Michael Miller and his colleagues generated the data (Miller et al. 2007) and the following data description was obtained from the web site http://genetsim.org/gaw15/answers/. Each replicate includes 1500 nuclear families each with two parents and an affected sib pair and 2000 unrelated controls. The data contain three types of autosomal markers: (i) 730 microsatellite markers with an average spacing of 5 cM, (ii) 9187 SNPs distributed on the genome to mimic a 10K SNP chip set, and (iii) 17,820 SNPs on chromosome 6. The data include map information, with lists of markers and their locations, and simulated family, marker, and phenotype data. The HLA DR genotype was also available and the phenotype/covariate data included rheumatoid arthritis affection status, age at ascertainment, lifetime smoking, anticyclic citrullinated peptide antibody (anti-CCP), immunoglobulin M (IgM), severity, age at onset, and age at death.
This simulated data set mimics the epidemiology and familial pattern of RA, a complex genetic disease in which it is hypothesized that several loci contribute to disease susceptibility. As summarized in Table 1, the data set models interactions of nine loci: C, DR, and D on chromosome 6, A on chromosome 16, B on chromosome 8, E on chromosome 18, F on chromosome 11, and G and H on chromosome 9. In addition, sex, age, smoking status, anti-CCP measure, IgM measure, severity, DR allele from father, DR allele from mother, age at onset, and age at death are included as covariates. The biomarkers, anti-CCP measures, and IgM measures are defined for the cases only. All SNP loci are diallelic and alleles are coded as 1 and 2.
TABLE 1.
Effects of major trait loci and covariates in the GAW15 data set
| Locus | Chr. | SNP no. | Phenotype | Effects |
|---|---|---|---|---|
| DR | 6 | 152–155 | RA | Affects risk of RA |
| A | 16 | 30–31 | RA | Controls effect of DR on RA risk |
| B | 8 | 442 | RA | Controls effect of smoking on RA risk |
| C | 6 | 152–155 | RA | Increases RA risk only in women |
| D | 6 | 161–162 | RA | Rare allele increases RA risk fivefold |
| E | 18 | 268–269 | RA, anti-CCP | Controls effects of DR on anti-CCP and increases RA risk |
| F | 11 | 387–389 | IgM | QTL for IgM |
| G | 9 | 185–186 | Severity | 25% QTL for severity |
| H | 9 | 192–193 | Severity | 25% QTL for severity |
| Age | — | RA | Affects RA risk through smoking and sex ratio | |
| Sex | — | RA | Affects RA risk with locus C | |
| Smoking | — | RA, IgM | Affects RA risk with locus B and through IgM |
For our analysis, which aimed to evaluate the effectiveness of AMBIENCE, we used the set of 9187 SNPs along with sex, age, and smoking status as covariates. We used all 100 replicates to obtain KWII and PAI values and the corresponding 95% confidence intervals for each combination of variables.
We refer to this data set as the “10K GAW15 data set.” The age, anti-CCP, and IgM variables, which are continuous measures, were discretized by simple binning into five intervals of equal width. Although haplotype-phase information was provided, we chose to not include it and treated the data as unphased genotype data. We conducted separate analyses with RA affection status, anti-CCP, and IgM as phenotypes of interest. The IgM variable was included as a covariate in the analysis of anti-CCP as phenotype and vice versa. All the analyses were performed with AMBIENCE input parameter values of θ = 50 and τ = 3.
GGI analysis of interactions in chromosome 5:
We assessed the effectiveness of the KWII and TCI spectra for identifying key interactions in a genotype data set from Daly et al. (2001) containing 103 SNPs spanning a 616-kb region of chromosome 5q31 that has been linked to Crohn's disease (Rioux et al. 2001; Onnie et al. 2006). The data set contains genotypes for 129 parent–child trios composed of 144 cases and 243 controls (Daly et al. 2001). For our analysis, SNPs whose genotypes were missing in ≥20% of subjects were excluded.
To obtain corresponding P-values for the KWII and PAI metrics, we permuted the case–control labels 5000 times. The family information in the data set was not considered in the permutation procedure.
Comparison to other competing approaches:
We compared our approach to the MDR (Ritchie et al. 2001, 2003; Hahn et al. 2003; Bush et al. 2006), the GMDR (Lou et al. 2007), and the PDT. The data were coded using an additive genetic model for all methods.
The AMBIENCE approach was compared to the MDR, GMDR, and PDT methods for GGI analysis on the Daly et al. (2001) data set.
The ability of AMBIENCE to detect GEI in the presence of covariates was compared to that of the MDR, GMDR, and PDT methods on the GAW15 data set. For this head-to-head comparison of the performance of MDR, GMDR, and PDT to that of AMBIENCE on GAW15 data, we selected 100 SNPs from among the 9187 SNPs to create a smaller data set that could be analyzed by all three competing methods. We refer to this data set as the “100-SNP GAW15 data set.” Specifically, this data set included the covariates smoking, age, and sex and contained key informative loci and sufficient uninformative loci as follows: (i) SNPs 131–171 from the region of chromosome 6 containing loci C, DR, and D; (ii) SNPs 30–32 from the region of chromosome 16 containing locus A; (iii) SNPs 438–442 from the region of chromosome 8 containing locus B; (iv) SNPs 266–272 from the region of chromosome 18 containing locus E; (v) SNPs 387–391 from the region of chromosome 11 containing locus F; (vi) SNPs 181–196 from the region of chromosome 9 containing loci G and H; and (vii) the remaining 22 SNPs were selected randomly from the rest of the 9187 SNPs. The RA affection status was used as the phenotype.
MDR method:
The MDR implementation was downloaded from http://sourceforge.net/projects/mdr/. For MDR analysis of the Daly et al. (2001) data set, samples missing genotypes at ≥10% of the SNPs were excluded followed by the exclusion of SNPs whose genotypes were missing in ≥10% of subjects.
The binary covariates, sex and smoking, and age (discretized as for the AMBIENCE analysis) in the 100-SNP GAW15 data set were input as additional markers for MDR analysis.
GMDR:
The GMDR implementation was downloaded from http://www.healthsystem.virginia.edu/internet/addiction-genomics/software/gmdr.cfm#.
Pedigree disequilibrium test:
The PDT (Martin et al. 2000) implementation in the software package UNPHASED v3.10 (Dudbridge 2003) was used. The program PDTPHASE v3.07 (see http://www.mrc-bsu.cam.ac.uk/BSUsite/Publications/Preprints/Unphased_manual.pdf) was used to perform tests of association of single SNPs and two-SNP haplotypes with disease status (Dudbridge 2003). The Daly et al. and the GAW15 data sets both included family information that was provided to the software program (Daly et al. 2001; Miller et al. 2007). For the GAW15 data set (Miller et al. 2007), the covariates of age, sex, and smoking, which are available for both cases and controls, were included in the analysis.
Computational speed estimate:
We tested the computational efficiency of the AMBIENCE algorithm using the GAW 15 data set problem 3 (http://www.gaworkshop.org/gaw15data.htm).
We used the dense map of chromosome 6 (17,820 diallelic SNPs) on chromosome 6 data because it has more markers that enabled assessment of the scalability–computational speed relationships for the AMBIENCE method. Three additional covariates (age, sex, and smoking) with the RA affection status as the phenotype were used. Together, this subset of the GAW 15 data set has a total of 17,823 genetic and environmental variables. From the simulation framework (i.e., the GAW15 “answers”) provided to us by Michael Miller (University of Minnesota) (Miller et al. 2007), it was known that the DR, C, and D loci in the chromosome 6 data were associated with the phenotype status. We therefore established data sets containing a total of 1000, 10,000, 17,823, or 100,000 variables in the following way: (i) all four data sets had the three informative DR, C, and D loci and three covariates (age, sex, and smoking) from the GAW15 data subset; (ii) the remaining SNPs were randomly selected from among the remaining 17,817 SNP variables; and (iii) the data set with 100,000 variables had additional randomly generated uninformative diallelic SNP variables added to make up the difference. We refer to this as the “computational speed GAW15 data set.”
The AMBIENCE algorithm was used to search for combinations containing up to three variables with θ = 50. The computations were conducted on a Hewlett-Packard Proliant server with four dual-core 2.8-GHz processors with 16 GB of memory and running the Linux operating system.
RESULTS
Performance of the PAI-search algorithm on simulated data:
In the following numerical experiments, we simulated data with known patterns of GEI and examined their relationships with the KWII, TCI, and PAI spectra.
Case studies 1A and 1B:
In case studies 1A and 1B, the GEI scheme (Figure 2A) contained multiple environmental variables and SNP variables. The model represents a challenging scenario with environmental heterogeneity; i.e., the two different environmental variables increase disease risk independently via the same genetic variables.
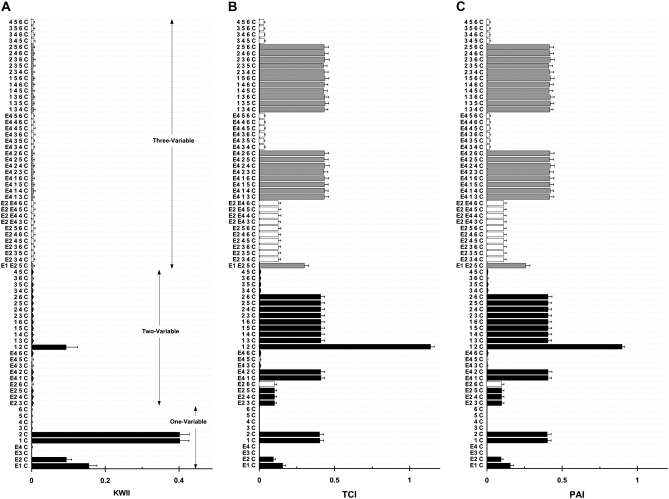
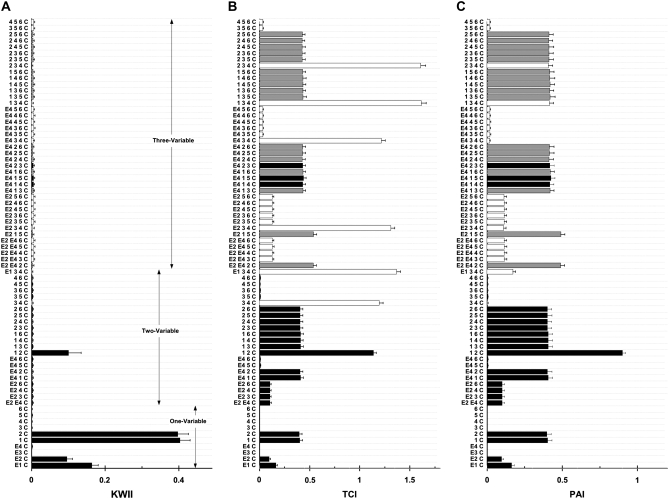
In Figure 3, the KWII (Figure 3A), TCI (Figure 3B), and PAI (Figure 3C) spectra, obtained using the PAI-based AMBIENCE search algorithm are compared to the corresponding results from an exhaustive search (EXS) of all combinations containing four variables or less for case study 1A. Figure 4, A–C, summarizes the spectra for case study 1B. The goal is to assess the effectiveness of the AMBIENCE search strategy by verifying that the critical interactions are identified.
Figure 3.—
A, B, and C are the KWII, TCI, and PAI spectra for case study 1A, respectively. All the one-variable-containing combinations and the 20 two-variable and 20 three-variable combinations with the highest KWII values are shown. The environmental variables are shown as E1, E2, E3, E4, the SNP variables are numbered 1–6, and phenotype is indicated as C. The combinations are indicated on the y-axis. The error bars represent the standard deviations. The solid bars identify the peaks obtained by both the PAI-based AMBIENCE search algorithm and EXS methods, the open bars indicate the peaks obtained by the EXS alone, and the shaded bars indicate the peaks obtained by AMBIENCE alone.
Figure 4.—
A, B, and C are the KWII, TCI, and PAI spectra of case study 1B, respectively. The legend is the same as that for Figure 3.
For each method of search, the 20 combinations with the highest KWII values are presented each for one-variable, two-variable, and three-variable combinations. The spectra for four-variable combinations are uninformative and not shown for clarity. The solid bars in Figure 4, A–C, identify the peaks obtained by both the PAI-based AMBIENCE search algorithm and the EXS methods, the open bars indicate the peaks obtained by EXS alone, and the shaded bars indicate the peaks obtained by AMBIENCE alone.
The KWII spectra in Figures 3A and 4A demonstrate that our PAI-based AMBIENCE search algorithm detects all peaks with significant GEI without the enumeration of all possible combinations that is required in an exhaustive search approach. The KWII values of combinations containing only informative variables are unaffected by the LD between uninformative variables.
The patterns in the TCI and PAI spectra of case study 1A (Figure 3, B and C) are identical. The TCI spectrum of case study 1B (Figure 4B) shows prominent peak changes relative to Figure 3B for combinations {2, 3, 4, C}, {1, 3, 4, C}, {E4, 3, 4, C}, {E2, 3, 4, C}, {E1, 3, 4, C} and {3, 4, C} that are caused by the LD between the uninformative variables SNP 3 and SNP 4. These peak changes are absent in the PAI spectrum of case study 1B (Figure 4C), demonstrating that PAI is unaffected in the presence of LD between uninformative SNP variables. Thus the PAI is more effective than TCI in detecting GEI when LD between uninformative SNP variables is present.
The KWII spectrum (Figure 4A) shows that the AMBIENCE search algorithm correctly identifies the one-variable-containing peaks that demonstrate the critical roles of E1, E2, SNP 1, and SNP 2 variables in the underlying model. A strong peak corresponding to the {1, 2, C} interaction is also identified. These peaks also feature in the KWII spectrum of EXS (as indicated by the shaded bars). None of the significant peaks involving an interaction between the known interacting variables are omitted in the spectrum of the PAI-based AMBIENCE search algorithm. All the peaks present in the KWII spectra of EXS only (open bars in Figures 3A and 4A) have very low magnitudes compared to the stronger peaks with known interactions. These results demonstrate that our search algorithm correctly identifies all known GEIs in both the case studies. Notably, the {E1, E2, C} combination was not present among the top 20 two-variable combinations with the highest KWII values in both the AMBIENCE search and EXS methods denoting the absence of any interaction between E1 and E2.
Case study 2:
In case study 2, the GEI scheme (Figure 2B) consists of multiple environmental, biomarker, and SNP variables whose interactions affect intermediate risk factors that contribute to the disease phenotype status. The schematic for the case study was motivated by the combinations of risk factors involved in congestive heart disease.
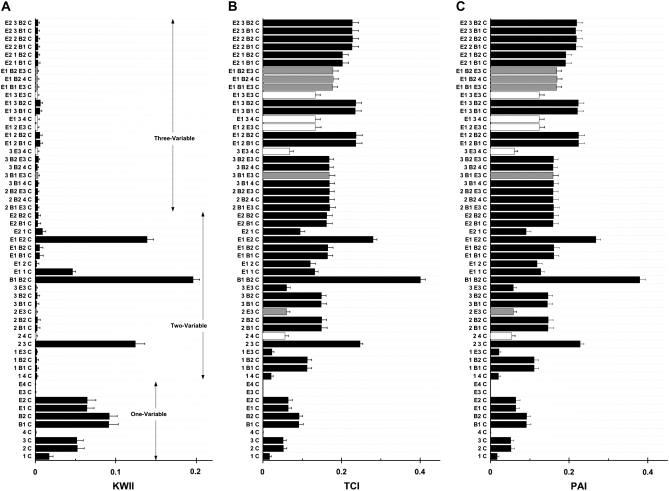
Figure 5, A, B, and C, summarizes the KWII, TCI, and PAI spectra, respectively, obtained using both the AMBIENCE algorithm and the EXS algorithm. For the KWII spectra (Figure 5A), combinations with the top 20 KWII values are presented each for one-variable, two-variable, and three-variable combinations.
Figure 5.—
A, B, and C are the KWII, TCI, and PAI spectra for case study 2, respectively. All the one-variable-containing combinations and the 20 two-variable and 20 three-variable combinations with the highest KWII values are shown. The environmental variables are shown as E1, E2, E3, E4, the SNP variables are numbered 1–6, the biomarker variables are B1 and B2, and the phenotype is indicated as C. The combinations are indicated on the y-axis. The error bars represent the standard deviations.
The one-variable-containing peaks in the KWII spectrum correctly detect the critical roles of E1, E2, B1, B2, SNP 1, SNP 2, and SNP 3 variables in the underlying model. Strong two-variable-containing interactions {E1, E2, C}, {E1, 1, C}, {B1, B2, C}, and {2, 3, C} were also identified. Again, all the peaks with significant KWII values that are detected by EXS are also identified by AMBIENCE. The KWII peaks that are detected by EXS alone (open bars in Figure 5A) are skipped during the search process by AMBIENCE because these have very low magnitudes compared to the other stronger peaks present. The TCI and PAI spectra show that AMBIENCE identifies combinations with higher values of TCI (shaded bars in Figure 5B) and PAI (shaded bars in Figure 5C) than EXS (open bars in Figure 5, B and C), respectively. These results demonstrate that AMBIENCE correctly and efficiently identified all significant interactions in this relatively complex model.
We have analyzed a diverse range of additional case studies. In each case, AMBIENCE identified the key interacting variables effectively (data not shown).
Assessing robustness of PAI to LD:
We critically assessed the variations in PAI values for different combinations in the presence of pairwise LD to evaluate the effectiveness of PAI for disease-associated GEI analysis.
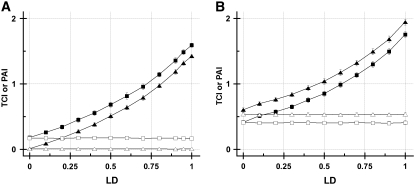
We first examined the effect of LD between two SNPs that were not associated with the disease phenotype variable on TCI and PAI. We varied the LD between SNP 3 and SNP 4 from 0 to 1 for case study 1B in this experiment. The representative combinations {3, 4, C} and {E1, 3, 4, C} are presented because they include the two SNP variables in LD with each other (SNP 3 and SNP 4), the risk-increasing environmental variable E1, and the phenotype variable. The results (Figure 6A) demonstrate that as expected, the increasing LD between SNP 3 and SNP 4 contributes to the TCI of the combinations containing these variables. In contrast to the TCI, which increases with increasing LD, the PAI remains unchanged: 0.0055 ± SD 0.0027 in the absence of LD and 0.0043 ± 0.0022 for LD = 0.9. Importantly for the {3, 4, C} combination the PAI remains at a value close to zero, indicating correct detection of no association between the SNPS and disease status despite the high LD. The TCI also correctly assessed no association between SNPs and phenotype in the absence of LD, 0.0086 ± 0.0032; however, when LD between SNPs 3 and 4 was increased to 0.9, the TCI increased to a value of 1.19 ± 0.037. In the second combination assessed, we include a risk-increasing environmental variable, E1, to {3, 4, C}. Because the {E1, 3, 4, C} combination contains the disease-associated E1 environmental variable, we correctly anticipated that both the PAI and the TCI values would be larger for {E1, 3, 4, C} than for {3, 4, C}. In the absence of LD, PAI and TCI were 0.170 ± 0.021 and TCI = 0.178 ± 0.021, respectively. When the LD between SNP 3 and SNP 4 was increased to 0.9, the TCI value combination increased >10-fold whereas the PAI was constant at 0.170 ± 0.019. The PAI retained the disease association due to the presence of E1 while remaining unaffected by the LD between SNP 3 and SNP 4. Thus, in the presence of LD, PAI is a more effective metric than TCI for detecting disease phenotype-associated GEI.
Figure 6.—
(A) TCI and PAI for various levels of LD between SNP 3 and SNP 4 (both are uninformative SNPs) for case study 1B. (B) The effects of LD between the informative SNP 2 and the uninformative SNP 3 when case study 1A was modified by introducing LD between SNP 2 and SNP 3. In A, the combinations {3, 4, C} and {E1, 3, 4, C} are shown as triangles and squares, respectively. In B, the combinations {2, 3, C} and {E1, 2, 3, C} are shown are shown as triangles and squares, respectively. In A and B, the solid symbols are TCI whereas the open symbols are PAI.
In the next set of experiments, we examined the effect of LD between two SNPs, one of which was associated with the disease phenotype variable. We modified case study 1A by introducing LD between SNP 3, which is not associated with the disease, and SNP 2, which is involved in the disease susceptibility. For this case (Figure 6B), the representative combinations {2, 3, C} and {E1, 2, 3,C} are presented. In the absence of LD, the TCI values of the {2, 3, C} and {E1, 2, 3, C} combinations were 0.411 ± 0.026 and 0.602 ± 0.032, respectively, and the PAI values were 0.408 ± 0.026 and 0.534 ± 0.026, respectively. The higher TCI and PAI values in Figure 6B compared with 6A reflect the presence of informative variables in each of the combinations. In the presence of LD = 0.9, the TCI values of the {2, 3, C} and {E1, 2, 3, C} combinations increased to 1.49 ± 0.046 and 1.68 ± 0.048, respectively. The PAI values of the {2, 3, C} and {E1, 2, 3, C} combinations remained constant at 0.400 ± 0.029 and 0.530 ± 0.024, respectively at LD = 0.9. Again, the results clearly indicate that the PAI effectively captured the genetic and environment risk-increasing information in the data while simultaneously filtering the spurious effects of LD in the {2, 3, C} and {E1, 2, 3, C} combinations.
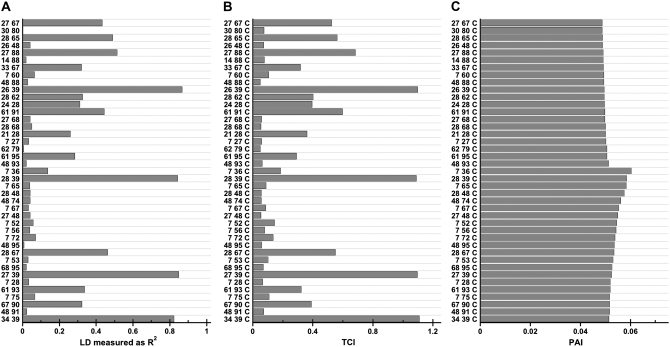
In Figure 7, we investigate the relationship between TCI and a measure of LD, R2, as well as the sensitivity of the PAI at varying levels of LD in real data for the Daly data set (Daly et al. 2001). We computed PAI and TCI values for all two-SNP-containing combinations with the case–control status phenotype; the corresponding R2 values for these same SNPs were also computed to measure LD. The R2, TCI, and PAI spectra for 40 representative combinations varying in R2 values are shown in Figure 7, A, B, and C, respectively. Comparisons of Figure 7A to 7B demonstrate that the TCI spectrum mimics the dependencies present in the patterns of LD as measured by R2 values. Figure 7C shows that in the presence of extensive pairwise LD, the TCI variations that closely resemble the LD patterns are not present in the PAI spectrum; consequently, PAI values are an order of magnitude (or more) smaller than the corresponding TCI values and the PAI spectrum is relatively independent of the LD patterns.
Figure 7.—
The R2 (A), TCI (B), and PAI (C) spectra for 40 representative two-SNP-containing combinations with varying levels of LD as measured by the R2 for the Daly data set (Daly et al. 2001). The SNP combinations are indicated on the y-axis.
These results indicate that the PAI is effective at detecting disease phenotype-associated GEI and is also robust to the confounding effects of complex patterns of dependencies among the genetic and environmental variables.
Performance of the PAI-based AMBIENCE algorithm on disease-relevant data sets:
Performance on the Daly data:
To assess the performance of AMBIENCE, we compared the results from the AMBIENCE analysis of the Daly data set (Daly et al. 2001) to those obtained by Rioux et al. (2001). Nine of the 11 SNPs on chromosome region 5q31 associated by Rioux et al. (2001) with the risk of Crohn's were present in the data set we analyzed (see Table 2); SNPs IGR2078a_1 and IGR2277a_1 were missing (Chanda et al. 2007).
TABLE 2.
A comparison of the various competing methods to AMBIENCE using the Crohn's disease-associated one-SNP combinations identified by Rioux et al. (2001) as a reference
| SNPs from Rioux et al. (2001)a | AMBIENCE | KWII P-valueb | MDR | GMDRc | PDT |
|---|---|---|---|---|---|
| IGR2055a_1 | ✓ | 0.0038 | ✓ | ||
| IGR2060a_1 | ✓ | 0.0072 | ✓ | ||
| IGR2063b_1 | ✓ | 0.0026 | ✓ | ✓ | ✓ |
| IGR2096a_1 | ✓ | 0.018 | ✓ | ||
| IGR2198a_1 | ✓ | 0.0044 | ✓ | ||
| IGR2230a_1 | 0.065 | ✓ | |||
| IGR3081a_1 | ✓ | 0.0038 | ✓ | ||
| IGR3096a_1 | ✓ | 0.029 | ✓ | ||
| IGR3236a_1 | ✓ | 0.0096 | ✓ |
The SNPs that were correctly identified in a one-SNP combination by each method are shown with a check mark.
Two SNPs IGR2078a_1 and IGR2277a_1 were missing in our data set and are not included.
The P-values of KWII values were obtained by permuting case–control labels and assessing the proportion of KWII values of the permutations that exceeded the observed KWII.
Results for GMDR are identical to those of MDR because there are no covariates.
In the AMBIENCE analysis, 8 of the 9 reported SNPs (see Table 2) were present among the 20 combinations with the highest KWII values (spectra not shown). The permutation-based P-values of the KWII for these SNPs (Table 2) ranged from 0.0028 to 0.029. We were unable to identify one SNP, IGR2230a_1 using AMBIENCE and it had a permutation-based P-value of 0.065. Of the 103 SNPs present in the Daly data set, only 17 single SNP combinations had KWII P-values ≤0.05 in permutation testing. AMBIENCE detected all 17 SNPs among the top 20 single SNP combinations with the highest KWII values.
10K GAW15 data set:
The underlying GGIs and GEIs in the simulations for this data set model the interaction of nine loci: C, DR, and D on chromosome 6, A on chromosome 16, B on chromosome 8, E on chromosome 18, F on chromosome 11, and G and H on chromosome 9 (see Table 1 for a summary) (Miller et al. 2007). However, the anti-CCP and IgM measures are defined for the cases only. Although phase information was provided, we treated the data as genotype data for the AMBIENCE analysis.
The GAW15 data set contained 100 replicates from repetitions of the simulation procedure (Miller et al. 2007) and the availability of these replicates enabled us to compute the 95% confidence interval for the KWII of each combination.
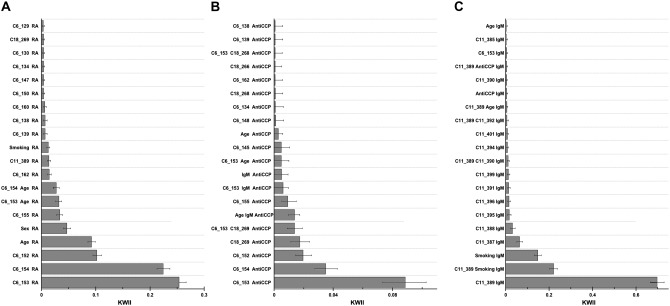
Figure 8 presents the KWII spectrum with RA affection status as the phenotype. In interpreting the KWII spectrum, a nonzero KWII value is significant and values greater than zero represent synergistic interactions. For example, in Figure 8A, we note that the KWII peaks for combinations {C6_153, RA}, {C6_154, RA}, {C6_152, RA}, {age, RA}, {sex, RA}, {C6_155, RA}, {C6_153, age, RA}, {C6_154, age, RA}, {C6_162, RA}, {C11_389, RA}, and {smoking, RA} are the combinations with the highest KWII values and also have 95% confidence intervals that do not include zero. These are therefore informative combinations in the KWII spectra. These combinations consist entirely of DR and locus C (both at SNPs C6_152-C6_155), locus D (C6_162), and locus F (C11_389) and the environmental variables age, sex, and smoking that had associations with the RA affection status in the simulated data set. Miller et al. (2007) built in pronounced effects of DR on RA affection status and this was confirmed by the highest values of KWII in Figure 8A that correspond to the DR locus. An interesting finding was the detection of the combination {C6_162, RA} corresponding to the locus D association with RA despite very low minor allele frequency (only 0.0083, making minor allele homozygotes very rare). Locus D has a direct effect on RA risk and each allele increases the hazard by fivefold (Miller et al. 2007).
Figure 8.—
The KWII spectra for one-variable- and two-variable-containing combinations for the “10K GAW15 data set” with rheumatoid arthritis (RA) affection status (A), anti-CCP antibody status (B), and IgM status (C) as the phenotype. The variable combinations are indicated on the y-axis; the chromosome number and the SNP identifiers are provided for SNPs. The bars represent mean values and the upper and lower error bars are the 95th and 5th percentiles of KWII values, respectively.
Figure 8B presents the KWII spectrum with anti-CCP measure as the phenotype. The peaks with the highest KWII values (Figure 8B) enabled the identification of the following loci and covariates associated with the disease: loci C and DR (chromosome 6), locus E (chromosome 18), age, and IgM. The strongest contributions to the anti-CCP in simulations were from loci E and DR; locus E affects anti-CCP by controlling which DR genotypes place a subject in the anti-CCP group with high mean values (Miller et al. 2007). Figure 8B demonstrates that the three highest KWII values correspond to the interaction between the DR locus (SNPs C6_152-C6_155) and the anti-CCP phenotype; the next two peaks, {C18_269, anti-CCP} and {C6_153, C18_269, anti-CCP}, correspond to the interactions of locus E alone and the locus E, DR combination with the anti-CCP phenotype.
Figure 8C presents the KWII spectrum with IgM as the phenotype. The peaks with the highest KWII values enabled the identification of the following loci and covariates associated with the IgM phenotype: loci C and DR (chromosome 6), locus E (chromosome 18), age, and smoking. When interpreting the KWII values of the {C11_389, IgM}, {C11_389, smoking, IgM}, and {smoking, IgM} combinations corresponding to the three largest peaks in Figure 8C, it is important to note that the KWII for each of these combinations does not contain redundant information; i.e., each of the combinations is significant on its own merit. Thus, the significant peaks for {C11_389, smoking, IgM} and {smoking, IgM} indicate that smoking alone is IgM associated but also contributes to the IgM phenotype synergistically in association C 11_389. Furthermore, the changes in the peak height should not be interpreted to imply any protective role for smoking in the disease association.
Thus of the nine loci and three key covariates reported to be associated with the disease, we were able to identify five loci and all three covariates. We were unable to identify loci A, B, G, and H. Nonetheless, the performance of the KWII spectrum derived from AMBIENCE can be considered promising particularly given that AMBIENCE in its current form does not utilize either the haplotype–phase information or the parent–child transmission information contained in the pedigree structures.
Comparison to other competing approaches:
We compared our AMBIENCE approach to the MDR technique (Ritchie et al. 2001, 2003; Hahn et al. 2003; Bush et al. 2006). All three methods were compared head-to-head on the SNP data set from Daly et al. (2001) and the 100-SNP GAW15 data set.
Daly data set:
The results from the head-to-head comparisons of AMBIENCE to MDR, GMDR, and PDT on the Daly data set are summarized in Table 2.
The MDR method identifies {IGR2063b_1}, {IGR2063b_1, IGRX100a_1}, {IGR2063b_1, IGR2198a_1 IGR3066a_1}, and {IGR2063b_1, IGR2198a_1 IGR3066a_1, GENS0202ex3_2} as significant combinations associated with the Crohn's disease phenotype. The MDR approach combination sets contained only two of the eight SNPs, IGR2063b_1 and IGR2198a_1, identified by Rioux et al. (2001) as being significantly associated with the Crohn's disease phenotype. As expected, because the Daly et al. (2001) data set lacked covariates, the GMDR results were identical to the corresponding MDR results. The PDT analysis, which was provided with the phase and family/transmission information in the Daly data set, identified all nine SNPs reported by Rioux et al. (2001).
100-SNP GAW15 data set:
The results from the head-to-head comparisons of AMBIENCE to MDR, GMDR, and PDT for the 100-SNP GAW15 data set are summarized in Table 3. The variables and the interactions identified by AMBIENCE have been previously discussed in the section Performance of the PAI-based AMBIENCE algorithm on disease-relevant data sets and are also summarized in Table 3.
TABLE 3.
A comparison of the various competing methods to AMBIENCE using the interactions used by Miller et al. (2007) in the GAW15 data set as a reference
| Combination | AMBIENCE | MDR | GMDR | PDT |
|---|---|---|---|---|
| DR | {DR, RA}, | {DR, RA} | {DR, age, RA}, | {DR, age, RA}, |
| {DR, age, RA} | {DR, age, RA} | {DR, sex, RA}, | {DR, sex, RA}, | |
| {DR, age, sex, RA} | {DR, smoking, RA} | {DR, smoking, RA} | ||
| A, DR | Not found | Not found | Not found | Not found |
| B, smoking | Not found | Not found | Not found | Not found |
| C, sex | {C, RA}, | {C, RA} | {C, sex, RA} | {C, RA}, |
| {Sex, RA} | {C, age, sex, RA} | {C, sex, RA}, | ||
| {C, smoking, RA} | ||||
| D | {D, RA} | Not found | {C, D, age, RA}, | {C, D, age, RA}, |
| {DR, D, age, RA} | {DR, D, age, RA} | |||
| E | {E, RA} | Not found | Not found | {E, RA, smoking} |
| Age, sex, smoking | {Age, RA}, | {DR, age, RA} | a | b |
| {Sex, RA}, | {C, age, RA} | |||
| {Smoking, RA}, | {DR, age, sex, RA} | |||
| {C, age, RA}, | {C, age, sex, RA} | |||
| {DR, age, RA} |
GMDR requires a priori calculation of covariate effects, which are then incorporated into the analysis. Covariates cannot be analyzed alone. For ease of interpretation, we have used the same notation for results from all the methods.
PDT analyzes covariates simultaneously with genetic data; however, UNPHASED v3.10 is not designed to analyze covariates without genetic data.
The MDR analysis detected {C6_153}, {C6_154, age}, and {C6_153, age, sex} as associated with RA. The SNPs C6_153 and C6_154 denote the chromosome loci C and DR, respectively. The MDR analysis did not detect locus D and E and smoking.
We analyzed the 100-SNP GAW15 data set using GMDR with sex, age, and smoking as the covariates and RA as the trait. The GMDR method identified the SNP combinations {C6_153}, {C6_153, C6_162}, {C6_153, C6_154, C11_389}, where SNPs C6_153, C6_154 denote the chromosome 6 loci C and DR, respectively; C6_162 denotes locus D on chromosome 6; and C11_389 denotes locus F on chromosome 11.
We analyzed the 100-SNP GAW15 data set using the PDT as implemented in UNPHASED v3.10. Two derived data sets were used for analysis, one including only nuclear families (6000 individuals) and one including all controls and one affected sibling selected at random from each family. Using both data sets we performed both single SNP analyses and analyses of all possible 2-SNP combinations with sex, age, and/or smoking status as effect modifiers of the trait RA. Both data sets identified the same loci as significant. After correction for multiple testing (Benjamini and Hochberg 1995) the PDT method identified loci DR, D, and E as associated with the RA phenotype and found locus C and sex as RA associated, specifically indicating an elevated risk of RA in women. As with the other methods, the PDT did not find locus A or B. Almost all of the false-positive associations were in regions contiguous with the true associations.
Time complexity and computational speed:
The AMBIENCE search algorithm is computationally much more efficient than exhaustive search, which requires computing all possible combinations and requires exponential time.
Here, we borrow the notation from complexity theory (Corman et al. 2001) to assess the computational complexity of the AMBIENCE algorithm. Let m be the sample size of the data and n be the number of variables (excluding the phenotype variable). Lines 2–5 take O(n × m2) computations because of PAI computation that consumes O(m2) computations and lines 6 and 16 take O(θ × n) computations each. Lines 7–15 take O(τ × n × θ × m2) computations since PAI computations are repeated for τ (for loop in line 7) × n (for loop in line 9) × θ (for loop in line 10) computations. Finally, lines 17–22 take O(τ × θ × 2τ × m2) time since KWII needs to be computed for all possible subsets for a maximum combination size of τ for each of θ combinations that were obtained at each step of τ iterations. However, in genetic applications, the range of τ-values of interest is small because of sample size constraints, which limits the computational complexity from becoming exponentially large.
The AMBIENCE algorithm was used to search for combinations containing up to three variables with θ = 50 using the computational speed GAW15 data sets as the test bed. The computations were conducted on a Hewlett-Packard Proliant server with four dual-core 2.8-GHz processors with 16 GB of memory and running the Linux operating system.
Table 4 summarizes the total time requirements and the time requirements for one-variable-, two-variable-, and three-variable-containing combinations. These results indicate that increasing the size of the combinations has only a modest effect on the computation time of AMBIENCE.
TABLE 4.
Computational speed for the AMBIENCE algorithm
| Computation time (hr)
|
||||
|---|---|---|---|---|
| No. of variables in data set | One-variable combinations | Two-variable combinations | Three-variable combinations | Total |
| 103 | 0.004 | 0.25 | 0.28 | 0.53 |
| 104 | 0.02 | 1.20 | 1.39 | 2.61 |
| 17,823 | 0.03 | 2.09 | 2.54 | 4.66 |
| 105 | 0.17 | 12.2 | 14.8 | 27.2 |
DISCUSSION
In our information theoretical framework, which is novel for GEI analysis, combinations with positive values of KWII are operationally defined as interactions. In this report, we developed and evaluated the PAI, a TCI-based information theoretic metric, to enable computationally efficient searching of the GEI combinatorial space. The PAI is more robust than the TCI when interdependencies among multiple variables such as those caused by LD are present. We also critically evaluated the effectiveness and computational efficiency of the PAI-based AMBIENCE search algorithm for GEI analysis. Our results demonstrate that these methods are effective for analyzing a diverse range of epidemiologic data sets containing complex combinations of direct effects and multiple GEI.
The information theoretic AMBIENCE approach is flexible and can be used when the genetic and environmental variables have different numbers of classes or when the phenotype has more than two classes. This means that SNP and microsatellite markers can be analyzed together if necessary. Another critical advantage with our approach is that it provides options for user interactions and visualization for small data sets. For example, the incremental effect of adding a SNP can be easily visualized on the PAI spectrum. The ability to interact with data enriches the user's experience and can enable detection of features that are otherwise difficult to find. In addition to its information theoretic underpinnings, which are novel for GEI analysis, a key difference between AMBIENCE and other methods such as MDR and GMDR is that the AMBIENCE approach uses a greedy search algorithm based on the PAI rather than dimensionality reduction. However, AMBIENCE may be compatible with dimensionality reduction methods. It is also noteworthy that the information theoretic metrics in AMBIENCE are sensitive to both linear and nonlinear dependencies in the data.
At first sight, our KWII-based definition of interaction would appear to differ from the more conventional definition of interactions in statistical genetics. Statistical interactions represent deviations from additivity that are present in data: they are said to occur when the probability of observing the phenotype states for a variable combination is greater (or less) than expected from the probabilities of the phenotype states for each of variable considered individually. Count data are commonly analyzed using logistic regression and in this framework, interactions are assumed to be present if the parameters for the product terms are significant. We have conducted simulations with a diverse range of models, many of which could not be included in this article in the interests of brevity, that indicate a remarkable degree of concordance between the GEIs identified by our method and those identified by other methods. Specifically, we have also conducted a KWII-based analysis of the two-locus interaction models of pure epistasis analyzed by Culverhouse (2007). These models are defined by penetrance matrices and result in two-locus interactions that are devoid of any main effects. We found (results not shown) that the KWII spectra successfully found the combination of the two variables involved in the interaction and did not contain peaks from any of the uninformative variables or combinations. The qualitative concordance of the KWII with the challenging models used by Culverhouse (2007) and its performance in the case studies further demonstrate the utility of the KWII-based definition for GEI applications and data sets is reassuring and represent an important step for our novel approach.
Although the KWII is effective at identifying two-locus interaction models of pure epistasis (Culverhouse 2007), AMBIENCE is likely to have less power than MDR at identifying informative combinations in such pure epistasis examples because it utilizes a marginal effect strategy. The Boolean XOR gate (Jakulin and Bratko 2003) is another example of a pure interaction that would be difficult to identify with AMBIENCE. Nonetheless, a pure epistasis interaction has stringent symmetry requirements that are rarely met in real data; this can be readily observed, e.g., in synthetic and symmetric appearance of the penetrance matrices employed by Culverhouse (2007). In real data, small differences in allele frequency cause traces of lower-order effects that can be detected by AMBIENCE. This weakness in AMBIENCE can be readily addressed by conducting an extensive search of two-variable combinations. However, in data sets with large numbers of genetic and environmental variables, MDR-based methods can also suffer from loss of power because the number of variables that can be analyzed is limited and users may not be able to identify the key variables for inclusion. Thus, MDR-based methods and AMBIENCE can suffer from loss of power under certain circumstances but for different reasons.
Although the KWII is very effective at detecting GEI, its correspondence with logistic regression is not exact (Jakulin 2005). The lack of exact correspondence is attributable in part to methodological differences: logistic models fit all the terms simultaneously to the data, whereas with the KWII approach, higher-order interactions are inferred after eliminating lower-order contributions.
The AMBIENCE algorithm was found capable of identifying the strongest interactions containing ≤3 variables in the 100,000 SNP-containing computational speed GAW15 data set with ∼27 hr of computational time. However, our goal is to extend the method so that it is capable of conducting 106- to 107-variable analyses and match the data acquisition capabilities of the Affymetrix and Illumina genotyping platforms. This goal should be considered feasible particularly given improvements, e.g., parallelization that can be used to boost the performance of the AMBIENCE algorithm.
Both MDR and AMBIENCE require the user to specify the maximum combination order, which is the principal determinant of computational load. However, methods based on MDR are computationally intensive because they conduct an exhaustive search of both the genotype and the variable spaces. AMBIENCE is focused on identifying interacting variables and derives its computational efficiency because it conducts a directed search that harnesses the PAI via a greedy search algorithm. The monotonic properties of the PAI assist in highlighting combinations with high KWII values.
To minimize estimation errors resulting from the limited cell counts for higher-order combinations, MDR conducts cross-validation of the multilocus genotypes in each variable combination. Although AMBIENCE currently implements a permutation-based P-value assessment after identifying the set of promising combinations, the inclusion of a permutation test within each stage can be expected to further improve its performance. Despite these weaknesses and differences vis-à-vis other methods, AMBIENCE has capabilities that are not present in any of the existing methods; e.g., it can handle data sets with three or more outcomes.
Nonetheless, the available GEI methods such as MDR, GMDR, and PDT that employ dimensionality reduction do different things and ask different questions. For example, PDT is a method that is particularly useful for family-based study designs and can accommodate missing data whereas MDR is a nonparametric dimensionality reduction method for case–control study designs. The GMDR method is capable of handling continuous covariates. To ensure a fair comparison of the competing methods, despite their underlying differences, we provided each competing method with relevant data that would enable it to deliver the best possible performance. We therefore provided the family relationships for the PDT analysis, the continuous covariates for GMDR, and the discretized covariates for MDR. All algorithms were compared using both real genetic data from Crohn's disease (Daly et al. 2001) and simulated data that were modeled on real data from rheumatoid arthritis (Miller et al. 2007). AMBIENCE differs from the entropy-based approach proposed by Dong et al. (2007) in that it is capable of assessing direct effects and two-locus and also higher-order interactions. The PAI metric in AMBIENCE can effectively reduce the confounding effects caused by pairwise (and higher-order) LD.
However, a potential criticism of AMBIENCE is that there is no specific genetic mechanism or particular linear or nonlinear mathematical form directly incorporated in the GEI assessment. These aspects of the AMBIENCE method are in direct contrast to methods such as logistic regression, which employs an explicit mathematical form, GMDR, which assumes that the variables conform to the exponential family of distributions, and the PDT, which is refined for family-based studies. On the other hand, the absence of such constraining assumptions may also be construed as a key strength of the AMBIENCE method as it nonetheless accomplishes the goal of detecting nonlinear and multidimensional relationships in epidemiological data sets. Another potential criticism is that the AMBIENCE algorithm employs a search strategy rather than dimensionality reduction for GEI analysis. The greedy search strategy utilizes marginal effects on the PAI of lower-order combinations to conduct a directed search of higher-order combinations that increase the PAI. These distinctions between AMBIENCE and the other approaches can theoretically impose certain limitations, e.g., susceptibility to local maxima, but also confer the advantages of enabling effective and efficient GEI analyses of larger data sets. Indeed, we selected the implementation method to showcase the unique advantages of the PAI. It may, however, be possible to combine other algorithmic strategies such as simulated annealing and genetic algorithms within the current AMBIENCE to further enhance its performance.
AMBIENCE is dependent on the input parameter θ, which represents the number of combinations retained in each the iteration of the search. In our experiments, we employed θ = 50 and were able to identify GEI in the Daly et al. and GAW15 data sets (Daly et al. 2001; Miller et al. 2007). The risk of missing informative combinations increases for lower values of θ whereas computational time increases at higher values. The input parameter τ determines the highest order of variable combination detected. Although biochemical pathways and biological processes involve numerous gene products, these are typically mediated by a sequence of molecular interactions and manifest as statistical interactions of lower order. In our experiments, we set τ = 3 and the choice of τ should be based on the expected complexity of the statistical interactions and the sample size. The computational time of AMBIENCE approaches that of an exhaustive search when the number of genetic and environmental variables in the data set is small or if the majority of the variables are involved in interactions of high order.
It is also important to note that we have employed the KWII and PAI spectra to highlight the relationships of these metrics to the underlying GEI models in simulations. We do not expect that such plots will be useful for large genomewide data sets because combinatorial explosion will make direct visual analysis difficult. However, we have developed a permutation-based statistical framework that provides P-values that can be deployed for decision making for data sets from genomewide association studies. Although AMBIENCE does not currently include corrections for multiple testing, the P-values from permutation testing can be corrected using approaches such as the SDMinP method of Obreiter et al. (2005) or the Benjamini–Hochberg method (Benjamini and Hochberg 1995).
In our comparisons, we used both simulated and real data. The major advantage to using simulated data is that the ground truth is established during the simulation. The GAW15 data set was also sufficiently rich and complex because it was modeled on the basis of a real rheumatoid arthritis data set and simulation details were available. The Crohn's disease data set from Daly et al. (2001) was obtained experimentally from a population of inflammatory bowel disease patient–parent trios with at least one unaffected parent. The genotype data involved a follow-up resequencing analysis and they contained essentially perfect haplotype-phase information (Rioux et al. 2001). These factors provided a sound framework for comparing the performance of AMBIENCE.
We also examined the variability of KWII, TCI, and PAI for a diverse range of simulated GEI case studies. For example, the error bars representing standard deviations in Figures 3–6 demonstrate that the effects of random variations caused by sampling on overall shapes of PAI and KWII spectra are small. For the Daly et al. (2001) data set we demonstrated that permutation testing can be used to compute P-values of the KWII and assess significance. Because of the availability of 100 replicates in the GAW15 data set, we were able to compute confidence intervals for the KWII. The distributions of KWII, TCI, and PAI of higher-order interactions have not been well characterized. However, for one-variable-containing interactions, KLD, KWII, and TCI are equal to each other and these metrics are asymptotically χ2-distributed (Jakulin and Bratko 2004).
In conclusion, our approach incorporates several features that are novel for GEI analysis. We have defined the PAI, a novel information theoretic metric that is robust to LD, and leveraged its mathematical properties to implement an algorithm, AMBIENCE, which is computationally efficient and effective at GEI analysis. Information-theoretic methods may have great potential in GEI analysis and statistical genomics and warrant more research.
Acknowledgments
This work was partly supported by the National Science Foundation and the National Institutes of Health. Support from the National Multiple Sclerosis Society (RG3743) is also gratefully acknowledged.
APPENDIX: PROPERTIES OF PHENOTYPE-ASSOCIATED INFORMATION
Property 1: the PAI is a nonoverlapping sum:
Here, we demonstrate the development of PAI as an information theoretic metric to efficiently search the combinatorial space to identify the variables involved in the strongest interactions. The interaction information involving three variables A, B, C can be written as
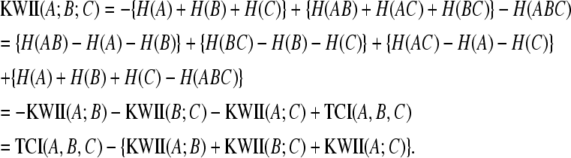 |
Thus
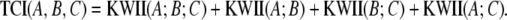 |
Similarly TCI for four variables A, B, C, D can be expressed as
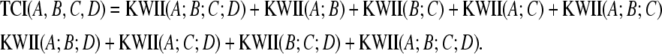 |
Generalizing to TCI for K variables X1, X2, … , XK,
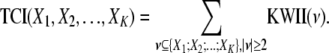 |
We assume a case–control study design for the problem of detecting the underlying GEI in a given data set with the genetic and environmental variables denoted by X1, X2, … , XN and the disease phenotype variable denoted by P. The TCI of K variables and the phenotype can be expressed as
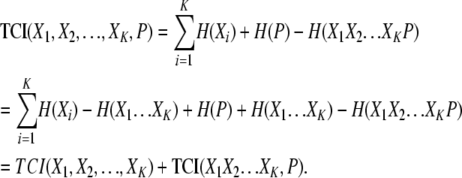 |
Alternatively,
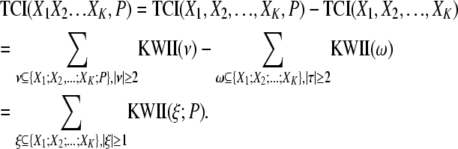 |
The term TCI(X1X2 … XK, P) is the TCI between the joint distribution of the K variables and the phenotype; the TCI(X1, X2, … , XK) term is the TCI among the K variables, and TCI(X1, X2, … , XK, P) is the TCI among the K variables and the phenotype. The above equation is the sum of all possible interactions involving variables X1, X2, … , XK, P that contains the phenotype variable P. This is defined as the PAI.
The PAI is derived from the TCI, which is the overall dependency among the genetic and environmental variables and the phenotype and removes the TCI contributions due to the interdependencies (caused by factors such as LD) among the genetic and environmental variables. Accordingly, the PAI is equal to
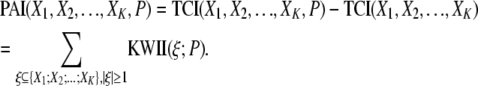 |
Because each KWII is nonredundant with every other combination and the PAI can be expressed as a sum of KWII values, the PAI is a nonoverlapping sum.
Property 2: PAI is greater than zero and increases monotonically:
We demonstrate two properties of PAI that make it suitable for designing hill-climbing algorithms to search the combinatorial space effectively: PAI is always greater than or equal to zero and increases monotonically with increased combination size.
For K genetic and/or environmental variables X1, X2, … , XK, and phenotype status variable P, we have
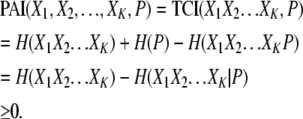 |
The value of H(X1, X2, … , XK) ≥ H(X1, X2, … , XK | P) because entropy decreases when information regarding phenotype P is known (the vertical line represents conditional entropy). As a result, PAI(X1, X2, … , XK) is thus nonnegative.
To demonstrate that PAI increases monotonically, we note that the PAI is equivalent to the mutual information between the joint distribution of K variables and phenotype status variable P. We have
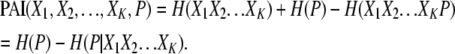 |
Thus,
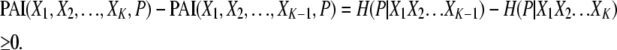 |
These equations demonstrate that the PAI increases monotonically with the inclusion of additional genetic or environmental variables because uncertainty about the variable P decreases when information on the additional variable XK is considered.
References
- Ambrosone, C. B., P. G. Shields, J. L. Freudenheim and C. C. Hong, 2007. Re: commonly studied single-nucleotide polymorphisms and breast cancer: results from the Breast Cancer Association Consortium. J. Natl. Cancer Inst. 99 487 (author reply 488–489). [DOI] [PubMed] [Google Scholar]
- Anderson, E. C., and E. A. Thompson, 2002. A model-based method for identifying species hybrids using multilocus genetic data. Genetics 160 1217–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arason, G. J., J. Kramer, B. Blasko, R. Kolka, P. Thorbjornsdottir et al., 2007. Smoking and a complement gene polymorphism interact in promoting cardiovascular disease morbidity and mortality. Clin. Exp. Immunol. 149 132–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini, Y., and Y. Hochberg, 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B Methodol. 57 289–300. [Google Scholar]
- Bhasi, K., L. Zhang, D. Brazeau, A. Zhang and M. Ramanathan, 2006. a Information-theoretic identification of predictive SNPs and supervised visualization of genome-wide association studies. Nucleic Acids Res. 34 e101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhasi, K., L. Zhang, D. Brazeau, A. Zhang and M. Ramanathan, 2006. b VizStruct for visualization of genome-wide SNP analyses. Bioinformatics 22 1569–1576. [DOI] [PubMed] [Google Scholar]
- Bush, W. S., S. M. Dudek and M. D. Ritchie, 2006. Parallel multifactor dimensionality reduction: a tool for the large-scale analysis of gene-gene interactions. Bioinformatics 22 2173–2174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caspi, A., and T. E. Moffitt, 2006. Gene-environment interactions in psychiatry: joining forces with neuroscience. Nat. Rev. Neurosci. 7 583–590. [DOI] [PubMed] [Google Scholar]
- Chanda, P., A. Zhang, D. Brazeau, L. Sucheston, J. L. Freudenheim et al., 2007. Information-theoretic metrics for visualizing gene-environment interactions. Am. J. Hum. Genet. 81 939–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho, Y. M., M. D. Ritchie, J. H. Moore, J. Y. Park, K. U. Lee et al., 2004. Multifactor-dimensionality reduction shows a two-locus interaction associated with type 2 diabetes mellitus. Diabetologia 47 549–554. [DOI] [PubMed] [Google Scholar]
- Corman, T. H., C. E. Leiserson and R. L. Rivest, 2001. Introduction to Algorithms. MIT Press, Cambridge, MA.
- Culverhouse, R., 2007. The use of the restricted partition method with case-control data. Hum. Hered. 63 93–100. [DOI] [PubMed] [Google Scholar]
- Daly, M. J., J. D. Rioux, S. F. Schaffner, T. J. Hudson and E. S. Lander, 2001. High-resolution haplotype structure in the human genome. Nat. Genet. 29 229–232. [DOI] [PubMed] [Google Scholar]
- Dong, C., X. Chu, Y. Wang, L. Jin, T. Shi et al., 2007. Exploration of gene-gene interaction effects using entropy-based methods. Eur. J. Hum. Genet. 16(2): 229–235. [DOI] [PubMed] [Google Scholar]
- Dudbridge, F., 2003. Pedigree disequilibrium tests for multilocus haplotypes. Genet. Epidemiol. 25 115–121. [DOI] [PubMed] [Google Scholar]
- Fano, R. M., 1961. Transmission of Information: A Statistical Theory of Communications. MIT Press, Cambridge, MA.
- Hahn, L. W., and J. H. Moore, 2004. Ideal discrimination of discrete clinical endpoints using multilocus genotypes. In Silico Biol. 4 183–194. [PubMed] [Google Scholar]
- Hahn, L. W., M. D. Ritchie and J. H. Moore, 2003. Multifactor dimensionality reduction software for detecting gene-gene and gene-environment interactions. Bioinformatics 19 376–382. [DOI] [PubMed] [Google Scholar]
- Han, T. S., 1980. Multiple mutual informations and multiple interactions in frequency data. Inf. Control 46 26–45. [Google Scholar]
- Jakulin, A., 2005. Machine learning based on attribute interactions, p. 240 in Computer Science. University of Ljubljana, Ljubljana, Slovenia.
- Jakulin, A., and I. Bratko, 2003. Analyzing attribute dependencies, pp. 229–240 in Proceedings of the 7th European Conference on Principles and Practice of Knowledge Discovery in Databases (PKDD 2003), edited by N. Lavrac, D. Gamberger, H. Blockeel and L. Todorovski. Springer, Cavtat-Dubrovnik, Croatia.
- Jakulin, A., and I. Bratko, 2004. Testing the significance of attribute interactions, pp. 409–416 in Proceedings of the Twenty-First International Conference on Machine Learning (ICML-2004), edited by R. Greiner and D. Schuurmans. Association for Computing Machinery (ACM), New York, USA.
- Li, Y., Y. Xiang, H. Deng and Z. Sun, 2007. An entropy-based index for fine-scale mapping of disease genes. J. Genet. Genomics 34 661–668. [DOI] [PubMed] [Google Scholar]
- Liu, Z., and S. Lin, 2005. Multilocus LD measure and tagging SNP selection with generalized mutual information. Genet. Epidemiol. 29 353–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lou, X. Y., G. B. Chen, L. Yan, J. Z. Ma, J. Zhu et al., 2007. A generalized combinatorial approach for detecting gene-by-gene and gene-by-environment interactions with application to nicotine dependence. Am. J. Hum. Genet. 80 1125–1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma, D. Q., P. L. Whitehead, M. M. Menold, E. R. Martin, A. E. Ashley-Koch et al., 2005. Identification of significant association and gene-gene interaction of GABA receptor subunit genes in autism. Am. J. Hum. Genet. 77 377–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin, E. R., S. A. Monks, L. L. Warren and N. L. Kaplan, 2000. A test for linkage and association in general pedigrees: the pedigree disequilibrium test. Am. J. Hum. Genet. 67 146–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin, E. R., M. D. Ritchie, L. Hahn, S. Kang and J. H. Moore, 2006. A novel method to identify gene-gene effects in nuclear families: the MDR-PDT. Genet. Epidemiol. 30 111–123. [DOI] [PubMed] [Google Scholar]
- McGill, W. J., 1954. Multivariate information transmission. Psychometrika 19 97–116. [Google Scholar]
- Miller, M. B., G. R. Lind, N. Li and S.-Y. Jang, 2007. Genetic Analysis Workshop 15: simulation of a complex genetic model for rheumatoid arthritis in nuclear families including a dense SNP map with linkage disequilibrium between marker loci and trait loci. BMC Genet. 1 (Suppl 1): S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore, J. H., J. C. Gilbert, C. T. Tsai, F. T. Chiang, T. Holden et al., 2006. A flexible computational framework for detecting, characterizing, and interpreting statistical patterns of epistasis in genetic studies of human disease susceptibility. J. Theor. Biol. 241 252–261. [DOI] [PubMed] [Google Scholar]
- Motsinger, A. A., B. S. Donahue, N. J. Brown, D. M. Roden and M. D. Ritchie, 2006. Risk factor interactions and genetic effects associated with post-operative atrial fibrillation. Pac. Symp. Biocomput. 584–595. [PubMed]
- Obreiter, M., C. Fischer, J. Chang-Claude and L. Beckmann, 2005. SDMinP: a program to control the family wise error rate using step-down minP adjusted P-values. Bioinformatics 21 3183–3184. [DOI] [PubMed] [Google Scholar]
- Onnie, C., S. A. Fisher, K. King, M. Mirza, R. Roberts et al., 2006. Sequence variation, linkage disequilibrium and association with Crohn's disease on chromosome 5q31. Genes Immun. 7 359–365. [DOI] [PubMed] [Google Scholar]
- Purcell, S., B. Neale, K. Todd-Brown, L. Thomas, M. A. Ferreira et al., 2007. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81 559–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rioux, J. D., M. J. Daly, M. S. Silverberg, K. Lindblad, H. Steinhart et al., 2001. Genetic variation in the 5q31 cytokine gene cluster confers susceptibility to Crohn disease. Nat. Genet. 29 223–228. [DOI] [PubMed] [Google Scholar]
- Ritchie, M. D., L. W. Hahn, N. Roodi, L. R. Bailey, W. D. Dupont et al., 2001. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am. J. Hum. Genet. 69 138–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie, M. D., L. W. Hahn and J. H. Moore, 2003. Power of multifactor dimensionality reduction for detecting gene-gene interactions in the presence of genotyping error, missing data, phenocopy, and genetic heterogeneity. Genet. Epidemiol. 24 150–157. [DOI] [PubMed] [Google Scholar]
- Rosenberg, N. A., L. M. Li, R. Ward and J. K. Pritchard, 2003. Informativeness of genetic markers for inference of ancestry. Am. J. Hum. Genet. 73 1402–1422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shields, P. G., and C. C. Harris, 2000. Cancer risk and low-penetrance susceptibility genes in gene-environment interactions. J. Clin. Oncol. 18 2309–2315. [DOI] [PubMed] [Google Scholar]
- Smith, M. W., J. A. Lautenberger, H. D. Shin, J. P. Chretien, S. Shrestha et al., 2001. Markers for mapping by admixture linkage disequilibrium in African American and Hispanic populations. Am. J. Hum. Genet. 69 1080–1094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talmud, P. J., and J. W. Stephens, 2004. Lipoprotein lipase gene variants and the effect of environmental factors on cardiovascular disease risk. Diabetes Obes. Metab. 6 1–7. [DOI] [PubMed] [Google Scholar]
- Tsai, C. T., L. P. Lai, J. L. Lin, F. T. Chiang, J. J. Hwang et al., 2004. Renin-angiotensin system gene polymorphisms and atrial fibrillation. Circulation 109 1640–1646. [DOI] [PubMed] [Google Scholar]
- Velez, D. R., B. C. White, A. A. Motsinger, W. S. Bush, M. D. Ritchie et al., 2007. A balanced accuracy function for epistasis modeling in imbalanced datasets using multifactor dimensionality reduction. Genet. Epidemiol. 31 306–315. [DOI] [PubMed] [Google Scholar]
- Watanabe, S., 1960. Information theoretical analysis of multivariate correlation. IBM J. Res. Dev. 4 66–82. [Google Scholar]
- Zhao, J., E. Boerwinkle and M. Xiong, 2005. An entropy-based statistic for genomewide association studies. Am. J. Hum. Genet. 77 27–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, J., E. Boerwinkle and M. Xiong, 2007. An entropy-based genome-wide transmission/disequilibrium test. Hum. Genet. 121 357–367. [DOI] [PubMed] [Google Scholar]