Adaptive Differentiation of Quantitative Traits in the Globally Distributed Weed, Wild Radish (Raphanus raphanistrum)

Abstract

Weedy species with wide geographical distributions may face strong selection to adapt to new environments, which can lead to adaptive genetic differentiation among populations. However, genetic drift, particularly due to founder effects, will also commonly result in differentiation in colonizing species. To test whether selection has contributed to trait divergence, we compared differentiation at eight microsatellite loci (measured as F_ST) to differentiation of quantitative floral and phenological traits (measured as Q_ST) of wild radish (Raphanus raphanistrum) across populations from three continents. We sampled eight populations: seven naturalized populations and one from its native range. By comparing estimates of Q_ST and F_ST, we found that petal size was the only floral trait that may have diverged more than expected due to drift alone, but inflorescence height, flowering time, and rosette formation have greatly diverged between the native and nonnative populations. Our results suggest the loss of a rosette and the evolution of early flowering time may have been the key adaptations enabling wild radish to become a major agricultural weed. Floral adaptation to different pollinators does not seem to have been as necessary for the success of wild radish in new environments.

ORGANISMS colonizing new environments likely face environmental conditions to which they are not well adapted. Thus, the colonization ability and persistence of organisms colonizing new habitats could be strongly influenced by the population's ability to evolutionarily adapt to new abiotic and biotic conditions (Blossey and Nötzold 1995; Ellstrand and Schierenbeck 2000). Alternatively, species may be preadapted to new environmental conditions by chance or through plasticity or may experience more benign environments in their introduced locations if there is an absence of competitors or predators (Elton 1958; Crawley 1987). However, the fact that many of the examples we have of rapid adaptation involve the establishment of populations in a novel environment (Reznick and Ghalambor 2001 and references therein) suggests that evolution plays a key role in the success of colonizations.

While divergent selection can create locally adapted populations, founder effects, drift, and migration among populations can all slow or prevent local adaptation from occurring depending on the strength of selection, population size, and the amount of gene flow between populations. Furthermore, drift or founder effects can also create nonadaptive differentiation that can be difficult to distinguish from local adaptation (Wright 1931; Lande 1976; Lynch 1990). One approach to determining the relative importance of drift and natural selection to population differentiation compares differentiation at presumptively neutral marker loci (F_ST) with differentiation of potentially adaptive quantitative traits (Q_ST) (Lande 1992; Spitze 1993). Since F_ST at truly neutral loci represents differentiation solely due to mutation and drift in the face of migration (Wright 1951), if Q_ST = F_ST, we cannot rule out that neutral processes alone have contributed to differentiation in the trait. However, if Q_ST > F_ST for a given trait, this suggests that natural selection has led to divergence of the populations. Conversely, a finding of Q_ST < F_ST indicates that convergent selection has prevented populations from diverging due to drift (Lande 1992; Spitze 1993; Whitlock 1999; McKay and Latta 2002). Comparisons of F_ST and Q_ST are especially useful for studying local adaptation in many populations due to the difficulty of making reciprocal transplants among multiple populations.

While comparisons of F_ST and Q_ST have been made for many species, few investigators have studied widely distributed organisms that have recently colonized new habitats. Koskinen et al. (2002) found remarkably rapid divergence in life-history traits of grayling fish in recently introduced populations in Norway with no migration between populations. Their findings indicate that local adaptation can be quite rapid in newly introduced organisms, despite low effective population sizes. However, similar studies on recently introduced populations across a large geographic area have not been done.

The success of widely occurring weedy and invasive species in new environments implies that selective pressures are similar across environments, that organisms exhibit phenotypic plasticity that enables them to survive and reproduce in different environments (Marshall and Jain 1968; Rice and Mack 1991; Parker et al. 2003), or that species are able to rapidly adapt to new habitats (Baker and Stebbins 1965; Baker 1974; Lee 2002). Flowering plants that are introduced to new habitats not only must survive under potentially different environmental conditions, but also must be successfully pollinated by potentially new pollinator species, particularly if they are outcrossing annuals. The abundance of effective pollinators in the new habitat and the ability to adapt to new pollinators could affect a plant species' ability to persist and spread (Parker 1997; Richardson et al. 2000).

One such widespread, introduced species is wild radish, Raphanus raphanistrum L. ssp. raphanistrum. Thought to be native to the Mediterranean basin (Hulten and Fries 1986; Holm et al. 1997), wild radish has successfully colonized a variety of locations, leading to its naturalization on all continents except Antarctica (Holm et al. 1997). Not only has wild radish colonized these new areas, but also it has become a major agricultural weed, causing yield losses in a variety of crops in North America (Webster and MacDonald 2001; Warwick and Francis 2005), Europe (Bostrom et al. 2003), and Australia (Streibig et al. 1989; Cousens et al. 2001). Due to the self-incompatibility system of wild radish (Sampson 1964) and its lack of vegetative reproduction, this species relies completely on pollination by insects for reproduction. Therefore, the successful reproduction of this species in its introduced locations indicates that it has been able to effectively use pollinators in its new habitats.

With the potentially large differences in abiotic and biotic environmental factors across continents (e.g., temperature, water availability, pollinators, herbivores), selection is likely to have played a role in the evolution of morphological, phenological, and vegetative traits of wild radish across both its native and introduced habitats, leading to locally adapted populations. Furthermore, pollinator-mediated selection has been found to be acting in North America on specific floral traits of wild radish such as anther exsertion, stamen dimorphism, and flower size (Conner et al. 1996a,b, 2003; Morgan and Conner 2001). Therefore, floral traits are likely candidates for experiencing divergent selection pressures across a wide geographic scale.

In this study we focus on potential differences in floral, phenological, and vegetative traits of wild radish across eight populations distributed across three continents. Specifically, we determine (1) the amount of additive genetic differentiation in floral, phenological, and vegetative traits (Q_ST); (2) genetic differentiation of the same populations at putatively neutral loci (F_ST); and (3) whether populations in closer proximity to one another are more genetically similar than those farther apart (isolation by distance). Results suggest that a loss of rosette formation and the evolution of earlier flowering time were key adaptations for colonization of agricultural habitats, but that less adaptive floral differentiation has occurred.

METHODS

Study system:

Wild radish is a self-incompatible, annual to biennial herb (Chater 1993) that is visited by at least 15 different genera of pollinators in three orders—Hymenoptera, Diptera, and Lepidoptera (Kay 1976, 1982; Conner and Rush 1996; Sahli and Conner 2007). It was first mentioned as an introduced weed in the eastern United States in the 1820s and 1830s (Torrey and Gray 1838) and has dispersed around the globe as a contaminant of grain seed (Woolcock and Cousens 2000).

Estimating Q_ST:

Seeds were collected from eight different populations located on three continents: Westonia, Australia (WA); Cowra, Australia (CA); Naracoorte, Australia (NA); Aura, Finland (AF); Masku, Finland (MF); Kalamazoo, Michigan (KM); Binghamton, New York (NY); and Madrid, Spain (MS) (Figure 1). All of the above populations were growing in grain fields, with the exception of MS, which was growing along the edge of a grain field, and MF, which was growing along a roadside (Table 1).

Figure 1.—

Location of populations. The map was prepared using a Mollweide projection.

TABLE 1.

Location of populations, the number of families per population used to estimate Q_ST, and the number of parental generation individuals used to estimate F_ST

Population	Location	Latitude/longitude	NQST	NFST
WA	Westonia, Australia	31°23′ S/118°32′ E	22	28
NA	Naracoorte, Australia	36°96′ S/140°73′ E	24	29
CA	Cowra, Australia	31°18′ S/152°20′ E	39	31
AF	Aura, Finland	60°36′ N/22°34′ E	36	30
MF	Masku, Finland	60°34′ N/22°6′ E	27	30
KM	Kalamazoo, Michigan	42°16′ N/85°35′ W	23	30
NY	Binghamton, New York	42°6′ N/75°54′ W	30	30
MS	Madrid, Spain	40°26′ N/3°42′ W	25	25

The Spanish population is native; all others are introduced agricultural weeds.

Parental measurements:

In 2003, one offspring from each of 50 field maternal plants per population was planted in 10-cm pots in MetroMix 360 potting soil (Scotts-Sierra, Marysville, OH) in the greenhouse at Kellogg Biological Station. We added 1.2 g Osmocote Plus 15-9-12 fertilizer (Scotts-Sierra) 12 days after seeds were planted. Pots were arranged in 50 blocks with each block containing one randomly assigned plant from each of the populations. This arrangement eliminates systematic environmental differences between populations.

Germination time, time to first flower, and height of first flower were recorded for each seed planted. Rosette score was determined by counting the total number of leaves produced below flowering branches. Leaf counts were made on photographs taken the day each plant first flowered. Plants that formed true rosettes made many more leaves than those that did not. The third flower from each plant was removed and photographed and the number of ovules in each flower was counted by gently pressing the pistil between two glass slides to view the ovules. Flower color was scored as either white or yellow and six floral traits were measured from the digital images of flowers using NIH Object Image (2.12; Vischer 2004): petal length and width, corolla tube length, length of one short and one long filament, and pistil length (Conner and Via 1993). Three composite traits were calculated from the above measurements due to earlier work showing selection on these traits (see Introduction): anther exsertion (long filament length minus corolla tube length), stamen dimorphism (long filament length minus short filament length), and flower size (first principal component of the above six traits). Tube and filament lengths were not analyzed separately due to their inclusion in these three composite traits. Because several plants (15%) from the Spanish population had not flowered after 4 months, any plants that had not flowered were placed in an environmental chamber with temperatures and day lengths simulating those typical of a winter in Spain. Over a period of 4 weeks the temperature was dropped to 12.8° during the day and 7.8° at night, and day length was shortened to 10 hr. Temperature and day length were dropped by 3.3° and 2 hr, respectively, each week. Plants were left at 12.8° at a day length of 10 hr for 74 days, after which time the temperature and day length were increased gradually to 22.2° and 15 hr of light, again over a period of 4 weeks. Plants that eventually flowered were measured as described above. Some of these plants were repotted into 15-cm pots and given an extra 2.4 g Osmocote fertilizer to induce flowering due to the long period of time they had spent in small pots.

After all of the above measurements were taken, plants were randomly mated within each population, with each plant serving as both a mother and a father. Using this mating design, 16–39 full-sib families per population were generated (Table 1). Leaf and bud tissue was collected from each plant and stored in an ultracold freezer (−80°) for later estimation of F_ST (see below).

Offspring measurements:

Four seeds from each family were planted in the greenhouse for a total of 877 offspring planted. One seed from each population was randomly assigned to one of 156 blocks to eliminate average environmental differences between populations. Due to differences in the number of families per population (16–39; Table 1), some blocks did not contain a plant from every population. All of the measurements made on the parents were made on these offspring as well. Plants that had not flowered after ∼3 months (53% of the MS population only) were exposed to a similar vernalization treatment to that described above, this time in the greenhouse. Plants were left at 12.8° at a day length of 10 hr for 30 days before increasing temperature and day length to 22.2° and 15 hr.

For the analysis, offspring were grouped into 9 blocks on the basis of their bench location in the greenhouse, and the parents were considered as a separate block since they were grown a year earlier. Thus all plants are grouped into 10 blocks. For each of the above quantitative traits, the statistical model

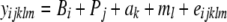(1)

was used, where y_ijklm is the observation of the mth individual in the ith block of the jth population with the lth maternal parent in the kth paternal family, B are block fixed effects, P are population random effects, a are additive genetic random effects, m are maternal environmental random effects, and e are random residual effects. The random effects were assumed to be normally distributed with mean zero and the usual covariance structures. Thus, all populations were analyzed simultaneously, except in the cases when certain populations were omitted for reasons described below. Fixed effects and variance components were estimated with REML using a modified version of Quercus (Shaw and Shaw 1992, 1994). Due to the extreme nonnormality of rosette score, log-transformed data were used for all analyses on this trait, which improved normality. Flowering time also had an extremely nonnormal distribution, which no transformation could improve. Q_ST was calculated as

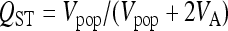(2)

as defined by Spitze (1993), where V_pop is the genetic variance between populations and V_A is the additive genetic variance within populations. To calculate confidence intervals for Q_ST estimates, we employed the “simulation method” (O'Hara and Merila 2005). For each trait, 1000 data sets were simulated in the design of the experiment from the maximum-likelihood estimates of the parameters and their dispersion matrices. For each data set, Q_ST was calculated, and from these, 95% confidence intervals for Q_ST were calculated using the empirical distribution of the approximate pivot quantity,

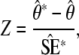(3)

where 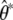are the simulated Q_ST (Efron and Tibshirani 1993, p. 160). The standard errors of the Q_ST from the simulated data sets, 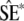, were approximated using the delta method. In the case of flower size, the among-population variance was too close to zero to reliably simulate data for the parametric bootstrap, so the delta method was used to obtain a 95% C.I. Confidence intervals based on the delta method (data not shown) were in general similar to those obtained from the parametric bootstrap.

Narrow-sense heritability (h²) was calculated for all traits in all eight populations as V_A/V_P, where V_A was determined using the program nf3.p in Quercus, and V_P is the phenotypic variance within a population. Significance of V_A was determined by using a one-tailed χ²-test, where the χ²-statistic was calculated as twice the difference between the log likelihood of the unconstrained estimate and the log likelihood when V_A was constrained to zero. The Q_ST estimate for each trait was regressed on heritability for that trait averaged across populations, to test whether h² predicts trait divergence among populations.

The flower color polymorphism in R. raphanistrum is controlled by a single locus, with white being completely dominant to yellow. Due to the dominant nature of this trait, we used a Bayesian approach to estimate F_ST for flower color using Hickory, version 1.1 (Holsinger et al. 2002), which estimates among-population differentiation (θ^II) from dominant data under the assumption that allele frequencies follow a beta distribution. The estimate of θ^II is directly comparable to Weir and Cockerham's (1984) F_ST and provides an estimate of differentiation among contemporaneous populations. Deviance information criteria (DIC) were used to determine the model that best fit the data of three models: (1) the full model where f and θ were free to vary, (2) no inbreeding (f = 0), and (3) no population structure (θ = 0). There was no difference between the full model (DIC = 17.2) and the model with no inbreeding (DIC = 17.1), but the model with no population structure did not fit the data (DIC = 53.8). θ^II-values from the model with no inbreeding are presented since wild radish is self-incompatible and since estimates did not differ. The posterior distributions for θ^II were used to estimate means and 95% credible intervals (CRI) of the estimate. Posterior distributions were approximated with Monte Carlo Markov chain (MCMC) simulations. We used uniform priors and a burn-in of 50,000 iterations.

Estimating F_ST for marker loci:

Total genomic DNA was extracted from 16–30 individuals per population (Table 1), using Qbiogene's (Carlsbad, CA) FastDNA kit and the FastPrep Instrument following the kit protocol. Individuals were genotyped at eight microsatellite loci derived from Brassica: Bn26a, Bn35d, Brms005, Na10-H06, Na12-E05, Na14-E08, Ra1-H08, and Ra2-E11 (UK CropNet Brassica database; http://ukcrop.net/brassica.html). Using data from eight loci reduces the chance that the F_ST estimate will be strongly influenced by nonneutral markers. Microsatellites were PCR amplified in 10-μl reactions consisting of 1.0 μl each of 10× buffer and 25 mm MgCl_2, 0.25 μl of 2 mm dNTPs, 7.05 μl of water, 0.1 μl of Taq polymerase, 0.15 μl of the 10-μm primers, with a fluorescently labeled forward primer, and 0.3 μl (∼6 ng) of DNA. The PCR program consisted of one initial denaturing phase at 94° for 10 min, followed by 25 cycles, each consisting of 94° for 1 min, annealing at 50°–61° (depending on the primer) for 45 sec, and an extension at 72° for 1 min. The 25 cycles were followed by an additional elongation step of 72° for 10 min. Microsatellite samples were run on 6% polyacrylamide gels, with 8 μl Temed and 400 μl 10% APS added to each gel. Bands were visualized on an FMBIO II Multiview scanner (Hitachi Software Engineering, San Francisco). Alleles were scored using FMBIO Analysis 8.0 (Hitachi Software Engineering 1991–1999) and placed in bins using Allelogram 1.2 (Manaster 1998).

A multilocus estimate of F_ST was calculated in FSTAT 2.9.3.2 (Goudet 1995) following Weir and Cockerham (1984) and 95% confidence intervals were determined by bootstrapping over loci. Q_ST was considered to be statistically different from F_ST when 95% confidence intervals of Q_ST did not overlap 95% confidence intervals of F_ST. Mantel permutations were used to test for independence between geographic and genetic differences in the ISOLDE option in GENEPOP (Raymond and Rousset 1995). No information on linkage relationships among these markers is available.

Two different estimates of Q_ST and F_ST were made, one with all eight populations included and one with only the seven weedy nonnative populations. The last analysis was made to test whether the nonnative populations have diverged from one another. Furthermore, because the Spanish population flowered much later than the other seven populations, floral measurements made on the Spanish population were not done in a common environment with the other populations. Because conditions in a greenhouse are not constant over time, we cannot rule out the possibility that differences in floral traits between the native and nonnative populations are due to environmental differences rather than genetic differences. However, differences in germination time, leaf number, and flowering time should be due to genetic differentiation.

RESULTS

Population differentiation based on microsatellite markers:

All loci were polymorphic in all populations (Table 2). Several alleles were unique to particular populations: NA, MF, and CA each had one unique allele, KM and WA each had two, and MS had four.

TABLE 2.

Number of alleles per locus for each population

Population	WA	CA	NA	AF	MF	KM	NY	MS	Total no. alleles
Bn35d	6	6	5	6	6	8	7	3	13
Brms-005	10	9	7	6	9	11	6	8	22
Na14-E08	6	6	4	6	4	5	6	6	12
Ra2-E11	8	5	6	3	4	4	7	5	10
Ra1-H08	4	5	4	5	5	4	5	6	7
Na12-E05	9	8	5	3	5	6	5	6	13
Na10-H06	4	4	4	3	4	4	4	3	5
Bn26a	6	6	7	3	4	5	5	5	11

Overall F_ST values ranged from 0.11 (among nonnative populations), to 0.14 (among all populations; Table 3). Pairwise F_ST values for the nonnative weedy populations (North America, Finland, and Australia) were all <0.18, with very low differentiation within North America and Finland (Table 4). The native Spanish population (MS) was less differentiated from the North American populations (F_ST = 0.15–0.19) than from the Finnish and Australian populations (F_ST = 0.24–0.27). A Mantel test with 1000 permutations could not detect a relationship between genetic differences and geographic distance (P = 0.23), consistent with long-distance gene flow due to shipment of contaminated grain seed as well as with previous results from North America (Kercher and Conner 1996).

TABLE 3.

F_ST values for each locus in each analysis, plus average values with 95% confidence intervals estimated by bootstrapping over the eight loci

Locus	All populations	All nonnative populations
Bn35d	0.15	0.09
Brms005	0.11	0.11
Na14E08	0.14	0.15
Ra2E11	0.18	0.11
Ra1H08	0.07	0.03
Na12E05	0.11	0.09
Na10H06	0.15	0.13
Bn26a	0.21	0.19
Mean	0.14 (0.11, 0.17)	0.11 (0.09, 0.14)

TABLE 4.

Pairwise F_ST values for the eight populations

	CA	NA	AF	MF	KM	NY	MS
WA	0.17	0.13	0.14	0.13	0.11	0.12	0.26
CA		0.15	0.16	0.14	0.14	0.14	0.25
NA			0.14	0.14	0.11	0.13	0.24
AF				−0.01a	0.07	0.09	0.27
MF					0.06	0.08	0.26
KM						0.04	0.19
NY							0.15

^aNot significantly different from zero; all other F_ST values are significant at P < 0.05 by permutation tests.

Quantitative traits:

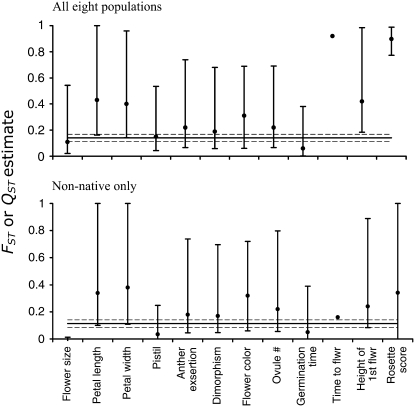
The traits studied had significant heritabilities in most populations except for petal length and germination time (Table 5). A one-way ANOVA revealed that populations differed in their average heritability (N = 88; F = 2.34; P = 0.03), where the Kalamazoo population had the highest average heritability, which was significantly greater than that of the CA and MS populations (Table 5). Population Q_ST values ranged from 0 (flower size, nonnative populations, Figure 2) to 0.93 (rosette score, all populations, Figure 2), with an average Q_ST estimate of 0.37 among all populations and 0.19 among only the nonnative populations, indicating that the nonnative populations have experienced little divergence in quantitative traits.

TABLE 5.

Narrow-sense heritability (h²) estimates for each trait in each population of R. raphanistrum calculated as V_A/V_P

Trait	WA	CA	NA	AF	MF	KM	NY	MS
Flower size	0.24**	0.11	0.16*	0.27***	0.38***	0.17	0.29***	0.08
Petal length	0.17	0.05	0.12	0.20**	0.36***	0.01	0.23**	−0.03
Petal width	0.31*	0.54***	0.51*	0.19*	0.27**	0.59***	0.14	0.17
Pistil length	0.38**	0.17*	0.41***	0.37***	0.70***	0.55***	0.35**	0.27*
Anther exsertion	0.14	0.20**	0.35**	0.40***	0.32**	0.32**	0.03	0.38**
Stamen dimorphism	0.21	0.36***	0.15	0.61***	−0.01	0.72***	0.49***	0.32**
Ovule no.	0.45***	0.17*	0.38***	0.41***	0.41***	0.49***	0.30**	0.33**
Germination time	0.04	0.06	0.23	0.28**	0.13	1.37***	0.13	0.09
Flower time	0.40***	0.38***	0.66***	0.28**	0.25**	0.58***	0.52***	0.09
Flower height	0.33**	0.47***	0.76***	0.28**	0.26**	0.27*	0.54***	0.31*
Leaf no.	0.62***	0.04	0.18	0.22*	0.28**	0.52***	0.58***	0.12
Average heritability	0.30 (a, b)	0.23 (b)	0.36 (a, b)	0.32 (a, b)	0.30 (a, b)	0.51 (a)	0.33 (a, b)	0.19 (b)

V_A was measured using restricted maximum-likelihood analysis in Quercus and significance values are based on V_A. Average heritabilities not sharing a letter in common are significantly different at P = 0.05 according to Tukey's HSD test. *P ≤ 0.05; **P ≤ 0.01; ***P ≤ 0.001.

Figure 2.—

F_ST and Q_ST estimates: among all populations and among nonnative populations. The horizontal line is the F_ST estimate with the dashed lines indicating 95% confidence limits. Error bars on the Q_ST estimates are 95% confidence limits based on a parametric bootstrap. Flower color differentiation was estimated using a Bayesian approach and error bars are 95% credible intervals. We were unable to accurately estimate C.I.'s for flowering time due to nonnormality of the data.

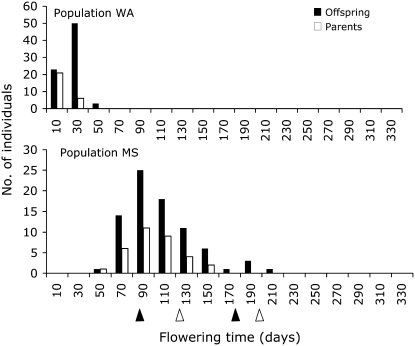
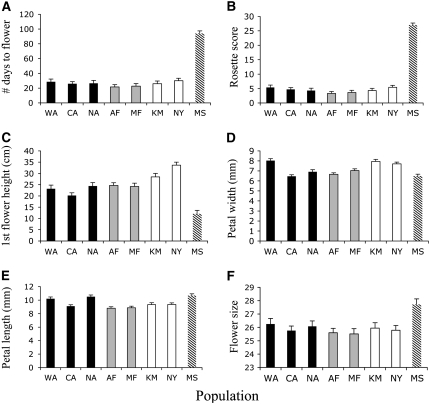
Petal length and width, flowering time, height of first flower, and rosette score generally had the highest values of Q_ST, but some of these estimates were greatly influenced by the Spanish population (Figure 2). Due to the extreme nonnormality of the distribution for flowering time (Figure 3; Shapiro-Wilks test for goodness of fit to a normal distribution, P < 0.0001), which no transformation could improve, we were unable to estimate confidence limits for our estimates of Q_ST for this trait. However, Q_ST for flowering time among all populations was extremely large, and the Spanish population flowered much later than the other seven populations (Figures 3 and 4A). Fifteen percent to 53% of the plants in the MS population were induced to flower upon a vernalization treatment (Figure 3), while all of the nonnative plants flowered without a vernalization treatment. Q_ST for rosette score followed a similar pattern, where Q_ST for this trait was significantly greater than F_ST when all populations were included (Figure 2), but not when only the nonnative populations were analyzed. Plants from the Spanish population produced clearly defined rosettes with many small leaves, while none of the weedy plants did (Figure 4B).

Figure 3.—

Distribution of flowering time for parents and offspring in a representative nonnative population (WA) and the native Spanish population, MS. Arrowheads indicate beginning and end dates of vernalization treatments.

Figure 4.—

Population means (+1 SE) for traits with Q_ST significantly different from F_ST. (A) flowering time, (B) rosette score, (C) height of first flower, (D) petal width, (E) petal length, and (F) flower size (first principal component of all floral traits measured).

Q_ST for height of the first flower was significantly larger than F_ST among the eight populations (Figure 2), with the Spanish population having the shortest flower stalks (Figure 4C). Finally, Q_ST for both petal length and width was marginally significantly >F_ST in both analyses (Figure 2). In general, the two Finland populations and one Australian population (AC) had shorter and more narrow petals than the other populations (Figure 4, D and E). Q_ST for flower size was significantly <F_ST among the nonnative populations (Figure 2), indicating convergent selection among the nonnative populations (Figure 4F). Heritability was not predictive of a trait's past divergence among populations, as the regression of h² on Q_ST was not significant (all populations, R² = 0.04; all nonnative populations, R² < 0.01; both P > 0.52).

Flower color:

Most populations were fixed for yellow flowers, with only the Australian populations containing white-flowered individuals. From the parental generation, white (dominant) frequencies in the Australian populations were WA = 0.37, CA = 0.07, NA = 0.06. The mean θ^II estimate for flower color was 0.31 among all populations and 0.32 among only the nonnative populations; however, the credible intervals were large for this estimate (Figure 2). We found no evidence of flower color alleles from the domestic radish, R. sativus, in any of these populations, as there were no pink- or bronze-flowered individuals (Stanton 1987).

DISCUSSION

Floral differentiation:

To our knowledge, this is the first study to compare F_ST and Q_ST among populations distributed across the globe. However, despite the large geographic distances among the populations we sampled, we found little evidence for adaptive differentiation in several floral traits, especially among those traits such as anther exsertion, stamen dimorphism, and flower size that are under pollinator-mediated selection (Conner et al. 1996a,b, 2003; Morgan and Conner 2001), and flower color, for which pollinators are known to differ in their preference for different color morphs (Kay 1976, 1978, 1982). This finding is unlikely to be due to the error around our estimates of Q_ST, as Q_ST point estimates for pistil length, anther exsertion, and stamen dimorphism were similar to F_ST in all analyses and hovered around the upper confidence limit for our estimate of F_ST. It is also not due to a high value of F_ST, as accidental movement of wild radish seeds by humans as contaminants of grain seed has kept neutral differentiation low on a global scale. Our finding of little divergence in these floral traits relative to divergence at neutral loci does not mean that the divergence must be attributed to drift alone, but rather indicates there is little evidence for strong divergence due to natural selection.

The only floral traits for which we found slight evidence for divergent selection were petal length and width, which had Q_ST values marginally significantly greater than F_ST in both comparisons. Petal size has been shown to influence visitation rates in a variety of species (e.g., Clements and Long 1923; Bell 1985; Galen 1989; Young and Stanton 1990; Eckhart 1991; Conner and Rush 1996). In their studies on the closely related R. sativus, Mazer and Meade (2000) found that populations with a large petal area were associated with high honeybee densities. However, this finding went against their expectation based on selection estimates where there was selection to increase petal area in the absence of honeybees, whereas in the presence of honeybees there was no selection on this trait. Unfortunately, little is known about the pollinators in the populations we studied except for those in Finland and North America. The dominant pollinator taxon can change across space, where Finland populations are dominated by honeybees, syrphid flies, and bumblebees (K. Lehtila, personal communication), and in New York and Michigan, small bees, syrphid flies, and honeybees often dominate (Conner and Rush 1996; Sahli and Conner 2007). Populations in Britain are visited by a mix of honeybees, bumblebees, cabbage butterflies, and syrphid flies (Kay 1976, 1978, 1982). Observations of populations in Australia and the Mediterranean, combined with more estimates of differences in selection by different pollinators, would be useful for understanding divergence in petal size.

Although petal size seems to have been under divergent selection, convergent selection has been acting on overall flower size among all the nonnative populations. Our estimation of flower size as the first principal component of all measured floral traits indicates that although petal size may have diverged, the overall size of the flowers did not change. Whether such convergent selection is imposed by biotic factors, abiotic factors, or some trade-off in flower size and flower number is currently unknown.

The lack of significant divergence in many floral traits is not due to a lack of genetic variation for selection to act on. In fact, the floral traits we measured were highly heritable in most populations. Thus, selection must not be strongly different in these populations, preventing strong divergence due to natural selection in the <200 generations that have occurred since the introduction to nonnative regions. Our findings suggest that, except for petal size, R. raphanistrum flowers are well adapted to pollinators across the globe, which is one possible reason why it is a successful weed despite being dependent on pollination.

Life history and vegetative differentiation:

While R. raphanistrum has been successful at colonizing agricultural fields across the globe without significant adaptive divergence in floral traits, the same is not true for two life-history traits: rosette production and flowering time. These traits had Q_ST values approaching 1 when all populations were included, but <0.4 for the nonnative populations only. The production of a rosette and delayed flowering are adaptations for overwintering, consistent with the Spanish population being a winter annual. These traits would be maladaptive in agricultural fields where a destructive harvest or tillage would kill the plant before flowering. There seems to have been strong selection among the nonnative populations to rapidly evolve loss of the rosette and any vernalization requirement to match the phenology of annual crops. This rapid evolution may have played a crucial role in the emergence of wild radish as a serious agricultural weed across the globe. Whether this adaptation to agricultural fields has occurred multiple times or just once is currently unknown.

An important caveat to this interpretation is that we sampled only one population in the native range; therefore, we cannot know for certain that the ancestral life-history state was late flower production and rosette formation. However, other lines of evidence suggest that rosette production and late flowering time may be the dominant form among native populations in Europe. We have also grown two other European subspecies of wild radish, one population of ssp. landra and one population of ssp. maritimus, and these other subspecies also formed a rosette, were perennial, and required an even more stringent vernalization treatment to induce flowering than the Spanish population of ssp. raphanistrum grown in this study. Thus, it seems likely that the evolution of shorter flowering time and loss of rosette formation has evolved in agricultural environments. Future studies of multiple nonweedy populations of all three subspecies would help directly test whether this pattern of rosette formation and vernalization requirement is indeed the ancestral, native form.

The vegetative trait of plant height has also diverged among all populations due to natural selection. Once again, most of this divergence was due to differences between the Spanish population and all of the nonnative populations, with the Spanish population having much shorter flowering stalks than the introduced populations. Increased plant height has been shown to directly increase pollinator visitation rates in some plant species (Campbell 1989; Engel and Irwin 2003), but the presence of herbivores can lead to selection for shorter plants (Gomez 2003). Thus a reduction of native herbivores may have led to an increase in flower height among nonnative populations of wild radish. Furthermore, an agricultural lifestyle may also select for taller flowering stalks, allowing pollinators to detect flowers growing amid tall-statured grain crops. Further investigations of herbivore differences and differences in the height of co-occurring plants in the Mediterranean region and in nonnative regions are needed.

Sampling and design of Q_ST studies:

Our findings of little differentiation despite large geographic sampling are particularly interesting when compared with previous comparisons of F_ST and Q_ST. In general, previous studies have found most traits have diverged more than neutral loci, indicating that divergent selection is rampant and strong enough to overcome the neutral effects of drift and migration (reviewed in Merila and Crnokrak 2001; McKay and Latta 2002; Leinonen et al. 2008). However, because most of our populations were from an agricultural setting, environmental conditions may have been more similar than if populations were occurring in a more natural environment.

Another major difference between our study and the vast majority of previous studies is that we estimated Q_ST on the basis of additive genetic variance, whereas most previous studies used variance estimates based on analysis of clonal or full-sib families, which also include dominance variance and variance due to shared maternal environment (but see Leinonen et al. 2008 for a list of those that have used additive genetic variance). Including dominance variance is appropriate for understanding evolutionary change in clonal or highly selfing species, but not for sexual ones, and including nonadditive variance in estimates can either increase or decrease Q_ST (Whitlock 1999; Lopez-Fanjul et al. 2003). Sampling error for Q_ST is also likely to be reduced for a given number of individuals by using full-sib families rather than estimating additive variation; this may be why the standard errors of our estimates of Q_ST are larger than those of previous studies. However, a recent meta-analysis found no effect of study design on Q_ST–F_ST comparisons (Leinonen et al. 2008).

In addition to differences in our study design, our estimation of the variance in Q_ST differed from those most commonly used—the nonparametric bootstrap and the delta method. These latter two methods have been found to underestimate the variance of Q_ST, while the simulation method (primarily used in our study) or a Bayesian approach produces the most accurate estimates (Morgan et al. 2005; O'Hara and Merila 2005). Thus, it may be difficult to detect significant differences among F_ST and Q_ST based on additive variance without very large sample sizes. However, we were able to detect significant differences among several traits that had diverged among populations, indicating that the large confidence intervals did not prevent us from detecting the signature of divergent selection.

Finally, our focus on floral traits may have prevented us from detecting many Q_ST estimates exceeding F_ST if most divergent selection occurs in life-history traits rather than in morphological traits. It is interesting that two of the four life-history traits we looked at, flowering time and rosette score at reproduction, had Q_ST estimates exceeding F_ST. Q_ST estimates of more morphological and life-history traits would allow us to further test whether life-history traits have, indeed, diverged more than morphological traits. However, previous studies have found life-history traits to be less divergent than morphological traits (Merila and Crnokrak 2001). Merila and Crnokrak (2001) suggest that the reason for such small differentiation in life-history traits of past studies may be due to the large amount of nonadditive genetic variation contributing to life-history traits as opposed to morphological traits (Crnokrak and Roff 1995). If the inclusion of nonadditive genetic variance causes a downward bias in Q_ST, past studies may have underestimated differences in life-history traits relative to morphological traits. Indeed, previous studies by Koskinen et al. (2002) and Palo et al. (2003) that also used additive genetic variance to estimate Q_ST found extreme divergence in most of the quantitative life-history traits they studied, relative to F_ST of neutral loci. Furthermore, a recent meta-analysis (e.g., Leinonen et al. 2008) that includes more studies using additive genetic variance to estimate Q_ST found no difference between life-history and morphological traits. Future studies comparing divergence in life-history traits to morphological traits using additive genetic variance are clearly needed.