Abstract
Understanding the interactions among different brain regions is fundamental to our understanding of brain function. Here we describe a complete map of functional connections in the human brain derived by an automatic meta-analysis of 825 neuroimaging articles, representing 3402 experiments. The likelihood of a functional connection between regions was estimated by studying the interdependence of their “activity,” as reported in each experiment, across all experiments. We obtained a dense coactivation map that recovers some fundamental principles of the brain's functional connectivity, such as the symmetric interhemispheric connections, and important functional networks, such as the fronto-parietal attention network, the resting state network and the motor network.
Keywords: brain mapping, database, functional connectivity, human brain, meta-analysis
Introduction
The most frequent source of brain stimulation is the brain itself. The cerebral cortex, the fastest growing structure in mammalian evolution, is a particularly striking example: here more than 95% of the afferent connections appear to be corticocortical (Braitenberg and Schüz 1991).
There are 2 main features important for understanding brain connectivity. One is the organization of efferent and afferent axonal fibers, which determines the brain's structural connectivity. The other is the organization of coordinated functional activation of different brain regions, which determines its functional connectivity.
Most of our knowledge about structural connectivity of the primate brain comes from post-mortem studies using retrograde and anterograde tracers in nonhuman primates. One of the major caveats of traditional tracing techniques is that they provide only a sparse representation of all the possible connections in the brain, a problem alleviated to some extent by systematic meta-analyses, such as those by Felleman and Van Essen (1991), Young et al. (1995), and Stephan et al. (2001).
Functional connectivity studies, on the other hand, are aimed at understanding the coordinated activity of brain regions during a cognitive task (Friston 1994). Neuronal activity may be measured, for example, by electric recordings as in electroencephalography, or by magnetic resonance imaging (MRI) of variations in blood oxygenation, as in functional MRI (fMRI). Interregional coordination of brain activity can then be estimated, for example, through the cross-correlation coefficient of such signals. Functional and structural connectivity, whereas obviously related, are not equivalent. Callosal fibers, for example, represent only 1% of the total corticocortical fibers (Schüz et al. 2006) and yet left–right symmetric patterns of interhemispheric activation are among the most frequent findings in neuroimaging studies. In fact, studies of functional connectivity provide information not only about the presence of a connection between 2 regions, direct or indirect, but also about the strength of this connection given the particular context (e.g., task). It would be impossible, however, to obtain a complete map of the brain's functional connectivity in an individual's brain using current functional connectivity methods; this would require collecting data in a group of subjects performing many different tasks.
Here we propose a different approach to the problem of mapping functional connectivity, which has allowed us to obtain a dense 6-dimensional map of functional connections across a large variety of tasks. We based our map on a large automatic meta-analysis of the neuroimaging studies in the BrainMap database (Laird et al. 2005). We interpreted the fact that a group of regions is reported together across experiments as evidence of their functional connection. We assessed the strength and significance of this connection by calculating the likelihood ratio between the hypothesis of interdependence of their activity compared with the null hypothesis of independence.
Using this approach, we observed that such a “meta-coactivation” map recovers some fundamental principles of the brain's functional connectivity, such as the symmetric interhemispheric coactivations, and some important functional networks, including the fronto-parietal attention network (Fox et al. 2005), the resting state network (Greicius et al. 2003) and the motor network (Paus et al. 1998; Postuma and Dagher 2006).
Methods
Database
Our meta-analysis included all the articles contained in the BrainMap database (Laird et al. 2005) of studies using positron emission tomography and fMRI. Articles in BrainMap are organized as “experiments” representing, for example, a particular contrast between 2 scanning conditions. Each experiment contains a variable number of “locations,” corresponding to the stereotaxic coordinates of the regions reported as “active.” As of June 2006, 825 articles were available in BrainMap, and have been used in our meta-analysis; these articles contained 3402 experiments with a total of 27 909 locations.
Locations in BrainMap are stored as 3-dimensional coordinates in standardized stereotaxic space (Talairach and Tournoux 1988). Whenever a study reports locations in MNI305 or ICBM152 space, they are converted into the standardized Talairach space using a piece-wise linear transformation (Brett 1999). We used the inverse of this transformation to convert location coordinates back to MNI305 space.
Each experiment was then transformed into a binary volume where the dimension-less locations were replaced by spherical regions of interest with a volume of 1[cm3]. The voxel-size of the binary volumes was set to 4[mm] isotropic.
Map of Coactivations
The coactivation between pairs of voxels in our map was defined by their statistical dependence across experiments. The activation of every voxel was modeled as independent and identically distributed samples of binary random variables whose values are equal to 1 when voxels are reported active, and 0 otherwise. For 2 such random variables A and B, corresponding to the activation of voxels v and w, the null hypothesis H0 states that the probability of B being active does not depend on the value observed for A, whereas the alternative hypothesis H1 states that a dependence does exist. Formally:
From the data, we can compute the maximum likelihood estimate 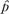 for the value p in the model under H0,
for the value p in the model under H0, 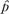 = m/N, where m is the number of experiments where voxel w was active, and N is the total number of experiments. Similarly, the values of p0 and p1 under H1 can be estimated by
= m/N, where m is the number of experiments where voxel w was active, and N is the total number of experiments. Similarly, the values of p0 and p1 under H1 can be estimated by 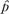 0 =(m − k)/(N − n) and
0 =(m − k)/(N − n) and 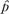 1 =k/n, where n is the number of experiments where voxel v was active, and k is the number of experiments where voxels v and w were active together.
1 =k/n, where n is the number of experiments where voxel v was active, and k is the number of experiments where voxels v and w were active together.
We used the likelihood ratio λ = L (H1)/L (H0) to evaluate how much more likely the alternative hypothesis is, compared with the null hypothesis (Manning and Schütze 1999). Here, L (H0) and L (H1) are the maximum likelihood of the data under the null and alternative hypotheses respectively,
where B(i, j, x) is the binomial distribution for the probability of i successes out of j trials, each having a success probability of x. Then,
The false-positive rate when rejecting the null hypothesis H0 for the alternative hypothesis H1 was estimated through 2log(λ), which is asymptotically χ2 distributed with 1 degree of freedom (Mood et al. 1974).
For every voxel in the brain, the coactivation map provides a 3-dimensional volume containing its coactive regions. We used a false-discovery rate of 0.01 to assess the statistical significance of the coactivations in each of these volumes while controlling for the multiple comparisons (Genovese et al. 2002).
Reproducibility
To verify that the coactivation map was not dependent on a particular choice of experiments, we computed partial coactivation maps using disjoint pairs of randomly selected subsets of experiments, with sizes of 500, 700, 900, 1100, 1300, 1500, and 1700 experiments. Twenty pairs of partial coactivation maps were computed for each subset size. We compared the similarity of each pair M0, M1 of partial maps using Pearson's correlation coefficient r,
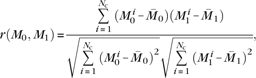 |
where  0 and
0 and  1 are the average coactivation of the maps M0 and M1, respectively, and Nc is the total number of coactivations in the maps.
1 are the average coactivation of the maps M0 and M1, respectively, and Nc is the total number of coactivations in the maps.
There were in total 280 partial coactivation maps, everyone occupying up to 300 MByte (up to 10 GByte uncompressed). The reproducibility computations took 3 days in a grid of 8 computers (16 Motorola G5 processors) running at 2 GHz with 2 GByte of memory.
Results
Map of Functional Coactivations
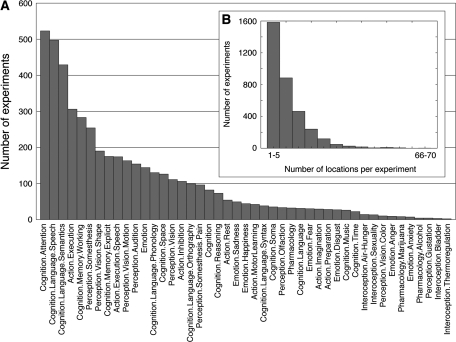
The experiments in our database represented a wide variety of cognitive domains (Fig. 1A), and involved on average 8 different locations, with values ranging from 1 to 68 (Fig. 1B). Locations were not distributed uniformly throughout the brain. The preSMA/SMA cortex was the most frequently reported region, followed by left/right symmetric regions in the premotor, intraparietal, and ventral temporo-occipital cortices. The least reported regions included the central sulcus, anterior temporal cortex and dorsal prefrontal cortex, as well as the inferior half of the cerebellum; the latter likely reflects a rather common omission of the inferior part of the cerebellum in the scanned volumes.
Figure 1.
Characterization of the experiments used in the coactivation map. Distribution of the different cognitive domains represented by the experiments after the BrainMap classification (A). Histogram of the number of locations per experiment (B). Experiments reported on average 8 locations, and a decreasing number of experiments reported large numbers of locations.
The meta-coactivation map consists of almost 45 000 individual volumes, 1 for every 4[mm3] voxel in the brain. Coactivation volumes showed a characteristic structure. Coactivation was stronger in the neighborhood of the seed-voxel, and often also in the left/right symmetric region. Depending on the particular position of the seed-voxel, other inter- and intrahemispheric regions, as well as subcortical structures, presented also strong coactivations (see, e.g., Figs 4–6).
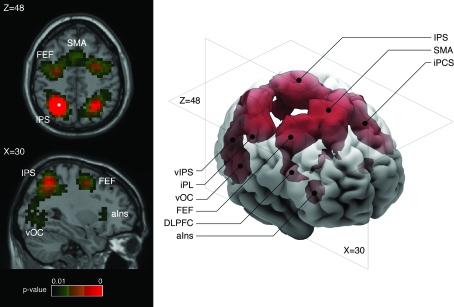
Figure 4.
Fronto-parietal “attention” network. Three-dimensional reconstruction and axial (z = 48) and para-sagittal (x = 30) stereotaxic slices of the network recovered with a seed-voxel at the left intraparietal sulcus (IPS, x = −26, y = −58, z = 48). It includes the supplementary motor area (SMA) and preSMA, left and right anterior insula (aIns), frontal eye fields (FEF), dorsolateral prefrontal cortex (DLPFC), inferior precentral sulcus (iPCS), ventral occipital cortex (vOC), inferior parietal lobule (iPL), and the ventral IPS (vIPS). The network clusters are isosurfaces for P = 0.01, and the location of the seed-voxel is indicated in the axial slice by a white square.
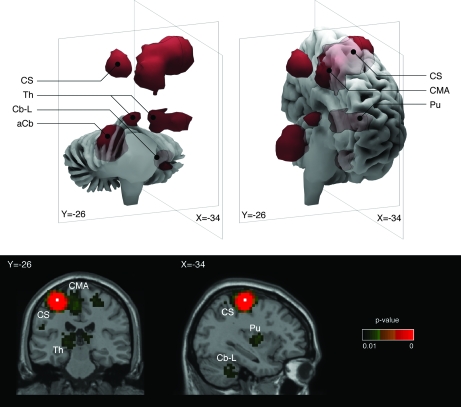
Figure 6.
Cortico-diencephalo-cerebellar “motor” network. Three-dimensional reconstructions and coronal (y = −26) and para-sagittal (x = −34) stereotaxic slices of the network recovered with a seed-voxel at the dorsal part of the left central sulcus (CS, x = −34, y = −26, z = 60). The network includes the right central sulcus, caudal cingulate motor area (CMA), ipsilateral putamen (Pu), thalamus (Th), and left cerebellum (Cb-L), and the contralateral anterior lobe of the cerebellum (aCb). The network clusters are isosurfaces for P = 0.01, and the seed-voxel is indicated by white squares in the coronal and sagittal slices.
Reproducibility
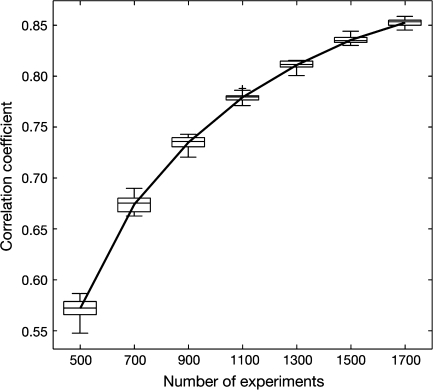
Reproducibility of the coactivation map was assessed by estimating the similarity between pairs of partial coactivation maps that used disjoint random subsamples of experiments. Figure 2 shows that the correlation between maps was significant and increased asymptotically with the number of experiments, being reasonably high with only 500 experiments. Thus, the meta-coactivation map does not depend on a particular choice of experiments, and there exists a robust structure in the functional coactivations that can be recovered even with a moderate number of studies.
Figure 2.
Reproducibility of the coactivation map. Pairs of partial coactivation maps computed from disjoint random subsets of the total database of experiments were progressively more similar as the number of experiments increased. The plot shows the distribution of the correlation coefficient for 20 pairs of partial coactivation maps computed from independent sets of 500, 700, 900, 1100, 1300, 1500, and 1700 experiments.
Networks
For every voxel in stereotaxic space, the coactivation map contains a complete 3-dimensional volume of its coactivations with the whole brain. These volumes represent networks of varying complexity, from those with significant coactivations only around the seed-voxel, to those showing a rich pattern of cortical and subcortical coactive regions. Here we illustrate that the coactivation map does recover meaningful networks by describing some well-known cases of functional connectivity.
Symmetric Interhemispheric Coactivations
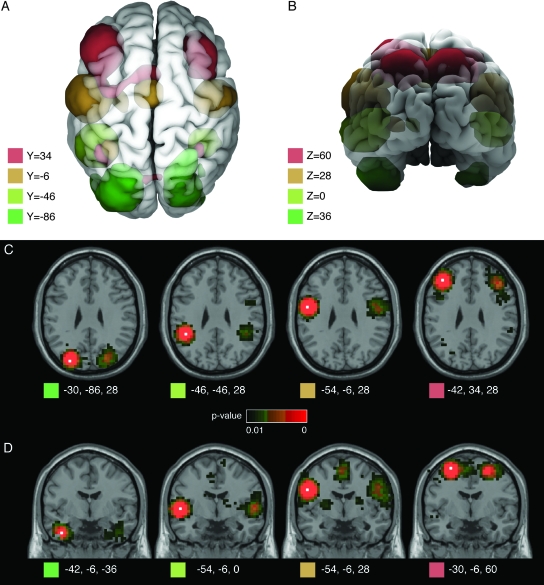
Figure 3 shows examples of symmetric interhemispheric coactivations between different regions of the cerebral cortex. Symmetric coactivations of this kind are among the strongest functional correlations that we can observe in the brain; and almost 2/3 of the voxels in the coactivation map have them. These coactivations are likely mediated by interhemispheric callosal fibers. Given that the number of callosal fibers is minimal compared with intrahemispheric corticocortical fibers, the strength of symmetric interhemispheric coactivations is impressively high.
Figure 3.
Symmetric interhemispheric coactivations. Coactivations of regions in the left hemisphere included most of the time the symmetric region in the right hemisphere, and vice versa. The figure shows 3-dimensional reconstructions (A, B) and stereotaxic slices of 4 networks corresponding to 4 seed-voxels in the axial plane z = 28 (C), and 4 networks in the coronal plane y = −6 (D). The network clusters are isosurfaces for P = 0.01, and the location of the seed-voxels is indicated by white squares in the stereotaxic slices.
Examples of Specific Networks
As an illustration of the type of network represented in the coactivation map, we have chosen seed-voxels for 3 well-known networks, based on the stereotaxic coordinates reported in the literature. We show the fronto-parietal “attention” network, cingulo-parietal “resting state” network, and the cortico-diencephalo-cerebellar “motor” network.
Fronto-parietal network.
A network including the SMA/preSMA, left and right anterior insula, frontal eye fields, dorsolateral prefrontal cortex, precentral sulcus, ventral occipital cortex, thalamus, and cerebellum (Fig. 4) was recovered with a seed-voxel of stereotaxic coordinates x = −26, y = −58, z = 48. This coordinate corresponds to the left intraparietal cortex in Fox et al. (2005). The likelihood ratios in this network are among the highest that we could observe in the coactivation map. In functional connectivity analyses, activity within this network is frequently observed during the performance of a task, and it has been named the “attention” network because of its involvement in top-down modulation of attention and working memory tasks (Fox et al. 2005).
Cingulo-parietal network.
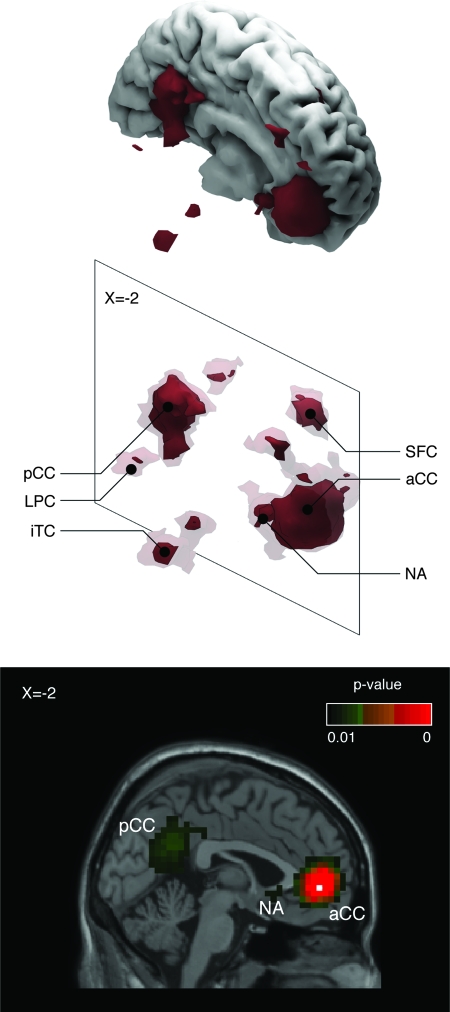
A network including the anterior cingulate cortex, nucleus accumbens in the subcallosal region, ventral and dorsal parts of the precuneus, inferior temporal cortex, lateral parietal cortex, and the part of the superior frontal cortex just anterior to the frontal eye field (Fig. 5) was recovered with a seed-voxel of coordinates x = −2, y = 46, z = −4. This seed-voxel corresponds to the anterior cingulate cortex region in Fox et al. (2005). The cingulo-parietal network is frequently found in functional connectivity analyses when subjects do not perform any task, having been named “resting state” or “default mode” network (Greicius et al. 2003; Fox et al. 2005).
Figure 5.
Cingulo-parietal “resting state” network. Three-dimensional reconstructions and sagittal stereotaxic slice (x = −2) of the network recovered with a seed-voxel at the anterior cingulate cortex (aCC, x = −2, y = 46, z = −4). It includes the posterior cingulate cortex (pCC), nucleus accumbens (NA), lateral parietal cortex (LPC), inferior temporal cortex (iTC), and the superior frontal cortex (SFC). The network clusters are isosurfaces for P = 0.01 (strong red), and P = 0.5 (in transparency). The location of the seed-voxel is indicated by a white square in the sagittal slice.
Cortico-diencephalo-cerebellar network.
A seed-voxel in the left central sulcus, coordinates x = −34, y = −26, z = 60 in Paus et al. (1998), was used to recover a network including the caudal cingulate motor area; ipsilateral putamen, thalamus and middle cerebellar peduncle; and the contralateral anterior lobe of the cerebellum (Fig. 6). These regions, related to the execution of motor tasks, constitute the “motor” network (Paus et al. 1998; Postuma and Dagher 2006).
Discussion
We have described a map of the functional coactivations for the whole human brain, constructed from an automatic meta-analysis of 825 articles and 3402 experiments. This meta-coactivation map represents what appears to be an invariant structure in the pattern of brain coactivations, independent of any particular choice of articles and experiments. The networks represented in the map are meaningful; we have shown that, for example, the fronto-parietal “attention” network, the cingulo-parietal “resting state” network and the cortico-diencephalo-cerebellar “motor” network can be found within the map.
Meta-analysis has been previously used to characterize patterns of functional coactivations in the human brain (Koski and Paus 2000; Lancaster et al. 2005; Postuma and Dagher 2006). This is, however, the first time that meta-analysis is used to produce a dense 6-dimensional map of coactivations across the entire brain (i.e., of every brain location with every other location).
Compared with standard analyses of functional connectivity, the meta-analytical approach poses several challenges. Our raw data are nondimensional points that intend to represent whole clusters of activation. Furthermore, these coordinates are obtained from studies using different methodologies, with different scanners and scanning methods, different numbers of subjects, and different statistical methods used to detect “activation.” In addition to the methodological problems, we need to consider the large intrinsic variability in the anatomy and function of the human brain, a difficulty that different studies address through different normalization techniques, and even using different stereotaxic spaces (Brett et al. 2002). These restrictions represent a strong filter to the kind of functional connection that we are able to recover, and only the most reproducible traits of functional networks will be captured by our meta-coactivation map.
Given all these limitations, it is striking to observe that we can recover the structure of some well-known networks with high accuracy. As an example, Table 1 shows a comparison between the fronto-parietal and the cingulo-parieto-temporal networks in the meta-coactivation map (Figs 4 and 5), and the corresponding “task-positive” and “task-negative” networks obtained through direct analyses of fMRI data by Fox et al. (2005). In their work, Fox and collaborators used 3 different seed-voxels to produce a conjunction map for each of the networks (left intraparietal sulcus, right frontal eye field and left ventral occipital cortex for the task-positive network; anterior cingulate cortex, posterior cingulate cortex and left medium temporal cortex for the task-negative network). The top half of Table 1 compares the peaks in the task-positive network to peaks detected automatically in the meta-coactivation map obtained with the left intraparietal sulcus seed-voxel. Nineteen peaks were detected, containing 13 out of the 16 peaks reported by Fox and collaborators, with an average Euclidean distance between corresponding cluster maxima of 1.25 ± 0.78 cm. The clusters of the 3 absent locations, the left and right inferior parietal lobules, and left dorsolateral prefrontal cortex, were fused with the clusters of the left and right intraparietal sulci and the left frontal eye field respectively, which explains why they were not identified as independent peaks. The same may be the case for the 4 cortical peaks in the coactivation map that were not reported in the task-positive network, as these locations seem to be included in a larger cluster in the conjunction map of Fox and collaborators. The bottom half of Table 1 compares the task-negative network to that obtained with the anterior cingulate seed-voxel. From the 12 peaks detected, 10 out of the 13 peaks reported by Fox and collaborators were found, with an average Euclidean distance between cluster maxima of only 1.03 ± 0.59 cm. Among the 3 absent peaks, the right medial prefrontal cluster was fused with the anterior cingulate cluster, which explains why it was not detected. Finally, we found the nucleus accumbens, which is not reported by Fox et al. (2005) but is present in the analysis of the same network by Greicius et al. (2003).
Table 1.
Comparison of peak locations
| Region |
Fox et al. (2005) |
Coactivation map |
||||
| x | y | z | x | y | z | |
| Fronto-parietal network | ||||||
| IPS-L | −23 | −66 | 46 | −26 | −58 | 48 |
| IPS-R | 25 | −58 | 52 | 26 | −58 | 48 |
| iPL-L | −42 | −44 | 49 | — | ||
| iPL-R | 47 | −37 | 52 | — | ||
| vIPS-L | −26 | −80 | 26 | −26 | −82 | 20 |
| vIPS-R | 35 | −81 | 29 | 30 | −82 | 16 |
| FEF-L | −24 | −12 | 61 | −30 | −10 | 48 |
| FEF-R | 28 | −7 | 54 | 26 | −6 | 52 |
| iPCS-L | −54 | 0 | 35 | −46 | −2 | 40 |
| SMA/preSMA | −2 | 1 | 51 | −2 | 10 | 48 |
| DLPFC-L | −40 | 39 | 26 | — | ||
| DLPFC-R | 38 | 41 | 22 | 38 | 26 | 32 |
| vOC-L | −47 | −69 | −3 | −46 | −66 | −4 |
| vOC-R | 54 | −63 | −8 | 34 | −74 | −4 |
| aIns-L | −45 | 5 | 8 | −30 | 22 | 0 |
| aIns-R | 45 | 4 | 14 | 30 | 22 | 8 |
| aIns-R2 | — | 30 | 18 | −4 | ||
| vFEF-L | — | −46 | −2 | −40 | ||
| vFEF-R | — | 46 | 2 | 24 | ||
| vOC-L2 | — | −18 | −90 | −16 | ||
| Th-L | — | −18 | −14 | 8 | ||
| Cb-R | — | 18 | −54 | −44 | ||
| Cingulo-parietal network | ||||||
| pCC1 | −2 | −36 | 37 | −6 | −58 | 28 |
| pCC2 | 3 | −51 | 8 | 6 | −46 | 8 |
| LPC-L | −47 | −67 | 36 | −46 | −66 | 24 |
| LPC-R | 53 | −67 | 36 | — | ||
| aCC1 | −3 | 39 | −2 | −2 | 46 | −4 |
| aCC2 | 1 | 54 | 21 | 6 | 50 | 28 |
| SFC-L | −14 | 38 | 52 | −18 | 34 | 48 |
| SFC-R | 17 | 37 | 52 | 14 | 38 | 48 |
| iTC-L | −61 | −33 | −15 | — | ||
| iTC-R | 65 | −17 | −15 | 50 | −14 | −20 |
| paraHipp-L | −22 | −26 | −16 | −22 | −22 | −20 |
| paraHipp-R | 25 | −26 | −14 | 18 | −22 | −20 |
| Cb | 7 | −52 | −44 | — | ||
| NA | — | 2 | 14 | −12 | ||
| iTC-R2 | — | 34 | −6 | −36 | ||
Note: pCC, posterior cingulate cortex; aCC, anterior cingulate cortex; NA, nucleus accumbens; iTC, inferior temporal cortex; LPC, lateral parietal cortex; SFC, superior frontal cortex; SMA, supplementary motor area and preSMA; aIns, left and right anterior insula; FEF, frontal eye fields; DLPFC, dorsolateral prefrontal cortex; iPCS, inferior precentral sulcus; vOC, ventral occipital cortex; iPL, inferior parietal lobule; IPS, intraparietal sulcus; vIPS, ventral IPS; Th, thalamus; Cb-R, right cerebellum; paraHipp, para-hippocampus.
Neural networks are an essential component of our current understanding of cognition (Jirsa and McIntosh 2007). The possibility of quickly obtaining a map of frequently active regions given a particular seed-voxel may be of broad interest for experimental and theoretical research. It can provide researchers a priori hypotheses on human brain connectivity that can be then empirically tested, or used to constrain structural equation models (McIntosh and Gonzales-Lima 1994). A number of recent theoretical models have used structural connectivity data to study the functional dynamics allowed by anatomical networks (Izhikevich et al. 2004; Sporns et al. 2005; Bressler and Tognoli 2006). The dense map of functional coactivation networks that we have described can provide further information on the relationship between the patterns of white matter connectivity and the functional networks of the human brain.
Source code and binaries for a graphic user interface to browse through the coactivation map have been made available, and can be downloaded at http://coactivationmap.sourceforge.net.
Funding
National Institutes of Health/National Institute of Mental Health (R01 MH074457) to P.T.F., Principal Investigator.
Acknowledgments
We thank Pierre Bellec for his comments and suggestions. Conflict of Interest: None declared.
References
- Braitenberg V, Schüz A. Anatomy of the cortex: statistics and geometry. Berlin: Springer; 1991. [Google Scholar]
- Bressler SL, Tognoli E. Operational principles of neurocognitive networks. Int J Psychophysiol. 2006;60:139–148. doi: 10.1016/j.ijpsycho.2005.12.008. [DOI] [PubMed] [Google Scholar]
- Brett M. 1999. The MNI brain and the Talairach atlas. [Google Scholar]
- Brett M, Johnsrude I, Owen A. The problem of localization in the human brain. Nat Rev Neurosci. 2002;3:243–249. doi: 10.1038/nrn756. [DOI] [PubMed] [Google Scholar]
- Felleman DJ, Van Essen DC. Distributed hierarchical processing in primate cerebral cortex. Cereb Cortex. 1991;1:1–47. doi: 10.1093/cercor/1.1.1-a. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Nat Acad Sci USA. 2005;102:9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ. Functional and effective connectivity in neuroimaging: a synthesis. Hum Brain Mapp. 1994;2:56–78. [Google Scholar]
- Genovese CR, Lazar N, Nichols TE. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage. 2002;15:870–878. doi: 10.1006/nimg.2001.1037. [DOI] [PubMed] [Google Scholar]
- Greicius M, Krasnow B, Reiss I, Menon V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Nat Acad Sci USA. 2003;100:253–258. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM, Gally JA, Edelman GM. Spike-timing dynamics of neuronal groups. Cereb Cortex. 2004;14:933–944. doi: 10.1093/cercor/bhh053. [DOI] [PubMed] [Google Scholar]
- Jirsa VK, McIntosh AR. Handbook on brain connectivity. Berlin: Springer; 2007. [Google Scholar]
- Koski L, Paus T. Functional connectivity of the anterior cingulate cortex within the human frontal lobe: a brain-mapping meta-analysis. Exp Brain Res. 2000;133:55–65. doi: 10.1007/s002210000400. [DOI] [PubMed] [Google Scholar]
- Laird AR, Lancaster JL, Fox PT. BrainMap: The social evolution of a functional neuroimaging database. Neuroinformatics. 2005;3:65–78. doi: 10.1385/ni:3:1:065. [DOI] [PubMed] [Google Scholar]
- Lancaster JL, Laird AR, Fox M, Glahn DE, Fox PT. Automated analysis of meta-analysis networks. Hum Brain Mapp. 2005;25:174–184. doi: 10.1002/hbm.20135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manning CD, Schütze H. Foundations of statistical natural language processing. Cambridge (MA): MIT Press; 1999. [Google Scholar]
- McIntosh AR, Gonzales-Lima F. Structural equation modelling and its application to network analysis in functional brain imaging. Hum Brain Mapp. 1994;2:2–22. [Google Scholar]
- Mood AM, Graybill FA, Boes DC. New York: McGraw-Hill; 1974. Introduction to the theory of statistics. [Google Scholar]
- Paus T, Jech R, Thompson CJ, Comeau R, Peters T, Evans AC. Dose-dependent reduction of cerebral blood flow during rapid-rate transcranial magnetic stimulation of the human sensorimotor cortex. J Neurophysiol. 1998;79:1102–1107. doi: 10.1152/jn.1998.79.2.1102. [DOI] [PubMed] [Google Scholar]
- Postuma RB, Dagher A. Basal ganglia functional connectivity based on a meta-analysis of 126 positron emission tomography and functional magnetic resonance imaging publications. Cereb Cortex. 2006;16:1508–1521. doi: 10.1093/cercor/bhj088. [DOI] [PubMed] [Google Scholar]
- Schüz A, Chaimow D, Liewald D, Dortenmann M. Quantitative aspects of corticocortical connections: a tracer study in the mouse. Cereb Cortex. 2006;16:1474–1486. doi: 10.1093/cercor/bhj085. [DOI] [PubMed] [Google Scholar]
- Sporns O, Tononi G, Kötter R. The human connectome: a structural description of the human brain. PLoS Comput Biol. 2005;1:e42. doi: 10.1371/journal.pcbi.0010042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephan KE, Kamper L, Bozkurt A, Burns GAPC, Young MP, Kötter R. Advanced database methodology for the collation of connectivity data on the macaque brain (CoCoMac) Phil Trans R Soc Lond B. 2001;356:1159–1186. doi: 10.1098/rstb.2001.0908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talairach J, Tournoux P. Co-planar stereotaxic atlas of the human brain. New York: Thieme; 1988. [Google Scholar]
- Young MP, Scannell JW, Burns GAPC. The analysis of cortical connectivity. Austin (TX): R.G. Landes; 1995. [Google Scholar]