Kinetic regulation of coated vesicle secretion

Abstract

The secretion of vesicles for intracellular transport often relies on the aggregation of specialized membrane-bound proteins into a coat able to curve cell membranes. The nucleation and growth of a protein coat is a kinetic process that competes with the energy-consuming turnover of coat components between the membrane and the cytosol. We propose a generic kinetic description of coat assembly and the formation of coated vesicles and discuss its implication to the dynamics of COP vesicles that traffic within the Golgi and with the endoplasmic reticulum. We show that stationary coats of fixed area emerge from the competition between coat growth and the recycling of coat components, in a fashion resembling the treadmilling of cytoskeletal filaments. We further show that the turnover of coat components allows for a highly sensitive switching mechanism between a quiescent and a vesicle producing membrane, upon a slowing down of the exchange kinetics. We claim that the existence of this switching behavior, also triggered by factors, such as the presence of cargo and variation of the membrane mechanical tension, allows for efficient regulation of vesicle secretion. We propose a model, supported by different experimental observations, in which vesiculation of secretory membranes is impaired by the energy-consuming desorption of coat proteins, until the presence of cargo or other factors triggers a dynamical switch into a vesicle producing state.

The plasma membrane and the membrane of cell compartments such as the endoplasmic reticulum (ER) and the Golgi continually produce vesicles for cargo transport. Vesicle formation generally involves specific proteins that aggregate into semirigid coats of dimensions in the 100-nm range, well visible by electronic microscopy (1–3). The process of vesicle formation is now rather well established (4) and is sketched in Fig. 1. First, various cytosolic proteins assemble on the membrane into elementary coat-building units, called monomers. The membrane-bound monomers then polymerize into coat structures that locally bend the membrane and recruit cargo molecules. As the coat expands, the coated membrane invaginates until it forms a nearly spherical vesicle containing cargo (5,6) that is eventually released from the membrane. The coat components soon disassemble and are ready to participate in the formation of a new vesicle.

Fig. 1.

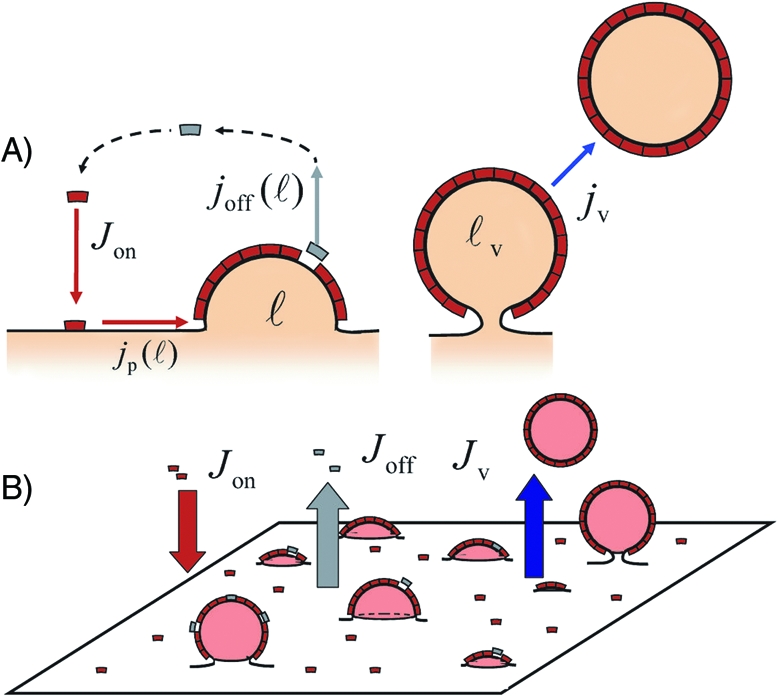
(A) Kinetic model of coated vesicle formation. A monomer cycle: activation/membrane binding (J_on), aggregation [j_p(ℓ)], membrane unbinding via inactivation [j_off(ℓ)] or vesiculation (j_v). (B) Coat population and the global fluxes in and out of the membrane.

The coats are classified in three major classes, COPII, COPI, and clathrin. Although they involve distinct proteins, the three types of coat share many common features, from their size and shape to the mechanism by which polymerization, cargo recruitment, and membrane deformation is achieved (4). Our approach is primarily aimed at studying the formation of COPI and COPII vesicles. However, the generality and robustness of its outcome suggest relevance for the more sophisticated clathrin coats as well. The assembly of COPs and clathrin and the fission of COP vesicles can now be reconstituted on purified liposomes with a restricted number of components (7–9). Those experiments point out the robustness of the coat-formation process. They also confirm that coat polymerization is spontaneous, only driven by weak short-range attractions between the monomers, whereas coat disassembly requires the presence of an energy source. More precisely, the assembly and disassembly of COP coat components follow the cycle of activation–inactivation of a GTPase protein, Sar1 for COPII and Arf1 for COPI (4). Once activated, the GTPases bind to the membrane and recruit individual coatomer complexes (the monomers) that later polymerize into coats (10). The inactivation of the GTPase, triggered by the hydrolysis of its bound GTP, leads to its unbinding from the membrane and to the monomer disassembly if the GTPase belongs to a monomer.

Strikingly, fluorescence recovery after photobleaching (FRAP) experiments suggest that the exchange kinetics of coat components is much faster than the rate of vesicle secretion (10). In other words, many futile monomers are released to the cytosol during the expansion of a coat. So, whereas new membrane-bound monomers polymerize at the coat periphery, others within the coat disassemble and are expelled to the cytosol. Paradoxically, the consumption of energy via GTP hydrolysis seems to work against coat growth and to prevent vesicle formation. This resembles microtubules dynamics and by analogy to the treadmilling of microtubules, it has been suggested that the competition between growth and unbinding may produce stable coats of fixed area (10–13).

In this article, we investigate theoretically the consequence of futile release of coat components on the distribution of size and shape of protein coats and, more practically, on the amount of secreted vesicles. In our model (Fig. 1), monomers are continuously “dropped” onto a membrane and proceed to aggregate into coats of growing size that curve the membrane. Monomers leave the membrane either individually after GTP hydrolysis or collectively as part of a completed vesicle. Intuitively, one expects GTPase inactivation to decrease the rate of vesicle formation by reducing the lifetime of membrane-bound monomers. However, our generic approach reveals that a deeper understanding of vesicle secretion requires a quantitative statistical model. Indeed, we report the existence of a discontinuous dynamical transition from a quiescent to a vesicle-producing membrane, upon variation of the rate of GTP hydrolysis. In other words, the apparently counterproductive energy consumption that favors the unbinding of coat components provides secretory membranes with a highly sensitive switch to regulate vesicle release, triggered, for instance, by a variation of the cargo concentration or the mechanical tension of the membrane.

Description of the Model

Our goal is to describe the collective behavior of a population of evolving membrane domains (coats) formed by the aggregation of identical units (monomers), which are themselves continuously recycled between the membrane and a reservoir (the cytosol). Our starting point is the course of events depicted in Fig. 1. We consider a patch of membrane much larger than the size of individual coats, which is subjected to a constant and homogeneous influx of monomers J_on. The monomers have a finite lifetime on the membrane before being recycled to the cytosol, at a rate k_off. While on the membrane, they diffuse and eventually aggregate into curved protein coats. Coats that manage to reach a critical size leave the membrane as coated vesicles.

Monomers.

The formation of a new monomer on the membrane involves a succession of steps (GTPase binding on membrane and activation and the recruitment of coat proteins) that are not individually described in the present model. The rates associated with these processes enter a unique parameter, the mean number of monomers J_on formed on the membrane per units of time and area.

Coat Growth.

Coat expansion proceeds by polymerization of monomers at the coat edge. Monomer–monomer binding is spontaneous and results from weak short-range interactions. The binding energy γ should be in the range of a few k_BT (k_BT is the energy available from thermal fluctuations, with k_B the Boltzmann constant and T the temperature in Kelvin), because the 10k_BT provided by GTP hydrolysis is sufficient to break the bonds. The polymerization is thus thermally reversible and solely driven by the minimization of the free energy of the coat.

Coat Structure.

Electron microscopy (1,2) supports the assumption that the optimal area per monomer s₀ (≈100 nm²) and the optimal radius of curvature of the coat R₀ (≈50 nm) are homogeneous within the coat and remain constant during coat growth. We thus adopt a model in which the state of a coat is fully characterized by a single, slowly varying parameter: the number of polymerized monomers ℓ it contains, taken as a continuous variable for commodity. All other internal degrees of freedom in the coat (protein density and coat shape) are considered to adjust to their optimal configuration faster than the typical rates of coat growth and GTP-hydrolysis. Under these assumptions, a given coat of size ℓ can be described as a spherical cap of constant curvature (defined as the dimensionless quantity $c=\sqrt{s_0/(4\pi R_0^2)}\approx 1/20$). A full spherical coat (ℓc² = 1) with these properties contains several hundred monomers.

Monomer Release.

Contrary to the reversible monomer polymerization, monomer desorption is an energy-consuming process driven by GTP hydrolysis. It occurs at a rate k_off, assumed constant here for simplicity [see supporting information (SI) Appendix for a discussion of this assumption]. This rate can be estimated from FRAP experiments (10,12,14,15), k_off ≈ 0.1 – 10 s⁻¹. Under the assumption of constant protein density in the coat, the dissociation of monomer from the coat is followed by a rapid rearrangement of the coat structure and by a slight shrinkage of the coat; monomer inactivation thus opposes coat expansion.

Vesicle Release.

A mature coat containing a number ℓ_v (ℓ_vc² ≲ 1) of bound monomers forms a nearly closed sphere connected to the rest of the membrane by a thin neck. At this stage, the coat cannot grow further and is eventually released into the cytosol as a coated vesicle. The details of the scission mechanism vary between classes of coat, and may involve additional proteins (4). Here, we merely assume that once a domain reachs the critical size ℓ = ℓ_v, it leaves the membrane as vesicles at a constant rate k_v.

Membrane Properties.

The curvature of the coat imposes a deformation to the membrane that is opposed by membrane tension (16). The membrane tension σ thus favors coat depolymerization, and can have a sizable effect on coat growth if it is larger than $\gamma /(s_0\sqrt{{\ell }_v})\simeq {10}^{-5}J/m^2$ (A detailed model for the elastic properties of the protein-covered membrane is discussed in SI Appendix, section II.B). Tensions of the Golgi, the ER, and the plasma membranes are typical in the range σ ≈ 10⁻⁶ – 10⁻⁴J/m² (17), and may thus play a role in vesicle secretion. Hereafter, membrane tension will be expressed in natural units: $\bar{\sigma }=\sigma s_0\approx {10}^{-2}-1k_{\text{B}}T$.

The population of membrane coats is characterized by its size distribution n(ℓ). The mean concentration of coats of size ℓ (between ℓ and ℓ + dℓ) at a time t is n(ℓ,t)dℓ, and the mean concentration of isolated monomers is n₁(t). Our purpose is thus to compute, n(ℓ) and n₁ at steady state, for given values of the parameters γ, $\bar{\sigma }$, k_off, J_on, k_v and ℓ_v. More practically, we will compare the fluxes of coat elements leaving the membrane as inactive monomers J_off and as part of a vesicle J_v (Fig. 1).

Theoretical Framework

Monomer Fluxes and Conservation Relations.

In this section, we derive the kinetic equations for the evolution of the coat size distribution n(ℓ). The monomer cycle can be divided into four steps, to which correspond four different fluxes, as shown in Fig. 1.

• J_on(t) is the influx of single monomers binding to the membrane, taken as an input in our model.

• j_p(ℓt) is the flux of monomer-joining domains of size ℓ, a balance between polymerization and depolymerization for this domain size. Integrated over the entire population, it gives the total flux of monomers incorporated into domains J_p = ∫₁^ℓ_v dℓ j_p(ℓ,t).

• j_off(ℓ,t) is the flux of monomers expelled from domains of size ℓ into the cytosol after GTP hydrolysis. Under the assumption of uniform release, it is given by j_off(ℓ) = k_offn(ℓ)ℓ. Integrated over the entire population, it gives the total flux of individual inactive monomers leaving the membrane J_off = ∫₁^ℓ_v d ℓ j_off(ℓ,t).

• j_v(t) is the flux of mature coats released as vesicles. Introducing the rate of vesicle formation k_v, we have j_v = k_v n(ℓ_v). The total flux of monomers leaving the membrane as part of a vesicle is J_v(t) = j_vℓ_v.

The evolution of the coat size distribution satisfies (see SI Appendix):

and the polymerization current j_p reads:

j_p is proportional to the density of available monomers n₁, and to the rate of monomer binding onto coats k_p (see below). It contains a diffusive term accounting for random polymerization and depolymerization induced by thermal noise and a convective term describing the drift of monomers toward domains of lower energy, driven by the “force” − ∂_ℓ ΔE. The free energy difference ΔE (in k_TT units) between a coat of size ℓ and ℓ isolated monomers diffusing on the membrane is obtained treating the coat as a rigid spherical cap (18) (see also SI Appendix):

where

is a chemical potential including the entropy of the freely diffusing monomers, see SI Appendix.

The net current j (ℓ) = j_p(ℓ) - j_off(ℓ) accounts for polymerization and desorption. It can be written in terms of an effective energy $\tilde{E}(\ell )\equiv \Delta E(\ell )+\frac{k_{\text{off}}}{2k_{\text{p}}{n}_1}({\ell }^2-1)$:

with

This equation introduces an effective tension Σ that illustrates the fact that desorption of inactive monomers and membrane tension formally play the same role in hindering coat maturation and vesicle secretion. Note that more generally, the coatomer binding or inactivation rates may depend on the coat size, in which case monomer desorption enters the effective energy as ∫d ℓ ℓ (k_off(ℓ)/k_p(ℓ)).

Finally, the monomer influx J_on and the flux of secreted vesicle j_v are accounted for via the boundary conditions (see SI Appendix)

Steady State.

At steady state, all fluxes are balanced and ∂ _t n = 0. Eqs. 1–9 reduce to two conditions to be satisfied by n₁ and n(ℓ):

The former equation enforces that the size distribution is constant, and the latter that the flux of monomer binding to the membrane balances the flux of monomer leaving the membrane, either after inactivation or by vesiculation.

Results

In this section, we focus on the steady state of a membrane receiving a constant influx of monomer, each having a finite lifetime at the membrane. The full characterization of the coat population and of vesicle secretion follows two steps. First, the stationary distribution of coat size n(ℓ) is computed for a given concentration of free monomers n₁ with Eq. 10. Second, n₁ is self-consistently derived for a given monomer influx J_on by imposing that the influx matches the total monomer outflux (Eq. 11). While the first step relies entirely on the properties of the free energy landscape $\tilde{E}$(ℓ), the second introduces collective effects emerging from the competitive growth of many domains, which ultimately give rise to the “secretory switch.”

Effective Energy Landscape and Steady-State Distribution.

Apart from thermal fluctuations, a coat is driven toward growth or shrinkage by the effective “force” − ∂_ℓ$\tilde{E}$(ℓ) (Eq. 5). Coat growth is thus formally analogue to thermal diffusion along the effective energy landscape $\tilde{E}$(ℓ) (Eq. 6). The analytical expression of the coat size distribution is given in SI Appendix. Several different regimes can be distinguished under increasing monomer concentration (Fig. 2).

Fig. 2.

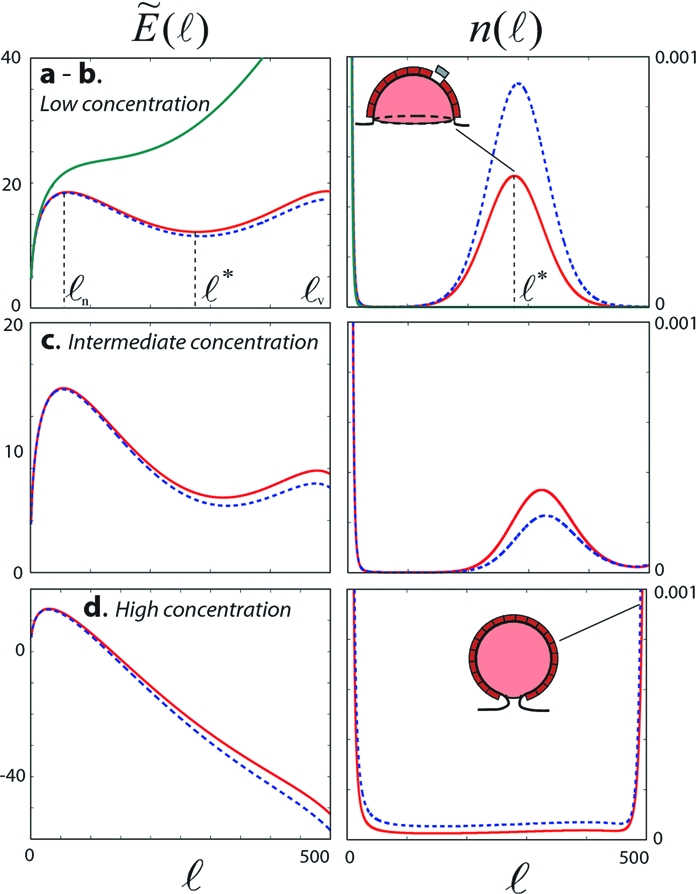
Effective energy landscape $\tilde{E}$(ℓ) (Left, in k_BT units, from Eq. 6) and the corresponding coat size distribution n(ℓ) (Right, in n₁^cmc units, from Eqs. 5–10), for different values of the free monomer density n₁. n₁/n₁^cmc = 0.986 (state a - Top green curve), 1.039 (state b - Top red), 1.054 (state c - Middle) and 1.160 (state d - Bottom). The variation of $\tilde{E}$(ℓ) and n(ℓ) upon a slight increase of n₁ above the given value are shown in blue dashed lines. Other parameters are γ = 5 k_BT, σ = 0, k_v = 0.13s⁻¹, k_off = 0.12s⁻¹, and ℓ_v = 500. With those values, n₁^cmc = 0.009.

The energy landscape illustrates the interplay between antagonistic effects; short-range attractions between monomers promotes polymerization, whereas the entropy of the free monomer favors their dispersion. The γ and μ terms in Eq. 6 reflect this competition. Furthermore, monomer inactivation and unbinding and membrane mechanical tension hinder coat growth (k_off and σ, respectively, combined in the effective tension Σ, Eq. 7). Depending on the monomer concentration, the landscape may show a local maximum at a small size ℓ_n (Fig. 2 states b–d), which indicates a nucleation process. Coats must reach the critical size ℓ_n (through fluctuations in the pool of free monomers) in order to consistently grow further, and the rate of nucleation is controlled by the height of the energy barrier. The effective energy may also show an barrier to vesiculation for large coat size ℓ ∼ ℓ_v (Fig. 2 states b and c), indicating that large coats are suppressed by the effective membrane tension Σ. A local minimum then exist for an intermediate size ℓ*, corresponding to kinetically stable coats.

Low monomer concentration.

At low monomer concentration, the large energy barrier to vesiculation at ℓ = ℓ_v prevents coats to mature into vesicles (J_v ≃ 0) (Fig. 2, states a and b). The coat size distribution resembles a distribution at thermal equilibrium: n(ℓ) ≃ e^{-$\tilde{E}$(ℓ)}, and the membrane follows a classical scheme common to many self-assembling systems [e.g., surfactants in solution (19)]. The local energy minimum at ℓ* appears above a critical concentration n₁^cmc, analogue to the “critical micellar concentration,” or “cmc” at which surfactants in solution start forming micellar aggregates (see ref. 19 and SI Appendix). For n₁ < n₁^cmc (Fig. 2 state a), entropy dominates, and the effective energy increases monotonously with the coat size ℓ. Monomer aggregation is unfavorable, and the membrane contains mainly single monomers and few small transient domains formed by fluctuation. For n₁ > n₁^cmc (Fig. 2 state b), long-lived coats can nucleate, at a rate fixed by the nucleation barrier, and grow up to the optimal size ℓ*. Maturation into coated vesicles (ℓ = ℓ_v) is prevented by monomer desorption and membrane tension.

Larger monomer concentration.

The height of the energy barrier to vesiculation at ℓ = ℓ_v decreases with increasing monomer concentration. When it falls below the nucleation energy barrier (Fig. 2 state c), domains may mature into fully formed vesicles and vesicle secretion becomes increasingly probable. The optimal coat size ℓ* increases with n₁ and eventually exceeds the critical size for vesiculation ℓ_v at high monomer concentration (Fig. 2 state d), under which conditions any nucleated domain matures into a fully formed vesicle.

The growth of individual coats is controlled by the amount of free, active monomers n₁. On the other hand, the pool of free monomers is depleted by their binding onto growing coats and is thus influenced by the coat population. As we shall see next, this feedback induces remarkable collective effects within the coat population, which presents a discontinuous transition between a state of arrested growth and a state of abundant vesiculation within a narrow range of kinetic parameters.

Vesicle Secretion is Controlled by Collective Effects.

The solution of the coupled Eqs. 10 and 11 is graphically represented on Fig. 3 as the intersection of the monomer in-flux J_on and total outflux J_off + J_v. It may fall in four different regimes (a–d), corresponding to the four distributions plotted in Fig. 2. In a wide range of parameters (see below), J_off displays the remarkable property of being nonmonotonous, with a sharp peak at a critical concentration of free monomers. This behavior dramatically influences the membrane's ability to secrete vesicles. Indeed, a given monomer influx may correspond to three distinct dynamical states of the membrane. We will show below that regimes b and d represent respectively a quiescent membrane and a membrane secreting large amount of vesicles, whereas regime c is dynamically unstable. The secretory membrane thus constitutes a bistable dynamical system able to abruptly switch vesicle secretion on and off at prescribed monomer turnover rates.

Fig. 3.

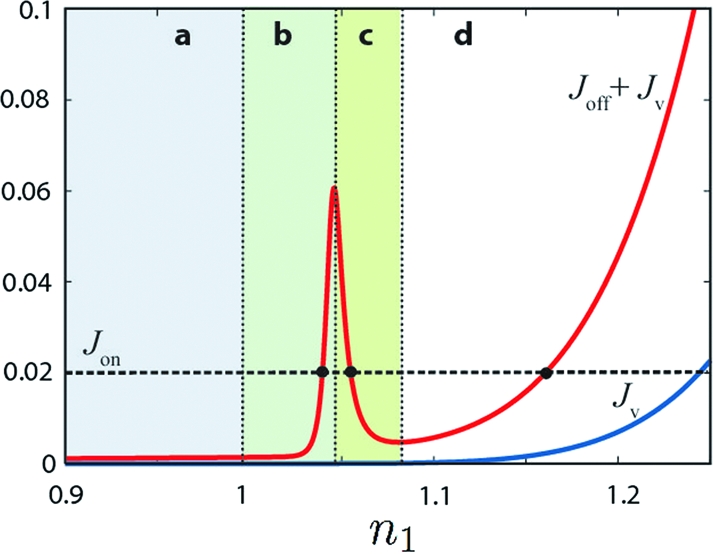
The fluxes of monomers leaving the membrane at steady state, as a function of the density of active monomer n₁ (in n₁^cmc unit). J_v (blue) is the vesiculation flux and J_off (red) the sum of vesiculation and inactivation. At stationary state, the total outgoing flux balances the incoming flux (J_off + J_v = J_on) (horizontal dashed line). Fluxes are in k_p(n₁^cmc)² unit and the black dots correspond to the three different states (b, c, d) depicted in Fig. 2.

Because all membrane-bound monomers are inactivated with the same rate k_off, the total flux of monomer leaving the membrane after inactivation J_off is directly proportional to the total amount of monomer on the membrane. The peak of J_off in Fig. 3 stems from the complex relationship between the concentration of isolated monomer n₁ and the total amount of coat components on the membrane.

No vesicle secretion regimes a and b.

If no coat can form (low monomer concentration: state a), the monomers outflux is dominated by the desorption of free monomer: J_off ≃ k_offn₁. If coats can form, but do not mature into vesicles (state b), the outflux is dominated by the desorption of monomers belonging to coats of size ℓ*: J_off ≃ k _offℓ*n(ℓ*). In this regime, monomers reaching the membrane tend to join a coat and the density of free monomer is almost insensitive to the fluxes: (n₁ ≈ n(ℓ*)^1/ℓ* with ℓ* ≫ 1, see SI Appendix). A small increase of n₁ requires a pronounced increase of the total amount of coat material on the membrane, which explains the sharp rise of the total monomer out-flux J_off with n₁ in Fig. 3. In this regime, the optimal coat size is also insensitive to the monomer fluxes, and is obtained from the minimization of the effective energy $\tilde{E}$ (Eq. 6)

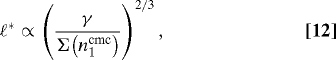The unstable regime c.

For intermediate monomer density, metastable coated pits have a high probability to grow into fully formed vesicle owing to the small barrier to vesiculation (Fig. 2 state c). The rate of vesicle formation increases with n₁, so the total amount of membrane-bound material actually decreases with increasing concentration of free monomer. This is shown by the dashed blue line in Fig. 2 state c, and explains the decrease of J_off in Fig. 3. This situation cannot be maintained at steady state, and spontaneously evolves toward either state b or d.

Steady Vesicle Secretion Regime D.

If the monomer concentration on the membrane is large, the effective coat energy exhibits a nucleation barrier but no intermediate minimum (Fig. 2 state d). After nucleation, a coat grows at nearly constant velocity until it reaches the critical size ℓ_v where it remains trapped for a time 1/k_v before being released as a vesicle. In this regime, both J_off and J_v increase with n₁, Fig. 3.

The bistability exhibited by the coats dynamics relies on the existence of an unstable steady state and holds as long as there exist a (meta)stable coat of intermediate size. This feature is conserved even if the effective energy contains higher-order terms, to be expected if the ratio of monomer dissociation to binding rates (k_off/k_pn₁) increases with the coat size (see SI Appendix). Furthermore, the switch exists if there is a metastable state within the accessible size range: ℓ*/ℓ_v( ≈ ℓ*c²) < 1. From Eq. 12, this condition amounts to Σ > γc³(≈10⁻⁴). The effective tension Σ (Eq. 7) accounts both for the membrane mechanical tension ($\bar{\sigma }$c² ≃ 10⁻⁵ - 10⁻³) and the ratio (k_off / k_pn₁). The binding rate is assumed to be limited by monomer diffusion and is expected to be of the order of the inverse monomer diffusion time over its own size (k _p ≈ D /s₀ ≈ 10⁴s⁻¹, with D ≈ μm²/s the membrane diffusion coefficient). With a dissociation rate k_off ≃ 1s⁻¹, and a monomer density n₁ ≈ 1% (or k_pn₁ ≈ 10²s⁻¹), we find that secretory membranes are well into the bistable regime (Σ ≃ 10⁻² ≫ γc³) and should exhibit the secretory switch discussed below.

Discussion

The growth of coated pits and the secretion of coated vesicles result from a kinetic balance between the polymerization and the inactivation of coat components. It is thus to be expected that coat maturation can only proceed if the coatomers turnover at the membrane is sufficiently slow (10,11,13). Our model goes beyond this intuitive analysis, and shows that secretory membranes are able to abruptly switch between a quiescent and a vesicle-producing state upon a slowing down of coatomer recycling. Switch-like behaviors are clearly advantageous for biological systems. The highly nonlinear nature of a switch confers evident robustness with respect to the noisy environment and allows for a precise regulation of the system's activity. The biological consequences of the secretory switch are discussed below, together with the influence of important factors, such as the density of cargo or the membrane tension, in regulating the activity of secretory membranes. We also show how some apparently unrelated observations on COPs vesicles naturally fit into our global picture of coated-vesicle secretion.

The Secretory Switch.

Consider a secretory membrane receiving a fixed amount of coatomer per unit time. As coatomers accumulate and aggregate, the membrane eventually reaches a steady state in which the flux of coatomer leaving the membrane (by inactivation or vesicle secretion) balances the influx. If the influx is low, the membrane is covered by monomers and stationary coated pits, the latter being prevented from maturing into fully formed coated vesicles by the combined effect of coatomer recycling and the energy associated with membrane deformation. As the influx increases, the coated pits-to-monomer ratio increases (Fig. 2 state a, dashed blue line), but as long as the membrane remains in the “stationary pits” regime (state b, Fig. 3) the size and shape of the coated pits is weakly sensitive to the influx, and no vesicle is produced. However, beyond a threshold value of the influx, state b disappears (Fig. 3). Coated pits are not kinetically stable, and after a fast transient regime that sees the release of the previously stable coated pits, the membrane settles into a state of steady vesicle secretion (state d).

If the influx is now reduced, the membrane remains in the secretory state d, which possesses a stable branch for smaller influx (Fig. 3). The secretory regime disappears below yet another critical threshold, and the systems jumps back into the quiescent state∼b.

The coat population can thus undergo discontinuous dynamical transitions, characterized by an hysteretic cycle, between the two nonequilibrium steady states b and d. In other words, the secretory membrane works in an all-or-nothing fashion and can switch vesicle production on and off within a narrow range of control parameters such as the GTPase activation and inactivation rates and membrane tension. Fig. 4 shows the rate of vesicle secretion as a function of the GTP hydrolysis rate k_off. The discontinuous transition between quiescent and vesicle-producing membrane is clearly apparent and is characterized by two hydrolysis rates (high and low thresholds). Between these two rates, the secretory membrane may be in either state, depending on the system's history (hysteresis).

Fig. 4.

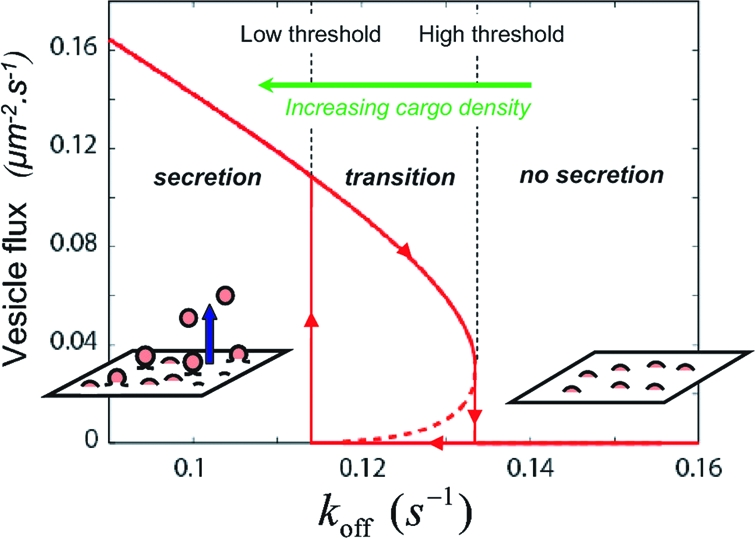
Number of secreted vesicle per μm².s (= j_v × 1μm/s₀) as a function of the rate of coatomer desorption from the membrane k_off. The transition to vesiculation is discontinuous, and is characterized by an hysteretic cycle (arrows), with high and low turnover thresholds. The parameters are the same as those used for Figs. 2 and 3.

Regulation of Vesicle Secretion by Cargo.

The adsorption flux J_on and the desorption rate k_off of coat components at the membrane tightly control vesicle secretion. Recent fluorescence experiments on COPs coat suggest that these rates vary with the amount of cargo present at the membrane. For COPI, the presence of extra cargo leads to significant increase of the amount of coat components at the Golgi membrane, which could reflect either the increase of J_on or the decrease of k_off (12). For COPII, FRAP experiments show that the coatomer exchange rate between the ER membrane and the cytosol is doubled in the absence of cargo. This has been attributed to the increase of k_off with decreasing cargo density (15).

Our model predicts that vesicles can only be secreted if the recycling rate k_off is below a critical value (Fig. 4). By increasing the lifetime of the coatomers at the membrane, the presence of cargo is thus expected to promote vesicle secretion, and a minimal amount of cargo at the membrane might actually be required for transport vesicle to be secreted. The two, high and low, recycling thresholds of Fig. 4 would then corresponds to two critical cargo densities (low and high, respectively).

Considering that newly synthesized cargo is brought to the membrane at a (slow) steady rate and is removed by vesiculation, membrane-bound cargo accumulates in the no-secretion regime, thereby decreasing k_off and moving the system toward the secretion regime. Above the high cargo-density threshold, the coat machinery abruptly escapes the stationary-pits regime and switches to vesicle production (Fig. 4). This results in a decrease of membrane-bound cargo, which increases k_off and moves the system toward the quiescent state. Below the low cargo-density threshold, vesicle secretion is switched off, letting the cargo accumulate until the high-density threshold is reached and vesicle production is resumed, starting a new cycle. Under constant cargo influx, the system should thus periodically switch between quiescent phases and phases of vesicle secretion, following the hysteretic loop of Fig. 4. If cargo synthesis is irregular, the membrane waits for sufficient accumulation of cargo between transient residences in the secreting state, where the accumulated cargo is released. The vesicle flux over time should then appear as an irregular pulsed signal. Recording the total vesicle outflux over an extended patch of secretory membrane over time should thus be of high interest. Oscillatory or pulsed vesicle secretion would be a signature of the secretory switch uncovered by our theoretical analysis (within our framework, steady secretion would indicate that cargo synthesis is sufficiently fast to compensate the secreted cargo).

This accumulator mechanism would provide functional efficiency to the secretory membrane, because it would prevent the futile delivery of empty vesicles. Strikingly, analysis of COPI vesicles in mutant cells where arf1 is unable to hydrolyse GTP have revealed a much lower cargo content than in normal cells (20). This observation supports our prediction. Indeed, in the absence of GTP hydrolysis (k_off = 0), the switch is gone, and vesicle secretion remains “on” regardless of the available amount of cargo.

The existence of an hysteretic cycle can also positively impact on the rate of cargo delivery. At steady state, the flux of cargo delivered by a secretory membrane that would not possesses an unstable regime would automatically adjust to the flux of synthesized cargo. Here, and while the system is traveling along the secretion branch of the hysteretic cycle, the flux of secreted cargo is mainly controlled by the kinetics of coat formation and can potentially be much larger than the rate of cargo synthesis.

Effects of the Membrane Tension: Regulation of Vesicle Formation and Coat Flattening.

Our calculation has shown that membrane tension plays essentially the same role as coatomer recycling in opposing vesicle secretion (Eq. 6). Vesiculation is only possible below a high tension threshold, and the oscillatory behavior described above may also result from variations of tension. Secretion removes membrane area from the organelle and may increase its tension, whereas the fusion of incoming vesicles (21) or other regulatory mechanisms (18), dynamically relaxes tension. Vesicle secretion would thus occur only when enough membrane area has been accumulated to relax the tension. Such a mechanism suggests a coordination of purely mechanical origin between absorption and release of vesicles and could prevent the uncontroled shrinking of secretory compartments. Remarkably, the Golgi strikingly crumbles in cells where the GTP hydrolysis in COPI-coat is rendered inoperant (20).

In Eq. 3, the effect of membrane tension was computed assuming that the coat rigidity κ (unit of energy) was sufficiently strong to impose the domain curvature, which remained constant regardless of the coat size and the membrane properties. This simplification ceases to be valid under high membrane tension (σ ≈ κ/R₀², where R₀ is the radius of curvature of a tensionless coat). Higher tensions result in a flattening of the coat (see SI Appendix, section II.B). Beyond a tension threshold σ > κ/(2R₀²) (≃ 10⁻⁴J/m² for the coat rigidity κ = 100k_BT), the formation of a closed sphere becomes impossible, and protein aggregates should grow as flat patches. High membrane tension would thus favor the formation of flat coatomer aggregates whose size is limited by coatomer recycling (22). Such “flat lattice” are indeed observed for clathrin coats at the basal membrane of adhered cells (23), where adhesive proteins are expected to generate high membrane tensions.

Concluding Remarks.

The model presented here is the simplest implementation of a kinetic model of coated vesicle formation where coat growth competes with the inactivation of coat components. The secretory switch revealed by our work is very robust and relies solely on the (nonequilibrium) thermodynamics of coat formation. Beyond the qualitative agreement with experimental findings discussed in the previous section, we hope that future experiments can further test some of our predictions, which include: (i) the existence of metastable domains of intermediate size, (ii) the role of membrane tension in preventing the formation of curved protein coat and eventually its involvement in the formation of flat lattices, and (iii) the oscillatory or pulsed secretion of vesicles in time.

In this study, we have used the crudest possible description of the coat structure, thus avoiding having to deal with structural details of specific protein coats. Further experimental observation, e.g., on biomimetic systems, could motivate the building of models focusing on the dynamics of a single coat. Supplementary degrees of freedom for the coat shape could be considered, allowing for the competitive growth of structures of various morphologies [tubules (6), spherical caps, and flat lattices (23)], observed in living cells and biomimetic systems.

In the same spirit, the heterogeneties of the coat structures may be included in the model. The coupling beween the GTP hydrolysis rate and the curvature (COPI) or the degree of polymerization (COPII) revealed in recent experiments (14,24), suggest that monomers inactivation may be enhanced at the coat center and limited at the boundary. One could then imagine the formation of layers of active monomers preventing coat disassembly (14,24). Such properties suggest a strong analogy with microtubules (11), and it is tempting to imagine exotic growth dynamics with shrinking cascades such as those observed for microtubules (25).