A case of selective impairment of encyclopaedic numerical knowledge or ‘when December 25th is no longer Christmas day, but ‘20 + 5’ is still 25’

Abstract

This study investigates encyclopaedic numerical knowledge in a patient with a presumed left temporal dysfunction, associated with temporal lobe epilepsy. Encyclopaedic numbers are those used as nominal labels (such as in ‘British Broadcasting Corporation – BBC 1’ or ‘Levis 501’) to express familiar or historical dates (e.g., our birthday or the French revolution, 1789) and to indicate other general or autobiographical numerical information (e.g., Personal Identification numbers – PINs, post-codes, telephone numbers). We showed a dissociation between impaired processing of encyclopaedic numbers and preserved processing of non-encyclopaedic numbers (e.g., the larger between 54 and 65 or the result of ‘6 × 9’). This dissociation complements the existing data showing the reverse pattern of performance, namely an advantage for encyclopaedic compared to non-encyclopaedic numbers. These data add important information on an aspect of numerical processing that has not yet been systematically explored and reinforce the distinction between numerical and non-numerical knowledge in the semantic system.

1. Introduction

Numerical expressions typically refer to quantities, either in terms of the number of things in a set (e.g., three coins in the fountain) or amount of stuff (e.g., 3 kilos); but they can also be used to refer to the order of things (e.g., p. 3, or third page) which is not strictly a quantity (Butterworth, 1999; Dehaene, 1998; Nieder, 2005). Some numerical expressions acquire additional meanings which are not derived from their quantity or ordinal features. We term these as “encyclopaedic numbers”. Typically they have a nominal use, for example, when they identify objects like commercial brands (e.g., ‘Levis 501’), movies (e.g., ‘2001: A Space Odyssey’), and TV channels (e.g., ‘British Broadcasting Corporation – BBC 1’ in the UK). Encyclopaedic numbers also refer to familiar (e.g., our birthday) and famous or historical dates (e.g., ‘September 11th’ or ‘1789’), zip codes (e.g., ‘22063’), telephone numbers (e.g., ‘999’), and other general and autobiographical numbers (e.g., age of consent, PINs, wedding anniversary). Nominal number assignments are exclusively verbal and are found only in linguistic humans (Butterworth, 1999; Nieder, 2005). Understanding and using nominal encyclopaedic numbers entail acquiring additional knowledge. Thus, it is not sufficient to know that “747” is the number that follows 746 to understand that it refers to a type of aircraft. Some encyclopaedic numbers also imply the processing of quantity, i.e., cardinal encyclopaedic numbers. Those numbers provide the answer to questions such as “How many people are in a football team” or “How many sections are in Dante's Divine Comedy?”. As they are stored in a propositional format, cardinal encyclopaedic numbers differ from more general cardinal numbers which can only be calculated or approximated (e.g., ‘3 × 4’ or the approximate result of ‘342 + 709’). This distinction may seem inappropriate for cardinal encyclopaedic numbers that can be inferred without accessing encyclopaedic knowledge, for instance, when counting techniques are applicable like in ‘How many legs does a horse have’. However, most cardinal encyclopaedic numbers cannot be inferred by counting or calculating but only by retrieving additional information stored in long-term memory. For instance, in the previous case of ‘How many sections are in Dante's Divine Comedy?’, either we know the answer as it is stored in long-term memory or we cannot infer it by any visual representation.

Little is known about the processing of encyclopaedic numbers compared to cardinal or ordinal numbers (see Nieder, 2005, for a review). One study by Alameda et al. showed that number naming is faster after an associative prime than after an unrelated prime. Subjects were faster at naming the target number ‘747’ when it was preceded by the prime ‘Boeing’ compared to an unrelated prime (Alameda et al., 2003). Moreover, lesion studies showed that some neurological patients perform better in tasks involving encyclopaedic numbers compared to non-encyclopaedic numbers. For instance, a patient was better at reading numbers ‘familiar’ to him, as in the case of famous historical dates (e.g., ‘1789’ for the French revolution), brands (e.g., ‘504’ for Peugeot) or zip codes (e.g., ‘75’ for Paris), compared to unfamiliar numbers (Cohen et al., 1994). Similarly, Delazer and Girelli (1997) showed that semantics might facilitate verbal number production: patient ZA performed better at reading encyclopaedic numbers than numbers not familiar to him.

At present there is not much evidence on which brain areas are involved in encyclopaedic numerical knowledge. While researchers have identified the parietal regions as the brain areas most involved in quantity meanings (see Dehaene et al., 2003 for a review), there is still uncertainty over whether those same areas or distinct areas are also engaged in encyclopaedic numerical knowledge. Suggestive evidence of a neuronal distinction between quantitative and encyclopaedic numerical knowledge comes from a recent neuroimaging study. Lochy and Van Turennout (2005) used an adaptation paradigm to compare arithmetic numbers, e.g., ‘6 × 70 = 420’, and encyclopaedic numbers, e.g., ‘Discovery of America = 1492’, and showed that arithmetical numbers are represented in the classical parietal areas whereas encyclopaedic numbers engage the left temporal areas.

The existing research indicates that encyclopaedic numbers can be selectively preserved than non-encyclopaedic numbers (Cohen et al., 1994; Delazer and Girelli, 1997), and can be more easily accessed (Alameda et al., 2003), but the opposite dissociation has not been demonstrated yet. Moreover, the possible functional distinction between nominal and cardinal encyclopaedic numbers has not been investigated so far. This study addresses these issues by reporting a patient with better performance for non-encyclopaedic (i.e., cardinal and ordinal numbers) than encyclopaedic numbers.

2. The present study

2.1. Case history

At the time of the investigation (November 2004–March 2006), JR was a 47 year-old right-handed man with 11 years of education and previously working for British Railways. In 1998, as a result of an assault JR suffered from a brain injury and developed post-traumatic amnesia. Since then, the patient has been complaining of memory loss, poor concentration and difficulty in making plans and monitoring them. In addition, JR reported being forgetful for numbers, in particular personal and historical dates, telephone numbers, PINs and addresses, i.e., encyclopaedic numerical knowledge. A computed tomography (CT) scan in 1998 was reported normal, although as a consequence of the assault the patient developed seizures with the characteristic features of temporal lobe epilepsy.

3. Neuropsychological investigation

JR was administered a neuropsychological battery evaluating general intellectual functioning, memory, semantic knowledge, executive functions and word retrieval. The results of the neuropsychological assessment are reported in Table 1. JR's scores in general intelligence tests measured with a task based on reading skills (Wechsler Test of Adult Reading (WTAR), Wechsler, 2001) indicated a significant degree of intellectual under-functioning. However, JR's general intelligence measured with a non-reading test (i.e., Progressive Matrices) was within the normal range (Spreen and Strauss, 1998). Memory processing was preserved. Similarly, semantic processing measured in terms of general semantic knowledge (Pyramids and Palm Tree Test, Howard and Patterson, 1992) and of a category-specific semantic task previously used by Bozeat et al. (2000) was well preserved. Good performance in the Pyramids and Palm Tree Test is usually considered an index of preserved semantic knowledge (Howard and Patterson, 1992). However, JR's performance on a more demanding semantic task, i.e., the concrete and abstract synonyms test (Warrington et al., 1998), was below the normal range. Frontal executive functions (Shallice and Evans, 1978) were preserved. In contrast, JR's word retrieval was impaired, although his spontaneous speech was syntactically correct and well articulated. Autobiographical memory processing was moderately impaired, although this could be partially accounted for by the patient's inability to process numbers. Indeed, in the ‘personal semantics’ section of the Autobiographical Memory Interview (Kopelman et al., 1989) the patient lost overall 13 points because he could not report relevant numerical information. These results together with the patient's report of his difficulties in dealing with numbers in specific contexts motivated the present experimental investigation.

Table 1. Summary of cognitive scores (number correct; standard deviations are reported in brackets).

Tasks performed	Number correct	Scaled score or Controls' performance
General intelligence
WTAR	23	I.Q. 76
Progressive Matrices (from WAIS-III)	16/26	Age-scaled score = 11 (controls mean 10, sd = 3)
Memory
Doors and People	9/12	Age-scaled score = 36
Famous Faces	19/30	High superior
AMI	PS 45/63, AI 27/27	Normal range
Digit Span
Forward	5	6.8 (.9)
Backwards	4	4.7 (1.2)
Semantic knowledge
Pyramids and Palm Tree Test	51/52	51.2 (1.4)
Word–Picture Matching	63/64	63.7 (.5)
Synonyms
Concrete	15/25	23.7 (1.3)
Abstract	11/25	23.0 (2.1)
Frontal/executive
Cognitive Estimates		Normal range
Word retrieval
GNT	18/30	>25 < 50 percentile, scaled score > 8 < 10

WTAR = Wechsler Test of Adult Reading.

WAIS = Wechsler Adult Intelligence Scale-Revised.

AMI = Autobiographical Memory Interview.

PS = personal semantic; AI = autobiographical incidents.

GNT = Graded Naming Test, McKenna and Warrington, 1983.

4. Experimental investigation

A set of experiments was designed and administered to JR to systematically investigate his cardinal, ordinal and more specifically encyclopaedic numerical knowledge.

4.1. Control subjects

Control subjects for the cardinal and ordinal numerical tests were three males matched to JR for age and education (mean age = 48.33 years, sd = 2.01; education = 11.7, sd = 2.52). These subjects were selected from a larger group of controls that was originally tested to validate the numerical battery used (Cappelletti et al., 2001; Cappelletti, 2002). A total of six different control subjects (five males) were tested on the specific tasks assessing encyclopaedic numerical knowledge (mean age = 46.6 years, sd = 5.3; education = 11.2, sd = 3.7).

5. Part 1: investigation of numerical knowledge

5.1. Methods and materials

JR's numerical knowledge was tested with a set of numerical tasks previously used to assess neuropsychological patients (Cappelletti et al., 2001; Cappelletti, 2002). The numerical tasks explored cardinal, ordinal numerical processing and other numerical skills (e.g., transcoding, parity judgement). Tasks were presented on a computer screen or on paper-and-pencil in which case there was no time constraint to produce an answer.

5.1.1. Cardinal numerical processing

The following tasks were used:

5.1.1.1. Magnitude comparison

JR was administered a computerised number comparison task, typically used as an index of intact number quantity processing. He was presented with two-digit Arabic numbers (range: 31–99) and asked to judge whether each stimulus was larger or smaller than the reference number ‘65’. JR was asked to indicate his response by depressing a right (for smaller numbers) or left key (for larger numbers) on the computer keyboard as quickly as possible. The experiment was controlled by a Sony S2VP laptop computer running E-prime software (Psychology Software Tools, Inc.). A total of 116 two-digit numbers displayed in black were presented in the centre of a white liquid crystal display computer screen for comparing their magnitude. Before each pair appeared, a fixation point was presented for 300 msec. The presentation time for the stimuli terminated when the patient produced an answer. Numbers could be grouped into: smaller and far from the reference (e.g., ‘39’), smaller and close to the reference (e.g., ‘61’), larger and close to the reference (e.g., ‘72’), larger and far from the reference (e.g., ‘84’). Accuracy and response times were recorded. Preserved number quantity processing is usually indicated by the increase in response times as the distance between the two numbers decreases (i.e., it takes longer to judge whether ‘63’ is larger or smaller than the target ‘65’ compared to ‘36’). This effect is known as ‘distance effect’ (Moyer and Landauer, 1967). If the automatic access to the magnitude of numbers is difficult or impossible, alternative strategies, such as counting, have to be employed to compare the two numbers. In this case, the longer the distance between the numbers, the longer it takes to indicate the larger. This would result in ‘abnormal’ distance effect.

Prior to this task, JR was invited to familiarize himself with the procedure of comparing numbers by performing a paper- and-pencil number comparison task. Twenty pairs of single- to four-digit Arabic numerals were presented to the patient who was asked to point to the larger of the two numerals. Pairs of numerals were printed in font 24 and presented to the patient on separate cards for comparison. This procedure, which is slightly different from the one used in the computerised task where one number had to be compared to the same reference, was part of the larger numerical battery previously used to assess neuropsychological patients and control participants (Cappelletti et al., 2001; Cappelletti, 2002). We used the same procedure in order to compare JR to the existing matched controls.

5.1.1.2. Composing the value of numbers with chips

The patient was asked to select the chips corresponding to the value of numbers orally presented by the examiner for a total of 24 stimuli. Chips consisted of rounded plastic poker tokens whose values ranged from 1 to 100 (i.e., ‘1’, ‘2’, ‘5’, ‘10’, ‘20’, ‘50’ and ‘100’) and with different colour assigned to each value.

5.1.1.3. Size judgement

JR was orally presented with pairs of objects' names (total = 10 pairs of stimuli), e.g., ‘chair’ and ‘bed’, and asked to indicate the larger (in half of the trials) or smaller (in the other half) in real size. Pairs of written words were presented one at a time on individual cards.

5.1.1.4. Quantity judgement with quantifiers

The patient was presented with pairs of quantifier words (total = 10 pairs of stimuli) and asked to indicate the one referring to the larger quantity (e.g., ‘more’ in the pair ‘more’ and ‘less’). Pairs of stimuli were presented one at a time on individual cards.

5.1.1.5. Calculation

5.1.1.5.1. Mental calculation

JR was asked to perform simple arithmetical problems comprising single-digit numbers (e.g., 2 + 1, 3 × 2). All problems were orally presented to the patient and an oral answer was required. Ten additions, subtractions and multiplication problems were tested in blocks of operations for a total of 30; division problems could not be tested.

5.1.1.5.2. Written calculation

Multi-digit problems of progressive difficulty were presented to the patient in Arabic format to be solved in written format. Addition, subtraction and multiplication problems were presented one at a time in blocks of operations for a total of 30; division problems could not be tested.

5.1.1.6. Approximation

5.1.1.6.1. Placing numbers on a number line

The patient was presented with a set of lines, each with the indication of the possible extremes (0–10, 0–100 or 0–1000) and was asked to perform two tasks. In Task 1, he was requested to estimate the position of a given number along the line. In Task 2, he was asked to indicate the number corresponding to a mark on the line (total = 18 stimuli for each task).

5.1.2. Ordinal number processing

The following tasks were used:

5.1.2.1. Counting backwards and forwards

JR's knowledge of the counting sequence was tested verbally: the patient was asked to count backward and forward in canonical (by one) and non-canonical order (by two and three) for a total of 60 stimuli.

5.1.2.2. Reciting non-numerical sequences

The patient was asked to recite different non-numerical sequences backwards and forwards, i.e., the alphabet (only forward), days of the week and months for a total of 64 stimuli. The use of non-numerical sequences allowed us to exclude any general output or memory problems should errors occur in performing the numerical sequences.

5.1.2.3. What comes before/after a number

JR was asked to indicate the number coming before or after a given number that was orally presented by the experimenter (total = 20 stimuli).

5.1.2.4. Bisection task

The patient was asked to verbally indicate the middle between two numbers, two letters or 2 days orally presented by the experimenter (10 stimuli for each category for a total of 30).

5.1.3. Other numerical skills

The following tasks were used:

5.1.3.1. Transcoding numbers in Arabic-to-verbal and verbal-to-Arabic formats

The patient was presented with Arabic numbers and asked to write them in letters (20 stimuli), or with written number words and asked to write the correspondent numbers in Arabic format (20 stimuli). In each task, stimuli ranged from single- to four-digit numbers (five items for each category of single-, two-, three- and four-digit numbers).

5.1.3.2. Reading and writing Arabic numbers and number words

JR was presented with one- to four-digit Arabic numbers and number words and asked to read each stimulus aloud or to write it to dictation (total = 20 stimuli for each task).

5.1.3.3. Parity judgement

The patient was asked to decide whether 20 single- to four-digit numbers orally presented in random order were odd or even.

5.2. Results and comments

JR's performance in ordinal and cardinal numerical tasks was equivalent to that of control subjects. The patient also performed well in other numerical tasks such as transcoding (see Table 2). In the magnitude comparison task, JR showed a normal ‘distance effect’ as his reaction times (RTs) to close numbers were slower than to far numbers (mean RTs for far and close distances: 744.18 and 678.92 msec, respectively, t(57) = 4.644, p < .001). Although in the magnitude comparison task the patient was slower than controls (t(115) = 7.867, p < .001), his performance in terms of accuracy (only two mistakes made) and RTs indicates that his number quantity processing was intact (see Fig. 1). In multi-digit arithmetical operations, the patient made a few errors only in multi-digit multiplications and division problems could not be tested.

Table 2. Summary of results in number and calculation tasks (percent correct).

Tasks performed	Patient JR	Controls
Cardinal numerical tasks
Numerical quantity knowledge	100	100
Magnitude comparison	83.3	90
Number line	100	100
Composing the value of num with chips	100	100
Non-numerical quantity knowledge
Size judgement (of pictures and objects)	100	100
Quantity judgement with quantifiers	100	100
Calculation
Simple calculation
Addition	100	100
Subtraction	100	98.5
Multiplication	100	95.4
Division	n.t.	–
Multi-digit calculation
Addition	100	100
Subtraction	100	100
Multiplication	40	93.5
Division	n.t.	–
Ordinal numerical tasks
Counting
Forwards	100	100
Backwards by 1	100	100
Backwards from 21 to 1 by 2	100	100
Backwards from 21 to 1 by 3	90.9	99
Reciting non-number sequences
Letters	100	100
Days	100	100
What comes
Next	90	90
Before	100	100
Bisection test
Numbers	100	100
Letters/days	85.7	100
Other numerical tasks
Transcoding A–V/V–A	100; 100	98; 99
Reading Arabic numbers and number words	100; 100	97; 98
Writing Arabic numbers	80	100
Parity judgement	100	100

n.t. = Not tested; A = Arabic numbers; V = Verbal numbers.

Fig. 1.

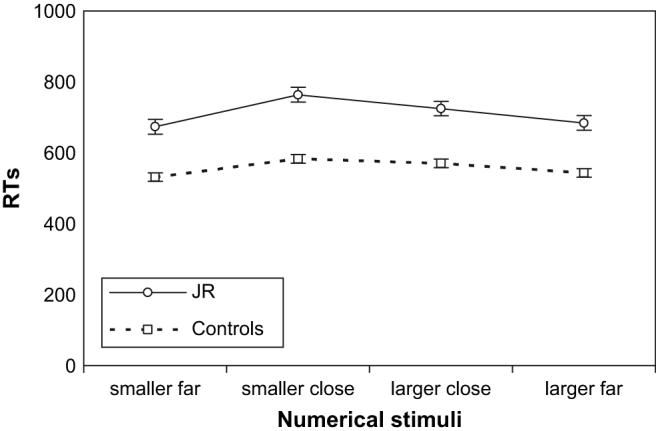
Number comparison task. Patient JR and control subjects' RTs.

Overall, these results indicate that JR's numerical and calculation abilities assessed in terms of cardinal, ordinal number processing and other numerical skills were preserved.

6. Part 2: investigation of encyclopaedic numerical knowledge

6.1. Methods and materials

The patient's encyclopaedic numerical knowledge was tested with a series of tasks based on verbal and pictorial materials.

6.1.1. Task 1: encyclopaedic numbers in terms of nominal assignments

Task 1 systematically investigated JR's encyclopaedic numerical knowledge in terms of nominal assignments, i.e., numbers used as labels (e.g., ‘BBC 4’). Two tasks were used.

6.1.1.1. Task 1A: Retrieval of numerical information based on personal and public knowledge

JR was presented with 75 questions concerning personal, historical dates and number facts, for instance, “When is your wedding anniversary” and ‘Which day is Valentine's Day?’. As it was not possible to establish JR's pre-morbid encyclopaedic knowledge, the questions in this set referred to information that was expected to be familiar to the patient and that was not likely to depend on the level of education.

6.1.1.2. Task 1B: Naming well-known items whose name contains a number

The patient was asked to name 25 items such as movies, drinks, cars whose name contained a number, for example, ‘2001: A space odyssey’, ‘7UP’ and ‘Renault 4’. For this task, the patient was presented with a set of pictures and was asked to name the stimuli depicted in each of them. Prior to this, JR was invited to give some information of the items illustrated (their colours, where to find them, characters involved) to assure that he could recognise and identify the stimuli. The pictures showed the whole objects, only omitting the verbal parts of their names or other words.

6.1.1.3. Control Task 1

JR was presented with a set of 35 questions of similar complexity of the previous ones (Task 1A) but not requiring a numerical answer. For example, a numerical question such as “What is your house number?” was matched to a non-numerical one like “What colour is your house?”. Non-numerical questions were matched to numerical questions referring to personal (10 questions), historical dates (10 questions) and other number facts (15 questions). This task allowed us to test whether JR had specific difficulties in processing only the numerical information of an event or if the impairment concerned the entire event. Moreover, questions in the experimental and in the control set were similar in terms of length, grammatical complexity and type of words used. This allowed us to exclude that any difference in performance could be attributed to difficulty effect or to other general cognitive abilities involved (e.g., comprehension or memory). Questions requiring and not requiring numerical answers were presented in random order and there was no time constraint to answer. The accuracy of JR's responses to questions tapping personal information was checked with a family member.

6.1.1.4. Control Task 2

In order to test JR's general non-numerical semantic knowledge, he was administered the ‘Information’ subtest of the Wechsler Adult Intelligence Scale-Revised (WAIS-R) (28 questions). As this test may be sensitive to education and I.Q., we designed another set of 50 easier questions assessing JR's semantic knowledge of exact, non-numerical facts tapping public events, general knowledge and the meaning of words or expressions (e.g., ‘What is the name of the British Prime minister?’, or ‘What do we use lungs for?’). Questions from the ‘Information’ subtest and those specifically designed were orally presented one at a time with no time constraint to produce an answer.

6.1.2. Task 2 encyclopaedic numbers in terms of cardinal assignments

Task 2 aimed at examining JR's processing of encyclopaedic numerical knowledge in terms of exact and approximate cardinal assignments, i.e., quantity information stored in propositional format in long-term memory. Two tasks were used:

6.1.2.1. Task 2A: Processing exact cardinal encyclopaedic numbers

JR was asked to answer 70 questions presented orally. Some of these questions could be answered by referring to a stored visual image, e.g., ‘How many colours are in the British flag?’ whereas others are probably stored in a propositional format in long-term memory, e.g., ‘How many minutes are in 1 h?’. Similar to Task 1A, as JR's pre-morbid encyclopaedic knowledge could not be established, questions in this set tapped information that was expected to be familiar to JR and that was unlikely to rely on high education.

6.1.2.2. Task 2B: Estimation of cardinal encyclopaedic numbers

The patient was asked to estimate the magnitude of sets. Questions corresponding to four different types of estimation were orally presented to JR for a total of 20 items: (i) estimation of time, e.g., ‘What is the average length of a movie?’; (ii) estimation of space, e.g., ‘How far is London from Paris in miles?’; (iii) estimation of numerosity, e.g., ‘How many people can fit in a double-decker bus?’; and (iv) estimation of magnitude, e.g., ‘How much does a pint of beer weight?’.

6.1.3. Task 3: peripheral processing of encyclopaedic numbers

The patient was asked to read and write to dictation a subset of the stimuli used in Tasks 1 and 2 (total = 30 stimuli). Although the patient's ability to read and write numbers has already been explored (see Part 1, Investigation of numerical knowledge ‘General assessment of numerical skills’), Task 3 specifically focused on the numerical stimuli the patient could not perform in encyclopaedic contexts. Stimuli referred to personal, historical dates and number facts (10 stimuli each) and consisted of 1 to 4-digit stimuli (N = 27) and of numbers expressed in other formats (e.g., 9½ referring to the title of a movie, 3 stimuli). In the reading task, JR was presented with individual Arabic numbers on separate cards and asked to read them aloud. In the writing task, JR was asked to write Arabic numbers to dictation. Stimuli were read aloud by the experimenter one at a time. There was no time constraint to perform the tasks.

6.2. Results

In Tasks 1 and 2, correct responses counted 1 point when the target item was correctly produced in its entire form. In Task 2B (‘Estimation of cardinal encyclopaedic numbers’), correct responses were those within one standard deviation from the control subjects’ responses. The patient was unable to process nominal encyclopaedic numbers or to name stimuli whose name contained a number (Tasks 1A and B). In contrast, he performed significantly better at answering non-numerical questions of similar difficulty, i.e., Control Task 1 (16 vs 97% correct answer, χ²(1) = 73.20, p < .001), general semantic questions, i.e., Control Task 2 (16 vs 84.6% correct answers, χ²(1) = 30.55, p < .001), and cardinal encyclopaedic questions, i.e., Task 2 (16 vs 68.6% correct answer, χ²(1) = 21.28, p < .001, see Fig. 2). In order to match JR's performance in answering exact encyclopaedic questions, a further analysis was performed comparing JR's answers to encyclopaedic nominal questions (Tasks 1A and B) and to exact encyclopaedic cardinal questions (Task 2A). This revealed a significant difference between exact nominal and exact cardinal encyclopaedic numbers (χ²(1) = 22.65, p < .001). Additionally, we compared only the subset of encyclopaedic numerical questions that had matched non-numerical control questions (Control Task 1), for instance ‘What is your house number?’ to ‘What colour is your house?’. This more stringent analysis revealed a significant difference between encyclopaedic numerical and non-numerical items (χ²(1) = 18.55, p < .01). JR's answers to some questions provide a clear example of his impairment with nominal encyclopaedic numbers. For instance, he could only correctly retrieve the letters but not the digits of his car registration number and of his post-code, which in the UK usually consist of a combination of letters and digits. He said his car registration number was “M something-KNS” instead of “M35 KNS” and his post-code was “EB-something-something-TE” instead of “EB23 5TE”.¹ This striking difference also allowed us to exclude the possibility that the patient’s impairment was due to difficulties in understanding the questions or to memory problems. This was also confirmed by JR's inability to name well-known items that he could nevertheless correctly describe. For instance, he could give a brief account of some of the movies whose title was unable to retrieve (e.g., “Ocean's 11” or “2001: A space odyssey”).

Fig. 2.

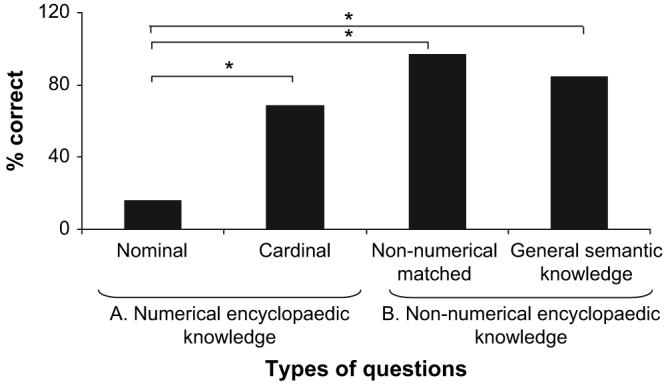
Patient JR's performance in questions tapping (A) numerical (Tasks 1 and 2) and (B) non-numerical encyclopeadic knowledge (control Tasks 1 and 2). Asterisks indicate a significant difference between tasks.

Although JR performed better with cardinal than nominal encyclopaedic numbers, cardinal numbers relying on a visual representation (e.g., “How many colours are in the British flag?”) were performed better than cardinal numerical information stored in propositional format (e.g., “How many states are in the USA?”, χ²(1) = 10.372, p < .001). Control subjects performed equally well on all these tasks.

JR performed at ceiling in reading and writing the numerals he could not process as encyclopaedic (Task 3). This was in agreement with his good performance in transcoding tasks with numerical stimuli not matched to the encyclopaedic numbers (see Section 5). Although the stimuli used in Task 3 matched only a subset of the stimuli used in the encyclopaedic tasks, the patient's ceiling performance with numbers presented in both modalities strongly suggests that his impairment with encyclopaedic numbers cannot be accounted for by problems at peripheral level.

6.3. Intermediate discussion

Patient JR showed impaired knowledge of encyclopaedic numerical knowledge. A difference also emerged between nominal and cardinal encyclopaedic numbers. Other numerical and calculation skills were well preserved (even when the same stimuli were used), suggesting that the impairment with encyclopaedic numbers could not be accounted for by a general numerical deficit. Moreover, the patient's difficulties cannot be explained by a failure to understand the task's instructions, the questions asked or the items visually presented, as he performed at ceiling or near ceiling in answering difficulty-matched questions not requiring numerical information.

Given the marked dissociation between encyclopaedic and other types of numerical knowledge, we next tested whether JR's problem was in retrieving the encyclopaedic numerical information from memory or whether the information itself was lost, i.e., whether it was a storage or a retrieval problem. We investigated this issue with two priming experiments. In addition, we tested whether the patient could process newly learnt numerical information using two paired-associative learning tasks.

7. Loss of encyclopaedic numerical information or difficulty in retrieving it?

7.1. Task 4: priming encyclopaedic numerical information

The priming experiment aimed at testing whether the patient's impairment with encyclopaedic numerical information could be explained by a deficit in retrieving the encyclopaedic numerical information or by the loss of the information itself. We predicted that an impairment in retrieving the encyclopaedic information should result in the patient showing an advantage for targets preceded by encyclopaedically related primes. Conversely, if the encyclopaedic numerical information is lost, there should be no difference whether targets are preceded by encyclopaedically related primes or not.

7.1.1. Methods and materials

Four different sets each of 15 trials were used, each trial consisting of a prime and a target. Primes always consisted of a numeral or of an expression containing a numeral and targets consisted of a name. For example, the prime ‘1988’ was associated to the target ‘marriage’ (1988 being the year of JR's wedding). The patient was instructed to look at the prime and once the target appeared to decide whether it was a common or a proper name. The experimental set included primes and targets whose link was meaningful or was related to the patient's personal history. Specifically, there were five trials related to public information (e.g., ‘December 25th → Christmas'); five related to JR's personal history (e.g., JR's birthday ‘June 10th → birthday’); five related to other meaningful numbers (e.g., ‘0207² → ‘phone’). Three different control sets were also used. In the first (C1), the same primes were presented with different, unrelated targets (e.g., ‘December 25th → Beatles’), in the second (C2) the same targets were presented with a prime similar to the related one (e.g., ‘January 25th → Christmas’), in the third (C3) the targets were presented with unrelated primes (e.g., ‘June 3rd → Christmas’). The experiment was controlled by a Sony S2VP laptop computer running E-prime (Psychology Software Tools, Inc.). Each trial began with a fixation cross, which appeared in the centre of a white LCD computer screen for 500 msec. This was followed by the prime (e.g., ‘December 25th’) which appeared in the position of the fixation cross for 200 msec, and subsequently by the target (e.g., ‘Christmas’) which remained on the screen until the patient responded. The second trial began with the fixation point after a blank screen was presented for 1000 msec. The experimental and the control trials were presented in random order twice each for a total of 120 stimuli. The experiment was preceded by a detailed explanation of the task's instructions and by a practice session (with different stimuli) where JR was invited to familiarize with the task. The set of encyclopaedic numbers concerning personal information was adjusted to test control subjects that provided this information beforehand.

7.1.2. Results

The patient's accuracy and RTs were calculated for each condition and used as dependent measures to test the patient's performance in the priming task. Only correct answers were included in the data set. In addition, RTs faster than 200 msec (anticipatory responses) or slower than two standard deviations above the mean of correct responses (delayed responses) were excluded from the data set.

JR made 10 errors overall (6.6 and 8.8% in the experimental and the control trials, respectively). Mean RTs did not differ neither between the experimental and the control conditions (t(29) = .726, p = .47, n.s.), nor between any of the four conditions (F(3,106) = .265, p = .85, n.s., see Fig. 3a). A further analysis showed that there was no difference between the experimental trials and those of the third control set, i.e., unrelated prime and same target (χ²(1) = .094, p = .76, n.s.).

Fig. 3.

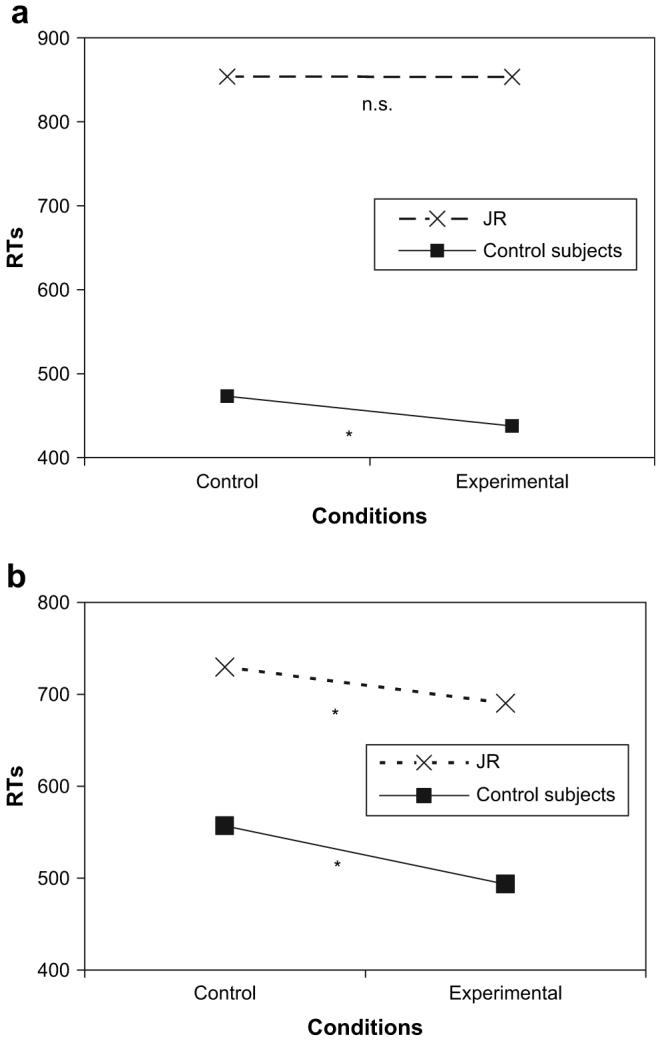
Priming experiments. Patient JR and control subjects' RTs in the priming experiment with numerical stimuli (a) and non-numerical stimuli (b). Asterisks indicate a significant difference between control and experimental conditions.

Contrary to patient JR, all control subjects showed an advantage for experimental compared to control trials (t(29) = 2.092, p = .04). Specifically, there was a facilitation for the experimental condition relative to C1 (t(29) = 9.376, p = .03) and C3 (t(29) = 2.092, p = .001), and only marginally to C2 (t(29) = 1.02, p = .052). This means that subjects were faster at deciding whether a target was a proper or a common name when this was proceeded by a meaningful prime (e.g., ‘December 25th → Christmas’) compared to a meaningless one (e.g., ‘June 3rd → Christmas’). This suggests that the prime activated semantic information that was relevant for the target and that facilitated (i.e., speeded) its processing.

7.1.3. Intermediate discussion

Task 4 indicated that patient JR did not benefit from semantically (encyclopaedically) related priming conditions relative to unrelated ones. Control participants showed a difference in performance between these conditions, suggesting that the experimental design was sensitive enough to discriminate between them. However, we cannot exclude that these results are due to JR not reacting to priming. To exclude this possibility, we constructed a second priming experiment with the same design as the previous one but testing non-numerical information. Both JR and matched controls were administered the second priming experiment.

7.2. Task 5: priming non-encyclopaedic information

7.2.1. Methods and materials

Similar to Task 4, four different sets each of 15 trials were used, each trial consisting of a prime and a target, which were always both names. For example, the prime ‘Cigar’ was associated to the target ‘Cuba’. The patient was instructed to look at the prime and once the target appeared to decide whether it was a common or a proper name. The experimental set included primes and targets whose link was meaningful (e.g., ‘Cigar → Cuba’ or ‘Cup → Tea’). Three different control sets were also used. In the first, the same primes were presented with different, unrelated targets (e.g., ‘Cigar → Heinz’); in the second the same targets were each presented with a prime similar to the related one (e.g., ‘Lighter → Cuba’); in the third the targets were each presented with unrelated primes (e.g., ‘Video → Cuba’). The experiment was controlled by a Sony S2VP laptop computer running E-prime (Psychology Software Tools, Inc.). The timings, the procedure and the experimental design were the same as Task 4. As before, the experiment was preceded by a detailed explanation of the task's instructions and by a short practice session (with different stimuli).

7.2.2. Results

The scoring criteria and method used to analyse the data were the same as Task 4. JR made no errors in any of the conditions, and there was a significant difference in mean RTs between the experimental and the control conditions (F(3,115) = 3.842, p = .012, see Fig. 3b). This means that JR was faster at deciding whether a target was a proper or a common name when this was proceeded by a meaningful prime (e.g., ‘Cigar → Cuba’). This suggests that the prime activated semantic information that was relevant for the target and that facilitated (i.e., speeded) its processing. Control participants also showed an advantage for experimental compared to control trials (F(3,119) = 5.373, p = .002).

7.3. Task 6: recognition of encyclopaedic numbers

In order to test whether JR's impairment consisted of the loss of the encyclopaedic numerical information or of a problem in retrieving it, we presented him a set of numbers and asked him to retrieve the associated event or concepts. The test was carried out in a different testing session in order to avoid any confound with previous exposure to the same material. Fifteen numerical stimuli were individually presented on separate cards in Arabic format. The stimuli were selected to represent a subset of the items used to test JR's encyclopaedic numbers: specifically, there were 5 stimuli concerning personal facts (e.g., ‘1957’, i.e., his year of birth), 5 historical facts (e.g., ‘09.11’, terrorist attack), and 5 numbers referring to other objects or information (e.g., ‘999’, emergency number in the UK). JR was invited to look at the numbers and to indicate the object or the event they referred to. If no answer was produced, the experimenter read each number aloud and invited the patient to produce an answer. JR answered correctly 4 out of 15 stimuli and could not produce an answer to the remaining stimuli irrespective of the modality they were presented in.

7.4. Task 7: multiple-choice of encyclopaedic numbers

A multiple-choice test was administered to JR to further explore his encyclopaedic numerical knowledge. The test was carried out in a different testing session in order to avoid any confound with previous exposure to the same material. Twenty encyclopaedic questions were individually presented to JR on separate cards. The questions were selected to represent a subset of the items previously used to test JR's encyclopaedic numbers: specifically, there were 10 questions concerning nominal encyclopaedic information and 10 concerning cardinal encyclopaedic information. Each question was orally presented with three possible answers: the correct one and two distracters in random order. JR chose the correct answer for 5 out of 20 questions (2 for nominal and 3 for cardinal stimuli). This result did not significantly differ from JR's performance in tasks where the same questions were presented with no multiple-choice answer (t(19) = 1.83, p = .083).

7.4.1. Intermediate discussion

In the first priming task (Task 4), patient JR did not benefit from the presence of a numerical prime: no difference was found between the conditions where primes and targets had a meaningful (i.e., encyclopaedic) link and the conditions where primes and targets had no meaningful link. Task 5 aimed to test the patient's sensitivity to priming in general, and to exclude the possibility that the lack of priming effect in Task 4 was attributable to the experimental design. Results of the second priming experiment showed that there was a significant difference between experimental and control conditions based on non-numerical information. Therefore, these results suggest that: (1) JR's impairment was due to the loss of the encyclopaedic numerical information itself rather than the inability to retrieve it; and that (2) the lack of priming effect could not be attributed to any experimental parameter. This was confirmed by Task 6 showing that JR could not retrieve the objects or concepts associated to given numbers irrespective of the modality of presentation. Moreover, Task 7 indicated that JR did not benefit from multiple-choice answers to encyclopaedic numerical questions. Given these results, the next series of tests assessed whether JR's impairment in processing encyclopaedic numerical information could be extended to new material. Two paired-associate learning tasks were used.

8. Is new encyclopaedic numerical information also impaired?

Two paired-associative learning experiments were administered to JR, the first based on numbers expressing dates, the second on numbers not referring to any particular event.

8.1. Task 8: paired-associate learning task with numbers as dates

8.1.1. Methods and materials

Three experimental sets, each with six pairs of stimuli, were constructed, similar to those used by Cohen (1990). The stimuli consisted of photographs of faces and of written stimuli presented in pairs on two separate cards. Written stimuli consisted of names (e.g., ‘James King’, set 1), jobs (e.g., ‘driver’, set 2), and dates (e.g., ‘July 23rd’, set 3). All the six names used were English, and consisted of a first and second name each of five letters on average; they were chosen so that they were not famous or familiar to the patient.³ Jobs consisted of the following professions: housewife, designer, receptionist, builder, driver and gardener. The jobs were not associated to the faces for any particular physical or semantic feature that could have influenced performance. Dates were expressed in terms of month in verbal format and day in Arabic format; dates were chosen so that they were not public holidays or well-known dates, and they were not related to the patient's personal life (e.g., no birthday or wedding anniversary). Months were only used once each and days were never repeated. Photographs were selected from the Rivermead Behavioral Memory Test (Baddeley et al., 1995) and represented the whole head in full-face pose of men and women between about 30 and 60 years of age, dressed in similar style and chosen to be dissimilar in appearance.

Faces with an associated item (name, job or date) were presented in random order on two cards for 3 sec each; subsequently, JR was presented with each face in a different order and asked to retrieve the associated information with no time constraint. After all the items had been presented once, the faces and their associated information were presented again for learning, and then the patient was asked to retrieve the information with the same procedure used before. Four trials (learning and recall) were given and the order of presentation of the items changed from trial to trial to prevent positional learning. Delayed recall could not be performed.

8.1.2. Results

Each correct response scored 1 point; months and days were scored separately as they consist of a verbal and a numerical component. A significant difference emerged between conditions (χ² (3) = 94.26, p < .0001, see Fig. 4a). Specifically, performance was better on jobs than months (χ²(1) = 6.480, p < .011) and days (χ²(1) = 24.543, p < .0001), but not better than names (χ²(1) = 1.025, p < .31). A significant difference was found between months and days (χ²(1) = 7.804, p < .005). In addition, an analysis was performed to compare JR's performance with names and dates only in the last trial (Trial 4). This revealed a significant difference between names and dates (χ²(1) = 6.316, p < .0012), suggesting that although JR had some difficulties learning names initially, he learnt them at the same level as control subjects by Trial 4. This was not the case of numbers. Control subjects showed no difference between the three categories (F(2,21) = 2.644, p = .09).

Fig. 4.

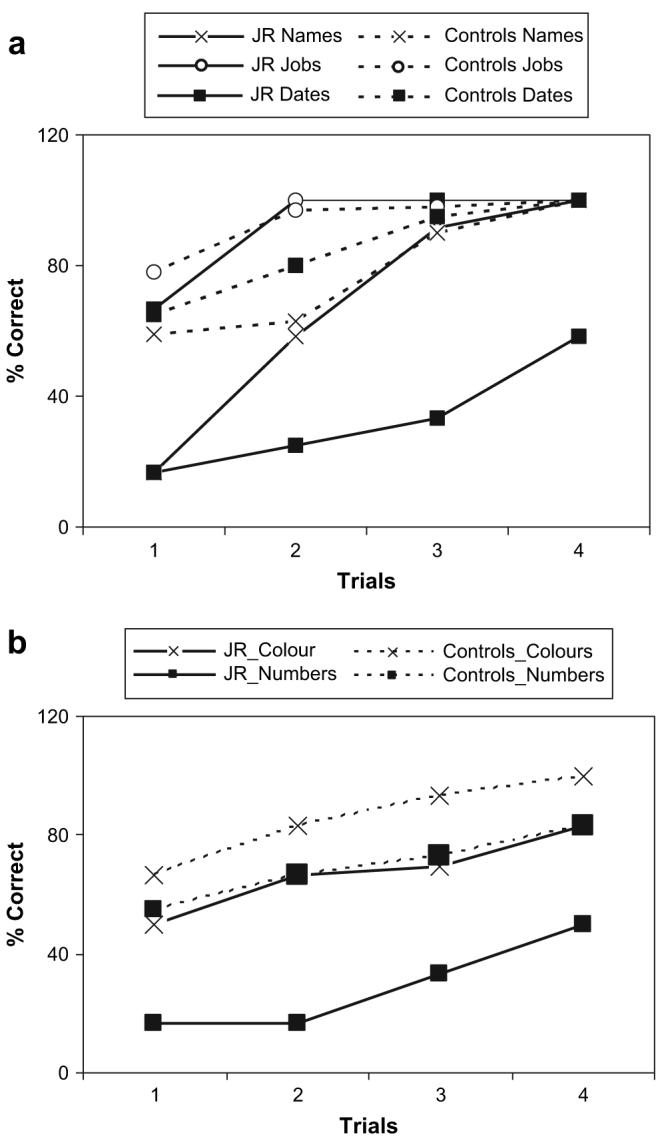
Paired-associate learning tasks. Patient JR and control subjects' accuracy in learning new numbers expressing dates contrasted to jobs and names (a) and new numbers in combination with letters of the alphabet contrasted to colour names (b).

8.1.3. Intermediate discussion

Results of Task 8 suggest that patient JR was impaired at learning new numerical stimuli expressed as dates compared to non-numerical ones. It is possible, however, that this partly depended on the nature of the stimuli used, since dates have specific properties; they are a small set (only 12 months and maximum 31 days) and are ordered. To test whether JR's performance partly reflected the nature of the stimuli used and to provide a more precise account of his ability to learn new numerical material, we devised and administered a second learning task.

8.2. Task 9: paired-associate learning task with numbers not expressing dates

There were two experimental sets consisting of six pairs of Arabic numbers (single-digit, e.g., ‘2’, set 1) and six pairs of written names of colours (e.g., ‘yellow’, set 2). Numerical stimuli were interleaved with letters of the alphabet to create strings resembling British postal codes, for instance, ‘N6 H5’ similarly, colour names were interleaved with letters of the alphabet, e.g., ‘Z Yellow J Red’ and used as control trials for the numerical stimuli. Numbers were not presented in any ordered sequence (e.g., ‘1–2’), colour names were not presented in any familiar association (e.g., ‘black–white’), and phonological or visual similarity was avoided (e.g., no ‘black–blue’ or ‘4–5’). Letters of the alphabet were never the same in the two sets and familiar or sequential patterns were avoided (e.g., no ‘A–Z’ or ‘A–B’). In the learning session, a trial consisting of a combination of letters and either numbers or colour names was presented for 3 sec; in the recall session, JR was presented with the letters of the alphabet of a given pair in a different order and asked to retrieve the associated stimuli (numbers or colour names) with no time constraint. After all the stimuli had been presented once, they were presented again in a different order, and the patient was asked to retrieve the information with the same procedure used in Task 8. Four trials (learning and recall) were given and the order of presentation of the items changed from trial to trial to prevent positional learning.

8.2.1. Results

Each correct response (i.e., both stimuli recalled) scored 1 point. JR was able to learn the associations between letters and colour names but not between letters and numbers (χ²(1) = 3.32, p = .019, see Fig. 4b).

8.2.2. Intermediate discussion

In the paired-associate learning experiments JR's performance depended on the stimulus used: in Task 8, he performed well on recalling names and jobs but poorly with numbers expressing dates. The difficulty with dates affected performance with days more significantly than months, possibly because months were expressed in alphabetic format. Results of Task 9 showed a similar pattern of results: JR could learn non-numerical stimuli (colour names) but not Arabic numbers. This suggests that the patient's difficulty in learning new encyclopaedic numbers was not limited to dates but extended to other numbers in arbitrary contexts. We shall note, however, that JR showed minimal improvement in learning new numerical stimuli (i.e., from 10 to 40%) after four learning-recall trials. Unfortunately, we have not explored how the patient would have performed in learning numbers after more learning-recall trials. Similarly, we could not test JR on a paired-associate learning test based on encyclopaedically associated events (e.g., ‘Channel 36’) compared to arithmetically associated events (e.g., ‘35² = 1225’).

9. General discussion

Although cardinal, ordinal and encyclopaedic numerical informations are intuitively distinct, most of the existing data can only support a dissociation between cardinal and ordinal numerical processes (see Dehaene et al., 2003; Delazer and Butterworth, 1997; Nieder, 2005). To our knowledge, this study is the first that systematically investigated encyclopaedic numerical knowledge and the first that has reported a dissociation between impaired encyclopaedic numbers and preserved non-encyclopaedic numbers. Specifically, three important results emerged from this investigation: (1) Patient JR's impairment in processing encyclopaedic numerical information contrasted with his preserved ability to process cardinal and ordinal numbers. This impairment seemed to be due to the loss of the encyclopaedic information and extended to new numerical material; (2) a dissociation emerged between nominal and cardinal encyclopaedic numbers; and (3) JR's impaired encyclopaedic numerical knowledge contrasted with his (almost) preserved general semantic knowledge. This case therefore provides evidence that allows us to draw a clear distinction between the processing of cardinal and ordinal numbers on the one hand, and of encyclopaedic numbers on the other. This complements the opposite dissociation, namely better performance with encyclopaedic than non-encyclopaedic numbers, although in previous cases the contrast was in terms of reading tasks based on encyclopaedic and non-encyclopaedic numbers (Cohen et al., 1994; Dehaene and Cohen, 1991; Delazer and Girelli, 1997).

JR's impaired encyclopaedic numerical knowledge did not seem related to his poor word retrieval, as the patient was also impaired in encyclopaedic numerical tasks that did not strictly depend upon word retrieval, for instance ‘Recognition of encyclopaedic numbers’ (Task 6) and ‘Multiple-choice of encyclopaedic numbers’ (Task 7). Moreover, although it is not possible to precisely establish the patient's pre-morbid semantic and general encyclopaedic knowledge, his impairment in processing encyclopaedic numerical information did not seem associated to his general semantic knowledge. While JR's performance in a highly demanding semantic task, i.e., the synonyms test, was outside the normal range, his performance in other tests (i.e., Pyramids and Palm Tree Test, category-specific matching task) did not differ from control subjects. In addition, the patient performed well on tasks assessing his ‘exact’ general semantic knowledge and on questions matching the encyclopaedic numerical items, suggesting that his poor performance with encyclopaedic numbers cannot be attributed to more general semantic impairments. Moreover, JR's impairment with encyclopaedic numbers did not seem to depend upon his general intelligence. Although the patient scored poorly in intelligence tests based on reading skills, his performance was within the normal range when assessed with the Progressive Matrices.

We would like to suggest that JR's impairment consisted of a loss of the encyclopaedic numerical information rather than an impairment in retrieving it. Two pieces of evidence support this hypothesis: first, the patient did not benefit from a priming task based on encyclopaedically related and unrelated stimuli (Task 4). This was not due to the patient not being sensitive to the priming paradigm in general or to the experimental design used as in a second priming task (Task 5). Indeed JR showed a significant advantage for targets preceded by semantically related, non-numerical primes. Second, the patient's performance did not change in a recognition and in a multiple-choice task suggesting that the encyclopaedic information numbers referred to were no longer available. This case therefore provides evidence that allows us to draw a clear distinction between the processing of cardinal and ordinal numbers on the one hand, and of encyclopaedic numbers on the other.

Previous studies have shown that both linguistic and numerical skills are necessary to process encyclopaedic numerical information. However, it is unclear to what extent these skills are also sufficient to process encyclopaedic numbers. A study of a semantic dementia patient showed very well preserved numerical skills in the context of encyclopaedic numbers being largely lost (Cappelletti et al., 2001, 2005). Similarly, another patient with linguistic disorders was selectively impaired at answering verbal questions requiring numerical answers when these implied the retrieval of verbal semantic information (Thioux et al., 1998). A group study on patients with degenerative conditions reinforces the idea that linguistic skills are necessary to process encyclopaedic numerical information. Crutch and Warrington (2002) showed that patients with semantic dementia are significantly more impaired than other demented patients in the ‘quantity facts measure’, an encyclopaedic numerical task that relies greatly on verbal skills.

JR's pattern of performance differs from these previously reported cases. The patient's impairment with encyclopaedic numbers contrasted with his preserved numerical skills and preserved non-numerical (i.e., linguistic) semantic knowledge. This suggests that numerical and linguistic skills are necessary but not sufficient to preserve encyclopaedic numerical knowledge. We propose that JR's disorder consisted of a selective impairment in the processing of nominal numerical assignments: he showed impairment only when numerals were used as labels to identify objects or events. Specifically, we suggest that the patient's impairment lies in the semantic link between an event and a numerical label identifying it, which resulted in the encyclopaedic information being lost rather than difficult to be retrieved. This impairment did not affect numerical processing in other contexts: the patient was able to read and write the same numbers he could not process as encyclopaedic and could perform calculation and quantity comparisons on them.

Patient JR not only showed a selective impairment in processing encyclopaedic numbers but also a dissociation between nominal and cardinal encyclopaedic numbers. This can be explained in terms of the cognitive processes supporting nominal and cardinal numbers. Cardinal encyclopaedic numbers can often be calculated or approximated when the precise information is not available: for instance, one can say that there are approximately 50 states in the USA or about 360 days in a year. Conversely, this is not the case of nominal encyclopaedic numbers, as a telephone number or a birthday cannot be an approximate series of digits or an approximate day. JR's better performance with cardinal than nominal encyclopaedic numbers suggests that he could have partly relied on calculation strategies when applicable and when the exact encyclopaedic information was not available. This hypothesis is also supported by JR's better performance with cardinal encyclopaedic numbers based on a visual image (e.g., ‘How many legs does a horse have’ or ‘How many fingers does a man have?’). JR could have easily obtained this type of encyclopaedic information through the inspection of a mental visual representation of the item or the event. However, this strategy is not available for nominal encyclopaedic numbers.

JR's pattern of performance in relation to his brain dysfunction does not allow any firm conclusion on the brain networks underlying the processing encyclopaedic numbers and to contrast them with those involved in quantity knowledge. At a speculative level, our results suggest that the parietal regions do not seem to be implicated in processing encyclopaedic numbers, as these areas were spared on the CT scan. Moreover, the patient performed well on numerical tasks requiring quantity processing which are thought to rely on the parietal regions (e.g., Dehaene et al., 2003). At present our results only allow us to indicate that encyclopaedic and other types of numerical knowledge are functionally distinct, and that preserved linguistic or non-numerical semantic processes are not sufficient for intact processing of encyclopaedic numerical knowledge. Further investigations are needed to complement this neuropsychological evidence and to provide information of the neuronal correlates of encyclopaedic numerical knowledge.

In sum, this case provides the first evidence that the processing of encyclopaedic numerical information is distinct from other numerical skills and from other non-numerical semantic information. In addition, we showed that there is a distinction between nominal and cardinal encyclopaedic numerals. Specifically, JR's processing of encyclopaedic numerical information was impaired unless the patient could rely on calculation or approximation processing or on the inspection of a visual representation of the items the encyclopaedic numbers refer to.