The Importance and Role of Intracluster Correlations in Planning Cluster Trials

Abstract

There is increasing recognition of the critical role of intracluster correlations of health behavior outcomes in cluster intervention trials. This study examines the estimation, reporting, and use of intracluster correlations in planning cluster trials. We use an estimating equations approach to estimate the intracluster correlations corresponding to the multiple-time-point nested cross-sectional design. Sample size formulae incorporating 2 types of intracluster correlations are examined for the purpose of planning future trials. The traditional intracluster correlation is the correlation among individuals within the same community at a specific time point. A second type is the correlation among individuals within the same community at different time points. For a “time × condition” analysis of a pretest–posttest nested cross-sectional trial design, we show that statistical power considerations based upon a posttest-only design generally are not an adequate substitute for sample size calculations that incorporate both types of intracluster correlations. Estimation, reporting, and use of intracluster correlations are illustrated for several dichotomous measures related to underage drinking collected as part of a large nonrandomized trial to enforce underage drinking laws in the United States from 1998 to 2004.

Cluster trials evaluate interventions delivered to intact social groups or clusters, such as communities, churches, schools, workplaces, and medical practices, whereas outcomes are measured on members of those groups.^1,2 The distinctive feature of cluster trials is the presence of intracluster (or intraclass) correlation among members within groups that arises from restricting assignment of the interventions to groups instead of to individuals. Failure to account for the intracluster correlation within clusters will likely lead to 2 shortcomings: an underpowered study and inflated Type I error rate of hypothesis tests relating to the intervention.^1,2 Proper planning of cluster trials is based upon sample size formulae that use hypothesized intracluster correlation values, often based on estimates from earlier trials.^3-6

Although sample size formulae based upon the intracluster correlation for a posttest-only cluster trial design are fairly well established, many cluster trials have multiple time points for which more than one type of intracluster correlation arises. In the case of a pretest–posttest nested cross-sectional design, characterized by different groups of individuals within clusters sampled at 2 time points, 2 intracluster correlations may be defined. The traditional intracluster correlation is the correlation among individuals within the same community at a specific time point. A second intracluster correlation is the correlation among individuals within the same community at different points in time. Extensions of the posttest-only sample size formulae are needed to refine sample size determination for multiple time point designs.

The sample size formula adopted in planning a cluster trial depends upon the statistical analysis to be used and, more specifically, the test statistic for the null hypothesis of “no intervention effect.” The proposed analysis will depend upon the trial's experimental design, including whether the intervention condition is randomized to groups. For example, in a randomized pretest–posttest nested cross-sectional design, the trial planners are concerned with how the statistical analysis should handle the pretest data to maximize statistical power for the test of intervention, given that a sufficiently large number of clusters are enrolled to ensure baseline balance among covariates and outcome. In short, the focus is on the comparison of posttest means. In contrast, potential bias from baseline imbalance is an additional concern in planning a nonrandomized cluster trial. In this case, a “time × condition” analysis may be appropriate because its test statistic is the difference in change in the mean outcome over time between intervention and control conditions. If the pretest intervention and control condition means are equal, a time × condition analysis will tend to have lower statistical power than a posttest only analysis because the former uses a test statistic that is a function of 4 means, resulting in greater variance than a test statistic that is a function of only 2 (posttest) means. In sum, the manner of accounting for pretest information in the analysis of a randomized cluster trial has implications for statistical power, whereas the choice may affect both power and bias for nonrandomized trials.

This article discusses the estimation of intracluster correlations and particularly their use in sample size formulae in the design of cluster trials. Although statistical analysis and power have received attention for modeling change in Gaussian outcomes,^7,8 insufficient consideration has been given to binary outcomes.^9,10 Focusing on large cluster trials with binary outcomes, a generalized estimating equations (GEE) approach is applied for the estimation of the 2 types of intracluster correlation.¹¹ In planning a nonrandomized cluster trial with a pretest–posttest nested cross-sectional design, the paper discusses a sample size formula for a GEE time × condition analysis that incorporates the 2 types of intracluster correlations.¹² Finally, the paper reports intracluster correlation estimates and estimates of their precision for several dichotomous measures of underage drinking from a large nonrandomized cluster trial to enforce underage drinking laws.¹²

METHODS

The Enforcing Underage Drinking Laws Program

The Enforcing Underage Drinking Laws Program, launched by the United States Office of Juvenile Justice and Delinquency Prevention in 1998, is the largest federal initiative focused on reducing underage drinking in United States history. Each of the 50 states and the District of Columbia received significant funding and technical assistance to support state and local efforts to enforce laws related to alcohol use by underage persons and to prevent underage drinking. A major component of the program involved discretionary grants provided to states on a competitive basis. Selected states awarded subgrants to communities (cities or counties) according to criteria that varied across states. Randomization was not employed, and the evaluation team had no control over the choice of intervention communities. However, control communities with characteristics similar to the intervention communities were selected by identifying those with propensity scores similar to the intervention communities.¹² The propensity score was a scalar summary of several community characteristics captured by federal census and other external sources, and identified a priori as being likely related to the grantee selection process and the major outcomes measured by the youth survey.

The evaluation of the impact of the discretionary grants, or “national evaluation,” was conducted with a nested cross-sectional design.^2,13,14 Data were collected using a variety of surveys; the focus in this work is on 3 annual telephone surveys using distinct samples of between 15 and 20 youths (age 16−20 years) in each selected community. For each community, data collection was conducted preintervention (or early in the intervention period), 1 year later, and 2 years later. A nested cross-sectional design was chosen over a nested cohort design because the long intervention period might result in substantial dropout in a cohort design.^1,14 Also, interest focused on the change in the population over time as opposed to within-individual change.¹²

The national evaluation was conducted using data collected during 3 funding cycles. The first began in 1999 with 52 intervention and 52 control communities in 9 states. The second began in 2000 with 16 intervention and 16 control communities from 7 states. The final cycle began in 2002 with 34 intervention and 34 control communities from 8 states. All but 2 communities participated in exactly one funding cycle. A total of 10,865 observations from 202 communities were used in the analysis of underage drinking outcomes.

Nine dichotomous measures of underage drinking use, alcohol risk behaviors, and negative consequences of alcohol use from the survey of youth were analyzed (Table 1). The following individual and contextual community-level variables were examined as covariates because they may partly explain the magnitude of intraclass correlations for alcohol use behaviors: age, sex, and community-level variables that are possibly characteristic of disadvantaged communities, namely, percentage of households with female head with no husband, percentage foreign born, and median income.

TABLE 1.

Description of Alcohol Use Measures From the Youth Survey of the Enforcing Underage Drinking Laws Program, 1998−2004

Measure	Description
Binge drinking	“Think back over the last 2 weeks. How many times have you had 5 or more drinks in a row?” Respondents who answered zero were coded “0” whereas those who answered one or more occasions were coded “1.”
DWI driving	Among ever-drinkers who reported ever driving, “During the last 30 days, how many times (if any) have you driven after drinking 2 or more drinks in an hour or less?” Those reporting zero, never drinkers, and ever drinkers who had never driven were coded “0”; those replying one or more occasions were coded “1.”
Past 30-day alcohol use	“When was the last time you drank alcohol?” respondents who answered “in the last 30 days” were coded “1.” Respondents who answered that they had consumed alcohol but not in the last 30 days, as well as never drinkers, were coded “0.”
Past 7-day use	Similar to “Past 30-day alcohol use”; response “in the last 7 days” coded “1.”
Attempt to purchase alcohol	“In the last 30 days, how many times did you try to buy alcohol from a bar, restaurant, or store (whether you were successful or not)?” Respondents who answered zero were coded “0”; those who answered one or more occasions were coded “1.”
Nonviolent consequences due to alcohol use	Experienced any of the following after they had been drinking: being cited or arrested for drinking, possessing alcohol, trying to buy alcohol, being cited or arrested for driving under the influence of alcohol; missing any school due to drinking; being warned by a friend about your drinking; passing out; being unable to remember what happened while drinking; breaking or damaging something; having a headache or hangover; being punished by your parents or guardian; and having sex without using birth control. Respondents who reported experiencing any these in the past year were coded “1”; others were coded “0.”
Perception of alcohol use among peers	“How many of your friends do you think have had any alcohol to drink in the last 30 days? Would you say none, a few, some, most, or all”? Respondents who reported that most of all or their friends had consumed alcohol in the past 30 days were coded “1”, while all others were coded “0.”
Perception of getting caught by police	“If you had been drinking, how likely would it be for the police to catch you? Very likely, somewhat likely, not very likely, or not at all likely?”, coded “1” if respondent answered “very likely” or “somewhat likely”; else coded “0.”
Commercial source of alcohol	“The last time you drank any alcohol, how did you get the alcohol?” those who answered that they obtained alcohol from a “commercial source” (businesses such as alcohol outlets, restaurants, and bars) were coded as “1.” Those who answered that they were given alcohol by their friends, family members, coworkers, acquaintances, or strangers at home or at events were coded “0.”

Statistical Analysis

The sample was predominantly white and well-balanced with respect to sex (Table 2). Sixteen and seventeen-year-olds were over-represented in the sample compared with 18, 19, and 20-year-olds. Observed prevalence for each outcome is reported in Table 3. Analyses of the intervention, reported elsewhere,¹⁵ used GEE with the simple “exchangeable” working correlation matrix^9,13,16 to fit time × condition logistic regression models; use of the “robust” empirical covariance estimator provided valid large sample inference even if the correlation structure was misspecified.

TABLE 2.

Sex, Race, and Age of Participants in the Youth Survey of the Enforcing Underage Drinking Laws Program for Control and Intervention Communities (All Rounds), 1998−2004

	Year 1		Year 2		Year 3
	Control (n = 1835)*	Intervention (n = 1784)*	Control (n = 1825)*	Intervention (n = 1822)*	Control (n = 1825)*	Intervention (n = 1775)*
Male; %	49.1	50.0	50.3	51.2	48.4	51.3
Race; %
White	85.4	87.5	86.6	88.1	83.1	87.6
Black	6.6	5.2	6.4	5.4	8.5	6.0
Other	8.0	7.3	7.0	6.4	8.7	6.5
Age (yrs); %
16	32.0	30.8	31.1	30.4	30.2	28.2
17	31.1	32.0	31.8	31.2	29.4	29.8
18	17.6	18.0	17.1	19.7	19.2	21.2
19	11.6	10.9	11.3	10.4	12.1	12.9
20	7.7	8.4	8.7	8.3	9.0	8.0
Community sample; mean†	18.0	17.8	17.9	18.2	17.7	18.0

^*Total number of youth sampled across communities.

^†Mean number of youth sampled per community.

TABLE 3.

Within-Time (α₀) and Between-Time (α₁) Intracluster Correlation Estimates (ICC) of Youth Alcohol Use Measures and Their 95% Confidence Intervals (CI) From the Youth Survey of the Enforcing Underage Drinking Laws Program, 1998−2004

Measure (Prevalence*) and Independent Variables†	Within-Time ICC (95% CI)	Between-Time ICC (95% CI)	Covariance‡
Binge drinking (0.1656)
Design variables	0.0185 (0.0048 to 0.0322)	0.0169 (0.0088 to 0.0251)	0.0000200
Age, sex	0.0193 (0.0060 to 0.0325)	0.0172 (0.0081 to 0.0262)	0.0000229
Community variables	0.0192 (0.0053 to 0.0330)	0.0166 (0.0069 to 0.0262)	0.0000226
DWI drive (0.0499)
Design variables	0.0027 (−0.0037 to 0.0092)	0.0074 (0.0019 to 0.0129)	0.00000252
Age, sex	0.0038 (−0.0032 to 0.0109)	0.0070 (0.0010 to 0.0131)	0.00000438
Community variables	0.0038 (−0.0033 to 0.0109)	0.0071 (0.0010 to 0.0133)	0.00000452
Past 30-day alcohol use (0.3939)
Design variables	0.0261 (0.0164 to 0.0358)	0.0219 (0.0134 to 0.0303)	0.0000128
Age, sex	0.0251 (0.0156 to 0.0346)	0.0217 (0.0133 to 0.0301)	0.0000117
Community variables	0.0234 (0.0139 to 0.0328)	0.0197 (0.0112 to 0.0282)	0.0000120
Past 7-day alcohol use (0.2174)
Design variables	0.0190 (0.0092 to 0.0288)	0.0158 (0.0088 to 0.0228)	0.00000745
Age, sex	0.0204 (0.0106 to 0.0301)	0.0156 (0.0082 to 0.0229)	0.00000785
Community variables	0.0197 (0.0099 to 0.0295)	0.0143 (0.0064 to 0.0222)	0.00000880
Attempt to purchase alcohol (0.0677)
Design variables	0.0191 (0.0096 to 0.0286)	0.0194 (0.0093 to 0.0295)	0.0000128
Age, sex	0.0178 (0.0069 to 0.0286)	0.0184 (0.0086 to 0.0281)	0.0000164
Community variables	0.0088 (−0.0003 to 0.0180)	0.0098 (0.0030 to 0.0165)	0.00000582
Nonviolent consequences to alcohol use (0.3609)
Design variables	0.0112 (0.0039 to 0.0184)	0.0115 (0.0056 to 0.0173)	0.00000500
Age, sex	0.0106 (0.0054 to 0.0169)	0.0111 (0.0054 to 0.0169)	0.00000451
Community variables	0.0087 (0.0022 to 0.0152)	0.0092 (0.0040 to 0.0145)	0.00000309
Perception of alcohol use among peers (0.5967)
Design variables	0.0222 (0.0124 to 0.0319)	0.0200 (0.0116 to 0.0284)	0.0000131
Age, sex	0.0208 (0.0115 to 0.0300)	0.0196 (0.0115 to 0.0276)	0.0000116
Community variables	0.0204 (0.0112 to 0.0296)	0.0192 (0.0110 to 0.0273)	0.0000117
Perception of getting caught by police (0.3988)
Design variables	0.0114 (0.0033 to 0.0195)	0.0125 (0.0061 to 0.0190)	0.00000672
Age, sex	0.0118 (0.0035 to 0.0200)	0.0127 (0.0062 to 0.0192)	0.00000694
Community variables	0.0087 (0.0010 to 0.0164)	0.0097 (0.0038 to 0.0157)	0.00000492
Commercial source of alcohol (0.0730)
Design variables	0.0163 (0.0036 to 0.0290)	0.0157 (0.0049 to 0.0265)	0.0000206
Age, sex	0.0164 (0.0040 to 0.0288)	0.0159 (0.0058 to 0.0262)	0.0000190
Community variables	0.0069 (−0.0026 to 0.0165)	0.0064 (−0.0004 to 0.0132)	0.0000339

^*Observed overall prevalence.

^†Design variables are condition, time, round and their pairwise interactions. Community variables are percent of household with female head with no husband, percent foreign born, and median income.

^‡Covariance between ${\widehat{\alpha }}_0$ and ${\widehat{\alpha }}_1$.

The estimation of intracluster correlations in this article employs an extension of GEE that jointly specifies one set of estimating equations for the parameters in the logistic model for the probability that an individual reports the behavior, and a second set of estimating equations to estimate the parameters in the correlation model.¹¹ In this approach, applied separately for the various behavior outcomes, a correlation model based upon 2 intracluster correlations is specified, the “within-time” correlation between outcomes from different youths at the same time (α₀), and the “between-time” correlation between 2 outcomes from different youths at different times (α₁).¹² The approach produces estimates of the standard error for both intracluster correlations as well as for their covariance. As in the ordinary GEE,¹⁶ the extended GEE approach provides valid inference for assessing intervention effects, assuming the marginal model for the probability of behavior is correctly specified, even if the correlation model is misspecified.

Three sets of logistic models are fit for the probability that a youth reports the behavior. An initial set of models includes the design variables of condition (ie, control versus intervention), time, and funding cycle, as well as their pairwise interactions. A second set of models includes these terms in addition to the individual characteristics of age and sex. A third and final set of models adds both individual and the community characteristics, which serves 2 purposes. First, it may help to address any postsample selection imbalances among covariates in this nonrandomized study. Second, it may partly explain the magnitude of within-cluster correlation.⁵ For example, smaller intracluster correlations in the third model, may suggest that intracluster correlations in the first or second models are partly explained by variation in community characteristics.

Sample Size Determination

A general approach to power calculations for cluster trials is based upon an analysis of community summary statistics according to the study design.¹² The general set-up is to specify the hypothesis of interest as H₀ : δ = 0 versus H₁ : δ ≠ 0 where δ = μ₁ – μ₂ is the intervention effect and μ_h = E(S_hi) is the expected value of the summary statistic, S_hi, for the i-th community receiving the intervention (h = 1) or control (h = 2) treatment condition. Specific examples of S_hi relevant in the application of GEE to the national evaluation data are discussed below. As communities are assumed to be statistically independent, deriving an expression for the variance of the community summary statistic in each condition (intervention and control) is the critical step in determining sample size. For the ith community receiving the hth condition, let σ_h² = Var(S_hi), and let m be equal to the number of subjects in each community at each time-point. Constant variance within condition results from assuming that m is constant. The number of communities needed per condition (n) to test the intervention using a two-sided test with α significance level and power 1 – β is

$$n=\frac{({\sigma }_1^2+{\sigma }_2^2){(z_{1-\alpha ∕2}+z_{1-\beta })}^2}{{\delta }^2}$$ (1)

where z_c is the (100× c)th percentile of the standard normal distribution. For small n, Equation 1 may be refined using the t-distribution.² Let ϕ(·) define the cumulative distribution function of the standard normal distribution, and

$$d=\sum _{i=1}^n{S}_{1i}∕n-\sum _{i=1}^n{S}_{2i}∕n,$$

an unbiased estimator of δ. Power (1 – β)is

$$1-\beta =\Phi \left(\frac{\delta }{\sqrt{\mathrm{var}\left(d\right)}}-z_{1-\alpha ∕2}\right)$$ (2)

where var(d) = (σ₁² + σ₂²)/n.

Of specific interest are sample size formulae for pretest-posttest nested cross-sectional designs as they pertain to binary outcomes. In this design, the total number of individuals sampled per community, or cluster size, is 2m. Let π_ht be the probability of the outcome for an individual at time t (t = 0 for pretest, t = 1 for posttest) from a community having condition h. Subscript i for the individual is not needed because the probability of outcome is assumed to depend only upon the treatment status and time point.

In randomized cluster trials with a moderate to large number of communities, a planned GEE analysis need not adjust for pretest since groups may be expected to be balanced with respect to outcomes and covariates as a result of randomization. Statistical inference may be based on the posttest-only logistic model

$$\mathrm{logit}\left({\pi }_{h1}\right)={\beta }_0+{\delta }_0{x}_1$$ (3)

where x₁ = 1 if h = 1 (intervention) and 0 if h = 2 (control); and δ₀ = μ₁ – μ₂, where μ₁ = logit(π₁₁) and μ₂ = logit(π₂₁), is the log odds ratio comparing odds of response in the posttest period for subjects in intervention communities to the odds of response for subjects in control communities. Suppose S_hi is the logit of the observed proportion reporting the behavior of those sampled at posttest from the ith community having condition h. Then d is an approximately unbiased estimator of δ₀ whose large sample variance depends upon the approximate variance of S_hi under H₁ : δ₀ ≠ 0:

$${\sigma }_h^2\approx \frac{\varphi }{m{v}_{h1}},$$ (4)

where ν_ht = π_ht (1 – π_ht) and ϕ = 1 + (m – 1)α₀ is the design effect. When α₀ > 0, ϕ represents a multiplicative increase on the sample size required in a cluster trial to obtain a given level of power relative to the sample size required in a clinical trial with randomization of individuals. Inserting Equation 4 into Equation 1 and substituting δ₀ for δ gives

$$n=\frac{\varphi (1∕v_{11}+1∕v_{21}){(z_{1-\alpha ∕2}+z_{1-\beta })}^2}{m{[\mathrm{logit}\left({\pi }_{11}\right)-\mathrm{logit}\left({\pi }_{21}\right)]}^2},$$ (5)

the posttest-only cluster trial design sample size for binary outcomes. Similarly, inserting Equation 4 into Equation 2 gives the power formula. The equivalency of Formula 5 to a general GEE method of sample calculation for the Wald test statistic corresponding to δ₀ in Equation 3 is shown in the Appendix. Alternatively, one can conduct sample size calculations for a planned linear model for the binary outcome (ie, use of identity link in Equation 3) using Equation 6 of Preisser et al.¹²

For a nonrandomized cluster trial with a nested pretest–posttest cross-section design, Formula 5 may be inadequate because adjustment for pretest response is needed in the analysis due to baseline imbalance. While, for the national evaluation, the estimation of intracluster correlations is based upon a model applied to data from 3 time points, sample size considerations for a future nonrandomized cluster trial address the anticipated effect at a single follow-up with respect to baseline. Thus, the comparison of intervention and control communities is operationalized as a one-degree-of-freedom contrast for the difference in the change in expected outcome from pretest to posttest. An appropriate sample size formula targets the contrast

$${\delta }_1=[\mathrm{logit}\left({\pi }_{11}\right)-\mathrm{logit}\left({\pi }_{10}\right)]-[\mathrm{logit}\left({\pi }_{21}\right)-\mathrm{logit}\left({\pi }_{20}\right)],$$

the regression coefficient for the time × condition interaction in the logistic regression model for a youth's response at time t under the hth condition:

$$\mathrm{logit}\left({\pi }_{ht}\right)={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\delta }_1(x_1\times x_2)$$ (6)

where x₂ = t. Specifically, δ₁ is the difference in log odds ratios for pretest/posttest changes between intervention and control conditions. Equivalently, exp(δ₁) is the multiplicative factor by which the pretest/posttest odds ratio for communities under the intervention condition exceeds that of the control condition. For a community i having condition h, define S_hi as the logit of observed proportion reporting the behavior at posttest minus the logit of the observed proportion reporting the behavior at pretest. The corresponding mean over all communities within a condition is Σ_tⁿ = 1 S_hi/n, an approximately unbiased estimator of μ_h = logit(π_h1) – logit(π_h0). The approximate variance¹² of S_hi is:

$${\sigma }_h^2=\frac{1}{m}\left\{\varphi \left(\frac{1}{v_{h1}}+\frac{1}{v_{h0}}\right)-\frac{2m{\alpha }_1}{\sqrt{v_{h1}{v}_{h0}}}\right\}$$ (7)

Inserting Equation 7 into Equation 1, and setting δ to δ₁ gives the pretest-posttest cluster trial design sample size formula for binary outcomes

$$n=\frac{\left\{\varphi \sum _{h=1}^2\sum _{t=0}^1\left(\frac{1}{v_{ht}}\right)-2m{\alpha }_1\left[\sum _{h=1}^2\left(\frac{1}{\sqrt{v_{h1}{v}_{h0}}}\right)\right]\right\}{(z_{1-\alpha ∕2}+z_{1-\beta })}^2}{m{\{[\mathrm{logit}\left({\pi }_{11}\right)-\mathrm{logit}\left({\pi }_{10}\right)]-[\mathrm{logit}\left({\pi }_{21}\right)-\mathrm{logit}\left({\pi }_{20}\right)]\}}^2}$$ (8)

Note that the resulting expression depends upon values of the 4 probabilities π_ht. Often researchers are unwilling or unable to specify particular values of the π_ht. Then values of π_ht may be chosen to give conservative values of σ_h² in Equation 4 or Equation 7 accordingly. Finally, inserting Equation 7 into Equation 2 and setting δ to δ₁ gives the corresponding formula for power. Alternatively, one can conduct sample size calculations for a planned linear model analysis of the proportions (ie, GEE identity link function) using Equation 9 of Preisser et al¹² and δ₁ = (π₁₁ – π₁₀) – (π₂₁ – π₂₀).

RESULTS

Intracluster Correlation Estimates

Table 3 provides intracluster correlation estimates for several binary outcomes from the national evaluation from the model based upon 3 timepoints and 3 funding cycles. Estimates obtained from the extended GEE approach for the within-time (α₀) and between-time intracluster correlation (α₁) as well as their 95% large sample confidence intervals are reported. The upper confidence bound for each intracluster correlation (eg, for α₀) is given by $\mathrm{UCB}={\widehat{\alpha }}_0+1.96\mathrm{se}\left({\widehat{\alpha }}_0\right)$ and the lower confidence bound is given by LCB = ${\widehat{\alpha }}_0-1.96\mathrm{se}\left({\widehat{\alpha }}_0\right)$, where se (${\widehat{\alpha }}_0$) is the standard error based upon the robust variance estimator.¹¹ The estimated covariance between ${\widehat{\alpha }}_0$ and ${\widehat{\alpha }}_1$ is also reported for the purpose of conducting power for a range of (α₀, α₁) as illustrated in the next section. Three different sets of intracluster correlations are reported based upon the covariates included in the model for the probability a youth reports a behavior. For each measure, the first row gives the intracluster correlations based upon the model for the probability of the behavior that depends only upon study design variables: time point (year), cycle, intervention versus control condition, and their twoway interactions. The second row gives intracluster correlation estimates based upon a probability model that also adjusts for covariates age and gender. The third row gives intracluster correlations based upon the logistic model that additionally adjusts for the community level variables.

Intracluster correlation estimates range from 0.003 to 0.026 with modest differences in within-time and between-time intracluster correlations. Within-cluster correlations estimates for binge drinking, past 30-day alcohol use and attempt to purchase alcohol are larger than estimates for those outcomes reported by some authors^4,17 but similar in magnitude to those reported by others.^5,18,19 Generally, correlations adjusting for individual and community variables are smaller than design-adjusted correlations or those adjusting for age and gender in addition to design variables. SAS/IML software for applying the extended GEE is available.²⁰

Sample Size Results

Consider a future cluster trial to reduce underage drinking. Suppose the primary outcome is past 30-day alcohol use, and a pretest-posttest (2 time-points) nested cross-sectional design is planned with equal numbers of intervention and control communities and m = 15 youth to be surveyed from each community at each time point. Assume π₁₀ = π₂₀ = π₂₁ = 0.40 and π₁₁ = 0.30 (ie, δ₁ = 0.44) such that a 25% decline in underage drinking is anticipated. Applying Equations 1 and 7, and using the unadjusted intracluster correlation values of α₀ = 0.0261 and α₁ = 0.0219 from Table 3, results in n = 48 communities per condition needed to provide approximately 80% power to detect the desired effect based upon a 2-sided test at the 0.05 significance level.

A sensitivity analysis of power considers a range of values for α₀ and α₁ using information in Table 3. Because combinations of the 2 types of intracluster correlation are required, the univariate confidence intervals reported in Table 3 have limited utility, since the joint 95% confidence region is not rectangular, but rather is defined by the ellipse

$$\{\alpha :{(\alpha -\widehat{\alpha })}^{\prime }{\left[\mathrm{Cov}\left(\widehat{\alpha }\right)\right]}^{-1}(\alpha -\widehat{\alpha })\le z_{0.025}^2\}$$ (9)

where α = (α₀, α₁)′, z_0.025² = 3.842 . Equivalently, the 95% joint confidence region consists of α values that satisfy

$$\frac{{({\alpha }_0-{\widehat{\alpha }}_0)}^2\mathrm{var}\left({\widehat{\alpha }}_1\right)-2({\alpha }_0-{\widehat{\alpha }}_0)({\alpha }_1-{\widehat{\alpha }}_1)\mathrm{cov}({\widehat{\alpha }}_0,{\widehat{\alpha }}_1)+{({\alpha }_1-{\widehat{\alpha }}_1)}^2\mathrm{var}\left({\widehat{\alpha }}_0\right)}{\mathrm{var}\left({\widehat{\alpha }}_0\right)\mathrm{var}\left({\widehat{\alpha }}_1\right)-{\left[\mathrm{cov}({\widehat{\alpha }}_0,{\widehat{\alpha }}_1)\right]}^2}\le z_{0.025}^2$$ (10)

Estimated variances for outcomes can be determined from Table 3, ie, $\widehat{\mathrm{var}}\left({\widehat{\alpha }}_0\right)={[(\mathrm{UCB}-{\widehat{\alpha }}_0)∕1.96]}^2$ or $\widehat{\mathrm{var}}\left({\widehat{\alpha }}_0\right)={[({\widehat{\alpha }}_0-\mathrm{LCB})∕1.96]}^2$, and similarly for α₁. Using national evaluation estimates for past 30-day alcohol use (i.e., ${\widehat{\alpha }}_0=0.0261$, ${\widehat{\alpha }}_1=0.0219$, $\mathrm{var}\left({\widehat{\alpha }}_0\right)=0.0000246$, $\mathrm{cov}({\widehat{\alpha }}_0,{\widehat{\alpha }}_1)=0.0000128$, and $\mathrm{var}\left(\widehat{\alpha }1\right)$ = 0.0000186 gives the ellipse plotted in Figure 1 along with contours of power to show how power varies over the joint confidence region for (α₀, α₁). First note the ellipse represents the boundary of the joint 95% confidence region for (${\widehat{\alpha }}_0,{\widehat{\alpha }}_1$). Second, the box is the intersection of the individual 95% confidence intervals, ignoring the covariance between the 2 correlation estimates. Third, the numbers on the plot represent power to reject H₀ : δ₁ = 0 in favor of H₁ : δ₁ ≠ 0, for the assumed values of probabilities described above. Fourth, the 3 bands within the ellipse indicate constant levels of power (77%, 80%, 83%) for different combinations of α₀ and α₁. Within the ellipse, power attains it highest value (85%) for the boundary values of (α₀ = 0.0210, α₁ = 0.0250), and its lowest value (76%) for the boundary values of (α₀ = 0.0311, α₁ = 0.0187). Thus, for a sample design with n = 48 and m = 15, the 95% joint confidence region for the 2 intracluster correlations indicates a range of power from 76% to 85%. This sensitivity analysis for power is a considerable refinement over a naive approach, represented by the box in Figure 1, that gives a range of power that is artificially low (71%) or high (90%). Given knowledge of the covariance of the 2 intracluster correlations, the joint elliptical confidence region approach represents a clear improvement in cluster trial planning.

FIGURE 1.

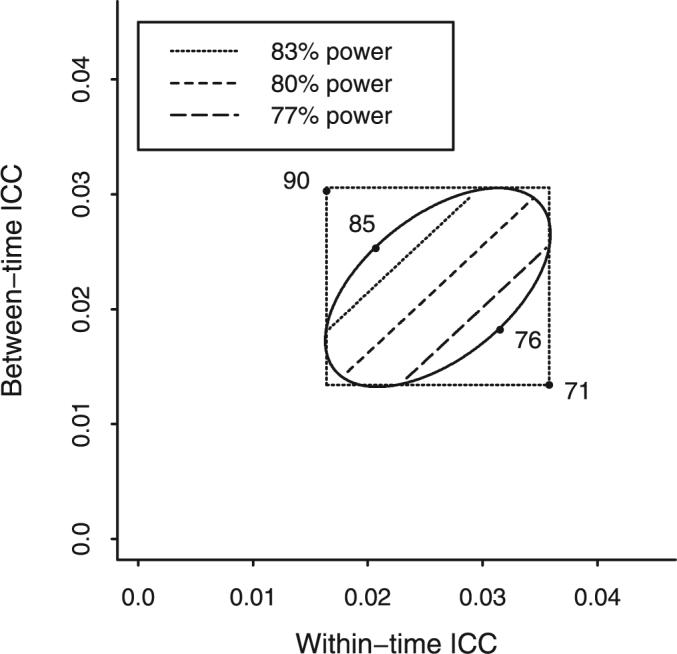
Power for detecting a difference in prevalence of past 30-day alcohol use of 0.10 between control and intervention conditions with a pretest–posttest nested cross-sectional design with n = 48 and m = 15. The diagonal lines indicate pairs of within-time and between-time intracluster correlation values that give a fixed level of power and that are useful values of correlations for planning a future trial as they lie in the ellipse that defines a 95% joint confidence region for the intracluster correlations.

Providing further rationale for use of the proposed 2 intracluster correlation sample size formula is the strong possibility that use of the posttest-only sample size formula when planning a pretest-posttest nested cross-sectional trial will underestimate the sample size needed to obtain a desired level of statistical power in a GEE time × condition analysis. Consider the ratio (r) of variances under the respective designs, var(d) based upon Equation 7 divided by var(d) based upon Equation 4. A ratio near 1 indicates that the formula for the posttest-only design is a good substitute for the pretest-posttest design formula. Figure 2 shows that generally r > 1 indicating that use of the posttest-only formula underestimates the required sample size. Using results for past 30-day alcohol use and m = 15, r ranges from 1.37 (corresponding to the highest value of power in the ellipse of Fig. 1) to 1.47 (based upon GEE estimates of intracluster correlations) to 1.56 (corresponding to lowest power). Figure 2 indicates that, in the case of (α₀ = 0.0210, α₁ = 0.0250), r < 1 only when m ≥ 30; note m = 30 and α₀ = 0.0210 gives ϕ = 1.61, a relatively large design effect. Comparatively, the observed design effect for past 30-day use, calculated as ϕ = 1 + ${\widehat{\alpha }}_0(\stackrel{‒}{m}-1)$, where $\stackrel{‒}{m}$ is the average number of youth from a community sampled at a timepoint, was 1.46. The fact that past 30-day use had the largest design effect among the 9 measures in the national evaluation suggests that observing a sufficiently large design effect in any cluster trial such that r ≤ 1 appears unlikely.

FIGURE 2.

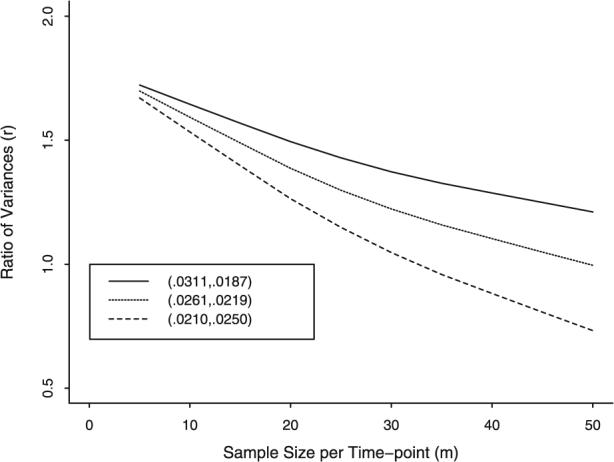
Ratio of variances of intervention effect from pretest–posttest to posttest-only design by sample size for 3 values for pairs of within-time and between-time intracluster correlations.

DISCUSSION

The utility of any sample size formulae for cluster unit trials depends upon the availability of intracluster correlation estimates for various outcomes. Given their typically high cost, many cluster trials enroll a small number of clusters. However, in many government and foundation-sponsored programs, such as the national evaluation, the resources available for the evaluation of the program may be distinct from funds for implementing the intervention, so a moderately large number of clusters may be studied. These larger studies offer a unique opportunity to report on the magnitude and precision of intracluster correlation estimates for health behavior outcomes.

Relative to equivalent general power methods for GEE,²¹ the sample size formulae for a time × condition analysis of binary outcomes presented in this paper are easy to apply. This article emphasized sample size formulae based upon a planned GEE analysis using a logit link, whereas Preisser et al¹² emphasized similar formulae based upon an identity link. As a rule, the choice of sample size formula should be based upon the planned statistical analysis. However, because the 4-parameter interaction model in Equation 6 places no structure on the 4 time × condition probabilities, correlation estimates obtained with the logit link model (eg, those in Table 3) may be used in sample size formula in equation 8 for a planned logit analysis or in Formulae 3 and 9 of Preisser et al¹² for an analysis using the identity link. The difference in the respective formulae pertains to a difference in the definition of the effect of interest as a contrast of logits, or a contrast of proportions. Applying the formula based upon the identity link would have given n = 50 communities per condition in the previous section instead of n = 48; it is not always the case that larger sample sizes will be required for the identity link.

One practical obstacle in applying the proposed sample size methods is that information regarding variances of intracluster correlations (usually, in the form of confidence intervals or standard errors) are only occasionally published, and it seems less realistic that covariances of the 2 types of intracluster correlation will be available. If the 2 intracluster correlations are approximately equal, the problem may be circumvented by conducting a sensitivity analysis of power using the pretest-posttest formula under the assumption that α ≡ α₀ = α₁; in this case, knowledge of a single intracluster correlation and its standard error are sufficient.

This article addressed the question of whether Formula 5 of the posttest-only design may be substituted for Formula 8 in planning a nonrandomized pretest-posttest nested cross-sectional cluster trial. Direct comparison of variances under the 2 designs showed that the posttest-only formula is generally not an appropriate substitute for the prettest-posttest design formula and will likely underestimate the required sample size and lead to an underpowered cluster trial. In other words, for nonrandomized cluster trials, pretest adjustment with a time × condition analysis is undertaken to address potential bias, at the price of loss of power. This is in contrast to the design and analysis of randomized cluster trials, where adjustment for pretest using a time × condition analysis may not be preferred because of the increased variance associated with Equation 7 relative to Equation 4. Rather, because communities tend to be similar across conditions due to randomization, covariate adjustment of cluster baseline response means may be undertaken to increase power.²²

The Enforcing Underage Drinking Laws Program that provided the intracluster correlation estimates in Table 3 had limitations. The sample under-represented 19- and 20-year-old subjects compared with 16-, 17-, and 18-year-old subjects. Such selection bias may lead to biased intracluster correlation estimates. However, for the national evaluation, stratified analyses of intracluster correlation estimates (not reported) were similar across age groups. Another limitation is that the random digit dialing methodology used to conduct the survey is known to underrepresent ethnic/racial minorities and lower socioeconomic status individuals.²³ These limitations should be considered when deciding whether to use the reported intracluster correlations in planning a future cluster trial.

Finally, there are limitations with respect to the extended GEE and proposed sample size methods. The simple sample size formulae applied to the national evaluation data are applicable only to cluster trial study designs without matching or stratification. For these more complicated designs, use of the general GEE power method²¹ is recommended. Finally, using the extended GEE to produce confidence intervals for intracluster correlations requires a large number of clusters (eg, 80 or more); otherwise, confidence intervals may suffer from severe under-coverage.²⁴ Small-sample bias adjustments to estimation of intracluster correlations,²⁵ and to their estimated variances and covariances by extension of corrections for ordinary GEE^26,27 may broaden the applicability of these methods. However, because the validity of estimating equation methods depends upon the assumption of asymptotic normality of parameter estimates, construction of (possibly asymmetric) confidence intervals based upon resampling strategies may be a better choice for small samples. In articular, bootstrap methods,²⁸ though more computationally intensive than the GEE approach, are often easy to implement.²⁹

APPENDIX

Equivalency of Sample Size Formula 5 for the Posttest-Only Analysis to the General GEE Sample Size Method

Rochon²¹ presents a general power analysis method for GEE regression coefficients for arbitrary working correlation and link and variance functions. Now, Equation 5 is the sample size formula for the summary statistic approach to power for the test statistic d/var(d), which in sufficiently large samples is normally distributed and equivalent to

$$Z=\frac{\mathrm{logit}\left({\pi }_{11}\right)-\mathrm{logit}\left({\pi }_{21}\right)}{\sqrt{\frac{\varphi }{nm}\left(\frac{1}{v_{11}}+\frac{1}{v_{21}}\right)}}$$

The following arguments show that the GEE Wald χ² statistic, Q_W in Expression 5 of Rochon,²¹ is equal to Z² thus demonstrating equivalency of the 2 power analysis approaches. This first step deduces the GEE estimator $\widehat{\beta }$ in Equation 2 of Rochon²¹ for the simple logistic model in Equation 3, binomial variance function ν_h1, and “exchangeable” working correlation matrix R = ϕ(J/m) + (1 – α₀) × (I – J/m), where I is the m × m identity matrix and J is the m × m matrix of 1's. Define 0 and 1 as m × 1 vectors of 0's and 1's, respectively. Following Equation 2 of Rochon,²¹ the GEE estimator for β = (β₀, δ₀)is

$$\widehat{\beta }={\left[\sum _{h=1}^2{X}_h^{\prime }{W}_h{X}_h\right]}^{-1}[\sum _{h=1}^2{X}_h^{\prime }{W}_h\left(1{\mathrm{g}}_{\mathrm{h}}\right)]\phantom{]}$$

where X₁ = [1, 1] and χ₂ = [1, 0], W_h = Δ_h⁻¹ Δ_h, Δ_h = diag{$\sqrt{v_{h1}}$}, and g_h = logit(π_h1) for h = 1, 2. Matrix computations and the result R⁻¹ = J/(mϕ) + (I – J/m)/(1 – α₀) lead to $\widehat{\beta }$ = (g₂, g₁ – g₂)′ and, from Equation 3 of Rochon,²¹ its model-based variance estimator is

$${\mathrm{COV}}_{MB}\left(\widehat{\beta }\right)=\frac{\varphi }{nm}\left[\begin{array}{cc}\hfill 1∕v_{21}\hfill & \hfill -1∕v_{21}\hfill \\ \hfill -1∕v_{21}\hfill & \hfill 1∕v_{21}+1∕v_{11}\hfill \end{array}\right].$$

Finally, the hypothesis H₀ : δ₀ = 0 can be expressed as H₀ : Hβ = 0, where H = [0, 1]. The Wald chi-square test statistic is

$$Q_W={\left(H\widehat{\beta }\right)}^{\prime }{\left[H{\mathrm{cov}}_{MB}{H}^{\prime }\right]}^{-1}\left(H\widehat{\beta }\right)=Z^2$$

proving the equivalency.