Abstract
Distortion-product otoacoustic emissions (DPOAEs) were measured in a New World primate, the common marmoset (Callithrix jacchus). We determined the optimal primary-tone frequency ratio (f2/f1) to generate DPOAEs of maximal amplitude between 3 – 24 kHz. The optimal f2/f1, determined by varying f2/f1 from 1.02 – 1.40 using equilevel primary tones, decreased with increasing f2 frequency between 3 – 17 kHz, and increased at 24 kHz. The optimal f2/f1 ratio increased with increasing primary-tone levels from 50 – 74 dB SPL. When all stimulus parameters were considered, the mean optimal f2/f1 was 1.224 – 1.226. Additionally, we determined the effect of reducing L2 below L1. Decreasing L2 below L1 by 0, 5, and 10 dB (f2/f1 = 1.21) minimally affected DPOAE strength. DPOAE levels were stronger in females than males and stronger in the right ear than the left, just as in humans. This study is the first to measure OAEs in the marmoset, and the results indicate that the effect of varying the frequency ratio and primary-tone level difference on marmoset DPOAEs is similar to the reported effects in humans and Old World primates.
Keywords: OAE, DPOAE, parameter optimization, primary-tone frequency ratio, primary-tone level difference, animal model, primate, marmoset
Introduction
Stimulating the ear with two pure tones, or primary tones, at frequencies f1 and f2 (with f1 < f2) can result in the generation of a number of nonlinear distortion-product otoacoustic emissions (DPOAEs) having frequencies algebraically related to the primary-tone frequencies. The strongest and most commonly examined of these nonlinear products is the cubic DPOAE, which has a frequency equal to 2f1-f2. In humans, cubic DPOAEs are presumed to arise from the micromechanical activity of outer hair cells (Kemp, 1978) at two distinct places. They are generated near the f2 region on the basilar membrane (e.g., Kim et al., 1980; Brown & Kemp, 1984; Martin et al., 1987; Harris et al., 1992) and are re-emitted at the location of the DPOAE frequency (fDP) region (e.g., Brown et al., 1996; Gaskill & Brown, 1996; Talmadge et al., 1998; Mauermann & Kollmeier, 1999; Shera & Guinan, 1999). DPOAEs then are propagated backwards along the basilar membrane, through the middle ear, to the external auditory canal where they can be recorded with a sensitive probe microphone. The relative amplitude of these emissions at specific frequencies may reflect the health of the basilar membrane at specific loci, and if so, DPOAEs provide a non-invasive method of measuring cochlear health.
DPOAEs have been studied in numerous non-primate species including (but not limited to) mice (e.g., Horner et al., 1985; Schrott et al., 1991; Parham, 1997; Varghese et al., 2005), rats (e.g., Brown, 1987; Khvoles et al., 1998), gerbils (e.g., Schmiedt, 1986; Brown & Kemp, 1984; Brown, 1987; Norton & Rubel, 1990; Mills & Rubel, 1994) guinea pigs (e.g., Canlon et al., 1983; Brown, 1987; Brown & Gaskill, 1990a), chinchillas (e.g., Kim, 1980; Zurek et al., 1982), rabbits (e.g., Lonsbury-Martin et al., 1987; Martin et al., 1987; Whitehead et al., 1992a,b), dogs (e.g., Sockalingam et al., 1998), spotted hyenas (McFadden et al., 2006b), cats (e.g., Kim, 1980; Wiederhold et al., 1986; Schmiedt, 1986), and bats (e.g., Kössl, 1994) to determine the effects of noise, drugs, anesthesia, temperature, age, and prenatal androgen exposure on the cochlea. However, these species exhibited DPOAEs that were approximately 30 – 40 dB SPL greater than those measured in humans (for a review, see Probst et al., 1991). Due to the inter-species differences, some investigators (Martin et al., 1988; Lasky et al., 1995; Park et al., 1995) have suggested that non-human primates may serve as a more appropriate model for cochlear function, though Brown and colleagues (Brown, 1987; Brown & Gaskill, 1990a; Gaskill & Brown, 1990) have shown these species differences to be most pronounced with high-level primary tones and less evident with low- to moderate-level primary tones. By contrast, the effect of f2/f1 on DPOAE level (LDP) varies considerably across species (Brown, 1987; Brown & Gaskill, 1990a), and the optimal f2/f1 is larger in rodents and rabbits (1.25 – 1.30) (Brown, 1987; Whitehead et al., 1992) than in humans (1.22 – 1.23) (e.g., Harris et al., 1989; Gaskill & Brown, 1990; Nielsen et al., 1993).
Indeed, DPOAEs in the rhesus monkey are more similar to human DPOAEs than are other laboratory animals (Martin et al., 1988; Park et al., 1995; Lasky et al., 1995, McFadden et al., 2006a). The strength of DPOAEs in rhesus monkeys can be approximately 45 – 60 dB SPL below (equilevel) primary-tone levels (McFadden et al., 2006a), while human DPOAEs are approximately 60 dB SPL below primary-tone levels (for a review, see Probst et al., 1991). Lasky et al. (1995) observed DPOAEs in rhesus monkeys that were 10 – 15 dB SPL stronger than those measured in humans. The mean optimal f2/f1 ratio in rhesus monkeys is 1.21 (Lasky et al., 1995) compared to 1.22–1.23 in humans (Harris et al., 1989; Gaskill & Brown, 1990; Nielsen et al., 1993). Decreasing L2 below L1 by 5 and 10 dB SPL had little effect on DPOAE levels in rhesus monkeys (Park et al., 1995) and humans with healthy ears (Whitehead et al., 1995).
For comparative purposes, we aim to determine whether cochlear function is similar in a New World primate, the common marmoset. This species has emerged as a model for biomedical research in reproductive biology (e.g., Tardif et al., 2005; Power et al., 2006), behavioral research (e.g., Sieden, 1957; Barros et al., 2007), and auditory function (e.g., Bendor & Wang, 2007; Bartlett & Wang, 2007; Schnupp et al., 2006; de la Mothe et al., 2006a, b). However, most auditory research in marmosets has focused on the central nervous system, particularly the auditory cortex, and only a few researchers have investigated the auditory periphery in this species (Wever & Vernon, 1961; Spatz & Löhle, 1995; Spatz, 1999). Sieden (1957), using a shock-avoidance technique, obtained behavioral audiograms from five marmosets (4 females and 1 male). These marmosets responded to pure tones as low as 100 Hz and as high as 25 – 37 kHz. Wever & Vernon (1961) measured cochlear potentials at frequencies up to 100 kHz in four (3 females, 1 male) of these same five marmosets. Spatz & Löhle (1995) showed that the marmoset cochlea takes about 2.5 turns, the same as in humans. To our knowledge, no one has systematically investigated cochlear function in this species. As a first step in this direction we have made detailed measurements of DPOAEs in the marmoset by varying stimulus parameters to determine the extent to which the response is similar to those reported for humans and Old World monkeys. Our results show that DPOAEs in the marmoset respond to these variations in a manner similar to humans and Old World monkeys. Therefore, this paper serves as a starting point for the study of OAEs in this species.
Materials and Methods
Subjects
DPOAEs were measured in 6 male and 6 female common marmosets ranging between 1.3 and 3.2 years of age (mean = 2.05 years). Subjects were located at the Southwest National Primate Research Center (SNPRC) at the Southwest Foundation for Biomedical Research (SFBR) in San Antonio, TX, housed either in group enclosures as family units or individually in rooms containing multiple enclosures. For four female marmosets, the optimal f2/f1 and L1 − L2 conditions were performed on separate days. For all male and two female marmosets both conditions were performed in a single session, permitting the same microphone placement for all measurements. All testing was conducted in a small procedure room at the SNPRC. Subjects were anesthetized with intramuscular injections of ketamine hydrochloride (Ketaset®, 10mg/kg) and butorphanol tartrate (0.5 mg, regardless of weight). A maintenance dose of ketamine was required after an hour to minimize movement in some male subjects. The subject was placed on its side during recordings. The subject’s temperature was maintained during recordings with an adjacent non-electrical heat source and monitored with a digital rectal probe thermometer at the beginning and end of each session. The average temperature change was minimal (−1.68 ± 1.49 º F). These procedures were approved by the SFBR Institutional Animal Care and Use Committee (IACUC; CJ 10441).
Procedures and equipment
A probe microphone/loudspeaker system with two loudspeaker ports (ER10B+, Etymotic Research, Inc.) was fitted tightly into the ear canal with a rubber immittance tip. Two loudspeakers (EC-1, Tucker-Davis Technologies, Inc.), with flat frequency response from 4 –100 kHz, were connected to the ER10B+ ports. Acoustic stimuli were delivered from an analog input/output (I/O) device (PXI-4461, 24-bit ADC, National Instruments, Inc.), through an electrostatic speaker driver (ED-1, Tucker-Davis Technologies, Inc.), to the EC-1 speakers. Each primary tone was delivered through a separate loudspeaker to avoid the generation of intermodulation products. Control measurements were performed with the microphone inserted into a 1-ml syringe (volume = 0.10 ml). No spurious intermodulation products generated by the electronics or by the acoustics of the canal were detectable at the DPOAE frequency in these control recordings.
The OAE response output from the ER10B+ microphone was amplified by 20 dB by a low-noise preamplifier (Etymotic Research, Inc.) and digitized at a 50-kHz sampling rate by the PXI-4461 module. The data-acquisition module was housed in a mobile chassis (PXI-1036DC, National Instruments, Inc.) and connected to a laptop computer (Latitude D800, Dell, Inc.) through the PC CardBus slot (PXI-8310 StarFabric® interface, National Instruments, Inc.). Custom software for acquiring DPOAEs was written in LabVIEW (National Instruments, Inc.) by one of the authors (E.G.P).
A modified CUBDIS procedure (Allen, 1990a) was used to estimate the level of the DPOAE. This procedure has been modified from that previously described by McFadden et al. (2006a, b). Briefly, the initial calibration procedure, which measures the frequency response of the ear canal to a single click, gave us information about the position of the probe tip in the ear canal. A smooth frequency response indicated a tight seal in the ear canal, and any deviation prompted us to reposition the probe. After ensuring a tight fit of the probe, two primary tones at specified frequencies and levels were presented continuously to one ear, and the response was simultaneously recorded for 4-sec from the stimulated ear. Primary tones were calibrated at each frequency to produce sound output at 65 dB SPL in the subject’s ear canal. The frequencies of the primary tones were chosen such that each segment of 1028 sample points contained an integral number of cycles (as did the DP component). The f2/f1 was as close to the desired f2/f1 as this sampling constraint allowed. Averaging in the time domain was performed using 2048-point segments of the waveform with 50% overlap. This procedure afforded a reduction in the noise floor level, and the 2048-point FFT analysis improved the frequency resolution, permitting testing at values of f2/f1 nearer to 1.0. The initial 2048 points and the strongest 15% of the other segments were discarded (to remove possible artifacts) and the remaining segments (about 165) were averaged to produce a waveform of 2048 points. This waveform was used to compute a power spectrum. The power in the frequency bin containing the DP was then converted to SPL and taken as the LDP. The strengths of the primary tones were similarly determined. The noise floor was estimated by averaging six adjacent frequency bins above and below the fDP (separated from fDP by at least 3 frequency bins). Also recorded in each case were the measured levels of f1 and f2; this permitted detection of conditions where the primary tones’ actual levels deviated from their target values.
Frequency ratio (f2/f1) optimization
DPOAEs were measured in the right ears of 12 (6 male, 6 female) marmosets. The left ear was also tested in a subset of these subjects (3 male, 2 female), so the total number of ears tested was 17. Right ears were tested first in every case. Seven f2 frequencies were selected in 0.5-octave spacing covering the range 3 – 24 kHz. For each value of f2, f1 was varied such that the f2/f1 ranged from 1.02 – 1.40 in 0.04 increments, except between 1.18 – 1.24 where step size was 0.02. At each f2/f1 ratio equilevel primary tones were presented in 6-dB increments between 50 – 74 dB SPL. DPOAE levels were averaged across all ears at each stimulus parameter and the f2/f1 which elicited the strongest mean LDP was taken as the optimal value.
The effect of decreasing L2 below L1
The effect of primary-tone level difference (L1 − L2) on the LDP was determined in the same 12 subjects described above (n = 18 ears). Right ears (6 male, 6 female) were tested before left ears (2 male, 4 female) in each case. The same f2 frequencies as above were used here. We chose an L1 − L2 paradigm in which L1 remained constant and L2 was decreased such that L1 − L2 = 0, 5, and 10 dB SPL. The f2/f1 was held constant (approximately 1.21) throughout. At each f2, a value of L1 − L2 was selected, and an input/output (I/O) function was obtained with L1 presented in 6-dB increments between 50 – 74 dB SPL. The values of LDP were averaged across all ears at each L1 − L2, and these mean DPOAE values were used to produce I/O functions (LDP vs. L1) and DPgrams (LDP vs. f2). Examination of theses I/O functions revealed them to be linear over the range of L1 values from 50 – 68 dB SPL. Linear-regression analysis was performed using this range to determine the slopes of the I/O functions.
Normative DPOAE audiograms and Input/Output functions
When evaluating normative marmoset DPOAE levels for any ear or sex differences, we will report the effect size (d) in place of statistical significance because the sample sizes were small. We calculated effect size by dividing the difference between the two means being compared by the square root of the weighted mean of the two variances. Cohen (1992) has suggested that effect sizes of 0.2, 0.5, and 0.8 should be considered small, medium, and large, respectively.
Data Omission
In some subjects there were calibration errors at higher f2/f1 ratios which resulted in frequency ranges (12 and 24 kHz) in which not all f2/f1 ratios were presented (see Discussion section). For these subjects, we did not include the incomplete frequency ranges in our final analysis to determine the optimal f2/f1 ratio. In one subject DPOAEs were not significantly greater than the noise floor at 24 kHz, so the data for this frequency were not included in our analysis. Data for another subject were excluded from the 24-kHz analysis as well because the voltage input (to the loudspeaker) required to produce 24-kHz tones was significantly larger than at all other frequency ranges in the same subject (and all other animals at 24 kHz), suggesting that, for this subject, the probe tip may have shifted between the 17- and 24-kHz measurements.
When f2 was at or below 8.5 kHz, an f2/f1 ratio of 1.02 (1.06 at 3 kHz) placed the f1 primary-tone frequency within nine frequency bins of the fDP, thereby including it in the average noise floor estimate. Because this resulted in a gross overestimation of the noise floor, we have omitted the affected data points from the appropriate figures.
Results
Frequency ratio (f2/f1) optimization
In general, the mean f2/f1 functions were bandpass in shape: as f2/f1 increased, the average DPOAE level increased to some maximum (usually occurring at mid-f2/f1 ratios) and then decreased as the f2/f1 was further increased. This was evident in the mean f2/f1 functions shown for 6 – 17 kHz (Figs. 1, 2) and in the individual f2/f1 functions (described later), although the f2/f1 which elicited the most robust DPOAE varied according to ear, sex, primary-tone level, and frequency. Table 1 summarizes the mean optimal f2/f1 at each f2 frequency and primary-tone level.
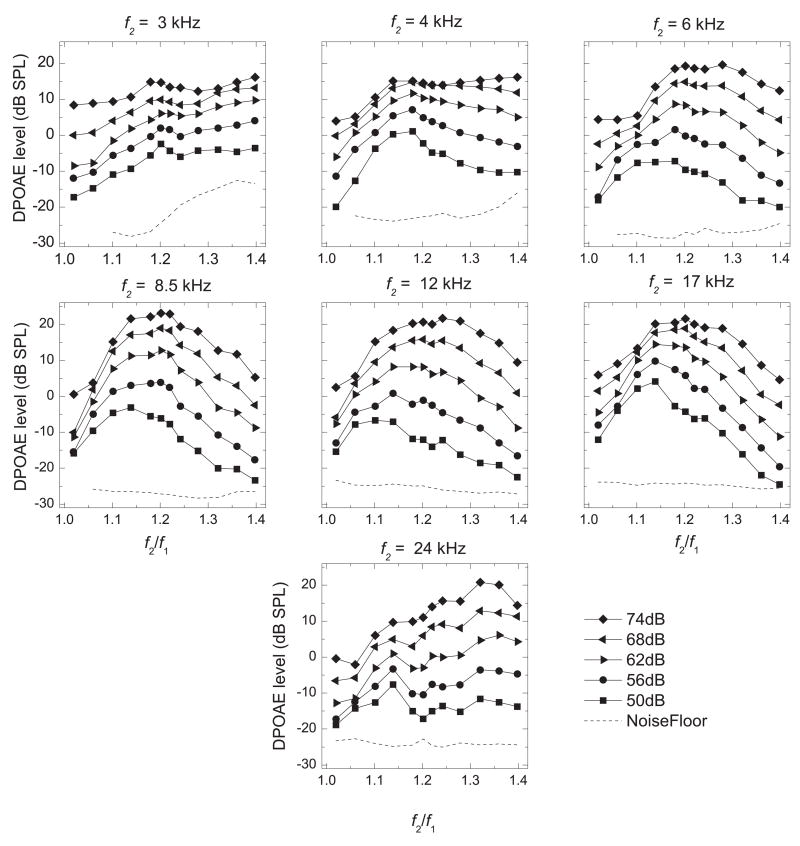
Figure 1.
Frequency-ratio (f2/f1) functions showing LDP (ordinate) vs. f2/f1 (abscissa) for each f2 frequency (f2 is specified above the individual panels). DPOAEs were obtained with equilevel primaries from 50 – 74 dB SPL (in 6-dB increments) as f2/f1 was increased from 1.02 – 1.40 in 0.04 increments (0.02 increments between 1.18 and 1.24). Responses were averaged across all ears (n = 17).
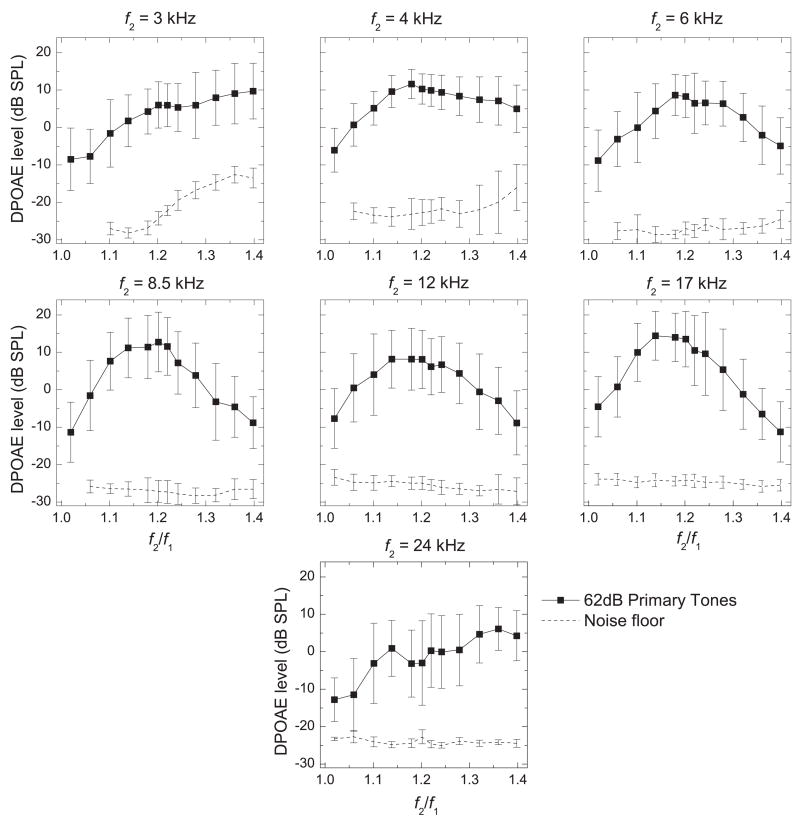
Figure 2.
Frequency-ratio (f2/f1) functions for each f2 frequency (axes as in Fig. 1). The DPOAEs shown here were obtained using equilevel primary tones at 62 dB SPL and were averaged across all animals and ears. Error bars are shown to demonstrate the typical amount of inter-subject and inter-ear variability observed in the DPOAE levels and the noise floor.
Table 1.
Mean optimal f2/f1 ratio for each combination of stimulus parameters.
| f2 (Hz)
|
||||||||
|---|---|---|---|---|---|---|---|---|
| 2978 | 4248 | 6005 | 8496 | 12,011 | 16,992 | 24,023 | Average | |
| Optimal frequency ratio all animals (both ears) | ||||||||
| L1 = L2 (db SPL) | ||||||||
| 50 | 1.196 | 1.160 | 1.140 | 1.137 | 1.119 | 1.141 | 1.139 | 1.147 |
| 56 | 1.386 | 1.176 | 1.183 | 1.174 | 1.139 | 1.141 | 1.272 | 1.210 |
| 62 | 1.371 | 1.176 | 1.194 | 1.200 | 1.174 | 1.174 | 1.359 | 1.235 |
| 68 | 1.371 | 1.213 | 1.202 | 1.208 | 1.208 | 1.190 | 1.339 | 1.247 |
| 74 | 1.386 | 1.360 | 1.235 | 1.208 | 1.242 | 1.200 | 1.339 | 1.282 |
| Average | 1.342 | 1.217 | 1.191 | 1.186 | 1.176 | 1.169 | 1.290 | 1.224 |
At 4 kHz (Fig. 1) the bandpass shape is seen most clearly at the lowest level of the primary tones, and as the primary-tone levels were increased from 50 – 74 dB SPL we observed less of an effect of f2/f1 on the average LDP. For example, with 68-dB SPL primary tones, the mean LDP elicited with f2/f1 ratios between 1.176 and 1.242 all were within 1.0 dB (with the maximum LDP occurring at 1.176).
At the lowest and highest f2 values that we tested (3 and 24 kHz), the f2/f1 functions did not exhibit the characteristic bandpass shape that was seen for all other frequency ranges. At 3 kHz (Fig. 1), the mean LDP increased with increasing f2/f1, with an initial peak at f2/f1 = 1.196 (1.173 for 74 dB SPL primary tones). In the mean functions, a small dip in LDP was observed following this peak, after which the DPOAE level increased again as the f2/f1 ratio was further increased. At 24 kHz, the effect of f2/f1 on the LDP differed greatly between individual subjects. None of the individual f2/f1 functions (at 24 kHz) was similar in shape to the mean f2/f1 function (data not shown).
Each plot of the mean DPOAE levels elicited by 62-dB SPL primary tones shown in Fig. 1 was selected and replotted in Fig. 2 to indicate the typical amount of inter-subject variability we observed at each point. Although the inter-subject variability was relatively high in most frequency ranges, the individual f2/f1 functions typically followed a similar pattern within a frequency range and differed mainly in overall DPOAE level (data not shown), although the optimal f2/f1 (the peaks of these functions), did vary somewhat between ears. The exceptions to this, as mentioned above, were the individual f2/f1 functions at 24 kHz. Generally, the noise-floor levels did not vary greatly between animals, with the exception of one frequency range (Fig. 2, 4 kHz) at high frequency ratios.
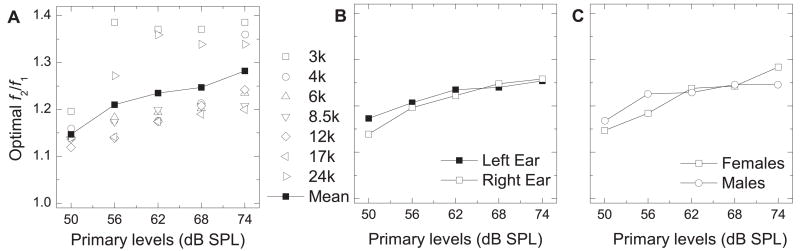
Figure 4.
Mean optimal f2/f1 ratio (ordinate) vs. primary-tone level (abscissa). A) The f2/f1 ratios which elicited the most robust DPOAEs for each ear were averaged to determine the mean optimal f2/f1. B) Right vs. left ear. DPOAEs were averaged only in subjects in which both ears were tested and the mean optimal f2/f1 was that which elicited the most robust mean DPOAE (n = 10 ears). C) Male vs. female. DPOAEs were averaged across both ears in males and females and the f2/f1 which elicited the most robust mean DPOAE was considered optimal.
At each value of f2/f1, the DPOAE levels were averaged across all subjects having complete ranges. The f2/f1 which elicited the strongest mean LDP at each f2 frequency and primary-tone level was considered the optimal f2/f1. There often were two or more f2/f1 ratios that elicited DPOAEs that were similar in strength. Such f2/f1 ratios were typically neighboring values, or at most separated by a small dip. If there were one or more DPOAEs within 1.0 dB SPL of the strongest DPOAE for a particular stimulus condition, the mean of the associated f2/f1 ratios was considered the optimal f2/f1. This mean was, in most cases, very similar to the f2/f1 ratio which elicited the strongest DPOAEs. Using this method meant that a single value was chosen to represent optimal f2/f1 ratio for each combination of stimulus parameters (e.g., L1 = L2 = 50 dB SPL at 3 kHz, L1 = L2 = 50 dB SPL at 4 kHz, etc.). Accordingly, we were not able to determine statistical significance or effect size of sex or ear differences in the optimal f2/f1.
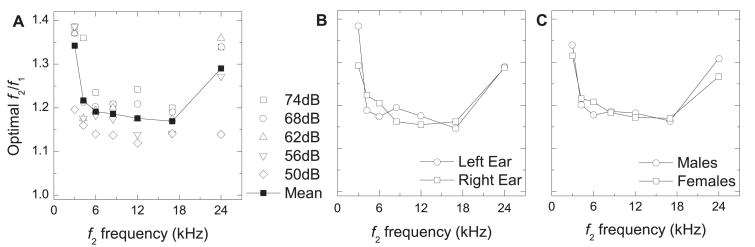
The mean optimal f2/f1 for each stimulus parameter ranged between 1.119 and 1.386 (Table 1). The mean optimal f2/f1 (averaged across all ears and all primary-tone levels) decreased with increasing frequency from 3 – 17 kHz, and then greatly increased for f2 = 24 kHz (Fig. 3A). The mean optimal f2/f1 for individual primary-tone levels exhibited a similar trend as the average across all primary-tone levels (Fig. 3A). When examining ear differences, only animals in which both ears were tested were considered. The ear difference in the mean optimal f2/f1 was minimal at most frequencies (no difference at 24 kHz), and was largest at 3 kHz (right ear mean = 1.292; left ear mean = 1.383) (Fig. 3B). Sex differences in the mean optimal f2/f1 ratio were minimal at all f2 frequencies (Fig. 3C). The mean optimal f2/f1 (across all frequencies and all ears) and the mean optimal f2/f1 for each individual f2 frequency (across all ears) both increased with increasing primary-tone level (Fig. 4A, Table 1). The mean optimal f2/f1 (across all frequencies) was similar in both ears (Fig. 4B), and both sexes (Fig. 4C), especially with 62 and 68 dB SPL primary tones.
Figure 3.
Mean optimal f2/f1 ratio (ordinate) vs. f2 frequency (abscissa). A) The f2/f1 ratios which elicited the most robust mean DPOAEs (averaged across all ears) were considered as the mean optimal f2/f1 ratios. B) Right vs. left ear. DPOAEs were averaged only in subjects in which both ears were tested and the mean optimal f2/f1 was that which elicited the most robust mean DPOAE (n = 5). C) Males vs. females. DPOAEs were averaged across both ears in males and females and the f2/f1 which elicited the most robust mean DPOAE was considered optimal.
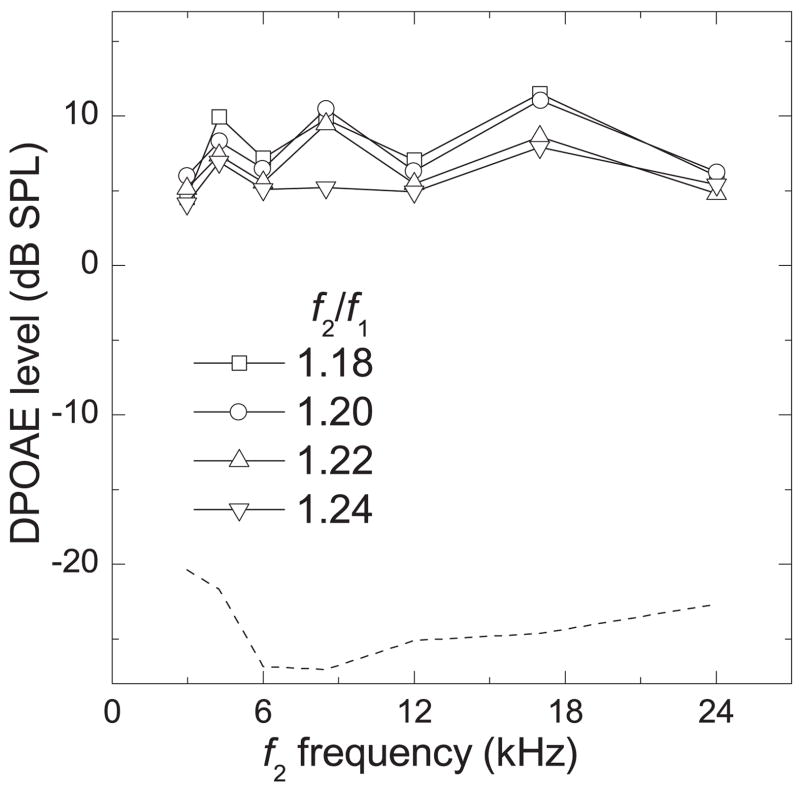
When all stimulus parameters and all subjects were considered (17 ears: 12 right, 5 left) the mean optimal f2/f1 was 1.224. For animals in which both ears were tested (n = 5), the mean optimal f2/f1 was 1.226. We have shown DPgrams in Fig. 5 to directly compare the effect of f2/f1 ratio over the limited range of 1.18 to 1.24 on the average LDP. The DPOAEs elicited by each of these f2/f1 ratios were very similar in amplitude within each f2 frequency, especially below 6 kHz.
Figure 5.
DPgram (LDP vs. f2 frequency) for f2/f1 values of 1.18 – 1.24. DPOAE levels were averaged across all ears (n = 17). Dashed line represents average noise floor.
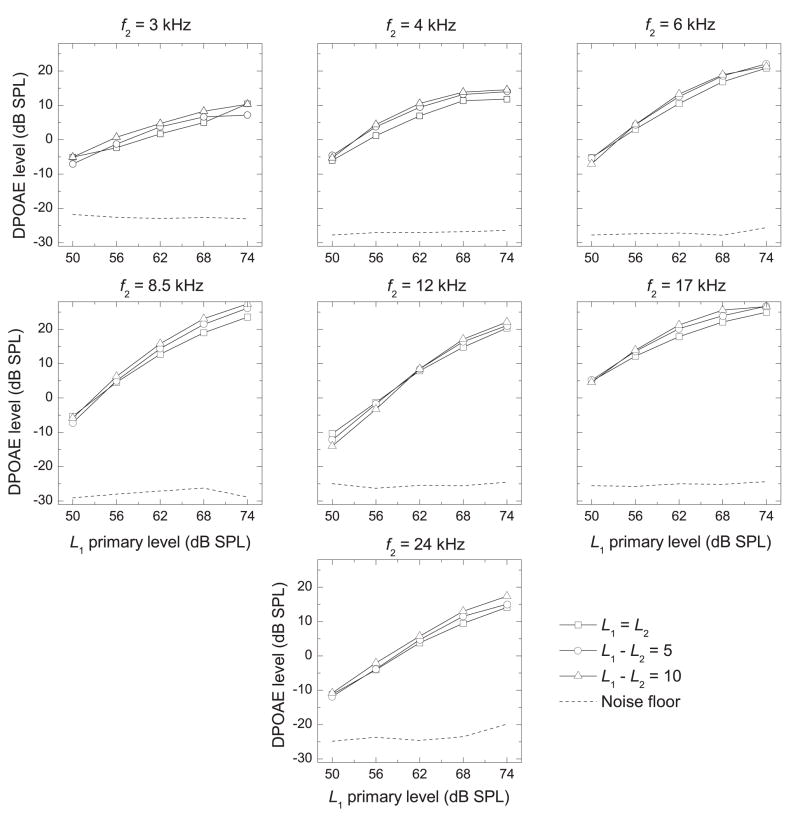
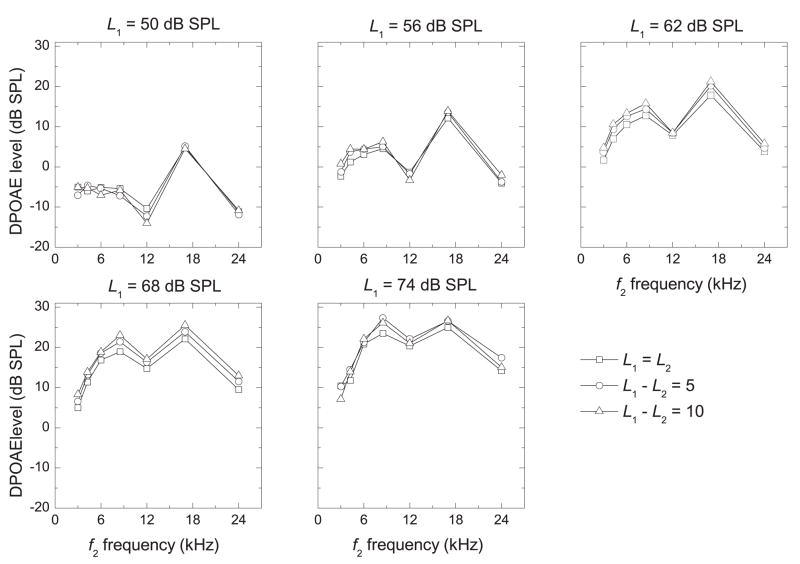
The effect of decreasing L2 below L1
Mean I/O functions (across all ears) are shown in Fig. 6 for each primary-tone level difference (L1 − L2 = 0, 5, 10 dB SPL). In general, the LDP increased as the primary-tone levels increased, and a maximum LDP was elicited when L1 = 74 dB SPL, the highest level tested. Figure 7 shows DPgrams for each L1 and L1 − L2. These DPgrams show significant maxima in LDP at 8.5 and 17 kHz at all primary-tone levels above 50 dB SPL. These peaks became more pronounced as primary-tone levels were increased. There was essentially no effect of decreasing L2 below L1 for most conditions, but for some conditions there was a small or, for even fewer conditions, a medium effect size. However, there was no consistent pattern to suggest that using a larger primary-tone level difference elicits stronger DPOAE levels in the ears of young, healthy marmosets.
Figure 6.
I/O Functions (LDP vs. L1 Primary Tone) at each f2 frequency (f2 indicated above the panel) for each primary-tone level difference. DPOAE levels were averaged across all ears (n = 18).
Figure 7.
DPgrams (LDP vs. f2 frequency) at each primary-tone level for each difference in primary-tone level. DPOAE levels were averaged across all ears (n = 18).
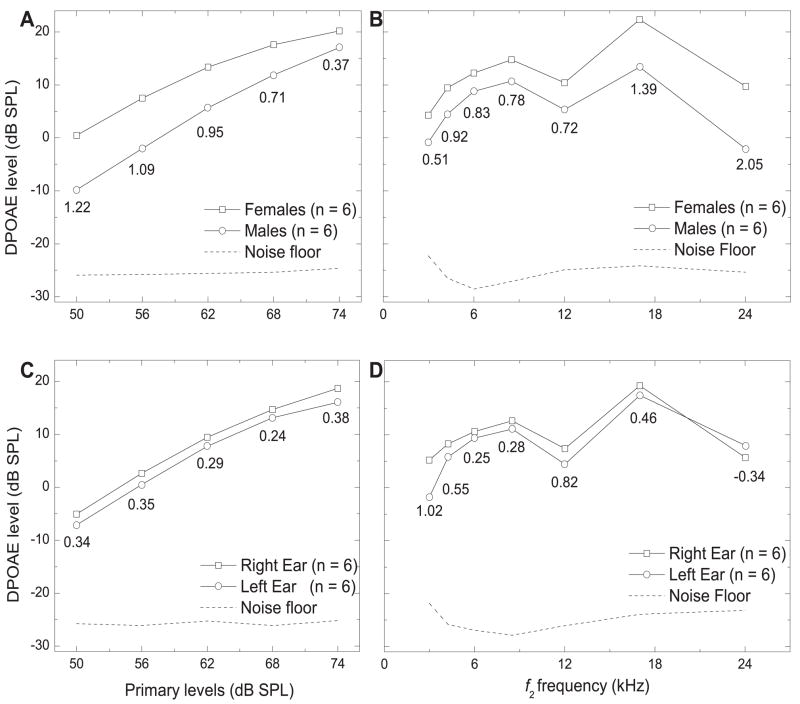
Sex and ear differences
Using equilevel primary tones, the effects of sex (6 males, 6 females, right ear only) and ear (6 right ears, 6 left ears) on LDP were determined (Fig. 8A–D). Female DPOAE levels were larger than those of the males, regardless of the primary-tone level (Fig. 8A) or f2 frequency (Fig. 8B). With 62 dB SPL primary tones, the absolute difference in mean LDP (mean female LDP –mean male LDP) ranged from 3.45 dB SPL (at 6 kHz) to 11.81 dB SPL (at 24 kHz). There was a medium effect size at 3, 8, and 12 kHz, and a large effect at 4, 6, 17, and 24 kHz (Fig 8B). The mean difference across frequencies (with L1 = L2 = 62 dB SPL) was 6.20 dB SPL. When averaged across all f2 frequencies, the absolute difference in mean LDP was highest at 50 dB SPL (10.27 dB SPL) and lowest at 74 dB SPL (3.15 dB SPL). The effect size was large when L1 = L2 = 50 to 68 dB SPL, and small when L1 = L2 = 74 dB SPL (Fig. 8A).The mean difference across frequencies and all primary-tone levels was 5.84 dB SPL.
Figure 8.
A) I/O Functions (LDP vs. L1 Primary Tone) for males vs. females (data was averaged across all f2 frequencies). B) DPgrams (LDP vs. f2 frequency) for males vs. females (L1 = L2 = 62 dB SPL). C) I/O Functions (LDP vs. L1 Primary Tone) for right vs. left ear (data was averaged across all f2 frequencies). D) DPgrams (LDP vs. f2 frequency) for right vs. left ear. Effect sizes are shown below the lower of the two compared mean LDP values.
DPOAEs tended to be slightly stronger in the right ear than the left ear (Fig. 8C), regardless of the primary-tone level (L1 = L2), though the effect size was small, similar to humans. As a function of f2 frequency, the mean LDP was stronger in the right ear than the left at each frequency, except 24 kHz, where it is reversed (Fig. 8D). The effect size was small at 6, 8, 17, and 24 kHz, but was in the opposite direction at 24 kHz. The effect size was medium at 4 kHz, and was large at 3 and 12 kHz.
I/O Functions
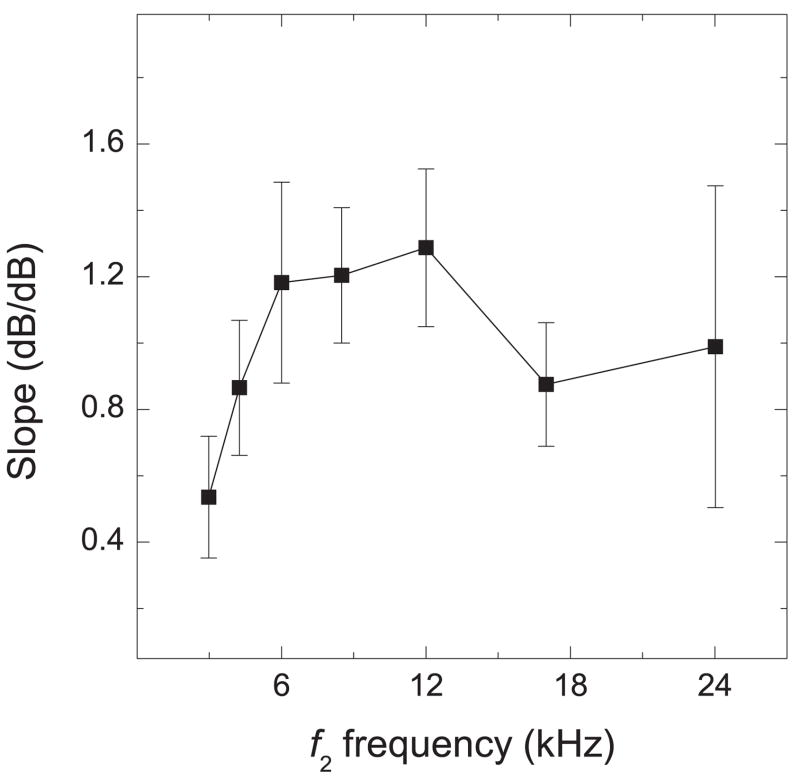
To determine the slopes of individual I/O functions obtained with equilevel primary tones (mean functions are shown in Fig. 6), we fitted a linear-regression equation to the most linear portion of the functions (Mills & Rubel, 1996; Coro & Kössl, 2001; Meenderink & van Dijk, 2004). The most linear growth occurred between L1 = L2 = 50 to 68 dB SPL (Fig. 6), and the functions began to saturate at 74 dB SPL. The slopes (in dB/dB) increased from 3 kHz (0.536) to 12 kHz (1. 287), decreased at 17 kHz (0.887), and increased at 24 kHz (0.989).
Discussion
Frequency ratio (f2/f1) optimization
Stimulus parameters such as the frequency and level of the primary tones, frequency ratio, and primary-tone level difference all contribute to DPOAE amplitude (Wilson, 1980; Harris et al., 1989; Brown & Gaskill, 1990a; Gaskill & Brown, 1990; Park et al., 1995; Lasky et al., 1995; Abdala, 1996; for a review, see Probst et al., 1991). The primary goal of this study was to determine the optimal stimulus parameters for eliciting robust DPOAEs in this species.
Historically, many methods have been employed to study the effects of varying f2/f1 on DPOAE amplitude. One method involves fixing one of the primary-tone frequencies, either f1 (Kim, 1980; Furst et al., 1988; Brown & Gaskill, 1990a; Gaskill & Brown, 1990) or f2 (Schmiedt, 1986; Lasky et al., 1995; Park et al., 1995; Dreisbach & Siegel, 2001) and systematically varying the second primary tone to satisfy a set of predetermined f2/f1 ratios. Other investigators have varied f1 and f2 to satisfy a set of predetermined f2/f1 ratios around a set of geometric mean frequencies (fGM) of the primary tones (fGM = (f1 × f2)0.5) (Nielsen et al., 1993) or a set of fixed DPOAE frequencies (Kim, 1980; Wilson, 1980; Horner et al., 1985; Lonsbury-Martin et al., 1987; Harris et al., 1989; Smurzynski et al., 1990). We have employed the fixed-f2 method which has been used to optimize the f2/f1 ratio in both rhesus monkeys (Park et al., 1995; Lasky et al., 1995) and humans (Schmiedt, 1986; Lasky et al., 1998; Dreisbach & Siegel, 2001). It is widely accepted that DPOAEs are first generated near the region where f2 is registered, so by using the fixed-f2 paradigm, we have attempted to ensure that any variation in DPOAE level is due solely to the effects of frequency ratio and not to the effect of changing the place of DPOAE generation (Moulin, 2000).
In humans, a number of studies have determined the optimal f2/f1, and the reported mean optimal f2/f1 (1.22 – 1.23) has been similar across studies, regardless of method (Harris et al., 1989; Gaskill & Brown, 1990; Nielsen et al., 1993). In fact, Nielsen et al. (1993) noted that robust DPOAEs could be elicited at all test frequencies with an f2/f1 between 1.21 – 1.25.
In non-human primates, DPOAE data so far have been reported only in the rhesus monkey (Macaca mulatta). Park et al. (1995) determined that the mean optimal f2/f1 for the rhesus monkey was 1.21 using a fixed-f2 paradigm (f2 = 1 – 8 kHz, L1 = L2 = 55 to 85 dB SPL). Lasky et al. (1995), also using the fixed-f2 paradigm, measured DPOAEs at four frequencies between 1 and 12 kHz using equilevel primary tones of 55, 60, and 65 dB SPL, and reported a similar optimal f2/f1 ranging from 1.175 – 1.225. Our data showed that strong DPOAEs could be elicited between 3 – 24 kHz with a frequency ratio between 1.18 – 1.24, and that the mean optimal f2/f1 ratio was 1.224. This agrees well with results from humans and Old World primates.
The mean optimal f2/f1 does not, however, elicit DPOAEs at maximum amplitude at all frequencies. Our results in the marmoset agreed with previous findings in humans (Wilson, 1980; Harris et al., 1989; Whitehead et al., 1992a; Bowman et al., 2000) and rhesus monkeys (Park et al., 1995); that the optimal f2/f1 increases with increasing primary-tone level. Additionally, in rabbits (Lonsbury-Martin et al., 1987; Whitehead et al., 1992a), bats (Kössl, 1994; Frank & Kössl, 1995), rhesus monkeys (Lasky et al., 1995; Park et al., 1995), and humans (Harris et al., 1989; Abdala, 1996; Bowman et al., 2000, Brown et al., 2000), the optimal f2/f1 ratio decreases with increasing f2 frequency. To our knowledge, there is only one study in humans in which the f2/f1 ratio has been optimized at frequencies greater than 9 kHz. Dreisbach and Siegel (2001) extended their test-frequency range to 13 kHz to determine if the same cochlear mechanics applied at higher frequencies. They showed that the optimal f2/f1 ratio continued to decrease through f2 frequencies of 10 kHz (when the emission probe was placed 10 – 15 mm from the eardrum). However, there was an increase in the f2/f1 ratio yielding the maximum amplitude DPOAEs at 13 kHz. In the marmoset, the optimal f2/f1 ratio continued to decrease through 17 kHz, but then increased at 24 kHz. In humans, Bowman et al. (2000) reported small sex differences in the optimal f2/f1 that were not statistically significant. The marmoset data agree well with this study; the mean optimal f2/f1 ratios shown here for male and female marmosets were very similar across f2 frequency and primary-tone level.
Between 6 – 17 kHz (and at low- to mid-primary-tone levels at 4 kHz) the marmoset DPOAE levels were lowest at narrow and wide frequency ratios and maximal at mid-f2/f1 ratios, exhibiting the characteristic bandpass shape that has been reported by other investigators (Wilson, 1980; Brown & Kemp, 1985; Lonsbury-Martin et al., 1987; Harris et al., 1989; Brown & Gaskill, 1990a, b; Gaskill & Brown, 1990, Whitehead et al., 1992; Brown et al., 1993; Stover et al., 1994; Park et al., 1995; Lasky et al., 1995; Abdala, 1996; Dreisbach & Siegel, 2001). Some researchers have suggested that the characteristic bandpass shape of these functions may be due to a second filter inherent in the cochlea (Allen, 1990b; Brown & Gaskill; 1990b; Neely & Stover, 1993; Stover et al., 1994). However, studies which have used models of the basilar membrane lacking a second filter suggest that this is not the case (Matthews & Molnar, 1986; Neely & Stover, 1997; Kanis & de Boer, 1997; van Hengel & Duifhuis, 2000). Fahey et al. (2006) hypothesized that vector cancellation of DPOAEs generated from different sources causes the f2/f1 functions to exhibit bandpass characteristics. They measured DPOAEs in humans using the fixed-f2 paradigm, but f1 was selected at frequencies which would minimize vector cancellation. Under these conditions the f2/f1 functions lost their bandpass shape, indicating that the characteristic decline in DPOAE amplitude on either side of the peak is primarily due to vector cancellations.
Studies in humans (Harris et al., 1989; Brown & Gaskill, 1990a; Whitehead et al., 1992; Stover et al., 1992; Abdala, 1996; Dreisbach & Siegel, 2001) have shown that the f2/f1 functions become sharper (steeper slopes on either side of the peak) with increasing frequency at f2 frequencies up to 4 – 13 kHz. Marmoset results agree well with these findings at f2 frequencies between 3 and 8.5 kHz and at 17 kHz. It has been suggested that the frequency-dependent increase in sharpness (of the f2/f1 functions) is due to sharper mechanical tuning at the basal end of the basilar membrane (Dreisbach & Siegel, 2001). However, a study in rhesus monkeys (Lasky et al., 1995) showed that at frequencies below 12 kHz, the f2/f1 functions became sharper as f2 was increased, but at 12 kHz the f2/f1 function exhibited a less sharp peak. We have seen the same trend to (what appears to be) an even greater extent in marmosets at 12 kHz (Figs. 1, 2).
Data Omission
We have reported that all errors in calibrating the primary tones occurred at 12 and 24 kHz when the frequency separation was large. Due to these calibration errors, the entire range of f2/f1 ratios was not presented and therefore we omitted data from two ears (1 right, 1 left ear) in our analysis of the12-kHz range and six ears (3 right, 3 left) in the 24-kHz range. While optimizing the f2/f1 ratio, we set stringent limits on the levels of the primary tones. They had to fall within 2.0 dB SPL of the target levels. Because it was easy to present 24-kHz tones to some ears and not others, we suspect that the problems we encountered at this frequency were due to the individual transfer functions of the subject’s ear canals. In these cases the data for the entire frequency range were excluded from analysis. These limits also suggest that the data we were able to collect at 12 and 24 kHz were reliable.
The effect of decreasing L2 below L1
Using the paradigm of holding L1 constant between 50 – 74 dB SPL and varying L2 such that L1 − L2 = 0, 5, and 10 dB SPL, we have reported that increasing L1 − L2 does not significantly increase DPOAE levels between 3 and 24 kHz in marmosets. This agrees very well with the results in rhesus monkeys (Park et al., 1995; Lasky et al., 1995) and humans (Gaskill & Brown, 1990; Whitehead et al., 1995). These human studies showed that DPOAE level is more dependent upon L1 than L2. Additionally, Whitehead et al. (1995) showed that the relative levels of primary tones (when L1 − L2 10 dB) only slightly affect the amplitude of DPOAEs in healthy ears.
Normative DPOAEs
The slopes of the marmoset I/O functions are similar to the results of Lasky et al. (1995), who reported an increase in slope with increasing frequency in both humans and rhesus monkeys, with the slopes of the I/O functions between 3 – 4 kHz being approximately 1.0. The slopes of the marmoset I/O functions at 3, 4, 17 and 24 kHz were below 1.0 (compressive power functions – the level of the DPOAE increased at a slower rate than the level of the primary tones), and at 6 and 8 kHz the slopes were greater than 1.0 (expansive power functions – the level of the DPOAE increased at a faster rate than the level of the primary tones). Lasky et al. (1995) measured DPOAEs at frequencies up to 20 kHz and reported a general increase in the slopes of the I/O functions through 20 kHz, although there were non-monotonicities throughout the function (slope vs. frequency) where the slope decreased at 16 kHz and increased again at 24 kHz. The non-monotonicities observed in the marmoset slope function followed a similar trend, though the f2 frequencies showing inflections were not identical to Lasky’s (16 vs 17 kHz and 20 vs 24 kHz). The differences observed in the slopes of the I/O functions in marmoset vs. rhesus monkey may be due to the methods used to determine the slopes of these functions. It is unclear to us which data points were used by Lasky’s group to determine the slopes of the I/O functions.
Park et al. (1995) found that the average DPOAE amplitude in six rhesus monkeys was 55 – 70 dB below the (equilevel) primary tones, depending on primary-tone level and frequency. McFadden et al. (2006a) showed that, on average, rhesus monkey DPOAEs were approximately 45 – 55 dB SPL below the (equilevel) primary tones. Lasky et al. (1995) reported average rhesus DPOAE levels to be stronger than human DPOAEs by 10 – 15 dB between f2 = 3 – 10 kHz (and less around f2 = 1 kHz). The mean DPOAE levels of the marmoset ranged from 50 to 60 dB SPL below the levels of the primary tones. These DPOAE levels are not equivalent to those of humans, which are approximately 60 dB SPL below the level of the primary tones (for a review, see Probst et al., 1991). These differences may be explained by size differences in the ear canals or by the effects of ketamine, which has been shown to increase DPOAE levels in mice (Harel et al., 1997).
The sex differences in the normative DPOAE level are in the same direction as has been reported in humans (e.g. Dunckley & Dreisbach, 2004), and other animals (e.g. frogs: Vassilakis et al., 2004; rhesus monkeys: McFadden et al., 2006a). These studies have shown that the mean LDP is slightly stronger in females than males. The sex differences we have reported seem to be the largest reported in primates thus far. In humans, Dunckley & Dreisbach (2004) investigated sex differences in LDP (with L1 = 60 dB SPL, L2 = 45, and f2/f1 = 1.22) and showed that the absolute difference in the mean LDP (mean female LDP − mean male LDP) ranged from -5.46 dB SPL (at 9 kHz) to 6.07 dB SPL (at 13 kHz) and the mean difference in LDP was reported to be 2.08 dB SPL. In marmosets, the absolute difference in mean LDP, with 62 dB SPL (equilevel) tones, ranged from 3.14 – 11.8 dB SPL (mean = 6.20 dB SPL). The sex difference in marmoset DPOAEs was even more pronounced when L1 − L2 was 10 dB SPL (L1 = 62 dB SPL), ranging from 4.32 – 15.48 dB SPL (mean = 7.60 dB SPL) (data not shown). The effect size for sex differences in rhesus monkeys was dependent on the frequency range and ear (McFadden et al., 2006a). In the right ear, the effect sizes (mean female LDP − mean male LDP) were -0.28, 0.17, and 0.02 for frequency ranges of 2.0 – 2.5, 3.0 – 3.5, and 5.0 – 5.5 kHz, respectively. In marmosets, the effect size for sex differences were much larger, ranging from 0.51 to 2.05 (with L1 = L2 = 62 dB SPL) as a function of frequency and from 0.37 to 1.22 as a function of primary-tone level (averaged across all f2 frequencies).
Conclusions
Strong DPOAEs were easily elicited in the common marmoset. The effect of varying stimulus parameters was similar to the effects reported in humans and rhesus monkeys. The mean optimal f2/f1 ratio was 1.22, but f2/f1 ratios between 1.18 – 1.24 elicited DPOAEs that were similar in strength. The mean optimal f2/f1 was slightly dependent on primary-tone level and strongly dependent upon f2 frequency. No systematic change in DPOAE amplitude was observed in the ears of these young, healthy marmosets when decreasing L2 below L1 by 5 or 10 dB SPL. The sex difference in DPOAE levels we reported is the largest observed in primates, including humans.
The data presented here suggest that the marmoset may be an excellent model to study the mechanisms underlying sex differences in otoacoustic emissions, but these differences should be further examined with CEOAEs, which typically exhibit much larger differences between sexes than DPOAEs (e.g. McFadden et al., 2006a). In future studies we will examine the effects of age and sex on normative DPOAEs and CEOAEs, with and without contralateral stimulation. To date, no SOAEs have been observed in marmosets, but the search will continue.
Figure 9.
Slope Functions (Slope vs. f2 frequency). The slopes of the linear-regression equations characterizing the I/O functions from 50 – 68 dB SPL (averaged across all ears of both sexes). Error bars are shown to indicate the amount of inter-subject and inter-ear variability in the slope of the I/O functions.
Acknowledgments
This work was supported in part by a student internship provided to M.D.V at the Southwest National Primate Research Center (SNPRC) at the Southwest Foundation for Biomedical Research in San Antonio, the Institute for Aging Research at UTSA, and NIH/NIDCD R03DC009050 (to R.R). One of the authors (M.D.V) was supported by the National Institute of Health/National Institute of General Medical Sciences Minority Biomedical Research Support- Research Initiative in Science Enhancement (MBRS-RISE) GM60655. Data-acquisition software was written by E.G.P while supported by research grant DC00153 awarded to D.M. by the National Institute on Deafness and other Communication Disorders (NIDCD). We would like to thank the SNPRC for their generous support, and in particular we thank Donna Layne-Colon and Dr. Suzette Tardif for their constant encouragement and assistance throughout this work.
Abbreviations
- OAE
otoacoustic emission
- f1, L1
frequency and level of lower-frequency primary tone
- f2, L2
frequency and level of higher-frequency primary tone
- f2/f1
frequency ratio
- L1 − L2
primary-tone level difference
- LDP
DPOAE level
- fDP
DPOAE frequency
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abdala C. Distortion product otoacoustic emission (2f1 – f2) amplitude as a function of f2/f1 frequency ratio and primary tone level separation in human adults and neonates. J Acoust Soc Am. 1996;100:3726–3740. doi: 10.1121/1.417234. [DOI] [PubMed] [Google Scholar]
- Allen JB. User Manual for the CUBDIS Distortion Product Measurement System. AT & T Bell Labs; 1990a. [Google Scholar]
- Allen JB. Modeling the noise damaged cochlea. In: Dallos P, Geisler CD, Matthews JW, Ruggero MA, Steele CR, editors. The Mechanics and Biophysics of Hearing; Proceedings of a conference held at the University of Wisconsin; Madison, WI. 25 – 29 June 1990; New York: Springer; 1990b. pp. 324–332. [Google Scholar]
- Barros M, Giorgetti M, Souto AA, Vilela G, Santos K, Baos NV, Tomaz C. Persistent anxiety-like behavior in marmosets following a recent predatory stress condition: reversal by diazepam. Pharmacol Biochem Behav. 2007;86:705–711. doi: 10.1016/j.pbb.2007.02.016. [DOI] [PubMed] [Google Scholar]
- Bartlett EL, Wang X. Neural representations of temporally modulated signals in the auditory thalamus of awake primates. J Neurophysiol. 2007;97:1005–1017. doi: 10.1152/jn.00593.2006. [DOI] [PubMed] [Google Scholar]
- Bendor D, Wang X. Differential neural coding of acoustic flutter within primate auditory cortex. Nat Neurosci. 2007;10:763–771. doi: 10.1038/nn1888. [DOI] [PubMed] [Google Scholar]
- Bowman DM, Brown DK, Kimberley BP. An examination of gender differences in DPOAE phase delay measurements in normal-hearing adults. Hear Res. 2000;142:1–11. doi: 10.1016/s0378-5955(99)00212-9. [DOI] [PubMed] [Google Scholar]
- Brown AM. Acoustic distortion from rodent ears: a comparison of responses from rats, guinea pigs, and gerbils. Hear Res. 1987;31:25–38. doi: 10.1016/0378-5955(87)90211-5. [DOI] [PubMed] [Google Scholar]
- Brown AM, Gaskill SA. Measurement of acoustic distortion reveals underlying similarities between human and rodent mechanical responses. J Acoust Soc Am. 1990a;88:840–849. doi: 10.1121/1.399733. [DOI] [PubMed] [Google Scholar]
- Brown AM, Gaskill SA. Can basilar membrane tuning be inferred from distortion measurement?. In: Dallos P, Geisler CD, Matthews JW, Ruggero MA, Steele CR, editors. The Mechanics and Biophysics of Hearing; Proceedings of a conference held at the University of Wisconsin; Madison, WI. 25 – 29 June 1990; New York: Springer; 1990b. pp. 164–169. [Google Scholar]
- Brown AM, Gaskill SA, Carlyon RP, Williams DM. Acoustic distortion as a measure of frequency selectivity: relation to psychophysical equivalent rectangular bandwidth. J Acoust Soc Am. 1993;93:3291–3297. doi: 10.1121/1.405713. [DOI] [PubMed] [Google Scholar]
- Brown AM, Harris FP, Beveridge HA. Two sources of acoustic distortion products from the human cochlea. J Acoust Soc Am. 1996;100:3260–3267. doi: 10.1121/1.417209. [DOI] [PubMed] [Google Scholar]
- Brown AM, Kemp DT. Suppressibility of the 2f1 – f2 stimulated acoustic emissions in gerbil and man. Hear Res. 1984;13:29–37. doi: 10.1016/0378-5955(84)90092-3. [DOI] [PubMed] [Google Scholar]
- Brown AM, Kemp DT. Intermodulation distortion in the cochlea: Could basal vibration be the major cause of round window CM distortion? Hear Res. 1985;19:191–198. doi: 10.1016/0378-5955(85)90138-8. [DOI] [PubMed] [Google Scholar]
- Brown DK, Bowman DM, Kimberley BP. The effects of maturation and stimulus parameters on the optimal f2/f1 ratio of the 2f1 – f2 distortion product otoacoustic emission in neonates. Hear Res. 2000;145:17–24. doi: 10.1016/s0378-5955(00)00064-2. [DOI] [PubMed] [Google Scholar]
- Canlon B, Marklund K, Borg E. Measures of auditory brain-stem responses, distortion product emissions, hair cell loss, and forward masking tuning curves in the waltzing guinea pigs. J Acoust Soc Am. 1993;94:3232–3243. doi: 10.1121/1.407229. [DOI] [PubMed] [Google Scholar]
- Cohen J. A power primer. Psychol Bull. 1992;112:155–159. doi: 10.1037//0033-2909.112.1.155. [DOI] [PubMed] [Google Scholar]
- Coro F, Kössl M. Components of the 2f1-f2 distortion product otoacoustic emission in a moth. Hear Res. 2001;162:126–133. doi: 10.1016/s0378-5955(01)00381-1. [DOI] [PubMed] [Google Scholar]
- de la Mothe LA, Blumell S, Kajikawa Y, Hackey TA. Cortical connections of the auditory cortex in marmoset monkeys: core and medial belt regions. J Comp Neurol. 2006a;496:27–71. doi: 10.1002/cne.20923. [DOI] [PubMed] [Google Scholar]
- de la Mothe LA, Blumell S, Kajikawa Y, Hackey TA. Thalamic connections of the auditory cortex in marmoset monkeys: core and medial belt regions. J Comp Neurol. 2006b;496:72–96. doi: 10.1002/cne.20924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dreisbach LE, Siegel JH. Distortion-product otoacoustic emissions measured at high frequencies in humans. J Acoustic Soc Am. 2001;110:2456–2486. doi: 10.1121/1.1406497. [DOI] [PubMed] [Google Scholar]
- Fahey PF, Stagner BB, Martin GK. Mechanism for bandpass frequency characteristic in distortion product otoacoustic emission generation. J Acoust Soc Am. 2006;119:991–996. doi: 10.1121/1.2146088. [DOI] [PubMed] [Google Scholar]
- Furst M, Rabinowitz WM, Zurek PM. Ear canal acoustic distortion at 2f1 – f2 from human ears: Relation to other emissions and perceived combination tones. J Acoust Soc Am. 1988;84:215–221. doi: 10.1121/1.396968. [DOI] [PubMed] [Google Scholar]
- Gaskill SA, Brown AM. The behavior of the acoustic distortion product, 2f1-f2, from the human ear and its relation to auditory sensitivity. J Acoust Soc Am. 1990;88:821–839. doi: 10.1121/1.399732. [DOI] [PubMed] [Google Scholar]
- Gaskill SA, Brown AM. Suppression of human distortion product: dual origin of 2f1 – f2. J Acoust Soc Am. 1996;100:3268–3274. doi: 10.1121/1.417210. [DOI] [PubMed] [Google Scholar]
- Harel N, Kakigi A, Hirakawa H, Mount R, Harrison R. The effects of anesthesia on otoacoustic emissions. Hear Res. 1997:25–33. doi: 10.1016/s0378-5955(97)00061-0. [DOI] [PubMed] [Google Scholar]
- Harris FP, Lonsbury-Martin BL, Stagner BB, Coats AC, Martin GK. Acoustic distortion products in humans: Systematic changes in amplitude as a function in f2/f1 ratio. J Acoust Soc Am. 1989;85:220–229. doi: 10.1121/1.397728. [DOI] [PubMed] [Google Scholar]
- Harris FP, Probst R, Xu L. Suppression of the 2f1 – f2 otoacoustic emission in humans. Hear Res. 1992;64:133–141. doi: 10.1016/0378-5955(92)90175-m. [DOI] [PubMed] [Google Scholar]
- Horner KC, Lenoir M, Bock GR. Distortion product otoacoustic emissions in hearing-impaired mutant mice. J Acoust Soc Am. 1985;78:1603–1611. doi: 10.1121/1.392798. [DOI] [PubMed] [Google Scholar]
- Kanis LJ, de Boer E. Frequency dependence of acoustic products in a locally active model of the cochlea. J Acoust Soc Am. 1997;101:1527–1531. doi: 10.1121/1.418173. [DOI] [PubMed] [Google Scholar]
- Kemp DT, Brown AM. A comparison of mechanical nonlinearities of man and gerbil from ear canal measurements. In: Klinke R, Hartman R, editors. Hearing –Physiological Bases and Biophysics. Springer; Berlin: 1983. pp. 82–88. [Google Scholar]
- Khvoles R, Freeman S, Sohmner I. Effect of temperature on the transient evoked and distortion product otoacoustic emissions in rats. Audiol Neurotol. 1998;6:349–360. doi: 10.1159/000013805. [DOI] [PubMed] [Google Scholar]
- Kim DO, Molnar CE, Matthews JW. Cochlear mechanics: Nonlinear behavior in two-tone responses as reflected in cochlear-nerve-fiber responses and in ear-canal sound pressure. J Acoust Soc Am. 1980;67:1704–1721. doi: 10.1121/1.384297. [DOI] [PubMed] [Google Scholar]
- Kössl M. Otoacoustic emissions from the cochlea of the ‘constant frequency’ bats, Pteronotus parnellii and Rhinolophus rouxi. Hear Res. 1994;22:105–114. doi: 10.1016/0378-5955(94)90206-2. [DOI] [PubMed] [Google Scholar]
- Lasky RE, Snodgrass EB, Laughlin NK, Hecox KE. Distortion product otoacoustic emissions in Macaca mulatta and humans. Hear Res. 1995;89:35–51. doi: 10.1016/0378-5955(95)00120-1. [DOI] [PubMed] [Google Scholar]
- Lasky RE. Distortion-product otoacoustic emissions in human newborns and adults. I Frequency effects. J Acoust Soc Am. 1998;103:981–991. doi: 10.1121/1.421215. [DOI] [PubMed] [Google Scholar]
- Lonsbury-Martin BL, Martin GK, Probst R, Coats AC. Acoustic distortion products in rabbit ear canal. I Basic features and physiological vulnerability. Hear Res. 1987;28:173–189. doi: 10.1016/0378-5955(87)90048-7. [DOI] [PubMed] [Google Scholar]
- Lonsbury-Martin BL, Harris FP, Stagner BB, Hawkins MD, Martin GK. Distortion product emissions in humans I. Basic properties in normally hearing subjects. Ann Otol Rhinol Laryngol. 1990;99:3–13. [PubMed] [Google Scholar]
- Martin GK, Lonsbury-Martin BL, Probst R, Scheinin SA, Coats AC. Acoustic distortion products in rabbit ear canal. II Sites of origin revealed by suppression contours and pure-tone exposures. Hear Res. 1987;28:191–208. doi: 10.1016/0378-5955(87)90049-9. [DOI] [PubMed] [Google Scholar]
- Martin GK, Lonsbury-Martin BL, Probst R, Coats AC. Spontaneous otoacoustic emissions in a nonhuman primate. I Basic features and relations to other emissions. Hear Res. 1988;33:49–68. doi: 10.1016/0378-5955(88)90020-2. [DOI] [PubMed] [Google Scholar]
- Matthews JW, Molnar CE. Modeling intracochlear and ear canal distortion product (2f1 – f2) In: Allen JB, Hall JL, Hubbard A, Neely ST, Tubis A, editors. Peripheral Auditory Mechanisms. Springer; Berlin: 1986. pp. 258–265. [Google Scholar]
- Mauermann M, Uppenkamp S, van Hengel PW, Kollmeier B. Evidence for the distortion product frequency place as a source of distortion product otoacoustic emission (DPOAE) fine structure in humans. I Fine structure and higher-order DPOAE as a function of the frequency ratio f2/f1. J Acoust Soc Am. 1999;106:3473–3483. doi: 10.1121/1.428200. [DOI] [PubMed] [Google Scholar]
- McFadden DM, Pasanen EG, Raper J, Lange HS, Wallen K. Sex differences in otoacoustic emissions measured in rhesus monkeys (Macaca mulatta) Horm & Beh. 2006a;50:274–284. doi: 10.1016/j.yhbeh.2006.03.012. [DOI] [PubMed] [Google Scholar]
- McFadden DM, Pasanen EG, Weldele ML, Glickman SE, Place NJ. Masculinized otoacoustic emissions in female spotted hyenas (Crocuta crocuta) Horm & Beh. 2006b;50:285–292. doi: 10.1016/j.yhbeh.2006.03.013. [DOI] [PubMed] [Google Scholar]
- Meenderink WF, van Dijk P. Level dependence of distortion product otoacoustic emissions in the leopard frog, Rana pipiens pipiens. Hear Res. 2004;192:107–118. doi: 10.1016/j.heares.2004.01.015. [DOI] [PubMed] [Google Scholar]
- Meenderink WF, van Dijk P. Temperature dependence of anuran distortion product otoacoustic emissions. J Assoc Res Otolaryngol. 2006;7:246–252. doi: 10.1007/s10162-006-0039-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mills DM, Rubel EW. Variation of distortion product otoacoustic emissions with furosemide injection. Hear Res. 1994;77:183–199. doi: 10.1016/0378-5955(94)90266-6. [DOI] [PubMed] [Google Scholar]
- Mills DM, Rubel EW. Development of the cochlear amplifier. J Acoust Soc Am. 1996;100:428–441. doi: 10.1121/1.415857. [DOI] [PubMed] [Google Scholar]
- Moulin A. Influence of primary frequencies ratio on distortion product otoacoustic emissions amplitude. I Intersubject variability and consequences on the DPOAE-gram. J Acoust Soc Am. 2000;107:1460–1470. doi: 10.1121/1.428433. [DOI] [PubMed] [Google Scholar]
- Neely ST, Stover L. Otoacoustic emissions from a nonlinear active model of cochlear mechanics. In: Duifhuis H, Horst JW, van Dijk P, van Netten SM, editors. Biophysics of Hair Cell Sensory Systems. World Scientific; 1993. pp. 64–71. [Google Scholar]
- Neely ST, Stover LJ. A generation of distortion products in a model of cochlear mechanics. In: Allen JB, Hall JL, Hubbard A, Neely ST, Tubis A, editors. Diversity in Auditory Mechanics. Springer-Verlag; New York, NY: 1997. pp. 258–265. [Google Scholar]
- Nielsen LH, Popelka GR, Rasmussen AN, Osterhammel PA. Clinical significance of probe-tone frequency ratio on distortion product otoacoustic emissions. Scand Audiol. 1993;22:159–164. doi: 10.3109/01050399309047462. [DOI] [PubMed] [Google Scholar]
- Norton SJ, Rubel EW. Active and passive components in mammalian and avian ears. In: Dallos P, Geisler CD, Matthews JW, Ruggero MA, Steele CR, editors. The Mechanics and Biophysics of Hearing. Springer-Verlag; Berlin, Heidelberg, New York: 1990. pp. 219–226. [Google Scholar]
- Park JY, Clark WW, Coticchia JM, Esselman GH. Distortion product otoacoustic emissions in rhesus (Macaca mulatta) monkey ears: normative findings. Hear Res. 1995;86:147–162. doi: 10.1016/0378-5955(95)00065-c. [DOI] [PubMed] [Google Scholar]
- Parham K. Distortion product otoacoustic emissions in the C57BL/6J mouse model of age-related hearing loss. Hear Res. 1997;112:216–234. doi: 10.1016/s0378-5955(97)00124-x. [DOI] [PubMed] [Google Scholar]
- Power ML, Bowman ME, Smith R, Ziegler TE, Layne DG, Schulkin J, Tardif SD. Pattern of maternal serum corticotrophin-releasing hormone concentration during pregnancy in the common marmoset. Callithrix jacchus. 2006;68:181–188. doi: 10.1002/ajp.20215. [DOI] [PubMed] [Google Scholar]
- Probst R, Lonsbury-Martin BK, Martin GK. A review of otoacoustic emissions. J Acoust Soc Am. 1991:2027–2067. doi: 10.1121/1.400897. [DOI] [PubMed] [Google Scholar]
- Rowoski JJ, Peake WT, White JR. Cochlear nonlinearities inferred from two-tone distortion products in the ear canal of the alligator lizard. Hear Res. 1984;13:141–158. doi: 10.1016/0378-5955(84)90105-9. [DOI] [PubMed] [Google Scholar]
- Schmiedt RA. Acoustic distortion products in ear canal. I Cubic difference tones: Effects of acute noise injury. J Acoust Soc Am. 1986;79:1481–1490. doi: 10.1121/1.393675. [DOI] [PubMed] [Google Scholar]
- Schnupp JW, Hall TM, Kokelaar RF, Ahmed B. Plasticity of temporal pattern codes for vocalization stimuli in primary auditory cortex. J Neurosci. 2006;26:4785–4795. doi: 10.1523/JNEUROSCI.4330-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrott A, Puel JL, Rebillardi G. Cochlear origin of 2f1-f2 distortion products assessed by using 2 types of mutant mice. Hear Res. 1991;52:245–254. doi: 10.1016/0378-5955(91)90204-m. [DOI] [PubMed] [Google Scholar]
- Shera CA, Guinan JJ., Jr Evoked otoacoustic emissions arise by two fundamentally different mechanisms: a taxonomy for mammalian OAEs. J Acoust Soc Am. 1999;105:782–798. doi: 10.1121/1.426948. [DOI] [PubMed] [Google Scholar]
- Sieden HR. Auditory acuity of the marmoset monkey, Hapale jacchus. Thesis, Princeton University; 1957. [Google Scholar]
- Smurzynski J, Leonard G, Kim DO, Lafreniere DC, Jung MD. Distortion product otoacoustic emissions in normal and impaired adult ears. Arch Otolaryngol Head Neck Surg. 1990;116:1309–1316. doi: 10.1001/archotol.1990.01870110081010. [DOI] [PubMed] [Google Scholar]
- Sockalingam R, Filippich L, Sommerland S, Murdoch B, Charles B. Transient-evoked and 2f1-f2 distortion product oto-acoustic emissions in dogs: preliminary findings. Audiol Neurootol. 1998;3:313–385. doi: 10.1159/000013807. [DOI] [PubMed] [Google Scholar]
- Spatz WB. Unipolar brush cells in the cochlear nuclei of a primate (Callithrix jacchus) Neurosci Lett. 1999;270:141–144. doi: 10.1016/s0304-3940(99)00493-0. [DOI] [PubMed] [Google Scholar]
- Spatz WB, Löhle E. Calcium-binding proteins in the spiral ganglion of the monkey, Callithrix jacchus. Hear Res. 1995;86:89–99. doi: 10.1016/0378-5955(95)00059-d. [DOI] [PubMed] [Google Scholar]
- Stover L, Neely ST, Gorga MP. Explorations of the ‘filter’ of distortion product otoacoustic emissions. Abstr Assoc Res Otolaryngol. 1994;17:54. [Google Scholar]
- Sutton LA, Lonsbury-Martin BL, Martin GK, Whitehead ML. Sensitivity of distortion-product otoacoustic emissions in humans to tonal over-exposure: Time course of recovery and effects of lowering L2. Hear Res. 1994;75:161–174. doi: 10.1016/0378-5955(94)90067-1. [DOI] [PubMed] [Google Scholar]
- Talmadge CL, Long GR, Tubis A, Dhar S. Experimental confirmation of the two-source interference model for the fine structure of distortion product otoacoustic emissions. J Acoust Soc Am. 1999;105:275–292. doi: 10.1121/1.424584. [DOI] [PubMed] [Google Scholar]
- Tardif SD, Ziegler TE, Power M, Layne DG. Endocrine changes in full-term pregnancies and pregnancy loss due to energy restriction in the common marmoset (Callithrix jacchus) J Clin Endocrinol Metab. 2005;90:335–339. doi: 10.1210/jc.2004-1064. [DOI] [PubMed] [Google Scholar]
- Taschenberger G, Manley GA. General characteristics and suppression tuning properties of the distortion-product otoacoustic emission 2f1-f2 in the barn owl. Hear Res. 1998;123:183–200. doi: 10.1016/s0378-5955(98)00120-8. [DOI] [PubMed] [Google Scholar]
- van Hengel PWJ, Duifhuis H. The generation of distortion products in a nonlinear transmission line model of the cochlea. In: Wada H, Takasaka T, Ikeda K, Ohyama K, Koike T, editors. Recent Developments in Auditory Mechanics. World Scientific; Singapore: 2000. pp. 409–415. [Google Scholar]
- Varghese GI, Zhu X, Frisina RD. Age-related declines in distortion product otoacoustic emissions utilizing pure tone contralateral stimulation in CBA/CaJ mice. Hear Res. 2005;209:60–67. doi: 10.1016/j.heares.2005.06.006. [DOI] [PubMed] [Google Scholar]
- Vassilakis PN, Meenderink SWF, Narins PM. Distortion product otoacoustic emissions provide clues to hearing mechanisms in the frog ear. J Acoust Soc Am. 2004;116:3713–3726. doi: 10.1121/1.1811571. [DOI] [PubMed] [Google Scholar]
- Wever EG, Vernon JA. Cochlear potentials in the marmoset. Physiology. 1961;47:739–741. doi: 10.1073/pnas.47.5.739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitehead ML, Lonsbury-Martin BL, Martin GK. Evidence for two discrete sources of 2f1 – f2 distortion product otoacoustic emission in rabbit. I Differential dependence on stimulus parameters. J Acoust Soc Am. 1992a;91:1587–1607. doi: 10.1121/1.402440. [DOI] [PubMed] [Google Scholar]
- Whitehead ML, Lonsbury-Martin BL, Martin GK. Evidence for two discrete sources of 2f1 – f2 distortion product otoacoustic emission in rabbit. II Differential physiological vulnerability. J Acoust Soc Am. 1992b;91:1587–1607. doi: 10.1121/1.402440. [DOI] [PubMed] [Google Scholar]
- Whitehead ML, McCoy MJ, Lonsbury-Martin BL, Martin GK. Dependence of distortion-product otoacoustic emissions on primary levels in normal and impaired ears: I. Effects of decreasing L2 below L1. J Acoust Soc Am. 1995;97:2346–2358. doi: 10.1121/1.411959. [DOI] [PubMed] [Google Scholar]
- Wiederhold ML, Mahoney JW, Kellogg DL. Acoustic overstimulation reduces 2f1 – f2 cochlear emissions at all levels in the cat. In: Allen JB, Hall JL, Hubbard A, Neely ST, Tubis A, editors. Peripheral Auditory Mechanism. Springer-Verlag; New York, NY: 1986. pp. 322–329. [Google Scholar]
- Wilson JP. The combination tone, 2fl-f2, in psychophysics and ear-canal recording. In: van den Brink G, Bilsen FA, editors. Psychophysical, physiological and behavioural studies in hearing. Delft Univ. Press, Delft; Netherlands: 1980. pp. 43–50. [Google Scholar]
- Zurek PM, Clark WW, Kim DO. The behavior of acoustic distortion products in the ear canals of chinchillas with normal or damaged ears. J Acoust Soc Am. 1982;72:774–780. doi: 10.1121/1.388258. [DOI] [PubMed] [Google Scholar]