External Ba²⁺ Block of Human Kv1.5 at Neutral and Acidic pH: Evidence for H_o⁺-Induced Constriction of the Outer Pore Mouth at Rest

Abstract

Previous studies have shown that low pH_o accelerates depolarization-induced inactivation and decreases the macroscopic conductance by reducing channel availability. To test the hypothesis that outer pore constriction underlies the decreased conductance at low pH_o, external Ba²⁺ was used to examine the accessibility of the channel pore at rest under neutral and acidic conditions. At pH_o 7.4, Ba²⁺ block of closed channels follows a monoexponential time course and involves a low-affinity superficial site (K_D ≅ 1 mM, −80 mV, 0 mM 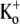) and a high-affinity site (K_D ≅ 4 μM) deeper in the pore. Depolarization promotes Ba²⁺ dissociation and an analytical model incorporating state-dependent changes of Ba²⁺ affinity is presented that replicates the frequency dependence of the time course and the extent of block. Open-channel block by Ba²⁺ is weak. At pH_o 5.5, both the access to and exit from the deep site is inhibited. These results are consistent with a low-pH_o-induced conformational change in the outer pore that prevents Ba²⁺ binding at rest or unbinding during depolarization. If a pore constriction is involved, similar to that proposed to occur during P/C-type inactivation, this would imply that closed-state inactivation in Kv1.5 occurs under acidic conditions.

INTRODUCTION

Kv1.5 is a Shaker-related, voltage-gated potassium (Kv) channel that, in the human heart, underlies the ultrarapid delayed rectifier current (I_Kur) that contributes to the repolarization of the atrial action potential (1,2). The inhibitory effects of low extracellular pH on Kv1.5 and Shaker channels, as well as the related mammalian Kv1.3 and Kv1.4 channels, have been studied by our group (3–6) and others (7–14).

Decreases in pH_o result in an inhibition of macroscopic Kv1.5 currents that is independent of the depolarizing shift of the conductance-voltage relationship caused by the charge-screening effect of the elevated [H⁺]_o (3,8,9,12). It has been suggested that this inhibition is due to an enhancement of slow inactivation; indeed, in addition to decreasing the peak current, low pH_o causes an acceleration of slow inactivation in Kv1.5 and in the fast-inactivation-removed mutants of Kv1.4 and Shaker (ShIR) channels (3,7,8,10,11,15). Slow inactivation is thought to proceed in two phases after channel activation. The first phase, known as the pore, or P-type, phase, involves constriction of the outer pore and loss of K⁺ conductance, and is followed, with continued depolarization, by the C-type phase, where the S4 transmembrane segments are stabilized in the “open” conformation through interactions with the pore (for a recent review, see Kurata and Fedida (16)). Here, we refer to these processes collectively as “P/C-type” inactivation. Consistent with H⁺-mediated enhancement of P/C-type inactivation, maneuvers that impede inactivation, such as raising external [K⁺] or mutating a specific outer pore residue (Kv1.5 R487, ShIR T449, or Kv1.4 K532) to a valine or tyrosine residue, also antagonize the inhibition of Kv1.5 current by low pH_o (3,10,11).

It is important to note, however, that an enhancement of the rate of depolarization-induced P/C-type inactivation and accumulation of channels in the inactivated state does not fully account for the decrease in peak macroscopic current observed at low pH_o. We have shown previously that the inhibition of Kv1.5 current at pH 5.9 does not show use dependence, as would be expected if it were caused by cumulative inactivation (3). In addition, analyses of single-channel currents show that low pH_o mainly blocks current by increasing the probability that closed Kv1.5 channels enter an unavailable mode (5). Fluorescence measurements from ShIR channels have also provided evidence that protons induce inactivation of channels from closed, resting states (6). These results therefore suggest that external acidification blocks Kv1.5 current by enhancing open- as well as closed-state inactivation.

Whether the 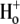-induced closed-state inactivation process involves the same conformational changes as P/C-type inactivation, however, remains unclear. In this article, we have used externally applied Ba²⁺ as a molecular probe to examine possible changes in the accessibility of the outer pore of Kv1.5 under acidic conditions. A Ba²⁺ ion has essentially the same radius as a K⁺ ion and is able to enter the pore of several classes of K⁺ channels from either side of the membrane (13,17–22). Regardless of the side of the channel to which it is applied, Ba²⁺ binding is thought to occur within the selectivity filter (19,20,23) and, perhaps because of its greater charge, Ba²⁺ tends to have a long mean dwell time, resulting in a block of K⁺ current. In ShIR channels, Ba²⁺ has been shown to bind to two sequential sites within the pore: a low-affinity superficial site that gives rise to a near-instantaneous component of block, and a deep site with a higher affinity for Ba²⁺ that is associated with a comparatively much slower block onset and offset (20).

Here, we first characterize the block of Kv1.5 by externally applied Ba²⁺ and show that for the block of resting channels there are two sequential binding sites, and that the affinity of the deep binding site is much higher than reported for ShIR. Again in contrast to ShIR, there is only weak fast block of open channels by Ba²⁺ in Kv1.5. We then assess whether Ba²⁺ can either access or exit the deep binding site at pH_o 5.5 and find that external acidification can prevent either the loading or unloading of the deep pore site. These results suggest that the decrease of channel availability caused by external acidification is associated with a constriction of the outer pore mouth and adds support to the hypothesis that a P-type inactivation process occurs at rest at low pH_o.

METHODS

Cell preparation

Wild-type hKv1.5 currents were recorded from channels stably expressed in a human embryonic kidney cell line (HEK293, American Type Culture Collection, Rockville, MD), as reported previously (3). Cells were passaged using trypsin-EDTA and maintained in minimum essential medium supplemented with 10% fetal bovine serum, 1% penicillin-streptomycin, and 0.5 mg ml⁻¹ geneticin at 37°C in an atmosphere of 5% CO₂ in air. All tissue culture supplies were obtained from Invitrogen (Burlington, ON, Canada).

Recording solutions

Unless otherwise stated, the standard, nominally K⁺-free bath solution contained (in mM): 143.5 NaCl, 2 CaCl₂, 1 MgCl₂, 5 glucose, and 10 HEPES, and was titrated at room temperature to pH 7.4 with NaOH. In experiments where 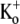was present, KCl was substituted for NaCl. Ba²⁺-containing solutions were prepared by isoosmotic substitution of NaCl with BaCl₂. The standard low-pH bath solution was prepared using 10 mM MES instead of HEPES and titrated to pH 5.5 with NaOH. The patch pipette solution contained (in mM): 130 KCl, 4.75 CaCl₂ (pCa²⁺ = 7.3), 1.38 MgCl₂, 10 EGTA, and 10 HEPES, and was adjusted to pH 7.4 with KOH. Chemicals were obtained from the Sigma Aldrich Chemical (Mississauga, ON, Canada).

In most experiments, a section of glass coverslip to which cells had attached was placed in a saline-filled recording chamber (volume 0.5 ml) and perfused with control solution (2 ml min⁻¹). We found no difference between experiments using continuous perfusion and those where control and test responses were recorded without perfusion (not shown).

Fast perfusion

For experiments requiring rapid solution exchange, a Warner Instruments (Hamden, CT) SF-77B Perfusion Fast Step system was used. Perfusion pipettes were made using borosilicate theta glass tubing (2 mm outer diameter; Warner Instruments) that was pulled in one step to an outer diameter at the tip of ∼300 μm and then cut into two parts using a ceramic wafer (for details, see Jonas (24)). Deactivated fused silica tubing (0.18 mm inner diameter, Agilent Technologies, Mississauga, ON, Canada) was then inserted into the back ends of the pipette barrels, advanced as far as possible toward the tip and fixed in place by back-filling with epoxy glue. The free ends of the silica tubing were then connected to the solution reservoirs via polyethylene tubing and the manifolds provided with the Fast Step system. While the bath was being constantly perfused with control solution, the assembled perfusion pipette was positioned as close as possible to the cell of choice, so that the cell was exposed to solution outflow from only one barrel. Rapid switching of the pipette position (200 μm movement) exposed the cell to the test solution that flowed continuously from the second barrel. Using a method described by Panyi and Deutsch (25), the time course of solution exchange, estimated from the decay in current amplitude at 0 mV when the [K⁺] of the perfusion solution was switched from 0.5 to 140 mM K⁺ (not shown), was ∼150 ms.

Electrophysiological procedures

Whole-cell currents were recorded at room temperature (20–25°C) using an EPC-8 patch-clamp amplifier and Pulse + Pulsefit software (HEKA Electronik, Lambrecht/Pfalz, Germany), connected through an ITC-18 digital interface (Instrutech, Port Washington, NY). Patch electrodes were made from thin-walled borosilicate glass (World Precision Instruments, Sarasota, FL) and had resistances of 1.0–2.5 MΩ measured in the bath with standard internal and external solutions. Capacitance and series resistance were compensated (typically 80%) using the circuitry of the amplifier. Leak subtraction was achieved using the online P/N protocol in Pulse, for which the holding potential was −100 mV and the scaling factor was −0.25. Current signals filtered at 3 kHz (−3 dB, 8 pole Bessel filter) were digitized (18 bit) at a sampling interval of 100 μs. Voltages were corrected for liquid junction potentials. Cells were held at −80 mV and a test potential of +50 mV was standard. Test pulses were 1.5 s long in experiments examining open-channel Ba²⁺ dissociation. In experiments involving repetitive stimulation at different frequencies, the pulse duration was 10 ms and the current amplitude was measured at the end of the voltage pulse. When applicable, current amplitudes were normalized to control measurements made at the beginning of an experiment. Data from cells showing <85% recovery to control levels were discarded.

Data analysis

Data are presented as mean ± SE, except for the values derived from non-linear least-squares fitting routines, which are expressed as mean ± SD (Igor, Wavemetrics, Portland, OR); n represents the number of cells. Due to the sigmoidal nature of current activation under control (0 mM Ba²⁺) conditions, the time course of activation was estimated by fitting the portion of the trace between 50 – 100% of the peak current to a single exponential function (using a 1.5 s pulse; Fig. 6). After Ba²⁺ exposure, the entire rising phase of the first current trace obtained upon the return to control conditions could be fit to an exponential function. The time courses of currents obtained using short pulses (10 ms) were not quantified (e.g., traces shown in Fig. 1).

FIGURE 6.

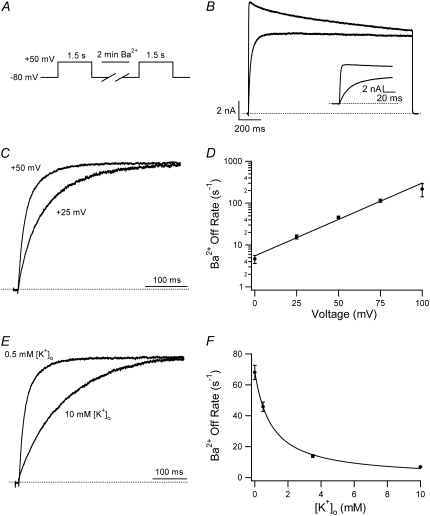
Ba²⁺ unbinding from the open state is voltage-dependent and inhibited by increasing the [K⁺]_o. (A) Schematic of voltage-pulse and Ba²⁺ application protocol. A 1.5 s pulse to +50 mV was applied under 0.5 mM [K⁺]_o, pH_o 7.4 conditions. The cell was then exposed to 5 mM Ba²⁺ for 2 min, followed by a 4-min wash in control solution, after which the test pulse was repeated. (B) After Ba²⁺ exposure (gray trace), the current activation was much slower and well fitted by a single exponential (τ_act,app = 28.14 ms; compare to τ_act = 1.25 ms for the control response (black trace). (Inset) Current activation on an expanded timescale. These results are representative of those obtained from 11 cells. (C) Normalized currents after a 2-min exposure to 5 mM Ba²⁺ (with 0.5 mM 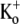) recorded at two different test-pulse potentials. The activation time course at both voltages was well fitted by a single exponential. At +50 mV, τ_act,app was 22.56 ± 1.25 ms (n = 11), which was significantly faster (p < 0.001) than at +25 mV (τ_act,app = 65.59 ± 7.33 ms; n = 3). Each trace was normalized with respect to its own peak current. (D) Plot of the Ba²⁺ off rate (1/τ_act,app) derived from experiments such as those described in C, obtained between 0 and +100 mV in 25-mV increments. A fit of the data to the Woodhull model (see Methods) gave an estimate for δ_Ba,off of 0.51 ± 0.04. Data points are from a total of 21 cells; 3–11 cells/point. (E) After Ba²⁺ loading (in 0.5 mM 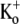), the time course of the current onset in 0.5 mM or 10 mM 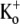was examined. The current activated significantly faster with 0.5 mM 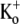(τ_act,app = 22.56 ± 1.25 ms; n = 11) than with 10 mM 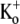(τ_act,app = 145.40 ± 6.15 ms; n = 5; p < 0.001). Traces were normalized as in C. (F) Plot of the Ba²⁺ off rate under varying [K⁺]_o at a test-pulse potential of +50 mV. The best fit of the data to the Hill equation (see Methods) gave a K_D for the 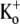inhibition of Ba²⁺ unbinding of 1.00 ± 0.08 mM. Data points are from a total of 31 cells, 5–11 cells/point.

FIGURE 1.

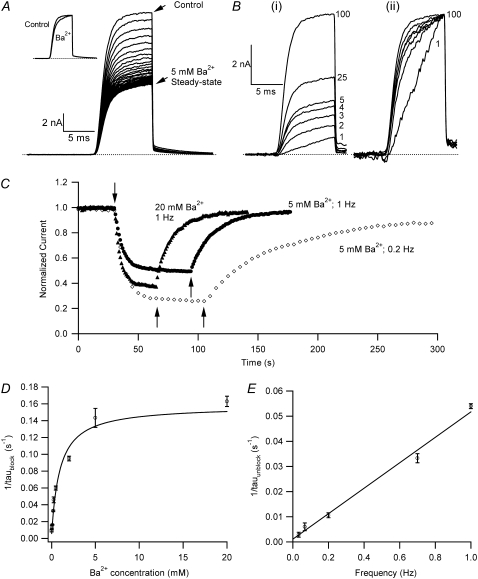
Ba²⁺ blocks Kv1.5 in a concentration- and frequency-dependent manner. (A) With 0 mM 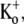pH_o 7.4 solution, 10-ms test pulses to +50 mV were applied at 1 Hz without (uppermost trace) and with 5 mM Ba²⁺. Shown are 65 consecutive traces from the time of Ba²⁺ application, which began immediately after the control trace. (Inset) The trace at the steady-state level of block was scaled 1.87× to match the peak amplitude of the control current. There was a small effect of Ba²⁺ on the onset of the K⁺ current. (B (i)) Trace 1 was recorded using a 10-ms pulse to +50 mV after a 1-min exposure to 1 mM Ba²⁺ in 0 mM 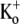at −80 mV. Traces 2–5 show the current from subsequent pulses applied at 1 Hz in the continued presence of Ba²⁺. Trace 25 shows the steady-state current in 1 mM Ba²⁺ with 1 Hz stimulation and Trace 100 is the steady-state current after recovery in 0 mM Ba²⁺. (B (ii)) Traces 1–5 and 25 are normalized with respect to Trace 100. There was a marked slowing of the rising phase of the current elicited by the first pulse after Ba²⁺ exposure, but this effect is diminished with subsequent pulses in the continued presence of Ba²⁺. (C) The time course of the onset and offset of the Ba²⁺ block. The average current amplitude in the last 1 ms of each pulse was normalized to the Ba²⁺-free control current. Down and up arrows indicate the time of fast Ba²⁺ application and withdrawal, respectively. Black circles (•) represent the normalized current amplitudes for the experiment shown in A. Single-exponential fits to the onset of and recovery from Ba²⁺ block give τ_block = 6.84 s and τ_unblock = 19.21 s, respectively. When the experiment was performed with the same stimulus protocol but with 20 mM Ba²⁺ (solid triangles), block onset was slightly faster (τ_block = 4.97 s) and the normalized steady-state current was smaller (0.37 vs. 0.50 for 5 mM Ba²⁺), but the time course of current recovery was the same. If the [Ba²⁺] was kept constant at 5 mM but the pulse frequency decreased to 0.2 Hz (open diamonds), the normalized steady-state level was also reduced (steady-state normalized current = 0.27). Although the onset of the block was not affected by the decrease in stimulation frequency, recovery with a 0.2-Hz pulse frequency was much slower (τ_unblock = 63.20 s) than that seen at 1 Hz. (D) The blocking rate (1/τ_block) is a nonlinear function of the [Ba²⁺]. τ_block values were assessed in 0 mM 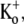with 10-ms pulses to +50 mV applied at 1 Hz. The solid line represents the best fit of the data to a sequential two-site binding model (Eq. 1; see text for fit parameters). Data points are from a total of 46 cells, 3–8 cells/point. (E) The unblocking rate is linearly related to the pulse frequency. Values for τ_unblock were assessed with 0 mM 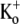and 20 mM 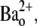using 10-ms pulses to +50 mV applied at 1, 0.7, 0.2, 0.066, or 0.033 Hz. The extrapolated off rate without pulsing (0 Hz) is 0.001 ± 0.002 s⁻¹. Data points are from a total of 53 cells, 5–24 cells/point.

The analysis of the relationship between the blocking rate (1/τ_block) and [Ba²⁺]_o (Fig. 1 C) was based on a sequential two-site binding model:

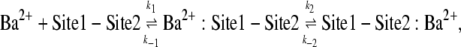(Scheme 1)

where Sites 1 and 2 are, respectively, the superficial and deep sites, k₁ and k₂ are the respective binding rates at Sites 1 and 2, and k₋₁ and k₋₂ are the respective rates of unbinding from Sites 1 and 2. This same model has been used previously to describe the concentration dependence of the slow block of ShIR channels by Ba²⁺ (20). At the superficial site, the binding rate is proportional to [Ba²⁺]. The deeper site is not directly exposed to the external bulk solution, or to the internal bulk solution by virtue of the closed activation gate and, as a consequence, k₂ is proportional to the probability that Site 1 is occupied. We make the assumption that k₋₂ is independent of the occupancy of Site 1; this arose from the assumption in the original model that a coulombic interaction precludes simultaneous occupation of the two sites by Ba²⁺. Even if this constraint is removed, there is little change in the outcome of the model, because k₋₂, derived independently from the time dependence of the current recovery in Ba²⁺-free medium (Fig. 1 E), is very small relative to k₂ at Ba²⁺ concentrations that produce a significant degree of block. Indeed, making the off rate a function of the probability that the superficial site is not occupied (i.e., k₋₂ × 1/(1 + [Ba²⁺]_o/K_Ba,s)) has minimal effect on the fit parameters (not shown). Thus, the data in Fig. 1 C were fit to the equation

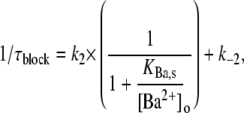(1)

where k₂ and k₋₂ are, respectively, the binding and unbinding rates at the deep site, K_Ba,s is the apparent equilibrium dissociation constant of the superficial site, and 1/(1 + K_Ba,s/[Ba²⁺]_o) is the probability that Ba²⁺ is bound to the superficial site.

Primarily to allow a comparison with the results of others, the [Ba²⁺]_o dependence of the steady-state residual current at a given pulse frequency was also quantified by fitting the data to the Hill equation:

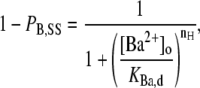(2)

where P_B,SS is the proportion of macroscopic current blocked at the steady state, K_Ba,d is the apparent equilibrium dissociation constant of the deep Ba²⁺ binding site and n_H is the Hill coefficient reflecting the number of Ba²⁺ ions binding per channel.

To model the frequency dependence of the Ba²⁺ block of Kv1.5, we employed Eqs. 3–7, which were originally applied by Starmer et al. (26) to describe the block of voltage-gated Na⁺ (Na_V) channels by the quaternary lidocaine derivative QX222. Briefly, a bimolecular scheme involving unblocked channels (U), drug (D), and blocked channels (B) is

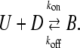(Scheme 2)

For a given channel conformation (i.e., open or closed), the steady-state level of block is k_on/(k_on + k_off) and the time constant for the block is (k_on + k_off)⁻¹. However, if the channel conformation affects the binding equilibrium, by virtue of an effect on the accessibility of the site and/or a change of k_on and/or k_off, and if the lifetime of a particular conformation is short-lived with respect to the blocking time constant, then the proportion of channels blocked can be critically influenced by the frequency and duration of test pulses that cycle channels in and out of different conformations. In the case of QX222, block is enhanced by increasing the pulse frequency, which increases the proportion of time spent in one or more conformations favoring drug binding and decreases the time spent in conformations favoring drug unbinding. As we will show, binding and unbinding of Ba²⁺ exhibits the opposite relationship: channel opening during test pulses to +50 mV promotes Ba²⁺ unbinding, whereas the reaction is biased toward binding in a closed channel at −80 mV. Consequently, increasing the frequency of depolarizing test pulses decreases the fractional block by Ba²⁺. The blockade with repetitive stimulation (see the Appendix of Starmer et al. (26) for details of the derivation) is described by the equation

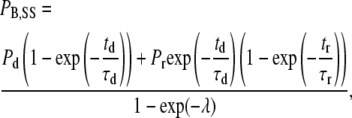(3)

where P_B,SS is the proportion of channels blocked at the steady state, P_d is the proportion of channels blocked at the deep site after a prolonged depolarization, P_r is the proportion of channels blocked at the deep site after a prolonged rest at the holding potential, t_d is the average amount of time that a channel is open during a depolarizing pulse, τ_d is the time constant for unblock during a depolarization to the test voltage, t_r is the time at the holding potential between test pulses, τ_r is the time constant for the block at the holding potential, and λ is equal to the unitless quantity (t_d/τ_d + t_r/τ_r). With the assumption that P_d is zero (20,21), Eq. 3 simplifies to

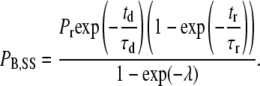(4)

Since Ba²⁺ can be trapped in open-inactivated channels (21,27), this equation is valid for prolonged depolarizations only if the value for t_d is appropriately adjusted; otherwise, the degree of unblock would be overestimated. With the 10-ms test depolarizations used in the quantification of the Ba²⁺ block, inactivation is not a significant mitigating factor, and the estimate of t_d is calculated from the open probability estimated from prior single-channel recordings (see Results).

The fractional block at the end of the xth pulse of a train (P_B,x) is

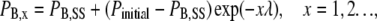(5)

where P_initial is the proportion of the current blocked at the point in time when the pulse frequency is changed, λ is as defined for Eq. 3, and x is the pulse number in the stimulus train. In words, Eq. 5 indicates that changing the stimulus frequency causes the proportion of current blocked during a pulse train to relax monoexponentially to a new steady-state level. The relationship between the time constant (τ) for that relaxation and λ is:

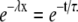(6)

Given that t, the time elapsed since the change of the pulse frequency, is equal to the product of the pulse number (x) and the cycle length (CL), then the time constant can be calculated by

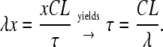(7)

To describe the [K⁺]_o dependence of the open-channel Ba²⁺ unbinding rate (see Fig. 6 F), the Ba²⁺ dissociation rates measured at +50 mV with different [K⁺]_o were fit to the Hill equation,

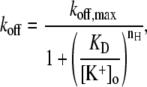(8)

where k_off is the apparent rate of Ba²⁺ unbinding from open channels at +50 mV (taken as 1/τ_act,app, where τ_act,app is the apparent activation time constant (see Fig. 6)), k_off,max is the unbinding rate with 0 mM 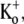K_D is the apparent equilibrium dissociation constant for the 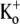inhibition of Ba²⁺ unbinding, and n_H is the Hill coefficient reflecting the number of K⁺ ions binding per channel to slow Ba²⁺ unbinding.

To quantify the voltage dependence of the open-channel Ba²⁺ dissociation rate (see Fig. 6 D), k_off was measured over a range of test potentials (with a fixed [K⁺]_o and [K⁺]_i), plotted against the test potential and fit to the Woodhull model:

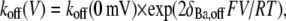(9)

where k_off(V) is the Ba²⁺ unbinding rate at the test voltage, k_off (0 mV) is the unbinding rate at 0 mV, V is the test potential, δ_Ba,off is the electrical distance between the deep Ba²⁺-binding site and the rate-limiting barrier for exit, and F, R, and T have their usual meanings (28).

RESULTS

Ba²⁺ blocks closed Kv1.5 channels at pH 7.4

Our first objective was to test the hypothesis that Ba²⁺ is able to access and bind within the pore of Kv1.5 channels and block current. We began by characterizing the effects of external Ba²⁺ on Kv1.5 currents at pH 7.4 using a stimulus protocol comparable to that used to investigate Ba²⁺ block of ShIR channels (20). Fig. 1 A illustrates a representative experiment examining the effect of 5 mM Ba²⁺ on currents evoked by 10-ms pulses to +50 mV applied at a frequency of 1 Hz from a holding potential of −80 mV. Tail current was recorded at −80 mV. Scaling of the steady-state current evoked in 5 mM Ba²⁺ and superimposition on the control current (Fig. 1 A, inset) revealed that the activation and deactivation kinetics of the steady-state current observed with 1 Hz stimulation were slightly affected by the 5 mM Ba²⁺ treatment.

For the currents shown in Fig. 1 B (i), 1 mM Ba²⁺ was applied for 1 min in the absence of pulses before initiating a train of 1-Hz pulses to +50 mV. The current in the first pulse had a small initial amplitude and slowly activating time course, which is consistent with the block of virtually all of the channels at the start of the pulse, followed by a slow unblock during the pulse (21). With continued pulsing in the presence of Ba²⁺, the degree of block at equilibrium (Trace 25) was nearly identical to that in Fig. 1 A. Trace 100 is the steady-state recovery response obtained in Ba²⁺-free medium. For Fig. 1 B (ii), select traces were normalized with respect to Trace 100 to better illustrate their relative activation time courses. These data suggest that repetitive pulsing has a substantial effect on the steady-state level of block of Kv1.5 by Ba²⁺, consistent with the observation made by Armstrong on the Ba²⁺ block of the squid giant axon delayed rectifier channels (17). A detailed analysis of the frequency dependence of Ba²⁺ block of Kv1.5 is presented below.

To illustrate the time dependence of the onset and offset of Ba²⁺ block, the normalized mean current in the last millisecond of each test pulse from the experiment described by Fig. 1 A has been plotted against time in Fig. 1 C (solid circles); the down arrow indicates the time at which the 5 mM Ba²⁺ fast perfusion began. In five experiments of this type, the relaxation of the normalized test current (I_norm) to a steady-state level of 0.52 ± 0.01 was well fitted by a single exponential with a time constant (τ_block) of 7.2 ± 0.6 s. After returning to Ba²⁺-free medium, marked by the up black arrow, the time course for complete reversal of the Ba²⁺ block was also monoexponential (τ_unblock = 18.5 ± 2.6 s). In an experiment with a fourfold higher concentration (20 mM) of Ba²⁺ (Fig. 1 C, solid triangles) but with the same pulse frequency of 1 Hz, the onset of the block was only slightly faster (τ_block = 4.8 ± 0.5 s; n = 9), and the steady-state block (1 − I_norm = 0.61 ± 0.01) was ∼20% greater. Note that after switching from 20 mM Ba²⁺ back to control solution τ_unblock was 12.8 ± 2.1 s, which was not significantly different (p > 0.05) from τ_unblock measured after the 5 mM Ba²⁺ treatment.

For the third set of responses (Fig. 1 C, open diamonds), a 5-mM concentration of Ba²⁺ was used but the stimulus frequency was 0.2 Hz. The τ_block (9.2 ± 0.3 s; n = 5) was similar to that observed with a 1-Hz pulse frequency using either 5 or 20 mM Ba²⁺. However, the degree of block (0.74 ± 0.01) was greater and unblock was slower (τ_unblock = 60.5 ± 2.9 s) than with the 1-Hz test-pulse frequency after channel loading using either 5 or 20 mM Ba²⁺. Thus, the Ba²⁺ block of Kv1.5 is similar to that reported for ShIR (20,21) in that the steady-state level of block and the kinetics of block onset are dependent on both the Ba²⁺ concentration and frequency of test pulses applied, whereas the time course of current recovery from Ba²⁺ block is sensitive only to the pulse frequency.

Despite these qualitative similarities in the features of the Ba²⁺ block of Kv1.5 (Fig. 1, A and C) and ShIR currents, the results of Fig. 1 also reveal substantial qualitative and quantitative differences, which is perhaps unexpected given the similarity of their pore structures (Fig. 2). For example, in ShIR with 20 mM Ba²⁺, the inhibition of current consists of a very rapid phase, attributable to fast block of open channels during the test pulse, as well as a slow phase that relaxes to the steady state with a time constant of ∼100 s (Fig. 2 of (20)). In contrast, but similar, to findings in Kv1.3 (13,14), there is no rapid component of block of Kv1.5 by 20 mM Ba²⁺ (Fig. 1 C) and the slow block occurs roughly 10 times faster than in ShIR. In light of these differences, in the second part of this article we undertook to analyze the Ba²⁺ block of Kv1.5 in more detail in the interest of highlighting mechanistic differences in the Ba²⁺ block of these closely related channels, and to validate the use of Ba²⁺ as a tool to probe the Kv1.5 pore at low pH_o.

FIGURE 2.

Sequence alignment of hKv1.5 and Shaker from the C-terminal end of S5 to the end of the selectivity filter. The putative regions forming the turret, pore helix, and selectivity filter are shown.

τ_block is not a linear function of [Ba²⁺]

To develop a kinetic model for the Ba²⁺ block, we examined the relationship between the blocking rate, taken as the inverse of τ_block after Ba²⁺ application in K⁺-free bath solution, and the concentration of Ba²⁺ applied (Fig. 1 D). As reported for ShIR, the blocking rate of Kv1.5 current saturated at a high [Ba²⁺]_o, indicating that a bimolecular blocking reaction was not involved. The data were fit very well to a sequential two-site binding model used to describe the Ba²⁺ block of closed ShIR channels (see Methods and Hurst et al. (20)). The best fit of the experimental data to Eq. 1, which is based on Scheme 1, is shown in Fig. 1 D (solid line) and gave an estimate of 0.93 ± 0.15 mM for the apparent equilibrium dissociation constant (K_Ba,s = k₋₁/k₁) of the superficial Ba²⁺ binding site, 0.16 ± 0.01 s⁻¹ for k₂, and 0.0025 ± 0.0019 s⁻¹ for k₋₂.

An independent estimate of k₋₂ was obtained from experiments where Kv1.5 channels were first loaded with Ba²⁺, and after switching back to Ba²⁺-free medium, τ_unblock was measured with test pulses to +50 mV applied at varying frequencies. The underpinning assumption of the experimental approach, which is validated below in Kv1.5 and supported by results in ShIR (21), is that because depolarization facilitates the unblocking reaction, and since recovery occurs in Ba²⁺-free medium, rebinding of Ba²⁺ is therefore unlikely to occur, and the relationship between τ_unblock and the pulse frequency allows k₋₂ to be estimated. Recovery time courses were always well fitted by a single exponential, regardless of the stimulus frequency (e.g., Fig. 1 C), and τ_unblock was independent of either the extent of the block or the Ba²⁺ concentration used in the loading phase of the experiment (not shown). As expected for an unblocking reaction that is facilitated by depolarization, the apparent unblocking rate (1/τ_unblock) is proportional to the stimulus frequency (Fig. 1 E) when the test-pulse duration is fixed and brief. Extrapolation of the fitted line to the y intercept provides an estimate of k₋₂ in the absence of pulsing, or, in other words, the value for the Ba²⁺ off rate from the deep binding site at the holding potential of −80 mV and with 0 mM external K⁺. The best estimate of k₋₂ derived from Fig. 1 E is 0.001 ± 0.002 s⁻¹ and buttresses the estimate of 0.0025 ± 0.0019 s⁻¹ in Fig. 1 D. However, both estimates have a large standard deviation and their accuracy is therefore uncertain. In comparison, the upper limit for the closed-state off rate in ShIR channels is 0.0132 s⁻¹ (21).

Ba²⁺ block of Kv1.5 is dependent on stimulation frequency

Although an effect of the test-pulse frequency on the steady-state level of Ba²⁺ block has been noted with ShIR and other K⁺ channels (17,21), to our knowledge, this relationship has not been systematically studied. Indeed, an explicit assumption has been made that a brief test pulse would have little effect on the slow component of block (20). Especially in view of the greatly enhanced block observed after a 1-min interpulse interval (Fig. 1 B), a more detailed examination of the frequency dependence of the Ba²⁺ block was warranted.

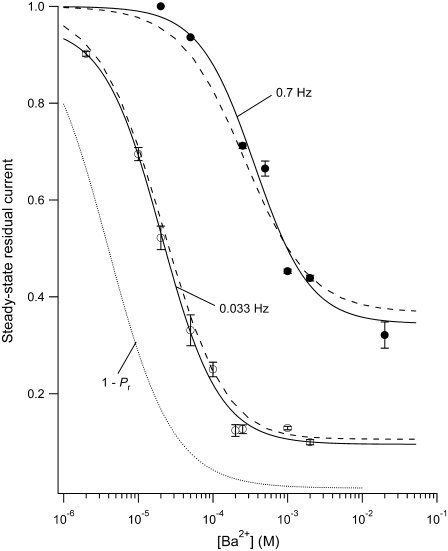
To quantify the relationship between the Ba²⁺ block and the test-pulse frequency, the steady-state level of block was assessed at two different stimulation frequencies over a range of [Ba²⁺]. Current amplitude was measured at the end of 10-ms test pulses to +50 mV applied once every 30 s (0.033 Hz) or once every 1.43 s (0.7 Hz). Ba²⁺ was applied by a computer-controlled fast perfusion system and the blocking reaction was allowed to proceed to the steady-state. Steady-state residual current was calculated by normalizing the peak test current at the steady state to the control test currents obtained before Ba²⁺ application. Fig. 3 shows the concentration-response relationship at 0.033 Hz (open circles) and at 0.7 Hz (solid circles). Separate fits of the two data sets to the Hill equation (Fig. 3, black lines, and Eq. 2) gave estimates for the apparent affinity of the deep Ba²⁺ binding site, K_Ba,d, and the Hill coefficient of 20.3 ± 2.6 μM and 1.12, respectively, for the 0.033-Hz pulse frequency, as compared to 361 ± 151 μM and 1.16 for responses evoked at 0.7 Hz. This demonstrates that increasing the pulse frequency from 0.033 Hz to 0.7 Hz causes an 18-fold increase of the midpoint of the concentration-response relationship while having no effect on the Hill coefficient, which had a value consistent with deep block arising from the binding of one Ba²⁺ ion. Increasing the pulse frequency to 0.7 Hz also caused an upward shift of the foot of the concentration-response relationship. This upward shift reflects the fact that with a saturating concentration of Ba²⁺ the degree of block with test pulses of a fixed duration (and a fixed t_d) is proportional to the time spent at rest (t_r). In other words, the decrease of t_r as the stimulus frequency increases means there is less time for the reestablishment of block at rest and, as a consequence, the proportion of unblocked channels increases.

FIGURE 3.

The steady-state level of Ba²⁺ block is dependent on the stimulation frequency and the [Ba²⁺]. Test pulses to +50 mV for 10 ms were applied at either 30-s intervals (0.033 Hz (open circles)) or 1.43-s intervals (0.7 Hz (solid circles)) with 0 and a pH_o of 7.4. Ba²⁺ was applied at various concentrations using a computer-controlled fast perfusion system. The steady-state residual current (1 − proportion of blocked (P_B,SS)) at the end of the test pulse was normalized to the control test current before Ba²⁺ application and plotted against the concentration of Ba²⁺ applied (2 μM – 20 mM). The black solid lines represent the best fits of the two data sets to the Hill equation. Estimates of the apparent K_Ba,d and the Hill coefficient are 20.3 ± 2.6 μM and 1.12, respectively, for the data collected at 0.033 Hz, whereas the estimates from the 0.7 Hz data are 361 ± 151 μM and 1.16, respectively. Gray dashed lines represent the outcome of a simultaneous fit of the two data sets to Eq. 4. From the fit, k₂, K_Ba,s, k₋₂, and τ_d were estimated to be 0.15 s⁻¹, 0.8 mM, 0.0006 s⁻¹, and 59 ms, respectively (see text). The dotted gray line represents the solution for the residual normalized current (1 − P_r), where P_r is the proportion of channels blocked after a prolonged rest at the holding potential, i.e., at 0 Hz. A fit of 1 – P_r to the Hill equation gave a Hill coefficient of 1 and a K_Ba,d of 4 μM, indicating that the apparent K_Ba,d is profoundly affected by the pulse frequency. Data points are from a total of 29 cells (2–8 cells/point) for the 0.7 Hz data; and 45 cells (3–9 cells/point) for the 0.033 Hz data.

To model the frequency dependence of the concentration-response relationship, the data obtained at 0.033 Hz and 0.7 Hz were simultaneously fit to Eq. 4; the outcome of the fit is represented by the gray dashed lines in Fig. 3. There are six parameters in the fitting equation: t_d, t_r, k₂, k₋₂, K_Ba,s, and τ_d. The value for τ_r in Eq. 4 arises from

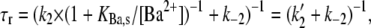and the value for P_r arises from

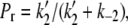where τ_r is the time constant for the Ba²⁺ block of the deep pore site at the holding potential, and P_r is the proportion of channels with Ba²⁺ occupying the deep site at the steady state. To estimate t_d, defined as the average open time during a 10-ms test pulse to +50 mV, the proportion of maximal charge conducted during a pulse was first calculated by dividing the integral for a control pulse current by the integral for the current if activation had been instantaneous (i.e., I_max × 10 ms). The t_d was then obtained by multiplying the proportion of maximal charge by the maximal open probability (P_o) of 0.8 measured from recordings of unitary Kv1.5 currents (5). The mean t_d calculated with this approach was 6.43 ± 0.25 ms (n = 7 cells). Ba²⁺ binding at the deep pore site is assumed to have no effect on t_d (but see Armstrong et al. (17)). For t_r, the time spent at the holding potential during one cycle length, a fixed value of 1/stimulus frequency in Hz − 0.01 s was used. Consequently, there were four free parameters in the global fitting routine, and of these, the values for k₂, k₋₂, and K_Ba,s were constrained to be in the range of the mean value ± 1 SD obtained from the fit of the data in Fig. 1 D. With these conditions, the best-fit values for the constrained parameters k₂, K_Ba,s, and k₋₂ were 0.15 ± 0.08 s⁻¹, 0.8 ± 0.3 mM, and 0.0006 ± 0.0009 s⁻¹, respectively. For τ_d, an unconstrained free parameter, the best estimate obtained from the simultaneous fit to the 0.033 and 0.7 Hz data was 59 ± 19 ms.

Apart from providing a good estimate of the shift of the concentration-response relationship at different frequencies, the best fit values derived in Fig. 3 can be used to approximate the proportion of unblocked channels at the deep site in the absence of test pulses. This is shown in Fig. 3 (gray dotted line) and represents the solution for 1 − P_r, where P_r is as defined above. A fit of 1 − P_r to the Hill equation gave a Hill coefficient of 1 and a K_Ba,d of 4 μM. In other words, with 4 μM Ba²⁺ the on-rate constant (k₂′) is equal to the off-rate constant (k₋₂) and half of the channels have Ba²⁺ bound at the deep site. This suggests that even with 10-ms test pulses applied only once every 30 s the K_Ba,d is overestimated roughly fivefold, whereas at 0.7 Hz the K_Ba,d is overestimated roughly 90-fold, and emphasizes the potential importance of taking the pulse frequency and duration into account when comparing the relative sensitivities of channels to block by Ba²⁺. Thus, reported millimolar values of K_Ba,d for ShIR (20,21) describe the apparent affinity of the deep site at a specific voltage and pulse frequency.

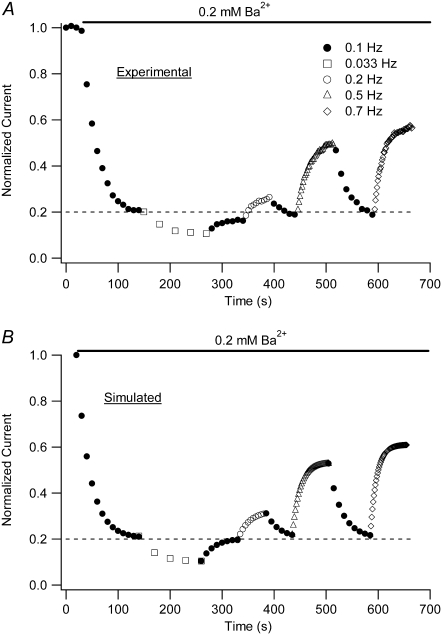
Equation 4 has been shown to fairly faithfully describe the frequency dependence of the concentration-steady-state block relationship; however, the analysis of Fig. 3 provides no indication of how well the model replicates the time dependence of either the onset of, or the recovery from, block. Experimental data addressing that issue are shown in Fig. 4 A. For this representative experiment, at the end of several 10-ms control test pulses to +50 mV, a computer-controlled, rapid changeover from zero to 0.2 mM Ba²⁺ was made and that concentration was then maintained while test pulses were applied at 0.1 Hz (solid circles). Once a steady level of block was attained, the stimulus frequency was decreased to 0.033 Hz (open squares) to monitor the progression of the block to a new steady state. Complete reversal of the enhanced steady-state block observed with 0.033 Hz pulsing was then obtained after reverting to the 0.1-Hz stimulus frequency. The same approach was subsequently repeated with trains of 0.2- (open circles), 0.5- (open triangles), and 0.7-Hz (open diamonds) pulses. Fig. 4 B shows the output of a simulation of the proportion of unblocked current (1−P_B,x) (see Eq. 5) at the end of the xth test pulse and was derived using the values for k₂, K_Ba,s, k₋₂, and τ_d obtained from the fit to the data of Fig. 3. The values for t_d, t_r, and τ_r were calculated as described in connection with Fig. 3; P_initial of Eq. 5 is 1 − the proportion of current at the end of the preceding epoch. Fig. 4 B illustrates that the analytical solution reproduces the experimental data quite well not only in terms of the steady-state level of residual normalized current, as expected, but also from the standpoint of the time dependence of the relaxations to a new level of residual current after a change of the test-pulse frequency. These results also suggest that the values of k₂, K_Ba,s, and k₋₂ are good estimates of the rate and equilibrium constants for Ba²⁺ binding to Kv1.5 channels, and they provide further support for the two-site binding model.

FIGURE 4.

A model of the frequency-dependent Ba²⁺ binding replicates the time dependence of block onset and reversal. (A) A representative experiment in which a cell was given four 10-ms test pulses to +50 mV in 0 mM Ba²⁺ before a rapid changeover to 0.2 mM Ba²⁺ while test pulses continued to be applied at 0.1 Hz (open circles). After steady-state block was achieved, the pulse frequency was decreased to 0.033 Hz (open squares) and the block was allowed to reach a new steady state. The enhanced steady-state block observed with 0.033-Hz stimulus frequency was reversed upon reverting to 0.1-Hz pulses. The effects of changing the pulse frequency to 0.2 (○), 0.5 (Δ) and 0.7 (◊) Hz were subsequently examined using the same approach. Data points show current amplitudes normalized to the peak current at the end of the initial control test pulses. (B) Plot of simulated proportion of residual normalized current (1 – P_B,x) at the end of each test pulse shown in A, calculated using Eq. 5 and the values for k₂, K_Ba,s,, k₋₂, and τ_d derived from fits to the data of Fig. 3. The values for t_d, t_r, and τ_r were those derived from Fig. 3 (see text), whereas P_initial of Eq. 5 is 1 − the proportion of current at the end of the preceding pulse train. At each stimulus frequency, the numerical simulation provides a good estimate both of the steady-state level of block and the time course of the relaxation to that steady state.

Ba²⁺ causes a weak fast block of open Kv1.5 channels

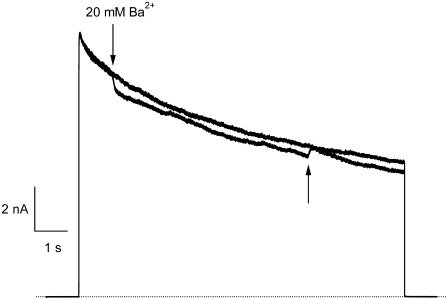
As noted above, the time course of Ba²⁺ block onset in Kv1.5 lacks the fast phase seen in ShIR channels (20,21) and instead exhibits a slow, monoexponential component (Fig. 1 C). However, our analysis of the [Ba²⁺] dependence of the blocking rate (1/τ_block; Fig. 1 D) suggested that, as with ShIR, Ba²⁺ binds first to a low-affinity (K_Ba,s ≅ 1 mM) superficial site and then to a high-affinity (K_Ba,d = 4 μM) deep site. Given the low value of K_Ba,s compared to the concentration of Ba²⁺ used in experiments such as those of Fig. 1 C, it was somewhat surprising that a fast phase of block onset related to Ba²⁺ binding to a superficial site was not seen. This motivated experiments where a brief pulse of 20 mM Ba²⁺was applied during a 10-s pulse to +50 mV (Fig. 5). At the onset of the Ba²⁺ application, the current amplitude rapidly decreased by ∼10%, with a time constant that we assume was governed primarily by the kinetics of the solution change. Upon the switch back to Ba²⁺-free solution, the current recovered to the same amplitude as that of the control current. These results indicate a fast but comparatively weak block of Kv1.5 by 20 mM Ba²⁺, likely by binding to the superficial pore binding site. If so, the affinity of this site for Ba²⁺ in the open state is apparently much lower than that estimated for the superficial site in the closed state (Fig. 1 D) and appears to account for the lack of a fast phase of block in experiments such as those shown in Fig. 1 C.

FIGURE 5.

Fast application of Ba²⁺ during a long depolarizing pulse reveals very weak open-channel block by 20 mM Ba²⁺. Current traces in response to depolarizing pulses to +50 mV for 10 s in 0 mM 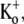Ba²⁺-free solution (black trace) and with a rapid application and withdrawal of a 0 mM 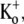20 mM Ba²⁺ solution during a subsequent pulse (gray trace). Down and up arrows indicate the start and end of the Ba²⁺ application, respectively. Exposure to Ba²⁺ caused a rapid fall in current amplitude of ∼10%. A similar effect was observed in six other cells.

Ba²⁺ block of Kv1.5 at rest and open-channel dissociation

As mentioned in connection to Fig. 1 B, when Ba²⁺ is applied for a prolonged period to resting channels, the first 10-ms pulse shows a slow activation time course mainly reflecting a slow unblock of channels. To characterize this unbinding of Ba²⁺ ions from open channels and determine whether it was dependent on factors such as the test voltage or [K⁺]_o, experiments were performed where Ba²⁺ was applied for 2 min to closed Kv1.5 channels at −80 mV in 0.5 mM 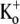(see experimental protocol in Fig. 6 A). After a 4-min wash to remove all Ba²⁺, a 1.5-s step to +50 mV was used to assess the time course of Ba²⁺ unbinding from the open channel. In agreement with findings in other K⁺ channels (17,19,21) and our estimate of k₋₂, Ba²⁺ remained bound to the channels even after the prolonged wash-out period, such that the first pulse elicited current with a much slower rise time than that seen before Ba²⁺ application (Fig. 6 B). The lack of either an initial delay or fast phase, which would be indicative of current moving through channels that were not blocked at the start of the pulse, together with the single exponential time course of the “post-Ba²⁺” current rising phase (τ_act,app = 22.56 ± 1.25 ms; n = 11) suggest that with the loading protocol used, all of the channels were Ba²⁺-bound before the pulse. (With 0 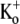there was, in addition to a slow component with τ_act,app = 15.30 ± 0.99 ms, which we take to reflect Ba²⁺ unbinding, a very slow component with τ = 1.08 ± 0.14 s (n = 10; data not shown). Investigation of the slower component of current was beyond the scope of this study, but we do note that confounding results with 0 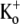solutions and Ba²⁺ have also been reported by others (21).) The first sweep after Ba²⁺ loading showed little or no decay over the course of the pulse, perhaps because of the overlap of inactivation and Ba²⁺ unblocking. From the rising phase of the current, the Ba²⁺ unbinding rate (1/τ_act,app) was calculated to be 45.79 ± 3.08 s⁻¹, although this may be an underestimate if substantial inactivation, and hence Ba²⁺ trapping, occurs during the rising phase. Additional depolarizations (not shown) evoked currents with activation kinetics similar to that of control, with a small (<10%) slow component, perhaps associated with residual Ba²⁺ that did not unbind during the initial 1.5-s pulse. With subsequent pulses, the contribution of the slow component diminished and current amplitude recovered toward control values.

As reported by others (19,21), we found that in Ba²⁺-free medium the dissociation rate of Ba²⁺ depended on both the step potential and [K⁺]_o. Ba²⁺ unbinding was faster at more positive potentials (Fig. 6, C and D), suggestive of outward, voltage-dependent dissociation. Using the Woodhull model (28), the electrical distance (δ_Ba,off) between the deep Ba²⁺ binding site and the rate-limiting barrier for exit was estimated to be 0.51 ± 0.04. This value is similar to those calculated for ShIR (δ_Ba,off = 0.37) and BK_Ca channels (δ_Ba,off = 0.45) (18,19,21). When [K⁺]_o was changed the properties of control currents were unaffected (not shown), which is consistent with previous reports that at pH_o 7.4, Kv1.5 open probability is insensitive to changes in [K⁺]_o (9). After a 2-min loading period with 5 mM Ba²⁺ (in 0.5 mM 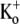) to block all channels (see Fig. 6 B), the cells were washed with solutions of varying [K⁺]_o and test pulses to +50 mV were repeated. As shown in Fig. 6, E and F, Ba²⁺ unbinding was slowed by increasing [K⁺]_o. A fit of the unbinding rates and [K⁺]_o to the Hill equation (see Methods) gave an apparent K_D of 1.00 ± 0.08 mM [K⁺]_o for this effect, with a Hill coefficient of 1.02 ± 0.06. We take this to be the dissociation constant at +50 mV for a K⁺ binding site external to the deep Ba²⁺ ion binding site that needs to be vacant for Ba²⁺ unbinding, and that would be analogous, if not homologous, to the “lock-in” site described in BK and ShIR channels (19–21).

Ba²⁺ does not block Kv1.5 at low pH_o

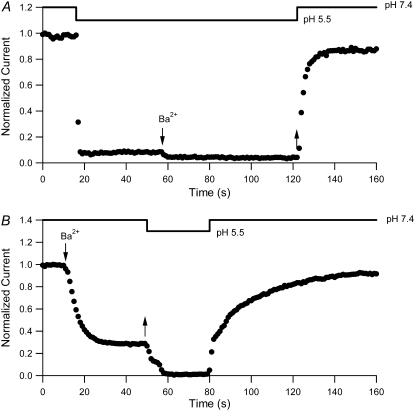
The results presented thus far are consistent with Ba²⁺ binding sequentially to two sites in Kv1.5, with the stable block of the channel resulting from Ba²⁺ occupancy of the deeper, higher-affinity site. Having established that Ba²⁺ can access and bind within the pore of Kv1.5 at rest, we proceeded to examine the hypothesis that extracellular acidification results in outer pore constriction and an altered ability of Ba²⁺ to bind to the pore. Fig. 7 A illustrates the results of experiments monitoring the current amplitude with 10-ms pulses to +50 mV applied at 1 Hz during the fast application of Ba²⁺ at low pH_o. When the pH_o was decreased from pH 7.4 to pH 5.5, current amplitude fell quickly to ∼6% of the control level. The small residual current is consistent with our previous findings that at low pH_o, an equilibrium exists between the available and unavailable states of the channel (5); it also likely includes a small contribution from endogenous K⁺ currents in the HEK293 cell line (3). Subsequent application of 20 mM Ba²⁺ at pH_o 5.5 caused a small additional decrease of the current amplitude. Upon the rapid washout of Ba²⁺ and return to pH_o 7.4, the recovery time course was fast (τ_recov = 4.01 ± 0.85 s; n = 4) and was not significantly different (p > 0.05) from that after pH_o 5.5 treatment alone (τ = 2.60 ± 0.18 s; n = 5; not shown). If lowering pH had no effect on Ba²⁺ accessibility, we would have expected to see ∼70% block of current under these conditions and, thus, a significant slowing of the recovery time course upon the return to pH_o 7.4. These results suggest that lowering pH_o before and during Ba²⁺ application largely prevents Ba²⁺ from accessing its blocking site in most of the channels, allowing them to quickly return to a conducting state after changing back to pH_o 7.4.

FIGURE 7.

Low pH_o inhibits both Ba²⁺ binding and unbinding from Kv1.5. (A) Diary plot of normalized current amplitudes at the end of 10-ms pulses to +50 mV applied at 1 Hz. Experiments were started in 0 mM 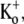pH 7.4 bath solution. Rapid switching to pH 5.5 solution caused a rapid fall of the current amplitude. Subsequent application of 20 mM Ba²⁺ (down arrow), still at pH 5.5, caused a further small decline. The rapid return (up arrow) to Ba²⁺-free, pH_o 7.4 solution resulted in a quick recovery of current amplitude (τ_recov = 3.1 s), which would not be expected had Ba²⁺ accessed the deep pore site. (B) In the converse of the experiment shown in A, 20 mM Ba²⁺ was applied (down arrow) at pH_o 7.4, resulting in 71% block of current, and was followed by a rapid wash-off of Ba²⁺ (up arrow) with pH 5.5 solution that caused an almost complete loss of current. Fast change of the bath solution back to pH 7.4 caused a rapid component of current recovery, followed by a large slow component (64% of total recovery) with a time constant of 23.6 s. These results are consistent with the interpretation that the proportion of Ba²⁺-loaded channels is not affected by high-frequency pulsing when the pH_o is low.

Ba²⁺ unbinding is inhibited at low pH_o

To test whether the lack of Ba²⁺ block at pH_o 5.5 is due to H⁺-induced unbinding of Ba²⁺, which would be indistinguishable from an inability of Ba²⁺ to bind in the experiments shown in Fig. 7 A, experiments were also performed where the pH of the bath solution was decreased after Ba²⁺ loading. Fig. 7 B shows the results from a representative experiment where the current level was allowed to reach a steady state (72 ± 2% block; n = 6) in 20 mM Ba²⁺ with pulses applied at 1 Hz, after which the cell was returned to Ba²⁺-free medium first at pH_o 5.5 and then at pH_o 7.4. Changing to the pH_o 5.5 solution caused a further, and almost complete, reduction in current magnitude. In contrast to the situation where Ba²⁺ was applied after switching to pH_o 5.5, the return to pH_o 7.4 saw current recovery proceed with a fast phase and a slow phase. The amplitude of the fast phase was similar to that of the residual current recorded at the end of the Ba²⁺ loading protocol at pH_o 7.4 (39 ± 4% vs. 28 ± 2% of control amplitude, respectively) and, thus, reflects the relatively rapid recovery of Ba²⁺-free channels from the action of pH 5.5 solution. Had significant Ba²⁺ unbinding occurred at the same rate as at pH 7.4 (Fig. 1 C), then 63% recovery from the Ba²⁺ block would have occurred. In addition, the time constant of the slow recovery phase (τ_slow = 25.59 ± 5.32 s) was not significantly different (p > 0.05) from that observed for current recovery at pH_o 7.4 after Ba²⁺ loading (Fig. 1 C). These results are consistent with an inability of Ba²⁺ to unbind from Kv1.5 at low pH_o. Together with the findings from the previous section, this suggests that the conduction pathway between the deep pore binding site and the external solution is changed sufficiently under acidic conditions to restrict free ingress and egress of Ba²⁺ to and from its binding sites and is supportive of a low-pH_o-mediated constriction of the outer pore of resting channels.

DISCUSSION

Ba²⁺ block at pH 7.4

The first series of experiments presented in this article show that in Kv1.5, at pH_o 7.4, external Ba²⁺ ions cause a high-affinity, slow block of closed channels (Figs. 1, 3, and 4) and a low-affinity, fast block of open channels (Fig. 5). Although the time course of the onset of closed-channel block (τ_block) followed a single exponential, rather than showing distinct fast and slow phases as in ShIR, the dependence of τ_block on [Ba²⁺]_o with 0 mM 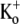was still well described by a sequential two-site binding model (Fig. 1 D) in which the loading of a deep site with an apparent equilibrium dissociation constant (K_Ba,d) in the low micromolar range depends on the occupancy of a superficial site with an apparent dissociation constant (K_Ba,s) of ∼1 mM. Near-saturation of the superficial site with 5–20 mM Ba²⁺ explains why τ_block was not linearly related to [Ba²⁺]_o (Fig. 1 D), as would occur for a simple bimolecular reaction. It is unlikely that the slow Ba²⁺ block and/or lack of an apparent fast block are due to nonspecific effects of charge screening since 1), the block induced by either 1 mM or 20 mM Ba²⁺ is qualitatively similar; and 2), charge screening would be expected to cause a fast change in current amplitude both when Ba²⁺ is applied and when it is removed (see Hurst et al. (20)).

Using three different approaches, a very rough estimate of ∼0.001 s⁻¹ (with a large standard deviation) was obtained for k₋₂, the rate constant for unblocking of the deep site from closed channels at −80 mV with nominally zero 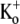(Figs. 1, D and E, and 3). The apparent off rate from the deep site was substantially increased either by raising the frequency of 10-ms test steps to +50 mV (Fig. 1 E), by increasing the test-pulse duration (Fig. 6 B), or by increasing the intensity of depolarizing pulses (Fig. 6 D). Indeed, extrapolation of the open-channel dissociation rate (Fig. 6 D) for Ba²⁺ to −80 mV, assuming δ_Ba,off = 0.51, gives an estimate that is >200 times faster than the measured closed-state off rate at −80 mV (Fig. 1 E). This facilitation of Ba²⁺ unbinding by depolarization, which is consistent with results from studies on K⁺ channels of the squid giant axon (17), BK channels (19) and ShIR (21), is likely due to a combination of several factors: 1), the deep site is in the pore and therefore “senses” part of the electric field so that depolarization decreases the on rate and/or increases the off rate; and 2), channel opening, which for Kv1.5 is maximal at voltages ≥+20 mV (3), may cause a conformational change of the binding site and may also permit a knock-off effect by intracellular K⁺ ions entering the pore.

The Ba²⁺ unbinding rate from open channels at +50 mV was slowed by increasing [K⁺]_o (see Fig. 6, E and F). It is interesting to note that the apparent K_D (1 mM) for the inhibition of Ba²⁺ unbinding by 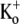is similar to the K_D (1 mM) for the antagonism by 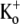of the low pH_o-induced loss of channel availability (3), suggesting that the same K⁺-binding site may be involved in both situations. This site is perhaps homologous to the “lock-in” binding site for the K⁺-dependent inhibition of Ba²⁺ unbinding in ShIR and BK channels (19–21). Indeed, the affinity of the lock-in site for K⁺ in ShIR (K_D = 0.75 mM (21)) is quantitatively similar to what we observed in Kv1.5. It should be noted that we measured the K_D of the lock-in site in Kv1.5 with a Ba²⁺ ion already bound to the deep site, as was done in ShIR. The actual affinity of the lock-in site for K⁺ may therefore be underestimated due to the possible coulombic interaction with a bound Ba²⁺ ion.

Ba²⁺ block of Kv1.5 versus ShIR

The divergence of the K_Ba,d estimates for Kv1.5 and ShIR can probably be accounted for, at least in part, by the test-pulse frequency and duration, but there are other significant differences in the Ba²⁺ block of Kv1.5 and ShIR channels. The fast phase of Ba²⁺ block, which is not seen in Kv1.5, arises because Ba²⁺ (K_Ba,s (0 mV) = 19 mM (20)) causes a rapidly equilibrating (flickery) block of open channels during test pulses used to monitor the development of block. We attribute the absence of a fast phase of Ba²⁺ block in Kv1.5 to the comparatively much weaker open-channel block.

Given the estimate of 1 mM for the K_Ba,s of the superficial site, this weak open channel block is perhaps unexpected. For example, if this binding site is assumed to be outside the electric field, then 20 mM Ba²⁺ would be expected to cause 95% inhibition when applied, as in Fig. 5, to open channels. If it is also assumed, for simplicity, that the superficial site that contributes indirectly to the slow block also accounts for the fast open-channel block, then possible explanations for the weak open-channel block are that the transition to the open conformation changes the site's affinity for Ba²⁺ or that the efflux of K⁺ through the open pore competitively antagonizes the fast Ba²⁺ block. In support of the K⁺ inhibition of Ba²⁺ block, with 3.5 mM 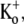only ∼40% of channels were blocked at rest by 1 mM Ba²⁺, compared to ∼90% with 0 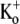(measured using 10-ms pulses to +50 mV at 0.033 Hz; data not shown). The effect of K⁺ is likely to be even greater when the channels are open, since, it has been suggested, even when the bulk [K⁺]_o is zero, outward K⁺ current through ShIR channels leads to an accumulation of K⁺ in the outer pore mouth, resulting in a [K⁺] of ∼15 mM (29).

Although Kv1.5 and Shaker have identical primary sequences from the N-terminus of the pore helix through to the GYGDM sequence of the selectivity filter (Fig. 2), the much weaker open-channel Ba²⁺ block of Kv1.5 points to significant structural differences between Kv1.5 and Shaker. The residue at position 449 in the outer pore mouth, which is threonine in wild-type Shaker, can be an important molecular determinant of Ba²⁺ block in ShIR (30) and it seems reasonable to propose that the presence in Kv1.5 of arginine (R487) at the position homologous to Shaker T449 contributes to their divergent responses to Ba²⁺. It is interesting to note that in Kv1.3, the mutation H399K, which is the positional equivalent of Kv1.5 R487, causes a marked decrease of τ_block (13,14), implying, albeit counterintuitively, that a basic side chain enhances Ba²⁺ loading. In light of the latter observation, the fact that onset of the slow block in Kv1.5 (τ_block ≈ 6 s at −80 mV with 0 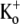and 20 mM Ba²⁺; Fig. 1 D) is more than an order of magnitude faster than in ShIR (τ_block ≈ 100 s at −90 mV with 2 mM 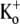and 20 mM Ba²⁺ (Fig. 9 of Hurst et al. (20)) might also be due to the arginine at position 487.

Low pH_o prevents movement of Ba²⁺ to and from its deep binding site

In support of an inactivation-mediated constriction of the outer pore, the movement of Ba²⁺ from its deep pore binding site to the bulk solution is significantly slowed in P/C-type inactivated ShIR channels, to the extent that Ba²⁺ is effectively trapped within the pore of P/C-type inactivated ShIR (21,27). We have shown here that with external acidification, external Ba²⁺ cannot access the deep pore binding site at rest (Fig. 7 A), nor can Ba²⁺ that is already bound at the deep site in the pore leave that binding site (Fig. 7 B). These results are therefore consistent with the hypothesis that an outer pore constriction, perhaps similar to that proposed to underlie P/C-type inactivation, also underlies the 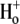-mediated decrease in Ba²⁺ access to, or egress from, the pore.

Is the H⁺-induced pore constriction indicative of closed-state P/C-type inactivation?

It remains an open question whether the proposed constriction of the outer pore of a closed Kv1.5 channel under resting, acidic conditions is the same conformation the channel enters during P/C-type inactivation, which is typically thought to be strongly coupled to channel activation. Unfortunately, we were unable to assess the Ba²⁺ block of P/C-type inactivated channels at pH_o 7.4, because the inactivation is slow and incomplete, even with long depolarizing pulses (3). Although the molecular mechanism for the low-pH_o-induced block of Kv1.5 is still unclear, we (3) and others (8,9) have proposed that the H463 residue in the outer turret acts as the putative pH_o sensor, since both the decrease in channel availability and enhanced depolarization-induced inactivation are substantially diminished in Kv1.5 H463Q. The ability of the noninactivating Kv1.5 R487V mutant, which is analogous to Shaker T449V, to mitigate the effects of low pH_o block are suggestive of an inactivation mechanism involving this residue, but the nature of the coupling mechanism between protonation of H463 and channel inactivation is unknown at this time.

Acidosis of cardiac muscle is a common outcome of a number of pathological conditions, such as myocardial ischemia, and can induce arrhythmias (31). Although the extent of extracellular acidification in native cardiac tissue is seldom likely to be as low as pH_o 5.5, the pK_a of the 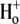-block of Kv1.5 in 5 mM 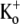is ∼6.2 (3,5), such that even small decreases in pH_o can result in a decrease in channel availability and faster macroscopic inactivation. Thus, pathological cardiac acidosis may be associated with reduced availability of Kv1.5 channels due to closed-state inactivation, which, coupled with faster inactivation of the remaining channels and a right shift of the activation curve (32), results in reduced I_Kur.