Rate Constant and Reaction Coordinate of Trp-Cage Folding in Explicit Water

Abstract

We report rate constant calculations and a reaction coordinate analysis of the rate-limiting folding and unfolding process of the Trp-cage mini-protein in explicit solvent using transition interface sampling. Previous transition path sampling simulations revealed that in this (un)folding process the protein maintains its compact configuration, while a (de)increase of secondary structure is observed. The calculated folding rate agrees reasonably with experiment, while the unfolding rate is 10 times higher. We discuss possible origins for this mismatch. We recomputed the rates with the forward flux sampling method, and found a discrepancy of four orders of magnitude, probably caused by the method's higher sensitivity to the choice of order parameter with respect to transition interface sampling. Finally, we used the previously computed transition path-sampling ensemble to screen combinations of many order parameters for the best model of the reaction coordinate by employing likelihood maximization. We found that a combination of the root mean-square deviation of the helix and of the entire protein was, of the set of tried order parameters, the one that best describes the reaction coordination.

INTRODUCTION

Neidigh et al. (1) designed the Trp-cage mini-protein (NLYIQ WLKDG GPSSG RPPPS) to be a fast two-state folder, with a native state that has both secondary and tertiary structures. The native structure of the 20-residue polypeptide contains an α-helix (residues 2–8), a 3₁₀-helix (residues 11–14), and a polyproline II helix (residues 17–19) (see Fig. 1). The three helices form a hydrophobic cavity in which Trp-6 is buried. This hydrophobic core is further stabilized by a salt bridge (between residues 9 and 16). Laser temperature-jump spectroscopy experiments by Qiu et al. (2) indicated that the mini-protein folds in a two-state manner from an unfolded to a native state, with a folding rate k ≈ (4.1 μs)⁻¹. Using fluorescent correlation spectroscopy, Neuweiler et al. (3) reexamined the two-state folding mechanism hypothesis. Their experiments showed that the protein (un)folds in a more complicated manner via an intermediate molten globulelike state, characterized by exposure of the tryptophan to the solvent. It remains unclear at what stage of folding the helix is being formed. The correlation between tryptophan fluorescence and circular dichroism melting data was proposed as evidence of simultaneous breaking of the hydrophobic core and helix solvation during (un)folding (2). UV-resonance Raman spectroscopy measurements show some evidence of a helical structure in the denaturated state of Trp-cage and thus suggest an early formation of the helix is possible (4). The helix-melting curve is also broader than usual; the α-helix is stable until 30°C and melts between 40 and 70°C (4). Recent experiments by Streicher and Makhatadze (5) suggest a slightly more stable native state of Trp-cage compared to the data of Qiu et al. (2).

FIGURE 1.

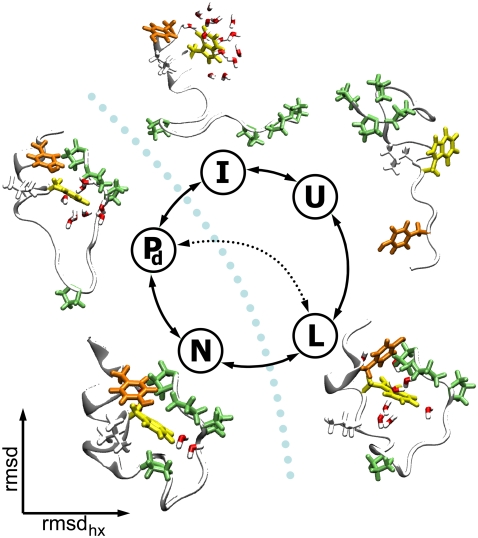
(Un)folding routes of Trp-cage mini-protein. The backbone of the configurations is plotted in white, in cartoon representation. Hydrophobic side chains forming the tryptophan pocket are plotted in licorice: tryptophan side chain in yellow, proline amino acids in green, tyrosine in orange, and lysine in white. Water molecules within 3 Å of the side chain of Trp-6 are plotted in licorice, with oxygen atoms in red and hydrogen in white. Two major routes between the native state (N) to the unfolded state (U) are possible from Juraszek and Bolhuis (18): one passing through state L, the other one through state I. The rate-limiting barrier is schematically represented by the light blue dotted line. The close-to-native intermediate state P_d is still in the basin of attraction of the native state, allowing for a mixed-mechanism pathway N – P_d – L, indicated by the black dotted line.

Being a small and fast folder, the Trp-cage protein can be studied by all-atom force-field molecular dynamics simulation. In the past six years, the Trp-cage has therefore become a model system that can bridge the gap between folding experiments and simulation. Folding events of Trp-cage have been observed in all-atom implicit solvent MD simulations (6–8), for an all-atom Gō model (9), and for a coarse-grained model (10). Work by Rhee et al. suggests that the solvent does play a crucial role in protein folding, one that current implicit solvent models are not able to capture (11). However, even for fast folders like Trp-cage a computational study of the kinetics of folding in explicit solvent using all-atom force fields still presents a challenge. A straightforward MD run could give all kinetic and thermodynamic folding information, but as the microsecond folding process is a rare event on the fundamental timescale of the MD, this approach would be still beyond the capability of current computing power. These long (microsecond and longer) timescales in protein folding are caused by a rough free-energy landscape with high folding barriers. Employing distributed computing, Snow et al. directly access the kinetics by initiating many simultaneous simulations, of which a small percentage succeeds in crossing the barrier (7).

A more efficient way to overcome the high free energy barriers is by increasing the temperature, as is done in high temperature MD (12), temperature-accelerated dynamics (13), and replica-exchange MD (REMD) (14). Zhou performed REMD simulations of Trp-cage in explicit solvent (15) and confirmed the two-state nature of the folding. Zhou also proposed an intermediate (I) state structure, containing two hydrophobic cores, because of Trp-cage being such a fast folder. More recently, Paschek et al. (16) observed folding events in an explicit solvent REMD simulation using the AMBER force field. In previous work (18) we concluded that our REMD simulations of Trp-cage in explicit water using the OPLSAA force field did not converge well and in fact did not show folding at all (in the available simulation time). In addition, REMD does not directly yield accurate information about the rare event at room temperature, because transitions only occur at high temperatures.

Other rare event methods therefore employ biasing potentials to enhance conformational sampling at room temperature (e.g., umbrella sampling (17), metadynamics (19), hyperdynamics (20), and flooding (21)). Piana and Laio successfully applied metadynamics to the Trp-cage system (22). Such biasing methods enable the computation of thermodynamic properties, but cannot be used to obtain accurate kinetics and mechanisms in complex systems, as they do not preserve the dynamics. Moreover, applying the biasing potential as a function of an order parameter requires a priori knowledge of the important reaction coordinate. A wrong choice of reaction coordinate in these methods leads to poor statistics, a wrong mechanism, and overestimation of the rate constants. To address this so-called reaction coordinate problem, Dellago et al. (23,25) and Bolhuis et al. (24) developed the transition path sampling (TPS) methods (23–25), a suite of techniques that enable the collection of an ensemble of transition paths (the path ensemble) between an initial and final state, without prior knowledge of the reaction coordinates. Applied to protein folding, the TPS algorithm samples trajectories of several nanoseconds long, connecting the native and unfolded states of the protein at room temperature. A straightforward molecular dynamics achieving a similar connecting trajectory would take many microseconds. In addition, analysis of the path ensemble yields the mechanism, transition state ensemble, and the rate constant. The TPS rate constant evaluation is rather computationally intensive. The transition interface sampling (TIS) method is a more efficient implementation of path sampling to evaluate the rate (26). Recently, Allen et al. proposed the forward flux method as an efficient alternative for TIS (27). While originally developed for nonequilibrium dynamics, for which there is no microscopic reversibility, the method is also valid for equilibrium dynamics (see, for instance, (28)).

In previous work (18), we studied the rate-limiting folding process with TPS and found that the protein follows two major (un)folding routes, resembling two generic protein-folding mechanisms: nucleation-condensation (NC) and diffusion-collision (DC). In Fig. 1, we show a summary of these results. Along one route (U – I – P_d – N), the polypeptide first forms the main secondary structure—the α-helix, followed by the appearance of the tertiary contacts (DC). On the second pathway (U – L – N) the tertiary contacts precede the formation of the secondary structure elements (NC). Two different folding routes, the predominant one in agreement with intermediate (I) found by Zhou, have also been predicted by an all-atom Gō model (9). In contrast to these predictions we find that 20% of the paths first form the helix, whereas 80% first form the tertiary contacts. The fact that there are two pathways suggests that the secondary structure (the helix) is by itself only marginally stable, and has to be stabilized by tertiary interaction. Because the helix is rather small, this is not unlikely. The prediction of the preference of the U – L – N route could also be an artifact of the force field.

In this article, we employ TIS (26) to calculate the rate constants for the folding and unfolding of the Trp-cage in explicit solvent. Because the TIS method can only tackle one barrier at the time, we choose the most likely of the two possible folding routes, the U – L – N pathway (see Fig. 1) because this route will contribute mostly to the rate. On this pathway, the protein first forms its native state tertiary contacts, while the secondary structure is still solvated. We compare the TIS calculations with forward flux sampling (FFS) simulation results.

The reaction coordinate of a process is an important ingredient for understanding this process. The lack of knowledge of the reaction coordinate is the reason why TPS was developed in the first place. As stated above, analysis of the path ensemble can reveal the reaction coordinate. Extracting a reaction coordinate is difficult, and in the past, a prospect candidate for reaction coordinate had to be tested by committor analysis (29). The committor is the probability of a structure to relax into the initial or final state (in the protein community, this is known as the p-fold). The committor is the ideal reaction coordinate as it smoothly changes from zero in the initial state, to 0.5 for the transition state ensemble, and to unity for the final state. However, the committor does not give physical insight in the mechanisms. Instead, we seek a reaction coordinate that predicts the committor. A prospect reaction coordinate can be tested for this property by computing the committor probability distribution for a constrained ensemble of configurations at a certain value of this reaction coordinate candidate (29). This is an extremely costly procedure, and might require many iterative cycles of proposing and testing a reaction coordinate. Ma and Dinner devised a genetic neural network approach to automate this analysis (30). However, prospect reaction coordinates can also be screened, based on information from just the TPS path ensemble itself. Peters and Trout (31) and Peters et al. (32) recently introduced a likelihood maximization (LM) method that only takes data from the TPS ensemble as in input, thus reducing the computational effort analysis of the reaction coordinate dramatically. In this article, we use this method to obtain the reaction coordinate for the Trp-cage.

The article is organized as follows. After the description of the path sampling and the LM method, we describe the results of the TIS rate constant calculation and the comparison between TIS and the FFS results. Subsequently, we discuss the reaction coordinate analysis. We end with concluding remarks.

METHODS

System preparation

The 304-atoms protein NMR structure (PDB entry 1L2Y) was solvated in 2797 SPC water molecules in a rhombic dodecahedral box of the diameter of 50 Å. All MD simulations were done with the GROMACS molecular simulation package (33), together with OPLSAA FF (34) and the SPC water model (33). After energy minimization and a protein position restraint run of 100 ps, the system underwent equilibration at ambient conditions of 1 bar and 300 K for 10 ns. These equilibration runs were performed using a Nosé-Hoover thermostat and the Berendsen box scaling method for the pressure coupling. Subsequently the box size was changed to 50.4 Å, corresponding to ambient pressure. All of the MD simulations in this article were performed at this constant volume, with a time-step of 2 fs. Furthermore, dodecahedral periodic boundary conditions were applied; long-range electrostatic interaction were treated by fast particle-mesh Ewald (35,36) with a grid spacing of 1.2 Å, and the Nosé-Hoover thermostat (37,38) ensured a constant temperature.

Molecular dynamics with a stochastic thermostat

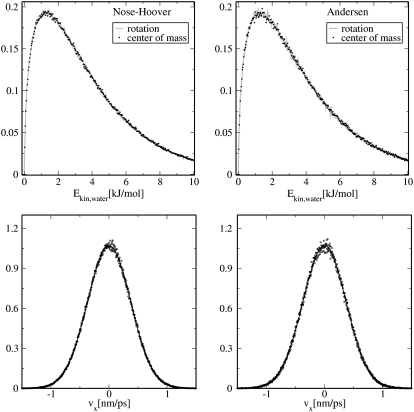
All of our TPS and TIS simulations were performed using molecular dynamics with a simplified version of Andersen temperature coupling, applied only to the center-of-mass motion of water molecules. We employ a very weak coupling, so that the dynamical properties of the system do not diverge significantly from their deterministic counterparts (1). We choose the coupling constant in such a way that the diffusion of water molecules is the same as in a simulation using a Nosé-Hoover thermostat. For the box size we use, this coupling frequency turns out to be slightly less than one water molecule per MD step. We tested this procedure on an SPC water system, to check whether the system couples correctly to the desired temperature and the velocity distribution is preserved compared to the Nosé-Hoover MD. These test simulations were carried out on a system of 2797 SPC water molecules in a rhombic dodecahedral box, using the same settings as described in System Preparation. Fig. 2 shows that this procedure yields velocity distributions identical to the ones obtained using Nosé-Hoover MD and that the equipartition of energy is fulfilled. The velocity of the center-of-mass of water molecules are Maxwell-Boltzmann distributed for both the Nosé-Hoover thermostat and our version of the Andersen thermostat. Equipartition of energy is fulfilled, meaning that the kinetic energy is equally distributed between rotation of water molecules and the motion of their center of mass. Both kinetic energy contributions are depicted in Fig. 2 and are identical for both simulations.

FIGURE 2.

A comparison between the simulations using our version of Andersen thermostat (right panels) and a Nosé-Hoover (left panels) MD shows that the rotational and center-of-mass velocities (bottom) and kinetic energies (top) of water molecules are correctly distributed.

After insertion of the protein, we observed that the system temperature rose ∼2° above the imposed temperature. This phenomenon is caused by a small energy drift related to the temperature-uncoupled polypeptide. Many factors could cause the uncoupled system to overheat but the single precision MD of GROMACS is probably the most significant one. Although a difference of 2° does not have a significant impact on the (un)folding rate we compensate for the mild overheating of the protein by decreasing the imposed temperature of water by ∼4° to 296 K. We could have increased the Andersen coupling constant to remove heat faster from the water shell surrounding the protein, but this in return would slow down the water diffusion with respect to the Nosé-Hoover MD reference.

While Trp-cage is considered one of the fastest folding polypeptides forming secondary and tertiary structure elements, the free-energy barrier separating unfolded from the folded state is still too high to observe a folding event in a regular MD simulation in explicit solvent. The experimental folding time is τ_fol = 4.1 μs (2), and one would have to run on average 4.1 μs MD to observe one folding event. We know from our previous work that transition paths crossing the rate-limiting barrier are, on average, τ_trans = 3 ns long—three orders-of-magnitude shorter than the folding time. Hence, the probability to find the protein on a transition path is ∼7 × 10⁻⁴, and it would be a waste of computational effort to examine the folding rare events with a straightforward MD. Moreover, 4.1 μs is still far beyond today's computational limits (on a single node this would take more than two years). Therefore, we use TPS to sample transition pathways effectively.

Path sampling

Transition path sampling

Transition path sampling (TPS) (23–25) comprises a set of techniques designed for sampling the ensemble of transition paths that connect two stable states, the initial state A and the final state B, without prior knowledge of either the transition states or the reaction coordinate of the process. TPS performs an importance sampling of trajectory space by generating new trial paths, and accepting or rejecting those paths according to their weight in the path ensemble by applying a Metropolis Monte Carlo criterion based on the detailed balance condition. The transition path sampling method generates trial paths by the shooting algorithm (25), which alters a randomly chosen time-slice (the shooting point) on an existing path randomly and integrates the equations of motion both forward and backward in time. In the basic fixed path-length implementation of TPS, the Monte Carlo criterion consists of checking whether the new trial path connects the states A and B. If so, the trial is part of the path ensemble, and can be accepted as the current path, otherwise it is rejected. The more efficient flexible path length TPS algorithm stops the generation of a path as soon as it enters one of the stable states (18,26). To maintain detailed balance, the acceptance criterion then depends on the path-length ratio of the old and the new paths.

The deterministic shooting algorithm runs into problems for long diffusive folding trajectories (long compared to the time-step, i.e., longer than a few picoseconds). While a random shooting point might seem to lie in the barrier region (i.e., outside of the stable state definitions), it can in fact already be completely committed to one of the stable states. In that case, the acceptance ratio will be extremely low. Only when shooting from points around the true transition-state region can we expect a reasonable acceptance. To alleviate this problem we employ the stochastic shooting algorithm (39) allowing shooting in one direction, either forward or backward. Application of deterministic MD to generate stochastic trajectories requires the introduction of a small amount of stochasticity in the trajectories, for instance by the Andersen thermostat. As mentioned above, the Andersen coupling constant can be made small enough so that there is no noticeable difference from completely deterministic dynamics (1). (The details of the algorithm can be found in (18).)

The advantage of stochastic sampling is an improved acceptance ratio of ∼50%. However, on the other hand, we have to wait several successful shots before an entirely new pathway is generated, because a single successful shooting replaces only one part of the trajectory. In the case of Trp-cage in explicit solvent, the method was two orders-of-magnitude more efficient than regular MD (18), based on the uncorrelated transition pathways.

We note that the TPS simulation require an initial pathway to bootstrap the sampling. While there are many ways to create such an initial pathway (see, e.g., (40)), we rely on a high temperature unfolding pathway.

Transition interface sampling

The TIS algorithm, contrived for the calculation of rate constants (26), adopts the TPS shooting algorithm for sampling the transition path ensemble. Similar to TPS, the method does not strongly depend on the choice of an order parameter, and thus can be applied to complex systems in which the reaction coordinate is not a priori known. The major requirement is that an order parameter λ can distinguish between the initial state A and the final state B. The next step is to divide the configuration space of the system in a number of subspaces by introducing n_I + 2 interfaces λ = λ_i, where i = 0, …, n_I + 1, chosen such that 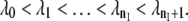The first interface λ₀ ≡ λ_A is identified with the boundary of stable state A, whereas the last interface 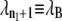is the boundary of state B. The calculation of the rate constant is then reduced to the subsequent calculation of the conditional crossing probabilities P_A(λ_i+1|λ_i) that a trajectory, starting in state A and passing through interface λ_i, will also cross interface λ_i+1 before returning to A. Multiplying these crossing probabilities together with the effective positive flux through the first interface 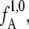as defined in van Erp et al. (26), yields the rate constant k_AB:

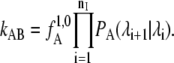(1)

The flux factor 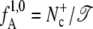in Eq. 1 can be calculated by performing an MD simulation of time 𝒯 in the initial state A and counting the number 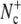of effective positive crossing events of the first interface λ₁. The conditional probabilities P_A(λ_i+1|λ_i) can be determined by performing a TIS simulation (26).

The biased stochastic TIS shooting algorithm

We employ the stochastic version of the shooting algorithm, in which we modify neither positions nor momenta of the shooting point (39). The stochasticity introduced by the mild Andersen coupling will cause the trajectory to diverge from the initial one, taking care of the constant temperature at the same time. To increase the efficiency of sampling we introduce a bias causing the shooting points to be drawn around the interface, with a Gaussian distribution, to assure that nearly every trajectory will cross the interface. This bias is introduced by assigning to each time-slice τ a nonuniform weight w(τ) that depends on the values of the order parameter λ(τ) and λ_i. The probability of selecting a given time-slice as a shooting point can be written as

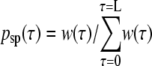(2)

and becomes 1/L, in the case no bias is introduced, with L denoting the number of time-slices in the path. In our version of the TIS algorithm, p_sp(τ) equals to

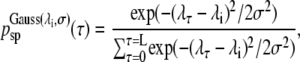(3)

where σ is of the order of the picosecond fluctuations in the parameter λ around interface λ_i.

Instead of using a fixed path length, we rely on a flexible path length definition (26). From an existing path o with L^(o) time-slices, we choose a random time-slice τ as our shooting point. We randomly choose either the forward or backward direction for shooting and reverse the momenta for a backward shot. We then integrate the equations of motion using Andersen-coupled MD until after a time τ_f we reach either region A or B. A trial path is constructed in which the newly shot trajectory replaces a part of the old path starting at τ. In the case of the backward shot, all momenta are reversed again. The new trial path n has a path length L⁽ⁿ⁾ = τ + τ_f in the case of forward trial shot, and L⁽ⁿ⁾ = (L^(o) – τ) + τ_f in the case of a backward shot. If the trial path does not start in A or does not cross λ_i, it is rejected straightaway. Otherwise, to obey detailed balance, it may be accepted with the Metropolis acceptance ratio

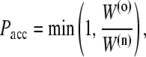(4)

where the min function returns the smaller of its arguments and 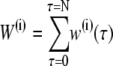is a sum of all weights w(τ) of trajectory i (a path weight). To avoid having to reject paths that do connect A and λ_i but are too long, in practice we choose a random number ξ = (0, 1) and determine the maximum path weight W_max = W^(o)/ξ in advance. The MD integration can then be halted if the total trial path weight exceeds W_max. As the shooting point bias enhances the acceptance ratio we also perform simultaneous shots in the forward and backward time directions. We set the percentage of these two-way shots to 20%.

Note that our implementation of TIS differs from the original TIS implementation (26) in the use of the stochastic algorithm. We believe that our implementation here is an efficient path-sampling algorithm for diffusive processes.

In summary, our stochastic TIS algorithm consists of the following steps:

1. With a probability 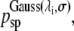given by Eq. 3, select a random time-slice τ_sp on the current trajectory o to act as the shooting point for the new trajectory n.

2. Draw a random number ξ ∈ (0, 1) and calculate the maximum allowed sum of weights 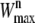for the new path from 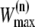= W^(o)/ξ.

3. Draw a random number p_1way ∈ (0, 1). If p_1way ≤ 0.8, decide to shoot either forward or backward with the same probability. In the case of a backward shot, reverse the momenta of the shooting point τ_sp. Initiate a single MD simulation. Note that for the Leap Frog algorithm, reversal of the momenta consists of integrating the system half time-step to obtain 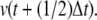The reversed time-slice is of the form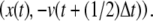

4. If p_1way > 0.8, initiate two molecular dynamics simulations: forward from unchanged time-slice τ_sp and backward from τ_sp with reversed momenta.

5. Continue the MD simulation(s), with Andersen temperature coupling as defined in Methods, until the sum of weights of the resulting trajectory (after gluing with a part of the old trajectory o in the case of one-way shooting, or gluing backward and forward trajectories in the case of the two-way shooting) exceeds 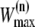or one of the two stable states is reached.

6. In the case where the resulting trial trajectory is not of the form A → λ_i → A or A → λ_i → B, reject it. Otherwise, the trajectory is accepted and trajectory n becomes the current trajectory.

7. Update path averages and restart the procedure at point 1.

Forward flux sampling

Forward flux sampling (FFS) (27) is a method that allows the sampling of stochastic dynamical pathways connecting two stable states separated by a free-energy barrier and calculates the rate constant for the transition. While initially derived for nonequilibrium dynamics, FFS can also be used for equilibrium transitions (28). Similar to TIS, FFS divides the phase space with nonoverlapping interfaces defined by a parameter λ. As in Transition Interface Sampling, λ does not have to be a reaction coordinate; nonetheless, it should be able to distinguish between the initial and final states A and B. The interfaces are such that 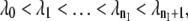and if λ < λ₀ = λ_A, this means the system is in state A; and if 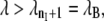the system is in state B. The rate constant k_AB for the transition from A to B is given by Eq. 1. The flux factor calculation has already been explained in Transition Interface Sampling and consists of counting the positive effective crossings of the interface λ_A per time in an MD simulation under ambient conditions. The difference between the TIS and FFS framework lies in the calculation of the crossing probabilities. First, one collects the set of time-slices associated with the positive recrossings of interface λ₁. Time-slices are randomly picked and used as shooting points for MD simulations without modifying the initial conditions. The trajectories resulting from a single point are different because of the use of stochastic dynamics. The MD integration can be stopped after having reached either the initial state A or the next interface λ₂. The estimator of the crossing probability is P(λ₂|λ₁) ≈ N₂/N, where N₂ equals the number of trajectories reaching the next interface and N is the total number of trajectories shot from the interface λ₁. This procedure is iteratively executed for the subsequent interfaces, until λ_B (state B) is reached. The total crossing probability P(λ_B|λ₁) is calculated by multiplying all the intermediate crossing probabilities according to the Eq. 1. The transition path ensemble can be obtained by gluing all the pathways starting from those that reached the last interface. The resulting glued trajectories are true dynamical trajectories, as the shooting points were not modified.

Reaction coordinate analysis

An order parameter can be considered a good reaction coordinate if it describes the progress of a reaction. As stated in the Introduction, the best reaction coordinate one could imagine is undoubtedly the committor. Calculating the committor of a structure consists of shooting a number of trial trajectories from that particular configuration each time with randomly reinitialized momenta (25). This procedure, known as p-fold analysis for proteins (41), is computationally expensive. Moreover, while the computation of committors along transition paths yields the transition-states ensemble, the committor itself is an abstract coordinate that fails to give insight into the reaction mechanism. Instead, we seek a physically relevant order parameter that would predict the committor well, but would still be a straightforward function of the configuration.

Committor analysis can test candidate reaction coordinates by computing the probability distribution of committor values for an ensemble of configurations constrained to a certain value of the prospect reaction coordinate (29). A committor distribution that is sharply peaked for a given value of an reaction coordinate is the signature of a good reaction coordinate having a good correlation with the committor. Needless to say, such analysis is event more expensive than the committor computation.

Peters and Trout (31) and Peters et al. (32) have recently formulated an approach that screens candidate reaction coordinates for the one that best predicts the committor, based on information from a TPS ensemble alone. In this algorithm, known as likelihood maximization (LM), a number of linear combinations of all available order parameters are tested for the best correlation with the committor function. For an existing TPS ensemble, the method yields insight into the reaction coordinate and allows us to approximate the transition states at no significant additional computational expense. As the crucial input for the LM algorithm, one can extract from the path ensemble the set of forward shooting points, together with the information whether they relax to state A or state B. In a sense, each of the TPS shooting trajectories can be regarded as an instance of a committor computation.

Peters and Trout (31) and Peters et al. (32) assume a sigmoidal shape of the committor p_B(x) as a function of a trial reaction coordinate r:

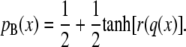(5)

The trial reaction coordinate r(q) is estimated as a linear combination of n order parameters q_i,

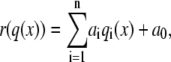(6)

where a_i values are the model's fitting parameters, to be optimized by the LM method. The likelihood function L(a) gives the probability to observe the measured data, as a function of the model parameters a,

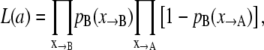(7)

where the products run over, respectively, the accepted and rejected shooting points obtained by TPS. X_→B denotes the set of forward shooting points ending up in B, and X_→A the ones that end up in A. Maximizing (the logarithm of) the function L(a) with respect to the parameters a, results in the reaction coordinate that best describes the observed data, given the model, Eq. 5.

We analyze the TPS shooting points using the LM method according to the following procedure. For each configuration x we compute all the parameters defined in Order Parameters (see below). We then construct linear combinations of n of these order parameters, and maximize the likelihood in Eq. 7 using the Broyden-Fletcher-Goldfarb-Shanno method (42). The linear combination of order parameters with the highest likelihood, as given by the coefficients a, corresponds to the best collective variable. We repeat this analysis by incrementing the number of order parameter n by one, until there is no further significant improvement in the maximum likelihood (32).

Order parameters

All TPS-based algorithms, including TIS, rely on the proper definition of the stable states. The order parameters used in these definitions should not only distinguish between the stable states but also be representative for these states (25,43,44). We obtain the set of state-defining order parameters from straightforward MD and REMD simulations (18). For Trp-cage, in all of the simulations, we monitor the following order parameters: the protein radius of gyration using the α-carbons only (rg); the fraction of native contacts (ρ); the root mean-square deviation from the native α-carbons structure (rmsd); the root mean-square deviation of the α-helical residues 2–8 from an ideal helix (rmsd_hx); RMSD of the hydrophobic core, i.e., the tryptophan and the prolines 12 and 17–19 (rmsd_core); the solvent-accessible surface (sas) of the whole protein; the distance (sb) between donors and acceptors in the hydrogen bonds of the salt-bridge between Arg-16 and Asp-9; and the number of water molecules around tryptophan (nw_trp). We use these order parameters to construct free-energy diagrams, extract stable state definitions, and for the reaction coordinate analysis.

RESULTS AND DISCUSSION

Transition path sampling

The TPS results have been discussed extensively in Juraszek and Bolhuis (18). We summarized these findings in Fig. 1. Specifically, by sampling pathways between the native state and unfolded states we found that Trp-cage can fold via two routes: Along one route (U – I – P_d – N), the polypeptide first forms the main secondary structure—the α-helix, followed by the appearance of the tertiary contacts. On the other pathway (U – L – N), the tertiary contacts in the loop state L precede the formation of the secondary structure elements.

The route via L occurs four times more in the path ensemble than the route along intermediate I. Because all trajectories start in N, this means that the unfolding reactive flux and hence the rate through the N – L route is four times higher than the flux via the N – I route. This translates roughly to a difference of ΔG = −k_BT ln(k_N–L/k_N–I) ≈ −1.3 k_BT in the unfolding barrier height of the two routes. At this point we cannot say much about the folding rates and barrier, because of the unknown relative stability of the intermediate states. However, TPS was able to switch between the major routes several times, indicating that the path ensemble has equilibrated. Hence, as the TPS represents true unbiased pathways (within the accuracy of the force field), we concluded that the unfolding rate is mainly (for 80%) determined by the N – L route. For a thorough discussion on the path ensemble results, we refer to Juraszek and Bolhuis (18). In the current work we use the TPS result primarily as input for the TIS rate calculation and for the reaction coordinate analysis (see Analysis of Reaction Coordinates). As we can tackle only one barrier at a time with TIS, we have chosen the most likely one of the two possible (un)folding pathways of Trp-cage, namely the N – L route (Fig. 1). On this route the protein unfolds the helix and water solvates the core while the overall U-shape, tertiary contacts, and small size are preserved. As mentioned above, this choice is justified by the fact the TPS results indicated that most of the contribution to the unfolding rate comes from this transition. The TPS ensemble revealed also that there are no additional intermediates on the N – L route.

The TPS ensemble for the N – L transition is plotted as density maps (seen later in Fig. 4, a and d). These maps are prepared as follows. We discretize the given order parameters according to a desired resolution. At the beginning, all bins are assigned with a zero value. For each pathway in the ensemble we check what bins are visited, and increased the value in these visited bins by the weight of the pathway. We scale the resulting two-dimensional histograms, dividing by the maximum. These density maps are a summary of the entire path ensemble as a function of the order parameters. Here, we primarily use these density maps to compare the TPS, TIS, and FFS ensembles, and to test the reaction coordinate analysis. We come back to this comparison in Comparing FFS and TIS/TPS and in Analysis of Reaction Coordinates sections.

FIGURE 4.

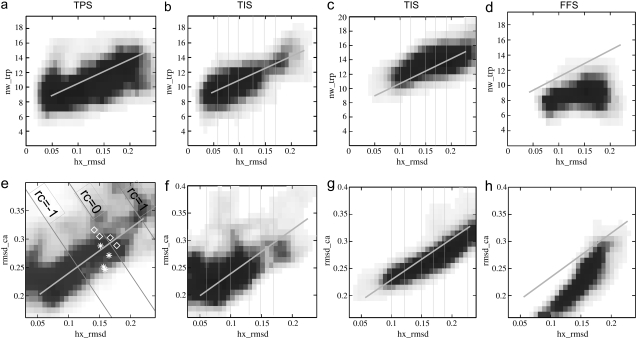
TPS ensemble of the N – L transition (a and e) versus the TIS ensembles of the N – L (b and f) and L – N (c and g) routes for their extreme interfaces and FFS transition path ensemble (d and h), respectively, in two representations: rmsd_hx[nm] – nw_trp (a–d) and rmsd_hx [nm] – rmsd_ca [nm] (e–h). Color scheme: red indicates that at least 70% of pathways visited through the bin; white indicates that no pathways passed that bin. Interfaces have been demarked with vertical lines for the TIS ensembles. The black thick solid line in the middle of the plots connects the native state, characterized by rmsd_hx = 0.05nm, nw_trp ≈ 9 and rmsd_ca = 0.19 nm with the L state, which has an unfolded helix (rmsd_hx = 0.23 nm), more waters within the cutoff distance of the Trp-6 (nw_trp ≈ 15), and rmsd_ca ≈ 0.35 nm. In the TPS ensemble plot (e), thin gray solid lines along rc_NL = const indicate the reaction coordinate found by the LM analysis. In the same plot, the stars show the location of the p_B = 0.5 TSE structures from Juraszek and Bolhuis (18), whereas the diamonds denote the transition state structures predicted by the LM analysis.

TIS rate constant calculation of the N – L transition

We have performed two sets of TIS simulations, one for the (N – L) unfolding (TIS-unf simulation) and another one for the folding (L – N) transition (TIS-fol simulation). The order parameter we chose to describe the interfaces was the helix RMSD: λ ≡ rmsd_hx. This order parameter sufficiently distinguishes the two states.

During the TIS simulation we encountered several problems related to the following observations:

1. There are two distinct pathways for the (un)folding process (N – L and N – I), and when we start the TIS simulation for an interface close to the initial state, there exists a nonnegligible probability that the system will choose the other pathway, which we want to exclude.

2. Parameter λ = rmsd_hx does not distinguish between the native state and the other intermediate state I. This problem is especially prevalent in the folding TIS simulation, as a trajectory started in state L may easily end up in state I.

3. There is a close-to-native metastable state (P_d), which is on-pathway for the N – I, but not for the N – L transition. For the interfaces λ < 1 Å the system is sometimes attracted to this metastable state P_d, rather than to the native state N.

We tried to circumvent the above-mentioned problems by carefully monitoring our TIS simulations. In the case where a TIS run was switching to sample a different free-energy barrier, we rejected it and restarted at the previous step. We also use TPS trajectories connecting both N and L states as an input for each of the interfaces, to ensure the sampling on the correct barrier.

The flux factors 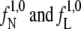(Eq. 1) were calculated based on 10-ns-long MD simulations in the native state (N) and in the loop state (L), respectively. To initiate the loop-state flux calculation, we picked 10 structures randomly from the endpoints of the TIS-unf trajectories. When we calculate the flux, we count only the crossings on the way from the stable state through the given interface: the effective positive flux (26). After each recrossing event we check whether the trajectory relaxes back to the stable state (crosses through λ₀), before a new crossing event can be counted. The procedure yielded an unfolding flux 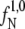= 6.7 [ns⁻¹] through the interface λ₁ = 0.06 [nm] for the native state and a folding flux 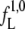= 1.0 [ns⁻¹] through the interface λ₁ = 0.23 [nm] for the loop state.

For the calculation of the unfolding crossing probability P(λ_L|λ_N) we defined the following interfaces: λ_i = rmsd_hx = 0.06, 0.08, 0.10, 0.13, 0.15, and 0.17. For the folding transition crossing probability P(λ_N|λ_L), we chose λ_i = rmsd_hx = 0, 23, 0.19, 0.17, 0.15, 0.12, and 0.10. For each of the above interfaces we performed a TIS simulation, resulting in an ensemble of trajectories of the form N → λ_i → N or N → λ_i → L for the unfolding process and L → λ_i → L or L → λ_i → N for the folding. The statistics of all ensembles are presented in Table 1. The TIS ensemble density maps are also plotted later in Fig. 4, b, c, f, and g. Although they overlap with the TPS ensemble, which connects both L and N states, the interfaces farthest from the respective initial states (λ = 0.17 for N – L and λ = 0.10 for L – N) do not precisely coincide with the transition state region (rmsd_hx ≈ 0.15 ± 0.025). This indicates that the transition state ensemble (TSE) is actually quite broad in rmsd_hx.

TABLE 1.

Statistics of the TIS ensembles. The total aggregate simulation time was 26 μs (unfolding 11 μs, folding 15 μs)

Transition
N – L
λ	0.06	0.08	0.10	0.13	0.15	0.17
Acceptance	52%	47%	53%	44%	43%	20%
Average path length*	260 ps	634 ps	1.2 ns	1.8 ns	1.9 ns	3.0 ns
Accepted pathways	1548	730	1209	386	708	102
Aggregate time†	780 ns	990 ns	3.0 μs	1.2 μs	3.3 μs	1.7μs
L – N
λ	0.23	0.19	0.17	0.15	0.12	0.10
Acceptance	55%	47%	47%	50%	38%	40%
Average path length*	1.8 ns	1.7 ns	2.1 ns	1.4 ns	2.6 ns	2.8 ns
Accepted pathways	415	226	332	1051	684	481
Aggregate time†	1.4 μs	800 ns	1.5 μs	3 μs	4.7 μs	3.6 μs

^*Weighted average over the whole ensemble.

^†The ensemble aggregate length.

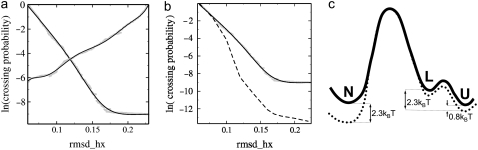
For each of the interfaces we can plot the crossing probability as a histogram of λ. By matching and reweighting these histograms we obtain the total crossing probability curve (Fig. 3 a). When plotted on a log scale, the functions P(λ|λ_N) and P(λ|λ_L) both reveal a plateau beyond (or below) a certain value of λ. The appearance of the plateau is a consequence of having crossed the transition state. Beyond (or below) a certain value of λ, the trajectories are committed to the final state, and thus the crossing probability becomes constant. The value of the plateau equals to the total crossing probability. From the TIS simulations, P(λ_L|λ_N) = 1.2 × 10⁻⁴ and P(λ_N|λ_L) = 2.5 × 10⁻³. These results give the following rates for folding and unfolding:

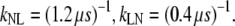(8)

The error in these numbers is difficult to estimate, but should not be higher than a factor of 3 (∼1 k_BT in free energy).

FIGURE 3.

(a) Crossing probabilities for both N – L and L – N transitions as a function of the TIS order parameter (rmsd_hx [nm]). The data points were fitted with polynomials of ∼7. (b) Comparison of the crossing probabilities for the N – L route calculated with TIS (solid line) and FFS (circles) (c) Schematic free-energy landscape of the calculated N – L – U unfolding route (solid line), compared to experimental measurements (dotted line). The calculated unfolding rate is lower by ∼2.3 k_BT than the experimental one. The folding rate differs with experimental measurement only by 0.5 k_BT.

The calculated rate constants yield a free-energy difference 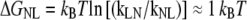between the folded N and the intermediate L state.

Comparison to experiments

The computed rate constants can be directly compared to the experimental values (2):

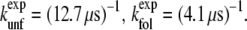(9)

Thus, the computed folding and unfolding rates seem both one order-of-magnitude higher than the experimental ones. Nevertheless, the computed free-energy value ΔG_NL ≈ 1 k_BT is at first sight the same as the experimental free-energy difference between the native and unfolded state Δ 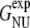 = 1 k_BT. However, we have to keep in mind that the experimental results are relative to the unfolded, not the loop state. From our replica-exchange simulation of Trp-cage (18) the free-energy difference between the loop and unfolded states was estimated to be ΔG_LU ≈ 1.5 k_BT. Using this value, the computed free-energy difference between the folded and unfolded state equals to ΔG_NU = ΔG_NL – ΔG_LU ≈ −0.5 k_BT. (A schematic free-energy landscape summarizing these values is given in Fig. 3 c.) The discrepancy of 1.5 k_BT with the experimental value might be due to the OPLSAA force field. We also speculate that the lower stability of the native state of Trp-cage in the OPLSAA force field (2.3 k_BT difference with experiment) may be an OPLSAA force-field issue.

Interestingly, the folding rate seems to agree better with experimental measurements. Assuming a simple steady-state approximation for the L-state, we can estimate k_UN by multiplying k_LN with the exponent of the free-energy difference between the L and U state, yielding 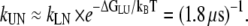This value differs only by a factor of 2 from the experimentally measured folding rate, presumably within the error of the computation. We note that because the other route N – P_d – I – U is four-times less likely, it will not influence the overall folding rate significantly.

Forward flux sampling

We performed an FFS simulation for Trp-cage starting from the native state, using rmsd_hx as the order parameter (λ). The interfaces we used are presented in Table 2. This set of interface values was obtained recurrently by trial and error. In case we were not able to reach the subsequent trial interface often enough, we decreased the gap in λ, until the desired minimal ratio was approximately reached. Our arbitrary choice was P_min(λ_i|λ_i+1) ≈ 0.1. When the probability of crossing through the next interface was >0.1, we continued the simulation with the next interface. The conditional probabilities P(λ_i|λ_i+1) for the resulting set of interfaces are presented in Table 3. The aim of this calculation was to sample the N – L transition with a method potentially faster than TIS, while computing the rate constant at the same time. The transition-path ensemble density plots in the rmsd_hx – nw_trp and rmsd_hx – rmsd_ca planes are presented in Fig. 4. The corresponding crossing probability curve is plotted in Fig. 3 b. The FFS crossing probability is 1.5 × 10⁻⁶, a factor-80 smaller than the one obtained with TIS, resulting in the rate constant k_NL = (100 μs)⁻¹ ≈ (1/8) × 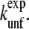This decrease of the rate constant (80 ≈ e^4.4-fold with respect to TIS) arises because FFS did not sample the correct barrier. By increasing the rmsd_hx the system was biased to unfold the α-helix (see Fig. 4, d and g). This process did not occur via the lowest free-energy path possible. On the contrary, the barrier crossed was higher by 4.4 k_BT than the one found with TIS. In some cases, the protein completely unfolded without even visiting the L state, indicating that direct N – U transitions are possible, although very improbable. None of the FFS trajectories ended up in the L-state, and a committor calculation showed their endpoints are either committed to the U or N state.

TABLE 2.

The summary of FFS results: crossing probabilities P(λ_i|λ_i+1) and the total number of generated trajectories

i	λi	λi+1	P(λi|λi+1)	Ntraj
0	0.06	0.08	0.1914	789
1	0.08	0.10	0.0829	1810
2	0.10	0.11	0.1112	2698
3	0.11	0.12	0.1250	1108
4	0.12	0.13	0.1472	1019
5	0.14	0.16	0.1708	896
6	0.16	0.17	0.6085	493
7	0.17	0.18	0.7979	376
8	0.18	0.19	0.8779	374
9	0.19	0.20	0.8761	347
10	0.20	0.22	0.7143	35

TABLE 3.

Order parameters defining the upper (max) and lower (min) boundaries of the stables state N (native) and L (loop)

Order parameters	Nmin	Nmax	Lmin	Lmax
rmsd(nm)	0	0.25	0.45	0.8
rmsdhx(nm)	0	0.05	0	1
sas(nm2)	17	18.5	0	30
ρ	0.75	0.90	0.20	0.50
nwtrp	0	7	12	25

Comparing FFS and TIS/TPS

It is interesting to note the differences between the FFS and the TIS/TPS transition path ensembles (Fig. 4). Projected on the rmsd_hx – rmsd_ca plane, the slope of the FFS ensemble is higher than the slope of the TPS ensemble, suggesting that the FFS pathways follow a different route. Indeed, on the FFS pathways, the α-helix unfolds from the N-terminus. Even when the whole helix is solvated the Trp-6 still stacks in between the proline residues, resulting in a low, essentially constant value of nw_trp along the FFS pathways. In contrast, the TPS path ensemble, when viewed from the unfolding perspective, shows slow but steady solvation of the hydrophobic core.

Even though the two simulations were started from the same equilibrated PDB structure (the TPS was started from an unfolding pathway initiated with this configuration), the initial states for the two cases are different. The FFS pathways are all anchored in the initial native configuration, while the TPS paths can relax the initial N state within the allowed definition, causing a difference of 1 Å in rmsd_ca between the initial configurations of the TIS/TPS ensemble and FFS pathways. The TPS pathways show that the last step of folding (or the first step of unfolding) of Trp-cage is a rearrangement of parts of the backbone not belonging to the helix, corresponding to a change in rmsd_ca. In contrast, FFS does not allow the pathways to increase the rmsd_ca at the beginning of the simulation. This sampling problem with FFS might be overcome by moving the first interface further from the initial state, but then the FFS method would become much less efficient.

Both FFS and TPS are sampling the same ensemble and the FFS results should eventually relax to the proper transition path ensemble, but this might be problematic if there are two valleys separated by a free-energy barrier in an orthogonal direction to the order parameter λ. If this is the case, and the order parameter λ is not the best reaction coordinate, then the FFS method might channel all pathways to the nearest valley, even if the free-energy barrier will eventually turn out higher. An alternative explanation is that rmsd_hx is a fast fluctuating variable and the FFS accepts any path that shows a fluctuation in this fast variable, not allowing for a proper relaxation of the pathways in directions orthogonal to the imposed order parameter. Our implementation of the TIS algorithm does not have this problem as we guide our ensemble in the right valley, using initial TPS trajectories, anchored in both the final and initial states. While TIS is less efficient than FFS in the generation of trajectories, TIS trajectories are more decorrelated from each other than the FFS path due to the backward shooting move.

We note that we did not put as much effort in the FFS simulation as we did in the TIS rate computation. Our TIS results are therefore probably more reliable. The point we would like to make here is that it is difficult to judge whether the path sampling result is trustworthy. A naive implementation of FFS will almost certainly lead to the wrong results. We therefore recommend a careful approach when using either FFS or TIS.

Analysis of reaction coordinates

The reaction coordinate analysis is based on the TPS simulation results (18). We collected all configurations of the forward shooting points, together with the destination of their trajectories: the initial or the final state. We divided this shooting point ensemble in two parts: one belonging to the N – I route and the other to the N – L path. We subjected both subensembles to the likelihood-maximization (LM) procedure (32). For the N – I subensemble the single most committor-correlated order parameter appeared to be rmsd_ca. No significant improvements were obtained for double combinations of trial order parameters. The resulting reaction coordinate is rc_NI = −3.7 + 12rmsd_ca, where the RMSD is given in nanometers. For the N – L subensemble the helix RMSD rmsd_hx yielded the maximum likelihood among the single order parameters. By adding another order parameter to our trial reaction coordinates, we were able to increase the maximum likelihood by a significant amount (32) for the combination of rmsd_hx and rmsd_ca. Reaction coordinates of the third order did not result in significant improvement. The reaction coordinate for the N – L route can thus be written as rc_NL = −4.5 + 13rmsd_hx + 8rmsd_ca.

From the shooting point ensemble we extract the configurations that have rc ≈ 0, corresponding to a predicted p_B ≈ 0.5. Inspection of these configurations reveals basically two kind of structures, differing by the position of Ala-12. In all cases water molecules penetrate the cavity between the tryptophan side chain and protein backbone. The side chain of Tyr-3 is twisted compared to the native state, allowing for solvation of the core. Several p_B ≈ 0.5 configurations are presented in Fig. 5 and compared with configurations calculated by committor analysis (18). The configurations appear similar, indicating that the reaction coordinate analysis is reasonable.

FIGURE 5.

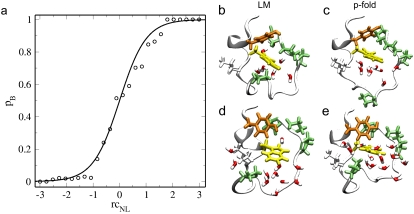
(a) The p_B values, based on the TPS shooting points, are plotted as dots in function of the calculated reaction coordinate rc_NL. The solid line is the fitted Tanh function given by Eq. 5. (b–d) Comparison of the structures with p_B ≈ 0.5 predicted by LM analysis (b and d) and real p_B ≈ 0.5 structures resulting from a full committor calculation from Juraszek and Bolhuis (18) (b and e).

Of course, the LM only predicts these structures to be transition states. To test this prediction, we performed an additional full committor calculation for several of these structures, using 10–50 independent trajectories (based on the error criterion of (25)). The committor values were mostly between 0.3 and 0.7, although there were also a few structures with a low p_B. The fact that the committor value is not exactly 0.5 might be due to the limited number of shooting points. We plotted the surfaces corresponding to rc_NL = – 1, rc_NL = 0, and rc_NL = 1 as solid lines in the TPS ensemble density maps in Fig. 4 e. The surfaces are roughly perpendicular to the guiding line connecting the N and L states, as expected. In the same plot we indicated the shooting points used for the full committor test, as well as the true TSE, as was published in Juraszek and Bolhuis (18). The first set lies on the rc_NL = 0 surface, but the true TSE lies at slightly lower values of rc_NL, indicating that the LM has not found the true reaction coordinate yet. While the LM approach could be improved by including more order parameters, the analysis is also hampered by the assumption of a linear reaction coordinate, and the limited number of shooting points in the ensemble.

The reaction coordinate analysis should be completed by performing a committor analysis for the ensemble of constraint configurations along these lines. Because there are many other configurations with the value of rc_NL = 0 that do not correspond to the TSE, this committor distribution along the rc_NL = 0 line will, almost certainly, not be peaked at ∼p_B = 0.5. Hence, we did not perform this expensive calculation. The reaction coordinate that we found, therefore, most likely provides only a local description of the L – N path ensemble, and will not be predictive for the total reaction. By improving the path ensemble, and computing more order parameters to test, the reaction coordinate could be refined. We leave this for a future study.

Our choice of TIS order parameter λ = rmsd_hx for the N – L transition could be the reason of some of the sampling problems in the folding TIS simulation. Although in principle TIS should not be very much dependent on the order parameter choice, including the rmsd_ca in the order parameter would have been useful for the TIS folding rate calculation, as any U – I transitions would have been forbidden. Nevertheless, successful sampling was still possible using only λ = rmsd_hx.

That the order parameter λ = rmsd_hx did not include the rmsd_ca in the FFS simulations is probably the cause for the serious underestimation of the rate. Performing the FFS with the above complete reaction coordinate would probably improve the FFS sampling.

CONCLUSIONS

We have performed a full transition interface sampling calculation of the folding and unfolding process between the rate-limiting intermediate loop state and the native state for the Trp-cage mini-protein in explicit solvent. To our knowledge, this is the first computation of such kind for a protein with tertiary structure formation.

The unfolding (N – L) rate constant calculated with the OPLSAA FF is one order-of-magnitude higher then the measured experimental value, while the folding (L – N) rate, including a minor correction reasonably agrees with the experiment. The discrepancy is probably the OPLSAA force-field related issue. The native state appears to be less stable than the unfolded state with a free-energy difference of ∼2 k_BT. A lower stability of the native state of Trp-cage in the OPLSAA force field has also been observed by others (A. Laio, International School for Advanced Studies (SISSA), personal communication, 2007).

The TPS and TIS ensembles follow the pathways corresponding to the lowest free-energy barriers. In contrast, forward flux sampling resulted in serious overestimation of the free-energy barriers and hence underestimation of the rate constant, because of the channeling of paths into the wrong direction. This is not caused by the fact that FFS is in principle wrong, but in practice more sensitive to the choice of order parameter than TIS.

Application of likelihood maximization for the TPS ensemble revealed that the reaction coordinate for the L – N transition is a combination of the rmsd_hx and the rmsd_ca. Using this reaction coordinate instead of only the rmsd_hx might improve the TIS sampling, and will almost certainly improve the FFS results.

A future study might improve and test the proposed reaction coordinate thoroughly by committor analysis. TIS can also be used to compute the rate for the other transitions in the Trp-cage system, i.e., N – I, I – U, and L – U, and possible transitions to misfolded states.

As a final remark, the methodology presented in this article opens the way for the investigation of the kinetics of other proteins, leading to improved insight in protein folding and conformational change.