The Membrane Potential and its Representation by a Constant Electric Field in Computer Simulations

Abstract

A theoretical framework is elaborated to account for the effect of a transmembrane potential in computer simulations. It is shown that a simulation with a constant external electric field applied in the direction normal to the membrane is equivalent to the influence of surrounding infinite baths maintained to a voltage difference via ion-exchanging electrodes connected to an electromotive force. It is also shown that the linearly-weighted displacement charge within the simulation system tracks the net flow of charge through the external circuit comprising the electromotive force and the electrodes. Using a statistical mechanical reduction of the degrees of freedom of the external system, three distinct theoretical routes are formulated and examined for the purpose of characterizing the free energy of a protein embedded in a membrane that is submitted to a voltage difference. The W-route is constructed from the variations in the voltage-dependent potential of mean force along a reaction path connecting two conformations of the protein. The Q-route is based on the average displacement charge as a function of the conformation of the protein. Finally, the G-route considers the relative charging free energy of specific residues, with and without applied membrane potentials. The theoretical formulation is illustrated with a simple model of an ion crossing a vacuum slab surrounded by two aqueous bulk phases and with a fragment of the voltage-sensor of the KvAP potassium channel.

INTRODUCTION

The transmembrane potential across the cellular membrane is a fundamental driving force affecting the translocation of permeating ions and the opening and closing transitions of voltage-gated channels (1). Although it is possible to impose a potential difference across a membrane using ion-exchanging electrodes and an electromotive force (EMF) (2), the potential difference in living cells arises from the unequal distribution of ions on both sides of the membrane. In both cases, the bulk ionic solutions remain electrically neutral and the potential difference across the membrane arises from a very small charge imbalance distributed in the neighborhood of the membrane-solution interface.

In the ideal case of a perfectly planar geometry, the transmembrane electric field is expected to be constant (3,4). A constant field is, however, probably unrealistic in the neighborhood of an embedded protein, where there can be aqueous pores and crevices of irregular shapes. It is thus necessary to develop general computational approaches to model the membrane potential for these more complex situations. Much insight can be gained from a continuum electrostatic Poisson-Boltzmann theory modified to account for membrane voltage (PB-V) (3). Calculations based on the PB-V theory have been used to simulate ion permeation (5–7), the voltage-dependence of pore blockers (8,9), and illustrate fundamental principles about the coupling between the conformation of voltage-gated potassium channels and the transmembrane voltage (10–13). Nevertheless, while the PB-V continuum electrostatic theory is useful, it is not designed to permit a realistic implementation of the membrane potential in simulations with explicit solvent molecules.

Achieving a realistic representation of the transmembrane potential in the context of all-atom computer simulations of biological membrane systems, although highly desirable, is not as straightforward as it may seem. For instance, a transmembrane potential cannot be naively controlled by imposing a physical charge imbalance across the bilayer in typical all-atom simulations where conventional periodic boundary conditions are applied in all directions (i.e., the two solutions across the membrane are actually one and the same). One of the simplest approaches to implement a transmembrane potential is to apply a constant external electric field E, perpendicular to the membrane plane (14–17). The external electric field drives a voltage difference over the whole system V = LE, where L is the length of the simulation box in the direction of the applied field. The external constant field method is convenient and easy to implement and has been widely used in a wide range of simulations (see (18–23) for a few recent examples). It has, however, a certain appearance of artificiality that is cause for some concerns (24,25). In particular, it is understood that the transmembrane potential arises from charge distributions at the microscopic level. Yet, the external force q_iE in the constant field method adds a constant force acting on all the charge q_i in the system, regardless of their position.

Alternative approaches have been sought, in part to circumvent those concerns. For example, Sachs et al. (24) developed a strategy to simulate a realistic Nernst potential based on a twin phospholipid bilayer system that included explicitly two bulk phases with unequal ion distributions. While the results were fascinating, the computational overhead associated with the twin bilayer system was significant. A reformulation of the charge imbalance strategy, using a reduced simulation system with a single-bilayer and an air-solvent interface, has been recently proposed to decrease the computational cost (25).

An important drawback of methods based on unequal ion distribution is that the potential may vary significantly (by hundreds of millivolts) upon a single permeation event (25). Similarly, large potential variations can also occur if an embedded membrane protein carrying charged residues undergoes a significant conformational change. For example, limiting the variations in the transmembrane to <∼50 mV during the opening of one voltage-gated potassium channel (∼15 unit charge) would require a simulation system comprising a bilayer of nearly 16,000 lipids and covering an area of 712 × 712 Ų. In that sense, it is very difficult to maintain a constant potential difference using a charge imbalance strategy with a finite simulated system—the same way in which it is difficult to maintain a constant pressure in simulations carried out at constant volume. In contrast, the external constant field is introduced as an invariant boundary condition on the simulation system, even though it is regarded as being somewhat unphysical (see discussion in (24,25)).

A first goal of this article is to clarify the physical significance of the external constant field in membrane simulations. A second goal of this article is to elaborate a theoretical formulation of the influence of the transmembrane potential on the configurational free energy of an intrinsic protein. The reduction of a thermodynamic system with applied potential to a finite simulation subsystem is discussed in the next section. This is followed by a theoretical development where several concepts associated with the transmembrane potential are introduced. From this analysis emerge three formal routes for characterizing the free energy of a charged protein system embedded in a membrane that is submitted to a voltage difference. Those three different approaches are illustrated with simulations of simple model systems. The article is concluded with an outlook on the various advantages of those different approaches.

THEORETICAL DEVELOPMENTS

Reduction to finite subsystem

Let us consider a system in thermodynamic equilibrium, comprising a protein embedded in a lipid membrane surrounded by two infinite aqueous salt solutions that are submitted to an electrostatic potential difference V. The potential difference between sides I and II is applied via ion-exchange electrodes (e.g., AgCl) that are connected through an electromotive force (EMF). Furthermore, it is assumed that the electrode on side II is grounded (V = 0) and that the membrane is centered at z = 0 and extends in the xy plane. The system is illustrated schematically in Fig. 1, A and B. For the sake of simplicity, it is assumed that the EMF and the electrodes are ideal and that one ionic species can be transported directly from one side to the other by going through the circuit. In a realistic system, e.g., with AgCl electrodes, the chloride anion is chemiabsorbed at the surface of the electrode on one side, releasing one electron that is transported by the EMF to the other side to yield a chloride anion on the other side (2). However, the exact details of the chemiabsorption process are unimportant in this treatment and will be ignored. The potential difference across the membrane arises from a small charge imbalance between the two bulk aqueous phases, which is transferred by the EMF via the electrodes (located far away in solution). This suggests that it should be possible to describe the situation realistically without having to treat explicitly all the details about the electrodes ion-exchange process (see discussion in (3)).

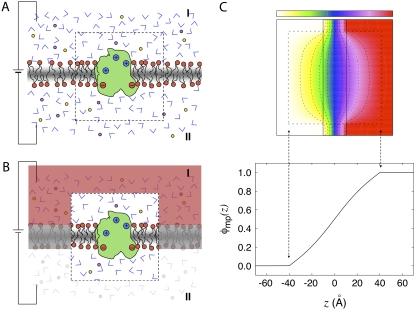
FIGURE 1.

Schematic representation of the reduction to a finite system and Poisson-Boltzmann calculation. (A) A thermodynamic membrane system with a transmembrane potential is separated into a microscopic subsystem (inner region) and its surrounding baths (outer region). The inner region (delineated by the dashed box) comprises the protein as well as the membrane and bulk solution in its neighborhood, while the outer region includes the aqueous salt solutions, the electrodes, and the EMF. The membrane is centered at z = 0 and extends in the xy plane. The electrode on side II is grounded (V = 0). (B) Representation of the same system with the degrees of freedom of the outer region integrated out and their influence on the inner region approximated using a continuum electrostatic Poisson-Boltzmann theory based on Eq. 4. (C) The effect of the transmembrane potential from an infinite thermodynamic system onto the finite subsystem is illustrated using a continuum electrostatic calculation based on the modified Poisson-Boltzmann theory (3). At the top is shown the dimensionless function φ_mp acting on a cubic central inner region of 80 Å on the side (indicated by the dashed line box). The dimensionless function φ_mp varies from 0.0 of the left (white) to 1.0 on the right (red); the contour levels indicated by colors and dashed lines are set to 0.0 (white), 0.20 (yellow), 0.35 (green), 0.50 (blue), 0.65 (purple), 0.80 (violet), and 1.0 (red). The variation of φ along the z axis cutting through the center of the box is shown at the bottom. The function φ was calculated by solving Eq. 4 numerically. In the inner region, the dielectric constant is set to 1 and the ionic screening constant is set to zero. For the aqueous phase of the outer region, a dielectric constant of 80 and an ionic concentration of 150 mM were assumed. The thickness of the membrane slab in the outer region is 20 Å and its dielectric constant is set to 2. The continuum electrostatic calculations were carried out using the PBEQ module of CHARMM using a cubic grid of 201 points spaced by 1 Å. The equation was solved by using the overrelaxation method and ∼500 iterations were required to reach convergence.

The total potential energy of the system is [U – Q_extV], where U is the microscopic potential energy of the system, and Q_ext is the net charge that transits through the external circuit. The extensive variable Q_ext and the intensive variable V are thermodynamically conjugated (26). There is a minus sign in front of the Q_extV contribution because the energy of a charge q going through the EMF from side I to side II is −qV. Yet, the accumulated net charge Q_ext is very small and the salt solutions remain globally neutral because any macroscopic charge imbalance in the bulk region would yield a prohibitively large energy.

To make progress, we choose to separate the complete system into two regions: a microscopic subsystem (inner region), embedded in the surrounding baths held at the potential difference V (outer region) (27,28). The separation is illustrated schematically by the box drawn with dashed lines in Fig. 1, A and B. The subsystem comprises the protein as well as the membrane and bulk solution in its neighborhood, while the outer bulk region corresponds to the rest of the system, including the electrodes and the EMF. The degrees of freedom of the inner and outer regions are denoted by X and Y, respectively. A formal thermodynamic reduction to the finite subsystem requires integrating out all the Y degrees of freedom of the outer region. This yields the effective potential energy function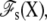

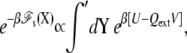(1)

which formally incorporates the influence of the surrounding baths, including the applied voltage V (the prime on the integration symbol means that the Y degrees of freedom are restricted to the outer region). The concept of the inner subsystem embedded in the surrounding baths shown schematically in Fig. 1 B, and the statistical mechanical reduction expressed by Eq. 1 underlie the physical picture that is used throughout the rest of the article.

Assuming that the aqueous ionic solutions surrounding the subsystem can be approximated using continuum electrostatics, it has been shown previously that 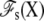can be written as

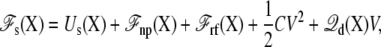(2)

where U_s is the microscopic potential energy of the subsystem, 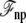is the nonpolar confinement acting on the subsystem from the surrounding baths, 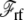is the electrostatic reaction field energy arising from the polarization of the surrounding baths, C is the capacitance of the subsystem, and 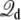is the displacement charge. The first three terms are actually independent of any applied voltage and are typical of the influence of an infinite bath surrounding a finite subsystem (27). The last two terms in Eq. 2 represent more specifically the coupling to the applied voltage. The capacitance C is independent of the internal configuration of the subsystem. In contrast, the displacement charge is highly sensitive to all charge movement within the subsystem. It may be expressed as (3)

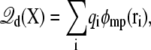(3)

where the dimensionless function φ_mp(r) represents the fraction of the membrane potential at position r in the subsystem (i.e., the ratio between the potential induced by the transmembrane potential at r and the value of the transmembrane potential V itself), and q_i is the i-th charge. The function φ_mp is defined from the Poisson-Boltzmann (PB) equation modified to account for the transmembrane potential V (3),

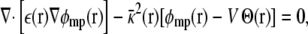(4)

where Θ(r) is a step function equal to 1 for z > 0 and ε(r) and 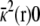represent the dielectric constant and ionic screening, respectively. At all points inside the subsystem where the surrounding bulk is explicitly excluded, ε(r) = 1 and 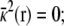however, in the outer region they assume bulklike values. It is particularly noteworthy that there are no source charges in the PB-V Eq. 4, showing that the dimensionless field φ_mp(r) is independent of the charge density ρ_s(r) inside the subsystem.

The function φ_mp embodies the coupling between the charges in the subsystem and the transmembrane voltage applied by the EMF via the electrodes in the outer aqueous salt solutions. The significance of φ_mp, however, runs deeper because it also transduces the microscopic charge movement in the subsystem into observable charge movement in the external circuit (see below). This can be made explicit by first considering the general solution to the PB-V equation,

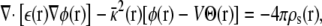(5)

which is expressed formally as the sum of two separate terms, φ(r;V) = Vφ_mp(r) + φ_rf(r), with

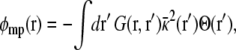(6)

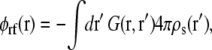(7)

using the Green's function defined by

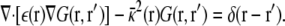(8)

A net variation in the total charge in the ionic solution on one side of the membrane implies that a charge Q_ext must have transited through the external circuit. Charge movements in the subsystem are actually detected because they induce a reorganization of the ions in the surrounding salt solution 〈ρ^ions(r)〉. For example, assuming an imposed zero potential (V = 0), the total ionic charge on the side I of the membrane (z > 0), is

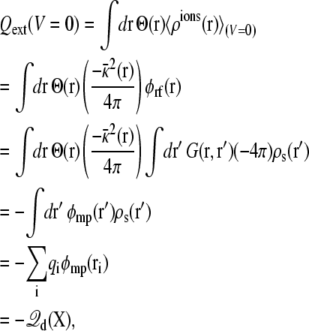(9)

where the property G(r, r′) = G(r′, r) of the Green function has been exploited (note the ion density 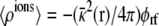in the linearized PB-V theory when the transmembrane potential is zero). Using similar arguments, it can be shown that the total charge induced in the solution at nonzero V is (3)

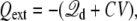(10)

at nonzero voltages. This relation implies that any atomic charge movements in the explicit subsystem gives rise directly to a detectable current going through the electrodes and the EMF. The latter are part of a virtual circuit, since those degrees of freedom have been integrated out and do not appear explicitly anymore in the reduced simulation system. The minus sign implies that, on average, when a microscopic charge q crosses the membrane from side I to side II, it pushes a charge q in the opposite direction through the virtual circuit.

According to these general considerations, a reasonable approach to simulate a finite subsystem of arbitrary shape under the influence of a membrane potential might be to generate the configurations according to the Boltzmann probability, exp[−ℱ_s(X)]. Rigorously speaking, this would require some grand canonical Monte Carlo scheme allowing particle insertion and annihilation to properly simulate the finite subsystem in open equilibrium with the buffers on side I and II of the membrane (28,29). Rather than pursuing these ideas at this point, we wish to discuss the overall shape of the function φ_mp for the particular case of a subsystem chosen with a simple cubic geometry. This is illustrated in Fig. 1 C. Although there are some local variations near the edges of the boundary, it is clear that the dimensionless coupling field φ_mp is nearly linear across the center of the subsystem (Fig. 1 C, bottom). Obviously, as the size of the subsystem is increased, the field becomes constant over most of the central region. Alternatively, if multiple copies of the subsystem were tilled together to form a two-dimensional periodic array parallel to the membrane, then the function φ_mp would be exactly linear by symmetry, and the displacement charge would then be rigorously

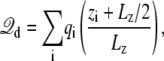(11)

where L_z is the length of the box along the z axis (the offset constant is chosen to be consistent with the grounded electrode at z → ∞). The coupling term 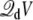then gives rise to a force equivalent to that of a constant electric field E = V/L_z, applied in the direction perpendicular to the membrane and acting on all the charges q_i in the subsystem.

As mentioned above, a correct simulation of such a subsystem in open equilibrium with its surrounding baths would still require a grand canonical Monte Carlo scheme (28,29). In practice a simpler and practical approach to ensure continuity and avoid the need to account for particle number fluctuations, is to impose periodic boundary conditions in the z direction. Furthermore, periodic boundary conditions alleviate the need to include the contributions from 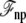and 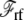required in simulations of finite systems with solvent boundaries (27). Additional considerations, however, are required to account correctly for the energy associated with the movement of ions wrapping around the central cell of the periodic system. For example, this occurs when an ion with net charge q_i leaves the cell at z = L_z/2 to reenter at z = −L_z/2. In an open ensemble simulation, such a process requires the annihilation of the ion i on side I of the system, followed by the immediate reinsertion of the ion on side II of the system. The probability for annihilating the ion i by an exchange with the buffer on side I is governed by the energy difference 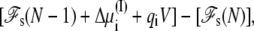where Δ 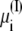+ q_iV is the excess chemical potential of the ion on side I (3,29). Similarly, the probability for inserting the ion i by an exchange with the buffer on side II is governed by the energy difference 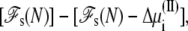where Δ 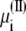is the excess chemical potential of an ion on side II (3,29). Thus, accounting for the movement of ion i wrapping around the periodic boundary, 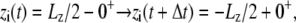requires a change in the total effective energy equal to +q_iV (the sign is negative if the ion wraps around in the opposite direction). This implies that the configurational probabilities in the periodic system are governed by the effective potential energy 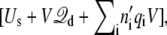where n′_i is the net number of times that the charge q_i has wrapped around the periodic coordinate system. Because of the linearity of 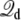in Eq. 11, this expression may be written equivalently as

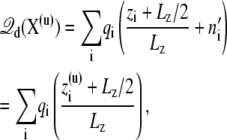(12)

where X^(u) and 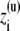represents unwrapped coordinates. Using Eq. 12 with unwrapped coordinates is essential when mobile ions carrying a net charge are part of the bulk solution (though this makes no difference for the neutral species such as water molecules).

This analysis leads us to conclude that a simulation with periodic boundary conditions in all directions, using the effective potential energy 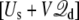with 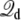given by Eq. 12, finds its roots directly in a proper reduction of a thermodynamic membrane system at voltage V by integrating out the external degrees of freedom of the infinite baths (including the electrodes and the EMF). In other words, applying a constant external electric field E = V/L_z in the direction perpendicular to the membrane, despite its apparent artificiality, correctly incorporates the influence of the surrounding infinite baths together with the transmembrane voltage applied via the electrodes and the EMF. In addition, Eq. 10 shows that the displacement charge in such system tracks the charge movement through the (virtual) external circuit. Although this conclusion was reached via an analysis based on the linearized PB-V Eq. 4 to describe the aqueous salt solution in the outer region, the physical interpretation of the constant external field should not be limited by a continuum electrostatic approximation.

To avoid the artifacts caused by truncation of the Coulomb potential, the resulting three-dimensional periodic array must be treated according to a Ewald lattice sum technique with standard conducting boundary conditions assumed at infinity to exclude the self-energy of the total dipole of the unit cell from the total energy (30,31). The widely used particle-mesh Ewald method developed by Essmann et al. (32), which relies on the fast-Fourier transform techniques to compute the periodic electrostatic potential by resolving Poisson's equation in reciprocal space, fulfills those conditions. The molecular electrostatic potential arising from the explicit charges handled by the lattice sum is periodic, Φ_mol(x, y, z + nL_z) = Φ_mol(x, y, z). The additional external constant field Φ_tot(x, y, z + nL_z) = Φ_tot(x, y, z) + nV, breaks the periodicity of the total electrostatic potential, though the total electric field (spatial derivative) is periodic and continuous everywhere. Thus, the total electrostatic forces comprises the lattice sum for the explicit charges together with the additional forces arising from the constant external field applied in the z direction. Although the electrostatic forces used to generate a MD trajectory are unambiguous, the results extracted from the periodic three-dimensional system must, however, be interpreted carefully. It is helpful to recall the original reduction to the inner region shown in Fig. 1 B to ensure that the results are interpreted in a physically meaningful way. At the edge of the inner region (the box drawn in dashed lines in Fig. 1 B), the total electric field should decay to zero and there is an offset V in the electrostatic potential between the aqueous salt solutions on sides I and II. In the periodic simulation system, those limits are replaced by z = −L_z/2 and z = +L_z/2, and L_z must be sufficiently large to avoid size artifacts.

It shall be noted that, in the effective potential energy 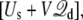the displacement charge 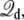an extensive variable, and the applied voltage V, an intensive variable, are thermodynamically conjugated. Interestingly, one can draw from the analogy of simulations at constant-volume (extensive) or constant-pressure (intensive) to contrast simulations generated with the constant external field or with the finite unequal distribution of charge. It is worth noting that simulations generated with a constant-pressure algorithm also have some elements of artificiality, even though they correctly yield time-averaged configurations in the isobaric ensemble (33).

From this point on, we consider a molecular subsystem for MD simulations comprising a protein embedded in a fully solvated membrane, which is simulated with periodic boundary conditions and a constant electric field acting on all the charges q_i. The total potential energy of the system is 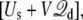where U_s is the microscopic potential energy of the simulated system, and 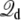is the total displacement charge given by Eq. 12 in terms of unwrapped coordinates. In the following we examine the statistical mechanical consequences of this construct.

Free energy and voltage coupling

For the sake of concreteness, let us consider the case of a voltage-activated protein with two conformational states, “a” and “b”. The normalized voltage-dependent probability for state “a” is

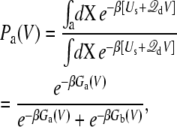(13)

where the subscript implies that the configurational integrals are restricted to a given conformation (i.e., “a” or “b”). In Eq. 13, G_a(V) represents the total free energy of the configurational state “a”,

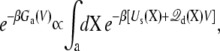(14)

with a similar expression for G_b(V) (the total free energy of the states is determined within an arbitrary constant).

It is useful to define the state-dependent excess free energy ΔG_a(V) arising from the applied membrane voltage:

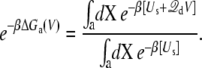(15)

Thus, the voltage-dependent probability of the state “a” is then

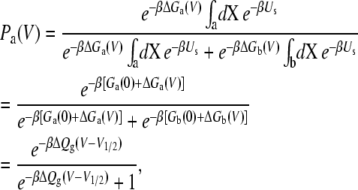(16)

where ΔQ_g is the gating charge for the two-state system,

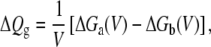(17)

and V_1/2 is the midpoint equilibrium of the two-state system,

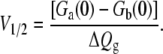(18)

These expressions describing the voltage-dependent equilibrium population of a two-state system are familiar in the field of voltage-gated potassium channels (34–37).

Displacement charge and voltage coupling

The key quantities that relate the coupling between the protein conformation and the applied voltage are the excess free energies, ΔG_a(V) and ΔG_b(V). A particularly simple relation exists between the excess free energies and the average of the displacement charge. Starting from Eq. 15, the excess free energies can be expressed as a thermodynamic integration over V,

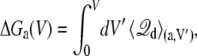(19)

where 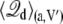is the average displacement charge of the (entire) subsystem with applied membrane voltage V′, restricted to the protein conformation a. Based on general linear response considerations, the average displacement charge is given by

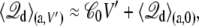(20)

where 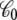is the apparent solvent-averaged capacitance of the subsystem (the subscript 0 means V = 0), which can be expressed in terms of the equilibrium fluctuations of the displacement charge at zero voltage (26). 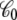should not be confused with the capacitance C appearing in Eq. 2, which does not depend on the internal configuration of the subsystem and has little impact on the analysis. In principle, the apparent solvent-averaged 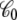depends on the shape and conformation of a protein embedded into the membrane. However, as shown previously in Roux (3), the dependence of 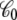upon changes in the protein conformation is negligible and can be safely ignored because the magnitude of 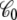is largely dominated by the membrane area A, thickness d, and permittivity ε₀ε_m (e.g., for an ideal parallel plate capacitor, ).

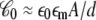Proceeding from Eqs. 19 and 20, the dominant effect of voltage on the excess free energy ΔG_a(V) can be expressed as

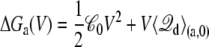(21)

(the argument is similar for ΔG_b(V)). Relying on Eqs. 14, 15, and 17, the voltage-dependent free energy difference between the states a and b can be expressed as

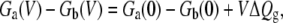(22)

and the gating charge defined in Eq. 17 is

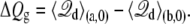(23)

This relation can be used to extract the gating charge ΔQ_g of a protein directly from MD simulations by calculating the average of 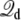for each of the two conformations at a given voltage V (the voltage must be the same for the two states a and b). The above analysis assumes that the total gating charge is independent of the applied voltage V, which is a valid assumption as long as V is sufficiently small.

It should be noted that ΔQ_g = −ΔQ_ext by virtue of Eq. 10. This points to the fundamental relationship between the total charge flowing through the external circuit comprising the electrodes and the EMF when the protein makes a transition from the conformation a to the conformation b (ΔQ_ext) and the effective charge that couples the protein to the applied membrane voltage and controls the relative free energy of the two states (ΔQ_g) (35).

Potential of mean force and voltage coupling

The above analysis showed that the applied membrane potential couples to the energetics of the microscopic system via the average displacement charge. A similar analysis can be extended to the solvent-averaged potential of mean force (PMF) of a protein embedded in a system with membrane potential V. The PMF is a central concept in modern discussion of the conformational free energy of a protein (38). The PMF can be expressed as a ratio of configurational integrals,

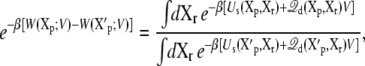(24)

where X_p and X_r values represent the coordinates of the proteins and of the remaining atoms (i.e., water, ions, and membrane lipids), respectively. Alternatively, it can be expressed from the reversible work

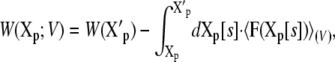(25)

where X′_p is some reference configuration of the protein, and X_p[s] represents the pathway for the conformational transition (i.e., the reaction coordinate). A complete conformational transition pathway can be determined using sophisticated computational methods (see (39,40) and references therein). With these definitions, it can be shown that the W(X_p;V) relative to the PMF at zero potential,

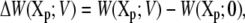(26)

is related to the variations in the average displacement charge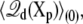

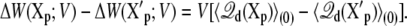(27)

Furthermore, the voltage-dependent probability of the state “a” expressed in Eq. 16 can also be written in terms of the PMF,

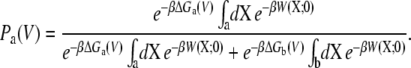(28)

Residue-based fractional field and voltage coupling

While the total gating charge is important, it is often of interest to have the ability to characterize individual contributions from specific residues of the protein. In this regard, it is useful to consider the free energy difference,

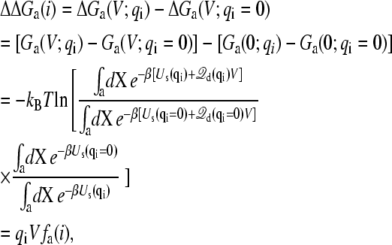(29)

where f_a(i) represents the coupling of the charge q_i to the transmembrane potential. The significance of f_a(i) may be clarified from a straightforward linear response argument. Introducing the thermodynamic coupling parameter q_i → λq_i, the charging electrostatic free energy is

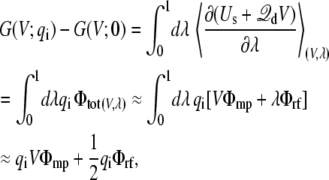(30)

where Φ_tot is the total average electrostatic potential felt by the charge q_i (the subscript “a” is omitted for simplicity). It comprises two contributions: VΦ_mp arising from the applied membrane potential (linearly proportional to V and independent of λ), and λΦ_rf arising from the reaction field (linearly proportional to λ, and independent of V). In the context of a linearized continuum electrostatic theory Φ_rf and Φ_mp are independent from one another [3], and Φ_rf cancels out in the difference in Eq. (29), yielding f_a(i) = Φ_mp. This analysis shows that f_a(i) corresponds to the fraction of the membrane potential acting on the charge q_i when the protein is in conformation a. It may actually be possible to estimate f_a(i) directly as an end-point average at λ = 1, without performing any free energy perturbation (FEP) calculation (although the accuracy of this approximation would have to be tested for specific cases). In this limit, 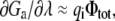and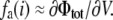

In practice, the value of f_a(i) can be obtained more accurately as the finite difference between two free energy perturbation calculations performed at two different transmembrane voltages V₁ and V₂, i.e.,

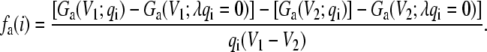(31)

The total displacement charge for the state “a”, including the contribution of all residues, may be expressed from individual residue contributions as

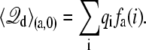(32)

A similar expression holds for 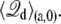It follows that the individual contribution of a given residue to the total gating charge is q_i[f_a(i) – f_b(i)], the difference in the residue-based fractional field for the two conformations, “a” and “b”.

COMPUTATIONAL DETAILS

For the sake of clarity, we considered a simple system comprising two aqueous phase regions separated by a vacuum slab of 20 Å meant to represent a low dielectric nonpolar membrane region. The water molecules were prevented from entering the slab region by using a flat-bottom harmonic potential with a force constant of 10 kcal/mol/Ų imposed using the GEO module of CHARMM (41). The initial system was constructed using a preequilibrated water system and contains a total of 1000 water molecules. The size of the simulation box is L_x = 31.1032009 Å, L_y = 31.1032009 Å, and L_z = 51.1032028 Å. Periodic boundary conditions were applied in all directions.

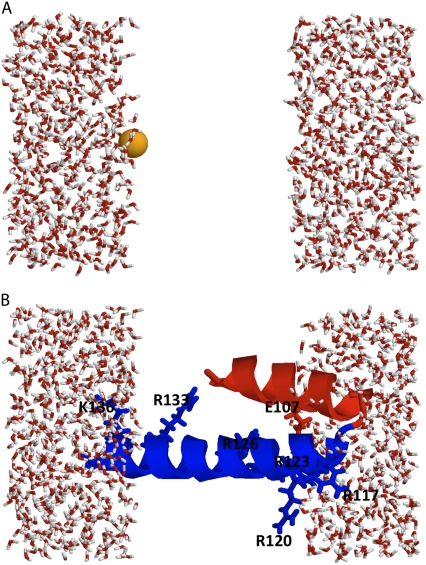
The simulation systems are shown in Fig. 2, A and B. The first simulation system (Fig. 2 A) includes a single K⁺ ion at different locations along the z axis. The second simulation system (Fig. 2 B) includes a 41-residue segment from the voltage-sensing domain of the KvAP bacterial channel, starting from Pro⁹⁹ (near the center of the S3 helix) to Ser¹³⁹ (near the C-terminus of the S4 helix) (42). The S3-S4 segment, taken from the x-ray structure of the isolated voltage sensor (PDB id 1ORS), was oriented with the residue Arg¹¹⁷ near the membrane-solvent interface and the C-terminus of the S4 helix on the other side of the membrane, as proposed in a number of previous models (43,44). Nonetheless, the purpose of these calculations is only to be illustrative of the methodology. The protein segment was held fixed during all the simulations with the KvAP fragment.

FIGURE 2.

(A) Simulation systems. Simulation system with a K⁺ ion solvated by water. To mimic the effect of a nonpolar membrane region, the water molecules are prevented to enter between −10 and +10 Å using a half-harmonic potential. (B) Simulation system with a 41-residue fragment of the voltage sensor of the KvAP channel, starting from Pro⁹⁹ (near the center of the S3 helix, shown in red) to Ser¹³⁹ (near the C-terminus of the S4 helix, shown in blue). To mimic the effect of a nonpolar membrane region, the water molecules are prevented to enter between −10 and +10 Å using a half-harmonic potential. The structure of the S3-S4 segment is directly taken from the x-ray structure of the voltage sensor (PDB id 1ORS). The important charged residues are displayed as sticks and the position of their center of charge are (z = 0 is at the center of the membrane): Glu¹⁰⁷ (10.8 Å), Arg¹¹⁷ (14.1 Å), Arg¹²⁰ (9.7 Å), Arg¹²³ (10.0 Å), Arg¹²⁶ (4.4 Å), Arg¹³³ (−4.2 Å), and Lys¹³⁶ (−12.7 Å).

All the configurational sampling was generated using Langevin dynamics at constant volume. A friction of 10 ps⁻¹ was used for all nonhydrogen atoms. The SHAKE algorithm was used to keep the geometry of the water molecules rigidly fixed (45), and a timestep of 2 fs was used to integrate the equation of motion. The nonbonded interactions were truncated at 12 Å and all electrostatic interactions were treated with the particle mesh Ewald method (32), using a fourth-order spline, 0.30κ, and a 32 × 32 × 64 grid for the fast-Fourier transform. The transmembrane potential V was implemented by introducing an external constant electric field applied along the z axis according to Eq. 12. The TIP3P potential was used for the water molecules (46). The all-atom CHARMM force field was used for the K⁺ (47) and the protein (48). All computations were performed using the CHARMM simulation program (41).

The voltage-dependent potential of mean force (PMF) for a K⁺ along the z axis was calculated by integrating the average force acting on the ion held fixed at 103 positions, going from z = −20 to +20 Å and spaced by 0.5 Å. The system is shown in Fig. 2 A. For each position, the configurational sampling was generated from 100 ps of simulation. Results for −5.0, −1.0, −0.5, 0.0, 0.5, 1.0, and 5.0 V are analyzed, though the results for −5.0, −1.0, and −0.5 were reconstructed from the results with 5.0, 1.0, and 0.5 V by symmetry (i.e., using the property that W(z;V) → W(−z; −V) + B, where B is an offset constant). A free energy perturbation (FEP) for charging the K⁺ ion held fixed at five specific locations along the z axis (−20, −10, 0, 10, and 20 Å) was carried out at 0 V and 1 V (49). Five forward and backward FEP simulations were generated with the thermodynamic coupling parameter λ = 0.0, 0.25, 0.50, 0.75, and 1.00 using the PERT module of CHARMM, and then postprocessed using the weighted histogram analysis method (50,51). The total simulation for each FEP calculation is 250 ps.

To further illustrate the method, a similar charging free energy calculation was carried out at 0 and 1 V for the seven charged residues that are part of the fragment of the KvAP voltage sensor (Glu¹⁰⁷, Arg¹¹⁷, Arg¹²⁰, Arg¹²³, Arg¹²⁶, Arg¹³³, and Lys¹³⁶). The protein fragment was held fixed during the FEP simulations in the orientation shown in Fig. 2 B. Five forward and backward simulations for the thermodynamic coupling parameter λ = 0.0, 0.25, 0.50, 0.75, and 1.00 were generated using the PERT module of CHARMM, and then postprocessed using the weighted histogram analysis method. The total simulation time for each FEP calculation was 250 ps.

RESULTS AND DISCUSSION

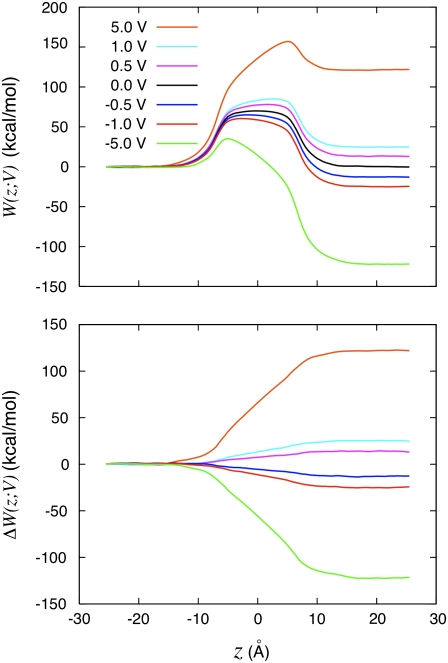
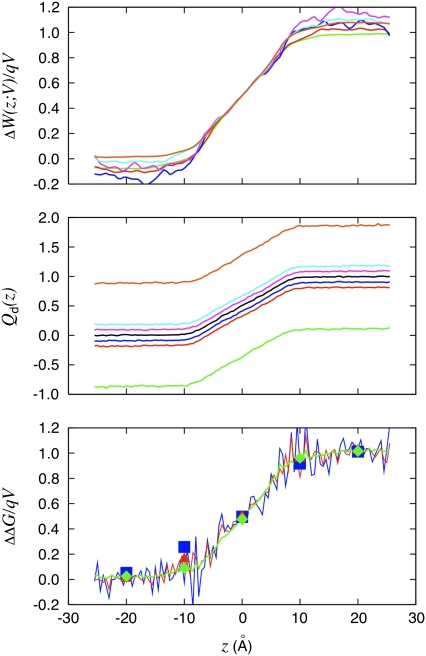
We first illustrate the effect of the transmembrane potential on a charged particle translated along an axis perpendicular to the membrane plane. In Fig. 3 (top) is shown the voltage-dependent PMF of a K⁺ ion along the z axis. The PMF at zero membrane potential is symmetric and displays a high free energy barrier of ∼70 kcal/mol, which is typical of the hydration free energy of K⁺. At different applied membrane potentials, the large central barrier remains although the symmetry is broken. An offset appears between the two sides of the membrane. While the voltage-dependent PMFs retain the original complexity observed at zero potential, the differences [W(z;V) – W(z;0)] display a much simpler structure. The difference of those PMFs with the PMF at zero voltage is shown in Fig. 3 (bottom). In fact, the coupling between the charged ion and its membrane environment with applied voltage can be summarized largely by a single dimensionless function f(z). Three different formal routes for characterizing f(z) are accessible for characterizing the coupling and are compared in Fig. 4. In Fig. 4 (top), the dimensionless coupling f(z) has been extracted from the variations in the PMF of the K⁺ ion along the z axis as

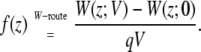(33)

In Fig. 4 (middle), the coupling is extracted from the variations of the total displacement charge calculated for the K⁺ ion along the z axis at a different voltage as

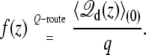(34)

The offset in the displacement charge at nonzero voltage (Fig. 4, middle) is the buildup of capacitive charge in the system, 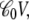according to Eq. 20. Fig. 4 (bottom) shows the coupling extracted from the variations of the voltage-dependent solvation free energy of the K⁺ ion along the z axis relative to zero voltage (plotted as dots),

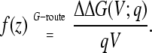(35)

It is observed that the character of f(z) from the three different routes is essentially identical, although the results appear to have different convergence efficiencies. For instance, the end-point estimator 〈Φ_tot(z)〉_(V)/qV, shown in Fig. 4 (bottom, solid line), is very noisy when the charging free energy from 0.5 V is used, whereas the finite charging free energy perturbation (Fig. 4, symbols) appears to be more accurate. For the particular system considered, the least noisy results are apparently obtained via the Q-route, by monitoring the average displacement charge according to Eq. 34. The fluctuations of 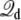are related to the effective capacitance 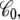which is roughly equal to ε₀ε_mA/d. Thus, the Q-route converges rapidly in this case because the membrane area A of the simulation system is modest. One may expect that obtaining accurate averages of 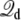could be more challenging in the case of a very large simulation system.

FIGURE 3.

Potential of mean force analysis. (Top) Calculated PMF W(z;V) for a K⁺ ion along the z axis of the system shown in Fig. 2 at various transmembrane potentials. The PMFs were calculated by integrating the mean force acting on the K⁺ held fixed at a series of positions along the z axis. All the PMFs were offset to be equal to zero at z = −20 Å. The results for −5.0, −1.0, and −0.5 were reconstructed from the results with 5.0, 1.0, and 0.5 V by symmetry (i.e., using the property that W(z;V) → W(−z; −V) + B, where B is an offset constant). (Bottom) Perturbative effect of the applied voltage obtained by subtracting the PMF at zero voltage from all the other PMFs, ΔW(z;V) = W(z;V) – W(z;0). The color legend is 5.0 V (orange), 1.0 V (cyan), 0.5 V (magenta), 0.0 V (black), −0.5 V (blue), −1.0 V (red), and −5.0 V (green).

FIGURE 4.

The dimensionless coupling of the K⁺ to the applied transmembrane voltage deduced from three different routes is shown. The W-route: voltage-dependent PMF technique is based on Eq. 33. The Q-route: average of the displacement charge based on Eq. 34; the offset in the displacement charge is caused by the apparent capacitance of the system according to Eq. 20. The G-route: relative charging free energy based on Eq. 35 (squares). The end-point averaging technique based on Eq. 30 is also shown (solid lines). The color legend is 5.0 V (orange), 1.0 V (cyan), 0.5 V (magenta), −0.5 V (blue), −1.0 V (red), and −5.0 V (green).

In the case of a single charged particle, the three different routes to characterize the dimensionless fraction of the field, f(z), yield essentially equivalent results and can be directly compared. Such a straightforward comparison cannot be carried out in the case of more complex molecular structures. Fig. 5 shows the dimensionless coupling f(i) calculated from the voltage-dependent solvation free energy ΔΔG(V;q)/qV for the seven charged residues of the fragment of the KvAP voltage sensor held in the fixed configuration shown in Fig. 2 B. The coupling extracted for the K⁺ from Fig. 4 (bottom) is shown as a dashed line for reference. While these calculations are not meant to reproduce experimental data about voltage-gating, they are useful to illustrate this methodology.

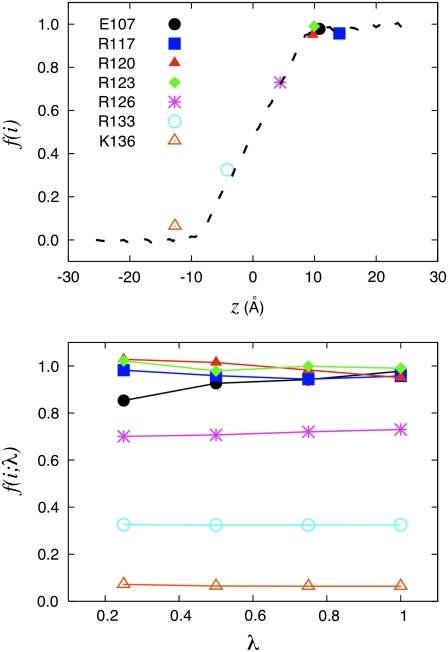
FIGURE 5.

KvAP voltage sensor. Illustration of the charging FEP technique based on Eq. 29 to determine the fraction of the field for specific residues for the fragment of the voltage sensor of the KvAP bacterial channel. (Top) The fraction of the field felt at each of the charged residues is shown with the position of their center of charge along the z axis: Glu¹⁰⁷ (10.8 Å); Arg¹¹⁷ (14.1 Å); Arg¹²⁰ (9.7 Å); Arg¹²³ (10.0 Å); Arg¹²⁶ (4.4 Å); Arg¹³³ (−4.2 Å); and Lys¹³⁶ (−12.7 Å). (Bottom) The variation of the fraction of the field extract at different values of the thermodynamic coupling parameter λ during the FEP calculations. The position assigned to each residue along the z axis is based on the geometric center of charge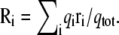

Consistent with the view suggested by Eq. 30, the results show that the coupling is essentially equivalent to the fraction of the transmembrane voltage, f(i), felt by each residue i in its environment. For this reason, the extracted values are fairly insensitive to the thermodynamic coupling λ (Fig. 5, bottom). Lastly, as shown by the close relationship between the results for the KvAP voltage sensor fragment and those from the K⁺ ion system (where the low dielectric region of the fixed protein is absent), the results are not exquisitely sensitive to the microscopic details of the interface. This is the main reason why a continuum electrostatic calculation based on the modified Poisson-Boltzmann Eq. 4 offers a useful approximation to analyze and dissect the gating charge of voltage-gated potassium channels (10,12,13). It should be noted that only the G-route, based on the excess free energy, can provide an absolute estimate of the voltage coupling of a single site in a single configuration, because the reference potential φ_mp is chosen to be zero at the edge of the box by virtue of Eq. 12. This confers a special advantage to this method in dealing with complex molecular structures, such as the voltage-gated potassium channel, because it can be applied even when a single conformational state is available. From this point of view, it permits a more incisive analysis of the contribution of each residue in a given conformational state. It may also be noted that the residue-based dimensionless voltage couplings f(i) calculated from the excess free energy method with explicit solvent are analogous to the results previously calculated using the PB-V theory on the Kv_1.2 channel (see Fig. 8 c in (13)).

Some practical issues deserve special attention concerning an analysis based on the Q- and G-routes. Concerning the G-route, it should be noted that the results are sensitive to the position of the zero potential reference along the z axis. For example, some simulation programs set the energy arising from the constant field to be 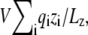where the electrostatic potential is set relative to the center rather than at the edge of the simulation box. As a consequence, usage of Eq. 35 will yield the value of the dimensionless fraction of the field relative to the center of the simulation box, rather than relative to the ground reference value in the aqueous salt solution on side II (at the lower edge of the simulation box). In this case, the resulting charging free energy must be shifted by an offset constant to recover the convention used here. To clarify any formal ambiguity, it is advisable to return to the original construction with the inner region surrounded by bulk salt solutions, as illustrated in Fig. 1 B. Concerning the Q-route, it is essential to utilize Eq. 12, with unwrapped coordinates (particularly if there are mobile ions in the bulk). This is necessary to extract physically meaningful results for the average displacement charge 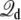based on Eq. 34 and the gating charge between different protein conformation based on Eq. 23. While the Q-route was illustrated here for a simple simulation system comprising two aqueous phase regions separated by a vacuum slab, additional tests demonstrate that this analysis is also valid when the bulk phase includes mobile ions (results not shown).

In closing, a few comments concerning size effects and dynamical properties are in order. This theory was elaborated for a system in thermal equilibrium. Under such conditions, the applied potential can affect the equilibrium properties of the system, but does not generate any steady-state current. Historically, a constant electric field has been frequently used to simulate nonequilibrium ion fluxes through membrane channels (14,15,17,18,22,23,25). The analysis shows that simulations with periodic boundary conditions based on the effective energy 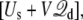where 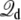is given by Eq. 12, offers a proper representation of the influence of the surrounding bulk with applied transmembrane potential onto the finite system. The results with the simple system shown in Fig. 4 illustrate that the average behavior can actually be maintained, even up to 5 V. In practice, it remains important to construct a system that is sufficiently large to avoid obvious size effects. It is also worth pointing out that a realistic simulation of the transmembrane potential should not only be concerned by thermodynamics, but also by fluctuations. For the sake of concreteness, let us consider the case of a permeating ion in the lumen of a channel. Let us assume that the size L of the simulation system is sufficiently large to generate the correct total mean force on the ion, 〈F^tot〉 = 〈F^(MD)〉_L + qV/L. According to the fluctuation-dissipation theorem, the time correlation function of the force acting on a tagged ion is related to the friction (the memory function) in a generalized Langevin equation dynamic description (52). The quantity 〈(F^tot – 〉F^tot〉)²〉 could be underestimated even if the mean force 〈F^tot〉 is accurate, because the time-independent force arising from the constant field, qV/L, does not contribute to the fluctuations. This will happen when the magnitude of qV/L approaches that of 〈F^(MD)〉_L. An underestimated friction will unavoidably lead to an artificially enhanced rate of transport at high voltage (53–56), a phenomenon that has been observed in a recent study of ion conduction (25). Therefore, while a given system size may be sufficient to yield an accurate PMF, it is possible that a sufficiently large system is needed to accurately simulate transport properties such as permeation.

CONCLUSION

It has been shown that the familiar constant external electric field applied in the direction normal to a membrane corresponds to a proper reduction of the influence of an infinite bath imposing a membrane voltage via electrodes connected to an electromotive force (EMF). Furthermore, the linear displacement charge consistent with the external field tracks all external charge movements through the (virtual) electrodes-EMF circuit. The reduction of the bath influence onto the subsystem leads to a statistical mechanical formulation that helps clarify the nature of the free energy of a charged system embedded in a membrane submitted to a voltage difference. This analysis led to the formulation of three formal approaches, the W-, Q-, and G-routes, for characterizing the voltage coupling were formulated. The theoretical formulation was illustrated with simple models of a charged ion and a fixed fragment of the voltage sensor of the KvAP channel.

The W-route considers the variations in the potential of mean force (PMF) along a reaction path connecting two conformations of the system. This is the most physical, since it deals directly with the concept of the free energy surface associated with the protein conformation changes. From this point of view, it allows a direct computation of the gating charge controlling the voltage-dependent population equilibrium of a protein. However, this approach also puts the highest demand on simulations since one is required to provide more than a single conformational state of the protein, and also a path linking those conformations to compute the reversible work between them.

The Q-route considers the average displacement charge as a function of the conformation of the system. This approach is perhaps the most straightforward to use. The only requirement is to perform end-point averages of the displacement charge at various voltages and in different conformational states of the protein. This is less demanding than the PMF-route since the pathway linking the various conformations is not needed, although the Q-route also requires a comparison between protein conformations. One disadvantage, however, is that it yields only the value of the total gating charge, with no simple way of achieving a residue-by-residue analysis.

The G-route considers the charging free energy of specific residues to extract the residue-based fractional field. This technique is slightly more involved because it requires FEP simulations for each residue, performed at two different membrane voltage V. It might be possible to extract rough estimates of the dimensionless coupling per residue by performing only end-point averages of the total electrostatic potential, although these tests suggest that the accuracy is better with FEP simulations. An important advantage of the G-route is that it allows a detailed decomposition of the contribution from each residue to the total gating charge. Furthermore, this technique makes it possible to extract the coupling of individual residues in a single protein conformation. Therefore, this technique can be used even when only a single conformation of the protein is available (i.e., the open-activated state of a potassium channel).