Experimental Verification of the Behavioral Foundation of Bacterial Transport Parameters Using Microfluidics

Abstract

We present novel microfluidic experiments to quantify population-scale transport parameters (chemotactic sensitivity χ₀ and random motility μ) of a population of bacteria. Previously, transport parameters have been derived theoretically from single-cell swimming behavior using probabilistic models, yet the mechanistic foundations of this upscaling process have not been verified experimentally. We designed a microfluidic capillary assay to generate and accurately measure gradients of chemoattractant (α-methylaspartate) while simultaneously capturing the swimming trajectories of individual Escherichia coli bacteria using videomicroscopy and cell tracking. By measuring swimming speed and bias in the swimming direction of single cells for a range of chemoattractant concentrations and concentration gradients, we directly computed the chemotactic velocity V_C and the associated chemotactic sensitivity χ₀. We then show how μ can also be readily determined using microfluidics but that a population-scale microfluidic approach is experimentally more convenient than a single-cell analysis in this case. Measured values of both χ₀ [(12.4 ± 2.0) × 10⁻⁴ cm² s⁻¹] and μ [(3.3 ± 0.8) × 10⁻⁶ cm² s⁻¹] are comparable to literature results. This microscale approach to bacterial chemotaxis lends experimental support to theoretical derivations of population-scale transport parameters from single-cell behavior. Furthermore, this study shows that microfluidic platforms can go beyond traditional chemotaxis assays and enable the quantification of bacterial transport parameters.

INTRODUCTION

Chemotaxis is the ability of cells to detect and respond to a gradient in chemical concentration. The motility and chemotaxis phenotypes have significant impact in a wide range of fields, including reproduction science (1,2), biofilm formation (3,4), contaminant bioremediation (5–7), disease pathogenesis (8–10), and nutrient cycling in the ocean (11–15). A quantification of chemotactic motility is therefore essential to predict the ability of a bacterial population to disperse and migrate in the presence of chemical gradients.

Bacterial motility is often described as a three-dimensional (3D) random walk (16). For the enteric bacterium Escherichia coli, 3D tracking (17) revealed that the random walk is composed of nearly straight segments (“runs”) interrupted by rapid changes in direction (“tumbles”). When bacteria experience favorable chemical gradients, tumbles are suppressed (18,19), resulting in a net chemotactic drift with velocity V_C toward an attractant or away from a repellent. At the population scale, this behavior has been characterized by a phenomenological model for the flux of cells J proposed by Keller and Segel (20), which in one dimension (x) reads

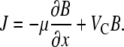(1)

Here, B(x,t) is the concentration of bacteria, t is time, and μ is the random motility coefficient, measuring the diffusivity of a population of bacteria resulting from their random walk behavior. Coupled with the conservation equation ∂B/∂t = −∂J/∂x, Eq. 1 gives an advection-diffusion equation for the bacterial population, known as the bacterial transport equation:

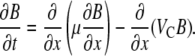(2)

In the absence of chemoattractants, V_C = 0 and Eq. 2 reduces to the diffusion equation. When a chemoattractant is present, the chemotactic velocity V_C depends on the chemoattractant concentration gradient and hence is not an intrinsic property of a bacterium-chemoattractant pair. Instead, such a role is played by the chemotactic sensitivity coefficient χ₀, expressing the strength of attraction of a population to a given chemical. The relation between V_C and χ₀ is discussed below. It follows from Eq. 2 that knowledge of μ and χ₀ enables one to predict bacterial transport in any given concentration field. Conversely, observed bacterial distributions can be used to determine μ and χ₀ by fitting Eq. 2.

A wide range of chemotaxis assays has been developed to measure the strength of attraction of a bacterial population to a given chemical. The classic “capillary assay” (21) is the most widespread, due to its simplicity. However, capillary assays are not conducive to the measurement of transport parameters (22,23), as chemoattractant gradients are exceedingly difficult to quantify and can be easily perturbed even by minor residual flows (24). Furthermore, the need for plate-counting considerably increases processing time and reduces accuracy. Quantification of transport parameters has typically relied on more controlled gradient-generation devices, such as the stopped-flow diffusion chamber (25) coupled with direct measurement of B(x,t) using light scattering or related techniques (25–27). These studies all have employed a population-scale approach, requiring a rather complex procedure to determine μ and χ₀ based on seeking time-dependent, numerical solutions of Eq. 2 for the particular geometry at hand and fitting them to the observed bacterial distribution B(x,t). In addition, most studies have relied on theoretical predictions of the chemoattractant concentration instead of measurements (25–27), considerably increasing uncertainty in light of the extreme sensitivity of the concentration field to perturbations. Here we present a direct approach to compute bacterial transport parameters from single-cell swimming information and direct measurements of the concentration field, thus bypassing the need to solve the bacterial transport equation.

The theoretical link between population-scale transport and single-cell chemotactic motility behavior has been derived by Rivero et al. (28) based on a previous model by Othmer et al. (29). Farell et al. (30) verified Rivero's model experimentally for surface-attached leukocytes. For free-swimming bacteria, the mechanistic foundation of a population-scale transport formulation has, to date, gone untested, partly due to the experimental difficulty of obtaining single-cell data of freely swimming organisms in a controlled concentration field. Besides, the chemotactic response of bacteria differs fundamentally from that of leukocytes: leukocytes bias the direction of their movement (28), whereas bacteria modulate run lengths (17). Here we test Rivero's model experimentally by tracking individual E. coli exposed to a range of well-defined chemoattractant gradients, generated using microfluidic devices.

Microfluidic devices consist of micrometer- to millimeter-sized flow channels that can be fabricated rapidly and precisely (31,32) and have extensively been used to generate accurate chemical gradients (1,33–37). In the context of chemotaxis, these devices have been designed and applied primarily to study chemotaxis of surface-attached cells (33,34,36,38). Microfluidic investigations of chemotaxis of free-swimming microorganisms have been more limited (35,39–41), neither attempting to compute chemotaxis parameters nor investigating the bacterial response at the single-cell level. Here we show that microfluidics optimally lends itself to quantitative chemotaxis assays to determine population-scale transport parameters directly from single-cell trajectories.

Theoretical background

Rivero et al. (28) present a mathematical model that links single-cell and population-scale descriptions of chemotaxis for bacteria swimming in a one-dimensional (1D) domain (x) at speed v_1D, with a chemoattractant gradient along x. For completeness, the main steps in their derivation are reproduced here. Bacteria are modeled as two subpopulations of concentrations n⁺ and n⁻, swimming in opposite directions (+x and −x, respectively). Cell conservation dictates:

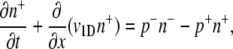(3)

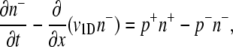(4)

where p⁺ is the probability per unit time that an n⁺ cell tumbles and becomes an n⁻ cell (and vice versa for p⁻). Tumbles are assumed to be instantaneous. Addition of these two equations yields the cell conservation equation ∂B/∂t = −∂J/∂x, where B = n⁺ + n⁻ is the overall bacterial concentration and J = v_1D (n⁺ − n⁻) is the bacterial flux. An equation for the bacterial flux can be obtained by subtracting Eq. 3 from Eq. 4 and rearranging:

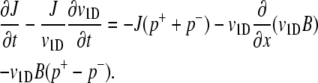(5)

For observation times larger than the persistence time (p⁺ + p⁻)⁻¹, a quasi-steady-state value for the local flux can be assumed (∂J/∂t = 0). The persistence time for E. coli is ∼0.5 s, considerably shorter than the observation time in our experiments. With the further assumption that swimming speed is constant over space and time, Eq. 5 reduces to

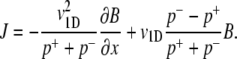(6)

This is equivalent to Eq. 1, with μ = (v_1D)²/(p⁺ + p⁻) and V_C = v_1D (p⁻ − p⁺)/(p⁺ + p⁻). Chen et al. (42) show that Eq. 1 also applies to cells swimming at speed v_3D in a 3D domain with a chemoattractant gradient along a single dimension x, with somewhat modified expressions for V_C (= (2/3)v_3D (p⁻ − p⁺)/(p⁺ + p⁻)) and μ (=(2/3)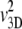/[(p⁺ + p⁻)(1 − ψ)]), where ψ is the directional persistence (∼0.3 for E. coli (17)). Ford and Cummings (43) further demonstrate that, if one measures the two-dimensional (2D) velocity v_2D resulting from the projection of the 3D swimming speed v_3D onto a 2D plane, as is often done in microscopy, one can still use these same expressions for V_C and μ, after replacing v_3D with 4v_2D/π. In summary, we have the following expressions for V_C and μ:

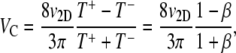(7)

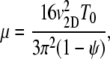(8)

where the mean run times are given by T⁺ = 1/p⁺ and T⁻ = 1/p⁻ (T⁺ = T⁻ = T₀ in the absence of chemoattractant gradients), and we defined the swimming direction asymmetry β = T⁻/T⁺ (β = 1 represents no chemotaxis, β = 0 is deterministic motion up the gradient).

Again, V_C is not an intrinsic property of a population, as it varies with the gradient dC/dx of the chemoattractant concentration C(x). The parameter intrinsically measuring the attraction of a population to a given chemical is the chemotactic sensitivity χ₀, which Rivero's model relates to V_C as (28,42)

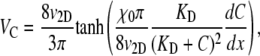(9)

where K_D is the receptor/ligand dissociation constant. The derivation of Eq. 9 for the 1D case is given in the Appendix. For E. coli exposed to α-methylaspartate, K_D has been estimated as 0.125 mM (44) or 0.160 mM (45). For our purposes, it proves convenient to rewrite Eq. 9 as

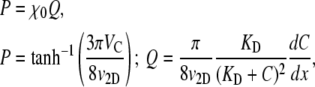(10)

and determine χ₀ as the slope of the best-fit line of Q vs. P. Here, we will directly measure β and v_2D to calculate V_C from Eq. 7, and further measure C and dC/dx to compute χ₀ from Eq. 10.

Finally, to measure the random motility μ of a bacterial population we will create a 1D band of bacteria (of initial width (2μt₀)^1/2) and observe them spread as a result of their random walk behavior. We compute μ by fitting the observed spatiotemporal distributions of bacteria to the analytical solution of the diffusion equation (Eq. 2 with V_C = 0) in an infinite domain, given by

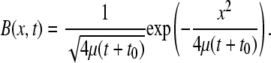(11)

MATERIALS AND METHODS

Bacteria, growth conditions, and chemoattractants

E. coli HCB1 (provided by H. Berg) was grown in Tryptone broth at 34°C on an orbital shaker (220 rpm) to midexponential phase (optical density = 0.4), then washed thrice by centrifuging at 2000g for 5 min and resuspending the pellet in motility buffer (10 mM potassium phosphate, 0.1 mM EDTA, 10 mM NaCl; pH = 7.5). The suspension was further diluted (1:5–1:2) in motility buffer to ensure optimal cell concentration for tracking.

For chemotaxis experiments, E. coli cells were exposed to the nonmetabolizable chemoattractant α-methylaspartate (Sigma-Aldrich, St. Louis, MO) diluted in motility buffer. Three sets of experiments were performed, corresponding to initial chemoattractant concentrations in the microchannel of C₀ = 0.1, 0.5, and 1.0 mM. A different bacterial batch was used for each set of experiments. Fluorescein (Sigma-Aldrich) was added to α-methylaspartate solutions to visualize the concentration field by epifluorescence microscopy, using an EXFO X-Cite 120 fluorescent lamp (Photonic Solutions, Ontario, Canada). Fluorescein has a diffusion coefficient of 5 × 10⁻¹⁰ m² s⁻¹, nearly identical to α-methylaspartate (5.5 × 10⁻¹⁰ m² s⁻¹ (46)). We previously verified that fluorescein does not induce chemotaxis in E. coli (47). For random motility experiments, nine realizations were performed, using two different batches of bacteria.

Microchannel fabrication

Microfluidic devices were fabricated using soft lithography techniques (31,33). The channel design was produced using computer-aided design software (Autodesk, San Rafael, CA) and printed onto transparency film with a high-resolution image setter (Fineline Imaging, Colorado Springs, CO), creating a design “mask”. A 60-μm-thick layer of negative photoresist (SU8-2100; Microchem, Newton, MA) was applied to a 4-inch silicon wafer (University Wafer, South Boston, MA) by spin-coating. With the mask laid onto the coated wafer, exposure to ultraviolet light was used to polymerize exposed regions of the photoresist, appending an impression of the channel design onto the silicon wafer (the “master”). Positive replicas with embossed channels were fabricated by molding polydimethylsiloxane (PDMS, Sylgard 184; Dow Corning, Midland, MI) against the master and baking at 65°C for 12 h. The hardened PDMS, containing the channel structure, was then peeled from the master and cut to size. Access holes for tubing were punched using a sharpened lure tip. The PDMS layer was then sealed against a glass microscope slide by exposure to oxygen plasma (Harrick Plasma Cleaner/Sterilizer; Harrick Scientific, Ossing, NY) for 1 min, forming a covalent bond and completing the microfluidic channel. Peek tubing (Upchurch Scientific, Oak Harbor, WA), with inner/outer diameters of 0.76/1.59 mm, was inserted into inlets and outlet.

Microchannel layout and operation

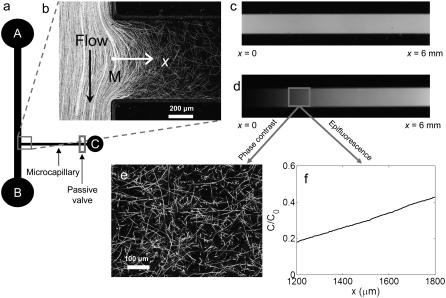
Two different microchannels were fabricated. The first (Fig. 1 a) was used to determine χ₀ and consisted of a 20-mm-long, 1-mm-wide, and 60-μm-deep main channel, with a 9-mm-long, 0.6-mm-wide, and 60-μm-deep side channel (the “microcapillary”), branching off from the main one at a right angle. The direction along the microcapillary will be denoted by x, with x = 0 at the mouth of the microcapillary (M, in Fig. 1 a). Before the start of an experiment, a solution of α-methylaspartate and fluorescein was injected into the microcapillary via inlet C (Fig. 1 a) using a 1 ml plastic syringe. Inlet C was equipped with an on-chip passive valve (38), which allowed flow under sufficient pressure, such as that exerted by gentle manual injection, and prevented it otherwise, so that the microcapillary was sealed from external perturbations.

FIGURE 1.

Experiments to determine the chemotactic sensitivity χ₀ of E. coli. (a) Schematic of the microfluidic channel. Chemoattractant and fluorescein were injected in the microcapillary via inlet C by means of a passive valve. (b) Flow in the main channel (from A to B) was used to transport E. coli past the mouth (M) of the microcapillary, where a fraction of the population had swum into the microcapillary. Each white path is an E. coli trajectory. The image is a superposition of 200 frames captured over 6.2 s. (c and d) Epifluorescence images (using a 2× objective) of the microcapillary, initially filled uniformly with α-methylaspartate (t = 0; c), and later exhibiting a nonuniform concentration profile (t = 45 min; d). The latter was used to probe the chemotactic response of the E. coli cells that had swum into the microcapillary. 100 μM fluorescein was added to variable concentrations of α-methylaspartate (0.1, 0.5, or 1.0 mM) for visualization. (e) Trajectories of E. coli from 300 frames recorded over 9.4 s using a 20× objective. (f) Concentration profile C(x) obtained from d and normalized by the initial concentration C₀ in the microcapillary. The field of view is the same as in e.

After completely filling the microcapillary with chemoattractant, motility buffer was injected into the main channel via inlet A at a constant flow speed of 300 μm s⁻¹, using a 1 ml plastic syringe driven by a syringe pump (PHD 2000, Harvard Apparatus, Holliston, MA) and collected at the outlet B. The continuous buffer flow washed out any chemoattractant that had leaked from the microcapillary into the main channel and established a boundary condition of zero chemoattractant concentration (C = 0) at the mouth M of the microcapillary. From this time on, the concentration profile of chemoattractant C(x) in the microcapillary evolved as a result of molecular diffusion and C = 0 at M. After ∼45 min, injection from inlet A was switched from buffer to a suspension of E. coli using an external valve. Maintaining the same flow speed prevented any flow disruption in the microchannel. A fraction of the bacteria advected past the mouth of the microcapillary swam into it and moved up the concentration gradient (Fig. 1 b). Their trajectories were subsequently recorded, along with the concentration gradient, as described in the next section.

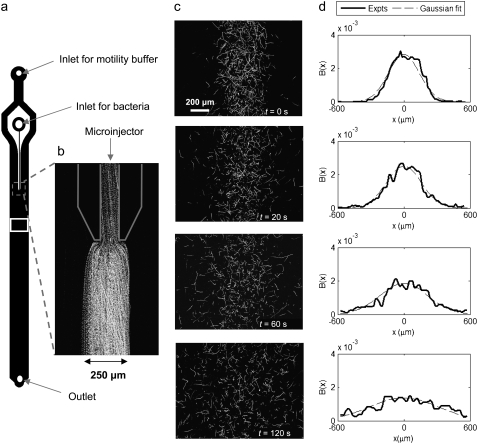
A second microchannel (see Fig. 7 a) was used to measure the random motility μ of E. coli from the lateral diffusion of a thin band of cells. This microchannel, described in detail elsewhere (47), consisted of a 45-mm-long, 3-mm-wide, and 50-μm- (three realizations) or 100-μm- (six realizations) deep channel, with two in-line inlet points, used to separately introduce motility buffer and bacteria with the syringe pump. The inlet through which bacteria were introduced led to a 100-μm-wide PDMS microinjector, which focused the bacteria in a thin band at the center of the main channel. The second inlet was used to flow buffer into the channel, so that the bacterial band was sandwiched between two buffer streams. The three streams flowed side by side, at the same mean speed of 240 μm s⁻¹, until the experiment was started by turning off the flow. This “released” the thin bacterial band, which thereafter spread laterally due to random motility. The distribution of bacteria across the channel was captured over time using videomicroscopy at a fixed location 5 mm downstream of the microinjector tip.

FIGURE 7.

Experiments to determine the random motility μ of E. coli. (a) Schematic of the microfluidic channel. The observation region is marked by a white rectangle. (b) Close-up of the microinjector, showing the 250-μm-wide band of E. coli. The image is composed of 100 frames recorded over 3.1 s, and white tracks represent individual bacterial trajectories. (c) Bacterial trajectories at four times after the flow was stopped (t = 0), “releasing” the band of bacteria. Because no chemoattractant is present, lateral spreading is due to random motility alone. Images are acquired as in b. (d) Profiles of bacterial positions across the channel, B(x), along with the best Gaussian fit. Each profile was normalized to a total area of 1 and corresponds to the adjacent panel in c.

Data acquisition and processing

All experiments were conducted using a computer-controlled inverted microscope (TE2000-E, Nikon, Tokyo, Japan), equipped with a 1600 × 1200 pixels, 14-bit charge-coupled device camera (PCO 1600, Cooke, Romulus, MI). For the set of experiments designed to quantify χ₀, chemoattractant concentrations and gradients in the microcapillary were measured by the addition of 100 μM fluorescein to α-methylaspartate solutions, and epifluorescence imaging with a 2× objective (Fig. 1, c and d). Fluorescein was visualized using a fluorescein isothiocyanate (FITC) filter cube, with excitation at 460–500 nm and emission at 515–560 nm. An earlier study showed that 300 ms pulses of blue light can briefly (<2s) affect motility of E. coli (48). In our experiments, epifluorescent light pulses lasted 200 ms and at least 15 s elapsed between a pulse and data collection. Furthermore, swimming speeds recorded before and 8 s after a 200 ms pulse showed negligible variation (<5%). Fluorescent intensity was converted to concentration via a previously determined calibration curve, which was found to be linear in the range of interest (0–1 mM α-methylaspartate). Across-channel averaging gave a 1D concentration profile C(x) along the microcapillary (Fig. 1 f).

Bacteria were observed at mid-depth of the microcapillary, using phase contrast microscopy and a 20× objective. For each experimental run, a sequence (“movie”) of 300 frames was captured over 9.4 s (32 frames/s). Each movie was analyzed using BacTrack, in-house cell tracking software, to obtain bacterial trajectories: first, each frame was subtracted from the following one to remove background and obtain a cleaner image; then, bacteria in each frame were located as peaks in a monochrome intensity field; finally, bacteria were tracked between frames using particle tracking algorithms. Postprocessing of trajectories in MATLAB (The Mathworks, Natick, MA) yielded the 2D swimming speed of each bacterium and thus the population-average velocity v_2D, as well as the swimming direction asymmetry β. The latter, as defined above, is the ratio of times spent traveling down and up the gradient, respectively. Because individual trajectories tended to be short as a result of bacteria swimming out of the focal plane, it was not possible to calculate β for each trajectory. Instead, β was equivalently calculated as the ratio of the sums of travel times for all trajectories down and up the gradient, respectively. Using v_2D and β we then calculated the chemotactic velocity V_C from Eq. 7.

To sample a range of concentration/concentration-gradient pairs while ensuring nearly simultaneous measurement of bacterial trajectories, we adopted the following automated acquisition sequence: i), a 2× (the number refers to the power of the objective) epifluorescent image of a 6-mm-long segment of the microcapillary (e.g., Fig. 1 d); ii), five to six 20× phase-contrast movies at different locations within the previous 2× field of view (e.g., Fig. 1 e), using computer-controlled motion of the microscope stage; and iii), a second 2× epifluorescent image at the same location as (i). This routine lasted ∼4 min, which accounts for switching objectives, filters, and illumination source as well as stage motion. Comparison between the two epifluorescent images allowed us to quantify the change in the concentration profile over the 4 min time interval. The mean between the two profiles was used for further analysis and denoted C(x). By selecting the region of C(x) corresponding to each 20× movie, we obtained a mean concentration C (as the average of C(x) over the 20× window) and a concentration gradient dC/dx (by a linear fit to C(x) over the 20× window).

For the set of experiments performed to quantify μ, bacteria were imaged at mid-depth, 5 mm downstream of the microinjector tip (see Fig. 7 a), using phase-contrast microscopy and a 10× objective, by taking a 100-frame movie at 32 frames/s every 20 s for 2 min after release of the bacterial band. Bacterial positions in the direction across the channel (x) were determined over all frames in a movie by image analysis as described earlier, yielding the cell distribution B(x,t). Each profile B(x,t) comprised at least 400 bacterial counts, and the experiment was repeated nine times.

RESULTS

Generation and measurement of chemoattractant gradients

To reliably quantify the chemotactic sensitivity χ₀, it is crucial to generate stable chemoattractant concentration profiles and measure them accurately. The on-chip passive valve allowed flow during manual injection to fill the microcapillary with α-methylaspartate solutions while otherwise successfully preventing any external perturbation from inlet C. This was confirmed by visually observing 2 μm fluorescent latex beads, which were found to not move except by Brownian motion. In addition, epifluorescent imaging of fluorescein concentration showed that switching the external valve controlling inflow in the main channel (inlet A) from buffer to bacterial solution did not perturb the concentration profile in the microcapillary.

At the mouth (M) of the microcapillary, flow from the main channel partially intruded into the microcapillary (∼600 μm; Fig. 1 b), exposing bacteria to chemoattractant gradients. A fraction of the bacteria swam out of the flow and into the microcapillary (Fig. 1 b). Because motility is required to move into the microcapillary, this setup guaranteed that only motile cells were subsequently assayed, whereas dead cells and debris from the bacterial culture (e.g., the thicker streaks in the main channel, Fig. 1 b) were washed away. Incidentally, the observed flow intrusion generates a more complex concentration field in the mouth region than predicted by analytical solutions used in previous chemotaxis studies (49) and underscores the importance of direct visualization of the fluid mechanical and chemical environment in a chemotaxis assay. In our experiments, this did not represent a problem, because direct measurement of concentration prevented artifacts associated with the use of analytical solutions. Furthermore, flow in the main channel was turned off well before data collection in the microcapillary began. Flow, then, was used only to initially set up a concentration profile inside the microcapillary and advect bacteria to the mouth of the microcapillary.

Data were collected in the microcapillary between x = 0 and 3 mm at different times, to ensure the chemotactic response of bacteria was captured for a wide range of (C, dC/dx) pairs. Fluorescent intensity images revealed that concentration varied only along the microcapillary (x) and was uniform across it (not shown). We performed three series of experiments with different initial concentrations of α-methylaspartate (C₀ = 0.1, 0.5, and 1.0 mM). The measured values of C and dC/dx ranged from 0.007 to 0.970 mM (0.06–7.76 K_D; K_D = 0.125 mM (44)) and from 0.02 to 0.5 mM/mm, respectively (see Fig. 6). Larger values of C were prevalently sampled at locations farther inside the microcapillary, where dC/dx was smaller, whereas cases with smaller C came primarily from closer to the mouth, where dC/dx was initially large and progressively decreased.

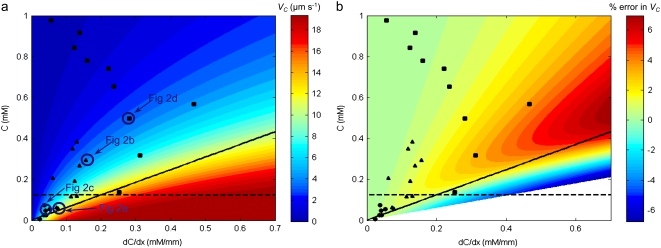
FIGURE 6.

(a) The chemotactic velocity V_C of E. coli exposed to α-methylaspartate as a function of the concentration C and concentration gradient dC/dx. V_C was calculated from Eq. 9 using the experimentally determined values v_2D = 29.8 μm s⁻¹ and χ₀ = 12.4 × 10⁻⁴ cm² s⁻¹. Symbols represent the experimental runs, separated based on initial chemoattractant concentration (•: C₀ = 0.1 mM; ▴: C₀ = 0.5 mM; ▪: C₀ = 1.0 mM). Bacterial trajectories corresponding to four cases (circled symbols) are shown in Fig. 2. The dashed line indicates C = K_D. The solid line represents C = (dC/dx) × v_1D/a_crit (with v_1D = v_3D/2 = 19 μm s⁻¹ and a_crit = 0.03 s⁻¹ (52)). The parameter space below this line represents experimental conditions for which saturation of the adaptation response is expected (52). Only two points fall below the saturation line. (b) The error incurred in estimating V_C (Eq. 9) using the mean nutrient concentration C over the entire field of view, expressed as a percentage deviation from the average V_C calculated for a linearly varying concentration profile, as a function of C and dC/dx. Symbols and lines as in (a). The error is <4% for all experiments. In the white region comparison with a linear concentration scenario is not possible, as it would correspond to negative concentrations.

Measurement and analysis of bacterial trajectories

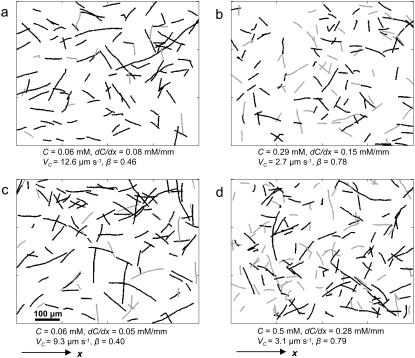
Simultaneously to concentration profile measurements, we tracked individual bacteria swimming in the microcapillary. The mean 2D swimming velocity was v_2D = 29.8 ± 2.7 μm s⁻¹, corresponding to v_3D = 4v_2D/π = 37.9 μm s⁻¹. Statistical analysis revealed no correlation of v_2D with either C or dC/dx, confirming the absence of chemokinetic behavior. On the other hand, the swimming direction asymmetry β and the chemotactic velocity V_C were strongly correlated with the chemoattractant concentration field. Differences in β were so strong as to be discernible visually from sample trajectories (Fig. 2). When concentration gradients were large and concentration was well below saturation (C ≪ K_D; Fig. 2, a and c), trajectories showed a clear bias of motion up the gradient (black) compared to down the gradient (gray). This resulted in small values of β (0.46 and 0.40 for panels a and c, respectively) and large values of V_C (12.6 and 9.3 μm s⁻¹). In contrast, trajectories were nearly equally partitioned between up and down the gradient when concentration exceeded saturation values (C ≫ K_D; Fig. 2, b and d), resulting in considerably larger β (0.78 and 0.79 for panels b and d, respectively) and smaller V_C (2.7 and 3.1 μm s⁻¹).

FIGURE 2.

Digitized trajectories of E. coli corresponding to different combinations of chemoattractant concentration C and concentration gradient dC/dx. Concentration increased along x. Black (gray) trajectories had a net positive (negative) displacement in the direction of the gradient and contributed to the total cumulative time T⁺ (T⁻) cells spent traveling up (down) the gradient. (a and c) C ≪ K_D (K_D = 0.125 mM): most cells had swum up the gradient, resulting in a small swimming direction asymmetry β and a large chemotactic velocity V_C. (b and d) C ≫ K_D: receptors saturated, chemotaxis diminished, and trajectories were nearly equally partitioned between up and down the gradient.

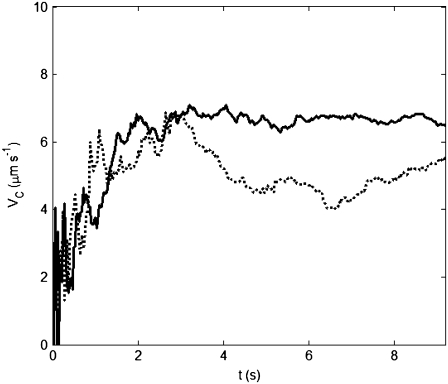
For each value of the initial chemoattractant concentration (C₀ = 0.1, 0.5, 1.0 mM), we computed V_C from Eq. 7 for a range of times and positions along the microcapillary. V_C ranged from 0.6 μm s⁻¹ (β = 0.95) to 13.8 μm s⁻¹ (β = 0.36), corresponding to 1.8% and 35% of the swimming speed v_3D, respectively. To ensure statistical significance of V_C, a convergence test was performed for each experiment, by calculating V_C from a progressively increasing portion of time t of a movie. Two examples are shown in Fig. 3, for a successful (solid line) and a failed (dotted line) converge tests. The estimate of V_C was considered statistically significant when the standard deviation computed from t = 6.6–9.4 s (i.e., the final 30% of a movie) did not exceed 0.5 μm s⁻¹. For most experiments, 9.4 s of data were sufficient to achieve convergence. This corresponded to cumulative trajectory time (i.e., the sum of the durations of all trajectories in a movie) ranging from 376 to 1164 s, or an average of 40–120 bacteria in the field of view. Only in 2 out of 28 cases was convergence not achieved, and those cases were discarded from the analysis.

FIGURE 3.

The chemotactic velocity V_C as a function of time t elapsed in a movie to test for convergence of V_C as described in the text. The solid line shows an experiment where V_C converged to 7.1 μm s⁻¹, and the dotted line corresponds to a run where V_C did not converge. The latter case was discarded from further analysis. The cumulative trajectory time for the two cases was 907 and 494 s, respectively. A recording time of 9.4 s was typically sufficient to ensure convergence, and only 2 out of 28 experiments failed to converge.

Chemotactic sensitivity coefficient χ₀

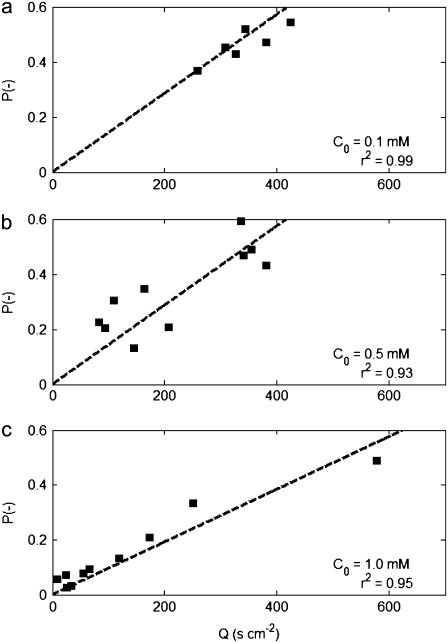
Direct measurement of v_2D and V_C for the 26 pairs of C and dC/dx described above (see Fig. 6 a) enabled us to test the relation between chemotactic velocity and chemotactic sensitivity (Eq. 9). We did so separately for the three sets of experiments corresponding to three initial chemoattractant concentrations C₀. A successful verification of Eq. 9 would have two features: a linear variation of P = tanh⁻¹[3πV_C/(8v_2D)] with Q = π/(8v_2D)[K_D/(K_D + C)²](dC/dx) (Eq. 10), and a slope χ₀ = P/Q that is independent of C₀.

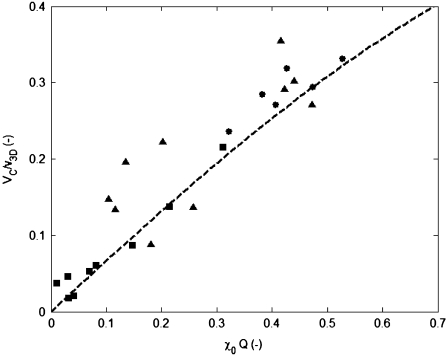
Experimentally determined values of v_2D, V_C, C, and dC/dx were used to compute P and Q for each of the 26 experiments, assuming K_D = 0.125 mM (44). In Fig. 4, we plot P as a function of Q for C₀ = 0.1, 0.5, and 1.0 mM. In all three cases a linear relation satisfactorily describes the dependence of P on Q, as supported by the large value of the correlation coefficient r², with the biggest scatter in the 0.5 mM data (r² = 0.93). A least-squares fit constrained to go through the origin gave χ₀ = 13.5 × 10⁻⁴, 14.3 × 10⁻⁴, and 9.6 × 10⁻⁴ cm² s⁻¹ for C₀ = 0.1, 0.5, and 1.0 mM, respectively, with an average of χ₀ = (12.4 ± 2.0) × 10⁻⁴ cm² s⁻¹, showing good agreement between the three sets of data. This is further emphasized by the agreement between the measured chemotactic velocity and its theoretical prediction, plotted in Fig. 5 as V_C/v_3D vs. χ₀Q, where the experimentally determined mean value was used for χ₀. These results then support the dependence of chemotactic sensitivity on chemotactic velocity derived in Rivero's model.

FIGURE 4.

Determination of the chemotactic sensitivity coefficient χ₀, for three initial concentrations C₀: (a) 0.1 mM; (b) 0.5 mM; (c) 1.0 mM. Each square represents one experiment. Here P = tanh⁻¹(3πV_C/8v_2D), Q = π/(8v_2D)[K_D/(K_D + C)²]dC/dx and the slope P/Q corresponds to χ₀ (Eq. 10). A least-square linear fit constrained to go through the origin (dashed line) gave χ₀ = 13.5 × 10⁻⁴, 14.3 × 10⁻⁴, and 9.6 × 10⁻⁴ cm² s⁻¹ for the three cases, respectively. The average is χ₀ = 12.4 × 10⁻⁴ cm² s⁻¹.

FIGURE 5.

Observed values of the relative chemotactic velocity V_C/v_3D of E. coli toward α-methylaspartate, as a function of χ₀Q (Eq. 10), where χ₀ = 12.4 × 10⁻⁴ cm² s⁻¹ from the experiments. Symbols correspond to the three initial concentrations C₀ = 0.1 (•), 0.5 (▴), and 1.0 mM (▪). The highest value of V_C/v_3D achieved in our experiments was 0.35. The dashed curve represents the theoretical prediction (Eq. 9), which plateaus at V_C/v_3D = 2/3 (not shown).

Having established that the behavioral foundation of the bacterial transport model of Rivero et al. (28) is supported experimentally, one can now use the model along with our measured value of χ₀ to predict the chemotactic velocity of E. coli toward α-methylaspartate as a function of C and dC/dx (Fig. 6 a). When C ≪ K_D, increasing values of V_C are related primarily to increases in dC/dx. In our experiments, this regime often occurred near the mouth of the microcapillary, where dC/dx was relatively large and C was low. Conversely, in the region of Fig. 6 a where C ≫ K_D (corresponding to receptor saturation), V_C ≈ 1/C² and changes in V_C are dominated by changes in C: this regime occurred farther into the microcapillary.

Effect of temporal and spatial averaging

Our approach for calculating χ₀ relied on both temporal and spatial averaging of the chemoattractant concentration to obtain C and dC/dx. As bacteria experienced local and instantaneous concentrations, rather than mean values, it is important to quantify the error associated with these averaging processes. Temporal averaging comes from taking the mean of the concentration profiles from two epifluorescent images recorded ∼4 min apart. Comparison of the two images showed that C and dC/dx varied at most by 4.2% and 8.2%, respectively, translating into an error in V_C that is always <8.1% and 8.2%, respectively, for all experiments. As for spatial averaging, the use of a constant value of dC/dx was justified because C(x) was nearly perfectly linear (r² > 0.96) over each 20× field of view. On the other hand, changes in C(x) over a field of view (L = 600 μm) could be substantial (ΔC = 0.30 mM for the steepest gradient, dC/dx = 0.50 mM/mm). Because Q (Eq. 10) is related nonlinearly to C [Q ≈ (1 + C/K_D)⁻²], use of a mean concentration could bias the calculation of χ₀. To investigate this further, we computed the average V_C over the field of view, as 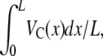using Eq. 9 with a linearly varying C(x) (and v_2D = 29.8 μm s⁻¹, K_D = 0.125 mM, χ₀ = 12.4 × 10⁻⁴ cm² s⁻¹). Compared to this value of V_C, the one computed using the mean concentration never differed more than 4% (Fig. 6 b) for our experimental conditions, justifying the use of the mean concentration C in determining χ₀.

Random motility coefficient μ

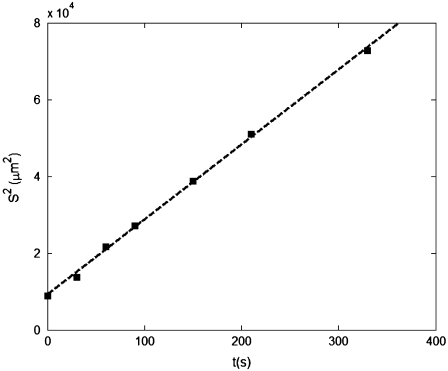
To fully characterize bacterial transport at the population scale, one further requires the random motility coefficient μ. We proceeded to measure μ for E. coli by observing the spreading of a band of bacteria. Using a microchannel equipped with a microinjector, we successfully generated a 250-μm-wide band of E. coli (Fig. 7 b). The experiment started by turning off the flow (at time t = 0), causing the bacterial suspension to stop nearly immediately (<3 s). The band of bacteria diffused laterally, due to random motility, and the cell distribution B(x,t) across the channel was recorded at a range of times after release of the band. At each observation time t, a 1D Gaussian (Eq. 11) was fitted to B(x,t) (Fig. 7 d), and the standard deviation S of the Gaussian was taken as a measure of the lateral width of the bacterial band. The linear increase of S² with time (Fig. 8) confirmed the diffusive nature of random motility. A linear least-squares fit to S² = 2μ(t + t₀), where (2μt₀)^1/2 is the initial width of the bacterial band, yielded values of μ ranging from 1.8 × 10⁻⁶ to 4.8 × 10⁻⁶ cm² s⁻¹ for nine realizations, with an average of μ = (3.3 ± 0.8) × 10⁻⁶ cm² s⁻¹. Negligible differences were observed among the two bacterial batches and for the two different channel depths (50 and 100 μm). In this analysis, effects from side boundaries were ignored because the observation time (2 min) was much shorter than the diffusive time for the bacterial band to reach the sidewalls (∼(1.5 mm)²/(2μ) ≈ 56 min). The mean swimming speed recorded for the random motility experiments was v_2D = 23.3 μm s⁻¹, somewhat lower than for the chemotaxis experiments.

FIGURE 8.

The squared standard deviation S² of the across-channel bacterial distribution corresponding to the experiments in Fig. 7 d, as a function of time t elapsed since release of the bacterial band. The dashed line represents the best linear fit, and its slope is 2μ. This experiment yielded μ = 3.6 × 10⁻⁶ cm² s⁻¹. The average random motility over nine experiments was μ = 3.3 × 10⁻⁶ cm² s⁻¹.

DISCUSSION

In many phenomena, the macroscopic behavior of a system emerges from the aggregate effect of a large number of players acting at smaller scales. It is then convenient to seek averaging procedures to achieve predictive power over the system's behavior without accounting for the microscale details of individual processes. Yet, before confidently doing so, it is both necessary and instructive to test such upscaling procedures experimentally, to ensure that macroscopic formulations adequately reflect the underlying microscopic dynamics. Also, observations at the scale of individual processes can shed light on additional detail lost in the averaging procedure. In the case of bacterial chemotaxis, the fate of a population emerges from the aggregate behavior of individual cells. The probabilistic model of Rivero et al. (28) provides the mechanistic basis, at the single-cell level, for the population-scale formulation of bacterial transport (Eq. 2), which in turn enables one to predict the fate of a bacterial population under arbitrary chemoattractant concentration conditions. Here, we used microfluidics and single-cell tracking to provide an experimental validation of the behavioral foundation for the mathematical upscaling at the basis of the bacterial transport equation.

We fabricated microfluidic devices to generate and measure a range of chemoattractant concentrations and concentration gradients, simultaneously capturing single-cell chemotactic behavior. This enabled us to directly determine the chemotactic sensitivity coefficient χ₀. Our observed value of χ₀ was somewhat larger than literature results for E. coli exposed to α-methylaspartate (Table 1) but in the same order and not statistically different (Student's t-test, p < 0.05). Variation in α-methylaspartate concentrations and use of different bacterial batches resulted in <50% variation in χ₀, a variability that compares very favorably with the five- to sevenfold change in χ₀ typically reported for replicate experiments of bacterial chemotaxis (25). Our study, then, provides a quantitative experimental verification of the behavioral basis of the bacterial chemotactic migration model proposed by Rivero et al. (28) and complements their initial validation based on previous population-scale data (50).

TABLE 1.

Chemotactic sensitivity χ₀ of E. coli to α-methylaspartate

χ0 (10−4 cm2 s−1)	Chemotaxis assay	Reference
7.5	Capillary	(44)
4.1 ± 0.2	SFDC	(80)
2.4 ± 0.6	SFDC	(46)
12.4 ± 2.0	Microfluidic capillary	This study

SFDC = stopped-flow diffusion chamber.

Our measurements (Fig. 5) revealed chemotactic velocities as high as 35% of swimming speed (v_3D), larger than most literature values (17,50,51). For example, Berg and Brown (17) measured V_C = 0.9 μm s⁻¹ = 0.06v_3D for E. coli in aspartate and V_C = 2 μm s⁻¹ = 0.14v_3D in serine, whereas Dahlquist et al. (50) found V_C = 3.5 μm s⁻¹ = 0.23v_3D for Salmonella in serine. The wider range of V_C/v_3D observed here is likely due to the broader set of concentration conditions explored in our setup, whereas those earlier studies focused on the mechanistic and molecular underpinnings of chemotaxis by working prevalently in shallow gradients.

Fig. 6 a shows that one could in principle attain even higher chemotactic velocities, with a theoretical limit of V_C/v_3D = 2/3 (Eq. 9), by exposing cells to larger concentration gradients. However, when dC/dx is too large the adaptation response of E. coli saturates (the adaptation response is the change in counterclockwise bias of motors during an attractant stimulus that varies exponentially in time t from an initial concentration C₀, i.e., C(t) = C₀ e^at, where a is the ramp rate) (52). Using tethered cells, Berg and co-workers (52) found the adaptation response to depend on the ramp rate a = (1/C) × (dC/dt), characterizing the fractional time rate of change in concentration experienced by a bacterium. For a < a_crit, E. coli's response to chemoattractants is a function of the time rate of change of chemoreceptor occupancy, as in the model of Rivero et al. (28). On the other hand, the adaptation response saturates above a critical ramp rate a_crit, with a_crit ∼0.03 s⁻¹ for α-methylaspartate (Fig. 6 A in Berg et al. (52)). For a > a_crit, cells can take seconds to minutes to adapt (45,53) and the model of Rivero et al. (28) is no longer applicable. For a swimming cell, the ramp rate is a = (dC/dx) × v_1D/C, where v_1D = v_3D/2 (43). Thus, the response saturates (a > a_crit) at high concentration gradients dC/dx and low concentrations C.

The threshold for saturation (a = a_crit) can then be expressed as C = (dC/dx) × v_1D/a_crit, a straight line in the (C, dC/dx) space (Fig. 6 a): below this line, saturation is expected to occur. Fig. 6 a shows that 24 out of 26 of our experiments were conducted in the linear regime of the adaptation response (i.e., above the saturation line), as a result of letting the initial step in concentration diffuse substantially before exposing bacteria to chemoattractants, unlike previous approaches (49,54). Only two data points fall in the saturation regime (below the line), one of them corresponding to the “outlier” (rightmost point) in Fig. 4 c. It is noteworthy that if one removed this data point from the analysis (removal of the second point has no effect), one would obtain χ₀ = 12.8 × 10⁻⁴ cm² s⁻¹ for C₀ = 1 mM (Fig. 4 c), bringing the average to χ₀ = (13.5 ± 0.6) × 10⁻⁴ cm² s⁻¹ and further improving the agreement among the three sets of experiments. Finally, the requirement that adaptation should not saturate reduces the maximum predicted value of V_C, which can be computed as the maximum from Eq. 9 under the constraint dC/dx = (1/C) × v_1D/a_crit. The new maximum V_C is reduced by a factor tanh(χ₀a_crit/4v_3D) compared to the theoretical one V_C/v_3D = 2/3 and occurs when C = K_D (the intersection between solid and dashed lines in Fig. 6 a). With χ₀ = 12.4 × 10⁻⁶ cm² s⁻¹ and v_3D = 37.9 μm s⁻¹, we find V_C/v_3D = 0.38, which compares favorably with our largest measured value of chemotactic velocity (V_C/v_3D = 0.35).

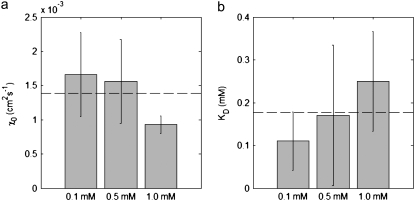
Although our quantification of χ₀ was based on previous knowledge of the dissociation constant K_D, the approach is also applicable to bacteria with unknown K_D. In this case, K_D and χ₀ can be determined simultaneously from nonlinear least-square fitting of Eq. 10 to the data. We implemented this simultaneous fitting of K_D and χ₀ for each of the three series of experiments using MATLAB's curve-fitting toolbox and report results in Fig. 9. Although some scatter is apparent in the estimate of χ₀, mean values for both parameters (χ₀ = 13.8 × 10⁻⁴ cm² s⁻¹; K_D = 0.171 mM) are in good agreement with our earlier estimate of χ₀ (Table 1) and values from the literature for K_D (0.125 mM (44) to 0.160 mM (45)). This demonstrates that a priori knowledge of K_D is in fact not required in estimating χ₀.

FIGURE 9.

Simultaneous determination of (a) χ₀ and (b) K_D, obtained by the nonlinear fitting of Eq. 9 to the experimental data for the initial conditions C₀ = 0.1, 0.5, and 1.0 mM. The dashed line represents the mean of the three sets of experiments, and the error bars indicate 95% confidence intervals.

It remains to be seen whether Eq. 9 is an accurate model for bacteria other than E. coli. The upscaling of simple mechanistic movement rules (28) is generally applicable, but the relation between V_C and C as well as dC/dx (Eq. 9) might be specific to E. coli, and different functional dependences might be appropriate for other bacteria. Furthermore, Eq. 9 does not account for chemokinetic behavior (i.e., changes in swimming speed associated with local concentration conditions). Although this was accurate in our case, for the swimming speed of E. coli was found to be independent of C and dC/dx, other bacteria are known to display chemokinesis (55,56), and the corresponding term in the model of Rivero et al. (28) would then have to be included in the analysis.

Why were we able to use a single-cell approach to determine χ₀, but not μ? The small depth of focus of traditional microscopy severely limits the duration over which individual bacteria can be tracked. Thus, individual run times (T₀) as well as directional persistence (ψ), elegantly measured by Berg and Brown (17) with a 3D tracking microscope, are difficult to obtain reliably with a 2D setup. Fortunately, this does not affect the determination of V_C (hence χ₀), as only the swimming speed and the ratio of run times β are required in this case (Eq. 7), both of which are independent of trajectory duration. The situation is different for μ (Eq. 8), which directly depends on average run time (T₀), making a single-cell approach more challenging. To obtain longer trajectories, one could use shallower microchannels, at the expense of increased confinement artifacts, or recently developed 3D visualization techniques, such as defocused particle tracking (57) and digital holographic microscopy (58).

On the other hand, unlike χ₀, μ can easily be determined from population-scale data, as neither concentration gradients nor numerical solutions of the transport equation (Eq. 2) are required in this case. Hence, a single-cell approach is primarily of interest for determining χ₀, whereas μ is best obtained from population-scale methods. Here, we illustrated one such method by using microfluidics to generate a band of bacteria and tracking its diffusion over time. We found a value of random motility (μ = (3.3 ± 0.8) × 10⁻⁶ cm² s⁻¹) of magnitude comparable to that obtained from the single-cell estimate from Eq. 8 (μ = 4.2 × 10⁻⁶ cm² s⁻¹, using v_2D = 23.3 μm s⁻¹ and assuming T₀ = 1 s and ψ = 0.3), particularly in light of the three orders of magnitude variability in literature values of μ for E. coli ((0.1–72) × 10⁻⁶ cm² s⁻¹ (46)), likely associated with differences in bacterial strains, growth, and experimental conditions.

Our microfluidic capillary assay presents several advantages over traditional chemotaxis assays. First, the laminar nature of the flow (59) prevents mixing except by molecular diffusion and allows fine-scale concentration profiles to be generated and accurately measured, bypassing the need for theoretical predictions. This eliminates the risk of unpredictable perturbations (25) arising from natural (60) or operator-induced convection (51). Second, the size and transparency of microchannels are optimally suited for microscopy, enabling direct observation of single bacteria and quantification of their chemotactic response by automated image analysis and cell tracking. This method of quantifying chemotaxis bypasses plate counting, which is both time-consuming (1–3 days (61)) and inaccurate. Third, by relying on single-cell information, one can analyze cultures with lower cell densities (<10⁷ cells/ml) compared to population-scale assays (∼10⁸ cells/ml (46)), reducing consumption of metabolizable chemoattractants, which generates unpredictable secondary gradients (49,62). Fourth, analysis of chemotaxis in a microcapillary accessible only to motile bacteria excludes nonmotile cells and debris, unlike previous approaches (7,25,27,46), enhancing the signal/noise ratio in the measurements. Fifth, studying chemotaxis under no-flow conditions prevents potential artifacts associated with flow-based gradient generators (33,36–38) where hydrodynamic shear might reorient cells (34,63,64) and potentially impair chemotaxis (63). Finally, the use of an unsteady concentration profile allows the sampling of a range of gradients within a single experiment. In this respect, steady gradients might allow greater repeatability, but microfluidic devices that generate steady gradients have only recently been proposed (39,40,65) and have seen limited application to bacterial chemotaxis, always at the population scale. We are currently working on applying steady-gradient microfluidic devices to single-cell investigations.

We see two potential drawbacks in our approach. First, measurements of V_C were based on quantification of bacterial fluxes. For uniform bacterial distributions, the only flux is the one associated with chemotaxis (BV_C in Eq. 1), as dB/dx = 0: thus, one is justified in calculating V_C from measured bacterial fluxes. In our experiments, however, bacteria moved freely within the microcapillary, giving rise to nonuniform distributions B(x,t). The ensuing diffusive flux of bacteria, −μ(dB/dx), contributed to the total observed flux and could thus have potentially affected our measurement of V_C. We verified that this was not the case by comparing diffusive and chemotactic fluxes and found that in all experiments the diffusive flux was negligible, since |μ(dB/dx)/(BVc)| < 4 × 10⁻³ ≪ 1. This was a result of allowing sufficient time for redistribution of bacteria before data collection. Second, the confined microchannel environment could potentially have influenced V_C by affecting bacterial motility. Boundaries are well known to alter motility in complex fashions (66–73). Although one cannot completely rule out boundary effects on V_C, these are confined to within 5 (74) to 10 (71) μm from boundaries, whereas the microcapillary depth (60 μm) is twice a typical E. coli run length (∼30 μm (16)). Besides, the use of fluorescein as a proxy for chemoattractant concentration holds only for low-molecular-weight attractants: for less-diffusive compounds, one would have to seek fluorescent dyes of higher molecular weight.

In conclusion, we have shown that single-cell swimming information accurately and reproducibly encodes the parameters governing chemotaxis of a bacterial population, enabling the direct quantification of chemotactic velocity and chemotactic sensitivity for a broad range of chemoattractant concentration conditions. This bypasses the need to fit the bacterial transport equation to observed bacterial distributions. At the same time, the ability to carefully measure the concentration field bypasses the use of theoretical predictions. Thus, our approach removes two key drawbacks (and the associated uncertainties) characteristic of most existing assays. The use of microscopic information provides a complementary approach to study microbial processes compared to traditional population-scale methods and allows the experimental verification of the behavioral foundation of chemotactic transport. This, in turn, lends confidence to the predictive use of population-scale models to a wide range of applications whenever bacteria are exposed to chemically heterogeneous environments.

Furthermore, individual-based data can reveal mechanistic details that are not observable at the population scale (75), and important questions in microbial ecology hinge on the behavior of individuals, including cell-cell interactions, quorum sensing (76), predation (77), and resource tracking (78). The relevance of single-cell information is directly proportional to the level of resolution at which one wishes to investigate a given process. The quantitative understanding of population-scale processes ultimately emerges from an accurate mechanistic description of the underlying dynamics at the single-cell level. Here, we used novel experimental tools to provide what is, to our knowledge, the first experimental verification of the mechanistic processes underlying a macroscopic bacterial transport model. We foresee that, by providing high-resolution information at the behavioral level, microfluidic techniques will trigger a deeper understanding of the ecology of motile microorganisms.

APPENDIX

For completeness, we provide a derivation of the expression for chemotactic velocity V_C, focusing on the 1D case for simplicity. Rivero et al. (28) derived an expression for V_C in terms of cell speed and tumbling probability:

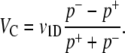(A1)

Brown and Berg (79) observed an exponential increase in run times (T) with the time rate of change in the number of bound receptors (N), relative to run times measured in the absence of chemical gradients (T₀). This led them to propose the empirical relation

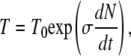(A2)

where σ is a proportionality constant describing the fractional change in mean run time per unit rate of change in bound receptors. For a single homogeneous cell receptor population, at receptor/ligand binding equilibrium N is given by

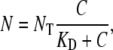(A3)

where N_T is the total number of receptors for that ligand. Since the mean run time is the reciprocal of the tumbling probability, Eq. A2 can also be written in terms of the tumbling probability:

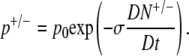(A4)

Here we separated the cases of cells swimming up (p⁺ = 1/T⁺) and down (p⁻ = 1/T⁻) the gradient, and p₀ (= 1/T₀) is the tumbling probability in the absence of chemical gradients. The material derivative D/Dt is necessary to account for both temporal and spatial changes in attractant concentrations experienced by cells swimming at speed v_1D and is defined as

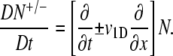(A5)

Substituting Eqs. A4 and A5 into Eq. A1 yields, after some algebra,

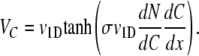(A6)

From Eq. A3 we further obtain

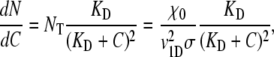(A7)

where χ₀ =N_T 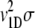represents a fractional change in dispersal capability per unit fractional change in receptor occupancy (54). Substituting Eq. A7 in Eq. A6 gives

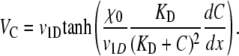(A8)

This relation expresses the dependence of the chemotactic velocity on the time rate of change of bound receptors. The case of bacteria swimming in 3D is treated in Chen et al. (42) and results in Eq. 9, which expresses the same relation, only with different numerical prefactors to account for the dimensionality of the problem.