Peptide Aggregation and Pore Formation in a Lipid Bilayer: A Combined Coarse-Grained and All Atom Molecular Dynamics Study

Abstract

We present a simulation study where different resolutions, namely coarse-grained (CG) and all-atom (AA) molecular dynamics simulations, are used sequentially to combine the long timescale reachable by CG simulations with the high resolution of AA simulations, to describe the complete processes of peptide aggregation and pore formation by alamethicin peptides in a hydrated lipid bilayer. In the 1-μs CG simulations the peptides spontaneously aggregate in the lipid bilayer and exhibit occasional transitions between the membrane-spanning and the surface-bound configurations. One of the CG systems at t = 1 μs is reverted to an AA representation and subjected to AA simulation for 50 ns, during which water molecules penetrate the lipid bilayer through interactions with the peptide aggregates, and the membrane starts leaking water. During the AA simulation significant deviations from the α-helical structure of the peptides are observed, however, the size and arrangement of the clusters are not affected within the studied time frame. Solid-state NMR experiments designed to match closely the setup used in the molecular dynamics simulations provide strong support for our finding that alamethicin peptides adopt a diverse set of configurations in a lipid bilayer, which is in sharp contrast to the prevailing view of alamethicin oligomers formed by perfectly aligned helical alamethicin peptides in a lipid bilayer.

INTRODUCTION

Antimicrobial peptides provide an opportunity to develop novel and more efficient antibiotics against organisms that continue to develop resistance to conventional antimicrobial agents. An improved understanding of the mechanism of these peptides is therefore not only of interest from a biophysical point of view but also relevant to biomedical research. Alamethicin is a 20-amino acid antimicrobial peptide isolated from the fungus Trichoderma viride (1). Similar to many other antimicrobial peptides, alamethicin is believed to exert its effects through direct interaction with the cellular membrane, resulting in disruption of the ionic gradients and electric potential across the membrane (2). It is assumed that the peptides accomplish this by forming nonselective pores or channels in the membrane, allowing water and ions to traverse the membrane freely.

As alamethicin represents a simple example of a membrane channel, numerous experimental studies have been conducted to investigate its physicochemical properties; see reviews (3–6) and references therein. Both experimental and simulation studies of alamethicin suggest that there are at least two distinct membrane-bound states for individual alamethicin peptides: a surface-bound state and a membrane-spanning state (7–12). It is also suggested that the peptide reaches the membrane-spanning state through insertion and translocation of its N-terminus across the bilayer (13,14). A detailed structure of individual alamethicin peptides in the pore forming state is unknown, but experiments indicate a mostly α-helical structure for the peptide in environments such as methanol and sodium dodecyl sulfate micelles (15,16) suggesting that alamethicin is likely in its helical form when forming pore-like structures in a lipid bilayer, in agreement with solid-state NMR experiments of alamethicin in di-myristoyl phosphatidylcholine (DMPC) bilayers by Bak et al. (7). Moreover, the oligomeric structure of alamethicin pores is also largely unknown. For example, there is no direct evidence for the number of peptides and their arrangement in a pore. The most widely accepted model packs 4–11 ordered helices in a barrel-stave like manner, forming a channel with hydrophilic side chains lining the pore. However, alamethicin only has three hydrophilic side chains, two of which are positioned at the C terminus, i.e., outside the transmembrane segment, perfectly placed for interactions with the lipid headgroups. It is thus not evident that the stabilization gained from clustering of the hydrophilic side chains is the main determinant of the aggregates' structure in a lipid bilayer. Investigation of the interactions of alamethicin peptides within a lipid bilayer and the process of aggregation and pore formation is therefore of high relevance to our understanding of its biological effects. The results of such investigations might also provide insight in regard to the general rules governing the assembly of helical membrane proteins.

Molecular dynamics (MD) simulations offer an effective approach for developing a dynamical view of various molecular processes at an atomic level. Several simulation studies of the alamethicin monomer and preformed alamethicin channels in a lipid bilayer have been reported (11,17–23). However, the all-atom (AA) representation of the system in these studies limited the timescales reached to a few 10s of nanoseconds. In a recent study by Marrink et al. (24), magainin peptides insert into a di-palmitoyl phosphatidylcholine bilayer and form a toroidal pore in the membrane within only 60 ns. Tieleman et al. (25) have also observed spontaneous peptide aggregation in an octane slab within 45 ns, and Esteban-Martin and Salgado (26) have captured the most favorable insertion of a peptide in a lipid bilayer, from self assembly of the lipid bilayer around the peptide in 50–100 ns. Still, a timescale around 100 ns is not expected to be sufficient for the complete description of such processes as spontaneous peptide aggregation in a lipid bilayer and pore formation.

To circumvent the timescale problem, the molecular system can be described using a coarse-grained (CG) model, representing groups of atoms as single units (beads), thereby, reducing the number of degrees of freedom and the number of pair interactions in the system significantly. CG models of lipid/water systems (27–31), and, more recently, systems including proteins (32–40) have proven very useful in simulations of various biomolecular systems and in reproducing certain physicochemical properties. CG simulations can be carried out on the microsecond timescale for problems where detailed atomistic interactions are not critical, because the process is largely driven by coarser interactions, e.g., separation of hydrophobic and hydrophilic clusters. Despite their efficiency in regard to the timescale, CG models naturally come short in describing certain aspects of molecular phenomena that rely on atomic-detailed interactions. Very often, the two levels of description need to be applied to various parts of the system simultaneously (multiscale simulations) to describe the process. Such methods are of great interest and actively pursued in the field (41–45), however, accurate description of the interaction between different resolution scales continues to pose a challenging problem.

We present a problem (peptide aggregation and pore formation of alamethicin) that can only be described through a different form of such multiscale methodologies in which CG and AA simulations are used sequentially to benefit both from the long timescale of CG simulations and from the high resolution of AA simulations, which proved necessary to complete the process. During the CG simulations, the peptides spontaneously aggregate in a lipid bilayer and transition between the membrane-spanning and the surface-bound states. However, due to the large size of CG water, the CG simulations are unable to describe detailed water-bilayer interactions such as the process of water file formation across the bilayer, thus, clearly requiring the model to be converted back to an AA representation. In the AA simulation we are then able to describe the completion of the pore formation process, identifying major defect regions in the bilayer and the role of the peptides in the pore formation.

METHODS

A more comprehensive and detailed description of the methods is provided as Supplementary Material, Data S1. In short, an equilibrated AA system consisting of alamethicin peptides, DMPC lipids, and water was used to generate a CG model, which was simulated in several independent simulations each for 1 μs to describe and investigate the behavior and aggregation of the peptides in the membrane. One of the CG systems at t = 1 μs was then converted back to an AA representation (reverse coarse grained using the procedure described in Shih et al. (46) and Freddolino et al. (47)), and subjected to a 50-ns AA simulation, in which the properties of the peptide aggregates and the lipid bilayer, particularly in regard to water conduction across the membrane, were studied. Furthermore, solid-state NMR experiments were carried out on a setup similar to the MD setup to investigate the conformational state of alamethicin with respect to the membrane.

Alamethicin

Alamethicin (Fig. 1, a-d) is rich in small, α-helix-promoting amino acids, namely alanine (Ala) and the nonstandard amino acid α-methylalanine (Aib). It exists in two naturally occurring variants: the R_f30 form (Fig. 1 d) and the R_f50 form, where a glutamate (Glu¹⁸) is replaced by a glutamine (Gln). The protonation state of Glu¹⁸ at neutral pH has been studied by AA simulations of a channel model with different protonation states of this residue (20), indicating that the channel was more stable when Glu¹⁸ was protonated. Therefore, this residue was kept protonated in our simulations. Other important features include an acetylated N-terminus and the presence of a modified phenylalanine (phenylalaniol, Phl) in the C terminus. The peptide is consequently neutral.

FIGURE 1.

(a–d) Alamethicin. (a) AA representation of a peptide after 1 ns of equilibration of the system setup shown in (g). Side chains are shown in licorice, with hydrophilic side chains in orange. (b) NAMD CG representation of the peptide shown in a. Backbone shown in cyan licorice, apolar beads (class C) are gray, and nonpolar with hydrogen bond donor and acceptor properties (class Nda) are orange. The bead classes are defined in Data S1. (c) MARTINI CG representation of the peptide shown in a. Backbone shown in cyan licorice, apolar beads (class C) are gray, and polar beads (class P) are orange. (d) The amino acid sequence aligned approximately to the structures shown in a–c. (e, f) DMPC lipid. (e) AA representation. The choline moiety is colored purple, the phosphate group pink, the glycerol linkage green, and the lipid tails gray. (f) NAMD CG representation. Apolar beads (class C) are gray, nonpolar with hydrogen bond acceptor properties (class Na) are green, and charged beads are either purple (class Q0) or pink (class Qa). (g) Initial AA setup. Water is excluded for clarity. Lipid bilayer with transmembrane peptides (cyan ribbons) shown from the top view. Lipids are gray with phosphates in pink. The lipids have been equilibrated for 0.2 ns. (h) The reverse coarse-graining procedure for a peptide (top row) and a lipid (bottom row). In the first column the structures taken from the initial equilibrated AA setup are shown. In the second column they are mapped to their CG representation. The third column depicts the peptide and the lipid after 1 μs of CG simulation. The reverse coarse-graining is then done by translating the respective atom groups from the initial equilibrated AA setup to the CG beads position at t = 1 μs (fourth column). The fifth column is the AA representation of the system at t = 1 μs after a simulated annealing (SA) where the COM of atoms corresponding to a bead was constrained to the position of the CG bead at t = 1 μs.

System setup

From oriented circular dichroism studies it is known that the ratio of membrane-spanning alamethicins versus the surface-bound form depends on the peptide/lipid ratio (48,49). Based on these experiments a molar peptide/lipid ratio of 1:13.2 was chosen to maximize the population of membrane-inserted alamethicins, which is likely the active state of the peptide. The system was thus built from 25 peptides and 330 lipids. Moreover, this ratio compares well with the ratio of 1:15 applied in the solid-state NMR experiments described below. Two additional setups including higher and lower concentrations of the peptide (49 peptides in 326 lipids and 16 peptides in 328 lipids) were also studied in 1 μs CG simulations, but the AA simulation and most of the results discussed here will be based on the simulations with the 25 peptides in 330 lipids setup.

The C monomer from the x-ray crystal structure of alamethicin in acetonitrile/methanol (15) (pdb-file 1AMT) was used for the initial AA system setup. The helical peptides were placed strictly parallel to the membrane normal (the z axis) and only translated in the xy plane to form a 5 × 5 lattice, with the centers of the peptides masses separated in the x and y directions by 28.5 Å (Fig. 1 g). With the peptides in place, a DMPC lipid molecule (Fig. 1 e) was replicated, randomly rotated around its long axis (z), and translated in the xy plane to fill the space between the peptides in the model. The lipid bilayer with the peptides was then solvated with water. As no charged residues are present in alamethicin, and the used lipids are electroneutral, the system was electrically neutral and, thus, no ions were needed. The AA system (∼125,000 atoms) was energy-minimized and equilibrated for 200 ps with the peptides fixed. The peptides were then released and the entire system energy-minimized and equilibrated for 1 ns in the NPT ensemble (T = 323 K, P = 1 atm) using NAMD 2.6b1 (50) and the CHARMM27 parameter set (51). Necessary additions to the topology and parameter files due to the nonstandard amino acids in alamethicin are described in Data S1.

Coarse-graining the system

The three setups with different peptide concentrations as described above were each simulated for 1 μs of NAMD CG simulation. To test the reproducibility of the results, two additional 1-μs NAMD CG simulations and one 1-μs GROMACS-MARTINI CG simulation were also carried out for the setup with 25 peptides and 330 lipids.

Both the NAMD and the MARTINI CG models are based on the CG model developed by Marrink et al. (29) for lipid-water systems. In this model a small group of atoms (about four heavy atoms and their hydrogens) are mapped to a CG particle (or bead). Four water molecules are mapped to one CG water bead, and the lipids are described by four headgroup beads, and a bead for every four carbon atoms in the tails as illustrated in Fig. 1, e and f.

NAMD CG simulation

For the NAMD CG simulations the original lipid-water CG model (29) is applied, and extended to proteins by Shih et al. (36). The protein CG model converts each amino acid into two CG beads: a backbone (BB) bead and a side chain (SC) bead. The exceptions are glycine (Gly) which does not have a SC bead, and the nonstandard residue Aib. The only difference between Ala and Aib is an extra methyl group on Cα in Aib, and it is therefore represented by two Ala SC beads attached to the BB bead. The NAMD coarse-graining of alamethicin is illustrated in Fig. 1 b. More details on the NAMD coarse-graining of the system can be found in Data S1.

From the equilibrated AA setup, the lipid-peptide part of the system was coarse-grained and re-solvated with CG water resulting in a CG setup (25 peptides, 330 lipids) with 11,773 beads and a unit cell with dimensions of 120 Å × 124 Å × 90 Å. After energy-minimization of the CG system, the NAMD production runs of 1 μs were carried out using a modified version of NAMD 2.5 (50) as described in Shih et al. (36). The temperature was kept at 323 K using a Langevin thermostat with a damping coefficient of 0.5 ps⁻¹. The choice of this parameter is very important, as it effects the diffusion of lipids and peptides within the bilayer, particularly in CG simulations. Periodic boundary conditions (PBC) were used and the pressure was kept at 1 atm using a Nosé-Hoover Langevin piston (52) with a piston period of 200 fs and a decay time of 100 fs. Nonbonded interactions were cut off at 12 Å, with shifting throughout the interaction range for electrostatic interactions and beginning at 9 Å for vdW interactions to implement a smooth cutoff. Pair lists were updated at least once per 20 steps, with a 16 Å pair list cutoff. The simulations were performed using a 20 fs time step. The computational cost for a 1 μs simulation was 8.5 days on 12 processors (6 Sun X2100 nodes; 2.2 GHz dual core AMD/Opteron, 2 GB memory; connected through a gigabit switch).

GROMACS-MARTINI CG simulation

MARTINI is the continued work of Marrink and coworkers on their original lipid-water CG model (29). It includes a fine-tuned version of the lipid model (MARTINI v2.0 (31)), and a protein CG model (MARTINI v2.1 (40)) developed in the same framework. Amino acids are represented by 1–5 CG beads; Gly and Ala are only represented by their BB bead, whereas other amino acids are represented by a BB bead and 1–4 SC beads depending on the size of the side chain and the involvement of a ring structure. In the MARTINI coarse-graining of alamethicin, Aib is represented by only one bead, i.e., same as Ala. MARTINI describes Ala to be slightly less polar than Gly; analogously, Aib is described as being slightly less polar than Ala. The MARTINI coarse-graining of alamethicin is illustrated in Fig. 1 c. Whereas DMPC lipids were modeled with four beads in each tail in the original CG model (29), only three beads in each tail is used in MARTINI v2.0. The coarse-graining of the lipids is done as illustrated in Fig. 1 f, but without the terminal beads in the lipid tails. More details on the MARTINI coarse-graining of the system can be found in Data S1.

From the equilibrated AA setup, the peptide part of the system was coarse-grained. The lipid-water part of the system was mapped from the NAMD coarse-graining of the AA setup, simply removing the terminal beads in the lipid tails. This resulted in a CG setup with 10,688 beads (25 peptides, 330 lipids) and a unit cell with dimensions of 120.5 Å × 123.7 Å × 92 Å. After energy-minimization of the CG system, the production run of 1 μs was carried out using GROMACS version 3.3.3 (53–55). The temperature for each molecular group (lipids, water, and peptides) was kept constant using the Berendsen temperature coupling algorithm (56) with a time constant of 0.1 ps. PBC and semi-isotropic pressure coupling was applied using the Berendsen algorithm (56), with a pressure of 1 bar independently in the plane of the membrane and perpendicular to the membrane. A time constant of 0.2 ps and a compressibility of 3 × 10⁻⁵ bar⁻¹ were used. As part of the MARTINI CG model for amino acids the bond lengths in the SC of Phl and the BB-SC bonds for valine were constrained with the LINCS algorithm (57) to avoid numerical instabilities arising from fast fluctuations (40). For nonbonded interactions the same cut off and shifting were used as for the NAMD CG simulations. Pair lists were updated every 10 steps, with a 12-Å pair list cutoff. The simulation was performed using a 30 fs time step. The computational cost for the total 1 μs simulation was 2.8 days on eight processors (four Dell SC1435 nodes; 2.6 GHz dual core AMD/Opteron, 8 GB memory; connected through a gigabit switch).

Comparing NAMD and MARTINI CG simulations

The timescale in CG simulations is very difficult to define. How fast the dynamics is depends on the CG model (and to some degree the temperature and pressure settings). Although in this study we are interested primarily in the configuration of the peptide clusters and not much in the timescale they require to form, to compare the NAMD and MARTINI CG simulations also from a dynamics point of view, we calculate the diffusion constants for water, lipid, and alamethicin peptides in the simulations, in an attempt to generate an internal measure that would allow us to compare the dynamics in the two types of CG simulations. For the MARTINI simulation the dynamics of water, lipids, and the peptides are 1.3, 5.3, and 1.2 times faster than those for the NAMD simulations, respectively (more details in Data S1). Because the analysis of the CG simulations in this study relates to bilayer dynamics only, the time axis of the MARTINI simulation is scaled by a factor of 4 as a very approximate value between the relative differences in diffusion coefficients for lipids and alamethicin. To scale the time axis by 4 is also standard procedure in the MARTINI articles (31,40). This means that we effectively have 4 μs of MARTINI CG simulation, and in all analysis and discussion in the study, the effective time will be used. Therefore, when reporting analysis of the NAMD and MARTINI CG simulations together, we only make use of the first quarter of the MARTINI simulation.

Other aspects that might give rise to differences between the NAMD and MARTINI simulations are the hydrophobic thickness of the bilayer and the helix end-to-end distance. The hydrophobic thickness of the bilayer (the average distance between the beads representing the DMPC glycerol linkage in the two leaflets of the bilayer) is 30.1 Å for the NAMD CG simulations and 25.1 Å for the MARTINI CG simulation. The difference arises because of the fewer lipid tail beads used in the MARTINI CG model of the lipids. The helix end-to-end distance is on average 33.5 Å for the NAMD simulations and 31.0 Å for the MARTINI simulation (details are found in Data S1).

Reverse coarse-graining

Although peptide aggregation was described effectively by the CG simulations, we soon realized that the process of water penetration into the membrane, which would be indicative of formation of pores, could not be described in the CG simulation, primarily due to the large size of the CG water beads. This is a clear case in which the fine details necessary for the complete description of the problem at hand can only be captured at the atomic level. Therefore, it became necessary to revert the structure of the peptide-lipid assembly to an AA representation. For one of the NAMD CG simulations at t = 1 μs, the atomic details were reintroduced by reverse coarse graining of the system back to an AA representation, using the procedure described in (46,47). The group of atoms in the initial equilibrated AA system corresponding to a CG bead was translated such that the center of mass (COM) of the group was on the CG bead's position (Fig. 1 h) This procedure leads usually to unphysical bonds between the atoms of different beads. The new AA system was therefore subjected to thorough energy minimization followed by simulated annealing for 19 ps (T_init = 610 K, T_end = 300 K, ΔT = −10 K), during which the COMs of the individual atom-groups were restrained to the position of their respective beads. This treatment relaxed the unphysical bonds while keeping the overall CG structure. Because CG water beads do not provide sufficient hydration for the lipid headgroups, we completely ignored CG water and re-solvated the resulting lipid-peptide system with AA water.

An AA simulation was carried out for 50 ns using the standard distribution of NAMD 2.6 (50) and the CHARMM27 parameter set (51). Similar to the NAMD CG simulations, PBC were used, but to avoid lipids entering the gel phase, the area of the unit cell was fixed at the value obtained at the end of the 1-μs NAMD CG simulation (127.9 Å × 102.1 Å). The pressure in the z-direction was kept at 1 atm using the Nosé-Hoover Langevin piston (52) with a piston period of 100 fs and a decay time of 50 fs. The temperature and thermostat settings were the same as for the NAMD CG simulations. The vdW interactions were cut off at 12 Å as for the CG simulations, but with the shifting beginning at 10 Å. Electrostatic interactions were calculated using the particle mesh Ewald algorithm (58) in the multiple time stepping integration scheme, where interactions within 12 Å were considered short-range and evaluated each time step, whereas the long-range interactions were evaluated every fourth time step. Pair lists had a 14 Å cutoff and were updated at least once per 20 steps. The simulation was carried out using a 1 fs time step. The computational cost for the total 50 ns simulation was 13 days on 128 processors (32 Sun X2200 nodes; 2.6 GHz 2-dual core AMD/Opteron, 16 GB memory; Voltaire infiniband interconnect).

Solid-state NMR experiments

The ¹⁵N NMR experiments were carried out on a 16.45-T (700 MHz) Bruker Avance-2 spectrometer (Bruker Biospin, Rheinstetten, Germany) using ¹H-¹⁵N cross-polarization and ¹H homonuclear decoupling during acquisition. Thereby, the sample of ¹⁵N-Aib⁸ alamethicin in macroscopically oriented DMPC lipid bilayers (peptide/lipid molar ratio 1:15) displayed a doublet splitting around the effective chemical shift due to the ¹H-¹⁵N dipole-dipole coupling which is not removed, but only scaled by the factor because of the homonuclear decoupling. Further experimental details may be found in Vosegaard et al. (59).

RESULTS AND DISCUSSION

The combination of CG and AA simulations allowed for a complete description of the processes of peptide aggregation and pore formation by alamethicin molecules in the lipid bilayer. In addition to peptide aggregation, we also observe transitions between the membrane-spanning and the surface-bound states of the peptides during the CG simulations. The AA simulation shows penetration of water molecules into the lipid bilayer through interactions with the formed peptide aggregates as well as deviation of the peptides from perfect α-helical structures. The results are discussed in detail in the following subsections.

Spontaneous peptide aggregation

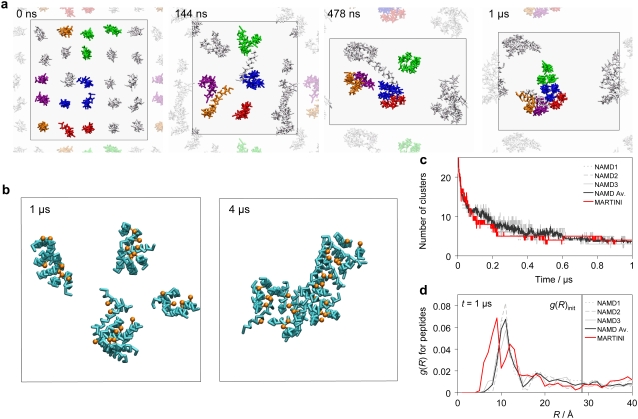
Most of the peptides remain in the membrane-spanning state throughout the CG simulations and laterally diffuse to assemble in aggregates that slowly grow in size. The development in the number of peptide clusters (if the COMs of two peptides are within 15 Å they belong to the same cluster as defined in Data S1) is shown in Fig. 2 c. The simulations provide a detailed view of the steps involved in the formation of oligomeric structures of alamethicin. At t = 150 ns, several small clusters of two or three peptides have formed, as shown in Fig. 2 a for one of the NAMD CG simulations. The clusters are approximately evenly distributed in the bilayer and have grown through random peptide diffusion. The coloring of the peptides in Fig. 2 a allows one to recognize the trajectories of the peptides and illustrates the way small clusters meet and join to form larger clusters. Once formed, the clusters diffuse as a unit and there is no exchange of peptides between the clusters (see Fig. S2 in Data S1). For the MARTINI CG simulation, which likely represents a longer timescale than 1 μs, the number of clusters continues to decrease slowly until only one cluster exists after 3.1 μs and for the rest of the simulation (Fig. 2 b).

FIGURE 2.

Peptide aggregation. (a) Peptide aggregation from one of the NAMD CG simulations, the other CG simulations show similar aggregation patterns. Snapshots taken at 0 μs, 0.144 μs, 0.478 μs, and 1 μs, respectively. The membrane is shown from the top view with only the peptides drawn. Peptides are colored to illustrate the aggregation mechanism. The neighboring unit cells are partially shown using a dimmer representation. Note the change of the aspect ratio of the periodic box, indicated by a black line, during the simulation. (b) Peptide aggregation in the MARTINI CG simulation. Peptide backbone in cyan with Gln⁷ side chains in orange. The periodic box is indicated by a black line. Clusters at t = 1 μs and t = 4 μs. (c and d) Peptide aggregation in the CG simulations. NAMD1-NAMD3 are the three NAMD CG simulations with NAMD Av. being the average of the three. MARTINI is the MARTINI CG simulation. (c) Number of peptide clusters over time. (d) Radial distribution of the peptides at t = 1 μs. The solid vertical line indicates the interpeptide distance in the initial (t = 0) structure.

To quantify peptide packing in the membrane, the radial distribution function (RDF) (see Data S1) of the transmembrane peptides was calculated at 1 μs (Fig. 2 d). The distribution peaks at a peptide-peptide distance of 11 Å for the NAMD simulations and at 9 Å for the MARTINI simulation. For both CG models this corresponds to a close packing of the peptides. An explanation for the difference in the distance could be found in the representations of Ala and Aib in the two CG models. These amino acids are abundant in alamethicin (10 of 20 amino acids) and as the models use the same size for all protein beads (except for ring beads in MARTINI), the BB-SC bond length of 2.0 Å for Ala and Aib comes in addition in the NAMD CG model because MARTINI has no SC beads for these amino acids. The RDF peak patterns fit a primarily hexagonal packing of the peptides in the NAMD simulations and a primarily square packing in the MARTINI simulation. The RDF for the initial model (Fig. 1 g) would have a thin sharp peak at R = 28.5 Å, because the peptides are placed with a distance of exactly 28.5 Å between them. It is therefore clear from Fig. 2 d, as well as from Fig. 2, a–c, that considerable peptide aggregation and packing have been achieved during the CG simulations.

The extent of peptide aggregation naturally depends on the parameters used in the simulations, particularly on the nonbonded terms for the amino acids. In the MARTINI protein force field, the partitioning free energy of amino acid side chains between aqueous and oil phases has been used in setting the nonbonded interaction terms (40), similar to the protocol used for the lipid parameterization of the force field. The quality of side-chain–side-chain interactions was evaluated by computing the association constants between lysine and glutamate, and between a leucine pair in water, the latter representing general hydrophobic interactions between protein side chains (40). The association constants obtained by MARTINI were found to be comparable to atomistic simulations, though it appeared to slightly underestimate the strength of the nonbonded amino acid interactions. The performance of the force field for other types of amino acid interactions has not been tested specifically. However, the partitioning of a hydrophobic peptide in a lipid bilayer is studied, and a polyleucine peptide that is made gradually less hydrophobic by changing more and more leucines to alanines behaves qualitatively as expected, showing that the CG model is sufficiently sensitive to capture the minor differences between two hydrophobic amino acids. A preliminary version of MARTINI has also been used to study the self-assembly of rhodopsin in lipid bilayer (38) showing oligomerization in agreement with experiments. We also note that hydrophobic interactions, which seem to be described adequately by MARTINI, are the most abundant type of interaction in the case of alamethicin and likely dominate the aggregation of the peptides in our simulations.

The architecture of the clusters

A large variation in position and tilt of the peptides with respect to the membrane is observed in our simulations as illustrated in Fig. 3 a. A few peptides completely emerge to the surface of the bilayer assuming a tilt angle of ∼90° with respect to the membrane normal, but most retain their membrane-spanning state. However, all possible positions in between these two extreme configurational states are sampled by the peptides for varying periods of time. Generally the C terminus is anchored to and interacts with the lipid headgroups regardless of the position and tilt of the peptide helix. In other words, transition of the peptide between various membrane bound states takes place through penetration and movement of the N-terminus across the hydrophobic part of the bilayer. As established previously, the tilt of membrane-spanning helical peptides is connected to the hydrophobic thickness of the membrane (34,60–62). The reason for the slightly higher helix tilt in the MARTINI simulation (Fig. 3 a) can therefore be explained by the differences in membrane thickness and peptide end-to-end distance (see Methods) between the two CG models. The helix tilt distribution calculated for the isolated peptides (i.e., before aggregation) and peptides in the clusters (see Fig. S3 a in Data S1), show no significant differences. Also, the helix kink around Pro¹⁴, which has been speculated to be important for the function of alamethicin (7,18,63–65), does not change as the peptides aggregate and form clusters (see Fig. S3 b in Data S1).

FIGURE 3.

(a) Distribution of helix tilt angles. NAMD1-NAMD3 are the three NAMD CG simulations, and NAMD Av. is the average of the three. MARTINI is the MARTINI CG simulation. (b–d) ¹⁵N solid-state NMR spectra of ¹⁵N-Aib⁸ alamethicin in aligned lipid bilayers. (b) Experimental spectrum obtained using ¹H homonuclear decoupling. (c) Simulated spectrum assuming a perfectly aligned sample and a helix tilt angle of 10°. (d) Simulated spectrum based on the structure diversity seen in the three NAMD CG simulations.

To obtain experimental values for the helix tilt angle, solid-state NMR spectroscopy of ¹⁵N-Aib⁸ labeled alamethicin in macroscopically-oriented DMPC lipid bilayers was carried out. A spectrum recorded using ¹H homonuclear decoupling is shown in Fig. 3 b (59). Such an experiment is very sensitive to local variations in the peptide conformation relative to the external magnetic field. The spectrum shows the expected doublet due to the ¹H-¹⁵N dipole-dipole coupling, but also shows a significant orientational disorder, which manifests itself by the differential line broadening and intensity of the two peaks in the doublet. To substantiate the experimental observation of orientational disorder, we have made a simulated spectrum, assuming that the bilayers are perfectly aligned and that all the peptides adopt the same configuration with respect to the membrane, that is, one specific helix tilt angle and rotational pitch (rotation angle of the α-helix with respect to the tilt angle; definitions in Data S1). Given these assumptions, the best fit to the recorded spectrum is seen in Fig. 3 c, which corresponds to a helix tilt angle of 10° in good agreement with previous solid-state NMR experiments carried out for alamethicin, with different ¹⁵N labeled alanine and valine residues, in DMPC lipid bilayers (7). However, because this fit does not reproduce the asymmetries of the spectrum in Fig. 3 b, we simulated a spectrum using the tilt angle and rotational pitch distributions of helical peptides in the three NAMD CG simulations including a term accounting for imperfect macroscopic alignment of the bilayers (59) (the construction of the simulated spectrum is described in Data S1). The obtained spectrum (Fig. 3 d) is in close agreement with the experimental spectrum, strongly supporting our finding that alamethicin peptides adopt a diverse set of mostly tilted configurations in a lipid bilayer.

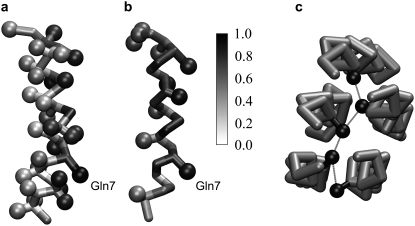
The observed configurations of the clusters do not fit the highly regular barrel-stave models suggested previously for alamethicin, and present a significantly larger degree of irregularity in their arrangement. However, despite a significant variation in the arrangement of the peptides within different clusters, common interaction patterns can be recognized. Fig. 4, a and b shows the probability for different residues to be involved in peptide-peptide contacts (as defined in Data S1). Clearly not all residues contribute equally to interpeptide contacts. One might define an oligomer-forming face for the peptide where the hydrophilic side chain of Gln⁷ with the high probability (>90% for the NAMD simulations, >85% for the MARTINI simulation) of contact with other peptides is located. Because glutamine has the ability to form two hydrogen bonds at the same time, a hydrogen bond network can be established among several peptides (as exemplified in Fig. 4 c), which will stabilize the cluster. Alamethicin is composed primarily of hydrophobic residues, particularly in the membrane-spanning region. Our results suggest that the single hydrophilic residue (Gln⁷) likely accounts for a significant part of the observed peptide aggregation, but not for all interpeptide interactions.

FIGURE 4.

(a and b) Alamethicin colored according to the propensity of individual residues in participating in interpeptide contacts in the lipid bilayer calculated over the period t = 0.8–1 μs. A probability of 1 represents contact at all times and 0 is no contact at any time. (a) An average of the three NAMD CG simulations. (b) The MARTINI CG simulation. (c) Example of clustering of Gln⁷ residues (black spheres) through a hydrogen bond network, taken from one of the NAMD CG simulations.

Alamethicin insertion in the membrane

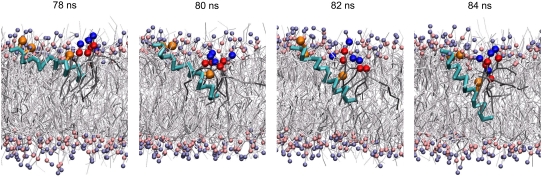
During the CG simulations several alamethicin peptides undergo clear transitions between the initial membrane-spanning state and the surface-bound state. Generally, once surfaced the peptides stay at the membrane surface for the rest of the simulation, showing that the surface bound configuration is also a stable configuration of the peptide. However, in one case the peptide recovered its membrane-spanning configuration during the simulation, a process that corresponds to and, thus, can describe the insertion of alamethicin peptides into the membrane. The insertion event is practically identical to the reverse of the observed transitions from the membrane-spanning to the surface-bound state. Fig. 5 illustrates the insertion process and shows how the bilayer is slightly deformed. In particular, a number of lipid molecules penetrate deeply into the core region of the bilayer along with the N-terminus, stabilizing the insertion of the hydrophilic Gln⁷ through interactions with the lipid headgroups. The membrane-spanning and surface-bound configurations observed here are similar to the low energy configurations reported by Mottamal and Lazaridis (66), where a single copy of alamethicin in AA representation was subjected to several 1-ns simulations within an implicit membrane model.

FIGURE 5.

Transition between the surface-bound and membrane-spanning states. The backbone of alamethicin is shown in cyan, with the hydrophilic side chains Gln⁷, Glu¹⁸, and Gln¹⁹ in orange. Lipids are colored gray with headgroups in purple and pink. The three highlighted lipid molecules with their headgroups in red-blue facilitate the insertion of the peptide. This event is taken from the NAMD CG simulation of the 16 peptides in 328 lipids setup.

Direct involvement of the N-terminus in insertion and emergence of individual peptides is clearly shown by our results. This is consistent with several experimental and simulation studies (13,14,23) suggesting that it is always the N-terminus, and not the C terminus, that traverses the bilayer during the insertion of alamethicin. One of the mechanisms proposed to be behind this behavior is the more hydrophilic nature of the C terminus (in contrast to the N-terminus) that results in its strong anchoring to the polar headgroup region and its lower propensity of inserting into the membrane. This hypothesis is consistent with what we observe in our equilibrium CG simulations. The role of the helix dipole and its alignment with the electric field across the membrane in a living cell environment has also been implicated (66,67). However, because our simulations do not include an electric field, and, more importantly, because the CG representations of the system do not take into account the helix dipole, we cannot evaluate the role of this effect in the observed directionality of membrane insertion of alamethicin.

Formation of water pores in the AA simulation

Monitoring the penetration of water into holes and cavities formed by proteins and peptide aggregates, or even those formed within a pure lipid bilayer is a very effective way to assess pore formation in a membrane patch in MD simulations. During the CG simulations only very few water beads interact with alamethicin inside the lipid bilayer. Due to the coarse representation of water, however, insufficient visits of water and lack of permeation of water across the membrane in the CG simulation cannot be equated to an absence of pores in the system. The CG water model used in this study uses a single bead to represent four water molecules and was constructed to describe bulk water properties and water-oil interfaces (29). Specific peptide-water interactions and finer penetration of water into the membrane, e.g., in the form of a single file structure, cannot be described with this model. The effective CG water bead diameter of 5.0 Å, compared to 2.8 Å for an AA water molecule, makes it difficult for the CG water beads to penetrate deep enough into the membrane and to interact with the lipid headgroups and alamethicin (see Fig. S4 in Data S1).

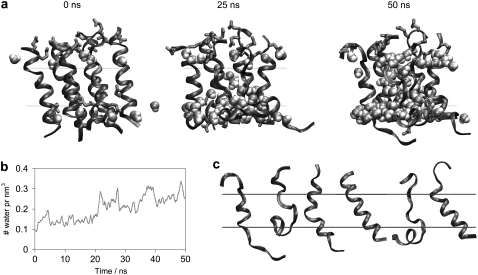
This shortcoming of the CG simulations prompted us to resort to an AA simulation to study the water leakage of the system after peptide aggregation in the CG simulations and to investigate in atomic detail the interactions of water with the alamethicin clusters. After 1 μs of CG simulation, clusters with the potential to form pores had been formed and an AA simulation was therefore set up using the configuration obtained at t = 1 μs from one of the NAMD CG simulations. During the 50 ns of AA simulation the amount of water content of the bilayer core gradually increased as shown in Fig. 6 b, indicating clearly the formation of a leaky lipid bilayer due to the presence of alamethicin peptides. Approximately 95% of the water molecules inside the bilayer are in direct contact with at least one peptide (water oxygen within 4 Å of a peptide atom) and the rest typically participate in water networks with the peptide-interacting waters. The diffusion of water inside the bilayer is extremely slow, particularly during the initial part of the AA simulation, because strong hydrogen bond interactions are established between the backbone of the peptides and the water molecules. However, in the course of the simulation the water pores are better established. Fig. 6 a illustrates the development of one of the water pores formed by six alamethicin peptides in a cluster. After ∼35 ns of AA simulation the pore is sufficiently expanded to allow water molecules to diffuse in and out and all the way across the bilayer. Such water pores connecting the two sides of the membrane could form during the initial stage in the development of large, nonspecific pores that would destroy the membrane gradients and thereby disrupt the cell.

FIGURE 6.

(a) Formation of the leaky membrane by alamethicin peptides. Six alamethicin peptides shown in ribbon with the hydrophilic side chains in licorice. Water in the middle 20 Å of the bilayer and within 8 Å of the six peptides is shown in VDW representation. The middle 12 Å of the bilayer is marked by black lines. (b) Water content of the bilayer. The density of water in the middle 12 Å of the bilayer (calculated at each time step, and subjected to a running average over windows of 0.5 ns) is depicted. (c) Individual conformations of the peptides from the cluster shown in a at t = 50 ns of the AA simulation.

Another shortcoming of CG simulations that can be alleviated by an AA refinement is regarding the secondary structure of the peptides. During the CG simulation the peptides remain mainly α-helical, regardless of the membrane-bound state (inserted or surface-bound) of alamethicin. This is, at least partially, due to the constraints of the CG model (see Data S1) that biases the peptides toward maintaining their original secondary structure, i.e., an α-helical structure in this case. This bias is removed in the AA simulation, and, therefore, it is possible to provide a better description of the secondary structure of the peptides in the clusters. Comparison of the secondary structure of the peptides at the beginning and at the end of the AA simulation shows that only 18 of 25 peptides remain α-helical, whereas the rest partially unfolds. The unfolding is in particular significant for the surface-bound peptides and for the peptides interacting strongly with water inside the bilayer. These secondary structure modulations for the six peptides surrounding the water pore depicted in Fig. 6 a are shown in Fig. 6 c. After 50 ns of AA simulation, only one of these peptides remains fully α-helical, whereas the other five have been partially unfolded into random coil structures. The unfolded backbone forms hydrogen bonds to the water molecules, thereby, stabilizing both the unfolded peptide and the water formation inside the bilayer. Apart from the unfolding of certain peptides, the composition of the clusters does not change during the time span (50 ns) of the AA simulation. The observed alamethicin clusters are thus clearly different from the model suggested previously, where close-to-perfect α-helices join in a bundle to form a highly symmetric channel with Gln⁷ pointing to the center. We see a large diversity in the form of the clusters and the structure of the individual alamethicins participating in the cluster.

CONCLUSION

This study of alamethicin peptides in a hydrated lipid bilayer is one of the first examples where CG and AA simulations needed to be combined to exploit their individual strengths, to describe fully the problem at hand. In this particular case, combining the two levels of resolution was a necessity, and not merely for partially refining the CG model. Although the two different types of CG simulations used resulted in some differences in the clusters, e.g., the packing of helices within the cluster or the timescale of aggregation, those aspects important for our discussion are consistently found by both simulations. From the CG simulations it is observed how the monomeric alamethicin peptides readily form aggregates. The aggregates do not consist of a specific number of peptides, but rather they grow in size over time. An oligomer-forming face of the peptide helix can be resolved, determining the overall structure of the aggregates. The individual peptides, however, sample a diverse set of structures with respect to the membrane; most are membrane-spanning with the helix axis close to parallel to the membrane normal, but all other configurational states up to a surface-bound position with the helix axis orthogonal to the membrane normal are observed. Transitions between the surface-bound and the membrane-spanning states are also observed during the CG simulations showing possible dynamics for the insertion of alamethicin into the membrane.

After aggregates of alamethicin had formed, the molecular system was reverse coarse-grained to an AA representation and 50 ns of AA simulation was carried out. This allowed for a more detailed description of the molecular system and especially the water interactions with the bilayer. The AA simulation showed clear deviations from an α-helical structure of the peptides. Whereas the CG water beads had difficulties entering the bilayer due to their size, the AA water molecules interacted extensively with the alamethicin clusters deep in the bilayer. Water pores going all the way across the lipid bilayer are formed, and the membrane therefore leaks water around the alamethicin clusters. These water formations could be the initial stage in a membrane disruption mechanism caused by the peptides. The observed alamethicin clusters are clearly different from the previously suggested model, where close-to-perfect α-helices join in a bundle to form a symmetric channel. We observe a large diversity in the form of the clusters and the structure of the individual alamethicins within the cluster. Solid-state NMR results presented here strongly support the diversity of the peptides' configuration with respect to the membrane as observed in the simulations.

The results could not have been obtained without using the combination of the microsecond timescale of the CG simulations and the detailed representation of molecular interactions in the AA simulation. We believe that reverting the system to an AA representation is clearly necessary to obtain information that is only accessible on the fine grained scale, and our simulations provide a clear case for such application, namely description of water penetration into and interaction with lipid bilayers.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.