Abstract
Pathways of structural relaxation triggered by ionization of internal groups in staphylococcal nuclease (SNase) were studied through multiple self-guided Langevin dynamics (SGLD) simulations. Circular dichroism, steady-state Trp fluorescence, and nuclear magnetic resonance spectroscopy have shown previously that variants of SNase with internal Glu, Asp, and Lys at positions 66 or 92, and Arg at position 66, exhibit local reorganization or global unfolding when the internal ionizable group is charged. Except for Arg-66, these internal ionizable groups have unusual pKa values and are neutral at physiological pH. The structural trends observed in the simulations are in general agreement with experimental observations. The I92D variant, which unfolds globally upon ionization of Asp-92, in simulations often exhibits extensive hydration of the protein core, and sometimes also significant perturbations of the β-barrel. In the crystal structure of the V66R variant, the β1 strand from the β-barrel is domain-swapped; in the simulations, the β1 strand is sometimes partially released. The V66K variant, which in solutions shows reorganization of six residues at the C-terminus of helix α1 and perturbations in the β-barrel structure, exhibits fraying of three residues of helix α1 in one simulation, and perturbations and partial unfolding of three β-strands in a few other simulations. In sharp contrast, very small structural changes were observed in simulations of the wild-type protein. The simulations indicate that charging of internal groups frequently triggers penetration of water into the protein interior. The pKa values of Asp-92 and Arg-66 calculated with continuum methods on SGLD-relaxed structures reached the normal values in most simulations. Detailed analysis of accuracy and performance of SGLD demonstrates that SGLD outperforms LD in sampling of alternative protein conformations without loss of the accuracy and level of detail characteristic of regular LD.
INTRODUCTION
Ionizable groups buried in the interior of proteins play essential functional roles in bioenergetics, including catalysis, H+ transport, and e− transfer reactions. The ionization of internal group is often coupled to structural relaxation. A drastic example is represented by the photoactive yellow protein, in which ionization of an internal group triggers structural reorganization that exposes up to 23% of the buried backbone amide groups to solvent. This effectively transforms the protein into a molten globule (1–3). In bacteriorhodopsin, a cascade of conformational changes triggered by a charge separation event drives the pumping of a H+ from the cytoplasmic to the extracellular side of the purple membrane (4–6). In ATPase, protonation of Asp-61 triggers structural changes that lead to H+ translocation by the c subunit (7,8).
Structural relaxation coupled to the ionization of internal groups has been studied by x-ray crystallography, nuclear magnetic resonance (NMR), Fourier transform infrared, and single molecule spectroscopy, hydrogen exchange, etc. Despite the wealth of structural detail that such experiments provide, they do not contribute detailed understanding of the mechanism and pathways of conformational reorganization at the atomic level. Computational methods, when benchmarked against experiments, offer the possibility of obtaining microscopic level descriptions necessary for understanding the structural basis of function governed by the ionization of internal groups.
Computational modeling of conformational rearrangements triggered by the ionization of internal groups is challenging. Standard molecular dynamics (MD) simulations in which protonation states of ionizable groups are fixed fail to reproduce protonation and deprotonation of ionizable groups; these processes are coupled to the properties of the local environment, which may change during the simulations. Constant pH MD simulations, in which the charged state of ionizable groups is allowed to vary, are being developed to circumvent these problems (9–17).
Conformational rearrangements triggered by ionization of internal groups may occur on a variety of timescales, as demonstrated in bacteriorhodopsin (6). Although MD simulations can describe processes at timescales of ns and faster, they fail to sample conformations that arise through processes at timescales of μs and longer. New computational and theoretical methods with improved abilities for conformational search are the focus of intense research. Emerging methodologies are based on different algorithms, e.g., coarse-graining (18–22), smoothing protocols (23–26), generalized ensembles (27,28), optimization of actions (29), or additions of constraints or forces (30–32). The ability of these methods to reproduce ligand-driven conformational transitions needs to be tested.
Variants of staphylococcal nuclease (SNase) with internal ionizable groups are useful benchmarks for computational methodologies. Because the protein is not as polarizable as water, these groups usually titrate with pKa values shifted in the direction that promotes the neutral state (depressed for basic groups and elevated for acidic ones (33,34)). In most variants, the internal ionizable groups are neutral at physiological pH. Crystal structures and circular dichroism, steady-state fluorescence, and NMR spectroscopies show that the response of the proteins to the ionization of internal groups depends strongly on the nature of the group and on its location inside the protein. In principle, electronic polarization, relaxation of dipoles from backbone and side chains, and water penetration can all be a part of the protein's response to the ionization of the internal groups. In certain cases, dielectric breakdown (i.e., local or global changes in the protein secondary and tertiary structure) may occur.
If the dielectric response involves small structural changes, standard computational methods should easily reproduce them. For example, in the L38K variant of SNase the experimental pKa value of Lys-38 was reproduced with Poisson-Boltzmann calculations on structures relaxed through simple energy minimization and short MD runs using a relatively low dielectric constant of 4 to account for electronic polarizability and minor structural relaxation (35). In contrast, a dielectric constant of 10 was needed to reproduce the pKa value of 5.7 of Lys-66 (36). The high dielectric constant needed in the continuum calculations to reproduce the experimental pKa value suggests that other mechanisms of dielectric response occur when Lys-66 is ionized, which were not treated explicitly in the Poisson-Boltzmann calculations. MD simulations of the V66K variant with Lys-66 in charged form (37) have indicated that Lys-66 side chain may twist, exit the protein interior, and become hydrated by the bulk water, suggesting that in this case, rearrangement of the side chain may be the dominant mechanism of dielectric relaxation. In another study, conformational changes in the related V66E variant were studied through a new method in which the charge assigned to an internal group is increased beyond its physical value (38). With the increased charge, side-chain twisting and hydration were achieved, and the correct pKa value shift for Glu-66 was reproduced while using a low dielectric constant.
Recent NMR studies have shown that structural changes coupled to the pH-induced ionization of Lys-66 in SNase are more complex than simple side-chain twisting (M. S. Chimenti and B. García-Moreno E., 2008, personal communication). These studies show that several residues of the β-barrel experience changes in proton chemical shifts, consistent with local structural reorganization. Six residues at the C-terminus of helix α-1 experience additionally line broadening, which is suggestive of a structural reorganization on a microsecond or longer timescale. In contrast, crystallographic studies of the variant with an Arg in position 66 show domain swapping of strand β1 (D. A. Karp and B. García-Moreno E., 2008, personal communication). The pH-induced ionization of internal group at another interior location, position 92, unfolds the protein globally (39). Owing to the extreme sensitivity of the observed conformational changes to the nature and location of inserted charges, these proteins are an excellent model system for studying the interplay between electrostatic interactions, local geometry, protein flexibility, and hydration in determining the nature of structural relaxation processes in response to the binding/release of a ligand (i.e., H+).
To gain insight into pathways of pH-induced conformational rearrangements observed experimentally in variants of SNase (global unfolding in the I92D variant, and local structural rearrangements in V66K and V66R variants), we used the self-guided Langevin dynamics (SGLD) method (32). No well-established computational method has described conformational rearrangements in a protein of this size and complexity, while maintaining the same level of detail (all atom and explicit solvent simulations) necessary for understanding transition pathways. SGLD increases searching efficiency by enhancing systematic conformational changes. The earlier version of this method, self-guided molecular dynamics (40) was based on a local average of nonbonded forces to guide systematic motions of a simulated system. It was found that the guiding forces calculated from nonbonded forces bias low energy conformations. In addition, in stochastic dynamics simulations, this kind of guiding force is often overwhelmed by random force noise and provides little guiding effect. To overcome these drawbacks, momentum-based guiding forces are used in the newly developed momentum-enhanced hybrid Monte Carlo (41) and in SGLD (32). In these methods, three parameters are used to control the guiding effect. One is the local averaging time, which defines the slow motions that are to be enhanced. A second is the guiding factor, which controls the strength of enhancement. The third is the friction coefficient that is used. The optimal choice of friction is typically an order-of-magnitude or two weaker than friction involving solvent. Weak friction is used to enhance conformational transitions rather than to mimic the effect of the solvent. Because of the guiding component of these simulations, information about the timescales of protein dynamics is lost. SGLD has been tested extensively in peptide folding simulations and other small systems, and has been shown to keep the density of states unaltered with reasonable choice of guiding parameters, while enhancing the conformational search ability (32).
METHODS
Simulated proteins and system setup
Four variants of SNase were simulated:
Δ+PHS, a hyperstable variant of SNase that differs from the wild-type in five substitutions (G50F, V51N, P117G, H124L, S128A) and a 44–49 deletion (39). Since this variant does not contain ionizable groups in the hydrophobic core of the protein, it will be referred to as the wild-type or background protein.
Δ+PHS/V66K, referred to as V66K. The pKa value of Lys-66 is 5.7 (33); therefore, Lys-66 is neutral at physiological pH. Studies with NMR spectroscopy suggest that the C-terminus of helix α1 becomes more dynamic upon pH-induced charging of Lys-66.
Δ+PHS/V66R, referred to as V66R. At physiological pH, Arg-66 is charged. Crystallographic studies showed that the β1 strand domain swaps. In the process, the side chain of Arg-66 becomes exposed to water.
Δ+PHS/I92D, referred to as I92D. Asp-92 has an apparent pKa value of 7.5. This protein undergoes global unfolding upon pH-induced charging of Asp-92.
The starting structure used for the simulations was the structure of the Δ+PHS/V66K variant obtained with the internal Lys-66 in the neutral form (33). The starting structures for the other variants were derived from this structure by mutating residue 66 or 92 into the appropriate amino acid. The orientation of Asp-92 in I92D and the locations of two water molecules surrounding the Asp-92 residue were determined through alignment with the crystal structure of the I92E variant (42). For the system setup and subsequent MD and SGLD runs, the program CHARMM (43) was used. The CHARMM force field, version 27 was employed (44). Lys-66 and Arg-66 were positively charged, and Asp-92 was negatively charged. Briefly minimized protein was embedded in a water box. Water molecules within 2.5 Å of the protein or crystallographic water molecules were removed. The protein was centered at the coordinate origin, and all water molecules further than 36 Å from the origin were also removed. The total number of water molecules and ions for the simulated systems were: wild-type (WT) (5245 water molecules, 8 Na+ ions, 14 Cl− ions), V66K (5237 water molecules, 8 Na+ ions, 17 Cl− ions), V66R (5221 water molecules, 8 Na+ ions, and 17 Cl− ions), I92D (5245 water molecules, 8 Na+ ions, 13 Cl− ions). The systems were subjected to minimizations under rhombic dodecahedral symmetry.
Modeling of the pH-induced ionization of internal groups in this study was achieved by charging the groups. The abrupt change in the state of ionization of the internal ionizable groups is artificial. It is only meant as a device to probe the conformational changes that would be reflected in the ensemble in solution under conditions of pH where the ionizable groups are fully charged.
MD and SGLD simulations
The systems were first heated up in steps of 2 K, from 100 K until 300 K. Equilibration for 100 ps in an NPT ensemble followed. The extended system formalism was used to maintain constant pressure and temperature via the Hoover thermostat (45) with a thermostat coupling constant of 1000 kcal/mol/ps2, while the normal pressure was maintained with a barostat with a piston mass of 500 amu, and piston collision frequency of 20/ps (46). Rhombic dodecahedral periodic boundary conditions and particle mesh Ewald method (47) for electrostatic interactions were employed, with the following parameters for Ewald simulations: κ = 0.45, interpolation order of 6, grid spacing of ∼1 Å, and real-space interaction cutoff of 10 Å. Lennard-Jones interactions were shifted to zero after 10 Å. The leapfrog Verlet algorithm was used with a timestep of 1 fs. For each of the four protein systems five different heating and equilibration runs were initiated, with five different seed numbers for the random number generator used for assigning initial velocities.
SGLD simulations (32) were performed for each of the completed equilibration runs. The equation of motion for the SGLD dynamics of an N particle system is
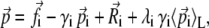 |
(1) |
where γi is the collision frequency, 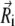 is a random force, and λi is the guiding factor. Here L represents the number of timesteps over which the averaging is performed, while the averaging time is tL = L δt, where δt is the timestep. The same friction coefficient γ and guiding factor λ was used for all particles. The following guiding parameters were tested: A: tL = 0.1 ps, λ = 0.0; B: tL = 0.1 ps, λ = 0.25; C: tL = 0.1 ps, λ = 1.0; D: tL = 0.5 ps, λ = 0.25; and E: tL = 0.5 ps, λ = 1.0.
is a random force, and λi is the guiding factor. Here L represents the number of timesteps over which the averaging is performed, while the averaging time is tL = L δt, where δt is the timestep. The same friction coefficient γ and guiding factor λ was used for all particles. The following guiding parameters were tested: A: tL = 0.1 ps, λ = 0.0; B: tL = 0.1 ps, λ = 0.25; C: tL = 0.1 ps, λ = 1.0; D: tL = 0.5 ps, λ = 0.25; and E: tL = 0.5 ps, λ = 1.0.
SGLD runs were performed in an NVT ensemble at 300 K. The friction coefficient was γ = 1/ps for both Langevin dynamics (λ = 0.0) and SGLD. Each SGLD simulation was run for 10 ns, for a total of 250 ns of simulation time for each of the four proteins.
Assignment of secondary structure
Automated identification of elements of secondary structure depends on the criteria used to catalog secondary structure. The criteria may include hydrogen-bond patterns (e.g., DSSP (48)), a combination of hydrogen-bond patterns and Φ/Ψ angles (e.g., STRIDE (49)), or Cα distances and Φ/Ψ angles (e.g., KAKSI (50)). Because different methods use different criteria they often disagree, especially at the edges of helices and strands, which are of special interest in this study.
Secondary structure assignments were performed on snapshots from SGLD trajectories. Coordinates were recorded every 10 ps (a total of 25,000 snapshots were taken for each simulated system). For each coordinate set the secondary structure was assigned with DSSP and KAKSI. Secondary structure assignment was performed for residues that were characterized as belonging to an α-helix or a β-strand in the crystal structure, and for a few residues around those residues. Remaining residues were assigned zero helical or strand character. Residues in α-helices were labeled “H,” and those in β-strands were labeled “E” in DSSP, or “b” in KAKSI.
Identification of conformational changes and additional simulations
Changes in the conformation of each residue were identified by following the time evolution of secondary structure assignments through DSSP and KAKSI. To filter out small fluctuations in the secondary structure a stringent set of criteria were applied: 1), only changes that persisted longer than 100 ps were considered; 2), only changes that were registered through both DSSP and KAKSI were kept; and 3), the structures chosen had to be recorded as frayed when visually inspected with VMD (which uses STRIDE to assign secondary structure).
Because the observed structural changes were often small, additional SGLD runs were performed to enhance them. These additional runs were performed starting from structures that satisfied the above criteria. They were each 5 ns long, and were performed with the guiding factor 1.0 while the averaging times were varied from 0.1 to 0.5 in steps of 0.05. In the case of the I92D variant, the observed conformational changes were larger than for other variants. Thus, in this case, instead of amplifying only the chosen simulations, each of the 10-ns-long SGLD runs with nonzero guiding factors was extended for an additional 6 ns.
Effective energies
To examine whether observed conformational changes contribute to the energetic relaxation of the protein, the evolution of the protein's effective energies was recorded. The effective energy was calculated as the sum of the self-energy, equal to the potential energy of the protein, and the solvation free energy. The solvation free energy was estimated through the linear response method (51). Thus,
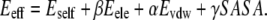 |
(2) |
Here α, β, and γ are empirical parameters. The values employed were α = 0.4, β = 0.5, and γ = 0.0072 kcal/mol/Å2 (52). Eint and Evdw are the electrostatic and van der Waals energies of interaction of the protein with water molecules and ions. All electrostatic and van der Waals energies were shifted to zero beyond 10 Å. The last term in this equation accounts for the so-called cavitation term, and is proportional to the solvent-accessible surface area (SASA). SASA was calculated through the analytic method of Richmond (53). The atomic radii and parameters are those of Kyte and Doolittle (54). The probe radius was 1.4 Å. All energy terms are determined as averages over 1000 conformations recorded every picosecond of trajectory.
pKa calculations
Structural relaxation coupled to the ionization of internal ionizable groups should lead toward states in which the pKa values of the internal groups are normal. As a measure of the completeness of structural relaxation, the pKa values of internal ionizable groups were calculated with the finite difference Poisson-Boltzmann method in the UHBD package (55) on snapshots from SGLD simulations. Details of the finite difference Poisson-Boltzmann calculations with SNase have been described elsewhere (36).
If sampling were not a problem, MD calculations would be able to capture the effects of ionization-induced conformational relaxation of proteins. If this were the case, a low dielectric constant of 2 (to account for electronic polarizability) would be appropriate for the calculation of pKa values with continuum methods when the continuum calculations are coupled to MD simulations to sample conformational reorganization explicitly. Empirically it has been shown that the combination of MD simulations and continuum electrostatics calculations yield the most reasonable results when a protein dielectric constant of 4 is used (56). The nature of these calculations still remains approximate, not only in the choice and meaning of the protein dielectric constants used in the continuum methods, but also because of discrepancies in the treatment of electrostatics in the MD simulations and in the continuum electrostatic calculations. The calculation of pKa values in our study is only meant as a metric to assess the extent of structural rearrangement. This is a useful approach because the pKa values of the groups of interest are shifted by dehydration when they are in their buried positions, and this effect should diminish dramatically as the structure reorganizes and the ionizable group becomes hydrated (36).
pKa values were determined on structures recorded every 100 ps along the trajectory, as well as for the final snapshots of 10-ns-long MD simulations. The Born energy, which accounts for the energetic penalty of removing the ionizable group from bulk solvent and placing it into the protein, is described along with the pKa value.
RESULTS AND DISCUSSION
Structural consequences of ionization: fraying of helices and strands
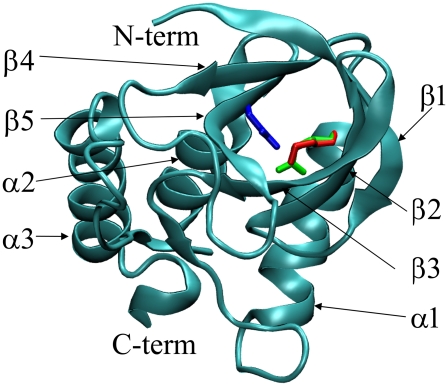
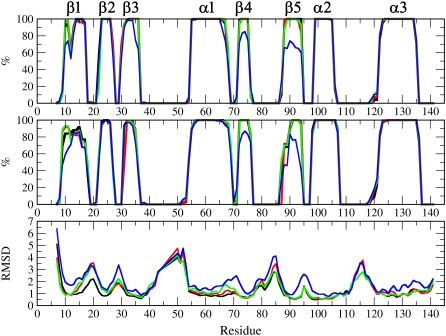
The secondary and tertiary structure of SNase and the location of the substituted ionizable groups in the initial structure is shown in Fig. 1. It has been shown experimentally that the ionization of Lys-66 triggers reorganization of the C terminus of helix α1, the ionization of Arg-66 leads to the release of strand β1, and the ionization of Asp-92 triggers global unfolding (B. Cannon and B. García-Moreno E., 2008, personal communication). To quantify the extent of unfolding observed in the simulations, the percentages of total simulation time that protein residues spent in an α-helical or a β-strand conformation were determined through DSSP and KAKSI calculations on snapshots recorded every 10 ps. The values, representing averages over the 25 10-ns SGLD runs, are shown in Fig. 2.
FIGURE 1.
Crystal structure of SNase (60) and position of Lys-66 (red), Arg-66 (green), and Asp-92 (blue) side chains.
FIGURE 2.
Percentage of total simulation time that residues in WT (black), V66K (red), V66R (green), or I92D (blue) spent in an α-helical or a β-strand conformation. Secondary structure was assigned with DSSP (top graph) and KAKSI (middle graph). Bottom graph shows average RMSD values for backbone atoms of each residue.
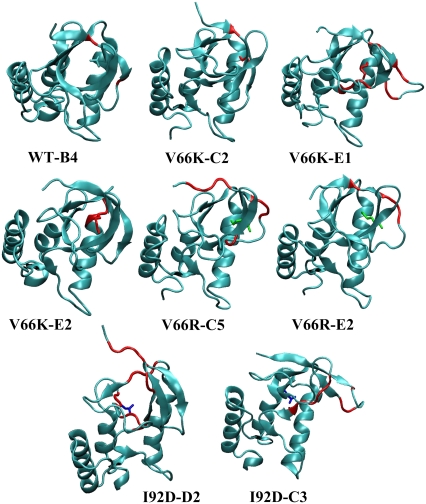
The I92D variant displays large changes in the secondary structure, especially in regions of strands β1, β3, β4, β5, and of helix α1 (Fig. 2). To amplify these changes, simulations with a nonzero guiding force were extended for an additional 6 ns. Structures that illustrate the largest changes in secondary structure after 16 ns of simulation time are shown in Fig. 3.
FIGURE 3.
Snapshots from SGLD simulations representative of observed secondary structure changes. The residues undergoing change in the secondary structure are shown in red. The substituted ionizable groups are shown in stick representation.
The average secondary structures of WT, V66K, and V66R variants are almost overlapping, as indicated in Fig. 2. Changes observed in the helical and strand structure of the three proteins were very small and usually short-lived and reversible. Thus, the strategy to simply extend all simulations to enhance the probability of observation of structural changes may not be the most productive way of searching conformational space. Therefore, additional runs were started only for structures that showed significant deviation from the initial secondary structure. To identify such structures, the time dependence of assigned secondary structures was followed, and only changes that persisted for longer than 100 ps were selected for further studies. Table 1 lists the residues that exhibited such fraying and the simulations in which they occurred.
TABLE 1.
List of residues that fray and simulations in which these fraying events occur
| Protein, end | Fraying events | Protein, end | Fraying events |
|---|---|---|---|
| WT, β1N | 9 (often), 9–10 (B1, E5), 9–11 (E2), 9–12 (C2) | WT, β4N | none |
| V66K, β1N | 10 (B4) | V66K, β4N | none |
| V66R, β1N | 9 (B1), 9–11 (C1) | V66R, β4N | none |
| WT, β1C | 17 (B4*) | WT, β4C | none |
| V66K, β1C | 15–17 (E1*) | V66K, β4C | none |
| V66R, β1C | 17 (C5*, E2*) | V66R, β4C | none |
| WT, β2N | 22 (often) | WT, β5N | 87 (A1, C3) |
| V66K, β2N | 22 (often) | V66K, β5N | 88 (A4, B2, D4) |
| V66R, β2N | 22 (often) | V66R, β5N | 88 (A3, B5, C1, C3) |
| WT, β2C | 27 (often) | WT, β5C | none |
| V66K, β2C | 27 (often) | V66K, β5C | 94 (E2*) |
| V66R, β2C | 27 (A4, A5, B4, B5, C2, C3, D3, E5) | V66R, β5C | 94 (C5*) |
| WT, β3N | none | WT, α2N | none |
| V66K, β3N | none | V66K, α2N | none |
| V66R, β3N | 31–32 (B1) | V66R, α2N | none |
| WT, β3C | 36 (A4, A5, B3, D5, E2, E3, E5) | WT, α2C | 106 (B3,C5) |
| V66K, β3C | 36 (often) | V66K, α2C | 106 (A4) |
| V66R, β3C | 36 (often) | V66R, α2C | 106 (C1) |
| WT, α1N | 54 (C1, C4, D3, E3) | WT, α3N | 119–121 (D3, E3), 120–121 (D1, E4), 122 (B4, E4) |
| V66K, α1N | 54 (B5, C5, D4) | V66K, α3N | 119–121 (E5), 120–121 (A1, B5, E2), 122 (D5) |
| V66R, α1N | 54 (B3, C1, C2, C4, E2, E3, E4) | V66R, α3N | 119–121 (B2, B4, B5, C1, D2, E1), 120–121 (C2) |
| WT, α1C | 68 (often) | WT, α3C | 135 (often) |
| V66K, α1C | 68 (often) | V66K, α3C | 135 (often) |
| V66R, α1C | 68 (often) | V66R, α3C | 135 (often) |
If a residue frayed in >10 simulations “often” is stated. Simulations for which additional SGLD runs were performed are indicated with an asterisk. I92D variant is not listed because fraying occurred in a large number of simulations.
Table 1 lists a large number of fraying events. Owing to limited access to computational resources, only secondary structure changes that initiated near the site of substitution were amplified with further simulations. The simulations that recorded such changes are B4 in WT; E1 and E2 in V66K; and C5 and E2 in V66R. Since Lys-66 in the C2 simulation of V66K leaves the interior and is fully solvated by bulk water, this simulation was amplified even though no significant changes in secondary structure changes were observed.
Snapshots representative of the largest secondary structure changes observed in additional simulations are shown in Fig. 3. For the WT, only fraying of C-terminus of strand β1 is observed. In the V66K variant strands β1, β2, β3, and the C-terminus of helix α1, were frayed. For the V66R variant, both ends of the β1 and β2 strands were frayed. More detailed analysis of the types and pathways of observed secondary structure changes is given in Relaxation Pathways.
Consequences of ionization: water penetration
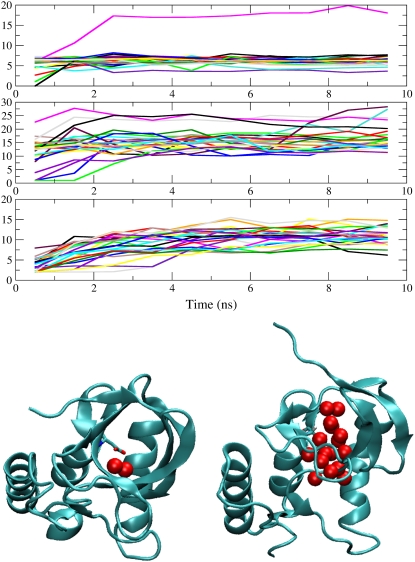
To study the state of hydration of charged internal groups, the number of water molecules within 6 Å of polar side-chain atoms was calculated. Averages over each nanosecond of every simulation are shown in Fig. 4.
FIGURE 4.
(Top) Number of water molecules within a 6 Å radius of side-chain polar atoms of substituted ionizable groups, averaged over 1 ns. (Graphs from top to bottom) Lys-66, Arg-66, and Asp-92. Different colors represent different simulations. (Bottom) Snapshots from simulation of I92D variant when Asp-92 is neutral (left) and charged (right). Red spheres represent internal water molecules.
The figure shows that internal ionizable groups become solvated by a large number of water molecules during the course of the simulations. In the case of the V66R variant, the side chain was hydrated by water in the bulk phase, whereas in the cases of V66K and I92D variants the ionizable groups remained internal in the majority of simulations. Simulations in which ionizable groups are neutral are available for both the V66K and I92D variants (57). These simulations showed that the Lys-66 side chain is dehydrated and the Asp-92 side chain is surrounded by approximately two water molecules, in full agreement with crystallographic observations. Upon charging of the internal ionizable groups the number of surrounding water molecules increases from 0 to ∼3–8 in the case of Lys-66, and from 2 to 10–15 in the case of Asp-92. Evidently, charging of an internal group promotes water penetration. This is illustrated graphically by representative snapshots from the simulation of the I92D variant with neutral and charged Asp-92 (Fig. 4).
Relaxation pathways
In all cases, the simulations suggest that the structural relaxation that is coupled to the ionization of internal groups can follow multiple pathways. The pathways involve both penetration of water into the protein interior as well as relaxation of protein backbone and side chains.
The initial response to the ionization of Lys-66 involves fast hydration of the side chain by water penetration. This was observed in all simulations. Between three and eight water molecules penetrate and hydrate the amino moiety of Lys-66, usually during the equilibration stage or during the first two nanoseconds (Fig. 4). Visual inspection of selected trajectories reveals that two major pathways are used for water penetration; a passage between α1 and β1, and a passage between β2 and β3. Several secondary relaxation processes were observed: exiting of the Lys-66 side chain from the protein interior, disruption of the structures of β1, β2, or β3 strands, separation of β1 and β2 strands from the remainder of the protein, or fraying of residues in the C-terminus of helix α1.
The initial relaxation in the V66R variant involves both hydration of the guanidium groups of Arg-66 and hydrogen bonding to the turn between β1 and β2. Fig. 4 shows that the hydration of this group happens in timescales ranging from the equilibration time to up to four ns. The number of water molecules surrounding Arg-66 ranges between 2 and 23 during the first nanosecond and between 12 and 28 during the last nanosecond. Inspection of selected trajectories suggests that the side chain of Arg-66 samples different rotameric states and protein hydrogen-bonding partners. The latter involve residues belonging to the β1-β2 turn, β1 strand, and the α1 helix. Backbone relaxation observed in the simulations of the V66R variant involve fraying of both ends of β1 and β2 strands.
In simulations of the I92D variant the number of water molecules in the neighborhood of the carboxylic moiety of Asp-92 increases more slowly than for the other two variants. As shown in Fig. 4, the average number of water molecule within the 6 Å radius of polar groups of Asp-92 is between 3 and 8 during the first nanosecond of simulation time, and between 12 and 15 during the 10th nanosecond. Through inspection of the snapshots taken at the end of the 10th nanosecond, two major relaxation pathways can be identified. In one, the Asp-92 side chain is hydrogen-bonded to the backbone of the strand β5 (in most cases it is the backbone of Tyr-81). This conformation is present in 10 out of 25 simulations. Approximately half of those simulations are accompanied by partial disruption of the β5 strand, complete disruption of the β4 strand, and absence of water molecules from the protein core. In the other half, water is present in the core. In the remaining 15 simulations, Asp-92 is hydrated in the interior of the protein. Water penetration occurs through multiple routes. Various levels of disruption of the β-barrel are registered, including complete disruption of strands β3, β4, or β5, and partial disruption of strands β1 and β2. Partial fraying of C-terminus of α1 is also registered.
Energetics
A detailed energetic analysis was performed for simulations that displayed the largest changes in secondary structure near the site of substitution (B4 for the WT, E1 and E2 for the V66K, C5 and E2 for the V66R, and D2 and C3 for the I92D). The analysis was performed for two additional simulations: A1 of the WT, which serves as a control since it does not have guiding nor internal ionizable groups, and C2 of the V66K, in which Lys-66 side chain leaves the protein interior. The number of water molecules that hydrate internal ionizable groups and the pKa values of these groups were determined for the simulations selected for analysis. Fig. 5 illustrates the analysis performed for each of the selected simulations.
FIGURE 5.
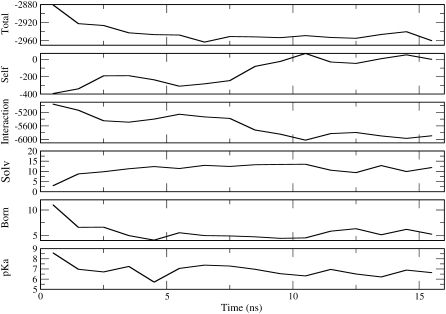
Energetic analysis of simulation D2 with the I92D variant. (From top to bottom) Total effective energy, self-energy, electrostatic interaction energy, number of solvent molecules around Asp-92, Born term, and pKa value of Asp-92. All energies are in kcal/mol. All numbers represent averages over 1 ns of SGLD runs.
Analysis of the control case (A1 simulation with WT), indicated that in the absence of internal ionizable groups, the effective energies can drop by as much as 40 kcal/mol during the course of the simulation. Analysis of the B4 simulation with WT indicates a drop in energy of 30 kcal/mol. Inspection of the contributions of individual secondary structure elements to total protein energy indicates that in many cases rearrangements in the loop regions give rise to changes in energy that are >5 kcal/mol. In the B4 simulation of WT, the observed secondary structure change that was observed, consisting of the breaking of a hydrogen bond between β1 and β2, did not contribute significantly to the overall change in energy.
Analysis of selected trajectories of V66K, V66R, and I92D variants indicates that ionization of internal groups sometimes contributes to an additional decrease in energy. For example, in the C2 simulation with V66K, the hydration of Lys-66 contributed to a decrease in energy of 12 kcal/mol. In simulations of the I92D variant, hydration of Asp-92 contributed to a 30 kcal/mol decrease in energy. Since the errors related to cutoffs used to calculate electrostatic energies and to the use of empirical coefficients in Eq. 2 are large, the analysis yielded only a qualitative understanding of the energetics of protein conformational changes.
Comparison of experiments and simulations
The simulations of the WT protein showed small frayings of various secondary structure elements (Table 1). Such local unfolding events are not the focus of this study since they are observed consistently in simulations of all variants, and are thus considered background fluctuations. To ensure that parts of the WT protein that were supposed to be folded did not unfold during the SGLD simulations, hydrogen protection factors were determined by calculating the average number (over all 25 SGLD runs) of water oxygen atoms within a 3 Å radius of the backbone NH atoms (58). The calculation suggested that the hydrogens that are well protected in the experiment (59) are also well protected during the simulations. Some of the hydrogens that show exchange in experiments are dehydrated in the simulations. This discrepancy is attributed to limited simulation time and the fact that the simulated protein differs slightly from the protein used in hydrogen exchange experiments.
Circular dichroism and steady-state fluorescence suggest that the I92D variant undergoes global unfolding upon charging of the substituted ionizable group, and that the V66K and V66R variants undergo local reorganization. The trends observed in the simulations are fully consistent with these experimental trends. Of the four proteins that were studied, the I92D variant displayed the largest change in secondary structure and the largest root mean-square deviation (RMSD) values (Fig. 2). Changes in the V66K and the V66R variant were less dramatic. Their RMSD values are similar to each other and they are in between those of the WT and the I92D variant. Even though secondary structure assignments during SGLD trajectory in Fig. 2 cannot distinguish between the WT and the V66K and V66R variants, additional simulations indicate that the secondary structure of the WT protein is perturbed much less than the secondary structure of V66K and V66R. This is illustrated in snapshots from additional simulations shown in Fig. 3.
The observed changes in secondary structure and calculated RMSD values for V66K and V66R variants are similar. Both variants show significant perturbations in the strand β1, and sometimes also strands β2 and β3, as shown in Fig. 3. The perturbations in strand β1 are consistent with the crystal structure of the V66R variant, which shows domain swapping of this strand when Arg-66 is in the charged state. No simulations of the V66R variant showed perturbations in the C-terminus of helix α1, but in a simulation of the V66K variant fraying of three residues (up to residue 65) was observed. This is consistent with results from NMR spectroscopy studies with V66K, which show that six residues in the C-terminus of helix α1 are rendered more dynamic by the ionization of Lys-66. NMR experiments suggest that these residues are in the intermediate exchange regime, which occurs on a μs-to-ms timescale (M. S. Chimenti and B. García-Moreno E., 2008, personal communication). These timescales are still orders-of-magnitude away from what can be achieved by multiple and enhanced SGLD simulations, thus it is not surprising that full fraying of the C-terminus of helix α1 was not observed in the simulations. The pKa values calculated for 10-ns snapshots from SGLD runs suggest that after 10 ns, the protein has not fully relaxed in response to ionization of Lys-66, as only one of 25 calculated pKa values is 10.4 or larger. The calculated pKa values of Lys-66 have a mean value of 5.6 and a standard deviation of 2.2. The pKa values calculated on the last snapshots of additional runs indicate that certain conformational changes can lead to normalization of the Lys pKa value. These include: twisting of the Lys-66 side chain and its hydration by the bulk water; fraying of C-terminus of helix α1; and fraying of strands β1, β2, and β3.
The pKa values of Arg-66, calculated for the last snapshots of V66R simulations, display a mean value of 12.3 and a standard deviation of 1.1. These pKa values are characteristic of a fully solvated Arg, which has a pKa value of 12. This indicates that the protein relaxation in response to ionization of Arg-66 might be complete. The perturbation in the structure of strand β1, as well as the breaking of several hydrogen bonds between strands β1 and β2 that were observed in the simulations, might correspond to the solution structure of the V66R variant. Domain swapping of strand β1, observed in the crystal structure, might be an artifact of crystallization. A number of other experiments indicate that in solution this protein is monomeric (D. A. Karp and B. García-Moreno E., 2008, personal communication).
In 20 of 25 simulations of the I92D variant the protein's core is fully hydrated. The pKa values of Asp-92 approach the value of 4.0 expected from a fully solvated Asp; the pKa values calculated for last snapshots of I92D simulations display a mean value of 5.5 and a standard deviation of 2.1.
Accuracy and performance of SGLD simulations
Comparison of the results obtained with different guiding factors yields an estimate of the accuracy and performance of SGLD simulations. Statistical analysis of secondary structure content resulting from simulations with different guiding factors has been performed. Results for a representative simulation (i.e., V66R) and for a representative secondary structure element (i.e., helix 1) are shown in Table 2. The table lists the percentage of total simulation time that each residue was α-helical. The table, however, does not contain information on how often particular residues frayed. The information about the frequency of occurrence of fraying events that last longer than 100 ps is in Table 1. This table shows that, for example, residue 68 of helix 1 frayed in more than 10 simulations while residue 54 frayed in seven simulations. When fraying events are sampled well (i.e., when they occur often and in many simulations), such as in case of residue 68 of helix 1, all guiding factors yield similar results. In cases when changes in secondary structure occur infrequently, such as for residue 54 of helix 1, there are differences in performances of different guiding factors. Results for other secondary structure elements and other simulated proteins (data not shown) yield the same conclusion.
TABLE 2.
Percentage that residues 50–69, which include the α1 helix, were helical in simulations with different guiding factors
| V66R, helix α1
| |||||
|---|---|---|---|---|---|
| Residue | Regular LD | tl = 0.1,λ = 0.25 | tl = 0.5,λ = 0.25 | tl = 0.1,λ = 1.0 | tl = 0.5,λ = 1.0 |
| 50 | 0 | 0 | 0 | 0 | 0 |
| 51 | 0 | <1 | 0 | <1 | <1 |
| 52 | 0 | <1 | 0 | <1 | <1 |
| 53 | 0 | <1 | 0 | <1 | <1 |
| 54 | 0 | <1 | <1 | 17 | 18 |
| 55 | >99 | >99 | 98 | 99 | 99 |
| 56 | >99 | >99 | 99 | >99 | >99 |
| 57 | >99 | 100 | 100 | >99 | >99 |
| 58 | >99 | 100 | 100 | >99 | 100 |
| 59 | 100 | 100 | >99 | >99 | >99 |
| 60 | 100 | 100 | 100 | >99 | 100 |
| 61 | 100 | 100 | 100 | 100 | 100 |
| 62 | 100 | 100 | 100 | >99 | 100 |
| 63 | 100 | 100 | 100 | >99 | 100 |
| 64 | >99 | 100 | >99 | >99 | >99 |
| 65 | >99 | >99 | >99 | >99 | >99 |
| 66 | >99 | >99 | >99 | 99 | >99 |
| 67 | 98 | 95 | 98 | 94 | 98 |
| 68 | 71 | 67 | 77 | 62 | 63 |
| 69 | 0 | 0 | 0 | 0 | 0 |
Performance of guiding factors in sampling infrequent events that last longer than 100 ps can be inferred by counting fraying events from Table 1. The results, shown in Table 3, indicate that guiding parameters B (tl = 0.1, λ = 0.25), C (tl = 0.1, λ = 1.0), and E (tl = 0.5, λ = 1.0) perform approximately two times better than guiding parameters D (tl = 0.5, λ = 0.25), or A (regular LD simulations) in sampling infrequently occurring events. The trends that were observed in the performance of guiding parameters were expected as a large guiding factor λ yields a large guiding force, while a large averaging time yields a small guiding force.
TABLE 3.
Performance of different guiding factors in sampling infrequent fraying events
| Parameters | # < 10 | # < 4 |
|---|---|---|
| Regular LD | 9 | 4 |
| tl = 0.1, λ = 0.25 | 18 | 10 |
| tl = 0.1, λ = 1.0 | 21 | 9 |
| tl = 0.5, λ = 0.25 | 9 | 5 |
| tl = 0.5, λ = 1.0 | 19 | 10 |
Numbers in column labeled “# < 10” included all events listed in Table 2, i.e., events that occurred in <10 simulations; numbers in column labeled “# < 4” included only events that occurred in <4 simulations.
Despite the apparently small advantage in sampling of rare events achieved by addition of guiding forces, the largest fraying of the secondary structure in the vicinity of the substituted ionizable groups are registered in simulation with nonzero guiding force. This becomes apparent by counting fraying events for the C-termini of strands β1 and β5 in Table 1. This is expected since charging of a neutral residue perturbs the system away from its equilibrium, and drives the system toward a new equilibrium. SGLD enhances such motions and accelerates the conformational changes associated with these ionization events.
The average RMSD values of each residue obtained in simulations with different guiding factors were compared (data not shown). In regions of compact secondary structure where fluctuations are small, i.e., α-helices and β-strands, all guiding factors exhibited approximately the same RMSD values. The exception are the region of strands β1 and β2 of the V66K variant, where the guiding parameters C and E, which utilize λ = 1, yield slightly larger RMSD values. The same two guiding parameters sometimes yield large RMSD values in loop regions, where fluctuations are large. In terms of hydration of interior groups, all guiding parameters yield comparable results (data not shown).
SUMMARY
Structural consequences of the ionization of internal groups in proteins were explored through multiple SGLD simulations. The structural changes that were observed include small rearrangements (such as side-chain rotations), small and large-scale water penetration, and loss of secondary structure. The structural trends observed in the simulations are fully consistent with the trends observed experimentally. The structural changes in the vicinity of sites 66 and 92 in the simulations of the WT are rather small. In contrast, the V66K, V66R, and I92D variants show noticeable structural changes in the vicinity of the internal ionizable group, suggesting that these changes are indeed a consequence of the substitutions and of the ionization of these internal groups.
The largest changes were observed for the I92D variant. For this variant, which is known to unfold globally upon ionization of Asp-92, all simulations recorded the disruption of the β-barrel. The extent of disruption ranged from perturbations of a few residues in some simulations, to the complete unraveling of two β-strands. The two strands closest to the substitution site, β4 and β5, unraveled most often. Fraying at the C-terminus of helix α1 was observed in some simulations. Charging of the internal Asp-92 in the I92D variant promoted water penetration: the protein core became hydrated by a large number of water molecules in the majority of simulations. In contrast, Asp-92 was hydrated by only one or two water molecules in simulations in which Asp-92 is neutral (57).
In simulations of the V66K and V66R variants, structural changes on a smaller scale were observed, in agreement with experimental observations. In simulations of the V66R variant, changes in the structure of the β1 and β2 strands were recorded, with sometimes up to five hydrogen bonds broken between them. This is consistent with the x-ray structure of V66R in which the β1 strand is released and the domain swapped. In the simulations of the V66K variant, changes in the β1, β2, and β3 strands are observed. In one simulation, fraying of helix α1 was observed. Changes in the β-barrel structure and C-terminus of helix α1 are both consistent with observations by NMR spectroscopy.
The pKa values calculated on the final 10-ns snapshots (12.3 ± 1.1 for Arg-66 and 5.5 ± 2.1 for Asp-92) are close to the normal pKa values of 12 and 4 for Arg and Asp, respectively. In contrast, the pKa values of Lys-66 (5.6 ± 2.1) was still far away from the normal value of 10.4. The pKa values of Lys-66 reach the model compound pKa values only in a few cases: when the side chain of Lys-66 left the protein interior, when fraying of C-terminus of helix α1 occurred, or when fraying of strands β1, β2, and β3 occurred.
An assessment of the accuracy and performance of SGLD was performed by comparing results of multiple simulations with nonzero and zero guiding force (regular Langevin dynamics). Four different sets of guiding parameters were tested. Populations of conformations that were easily accessible through regular LD simulations were comparable for LD and SGLD with all guiding factors, suggesting that SGLD does not alter population distributions. In sampling of rare protein conformations some SGLD parameters, particularly those that employed a guiding factor λ = 1, performed twice as well as LD. For V66K and V66R variants, conformational rearrangements coupled to ionization of internal groups were observed exclusively in the SGLD simulations with nonzero guiding force. This suggests that, despite the evidence that for one of the variants the conformational sampling achieved with SGLD is still insufficient, SGLD represents a significant improvement over MD and LD in sampling of conformations induced by proton binding events.
Acknowledgments
We thank Michael J. Harms for help with pKa calculations. All SGLD runs were performed on the National Institutes of Health Biowulf cluster.
This work was supported by a National Institutes of Health grant (No. R01 GM061597) to B.G.M.E. This research was supported in part by the Intramural Research Program of the National Institutes of Health, National Heart, Lung, and Blood Institute.
Editor: Helmut Grubmuller.
References
- 1.Hoff, W. D., A. Xie, I. H. M. van Stokkum, X.-J. Tang, J. Gural, A. R. Kroon, and K. J. Hellingwerf. 1999. Global conformational changes upon receptor stimulation in photoactive yellow protein. Biochemistry. 38:1009–1017. [DOI] [PubMed] [Google Scholar]
- 2.Lee, B.-C., P. A. Croonquist, T. R. Sosnick, and W. D. Hoff. 2001. PAS domain receptor photoactive yellow protein is converted to a molten globule state upon activation. J. Biol. Chem. 276:20821–20823. [DOI] [PubMed] [Google Scholar]
- 3.Xie, A., L. Keleman, J. Hendriks, B. J. White, K. J. Hellingwerf, and W. D. Hoff. 2001. Formation of a new buried charge drives a large-amplitude protein quake in photoreceptor activation. Biochemistry. 40:1510–1517. [DOI] [PubMed] [Google Scholar]
- 4.Brown, L. S., H. Kamikubodagger, L. Zimanyi, M. Kataoka, F. Tokunaga, P. Verdegem, J. Lugtenburg, and J. K. Lanyi. 1997. A local electrostatic change is the cause of the large-scale protein conformation shift in bacteriorhodopsin. Proc. Natl. Acad. Sci. USA. 94:5040–5044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Luecke, H., B. Schobert, H. T. Richter, J. P. Cartailler, and J. K. Lanyi. 1999. Structure changes in bacteriorhodopsin during ion transport at 2 Å resolution. Science. 286:255–260. [DOI] [PubMed] [Google Scholar]
- 6.Lanyi, J. K. 2004. Bacteriorhodopsin. Annu. Rev. Physiol. 66:665–688. [DOI] [PubMed] [Google Scholar]
- 7.Rastogi, V. K., and M. E. Girvin. 1999. Structural changes linked to proton translocation by subunit c of the ATP synthase. Nature. 402:263–268. [DOI] [PubMed] [Google Scholar]
- 8.Nakano, T., T. Ikegami, T. Suzuki, M. Yoshida, and H. Akutsu. 2006. A new solution structure of ATP synthase subunit c from thermophilic bacillus PS3, suggesting a local conformational change for H+-translocation. J. Mol. Biol. 358:132–144. [DOI] [PubMed] [Google Scholar]
- 9.Mertz, J. E., and B. M. Pettitt. 1994. Molecular dynamics at a constant pH. Int. J. Supercomput. Appl. High Perform. Comput. 8:47–53. [Google Scholar]
- 10.Baptista, A. M., P. J. Martel, and S. B. Petersen. 1997. Simulation of protein conformational freedom as a function of pH: constant-pH molecular dynamics using implicit titration. Proteins Struct. Funct. G E N. 27:523–544. [PubMed] [Google Scholar]
- 11.Börjesson, U., and P. H. Hünenberger. 2001. Explicit-solvent molecular dynamics simulation at constant pH: methodology and application to small amines. J. Chem. Phys. 114:9706–9719. [Google Scholar]
- 12.Bürgi, R., P. A. Kollman, and W. F. van Gunsteren. 2002. Simulating proteins at constant pH: an approach combining molecular dynamics and Monte Carlo simulation. Proteins Struct. Funct. G E N. 47:469–480. [DOI] [PubMed] [Google Scholar]
- 13.Dlugosz, M., and J. M. Antosiewicz. 2004. Constant-pH molecular dynamics simulations: a test case of succinic acid. Chem. Phys. 302:161–170. [Google Scholar]
- 14.Mongan, J., D. A. Case, and J. A. McCammon. 2004. Constant pH molecular dynamics in generalized born implicit solvent. J. Comput. Chem. 25:2038–2048. [DOI] [PubMed] [Google Scholar]
- 15.Baptista, A. M., V. H. Teixeira, and C. M. Soares. 2002. Constant-pH molecular dynamics using stochastic titration. J. Chem. Phys. 117:4184–4200. [Google Scholar]
- 16.Lee, M. S., F. R. Salsbury, Jr., and C. L. Brooks III. 2004. Constant-pH molecular dynamics using continuous titration coordinates. Proteins Struct. Funct. G E N. 56:738–752. [DOI] [PubMed] [Google Scholar]
- 17.Khandogin, J., and C. L. Brooks III. 2005. Constant pH molecular dynamics with proton tautomerism. Biophys. J. 89:141–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Laio, A., and M. Parrinello. 2002. Escaping free energy minima. Proc. Natl. Acad. Sci. USA. 99:12562–12566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hummer, G., and I. G. Kevredikis. 2003. Coarse molecular dynamics of a peptide fragment: free energy, kinetics and long-time dynamics computations. J. Chem. Phys. 118:10762–10773. [Google Scholar]
- 20.Bahar, I., and A. J. Rader. 2005. Coarse-grained normal mode analysis in structural biology. Curr. Opin. Struct. Biol. 2005:586–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zheng, W., and B. R. Brooks. 2005. Normal-mode-based prediction of protein conformational changes guided by distance constraints. Biophys. J. 88:3109–3117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chu, J.-W., and G. A. Voth. 2005. Allostery of actin filaments: molecular dynamics simulations and coarse-grained analysis. Proc. Natl. Acad. Sci. USA. 102:13111–13116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Torrie, G. M., and J. P. Valleau. 1977. Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling. J. Comput. Phys. 23:187–199. [Google Scholar]
- 24.Grubmüller, H. 1995. Predicting slow structural transitions in macromolecular systems: conformational Flooding. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 52:2893–2906. [DOI] [PubMed] [Google Scholar]
- 25.Voter, A. F. 1997. Hyperdynamics: accelerated molecular dynamics of infrequent events. Phys. Rev. Lett. 78:3908–3911. [Google Scholar]
- 26.Hamelberg, D., J. Mongan, and J. A. McCammon. 2004. Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules. J. Chem. Phys. 120:11919–11929. [DOI] [PubMed] [Google Scholar]
- 27.Sugita, Y., and Y. Okamoto. 2000. Replica-exchange multicanonical algorithm and multicanonical replica-exchange method for simulating systems with rough energy landscape. Chem. Phys. Lett. 329:261–270. [Google Scholar]
- 28.Sanbonmatsu, K. Y., and A. E. García. 2002. Structure of Met-encephalin in explicit aqueous solution using replica exchange molecular dynamics. Proteins Struct. Funct. G E N. 46:225–234. [DOI] [PubMed] [Google Scholar]
- 29.Olender, R., and R. Elber. 1996. Calculation of classical trajectories with a very large time step: formalism and numerical examples. J. Chem. Phys. 105:9299–9315. [Google Scholar]
- 30.Schlitter, J., M. Engels, P. Krüger, E. Jacoby, and A. Wollmer. 1993. Targeted molecular dynamics simulation of conformational change—application to the T ↔ R transition in insulin. Mol. Simul. 10:291–308. [Google Scholar]
- 31.Izrailev, S., S. Stepaniants, M. Balsera, Y. Oono, and K. Schulten. 1997. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 72:1568–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wu, X. W., and B. R. Brooks. 2003. Self-guided Langevin dynamics simulation method. Chem. Phys. Lett. 381:512–518. [Google Scholar]
- 33.García-Moreno E., B., J. J. Dwyer, A. G. Gittis, E. E. Lattman, D. S. Spencer, and W. E. Stites. 1997. Experimental measurement of the effective dielectric in the hydrophobic core of a protein. Biophys. Chem. 64:211–224. [DOI] [PubMed] [Google Scholar]
- 34.Dwyer, J. J., A. G. Gittis, D. A. Karp, E. E. Lattman, D. S. Spencer, W. E. Stites, and B. García-Moreno E. 2000. High apparent dielectric constants in the interior of a protein reflect water penetration. Biophys. J. 79:1610–1620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Harms, M. J., J. L. Schlessman, M. S. Chimenti, G. R. Sue, A. Damjanovic, and B. García-Moreno E. 2007. Flexibility of the protein-water interface is responsible for the normal pKa value of a buried Lys in staphylococcal nuclease. Protein Sci. In press. [DOI] [PMC free article] [PubMed]
- 36.Fitch, C. A., D. Karp, K. Lee, W. Stites, E. Lattman, and B. García-Moreno E. 2002. Experimental pKa values of buried residues: analysis with continuum methods and role of water penetration. Biophys. J. 82:3289–3304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Damjanović, A., B. García-Moreno E., E. E. Lattman, and A. E. García. 2005. Molecular dynamics study of water penetration in staphylococcal nuclease. Proteins Struct. Funct. G E N. 60:433–449. [DOI] [PubMed] [Google Scholar]
- 38.Kato, M., and A. Warshel. 2006. Using a charging coordinate in studies of ionization induced partial unfolding. J. Phys. Chem. B. 110:11566–11570. [DOI] [PubMed] [Google Scholar]
- 39.Nguyen, D. M., R. L. Reynald, A. G. Gittis, and E. E. Lattman. 2004. X-ray and thermodynamic studies of staphylococcal nuclease variants I92E and I92K: insights into polarity of the protein interior. J. Mol. Biol. 341:565–574. [DOI] [PubMed] [Google Scholar]
- 40.Wu, X., and S. Wang. 1998. Self-guided molecular dynamics simulation for efficient conformational search. J. Phys. Chem. B. 102:7238–7250. [Google Scholar]
- 41.Andricioaei, I., A. R. Dinner, and M. Karplus. 2003. Self-guided enhanced sampling methods for thermodynamic averages. J. Chem. Phys. 118:1074–1084. [Google Scholar]
- 42.Schlessman, J. L., C. Abe, A. Gittis, D. A. Karp, M. A. Dolan, and B. García-Moreno E. 2007. Crystallographic study of hydration of an internal cavity in engineered proteins with buried polar or ionizable groups. Biophys. J. 94:3208–3216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 44.MacKerell, A. D., Jr., D. Bashford, M. Bellott, R. L. Dunbrack, Jr., J. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, I. W. E. Reiher, B. Roux, M. Schlenkrich, J. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-hydrogen empirical potential for molecular modeling and dynamics studies of proteins using the CHARMM22 force field. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- 45.Hoover, W. 1985. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A. 31:1695–1697. [DOI] [PubMed] [Google Scholar]
- 46.Feller, S. E., Y. H. Zhang, R. W. Pastor, and B. R. Brooks. 1995. Constant pressure molecular dynamics simulation—the Langevin piston method. J. Chem. Phys. 103:4613–4621. [Google Scholar]
- 47.Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald. An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 48.Kabsch, W., and C. Sander. 1983. How good are predictions of protein secondary structure? FEBS Lett. 155:179. [DOI] [PubMed] [Google Scholar]
- 49.Frishman, D., and P. Argos. 1995. Knowledge-based secondary structure assignment. Proteins Struct. Funct. Genet. 23:566–579. [DOI] [PubMed] [Google Scholar]
- 50.Martin, J., G. Letellier, A. Marin, J.-F. Taly, A. G. de Brevern, and J.-F. Gibrat. 2005. Protein secondary structure assignment revisited: a detailed analysis of different assignment methods. BMC Struct. Biol. 5:1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Carlson, H. A., and W. L. Jorgensen. 1995. An extended linear response method for determining free energies of hydration. J. Phys. Chem. 99:10667–10673. [Google Scholar]
- 52.Wu, X., and B. R. Brooks. 2004. β-hairpin folding mechanism of a nine-residue peptide revealed from molecular dynamics simulations in explicit water. Biophys. J. 86:1946–1958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Richmond, T. J. 1984. Solvent accessible surface area and excluded volume in proteins. J. Mol. Biol. 178:63–90. [DOI] [PubMed] [Google Scholar]
- 54.Kyte, J., and R. F. Doolittle. 1982. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 157:105–132. [DOI] [PubMed] [Google Scholar]
- 55.Davis, M. E., J. D. Madura, B. A. Luty, and J. A. McCammon. 1991. Electrostatics and diffusion of molecules in solution: simulations with the University of Houston Brownian Dynamics Program. Comput. Phys. Commun. 62:187–197. [Google Scholar]
- 56.van Vlijmen, H. W. T., M. Schaefer, and M. Karplus. 1998. Improving the accuracy of protein pKa calculations: conformational averaging versus the average structure. Proteins Struct. Funct. G E N. 33:145–158. [DOI] [PubMed] [Google Scholar]
- 57.Damjanović, A., J. L. Schlessman, C. A. Fitch, A. E. García, and B. García-Moreno E. 2007. Role of flexibility and polarity as determinants of the hydration of internal cavities and pockets in proteins. Biophys. J. 93:2791–2804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.García, A. E., and G. Hummer. 1999. Conformational dynamics of cytochrome c: correlation to hydrogen exchange. Proteins Struct. Funct. G E N. 36:175–191. [PubMed] [Google Scholar]
- 59.Loh, S. N., K. E. Prehoda, J. Wang, and J. L. Markley. 1993. Hydrogen exchange in unligated and ligated staphylococcal nuclease. Biochemistry. 32:11022–11028. [DOI] [PubMed] [Google Scholar]
- 60.Loll, P., and E. Lattman. 1989. The crystal structure of the ternary complex of staphylococcal nuclease, Ca+2, and the inhibitor pdTp, refined at 1.65 Å. Proteins Struct. Funct. G E N. 5:183–201. [DOI] [PubMed] [Google Scholar]