Alternating Carrier Models of Asymmetric Glucose Transport Violate the Energy Conservation Laws

Abstract

Alternating access transporters with high-affinity externally facing sites and low-affinity internal sites relate substrate transit directly to the unliganded asymmetric “carrier” (Cⁱ) distribution. When both bathing solutions contain equimolar concentrations of ligand, zero net flow of the substrate-carrier complex requires a higher proportion of unliganded low-affinity inside sites (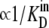) and slower unliganded “free” carrier transit from inside to outside than in the reverse direction. However, asymmetric rates of unliganded carrier movement, k_ij, imply that an energy source, ΔG_carrier = RT ln (k_oi/k_io) = RT ln (Cⁱⁿ/C^out) = RT ln (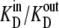), where R is the universal gas constant (8.314 Joules/M/K°), and T is the temperature, assumed here to be 300 K°, sustains the asymmetry. Without this invalid assumption, the constraints of carrier path cyclicity, combined with asymmetric ligand affinities and equimolarity at equilibrium, are irreconcilable, and any passive asymmetric uniporter or cotransporter model system, e.g., Na-glucose cotransporters, espousing this fundamental error is untenable. With glucose transport via GLUT1, the higher maximal rate and K_m of net ligand exit compared to net ligand entry is only properly simulated if ligand transit occurs by serial dissociation-association reactions between external high-affinity and internal low-affinity immobile sites. Faster intersite transit rates occur from lower-affinity sites than from higher-affinity sites and require no other energy source to maintain equilibrium. Similar constraints must apply to cotransport.

INTRODUCTION

Glucose transport across cell membranes, via members of the GLUT branch of the major facilitator superfamily, is passive, so net transport continues by facilitated diffusion only until the chemical potential difference across the membrane of the transported substrate, or ligand, is nullified, when equimolar concentrations are present in the solutions bathing both sides of the transporter. Despite the passive nature of the transport process, the observed sugar affinity at the inside site, or internal or inward-facing site (∝1/K_m), as obtained by the concentration at half-maximal rates of export, has often been found to be lower than at the outside, outward-facing site or import face of the carrier or transporter.

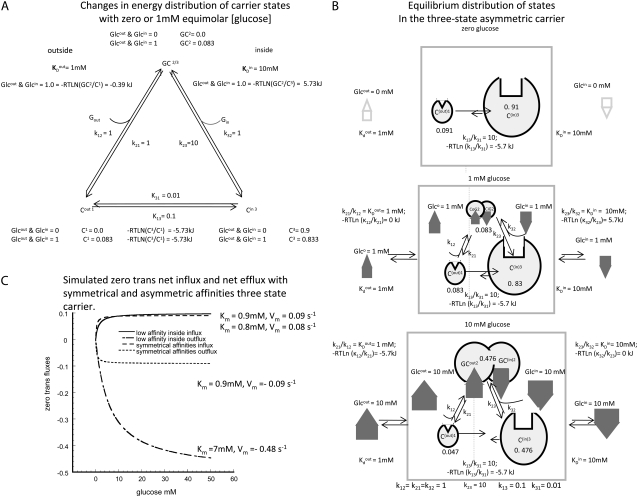
The asymmetric transport process for glucose in erythrocytes has traditionally been described in terms of a mobile circulating carrier, using a four-node cyclic network (1–9). This scheme can be simplified to a three-node cycle, as adopted by Stein (9), in which the internal and external faces of the carrier-glucose complex are condensed to a single node and assumed to be centrally positioned (Figs. 1 A and 2).

FIGURE 1.

(A) The proportions of each carrier state, C₁, GC₂, and C₃, are shown with equimolar glucose concentrations in the external solutions of 0 and 1 mM with the asymmetric affinities and rates shown in C. (B) Illustration of the relative proportions of carrier form predicted by the three-state asymmetric mobile carrier assuming the inside site has K_D = 10 mM, the outside site has K_D = 1 mM, and both external solutions contain 1 mM glucose. All the rate constants are as shown in B for the asymmetric carrier. The relative sizes of the carrier forms 1 = 2 = 0.083 and 3 = 0.83 illustrate the relative proportions of each carrier state, and the energy differences between these states are shown beside the connecting arrows between the states. (C) Simulated zero-trans net influx and efflux via the three-node mobile carrier as illustrated in C, with either symmetrical or asymmetrical affinities. The lines with positive flux values are the influx rates and those with negative values are the efflux rates at varying concentrations of glucose in either external solution (influx) or internal solution (efflux). The symmetrical transporter generates operational K_ms for import or export of 0.9 mM and V_m of 0.09 s⁻¹ with assigned affinities of 1 mM on each side with the rates of association and dissociation between solutions and sites 1 and 3 = 1.0 s⁻¹ and the inverse rates of free-carrier transit = 0.1 s⁻¹. The asymmetric carrier is assigned a dissociation rate k₂₃ = 10 s⁻¹ and k₃₁ = 0.01 s⁻¹, and all other constants are the same as for the symmetrical carrier. The operational K_m for exit is 7 mM and V_m for net exit = 0.48 s⁻¹, whereas the K_m and V_m for net entry become 0.8 mM and 0.08 s⁻¹, respectively.

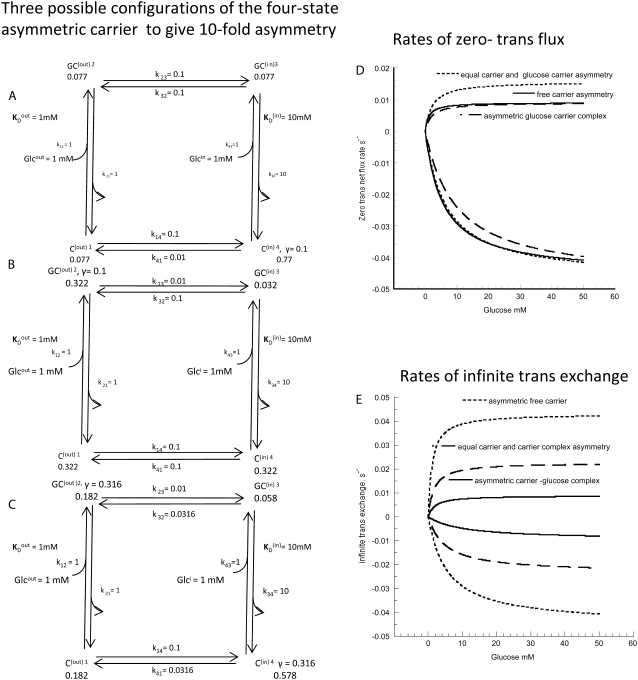
FIGURE 2.

Diagrams showing the rates and steady-state proportions of carrier forms of the four-state alternating carrier in which the inside carrier forms have a 10-fold-lower affinity, 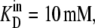than the outside site, 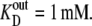(A) The rates of ligand-free carrier transit k₁₄/k₄₁ = 10 compensate for the asymmetric affinities between the inside and outside sites. (B) The rates of ligand-carrier complex transit, k₃₂/k₂₃ = 10, compensate for the asymmetric affinities between the inside and outside sites. (C) The rates of ligand carrier complex and free carrier compensate equally for the asymmetric affinities between the inside and outside sites. (D) The simulated flux rates for net influx and net efflux at varying external or internal glucose concentrations are shown with model parameters as shown in Fig. 2, A–C. The trans side contains zero glucose at all times. (E) The simulated flux rates for infinite trans exchange influx and efflux, where “unlabeled” glucose is present either inside or outside at 100 mM and the solution in the opposite side has varying concentrations of labeled sugar from which the rates are measured.

The important attributes of the three-node cyclic transporter are the possibility of differing ligand affinities at the outside and inside faces (K_D = k₂₁/k₁₂ and k₂₃/k₃₂, respectively); the asymmetries of maximal rates, V_m, of net ligand export and import match the affinity asymmetries, so that the V_m/K_m ratios for import and export, the Haldane relationships, are equal. Consequently, when the transported ligand has equal concentrations on both sides, net solute flow across the transporter is zero, despite the asymmetric affinities. The model apparently satisfies the thermodynamic requirement that solute transport be passive, as no exogenous energy source is coupled to the transport process. It also meets the microscopic reversibility constraint (9–13), since the product of all the clockwise rates, k₁ × k₂ × k₃, is equal to the product of all anticlockwise rates, k₋₁ × k₋₂ × k₋₃ (Fig. 1, B and C). However, it will be shown that these conventional views, although very influential, are fallacious, and have, for the last half-century, led to misunderstanding of biological transport processes.

As the asymmetric alternating carrier transporter is an accepted and orthodox explanation of transport asymmetry, it is important to explain where it is deficient, describe how this misunderstanding arose, and provide an alternative template for asymmetric transport that complies with the energy conservation laws.

The illustrations of the flaws in the asymmetric carrier model will be taken mainly from the three-node, or three-state, digraph (Fig. 1), as this is the most transparent and basic model; it exemplifies all the important attributes of the more complex models, but avoids their obscuring algebraic complexity. However, these criticisms of passive carrier asymmetry apply equally to the more complex four-node transporter (Fig. 2) and the cotransporter carrier models, most notably to the Na-glucose cotransporter SGLT1 and 2 (14–16) (Fig. 3), which also relies on asymmetric mobile carrier affinities to explain the apparent asymmetric affinities and maximal rates of influx and efflux. In addition, asymmetric carrier transport theory as applied to a variety of ligand transport systems in which asymmetric transport has been observed, e.g., nucleosides (17,18), choline (19,20), and gamma amino butyric acid (GABA) (21), suggests that asymmetric ligand transport is a widely replicated characteristic of biological transport processes.

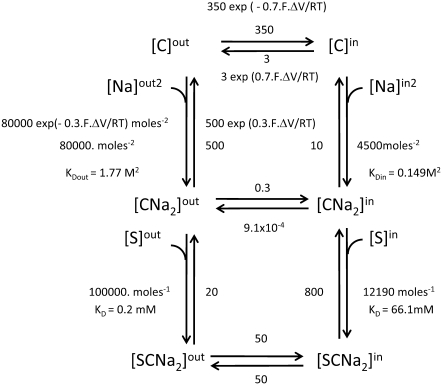
FIGURE 3.

The rate constants and affinities of α-methyl-glucoside (αMG) and Na⁺ at the inside and outside faces of the sodium glucose cotransporter SGLT1 (13). The K_Ds of αMG and Na⁺ at the cytoplasmic surface are 67 and 47 mM, respectively. At the external surface, the observed K_0.5^αMG = 0.33 mM at 100 mM Na⁺ and 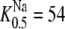at 1 mM αMG.

METHODS

All the numerical solutions to the transport models were obtained using Berkeley Madonna, a program for modeling and analysis of dynamic systems developed by R. Macey and G. Oster, version 8.01 http://www.berkeleymadonna.com. The simulations were carried out using the variable-step-length method of integration, using a minimum time step of 100 μs. The equations for mobile three- and four-state carrier flow are shown in Figs. 1 and 2, respectively, and those for intersite flow between fixed sites are shown in Fig. 4. The operational Michaelis-Menten parameters, K_m and V_m, derived from the simulated glucose fluxes with the three- and four-node transport schemes, are illustrated in Figs. 1, B and C, and 2, D and E, and Tables 1 and 2. The two-fixed-site model (Fig. 4 A, with outputs illustrated in Fig. 4 C and Tables 1 and 2) was obtained using Levenberg-Marquardt least-squares nonlinear fitting of the Michaelis-Menten equation to the simulations of the varying rates of “glucose” flow in the appropriate flux mode versus glucose concentration. The derived operational K_m and V_m values of these curves all have errors of <1%.

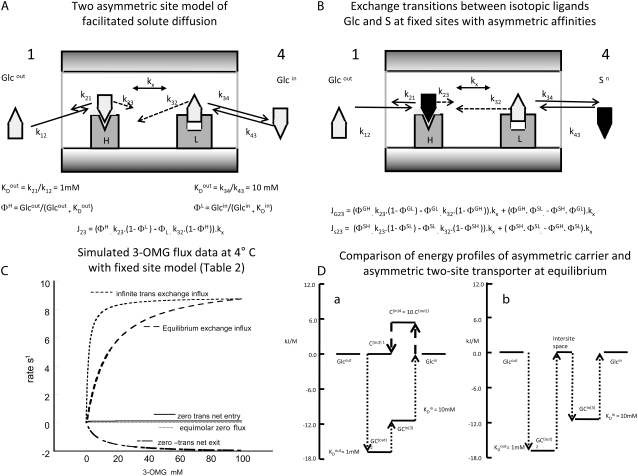
FIGURE 4.

(A) An illustration of the two-asymmetric-site model for facilitated diffusion of glucose, which closely simulates the net fluxes of glucose shown in Fig. 3 C. The high-affinity site on the outside has K_D = 1 mM and the low-affinity site L has K_D = 10 mM. The assigned rate constants for association and dissociation are the same as in Fig. 1 for the symmetrical or asymmetrical three-state mobile carriers. Because two independent ligand binding sites are assumed for the fixed-site network, the number of nodes is extended from three, in the case of the mobile carrier (Fig. 1 A) to four with the fixed-site network so the external solution is assigned as phase 1 and the internal bathing solution as phase 4. (B) Illustration of the mode of ligand exchange between isotopes of glucose in the free solution, where unlabeled glucose is present in the external solution and labeled glucose (black) in the inside solution. The ligands can exchange between connected sites or between the external solutions and adjacent binding sites, as shown. The equations shown simulate exchange fluxes shown in C. (C) Simulation of asymmetrical glucose (3-OMG) transport in erythrocytes at 4°C. The data simulated are those published by Cloherty et al. (21). The derived Michaelis-Menten parameters are shown in Table 2. The rates and affinities were adjusted to obtain a good fit to the observed data. There are several other possible fits obtainable, but the key point is that fitting requires asymmetric affinities with a low-affinity internal site, K_D = 12 mM, and a high-affinity external site, K_D = 0.5 mM. It should be noted that the observed ratio of K_{m out}/K_{m in} = 0.38/4.35 = 0.87 < the assigned ratio = 0.5/12 = 0.41. The masking of the asymmetry ratio is due to crossover of ligands between the internal and external binding sites. The higher the ratio of intersite transition rates relative to net flux rates the greater the ligand crossover and masking of asymmetry. Infinite-trans exchange flux is obtained by maintaining internal unlabeled [3-OMG] at 100 mM and varying external labeled [3-OMG] from zero to 100 mM (see B); equilibrium exchange is obtained by varying internal and external [3-OMG] from zero to 100 mM simultaneously; zero-trans net entry and exit are obtained by varying the external or internal [3-OMG] from zero to 100 mM while maintaining the concentration in the trans solution at zero. Zero net flux with equimolar concentrations is obtained when external [3-OMG] and internal [3-OMG] are both varied equally and simultaneously from zero to 100 mM. (D) Comparison of energy profiles at equilibrium of the ΔG for glucose as it traverses the transporter from outside to inside. (a) The change in glucose energy as it traverses from the external solution to the high-affinity site, C(1), where it forms a complex with carrier GC(2) (−17.2 kJ). It transits to the inside gaining ΔG to form the inside low-affinity GC(3) complex (−11.49 kJ) before dissociating into the inside solution. During return transit, the free carrier C⁴ loses unsourced energy (5.74 kJ), which compensates for the energy gain on GC transit. (b) As glucose traverses the two-site transporter from outside, it first binds to a high-affinity site (−17.2 kJ), then dissociates to the intersite space, where it reverts to the same energy level as in the external solutions (0 kJ). It then binds to the low-affinity site (−11.49 kJ) before dissociating to the inside pool. No transferences of energy between the ligand binding sites occur with this model.

TABLE 1.

Operational influx and efflux parameters of a four-state asymmetric carrier model

Operational Michaelis-Menten parameters of simulated zero-trans net fluxes and infinite-trans exchange fluxes*	Km (mM)	Vm (s−1)	Km ratio (efflux/influx)	Vm ratio efflux/influx
Zero-trans influx, free-carrier asymmetry	1.1	0.009
Zero-trans efflux, free-carrier asymmetry	5.5	−0.045	5.5	5.0
Zero-trans influx, carrier-glucose complex asymmetry	1.8	0.009
Zero-trans efflux, carrier-glucose complex asymmetry	9.7	−0.047	5.4	5.2
Zero-trans influx, equal carrier glucose complex asymmetry	2.2	0.0157
Zero-trans efflux, equal carrier glucose complex asymmetry	6.4	−0.047	2.9	3.0
Infinite-trans influx, free-carrier asymmetry Ratio infinite-trans/zero-trans	1.1 (1)	0.043 (4.7)
Infinite-trans efflux, free-carrier asymmetry Ratio infinite-trans/zero-trans	5.5 (1)	−0.045 (1)	5.5	1.0
Infinite-trans influx, carrier-glucose complex asymmetry Ratio infinite-trans/zero-trans	1.9 (1)	0.0089 (1)
Infinite-trans efflux, carrier-glucose complex asymmetry Ratio infinite-trans/zero-trans	10.1 (1)	−0.0096 (0.2)	5.3	1.1
Infinite-trans influx, equal carrier glucose complex asymmetry Ratio infinite-trans/zero-trans	1.6 (0.7)	0.022 (1.4)
Infinite-trans efflux, equal carrier glucose complex asymmetry Ratio infinite-trans/zero-trans	4.8 (0.7)	−0.023 (0.5)	3	1.0

^*The parameters shown are for the model depicted in Fig. 2. For the four-site alternating carrier, the model parameters are k₁₂ = k₂₁ = 1 s⁻¹, k₄₃ = 1 s⁻¹, k₃₄ = 10 s⁻¹, 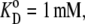and 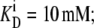for free-carrier asymmetry, they are k₄₁ = 0.01 s⁻¹, k₁₄ = 0.1 s⁻¹, and k₂₃ = k₃₂ = 0.1 s⁻¹; for glucose carrier asymmetry, they are k₂₃ = 0.01 s⁻¹, k₃₂ = 0.1 s⁻¹, and k₁₄ = k₄₁ = 0.1 s⁻¹; and for mixed asymmetry, they are k₂₃ = k₄₁ = 0.0316 s⁻¹ and k₁₄ = k₃₂ = 0.1.

TABLE 2.

Simulated operational Michaelis-Menten parameters of observed 3-OMG fluxes at 4°C obtained with the asymmetric two-fixed-site model

Condition	Km (mM) (observed)	Vm (mM L−1 min−1) (observed)	Vm/Km (observed)	Km (mM)	Vm s−1	Vm/Km
Zero-trans entry	0.38	0.18	0.47	0.4	0.12	0.30
Zero-trans exit	4.35	1.62	0.37	7.3	2.10	0.29
Equilibrium exchange	22.62	9.17	0.41	14.7	10.0	0.68
Infinite-trans entry	1.57	5.62	3.58	1.38	8.8	6.37

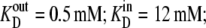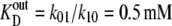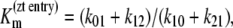Parameters for “two-fixed site” simulation (Fig. 4) to fit the flux parameters obtained by Cloherty et al. (21) for 3-O methyl D-glucoside fluxes in human erythrocytes at 4°C: k₀₁ = 10 s⁻¹; k₄₃ = 12 s⁻¹; k₂₃ = k₃₂ = 0.025 s⁻¹; k_exchange = 10 s⁻¹. Note that since and ligand transport by binding to a single-site model ligand followed by dissociation with zero ligand reflux gives k₂₁ ≈ 0 during zero-trans entry and k₁₂ ≈ 0 in zero-trans exit. It follows that in this condition the ratio 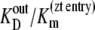reduces to 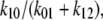and this fraction should always exceed 1.0.

The results in Table 2 show that 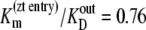and 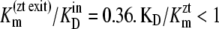can only occur if there is significant ligand reflux, i.e., k₂₁ or k₁₂ are significant factors during zero-trans influx and efflux, respectively.

Assuming that the model parameter assignments are accurate, these calculations indicate that at 4°C, twice as much reflux occurs from the high-affinity outside site to the low-affinity inside site during zero-trans efflux than in the reverse situation. This finding corroborates the view that the glucose transporter behaves similarly to an asymmetric multisite channel (41).

RESULTS

The asymmetric passive alternating transporter model (three-state model)

The rate of net glucose transport, as observed in human erythrocytes, is measured from a solution containing glucose (cis solution) into the other, nominally glucose-free (trans) solution across the cell membrane. The concentration at which the transport rate is half maximal, i.e., the K_m, is a measure of the apparent affinity of the transported ligand for the adjacent binding site. However, this apparent affinity of transport may differ from the binding affinity, K_D, as transport rates are compounded of rate constants pertaining to both binding and transport. The erythrocyte glucose transporter GLUT1 has an ∼10-fold-lower affinity for D-glucose, K_m ≈ 10–15 mM, at the inside face for net export than on the outside (K_m = 1–2 mM) for net import of glucose (zero-trans net flux) at 24°C (22). The affinities are higher at 4°C (as simulated in Figs. 1 C, and 2, A and B, and Tables 1 and 2), and the asymmetry is exaggerated at the lower temperatures.

If the glucose transporter with asymmetric affinities (modeled in Figs. 1 and 2) had equal transition rates for the unliganded carrier, C^ij, between inner and outer membrane phases, i and j, at equilibrium, it would generate a higher sugar concentration in the inside solution adjacent to the low-affinity glucose export site. This is because the transporter reacts with the “reduced” concentration of the external sugar ligand, (superscripts j and i denote the outside or internal solutions, respectively, and are the ligand dissociation constants at the external and inward-facing transporter sites), rather than the real concentration, Glcⁱ (see Eq. 10 below), and the ligand only permeates the membrane via the transporter. However, if the glucose concentration at equilibrium was higher in the inside than in the outside solution, an energy source would be required to sustain the concentration difference. This is thermodynamically impermissible, as no energy source other than that supplied by the ligand concentrations in the aqueous solutions on either side of the membrane is available to generate a transmembrane sugar concentration gradient when the solutions are at equal temperature and pressure.

Regen (7,8), Baker and Widdas (1), and Geck (2) immediately realized the importance of reconciling the kinetic with the thermodynamic implications of asymmetric transport. The solution they provided, and which was reiterated by Stein and colleagues (3,4,9,12), was to introduce a factor altering the relative transition rate of free carrier between the outside and inside of the membrane, so that when equal concentrations of transported ligand are present in the external and internal bathing solutions, the transit rate of the low-affinity liganded carrier from inside to outside equals that of the high-affinity liganded carrier from outside to inside (Fig. 1 C). As shown below, the assumption that asymmetric rates of free-carrier transit provide a satisfactory solution to the problem is erroneous.

Thermodynamics of alternating transporter equilibrium

If the internal and external solutions consist of dilute glucose in an ideal aqueous solution, then the thermodynamic equations governing glucose equilibration across the membrane are as follows:

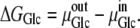(1)

Since

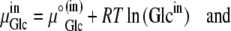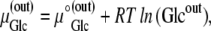(2)

where R is the universal gas constant (8.314 Joules/M/K°), and T is the temperature, assumed here to be 300 K°, then

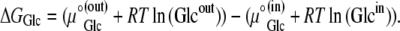(3)

The standard free energies of glucose in both ideal aqueous bathing solutions are the same. Hence,

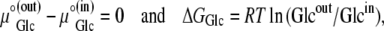(4)

where ΔG_Glc is the Gibbs free energy for glucose movement (Joules) between solutions i and j; Glc^ij is the glucose concentration (mol L⁻¹) in solutions i and 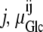is the chemical potential of glucose in phases i and j, μ°^ij is the standard molar free energy of glucose (Joules), and RT ln C^ij is the energy (Joules) generated by the concentrations of ligand in phases i and j; hence, a 10-fold glucose concentration gradient between the solution phases on either side of the transporter ≡ 5.74 kJ; phases i and j refer here to the external and internal solutions and inside- and outside-facing membrane domains (Figs. 1, A and B, and 2, A–C).

If the dissociation constant of glucose from the external site, 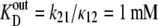and the dissociation constant from the inside site, 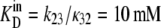(where k_ij is the rate constant of transition from states i to j, and κ is a pseudo-first-order rate constant (s⁻¹), in fact a second-order constant in which the concentration term Glcⁱ (M), and the second-order rate term for ligand association from the external bathing solution with the adjacent binding site (M⁻¹ s⁻¹) are conjoined (Fig. 1, A and B),

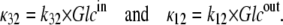(5)

The 10-fold affinity asymmetry, together with the principle of detailed balance, when applied to the trinodal cyclic path requires that

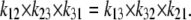(6)

For descriptive convenience, the ligand rates of association with carriers, k₁₂ and k₃₂, on both sides are assumed to be diffusion-limited and are initially assigned equal values, i.e., k₁₂ = k₃₂, so the affinity differences between the outside and inside sites are ascribable only to differences in dissociation rates, and the 10-fold asymmetric affinity ratio between the inside and outside of the transporter then depends only on k₂₃/k₁₂ = 10.

Since k₁₂ = k₃₂ and k₂₃/k₁₂ = 10, Eq. 6 reduces to

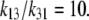(7)

However, the ratio of free-carrier mobilities, k₁₃/k₃₁ = 10, also determines the ratio of free-carrier distribution between the two sides of the membrane at equilibrium. Hence,

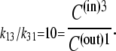(8)

C⁽ⁱⁿ⁾³ and C^(out)1 are the probabilities of free carriers facing toward the inner or outer surfaces, respectively (Fig. 1, A and B).

As there are only three possible carrier states to be considered, C¹, GC², and C³, where GC² is the centrally positioned glucose-carrier complex probability, the total probability of all carrier forms is C¹ + GC² + C³ = 1, and therefore

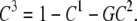(9)

This relationship reduces the number of degrees of freedom of the three-state carrier model to two independent components and the number of independent rate constants by one.

The law of mass action and carrier energy distribution

The set of rate constants in Fig. 1 B describes the kinetics of asymmetric glucose transport, with a low affinity operational (high K_m = 7 mM) for net outflow and high affinity (K_m = 0.9 mM) for net inflow and also the observed matching higher maximal rate of net outflow compared to inflow, 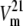> 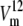(Fig. 1 C). These Michaelis-Menten parameters were obtained from the simulations using Levenberg-Marquardt least-squares fitting, as described in Methods and shown in Fig. 1 C.

With equal ligand concentrations (glucose) present in the solutions on either side of the membrane, the law of mass action requires that

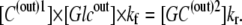(10)

Since

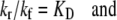(11)

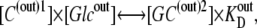(12)

similarly,

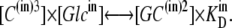(13)

At equilibrium, as fluxes of the carrier-ligand complex GC in both directions are equal, from Eqs. 12 and 13, it follows that

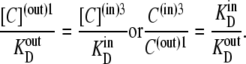(14)

Since the transporter affinity ≡ 1/K_D for glucose is 10-fold lower on the inside than on the outside, i.e., 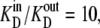obtaining equal rates of glucose-carrier-complex (GC) flowing in opposite directions at equilibrium when equal glucose concentrations are present in the internal and external bathing solutions requires that the probability of the unliganded carrier on the inside, C⁽ⁱⁿ⁾³, be 10-fold higher than that of C^(out)1 to offset their affinity differences.

Thus, although the energy change of glucose interaction, 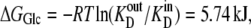with the carrier form is greater at the external site, which has 10-fold higher affinity than the inside site, because the carrier “concentration” inside is greater than outside, 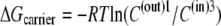= 5.74 kJ, the total energy of the carrier-glucose complex is equal on both sides. It therefore would seem that at equilibrium, because the energy imbalance caused by the asymmetric affinities on the two sides of the carrier is offset by the energy imbalance of the unliganded free-carrier distribution between the two sides, the system is in energetic and kinetic or “thermokinetic balance” (13) (Fig. 1, A and B).

A major problem with this assumption is that maintenance of steady-state asymmetric rates of free-carrier movement and the consequent asymmetric free-carrier distribution ratios requires an exogenous energy source to sustain the time-averaged concentration difference of the free carrier. With the cyclic asymmetrical carrier model, when equal glucose concentrations are present in the inside and outside bathing solutions, zero net flow can only occur when an exogenous energy source counterbalances the energy difference between the affinities of glucose-carrier complexes between the membrane phases (23–25). The assumption implicit with the asymmetric rates of unliganded carrier transit is that the asymmetric free-carrier distribution is self-generated.

The phase equilibrium fallacy

A valid explanation for the higher concentration of free-carrier form inside than outside at equilibrium is that the Nernst phase distribution coefficient of free carrier favors a higher “concentration”, or probability, of C⁽ⁱⁿ⁾³ than C^(out)1 (26,27).

The phase equilibrium condition requires that all the chemical potentials of mobile components (k) between communicating or connected phases (i and j) must be equal (26,27).

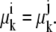(15)

This aspect of the Gibbs phase rule applies equally to mobile free carrier transiting between the membrane phases only, and mobile ligands transiting between both membrane phases and external solutions. If the carrier asymmetry arises because of a difference in standard free energy of the free carrier between the two sides of the membrane 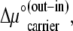resulting either from a difference in the local environment at the two membrane surfaces or from carrier conformational differences, then since

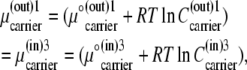(16)

where 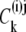represents a density of distribution, either a concentration (in M), or a probability (p) or mole fraction (x) of the component (subscript k) in phases (superscripts (i,j)) and carrier states (superscripts i,j).

Then

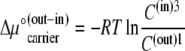(17)

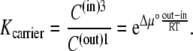(18)

C^(out)1 and C⁽ⁱⁿ⁾³ refer to the probabilities of free-carrier forms 1 and 3 being in the outside membrane, phase^(out), and the inside membrane, phase⁽ⁱⁿ⁾, respectively (Fig. 1 B). The slower carrier movement from C⁽ⁱⁿ⁾³ phaseⁱⁿ → phase^out C^(out)1 could result from an unfavorable endergonic phase transition process, which is the converse of the faster exergonic phase carrier transition, phase^out → phaseⁱⁿ.

If the concentration difference of free carrier is generated only by the standard free-energy difference, 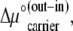between the adjacent membrane phases, then the ratio of carrier distribution, the distribution coefficient K_carrier, can be estimated as

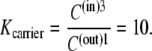(19)

From Eq. 15, at phase equilibrium (26,27), the activities of the all-mobile components (a_k) must be equal in all phases (i and j) to which components k have access; hence, at equilibrium,

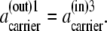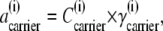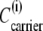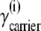Since where and are the concentration and activity coefficients, respectively, of carrier in membrane phase i, it follows from Eqs. 15–18, that

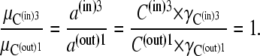(20)

From Eqs. 19 and 20, the ratio of free-carrier activity coefficients can be computed,

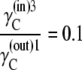For the three-state carrier (Fig. 1), as the glucose-carrier complexes are formed within each separate membrane phase space, the constraints on phase transition that apply to the free-carrier state must also apply to the glucose-carrier complex.

As K_carrier = 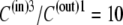(Eq. 19), then equal flow rates of GC_in→out and GC_out→in require that also

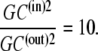(21)

This situation occurs when the glucose concentration ratio between the inside and outside solutions is 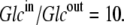Thus, thermodynamic analysis of the circulating carrier model shows that equal rates of inward and outward diffusion of the glucose-carrier complex GC only occur when the glucose concentration in the inside solution exceeds that in the external solution by 10-fold, and not with equimolar glucose concentrations, as the asymmetric alternating carrier would seem to imply.

It should be noted that the standard free energy of the carrier refers to both interactions between the carrier and membrane lipids and conformational changes occurring within the membrane that alter the probabilities of transporter distributions within the membrane.

Application to the conventional four-node passive carrier format

Condensation of the traditional four-node transporter to a three-node scheme introduced two simplifications to illustrate more clearly the underlying anomalies with asymmetric carrier transport. These simplifications enforce equality of the ligand-carrier complex on both sides of the membrane and, implicitly, also equality of the rates of flow of ligand-carrier complex between the alternate sides. This is consistent with the usual assignment of asymmetry as being generated by the slow rate of unliganded carrier movement from inside to out (1,2,4,8,9). It is also evident that the three-state model does not model the phase equilibrium of the carrier-ligand complex GC satisfactorily, since with the three-state model, it is assumed to be in a central position between the two free-carrier states, although paradoxically it is required to have two activity coefficients. Additionally, it has been shown experimentally, at least for choline transport, that a four-, rather than three-node transporter, is a more consistent model (19).

Because of the extra degrees of freedom allocated to the traditional four-node carrier model, it permits asymmetries of either the free-carrier, Cⁱ, or the unliganded carrier, GCⁱ, distributions, or both. Energy compensation for the asymmetric affinity difference can now be shared between two pairs of asymmetric rates (5), instead of one pair, as with the three-state model.

The assumptions involving asymmetric rates of the carrier-glucose complex, GC are identical to those made for unliganded carrier. The following brief analysis will show that the same fallacies that applied to the three-node model (Fig. 1) also apply to the conventional four-node digraph model of passive alternating carrier-mediated transport (Fig. 2 A).

Asymmetric rates of free-carrier transit

As no additional ligands are added to or subtracted from the ligand-carrier complex GC during transit, the affinity changes occurring during its phase transition, as with the unliganded carrier transits, are not ascribable to an exogenous energy source.

As with the three-state model, the model requires that the product of the clockwise rates is equal to that of the anticlockwise rates (Fig. 2).

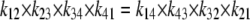(22)

Thus, the conditions for “detailed balance” are satisfied.

However, as before, this assumption ignores Gibbs' phase rule requirement of equality at equilibrium of the chemical potentials, 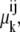of all mobile components k in all phases i and j to which k has access. Thus, phase equilibrium for the free carrier Cⁱ between the outside and inside membrane phases (Fig. 2 A) requires

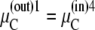and its activity

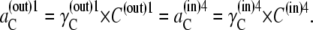Similarly, phase equilibrium for the glucose-carrier complex requires that

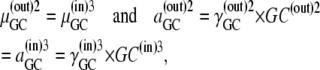(23)

where the numerical superscripts (also in Eqs. 24–40) refer to the carrier states shown in Fig. 2.

It follows that

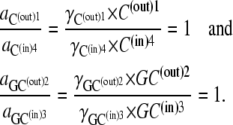(24)

Since the law of mass action requires that for the reversible reaction Glcⁱ + Cⁱ ↔ GCⁱ at equilibrium,

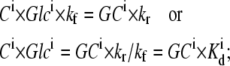(25)

hence,

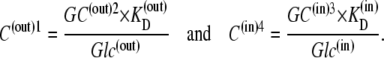(26)

There are three main modes by which apparent equilibrium can be maintained when the inside export site has a 10-fold-lower affinity than the outside site with the four-node transporter.

The asymmetric equilibrium with detailed balance may be determined by asymmetric rates of free-carrier movement, Cⁱ, i.e., k₁₄/k₄₁ = 10 and where k₃₂/k₂₃ =1. This is similar to the asymmetric equilibrium discussed in relation to the three-state transporter. Second, equilibrium may be determined by asymmetric rates of carrier-glucose complex, GCⁱ, i.e., k₃₂/k₂₃ = 10, with symmetrical rates of ligand-free carrier, Cⁱ, transit, i.e., k₁₄/k₄ = 1. Third, the compensating asymmetry can be shared in any proportion between the rates of free carrier, Cⁱ, and glucose-carrier complex, GCⁱ, movements so that k₁₄/k₄₁ × k₃₂/k₂₃ = 10.

Asymmetric rates of free-carrier, C, transit

If the asymmetry is determined solely by asymmetric free carrier movement, as in Fig. 2 A, k₁₄/k₄₁= 10, then from Eq. 26,

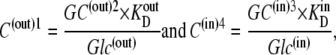(27)

and at equilibrium, when Glc⁽ⁱⁿ⁾ = Glc^(out), then GC^(out)2 = GC⁽ⁱⁿ⁾³. It follows that

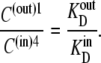(28)

Although there may be inequality of free carrier concentration distribution, Cⁱ, at equilibrium, the chemical potentials, or activities, of the free carrier must still remain equal between the external and internal membrane phases.

Hence, at equilibrium, the activity coefficients γⁱ of Cⁱ must be inversely proportional to the concentrations of free carrier Cⁱ in both internal and external membrane phases. Thus,

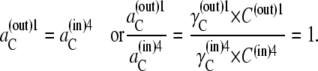(29)

However, since

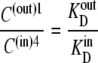(30)

and hence 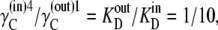therefore, if 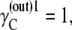then

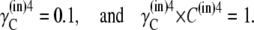(31)

It follows that no energetic benefit can be derived from the asymmetric distribution of free carrier. Thus, 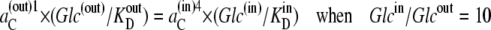and not when Glc⁽ⁱⁿ⁾ = Glc^(out).

Asymmetric rates of carrier-ligand complex GC transit

In the second case, all the compensation for the asymmetric affinities is assumed to be due to asymmetric rates of carrier-glucose complex movement, as in Fig. 2 B, where k₃₂/k₂₃ = 10. In this condition, C^(out)1 = C⁽ⁱⁿ⁾⁴ and Glc^(out) = Glcⁱⁿ, and from Eq. 26,

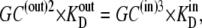(32)

hence,

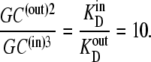(33)

However, since phase equilibrium of GC^ij requires that 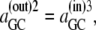it follows that

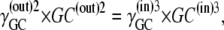(34)

and thus

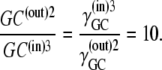(35)

Hence, although the concentration ratio 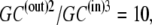the activity coefficient ratio reduces the activity ratio of GC to 1. It follows that no energetic benefit can be derived from the asymmetric concentration distribution carrier-ligand complex GCⁱ between the outside and inside membrane phases, and again, when 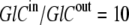and not when Glc⁽ⁱⁿ⁾ = Glc^(out).

Equally divided asymmetries between unliganded carrier and carrier-ligand complexes

The third case permits asymmetry to occur with both free carrier and carrier-glucose complexes, as illustrated in Fig. 2 C.

In the simplest case, where the asymmetry is equally divided between the free-carrier, Cⁱ, and the carrier-glucose complex, GCⁱ, then

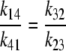and hence

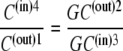(36)

and

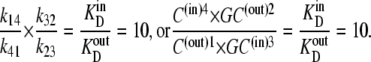(37)

Since at equilibrium

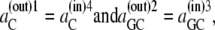(38)

it follows from Eqs. 36–38 that

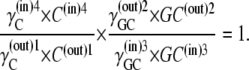(39)

Assuming that 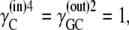then

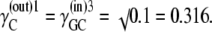(40)

Thus, in this third case, where the asymmetries are equally divided between the free carrier and ligand-carrier transits, again no energetic benefit accrues from the asymmetric distributions of free carrier and carrier-ligand complexes, as the combined activity coefficients of both carrier and carrier-ligand complex negate all energetic benefit obtained from the combined concentration gradients of the carrier forms. Again, equal transit of GCⁱ only occurs when 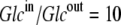and not when Glc⁽ⁱⁿ⁾ = Glc^(out).

In summary, the previous section shows that whether the asymmetry is confined to the unliganded carrier forms or to the carrier-ligand complex, or distributed between all possible forms, asymmetric distributions of carrier forms cannot supply energy to the transport process at equilibrium. This follows directly from the requirement that at equilibrium, the chemical potentials of all mobile components must be equal in all the phases to which they have access (26,27). Hence, the energy difference generated by ligands binding with asymmetric affinities to sites on opposite sides of the membrane transporter cannot be compensated by any asymmetry in carrier transit rates. Therefore, the asymmetric alternating carrier model does not and cannot account for the asymmetric transport parameters observed with glucose and a large number of other transport systems.

In addition to passive facilitated transport of sugars via GLUTs, asymmetric carriers have been invoked to describe the transport of a wide range of organic solutes via uniporters, e.g., choline (19,20), purines, and nucleosides (16,17), and organic acids (21). The above analysis shows that where transport model systems rely on a cyclic carrier system with asymmetric rates of free carrier movement to account for observed asymmetric affinities, they are, without exception, invalid.

Nonequilibrium thermodynamic systems have been found in which exogenous energy sources generated by ATP are used to change affinities of enzyme systems (23,24). However, such systems do not apply to the case of facilitated transporters described in this article, as these function without the need for any exogenous energy source. This merely emphasizes the point that energy is required to change the affinity of a bound ligand. Some other explanation must be sought for the passive asymmetrical transport process. In some cases, as with choline, transmembrane electrical potential could provide an external energy source to alter the equilibrium distribution of the charged ligand. However, many cotransporter models assume that the free (uncharged) carriers have rate constants that are asymmetric even when membrane potential is held at zero (see below).

Cotransport and asymmetry

Asymmetrical carrier transport has been applied to describe cotransport (symport) between ligands, such as Na⁺ and glucose, via the Na-dependent cotransporters SGLT1 and SGLT2 (14–16). These carrier transport systems are necessarily more complex than uniporter facilitated diffusion systems, as they involve more ligands that may associate in either an ordered or a random fashion with both sides of the carrier, and may involve polyvalent stoichiometries and electrical potential, which has been invoked to impinge not only on the mobilities of charged ligands, e.g., Na⁺, but also on the transit rates of free and complexed carrier. Many cotransport models also incorporate the assumption already examined for uniport facilitated diffusion systems, namely, that free carriers are very asymmetrically distributed even when the electrostatic potential difference across the membrane is zero (14,15) (Fig. 3).

In this model description of Na-glucose cotransport via SGLT1 (14), the assigned rates for free carrier movement at zero potential difference are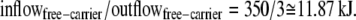

This asymmetry is required to explain why glucose export flux against the direction of the Na⁺ electrochemical potential gradient is much slower (virtually zero) than predicted on the basis of the energy generated by the Na⁺ electrochemical potential difference between the bathing solutions.

Cotransport models require that transport “equilibrium” no longer occurs when there is a uniform distribution of all mobile ligands in all accessible phases. With cotransporter-induced static-head equilibrium, it is assumed that the electrochemical potentials of the cotransported ligand species in the external solutions are summated, in a manner similar to the way electrical and chemical potentials combine to affect the movements of charged mobile ions across an ion-selective membrane (9,16,20).

Thus, for cotransport via SGLT1, static-head equilibrium occurs when

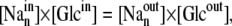(41)

where n = 2 is the stoichiometric coefficient of Na⁺ binding to the SGLT1 carrier and cotransported with glucose, and the import and export rates of the mobile component of the ligand-carrier complex are equal (14,15):

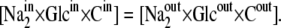(42)

Thus, static-head equilibrium effectively defines the limit for the maximum accumulation ratio of the driven ligand, e.g., glucose in the case of SGLT1 and SGLT2. This equilibrium is also sustained by asymmetric rates of the carrier-Na₂ complex at zero potential difference:

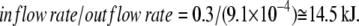In addition to the implicit hypotheses that external energy sources are needed to sustain asymmetric permeabilities of the free carrier and the divalent Na₂-carrier complex, the model requires that neither free Na⁺, nor glucose within the membrane, nor the isolated carrier-complex with Na⁺ or glucose, i.e., NaCⁱ and GCⁱ, permeate the intramembrane phase boundaries of the transporter (14). If Na⁺ were permitted to permeate passively within the carrier phase spaces, then at phase equilibrium the Na⁺ gradient would dissipate entirely. If the leak pathways lie outside the transporter, then, in theory at least, Na⁺ equilibration between the membrane phases of mobile ligand can be avoided.

The cotransport model explicitly assumes that the mobile Na₂Cⁱ complex is asymmetrically sustained by asymmetric rate constants that are independent of membrane potential and unsourced from any overt energy input. This prevents Na⁺ equilibration between the inside and outside phases of the cotransporter and circumvents the problem of phase equilibration of Na⁺.

It is evident that although the SGLT cotransport kinetic models provide good heuristic descriptions of steady-state and pre-steady-state ionic flows across isolated cotransporters, they are not based on secure thermodynamic or mechanistic foundations, and therefore cannot be regarded as valid.

Detailed balance, microscopic reversibility, and asymmetric transport

It has been argued that microscopic reversibility constraints can only properly be applied to particles of equal energy in the gas phase (13). Since the products of chemical reactions generally have energies different from those of the reactants, the forward and backward reaction rates differ at equilibrium. Tolman (28) refers to this as an inverse process where k_reverse/k_forward = K_D; hence, unless K_D = 1,

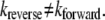(43)

In the case of the trinodal network (Fig. 1, A and B), illustrating the asymmetric carrier, there are two asymmetric inverse chemical reactions along the edges between nodes 1 and 2 and nodes 3 and 2 in which the product GC is formed as a result of association between glucose in either external solution, Glcⁱ, and carrier, Cⁱ. This leaves only the unliganded transitions of free carrier between nodes 1 and 3 needing to fulfill the microscopic reversibility and detailed balance criteria. With the four-node network (Fig. 2), the transitions of Cⁱ between nodes 1 and 4 and GCⁱ between nodes 2 and 3 must fulfill the criteria of both microscopic reversibility and detailed balance.

Thomsen (29) outlined these criteria very precisely. The first criterion is that equilibrium between two states occurs only if the two states are interconnected—if it is possible to go from one to the other in both directions. The digraph in Fig. 1 A shows that carrier states 1 and 3 on either side of the membrane are interconnected, and in Fig. 2, carrier states 1 and 4 and 2 and 3 are both interconnected.

The second criterion, microscopic reversibility {M}, requires that transition probabilities, λ_ij, between states i and j are the same in either direction for every i and j. This means that equal flows between i and j must occur via all possible routes, in this case along both the direct path in Fig. 1 A, 1 ↔ 3, and also via the indirect path, 1 ↔ 2 ↔ 3.

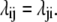(44)

The third criterion, detailed balance {D}, requires that transitions occur with equal frequency between any two states at equilibrium:

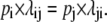(45)

This criterion of detailed balance is fulfilled in the asymmetric carrier model, since the net flows at equilibrium of the asymmetric carrier are zero along all branches of the network at equilibrium.

From the previous discussion, it is evident that at equilibrium the probabilities p_i of asymmetric carrier states on either side of the membrane are unequal, since with the three-node carrier, C¹/C³ = 0.1 (Eq. 14), and with the conventional four-node carrier, either C₁/C₃ = 0.1 (Eq. 30) or GC¹/GC³ = 10 (Eq. 33), and similarly in the four-state model.

Hence,

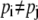(46)

The ergodic hypothesis {E}, the fourth criterion, assumes that all accessible states i are equally probable at equilibrium. The asymmetric distribution of unliganded carrier is a consequence of the asymmetric rates of free carrier movement across the membrane between nodes 1 and 3 (Fig. 1) or, with the four-state transporter, between nodes 1 and 4 and 3 and 4 (Fig. 2, A and C).

For every state i,

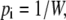(47)

where W is the number of accessible quantized states i.

The asymmetric mobile carrier, as formulated, matches neither the ergodic hypothesis {E} nor microscopic reversibility {M} criteria, and only obeys the principle of detailed balance {D} by assuming that an imaginary source of energy is available to maintain the balanced condition.

Previously, the possibility has been considered that carrier particles within a membrane can exist in different conformations or energy states and the transition rates between these states could be functions of electrical potential (14,21) or nontransported ligands (19). Where these forces act unilaterally, they must be considered as affecting only the standard free energies of the transported ligand, and not the concentration-dependent component of energy, and therefore, as has been illustrated above, they affect only the distribution coefficient of free carrier, K_carrier. It should be noted that when the affinities are symmetrical, the mobile carrier scheme fulfills all four criteria for equilibrium outlined above.

Alternative forms of asymmetric transport

Cyclic carriers, as illustrated in Fig. 1, A and B, make the fundamental assumption that there is only a single ligand binding site for uniporters, or conjoined multiple sites for cotransporters, which alternate between the two sides of the membrane. The process of carrier disappearance from one side and its automatic reappearance on the other side implies motion. In addition, in the case of carrier asymmetry, disappearance of the high-affinity site from the outside followed by its reincarnation on the inside, as a low-affinity site and vice versa, implies an energy change during translation (Fig. 4 D). Integral with these assumptions, microscopic reversibility requires reciprocal and equal translation rates of the carrier-ligand complex at equilibrium. These two conflicting constraints are ostensibly reconciled by assuming that the free-carrier energy change on translation can compensate for the energy difference due to different ligand affinities on the two sides of the transporter.

It is evident that the triple constraints of mobile carrier path cyclicity, combined with asymmetric ligand affinities and the absolute requirement to maintain equimolar equilibrium in the external solutions, are mutually irreconcilable, since this requires unequal unliganded carrier distribution at equilibrium, i.e., failure to observe the ergodic hypothesis {E} (Eq. 47). In macroscopic terms, this translates to Gibbs' phase rule, which requires the chemical activities of all mobile components to be equal in all phases at equilibrium.

This fundamental flaw is averted if the assumption of a mobile site is relinquished and two or more fixed interconnected sites on each membrane side are assumed instead. Ligand flows then occur by serial jumps resulting from ligand dissociation and reassociation reactions between the connected vacant sites or nodes in the network. With cotransport, the altered kinetic energy from frictional interactions resulting from collisions between the mobile ligands within the transporter also affects the rates and direction of flows. Although conformational changes of the transporter protein are not precluded in this model, no such change leading to ligand position or affinity changes within the binding site is necessary.

The major kinetic and thermodynamic differences between mobile-site- and fixed-site-mediated transport are that ligand(s) only dissociate from mobile carriers to the external solutions, whereas with fixed-site models, ligand(s) dissociate between sites on opposing membrane sides, as well as to the adjacent external solution but, in contrast to carriers, not to the solution on the opposite side of the membrane (Fig. 4, A and D).

These differences have important implications. Asymmetric mobile carriers are hypothetically able to couple the energy from their asymmetric distribution to that of the bound ligand(s) during ligand transference (Fig. 4 D, a). This is avoided with fixed-site transporters, because the ligands have to dissociate from one site before reassociating with the alternate site. At equilibrium, ligand dissociation into the intermediate space between sites causes the dissociated ligand to revert to its energy status in its source solution (Fig. 4 D, b). Thus, no energy change is conferred on the ligands during transit from the high- to the low-affinity site, or vice versa.

Furthermore, the higher rate of ligand dissociation from the low-affinity inside (fixed) site is reflected in a higher rate of ligand transit from lower-affinity inside sites to outside sites (Fig. 4 A). Thus, equal rates of ligand flow between sites with asymmetric affinities automatically occur when equal concentrations of ligand are present in both external bathing solutions. This contrasts sharply with the mobile carrier model, where ligand translation between the two membrane sides is rate-determined only by the carrier mobility and not directly by the ligand dissociation rate (Figs. 1, A and B, and 2 A).

In the fixed-site transporter (Fig. 4 A), the rates of ligand (glucose) transit between sites i and j are

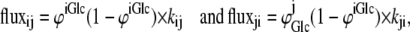(48)

where ϕ^ijGlc is the fractional saturation of sites i and j with glucose.

If the rates of association and dissociation of glucose to external solutions 1 and 4 are much faster than the intersite transitions, then

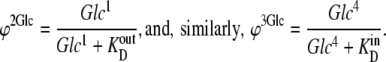(49)

As the intersite dissociation rates k_ij are proportional to the dissociation rates between binding sites and adjacent solution,

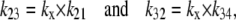(50)

where k_x is the symmetrical diffusion coefficient for intersite ligand diffusion within the intersite space.

At equilibrium, the unidirectional intersite fluxes 2 → 3 and 3 → 2 are equal, and Glc^out = Glcⁱⁿ; hence,

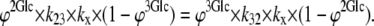(51)

If k₃₂/k₂₃ = 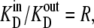then from Eq. 48,

which simplifies to

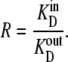(52)

Thus, the unidirectional fluxes are equal when equal concentrations of transported ligand in the external solutions and the unidirectional rates of dissociation from a site i to the intersite space are proportional to 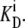Therefore, at equilibrium, the multisite transporter is in detailed balance. A numerical example illustrates this point.

If Glc^out = 1 mM = 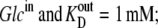and k₂₃ = k_x × 1; 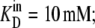and k₃₂ = k_x × 10, then, from Eq. 49, ϕ^2Glc = 0.5 and ϕ^2Glc = 0.091.

At equilibrium, where the concentrations in both bathing solutions are 1 mM,

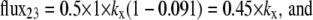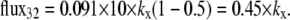The generality of this point is illustrated in Fig. 4 C, where it is shown that zero net glucose flux occurs with equimolar external glucose concentrations on either side of the asymmetric fixed-two-site transporter. The intersite dissociation rates from each site are proportional to their dissociation rates to the external solutions.

Exchange transport via mobile or fixed-site asymmetric transporters

One of the most appealing aspects of the alternating carrier model is that it readily accounts for most of the phenomena related to accelerated exchange, for example, the higher maximal rate of exchange flux compared to net influx. Exchange flux refers here to the exchange of labeled sugar ligand with unlabeled sugar, initially present only in the solution on the opposite side of the membrane. Net flux is simply the flux of sugar into the opposite solution, which initially is sugar-free. With an asymmetric transporter, the higher ratio of maximal exchange flux to maximal net influx than to maximal net efflux, and the higher K_m for equilibrium exchange than for net influx, or infinite-trans exchange are equally predictable by the mobile carrier theory and are similar to the observed parameters (21) (Table 2).

The mobile-carrier explanation for accelerated ligand exchange is that the path for ligand exchange via the mobile carrier nodes, (1 → 2 → 3), (3 → 2 → 1), bypasses the slow path of free-carrier transit (3 → 1) or (1 → 3) (Fig. 1 A), which is obligatory for completion of a net transport cycle. The higher ratio of maximal exchange flux to maximal net influx than to maximal net efflux (Fig. 1 A) arises because the slow rate of return of empty carrier to the outside retards net influx more than the faster return of empty carrier to the inside slows exit. The higher K_m for exchange than for net flux arises because both inside and outside sites must be saturated before exchange flux is maximal. Consequently, the K_{m(equilibrium exchange)} is determined by the low-affinity inside site, whereas the K_{m(net influx)} is determined only by the high-affinity outward-facing site.

With infinite-trans exchange, where rates of exchange uptake from variable concentrations of labeled external glucose concentrations are measured into cells preloaded with high unlabeled glucose concentrations sufficient to completely saturate the inside site, exchange flux now reaches a maximum when the outside site becomes saturated with labeled sugar, so the K_m for infinite-trans exchange entry is close to that of the high-affinity external site, 1–3 mM.

The fixed-site transporter model requires that accelerated exchanges between free ligand in solution, or ligand in the intersite space within the membrane, and ligands bound to the transporter are faster than net flux, i.e., a complete ligand association-dissociation cycle with a vacant site to explain accelerated exchange. More rapid exchange will occur between bound and free ligand providing the “activation energy” is lower for exchange than for the net association-dissociation reaction between free ligand and a binding site (Fig. 4 B). If the activation energy is higher for exchange than for net uptake and dissociation of ligands from a binding site, then exchange retardation will occur, as has been observed with exchanges between different hexoses (30).

Implementation of this assumption permits all the kinetics of both net and exchange glucose to be simulated (Fig. 4 C, and Tables 1 and 2), as has been observed with glucose transport in human erythrocytes via GLUT1 (1–4,6,9,11,12,22,31–33).

DISCUSSION

The hypothetical asymmetry of free-carrier flow was postulated so that the alternating carrier model could achieve the balance condition {D} at equilibrium (see Eqs. 6, 22, and 45). Paradoxically, the cyclic carrier model at equilibrium cannot both encompass detailed balance and retain the asymmetric affinities without implicitly introducing an imaginary energy source to maintain the asymmetric distribution of unliganded carriers.

The energy obtained from asymmetric flux ratios, ΔG_carrier = RT ln (k_ij/k_ji), is well understood, as this flux ratio equation was introduced by Ussing (25) to explain active Na⁺ transport by isolated frog skin and differentiate it from passive transport. Thus, it is surprising that it has been accepted for so long that asymmetric rates of free-carrier movement provide a solution to the asymmetric affinities of passive mobile carriers.

Since cyclic asymmetric alternating carriers can no longer be used to explain glucose transport kinetics, some alternative multisite transport model must be invoked to account for glucose transport. This lends support to recent observations from docking studies that there are multiple low-affinity glucose docking sites present within the central transport channel of GLUT1 (34,35).

Recently, fixed-site collision models have been suggested to explain some cotransport phenomena, e.g., serotonin transport via the human serotonin transporter without mobile carriers (36,37) and lactose transport via LacY (38). These may be better analogs of cotransport than the more accessible, but erroneous, carrier models, which derive their asymmetry from energy-requiring asymmetric rates of free-carrier transit.

An earlier version of cotransport in which coupled Na⁺ and glucose movements are viewed as deriving from frictional coupling and aided by convective flow (39) may provide a working basis for future cotransport models. The presence of a central osmotically active vestibular compartment within SLGT1 and 2 could be a basis for development of convective flow of Na⁺ and sugar generated by the osmotic pressure from actively accumulated solutes (34,35,40).

Comparison of the two-site transport model with asymmetric multioccupancy ionic channels

The two-site model of sugar transport shown in Fig. 4 has similarities to a model of asymmetric, multioccupancy ion channels discussed by Eisenman and Horn (41). This describes asymmetric channel ionic permeability, P_i, in terms of two parameters, an ion affinity of binding, K_i, to each site and an activation energy, k*_i = A_i × exp(−G*/RT). These parameters are combined, so the permeability ratios of two or more ions can be compared using the relationship 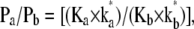where k_i* is the rate constant of permeation of ion species i. Even with singly occupied channels, providing there are asymmetric selectivity barriers present within the channel, this linear model generates different patterns of ion selectivity as ion concentrations are varied. Interpretation of the selectivity properties of the ion channels becomes difficult when multiple barriers of differing height and ion selectivity are present. Multisite channels with variable site affinities and occupancy makes interpretation of ion selectivity patterns more difficult, as differential binding can arise with different ion concentrations that may involve blockage or inhibition of ion flow by ions bound to distal sites or by geminate recombination between channel sites.

A recent simulation of ion permeation through the α-hemolysin channel using Monte Carlo Brownian dynamics (42) has established that a major cause of asymmetric ion permeability is the asymmetric distribution of fixed charges, e.g., aspartate and lysine, which create a large potential barrier within the channel opening separated from a salt bridge between a glutamate and lysine residue in a narrow region near the inside opening of the channel with weak anion selectivity. When combined with a transmembrane potential of ±150 mV, these fixed charges generate large differences in the free-energy profiles for K⁺ and Cl⁻ and changes in the number and distribution of ions within the channel.

Several features of the fixed-site model for sugar transport (Fig. 4) resemble the Eisenman-Horn channel model (41). The fixed sugar-binding sites have ligand specificity assigned in terms of Michaelis-Menten kinetic parameters for binding and transference between sites. This simple unitary behavior is also complicated by the presence of multiple binding sites, which create the possibility of asymmetric flow with a wide range of kinetics, including self-inhibition by ligands binding to the alternate site, or acceleration or retardation exchange flux resulting from the activation energies of exchange process being lower or higher, respectively, than net flux (22,33). The data shown in Table 2 and simulated in Fig. 4 C are consistent with more geminate recombination during zero-trans exit than during entry, as would be expected if the external site has a higher affinity than the inside site(s) (Table 2). Allowing for multisite kinetics in combination with site-specific mutations may provide a useful strategy for future investigations into the complex nature of transporter specificity to sugars and other ligands.

CONCLUSIONS

The conventional description of asymmetric passive facilitated diffusion, where an alternating carrier with asymmetric rates, k_ij, of unliganded free-carrier movement is used to account for the transporter's asymmetric affinities for ligand, is shown to be invalid. It implicitly requires an energy source, ΔG_carrier = RT ln (k_ij/k_ji) = −RT ln (Cⁱ/C^j) = − RT ln (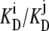), to maintain the asymmetric distribution of unliganded carrier, C^ij, at equilibrium in phases^i,j. Asymmetric distributions of carrier forms within different membrane phases also cannot account for the asymmetry, as phase equilibrium requires that all mobile forms have equal activity in all phases to which they have access. If the concept of the cyclic nature of ligand transport linked to a mobile binding site is relinquished, and instead transport is viewed as a series of reversible association-dissociation reactions of the transported ligand between sites of variable affinity within a channel, no exogenous energy is required to maintain equimolar equilibrium of the transported ligand. In this case, no transporter-derived energy transference occurs between the internal and external transporter phases, and the asymmetric rates of ligand flow are due to the variable rates of ligand dissociation from the high- and low-affinity binding sites.