Robust Linearized Image Reconstruction for Multifrequency EIT of the Breast

Abstract

Electrical impedance tomography (EIT) is a developing imaging modality that is beginning to show promise for detecting and characterizing tumors in the breast. At Rensselaer Polytechnic Institute, we have developed a combined EIT-tomosynthesis system that allows for the coregistered and simultaneous analysis of the breast using EIT and X-ray imaging. A significant challenge in EIT is the design of computationally efficient image reconstruction algorithms which are robust to various forms of model mismatch. Specifically, we have implemented a scaling procedure that is robust to the presence of a thin highly-resistive layer of skin at the boundary of the breast and we have developed an algorithm to detect and exclude from the image reconstruction electrodes that are in poor contact with the breast. In our initial clinical studies, it has been difficult to ensure that all electrodes make adequate contact with the breast, and thus procedures for the use of data sets containing poorly contacting electrodes are particularly important. We also present a novel, efficient method to compute the Jacobian matrix for our linearized image reconstruction algorithm by reducing the computation of the sensitivity for each voxel to a quadratic form. Initial clinical results are presented, showing the potential of our algorithms to detect and localize breast tumors.

I. Introduction

THERE has been considerable recent interest in the use of adjunctive technologies to mammography in screening for and diagnosing breast cancer. This interest is motivated by the observation that X-ray mammography, while effective in reducing breast cancer mortality [1], [2], fails to detect a considerable proportion of breast tumors [3], [4]. In addition, due to the relatively high false-positive rate of standard screening methods[5], many women are needlessly subjected to the physical and emotional trauma of biopsy.

Electrical impedance tomography (EIT) shows promise for a number of biomedical applications, including the noninvasive monitoring of pulmonary function [6], monitoring of gastric emptying [7], functional brain imaging [8], and breast cancer detection [9]–[11], the subject of the present study. To a great extent, current research in EIT of the breast has been motivated by ex vivo studies of freshly excised tissue [12] which showed significant differences between the impedance spectra of malignant carcinomas and those of normal tissue. Additionally, a handheld impedance-based scanning device has been developed and approved for clinical use by the American Food and Drug Administration (FDA), with promising initial clinical results [13].

Motivated by this work, we have developed a multifrequency impedance imaging system, the Adaptive Current Tomograph (ACT) 4 [14], [15], which operates in conjuction with an X-ray tomosynthesis instrument [16] currently being clinically evaluated at Massachusetts General Hospital. Our system makes use of 60 radiolucent rectangular electrodes [17] attached to the mammography paddles on either side of the breast, in a transmission configuration. We apply patterns of voltages to the electrodes and measure the resulting currents and voltages at each of six temporal frequencies logarithmically spaced between 3 kHz and 1 MHz. Although the electrodes themselves are radiolucent, the connections to the electrodes are visible at the edges of a number of slices of a breast’s tomosynthesis reconstruction, making it possible to accurately coregister the imaging results from these two modalities. The Rensselaer ACT 4, attached to a digital tomosynthesis instrument is shown in Fig. 1(a). The radiolucent electrode arrays are detailed in Fig. 1(b).

Fig. 1.

Imaging hardware used in clinical studies. (a) Combined EIT-Tomo imaging configuration. (b) Radiolucent arrays which make possible the coregistered imaging using the two modalities.

The ACT 4 has been designed to either apply patterns of voltages to the electrodes, measuring the resulting currents, or to apply patterns of currents, measuring the corresponding patterns of voltages. In fact, the instrument measures both the currents and voltages on the electrodes in all instances. However, the capacitance of our radiolucent electrode array [17] is such that it is very difficult to design current sources that will maintain accuracy over a relatively wide range of frequencies. Thus, we instead apply patterns of voltages that maximize distinguishability [18], [19] for a rectangular, homogeneous medium. In the image reconstruction, we then synthesize the voltages that we would have obtained, had we applied the canonical set of currents that maximizes distinguishability. In this case, as opposed to computing the Jacobian matrix with respect to the currents actually applied, we compute the Jacobian with respect to application of a single canonical set of current patterns. This canonical set, which can be precomputed, is comprised of the eigenvectors of the Neumann-to-Dirichlet map for a rectangular parallelpiped. For measurements at each temporal frequency, we compute the best fit for the homogeneous admittivity γ₀ of the medium at that frequency, which is then the scalar scaling factor applied to the Jacobian matrix for the measurements at the specified frequency. Finally, the forward model which we use is much easier to implement if we consider the mapping between a Neumann boundary condition and Dirichlet measurements.

If EIT of the breast is to have real clinical utility, then algorithms must be developed which are computationally efficient and which are robust to the types of noise and modeling error actually encountered in practice. Two specific forms of modeling error that we have found to be of great importance in analyzing EIT data are: electrodes which make poor contact with the breast and the reconstruction of objects embedded in a layered structure. For the former problem, we have developed a data screening procedure to automatically detect electrodes which make poor contact with the breast and exclude data from these electrodes from use in the image reconstruction. In order to mitigate the effect of a thin, highly resistive skin layer, we make use of a scaling procedure which effectively calculates a different complex admittivity for each current pattern. Since we use a canonical set of voltage patterns, which probe the breast using patterns of varying spatial frequency, the proportion to which each pattern is influenced by the skin is different. Patterns of higher spatial frequency tend to see the medium as being more resistive overall, particularly at lower temporal frequencies, at which the skin is more resistive.

We have previously reported the use of the complete electrode model in the mammography configuration [20], solving the forward problem using the Galerkin method. Here, however, we use the ave-gap mode [21]–[23] to model the voltages on the electrodes due to a given current pattern. The motivation for the selection of the ave-gap model is that, in the rectangular geometry, we are able to compute the potential inside of the medium and the voltages on the electrodes extremely rapidly, suitable for a real-time implementation. In addition, in the complete electrode model it is necessary to estimate the surface impedance of each electrode, a problem we will leave for a future publication.

Using the ave-gap model, then, we are then able to compute the forward model analytically. Likewise, we can analytically compute the Jacobian matrix relating the measurements to the spatial distribution of conductivity. We also present a novel approach which allows us to compute this Jacobian matrix in a computationally efficient manner, as compared to that presented in [21], with the matrix element for each set of current patterns for a given voxel computed as a quadratic form. Experimental results from a homogeneous breast-shaped phantom containing an inclusion at several different locations clearly show the utility of our analytical approximation.

Finally, we have used our algorithms for the analysis of clinical EIT measurements from human subjects. We present a novel multispectral parameter which shows promise for detecting and localizing malignant carcinomas in a limited sample of subjects.

II. Methods

A. Forward Modeling

In the quasi-static approximation, Maxwell’s equations can be simplified such that the potential, u satisfies the following condition in the interior of a source-free region with finite complex admittivity γ

$$\nabla \cdot \gamma \left(p\right)\nabla u\left(p\right)=0,\text{for}p\text{in}\Omega .$$ (1)

We attach electrodes to the two plates used to apply pressure to the breast during mammography. As the electrode array is generally smaller than the breast, we are able to successfully model the breast as a homogeneous rectangular parallelpiped whose boundaries extend 2 cm beyond the boundaries of the electrode array, as depicted in Fig. 2.

Fig. 2.

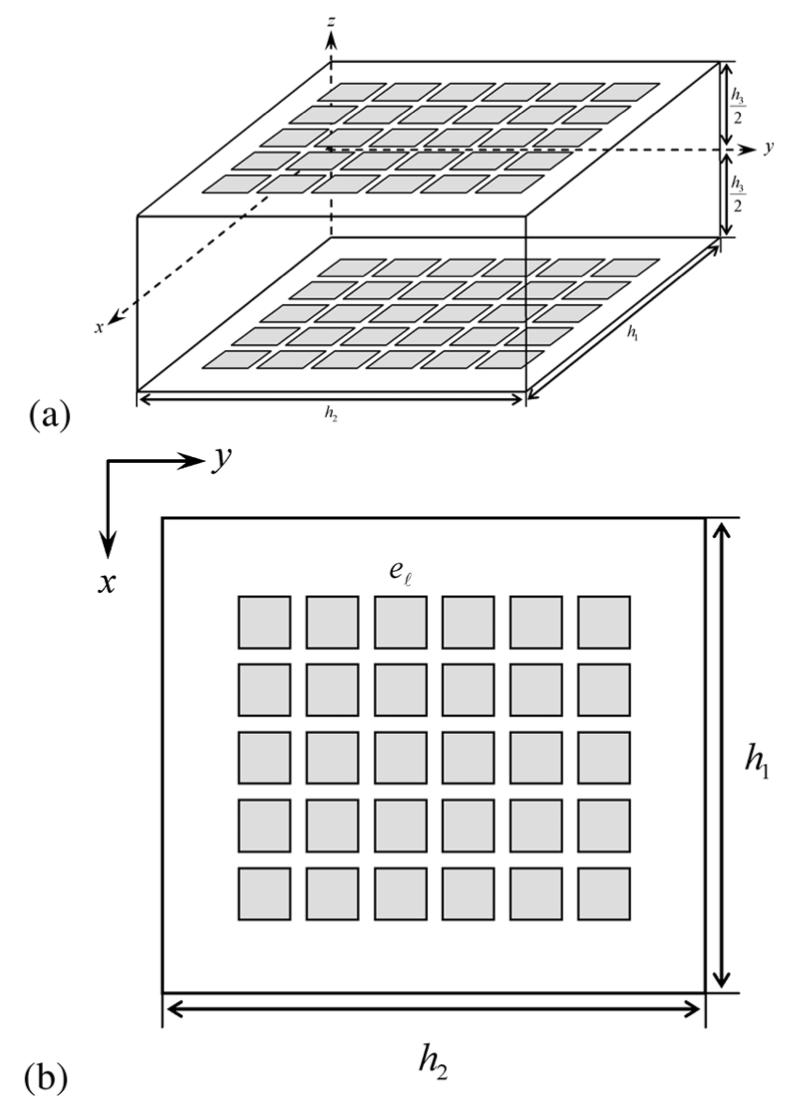
Simplified model of the breast as a rectangular parallelpiped. (a) Side view. (b) Top view.

The resulting partial differential equation which we solve is then

$$\{\begin{array}{cc}\nabla \cdot \gamma \nabla u(x,y,z)=0,\hfill & x\le h_1,y\le h_2,-\frac{h_3}{2}\le z\le \frac{h_3}{2}\hfill \\ \gamma \frac{\partial u}{\partial v}=j^{\mathbb{T}}(x,y),\hfill & z=\frac{h_3}{2}\hfill \\ \gamma \frac{\partial u}{\partial v}=j^{\mathbb{B}}(x,y),\hfill & z=-\frac{h_3}{2}\hfill \\ \gamma \frac{\partial u}{\partial v}=0,\hfill & x=0,x=h_1,y=0,y=h_2\hfill \end{array}\phantom{\}}$$ (2)

where $j^{\mathbb{T}}$ and $j^{\mathbb{B}}$ denote the current densities at the top and bottom planes, respectively, and v is the unit outward normal to the body.

Using separation of variables and assuming that γ is constant, it is easy to see that the solution to (2) can be written as an infinite series, which we truncate to a finite number of terms

$$\begin{array}{c}\hfill u(x,y,z)\approx b_{0}z+\sum _{n=0}^N\sum _{m=0}^N\cos \left({\lambda }_{n}x\right)\cos \left({\lambda }_{m}y\right)\hfill \\ \hfill \times [a_{n,m}\cosh \left({\lambda }_{n,m}z\right)+b_{n,m}\sinh \left({\lambda }_{n,m}z\right)]\hfill \end{array}$$ (3)

where a_n,m = 0, b_n,m = 0, N is the number of Fourier terms in our Fourier approximation, and

$$\{\begin{array}{c}{\lambda }_n=\frac{n\pi }{h_1},\hfill \\ {\lambda }_m=\frac{m\pi }{h_2}\hfill \\ {\lambda }_{n,m}=\sqrt{{\lambda }_n^2+{\lambda }_m^2}\hfill \end{array}\phantom{\}}$$

where n, m = 0, 1, 2,..., N.

In the ave-gap model [21], we assume that the current density is uniformly distributed over the electrode region and that it is zero outside of the support of all of the electrodes

$$j(x,y)=\{\begin{array}{cc}{I}_{\ell }∕\mid e_{\ell }\mid \hfill & \text{on}{e}_{\ell },\ell =1,2,...,L\hfill \\ 0\hfill & \text{off}{\bigcup }_{\ell =1}^L{e}_{\ell }\hfill \end{array}\phantom{\}}$$ (4)

where $\mid e_{\ell }\mid$ is the area of the ℓth electrode, Iℓ is the current applied, and L is the number of electrodes.

We are then able to derive explicit formulas for the coefficients b₀, a_n,m,, and b_n,m in (3) for all current patterns, as described in [21].

B. Linearized Reconstruction and Measurement Scaling

In our image reconstruction, we make use of the approach taken in [24] and [21] where the assumption is made that the admittivity γ within the medium differs only slightly from a constant admittivity γ0. The linearization method follows from the identity, which arises by an application of the divergence theorem

$$\begin{array}{c}{\int }_S\left[u_{\alpha }\left({\gamma }_0\right)\gamma \frac{\partial u_{\beta }\left(\gamma \right)}{\partial v}-u_{\beta }\left(\gamma \right){\gamma }_0\frac{\partial u_{\alpha }\left({\gamma }_0\right)}{\partial v}\right]dS\hfill \\ \hfill ={\int }_{\Omega }\eta \nabla u_{\alpha }\left({\gamma }_0\right)\cdot \nabla u_{\beta }\left(\gamma \right)dp\end{array}$$ (5)

where η≡γ—γ₀. The subscripts α and β denote pairs of current patterns. In order to reconstruct an image of the admittivity, we apply K linearly independent patterns, where it is generally true that K = L — 1. The term on the left-hand side of (5) represents the data matrix $\mathbf{D}\in {\mathbb{C}}^{K\times K}$

$$D_{\alpha ,\beta }=\sum _{\ell =1}^L[I_{\ell ,\alpha }{U}_{\ell ,\beta }\left({\gamma }_0\right)-I_{\ell ,\beta }{V}_{\ell ,\alpha }\left(\gamma \right)]$$ (6)

where U_ℓ,α (γ₀) is the forward solution for a homogeneous complex admittivity γ0 and V_ℓ,α(γ) is the experimental data, both corresponding to current pattern α. Alternatively, we can write the data matrix as follows:

$$D_{\alpha ,\beta }=\sum _{\ell =1}^L\left[\frac{1}{{\gamma }_0}{I}_{\ell ,\alpha }{U}_{\ell ,\beta }\left(1\right)-I_{\ell ,\beta }{V}_{\ell ,\alpha }\left(\gamma \right)\right]$$ (7)

where U_ℓ,α (1) is the voltage on electrode ℓ due to pattern β for a medium with conductivity 1 S/m.

In order to estimate the optimal constant admittivity about which to perturb, we introduce the residual, $E={\sum }_{\alpha =1}^K{\sum }_{\beta =1}^K{D}_{\alpha ,\beta .}^2$. We can find a closed-form expression for the value of γ0 that minimizes E by differentiation.

In [25], a method was introduced to compensate for the different effective admittivities “seen” by each current pattern. In this method, we replace γ0 in (6) and (7) by a current-pattern-specific admittivity, γ0,β as follows:

$$D_{\alpha ,\beta }=\sum _{\ell =1}^L\left[\frac{1}{{\gamma }_{0,\beta }}{I}_{\ell ,\alpha }{U}_{\ell ,\beta }\left(1\right)-I_{\ell ,\beta }{V}_{\ell ,\alpha }\left(\gamma \right)\right].$$ (8)

It is still possible to compute a closed-form solution for the optimizing value of γ0,β for each current pattern β by differentiation.

In the linearized reconstruction, we replace ∇u_α (γ) in (5) with ∇u_α (γ0). Discretizing by setting $\eta ={\sum }_{s=1}^{N_s}{\eta }_s{\chi }_s\left(p\right)$ where ϰ_s (p) is the characteristic function of η_s voxel, we than have

$$D_{\alpha ,\beta }\approx \sum _{s=1}^{N_s}{\eta }_s{J}_{\alpha ,\beta }^s$$ (9)

$$J_{\alpha ,\beta }^s={\int }_{{\Omega }_s}\nabla u_{\alpha }\left({\gamma }_0\right)\cdot \nabla u_{\beta }\left({\gamma }_0\right)dp$$ (10)

where J is the Jacobian of the forward model with respect to a small perturbation in admittivity, Ω_s is the spatial extent of voxel s, and N_s is the total number of voxels.

We then obtain the solution of the regularized linear inverse problem as

$$\eta \approx {[{\mathbf{J}}^T\mathbf{J}+r_1\mathrm{diag}\left({\mathbf{J}}^T\mathbf{J}\right)+r_2\mathbf{I}]}^{-1}{\mathbf{J}}^{T}D.$$ (11)

where r₁ and r₂ are regularization parameters for NOSER-type and Tikhonov regularization, respectively, and we have reordered D_α,β and J^s_α,β into the vector D and the matrix J of sizes K² × 1 and K² × N_s, respectively.

C. Efficient Computation of the Jacobian Matrix

Here we are concerned with the efficient computation of the Jacobian matrix (10) used in the image reconstruction. The approach described here is a simplification of the approach given in [21]. In our experimental work, we decompose the region being reconstructed into rectangular voxels, but, with some modifications, the method described below is applicable to voxels with other shapes as well.

We rewrite (10) as

$$\begin{array}{cc}\hfill & J(\alpha ,\beta ,i,j,k)\hfill \\ \hfill & ={\int }_{x=x_i}^{x=x_{i+1}}{\int }_{y=y_j}^{y=y_{j+1}}{\int }_{z=z_k}^{z=z_{k+1}}\frac{\partial u_{\alpha }}{\partial x}\frac{\partial u_{\beta }}{\partial x}\hfill \\ \hfill & +\frac{\partial u_{\alpha }}{\partial y}\frac{\partial u_{\beta }}{\partial y}+\frac{\partial u_{\alpha }}{\partial z}\frac{\partial u_{\beta }}{\partial z}dzdydx\hfill \\ \hfill & =J_x(\alpha ,\beta ,i,j,k)+J_y(\alpha ,\beta ,i,j,k)\hfill \\ \hfill & +J_z(\alpha ,\beta ,i,j,k).\hfill \end{array}$$ (12)

If we interchange the order of summation of integration, we can write the contributions to the Jacobian matrix of the gradients in the x,y, and z directions, respectively

$$\begin{array}{cc}\hfill & J_x(\alpha ,\beta ,i,j,k)\hfill \\ \hfill & \approx \sum _{n=0}^N\sum _{m=0}^N\sum _{n\prime =0}^N\sum _{m\prime =0}^N{\lambda }_n{\lambda }_{n\prime }{P}_x^{n,n\prime }\left(i\right)Q_y^{m,m\prime }\left(j\right)\hfill \\ \hfill & \times [a_{n,m}^{\alpha }{a}_{n\prime ,m\prime }^{\beta }{R}_z^{n,m,n\prime ,m\prime }\left(k\right)\hfill \\ \hfill & +a_{n,m}^{\alpha }{b}_{n\prime ,m\prime }^{\beta }{S}_z^{n,m,n\prime ,m\prime }\left(k\right)\hfill \\ \hfill & +b_{n,m}^{\alpha }{a}_{n\prime ,m\prime }^{\beta }{T}_z^{n,m,n\prime ,m\prime }\left(k\right)\hfill \\ \hfill & +b_{n,m}^{\alpha }{b}_{n\prime ,m\prime }^{\beta }{V}_z^{n,m,n\prime ,m\prime }\left(k\right)]\hfill \end{array}$$ (13)

$$\begin{array}{cc}\hfill & J_y(\alpha ,\beta ,i,j,k)\hfill \\ \hfill & \approx \sum _{n=0}^N\sum _{m=0}^N\sum _{n\prime =0}^N\sum _{m\prime =0}^N{\lambda }_m{\lambda }_{m\prime }{Q}_x^{n,n\prime }\left(i\right)P_y^{m,m\prime }\left(j\right)\hfill \\ \hfill & \times [a_{n,m}^{\alpha }{a}_{n\prime ,m\prime }^{\beta }{R}_z^{n,m,n\prime ,m\prime }\left(k\right)\hfill \\ \hfill & +a_{n,m}^{\alpha }{b}_{n\prime ,m\prime }^{\beta }{S}_z^{n,m,n\prime ,m\prime }\left(k\right)\hfill \\ \hfill & +b_{n,m}^{\alpha }{a}_{n\prime ,m\prime }^{\beta }{T}_z^{n,m,n\prime ,m\prime }\left(k\right)\hfill \\ \hfill & +b_{n,m}^{\alpha }{b}_{n\prime ,m\prime }^{\beta }{V}_z^{n,m,n\prime ,m\prime }\left(k\right)]\hfill \end{array}$$ (14)

$$\begin{array}{cc}\hfill & J_z(\alpha ,\beta ,i,j,k)\hfill \\ \hfill & \approx \sum _{n=0}^N\sum _{m=0}^N\sum _{n\prime =0}^N\sum _{m\prime =0}^N{\lambda }_{n,m}{\lambda }_{n\prime ,m\prime }{Q}_x^{n,n\prime }\left(i\right)Q_y^{m,m\prime }\left(j\right)\hfill \\ \hfill & \times [a_{n,m}^{\alpha }{a}_{n\prime ,m\prime }^{\beta }{V}_z^{n,m,n\prime ,m\prime }\left(k\right)\hfill \\ \hfill & +a_{n,m}^{\alpha }{b}_{n\prime ,m\prime }^{\beta }{T}_z^{n,m,n\prime ,m\prime }\left(k\right)\hfill \\ \hfill & +b_{n,m}^{\alpha }{a}_{n\prime ,m\prime }^{\beta }{S}_z^{n,m,n\prime ,m\prime }\left(\alpha \right)\hfill \\ \hfill & +b_{n,m}^{\alpha }{b}_{n\prime ,m\prime }^{\beta }{R}_z^{n,m,n\prime ,m\prime }\left(k\right)]\hfill \\ \hfill & +\sum _{n=0}^N\sum _{m=0}^N{b}_0^{\alpha }{\lambda }_{n,m}[a_{n,m}^{\beta }{Q}_x^{n,0}\left(i\right)Q_y^{m,0}\left(j\right)T_z^{n,m,0,0}\left(k\right)\hfill \\ \hfill & +b_{n,m}^{\beta }{Q}_x^{n,0}\left(i\right)Q_y^{m,0}{V}_z^{n,m,0,0}\left(k\right)]\hfill \\ \hfill & +\sum _{n=0}^N\sum _{m=0}^N{b}_0^{\beta }{\lambda }_{n,m}[a_{n,m}^{\beta }{Q}_x^{n,0}\left(i\right)Q_y^{m,0}\left(j\right)T_z^{n,m,0,0}\left(k\right)\hfill \\ \hfill & +b_{n,m}^{\alpha }{Q}_x^{n,0}\left(i\right)Q_y^{m,0}\left(j\right)V_z^{n,m,0,0}\left(k\right)]\hfill \\ \hfill & +b_0^{\alpha }{b}_0^{\beta }{I}_v(i,j,k)\hfill \end{array}$$ (15)

and

$$\{\begin{array}{c}{P}_x^{n,n\prime }\left(i\right)={\int }_{x=x_i}^{x=x_{i+1}}\sin {\lambda }_{n}x\sin {\lambda }_{n\prime }xdx\hfill \\ P_y^{m,m\prime }\left(j\right)={\int }_{y=y_j}^{y=y_{j+1}}\sin {\lambda }_{m}y\sin {\lambda }_{m\prime }ydy\hfill \\ Q_x^{n,n\prime }\left(i\right)={\int }_{x=x_i}^{x=x_{i+1}}\cos {\lambda }_{n}x\cos {\lambda }_{n\prime }xdx\hfill \\ Q_y^{m,m\prime }\left(j\right)={\int }_{y=y_j}^{y=y_{j+1}}\cos {\lambda }_{m}y\cos {\lambda }_{m\prime }ydy\hfill \\ R_z^{n,m,n\prime ,m\prime }\left(k\right)={\int }_{z=z_k}^{z=z_{k+1}}\cosh {\lambda }_{n,m}z\cosh {\lambda }_{n\prime ,m\prime }zdz\hfill \\ S_z^{n,m,n\prime ,m\prime }\left(k\right)={\int }_{z=z_k}^{z=z_{k+1}}\cosh {\lambda }_{n,m}z\sinh {\lambda }_{n\prime ,m\prime }zdz\hfill \\ T_z^{n,m,n\prime ,m\prime }\left(k\right)={\int }_{z=z_k}^{z=z_{k+1}}\sinh {\lambda }_{n,m}z\cosh {\lambda }_{n\prime ,m\prime }zdz\hfill \\ V_z^{n,m,n\prime ,m\prime }\left(k\right)={\int }_{z=z_k}^{z=z_{k+1}}\cosh {\lambda }_{n,m}z\cosh {\lambda }_{n\prime ,m\prime }zdz\hfill \\ I_v(i,j,k)={\int }_{x=x_i}^{x=x_{i+1}}{\int }_{y=y_j}^{y=y_{j+1}}{\int }_{z=z_k}^{z=z_{k+1}}1dzdydx\hfill \end{array}\phantom{\}}.$$ (16)

Next, we notice that each summation over n, m, n′, m′ is a quadratic form, and thus we can rewrite J_x (α, β, i, j, k), J_y (α, β, i, j, k), and J_z (α, β, i, j, k) as follows:

$$\begin{array}{cc}\hfill & J_x(\alpha ,\beta ,i,j,k)\hfill \\ \hfill & ={\left({\mathbf{a}}^{\alpha }\right)}^T{\mathbf{A}}_x^{c,c}{\mathbf{a}}^{\beta }+{\left({\mathbf{a}}^{\alpha }\right)}^T{\mathbf{A}}_x^{c,s}{\mathbf{b}}^{\beta }\hfill \\ \hfill & +{\left({\mathbf{b}}^{\alpha }\right)}^T{\mathbf{A}}_x^{s,c}{\mathbf{a}}^{\beta }+{\left({\mathbf{b}}^{\alpha }\right)}^T{\mathbf{A}}_x^{s,s}{\mathbf{b}}^{\beta }\hfill \end{array}$$ (17)

$$\begin{array}{cc}\hfill & J_y(\alpha ,\beta ,i,j,k)\hfill \\ \hfill & ={\left({\mathbf{a}}^{\alpha }\right)}^T{\mathbf{A}}_y^{c,c}{\mathbf{a}}_{\beta }+{\left({\mathbf{a}}^{\alpha }\right)}^T{\mathbf{A}}_y^{c,s}{\mathbf{b}}^{\beta }\hfill \\ \hfill & +{\left({\mathbf{b}}^{\alpha }\right)}^T{\mathbf{A}}_y^{s,c}{\mathbf{a}}^{\beta }+{\left({\mathbf{b}}^{\alpha }\right)}^T{\mathbf{A}}_y^{s,s}{\mathbf{b}}^{\beta }\hfill \end{array}$$ (18)

$$\begin{array}{cc}\hfill & J_z(\alpha ,\beta ,i,j,k)\hfill \\ \hfill & ={\left({\mathbf{a}}^{\alpha }\right)}^T{\mathbf{A}}_z^{c,c}{\mathbf{a}}^{\beta }+{\left({\mathbf{a}}^{\alpha }\right)}^T{\mathbf{A}}_z^{c,s}{\mathbf{b}}^{\beta }\hfill \\ \hfill & +{\left({\mathbf{b}}^{\alpha }\right)}^T{\mathbf{A}}_z^{s,c}{\mathbf{a}}^{\beta }+{\left({\mathbf{b}}^{\alpha }\right)}^T{\mathbf{A}}_z^{s,s}{\mathbf{b}}^{\beta }\hfill \\ \hfill & +b_0^{\alpha }({\mathbf{N}}_a^T{\mathbf{a}}^{\beta }+{\mathbf{N}}_b^T{\mathbf{b}}^{\beta })+b_0^{\beta }({\mathbf{N}}_a^T{\mathbf{a}}^{\alpha }\hfill \\ \hfill & +{\mathbf{N}}_b^T{\mathbf{b}}^{\alpha })+b_0^{\alpha }{b}_0^{\beta }{I}_v\hfill \end{array}$$ (19)

where

$$\{\begin{array}{c}\mathbf{a}={\left[a_{0,0}{a}_{0,1}\dots a_{N,N}\right]}^T\hfill \\ \mathbf{b}={\left[b_{0,0}{b}_{0,1}\dots b_{N,N}\right]}^T\hfill \end{array}\phantom{\}}$$ (20)

and:

$$\{\begin{array}{c}{\mathbf{N}}_a={\left[N_{0,0}^a{N}_{0,1}^a\dots N_{N,N}^a\right]}^T\hfill \\ {\mathbf{N}}_b={\left[N_{0,0}^b{N}_{0,1}^b\dots N_{N,N}^b\right]}^T\hfill \end{array}\phantom{\}}$$ (21)

$$\{\begin{array}{c}{N}_{n,m}^a={\lambda }_{n,m}{Q}_x^{n,0}\left(i\right)Q_y^{m,0}\left(j\right)T_z^{n,m,0,0}\left(k\right)\hfill \\ N_{n,m}^b={\lambda }_{n,m}{Q}_x^{n,0}\left(i\right)Q_y^{m,0}\left(j\right)V_z^{n,m,0,0}\left(k\right)\hfill \end{array}\phantom{\}}.$$ (22)

For each voxel, we precompute the matrices A^c,c, A^c,s, A^s,c, A^s,s and the vectors N_a and N_b where

$${\mathbf{A}}^{c,c}={\mathbf{A}}_x^{c,c}+{\mathbf{A}}_y^{c,c}+{\mathbf{A}}_z^{c,c}$$ (23)

$${\mathbf{A}}^{c,s}={\mathbf{A}}_x^{c,s}+{\mathbf{A}}_y^{c,s}+{\mathbf{A}}_z^{c,s}$$ (24)

$${\mathbf{A}}^{s,c}={\mathbf{A}}_x^{s,c}+{\mathbf{A}}_y^{s,c}+{\mathbf{A}}_z^{s,c}$$ (25)

$${\mathbf{A}}^{s,s}={\mathbf{A}}_x^{s,s}+{\mathbf{A}}_y^{s,s}+{\mathbf{A}}_z^{s,s}$$ (26)

These matrices and vectors can be quickly populated if we precompute the integrals, (16) for all i, j, k. Finally, we compute J(α, β, i, j, k) for voxel (i, j, k) and each pair of current patterns as

$$\begin{array}{cc}\hfill & J(\alpha ,\beta ,i,j,k)\hfill \\ \hfill & ={\left({\mathbf{a}}^{\alpha }\right)}^T{\mathbf{A}}^{c,c}{\mathbf{a}}^{\beta }+{\left({\mathbf{a}}^{\alpha }\right)}^T{\mathbf{A}}^{c,s}{\mathbf{b}}^{\beta }\hfill \\ \hfill & +{\left({\mathbf{b}}^{\beta }\right)}^T{\mathbf{A}}^{s,c}{\mathbf{a}}^{\beta }+{\left({\mathbf{b}}^{\alpha }\right)}^T{\mathbf{A}}^{s,s}{\mathbf{b}}^{\beta }\hfill \\ \hfill & +b_0^{\alpha }({\mathbf{N}}_a^T{\mathbf{a}}^{\beta }+{\mathbf{N}}_b^T{\mathbf{b}}^{\beta })\hfill \\ \hfill & +b_0^{\beta }({\mathbf{N}}_a^T{\mathbf{a}}^{\alpha }+{\mathbf{N}}_b^T{\mathbf{b}}^{\beta })\hfill \\ \hfill & +b_0^{\alpha }{b}_0^{\beta }{I}_v\hfill \end{array}$$ (27)

Thus, for each voxel, the Jacobian for a given pair of current patterns can be easily computed as a set of matrix-vector and scalar multiplies.

D. Detection of Poorly Contacting Electrodes

In our initial clinical experiments, we found that it was quite difficult to ensure that all electrodes make sufficiently good contact with the breast. Quite often it was the case that some subset of the electrodes experienced a relatively high impedance, perhaps due to local variation in the pressure applied to different portions of the breast under compression. If the gap model is used, these high-impedance interfaces tend to produce low-admittivity artifacts in the reconstructed images.

Our approach is to use an automated criterion to detect poorly contacting electrodes, by considering the relative error of the voltages actually measured on these electrodes, as compared to the voltages that would have been expected given a homogeneous medium and the gap model. Those electrodes which meet or exceed a given threshold for the relative error are excluded from the image reconstruction, where the exclusion is accomplished by replacing the measured data from these electrodes with data generated by the ave-gap model applied to a homogeneous medium.

In order to detect electrodes making insufficiently good contact with the breast, we compute the following error metric for each electrode:

$$E\left(\ell \right)=\frac{\sqrt{\sum _{\alpha =1}^K{\mid \frac{1}{{\gamma }_0}{U}_{\ell ,\alpha }\left(1\right)-V_{\ell ,\alpha }\mid }^2}}{\sqrt{\sum _{\alpha =1}^K{\left(\frac{1}{{\gamma }_0}{U}_{\ell ,\alpha }\left(1\right)\right)}^2}}$$ (28)

where U_ℓ,α (1) is the voltage on electrode ℓ for current pattern α for a region with a conductivity of 1 S/m, V_ℓ,α is the measured on electrode ℓ, and where γ0 is chosen to minimize the numerator of this expression.

Our strategy in ameliorating errors from poorly contacting electrodes is to replace measured data from these electrodes with values that we would have expected, given a homogeneous gap model. In order to accomplish this, we replace (5) with the following expression:

$$\begin{array}{c}\hfill \sum _{\ell \notin B}{\int }_{e_{\ell }}\left[u_{\beta }\left({\gamma }_0\right)\frac{\partial u_{\alpha }\left(\gamma \right)}{\partial v}-u_{\alpha }\left(\gamma \right)\frac{\partial u_{\beta }\left({\gamma }_0\right)}{\partial v}\right]dS\hfill \\ \hfill \approx {\int }_{\Omega }\eta \nabla u_{\beta }\left({\gamma }_0\right)\cdot \nabla u_{\alpha }\left({\gamma }_0\right)dp\hfill \end{array}$$ (29)

where B is the set of electrodes for which E(ℓ) is greater than a predetermined threshold, 70%.

III. Electrical Impedance Spectroscopy of the Breast

Motivated by previous research in the area of electrical impedance spectroscopy [12], we made electrical impedance measurements of the breast at each of six discrete, logarithmically spaced, frequencies from 3 kHz to 1 MHz. Using the methods described in this paper, we compute linearized reconstructions of the complex admittivity at each of these frequencies.

We plot the imaginary component of the admittivity versus the real component, parameterized by frequency, for each voxel within the breast, denoting the result as an “EIS plot.” We have examined a number of derived parameters, which condense the information within this EIS plot for each voxel into a single figure of merit. At present, a particularly promising derived parameters is the linear correlation metric (LCM), which essentially is a nonlinear transformation that quantifies the resemblance of the EIS plot to a straight line. In order to compute the LCM, we first compute the best least-squares fit for a linear relationship between the conductivity σ and the absolute permittivity ∈ for each point in space for which we compute a reconstruction

$${∊}_{\mathrm{lin}}=a\sigma +b1.$$ (30)

where σ is a vector composed of the reconstructed conductivities at all frequencies for which we collect data and 1 is the vector: [1 1 ... 1]^T. Here, we are fitting for the parameters a and b. We then compute the LCM at each point in space by applying a nonlinear transformation of the correlation between the reconstructed and linearly predicted permittivities, ∈ being a vector of the reconstructed permittivities

$$\mathrm{LCM}=\frac{1}{1-\frac{{∊}_{\mathrm{lin}}\cdot ∊}{{\Vert {∊}_{\mathrm{lin}}\Vert }_2{\Vert ∊\Vert }_2}}$$ (31)

We display the LCM in the center layer of the reconstructed image alongside the central slice of the tomosynthesis reconstruction.

IV. Results and Discussion

Here, we evaluate the algorithms presented for experimental data acquired in a breast-shaped tank filled with conductive saline solution and for a single clinical research subject.

A. Saline Phantom Experiments and Simulation Study

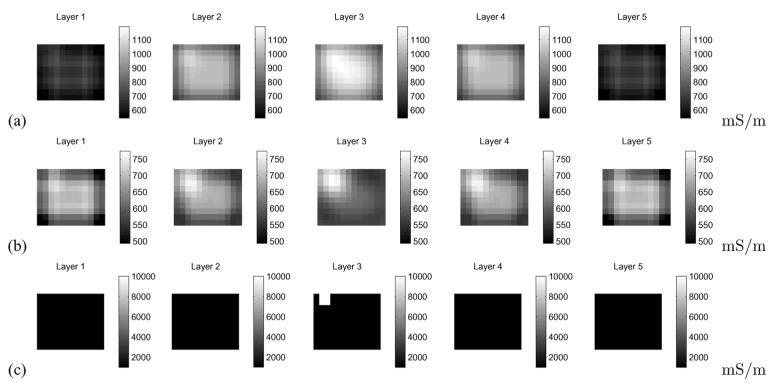
We conducted simulation studies to examine whether the simplified linearized methods and geometry described in this paper can compensate for significant sources of model mismatch likely to be encountered in practice. To this end, we used the complete electrode model, generating the forward data using the Galerkin method [20]. We assumed the presence of nontrivial electrode surface impedances (10^-3 Ωm). We simulated a medium with background admittivity 1.0 S/m and containing a 1 cm³ inclusion with admittivity 10.0 S/m. We also assumed the presence of a thin layer of “skin” of thickness 2 mm directly beneath the electrodes, with admittivity 0.1 S/m. The reconstruction in which we do not introduce an individual effective impedance, γ_0,β for each current pattern β [i.e., utilizing (6)], results in a wide dynamic range and nearly no evidence of the target [Fig. 4(a)]. In contrast, the reconstruction making use of (8) [Fig. 4(b)] reduces the dynamic range of the reconstruction and displays the target clearly and the true location of the inclusion and its contrast are shown in Fig. 4(c). We see that introducing an independent scaling factor for each current pattern significantly reduces the image artifacts present in the reconstruction when we have model mismatch due to the presence of skin and the use of a less accurate electrode model.

Fig. 4.

Illustration of the utility of data scaling in in the image reconstruction, simulation study. (a) Image reconstruction without scaling. (b) Image reconstruction making use of scaling. (c) True conductivity used in the simulation.

We further explored this issue with an experimental study, using the ACT 4 to make measurements in a breast-shaped saline tank, shown in Fig. 3. The phantom is constructed from plexiglass with a shape intended to simulate the breast under compression. The planar electrode arrays, each of which contains five rows of six electrodes each, are located on the front and back side walls, which correspond to the top and bottom electrode arrays of the mammography geometry model in Fig. 2(a). The size of each electrode is 10 × 10 mm, and the width of the gap between adjacent electrodes is 1 mm. In our forward modeling, we assume a cube with the following dimensions: 75(h₁) × 86(h₂) × 42(h₃) mm, where h₃ is the depth of the phantom, thus assuming a border of 10 mm at each edge of our electrode array. Here, we show reconstructions for data acquired at 10 kHz but the results for other temporal frequencies in the saline tank are very similar. We placed a 1 cm³ conducting inclusion near electrode 8, which is the second electrode from the left in the second row of Fig. 2(b), at a depth of approximately 1 cm. The phanton was filled with saline solution with a conductivity of 64 mS/m. Fig. 5 illustrates the importance of data scaling in the image reconstruction, where, by scaling, we mean the use of D_α,β in the image reconstruction obtained using (8), as opposed to using (6). Fig. 5(a) shows the image reconstruction without scaling applied, while Fig. 5(b) depicts that, when scaling is used, the target becomes much more clearly visible. For the purpose of comparison, a difference-imaging reconstruction, using the saline tank without the presence of the inclusion as a reference, is shown in Fig. 5(c). In all cases, the Jacobian matrix was created using the methods described in Section II-C, with N = 31 in the x and y directions, for a total of 2049 basis functions used to represent the potential resulting from the application of each current pattern. Thus, we observe that introducing a different scaling factor for each current pattern in the image reconstruction improves our ability to detect and localize targets. A possible explanation for this phenomenon is that we can compensate for electrode effects, which are not explicitly modeled by the ave-gap formulation, by applying this scaling approach.

Fig. 3.

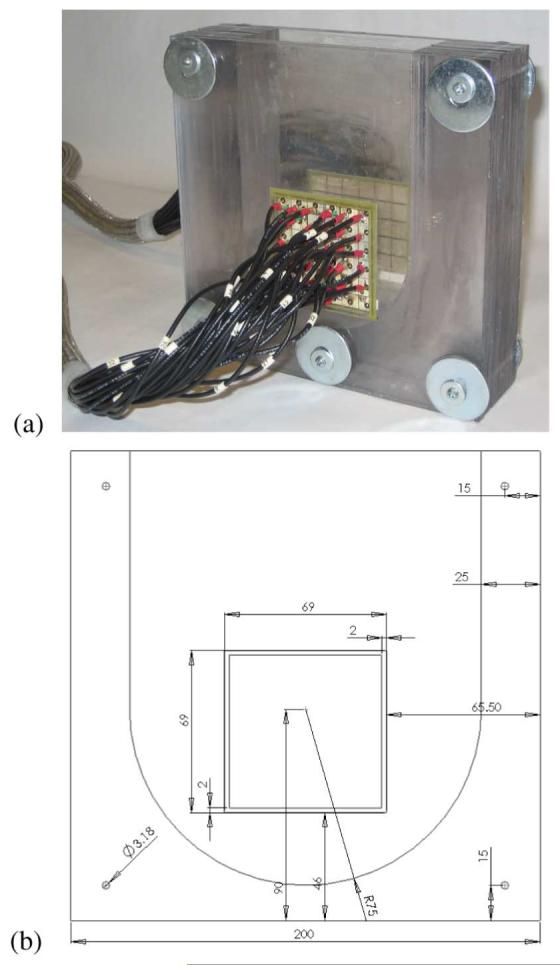
The 60-electrode test phantom for the 3-D mammography geometry used in the experiment. (a) Three-dimensional test phantom. (b) Front view.

Fig. 5.

Illustration of the utility of data scaling in the image reconstruction for experimental data. (a) Image reconstruction without scaling. (b) Image reconstruction making use of scaling. (c) Difference imaging reconstruction.

We next consider the problem of detecting and compensating for the presence of poorly contacting electrodes. In order to test for this condition experimentally, we partially occluded a single electrode, electrode 10, by covering a large portion of its surface with insulating tape, as shown in Fig. 6. The effect of this electrode on the measured voltages is shown in Fig. 7. Fig. 7(a) shows the measured (depicted as a dashed line) and expected (depicted as a solid line) voltages corresponding to a current pattern which imposes the same positive current on all of the bottom electrodes (electrodes 1–30) and the same negative current on all of the top electrodes (electrodes 31–60). A significant discrepancy between the two patterns of voltages is observed for electrode 10. In Fig. 7(b), we display E(ℓ) as computed for all electrodes, using (28). For electrode 10, the electrode norm error is greater than 90%, while for all other electrodes E(ℓ) is lees than 11%.

Fig. 6.

Illustration of the occlusion of electrode 10, the fourth electrode in the second row from the top, covered except for a circular hole about 5 mm in diameter.

Fig. 7.

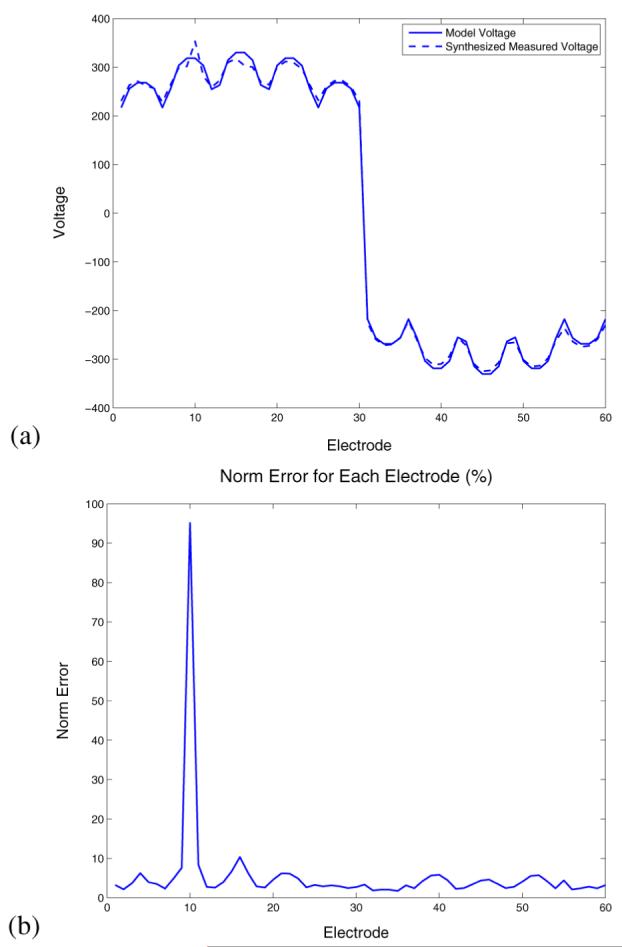
Effect of the occluded electrode on measured voltages and automatic detection of an occluded or noncontacting electrode. (a) Measured and model voltages corresponding to a particular current pattern. (b) Norm error for each electrode.

To experimentally validate our electrode contact compensation procedure, we partially occluded electrode 10 and placed a 1 cm³ conducting inclusion into a homogeneous saline-filled tank at a depth of approximately 1 cm near electrode 13, at the center left of the electrode array. The linearized reconstruction of the conductivity, using measurements made at 30 kHz and utilizing all of the measurements, is shown in Fig. 8(a). We notice that the reconstruction is dominated by a large negative artifact near the occluded electrode 10. In Fig. 8(b), we have computed the reconstruction using the compensation procedure in (29). We observe in this case that the artifact previously observed near electrode 10 is largely absent. The difference-imaging reonstruction shown in Fig. 8(c) is used to illustrate the actual target location and closely resembles the reconstruction in Fig. 8(b). Thus, we have developed a technique for mitigating the effect of a partially noncontacting electrode, a condition which we have frequently observed in our clinical studies.

Fig. 8.

Illustration of the efficacy of our technique for reducing artifacts due to noncontacting electrodes. (a) Image reconstruction using all data. (b) Image reconstruction substituting forward model data for data on the noncontacting electrode. (c) Difference imaging reconstruction.

B. Clinical Results

Here, we consider the use of the algorithms described in this paper for the analysis of human subject electrical impedance measurements. First, Fig. 9 shows the significance of poor electrode contact as a problem in the analysis of some data obtained in a clinical setting. Fig. 9(a) compares the actual, measured voltages obtained as a result of a particular input current pattern, to those expected given an gap model. A significant discrepancy is observed for electrode 30, a discrepancy which is quantified as a large peak in the value of E(ℓ) for this electrode, shown in Fig. 9(b).

Fig. 9.

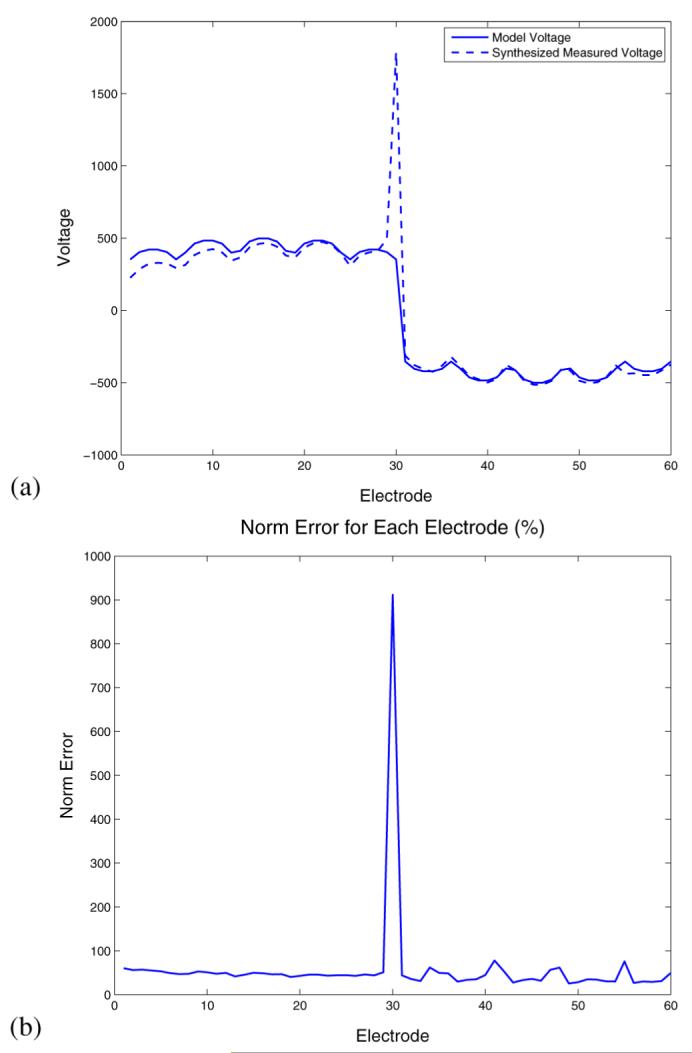
Electrode diagnostics for a clinical imaging subject, left breast.(a) Comparison of expected and measured voltages corresponding to a given current pattern. (b) E(ℓ) for each electrode.

We made use of the algorithms described in this paper to analyze the electrical impedance data from the left breast of a clinical imaging subject. Upon examination by biopsy, this breast was discovered to contain ductal carcinoma in situ (DCIS) as well as invasive ductal carcinoma. The results for the electrical impedance spectral analysis are shown in Fig. 10. A slice of the Tomosynthesis reconstruction, superimposed with the position of the electrode arrays, is depicted in Fig. 10(a). We display an image of the derived LCM spectral parameter for the region under the grid in Fig. 10(a) and (b). The region containing high values of the LCM parameter corresponds quite well to the region of the breast assessed as being abnormal by mammographic examination. Finally, the electrical impedance spectra for two voxels, one within the region identified by the radiologist to contain an invasive carcinoma and one within a presumed normal region of the breast are shown in Fig. 10(c). A striking difference between the two spectra is noted, with the voxel within the abnormal region of the breast having an EIS spectrum which much more closely resembles a straight line than that of the spectrum for the voxel within the presumably normal region.

Fig. 10.

Comparison of EIT and Tomosynthesis reconstructions for a clinical imaging subject, left breast. (a) Tomosynthesis reconstruction, superimposed with the electrode array. (b) LCM image in the center slice, corresponding to the region directly below the electrode array. (c) Electrical impedance spectra for two regions of interest within the breast.

V. Conclusion and Future Work

In this paper, we have described and implemented algorithms for the linearized reconstruction of conductivities within the breast given external measurements of the voltage and currents on a discrete set of electrodes in direct contact with the surface of the breast in a mammography configuration. An analytical forward model and an efficient method for computing the Jacobian matrix linking the measurements to the internal conductivities have been described. In addition, algorithms improving the robustness of the reconstruction to modeling error have been introduced and implemented. Specifically, we show the utility of making use of a different effective conductivity for the reconstruction of data from each applied current pattern and develop an algorithm for the automatic detection of poorly contacting electrodes as well as the mitigation of these electrodes’ effects on the reconstruction. Lastly, we demonstrate the utility of the methods described here for the reconstruction of data from a human subject found to have breast cancer. In the future, we plan to compare the methods described here to fully nonlinear reconstruction approaches, to determine if the very high computational cost of the latter is justified. We also plan to investigate the use of the complete electrode model and spectral parameters other than the LCM.