Optimized approach to decision fusion of heterogeneous data for breast cancer diagnosis

Abstract

As more diagnostic testing options become available to physicians, it becomes more difficult to combine various types of medical information together in order to optimize the overall diagnosis. To improve diagnostic performance, here we introduce an approach to optimize a decision-fusion technique to combine heterogeneous information, such as from different modalities, feature categories, or institutions. For classifier comparison we used two performance metrics: The receiving operator characteristic (ROC) area under the curve [area under the ROC curve (AUC)] and the normalized partial area under the curve (pAUC). This study used four classifiers: Linear discriminant analysis (LDA), artificial neural network (ANN), and two variants of our decision-fusion technique, AUC-optimized (DF-A) and pAUC-optimized (DF-P) decision fusion. We applied each of these classifiers with 100-fold cross-validation to two heterogeneous breast cancer data sets: One of mass lesion features and a much more challenging one of microcalcification lesion features. For the calcification data set, DF-A outperformed the other classifiers in terms of AUC (p<0.02) and achieved AUC=0.85±0.01. The DF-P surpassed the other classifiers in terms of pAUC (p<0.01) and reached pAUC=0.38±0.02. For the mass data set, DF-A outperformed both the ANN and the LDA (p<0.04) and achieved AUC=0.94±0.01. Although for this data set there were no statistically significant differences among the classifiers' pAUC values (pAUC=0.57±0.07 to 0.67±0.05, p>0.10), the DF-P did significantly improve specificity versus the LDA at both 98% and 100% sensitivity (p<0.04). In conclusion, decision fusion directly optimized clinically significant performance measures, such as AUC and pAUC, and sometimes outperformed two wellknown machine-learning techniques when applied to two different breast cancer data sets.

I. INTRODUCTION

Breast cancer accounts for one-third of all cancer diagnoses among American women, has the second highest mortality rate of all cancer deaths in women,¹ and is expected to account for 15% of all cancer deaths in 2005.² Early diagnosis and treatment can significantly improve the chance of survival for breast cancer patients.³ Currently, mammography is the preferred screening method for breast cancer. However, high false positive rates reduce the effectiveness of screening mammography, as several studies have shown that only 13–29% of suspicious masses are determined to be malignant.^4-6 Unnecessary surgical biopsies are expensive, cause patient anxiety, alter cosmetic appearance, and can distort future mammograms.⁷

Commercial products for computer-aided detection (CAD) have shown promise for improving sensitivity in large clinical trials. Most studies to date have shown CAD to boost radiologists lesion detection sensitivity.^8-11 To date, however, there are no commercial systems to improve specificity for breast cancer screening. To fill this need to improve the sensitivity of mammography, computer-aided diagnosis (CADx) has emerged as a promising clinical aid.¹²

There has been considerable CAD and CADx research based upon a rich variety of modalities and sources of medical information, such as: digitized screen-film mammograms,^13-17 full-field digital mammograms,¹⁸ sonograms,^19-21 magnetic resonance imaging (MRI) images,²² and gene expression profiles.²³ Current clinically implemented CADx programs tend to use only one information source, although multimodality CADx programs²⁴ are beginning to emerge. Moreover, most CADx research has been performed using relatively homogeneous data sets collected at one institution, acquired using one type of digitizer or digital detector, or using features drawn from one source such as human-interpreted findings versus computer-extracted features. Increasingly however, there is a trend toward boosting diagnostic performance by combining data from many different sources to create heterogeneous data. We defined heterogeneous data as comprising multiple, distinct groups. Specifically, for this study, we considered as heterogeneous any of the following data set characteristics: Multiple imaging modalities, multiple types of mammogram film digitizers, data collected from multiple institutions, and various types of features extracted from the same image, especially computer-extracted and human-extracted features. Combining heterogeneous data types for classification is a difficult machine-learning problem, but one that has shown promise in bioinformatics applications.^25-27

To meet the challenge of combining heterogeneous data types, we turned to a decision-fusion method that operates by the following two steps: (1) Classifiers use feature subsets to generate initial binary decisions, and (2) these binary decisions are then optimally combined by using decision-fusion theory. Decision fusion offers the following advantages: It handles heterogeneous data sources well, reduces the problem dimensionality, is easily interpretable, and is easy to use in a clinical setting. Decision fusion has effectively combined heterogeneous data in many diverse classification tasks, such as detecting land mines using multiple sensors,²⁸ identifying persons using multiple biometrics,²⁹ and CADx of endoscopic images using multiple sets of medical features.³⁰

The purpose of this study was to optimize a decision-fusion approach for classifying heterogeneous breast cancer data. We compared this decision-fusion approach to a linear discriminant and an artificial neural network (ANN), which are well-studied techniques that have frequently been applied to breast cancer CADx.^13,31-33 This study evaluates these classification algorithms on two breast cancer data sets using two different clinically relevant performance metrics.

II. METHODS

A. Data

For this study, we chose two different breast cancer data sets, which differed considerably in the type and number of patient cases as well as the type and number of medical information features describing those cases.

1. Microcalcification lesions

Data set C consisted of all 1508 mammogram microcalcification lesions from the Digital Database for Screening Mammography (DDSM).³⁴ The outcomes were verified by histological diagnosis and followup for certain benign cases, yielding 811 benign and 697 malignant calcification lesions. Figure 1 shows the feature group structure of this data set. The feature groups were 13 computer-extracted calcification cluster morphological features, 91 computer-extracted texture features of the lesion background anatomy, 2 radiologist-interpreted findings, 3 radiologist-extracted features from the Breast Imaging Reporting and Data System (BI-RADS™, American College of Radiology, Reston, VA) (Ref. ³⁵) and patient age. In total, data set C had 110 features and a sample-to-feature ratio of approximately 14:1. Each mammogram was digitized with one of four digitizers: A DBA M2100 ImageClear at a resolution of 42 microns, a Howtek 960 at 43.5 microns, a Howtek MultiRad850 at 43.5 microns, or a Lumisys 200 Laser at 50 microns. To study this large heterogeneous data set, no attempt was made to restrict cases only to a single digitizer, as was common in most previous studies. Moreover, no standardization step was applied to the images to correct for the differences in noise, resolution, and other physical characteristics from the various digitizers. We used a 512×512 pixel region of interest (ROI) centered on the centroid of each lesion (using lesion outlines drawn by the DDSM radiologists) for image processing and for generating the computer-extracted features. We extracted morphological and texture (spatial gray level dependence matrix) features, which were shown to be useful in a previous study of CADx by Chan et al.³¹

Fig. 1.

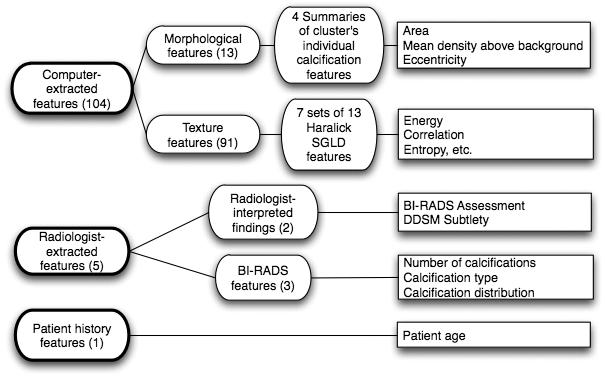
Feature group structure for calcification Data Set C (calcification lesions). The features of the calcification data set consisted of three main groups: Computer-extracted features, radiologist-extracted features, and patient history features. The computer-extracted features were morphological and shape features of the automatically detected and segmented microcalcification clusters within the digitized mammogram images. The radiologist-extracted features comprised both radiologist-interpreted findings and BI-RADS features. This data set consisted of 512×512 pixel ROIs of all 1508 calcification lesions in the DDSM. This data set had many heterogenic characteristics, such as that it was collected at four different institutions, scanned on four digitizers with different noise characteristics, and included both human-extracted and computer-extracted features, such as shape and texture features.

This data set had many heterogenic characteristics, such as that it was collected at four different institutions, scanned on four types of digitizers with different physical characteristics, and included both human-extracted and computer-extracted features, such as shape and texture features.

2. Mass lesions

Data set M consisted of 568 breast mass cases that were collected in the Radiology Department of Duke University Health System between 1999 and 2001. These cases were an extension of the data set described in detail in our previous studies.^36,37 Definitive histopathologic diagnosis from biopsy was used to determine outcome, yielding 370 benign and 198 malignant mass lesions. Figure 2 shows the feature group structure of this data set. Dedicated breast radiologists recorded all features.

Fig. 2.

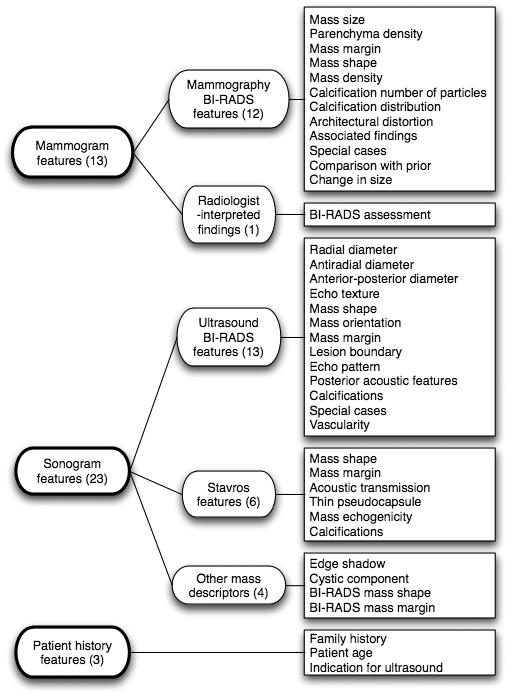
Feature group structure for mass Data set M (mass lesions). The features of the mass data set consisted of mammogram features, sonogram features, and patient history features. The mammogram features comprised both BI-RADS features and radiologist-interpreted findings. The sonogram features consisted of ultrasound BI-RADS features, Stavros features, and other ultrasound mass descriptors. All image features were radiologist-extracted features. The mass data set was heterogeneous in including both mammogram and sonogram views of the breast. Both mammogram and sonogram feature sets were as well as including patient history features.

The mass data set was heterogeneous because it was comprised of 3 distinct types of data: 13 mammogram features, 23 sonogram features in turn drawn from 3 different lexicons (Ultrasound Bl-RADS, Stavros, and others),³⁶ as well as 3 patient history features. In total, data set M had 39 features and a sample-to-feature ratio of approximately 15:1.

B. Decision fusion

There is a growing literature in the area of distributed detection. Although there is even some earlier work, several of the early classical references include the work of Tenney and Sandell,³⁸ who introduced distributed detection using a fixed fusion processor and optimized the local processors. Chair and Varshney³⁹ fixed the local processors, and optimized the fusion processor. Reibman and Nolte⁴⁰ extended these previous studies by simultaneous optimization of the local detectors while deriving the overall optimum fusion design. Dasarathy⁴¹ summarized some of the earlier work.

Decision-fusion theory describes how to combine local binary decisions optimally to determine the presence or absence of a signal in noise.^38-42 The local binary decisions can come from any arbitrary source.

Figure 3 provides a schematic of our decision-fusion method. Our algorithm is a two-stage process, each with a likelihood ratio calculation. The first stage applies a separate likelihood ratio to each feature. These feature-level likelihood ratios are then compared to separate thresholds to generate feature-level decisions. These feature-level decisions are then fused in the second stage by computing the likelihood ratio of the binary decision values. The second stage combines the feature-level decisions into one fused likelihood-ratio value, which can be used as a classification decision variable.

Fig. 3.

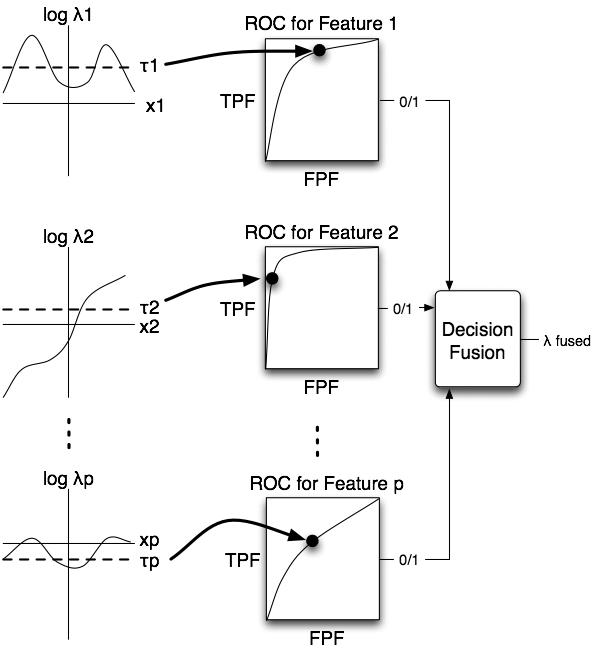
The role of likelihood-ratio thresholds for decision fusion. The first column shows plots of the log-likelihood-ratio versus feature value for each feature. The algorithm calculated the likelihood ratio and then thresholded it separately for each feature. The threshold determined the ROC operating point of the likelihood-ratio classifier of a particular feature. Next, the algorithm combined the binary decisions from the feature-level likelihood ratio classifiers using decision fusion theory to produce the likelihood ratio of the fused classifier.

Our technique offers the important advantage that it can reduce the dimensionality of the feature space of the classification problem by assigning a classifier to each feature separately. Considering only one feature at a time greatly reduces the complexity of the problem by avoiding the need to estimate multidimensional probability density functions (PDFs) of the feature space. Accurately estimating such multidimensional PDFs likely requires many more observations than a typical medical data set contains. Other benefits of decision fusion are that it is robust in noisy data⁴³ is not overly sensitive to the likelihood ratio threshold values,⁴² and can handle missing data values.⁴⁴ Our decision-fusion technique can also be tuned to maximize arbitrary performance metrics (as described later in Sec. II C) that may be more clinically relevant, unlike more traditional classification algorithms that minimize mean-squared error.

1. Detection theory approach - likelihood ratio

Although decision fusion combines binary decisions regardless of how those decisions were made, it is still important to choose the right initial classifiers in order to pass as much information to the decision fuser as possible. In our algorithm, we used the likelihood ratio as the initial classifier and applied a threshold to generate the binary decisions on each feature. Previous work has shown the likelihood ratio to be an excellent classifier for breast cancer mass lesion data.^45,46

According to decision theory, the likelihood ratio is the optimal detector to determine the presence or absence of a signal in noise.⁴⁷ For this study, the signal to be detected was the potential malignancy of a breast lesion. The null hypothesis (H₀) was that the signal (malignancy) is not present in the noisy features, while the alternative hypothesis (H₁) was that the signal is present:

$$\begin{array}{cc}\hfill H_0:X& =N,\hfill \\ \hfill H_1:X& =S+N.\hfill \end{array}$$ (1)

Sources of noise in the features included anatomical noise inherent in the mammogram or sonogram, quantum noise in the acquisition of the mammogram or sonogram, digitization noise and artifacts for data set C, and ambiguities in the mammogram reading process for the radiologist-interpreted findings in both Data sets C and M.

The likelihood ratio is the probability of the features under the malignant case divided by the probability of the features under the benign case:

$${\lambda }_{\text{features}}\left(X\right)=\frac{P(X\mid H_1)}{P(X\mid H_0)},$$ (2)

where P(X|H₁) is the PDF of the observation data X given that the signal is present, and P(X|H₀) is the PDF of the data X given that the signal is not present. The likelihood ratio is optimal under the assumption that the PDFs accurately reflect the true densities. We estimated the one-dimensional PDFs of the features with histograms. We used Scott's rule to determine the optimal histogram bin width,⁴⁵

$$h=3.5\sigma n^{-1∕3},$$ (3)

where h is the bin width, σ is the standard deviation, and n is the number of observations. The interval of two standard deviations around the mean, [μ −2σ,μ+2σ], was then subdivided by the bin width, h. We assigned the values falling outside this interval to the extreme left or right bins. Next, we applied a threshold value, τ, to the likelihood ratio to produce a binary decision about the presence of the signal.

$$u=\{\begin{array}{cc}1\hfill & \text{if}{\lambda }_{\text{feature}}\ge \tau \hfill \\ 0\hfill & \text{if}{\lambda }_{\text{feature}}<\tau .\hfill \end{array}\phantom{\}}$$ (4)

2. Fusing the binary decisions

For the signal-plus-noise hypothesis H₁, the probability of detecting an existing signal is P(u=1|H₁)= Pd and of missing it is P(u=0|H₁)=1−Pd. For the noise-only hypothesis H₀, the probability of false detection is P(u=1|H₀)= Pf and of correctly rejecting the missing signal is P(u=0|H₀)=1 −Pf. Using these probabilities, the likelihood ratio value of a binary decision variable has a simple form, as shown in Eq. (5):

$${\lambda }_{\text{decision}}\left(u\right)=\frac{P(u\mid H_1)}{P(u\mid H_0)}=\{\begin{array}{cc}\frac{\mathit{Pd}}{\mathit{Pf}}\hfill & \text{if}u=1\hfill \\ \frac{1-\mathit{Pd}}{1-\mathit{Pf}}\hfill & \text{if}u=0.\hfill \end{array}\phantom{\}}$$ (5)

We can then use the likelihood ratios of the individual local decision variables to calculate the joint likelihood ratio of the set of decision variables. Assuming that the local decision variables are statistically independent, the likelihood ratio of the fused classifier is a product of the likelihood ratios of the individual local decisions.

$$\begin{array}{cc}\hfill {\lambda }_{\text{fusion}}(u_1,\dots ,u_p)& =\prod _{i=1}^p{\lambda }_{\text{decision}}\left(u_i\right)\hfill \\ \hfill & =\prod _{i=1}^p\frac{P(u_i\mid H_1)}{P(u_i\mid H_0)}\hfill \\ \hfill & =\prod _{i=1}^p{\left(\frac{{\mathit{Pd}}_i}{{\mathit{Pf}}_i}\right)}^{u_i}{\left(\frac{1-{\mathit{Pd}}_i}{1-{\mathit{Pf}}_i}\right)}^{1-u_i}.\hfill \end{array}$$ (6)

Note that we assume statistical independence of only the local binary decisions, not of the sensitivity, false-positive rate, or even the features on which the local decisions were made.

In our decision-fusion theory approach, we have made the important assumption that all the local decisions are statistically independent. While this appears to be a very strong assumption, using it in decision fusion often does not lower classification performance substantially below the performance of the optimal decision fusion processor for correlated decisions. Although we can construct an optimal correlated decision-fusion processor with known decision correlations,⁴⁸ it is difficult to estimate the correlation structure of the decisions accurately, especially given many decisions but only few observations. However, even with correlated decisions, the simplifying assumption of independent decisions often does not lower decision fusion performance. Liao et al.⁴² have shown that, under certain conditions for the case of fusing two correlated decisions, the independent fusion processor exactly matched the performance of the optimal correlated decision fusion processor. Even in many situations when the optimality conditions were not kept, the degradation of the fusion performance was not significant.⁴² Another benefit of the independent local decisions assumption is that decision fusion can usually recover from weak signals and correlated features given enough decisions to fuse.⁴³ Because we have a large number of local decisions by setting a separate local decision for each feature, our algorithm takes advantage of this performance benefit.

C. Classifier evaluation and figures of merit

We used the receiver operating characteristic (ROC) curve to capture the classification performance of our decision-fusion algorithm. Assuming independent local decisions, the PDFs of the decision-fusion likelihood ratio have a similar product form.⁴²

$$\begin{array}{cc}\hfill P({\lambda }_{\text{fusion}}\mid H_1)& =\prod _{i=1}^p{\left({\mathit{Pd}}_i\right)}^{u_i}{(1-{\mathit{Pd}}_i)}^{1-u_i},\hfill \\ \hfill P({\lambda }_{\text{fusion}}\mid H_0)& =\prod _{i=1}^p{\left({\mathit{Pf}}_i\right)}^{u_i}{(1-{\mathit{Pf}}_i)}^{1-u_i}.\hfill \end{array}$$ (7)

Using the fusion likelihood ratio value as a classification decision variable, the probabilities of detection and false alarm are calculated as follows:

$$\begin{array}{cc}\hfill {\mathit{Pd}}_{\text{fusion}}\left(\beta \right)& =\underset{{\lambda }_{\text{fusion}}\ge \beta }{\Sigma }P(\lambda ={\lambda }_{\text{fusion}}\mid H_1),\hfill \\ \hfill {\mathit{Pf}}_{\text{fusion}}\left(\beta \right)& =\underset{{\lambda }_{\text{fusion}}\ge \beta }{\Sigma }P(\lambda ={\lambda }_{\text{fusion}}\mid H_0),\hfill \end{array}$$ (8)

where β is a threshold on λ_fusion that determines the operating point on the ROC curve. By varying the value of the threshold β, these Pd_fusion(β) and Pf_fusion(β) values trace the entire decision-fusion ROC curve.

One can use the ROC curve to quantify classification performance by calculating summary metrics of the curve. Certain performance metrics have more significance in a clinical setting than others, especially when high sensitivity must be maintained. This study used two clinically interesting summary metrics of the ROC curve: The area under the curve (AUC), and the normalized partial area under the curve (pAUC) above a certain sensitivity value.⁴⁹ For this study, we set the sensitivity value true positive fraction (TPF) =0.90 for pAUC to reflect that diagnosing breast cancer at high sensitivities is clinically imperative. We used the nonparametric bootstrap method ⁵⁰ to measure the means and variances of the AUC and pAUC values as well as to compare metrics from two models for statistical significance.

D. Genetic algorithm search for the optimal threshold set

The selection of the likelihood-ratio threshold values is important to maximize performance of the fused classifier. Threshold values very far from the best values often lowered the fused classifier's performance to near chance levels. A genetic algorithm searched over the likelihood-ratio threshold values for each feature to select a threshold set that maximized the desired performance metric or figure of merit (FOM),

$${\tau }_{\text{optimal}}=\mathrm{argmax}\mathrm{FOM}\left[{\lambda }_{\text{fusion}}(u;\tau )\right],$$ (9)

where the FOM is either AUC or pAUC, u is the set of local decisions, and τ is the set of feature-level likelihood-ratio thresholds. The fitness function of the genetic algorithm was set to the FOM in order to maximize the FOM value. We optimized for cross-validation performance the following genetic algorithm parameters: The number of generations, population size, and rates of selection, crossover, and mutation.

E. Decision fusion with cross-validation

We used k-fold cross-validation (k=100) to estimate the ability of the classifiers to generalize on our data sets. For each fold, a new model was developed, i.e., the likelihood ratio was formed on the k−1 subsets (99% of cases) used as training samples, and the genetic algorithm searched over the thresholds to maximize the performance metric on these training samples. Once the best thresholds had been found on the training set, they were then used to evaluate the algorithm on the one subset (1% of cases) withheld for validation. The resulting local decisions were then combined into the fused validation likelihood ratio λ_test,fusion, as in Eq. (6). The process was then repeated k times by withholding a different subset for validation, such that all cases are used for training and validation while simultaneously ensuring independence between those subsets.

Compiling all λ_test,fusion values at the end of the cross-validation computations created a distribution of λ_test,fusion(X) of the test cases. We constructed an ROC curve from the λ_test,fusion(X) values, as in Eq. (8), in order to measure the classification performance of the decision-fusion classifier with k-fold cross-validation.

F. Using decision fusion in a diagnostic setting

Once the model has been fully trained and validated, it can similarly be applied to new cases by setting all of the existing data to be the training data and applying the new clinical case as a new validation case. The decision-fusion algorithm would recommend to the physician either a biopsy with a malignant classification or short-term follow-up with a very likely benign classification.

G. Other classifiers: Artificial neural network and linear discriminant

We compared the classification performance of the decision fusion against both an ANN and Fisher's linear discriminant analysis (LDA), which are well-understood algorithms and are popular breast cancer CADx research tools.

For the ANN, we used a fully connected, feed-forward error backpropagation network with a hidden layer of five nodes, implemented using the nnet package (version 7.2-20) for statistical software (version 1.12, the R Project for Statistical Computing). For the LDA, we used the Statistics Toolbox (version 5.1) of matlab® (Release 14, Service Pack 2, Mathworks Inc, Natick, MA). Both models were carefully verified against custom software previously developed within our group. We implemented our decision-fusion algorithm in MATLAB, relying specifically on the Genetic Algorithm and Direct Search Toolbox (version 2) to find the best thresholds for the likelihood ratio values.

III. RESULTS

A. Classifier performance on data set C (calcification lesions)

Figure 4 shows the validation ROC curves for the calcification data. Table I lists the classification performances of the four classifiers, while Tables II and III list the two-tailed p values for the pairwise comparisons by AUC and pAUC, respectively. The AUC-optimized decision fusion (DF-A) showed the best overall performance, with AUC=0.85±0.01, and the pAUC-optimized decision fusion (DF-P) was slightly worse with AUC=0.82±0.01. Both decision-fusion ROC curves were well above those of the LDA and ANN, both in terms of AUC (p<0.0001) and pAUC (p<0.02). None of the features were particularly strong by themselves; we ran an LDA on each feature separately, yielding on average AUC=0.53±0.03, with a maximum of AUC=0.66 for the best feature.

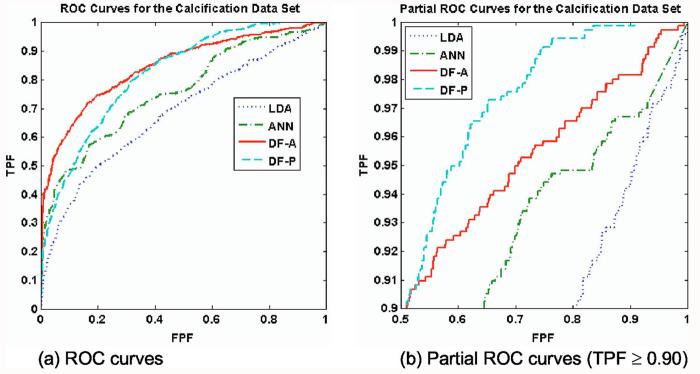
Fig. 4.

ROC curves for Data set C (calcification lesions). The classifiers' ROC curves for 100-fold cross-validation are shown. Figure 4(a) shows the full ROC curves, while Figure 4(b) shows only the high-sensitivity region (TPF≥0.90). For the calcification data set, the four classifiers yielded differing classification performance under 100-fold cross-validation. Both decision-fusion curves lay significantly above the LDA and ANN curves, both in terms of AUC and pAUC. As expected, the decision-fusion classifiers achieved the highest scores of all the classifiers for their target performance metrics; DF-A attained the greatest AUC, whereas DF-P attained the greatest pAUC. The DF-P curve surpassed the DF-A curve and dominated the other curves above the line TPF=0.90. In order to gain high-sensitivity performance, DF-P sacrificed performance in the less clinically relevant range of TPF<0.90.

Table I.

Classifier performance on Data set C (calcification lesions). The table shows the AUC and pAUC values for the ROC curves of the four classifiers under 100-fold cross-validation. The performance values exhibited a wide range. The DF-A scored the best for AUC, while DF-P scored highest for pAUC, as expected. The decision-fusion curves soundly outperformed both the ANN and LDA in terms of pAUC.

Classifier	AUC	pAUC
DF-A	0.85±0.01	0.28±0.03
DF-P	0.82±0.01	0.38±0.02
ANN	0.76±0.01	0.14±0.02
LDA	0.68±0.01	0.09±0.06

Table II.

P values for AUC comparisons for Data set C (calcification lesions). The confusion matrix shows the p values for the pairwise comparisons of the classifiers' AUC values. All pairwise comparisons were statistically significant.

	DF-A	DF-P	ANN	LDA
DF-A		0.018	<0.0001	<0.0001
DF-P			0.0001	<0.0001
ANN				<0.0001
LDA

Table III.

P values for pAUC comparisons for Data set C (calcification lesions). The confusion matrix shows the p values for the pairwise comparisons of the classifiers' pAUC values. All pairwise comparisons were statistically significant.

	DF-A	DF-P	ANN	LDA
DF-A		0.0084	0.018	<0.0001
DF-P			0.0001	<0.0001
ANN				0.016
LDA

The DF-P curve (pAUC=0.38±0.02) crossed the DF-A curve (pAUC=0.28±0.03) at the line TPF = 0.9. In order to gain high-sensitivity performance, DF-P sacrificed perfor- mance in the less clinically relevant range of TPF<0.9. The DF-A beat the DF-P in terms of AUC (p=0.018) but lost in pAUC (p<0.01). Both decision-fusion classifiers greatly outperformed the both the ANN (pAUC=0.14±0.02) and LDA (pAUC=0.09±.06) in terms of pAUC.

B. Classifier performance on data set M lesions (mass lesions)

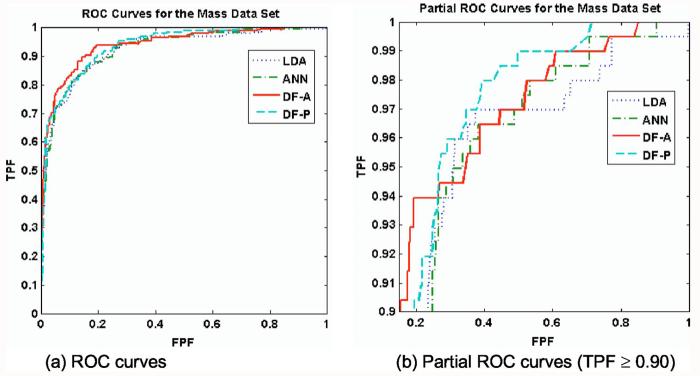
Figure 5 shows the validation ROC curves of the classifiers for the mass data set. Table IV lists the classification performances of the four classifiers, whereas Tables V and VI list the p values for the pairwise comparisons by AUC and pAUC, respectively. For this data set, all the classifiers had higher but very similar performance, with AUC ranging from 0.93±0.01 (LDA) to 0.94±0.01 (DF-A). With the exception of DF-P (p=0.50), the DF-A nonetheless significantly outperformed both the LDA (p=0.021) and the ANN(p=0.038) in terms of AUC. The LDA, ANN, and DF-P curves were all very similar, for both AUC (p>0.10) and pAUC (p>0.10). Figure 5(b) shows the ROC curves in the high sensitivity region above the line TPF = 0.90. The classifiers pAUC values ranged narrowly from 0.57±0.07(ANN) to 0.67±0.05 (DF-P), all close enough to show no statistically significant differences (p>0.10). However, the DF-P did have a higher specificity than the LDA at both 98% sensitivity (0.37±0.10 vs. 0.13±0.13, p=0.04) and at 100% sensitivity(0.34±0.08 vs. 0.09±0.12, p=0.03). The DF-P curve passed the DF-A curve approximately at the line TPF= 0.90 and yielded a slightly higher pAUC (0.67±0.05 versus 0.63±0.07), although this improvement was not statistically significant (p=0.48).

Fig. 5.

ROC curves for Data set M (mass lesions). For the mass data set, all classifiers had high levels of classification performance. The DF-A and DF-P achieved the highest AUC and pAUC, respectively. In terms of AUC, the DF-A outperformed both the ANN and LDA (p=0.038 and 0.021, respectively). In (b), the DF-P curve had slightly more partial area than the other curves. Despite having statistically equivalent partial areas, the DF-P had a greater specificity than the LDA at high sensitivities TPF=0.98 (p=0.03).

Table IV.

Classifier performance on Data set M (mass lesions). The table shows the AUC and pAUC values for the ROC curves of the four classifiers under 100-fold cross-validation. All four classifiers performed very similarly on this data set. The DF-A scored the best for AUC, whereas the DF-P scored highest for pAUC, although both were still within one standard deviation of each of the other classifiers' performances.

Classifier	AUC	pAUC
DF-A	0.94±0.01	0.63±0.07
DF-P	0.93±0.01	0.67±0.05
ANN	0.93±0.01	0.57±0.07
LDA	0.93±0.01	0.59±0.06

Table V.

P values for AUC comparisons for Data set M (mass lesions). The confusion matrix shows the p values for the pairwise comparisons of the classifiers' AUC values. The DF-A outperformed the ANN and LDA. Among the DF-P, ANN, and LDA, there were no statistically significant pAUC differences.

	DF-A	DF-P	ANN	LDA
DF-A		0.50	0.038	0.021
DF-P			0.20	0.17
ANN				0.53
LDA

Table VI.

P values for pAUC comparisons for Data set M (mass lesions). The confusion matrix shows the p values for the pairwise comparisons of the classifiers' pAUC values. None of the pAUC comparisons were statistically significant. Although pAUC scores were similar, the DF-P did have a higher specificity than the LDA at both 98% sensitivity (0.37±0.10 versus 0.13±0.13, p=0.04) and at 100% sensitivity (0.34±0.08 versus 0.09±0.12, p=0.03).

	DF-A	DF-P	ANN	LDA
DF-A		0.48	0.45	0.27
DF-P			0.14	0.12
ANN				0.46
LDA

IV. DISCUSSION

The multitude of medical data becoming available to physicians presents the problem of how best to integrate the information for diagnostic performance. Despite recent availability of this information, current CADx programs for breast cancer tend to use only one type of data, usually digitized mammogram films. Because many clinical tests provide complementary information about a disease state, it is important to develop a CADx system that incorporates data from disparate sources. However, combining disparate data types together for classification is a difficult machine-learning problem. This study used the likelihood-ratio detector and decision-fusion classifier to detect the presence of a malignancy (a signal) within medical data (noisy features). We also compared the performance of this classifier to two popular classifiers in the CADx literature, LDA and ANN, and we measured the diagnostic performance with two classification metrics, ROC AUC and pAUC. Finally, we performed these studies using two very different data sets in order to assess performance differences due to the data set itself.

Data set C (calcification lesions) had a stronger nonlinear component, indicated by the fact that the ANN AUC was much greater than the LDA AUC. The robustness of the decision-fusion algorithm is evident in its good performance on this weaker, nonlinear, and noisy data set. Decision fusion significantly outperformed the ANN and LDA on the calcification data set for both performance metrics. Figure 4 and Table I show that the biggest performance gain is in the pAUC metric, for which decision fusion doubled the performance of the other classifiers.

On Data set M (mass lesions), all four classifiers seemed to be saturated at a high level of performance in terms of both AUC and pAUC, as shown in Fig. 5 and Table IV. Performances were largely equivalent across all models, except for two trends. In terms of AUC, the DF-A outperformed both the ANN and the LDA (p=0.038 and 0.021, respectively). Although on this data set decision fusion offered only relatively modest gains in pAUC, it did achieve a significantly better specificity than the LDA at several of the highest sensitivities of the ROC curve (p<0.05).

This decision-fusion algorithm has many potential benefits over more traditional classification algorithms. Decision fusion can be optimized for any desired performance metric by incorporating the metric into the fitness function of the genetic algorithm for its search over the likelihood-ratio thresholds. This advantage has important clinical implications, as both the physician and the CADx algorithm are constrained to operate at high sensitivity. The performance metric can emphasize good performance at high sensitivities and deemphasize performance at clinically unacceptable low sensitivities. Therefore, we expect the DF-A curve to maximize AUC and the DF-P curve to maximize pAUC. The DF-P curve should fall under the DF-A curve for low FPF values but should cross the DF-A curve at the line TPF =0.90 to capture a greater pAUC value. Figures 4 and 5 show evidence that the DF-P did optimize pAUC. The DF-P ROC curves crossed the DF-A curves at the line TPF=0.90, and do in fact have a larger pAUC value than the DF-A curves. Another advantage is that decision fusion is robust and can recover from noisy weak features. The likelihood-ratio classifier passes information about the strength or weakness of a feature to the decision fuser, which adjusts the influence given to that feature. This feature-strength information is the ROC operating point (sensitivity and specificity) determined by the likelihood-ratio threshold that was found by the genetic algorithm search. Figure 3 shows a schematic of this information flow from the individual features to the decision fuser. The robustness of the algorithm also suggests that decision fusion may be able to reach the asymptotic validation performance with fewer data. This is important for most medical researchers who are starting to collect new databases and for any databases that are expensive to collect. Because our decision-fusion technique needs to estimate only one-dimensional PDFs, which require much fewer data points than multidimensional PDFs, decision fusion needs many fewer data points for training. For this reason, the decision-fusion algorithm may be able to handle typical clinical data sets with missing data, as shown in previous work with decision fusion.⁴⁴

Drawbacks of the decision-fusion algorithm include losing potentially useful feature information by reducing the likelihood-ratio values of the features to a binary value. Although the algorithm loses some feature information in this step, it recovers by optimally fusing the remaining binary feature information from that point forward. In the ideal case, if the true underlying multivariate distribution of the data happens to be known or can be estimated with a high degree of confidence, then the Bayes classifier can take this information into account and is theoretically optimal. However, since the true underlying distribution is almost never known in practice, decision fusion is a good alternative method, especially for small and noisy data sets.

V. CONCLUSIONS

We have developed a decision-fusion classification technique that combines features from heterogeneous data sources. We have demonstrated the technique on both a data set of two different breast imaging modalities and a data set of human-extraced versus computer-extracted findings. With our data, decision fusion always performed as well as or better than the classic classification techniques LDA and ANN. The improvements were all significant for the more challenging Data set C, but not always significant for the less challenging Data set M. Such a statement may not reflect the full diversity of these data sets, which differ in many respects, including linear separability, numbers of cases and features, and feature correlations. Future work will explore the contribution of such factors in order to understand the full potential and limitations of the decision-fusion technique. In conclusion, the decision-fusion technique showed particular strength in the task of combining groups of weak noisy features for classification.