Nuclear Pore Complex Number and Distribution throughout the Saccharomyces cerevisiae Cell Cycle by Three-Dimensional Reconstruction from Electron Micrographs of Nuclear Envelopes

Abstract

The number of nuclear pore complexes (NPCs) in individual nuclei of the yeast Saccharomyces cerevisiae was determined by computer-aided reconstruction of entire nuclei from electron micrographs of serially sectioned cells. Nuclei of 32 haploid cells at various points in the cell cycle were modeled and found to contain between 65 and 182 NPCs. Morphological markers, such as cell shape and nuclear shape, were used to determine the cell cycle stage of the cell being examined. NPC number was correlated with cell cycle stage to reveal that the number of NPCs increases steadily, beginning in G₁-phase, suggesting that NPC assembly occurs continuously throughout the cell cycle. However, the accumulation of nuclear envelope observed during the cell cycle, indicated by nuclear surface area, is not continuous at the same rate, such that the density of NPCs per unit area of nuclear envelope peaks in apparent S-phase cells. Analysis of the nuclear envelope reconstructions also revealed no preferred NPC-to-NPC distance. However, NPCs were found in large clusters over regions of the nuclear envelope. Interestingly, clusters of NPCs were most pronounced in early mitotic nuclei and were found to be associated with the spindle pole bodies, but the functional significance of this association is unknown.

INTRODUCTION

Nuclear pore complexes (NPCs) are organelles embedded in the nuclear envelope of eukaryotic cells whose major function is to facilitate the bidirectional exchange of materials between the nucleoplasm and the cytoplasm (reviewed Rout and Wente, 1994; Davis, 1995). In vertebrate cells, NPCs are cylindrical structures with a diameter of ∼120 nm, a thickness of ∼70 nm, and a mass of approximately 124 MDa (Rout and Wente, 1994; Davis, 1995). In the budding yeast Saccharomyces cerevisiae, the NPC is somewhat smaller, measuring approximately 97 nm in diameter. The yeast NPC has been highly enriched and this preparation was found to contain several NPC protein components called nucleoporins and upward of 80 additional peptides that are candidate nucleoporins (Rout and Blobel, 1993). The completion of the yeast genomic sequence should greatly facilitate the discovery of the genes that encode these proteins because limited protein sequence data can be quickly matched to yeast genes that may encode the sequence. Several of these genes have homologues in vertebrates and are likely to encode proteins that will be conserved in all NPCs (Davis, 1995). Despite these advances in the study of NPCs, little is known about the mechanism and dynamics of NPC assembly.

In vertebrate cells, NPC assembly occurs during the reformation of the nuclear envelope after mitosis and during interphase (Maul et al., 1971, 1972). It is not clear whether the same mechanism is used during these two periods of assembly. The in vitro analysis of NPC assembly has been largely pursued by using extracts from Xenopus oocytes, which contain stockpiles of components. Extracts from these cells will assemble NPCs into cytoplasmic membranes, termed annulate lamellae. Some of the nucleoporin and cofactor requirements for this assembly process have been identified (Macaulay and Forbes, 1996). Furthermore, some nucleoporins have been identified in subcomplexes that are thought to be precursors to assembled NPCs (reviewed in Davis, 1995).

Unlike vertebrate cells, yeast cells have a closed mitosis, in that the nuclear envelope remains intact during mitosis and throughout all stages of the cell cycle (Byers, 1981). It is presumed that NPC assembly in yeast occurs by insertion of NPCs into intact nuclear envelopes. The mechanism of this assembly event is unknown in S. cerevisiae. Mutations in genes encoding nucleoporins give rise to various ultrastructural phenotypes, as detected with the electron microscope, such as tight clustering of NPCs associated with nuclear envelope anomalies or the formation of a membrane cap over the cytoplasmic face of the envelope (reviewed in Rout and Wente, 1994; Doye and Hurt, 1995). The mutant strains exhibiting these morphological defects also display defects in NPC transport functions, so that it is unclear whether the observed morphological defects arise from improper NPC assembly or result from a defect in NPC function unrelated to assembly.

However, information concerning the assembly of NPCs in yeast cells is available. Cells depleted for the nucleoporin Nsp1p fail to form new NPCs, but the existing NPCs remain intact (Mutvei et al., 1992). Furthermore, a particular mutation in the nucleoporin Nic96p blocks NPC assembly at a restrictive temperature, and proteins that interact with Nic96p may be important in NPC assembly (Zabel et al., 1996). Nonetheless, the study of NPC assembly in S. cerevisiae could benefit from a thorough description of NPC number and distribution. Some general information pertaining to the number of NPCs has been obtained by freeze–fracture analysis of the nuclear envelope (Moor and Mühlethaler, 1963; Jordan et al., 1977), which offered some insight into changes in NPC number during the cell cycle. However, the use of freeze–fracture analysis is limited because the state of the entire nucleus is inferred from the region that is revealed in a fracture plane. In addition, other useful morphological markers that would reveal cell cycle stage are hard to assess in freeze–fracture replicas.

We have used computer-assisted three-dimensional (3D) reconstruction of the nuclear envelopes from serial thin sections of 32 yeast cells to analyze the number and distribution of NPCs at four distinct stages of the cell cycle. We report that both the number of NPCs and the surface area of the nuclear envelope increase throughout the cell cycle but at different rates, so that the density of NPCs peaks in S-phase cells. We also analyzed the distribution of NPCs over the surface of the nuclear envelope and found that NPCs are not equidistant from one another, but occur in clusters of higher density. Interestingly, the large clusters of NPCs in mitotic cells appear to be associated with the spindle pole body (SPB), the other nuclear-envelope–embedded organelle.

MATERIALS AND METHODS

Strain and Cell Culture

The S. cerevisiae strain S288c (genotype, a, gal2; source, R.K. Mortimer, University of California, Berkeley) was grown in YEPD (Sherman, 1991) at 30°C in a shaking water bath. Cells were harvested in midlogarithmic phase at a density of 1–5 × 10⁶ cells/ml.

Electron Microscopy

Cells were prepared for thin sectioning and electron microscopy as previously described in Winey et al. (1995). Briefly, cells were grown to midlogarithmic phase and collected onto a filter by vacuum filtration. The resulting yeast paste was transferred to sample holders and frozen in a Balzers HPM10 high-pressure freezer. The frozen cells were then freeze substituted in 0.1% tannic acid in acetone at −80°C for 4 d and then fixed in 2% osmium tetroxide in acetone at −20°C for 1 d and at 4°C overnight. Fixed samples were rinsed in acetone, gradually warmed to room temperature, and embedded in Spurrs resin (Polyscience, Warrington PA) for routine microscopy. Serial sections with a nominal thickness of ∼60 nm were cut by using a Reichert Ultracut E microtome and collected on Formvar-coated slot grids (1 × 2 mm). The sections were poststained with 2% uranyl acetate in 70% methanol for 5 min followed by aqueous lead citrate for 3 min.

Section thicknesses were approximated by the reflected color of the sections during microtomy, but we then derived an average section thickness for each of the two sectioning sessions on the microtome. Only nuclei that were nearly round in cross-section were used for this calibration. For each such nucleus, we determined the mean diameter of the nucleus at the largest section and the number of sections required to pass through the nucleus. If the nucleus were a sphere, the section thickness would be the diameter divided by the number of sections. If we assume that these nuclei were spherical on average, then an average section thickness can be derived from the mean of the diameter divided by the number of sections. Average section thicknesses, 53 and 60 nm, were determined for each of the two separate sectioning sessions and were used as the section thicknesses for each of the nuclei imaged from their respective sessions.

For freeze–fracture analysis, cells were either high-pressure-frozen or plunged into liquid propane just above its freezing point (Ding et al., 1993). Freeze–fracture replicas of the frozen samples were prepared in a BAL-TEC BAF 060 freeze etch system. Samples were fractured at −112°C and shadowed with 2 nm of Pt/C at an angle of 45° followed by 20 nm of C at 90°. Replicas were cleaned in 7.8% (wt/vol) potassium dichromate and 33% (vol/vol) sulfuric acid. The surface density of NPCs (NPCs/μm²) was determined from images of the nuclear envelopes of 36 cells. NPCs were counted on negatives within a circle centered over the optimally shadowed portion of the nuclear envelope, such as the top or bottom of the nucleus. The circle encompassed 0.88 μm² of the nuclear envelope as determined from the magnification and by assuming that the enclosed portion of the nuclear envelope represents a segment of a sphere with a radius of curvature of 0.8 μm. This radius is based on the data derived from the reconstruction of the nuclei from images of serial thin sections described below.

Sections or replicas were viewed in a Philips CM10 electron microscope (Philips Electronic Instruments, Mahwah, NJ) operating at 80 kV as previously described in Winey et al. (1995). Serial micrographs were taken at an approximate magnification of 15,500–21,000× on the microscope, and true magnification was measured by using a carbon replica grating of known spacing.

3D Reconstruction and Modeling

Electron micrographs of serial sections through nuclei were digitized as previously described in McDonald et al. (1991) and Ding et al. (1993). Negatives were digitized in serial order by using a Dage 81 MTI video camera connected to a Parallax 1280 graphics device in a Microvax III computer. The data set was copied to an Iris Indigo Silicon Graphics computer, converted to UNIX format, aligned, and modeled by using software described in detail in Kremer et al. (1996).

A good alignment of the serial sections was essential for an accurate measurement of surface area and analysis of the surface density of NPCs. Unaligned images would yield a model with many surface irregularities because of the section-to-section distortions that arise during sectioning and microscopy. Such distortions are typically about 4% and range up to 10%. Correction for these distortions with general linear transformations can adjust for changes in overall magnification and rotation and for stretch along one axis. To find these transformations, programs that allow one to adjust the amount of stretch and magnification while visualizing the quality of alignment between a given pair of successive images were used (Kremer et al., 1996). These transformations relating each section to the previous one were then combined in a way that aligned all of the images to each other and eliminated any systematic trends in the alignment. Specifically, any drift in position introduced during digitization was eliminated, resulting in more nearly spherical nuclei with lower surface areas. Some final models still show some irregularity. However, the residual uncorrected distortions should not have much effect on the surface area, because the error in surface area is proportional to the square of the distortion. These transformations resulted in alignment of organelles, vacuoles, and contours of the plasma and nuclear membranes in adjacent sections.

The software program IMOD was used to trace the contours of the outer nuclear envelope and to mark the positions of the NPCs and SPBs. The positions of the NPCs were marked by manually positioned points in the center of each organelle, and a sphere was inserted into the model. SPBs were entered into the models by tracing contours around each SPB in the adjacent sections where the SPBs could be seen. The 3D reconstruction could then be rendered in various ways to display the nuclear envelope with the NPCs and SPBs marked to scale (Kremer et al., 1996).

Data Analysis

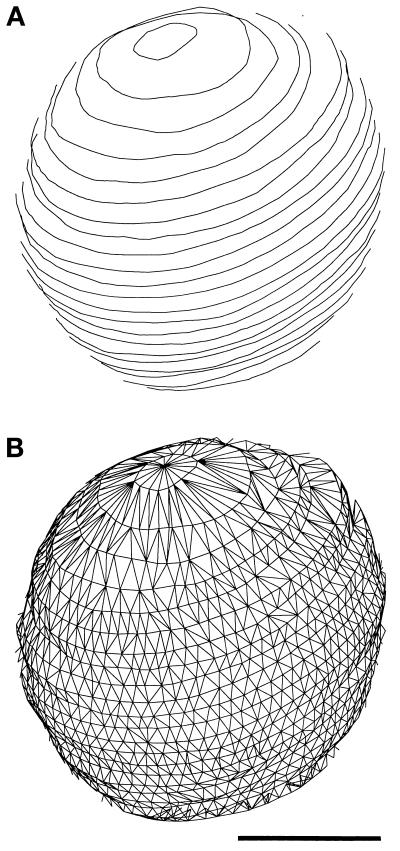
The identification of NPCs and the contours defining the nuclear membrane were used for the various quantitative analyses described below. After contours were drawn on aligned images, a mesh of triangles was constructed to completely cover the surface of the given nucleus (Kremer et al., 1996, see Figure 2). The triangles have their vertices on the contours and the area they cover defines a very small region of the surface of the envelope. The surface area of nuclear membrane was then calculated by summing the areas of all of the triangles in the mesh of triangles that covered the surface of the nucleus. An approximate or smoothed surface was not used because of the difficulties of fitting such a surface to the irregularly shaped mitotic nuclei. Surface density is calculated as the number of NPCs per unit surface area.

Figure 2.

Surface of the nuclear envelope models was defined by a mesh of triangles (see MATERIALS AND METHODS). The contours (A, front only) of the S-phase nucleus shown in Figure 1C are connected by a triangular mesh (B) covering the surface defined by the contours. Bar, 0.5 μm.

Surface density analysis (SDA) and display were carried out with newly developed tools in the IMOD software package. First, the nuclear envelope surface over which the local NPC density was analyzed was defined by the mesh of triangles technique described above (see Figure 2). An algorithm was developed to measure the distance between any two points (e.g., NPCs) on a surface (nuclear envelope). The path connecting two points was specified by the intersection between the surface and a single plane containing the two points. If the surface were a sphere, the shortest path between the two points could be found by taking the intersection between the surface and the plane passing through the two points and the center of the sphere. The same plane would also contain the normals, or lines perpendicular to the surface, at the two points (e.g., the centers of the NPCs; see Figure 5). On a nonspherical surface for which no center can be defined, the normals are not coplanar, so each normal defines a separate plane passing through the two points. The plane midway between the two planes defined by the normals was used in an initial attempt to find a path on the surface between the two points. Given the midway plane, the path was found by starting at one point, moving from one triangle defining the surface to the next, finding the intersections of the plane with the current triangle, and using that information to move to the edge of the next triangle. The procedure was reiterated until the other point was reached, and the length of the resultant path was recorded. Sometimes the path became a closed circle before the other point was reached, particularly if one point was in the bud neck. In these cases, the plane defining the path was adjusted to progressively greater angles from the plane midway between the normals until a path was found. Rarely, a path could not be found, and the distance between the two points was left undefined.

Figure 5.

Schematic representation of the SDA protocol. An individual NPC (black dots) is chosen as the point of reference and localized by a line (normal) through the center of the NPC perpendicular to the surface of the nuclear envelope (light gray). Density is measured in a series of concentric rings (medium gray, only one is shown) of defined inner and outer radii around the normal. The area within each ring is calculated and the number of NPCs within the ring is determined by measuring distances along the surface from the normal (see MATERIALS AND METHODS). With the area and NPC numbers determined, the NPC density in each ring can be derived. This analysis is reiterated for a given nuclear envelope model by using each NPC as the center with fixed ring sizes, so that the mean NPC density in a given ring can be determined and plotted as shown in Figure 6.

Having developed a general method to determine point-to-point distances (NPCs, SPBs, or triangles in the mesh being the points in this case) over the surface of irregularly shaped objects, tabulation of these distances could be used to define NPC surface densities. A graph of NPC density as a function of distance from a NPC is computed just as in a neighbor density analysis of points in a plane (McDonald et al., 1991). The value reported in each bin on the X-axis of the graph is the NPC density found in a range of distances (e.g., 0.4–0.5 μm) from a central point. Each NPC is taken in turn as a central point to measure the NPC density in a given range of distances (see Figure 5). The number of NPCs located at that range of distances from the central point is counted, and the area of the surface located there is also computed (triangles are subdivided as necessary to estimate the fraction of a triangle falling within the range of distances). These counts and areas are summed over all NPCs, having used each NPC as the center point of reference, to obtain a density for the bin at the given range of distances from the NPC. If the NPCs are randomly distributed over the nucleus, the graph will be flat and will show the overall mean density at any range of distances. A similar analysis was carried out for the NPC density at given distances from SPBs by simply using the SPBs in the models as the central point from which to tabulate the NPC densities.

To display relative NPC surface densities on the model of a nuclear envelope, a smoothed density value for each vertex on the surface of the envelope was obtained by kernel smoothing (Wand and Jones, 1995). A kernel is a function, in this case an inverted paraboloid, that is centered on the location of each NPC. At each vertex, the smoothed density is the sum of the values of all of the kernels overlapping that point. After experimenting with different kernel widths, a width was chosen so that the area covered by a kernel would contain 10 NPCs, on average. With such a width, the density at each vertex would be the sum of contributions from NPCs within about 0.5 μm of that vertex, where the contribution varies among NPCs depending on their distance from the vertex. Narrower kernels gave densities that appeared noisier and undersmoothed.

The same computations were done on a series of randomly placed points to evaluate the significance of features seen in the SDA graphs and in the smoothed density displays. In each nuclear envelope evaluated, the number of randomly placed points matched the number of actual NPCs for that model, and points were not allowed to be too close together. Points were randomly placed within a triangle on the surface that was also chosen at random. If this position was sufficiently close to any other previously placed random point, then the position was discarded with a probability based on the distance from the other point. These probabilities were adjusted so that the rising portion of the density graph for randomly selected points would match that seen for graphs derived from the analysis of actual NPC positions (see Figure 6).

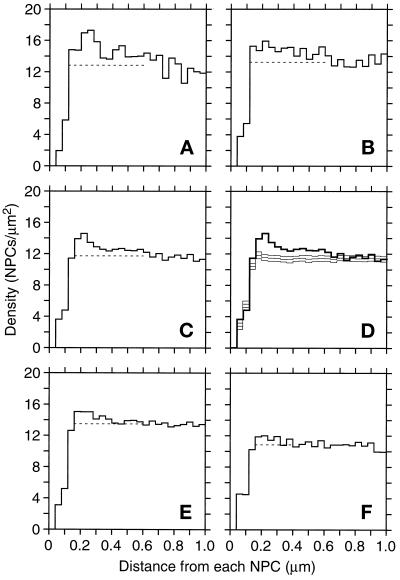
Figure 6.

NPC SDA (see MATERIALS AND METHODS) of nuclei showing NPC density (Y-axis) as a function of distance from an NPC, averaged over all NPCs in the model or sets of models. (A) SDA for the mitotic nucleus 23 (Table 1). (B) SDA for mitotic nucleus 26 (Table 1). (C) SDA for all the mitotic nuclei (Table 1, models 19–26). (D) SDA in C (thick lines) compared with results from 40 control SDAs. A control SDA was computed by randomizing NPC positions in each of the eight mitotic nuclei and summing the resulting SDAs. The three graphs in light lines are the mean and the mean plus and minus two standard deviations. (E) The cumulative SDAs for all the G₁- and S-phase nuclei (Table 1, models 1–10 and 11–18, respectively). (F) Cumulative SDA for the late anaphase nuclei (Table 1, models 27–32). The dashed lines show the mean density from 0.60 to 0.92 μm.

RESULTS

Nuclear Envelope Reconstructions

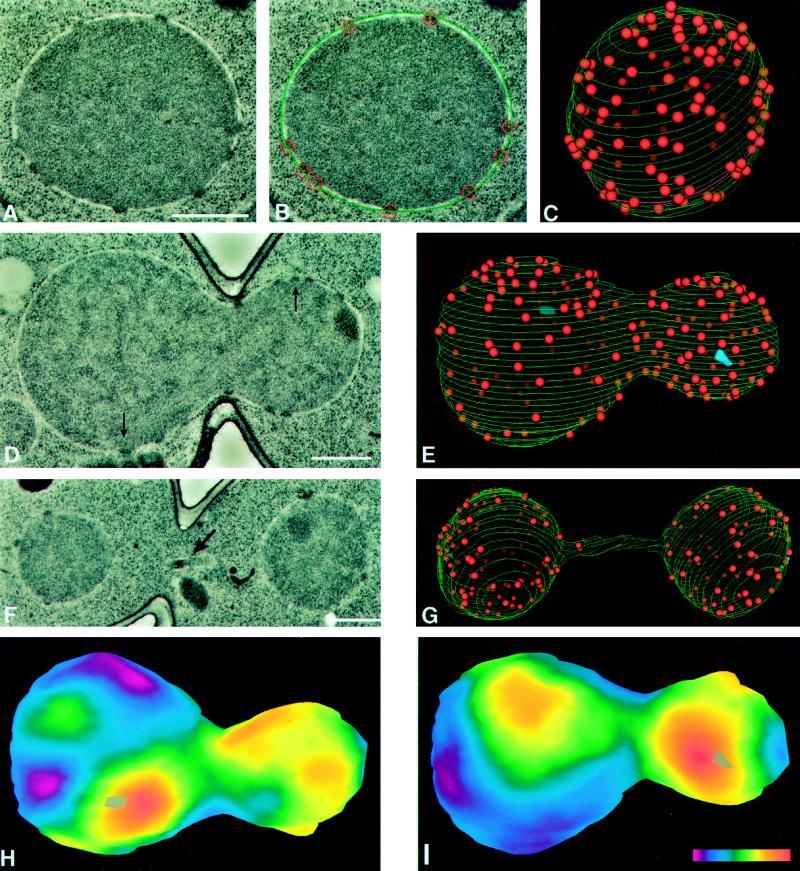
We created 3D reconstructions of entire nuclei from electron micrographs of serial thin sections to determine the number, surface density, and distribution of NPCs throughout the cell cycle of the budding yeast S. cerevisiae. As shown in an earlier study (Winey et al., 1995), fixation of the cells by high-pressure freezing followed by freeze substitution resulted in good morphological preservation of the cells. Critical for this study, the nuclear envelope exhibited smooth round profiles in cross-section, the membranes of the nuclear envelope were evenly spaced, and NPCs were clearly observed as dense bodies spanning the envelope (Figure 1A). To avoid any artificial perturbation of the cell cycle, samples were prepared from logarithmically growing cultures. Serial electron micrographs of the selected nuclei were digitized and models were constructed with the aid of the IMOD program (Kremer et al., 1996; see also MATERIALS AND METHODS for special features developed for this analysis). The models (Figure 1) have three components; nuclear envelope, NPCs, and SPBs. Tracings of the outer envelope in each section (Figure 1B) generated the lines that define the nuclear surface in the wire-basket style models (Figure 1, C, E, and G). The position of each NPC was marked by a sphere of appropriate size inserted into the model. As expected, individual NPCs spanned more than one section, because their 97-nm diameter (Rout and Blobel, 1993) exceeds the thickness of our sections (53 or 60 nm, MATERIALS AND METHODS). Detection of stained material in adjacent sections was one of the criteria used to confirm that the densely staining material was a NPC. The sphere used to mark the position of the NPC was displayed as a large circle on the section where the bulk of the NPC was found (Figure 1B) and as a smaller circle on adjacent sections. This feature, in combination with precise alignment of adjacent sections, allowed us to visualize the position of NPCs in adjacent sections and to avoid duplicate modeling of the same NPC. Finally, SPBs, which can be difficult to detect in cells prepared by the methods used herein, were unambiguously identified by their laminar morphology and/or the association of microtubules and mapped in 14 of the 32 nuclei modeled (Table 1).

Figure 1.

Model building of nuclear envelopes is carried out by using digitized electron micrographs of serially sectioned nuclei (A) on which the outer nuclear envelope and the position of the NPCs are manually indicated (B, outer nuclear envelope is green and NPCs are red). After modeling on images of every section of a given nucleus, the 3D model can be displayed (C). Perspective and a gradient of lighting with depth have been used to differentiate NPCs on the front and back surfaces of the model. The magenta-colored contour near the bottom of the model (C) represents the section shown in A and B. Various statistics from this model can be extracted using the IMOD program (MATERIALS AND METHODS, see Table 1). The spherical nucleus shown in A–C is from an S-phase cell (Table 1, cell 15) and is similar to the nuclei seen in all the G₁- and S-phase cells. Representative digitized electron micrographs of a mitotic (D; Table 1, cell 26; arrows indicate SPBs) and a late anaphase (F; Table 1, cell 32; arrow indicates a piece of the nucleus in the neck region) are shown, as well as the models of the nuclei in these cells (E and G, respectively; blue objects in E are SPBs). Two projections (H and I) of a smoothed surface density map of the mitotic nucleus in D and E, generated as described in MATERIALS AND METHODS. The projections show the front (I) and back (H) surfaces of the model with respect to the orientation shown in E. Positions of the SPBs are indicated by gray objects (one each in H and I). The color bar (I inset) shows the colors corresponding to densities from zero (magenta) to 26.7 NPCs/μm² (red). Scale bars, 0.5 μm.

Table 1.

NPC Number and Nuclear Dimensions for Individual Reconstructed Nuclei

Cell cycle stage	Model	No. NPCs	Surface area (μm2)	Density (NPC/μm2)	Volume (μm2)	SPB? (μm)a
G1	1	65	7.0	9.2	1.59
	2	70	7.5	9.4	1.64
	3	75	7.4	10.1	1.81
	4	75	6.5	11.6	1.38
	5	79	5.5	14.4	1.15
	6	91	7.1	12.7	1.63
	7	91	8.6	10.6	2.18	Y
	8	94	9.0	10.5	2.27
	9	108	9.2	11.8	2.39	Y
	10	113	6.8	16.6	1.54
		86 ± 16.0b	7.4 ± 1.15	11.6 ± 2.35	1.76 ± 0.41
S	11	95	8.4	11.3	2.15
	12	98	6.0	16.2	1.34
	13	111	6.8	16.3	1.60
	14	113	9.9	11.4	2.73	Y
	15	120	6.7	17.9	1.56
	16	125	7.1	17.6	1.61
	17	130	9.8	13.2	2.69
	18	146	11.4	12.8	3.35	Y
		117 ± 16.8	8.3 ± 1.92	14.6 ± 2.72	2.13 ± 0.72
Early mitosis	19	125	13.5	9.2	3.56	Y/2 (2.69)
	20	132	10.8	12.2	2.40
	21	134	11.5	11.6	2.64	Y/1
	22	135	13.1	10.3	3.52
	23	136	10.5	12.9	2.29
	24	140	14.9	9.4	3.96	Y/2 (3.14)
	25	156	12.4	12.6	2.92	Y/1
	26	176	13.5	13.0	3.49	Y/2 (1.96)
		142 ± 16.4	12.5 ± 1.50	11.4 ± 1.55	3.10 ± 0.62
Late anaphase	27	106	12.9	8.2	2.46	Y/2 (4.41)
	28	110	13.0	8.4	2.60	Y/2 (4.71)
	29	124	12.3	10.1	2.40
	30	145	16.6	8.6	3.76	Y/2 (6.16)
	31	155	13.6	11.4	2.62	Y/2 (5.60)
	32	182	14.2	12.8	3.16	Y/2 (3.94)
		137 ± 29.2	13.8 ± 1.62	10.0 ± 1.86	2.83 ± 0.53

^aSpindle length in μm. 

^bFor each group, the mean ± SD is shown. 

Nuclei from 32 cells at different points of the cell cycle were reconstructed and modeled. A critical aspect of the analysis was to define the stage of the cell cycle for each cell whose nucleus was modeled. Several criteria were used during examination of cells in the electron microscope to discriminate between four stages of the cell cycle, G₁, S, early mitosis, and late anaphase, that could be determined entirely by morphological criteria. The “G₁ group” was composed of mother–bud pairs that had completed cytokinesis but were still joined at the new septum. In these cells, the nuclei were spherical. We did not distinguish between mother and bud in the analysis. A representative model of a G₁ cell is shown in Figure 1C, and 10 such cells were modeled (Table 1). The “S-phase” group consisted of cells with minimal size buds. These very small buds are filled with the characteristic darkly stained vesicles described previously (Byers and Goetsch, 1975). As with the G₁ cells, the nuclei in these cells were spherical (Table 1, n = 8). A third class of cells in early mitosis forming the “early mitotic” group of eight models (Table 1) were identified as cells with the nucleus elongated through the bud neck (e.g., Figure 1, D and E). The nuclei included in the early mitotic group were just ballooning out slightly on the bud side of the neck. Both SPBs were identified in three of these nuclei, and the pole-to-pole distances were 1.96, 2.69, and 3.14 μm (taken to be spindle length; Table 1, models 26, 19, and 24, respectively), indicating that these cells are indeed in mitosis (Winey et al., 1995). Finally, the fourth class of cells were those in late anaphase, where extensive separation of the SPBs (anaphase B) has occurred such that there is a spherical nuclear body in both the mother cell and the bud (not distinguished) joined by the thin tube of envelope and spindle remnants (e.g., Figure 1G). Six such nuclei were modeled (Table 1) with spindle lengths of 3.94–6.16 μm, consistent with late anaphase (Winey et al., 1995).

The IMOD program was used to extract various parameters from the 32 models of yeast nuclei. These values include the number of NPCs per nucleus, as well as the volume and surface area of each nucleus (Table 1). Surface area was determined from a mesh of triangles over the surface of the nuclear models (Figure 2, see MATERIALS AND METHODS). By using the surface area and NPC values for each nucleus, an average NPC density (NPC/μm² of nuclear envelope) was derived (Table 1). The number of NPCs observed in models of individual nuclei ranged from 65 in a G₁ cell (Table 1, model 1) to 182 NPCs in a late anaphase cell (Table 1, model 32). The surface area of the nuclei ranged from 5.5 μm² in a G₁ cell to 16.9 μm² in a late anaphase cell (Table 1, models 5 and 30, respectively). The volume of the nuclei ranged from 1.3 μm³ in a S-phase cell to 4.0 μm³ in a mitotic cell (Table 1, models 12 and 24, respectively). The trend toward increasing numbers in later stages of the cell cycle is reversed for average NPC density per μm² of nuclear envelope, which ranged from 8.2 NPCs/μm² in a late anaphase cell to 18 NPCs/μm² in a S-phase cell (Table 1, models 27 and 15, respectively). Finally, the overall average number of NPCs/nucleus for this data set is 117 (SD = 29.7), with an average nuclear volume of 2.39 μm³ (SD = 0.78), average surface area of 10.1 μm² (SD = 3.08), and an average NPC density of 12.0 NPCs/μm² (SD = 2.66).

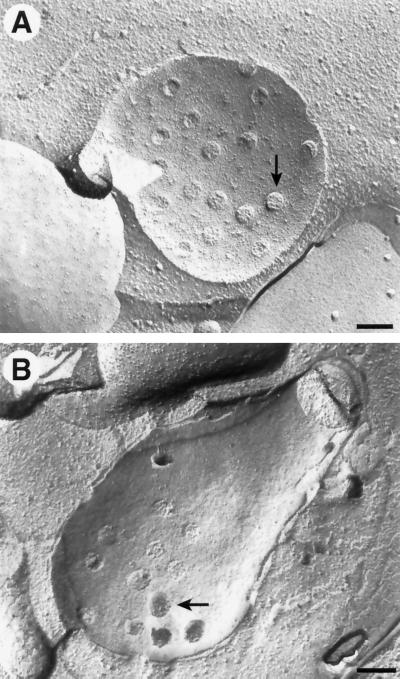
Another technique that has been used in a variety of cell types to examine NPC structure, number, and distribution is freeze–fracture analysis. Because membrane systems are frequent sites of fracture, this has been a popular technique to examine complexes embedded in membranes, such as NPCs. This technique has the advantage of sampling large regions of the nuclear envelope and of possibly showing fine structure of the organelle being examined (Figure 3). The disadvantage of freeze–fracture analysis for the type of analysis described herein is that it is usually difficult to determine the cell cycle stage of the cell whose nucleus is exposed, and it is difficult to estimate the size of the entire nucleus from the image of the fracture through part of the nuclear envelope. Nonetheless, we estimated the NPC density in fragments of 36 nuclei imaged by freeze fracture, as shown in Figure 3 (see MATERIALS AND METHODS). These cells were from all stages of the cell cycle and yielded an average NPC density of 9.4 NPCs/μm² of nuclear envelope (SD = 2.6 NPCs/μm²), which is similar to previously reported numbers (Moor and Mühlethaler, 1963). Because the sampling technique is so different, these results are not directly comparable to those from the 3D reconstructions of entire nuclei. Nonetheless, the number of 9.4 NPCs/μm² compares favorably with the average NPC density of 12.0 NPCs/μm² for the entire data set of 3D models. Furthermore, the NPC densities observed in the segments of the 36 nuclear envelopes imaged by freeze–fracture analysis corresponded to the range of NPC densities that were observed in areas of 32 nuclei modeled in 3D (Table 1). This result suggests that the NPC numbers presented herein are reliable because they can be derived by two independent techniques, indicating that we probably did not miss significant numbers of NPCs, if any, in the serial reconstructions.

Figure 3.

Freeze–fracture images of the nuclear envelope (see MATERIALS AND METHODS) from two different (A and B) cells, where B appears to be a mitotic nucleus. The position of a few NPCs is indicated by arrows. Bars, 0.2 μm.

Cell Cycle Trends

The selection of the 32 cells for modeling on the basis of their stage in the cell cycle allows us to derive average values for the different parameters described above at each of the cell cycle stages. Roughly equivalent numbers of nuclei were modeled for each of the four cell cycle stages (G₁, n = 10; S, n = 8; early mitosis, n = 8; late anaphase, n = 6). The values for the parameters were averaged within each cell cycle group, and the standard deviations were derived (Table 1). To complete the cell cycle by comparing results between late anaphase and G₁ nuclei, we have divided the anaphase numbers by two (anaphase/2) for some analyses. Because these late anaphase nuclei will give rise to two G₁ nuclei by karyokinesis, the anaphase/2 bin may approximate the lowest values that might be expected in G₁ cells.

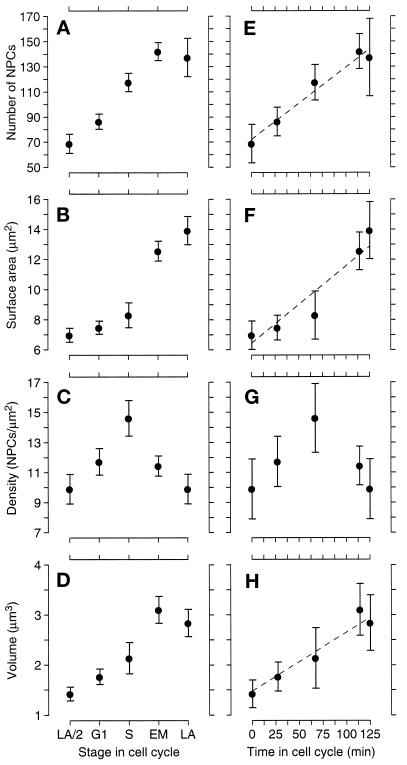
Figure 4 consists, in part, of graphs of these averages versus cell cycle stage. Figure 4A shows the change in average NPC number in the four cell cycle classes plus the anaphase/2 numbers. As expected, the G₁ class clearly has the lowest number of NPCs. The anaphase/2 numbers show that there is some increase in NPC number from late anaphase to G₁, which could occur during late anaphase, early G₁, or both. The average number of NPCs is higher in S-phase and even higher in early mitotic cells (G₁ versus S, p < 0.001; S versus early mitosis, p < 0.01; one-tailed t test), but the number of NPCs is approximately the same in the early mitotic and late anaphase cells. Interestingly, the volume of the nucleus follows a similar trend (Figure 4D), with a steady increase from anaphase/2 to early mitotic nuclei but no increase from the mitotic to late anaphase nuclei. However, the largest change in volume occurs from the S-phase group to the early mitotic group (anaphase/2 versus G₁, p = 0.09; G₁ versus S, p = 0.09; S versus early mitosis, p = 0.006; one-tailed t tests). The early mitotic and late anaphase nuclei are nearly twice the volume of the G₁ nuclei and are about the same as each other despite the contortions of the envelope during mitosis (see Figure 1 for examples). The nuclear envelope surface area increases throughout the cell cycle, but unlike the NPC number, the greatest increase is between the S and early mitotic classes of cells, and smaller increases are observed between the G₁ and S classes and the early mitotic and late anaphase classes (Figure 4B). The different trends in NPC number and envelope surface area combine to make for very interesting behavior of NPC density (Figure 4C), which is highest in the S-phase class cells (G₁ versus S, p = 0.03; S versus early mitosis, p = 0.01; two-tailed t test). This trend could be inferred by seeing that the NPC numbers rises steadily from G₁- to S-phase nuclei (Figure 4A), whereas the nuclear envelope surface area increases mainly between the S and early mitotic groups (Figure 4B).

Figure 4.

Graphs of mean NPC number (A), nuclear surface area (B), NPC density (C), and nuclear volume (D) versus cell cycle stage. The stages G₁, S, early mitotic (EM), and late anaphase (LA) are defined in the text. The category LA/2 is defined by dividing the value for the late anaphase cells in two to facilitate comparison between the late anaphase and the G₁ nuclei and is not significantly different from analyzing each lobe of the LA nuclei individually. The bars show 74% confidence limits, so that nonoverlapping bars indicate that the means are significantly different (p ≤ 0.05, one-tailed t test). These five cell cycle stages are also plotted (E–H) by their relative position in the cell cycle as defined by Yeh et al. (1995; see also RESULTS). For ease of plotting, the LA/2 numbers were put at time 0, and the points are then G₁, S, EM, and LA, from left to right. The error bars are 95% confidence intervals to facilitate comparison between the means and the straight lines.

The observations that the numbers of NPCs in late anaphase cells were similar to those in early mitotic cells and that late anaphase cells exhibited relatively low NPC density led us to examine whether undercounting of NPCs in the narrow connecting region of the late anaphase nuclei could account for both of these results. In fact, this region of the late anaphase nuclei has the very low mean density of 5.4 NPCs/μm² (compare to Table 1). It seemed possible that the number of NPCs was underestimated because of difficulty in detecting NPCs in the longitudinal view of the narrow portion of the nuclear envelope connecting the separating nuclear masses (see Figure 1, F and G). However, three such late anaphase cells analyzed in another study (Winey et al., 1995) had been cross-sectioned through the entire neck and the determination of NPC number was unambiguous when these cells were examined. The cells were found to contain 4, 6, and 9 NPCs in this region, whereas the six anaphase cells collected for this study have 2, 2, 3, 7, 11, and 12 NPCs in this region. The means of these two groups of cells match quite well (6.3 versus 6.2). Therefore, we consider the number of NPCs in the sample set collected from the longitudinally sectioned cells presented herein to be accurate.

Another possible explanation for the similarity between the NPC numbers in the early mitotic and late anaphase nuclei could be that these two cell cycle stages are not separated by much time in the cell cycle, so that we would not expect to see much change in the NPC number. The relative progression through the cell cycle between the bins that we have defined cannot be determined directly from our electron micrographs. However, we have correlated the stages of the cell cycle we examined with the kinetics of the cell cycle as determined by the examination of living cells with time-lapse and digital- and video-enhanced differential interference contrast microscopy. In this study the cell cycle time was an average of 125 min (±9 min), and our early mitotic nuclei correlate to stage IV and our late anaphase nuclei correlate to stage Va, which are only separated by approximately 12 min (Yeh et al., 1995; K. Bloom, personal communication). Although the distinction between G₁- and S-phase in Yeh et al. (1995) is not as clearly defined as the mitotic stages, our attempt to fit our data to the cell cycle clock defined by Yeh et al. (1995) is shown in Figure 4, E–H. A line indicating the doubling of the given value at a constant rate during the cell cycle has been placed on these graphs and shows a good fit for the increase in NPC number (Figure 4E) and nuclear volume (Figure 4H) but not for nuclear surface area (Figure 4F), which contributes to the behavior of the NPC density (Figure 4G). In conclusion, the lack of increase in NPC number and nuclear volume from the early mitotic to late anaphase stages appears to be a consequence of the close temporal proximity of these two stages and is consistent with a uniform increase of these parameters through the cell cycle.

NPC Distribution over the Nuclear Envelope

The high-resolution 3D models of nuclei and their NPCs proved useful not only for the analysis of general trends in NPC numbers and nuclear envelope accumulation during the cell cycle but also for the examination of the distribution of NPCs over the surface of the nuclear envelope. We first wished to determine whether NPCs were evenly dispersed over the surface of the nuclear envelope. To do this, an algorithm (see MATERIALS AND METHODS) was developed to determine a smoothed relative surface density of NPCs. These relative densities can be displayed in false color on the surface of the nuclear envelope model as shown in Figure 1, H and I. The mitotic nucleus shown in Figure 1 has a wide range of smoothed densities from 1.3 NPC/μm² to 26.7 NPC/μm². All nuclei showed similarly irregular distributions with at least a fourfold range of smoothed densities (Table 2). Thus, NPCs are not evenly distributed or regularly spaced apart from one another over the surface of the nuclear envelope.

Table 2.

SDs of smoothed density in modeled nuclei compared to SDs in 500 randomizations of each model

Cell cycle stage	Model	Smoothed densitiesa			%b
		Min	Max	SD
G1	1	2.1	19.9	3.5	5.2
	2	0.3	21.5	4.1	0.4
	3	0.2	18.3	4.8	0.0
	4	4.0	22.0	3.3	66.0
	5	3.3	33.3	5.2	8.6
	6	2.6	29.6	5.8	0.0
	7	0.4	19.8	3.9	10.6
	8	2.2	22.0	4.1	3.2
	9	1.6	24.0	4.1	11.8
	10	1.7	28.9	5.1	8.2
S	11	2.7	19.6	3.9	1.8
	12	2.8	30.9	5.9	0.8
	13	4.0	34.2	5.8	2.0
	14	2.6	27.8	4.3	3.2
	15	5.0	32.0	5.8	5.8
	16	1.9	34.5	6.5	1.0
	17	5.0	21.3	2.9	98.8
	18	2.9	22.0	3.8	29.8
Early mitosis	19	2.3	20.2	3.6	3.2
	20	0.1	25.4	5.7	0.0
	21	0.9	24.8	5.0	0.0
	22	1.1	18.7	3.7	11.8
	23	0.0	28.7	6.1	0.0
	24	0.4	19.8	4.3	0.0
	25	0.2	24.3	5.7	0.0
	26	1.3	26.7	5.8	0.0
Late anaphase	27	0.0	20.2	3.6	1.2
	28	0.6	23.6	4.8	0.0
	29	2.8	22.0	3.8	9.6
	30	1.0	17.4	3.3	2.8
	31	0.0	25.2	5.2	0.0
	32	0.0	29.3	5.2	0.0

^aSmoothed densities (NPCs/μm²) for individual nuclear models, reporting the minimal (Min) and the maximal (Max) densities, and the SD of the smoothed density. 

^bThe percentage of the SDs of the smoothed densities in 500 randomizations of each model that exceed the SD of the smoothed density of the real model. 

Because NPCs are not spread over the surface of the nucleus equidistant from one another, we endeavored to determine whether the organization of the NPCs was random or not. To do this, we used the SD of the smoothed density over the whole surface as a measure of the irregularity of the NPC distribution. For each model, the SD of the smoothed density was compared with a similar number derived from randomized data. The placement of NPCs was randomized in each of the models 500 times as described in the MATERIALS AND METHODS, and the SD of the smoothed density for each randomization was compared with the SD derived from the real data. Table 2 lists the percent of randomly generated data sets that had an SD greater than the SD of the real data set. Each of these percents estimates the probability that the actual data are equivalent to a sample from a random distribution, or in other words, the percentage is a measure of the statistical significance of nonrandomness of NPC distribution for each nucleus. The majority (n = 19) of nuclei were significantly nonrandom, having fewer than 4% of the random data sets being more irregular than the actual distribution. Another 8 nuclei had from 5.2 to 11.8% of the SDs of randomized data greater than the SD for real data, so their nonrandomness might be considered marginally significant. Only 3 nuclei showed no evidence of being more irregular than a random distribution (SD_random > SD_real, 30%, 66%, and 99%, see Table 2). The degree of nonrandomness is most striking for mitotic and late anaphase nuclei, wherein the 500 randomizations for each of 9 of 14 nuclei in these classes did not produce any single randomized model with an SD greater than that of the actual data. Although NPCs are not equidistant from one another, this analysis shows that they are also not randomly dispersed over the surface of the nuclear envelope.

Two kinds of nonrandom NPC arrangements that could contribute to the observed nonrandom, yet nonequidistant, arrangement are a preferred nearest neighbor distance and longer range clustering. In fact, such clustering is suggested by the high density of NPCs in the red regions of Figure 1, H and I. To explore NPC distribution over the nuclear envelope in more detail, SDA was developed (Figure 5, see MATERIALS AND METHODS). In SDA, ever larger concentric rings of defined radii (to the inner and outer circles that define the ring) are drawn around each NPC in a given nuclear envelope model. The NPC density found in each ring of given minimal and maximal radii is recorded, and these values are averaged over every NPC in the model (Figure 5). The data can be displayed as a graph of NPC density versus distance from the NPC (ring radii), as shown in Figure 6. The SDAs for two mitotic nuclei, model 23 and 26 (Table 1), are displayed in Figure 6, A and B, respectively. These SDAs are for a total of 136 NPCs in Figure 6A and 176 NPCs in Figure 6B.

Three trends are recognizable in these histograms. One is a region close to NPCs, up to 120 nm, that has very few NPCs, suggesting that few if any NPCs are touching each other or are very close to each other. This is easily verified by viewing the models (Figure 1). Next is a small peak of density around 240 nm, which is most obvious in Figure 6A. This small peak is suggestive of some preferred NPC nearest neighbor spacing. The SDA for another mitotic nucleus is shown to demonstrate that this feature is not necessarily evident in every model (Figure 6B). However, note that in both cases the density out to 600 nm is elevated above the dashed line that shows the average density from 600 to 920 nm. This is the third feature, a slight decline in density with distance. When an average SDA is formulated for all eight mitotic nuclei (Table 1, models 19–26), all three trends are apparent in this population (Figure 6C). This averaging makes it clear that density is elevated out to about 600 nm, which implies that NPCs occur in clusters approximately 0.5–1.0 μm across. A randomization control is shown in Figure 6D. SDAs were derived for one randomization of each of the eight mitotic nuclei and averaged. After performing 40 such averaged randomizations, the mean and SD of the density in each bin was computed. Figure 6D shows the mean SDA and the mean plus or minus two standard deviations (thin lines). In this analysis the most closely spaced NPCs were excluded so that the rising phase of the graph would match the same region of the graph of the actual data (thick lines). The SDAs derived from randomized data are basically flat from 200 nm to 1.0 μm, so the elevation of the graph from actual data out to 600 nm is clearly significant. Also, the small peak of actual density at about 200 nm is not simply an overshoot from the low density at short distances, because the randomizations have similarly low initial density without such a peak. Average SDAs for the 18 G₁- and S-phase nuclei and for the six late anaphase nuclei are presented in Figure 6, E and F, respectively. Both graphs show some elevation in density above the baseline level out to 400–600 nm, but the clustering effect is not as strong as it is for the mitotic nuclei. Randomization controls showed that these elevations, although small, were significant at a confidence level of at least 98%.

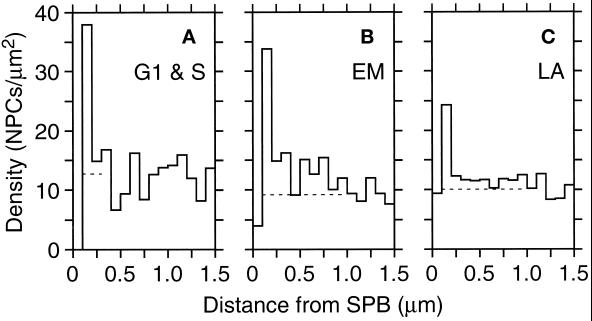
Finally, we examined the distribution of NPCs relative to the SPB, the other nuclear-envelope–embedded organelle. For this analysis, 19 SPBs were identified unambiguously in 13 cells. By using these SPBs, an SDA of NPC density around each SPB in all the models was performed (Figure 7). Like NPC SDAs, there is a small zone of exclusion around the SPB that does not contain NPCs, but then a high density of NPCs is observed just outside of that region (Figure 7, peaks in graphs). Again, mitotic cells showed the strongest effects, with two separate components (Figure 7B). The single high bin from 100 to 200 nm reflects that there are 3.3 NPCs within 200 nm of the SPB, whereas only 0.9 is expected based on the average density. In addition to this small local cluster, the elevated density out to 1.0 μm implies a more extended cluster of NPCs within that distance of the SPB. The late anaphase cells show both effects (Figure 7C), but less strongly than the mitotic nuclei, whereas the G₁ and S nuclei show only the local clustering (Figure 7A). To visualize this result, the location of the SPBs was examined on nuclear envelope models that had been pseudocolored to display relative NPC density as shown in Figure 1, H and I. As illustrated in Figure 1, H and I, all the SPBs identified in mitotic cells (n = 8) were found to be in or adjacent to a region of highest NPC density, whereas this relationship appeared for 4 of 7 SPBs in late anaphase and only 1 of 4 SPBs in G₁- or S-phase cells. The extended elevation in density seen in the SDA graphs of Figure 7 thus reflects the degree of colocalization of SPBs and regions of peak NPC density. This result suggests that nuclei in early mitotic cells may have some higher-order organization involving NPCs and SPBs.

Figure 7.

SDA of NPCs relative to SPBs as the center. The axes are as in Figure 6, but the scale on the Y-axis is different. The SDAs presented are cumulative for the G₁- and S-phase nuclei (A, n = 4 SPBs), the early mitotic nuclei (B, n = 8 SPBs), or the late anaphase nuclei (C, n = 7 SPBs) in which SPBs could be unambiguously placed. The dashed lines show the mean density from 1.0 to 1.5 μm.

DISCUSSION

We have determined the number of NPCs and the NPC distribution over the nuclear envelope in wild-type S. cerevisiae at different stages of the cell cycle by using computer-assisted 3D reconstruction of entire nuclear envelopes from electron micrographs of serial thin sections. We have found that both the number of NPCs and the surface area of nuclear envelope increase as cells proceed through the cell cycle. However, the NPC surface density (NPCs/μm² of envelope) is not constant through the cell cycle, but peaks in S-phase cells. In addition to determining the overall NPC surface density, new software tools have been developed to determine local NPC densities over the surface of the nucleus. With these tools, we have shown that NPCs are neither evenly nor randomly distributed over the nuclear envelope but that the NPCs are found in clusters. Clusters of NPCs are most striking in early mitotic nuclei, where these clusters are associated with the position of the SPBs.

NPC Assembly during the Cell Cycle

NPC assembly is clearly a cell cycle event in animal cells, in which the nuclear envelope breaks down during mitosis and is then reformed. As a result, NPCs are disassembled before mitosis and reconstructed after mitosis (Davis, 1995). NPCs are also assembled into the intact nuclear envelope of HeLa cells during interphase (Maul et al., 1971, 1972), which could be via a similar process to NPC assembly in yeast. Plotting our NPC numbers as a function of the yeast cell cycle by using a time scale based on cell cycle progression data suggests that the number of NPCs in the cells increases continuously, and nearly linearly, throughout the cell cycle. However, NPC surface density peaks in S-phase cells and then the density drops in mitotic cells. This behavior appears to occur because addition of nuclear envelope early in the cell cycle lags behind accumulation of NPCs, but later in the cell cycle more nuclear membrane accumulates leading to the drop in NPC density. Nonetheless, these data on the number of NPCs/nucleus at different points in the cell cycle can be interpreted as indicating that NPC assembly occurs continuously during the yeast mitotic cell cycle.

To accept that NPC assembly is continuous during the cell cycle, as suggested by the data presented herein, one must assume that the accumulation of NPCs results from new NPC assembly and not from increased stability of the NPCs leading to increased NPC number. We believe that the disassembly of NPCs in yeast is a slow process, if it occurs at all. Mutvei et al. (1992) blocked the de novo assembly of NPCs via the depletion of the yeast nucleoporin Nsp1p. In Nsp1p-depleted cells, NPC number and density decreases slowly through several cell divisions during which new NPCs are no longer synthesized. Apparently, preexisting NPCs are maintained but are diluted in the nuclear envelope during continued growth and cell divisions in the absence of new NPC assembly. This interpretation was also invoked by Zabel et al. (1996) to explain the decreased NPC number observed in nic96–1 cells after a shift to the restrictive temperature. Therefore, we consider the changes in NPC numbers through the cell cycle we report herein to result from the assembly of new NPCs with little or no background from NPC disassembly. Nonetheless, the demonstration that NPC assembly is continuous throughout the yeast cell cycle will not be conclusive until the assembly mechanism is understood in molecular terms and that mechanism can be assayed throughout the cell cycle.

Distribution of NPCs over the Nuclear Envelope

Analysis of the nuclear envelope models revealed that NPCs are not evenly distributed, nor are they randomly dispersed, over the nuclear envelope. Maul et al. (1971) similarly reported that NPC distribution in rat kidney cell nuclei is nonrandom, but a distributional pattern could not be identified. However, the organization that was detected herein in yeast is a modest level of clustering, in which some regions of the nucleus have higher local densities of NPCs but other regions have lower densities. This organization is most pronounced in early mitotic cells, where each lobe of a nucleus that spans the budneck has one region of high NPC density associated with a SPB. This observation suggests to us that there may be some functional significance to the clusters of NPCs. It seems possible that the clusters could be heritable, along with the SPB, into the daughter cells. Inheritance of a cluster of NPCs may serve as a founder event, ensuring that the new daughter nucleus receives a sufficient number of NPCs to function appropriately. Such a mechanism of NPC inheritance may also contribute to the very low NPC densities observed in the isthmus of nuclear envelope between the two lobes of the late anaphase nuclei. Another possibility to explain the observation of clusters includes limited dispersal of NPCs from the site(s) of assembly. However, NPCs have been shown to be quite mobile in the yeast nuclear envelope (Bucci and Wente, 1997). Finally, clustering may arise from other functional requirements in the cell, such as a need for high local transport activity between the nucleus and cytoplasm, which we do not yet recognize.

Interestingly, mutants in several yeast nucleoporins give rise to a phenotype called “clustering,” wherein the NPCs are found to be in tight clusters (reviewed in Rout and Wente, 1994; Davis, 1995; Doye and Hurt, 1995). The nuclear envelopes in these cells have been found to contain several tight clusters of NPCs, along with regions of the envelope that lack NPCs. Furthermore, these clusters have been observed to be associated with the SPB in one clustering mutant (Heath et al., 1995). It seems possible that the clustering phenotype is an exaggerated form of the normal distribution of NPCs reported herein. Clusters of NPCs have also been reported in starved cells (Moor and Mühlethaler, 1963). Further analysis of mutants and growth conditions may reveal both the basis of NPC clusters in the nuclear envelope and the function of these clusters.

Finally, little is known of the molecular process of NPC assembly in yeast. The determination of the absolute number of NPCs in individual yeast cells at distinct points in the cell cycle may help to define some aspects of NPC assembly in these cells where the molecular mechanism of NPC assembly should be accessible through genetic and biochemical analysis. Furthermore, this description of wild-type yeast cells will be important in the interpretation of mutants that can be characterized by using the techniques described herein. It is hoped that the 3D modeling procedures used herein will contribute to the analysis of yeast mutants to determine which genes are necessary in the process of NPC assembly.