Preferred Orientations of His-64 in Human Carbonic Anhydrase II

Abstract

Histidine at position 64 (His-64) in Human Carbonic Anhydrase II (HCA II) is believed to be the proton acceptor in the hydration direction and the proton donor in the dehydration direction for the rate limiting proton transfer (PT) event. While the biochemical effect of histidine at position 64 has been thoroughly investigated, the role of its orientation in the PT event is a topic of considerable debate. X-ray data of HCA II suggests that His-64 can adopt either an “in” or “out” orientation. The “in” orientation is believed to be favored for the hydration direction PT event because the N_δ of His-64 is closer to the catalytic zinc. This orientation allows for smaller water bridges, which are postulated to be more conducive to PT. In the present work, classical molecular dynamics simulations have been conducted to elucidate the role that the His-64 orientation may play in its ability to act as a proton donor/acceptor in HCA II. The free energy profile for the orientation of His-64 suggests that the histidine will adopt an “in” orientation in the hydration direction, which brings the delta nitrogen in close proximity to the catalytic zinc. When the histidine becomes protonated it then rotates to an “out” orientation creating a more favorable solvation environment for the protonated His-64. In this “out” orientation the imidazole ring releases the delta nitrogen’s excess proton into the bulk environment. After the second PT event and when the zinc bound water is regenerated the His-64 is again favored to reorient to the “in” orientation, completing the catalytic cycle.

One of the most extensively characterized enzymes that utilizes a proton transfer (PT) event is carbonic anhydrase (CA).(1–10) CA, one of the most efficient enzymes known, catalyzes the conversion of carbon dioxide to bicarbonate and an excess proton.(1, 11, 12)

$$C{O}_2+H_{2}O\leftrightarrow H^{+}+HC{O}_3^{-}$$ (1)

CA is key to the transport of CO₂ and can be found in plants, animals and certain bacteria. In humans, CA is fundamental to CO₂ transport, gluconeogenesis, ureogenesis and bicarbonate buffering.

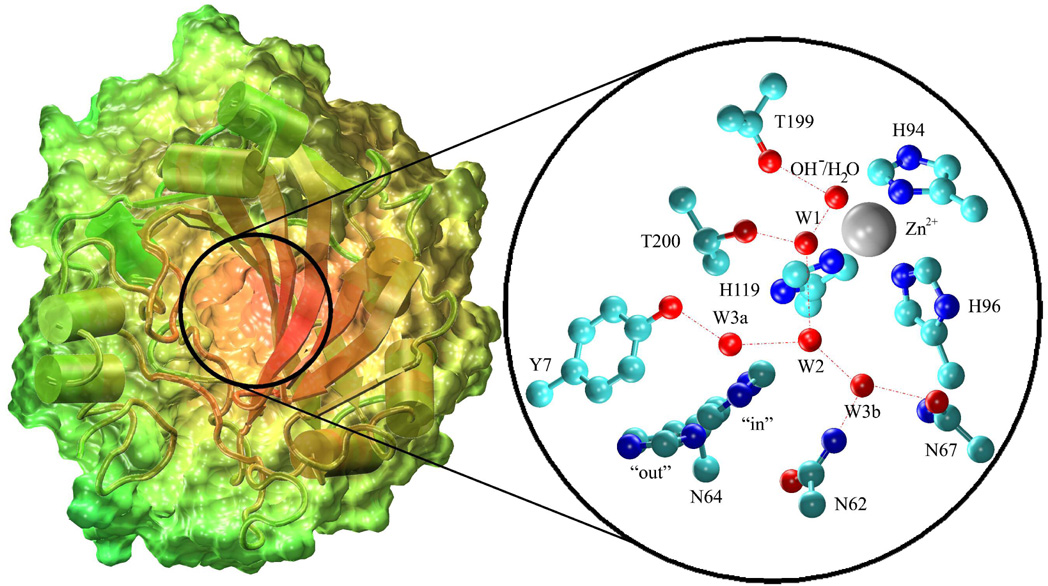
Human Carbonic Anhydrase II (HCA II) is the fastest of at least 14 CA isozymes with a maximal turnover number of 10⁶ s⁻¹.(13, 14) HCA II is a cytosolic enzyme consisting of a single polypeptide chain of 260 residues.(15) The catalytic center of the spherically shaped enzyme resides at the bottom of a conical opening that is 15 Å in diameter at the mouth and 15 Å deep.(5, 8) At the base of the conical cleft resides a zinc that is tetrahedrally coordinated to three histidines (His-94, His-96 and His-119) and a water/hydroxide (Figure 1).

Figure 1.

HCA II enzyme. This figure depicts the solvent accessible surface of the HCA II enzyme. The color scale of the enzyme is based on the distance from the center of mass of the enzyme. The subset depicts the active site of HCA II from the 2CBA(8) x-ray crystallographic data where amino acids Tyr-7, Asn-62, Asn-67, Thr-199 and Thr-200 are believed to stabilize the participating waters in the hydrogen bonding network that links the zinc bound water/hydroxide to His-64.(55, 56)

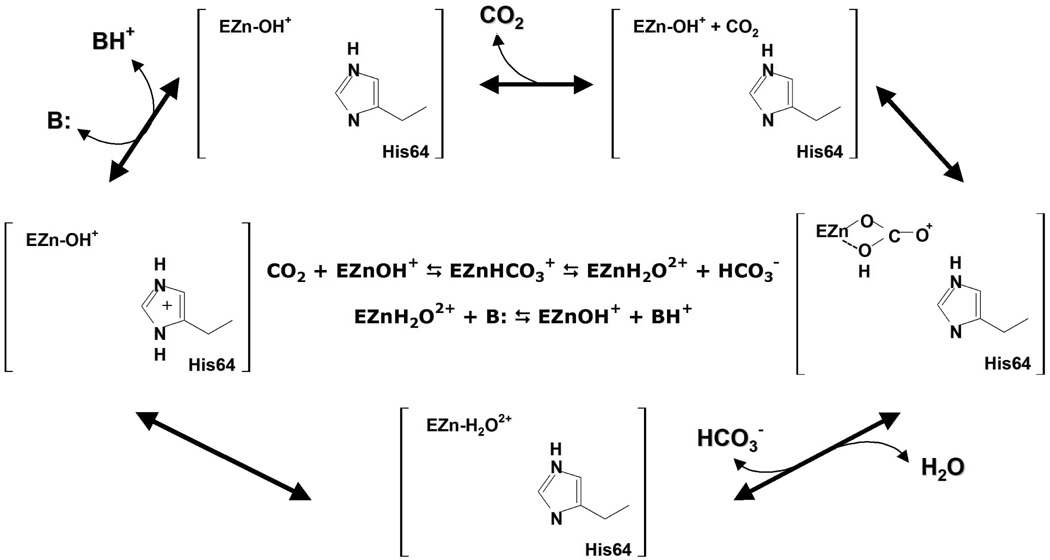
The catalysis of HCA II occurs in two distinctly separate steps referred to as ping-pong kinetics. The first step entails the nucleophilic attack of the zinc bound hydroxide by the carbonyl carbon of CO₂, generating a bicarbonate ion. The second step involves the PT between the zinc-bound water and an exogenous buffer, thereby regenerating the initial zinc-bound hydroxide species (Figure 2).(3, 12, 16, 17) The rate limiting step of catalysis is dependent on the exogenous buffer concentration and is either the PT from His-64 to the exogenous buffer at low buffer concentrations,(1) or the PT from the zinc bound water through the intramolecular water wire to His-64 at high buffer concentrations.(18) It has been suggested by both experiment and theory that the intramolecular water wire consists of 2 to 4 water molecules.(4, 5, 8, 19–23) These water molecules, which are believed to facilitate the transport of a proton 8–10 Å across the enzyme active site, are thought to be stabilized by Tyr-7, Asn-62, Asn-67, Thr-199 and Thr-200 (Figure 1).

Figure 2.

Catalytic mechanism of HCA II.(3, 12, 16, 17) The two end states studied are depicted in the bottom left two cells and labeled by EZn-H₂O²⁺ and EZn-OH⁺. E stands for the enzyme HCA II while the Zn-H₂O²⁺ refers to the zinc bound water and Zn-OH⁺ refers to the zinc bound hydroxide.

The importance of His-64 has been illuminated by mutation experiments where position 64 has been mutated to nonionizable residues, such as alanine, which lead to a 10 to 50 fold reduction in the catalytic turnover, k_cat , for CO₂ hydration.(24, 25) Subsequent studies have chemically rescued these impaired mutants with 4-methyl-imidazole, recovering up to 40% of the maximal activity observed in the wild-type (WT) system.(9, 24, 26) These mutation and chemical rescue experiments suggest that His-64 is intimately linked to the rate limiting PT event in HCA II. X-ray data reveals that His-64 adopts two orientations, labeled “in” or “out” (Figure 1).(8) It is not well-understood how the orientation of His-64 affects the rate limiting PT event, if at all.

This work presents classical molecular dynamics (MD) simulations of the fully solvated HCA II enzyme which were conducted to elucidate the role and behavior of His-64 in catalysis. Evaluation of two enzyme states was conducted to study the effects of the protonation state of His-64 and the active site on the orientation of His-64. These two states reflect the starting state in the hydration direction (zinc-bound water and a neutral His-64) and the starting state in the dehydration direction (zinc-bound hydroxide and a protonated His-64). In addition to studying different protonation states the orientation of His-64 was evaluated in both the “in” and “out” orientations. In the HCA II enzyme an integral part of the catalysis is the formation of an intramolecular water wire that connects the catalytic zinc to His-64. The ability of HCA II to form this critical water wire was evaluated for the two enzyme states and orientations of His-64. In addition, key amino acids in the active site were analyzed for their ability to stabilize the intramolecular water wire. These analyses provide a more detailed picture of the orientation of His-64 during the rate-limiting PT event at high buffer concentrations.

2. Methodology

Four systems were created to represent the CO₂ hydration/dehydration reaction in HCA II. The initial state for the hydration reaction was modeled by a zinc bound water and a neutral His-64 (EZnH₂O²⁺-His), while the initial state for the dehydration reaction was modeled by a zinc bound hydroxide and a protonated His-64 (EZnOH⁺-HisH⁺). To evaluate the role of His-64’s orientation on the reaction, each of these initial systems were subdivided into two subsystems, defined by the orientation of the His-64 residue. The starting configurations for the simulations were obtained from the 1.54 Å resolution x-ray structure (Protein Data Bank reference 2CBA).(8)

Partial Charges

To create a model that accurately represents a complex system it is crucial to adequately describe the electrostatic interactions. For classical MD simulations the electrostatic charge of an atom is represented by a point charge centered on the nuclear coordinates. In complex systems the environment in which an atom exists influences the charge density and susequetly the classical point charge counterpart. Therefore a two-layered ONIOM(27–35) method in the Gaussian 03(36) package was used to represent the HCA II system. The ONIOM method allows for a high-level electronic structure treatment on a small portion of the system without neglecting the effects of the overall system. This is crucial when dealing with enzymes, which use the total enzyme environment to catalyze a specific reaction. The two-layered ONIOM method consists of the total system and a small subset of the total system. The total system is treated with a low level of theory, while the small subset of the system is treated with both low and high level of theory. The total ONIOM energy E^ONIOM is determined by(28, 29)

$$E^{\mathit{\text{ONIOM}}}=E(\mathit{\text{high}},{\mathit{\text{Model}}}_{\mathit{\text{subset}}})+E(\mathit{\text{low}},{\mathit{\text{Model}}}_{\mathit{\text{total}}})-E(\mathit{\text{low}},{\mathit{\text{Model}}}_{\mathit{\text{subset}}})$$ (2)

where E(high, Model_subset) is the energy of the small subset plus the link atoms calculated at the high level of theory, E(low, Model_total), is the energy of the total system at the low level of theory, and E(low, Model_subset), is the energy of the small subset at the low level of theory. The nuclear coordinates for the HCA II enzyme used in the ONIOM calculations were taken from equilibrated molecular dynamics (MD) structures (described below). The density functional method B3LYP(37, 38) using the 6-31g(d) basis set was chosen as the “high” level of theory. The Model_subset system consisted of His-94, His-96, His-119, Zinc and the Zinc bound water/hydroxide (Figure 1). Hydrogen link atoms were used at the C_β site of the histidine backbone in order to fill exposed valence sites due to the truncation created at the ONIOM method boundary. The Model_total system was represented using the AMBER parm96(39) molecular mechanical (MM) force field. The MM parameters for the zinc active site were taken from previous MD simulation work.(20, 40) The Model_total system consisted of the equilibrated HCA II enzyme and solvent water molecules within a 20 Å radius from the catalytic zinc atom. The embedded charges flag was used in the ONIOM method to allow the Model_subset system to see the electrostatic charges of the Model_total system. The ONIOM (B3LYP/6-31G(d):AMBER) system was optimized to find minima describing the EZnH₂O²⁺-His and EZnOH⁺-HisH⁺ systems. Once minima were obtained, charge calculations were performed at the Hartee-Fock level of theory using the 6-31g(d) basis set. The MM point charges were determined using the restrained electrostatic potential fitting procedure(41) (RESP) in the AMBER(42) package. Residual charges were added onto the C_β of the histidine backbones to force an integer charge on the systems.

MD Setup

The Nuclear coordinates for the ONIOM RESP method calculations were taken from the first-round of equilibration MD simulations on the HCA II system. The simulations represented the EZnH₂O²⁺-His and the EZnOH⁺-HisH⁺ system, both having the His-64 in the “in” orientation. The HCA II protein and 220 x-ray waters from the 2CBA(8) x-ray structure were solvated in a cubic simulation box (L ≈ 75 Å) of modified TIP3P(43) water. A total of 13502 water molecules were added to the 4090 solute atoms for a total system size of 44596 atoms. The parm99(44) force field was used to describe the enzyme, while the parameters for the zinc active site were taken from Hoops et al.(40), and Lu and Voth.(20, 40) The modified parameters used to represent the active site are found in the supporting information. The first-round equilibration system was simulated for 250 ps in the constant NVE ensemble followed by 250 ps in the constant NPT ensemble.(45) The resulting system was then equilibrated for 1ns in the constant NVT ensemble.(45) All simulations were conducted at 298.15 K and used periodic boundary conditions with long-range Coulombic interactions calculated by Ewald summation.(46) The short-ranged nonbonded interactions and forces were subject to a 10 Å cutoff. The MD time integration step within the leap-frog Verlet integrator was 0.5 fs in all simulations. When applicable the simulations were run at 1 atm and utilized Langevin dynamics for the thermostat. The simulations were carried out using the AMBER 8 package. (42) The resulting geometries were then used as the initial geometries for the ONIOM RESP method calculations. The difference in Helmholtz free energy calculated in the current simulations is used interchangeable with differences in Gibbs free energy. This is accomplished due to the systems average volume and pressure being constant with small fluctuations about the average values as seen from the equilibration period. In the approximation of constant volume and pressure with small fluctuations about the average the differences in Gibbs and the differences in Helmholtz free energies may be directly compared.

Once new charges for the zinc active site were calculated for (His)₃-ZnH₂O²⁺ and (His)₃-ZnOH⁺ they were implemented into the previously equilibrated systems (first-round equilibration). The parameters for the active site and the new RESP charges can be found in the supporting information. The newly modified systems were then subdivided into EZnH₂O²⁺-His(IN/OUT) and EZnOH⁺-HisH⁺(IN/OUT). The “out” orientations were created by placing a harmonic restraint on the distance between the zinc and the N_δ of His-64, R_Zn–Nδ, and using a spring force constant, k , of 40 kcal mol⁻¹ Å. The four systems were then simulated for 250–500ps in the constant NPT ensemble. The resulting systems were then subjected to another round of equilibration (second-round equilibration) that consisted of 1000 steps of steepest descent and 5000 steps of conjugated gradient optimization. The optimized system was then subjected to 200 ps equilibration in the constant NPT ensemble and 2.5 ns in the constant NVT ensemble. (45) All other simulation parameters were identical to the previously conducted first-round equilibration simulations.

Biased Sampling

Sampling a free energy surface that has characteristic features with significant barriers (»k_BT) is problematic for classical MD simulations. On such a free energy surface, a classical simulation will become trapped in a local minimum if such barriers surround it. To sample the full free energy surface a biasing technique is required. With biased sampling it is also necessary to use an unbiasing technique to combine the biased sample data to create a complete unbiased data set. The biasing umbrella sampling technique and the unbiasing weighted histogram analysis method (WHAM)(47, 48) technique were used here to construct a Potential of Mean Force (PMF) along the N-C_α-C_β-C_γ dihedral reaction coordinate, ξ_dihedral. This reaction coordinate describes the rotation of the imidazole group between the “in” and “out” orientation. Between 15 to 30 harmonic restraining potentials (windows) of the form

$$U_n^{\mathit{\text{umbrella}}}\left({\xi }_{\mathit{\text{dihedral}}}\right)=\frac{k_n}{2}{\left({\xi }_{\mathit{\text{dihedral}}}-{\xi }_0^n\right)}^2$$ (3)

were used to generate the PMF. All windows used spring constants of k_n = 40 kcal mol⁻¹ rad² and spanned the range of ${\xi }_0^n=-65°\text{to}80°$. Each window was equilibrated for 250 ps followed by a data collection period of 1 to 2 ns in the constant NVT ensemble, depending on the convergence of the PMF. Convergence is considered achieved when there exists a negligible difference between a PMF calculated from the first half of the data and a PMF calculated from the second half of the data. In addition the error of the PMF must be relatively small, ≤ 0.1 kcal/mole

3. Results and Discussion

Active Site Geometries

The second-round of equilibration and subsequent umbrella sampling production runs for HCA II used the newly constructed RESP charges (supporting information) and modified parm99(44) parameters (supporting information).(20, 40) In addition to these modified parameters it was determined during the second-round of equilibration that the distance between the zinc and the zinc bound water was shorter than x-ray and ONIOM values. This shortening of the bond was most likely due to the new charge distributions. To rectify the inaccurate bond length, a modification of the spring constant or equilibrium distance was needed. In the second-round of equilibration and the umbrella sampling production runs the equilibrium distance, r_eq, was increased to 2.30 Å , which yielded a zinc to zinc bound water distance of 2.05 ± 0.09 Å. This value more closely reproduced the ONIOM results of 2.04 Å and is within the range of x-ray results of 1.99 to 2.08 Å, which were obtained over a range of pH values.(49) The zinc to hydroxide and zinc to nitrogen (His-94, His-96 and His-119) distances were not affected by the new charge distribution and resulted in good agreement with ONIOM and x-ray data.

His-64 Orientation

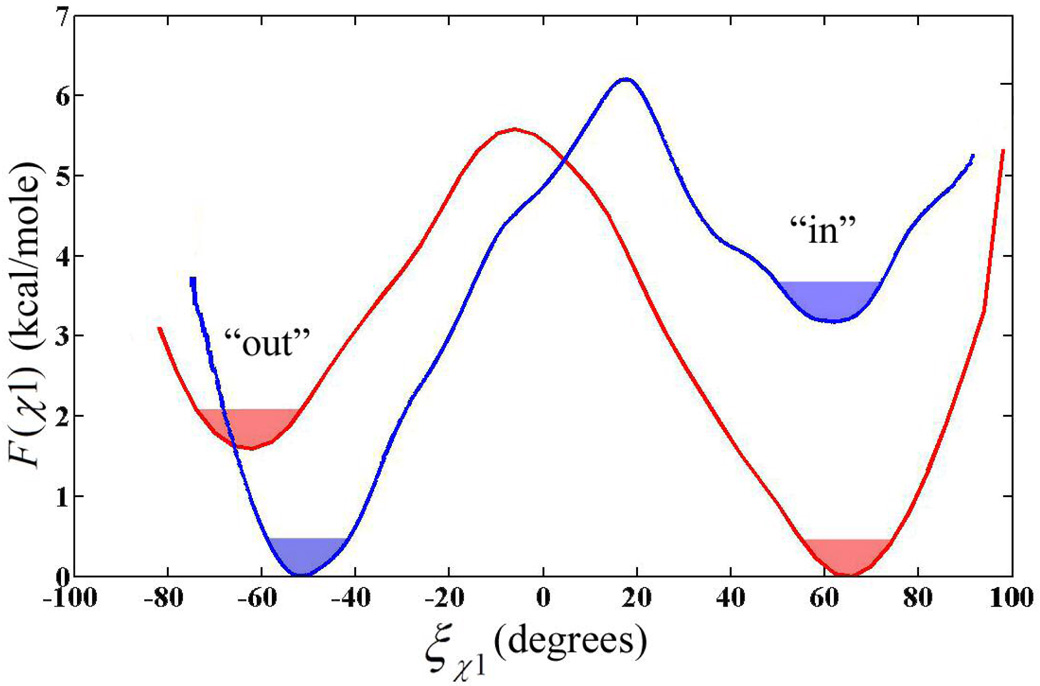
When evaluating the orientation of amino acids containing ring structures the χ1 and χ2 dihedral describes the spatial orientation of the side chain. The reaction coordinate (χ1) involves the atoms N-C_α-C_β-C_γ and describes the rotation about the C_α-C_β atoms. This dihedral and the R_Zn–Nδ distance are the primary factors in determining if the His-64 residue is in the “in” or “out” orientation. The χ2 dihedral containing the atoms C_α-C_β-C_γ-N_δ and describes the rotation about the C_β-C_γ atoms. The χ2 dihedral determines the orientation of the imidazole ring of His-64 and is often described as ring flipping. The free energy landscape as a function of χ1 and/or χ2 dictates the ability of the amino acid to sample its orientation space. The PMF for the rotation about the dihedral reaction coordinate, F(ξ_χ1) (Figure 3), provides information about the relative stability of His-64 in either the “in” or “out” orientation as well as the free energy barrier, F_b, between the two orientations. The relative distributions of the “in” and “out” orientations from the F(ξ_χ1) can be compared to x-ray data and possibly help explain why some orientations are more prevalent in the x-ray structures. Evaluating both the χ1 and χ2 dihedrals along with the R_Zn–Nδ distance will illuminate the spatial orientation of His-64 in HCA II during the hydration/dehydration reaction. The F_b from the F(ξ_χ1) can be used with transition state theory to determine the upper limit for the rate of transfer between orientations, which can be compared to the rate-limiting step. This comparison of the rates helps determine if the movement between orientations is a factor in the rate-limiting step.

Figure 3.

Free energy profile for rotation of His-64 about the χ1 dihedral angle in the EZn-H₂O²⁺-His system (red) and the EZn-OH⁺-HisH⁺ system (blue). Error for the PMF’s is less than 0.1 kcal/mole as determined by Monte Carlo bootstrap error analysis. The filled portion of the wells represents the thermally accessible region of the dihedral within k_BT/2 of the minimum.

The PMFs, F(ξ_χ1), for the EZnH₂O²⁺-His and the EZnOH⁺-HisH⁺ systems are displayed in Figure 3. For His-64 in the EZnH₂O²⁺-His system, the “in” orientation is described by the dihedral angles of −7° ≤ χ1 ≤ 100° while the “out” orientation is described by the dihedral angles of −100° ≤ χ2 ≤ −7° where the transition state region is around −7.0°. The F_b for rotation about the χ1 dihedral from “in” to “out” is 5.6 kcal mole⁻¹ with the “in” orientation being 1.6 kcal mole⁻¹ more stable. By contrast, the EZnOH⁺-HisH⁺ system’s “in” orientation is described by the dihedral angles of 17° ≤ χ1 ≤ 100° and the “out” orientation is described by the dihedral angles of −100° ≤ χ1 ≤ 17° where the transition state region is located near 17°. The F_b for rotation about the χ1 dihedral from “out” to “in” is 6.2 kcal mole⁻¹ with the “out” orientation being 3.2 kcal mole⁻¹ more stable. The F(ξ_χ1) free energy curve for the EZnOH⁺-HisH⁺ system not only has a higher F_b, but the stability of the “in” to “out” orientation is opposite of that for the EZnH₂O²⁺-His system. This suggests that the orientation of His-64 may be susceptible to long range electrostatic interactions with the active site and differing solvent environments for the two systems.

The rate at which His-64 transverses from the “in” to the “out” orientation is important in determining if this rotation plays a role in the rate limiting step of catalysis. The rate of transversal is also crucial in determining if the orientation of His-64 has time to reach equilibrium on the time scale of the rate limiting PT event. Transition state theory provides an approximate bridge between the F_b and the rate of transmission over the barrier by virtue of the formula

$$k_{\mathit{\text{TST}}}=\frac{{\omega }_0}{2\pi }{e}^{(-F_b/k_{B}T)}$$ (4)

where k_TST is the rate of transmission in the approximation of the TST limit, $\beta =\frac{1}{k_{B}T}$, where k_B is Boltzmann’s constant, T is the temperature, ω₀ is the fundamental frequency of the reactant state around its minimum, and F_b is the free energy barrier height. The fundamental frequency, ω₀, was calculated using normal mode analysis conducted on a subsystem of the HCA II enzyme. The first system consisted of residues 5, 6, 7, 63, 64 and 65 while the second system consisted of residues 3 to 8, 61 to 67 and 197 to 201. The coordinates for the normal mode systems were taken from the average structure of the 2.5 ns trajectory of the HCA II enzyme with His-64 in the “in” orientation. The α-carbons of all residues except 64 were constrained to their average positions and the system was then optimized using the steepest decent method. The optimized structure was then treated by normal mode analysis using the parm99 force field. The resulting frequencies were then analyzed for ω₀. Both the small and larger systems produced similar ω₀ values of 159.59 cm⁻¹ and 161.68 cm⁻¹, respectively. By then using equation 4, it is found that the “out” to “in” transition for the EZnH₂O²⁺-His system is over an order of magnitude faster than the “in” to “out” transition and three orders of magnitude faster than the hydration PT rate of native HCA II.(50) Conversely in the EZnOH⁺-HisH⁺ system the “in” to “out” transmission is two orders of magnitude greater than the “out” to “in” transmission and four orders of magnitude greater than the PT rate of native HCA II. This rate information suggests that the rotation of His-64 about the χ1 dihedral has ample time to reach equilibrium between PT events in HCA II for both the EZnH₂O²⁺-His and EZnOH⁺-HisH⁺ systems. Therefore using the equilibrium distribution from the F(ξ_χ1) curves becomes valid in analyzing the orientation of His-64 in HCA II on the time scale of the rate limiting PT event. Due to the transmission rates being significantly faster than the rate-limiting step of HCA II we can rule out these transmissions of His-64 as a direct factor in the rate-limiting step.

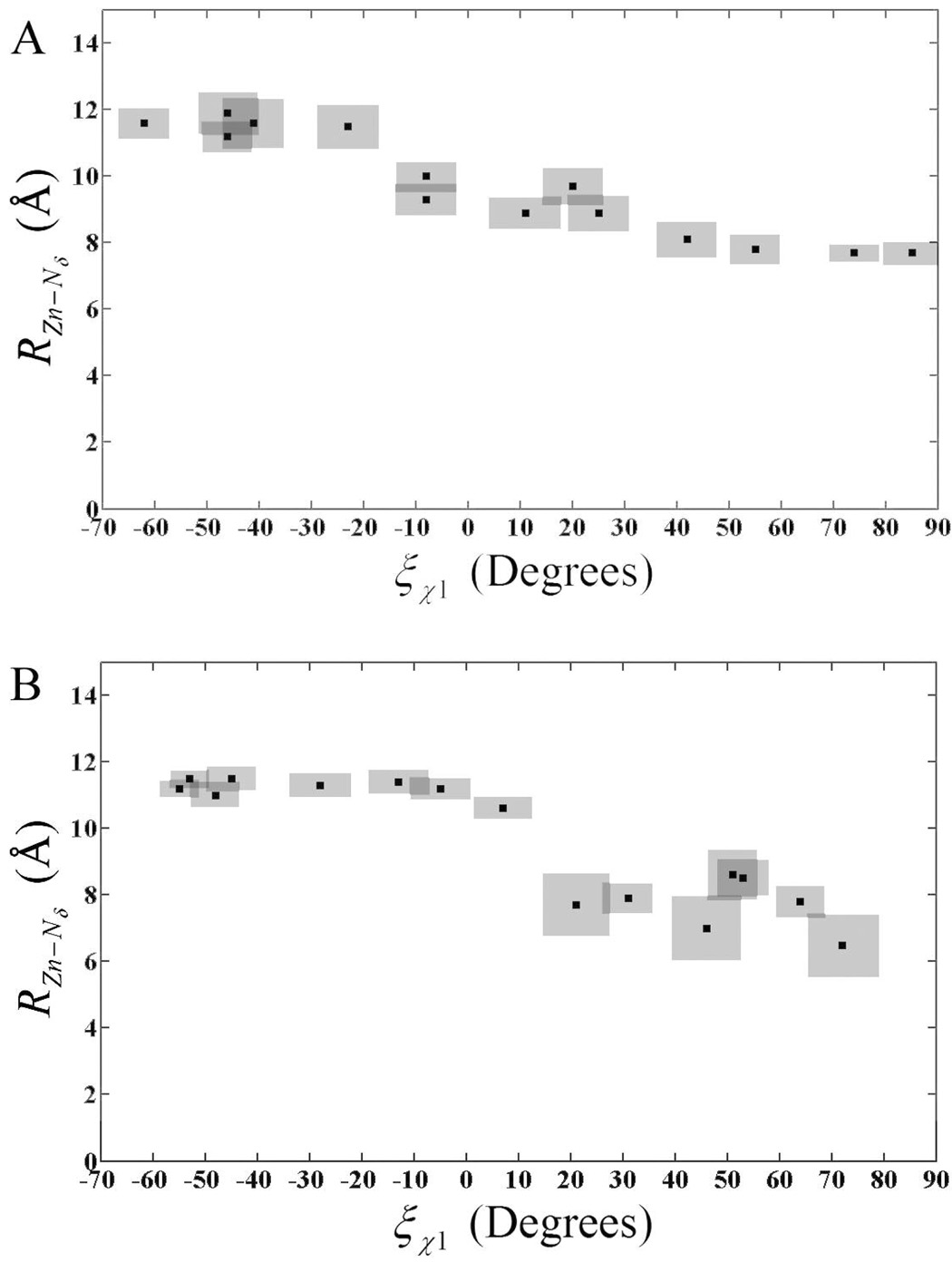
Inspection of the F(ξ_χ1) curves also reveals a shifting of the Transition State (TS) from χ1 = −7° in EZnH₂O²⁺-His to χ1= 17° in the EZnOH⁺-HisH⁺ system. To understand the cause of the χ1 dihedral shift the relationship between the χ1 dihedral and the distance between the catalytic zinc and the N_δ of His-64 (R_Zn–Nδ) was evaluated (Figure 4). From Figure 4 it is apparent that the shift in the χ1 dihedral corresponds to an increase in R_Zn–Nδ of around 2 Å. The increase in R_Zn–Nδ is most likely due to the repulsive nature of two positively charged bodies (active site and His-64). The “in” and “out” orientations previously defined by the χ1 dihedral can also be defined by R_Zn–Nδ with the “in” orientation corresponding to R_Zn–Nδ of around 7 Å and the “out” orientation corresponding to distances around 11 Å. Evaluating R_Zn–Nδ as a function of χ1 indicates that His-64 prefers to occupy very specific distances from the catalytic zinc over a range of χ1 (Figure 4). For the EZnH₂O²⁺-His system R_Zn–Nδ distances stay relatively stable at 11.5 Å, until the χ1 approaches the TS at −7° at which point the R_Zn–Nδ distance, after passing through the TS region, change to values around 7.5 Å. The majority of the R_Zn–Nδ change occurs in the range of −20° ≤ χ1 ≤ 10° and again at 25° ≤ χ1 ≤ 35°. Figure 4 shows that in the region where R_Zn–Nδ distances are typical of the “in” orientation, the dihedral samples a range of −70° ≤ χ1 ≤ −20° while the dihedral samples 35° ≤ χ1 ≤ 90° when in the “out” orientation. Inspection of the R_Zn–Nδ distances reveals an abrupt change at the TS, which indicates that the EZnH₂O²⁺-His system prefers to have His-64 at very specific distances that may correspond to environments that favor PT. Given that 7.5 Å is indicative of the “in” orientation three to four water molecules would be needed to bridge the span between the catalytic zinc and His-64. Indeed water wires containing three or four water molecule are seen in both MD simulation data (data not shown) and x-ray data(51). When His-64 occupies the “out” orientation the increased R_Zn–Nδ allows for the addition of one or more water molecules to the water wire, as seen in MD simulation data (data not shown). The discrete R_Zn–Nδ distances seen as the χ1 angle varies could be partially explained by the sequential insertion/deletion of water molecules from the water wire. The EZnOH⁺-HisH⁺ system also possesses this discrete distance characteristic for R_Zn–Nδ (χ1). For the EZnOH⁺-HisH⁺ system a stable R_Zn–Nδ region of 11 to 12 Å across the range of −60° ≤ χ1 ≤ 0°is representative of the “out” orientation. Near the TS the N_δ of His-64 abruptly moves to the “in” orientation with a R_Zn–Nδ of 7 to 8 Å. A distinct difference between the EZnH₂O²⁺-His system and the EZnOH⁺-HisH⁺ system is the wider transition region in the EZnH₂O²⁺-His system. The wider transition region is expected due to the broad transition region in the EZnH₂O²⁺-His system’s PMF when compared to the EZnOH⁺-HisH⁺ system (Figure 3).

Figure 4.

Distance from catalytic zinc to the N_δ of His-64 as a function of the χ1 dihedrals for the EZn-H₂O²⁺-His system (A) and the EZn-OH⁺-HisH⁺ system (B). Solid black squares represent the average R_Zn–Nδ (χ1) value. The shaded area around the solid squares represents the uncertainty in the calculated R_Zn–Nδ and the χ1 values.

To see more clearly the spatial orientation of the His-64 it is useful to evaluate the PMF as a function of χ1 as well as χ2 (Figure 5). The two-dimensional (2-D) PMF, F(ξ_χ1, ξ_χ2), can be constructed using the equation(52)

$$F({\xi }_{\chi 1},{\xi }_{\chi 2})=F({\xi }_{\chi 1})-k_{B}T\text{ln}\langle \rho ({\xi }_{\chi 2};{\xi }_{\chi 1})\rangle +C$$ (5)

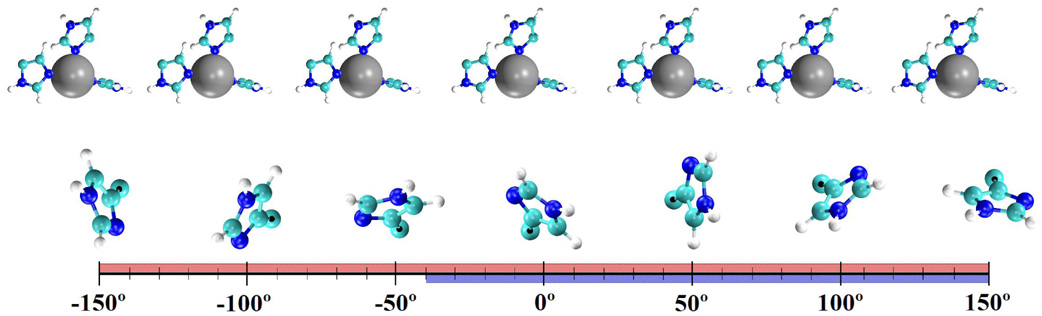
where F(ξ_χ1) is the free energy as a function of ξ_χ1, 〈ρ(ξ_χ2;ξ_χ1)〉 is the average density along ξ_χ2 at a given ξ_χ1, and C is a constant. When evaluating the 2-D PMF for the EZnH₂O²⁺-His system the χ2 dihedral transverses the range of 4° ≤ χ2 ≤ 140° when the χ1 dihedral is in the range depicting the “in” orientation and transverses the range of −148° ≤ χ2 ≤ 156° when the χ1 dihedral is in the range depicting the “out” orientation. When His-64 is inserted into the active site, “in” orientation, the imidazole ring adopts two stable orientations. The two orientations are the “parallel” orientation for dihedrals of ~20° ≤ χ2 ≤ ~70° and the “perpendicular” orientation for dihedrals of ~120° ≤ χ2 ≤ ~50°. The orientation of His-64 with respect to the catalytic zinc is shown in Figure 6. Figure 5(A) reveals a free energy barrier between the two local minima describing the “parallel” and “perpendicular” orientation of His-64, indicating that the χ2 dihedral between these two local minima is infrequently sampled. From the 2-D PMF the barrier for ring flipping, χ2, is around 7 kcal/mole, which is in close agreement with the proposal that ring flipping about the side chains χ2 dihedral has a barrier of ≤ 8 kcal/mole corresponding to rates of ≥ 10⁶ s⁻¹.(53) When His-64 adopts the “out” orientation there are less restrictions on the rotation of the imidazole ring as seen by the larger sampling of the χ2 dihedral, Figure 5(A). In the “out” orientation the imidazole ring of His-64 rotates from having the N_δ facing the catalytic zinc (“parallel”) to having the imidazole ring occupying two different “perpendicular” orientations. This increased ability for rotation could be explained by the fact that the His-64’s environment is less restrictive in the “out” orientation due to the His-64 occupying a more bulk water-like environment.

Figure 5.

Free energy profile for the rotation about the dihedral angles as a function of the χ1 and χ2. (A) F(ξ_χ1, ξ_χ2) for the EZnH₂O²⁺-His system and (B) F(ξ_χ1, ξ_χ2) for the EZnOH⁺-HisH⁺ system.

Figure 6.

Orientation of His-64 with respect to the catalytic zinc as a function of the χ2 dihedral. The black dot indicates the C_β of the His-64 backbone. The red line represents the range of the χ2 dihedral angles sampled for the EZnH₂O²⁺-His system while the blue line represents the range of the χ2 dihedral angles sampled for the EZnOH⁺-HisH⁺ system.(55, 56)

The χ1 and χ2 2-D PMF for the EZnOH⁺-HisH⁺ system is depicted in Figure 5(B). The overall χ2 range is smaller than that of the EZnH₂O²⁺-His system (Figure 6). When χ1 is in the “in” orientation the χ2 dihedral samples from ~40° ≤ χ2 ≤ ~150° with ~40° ≤ χ2 ≤ ~70° represented by the “parallel” orientation and ~120° ≤ χ2 ≤ ~150° representing the “perpendicular” orientation. One significant difference between the EZnH₂O²⁺-His and the EZnOH⁺-HisH⁺ system is the increased χ2 sampling for the EZnOH⁺-HisH⁺ system in the “in” orientation. This can be explained by the almost symmetric charge distribution on HisH⁺. This in turn supports the idea that the N_δ and N_ε of the HisH⁺ moiety are almost indistinguishable in the active site environment, allowing HisH⁺ of the EZnOH⁺-HisH⁺ system to rotate to either “perpendicular” orientation. This is not the case for the His moiety in the EZnH₂O²⁺-His system because the N_δ and N_ε are significantly different and therefore only one “perpendicular” orientation is sampled. When χ1 is in the “out” orientation, the χ2 for the EZnOH⁺-HisH⁺ system samples a reduced range of ~50° ≤ χ2 ≤ ~150°, which includes one of the two “perpendicular” orientations and the parallel orientation. Only one perpendicular orientation is sampled because the ring structure of Trp-5 interacts with the positively charged imidazolium ring of His-64 thereby restricting the rotation of His-64. Even though the Trp-5 is present in both the EZnH₂O²⁺-His and the EZnOH⁺-HisH⁺ system the extra proton of the HisH⁺ moiety now prevents certain rotations of the His-64 ring near Trp-5.

An important aspect of the free energy curve, F(ξ), is the ability to calculate the equilibrium probability of finding His-64 in either the “in” or “out” orientation, which can then be compared to experimental x-ray data. The relative distribution of the “in” to “out” orientation are found by integrating the PMF curve according to

$$P=\frac{{\displaystyle {\int }_a^b{e}^{-\beta F(\xi )}d\xi }}{{\displaystyle {\int }_{-180}^{180}{e}^{-\beta F(\xi )}d\xi }}$$ (6)

where P is the probability, ξ is the reaction coordinate, a and b represent the subset range of configurations and F(ξ) is the free energy. Typically the ranges for integration are −180° ≤ a ≤ TS and TS ≤ b ≤ 180°. Using equation 6 yields an “in” orientation probability of 86.2% and an “out” orientation probability of 13.8% for the EZnH₂O²⁺-His system, and a probability of 3.3% for the “in” orientation and 96.7% for the “out” orientation in the EZnOH⁺-HisH⁺ system. The appearance of both the “in” and “out” orientations is also seen in x-ray data where both the “in” and “out” are present at different ratios over the pH range of 6.1 to 10.(2, 49) The ratio values for the EZnH₂O²⁺-His system agree very well with recent x-ray data that indicates a ration of 80% “in” and 20% “out”.(51) This agreement would also indicate that the x-ray structure is representative of the EZnH₂O²⁺-His system and not the EZnOH⁺-HisH⁺ system. Analyzing the F(ξ) reveals that when His-64 is protonated, like in the EZnOH⁺-HisH⁺ system, it predominantly adopts the “out” orientation while adopting the “in” orientation for the EZnH₂O²⁺-His system. This suggests that when HCA II proceeds in the CO₂ hydration direction (EZnH₂O²⁺-His as reactant), the His-64 is in the “in” orientation. This moves the N_δ of His-64 closer to the catalytic zinc and maximizes the probability of PT from the zinc bound water to His-64. While in the EZnOH⁺-HisH⁺ system where His-64 prefers the “out” orientation, the PT from His-64 to the bulk medium is favored over the PT from His-64 to the catalytic zinc bound hydroxide.

His-64 Solvation Structure

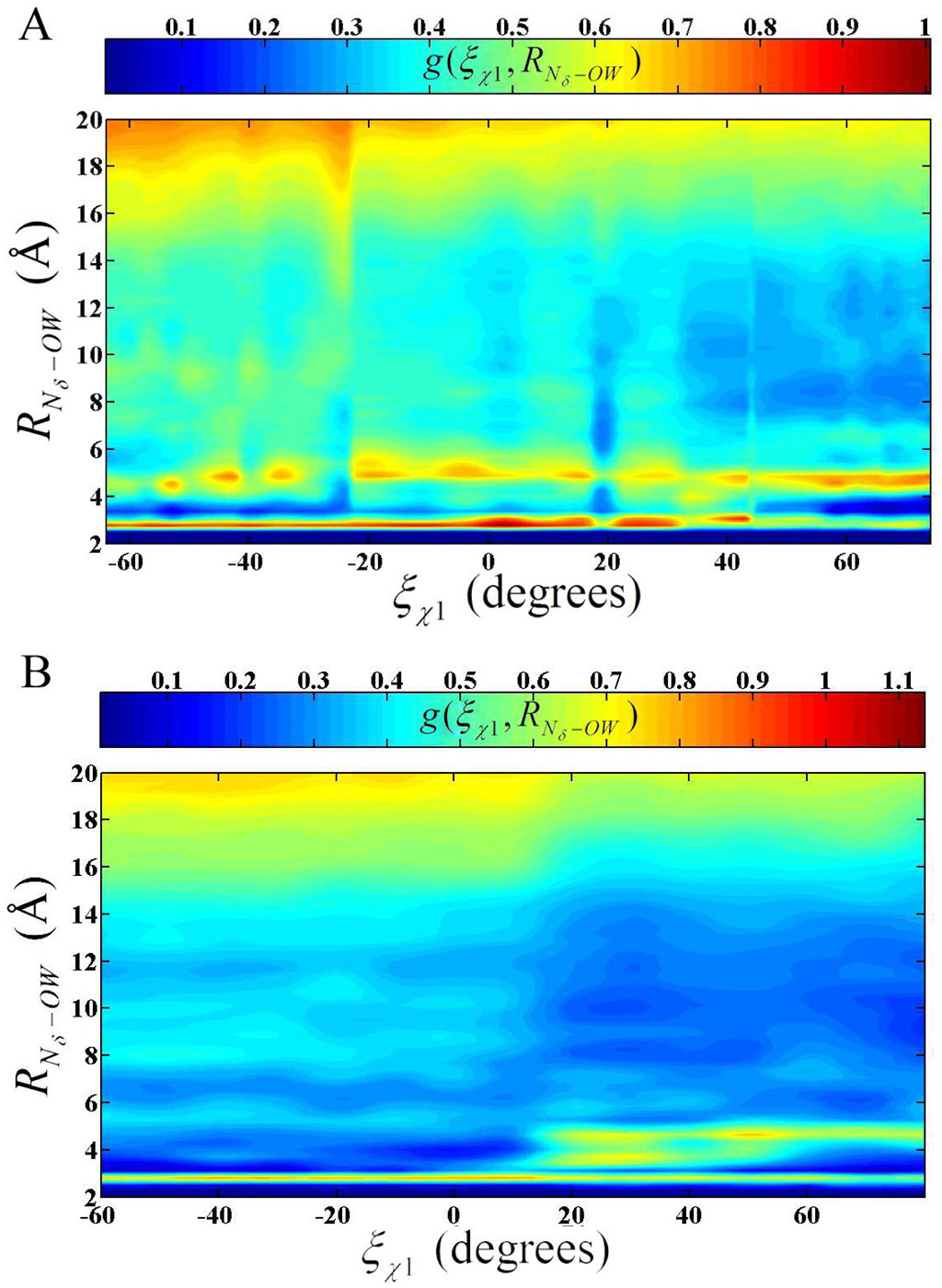
The solvent structure around His-64 should be crucial in the transport of a proton near the imidazole ring. It is the water solvent that is believed to transport the proton between the catalytic active site and His-64. The solvent is also responsible for the transport of the proton between the bulk water environment and His-64. Therefore 2-D radial distribution functions (RDF) were calculated on the HCA II simulations to evaluate how the solvent network adapts to the orientation of His-64. The 2-D RDF around the N_δ of His-64 at different χ1 dihedrals, g(ξ_χ1, ξ_RNδ–OW), was evaluated to clarify the behavior of the solvation shells for both the ZnH₂O²⁺-His and ZnOH⁺-HisH⁺ systems (Figure 7). It has been shown that the RDF for the modified TIP3P reasonably reproduces the experimentally determined RDFs for bulk water (data not shown). When His-64 adopts the “in” orientation in the ZnH₂O²⁺-His system the second solvation shells amplitude is slightly elevated above the first solvation shell. Closer inspection of the first solvation shell reveals an average occupancy of 1.1 (data not shown). The W3a (see Figure 1) water is clearly the major contributor of the peak’s amplitude with a minor portion being contributed by either W2 or another active site water. Due to the stabilizing hydrogen bonds and the reduced volume in the active site the W3a water is believed to be the predominant water in the vicinity of the N_δ of His-64. The W2 and other active site waters predominantly occupy the second solvation shell. The second solvation shell has a relatively elevated amplitude because these enzyme-stabilized waters have a reduced diffusion constant compared to bulk water(19) and occupy this solvation shell.

Figure 7.

2-D radial distribution function: (A) g(ξ_χ1, R_Nδ–OW) for the EZnH₂O²⁺-His system and (B) g(ξ_χ1, R_Nδ–OW) for the EZnOH⁺-HisH⁺ system.

The small amplitude in g(ξ_χ1, ξ_RNδ–OW) in Figure 7 at around 10 Å can be explained by the solution void created by the HCA II enzyme. As the His- 64 is retracted from the confined active site of the enzyme and starts to experience a more bulk-like solvated environment the amplitude of the second solvation shell decreases. This reduction in the second solvation shell’s amplitude is due to more labile waters occupying the second solvation shell, typical of a more bulk water like environment. In addition, the first solvation peak increases slightly as His-64 is removed from the solvent network in the enzyme environment and more waters are allowed to favorably interact with the first solvation shell. As the His-64 moves to the “out” orientation the elevated first solvation amplitude persists and the second solvation shells amplitude is reduced. The “out” orientation reflects a more classical bulk like RDF for histidine, with the major difference being that the bulk density values of the g(ξ_χ1, ξ_RNδ–OW) does not become apparent until R_Nδ–OW > 18 Å in the enzyme system, where one would expect a histidine in bulk water to reach bulk density at shorter distance (~6 Å). Again, this is explained by the solvation void created by the HCA II enzyme, which suppresses the amplitude of the radial distribution function because no water is present in the enzyme void.

The 2-D RDF for the EZnOH⁺-HisH⁺ system in Figure 7B, like the EZnH₂O²⁺-His system, shows significant changes in the solvation structure at different χ1 dihedrals. When His-64 is in the “in” orientation there are two prominent solvation shells followed by the void at around 10 Å. Once again it is evident that the second solvation shell has an elevated amplitude due to the stabilizing effect of the active site amino acids on the active site waters. The second solvation shell is also at a shorter R_Nδ–OW than seen in bulk water. This is an indication of the level of frustration in the solvent environment. Frustration in this case refers to the amount by which the solvation structure must deviate from bulk values in order to accommodate a particular environment. It can be concluded that HisH⁺ occupies a more frustrated environment in the “in” orientation than His because His deviates from the bulk like RDF in amplitude only, while HisH⁺ deviates from the bulk like RDF in amplitude and spacing. This frustration is postulated as one of the reasons the “in” orientation is less favorable for HisH⁺. As the χ1 dihedral is reduced and the His-64 begins to move to the “out” orientation a transition phase is seen in the behavior of g(ξ_χ1, R_Nδ–OW). The transition state at χ1 =17° is evident in the g(ξ_χ1, R_Nδ–OW) by the termination of the second solvation shell at around 4 Å. As His-64 moves to the “out” orientation the first solvation shell intensity increases, the second and third solvation shells move to longer R_Nδ–OW distances, and a noticeable void forms before and after the second solvation shell. This indicates that HisH⁺ is able to form an ordered and stable solvation structure when in the “out” orientation. The solvation structure is more ordered in EZnOH⁺-HisH⁺ than in the EZnH₂O²⁺-His system because the EZnOH⁺-HisH⁺ system’s His-64 carries a positive charge and therefore creates more electrostatic interactions. The “out” orientation’s behavior of g(ξ_χ1, R_Nδ–OW) is very similar to that of HisH⁺ in bulk water except for the shifted tail region at longer R_Nδ–OW distances. Again the bulk density value is not reached until greater R_Nδ–OW values due to the presence of the HCA II enzyme.

4. Conclusions

The present investigation into the orientation of His-64 in HCA II has revealed a complex interplay between His-64 and its environment. PMF data along the reaction coordinate, χ1, reveals the long-range electrostatic interactions between His-64, the solvent environment, and the active site of HCA II. In the HCA II system, transition state theory suggests that on the time scale of the rate limiting PT event the transfer between orientations for His-64 does not contribute to the rate limiting step and His-64 will have reached equilibrium between the “in” and “out” orientations. Once in equilibrium the His-64 of EZnH₂O²⁺-His system is favored to occupy the “in” over the “out” orientation. This indicates that His-64 favorably inserts into the active site, thereby decreasing the distance between the catalytic zinc and N_δ of His-64. This shortened distance between the catalytic zinc and His requires shorter water wires to connect the zinc bound water to the N_δ of His-64, which are believed to be more conducive to PT.

In the EZnOH⁺-HisH⁺ system the PMF data suggests the “out” orientation is favored at equilibrium over the “in” orientation. The protonated His-64 for the EZnOH⁺-HisH⁺ system is more likely to rotate to the “out” orientation and release the proton to the bulk water than to remain in the “in” orientation and back-donate the proton to the zinc bound hydroxide. This step appears to be a key feature of the overall enzyme functional cycle.

In addition to the χ1 dihedral effects reflecting the in versus out conformation, the χ2 dihedral, which describes the imidazole ring orientation, plays a roll in the ability for His-64 to find a favorable orientation relative to the enzyme active site. The His for the EZnH₂O²⁺-His system is restricted in its sampling of the χ2 dihedral when χ1 is in the “in” orientation due to the elevated χ2 barrier when compared to the EZnOH⁺-HisH⁺ system. The barrier height and subsequently the sampling of the χ2 dihedral causes an increase in the probability that His will be in the optimum orientation for PT from the zinc bound water to His-64. At the same time, the reduced χ2 barrier (Figure 5) and therefore the increased sampling of χ2 in the “in” orientation for the EZnOH⁺-HisH⁺ system reduces the probability that HisH⁺ will occupy the ideal conformation for PT to the zinc bound hydroxide. This intricate interplay between χ1 and χ2 dihedrals reveals how the enzyme environment manipulates His-64 to occupy the most favorable position for catalysis in HCA II. In future work, the present results will be integrated with those from simulations of explicit PT using the multi-state empirical valence bond (MS-EVB) model(54) as applied to HCA.

Supplementary Material

File002. Supporting Information Available.

Tables containing detailed information on modifications to the force field. This material is available free of charge via the Internet at http://pubs.acs.org.