A One-Dimensional Velocity Technique for NMR Measurement of Aortic Distensibility

Abstract

A technique is presented for rapidly and noninvasively determining aortic distensibility, by NMR measurement of wave velocity in the aorta. A two-dimensional NMR selective-excitation pulse is used to repeatedly excite a cylinder of magnetization in the aorta, with magnetization read out along the cylinder axis each time. A toggled bipolar flow-encoding pulse is applied prior to readout, to produce a one-dimensional phase-contrast flow image. Cardiac gating and data interleaving are employed to improve the effective time resolution to 2 ms. Wave velocities are determined from the slope of the leading edge of flow measured on the resulting M-mode velocity image. The technique is sensitive over a range of distensibilities from 10⁻⁶ to 10⁻³ m s²/kg. The average value in the descending thoracic aorta in seven normal subjects was found to be 4.8 × 10⁻⁵ m s²/kg, with a significant inverse correlation with age.

INTRODUCTION

Sudden aortic dissection or rupture in patients with aneurysmal dilatation secondary to atherosclerosis or connective tissue disease is common. Monitoring of aortic diameter is currently used as a guideline for surgical intervention because no practical noninvasive method exists to measure aneurysmal distensibility. A rapid and noninvasive technique for determining aortic distensibility could play an important clinical role in this context. Aortic compliance, a closely related measure of stiffness, has also been shown to influence left ventricular after-load, and is an important variable in the management of ventricular disease (1-3). Aortic stiffness appears as well to be a correlate (although nonspecific) of coronary artery disease and fitness (4-6).

We present here a noninvasive technique for determining aortic distensibility by means of wave-velocity measurements. An NMR phase-contrast pulse sequence employing cylindrical NMR selective excitation pulses is used to produce M-mode velocity images, in which propagating flow wavefronts in the aorta may be viewed. For an incompressible fluid in a stiff vessel, pressure changes are instantaneously transmitted down the vessel, but for a vessel with compliant walls, the pressure wave distends the vessel, and travels along it at a finite velocity which can be determined from the flow image.

THEORY

The distensibility, D, defined as the fractional change in vessel cross-sectional area/unit change in pressure, may alternatively be determined from the relation

$$D=1∕\rho C^2,$$

where ρ is the blood density and C is the wave speed in the vessel (7, 8). (The related parameter, compliance, is the change in volume/unit change in pressure.) The blood density is 1.057 ± 0.007 g cm⁻³ in normal subjects (9) and, even among patients, will vary much less than the experimental error of the wave-velocity measurements, and thus is taken to be constant. Proper determination of the wave velocity requires lack of interference from reflected waves, and also that the wave velocity be much larger than the blood velocity v_b (8). If the foot of the flow wave is followed, directly at the onset of systolic flow, both of these requirements are generally met.

The wave velocity is measured using a variant of an NMR flow-sensitive M-mode sequence. In the basic sequence (10), shown in Fig. 1, a cylinder or “pencil” of magnetization typically 1.5 cm in diameter is excited along the ascending or descending aorta, using a spiral-scan cylindrical excitation pulse (11). This employs a constant-gradient-slew-rate traversal of the spiral to maximize bandwidth (12) and a correction factor for the RF waveform to compensate for uneven coverage of k space by the spiral near the origin (13). Following the pencil excitation a toggled bipolar velocity-encoding gradient is applied in the direction of blood flow and then a half-echo readout gradient is played out along the pencil axis. Alternate acquisitions are subtracted, yielding a time-dependent phase-contrast flow profile with a time resolution on the order of 50 ms (10). Alternatively, the phase may be calculated first and subtracted to produce a phase-difference image, in which directional information is retained, but the signal from static tissue is no longer suppressed. For oblique pencil orientations the logical gradient axes GX, GY, and GZ in Fig. 1 are combined via rotation matrices to produce the physical gradient waveforms.

FIG. 1.

Basic one-dimensional velocity-profiling pulse sequence. Spiral-scan pulse excites a pencil of magnetization, and half-echo readout yields a profile along the pencil. The bipolar flow-encoding pulse shown at right may be added along any gradient axis to produce flow sensitivity in that direction, but is typically placed along GX. The bipolar waveform is toggled on alternate acquisitions, and the raw signal subtracted before 1D Fourier transformation, to yield a phase-contrast M-mode image.

This basic pulse sequence lacks the time resolution needed to follow propagating wavefronts to determine C. To achieve this, the sequence is gated to the cardiac cycle, with an incremented trigger delay, and the resulting data are interleaved into the proper time order. In this manner an effective time resolution of 2 ms can be obtained within 32 heart cycles.

It is useful to perform quantitation of the blood velocity to help determine whether any abnormal flow is present which would invalidate this wave-velocity technique. This is done using a cardiac-gated Fourier-velocity-encoded version of the basic pulse sequence of Fig. 1 (14). Here the bipolar gradient is stepped through a range of amplitudes and a Fourier transform is applied to generate velocity distributions at various phases of the heart cycle.

MATERIALS AND METHODS

The GE Signa MRI scanner is controlled interactively from a Sun SPARCserver with a Mercury MC860 array processor (AP) linked through a data path and a scan-control path (15). The data are reconstructed one line at a time on the AP and displayed in a scrolling fashion on the Sun monitor, under control of an Xview window system (Fig. 2). New pencil orientations and offsets are prescribed graphically on a scout image displayed on the Sun, and sent over the scan-control link to redirect the pulse sequence in real time. A convention has been adopted in which the prescription angles range from −45° to 135° relative to a horizontal axis. The right side of the flow image corresponds to the right end of the pencil in Fig. 2 (where the angle is −42°), and for all angles between −45° and 45°. For angles between 45° and 135°, the right side of the flow image corresponds to the top end of the pencil.

FIG. 2.

Sun display for interactive cardiac imaging system. Lines drawn on the scout image at left direct placement of the NMR pencil in real time, and a scrolling display of blood flow appears on the right. Here a phase-contrast reconstruction has been used; faster moving blood produces a brighter signal, and static tissue is suppressed.

To achieve sufficient temporal resolution to follow typical wave-propagation velocities of several hundred cm/s, the sequence of Fig. 1 is gated to the heart cycle in groups of 16 excitations/cycle, with the sequence delayed by an additional 2 ms relative to the R-wave trigger on each successive pair of cycles, as shown in Fig. 3. The data are then interleaved into the proper time order and a 1DFT is applied. This results in a flow image that has distance along the cylinder as one axis, and time relative to the R-wave as the other axis, with an effective time resolution of 2 ms, and spatial resolution on the order of 1 mm. The wave velocity is then determined by measuring the slope of the edge corresponding to the foot of the flow wave in this time-versus-distance image. The field of view was typically around 30 cm and the pencil diameter 1.5 cm. The pencil-excitation pulse was based on an 8-cycle k-space spiral, and was typically 11 ms in duration. Each lobe of the bipolar flow-encoding gradient was 1 ms long, with an amplitude of 0.5 G/cm.

FIG. 3.

Cardiac gating scheme for interleaved flow-profiling sequence. Sixteen phases of the heart are acquired in each heartbeat, with the trigger delay incremented by 2 ms with each pair of heartbeats, and the data interleaved into the proper time order after 32 heart cycles.

The Fourier-flow-encoded pulse sequence used to determine blood velocities employed 32 velocity-encoding steps, and was gated to the R-wave, with data acquired over 16 phases of the heart separated by 36 ms each. The sinusoidal bipolar gradient had a maximum amplitude of 1 G/cm, and each lobe was 6 ms long, yielding a velocity resolution of 5 cm/s. This resulted in aliasing for velocities greater than 80 cm/s, but since the flow direction was known, and flow was followed over the heart cycle, any ambiguity in the velocity profiles was removed. This aliasing could be easily eliminated at the cost of increased imaging time by employing 64 velocity-encoding steps.

RESULTS

Figure 4a shows a scout image from a volunteer, with the position prescribed for the pencil indicated as a line on the image. The Fourier velocity-encoded version of the sequence of Fig. 1 was applied, with the flow direction running orthogonal to the pencil and along the aorta. The resulting flow distribution, shown over 16 heart phases, is illustrated in Fig. 4b. The 16 long horizontal lines correspond to static tissue in the excited pencil, at each cardiac phase. Vertical displacements relative to each long line are proportional to velocity at that heart phase. Where the pencil intersects the aorta, a short segment can be seen in Fig. 4b rising and then falling over the heart cycle, arising from systolic blood flow in the aorta. The peak velocity for this volunteer was 70 cm/s, with essentially plug flow observed across the aorta.

FIG. 4.

(a) Oblique scout image of descending aorta of normal volunteer. Line indicates position of prescribed pencil for subsequent Fourier flow sequence. (b) Results of Fourier velocity-encoded pulse sequence over 16 heart phases. Long lines correspond to static tissue, and short lines to flow in the aorta, with velocity proportional to vertical displacement relative to each long line. Velocity in the aorta rises to 70 cm/s and then falls again to zero.

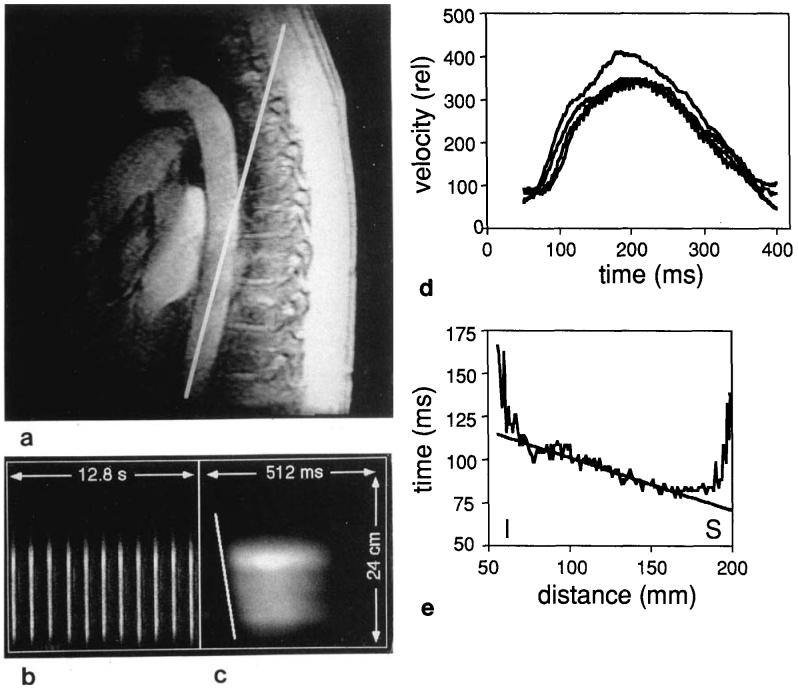
Figure 5a shows an oblique view of the descending aorta in a normal volunteer, acquired using a segmented gradient-echo pulse sequence. The line drawn on the image indicates the position of the pencil subsequently excited in the flow-encoding pulse sequence. Figure 5b shows a phase-contrast flow profile obtained using the nongated 1D velocity pulse sequence of Fig. 1. Here the horizontal dimension is time, and the vertical dimension is position along the cylinder axis. The long streaks correspond to systolic flow in that portion of the aorta intersecting the pencil. Roughly 11 heart cycles are covered in 256 lines.

FIG. 5.

(a) Quasi-sagittal scout image of descending aorta of normal volunteer. Line indicates position of prescribed pencil for subsequent flow sequence. (b) Phase-contrast flow profile obtained using the nongated 1D velocity pulse sequence of Fig. 1, and covering roughly 11 heart cycles. (c) Gated, interleaved flow profile obtained using the gating scheme of Fig. 3. Effective time resolution has been improved to 2 ms. Sloped line corresponds to foot of velocity wave. (d) Series of flow profiles obtained at 2-cm intervals along the image part c). The propagation of the leading edge of the flow is evident on the left side of the plot. Differences in wave speed of the higher frequency components of the pulse cause the shape of the curve to change slightly as the pulse moves down the aorta. (e) Best fit to the foot of the wavefront of part c). The end regions have been excluded from the fit. Slope of line yields wave velocity of 340 cm/s. I, inferior; S, superior.

In Fig. 5c, the gated, interleaved version of the pulse sequence has been used to measure flow in the same region with much higher effective time resolution. In this image the horizontal time axis extends over roughly the first half of one heart cycle (512 ms). The bright region corresponds to one of the streaks in Fig. 5b. The propagating wave front can be seen as the sloped region (marked with a line) in the leading edge of the systolic flow. Measurement of the slope yields a value for the velocity of propagation of the wave front. Figure 5d shows several flow profiles obtained by taking sections through the image of Fig. 5c. The delay-time of the foot of the flow wave is determined by setting a constant threshold which is higher than the baseline by roughly three times the noise level in the profiles, and finding the threshold crossing at each position. A best fit is then performed of this time versus position, as shown in Fig. 5e, to determine the wave velocity, which is in this case 340 cm/s. The first 1 cm at either end of the flow region is excluded from the fit, because the aorta is curving into or out of the pencil in these areas, and so is not completely aligned with the flow-encoding gradients. This also has the advantage of excluding blood which is first entering the pencil and so has not yet achieved equilibrium with the 30° pencil-excitation pulses.

Wave velocities have been determined in similar fashion from the ascending aorta. Figure 6a shows a scout image from a normal volunteer, with subsequent pencil position indicated again with a line. The free-running phase-contrast image is shown in Fig. 6b, with the corresponding interleaved, cardiac-gated image shown in Fig. 6c. Here systolic outflow from the left ventricle into the ascending aorta is evident as the long streak, followed by filling of the left ventricle from the left atrium, visible as the shorter streak in the left ventricle. This filling is in essentially the opposite direction from the systolic flow, as seen using a phase-difference reconstruction algorithm (15). The wave velocity in the ascending aorta from this subject was 270 cm/s.

FIG. 6.

(a) Scout image of left ventricle and ascending aorta of normal volunteer. Line indicates position of prescribed pencil for subsequent flow sequence. (b) Nongated and (c) gated phase-contrast flow images showing systolic and diastolic flow.

Wave velocity in the descending thoracic aorta was measured in seven volunteers ranging in age from 24 to 63 years. Figures 7a and 7b show free-running and gated flow images, respectively, from a 63-year-old subject. The slope of the wavefront is markedly steeper than in the 33-year-old subject of Fig. 5c, and corresponds to a wave velocity of 960 cm/s. Wave velocity is plotted versus age in Fig. 8a for all of the subjects. The best linear fit to these data yields v_p = 9.3X + 90, where X is age, with a correlation coefficient of R = 0.90. The error bars on the individual points in Fig. 8a are based upon a 0.5° uncertainty in the slope of the wavefronts, as measured for example on Fig. 5c. This uncertainty was determined by making repeated (between 3 and 6) NMR measurements on the same subject, for three different subjects, and calculating the standard deviation of the slope for each subject. Note that this yields a larger uncertainty as the wave velocity increases, as seen in Fig. 8a.

FIG. 7.

(a) Nongated and (b) gated phase-contrast 1D flow image of descending aorta of 63-year-old normal subject. Wave velocity is much higher than in 33-year-old subject of Fig. 5.

FIG. 8.

(a) Wave velocity in the descending thoracic aorta of seven normal subjects as a function of age, with linear fit and 95% confidence intervals. A best-fit line of Y = 9.3X + 90 was obtained, with an R-value of 0.90. (b) Aortic distensibility versus age for the same subjects. R = 0.91.

Distensibilities calculated using Eq. [1] are plotted on a logarithmic scale versus age in Fig. 8b. The best fit was D = −0.021X + 2.48 (on a log scale) and the correlation was R = 0.91. Here blood density was assumed to be 1.06 g/cm³.

DISCUSSION

We have developed a noninvasive technique for measuring aortic distensibility within a total of 64 heartbeats. NMR pencil excitation followed by Fourier flow encoding is used to determine aortic blood velocity to an accuracy of 5 cm/s with a time resolution of 36 ms, within 32 heartbeats, in order to characterize the flow. Wave velocity in the aorta is then measured within 32 heartbeats using a cardiac-gated phase-contrast pulse sequence with NMR pencil excitation, which yields an effective time resolution of 2 ms. These pulse sequences are both directed in a highly interactive fashion via a workstation interface to the MR scanner. The chief virtue of this technique is its ability to acquire regional measurements in a quick, noninvasive manner, over any portion of the aorta, along lengths as short as approximately 3 cm. It is sensitive over a range of distensibilities from approximately 10⁻⁶ to 10⁻³ m s²/kg, where the lower limit is determined by the time resolution of the technique, and the upper limit is reached as wave velocities approach the blood velocity.

Previous methods for directly or indirectly assessing distensibility or compliance have suffered from a variety of drawbacks. Ting et al. measured foot to foot flow intervals using micromanometers on a catheter inserted in the aorta via the femoral artery (16), a technique which is somewhat invasive. Changes in cross-sectional area of the aorta over the heart cycle have been determined using echocardiography (6) or MR imaging (5, 17) and the regional blood pressure estimated from sphygmomanometer measurements. Determining compliance from these measurements requires assumptions about the relationship between local and measured blood pressures and, in the case of echocardiography, is limited to accessible regions of the aorta, such as the aortic arch. Aortic wave velocities have recently been determined using MR cine velocity imaging in an oblique plane passing through the ascending and descending aorta, with calculation of the transit time of the foot of the flow wave between the two points, and with the distance measured from an oblique spin-echo image through the aortic arch (3, 18). This, however, is relatively time consuming and measures average wave velocity over the entire region between the two points. More recently a multi-planar excitation scheme with Fourier flow encoding has been used to measure distensibility of the femoral arteries (7). This typically requires 15 to 30 min for data acquisition, and is subject to interference from any vessels which may be overlying the vessel of interest, since it acquires projections across each slice.

Our values of aortic wave velocity fall somewhat above those determined previously by micromanometer measurements (16), and below those determined by phase-contrast MRI (3, 18). Ting et al. (16) obtained a foot-to-foot wave velocity of 374 ± 25 cm/s (all errors SEM) in the proximal descending aorta in eight normal subjects of average age 42.3 ± 3.1 years. This is not significantly different (P > 0.05) from the average value of 519 ± 81 cm/s obtained in the present study, which had a population of similar average age but wider age range (42.7 ± 5.3 years). Mohiaddin (18) found a linear dependence of wave velocity in the proximal aorta with age v_p = 8X + 300 (converted to cm/s). This line is roughly 20% higher on average than the curve of Fig. 8a, but has a similar slope. The 2D MRI measurements of wave velocity (3,18) are averages from the ascending aorta, around the aortic arch, to a point opposite on the descending aorta, and so are not entirely equivalent to our measurements in the descending aorta. Wave velocity (16) and compliance (5) both appear to vary with position along the aorta.

The distensibilities plotted in Fig. 8b are roughly a factor of 2 higher on average than those derived from excised human thoracic aorta. Learoyd et al. (19) obtained average values for the Young's modulus E of approximately 10⁷ dyn cm⁻² and for the ratio of wall thickness to diameter h/d of 0.04, in subjects between 10 and 50 years old. Using the relationship (8) between distensibility and these quantities, D = [E (h/d)]⁻¹, one obtains an average value of D = 25 μm s² kg⁻¹. This variation may be due in part to differences between excised and in vivo aorta. Dart et al. (6) found an in vivo value for the “beta index” in the aortic arch of β = 0.16X − 2.0, where X is age. They defined β as ln(P_s/P_d) D_d/(D_s − D_d), where P_s and P_d are systolic and diastolic arterial pressure, respectively, and D_s and D_d are maximum aortic diameter during systole and aortic diameter at end diastole, respectively. Using their mean values of P_s = 127.5 ± 2.5 mm Hg, P_d = 79.4 ± 1.2 mm Hg, and D_d = 24.4 ± 0.71 mm, one can calculate resulting average values for the distensibility. This yields 150 μm s² kg⁻¹ at age 20 years and 20 μm s² kg⁻¹ at age 60 years, which are somewhat higher than the values shown in Fig. 8b, and therefore even higher relative to the data from excised aorta (19). Mohiaddin et al. (5), on the other hand, in 1-cm thick slices through the ascending aorta, found average values of compliance of 10 raised to the power −0.01X + 1.79 (in μl/mm Hg), and a cross-sectional area of 0.09X + 2.1 (in cm²), where X is age. Converting units and dividing by area times thickness, yields an average value of 75 μm s² kg^−l for the distensibility at age 20 years, and 15 μm s² kg⁻¹ at age 60 years. Their values in the descending thoracic aorta were, on average, roughly 60% of their values in the ascending aorta.

This and other wave-velocity techniques ignore contributions from reflected waves, which have been found to be present, for instance, in the ascending aorta and near the renal arteries (16). If measurements are acquired immediately after a period of relatively constant or minimal flow, however, reflected waves will be insignificant, since pressure waves are not created during steady flow, and tend to attenuate quickly. For this reason, wave velocities were determined using the leading edge, or foot, of the velocity wave.

Equation [1] holds strictly only when v_b/C ≪ 1, because under these conditions convective accelerations in the blood are small compared with local accelerations (8). This condition generally is met in blood flow under normal physiological conditions, even in major vessels, and Eq. [1] has in fact been verified directly in dogs (8). However, when turbulent flow or jets are present, as in the case of valve disorders, the blood velocity may become comparable with or exceed the wave velocity, and Eq. [1] becomes invalid. Indeed, in these situations there is usually a loss of signal and the wave front cannot be followed in any event. This may limit any wave-velocity technique applied to aneurysms in the ascending aorta, if dilatation of the aorta has resulted in aortic insufficiency.

We found our determination of wave velocity to be adversely affected in some cases by breathing artifacts, which took the form of spurious signals running along the time axis of the flow profiles, notably in that portion of the descending aorta at the level of the diaphragm. Breath-holding was found to ameliorate this problem considerably, but may not be practical for all patients. The use of repeated short breath-holds would prove beneficial in these cases; data acquisition could be triggered by real-time scout views, which monitored the start of breath-holding.

Measurement of aortic distensibility typically requires knowledge of developed aortic pressure. Our method, in addition to being totally noninvasive, does not require in situ pressure measurements and can thus easily be applied clinically under various pharmacologic interventions.