Sensitivity of Inferior Colliculus Neurons to Interaural Time Differences in the Envelope Versus the Fine Structure With Bilateral Cochlear Implants

Abstract

Bilateral cochlear implantation seeks to improve hearing by taking advantage of the binaural processing of the central auditory system. Cochlear implants typically encode sound in each spectral channel by amplitude modulating (AM) a fixed-rate pulse train, thus interaural time differences (ITD) are only delivered in the envelope. We investigated the ITD sensitivity of inferior colliculus (IC) neurons with sinusoidally AM pulse trains. ITD was introduced independently to the AM and/or carrier pulses to measure the relative efficacy of envelope and fine structure for delivering ITD information. We found that many IC cells are sensitive to ITD in both the envelope (ITD_env) and fine structure (ITD_fs) for appropriate modulation frequencies and carrier rates. ITD_env sensitivity was generally similar to that seen in normal-hearing animals with AM tones. ITD_env tuning generally improved with increasing modulation frequency up to the maximum modulation frequency that elicited a sustained response in a neuron (tested ≤Hz). ITD_fs sensitivity was present in about half the neurons for 1,000 pulse/s (pps) carriers and was nonexistent at 5,000 pps. The neurons that were sensitive to ITD_fs at 1,000 pps were those that showed the best ITD sensitivity to low-rate pulse trains. Overall, the best ITD sensitivity was found for ITD contained in the fine structure of a moderate rate AM pulse train (1,000 pps). These results suggest that the interaural timing of current pulses should be accurately controlled in a bilateral cochlear implant processing strategy that provides salient ITD cues.

INTRODUCTION

Cochlear implantation is a widely used treatment for sensorineural deafness with > 100,000 adults and children implanted worldwide. While most cochlear implant users have only been implanted in one ear, bilateral implantation is rapidly becoming routine to restore the advantages of binaural hearing. However, commercially available cochlear implant sound processors have not been designed with binaural hearing in mind.

Binaural advantages for normal listeners include accurate localization of sound sources in the horizontal plane and improved speech reception in background noise (Blauert 1997; Durlach and Colburn 1978; Zurek 1993). The acoustic cues that lead to these advantages result from the physical separation of the two ears about the head and include interaural time and level differences (ITD and ILD). This study addresses issues of ITD coding with bilateral cochlear implants by studying the sensitivity of neurons to ITD using electric stimulation in an animal model. We focus on ITD because although bilaterally implanted subjects have good ILD discrimination (Grantham et al. 2008; Laback et al. 2004; van Hoesel and Tyler 2003), their ability to discriminate ITD is highly variable across subjects and comparable to normal performance only over a narrow range of stimulus parameters even in the best subjects, leaving much room for improvement in how this important binaural cue is encoded (Laback et al. 2007; Long et al. 2003; van Hoesel 2007; van Hoesel and Tyler 2003).

In a companion study (Smith and Delgutte 2007), we found that the ITD tuning of single units in the cat inferior colliculus (IC) for bilateral electric stimulation with low-rate, constant-amplitude pulse trains is as sharp at near-threshold intensities as for acoustic stimulation with broadband noise in normal-hearing animals. Such low-rate pulse trains have temporally punctate waveforms that make them ideal for revealing the intrinsic ITD sensitivity of binaural neurons, but they clearly differ from the more complex stimulation produced by cochlear implant sound processors. The present study focuses on ITD sensitivity for amplitude-modulated (AM) pulse trains that better mimic the types of stimulation used in clinical devices.

Cochlear implant sound processors typically split sound into multiple frequency bands and then use the filtered signals in each band to modulate the amplitude of current pulses delivered to tonotopically arranged intracochlear electrodes. For example, the popular continuous interleaved sampling (CIS) strategy (Wilson et al. 1991) uses the amplitude envelope of the filtered sound signal in each frequency channel to modulate the amplitude of a fixed-rate pulse train, which is temporally interleaved with the pulse trains in other channels to mitigate electrode interactions. In this scheme, as well as the majority of clinical processing strategies, the temporal fine structure of the original sound signal is discarded and only the amplitude envelope is delivered to the auditory nerve via the implanted electrodes. Thus the only ITD cues available to users of bilateral cochlear implants are contained in the amplitude envelope. While envelope cues in a limited number of frequency bands (e.g., 6–12) suffice for speech understanding in favorable acoustic environments (Shannon et al. 1995), they do not provide good speech reception in noise, fine pitch discrimination, and accurate localization of low-frequency sounds (Henning 1974; Henning and Ashton 1981; Qin and Oxenham 2003; Smith et al. 2002).

Neural sensitivity to ITD originates in the auditory brain stem. Neurons in the medial and lateral superior olive (MSO and LSO) create ITD tuning from convergent inputs from the contra- and ipsilateral ears. While MSO neurons are typically sensitive to ITD in the fine time structure of low-frequency sounds (Goldberg and Brown 1969; Yin and Chan 1990), a majority of LSO neurons are sensitive to ITD in the amplitude envelope of AM tones with high-frequency carriers (Joris and Yin 1995). LSO neurons are also highly sensitive to ILD (Boudreau and Tsuchitani 1968; Tollin and Yin 2005). Both MSO and LSO neurons have direct and indirect projections to the IC where neurons have ITD tuning that can resemble that in the MSO and LSO and can also be more complex (Batra et al. 1993; McAlpine et al. 1998; Yin and Kuwada 1983). Stimulation with broadband noise shows that ITD-sensitive IC neurons with low characteristic frequencies (CFs; <1 kHz) are primarily sensitive to ITD in the fine time structure, while neurons with high CFs (>3 kHz) are primarily sensitive to ITD in the envelope (Joris 2003).

The primary purpose of this paper is to determine the relative neural sensitivity to ITD in the amplitude envelope (ITD_env) versus the temporal fine structure (ITD_fs) with bilateral electric stimulation. Because ITD_fs is perceptually more salient than ITD_env in normal hearing (Macpherson and Middlebrooks 2002; Wightman and Kistler 1992), neuronal sensitivity in the IC of normal hearing animals is generally greater for ITD_fs than for ITD_env (Batra et al. 1993; Griffin et al. 2005; Yin et al. 1984), and electric stimulation of the cochlea elicits precise temporal responses to electric pulses in the auditory nerve (Javel and Shepherd 2000; Moxon 1967; van den Honert and Stypulkowski 1987), we hypothesize that ITD-sensitive neurons will be more sharply tuned to ITD_fs than to ITD_env with electric stimulation. To test this hypothesis, we investigated the ITD sensitivity of IC neurons to AM pulse trains delivered via bilaterally implanted intracochlear electrodes. We found that the majority of neurons in the central nucleus of IC are sensitive to ITD_env with tuning similar to that seen for acoustic stimulation with AM tones in normal-hearing animals. We also found that many neurons are sensitive to ITD_fs at a moderate pulse rate (1,000 pps) and that this tuning is sharper than that for ITD_env. Preliminary reports have been presented (Smith and Delgutte 2003a,b, 2005a,b).

METHODS

Experimental procedures

Methods for animal preparation, electric stimulation, and single-unit recordings were as described in detail by Smith and Delgutte (2007). All surgical and experimental procedures were approved by the internal animal care and use committees of both the Massachusetts Eye and Ear Infirmary and the Massachusetts Institute of Technology. Briefly, cats were deafened by coadministration of kanamycin (300 mg/kg sc) and ethacrynic acid (25 mg/kg iv) 7–14 days prior to the experiment (Xu et al. 1993). For all animals, no auditory brain stem response was seen on the day of the experiment when stimulated with acoustic clicks (110 dB SPL). On the day of the experiment, after induction of anesthesia by Dial in urethane (75 mg/kg), stimulating electrodes were surgically implanted into each cochlea through the round window. The electrodes were either custom-made Pt/Ir ball electrodes (0.45 mm diam), or eight-contact electrode arrays with 0.75 mm spacing (Cochlear, Englewood, CO; ring-type contacts with 0.45 mm diam). In all experiments, we used a wide bipolar configuration (~5 mm between electrodes) with the active electrode inserted ~5 mm into the scala tympani and the return electrode (either another Pt/Ir ball or the most basal contact of the array) just inside the round window.

Part of the skull overlying the occipital cortex was removed to allow for partial aspiration of cortical tissue and access to the IC. Single-unit activity in the IC was recorded using either parylene-insulated tungsten stereotrodes (Microprobe, Potomac, MD; ~2 MΩ impedance), or 16-channel silicon probes (NeuroNexus Technologies, 100 or 150 µm spacing between contacts, 177 µm² site area). Recording electrodes were advanced through the IC either from dorsolateral to ventromedial in the coronal plane tilted 45° off the sagittal plane or vertically from dorsal to ventral (Smith and Delgutte 2007). Stimulus artifact was reduced in real time by means of an adaptive digital filter (Smith and Delgutte 2007).

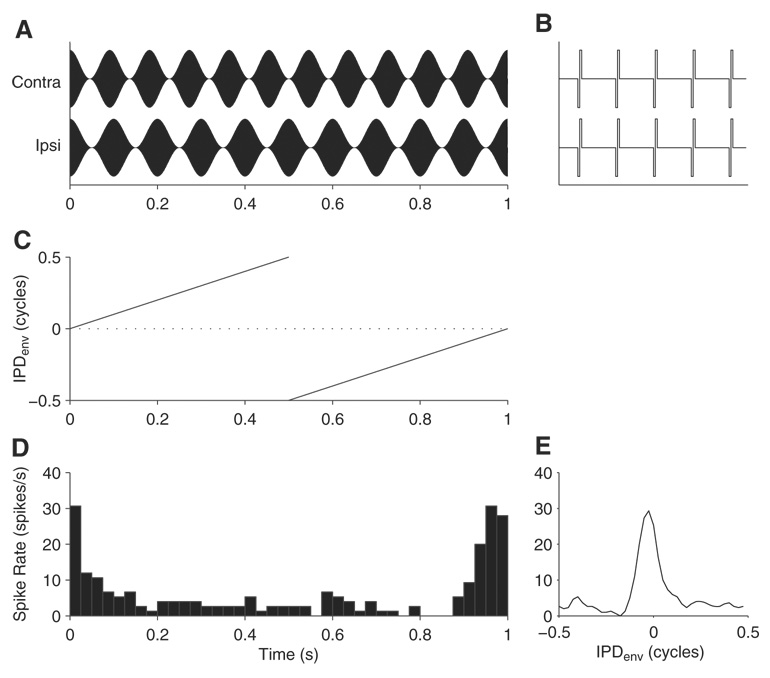
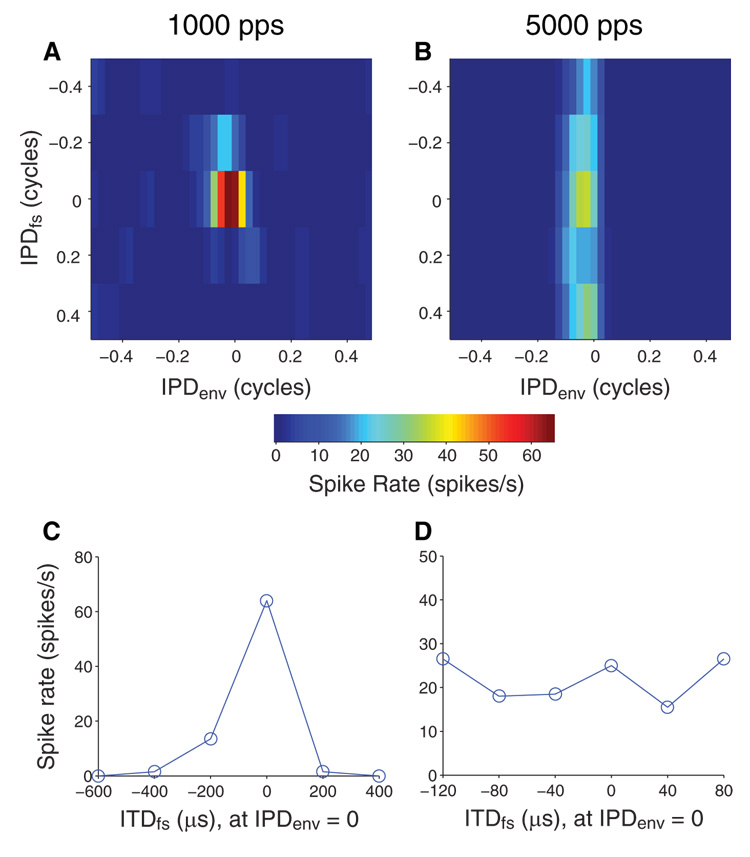
Once a single unit was isolated, its threshold was measured with monaural and diotic pulses. The basic ITD sensitivity was then assessed with constant-amplitude pulse trains at 40 pps (Smith and Delgutte 2007). Following this preliminary characterization, binaural responses to AM pulse trains were studied. AM stimuli were made up of electric pulse trains at a rate of either 1,000 or 5,000 pps. Individual current pulses were biphasic (cathodic-anodic, 50 µs/phase). Pulse trains were sinusoidally amplitude modulated using modulation frequencies (f_mod) of 10–200 Hz and a 100% modulation depth. The “standard” stimulus was a 40-Hz/1,000-pps AM pulse train. Stimuli with dynamic ITDs have been used to efficiently study envelope ITD tuning of single units in normal-hearing animals (Yin et al. 1984). Here a dynamic ITD was imposed in the envelope of AM stimuli by making f_mod in the contralateral ear 1 Hz higher than in the ipsilateral ear (Fig. 1A). The interaural phase difference in the amplitude envelope (IPD_env) of this “binaural modulation beat” (BMB) stimulus takes all possible values from −0.5 to +0.5 cycles over the 1-s beat period (Fig. 1C). The BMB stimulus was presented continuously for 30 s (30 beat cycles). The interaural timing of the carrier pulses was controlled independently and is shown for ITD_fs = 0 (synchronized carrier) in Fig. 1B. In some cases, ITD_fs tuning was measured simultaneously with ITD_env by systematically varying the static ITD_fs of the BMB stimulus (usually over 1 cycle of the 1,000-pps carrier in 100- or 200-µs steps). Unless otherwise stated, the stimulation current was 2 dB above the threshold current level required to elicit sustained responses with the standard AM stimulus in each neuron. All other dB current values are referenced to this threshold. In some units, the dependence of ITD_env tuning on stimulus level was also studied.

FIG. 1.

Binaural modulation beat (BMB) stimulus and example response from an inferior colliculus (IC) neuron. A: BMB stimulus. The modulation frequency in the contralateral ear is 1 Hz above that in the ipsilateral ear to create a dynamic interaural time difference in the envelope (ITD_env) that traverses the full range of interaural phase difference in the amplitude envelope (IPD_env; between −0.5 and 0.5 cycle) every second. For illustrative purposes, the modulation frequencies shown here are relatively low (11 Hz for the contralateral ear and 10 Hz for the ipsilateral ear). B: detailed (5-ms span) view of the stimulus waveforms shows that the carrier pulses are synchronized at the 2 ears (ITD_fs = 0 µs). C: IPD_env as a function of time for the BMB stimulus. D: period histogram of the response of a neuron to 30 s of stimulation by the BMB. Because the spike rate changes over time in synchrony with IPD_env, this neuron is sensitive to IPD_env. E: IPD_env tuning function obtained from response in D.

Data analysis

Spike times were processed to determine the discharge rate as a function of IPD_env. First, a period histogram was computed for 30 presentations of the 1-s modulation beat cycle using a 25-ms bin width. An example is shown in Fig. 1D for f_mod at 10 Hz. IPD_env functions were then computed from the period histograms by converting time to IPD_env cycles and then circularly convolving with a three-point smoothing kernel with values [0.25 0.5 0.25]. The IPD_env function derived from the PST histogram of Fig. 1D is shown in E. This function can also be expressed in terms of ITD_env by multiplying the IPD_env values by the period of f_mod. Positive values of IPD and/or ITD indicate contralateral-leading stimulation, whereas negative values indicate ipsilateral-leading stimulation. Note that because the 1-s beat cycle was analyzed with a 25-ms bin width, the resolution of our IPD_env curves is 1/40 cycle; at low modulation frequencies, this translates to a rather coarse resolution in ITD_env (e.g., 625 µs for 40-Hz modulation). We address this point in the DISCUSSION.

ITD_fs functions were obtained by presenting the BMB stimulus at several ITD_fs steps and plotting the average spike rate over the 30-s stimulus duration as a function of ITD_fs for a specific IPD_env (typically 0) chosen to get near-maximal firing rates.

Sensitivity to ITD was quantified by computing the mean interaural phase and the vector strength (Goldberg and Brown 1969) of the IPD_env and ITD_fs functions. The vector strength takes on a value between 0 and 1 and indicates how much the spike distribution over one cycle of IPD differs from uniform. Neurons are considered to be ITD sensitive if the vector strength of their IPD function is statistically significant (P < 0.001) as determined by the Rayleigh test of uniformity (Mardia and Jupp 2000).

Characteristic delay (CD) and characteristic phase (CP) were estimated in neurons that were tested at several values of f_mod. Mean interaural phase as a function of f_mod was fit with a regression line using a weighted least-squares procedure (Kuwada et al. 1987). Each phase point was weighted by the product of the vector strength and mean firing rate. Only data that passed the linearity test described by Yin and Kuwada (1983), with a criterion of P < 0.005, were analyzed for CD and CP. For these neurons, the slope of the regression line gives the CD and the intercept gives the CP.

We used a metric from signal detection theory to quantify ITD discrimination thresholds based on spike counts from single neurons in a way that can be compared with psychophysical thresholds (Jiang et al. 1997; Shackleton et al. 2003). Our metric D was a slight modification of standard separation (Sakitt 1973; Simpson and Fitter 1973)

$$D_{\mathrm{I}\mathrm{T}\mathrm{D},\mathrm{I}\mathrm{T}\mathrm{D}+\mathrm{\Delta }\mathrm{I}\mathrm{T}\mathrm{D}}=\frac{\left|{\mathrm{\mu }}_{\mathrm{I}\mathrm{T}\mathrm{D}}-{\mathrm{\mu }}_{\mathrm{I}\mathrm{T}\mathrm{D},\mathrm{\Delta }\mathrm{I}\mathrm{T}\mathrm{D}}\right|}{\sqrt{({\mathrm{\sigma }}_{\mathrm{I}\mathrm{T}\mathrm{D}}^2+{\mathrm{\sigma }}_{\mathrm{I}\mathrm{T}\mathrm{D}+\mathrm{\Delta }\mathrm{I}\mathrm{T}\mathrm{D}}^2)/2}}$$

where μ_ITD and μITD + ΔITD are the means of the spike counts and σITD and σITD + ΔITD their respective SDs. This metric expresses the difference in spike counts elicited by stimuli with two different ITDs in units of their combined SD. We use the arithmetic mean of variances rather than the geometric mean used in the original definition of D to avoid problems when the spike-count variance is 0 for one of the two ITDs. Standard separation is analogous to d′ which is often used to quantify discrimination in psychophysical studies (Green and Swets 1966). The just-noticeable difference (JND) in ITD was defined as the ΔITD, from a reference ITD of 0, needed for the standard separation to reach a value of 1. This criterion corresponds to ~76% correct in a two-interval, two-alternative forced choice discrimination task.

RESULTS

Results are based on responses of 47 IC neurons to bilateral electric stimulation of the cochlea with AM pulse trains in 17 deafened cats. While most neurons only exhibited onset discharges to constant-amplitude pulse trains at rates >300 pps (Smith and Delgutte 2007), applying low-frequency AM (<200 Hz) reintroduced ongoing firing at moderate and high pulse rates (1,000 and 5,000 pps). ITDs were applied to the modulation waveform and carrier pulses independently to test the hypothesis that neuronal selectivity would be greater for ITD in the temporal fine structure (ITD_fs) than for ITD_env. Neural sensitivities to ITD_env and ITD_fs were characterized at several intensities, modulation frequencies, and pulse rates.

The breakdown of the number of neurons sensitive to each type of ITD is given in Table 1. Of the 47 neurons studied, 46 responded throughout the duration of AM stimuli when probed with a 1,000-pps carrier at 10 or 40 Hz AM. Of these 46 neurons, 35 (76%) were sensitive to ITD in the amplitude envelope. This is slightly lower than the 86% of neurons that were previously found to be sensitive to ITD for low-rate (40 pps), unmodulated pulse trains (Smith and Delgutte 2007). Thirty one of these ITD_env-sensitive neurons were tested for additional ITD sensitivity in the fine structure with a carrier rate of 1,000 pps. 17/31 neurons were sensitive to both ITD_env and ITD_fs, while the remaining 14/31 neurons were only sensitive to ITD_env. Finally, seven neurons that showed good ITD_fs tuning at 1,000 pps were also tested at 5,000 pps. Only one neuron exhibited any significant ITD_fs sensitivity at this higher rate.

TABLE 1.

Number of neurons responsive to AM stimuli and sensitive to ITD

	Sustained Response to AM (any fmod)	Sensitive to Envelope ITD (any fmod)	Sensitive to Fine Structure ITD (1000 pps)	Sensitive to Fine Structure ITD (5000 pps)
Yes	46	35	17	1
Total Tested	47	46	31	7

Each successive column is a subset from the “yes” row of the previous column. AM, amplitude modulated; ITD, interaural time difference.

Envelope ITD sensitivity at 40 Hz

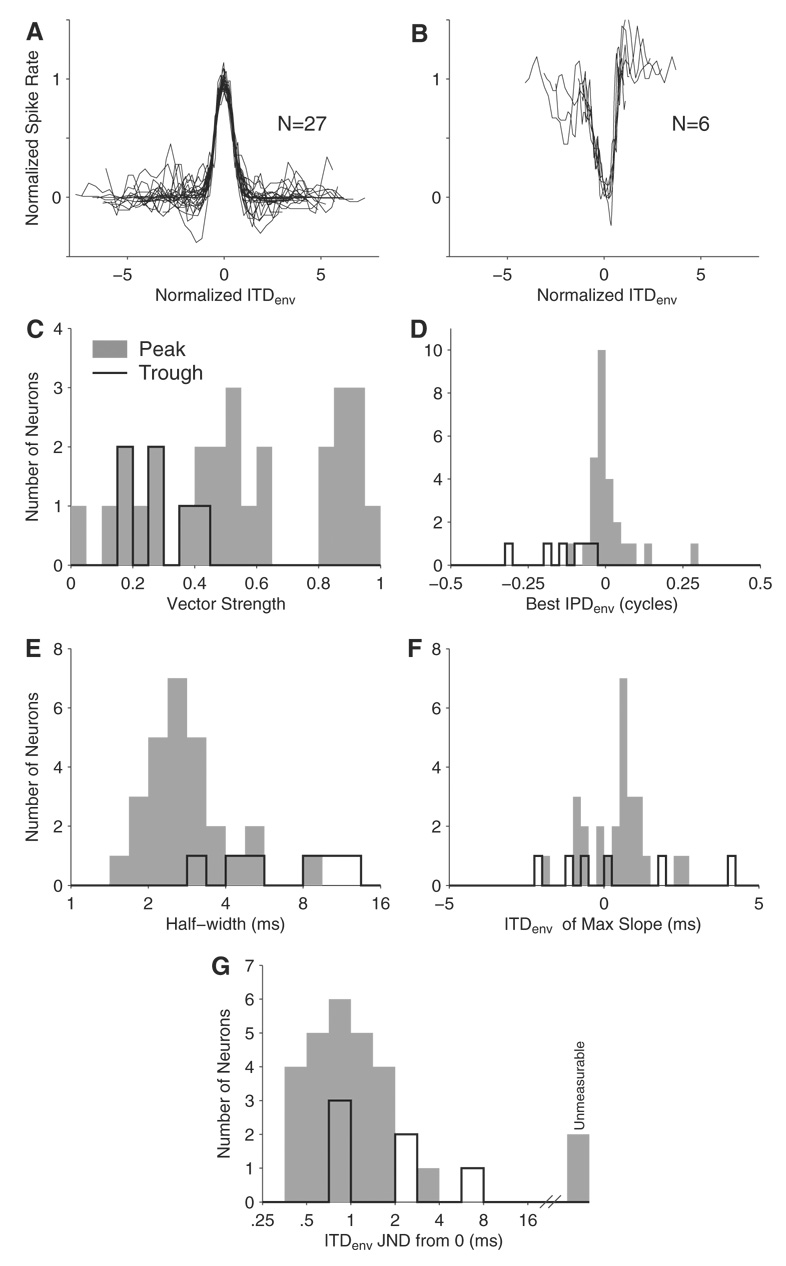
Neurons with sustained responses to AM stimuli were tested for sensitivity to ITD_env using a dynamic ITD_env stimulus (BMB). Because ITD_fs was usually fixed at 0 µs, this stimulus has mismatched envelope and carrier ITDs except for the brief moments when ITD_env passes through 0 µs. If a neuron showed no ITD_env sensitivity with zero ITD_fs, it was tested with other ITD_fs to make sure the lack of ITD_env sensitivity did not result from a choice of unfavorable ITD_fs. A total of 44 neurons were tested with AM pulse trains using a 1,000-pps carrier and f_mod = 40 Hz at 2 dB above threshold. These stimulus parameters were chosen because most neurons in the IC respond well to 40 Hz AM, and 1,000 pps lies within the range of pulse rates used in today’s cochlear-implant processors.¹ Thirty three of these neurons were found to be ITD_env sensitive by the Rayleigh test, and the majority of these (27/33) had peaked-shaped ITD_env tuning (Fig. 2A), whereas the remaining 6 neurons had trough-shaped tuning (Fig. 2B). Gaussian functions with either positive or negative amplitude were fit to peak- and trough-shaped ITD_env curves, respectively, and quantitative measures of ITD tuning (best IPD_env, half-width, ITD of maximum slope, etc.) were obtained from the fitted Gaussians. The Gaussian fits were also used to scale and shift the ITD_env curves in Fig. 2, A and B, so that they are all centered at 0 with a half-width and a height of 1. The peak-shaped curves are largely symmetric around the best ITD, whereas many of the trough-shaped curves show a sharper edge on the side contralateral to the worst ITD (toward positive ITDs from trough) than on the ipsilateral side.

FIG. 2.

ITD_env tuning for the standard BMB stimulus (pulse rate = 1,000 pps, f_mod = 40 Hz) across the population of ITD_env-sensitive IC neurons. A and B: normalized ITD_env functions for all neurons tested (1 trace per neuron) with the standard BMB stimulus. Peak-shaped tuning is shown in A and trough-shaped tuning in B. Responses are scaled and shifted along both axes to show the goodness of fit of the positive and negative Gaussians to the data. C–G: distributions of vector strength, best IPD_env, ITD_env half-width, maximum slope of ITD_env tuning, and neural ITD_env just noticeable differences (JNDs) for neurons with peak- and trough-shaped ITD_env tuning. G: single-unit neural ITD_env JNDs (from a reference of 0 ms) were measured in 31 of 33 neurons. The remaining 2 neurons with unmeasurable JNDs are shown to the right of the distributions.

The distributions of ITD_env tuning metrics are shown in Fig. 2, C–G, separately for peak-shaped (gray bars) and trough-shaped (black lines) curves. However, summary statistics reported below group both types of IPD_env tuning because there are not enough trough units to make strong statistical comparisons between the two. The distribution of vector strengths, which is a measure of the strength of IPD_env tuning (Fig. 2C), is very broad, with a mean of 0.51 and SD of 0.28 for ITD_env-sensitive neurons. The distribution of “best” IPD_env (Fig. 2D), which is defined as the location of the peak or trough of the Gaussian fit, is tightly clustered near 0 cycle with a mean of −0.02 cycles (corresponding to −0.5 ms for 40-Hz AM) and a SD of 0.09 cycles (2.3 ms). All six trough-type neurons had negative worst IPD_env. To characterize the precision of ITD_env tuning, we used the half-width, the width of the tuning curve at half the range of firing rates (sometimes called “full-width at half-max”). The half-width of each ITD_env tuning curve (Fig. 2E) was calculated from the Gaussian fits $(\text{half-width}=2\mathrm{\sigma }\sqrt{2\mathit{\text{ln}}2})$. Trough-type responses tended to have larger half-widths than peak-type responses. The geometric mean half-width (3.3 ms, or 0.13 cycles of the 40-Hz modulator) is much larger than the ±350 µs range of ITDs naturally encountered by a cat, suggesting poor ITD_env discrimination for the average IC neuron at this low AM frequency. However, wide ITD_env tuning may not preclude good discrimination as long as there is a large change in discharge rate within the range of naturally occurring ITDs. Using the fitted Gaussians, we determined the place of maximum slope of ITD_env tuning curves, where the sensitivity is high.² Because there are two ITD_env where the slope approaches maximum (1 on each side of the best/worst ITD), we only characterized the maximum closest to ITD_env = 0. Figure 2F shows that, for the majority of neurons (27/33), maximum slopes occur outside of the ±350 µs range of naturally occurring ITDs for cat, further suggesting poor discrimination of ITD_env by IC neurons.

To test this idea more directly, neural ITD_env discrimination thresholds, a.k.a. just noticeable differences (JNDs) in ITD_env, were estimated from rate responses of single-units using the procedures described in METHODS. Briefly, spike count statistics at each ITD_env step were used to determine the smallest ITD_env step from 0 that could be reliably detected by an ideal observer. ITD_env JNDs were obtained for 31/33 neurons; the other two had unmeasurable ITD_env JNDs because the standard separation D never reached criterion. The distribution of ITD_env JNDs is shown in Fig. 2G on a logarithmic scale. The geometric mean of the distribution (excluding the 2 neurons with unmeasurable JNDs) is 1.0 ms, and the best ITD_env thresholds are near 400 µs. This result confirms that ITD_env discrimination thresholds of IC neurons for 40-Hz modulation are poor compared with the natural range of ITDs encountered by the cat.

Effect of stimulus intensity on envelope ITD tuning

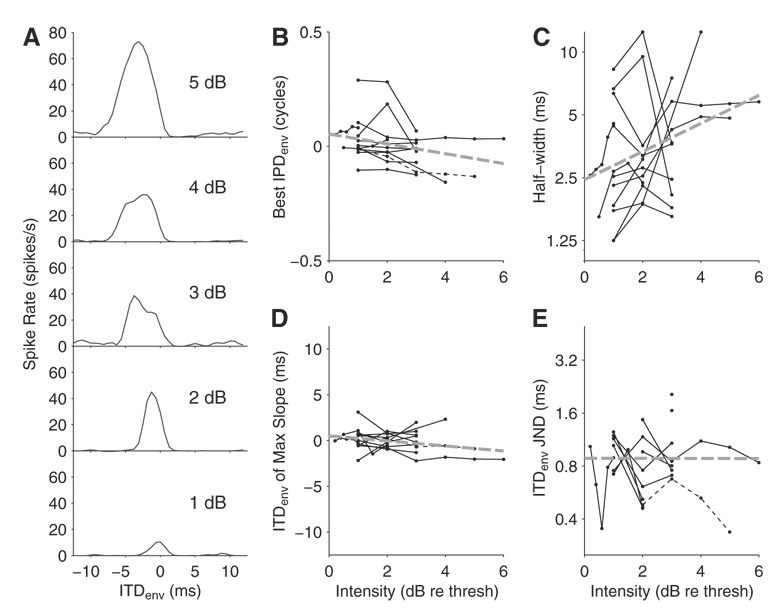
In 12 neurons with peak-shaped ITD_env tuning, ITD_env sensitivity was studied for several stimulus intensities with the standard AM stimulus parameters (carrier rate = 1,000 pps, f_mod = 40 Hz). Current level (in dB) was varied equally in both ears, typically in 1 dB steps, starting from threshold to 3–6 dB above threshold. Figure 3A shows ITD_env tuning curves for an example neuron at five intensities. With increasing intensity, the peak firing rate increases and ITD_env tuning broadens. Also the peak of the ITD_env function shifts toward more ipsilateral leading (negative) ITD_env. This shift results in a relatively stable location of the steep downwards slope of the function near 0 µs despite widening with increasing intensity. These trends are better appreciated by looking at changes with stimulus intensity over the entire sample of neurons. Figure 3B shows the best IPD_env for each neuron as a function of intensity. As for the example neuron in Fig. 3A, best IPD_env shifts toward more negative values (ipsilateral leading) for the majority of neurons. A linear regression (thick dashed line) reveals a significant negative correlation (r = −0.32, P = 0.037) between intensity and best IPD_env across the population, despite considerable scatter. Also as in Fig. 3A, ITD_env half-width increases with intensity for most neurons (Fig. 3C), and the correlation is significant (r = 0.36, P = 0.017). Figure 3D shows that there is also a significant shift toward move negative values in the location of the maximum slope of ITD_env curves with intensity (r = −0.33, P = 0.030). However, the slope of the regression line is shallower for the location of maximum slope than for the best ITD, indicating that the point of maximum sensitivity is more stable to changes in intensity than the best ITD.

FIG. 3.

Effect of stimulus intensity on envelope ITD tuning. A: ITD_env functions for an IC neuron at 5 different stimulus intensities (units are dB re threshold; threshold is 0.71 mA peak amplitude). The stimulus is a binaural modulation beat with a 1,000 pps carrier and 40 Hz AM. B–E: best IPD_env, ITD_env half-width, ITD_env of maximum slope, and neural ITD_env JND as a function of intensity for 12 neurons. Thin lines show data from individual neurons and thick dashed lines are linear fits to the population data. The thin dashed lines are the data from the neuron in A.

Neural ITD_env JNDs are shown as a function of intensity in Fig. 3E. Although there is no significant trend for the population data (r = −0.002, P = 0.99) due to the wide variation in JNDs across neurons, ITD_env JNDs seem to improve (decrease) with increasing intensity for most neurons. To quantify this observation, a straight line was fit to the data for each neuron with measurable JNDs. Across the population, the slopes were significantly <0 (t-test, P = 0.010) with a mean slope of −0.15 ms/dB (σ = 0.15) indicating that, on average, ITD_env JNDs decrease with increasing intensity (this was the case for all 10 neurons that had measurable JNDs at multiple intensities). Thus neural discrimination thresholds generally improved (smaller JNDs) with increasing stimulus intensity despite the broadening of the ITD_env functions. Because the neural thresholds depend on a significant change in firing rate between the reference ITD_env and a neighboring ITD_env, the reduction in JNDs at higher intensities could be caused by increases in slope and/or shifts in the location of the steep slope toward the 0 reference ITD. For the neuron in Fig. 3A (dashed lines in Fig. 3, B–E), the location of the steep slope shifted further away from 0 rather than toward 0, so the improvement in JND must be due to increases in slope relative to the variability of firing rates.

Effect of modulation frequency and carrier rate on ITD_env sensitivity

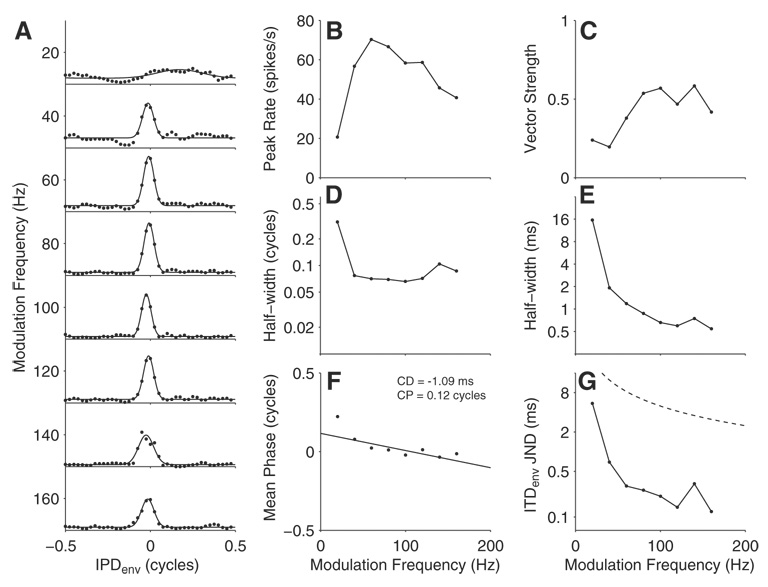
Because the modulation frequencies at the output of a cochlear-implant sound processor will vary over a wide range for stimulation by natural sounds, ITD_env tuning was tested as a function of modulation frequency (f_mod) between 20 and 160 Hz in several neurons with peak-shaped ITD_env tuning. Figure 4A shows IPD_env tuning curves for an example neuron stimulated at eight modulation frequencies with the same 1,000-pps carrier rate. The neuron responds poorly at the lowest f_mod tested (20 Hz); at higher f_mod, both the best IPD_env and the shapes of the tuning curves are fairly stable, although the peak firing rates vary substantially. Figure 4B shows the peak firing rate of each IPD_env curve as a function of modulation frequency, a measurement we call “peak rate modulation transfer function” (prMTF). This neuron responds best to BMB stimuli at f_mod = 60 Hz. The vector strength (Fig. 4C) is statistically significant (P < 0.001) for all f_mod and increases from a low value at 20 Hz to reach a plateau at ≥60 Hz. The half-width of the IPD_env curve (Fig. 4D) is relatively stable for all f_mod except 20 Hz when expressed in units of modulation cycles. Therefore the half-width decreases with increasing f_mod when expressed in ms (Fig. 4E). Mean interaural phase (Fig. 4F) decreases slowly with increasing f_mod. The dependence of mean phase on f_mod is fairly well characterized by a straight line (fit with the weighted least-squares procedure described in METHODS), indicating that the neuron has a CD (−1.08 ms). Finally, the neural ITD_env JND of this neuron (Fig. 4G) generally decreases with increasing f_mod, consistent with parallel drops in ITD_env half-width, and is always substantially below one half modulation cycle (- - -), which represents the maximum possible JND.

FIG. 4.

ITD_env tuning at 8 different modulation frequencies for an example neuron. A: IPD_env tuning curves for each f_mod.●, the measured data; —, Gaussian fits. The vertical axis is spike rate and the same scale is used for all 8 plots. B: peak spike rate as a function of f_mod. C–G: summary metrics from the data in A as a function of f_mod: vector strength (C), ITD_env half-width in units of cycles of the modulation period (D), ITD_env half-width in ms (E), mean interaural phase (F), and neural ITD_env JNDs (G). Line in F is the weighted least-squares fit to the phase data used to estimate characteristic delay and phase (CD and CP). - - - in G indicates half of the modulation period, which is the upper limit of measurable ITD_env JNDs.

We studied the effect of f_mod on ITD_env tuning in 15 neurons using a pulse rate of 1,000 pps and in 11 neurons using a pulse rate of 5,000 pps. Stimuli were presented at the same current level for both pulse rates. Stimulation at rates above the upper frequency limit of phase locking to pure tones in the auditory nerve (4,000–5,000 kHz) has been proposed as a means of improving speech reception with cochlear implants (Rubinstein et al. 1999). Such high-rate stimulation might also be beneficial for binaural hearing by mitigating the possible confounding effects of conflicting ITD_env and ITD_fs cues delivered by today’s processors.

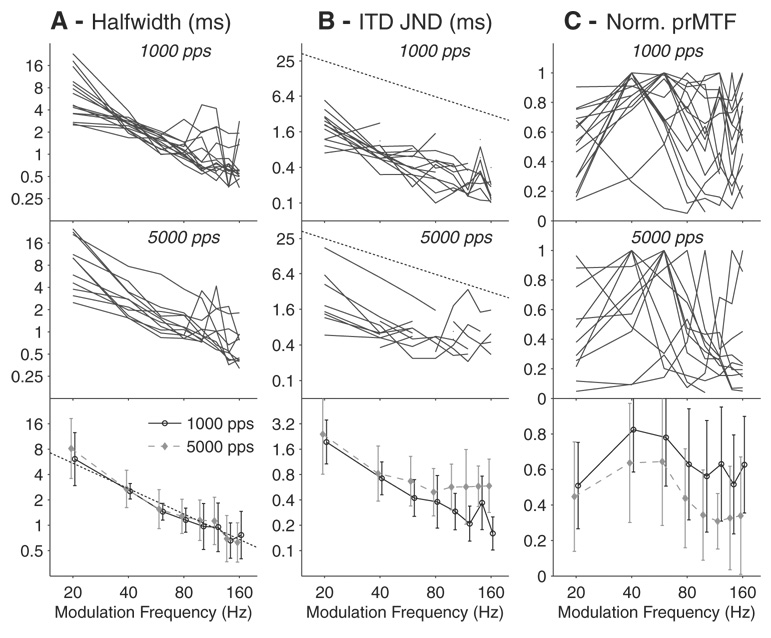
Figure 5 A–C, shows ITD_env half-widths, ITD_env JNDs, and prMTF as a function of f_mod for our entire sample of neurons. The top and middle rows show data from individual neurons for stimuli with pulse rates of 1,000 and 5,000 pps, respectively. The bottom row shows the population mean data for the two pulse rates. ITD_env half-width (Fig. 5A) tends to decrease monotonically with increasing f_mod between 20 and 80 Hz for both pulse rates. This trend continues to hold for a majority of the neurons >80 Hz, but some neurons deviate from monotonicity. The population mean ITD_env half-widths (Fig. 5A, bottom) are very similar for the 1,000- and 5,000-pps carrier rates. The thin dotted line in Fig. 5A, bottom, shows the equation κ/f_mod (where κ = 0.11 is a proportionality constant). This line is very close to the mean data for both pulse rates, meaning the mean half-widths are roughly a constant fraction of the modulation period, although the 5,000-pps curve falls slightly faster for low f_mod. A two-way ANOVA on the logarithms of the half-widths showed a main effect of f_mod (continuous predictor) as expected [F(1,198) = 223, P < 0.001] but no significant effect of carrier rate [F(1,198) = 1.6, P = 0.21] and no interaction.

FIG. 5.

Effect of modulation frequency and carrier rate on envelope ITD tuning. Top row: single neuron data (n = 15) for carrier rate of 1,000 pps. Middle row: single neuron data (n = 11) for carrier rate of 5,000 pps. Bottom row: mean values across the neural population for the two carrier rates, error bars show ±1 SD. A: ITD_env half-width as a function of modulation frequency. The thin dotted line in the bottom panel is κ/f_mod (κ = 0.11). B: ITD_env JNDs as a function of modulation frequency. Thin dotted lines show upper limit of measurable values. Population mean JNDs only include measurable JNDs from single neurons. See Fig. 6A for the proportion of measurable JNDs at each f_mod. C: peak firing rate of IPD_env curve as a function of modulation frequency. Rates are normalized to their maximum.

Neural ITD_env JNDs were computed from each neuron’s ITD_env tuning curves as a function of f_mod (Fig. 5B). The dotted line in each panel of Fig. 5B shows 1/(2f_mod), which is the maximum measurable JND. Unmeasurable JNDs are not plotted. In general, the neural JNDs decrease with increasing f_mod, consistent with the decrease in half-width in Fig. 5A. For the 1,000-pps carrier, the geometric mean ITD_env JND across the population drops steadily with increasing f_mod over the entire range (Fig. 5B, bottom). Mean ITD_env JNDs for the 5,000-pps carrier closely parallel the JNDs for the 1,000-pps carrier ≤80 Hz but become nearly flat >80 Hz unlike the decreasing trend seen for the 1,000-pps carrier. A two-way ANOVA on the logarithms of the JNDs showed a main effect of f_mod [F(1,143) = 61.5, P < 0.001] and a significant interaction between f_mod (continuous predictor) and carrier rate [F(1,143) = 4.64, P = 0.033], reflecting the different dependence of JNDs on f_mod for the two rates.

The difference in mean ITD JNDs between the two carrier rates at higher f_mod is unexpected because the mean ITD_env half-widths are very similar (Fig. 5A, bottom). However, these differences may be explained by taking into account the prMTFs shown in Fig. 5C. For both carrier rates, most prMTFs for individual neurons are band-pass, although the best f_mod varies considerably among neurons. The mean prMTFs across the population (Fig. 5C, bottom) are also band-pass for both carrier rates with best modulation frequencies near 40–60 Hz. However, the magnitude of the mean prMTF is greater for the 1,000-pps carrier than for the 5,000-pps carrier, and this difference is most prominent at higher f_mod where the mean prMTF for 5,000 pps shows a sharp drop-off. These differences in mean prMTFs reflect in part wider bandwidths of individual prRMTFs at 1,000 pps compared with 5,000 pps and in part a greater proportion of higher best f_mod at 1,000 pps. In any case, the lower firing rates in response to higher f_mod for the 5,000- pps carrier rate may largely account for the plateau in mean ITD JNDs seen in Fig. 5B.

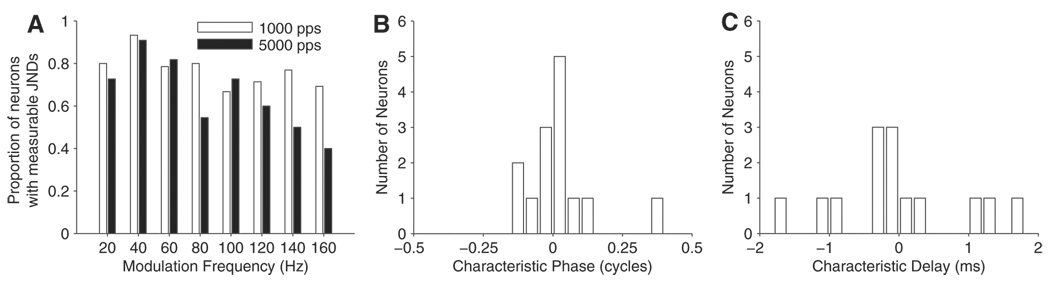
A further difference between the two carrier rates emerges when the proportion of measurable ITD_env JNDs is analyzed (Fig. 6A). For the 1,000-pps carrier, the proportion of neurons with measurable ITD_env JNDs is ~70% across the entire range of f_mod tested. For the 5,000-pps carrier, the proportion is similar to that for 1,000 pps for f_mod between 20 and 60 Hz but tends to fall at higher f_mod to reach ~40% at 160 Hz. This is also probably a result of the lower peak firing rates at higher f_mod for the 5,000-pps carrier compared with the 1,000-pps carrier (Fig. 5C). A similar tendency for neural MTFs to drop more rapidly at higher pulse rates has been reported in the auditory cortex for monaural electric stimulation of the cochlea (Middlebrooks and Lee 2004).

FIG. 6.

A: proportion of neurons with measurable ITD_env JNDs at different modulation frequencies. B and C: distributions of CP (B) and CD (C) calculated over f_mod from 20 to 160 Hz with a carrier rate of 1,000 pps (14/15 neurons had a linear phase-f_mod relationship and were included in this analysis).

The mean interaural phase of neurons that were tested over a range of modulation frequencies was analyzed. Only data for the 1,000-pps carrier was examined here because more neurons were tested at 1,000 pps than at 5,000 pps. Fourteen of 15 neurons had a linear phase-f_mod relationship (P < 0.005) and were used to calculate distributions of CP and CD. The distribution of CP (Fig. 6B) is centered near 0, with a mean of 0.03 ± 0.13 (SD) cycles, consistent with the observation that these neurons had peak-shaped IPD_env functions. The distribution of CD is broad, with a mean of −0.03 ± 0.91 (SD) ms.

ITD sensitivity to the temporal fine structure

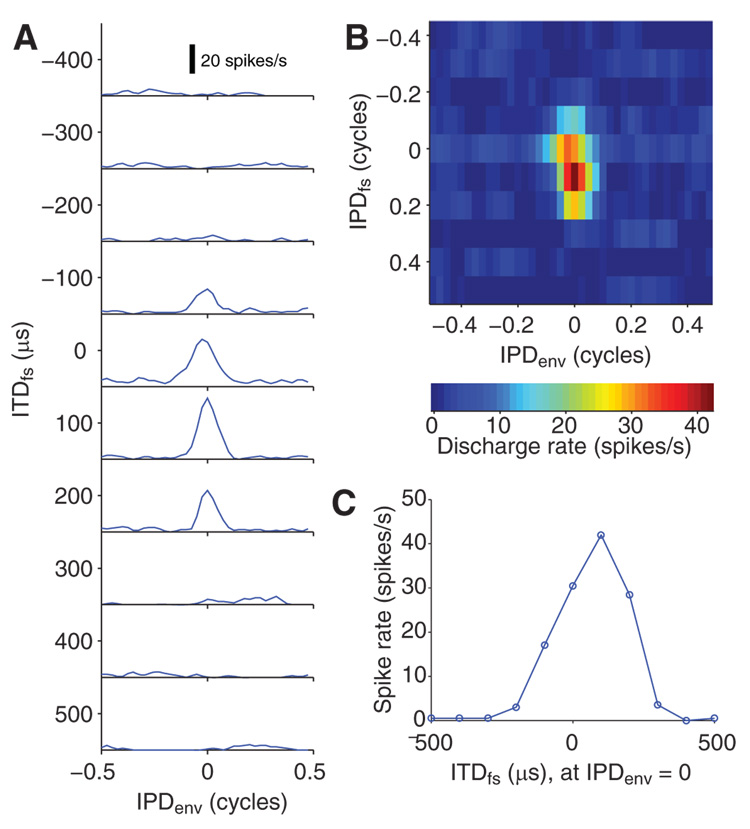
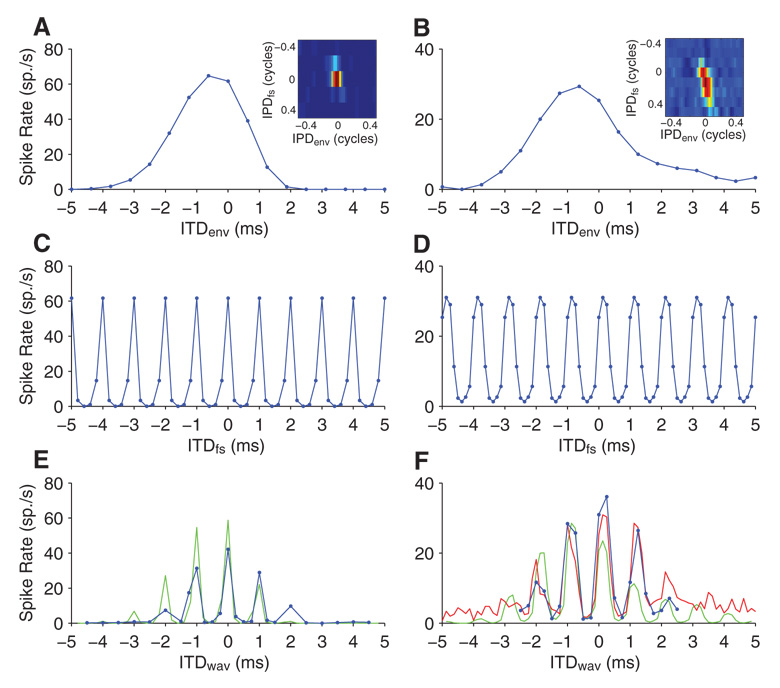
Sensitivity to ITDs in the temporal fine structure (ITD_fs) was measured simultaneously with ITD_env sensitivity by introducing static ITDs in the carrier of the dynamic ITD_env stimulus. Tests of ITD_fs sensitivity were always made at f_mod = 40 Hz, most frequently with a carrier rate of 1,000 pps. Figure 7A shows IPD_env curves for an example neuron at 10 different IPD_fs steps covering the 1,000-µs period of the 1,000-pps carrier. This neuron is sensitive to ITDs introduced to both the amplitude envelope and the temporal fine structure of the stimulus. It responds well to ITD_fs between −100 and +200 µs and IPD_env near 0 cycles. These curves can be combined into a two-dimensional pseudocolor display of discharge rate against both IPD_env and IPD_fs (Fig. 7B). ITD_fs tuning curves were derived from this display by taking one column and converting IPD_fs into ITD_fs by scaling by the 1,000-µs carrier period. The ITD_fs tuning curve for IPD_env = 0 cycles (Fig. 7C) shows sharp tuning centered at +100 µs. The half-width of ITD_fs tuning is 284 µs (from fitted Gaussian), compared with 2.57 ms for the half-width of ITD_env tuning. Note that, although IPD tuning is narrower in the modulation dimension, ITD tuning is narrower in the carrier dimension due to the large disparity in period between the AM and the carrier (25 vs. 1 ms, respectively).

FIG. 7.

Sensitivity to fine structure ITD. A: IPD_env tuning curves at for 10 different fine structure ITD (ITD_fs). B: joint IPD_env-IPD_fs tuning function derived from data in A. C: ITD_fs tuning at IPD_env = 0.

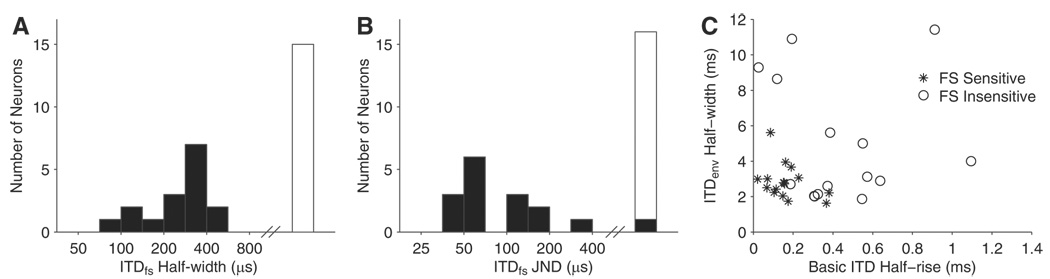
A total of 31 ITD_env-sensitive IC neurons were tested for sensitivity to ITD_fs at a carrier rate of 1,000 pps. Roughly half of these neurons (17/31) showed significant ITD_fs tuning (P < 0.001, as assessed with the Rayleigh coefficient of the IPD_fs vector strength). A histogram of ITD_fs half-widths for the 31 neurons is shown in Fig. 8A. ITD_fs sensitive neurons are shown by ■, and □ to the right indicates the neurons that were not sensitive to ITD_fs at 1,000 pps. The mean ITD_fs half-width for the 17 ITD_fs-sensitive neurons was 287 µs, which is narrower than the 691 µs mean half-width observed for 40-pps constant-amplitude pulse trains in a larger sample of IC neurons (Smith and Delgutte 2007). A histogram of ITD_fs JNDs (from a reference ITD_fs of 0 µs) for the population is shown in Fig. 8B. The mean ITD_fs JND for ITD_fs-sensitive neurons is ~100 µs, which is comparable to the 118 µs mean ITD JND for low-rate constant-amplitude pulse trains (Smith and Delgutte 2007).

FIG. 8.

Characteristics of ITD_fs sensitivity across IC population for 1,000-pps carrier and 40-Hz modulation. A: distribution of ITD_fs half-widths. ■, ITD_fs-sensitive neurons; □, ITD_fs-insensitive neurons. B: distribution of neural ITD_fs JNDs. C: scatter plot of half-rise of ITD tuning for 40 pps constant-amplitude pulse trains (Smith and Delgutte 2007) against ITD_env half-width at 40 Hz. *, ITD_fs-sensitive neurons; ○, ITD_fs-insensitive neurons for the 1,000-pps carrier.

ITD_fs tuning for the standard stimulus (1,000 pps, 40 Hz) is much sharper, when present, than ITD_env tuning over the range of f_mod tested (20–160 Hz; Fig, 5A). The mean ITD_fs JND is also significantly lower than the mean ITD_env JND (Fig. 5B) over the range of f_mod tested. While ITD_env tuning would presumably continue to sharpen at higher f_mod, the peak firing rate of most neurons would be expected to drop off sharply for f_mod >300 Hz based on IC data for monaural electric stimulation of the cochlea (Snyder et al. 2000). Thus ITD_env tuning may never “catch up” with ITD_fs even by using higher modulation frequencies.

Relating ITD_fs tuning to ITD tuning with low-rate, constant-amplitude pulse trains

Why is only a subset of neurons sensitive to ITD_fs at 1,000 pps, while most binaural neurons are sensitive to ITD_env and nearly 90% of neurons in a larger sample were sensitive to ITD for constant-amplitude, 40-pps pulse trains (Smith and Delgutte 2007)? About half of the neurons in the Smith and Delgutte (2007) study had ITD half-widths >500 µs, which is half the period of our standard 1,000-pps carrier, and thus would be unlikely to show ITD_fs sensitivity at this carrier rate. This corresponds roughly to the proportion of ITD_fs -insensitive neurons we observed, suggesting the hypothesis that ITD_fs sensitive neurons may just be those that have the sharpest ITD tuning. To test this hypothesis, we investigated possible differences in basic ITD tuning between the ITD_fs-sensitive and -insensitive neurons.

Basic ITD tuning characteristics measured with 40-pps constant- amplitude pulse trains include the ITD of maximum slope (ITD_MS), the half-rise (width of the rate-ITD function about ITD_MS between 25 and 75% normalized spike rate), and the physiological modulation depth (PMD; normalized change in spike rate within the natural range of ITD for the cat). ITD_MS and half-rise are used for comparison in lieu of best ITD and half-width because the latter are only defined for peak- and trough-shaped ITD curves, whereas the former are also defined for monotonic and biphasic ITD curves. These basic ITD tuning characteristics, as well as ITD_env half-width and electrode depth, were compared between ITD_fs-sensitive (n = 16) and ITD_fs-insensitive neurons (n = 15) using two-sample t-tests. Table 2 shows the means and SDs, and the result of the t-test, for each metric. ITD_fs-sensitive neurons have significantly narrower half-rises, ITD_MS closer to 0 (and within the natural range of ITD), and higher PMDs than ITD_fs-insensitive neurons, consistent with the hypothesis that this subset of neurons is more sharply tuned. ITD_fs-sensitive neurons also have significantly narrower ITD_env half-widths and were recorded at shallower electrode depths than ITD_fs-insensitive neurons, suggesting that these neurons would have lower CFs in normal-hearing animals.

TABLE 2.

Difference in basic ITD tuning between ITD_fs-sensitive and -insensitive neurons

	Basic Half-Rise, µs	Basic |ITDMS|, µs	Physiological Modulation Depth, %	ITDenv Half-Width, ms	Electrode Depth, µm
ITDfs sensitive (16)	161 ± 98	143 ± 173	84.8 ± 21.7	2.83 ± 0.97	2213 ± 740
ITDfs insensitive (15)	436 ± 292	398 ± 372	51.3 ± 27.4	4.95 ± 3.42	2711 ± 563
Significance	P = 0.0013	P = 0.019	P < 0.001	P = 0.024	P = 0.045

Numbers are means ± SD. P values are from two-sample t-tests comparing properties of ITD_fs-sensitive and -insensitive units.

Figure 8C shows basic ITD half-rise (measured with 40-pps pulse trains) plotted against ITD_env half-width for 40-Hz modulation for the population of neurons. Although there is no significant correlation between these two metrics (r = 0.14, P = 0.50), their combination provides a fairly clear segregation of ITD_fs-sensitive from ITD_fs-insensitive neurons: ITD_fs-sensitive neurons (*) cluster in the lower left corner of the plot. ITD_fs-sensitive neurons with larger basic ITD half-rise tend to have smaller ITD_env half-width, whereas those with larger ITD_env half-width tend to have smaller basic ITD half-rise. Overall, these analyses support the hypothesis that ITD_fs-sensitive neurons are fundamentally more sharply tuned to ITD than ITD_fs-insensitive neurons.

ITD_fs tuning at high carrier rates

In a small number of ITD_fs-sensitive neurons, the effect of using a higher pulse rate on ITD_fs tuning was tested. The standard stimulus had a carrier rate of 1,000 pps and therefore a period of 1,000 µs. The higher pulse rate was 5,000 pps with a period of 200 µs. ITD tuning would have to be very sharp to see a modulation of the response within the ±100 µs possible range of ITD_fs with a 5,000-pps carrier. Very few (3/92) neurons in our sample studied with 40-pps constant-amplitude pulse trains had ITD half-widths <200 µs (Smith and Delgutte 2007).

Figure 9, A and B, shows the IPD_env-IPD_fs tuning display for an example neuron with f_mod = 40 Hz for pulse rates of 1,000 and 5,000 pps, respectively. ITD_fs tuning at 1,000 pps is relatively sharp for this neuron (half-width = 108 µs, vector strength = 0.85) and the best ITD_fs is near 0 µs (Fig. 9C). When the carrier rate is increased to 5,000 pps (Fig. 9B), IPD_env tuning curves become very similar for all IPD_fs tested, indicating that ITD_fs tuning is essentially eliminated (Fig. 9D, vector strength = 0.02 and not statistically significant). The effect of carrier rate on ITD_fs tuning was tested in seven neurons with good ITD_fs tuning at 1,000 pps; in each case, ITD_fs tuning was eliminated or severely reduced with the 5,000-pps carrier. The mean vector strength was 0.68 for the 1,000-pps carrier and only 0.13 for 5,000 pps. Six of the seven vector strength measures for the 5,000-pps carrier were not significant at the 0.1% level.

FIG. 9.

Effect of carrier rate on ITD_fs tuning. A and B: joint IPD_env-IPD_fs tuning function for a neuron at a pulse rate of 1,000 pps (A) and 5,000 pps (B). f_mod was 40 Hz in both cases. C and D: ITD_fs tuning at IPD_env = 0 for 1,000 pps (C) and 5,000 pps (D).

Whole waveform ITD sensitivity for AM stimuli

All measures of ITD sensitivity reported so far involved independent manipulations of envelope and fine structure ITD. We also tested sensitivity to ITD imposed on the whole waveform of AM pulse trains in which envelope and carrier ITDs are matched. For acoustic stimulation, this would be a more natural stimulus because ITDs are normally contained in both the envelope and the fine structure in free field. While current processors for cochlear implants only deliver ITD in the envelope, whole-waveform ITDs might be implemented in future processing strategies to better mimic normal acoustic stimulation.

Figure 10A shows the dynamically derived ITD_env tuning curve (ITD_fs = 0 µs) for the same neuron as in Fig. 9A using 40-Hz AM and 1,000-pps carrier rate. The colored inset of Fig. 10A shows the joint ITD_env-ITD_fs tuning for this neuron; the main plot of Fig. 10A is a horizontal section (ITD_fs = 0 µs) through the colored inset. Because the 1,000-pps carrier rate has a period of 1 ms, the ITD_fs curve for this neuron over the range from −5 to +5 ms (Fig. 10C) is the same as the ITD_fs curve from Fig. 9C repeated every 1 ms. Comparison of Fig. 10C with Fig. 10A illustrates how much sharper the ITD_fs tuning is than ITD_env tuning. Whole waveform ITD (ITD_wav) tuning was also measured with static ITD stimuli for this neuron (Fig. 10E, blue). The shape of the ITD_wav curve is very close to the product of the ITD_env and ITD_fs curves (Fig. 10E, green line): the response peaks every 1,000 µs as does the ITD_fs curve but only over a range of ITDs of about the same width and shape as the ITD_env curve. However, the envelope of the ITD_wav curve is more symmetric ~0 ITD than the ITD_env curve, which is slightly offset toward negative ITDs. This may be because the ITD_env curve was measured dynamically, whereas the ITD_wav curve was measured with static stimuli. In any case, within the range of relevant ITDs for a cat or a human, the ITD_wav sensitivity of this neuron is clearly dominated by its sensitivity to ITD_fs.

FIG. 10.

Sensitivity to ITD in the whole waveform for 2 neurons using a 1,000-pps, 40-Hz AM pulse train. Left: neuron is the same neuron as in Fig. 9. A and B: ITD_env tuning for ITD_fs fixed at 0. Insets: joint ITD_env-ITD_fs tuning functions. C and D: ITD_fs tuning for ITD_env fixed at 0. E and F: tuning to ITD in the whole waveform (ITD_wav). Blue points are direct measurements, green lines show predictions of ITD_wav tuning from multiplication of ITD_env and ITD_fs tuning curves, and the red line (F only) shows predictions of ITD_wav tuning from resampling the joint ITD_env-ITD_fs tuning function.

That the whole-waveform ITD curve can be approximated by the product of the ITD_env and ITD_fs curves as in Fig. 10E would be predicted mathematically if the effects of ITD_env and ITD_fs on neural responses were separable, i.e., if the response as a function of both ITD_env and ITD_fs could be expressed as the product of a function of ITD_env alone and a function of ITD_fs alone. The joint responses as a function of ITD_env and ITD_fs (as in Fig. 7B and Fig. 10A) were analyzed with singular value decomposition (SVD) to assess their separability (Pena and Konishi 2001). The SVD of a completely separable response has only one nonzero singular value, and the original response can be perfectly reconstructed from the external product of two vectors (in this context representing the independent sensitivities to ITD_env and ITD_fs). We assessed the degree to which each distribution is separable by determining the fraction of the energy of the joint distribution contained in the first singular value for each ITD_fs-sensitive neuron. For example, the fractional energy in the first singular value for the distribution of Fig. 10A is 97.3%, indicating a high degree of separability and explaining the observed resemblance between the whole-waveform ITD curve and the product of the ITD_env and ITD_fs curves for this neuron. Across our sample of 16 ITD_fs-sensitive neurons, the mean fractional energy in the first singular value was 87.9 ± 5.7%, indicating that a multiplicative model, with separable ITD_env and ITD_fs tunings, accounts for ~88% of the variance in the joint ITD_env-ITD_fs tuning space.

Figure 10, right, show results for another ITD_fs-sensitive neuron. The joint ITD_env and ITD_fs tuning function for this neuron (Fig. 10B, inset) is less separable than that for the neuron of Fig. 10A as shown by the marked tilt in the high-amplitude region. SVD analysis confirms the lesser separability of tuning for this neuron, with a fractional energy of 84.6% in the first singular value. As expected, multiplying the ITD_env and ITD_fs curves (green line in Fig. 10F) gives a relatively poor prediction of the measured ITD_wav curve (blue line in Fig. 10F) with the best ITD occurring near −1 ms in the prediction versus 0 ms in the data. Responses to the ITD_wav stimulus can also be predicted by resampling the joint ITD_env-ITD_fs distribution along the diagonal line representing equal ITD_env and ITD_fs. The prediction based on resampling the joint ITD_env-ITD_fs tuning function (red line in Fig. 10F) better matches the measured ITD_wav curve than the multiplicative prediction based on the separability assumption (green line).

In summary, sensitivity to ITD in the whole waveform can be predicted from joint measurements of ITD_env and ITD_fs sensitivities. For a majority of neurons that have nearly independent sensitivities to ITD_env and ITD_fs, the prediction of ITD_wav sensitivity can be obtained more easily from separate measurements of these two sensitivities.

Phenomenological model of electric ITD tuning

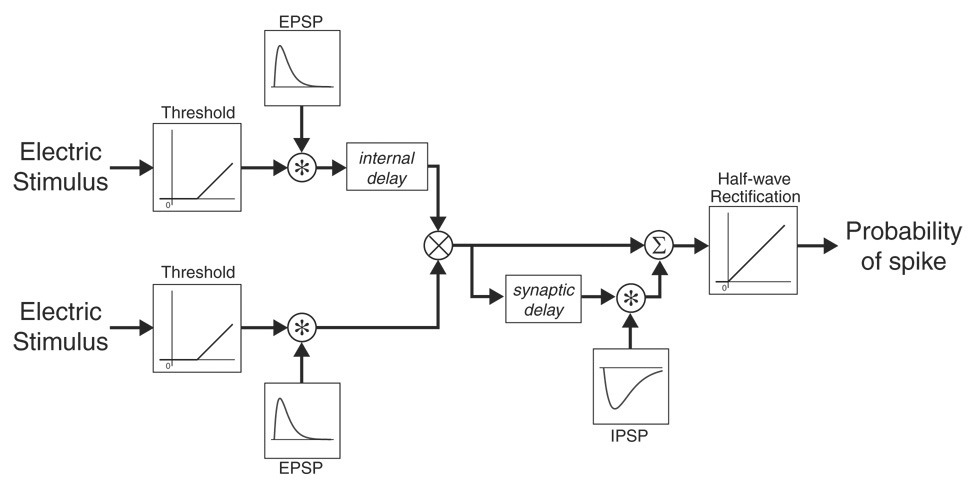
To gain some insight into the mechanisms that underlie the ITD sensitivity of IC neurons for bilateral electric stimulation, we developed a phenomenological model that captures key trends in the data. The model consists of a cascade of stages that convert the electric current waveforms delivered to each ear into the firing probability of a single IC neuron. By varying ITD as in our experiments, rate-ITD functions are derived by integrating the spike probability over time to get the predicted firing rate at each ITD.

Figure 11 shows a block diagram of our model; the parameter values used are given in Table 3. The model includes a highly simplified peripheral stage describing auditory-nerve responses to electric stimulation, an interaural coincidence detector giving rise to ITD sensitivity, and an envelope processing model similar to that developed by Nelson and Carney (2004) for IC neurons. Peripheral processing (stage 1) is modeled by subtracting a constant threshold from the input waveform and then half-wave rectifying. The resulting waveform is then convolved with an excitatory postsynaptic potential (EPSP) of the form: α_ete^−t/τe, where α_e is a scale factor, τ_e is the time constant. This convolution implements a low-pass filter and serves to add temporal jitter and limit phase locking to the carrier at high pulse rates. The binaural processor (stage 2) consists of an internal delay imposed on the output of the contralateral ear to model to neuron’s best ITD followed by a multiplication of the signals from the two ears to approximate interaural coincidence detection as in the Jeffress (1948) model. In stage 3, the output of the coincidence detector splits into two parallel branches. The first branch is excitatory and goes directly into a summation stage representing synaptic integration in the IC. The signal in the second branch is delayed (synaptic, 1 ms) and convolved with an inhibitory postsynaptic potential (IPSP) of the form: −α_ite^−t/τi, where α_i is a scale factor, and τi is the time constant. The negative sign makes the second branch inhibitory. The two branches are finally summed and half-wave rectified to obtain the probability of spiking in the IC neuron. The inhibitory branch in stage 3 serves to block sustained firing at high pulse rates and high modulation frequencies.

FIG. 11.

Phenomenological model of electric ITD tuning. Operations are shown in circles and include convolution (*), multiplication (×), and summation (∑).

TABLE 3.

Parameter values used in the phenomenological model of ITD tuning

Parameter	Value
τe, ms	0.1
τi, ms	2.0
αe/αi	1.25
Synaptic delay, ms	1.0

The model captures key aspects of the data for both constant-amplitude and AM pulse trains, including: the reduction in sustained responses to constant-amplitude pulses with increasing pulse rate (Smith and Delgutte 2007; Snyder et al. 1995), the restoration of sustained responses to high-rate pulse trains by low-frequency AM, the decrease in ITD_env half-width with increasing modulation frequency, the increase in ITD_env half-width with increasing stimulus intensity, sharper tuning to ITD_fs than ITD_env, and the loss of ITD_fs sensitivity at very high pulse rates.

In the following examples of model responses to various electric stimuli, the peak stimulus intensity is expressed in decibels relative to the model threshold. So if an AM pulse train stimulus is 1 dB re threshold, then only pulses occurring during the peaks of the amplitude envelope exceed threshold.

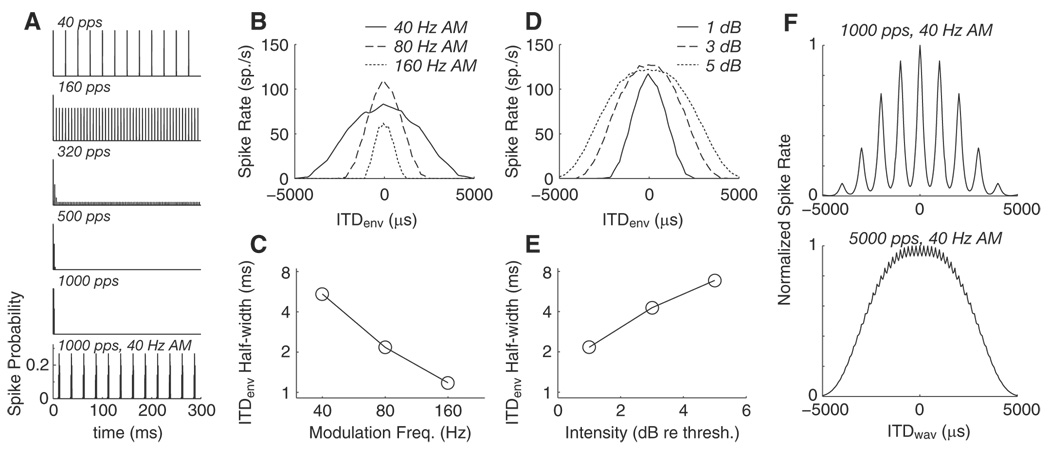
Figure 12A shows the model responses to pulse trains of different carrier rates with an ITD equal to the internal delay of the model neuron at 1 dB re threshold. These responses represent the spike probabilities as a function of time and can be compared with PST histograms of measured IC responses. The first five panels show the output of the model for constant-amplitude pulse trains with rates ranging from 40 to 1,000 pps. For 40 and 160 pps, the responses are sustained and locked to the individual stimulus pulses. For 320 pps, the response remains locked to the individual stimulus pulses, but firing probability is high at the onset and then is low throughout the remainder of the stimulus. For 500 and 1,000 pps, the spike probability is only greater than zero during a brief onset transient. The bottom panel shows the model output for a 1,000-pps pulse train with 40-Hz sinusoidal AM. Low-frequency AM restores a sustained response that is now phase-locked to the 40-Hz amplitude peaks of the stimulus. The key element of the model that creates a transition between sustained and onset-only responses is the delayed inhibition in stage 3. Because the time constant of the inhibition (τ_i = 2 ms) is an order of magnitude longer than that for the excitation (τ_e = 0.1 ms), the inhibition produced by one pulse builds up gradually and overlaps with the excitation produced by the next pulse for pulse rates >200 pps. At lower pulse rates, inhibition and excitation do not interact because they are interleaved in time. The temporal interaction between excitation and inhibition also imposes an upper limit on modulation frequencies that can elicit sustained responses to AM stimuli. A similar interplay between excitation and inhibition was proposed to account for neural responses to SAM tones in the MSO of the mustache bat (Grothe 1994).

FIG. 12.

Responses of phenomenological model to various ITD stimuli. A: temporal response patterns for constant-amplitude pulse trains as a function of pulse rate. All stimuli are 300 ms in duration, the peak intensity is 1 dB re model threshold, and the ITD equals the model neuron’s internal delay (ITD_best). The bottom trace shows the effect of 40-Hz AM on the response to a 1,000-pps pulse train. B: ITD_env tuning for a 1,000-pps AM stimulus at 3 modulation frequencies (1 dB re threshold). C: ITD_env half-width decreases with increasing modulation frequency. D: ITD_env tuning for a 1,000-pps, 80-Hz AM stimulus at 3 stimulus intensities (dB re threshold). E: ITD_env half-width increases with increasing intensity. F: model ITD_wav tuning for 1,000-pps, 40-Hz AM stimulus (top) and 5,000-pps, 40-Hz AM stimulus (bottom) at 1 dB re threshold.

Envelope ITD functions for the model were calculated as a function of modulation frequency (Fig. 12B) and overall intensity (Fig. 12D) for AM pulse trains with 1,000-pps carriers. Consistent with the neural results, ITD_env half-width decreases with increasing f_mod (Fig. 12C) and increases with increasing intensity (Fig. 12E). In the model, the width and shape of ITD_env tuning are primarily dependent on the width and shape of the suprathreshold peaks in each AM cycle. By increasing f_mod, the width of the suprathreshold portion of the modulation envelope narrows and thus ITD_env half-width narrows. Similarly by increasing the stimulus intensity, more pulses within each AM cycle lie above threshold and thus the ITD_env half-width increases. Finally, whole waveform ITD curves from the model are shown in Fig. 12F for 40-Hz AM pulse trains at 1 dB re threshold with carrier rates of 1,000 and 5,000 pps. For the 1,000-pps carrier (top), ITD tuning to the fine structure creates a 1,000-µs periodicity in the ITD function that is much narrower than the wide ITD_env tuning that gives the function is overall shape. For the 5,000-pps carrier (bottom), ITD_fs is essentially lost, and only ITD tuning to the envelope remains. These results are consistent with the neural data (Fig. 9 and Fig. 10). In the model, ITD_fs tuning is lost at 5,000 pps because of low-pass filtering by the EPSP (τ_e = 0.1 ms) before coincidence detection.

DISCUSSION

We studied single-neuron responses to amplitude-modulated trains of electric current pulses in the IC of anesthetized cats with bilateral cochlear implants. Sensitivity to envelope ITD was found to be similar in many respects to that seen with acoustic stimulation. In agreement with results using acoustic stimulation (Batra et al. 1993), the half-width of ITD_env curves decreased with increasing modulation frequency such that half-width was nearly constant when expressed in units of modulation phase. Neurons that had the best sensitivity to ITDs in low-rate constant-amplitude pulse trains were also the most likely to be sensitive to ITD_fs with a 1,000-pps carrier. Neural ITD_fs selectivity was relatively sharp when compared with ITD_env tuning for 1,000-pps carriers but was eliminated at the high carrier rate of 5,000 pps. This is similar to acoustic stimulation where neural sensitivity to ITD_fs in the IC drops rapidly >1,500 Hz (Joris 2003; Yin et al. 1984) and ITD_env JNDs to sinusoidal AM tones are poorer than JNDs for pure tones at the AM envelope frequency (Griffin et al. 2005).

Sensitivity to envelope ITD

The vast majority of neurons in the IC were sensitive to ITD_env at modulation frequencies that elicited a sustained response. The decrease in ITD_env half-width with increasing f_mod was consistent with constant IPD_env half-width over the range of f_mod tested (20–160 Hz). A similar result has been reported in high-CF neurons of the IC of the awake rabbit using acoustic stimulation with SAM tones over a higher range of f_mod (300–700 Hz) (Batra et al. 1993). As for acoustic stimulation (Batra et al. 1993; Yin et al. 1984), the dependence of best ITD_env on f_mod was fairly linear for the majority of our neurons, so that these neurons had a well-defined CD. The range of CDs was comparable to that seen acoustically for modulation frequencies <150 Hz (Batra et al. 1993), although the small size of our sample precludes a detailed comparison.

Our IPD_env curves were sampled at a resolution of 1/40 cycle, which translates to rather coarse sampling in ITD_env for low modulation frequencies (e.g., 625 µs for 40-Hz modulation). It is conceivable that this coarse ITD_env sampling at low f_mod might have obscured sharp features in the ITD_env curves, particularly near 0 ITD. We believe that this possibility is very unlikely for the following reasons. First, the ITD_env curves were all smooth and well-behaved (Fig. 1E, Fig. 3A, and Fig. 4A) and highly consistent across neurons (Fig. 2A). Because the points at which we sample the ITD_env curves differ in relation to each neuron’s best ITD_env, the shapes of the ITD_env curves would not be expected to be so consistent if they contained micro features. Second, the ITD_env curves maintain their shape as the modulation frequency is increased (Fig. 5), and the ITD_env resolution improves in proportion to f_mod (e.g., 156-µs resolution for 160-Hz modulation). Finally, none of the whole-waveform ITD curves we measured using a resolution of 250 µs showed any unusual feature (Fig. 10). These curves always consisted of a rapid oscillation reflecting ITD_fs sensitivity modulated by a smooth envelope resembling our dynamic ITD_env curves. Despite these arguments, a definitive resolution of the question of whether ITD_env curves might contain microfeatures would require repeating our dynamic IPD_env measurements using lower beat frequencies.

We found that using a higher f_mod leads to sharper ITD_env tuning and smaller ITD_env JNDs. Although values of f_mod >160 Hz were not systematically tested, previous studies with monaural electric stimulation suggest that there is a limit near 200–300 Hz above which most IC neurons would have a diminished sustained response (Snyder et al. 1995, 2000), similar to the rate limit seen previously (Smith and Delgutte 2007) with bilateral constant-amplitude pulse trains. If this upper limit is not a result of sampling bias or an artifact of anesthesia, then employing values of f_mod much greater than those tested in this study may not lead to better ITD_env sensitivity. Such an upper limit is not seen with acoustic stimulation, where some IC neurons give sustained responses to AM tones for f_mod of 1,000 Hz and above (Batra et al. 1989; Krishna and Semple 2000; Schreiner and Langner 1988).

Because ITD_env tuning half-width seems to be directly related to the width of each cycle of the amplitude envelope, temporal sharpening of the envelope might improve ITD_env tuning, while avoiding high stimulus rates that result in mostly onset responses in the IC. Temporal sharpening of the amplitude envelope is also achieved in acoustic studies of binaural hearing by the stimulus transposition technique, in which a high-frequency sinusoidal carrier is modulated by a half-waverectified, low-frequency stimulus (van de Par and Kohlrausch 1997). Transposed stimuli provide better behavioral (Bernstein and Trahiotis 2002) and neural (Griffin et al. 2005) ITD_env discrimination thresholds than conventional AM stimuli.

Although we did not observe a significant difference in ITD_env half-widths between carrier rates of 1,000 and 5,000 pps, ITD_env JNDs were somewhat poorer >80 Hz, and the proportion of units with measurable ITD_env JNDs was lower for the 5,000-pps carrier. Thus the theoretical benefit of using higher carrier rates to increase the upper limit of envelope frequencies that can be delivered with a cochlear implant may be partly offset by a moderate degradation of ITD_env sensitivity with higher carrier rates.

Sensitivity to fine structure ITD

While stimulation with a constant-amplitude 1,000-pps pulse train carrier elicited predominantly onset responses in IC neurons, low-frequency AM of the carrier restored sustained responses to bilateral stimulation, consistent with previous observations for monaural stimulation (Snyder et al. 2000). Despite a general lack of phase locking to the 1,000-pps carrier, over half of our IC neurons were sensitive to ITD_fs at this carrier rate when AM was imposed on the stimulus. One possible interpretation of this finding is that ITD_fs sensitivity arises at a level lower than the IC (such as the SOC) as suggested in previous studies of acoustic stimulation with AM tones in high-frequency neurons (Batra et al. 1993; Yin et al. 1984), while the mechanism responsible for the upper limit of phase locking occurs after ITD_fs processing. Our phenomenological model is consistent with this interpretation because the upper frequency limit to sustained responses is determined by the time constant τ_i of the inhibitory synapse occurring after the binaural coincidence detector, while the upper limit of ITD_fs sensitivity is determined by the time constant τ_e of the excitatory synapse preceding the coincidence detector. However, Colburn et al. (2007) developed an MSO neuron model without inhibition that can also simulate both the lack of sustained responses at higher pulse rates and the restoration of sustained responses and ITD sensitivity by introducing lowfrequency AM. In their model, the suppression of sustained responses is caused by the dynamics of ionic membrane channels, particularly low-threshold potassium channels. The two mechanisms (inhibition and hyperpolarizing membrane channels) are not mutually exclusive, and both may be necessary to account for all the data.

The ranges of ITD_fs half-widths and neural JNDs with the 1,000-pps carrier are consistent with the values previously obtained in the best neurons for low-rate (40 pps) constantamplitude pulse trains (Smith and Delgutte 2007). Neurons that are sensitive to ITD_fs tend to have sharp ITD tuning for low-rate constant amplitude pulse trains, while neurons that are insensitive to ITD_fs had broader ITD tuning. This is an intuitive result because the 1,000-pps carrier imposes a limited physical range (±500 µs) of ITD on the stimulus. It is also interesting to consider that ITD_fs -sensitive neurons tended to be located at shallower electrode depths in our dorsal-to-ventral penetrations and thus would lie in lower-CF regions of the IC in normalhearing animals (Table 2). Because MSO neurons mostly target low-CF regions of the IC (Adams 1979; Loftus et al. 2004), this might suggest that ITD_fs -sensitive IC neurons preferentially receive inputs from the MSO. However, in our previous study with bilateral electric stimulation (Smith and Delgutte 2007), there was no correlation between sharpness of ITD tuning and electrode depth in the IC, so this idea may be too simplistic. Mechanisms underlying the substantial variability in ITD tuning among IC neurons with electric stimulation are poorly understood.

Unlike acoustic stimulation, where phase locking in the auditory nerve begins to degrade above ~1,500 Hz (Johnson 1980; Joris et al. 1994), electric stimulation can produce significant phase locking well above 5,000 pps (Dynes and Delgutte 1992). The loss of ITD_fs sensitivity we observed at the higher carrier rate (5,000 pps) may result from the coincidence window of the ITD-processing neurons being relatively wide compared with the 200-µs period of the carrier, or alternatively may reflect a loss of phase locking beyond the auditory nerve in the binaural circuits that process ITD. The loss of ITD_fs sensitivity with high-frequency stimulation is also seen with acoustic hearing (Joris 2003; Yin et al. 1984). However, with electric stimulation, this effect can be observed within individual neurons since electric stimulation allows stimuli of any frequency to stimulate the same region of the cochlea, whereas in normal-hearing animals, the rapid increase in neural thresholds for frequencies above a neuron’s CF imposes an upper limit on the frequencies that can be tested for ITD_fs sensitivity in any individual neuron. Future studies will need to determine where between 1,000 and 5,000 pps the upper rate limit of ITD_fs sensitivity occurs in IC neurons with electric stimulation and whether this limit differs from that seen for acoustic stimulation.

Comparison of envelope and fine-structure ITD sensitivity

The result that IPD_env half-widths are nearly constant for a given neuron over a wide range of f_mod supports the notion that ITD_env sensitivity may have more to do with the instantaneous intensities of the stimulus at each ear rather than with the interaural timing of the amplitude envelopes. We showed previously that changing the rate of a constant-amplitude pulse train does not have a large effect on the half-width of ITD tuning (Smith and Delgutte 2007), but here with AM pulse trains, increasing f_mod proportionately decreased the half-width of ITD_env tuning. Varying f_mod changes both the rate and slope of each modulation cycle, so we cannot eliminate the possibility that the slope of the amplitude envelope is what determines the width of ITD_env tuning. Note also that the carrier pulses have infinite slope while the envelope has a slow rise-time. Future experiments using trapezoidal AM might help to separate the two factors.

Another line of evidence distinguishing ITD_env and ITD_fs sensitivities comes from measurements of neural sensitivity to ITD imposed on the whole waveform (Fig. 10, E and F). To a first-order approximation, these responses can be predicted from the product of separable sensitivities to ITD_env and ITD_fs , each of which can be measured by holding the other at a fixed value. There are, however, limits to the idea that ITD_env and ITD_fs sensitivities are independent. First, independence may no longer hold if the modulation and carrier frequencies were less disparate than in our measurements (40 Hz vs. 1,000 pps). Second, ITD_fs sensitivity for 1,000-pps carriers must vanish at very low f_mod as inferred from the lack of sustained responses to constant-amplitude pulse trains.

The phenomenological model presented in this paper may provide insight into the underlying factors that contribute to ITD_env and ITD_fs tuning. In the model, the width and shape of envelope ITD tuning with AM pulse trains are primarily controlled by the width and shape of each cycle of the stimulus AM that exceeds threshold. For fine structure ITD tuning with constant-amplitude or AM pulses, it is the width of the EPSP, or temporal jitter before binaural coincidence detection, that determines the width of ITD tuning.

Phenomenological model for ITD tuning

A relatively simple, phenomenological model of electric ITD tuning was created with the aim of better understanding the factors that influence electric ITD tuning at the level of the IC. The general structure of the model is broadly consistent with the organization of the auditory pathway and similar to that of existing models of IC responses to acoustic stimulation (Cai et al. 1998; Nelson and Carney 2004). Specifically, the model consists of three cascaded stages: a peripheral processor, a binaural coincidence detector, and an envelope processor. The peripheral processor roughly mimics the responses of auditory nerve fibers to electric stimulation. It is simpler than previous peripheral models of electric stimulation (Bruce et al. 1999, 2000) and only consists of a threshold followed by convolution with an EPSP. These effectively act to create a narrow dynamic range of stimulation and limit phase-locking at high pulse rates. The binaural processor is implemented as multiplication between a delayed input from the contralateral side and an undelayed input from the ispsilateral side. This architecture is comparable to Jeffress-type models of binaural coincidence detection (Jeffress 1948) and mimics the operation of the MSO when operating on spike probabilities (Batra and Yin 2004; Goldberg and Brown 1969; Yin and Chan 1990). The envelope processor implements the interaction between excitation from the output of the binaural coincidence detector with delayed inhibition from the same output. Possible anatomical substrates for an ITD-sensitive inhibitory input to the IC, include projections from the dorsal nucleus of the lateral lemniscus (Adams and Mugnaini 1984; Brugge et al. 1970) and intrinsic inhibitory connections within the IC (Oliver et al. 1994). The envelope processor stage of the model, with the interaction of short excitation with delayed, long-lasting inhibition, is similar to existing models of IC responses to AM acoustic stimuli (Nelson and Carney 2004).

The model captures several aspects of the data in this and our previous report (Smith and Delgutte 2007), including: the reduction in sustained responses to constant-amplitude pulse trains with increasing pulse rate, the restoration of sustained responses to high-rate pulse trains by low-frequency AM, the decrease in ITD_env half-width with increasing modulation frequency, the increase in ITD_env half-width with increasing stimulus intensity, sharper tuning to ITD_fs than ITD_env, and loss of ITD_fs tuning at very high pulse rates. Aspects of the data that are not captured by the model include: the saturation of ITD functions for constant-amplitude pulse trains at high stimulus intensities (Fig. 5 in Smith and Delgutte 2007), shifts in best ITD_env with changes in overall intensity (Fig. 3B), shifts in best ITD (for constant-amplitude pulse trains) with changes in ILD (Fig. 6 in Smith and Delgutte 2007), and stochastic responses. Because the model is deterministic, it only predicts the mean discharge rate and not variability and thus cannot be used to predict ITD discrimination thresholds. Some of these limitations could be dealt with by more carefully modeling responses to electric stimulation observed in the auditory nerve. For example, the threshold stage of our peripheral model could be replaced by a more complex stage consisting of a dynamic threshold, intensity-dependent latency, and stochastic spiking (Bruce et al. 1999). Other model limitations, for example the dependence of best ITD_env on intensity, may require changes to the binaural processor itself. For our purposes, however, the simple model suffices to capture the major trends in the data, and our data with AM stimuli are too limited to allow meaningful testing of more elaborate model structures. Even in its simple form, the model is useful for understanding the basic mechanisms that possibly underlie neural ITD sensitivity with electric stimulation and can also be used to predict responses to stimuli not tested in vivo.

Comparison with behavioral data from bilaterally implanted human subjects

Agreement between our results and psychophysical reports of ITD sensitivity for AM stimuli in bilaterally implanted human subjects is mixed. van Hoesel and Tyler (2003) measured behavioral ITD JNDs for an 800-pps carrier both with and without sinusoidal AM in three subjects. While none of the subjects had measurable ITD JNDs for the unmodulated pulse train, 55-Hz modulation of the pulse carrier restored ITD_wav sensitivity in all three subjects tested. One of these subjects was tested with ITDs presented in the envelope only as well as ITDs in the whole waveform; this increased the JND from 120 to 290 µs, suggesting the subject must have benefited from fine-structure cues in the whole-waveform condition. In another study of lateralization of short trapezoidal AM stimuli (Majdak et al. 2006), stimuli with whole waveform ITD were generally more strongly lateralized than those restricted to envelope ITD for carrier rates below an upper limit. This upper rate limit for carrier contributions to lateralization varied substantially across subjects and could reach 800 pps in some subjects. Several other studies have reported across-subject differences in the ability to use ongoing ITD_fs cues at high pulse rates (van Hoesel 2007). Together these studies suggest that up to a certain carrier rate, ITD discrimination for AM stimuli benefits from the inclusion of ITD in the carrier, even at rates that, in some subjects, yield unmeasurable ITDs when not modulated. These psychophysical observations are qualitatively similar to our neural results in cat IC. We previously found that neural ITD sensitivity for constant-amplitude pulse trains degrades with increasing pulse rates due to the gradual loss of a sustained response (Smith and Delgutte 2007), and here we show that amplitude modulating a 1,000-pps pulse train restores ITD_fs sensitivity in a majority of neurons by eliciting sustained responses.

Behavioral data on ITD_env discrimination as a function of modulation frequency for AM pulse trains subjects are only available from one study that used three subjects (van Hoesel 2007). In contrast to our results that show decreasing neural ITD_env JNDs with increasing f_mod (20–160 Hz), their psychophysical results, using a 6,000-pps carrier, show increasing ITD_env JNDs with increasing f_mod from 100 to 400 Hz. However, it is hard to draw firm conclusions from this comparison because the behavioral thresholds were measured in 100-Hz steps, and there is only one overlapping f_mod (100 Hz) between the two datasets. A possible physiological explanation for the degradation in behavioral ITD_env sensitivity at ≥200 Hz is the reduced numbers of neurons giving sustained responses at these modulation frequencies (Snyder et al. 1995, 2000). Future studies need to investigate both behavioral ITD_env sensitivity at additional f_mod <200 Hz and neural ITD_env sensitivity at f_mod >160 Hz to test this interpretation. Some of the neural studies need to be done in awake animals to test whether the loss of sustained responses to electric stimulation at higher pulse rates and f_mod is dependent on anesthesia. Behavioral data from bilaterally implanted animals such as cats would also be valuable to address possible species differences.

Significance for bilateral cochlear implant processing strategies

The neural responses in this study show tuning to envelope ITD similar to that seen in normal-hearing animals using AM tones. Over the range of modulation frequencies tested (≤160 Hz), IC neurons are more sharply tuned to ITD in the fine time structure of 1,000-pps AM pulse trains than in the amplitude envelope, although ITD_fs sensitivity is essentially eliminated at a higher carrier rate of 5,000 pps. ITD_env sensitivity in our study is likely to have been overestimated because our stimuli all had 100% AM depth, which is considerably higher than the modulation depths at the output of cochlear implant speech processors. Processors typically modulate pulse amplitude in each channel between threshold and the maximum comfortable level. We expect the reduced modulation depths produced by clinical processors to broaden ITD_env tuning, thereby exacerbating the contrast between the good ITD_fs sensitivity and the poor ITD_env sensitivity we observed with 100% modulation of 1,000-pps carriers.

Based on our single neuron results, we suggest that a bilateral cochlear implant strategy that successfully conveys ITD cues should control the precise timing of current pulses based on the fine timing of the sound sources at each ear. van Hoesel and Tyler (2003) implemented such a strategy but found it yielded little or no benefit over the standard clinical strategy for sound localization and speech reception in noise when tested in five bilaterally implanted subjects. One possible explanation is that to be effective, a fine-structure-based strategy may require each electrode channel to stimulate a highly specific population of neurons, an ability that may be limited by the large channel interactions observed with contemporary scala tympani electrodes (Boex et al. 2003; Chatterjee and Shannon 1998; Shannon 1983). Because the stimulation in neighboring channels is temporally interleaved, channel interactions effectively increase the pulse rates seen by individual neurons and may therefore reduce the ability of the binaural processor to make use of ITD_fs cues. A further caveat with fine-structure-based strategies is that only about half of our neurons were sensitive to ITD_fs with 1,000-pps carriers, so the decoding stages beyond the IC would have to be able to selectively “attend” to the subpopulation of sensitive neurons to effectively process the available ITD information.

An alternative processing strategy would use carrier rates above the upper limit of sensitivity to ITD_fs (e.g., 5,000 pps) to avoid creating conflicting ITD_fs and ITD_env cues. However, any benefits arising from the ability to encode higher modulation frequencies with such a high-rate strategy would be at least partially mitigated both by the somewhat poorer neural ITD_env JNDs seen at higher f_mod for the 5,000-pps carrier compared with the 1,000-pps carrier and by the poor behavioral ITD_env JNDs at modulation frequencies >200 Hz (van Hoesel 2007). With either strategy, further benefit from improved sensitivity to envelope ITD may potentially be achieved by temporally sharpening the amplitude envelope as in transposed stimuli (Bernstein and Trahiotis 2002; van de Par and Kohlrausch 1997), albeit with the possible side effect of distorting speech information. Clearly many interacting peripheral and central factors will influence the effectiveness of future processors designed to improve ITD sensitivity with bilateral cochlear implants.