Abstract
Accuracy of results from mathematical and computer models of biological systems is often complicated by the presence of uncertainties in experimental data that are used to estimate parameter values. Current mathematical modeling approaches typically use either single-parameter or local sensitivity analyses. However, these methods do not accurately assess uncertainty and sensitivity in the system as, by default they hold all other parameters fixed at baseline values. Using techniques described within we demonstrate how a multi-dimensional parameter space can be studied globally so all uncertainties can be identified. Further, uncertainty and sensitivity analysis techniques can help to identify and ultimately control uncertainties. In this work we develop methods for applying existing analytical tools to perform analyses on a variety of mathematical and computer models. We compare two specific types of global sensitivity analysis indexes that have proven to be among the most robust and efficient. Through familiar and new examples of mathematical and computer models, we provide a complete methodology for performing these analyses, both in deterministic and stochastic settings, and propose novel techniques to handle problems encountered during this type of analyses.
Keywords: Latin Hypercube Sampling (LHS), Partial Rank Correlation Coefficient (PRCC), Extended Fourier Amplitude Sensitivity Test (eFAST), Agent-Based Model (ABM), Sensitivity Index, Monte Carlo Methods, Aleatory Uncertainty, Epistemic Uncertainty
1. Introduction
Systems biology is the study of the interactions between the components of a biological system, and how these interactions give rise to the function and behavior of the system as a whole. The systems biology approach often involves the development of mathematical or computer models, based on reconstruction of a dynamic biological system from the quantitative properties of its elementary building blocks. The need to build mathematical and computational models is necessary to help decipher the massive amount of data experimentalists are uncovering today. The goal of the systems biologist or modeler is to represent, abstract, and ultimately understand the biological world using these mathematical and computational tools. Experimental data that are available for each system should guide, support, and shape the model building process. This can be a daunting task, especially when the components of a system form a very complex and intricate network.
Paraphrasing Albert Einstein, models should be as simple as possible, but not simpler. A parsimonious approach must be followed. Otherwise, if every mechanism and interaction is included, the resulting mathematical model will be comprised of a large number of variables, parameters, and constraints, most of them uncertain because they are difficult to measure experimentally, or are even completely unknown in many cases. Even when a parsimonious approach is followed during model building, available knowledge of phenomena is often incomplete, and experimental measures are lacking, ambiguous, or contradictory. So the question of how to address uncertainties naturally arises as part of the process. Uncertainty and sensitivity (US) analysis techniques help to assess and control these uncertainties.
Uncertainty analysis (UA) is performed to investigate the uncertainty in the model output that is generated from uncertainty in parameter inputs. Sensitivity analysis (SA) naturally follows UA as it assesses how variations in model outputs can be apportioned, qualitatively or quantitatively, to different input sources (Saltelli et al., 2000). In this work we review uncertainty and sensitivity analysis techniques in the context of deterministic dynamical models in biology, and propose a novel procedure to deal with a particular stochastic, discrete type of dynamical model (i.e. an Agent-Based Model -ABM1).
By deterministic model, we mean that the output of the model is completely determined by the input parameters and structure of the model. The same input will produce the same output if the model were simulated multiple times. Therefore, the only uncertainty affecting the output is generated by input variation. This type of uncertainty is termed epistemic (or subjective, reducible, type B uncertainty, see (Helton et al., 2006)). Epistemic uncertainty derives from a lack of knowledge about the adequate value for a parameter/input/quantity that is assumed to be constant throughout model analysis. In contrast, a stochastic model will not produce the same output when repeated with the same inputs because of inherent randomness in the behavior of the system. This type of uncertainty is termed aleatory (or stochastic, irreducible, type A, see (Helton et al., 2006)). This distinction has been and still is an area of interest and study in the engineering and risk assessment community (see (Apostolakis, 1990; Helton, 1997; Helton et al., 2007; Parry & Winter, 1981; Pate'-Cornell, 1996)).
Many techniques have been developed to address uncertainty and sensitivity analysis: differential analysis, response surface methodology (RSM), Monte Carlo Analysis, and variance decomposition methods. See (Iman & Helton, 1988; Saltelli et al., 2000) for details on each of these approaches and (Cacuci & Ionescu-Bujor, 2004; Draper, 1995; Helton, 1993; Saltelli et al., 2005) for more general reviews on uncertainty and sensitivity analysys. Here we briefly illustrate the most popular, reliable, and efficient uncertainty analysis techniques and sensitivity analysis indexes. In section 2, we describe two uncertainty analysis techniques: a Monte Carlo approach and Latin hypercube sampling (LHS). In section 3, we describe two sensitivity analysis indexes: partial rank correlation coefficient (PRCC) and extended Fourier Aamplitude Sensitivity Test (eFAST): PRCC is a sampling-based method, while eFAST is a variance-based method. In section 4, we perform US analysis on both new and familiar deterministic dynamical models (quantifying epistemic uncertainty) from epidemiology and immunology, and discuss results. Section 5 presents an ABM, where we suggest a method to deal with the aleatory uncertainty that results from the stochasticity embedded in the model structure, to facilitate the use of PRCC and eFAST techniques. We use Matlab (Copyright 1984-2006 The MathWorks, Inc. Version 7.3.0.298 R2006b) to solve all the differential equation systems of section 4 and to implement most of the US analysis functions described throughout the manuscript (available on our website, http://malthus.micro.med.umich.edu/lab/usanalysis.html).
2. Uncertainty Analysis
Input factors for most mathematical models consist of parameters and initial conditions for independent and dependent model variables. As mentioned, these are not always known with a sufficient degree of certainty because of natural variation, error in measurements, or simply a lack of current techniques to measure them. The purpose of uncertainty analysis is to quantify the degree of confidence in the existing experimental data and parameter estimates. In this section we describe the most popular sampling-based approaches used to perform uncertainty analysis, Monte Carlo methods, and their most efficient implementation, namely the LHS technique.
2.1. Monte Carlo simulation
Monte Carlo (MC) methods are popular algorithms for solving various kinds of computational problems. They include any technique of statistical sampling employed to approximate solutions to quantitative problems. A MC simulation is based on performing multiple model evaluations using random or pseudo-random numbers to sample from probability distributions of model inputs. The results of these evaluations can be used to both determine the uncertainty in model output and to perform SA. A large body of literature exists on the use of expert review processes to characterize epistemic uncertainty associated with poorly known model parameters (see for example (Cooke, 1991; Evans et al., 1994; Hora & Iman, 1989; McKay & Meyer, 2000)). For each parameter, sampling is guided by the specification of a probability density function (pdf) (i.e. normal, uniform, lognormal, etc.), depending on existing data and a priori information. If there are no a priori data, a natural choice is a uniform distribution (assigning some hypothetical, but large range with minimum and maximum values for the parameters). If biological knowledge exists suggesting a more frequent or expected value for a parameter, a normal pdf would be the best choice (setting the variance of the distribution as large as needed).
Several sampling strategies can be implemented to perform uncertainty analysis, such as random sampling, importance sampling or LHS (Helton & Davis, 2003; Mckay et al., 1979). To recreate input factor distributions through sampling, a large number of samples are likely required. If too few iterations are performed, not all values may be represented in the samples or values in the outer ranges may be under-sampled. The LHS algorithm was specifically developed to address this problem and it is by far the most popular sampling scheme for UA (Morris, 2000).
2.2. Latin Hypercube Sampling – LHS
Latin hypercube sampling (LHS) belongs to the MC class of sampling methods, and was introduced by McKay et al. (Mckay et al., 1979). LHS allows an un-biased estimate of the average model output, with the advantage that it requires fewer samples than simple random sampling to achieve the same accuracy (Mckay et al., 1979). LHS is a so-called stratified sampling without replacement technique, where the random parameter distributions are divided into N equal probability intervals, which are then sampled. N represents the sample size. The choice for N should be at least k+1, where k is the number of parameters varied, but usually much larger to ensure accuracy. If the interval of variation for some parameter is very large (several orders of magnitude), the sampling can be performed on a log scale to prevent under-sampling in the outer ranges of the interval where the parameter assumes very small values (see Supplement C and Figure C.1 and C.2 online).
The LHS method assumes that the sampling is performed independently for each parameter, although a procedure to impose correlations on sampled values has also been developed (Iman & Conover, 1982; Iman & Davenport, 1982). The sampling is done by randomly selecting values from each pdf (Figure 1A). Each interval for each parameter is sampled exactly once (without replacement), so that the entire range for each parameter is explored (Figure 1A). A matrix is generated (which we call the LHS matrix) that consists of N rows for the number of simulations (sample size) and of k columns corresponding to the number of varied parameters (Figure 1B). N model solutions are then simulated, using each combination of parameter values (each row of the LHS matrix, Figure 1B). The model output of interest is collected for each model simulation. Different model outputs can be studied if more than one model output is of interest.
Figure 1.
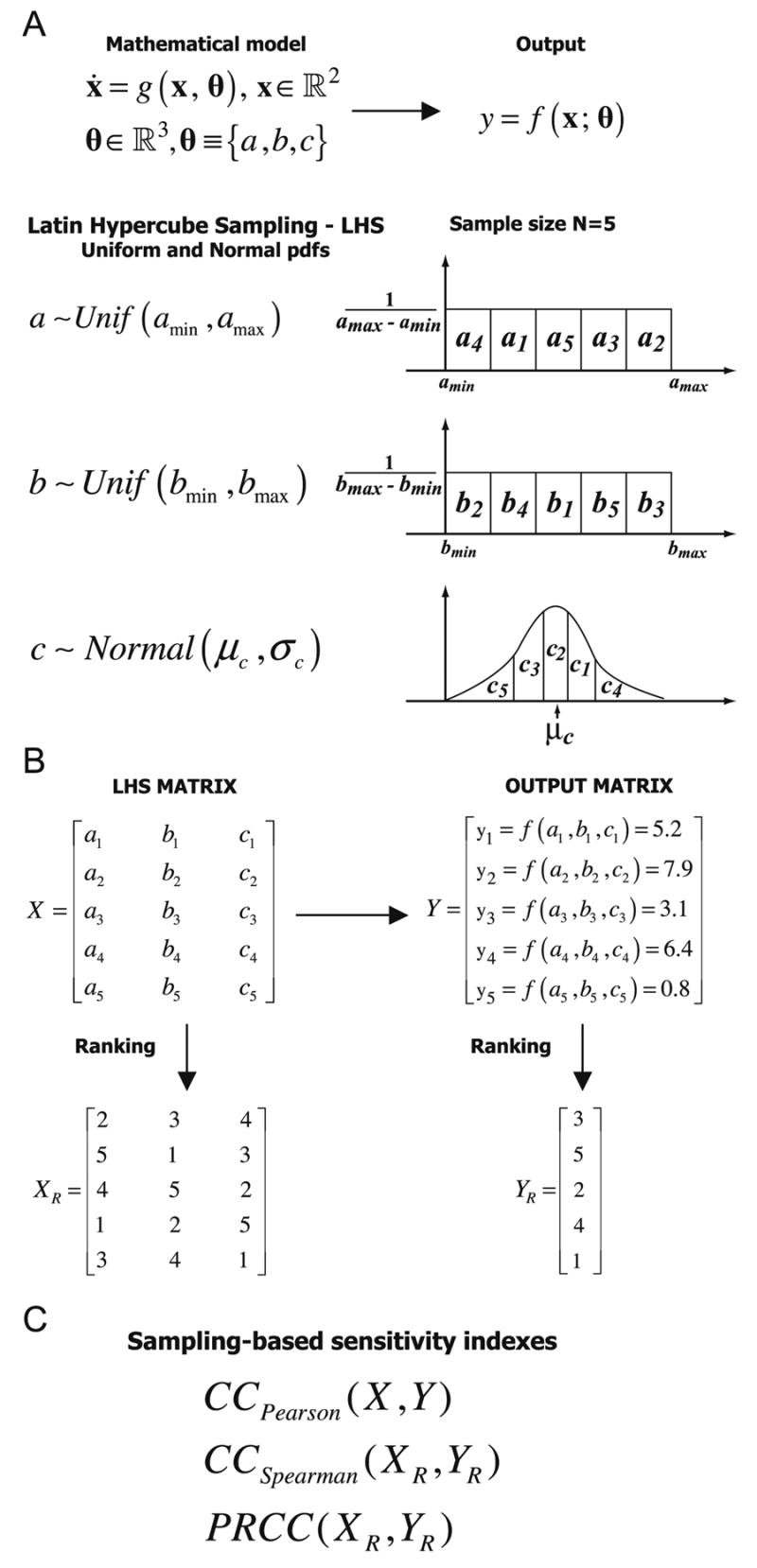
Scheme of uncertainty and sensitivity analysis performed with LHS and PRCC methods. The mathematical model is represented as an ordinary differential equations system, where x is the vector of state variables in a n-dimensional space ¡ n (n=2 in this example and θ is the parameter vector in ¡ k (k=3 in this example). For ease of notation, the output y is unidimensional and it is a function of x and θ.
Panel A: mathematical model specification (dynamical system, parameters, output) and the corresponding LHS scheme. Probability density functions (pdfs) are assigned to the parameters of the model (e.g. a, b, c). We show an example with sample size N equal to 5. Each interval is divided into 5 equiprobable subintervals, and independent samples are drawn from each pdf (uniform and normal). The subscript represents the sampling sequence. Panel B: the LHS matrix (X) is then built by assembling the samples from each pdf. Each row of the LHS matrix represents a unique combination of parameter values sampled without replacement. The model x = g(x, θ) is then solved, the corresponding output generated, and stored in the matrix Y. Each matrix is then rank-transformed (XR and YR).
Panel C: The LHS matrix (X) and the output matrix (Y) are used to calculate Pearson correlation coefficient (CCPearson). The rank-transformed LHS matrix (XR) and output matrix (YR) are used to calculate the Spearman or rank correlation coefficient (RCC) and the Partial Rank Correlation Coefficient (PRCC) (see section 3.1)
3. Sensitivity Analysis
Sensitivity analysis (SA) is a method for quantifying uncertainty in any type of complex model. The objective of SA is to identify critical inputs (parameters and initial conditions) of a model and quantifying how input uncertainty impacts model outcome(s). When input factors such as parameters or initial conditions are known with little uncertainty, we can examine the partial derivative of the output function with respect to the input factors. This sensitivity measure can easily be computed numerically by performing multiple simulations varying input factors around a nominal value. This technique is called a local SA because it investigates the impact on model output, based on changes in factors only very close to the nominal values. In biology, input factors are often very uncertain and therefore local SA techniques are not appropriate for a quantitative analysis; instead global SA techniques are needed. These global techniques are usually implemented using Monte Carlo simulations and are, therefore, called sampling-based methods.
Different SA techniques will perform better for specific types of mathematical and computational models. A natural starting point in the analysis with sampling-based methods would be to examine scatter plots. Scatter plots enable graphic detection of nonlinearities, non-monotonicities, and correlations between model inputs and outputs. See (Helton & Davis, 2002; Helton et al., 2006; Hora & Helton, 2003; Kleijnen & Helton, 1999; Storlie & Helton, 2008a; Storlie & Helton, 2008b) for a review on the indexes listed in the next paragraph.
For linear trends, linear relationship measures that work well are Pearson correlation coefficient (CC), Partial Correlation Coefficients (PCC) and Standardized Regression Coefficients (SRC). For nonlinear but monotonic relationships between outputs and inputs, measures that work well are based on rank transforms2 such as Spearman Rank Correlation Coefficient (SRCC), Partial Rank Correlation Coefficient (PRCC) and Standardized Rank Regression Coefficients (SRRC). For nonlinear non-monotonic trends, methods based on decomposition of model output variance are the best choice. Examples of these methods are the Sobol method and its extended version based on (quasi) random numbers and an ad hoc design (see (Saltelli, 2002) for details), the Fourier Amplitude Sensitivity Test (FAST) and its extended version (eFAST). Aside from those listed, there are alternative methods available that are less affected by nonmonotonic relationships between the inputs and the output, e.g. common means (CMNs), common distributions or locations (CLs), common medians (CMDs) and statistical independence (SI). These methods are based on gridding (placing grids on a scatter plot) to evaluate any non-randomness in the distribution of points across the grid cells and they are generally less computationally expensive than variance-based methods (such as eFAST).
In general, the computational execution time of the model is the major concern when performing US analysis. Screening methods, such as Morris (see (Morris, 1991)), are global and computationally compatible: they represent adequate available tools to efficiently address the problem, if the model is very large and the execution time is prohibitive (several hours or days), as it is usually the case for Agent- Based Models (see below).
We will focus and implement only PRCC and eFAST as two examples of SA methods. PRCC and SRRC appear to be, in general, the most efficient and reliable (giving similar results) among the sampling-based indexes (see (Saltelli & Marivoet, 1990)) while eFAST has proven to be one of the most reliable methods among the variance-based techniques (Saltelli, 2004), although computationally expensive (see (Ratto et al., 2007; Tarantola et al., 2006)).
It is important to note that PRCCs and variance decompositions obtained with eFAST measure two very different model properties. Specifically, PRCCs provide a measure of monotonicity after the removal of the linear effects of all but one variable. In contrast, the results obtained with eFAST returns measures of fractional variance accounted for by individual variables and groups of variables. Ideally both indexes should be calculated in order to have a complete and informative US analysis.
We review details for both PRCC and eFAST in the next section. We tested the correctness of our matlab implementation of LHS\PRCC and eFAST by running similar experiments with the softwares SaSat (see (Hoare et al., 2008)) and SimLab (see (SimLab, 2006)), or comparing with known results for eFAST (see Ishigami function, pages 41-42 in (Saltelli et al., 2000)) (data not shown).
3.1. Partial Rank Correlation Coefficient (PRCC)
Correlation provides a measure of the strength of a linear association between an input and an output. A correlation coefficient (CC) between xj and y is calculated as follows:
| (1) |
and varies between −1 and +1. Cov(xj,y) represents the covariance between xj and y, while Var(xj) and Var(y) are respectively the variance of xj and the variance of y (x̄ and ȳ are the respective sample means). If xj and y are the raw data, then the coefficient r is called sample or Pearson correlation coefficient (Figure 1C). If the data are rank-transformed, the result is a Spearman or rank correlation coefficient (Figure 1C). It is important to note that the process of rank-transforming data assumes that sampled model inputs are real-valued or can adopt many possible values. If a parameter takes only integer values and the range of possible values it can assume is less than N, there is insufficient information to break ties during ranking, resulting in poor correlations. We are currently pursuing methods to handle this problem3.
Partial correlation characterizes the linear relationship between input xj and output y after the linear effects on y of the remaining inputs are discounted. The PCC between xj and y is the CC between the two residuals (xj − x̂j) and (y − ŷ), where x̂j and ŷ are the following linear regression models:
| (2) |
Similarly to PCC, Partial Rank Correlation performs a partial correlation on rank-transformed data: xj and y are first rank transformed, then the linear regression models described in Eq. (2) are built. PRCC is a robust sensitivity measure for nonlinear but monotonic relationships between xj and y, as long as little to no correlation exists between the inputs (see Uncertainty and sensitivity functions and implementation on our website http://malthus.micro.med.umich.edu/lab/usanalysis.html for the use of scatter plot functions to enable graphic detection of non-monotonicities).
By combining the uncertainty analyses with PRCC, we are able to reasonably assess the sensitivity of our outcome variable to parameter variation (see for example (Blower & Dowlatabadi, 1994; Saltelli, 2004)). Figure 2 shows an example of a standard LHS-PRCC scheme, scatter plots with correlation indexes (Pearson, Spearman and PRCC, see Figure 2C) and p-values (see the titles of the scatter plots in Figure 2C) based on a classic ODE in population dynamics: a predator-prey (or Lotka-Volterra) model. The Lotka-Volterra model is the simplest model of predator-prey interactions and was developed independently by Lotka (1925) and Volterra (1926):
Figure 2.
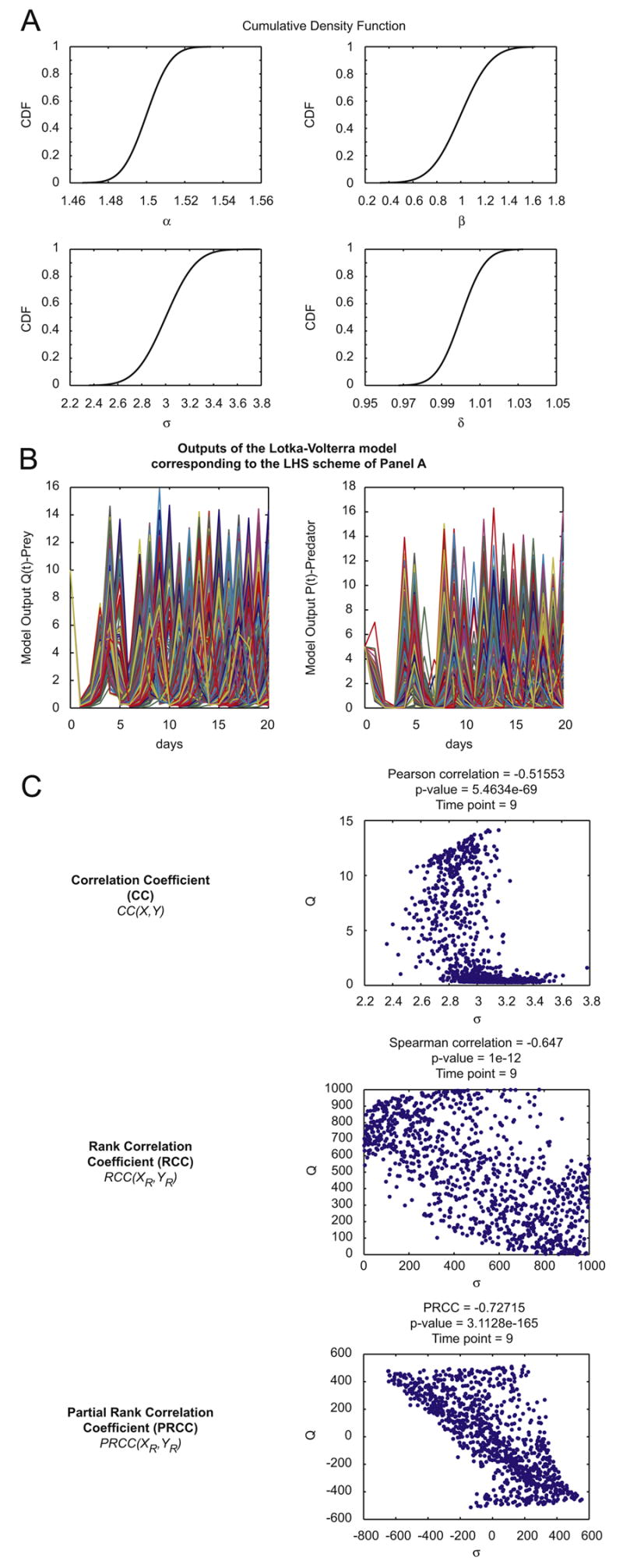
general LHS scheme and PRCC performed on the Lotka-Volterra model (model equations and parameters are as described in Section 3.1).
Panel A: Cumulative Distribution Functions – CDFs of 1000 samples independently drawn from normal pdfs (initialized following eqns. (3)) for the four parameters (α, β, σ, δ) of the Lotka-Volterra model described in Section 3.1, equations (1)-(2).
Panel B: outputs of the Lotka-Volterra model over time (days) corresponding to the parameter combinations of the LHS scheme illustrated in Panel A.
Panel C: Example of sampling-based correlation indexes calculated on the LHS matrix resulting from Panel A and from the output matrix resulting from Panel B. The reference output is the variable Q(t)-prey at time t=9 and it is shown on the ordinate. Parameter σ is taken as the parameter of interest and it is represented on the abscissa. Each dot represents the output value Q(9) for a specific sampled value of parameter σ.
Note that at each step of processing (correlation, rank correlation, partial rank correlation), the linear relationship between parameter and output variations becomes more apparent.
| (3) |
| (4) |
It has two state variables (Q, P) and several parameters. Q represents the density of prey, P represents the density of predators, α is the intrinsic rate of prey population increase, β is the predation rate coefficient, σ is the predator mortality rate, and δ is the reproduction rate of predators per prey consumed. As an example, we assume that these four parameters follow normal probability density functions (Figure 2A) with means given by
| (5) |
and initial conditions as shown in Eqs. (3)-(4). Standard deviations for parameters α and δ are set very small (i.e. std=0.01) while parameters β and σ are varied in a larger range (i.e., std=0.2). LHS is performed following the scheme below
| (6) |
The sample size N is set to 1000. Figure 2A shows the cumulative distribution functions (CDFs) for each parameter, while Figure 2B shows the outputs ((Q(t)-prey and P(t)-predator) over time corresponding to the LHS scheme illustrated in Figure 2A.
3.2. Inference on PRCCs
Significance tests can be performed to assess if a PRCC is significantly different from zero (thus, even small correlations may be significant) and if two PRCC values are significantly different from each other. Each PRCC (γ) generates a value T according to the following statistic (see (Anderson, 2003), pp. 143)
| (7) |
where T follows a t of Student distribution with (N−2−p) degrees of freedom. N is the sample size and p is the number of inputs/parameters whose effects are discounted when the PRCC is calculated. For example, if we vary 6 inputs/parameters (xi, i = 1, 2,…., 6) in LHS, p would be equal to 5 (PRCC(xi, y) = γxiy/xj, j = 1,…,6 j≠i). Equation (7) is exact for linear partial correlation when the inputs and output are normally distributed, but is a large-sample approximation otherwise. Fisher showed that the following transformation of a sample Pearson correlation coefficient r
| (8) |
is normally distributed with mean equal to the unknown Pearson correlation of the population (μ) and standard deviation equal to . In order to test if two Pearson correlation coefficients are different, the log transformation in Eq. (8) is applied to the respective sample Pearson correlation coefficients r1 and r2 and the following statistic z is calculated (z-test):
| (9) |
where N1 and N2 are the respective sample sizes. Since the distribution of sample partial correlation coefficients is of the same form as that of Pearson correlation coefficients, the z statistic given in Eq. (9) can be used to compare them (after applying the log transformation (8) to the partial correlation coefficients (pcc')):
| (10) |
where N1 and N2 are the respective sample sizes and p1 and p2 are the respective inputs/parameters whose effects are discounted when pcc1 and pcc2 are calculated. The extension of Eq. (10) to partial rank correlation coefficients can be inferred from Anderson (see (Anderson, 2003), pp. 144).
3.3. Extended Fourier Amplitude Sensitivity test – eFAST
Extended FAST (eFAST), developed by Saltelli et al. (Saltelli, 2004; Saltelli & Bolado, 1998; Saltelli et al., 2000; Saltelli et al., 1999), is based on the original Fourier Amplitude Sensitivity Test (FAST) developed by Cukier et al. (Collins & Avissar, 1994; Cukier et al., 1973; Schaibly & Shuler, 1973). eFAST is a variance decomposition method (analogous to ANOVA): input parameters are varied, causing variation in model output. This variation is quantified using the statistical notion of variance: where N=sample size (or equivalently, total number of model runs), yi=ith model output, ȳ =sample mean. The algorithm then partitions the output variance, determining what fraction of the variance can be explained by variation in each input parameter (i.e. partial variance). Partitioning of variance in eFAST works by varying different parameters at different frequencies, encoding the identity of parameters in the frequency of their variation (see Supplement A.1 for details). Fourier analysis then measures the strength of each parameter's frequency in the model output. Thus, how strongly a parameter's frequency propagates from input, through the model, to the output serves as a measure of the model's sensitivity to the parameter.
The sampling procedure implemented in eFAST defines a sinusoidal function of a particular frequency for each input parameter (i.e. a search curve), x = f (j), j = 1,2,…, NS, that assigns a value to x based on the sample number 1 through the total number of samples per search curve, Ns. The choice of sinusoidal function depends on the distribution of parameter values desired (e.g. uniform, normal, etc.). The frequencies assigned to parameters must meet several criteria so that they can be distinguished during Fourier analysis. See Supplement A.1 for a detailed discussion of how search curves are specified and frequencies are chosen. The minimum recommended value for NS is 65 (see (Saltelli et al., 2000), p. 187). Due to the symmetry properties of trigonometric functions, the sinusoidal function will eventually repeat the same samples. A resampling scheme is implemented to avoid this inefficiency (Saltelli et al., 1999): eFAST algorithm is repeated NR (the resampling size) times with different search curves specified by introducing a random phase shift into each sinusoidal function. So, the total number of model simulations, N, is given by N = NSx k x NR, where k is the number of parameters analyzed.
As an example, in Figure 3, we illustrate the steps within the eFAST algorithm to the Lotka-Volterra model described in section 3.1. We use 257 samples per search curve with no resampling (i.e. NS =257, NR=1). Parameter σ is taken as the parameter of interest. The algorithm assigns parameter σ a frequency of 31, and parameter β a frequency of 2. For simplicity, parameters α (frequency = 1) and δ (frequency = 3) are not illustrated. Figure 3A illustrates this sampling step. Each sampled parameter combination is then used to solve the model (Figure 3B).
Figure 3.
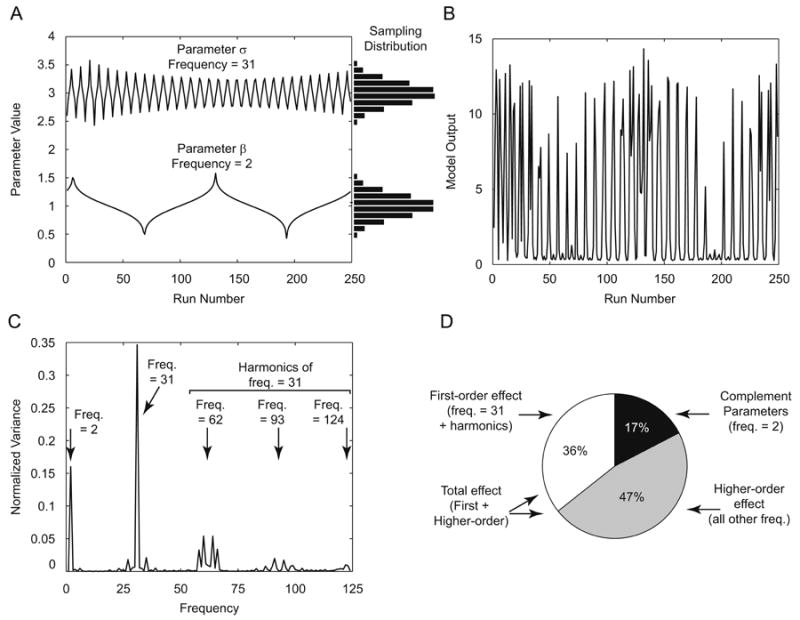
eFAST performed on the Lotka-Volterra model. Model equations and parameters are as described in Section 3.1. Panel A: Input Parameter Sampling: Parameters are varied according to a sinusoidal function based on run number. Note that the shapes of these search curves result in normal distribution of parameter values (see Eq. (6) for details) when sampled (horizontal histograms). σ is assigned a frequency of 31, and β is assigned a frequency of 2. α and δ are sampled at frequencies 1 and 3, respectively (not shown). These frequencies are chosen automatically to meet the criteria described in Appendix A.1. Panel B: Model Output: The model is solved for each parameter combination from Panel A. The number of prey at t=9 is taken as the model output. Note that both high- and low-frequency components are evident by inspection. Panel C: Fourier analysis and Variance Spectrum: The variance at each frequency is calculated from the model ouput (see text) and normalized to total variance. The variance at frequency 2, 31, and higher harmonics of frequency 31 are indicated (arrows). Panel D: Sensitivity Indexes: Taking parameter σ (varied at frequency 31) as our parameter of interest, first-order sensitivity index (Si) is calculated by the sum of variance at frequency 31 and higher harmonics, normalized to total variance (white pie slice). The sensitivity of the complementary set of parameters is calculated similarly (black pie slice). The remaining variance is assumed to be the result of non-linear higher-order interaction between parameters (gray pie slice). The total-order sensitivity index (STi) is calculated by the sum of Si and higher-order effects (white + gray pie slices).
The primary advantage of the eFAST method over the original FAST is the ability to calculate both the first-order sensitivity and total-order sensitivity of each input parameter (see Supplement A.2 online for details). A first-order sensitivity index, Si, of a given parameter i, is calculated as the variance at a particular parameter's unique frequency (and harmonics of that frequency) divided by total variance (Figure 3D, white pie-slice). First, variance ( ) is calculated from the Fourier coefficients at the frequency of interest, j,
| (11) |
then, the first-order Si is calculated as a fraction of total variance:
| (12) |
This index represents the fraction of model output variance explained by the input variation of a given parameter. To estimate the total-order sensitivity index, STi, of a given parameter i, eFAST first calculates the summed sensitivity index of the entire complementary set of parameters (i.e. all parameters except i) using their identification frequencies (Figure 3D, black pie-slice).
STi is then calculated as the remaining variance after the contribution of the complementary set, Sci, is removed (Figure 3D, gray pie-slice):
| (13) |
This includes higher-order, nonlinear interactions between the parameter of interest and the complementary set of parameters. eFAST indexes can also be used to determine the degree of additivity of a model (see Supplement A.3 online for details).
3.3.1. Inference on eFAST and the dummy parameter
Equation (7) allows statistical inference on PRCCs. Since an equivalent test for variance-based sensitivity indexes is not available, we propose a novel method based on dummy parameters for determining the significance of eFAST first- and total-order indexes. The use of dummy parameters is a standard practice in screening methods (see Chapter 4 in (Saltelli et al., 2000)), although, to our knowledge, it has never been applied in the context of eFAST with the purpose of testing the significance of first and total-order sensitivity coefficients.
eFAST implements random resampling (NR) of search curves for more efficient parameter sampling. Because different search curves will produce different combinations of parameter values, different search curves will lead to slightly different sensitivity measures. We take advantage of these repeated measures to perform statistical tests comparing eFAST sensitivity indexes. The algorithm already performs these repeated measures, thus the statistical tests entail no additional computationally intensive model simulations.
The eFAST method artifactually produces small but non-zero sensitivity indexes for parameters to which the model is completely independent. This is also true for the PRCC method. To illustrate this point, we run an example sensitivity analysis where we include a negative-control “dummy” parameter. This dummy parameter does not appear in the model equations and thus does not affect the model in any other way, so should ideally be assigned a sensitivity index of zero. Figure 4 shows eFAST and PRCC SA results with the use of a dummy parameter on the Lotka-Volterra model discussed in Sections 3.1.
Figure 4.
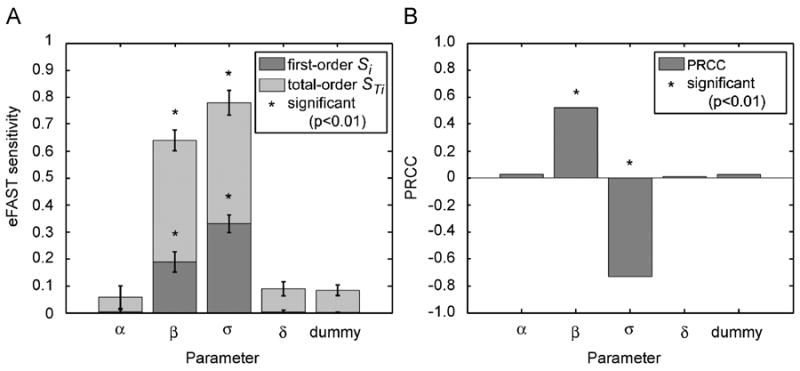
Dummy parameter on eFAST and PRCC performed on the Lotka-Volterra model. Model equations and parameters are as described in Section 4.1 and Table I. The reference output is Q(t)-prey Eq. (3), at t=9. Panel A: eFAST results with resampling and significance testing. Search curves were resampled 5 times (NR=5), for a total of 1285 model evaluations (NS=257). First-order Si and total-order STi are shown for each parameter, including a dummy parameter, as described in the text. Error bars indicate +/- 2 S.D on the mean of resamples. Parameters with first- or total-order indexes significantly different (p<0.01) from those of the dummy parameter are indicated with asterisks (*). Panel B: PRCC results. Sample size N=1000. (*) denotes PRCCs that are significantly different from zero.
The eFAST algorithm assigns this dummy parameter a small but non-zero first-order sensitivity index (Sdummy= 0.003), and total-order sensitivity index (STdummy) of approximately 0.11 (Figure 4A). The non-zero first-order index, Sdummy, likely derives from aliasing and interference effects (see Supplement A.1 online). The assignment of a larger artifactual value to the total-order index, STdummy, is more complicated, as this artifact is derived from imprecise simplifying assumptions used to calculate the total-order index (see Supplement A.4 online). Since we cannot test if those values are significantly different from zero, by taking a dummy parameter as the parameter of interest, we propose a way to quantify these artifacts and test for significance. Parameters with a total-order sensitivity index less than or equal to that of the dummy parameter should be considered not significantly different from zero.
We propose using a two-sample t-test4 on data generated by resampling the eFAST search curve to determine whether the sensitivity indexes of a parameter of interest are significantly different from the indexes calculated for the dummy parameter. The t-test compares two distributions, the or (j = 1, 2,…, NR) with the or (j = 1, 2,…, NR) (see Supplement A.5 online for more details).
Since NR is usually small (for ease of computation), the adequacy of this t-test procedure is limited, considering that the normality assumption4 is unlikely to hold for the first and total order sensitivity indexes. However, it can indicate on whether a small total-order sensitivity index should be considered an artifact of eFAST total-order estimation. The two-sample t-test might also be used to determine whether the indexes of multiple parameters of interest are significantly different from each other, allowing qualitative comparisons of effect size. Figure 4A illustrates the use of resampling and statistical significance testing. The LHS/PRCC algorithm (Figure 4B) assigns a PRCC value to the dummy parameter that is not significantly different from zero (0.04054, p-value>0.05 according to the statistic (7)).
Although not relevant for our examples, multiple test corrections should be considered if a large number of tests are performed in the US analysis (see Supplement B for details).
3.4. Is there an optimal choice for N?
There is no a priori exact rule for determining the adequate sample size for either LHS-PRCC or eFAST. A minimum value is known for both: N=k +1 for LHS and NS=65 for eFAST, where k is the number of uncertain parameters that are varied. A way to overcome the problem is to systematically increase the sample size and check if the sensitivity index used (in our case either PRCC or eFAST Si and STi) can consistently capture and rank a similar set of most important effects. If that holds between two consecutive experiments, there is no evident advantage in increasing the sample size, because the conclusions (in terms of US analysis) will be the same. A measure of this type of correlation is given by the top-down coefficient of concordance (TDCC).
TDCC is described in (Iman & Conover, 1980; Iman & Conover, 1987) where a concordance measure is designed to be more sensitive to agreement on the top rankings from a set of h different rankings. It is based on Savage scores (Savage, 1956), defined as follows:
| (14) |
where i is the rank assigned to the ith order statistic in a sample of size k5 (in our case k is the number of parameters varied).
If h=2, the top-down correlation rT is the simple correlation coefficient computed on Savage scores. If h>2, rT is the Kendall's coefficient of concordance (still computed on Savage scores). TDCC asymptotically follows a normal distribution, specifically . We implemented TDCC following (Iman & Conover, 1980; Iman & Conover, 1987), and it can be used for two purposes:
Selecting for an optimal sample size for LHS-PRCC and eFAST (see examples in section 4)
Comparing PRCC and eFAST to see if they are in agreement (not implemented).
An alternative method to assess the adequacy of sample size in LHS is based on the use of t-distribution with replicated sampling (see Sections 6 and 7 in (Helton et al., 2000)). The process of ranking in the Partial Rank Correlation method refers to ranking the raw data from the LHS matrix and model output in descending order to calculate the PRC coefficient. Here and elsewhere, when we state that a set of parameters is the “most important” in significance affecting model output, we mean that after listing the sensitivity indexes in descending order by value for either PRCC or eFAST, these parameters are always greatest in absolute value. PRC coefficients can be formally ranked by z-test (see Eq. (10)). We propose the use of a pairwise t-test and a dummy parameter to rank Si and STi6.
3.5. Time varying sensitivity indexes
PRCC and eFAST indexes can be calculated for multiple time points and plotted versus time. This allows us to assess whether significances of one parameter occur over an entire time interval during model dynamics (this is the usual presentation of SA indexes for dynamical systems analysis). This analysis can be performed in two ways. If specific time points are known to be crucial, then only those will be checked for significance. For example, a model of acute virus dynamics will focus on the first days post-infection. If we model a slow-growing pathogen (like Mycobacterium tuberculosis), we might be interested in later time points. If no particular time effect is known, the analysis can be done in an exploratory way, looking for any significant time-dependent relationships throughout the entire time course. Figure 5 shows an example of PRCCs plotted over time: the US analysis is performed on the ODE model described in Section 4.3 (only five parameters are shown). The grey area in Figure 5 indicates PRCCs that are not significantly different from zero (based on the statistic (7)). A similar plot can be displayed for eFAST indexes Si and STi (not shown).
Figure 5.
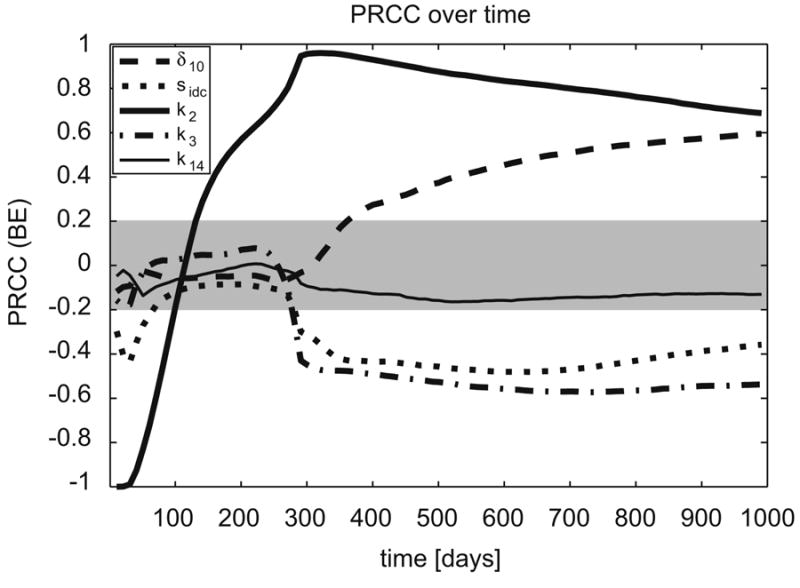
PRCCs of the two compartmental model US analysis performed in section 4.3, plotted over a time course. The gray area represents PRCC values that are not statistically significant. Note how the sensitivity of parameters change as system dynamics progress.
In this example we see that the effect of parameter k2 (maximum rate of infection of resting macrophages due to extracellular bacteria) changes with respect to bacterial load over time: it is negatively correlated (very strong PRCC, almost perfect negative correlation) right after infection (early time points), and then it becomes positively (very strongly) correlated as the infection progresses to its steady state. The positive sign of its PRCC indicates that if we increase parameter k2, bacterial load increases (and vice versa). The negative sign suggests that if we increase it, bacterial load decreases (and vice versa). So, the rate of infection of resting macrophages by M. tuberculosis (k2) is initially responsible for lowering the extracellular bacterial load (likely due to bacterial uptake). Then it becomes the most important source of infection, likely due to bacteria proliferation: the more bacteria internalized by macrophages, the more bacteria are released into the extracellular domain due to overproliferation and subsequent macrophage bursting or killing. Other mechanisms, such as the maximum rate of immature dendritic cells (IDCs) activation/maturation/migration from the lung to the lymph node compartment (δ10), only become significant later during infection (from 300 days on, see Figure 5).
3.6. Standard versus explorative US analysis
US analysis can be implemented by choosing a specific reference output for calculating sensitivity indexes (for example viral or bacterial load, if we track the progression of an infection). We define this type of approach a standard US analysis.
US analysis can be run on a list of several possible model outputs and the results can then be studied and classified depending on the goal of the analysis. We define this type of approach an explorative US analysis. For example, if the model comprises variables at different scales (e.g. intra-cellular vs extra-cellular, or molecular vs. cellular) or in different compartments (e.g. different organs), we can choose outputs to investigate effects of parameter changes on different scales or in different compartments (see section 4.3 for details). An intra-compartmental/intra-scale US analysis investigates how certain outputs generated in a specific compartment (scale) are affected by variations of parameters belonging to the same compartment (scale). An example of intra-compartmental US analysis can be to study how the rate of infection of resting macrophages in the lung affects the bacterial load in the lung (see Section 4.3).
Inter-compartmental US analysis explores how certain outputs generated in one compartment in a multi-compartment/scale model are affected by variations of parameters belonging to a different compartment/scale (for example how the percentage of particular immune cells migrating from the lymph node - compartment 1 - affects the bacterial load in the lung - compartment 2, see Section 4.3). The analysis can be performed either looking at specific inter- and intra-compartmental effects in which we are interested, or all the significant indexes can be listed and then classified as inter- or intra-compartmental effects. An example of multiscale sensitivity analysis can be found in (Chang et al., to appear in Infection and Immunity; Kirschner et al., 2007).
Whether a standard or an explorative US analysis is performed, the set of parameters that are varied is always under investigation and the parameters are continuously varied. The difference is in the goal of the analysis. Standard US analysis is applied for each of the examples shown in section 4, while explorative US analysis is only applied to the two compartmental ODE model of Mycobacterium tuberculosis infection (section 4.3).
4. Uncertainty and Sensitivity Analysis Examples
Since the relationship (including monotonicity) between parameters and outputs is not typically known a priori, then in principle using both PRCC and eFAST methods is ideal. The drawback is that issues related to accuracy of results and computational costs may arise. To illustrate the differences between these methods we implement both PRCC and eFAST and compare the results for different types of mathematical models in biology: three different ordinary differential equation (ODE) systems (Lotka-Volterra, cell population dynamics in HIV infection, and Mycobacterium tuberculosis infection), a delay differential equation (DDE) system in theoretical immunology, and an agent-based model (ABM) of granuloma formation. The results are model-specific. However, in the discussion at the end of the manuscript, we suggest a general approach to balance accuracy of analysis and computational costs.
4.1. Emphasizing PRCC is not accurate when non-monotonicities are present: Lotka-Volterra model
We now revisit the predator-prey (or Lotka-Volterra) model described in section 3.1. Our goal is to focus on two of the four parameters of model (3)-(4) and show how PRCC and eFAST give contradictory results, even with a simple prey-predator model. The cumulative distribution functions (CDFs) of the parameter samples resulting from the LHS scheme are illustrated in Figure 2A. We set the sample size N to 1000. Each parameter is independently sampled from normal pdfs (see Eq. (5)) and the model described by Eqs. (3)-(4) is simulated for each parameter combination. Figure 6A shows the Lotka-Volterra model outputs (Eq. (4), P(t)) corresponding to the LHS matrix and scheme defined in Eq. (5). The vertical dashed line represents the time point chosen to perform the sensitivity analysis (time=9 days). In order to test for non-linearities and non-monotonicities between input variations (parameter σ) and output results (P(t) (predator), we produce scatter plots of the raw or ranked output (y axis) versus raw or ranked input (x-axis, see Panel B, C and D of Figure 6).
Figure 6.
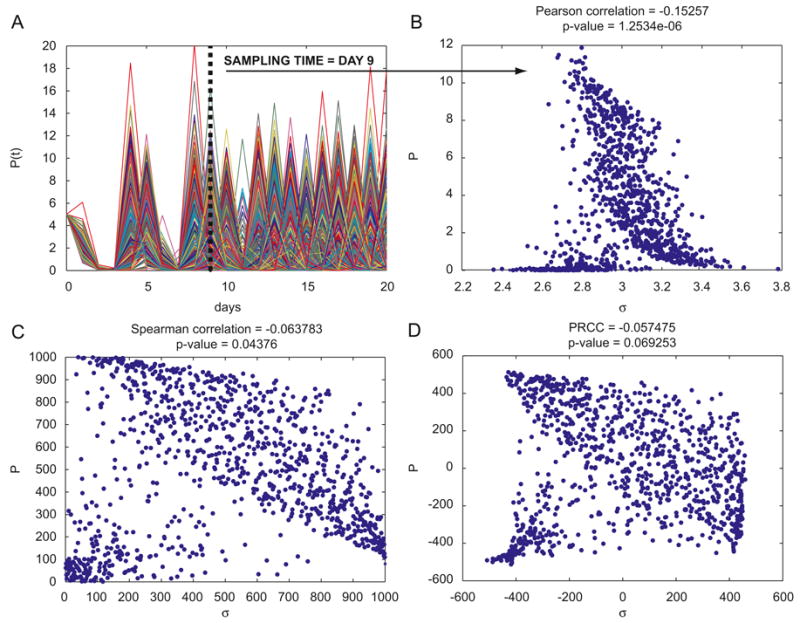
Panel A: plot of the output (1000 runs) of the Lotka-Volterra model. The y axis represents variable P(t), x axis represents time (days). Panel B: scatter plot (linear scale) of parameter σ (x axis) and the “slice” of the output of Panel A at time=9 (rPearson =-0.15257, p<0.001). Panel C: linear-linear plot of the rank-transformed data of Panel B (rSpearman =-0.0638, p>0.04, where rSpearman is the rPearson coefficient calculated on the data of Panel C.). Panel D: linear-linear plot of the residuals of the linear regressions of the parameter σ versus all the other parameters of the model (x-axis) and the residuals of the linear regression of the output versus parameter σ (y-axis) (PRCC =-0.0575, p>0.06). PRCC is the Pearson correlation coefficient calculated on the data of Panel D. Scatter plots of Panel B, C and D remains qualitatively invariant for different LHS simulations. The input parameter (and its rank-transformed values) shown on the x-axis is σ, although all four parameters are varied simultaneously.
Figure 6B shows the linear scatter plot of the 1000 output values at day 9 plotted versus input variation. Figure 6C shows the linear scatter plot of the rank-transformed data, while the scatter plot of two different residuals7 used to calculate PRCC is shown in Figure 6D (see Figure legends for details). There is clearly a non-monotonic, nonlinear relationship between σ and the output P(t) at time t=9 (Figure 6B-C-D) and the corresponding PRCC is not significantly different from zero (Figure 6D, PRCC=-0.0575, p>0.06).
We designed the simulations varying parameters β and σ over large intervals, while parameters α and δ are allowed to vary around their respective mean value following a normal pdf with a very small standard deviation (e.g. 0.01). We tested for significant PRCCs for all four parameters of the Lotka-Volterra model. By construction, parameters α and δ should not significantly affect the output (as confirmed by PRCC columns in Table I, where all PRCCs for α and δ are between −0.05 and 0.05 and not significant, except for the PRCC of α for output Q (-0.0916, p<0.004).
Table I.
Comparison of PRCC and eFAST values for Lotka-Volterra UA and SA (time point = day 9). Values for the columns related to Q(t) are illustrated in Figure 4.
| eFAST: | ||||||
|---|---|---|---|---|---|---|
| PRCC | ||||||
| Si (first order) | STi (total order) | |||||
| Parameters | Q(t) | P(t) | Q(t) | P(t) | Q(t) | P(t) |
| α | 0.0916* | 0.0055 | 0.0042 | 0.0584 | 0.0584 | 0.0018 |
| β | 0.5586* | -0.1655* | 0.1890* | 0.6395* | 0.6395* | 0.0342* |
| σ | -0.7272* | -0.0575 | 0.3306* | 0.7794* | 0.7794* | 0.2324* |
| δ | 0.0422 | 0.0115 | 0.0032 | 0.0893 | 0.0893 | 0.0025 |
| dummy | 0.0405 | -0.0054 | 0.0013 | 0.0840 | 0.0840 | 0.0032 |
significant (p<0.01)
Parameters β and σ should significantly affect the output: confirmed for the model output Q(t) (first PRRC column of Table I, 0.5586 and −0.7272, with p-values<0.001) but because of the non-monotonicity shown in Figure 6D, PRCC of σ versus the output P(t) is not significant (-0.0575, p-value>0.06).
On the other hand, the first- (Si) and total-order (STi) sensitivity indexes returned by eFAST are the highest for σ (see Table I, eFAST columns), suggesting that the contribution of σ to the variability of the output P(t) is in fact the most important. According to condition (A.9) in the Supplement A.5, the sampling size for each curve (NS=65) ensures accurate Si and STi estimates (average CV▽Si <6% and CV▽STi <2% for both outputs).
Summary
These contradictory results show how, even with a simple model, non-linear and non-monotonic relationship between input and output variation can lead to misleading conclusions during sensitivity analyses if PRCC is used.
4.2. Sampling (NS) and resampling (NR) in eFAST: an HIV-ODE model example
We next examine a model for the interaction of HIV with CD4+ T cells (see (Perelson et al., 1993)). It describes four cell population concentrations in the blood: uninfected T cells (T), latently infected T cells (T*, i.e. cells that contain the provirus but are not producing new virus), actively infected T cells (T**, i.e. cells that are producing virus) and free virus (V). The model comprises a total of nine parameters (see Table II) and the dynamics of the various populations are given by
Table II.
| Parameter | Description | Range | Baseline |
|---|---|---|---|
| s | Rate of supply of CD4+ T cells from precursors | [1e-2, 50] | 10 |
| μT | Death rate of uninfected and latently infected CD4+ T cells | [1e-4, 0.2] | 2e-2 |
| r | Rate of growth for the CD4+ T cell population | [1e-3, 50] | 0.03 |
| k1 | Rate constant for CD4+ T cells becoming infected by free virus | [1e-7, 1e-3] | 2.4e-5 |
| k2 | Rate latently infected cells convert to actively infected | [1e-5, 1e-2] | 3e-3 |
| μb | Death rate of actively infected CD4+ T cells | [1e-1, 0.4] | 0.24 |
| NV | Number of free virus produced by lysing a CD4+ T cell | [1, 2e3] | 1200 |
| μV | Death rate of free virus | [1e-1, 1e1] | 2.4 |
| Tmax | Maximum CD4+ T cell population level | 1500 | 1500 |
| (15) |
| (16) |
| (17) |
| (18) |
where T(0) = 1000 mm−3, T*(0) = T**(0) = 0 and V(0) = 10−3 mm−3. The model admits two equilibrium solutions: an uninfected steady state (EB, with no virus present) and an endemically infected steady state (EP). NV is a transcritical bifurcation parameter for EB, or in other words the system converges to the uninfected steady state EB only if
| (19) |
The system (15)-(18) reaches the endemically infected steady state EP if NV> Ncrit. The ranges over which parameters are varied (uniform pdfs) determine whether condition (19) is met or not. So, the parameters NV, μT, μV, k1, k2 (those included in (19)) should appear significant in our uncertainty and sensitivity analysis, depending on the intervals defined in Table II (Range column). Analytically, further conditions defined on other parameters play a role in determining the stability of EP: whether they show up or not in the US analysis depends on the range over which they are varied (see Supplement E for an example with PRCC).
Parameter values given in Table II (Baseline column) produce a stable EP, but stability can be lost through Hopf bifurcations occurring for several parameter combinations (see (Perelson et al., 1993) for details).
We ran LHS/PRCC and eFAST analyses for different sample sizes. For LHS/PRCC we used the following sample sizes 100, 200, 300, 400, 500 and 1000, while for eFAST we set NS respectively to 65, 129, 257, 513, 1025 and 2049 (with NR=5). We test the adequacy of the sample size for both PRCC and eFAST with the top-down coefficient of concordance (TDCC). The number of parameters varied is 8, so the TDCC gives only a trend (since the statistic is only correct for large values of k, i.e. asymptotically). The results are summarized below, while all the details can be found in Supplement D online (Table D.1-D.7).
4.2.1. PRCC and eFAST results for HIV model
PRCC results show how parameters NV, k2, μv (-) are consistently significant and the most important, with k1 and μT (-) always in fourth and fifth position (see Table D.1 online). TDCC suggests N=200 as the optimal sample size (see Table D.2 online).
As mentioned before, use of a uniform or log-uniform distribution (i.e. log-scale sampling) over a range spanning many orders of magnitude can produce very different results. In fact by using a log-scale sampling scheme, parameters k1, NV and μT are now consistently significant and the most important, with μV always in fourth position (see Table D.3 online). Thus, by sampling on a log scale, PRCC results are very different. Only parameter NV is still selected, while parameters k1 and μv are lost. The TDCC suggests again N=200 as the optimal sample size (see Table D.4 online).
eFAST results (both Si and STi) confirm that parameters μV, NV and k2 are consistently significant and the most important (see Table D.5 online). The TDCCs suggest NS=257 as the optimal sample size, although increasing NS does not improve the agreement in the results, except for NS=2049 (see Table D.7 online). The coefficients of variation (see Supplement A.5 online for implementation) are always very high for the first-order sensitivity indexes Si (likely because the values of Si are close to zero) and generally below 10-15% for the total-order sensitivity indexes STi (see Table C.6 online for details). Increasing NS only improves the coefficients of variation for STi. We did not implement a log-scale sampling for eFAST.
If we combine results from both PRCCs and eFAST Si and STi, parameters μT,, k1, k2, NV and μV indeed are significant, suggesting how a properly designed US analysis should return bifurcation parameters as significant. Note that in the original paper (Perelson et al., 1993) these were shown analytically to be bifurcation parameters.
Summary
PRCC and eFAST measure different things. This example shows how results can overlap for a subset of parameters (e.g. μV, NV and k2). However, the ranking of the most important effects is not preserved between the two methods. The TDCC shows how PRCC more efficiently (i.e. with a lower sample size) achieves a concordance in ranking the most important effects, while eFAST may need larger sample sizes.
4.3. Standard and Explorative US analysis: a two compartmental ODE model
We now examine a more complex ODE to address the use of uncertainty and sensitivity analysis in a multi-scale/multi-compartmental setting. As an example, we choose an ODE model of Mycobacterium tuberculosis (Mtb) infection in humans published by our group (Marino & Kirschner, 2004): it comprises a total of 17 equations, and a much larger set of 90 parameters, that describe dynamics between two physiological compartments (lymph node and lung). A detailed description of the model can be found in (Marino & Kirschner, 2004; Marino et al., 2004). Basic details on the biology are given in the Supplement E and Figure E.1.
We perform uncertainty and sensitivity analysis on the 12 parameters that are specifically involved in establishing infection and linking the two anatomical compartments (see Table E.1 for details). This set of parameters represents mechanisms whose action is elicited either in the lung or in the lymph node compartment. A more comprehensive analysis would include all the parameters of the model, or at least the uncertain ones. Here we focus on a subset for the purpose of illustrating both a standard and explorative US analysis. As discussed in Section 3.6, whether a standard or an explorative US analysis is performed, the set of 12 parameters varied is always under investigation and the parameters are continuously varied. The difference between the two analyses is subtle. A standard US analysis lists all the parameters with a significant sensitivity index with respect to one or more outputs of reference (in our example the output of reference is the extracellular bacterial load - BE, see Table III, Panel A).
Table III.
PRCC and eFAST results on the 2-compartmental ODE model. This table summarizes results shown in great detail in Supplement E online, where different sample sizes are used for both LHS/PRCC and eFAST. The time points tested are [100 500 1000]. The sign of PRCC is shown in parenthesis. The top two or three parameters are highlighted. The order they are listed reflect the magnitude of the coefficient (in absolute value, going from high to low). [(*): significant; i.e., p<0.01]. Panel A: PRCC and eFAST results grouped by significance over time. Bacterial load is the output of interest. Panel B: Inter and Intra-compartmental effects. PRCC and eFAST results for BE at time 1000. Panel C: Inter and Intra-compartmental effects. PRCC and eFAST results for MDC at time 500. Panel D: Inter and Intra-compartmental effects. PRCC and eFAST results for Th1 at time 100.
| Sensitivity index | Parameter with a significant sensitivity index | ||
|---|---|---|---|
| Day 100 | Day 500 | Day 1000 | |
| PRCC | sIDC(-), δ10, k2(-),k4(-), δ6 (-), k14(-) | k2(-), sIDC (-), k4, k3, k14(-), δ10, δ8, ξ(-) | k2 (-), δ10, k3, k4, sIDC(-), ξ(-), k14(-) |
| eFAST - Si(*) | k2 | k14, ξ, k2, k3, sIDC | k3, k14, k2, sIDC, ξ |
| eFAST - STi(**) | k2 | k14, ξ, k2, k3, sIDC, k4 | k3, k14, k2, sIDC, ξ, k4 |
| Panel A: US analysis for extracellular bacterial load (BE) over three time points | |||
| Sensitivity index | Parameter with a significant sensitivity index | ||
| Inter-compartment | Intra-compartment | ||
|
| |||
| PRCC | δ10, ξ(-) | k2(-), k3, k4, sIDC(-), k14(-) | |
| eFAST - Si(*) | ξ | k3, k14, k2, sIDC | |
| eFAST - STi(**) | ξ | k3, k14, k2, sIDC, k4 | |
| Panel B: US analysis for extracellular bacterial load (BE) at time 1000 days post infection | |||
| Sensitivity index | Parameter with a significant sensitivity index | ||
| Inter-compartment | Intra-compartment | ||
|
| |||
| PRCC | sIDC, k2, k3(-), δ9 (-) | δ10 | |
| eFAST - Si(*) | k14, k4, k3, sIDC | ξ | |
| eFAST - STi(**) | k14, k4, k3, sIDC, k2 | ξ | |
| Panel C: US analysis for mature dendritic cells (MDC) at time 500 days post infection | |||
| Sensitivity index | Parameter with a significant sensitivity index | ||
| Inter-compartment | Intra-compartment | ||
|
| |||
| PRCC | ξ, δ10 | k3, k2, sIDC, δ4, k14(-) | |
| eFAST - Si(*) | δ10 | k2, sIDC | |
| eFAST - STi(**) | δ10 | k2, sIDC, δ8 | |
| Panel D: US analysis for T Helper cells type I (Th1) at time 100 days post infection | |||
An explorative US analysis identifies which one of these effects (significant sensitivities) has an impact in the same compartment (intra) of the output of reference, or in a different compartment (inter). In our example, we examined two outputs in the lung compartment (extracellular bacterial load – BE, type I T helper cells – Th1) and one output in the lymph node compartment (mature dendritic cells –MDCs) (see Supplement E for details on the biology). Then we computed both PRCC and eFAST coefficients and classified all the parameters with significant sensitivity indexes either as intra- or inter-compartmental effects, as having effects, depending on the output of reference.
We performed LHS/PRCC and eFAST analyses for different sample sizes. For LHS/PRCC we used the following sample sizes 100, 200, 300, 400, 500 and 1000, while for eFAST we set NS respectively to 65, 129, 257, 513, 1025 and 2049 (with NR=5). We tested the adequacy of the sample size for both PRCC and eFAST with the top-down coefficient of concordance (TDCC). The number of parameters varied is small (i.e., 12), so TDCC gives only a trend (as in the previous example). Since analytical results are not available due to the size of the model and the complexity of the equations, conclusions are not as straightforward as in the previous examples. Standard US analysis results are shown in Table III Panel A, while an example of inter- and intra-compartmental analysis at specific time points is given in Table III Panels B-D. All the details can be found in Supplement E online. We analyze three different time points, namely 100, 500 and 1000 days post infection. Table III rows show both PRCC and eFAST Si and STi: they are ordered in descending order (the first listed have the largest absolute values and are highlighted) and the sign of the PRCCs is in parenthesis.
Overall, this example shows how the sets of significant Si and STi returned by efAST is consistent throughout the analysis, returning the same list of important parameters with the same ranking. eFAST results suggest (generally smaller) sets of significant parameters that are not always listed as significant by PRCC and are generally smaller. Moreover, when the same set of parameters is returned, the ranking is frequently different between the two methods (see Panel A).
Table III shows how the fraction of precursor T Helper cells (Th0) migrating out of the lymph node compartment into the blood (ξ) and the maximum rate of immature dendritic cells (IDCs) activation/maturation/migration from the lung compartment to the lymph node compartment (δ10) are alternatively classified as significant inter- (Panel B and D) or intra-compartmental (Panel C) parameters by PRCC and eFAST.
However, they are not consistently returned as significant by both indexes. For example, in Panel C, δ10 is significant only with PRCC and parameter ξ is listed as significant only by Si and STi: both are ranked as the most important by each respective method. Another example is given by parameter ξ in Panel D: only PRCC lists it as significant (while δ10 is returned as very important by PRCC and eFAST Si and STi).
Summary
This example shows how on a large complex model, the use of both indexes is recommended because often the set of the most important parameters is not consistent between the two methods.
4.4. A delay differential model example
We next apply uncertainty and sensitivity analysis to a delay differential equation model published by our group (see (Marino et al., 2007) for details). The model investigates the role of delays in innate and adaptive immunity to intracellular bacteria infection. It tracks five variables: uninfected target cells (XU), infected cells (XI), bacteria (B), and phenomenological variables capturing innate (IR) and adaptive (AR) immunity. A detailed description of the model is in (Marino et al., 2007). Here we only show the equations.
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
Two delays are included in the model. The delay for innate immunity, τ1, occurs on the order of minutes to hours and τ2 is the delay for adaptive immunity on the order of days to weeks. We assume that both responses are dependent solely on the bacterial load (f1 ≡ f2 = B(s)) in the previous τi time units (i = 1,2), where the kernel functions wi(s) (i = 1,2) weight the past values of the bacterial load, B(s).
We use a uniform kernel for innate immunity (with τ1 ≅ 1) and an exponential growth kernel for adaptive immunity (with τ2 ≅ 20). System (20)-(24) is comprised of 20 parameters (15 independent parameters), 7 of which are directly involved in existence condition for equilibrium solutions. Initial conditions for the model are given in Table G.1 (online Supplementary Material). We solved the system numerically using the Matlab solver dde238. The model admits two equilibria: boundary equilibrium EB (clearance of infection, no bacteria) and a positive equilibrium EP (damped or sustained oscillatory bacterial levels, depending on the values of τ1 and τ2). The positive equilibrium EP exists only if the following condition holds:
| (25) |
We sampled eight parameters simultaneously (τ1, τ2, α1, α2, α3, α 4, α 20,σ), defining uniform probability density functions for their distributions. The remainder of the parameters is held constant at their default values (see Table G.1 online). Table G.1 is used to initialize the sampling procedure (see Value column) and to define intervals for uncertainty analysis (see Range column). We set the dimension of the sample in LHS to N=1000, while eFAST is performed for 3 different NS (i.e. 65, 129 and 257) and resampling size to NR=5 (for inference on Si and STi), except for the sample NS=65 where we increased NR to 20 to improve accuracy (see Table G.3 online).
Some parameter combinations do not satisfy the existence condition for EP (i.e., condition (25).); thus, we calculate PRCCs both on the entire LHS dataset and on the subset of samples fulfilling condition (25)). In contrast, the same procedure cannot be applied to eFAST. Because of its unique sampling technique, eFAST must process the whole sampled dataset at once, and we can only compare the sensitivity indexes calculated on the whole parameter space.
We summarize the main US analysis results below, while all the details can be found in Tables G.2 and G.3 online. The indexes are evaluated at 5 different time points (10, 30, 50, 100 200 days) and the model output chosen for sensitivity analysis is bacterial load (Eq. (22)). Condition (A.9) is never satisfied by the choice of NS and NR (see Table G.3 online). Panels A, B and C (in Table G.2 online) show PRCC results, while Panels D and E show eFAST results. Both PRCC and eFAST suggest that bacterial load levels over time are mainly affected by variations in the parameters α3 and α20. PRCC scatter plots of these two parameters versus the bacterial load are shown in Figure 7 (using the whole LHS matrix), where the strong correlations are confirmed. Parameter α4 is found consistently significant only with the PRCC analysis (although the correlation is weak). Extended FAST (Table G.2 Panels D and E) and PRCC list delays τ1 and τ2 as important sources of variation for bacterial load (PRCC predicts they are significant with small negative correlations). Both delays are significant only with the subset of LHS matrix satisfying (25) (Table G.2 Panel C online), in line with analytical results where τ1 and τ2 play a role only when EP exists (τ1 and τ2 define the nature of the equilibrium, with either sustained or damped oscillations). The effect of τ2 is lost if the whole LHS matrix is used (Table G.2 Panel A, online) and both are lost (Table IV Panel B) if only the subset of LHS matrix not satisfying (25) is used (in fact EB is not affected by changes in τ1 and τ2). PRCC scatter plots (see Figure 7) do not show any clear nonlinear non-monotonic relationship between variations in the parameters τ1, τ2, α1 and the output (bacterial load). PRCC and eFAST confirm indirectly our analytical results: they return as significant those parameters that are involved in the existence condition (25) for equilibrium solutions.
Figure 7.
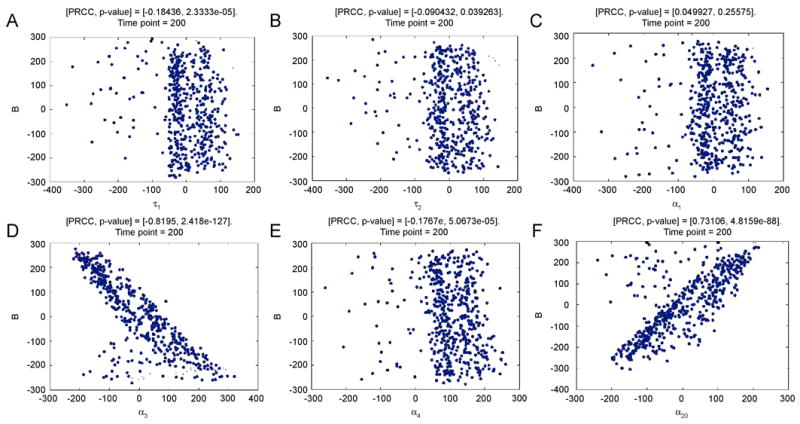
PRCC scatter plots of parameters τ1, τ2, α1 α3, α4 and α20 (calculated at day 200, all 8 parameters are varied simultaneously). Sample size N=1000. The abscissa represents the residuals of the linear regression between the rank-transformed values of the parameter under investigation versus the rank-transformed values of all the other parameters. The ordinate represents the residuals of the linear regression between the rank-transformed values of the output versus the rank-transformed values of all the parameter under investigation The title of each plot represents the PRCC value with the corresponding p-value (see Table G.2 at 200 days in Supplementary Material online)
Table IV.
Parameters analyzed in US analysis.
| Symbol | Description | Range of uniform pdf |
|---|---|---|
| λ | Chemokine diffusion coefficient | [0.4, 0.8] |
| δ | Chemokine degradation coefficient | [2.8811×10-4, 0.0011] |
| αBI | Intracellular growth rate | [0.002, 0.006] |
| Trecr | Probability of T cell recruitment | [0.10, 0.40] |
| Tmove | Probability of T cell movement | [0.01, 0.20] |
| Tactm | Probability of T cell activating macrophage | [0.05, 0.20] |
| Minit | Initial number of macrophages | [40, 400] |
| Mrecr | Probability of macrophage recruitment | [0.20, 0.70] |
| Masp | Activated macrophage speed | [200, 8000] |
| Ntact | Number of T cells needed to activate macrophage | [1, 6] |
| pk | Probability of bacteria killed by resting macrophage | [0.01, 0.10] |
| pTk | Probability of T cell kills a macrophage | [0.01, 0.10] |
Summary
This example shows how PRCC and eFAST results can overlap. However, since the nature of the relationship between inputs and output is not known a priori, PRCC and eFAST should be used together (as in this example), if eFAST computational cost is not prohibitive.
5. Uncertainty and Sensitivity Analysis in Agent-Based Models
Agent-Based Models (ABMs, also called “individual-based models”, IBMs) are a formalism evolved from early research in cellular automata and artificial life. The defining feature of ABMs is that elements of the system are represented as discrete agents that move and interact according to defined rules, in an explicitly defined spatial environment. Stochasticity enters the model as some decision-making rules can be based on random chance, such as a random walk movement of cells. In an ABM, the individual, possibly stochastic, interactions between agents give rise to global, system-wide dynamics and patterns. Thus, ABMs are ideal for studying complex systems in which stochasticity, and spatial and temporal heterogeneity are important, such as biological systems.
Stochastic models, such as the ABM we consider here, pose unique challenges to uncertainty and sensitivity analysis. Most uncertainty and sensitivity analysis techniques have been developed for use with deterministic models, such as those presented in previous sections of this work. To our knowledge, very few researchers have attempted extensive and systematic uncertainty and sensitivity analysis on ABMs (Lempert et al., 2002; Riggs et al., 2008; Segovia-Juarez et al., 2004).
To perform uncertainty and sensitivity analysis on an ABM, it is critical to keep in mind the distinction between aleatory and epistemic uncertainty during model building. In this analysis, epistemic uncertainty is handled by holding a parameter to a fixed value during a particular model simulation, but allowing probabilistic variation between model simulations to reflect uncertainty. In contrast, stochastic components vary randomly from moment to moment within a single ABM simulation. Some studies have applied a stochastic component to otherwise deterministic models by sampling a random sequence of values prior to running a model simulation (Helton, 1999; Helton & Breeding, 1993; Helton et al., 1995). However, this approach cannot be easily applied to ABMs as presented here: stochastic decisions made by each agent at each time step are based on conditional probabilities that depend on both random chance and the state of other interacting agents. Therefore it is impossible to correctly specify a random sequence of agent decisions prior to running the simulation. When performing uncertainty analysis on an ABM, epistemic uncertainty and aleatory uncertainty become conflated in the model output. It is difficult to know whether variability in model outcome is due to experimentally introduced variation in input parameters (epistemic uncertainty) or to the inherent stochastic components of the model (aleatory uncertainty). Therefore, it is difficult to apportion variability to input parameters during sensitivity analysis. In this section, we perform uncertainty and sensitivity analysis on an ABM, identify the strengths and weaknesses of the PRCC and eFAST techniques in dealing with aleatory uncertainty, and propose an averaging method to reduce the influence of aleatory uncertainty.
5.1. An agent-based model example
As an example, we present a published ABM describing granuloma formation during Mycobacterium tuberculosis infection (Segovia-Juarez et al., 2004). This was the first ABM to use a modification of a US analysis using PRCC. In this model, the spatial environment represents a 2mm square section of lung tissue. This area is subdivided into a 100×100 lattice of 20μm square micro-compartments. Agents (cells) populate this environment, representing resident or infiltrating macrophages and T-cells. Bacteria and chemokines also exist in the model, but are treated as a continuous quantity rather than discrete agents. Each micro-compartment can contain at most one macrophage and one T-cell agent (and a quantity of bacteria/chemokines, as these are assumed to have negligible size). Some micro-compartments are designated as vascular source compartments, through which new macrophage and T-cell agents arrive from the blood.
A simulation is initiated by distributing an initial population of resting macrophages randomly on the lattice and an initial load of extracellular bacteria in the center of the lattice. The simulation evolves by a series of discrete time steps, during which rules are evaluated governing the diffusion of chemokines, infection and replication of bacteria, and arrival, movement, interaction, and change in phenotype of immune cells. Parameters that we will analyze by US methods control initial conditions and rates or probabilities used to evaluate rules (Table IV). See (Segovia-Juarez et al., 2004) for a more detailed description of the model.
5.2. Aleatory Uncertainty
It is impossible to entirely separate model output variability due to either aleatory or epistemic uncertainty. However, it is useful to crudely quantify aleatory uncertainty in the absence of variability due to epistemic uncertainty by repeatedly solving the model, holding all parameters constant. Figure 8 represents two typical scenarios: containment of infection and dissemination. The baseline set of parameter values differs between the two scenarios (see (Segovia-Juarez et al., 2004) for definitions of these scenarios and baseline parameters). The variability around each scenario is determined by aleatory uncertainty, while epistemic uncertainty causes the emergence of this bimodal outcome. We find that the containment scenario produces a moderate level of aleatory uncertainty. To roughly quantify aleatory uncertainty, we calculate the coefficient of variation of 10 replicates, holding all parameters constant at their average values (middle value of the Range column in Table IV). For this model, coefficients of variation of the output for the containment scenario (extracellular bacterial load) are 3.5% at day 500 and 62.4% at day 30. The coefficient of variation at day 30 is much larger than at day 500, meaning that aleatory uncertainty at this early time point will more strongly mask any variability due to epistemic uncertainty introduced in subsequent analysis steps. We will focus our analysis on day 30, as this time point is analyzed in (Segovia-Juarez et al., 2004), providing a reference point to compare our results to, and because aleatory effects should be most problematic at this time point due to the high coefficient of variation.
Figure 8.
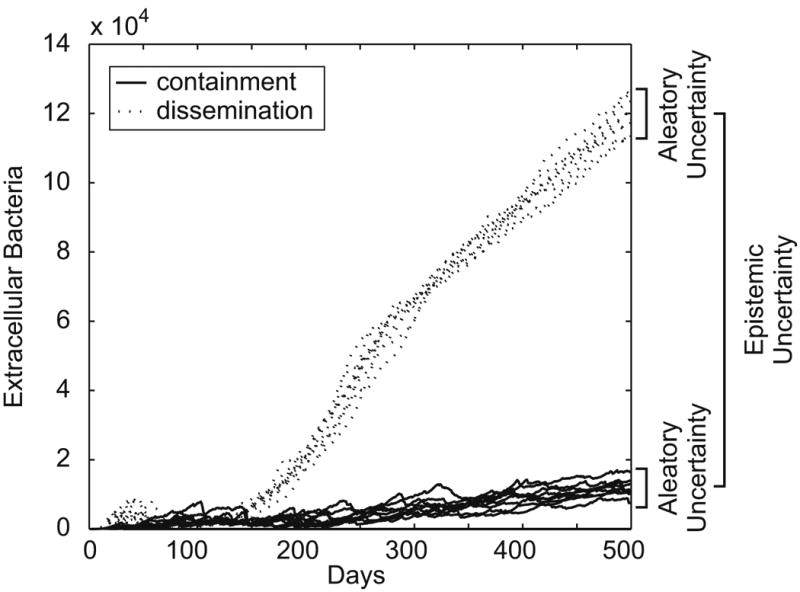
Variation in ABM output due to epistemic uncertainty and aleatory uncertainty. Differences in parameter values lead to either containment of extracellular bacterial load (solid lines), or dissemination of bacteria (dotted lines), as described previously in (Segovia-Juarez et al., 2004). Within each parameter combination, inherent stochasticity within the model causes aleatory uncertainty. At time points earlier than approximately day 150, aleatory uncertainty masks the epistemic difference that USA methodologies seek to measure.
5.3. Replication and averaging scheme for ABM
To study aleatory uncertainty, we propose a replication and averaging scheme that can be applied with either PRCC or eFAST. First, parameter combinations are created using the LHS or eFAST internal sampling algorithm. Next, multiple model simulations are repeatedly run for each parameter combination (replication step). Note that when using a pseudorandom number generator in the algorithm, we reinitialize the random seed for each model simulation. Finally, the sensitivity coefficients are calculated using the average of model outputs across replicates. By comparing these results with the sensitivity coefficients obtained from each replicate individually, we can assess whether US analysis is robust at a specific sample size. One caveat to this approach is that using the average to characterize the distribution of output values over aleatory uncertainty is reliable only if the output values are clustered around a central value (i.e. unimodal). We apply the replication and averaging scheme to the Segovia-Juarez ABM.
5.4. LHS/PRCC results
When aleatory uncertainty is moderate, as is in this example, LHS/PRCC produces consistent results at large LHS sample size: in the original analysis of this model, Segovia-Juarez et al use an LHS sample size of 1000. As sample size is reduced to less than approximately 200-300, two effects occur: first, PRCC becomes less reliable due to the influence of aleatory uncertainty; second, statistical power for PRCC significance is reduced due to the smaller sample size; therefore weakly correlated parameters are not found to be significant.
Next, we explore whether averaging replicates can reduce effects of aleatory uncertainty, allowing fewer computationally intensive model simulations. We find that averaging replicates has two beneficial effects. First, PRCC becomes reliable at smaller sample sizes due to the removal of some of the variability induced by aleatory uncertainty. Specifically, by using replicates (4 replicates in this case), a similar set of parameters with significant PRCC is achieved with a smaller number of samples (at least 50) compared to the standard scheme without replicates (at least 300 samples). Second, parameter values and model output becomes more tightly correlated due to the removal of some confounding aleatory noise, resulting in PRCC of greater magnitude (see Figure 9). This increase in PRCC magnitude that occurs by averaging is apparent even when PRCC is already reliable due to large sample size, e.g. 1000 samples (not shown). These benefits come at a cost, however: if the total number of model simulations is held constant, performing replicates reduces the number of samples available for statistical tests (e.g. 300 parameter samples simulated once, versus 100 parameter samples replicated 3 times, then averaged, yielding 100 sample averages). In Figure 9, we show that there are some situations where the gain in PRCC magnitude due to averaging is favorable despite the loss in statistical power. In the original analysis of this model, using a sample size of 1000 with no replication, Segovia-Juarez et al (Segovia-Juarez et al., 2004) find 9 significant parameters, including parameters αBI and λ. Reducing sample size to 300 with no replication (Figure 9, black bars), for a total of 300 model simulations, parameters αBI and λ are not significantly different from zero. Using 100 samples and averaging 3 replicates (Figure 9, gray bars), for a total of 300 model simulations, however, successfully identifies αBI and λ as significant, yielding performance similar to that of 1000 samples used by Segovia-Juarez et al. Therefore, for this ABM we suggest that performing replicate simulations of each parameter sample and averaging these replicates is a useful strategy that can provide better performance with fewer computationally intensive model simulations.
Figure 9.
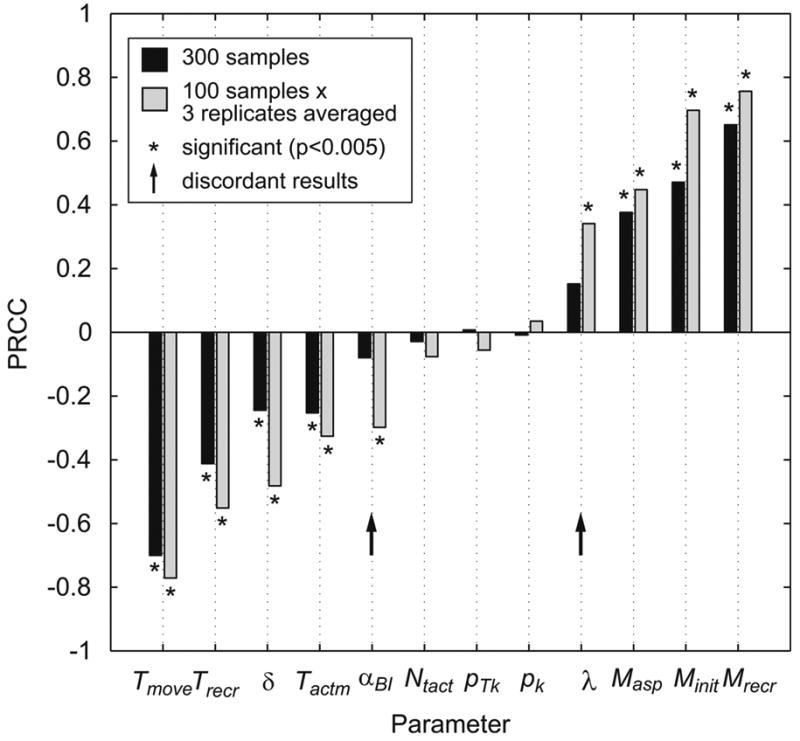
Effect of aleatory uncertainty on LHS/PRCC and the benefit of averaging replicates. Model parameters were sampled 300 (black bars) or 100 times (gray bars). For the 100 sample condition, the 3 replicate model simulations were performed for each sample and averaged. Parameters with a PRCC significantly (p<0.005) different from zero are indicated with (*). Parameters with discordant statistical significance between the two experimental conditions are indicated (arrow).
5.4.1. eFAST results
To our knowledge, eFAST has been used to analyze an ABM once before (Lempert et al., 2002), but details of the methodology used are lacking. To explore the suitability of the eFAST method in analysis of stochastic models, we analyze the Segovia-Juarez model, described above, taking advantage of the replication and averaging scheme (described in the previous section) and of the use of a dummy parameter (as developed in section 3.3.1). Extended FAST is performed using 257 samples per search curve (i.e., NS=257, chosen to satisfy condition (A.9)), a resampling size of 4 (i.e., NR=4), and 4 replicates for averaging. By allowing eFAST to partition variance to a dummy parameter, we find that the first-order index is relatively unaffected (Figure 10A). However, eFAST severely mishandles the variability induced by aleatory uncertainty by incorrectly partitioning it to the total-order sensitivity index, resulting in a large artifactual STi=24.3% (Figure 10B, dummy parameter, black bar). Thus, use of a dummy parameter to quantify this artifact reveals that parameters with a total-order STi in the range of ∼20-30% are likely artifactual. Using replication and averaging to limit variability induced by aleatory uncertainty successfully reduces this artifact by more than half (Figure 10B, dummy parameter, gray bar): this allows 7 of the 8 significant parameters identified by LHS/PRCC to exceed the dummy parameter background value for Si (Figure 10A). Increasing NS and NR, as well as performing averaging with additional replicates will likely further improve the limit of detection. Performing significance testing in combination with replication and averaging, we find that 8 of the 9 parameters identified as significant by LHS/PRCC are also identified by eFAST first-order Si (Figure 10A), while the STi coefficients are significantly different from the dummy only for 4 of the 8 parameters listed by LHS/PRCC (Figure 10B). Note that eFAST result come at a much higher computational cost: 53456 total model simulations using eFAST, as opposed to 300 total model simulations with LHS/PRCC.
Figure 10.
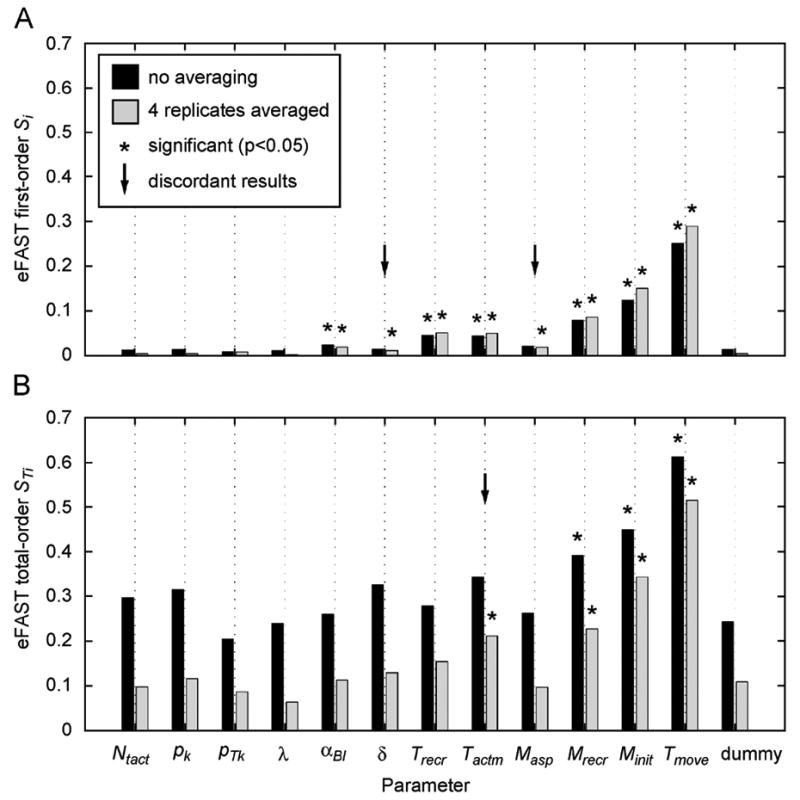
Performance of eFAST on the stochastic agent-based model of Segovia-Juarez et al. (Segovia-Juarez et al., 2004) Panel A: eFAST first-order sensitivity index Si. Replication and averaging (gray bars) has a small effect on Si, allowing additional parameters (indicated by arrow) to be identified as statistically significant (*). Panel B: eFAST total-order sensitivity index STi. eFAST artifactually assigns aleatory variance to the total-order index, resulting in a high dummy parameter background value (dummy parameter, black bar). Replication and averaging (gray bars) partially reduces this artifact, allowing an additional parameter (indicated by arrow) to be found significant (*).
Summary
This specific ABM example shows how LHS/PRCC and eFAST are typically in agreement, identifying a similar set of important parameters (with the eFAST sets of important parameter being smaller than PRCC, as shown in some of the deterministic model examples in section 4). However, these two methods have different relative strengths and weaknesses. eFAST requires many more model simulations, which is a particular problem as ABMs are often more computationally intensive than deterministic models. Also, when analyzing stochastic models, eFAST produces an artifact whereby aleatory variance is inappropriately partitioned to the total-order sensitivity index. Therefore, this example suggests how LHS/PRCC method (with the modifications presented here) can perform better than eFAST for a specific time point, reaching the same conclusions with much less computational cost.
The eFAST method has the strength of identifying non-monotonic sensitivities, however. Though we see no evidence of this strength in the ABM we analyze here, there is no a priori way of knowing if non-monotonic sensitivities are present in a model. Therefore, if computational cost is not prohibitive, use of eFAST on stochastic models can complement LHS/PRCC results. In this case, one should take steps to reduce the artifact of eFAST mishandling aleatory variance in the total-order sensitivity index, or one should rely solely on the first-order index, as it is unaffected by the artifact.
6. Discussion and Conclusion
Uncertainty and sensitivity analyses offer a way to assess the adequacy of models and establish what factors affect model outputs. We reviewed and compared two specific types of global sensitivity analysis indexes that have proven to be among the most reliable and efficient, namely a sampling-based method (Partial Rank Correlation Coefficient-PRCC) and a variance-based method (extended Fourier Amplitude Sensitivity Test-eFAST). All functions used throughout the paper are available on our website (http://malthus.micro.med.umich.edu/lab/usanalysis.html).
PRCC provides answers to questions such as how the output is affected if we increase (or decrease) a specific parameter (linearly discounting the effects of the uncertainty over the rest of the parameters). Thus PRCC can be informative on what parameters to target if we want to achieve specific goals (e.g., control or regulatory mechanisms). For example, the most significant set of parameters can be used to determine how to efficiently reduce viral load or increase immune response (by both timing and magnitude). eFAST, and all variance-based methods in general, indicate which parameter uncertainty has the greatest impact on output variability. In other words, our predictions will be strengthened if we can reduce uncertainty and get better estimates on specific parameters of the model (i.e., the ones with highest Si and STi sensitivity coefficients). This will also enhance any additional PRCC or sampling-based analysis, because any regulatory or control strategy will be more reliable.
A general finding was that a properly designed US analysis returns a set of bifurcation parameters as significant; thus US analysis can be an adequate alternative when an analytical solution to a mathematical system is not possible. This holds true for both sample and variance-based methods (at least if we consider the examples of section 4).
One critical point is the selection of adequate pdfs and the choice of parameter ranges used for sampling. The selection of probability distributions for the uncertain parameters depends in part on whether the intent of the analysis is an exploration of variable effects (i.e., a sensitivity analysis) or a propagation of uncertainty to assess the uncertainty in the outcomes of interest (i.e., an uncertainty analysis). For meaningful uncertainty analyses, the selected distributions are chosen based on the degree of our understanding of biology with respect to the appropriate values of model parameters. In contrast, the distributions might be selected simply to fully explore potential variable effects in a sensitivity analysis.
The choice of parameter range should also be guided by the available knowledge of the biological problem. If a parameter range is completely outside the biological realm, the practical relevance of the US analysis is lost. Unfortunately, exact or even hypothetical biological ranges are many times unknown. Unless the choice of very small ranges for certain parameters is guided by some a priori knowledge, the sampling should be performed within the whole range of plausible values, since US analysis results can be quite different (see Supplement F for examples of how PRCC and eFAST results can be affected by sampling different ranges). Moreover, if the range of variation for some parameter spans several orders of magnitude and we want to avoid under-sampling in the outer ranges of parameter space, the implementation of a logarithmic sampling scheme (for example, a log-uniform in place of a uniform pdf) would achieve the goal, but the final results will be affected (as shown in Supplement D online).
Our examples showed how PRCC and eFAST could give different results, where nonlinear and non-monotonic relationships between inputs and output lead to misleading conclusions, even with a simple prey-predator model (see section 4.1). eFAST is more general than PRCC (it deals with any type of relationship between inputs and outputs of a model) with one major drawback: its computational cost, especially for computing STi. Our examples highlight how a large number of iterations are needed to achieve a recommended degree of accuracy in eFAST (as also shown in Figure 8.9 at page 190 of (Saltelli et al., 2000)).
We designed a new method (together with an heuristic for its accuracy) to check for significant eFAST Si and STi. This new method is based on a two-sample t-test approach and uses a re-sampling scheme to compare each sensitivity index with that of a dummy parameter. The use of dummy parameters is a standard practice in screening methods (see Chapter 4 in (Saltelli et al., 2000)), although, to our knowledge, it has never been applied in the context of eFAST.
We built several functions to display scatter plots of sampled parameters versus the output under study (given on our website, see http://malthus.micro.med.umich.edu/lab/usanalysis.html): they can be extremely useful to detect non-monotonicities and non-linearities (as shown in section 4) and possibly explain why PRCC and eFAST results are different.
In the context of ABM, we also implemented a new averaging strategy to efficiently and reliably perform US analysis within the context of this particular class of stochastic models. By running the ABM multiple times with the same set of parameters and then averaging the output, we are able to attenuate the effect of aleatory uncertainty, obtaining more reliable results both for PRCC and eFAST.
We also implemented a concordance measure (top-down coefficient of concordance – TDCC) that informed on the adequacy of the sample size and can check if PRCC and eFAST return a similar set of important parameters.
Throughout our examples, we found that the set of significant first order Si and total order STi sensitivity indexes returned by eFAST is consistent and with the same ranking. eFAST generally returns smaller sets of parameter with significant Si and STi, compared to the set of parameters with significant PRCC. Also, eFAST often returns Si and STi for parameters that are not listed as significant by PRCC and, when a similar set of parameters is returned, the order of importance is frequently different between the two methods.
Based on the examples shown, we conclude that PRCC and eFAST Si and STi should both be computed, keeping in mind that they measure different things, and that eFAST is generally computationally more expensive. If the computational cost is not too high (i.e. cpu time per one model run), more efficient methods are available (e.g. methods that are less affected by non-monotonicities). A lower computational cost can be achieved by reducing NS and NR, (i.e. the total number of runs) but the accuracy of the results might be affected. To increase the accuracy of eFAST results, in general, it is better to increase NS first (and check for the top-down coefficient of concordance (TDCC) to see if that sample size is sufficient to capture a similar set of most important parameters), and then eventually increase NR (to improve the accuracy of inference on the indexes). We found that values and significances of first-order Si are affected by increasing NS: the values of the not significant Si get smaller, as does the dummy parameter Sdummy, making the t-test more reliable. Increasing NS does not affect STi values, although the t-test becomes more precise.
In general, the computational execution time of the model is the major concern when performing US analysis (although it was not a major issue for the examples given in section 4 and for the ABM). Models with several parameters and many complex nonlinear mechanisms likely result in high computational costs. Screening methods are available to address this problem. Within the class of screening methods, Morris (or elementary effects) is the most popular (see (Morris, 1991)): it is global, computationally efficient and should be implemented as a first preliminary US analysis when the execution time of the model is prohibitive (several hours or days).
In summary, characterizing uncertainty in parameter values and initial conditions in mathematical models in biology is attainable and is dependent on the type of system under study. For the math biology community to continue to gain a foothold and have an impact in important biology problems, it is clear that identifying uncertainty in our models is of key importance. By the very act of classifying this uncertainty, we can simultaneously identify the parameters (i.e. biological mechanisms) that are driving system outputs. These mechanisms can then be posed to the experimental community to test. This close interaction between theorists and experimentalists provides the greatest opportunity for the use of mathematical models.
Supplementary Material
Acknowledgments
NIH grants HL68526, LM 009027 and DAIT-BAA-05-10. We are grateful to Jennifer Linderman, Rick Riolo and to the members of the Kirschner laboratory for helpful discussions. Also comments by 2 anonymous reviewers were invaluable in making this manuscript as comprehensive and clear as possible.
Footnotes
IBM=Individual Base Modeling in fields like ecology
Definition of rank-transformation: the smallest value of a variable is assigned a rank of 1, the next largest value is assigned a rank of 2, tied values are assigned an average rank, and the largest value is assigned a rank equal to the sample size
The standard procedure when ties are encountered is to assign the tied values the average of what their values would have been if they have been consecutive but not equal. We are indirectly addressing the problem of integer-valued parameters with very few values by a single-parameter space exploration, holding them fixed during the UA and SA procedures.
We use the matlab function ttest2 to perform the two-sample t-test. We assume the most conservative options, e.g. two tails and that the two samples come from normal distributions with unknown and unequal variances. This is known as the Behrens-Fisher problem. ttest2 uses Satterthwaite's approximation for the effective degrees of freedom.
If k=3, and
The resampling size NR should be large enough to achieve accuracy in statistical significance.
We want to model y (response or dependent variable) as a function of x (regressor or independent variable), i.e. y=f(x). The error we make in the prediction is called residual (e=y-f(x)). In our case x is the parameter vector (α, β, δ, σ) and f is a linear combination of a subset of x. Thus the x-axis of Panel D represents [ex=σ-f(α, β, δ)], the y-axis represent [ey=y-f(σ)]., where the dependent and independent variables are rank-transformed.
(Version 6.5, R13, Copyright 1984-2002, The MathWorks, Inc)
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson TW. Wiley series in probability and statistics. 3rd. Wiley-Interscience; Hoboken, N.J: 2003. An introduction to multivariate statistical analysis. [Google Scholar]
- Apostolakis G. The Concept of Probability in Safety Assessments of Technological Systems. Science. 1990;250(4986):1359–1364. doi: 10.1126/science.2255906. [DOI] [PubMed] [Google Scholar]
- Blower SM, Dowlatabadi H. Sensitivity and Uncertainty Analysis of Complex-Models of Disease Transmission - an Hiv Model, as an Example. International Statistical Review. 1994;62(2):229–243. [Google Scholar]
- Cacuci DG, Ionescu-Bujor M. A comparative review of sensitivity and uncertainty analysis of large-scale systems - II: Statistical methods. Nuclear Science and Engineering. 2004;147(3):204–217. [Google Scholar]
- Chang ST, Linderman JJ, Kirschner DE. Multiple polymorphisms on antigen presentation and susceptilbity to M. tuberculosis infection. Infection and Immunity. doi: 10.1128/IAI.01677-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins DC, Avissar R. An Evaluation with the Fourier Amplitude Sensitivity Test (Fast) of Which Land-Surface Parameters Are of Greatest Importance in Atmospheric Modeling. Journal of Climate. 1994;7(5):681–703. [Google Scholar]
- Cooke R. Environmental ethics and science policy. Oxford University Press; New York: 1991. Experts in uncertainty : opinion and subjective probability in science. [Google Scholar]
- Cukier RI, Fortuin CM, Shuler KE, Petschek AG, Schaibly JH. Study of Sensitivity of Coupled Reaction Systems to Uncertainties in Rate Coefficients. 1. Theory. Journal of Chemical Physics. 1973;59(8):3873–3878. [Google Scholar]
- Draper D. Assessment and Propagation of Model Uncertainty. Journal of the Royal Statistical Society Series B-Methodological. 1995;57(1):45–97. [Google Scholar]
- Evans JS, Gray GM, Sielken RL, Smith AE, Valdezflores C, Graham JD. Use of Probabilistic Expert Judgment in Uncertainty Analysis of Carcinogenic Potency. Regulatory Toxicology and Pharmacology. 1994;20(1):15–36. doi: 10.1006/rtph.1994.1034. [DOI] [PubMed] [Google Scholar]
- Helton JC. Uncertainty and Sensitivity Analysis Techniques for Use in Performance Assessment for Radioactive-Waste Disposal. Reliability Engineering & System Safety. 1993;42(23):327–367. [Google Scholar]
- Helton JC. Uncertainty and sensitivity analysis in the presence of stochastic and subjective uncertainty. Journal of Statistical Computation and Simulation. 1997;57(14):3–76. [Google Scholar]
- Helton JC. Uncertainty and sensitivity analysis in performance assessment for the Waste Isolation Pilot Plant. Computer Physics Communications. 1999;117(12):156–180. [Google Scholar]
- Helton JC, Breeding RJ. Calculation of Reactor Accident Safety Goals. Reliability Engineering & System Safety. 1993;39(2):129–158. [Google Scholar]
- Helton JC, Davis FJ. Illustration of sampling-based methods for uncertainty and sensitivity analysis. Risk Anal. 2002;22(3):591–622. doi: 10.1111/0272-4332.00041. [DOI] [PubMed] [Google Scholar]
- Helton JC, Davis FJ. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliability Engineering & System Safety. 2003;81(1):23–69. [Google Scholar]
- Helton JC, Johnson JD, Oberkampf WL, Storlie CB. A sampling-based computational of epistemic uncertainty in model strategy for the representation predictions with evidence theory. Computer Methods in Applied Mechanics and Engineering. 2007;196(3740):3980–3998. [Google Scholar]
- Helton JC, Johnson JD, Sallaberry CJ, Storlie CB. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliability Engineering & System Safety. 2006;91(1011):1175–1209. [Google Scholar]
- Helton JC, Johnson JD, Shiver AW, Sprung JL. Uncertainty and Sensitivity Analysis of Early Exposure Results with the Maccs Reactor Accident Consequence Model. Reliability Engineering & System Safety. 1995;48(2):91–127. [Google Scholar]
- Helton JC, Martell MA, Tierney MS. Characterization of subjective uncertainty in the 1996 performance assessment for the Waste Isolation Pilot Plant. Reliability Engineering & System Safety. 2000;69(13):191–204. [Google Scholar]
- Hoare A, Regan DG, Wilson DP. Sampling and Sensitivity Analyses Tools (SaSat) for Computational Modeling. Theoretical Biology and Medical Modelling. 2008;5:4. doi: 10.1186/1742-4682-5-4. open access at http://www.tbiomed.com/content/5/1/4. [DOI] [PMC free article] [PubMed]
- Hora SC, Helton JC. A distribution-free test for the relationship between model input and output when using Latin hypercube sampling. Reliability Engineering & System Safety. 2003;79(3):333–339. [Google Scholar]
- Hora SC, Iman RL. Expert Opinion in Risk Analysis - the Nureg-1150 Methodology. Nuclear Science and Engineering. 1989;102(4):323–331. [Google Scholar]
- Iman RL, Conover WJ. Small Sample Sensitivity Analysis Techniques for Computer-Models, with an Application to Risk Assessment. Communications in Statistics Part a-Theory and Methods. 1980;9(17):1749–1842. [Google Scholar]
- Iman RL, Conover WJ. A Distribution-Free Approach to Inducing Rank Correlation among Input Variables. Communications in Statistics Part B-Simulation and Computation. 1982;11(3):311–334. [Google Scholar]
- Iman RL, Conover WJ. A Measure of Top-down Correlation. Technometrics. 1987;29(3):351–357. [Google Scholar]
- Iman RL, Davenport JM. Rank Correlation Plots for Use with Correlated Input Variables. Communications in Statistics Part B-Simulation and Computation. 1982;11(3):335–360. [Google Scholar]
- Iman RL, Helton JC. An investigation of uncertainty and sensitivity analysis techniques for computer models. Risk Anal. 1988;8(1):71–90. [Google Scholar]
- Kirschner DE, Chang ST, Riggs TW, Perry N, Linderman JJ. Toward a multiscale model of antigen presentation in immunity. Immunol Rev. 2007;216:93–118. doi: 10.1111/j.1600-065X.2007.00490.x. [DOI] [PubMed] [Google Scholar]
- Kleijnen JPC, Helton JC. Statistical analyses of scatterplots to identify important factors in large-scale simulations, 2: robustness of techniques. Reliability Engineering & System Safety. 1999;65(2):187–197. [Google Scholar]
- Lempert R, Popper S, Bankes S. Confronting surprise. Social Science Computer Review. 2002;20(4):420–440. [Google Scholar]
- Marino S, Beretta E, Kirschner DE. The role of delays in innate and adaptive immunity to intracellular bacteria infection. Mathematical Biosciences and Engineering. 2007;4(2):261–286. doi: 10.3934/mbe.2007.4.261. [DOI] [PubMed] [Google Scholar]
- Marino S, Kirschner DE. The human immune response to Mycobacterium tuberculosis in lung and lymph node. J Theor Biol. 2004;227(4):463–86. doi: 10.1016/j.jtbi.2003.11.023. [DOI] [PubMed] [Google Scholar]
- Marino S, Pawar S, Fuller CL, Reinhart TA, Flynn JL, Kirschner DE. Dendritic cell trafficking and antigen presentation in the human immune response to Mycobacterium tuberculosis. J Immunol. 2004;173(1):494–506. doi: 10.4049/jimmunol.173.1.494. [DOI] [PubMed] [Google Scholar]
- McKay M, Meyer M. Critique of and limitations on the use of expert judgements in accident consequence uncertainty analysis. Radiation Protection Dosimetry. 2000;90(3):325–330. [Google Scholar]
- Mckay MD, Beckman RJ, Conover WJ. Comparison of 3 Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics. 1979;21(2):239–245. [Google Scholar]
- Morris MD. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics. 1991;33(2):161–174. [Google Scholar]
- Morris MD. Three Technometrics experimental design classics. Technometrics. 2000;42(1):26–27. [Google Scholar]
- Parry GW, Winter PW. Characterization and Evaluation of Uncertainty in Probabilistic Risk Analysis. Nuclear Safety. 1981;22(1):28–42. [Google Scholar]
- Pate'-Cornell ME. Uncertainties in Risk Analysis: Six Levels of Treatment. Reliability Engineeering and System Safety. 1996;54(23):95–111. [Google Scholar]
- Perelson AS, Kirschner DE, De Boer R. Dynamics of HIV infection of CD4+ T cells. Math Biosci. 1993;114(1):81–125. doi: 10.1016/0025-5564(93)90043-a. [DOI] [PubMed] [Google Scholar]
- Ratto M, Pagano A, Young P. State dependent parameter metamodelling and sensitivity analysis. Computer Physics Communications. 2007;177(11):863–876. [Google Scholar]
- Riggs T, Walts A, Perry N, Bickle L, Lynch JN, Myers A, Flynn J, Linderman JJ, Miller MJ, Kirschner DE. A comparison of random vs. chemotaxis-driven contacts of T cells with dendritic cells during repertoire scanning. J Theor Biol. 2008;250(4):732–51. doi: 10.1016/j.jtbi.2007.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saltelli A. Making best use of model evaluations to compute sensitivity indices. Computer Physics Communications. 2002;145(2):280–297. [Google Scholar]
- Saltelli A. Sensitivity analysis in practice : a guide to assessing scientific models. Wiley; Hoboken, NJ: 2004. [Google Scholar]
- Saltelli A, Bolado R. An alternative way to compute Fourier amplitude sensitivity test (FAST) Computational Statistics & Data Analysis. 1998;26(4):445–460. [Google Scholar]
- Saltelli A, Chan K, Scott EM. Wiley series in probability and statistics. Wiley, Chichester; New York: 2000. Sensitivity analysis. [Google Scholar]
- Saltelli A, Marivoet J. Nonparametric Statistics in Sensitivity Analysis for Model Output - a Comparison of Selected Techniques. Reliability Engineering & System Safety. 1990;28(2):229–253. [Google Scholar]
- Saltelli A, Ratto M, Tarantola S, Campolongo F. Sensitivity analysis for chemical models. Chemical Reviews. 2005;105(7):2811–2827. doi: 10.1021/cr040659d. [DOI] [PubMed] [Google Scholar]
- Saltelli A, Tarantola S, Chan KPS. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics. 1999;41(1):39–56. [Google Scholar]
- Savage IR. Contributions to the Theory of Rank Order-Statistics - the 2-Sample Case. Annals of Mathematical Statistics. 1956;27(3):590–615. [Google Scholar]
- Schaibly JH, Shuler KE. Study of Sensitivity of Coupled Reaction Systems to Uncertainties in Rate Coefficients. 2. Applications. Journal of Chemical Physics. 1973;59(8):3879–3888. [Google Scholar]
- Segovia-Juarez JL, Ganguli S, Kirschner D. Identifying control mechanisms of granuloma formation during M. tuberculosis infection using an agent-based model. J Theor Biol. 2004;231(3):357–76. doi: 10.1016/j.jtbi.2004.06.031. [DOI] [PubMed] [Google Scholar]
- SimLab. 2006 http://simlab.jrc.ec.europa.eu/. distributed under the SimLab Software License, Version 1.0.
- Storlie CB, Helton JC. Multiple predictor smoothing methods for sensitivity analysis: Description of techniques. Reliability Engineering & System Safety. 2008a;93(1):28–54. [Google Scholar]
- Storlie CB, Helton JC. Multiple predictor smoothing methods for sensitivity analysis: Example results. Reliability Engineering & System Safety. 2008b;93(1):55–77. [Google Scholar]
- Tarantola S, Gatelli D, Mara TA. Random balance designs for the estimation of first order global sensitivity indices. Reliability Engineering & System Safety. 2006;91(6):717–727. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


