Polymer Models of Meiotic and Mitotic Chromosomes

Abstract

Polymers tied together by constraints exhibit an internal pressure; this idea is used to analyze physical properties of the bottle-brush–like chromosomes of meiotic prophase that consist of polymer-like flexible chromatin loops, attached to a central axis. Using a minimal number of experimental parameters, semiquantitative predictions are made for the bending rigidity, radius, and axial tension of such brushes, and the repulsion acting between brushes whose bristles are forced to overlap. The retraction of lampbrush loops when the nascent transcripts are stripped away, the oval shape of diplotene bivalents between chiasmata, and the rigidity of pachytene chromosomes are all manifestations of chromatin pressure. This two-phase (chromatin plus buffer) picture that suffices for meiotic chromosomes has to be supplemented by a third constituent, a chromatin glue to understand mitotic chromosomes, and explain how condensation can drive the resolution of entanglements. This process resembles a thermal annealing in that a parameter (the affinity of the glue for chromatin and/or the affinity of the chromatin for buffer) has to be tuned to achieve optimal results. Mechanical measurements to characterize this protein–chromatin matrix are proposed. Finally, the propensity for even slightly chemically dissimilar polymers to phase separate (cluster like with like) can explain the apparent segregation of the chromatin into A+T- and G+C-rich regions revealed by chromosome banding.

INTRODUCTION

The structure of condensed chromosomes on scales beyond the level of the basic 10-nm beads-on-a-string fiber is still controversial, in part because chromatin is dense yet labile and easily disturbed (van Holde, 1989). In this article, we use polymer statistical mechanics to elaborate the equilibrium properties of bottle-brush models of meiotic chromosomes and to outline how the kinetics of mitotic chromosome condensation directs the resolution of entanglements. Without any assumptions about well-ordered structures other than that of the chromatin fiber, we show how semiquantitative predictions about experiments can still be made. These predictions concern the morphology and mechanical properties of chromosomes on scales that can be studied via light microscopy in buffer or, in some cases, in vivo. If these predictions are borne out (several already have qualitative support), then it will lend credence to the starting assumptions and will allow inference of mechanical and kinetic parameters not obtainable by imaging fixed samples.

The phenomenological approach to polymer solutions has proved very powerful, because nontrivial and experimentally testable consequences can be derived with weak assumptions under general conditions (de Gennes, 1979; Doi and Edwards, 1986; Grosberg, 1994). Following Flory (de Gennes, 1979, chapter 4), all the chemical details can be lumped into three essential parameters, the effective monomer size a, the number of monomers per chain N, and a dimensionless interaction parameter χ that expresses the tendency for monomers to adhere to (or repel) one another. Monomer in this context is the smallest unit that can substantially reorient in thermal equilibrium and so naturally, in the context of chromatin, includes both the DNA and bound protein (e.g., several successive nucleosomes). The strongest predictions from this class of theories are frequently cast as scaling laws, valid for large N to within dimensionless order-unity constants. Chromosomes are without question the longest polymers known, so it is natural to ask whether aspects of their morphology can be explained using polymer phenomenology.

The first dichotomy to be faced in any discussion of polymers in solution is whether they are in good (χ <1/2) or bad (χ >1/2) solvent. By solvent we mean the water, ions, and other small (<10 nm) moieties in the cytosol that make up the medium surrounding chromatin fibers and chromosomes. A good solvent wets the monomers, making the polymers dissolve and disperse; a bad solvent is one in which the monomers and, therefore, the polymers aggregate, leading to phase separation between concentrated polymers and essentially polymer-free solvent. We will work exclusively in good solvent conditions (chromosomes in meiotic prophase) or marginal theta-solvent conditions (χ ∼ 1/2), which with several caveats we apply to mitotic chromosomes.

Brush models, in which chromatin loops are attached to a central axis but otherwise free to fluctuate, have been part of the debates over chromosome structure for many years. From the microscopic evidence, such a model is most clearly relevant to chromosomes in meiotic prophase [Moens, 1987; applications of the model to mitotic chromosomes are due to Laemmli and coworkers (Paulson, 1988)]. Once we add the assumption that the bristles behave as if in good solvent (for our purposes it is immaterial that they are loops rather than single fibers), the basic physical theory can be taken from the polymer brush literature (Li and Witten, 1994). The existing theory has not found many applications due to the difficulty of preparing synthetic brush-like polymers; the process by which chromosomes condense into brushes is therefore of interest to materials scientists as well as to biologists.

The most striking pictures of brushes have been obtained with certain solvent washes and drying that serve to comb out the bristles of an otherwise more compact structure (Miller and Hamkalo, 1972). The Christmas trees formed by the nascent RNA transcripts along certain heavily transcribed genes are classical, and similar pictures of flattened extended brushes have been obtained for meiotic prophase chromosomes (Moens and Pearlman, 1988). These preparations are a good assay for the arc length of individual bristles and their axial spacing, but by themselves do not rule out the possibility of proteinaceous attachments between bristles in vivo or that the bristles are collapsed or self-adhering. Similar caveats have been expressed about the high salt treatments of mitotic chromosomes that have been interpreted as evidence for a radial loop model (Paulson, 1988; Jackson et al., 1990).

Lampbrush chromosomes isolated from amphibian oocytes provide the best evidence for an open brush morphology suggestive of good solvent conditions in vivo and do so on two scales (Callan, 1986). The prominent DNA loops are themselves brushes with a DNA core and ribonucleoprotein (RNP) bristles and form in turn the bristles of a larger brush that is the chromosome itself. The loops appear to undergo Brownian motion when viewed free in buffer and the chromosomes themselves unfold when they emerge from a punctured nucleus (Macgregor and Varley, 1988). The theory to be developed below shows that the retraction of the loops when the RNA transcripts are snipped off and the ubiquitous oval shape of diplotene bivalents between chiasmata indicate that the bristles are in good solvent conditions.

Meiotic chromosomes in a variety of other species during leptotene through pachytene and in diplotene also evidence a brush-like morphology (Comings and Okada, 1970; Rattner et al., 1980, 1981; Heng et al., 1994). Preparations in these studies involve surface speads, fixation, and degrees of squashing, so that some distortion is occurring, though less than with classic Miller spreads. Microscopy on whole nuclei probably yields the most faithful measures of dimensions (Dawe et al., 1994). In all cases, an axial core is readily visible surrounded by a chromatin halo. For mammals a prominent protein constituent of the core has been identified and fluorescent antibodies are available (Dobson et al., 1994; Moens, 1994; Pearlman et al., 1992). We have interpreted a number of observations on fixed specimens, as evidence for good solvent conditions.

Mitotic chromosomes are typically denser than their meiotic (prophase) counterparts and the proteins that condense along with the chromatin fiber are only now being identified with the aid of cell extracts and genetics (Gasser, 1995; Hirano et al., 1995; Strunnikov et al., 1995; Koshland and Strunnikov, 1996). We accept the prevalent hypothesis that chromosome condensation plays an essential driving role in the resolution of entanglements and the separation of duplicate sister chromatid arms.

For entanglement resolution to occur by physical-chemical means (i.e., by a local mechanism rather than by an external process such as motors along tracks), we develop the hypothesis that the cell in early prophase tunes solvent quality (or equally well, physical properties of chromatin) toward theta-solvent conditions, i.e., χ = 1/2. Nonhistone proteins that coprecipitate with the chromatin are taken to act as a gentler and regulated version of the well-known polyanion condensing agents and come into play when 1/2 − χ is sufficiently small (but still positive). We insist that the solvent conditions for the chromatin must never become truly bad: if poor solvent conditions prevailed, all the chromosomes would condense together into a ball. In poor solvent, sister chromatid arms would remain intertwined until pulled apart by microtubule-based motors. Instead, in mitotically arrested cells, some delineation between the arms of the chromatids occurs in the absence of any known motor proteins and in the absence of microtubules (Shamu and Murray, 1992; Miyazaki and Orr-Weaver, 1994).

We stress that our discussion of mitotic chromosomes focuses on the thermodynamics of chromatin packing and the kinetics of its disentanglement along the chromatid arms and has nothing to say about how the chromatids are joined at the centromere. These attachments are known to be precisely regulated in response to tension across the kinetochore (Bickel and Orr-Weaver, 1996).

THEORY

In this section we rederive by elementary means some of the theoretical results on polymer brushes in good solvent as a way of summarizing the physics involved and making comprehensible the extensions needed to describe chromosomes. Two ingredients are needed. The first just formalizes the notion that two monomers cannot occupy the same region of space, which is expressed as an interaction contribution to the free energy of order Twn per monomer, where n is the local monomer density (units of number/volume) and w ∼ (1 − 2χ) a³ is the excluded volume per monomer with length a. For good solvent, we will set χ = 0, so as not to carry a parameter we have no hope of determining from the data. (For bad solvents, χ > 1/2 and w < 0, which corresponds to attraction between the monomers and their condensation into a dense phase.) The energy scale is set by the thermal energy T = 4.1 × 10⁻²¹ J or 4.1 pN·nm (the work done by a force of 4.1 × 10⁻¹² N during a displacement of 1 nm).

The second ingredient is intuitively less obvious but is just a restatement of the second law of thermodynamics in terms of an entropic force. Namely, to distort a flexible polymer (treated as a random walk and hence without an internal energy) from its most probable Gaussian configuration (so-called because the displacement between the ends of a random walk follows a Gaussian distribution) requires work that decreases the entropy and increases the free energy of the polymer. For forces < T/a, the free energy as a function of extension R is ∼ TR²/Na², where numerical factors of order unity are suppressed. Alternatively, this force law is just a restatement of what is meant by good solvent conditions, ignoring for the moment that the polymer is constrained not run into itself.

Brush Equilibrium Free Energy and Radius

To describe a brush, we ignore the obvious variation in monomer density as a function of distance from the axis and express the free energy per bristle G_b as a function of brush radius R, as the sum of the two terms above (Li and Witten, 1994):

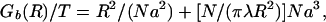1

where λ is the distance along the axis of successive bristles (1/λ is the number of bristles per length) and N is the number of monomers per bristle. The optimal R and G_b (denoted with a*) are obtained by minimizing Eq. 1 with respect to R; hence,

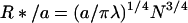2a

and

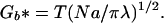2b

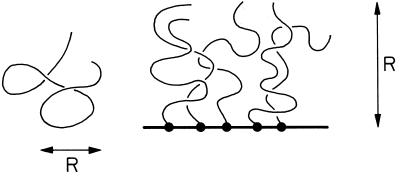
Note that the radius increases with N more rapidly than for a random walk (Figure 1), because of the excluded volume of the other bristles; i.e., the polymer must not run into itself. The equilibrium structure is just a balance between intermonomer excluded volume and the entropic stretching. Decreasing λ increases the monomer density, and R* increases as a result. For reasonable parameters, the free energy is always larger than T (we assume λ << R; for λ ∼ R, each bristle is an isolated coil), reflecting the energetic cost of confining the bristles to a common axis. Alternatively, the constraint that each bristle is anchored on the axis gives rise to a chromatin pressure, which stretches the bristles.

Figure 1.

An isolated chromatin bristle will be a random coil (left), but when attached to an axis and spaced by << R, interchain repulsion stretches it (right).

When one properly treats the variable density, the radius and free energy change by no more than 20% in the above formulas (Li and Witten, 1994). However, the detailed density profile is quite interesting: the free ends are found essentially only between 0.5R and R; the monomer density is very peaked around the core (as expected just for geometric reasons) and quite tenuous beyond 2R/3. The monomer density goes smoothly to zero at R.

Several other properties of brushes pertinent to chromosomes can be derived by similar dimensional reasoning. A given bristle will sample a cone-like region of space with its apex on the axis. The base (outer edge) has a radius characteristic of a random walk (in contrast with Eq. 2a)

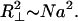3

Thinking of the polymer as a random walker starting out from the axis, one realizes that the radial steps will be biased outward by the chromatin pressure, but a finite fraction of the total steps will be transverse to the radius and otherwise unbiased, giving rise to a random walk transverse to the radial direction.

The R_⊥ is pertinent to chromosomes because it can be used to qualitatively assess the entanglement of adjacent bristles in one brush and of bristles in two overlapping brushes (e.g., paired chromatids at an early stage of entanglement resolution). From the study of both experiments on and simulations of flexible polymers, it is known that when eight random-walk polymers share the same volume, the chains will be constrained by entanglements (Kavassalis and Noolandi, 1989). Adopting this criterion, from the number of segments per volume in our brush [n* = N/(πR*2 λ)] and the volume occupied by a chain (R*R_⊥²), the number of chains that share the same volume follows as R*R_⊥²n*/N = [a³/(πλ³)]¼N¼. Because of the weak N dependence, this number will not reach 8 for typical chromosome parameters; shorter bristles can be considered as essentially unentangled once equilibrium has been reached.

Repulsive Force between Two Brushes

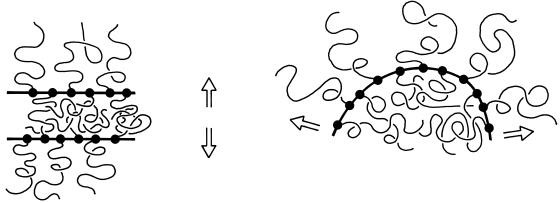
When two brushes overlap, they will push apart to lower the chromatin density; this is another manifestation of chromatin pressure (Figure 2). To calculate the order of magnitude of this repulsive force, note that if two brushes coincided the free energy per bristle would increase by 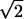(take λ → λ/2 in Eq. 2). This free energy could also be derived by integrating the inter brush force from a spacing of 2R, where it vanishes to zero. The dependence of the force on the radial spacing is nontrivial and could be calculated following established methods (Li and Witten, 1994) but its order of magnitude of this force per unit of axial length F_a is:

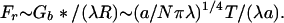4

Figure 2.

Chromatin pressure develops when the bristles are compressed, either when two brushes overlap (left) or when a brush is bent (right). Arrows indicate forces.

Tension between Bristles Inside Brush

There is also an axial force F_r exerted on whatever glue fastens the bristles together. Its magnitude is just G_b^* expressed per unit length of brush or

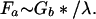5

Brushes Have a Long Bending Persistence Length

The last property of interest is the thermal persistence length of the brush or the length of brush that can be deflected by an angle of one radian at an energetic cost of T. Assume whatever constitutes the axis is completely flexible. Forcing the brush to bend with a radius of curvature ρ >> R will increase (decrease) the volume accessible to the outer (inner) bristles by a factor ∼ 1/(1 ± R/ρ). Redo the argument leading from Eq. 1 to Eq. 2 separately for the two populations of bristles to find

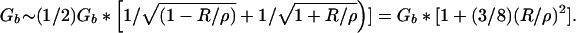Converting to units of per length of brush and extracting the persistence length yields

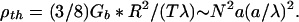6

This is typically a long distance compared with brush radius R. A polymer bottle brush is, therefore, a rather stiff object, on the scale of its radius, even if the axial core has no intrinsic stiffness. Chromatin pressure alone is sufficient to stiffen the brush. On the other hand, it should be noted that chromatin pressure provides no resistance to shear: twisting elasticity purely probes the stiffness of the axial attachments or of bristle cross-linking.

Brush in Theta Solvent

The above theory can be extended to the case of theta solvents, but we will merely sketch how the various scaling laws change, because when evaluated for parameters appropriate for meiotic chromosomes, the numerical results change by no more than 50%. The definition of a theta solvent is that the interaction energy per monomer is no longer proportional to n but rather to n². Such a situation arises when monomer–monomer avoidance and sticking approximately cancel one another (i.e., χ = 1/2) ; one is left with only three-body interactions that contribute a free energy per monomer proportional to n².

Hence Eq. 1 is replaced by

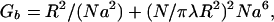7

and Eq. 2 becomes

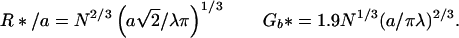8

Thus the monomer density is still lower than in a collapsed state (i.e., a melt of densely packed monomers where n ≈ 1/a³) by a factor of ∼ (N λ/a).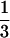

Gel Model of Chromosome

An alternative to a brush model where the chromatin attachments are all to a central axis, is a gel, where the cross linkages are uniform through out the volume (note that these two pictures are not mutually exclusive: cross-linked radial loops give rise to a gel). If there are N >> 1 monomers between successive cross-links, the resulting network can be elastic over a large range of extensions (i.e., five or more). A gel can be immersed in a good solvent and swollen so that a large part of its volume is liquid; alternately, if the solvent quality is poor the chains will collapse and the gel will be dense, like rubber.

If we assume the monomers in a gel are free to move, then the elasticity of a gel comes from the entropic elasticity of the constituent chains: to extend each chain a distance R, a force of TR/(Na²) must be applied. A key point is that synthetic polymer gels (e.g., cross-linked polystyrene chains) have a much smaller monomer size (a ≈ 0.5 nm) than chromatin (a ≈ 30 nm) and, therefore, a gel of chromatin will have intrinsically rather weak elasticity.

The elasticity of a gel is described by an elastic modulus E that has the dimension of a pressure. Its value reflects the pressure, or force per area, that must be applied to a gel to increase its length by a factor of two. If we consider a gel in good solvent, the inter-cross-link chains will be swollen and separated from one another. If before stretching, the radius of each chain is R₀, then the number of chains per cross-sectional area is just 1/R₀²; the force per area as a function of extension R of each chain is (1/R₀²)TR/(Na²) = (R/R₀)T/(NR₀a²). Therefore the elastic modulus is E = T/(Na²R₀). Because before stretching each chain is of radius R₀ ≈ 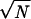a, the elastic modulus can also be expressed as E = T/R₀³ or roughly one thermal unit of energy per cross-link volume (de Gennes, 1979). Measurement of gel elasticity therefore leads to an estimate of cross-link density. In poor solvent, one must consider more carefully how the chains are packed and the effects of surface tension, but a value of a thermal unit per cross-link volume is in a good starting estimate for E.

Finally, we note that a gel can be deformed either while keeping its volume fixed, or while allowing its volume to change. The former type of deformation measures the shear modulus; the latter is sensitive also to the bulk modulus. Most mechanical measurements (e.g., stretching, bending, or twisting an elastic rod) are primarily sensitive to the shear modulus. On the other hand, the change in volume of a gel in response to a change in hydrostatic or osmotic pressure is dependent on its bulk modulus. For swollen gels, the two moduli are usually comparable.

Phase Separation of Bristles and Banding

So far we have assumed chemical homogeneity, but the well-known process of chromosome banding converts small differences in base composition to a pattern of nested stripes particular to the chromosome (Craig and Bickmore, 1993). We therefore note in this connection, one very characteristic feature of dense polymer solutions or melts, namely, their tendency to phase separate, i.e., spatially cluster together similar molecules. This can be understood semiquantitatively from a Flory theory because the entropy of mixing depends on the concentration of chains, each of which moves as a unit, while the van der Waals energy mismatch, which promotes phase separation, goes as the number of monomers. (van der Waals interactions may be overwhelmed by other interactions favoring separation, e.g., interactions between proteins that bind favorably to either A+T- or G+C-rich chromatin; however, simple van der Waals theory provides a starting point that may describe sequence-driven separation in purified DNA or chromatin fiber solutions)

A very crude estimate of this effect is (chapter 6 in Israelachvili, 1992).

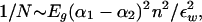9

where E_g ∼ 10⁴ is the frequency range in temperature units where the molecular dielectric polarizabilities [α]_1,2 differ appreciably. The dielectric constant of water, ε_w, although ∼80 for zero frequency, is a factor 10–40 smaller at the frequencies appropriate to the van der Waals interaction. Polarizabilities are of order the molecular volume, so the difference between [α]_A+T versus [α]_G+C could be ∼10%. The contrast in the A+T:G+C density is as high as 10% and the volume fraction of nucleotide pairs in condensed chromatin ∼10%. Hence, ([α]₁ − [α]₂)n ∼ 10⁻³. Larger contrasts could be produced by proteins or the dyes used to visualize the bands. Hence, individual bristles with N ∼ 100 could phase separate.

For chromosomes with the bristles anchored to a central axis, the loop size limits the degree of spatial phase separation, and conversely observing phase separation would measure the transverse loop radius R_⊥ Our prediction is therefore that the A+T:G+C ratio in chromosome bands will be enhanced over what would be predicted if the genome were layed down sequentially. Another consequence of chemical heterogeneity near the theta point is that certain regions may collapse while others remain extended.

Alternative Theory—Bad Solvent

Sikorav and Jannink (1994) envision a chromosome as a polymer melt (bad solvent conditions) and then show that topoisomerase (topo) II is necessary for the final stages of chromatin compaction by allowing strand passages. We feel that experiments on both native and in vitro-assembled mitotic chromosomes argue in favor of good solvent conditions as regards the chromatin-buffer system and that a third glue component is necessary to understand mitotic chromosomes, which they did not postulate. Topo II will certainly link dense chromatin, but this seems to us parasitic rather than essential to the condensation process and we feel that plausible chemical condensing agents alone can give densities compatible with experiments. Jannink et al. (1996) considered the kinetics of chromosome separation under melt conditions and concluded that some outside force (i.e., from the spindle) is needed when there is more than 10⁵ bp per chromosome. This is at variance with the in vitro and in vivo experiments summarized below.

RESULTS AND DISCUSSION

Meiotic Prophase Chromosomes

Brush Model Parameters.

The effective monomer size a is the length of the minimal unit that can reorient in thermal equilibrium. For chromatin in vivo, we will identify this with ≈30-nm-long segments of the 30-nm fiber seen via electron microscopy and x-ray scattering for a variety of preparations (Thoma et al., 1979; Widom, 1986, 1989). However, a density correlation on this scale does not imply thermally induced bending on the same scale. The interpretation of what is seen in these experiments as the monomer size for our purposes is suggested by atomic force microscopy experiments, sectioned cryoelectron microscopy, and modeling studies of interphase chromosomes (Woodcock et al., 1993; Horowitz et al., 1994; Leuba et al., 1994; Woodcock and Horowitz, 1995). These authors show how a random variation in the linker distance, plus the natural helicity of the DNA, can give rise to decorrelation in the direction of the fiber on the scale of 5–10 nucleosomes. Because the amount of linker DNA contained in such a segment is one or two thermal persistence lengths, thermal fluctuations should be comparable to those induced by the linker variability.

An important consistency check on this interpretation is provided by the fluorescence in situ hybridization measurements of Yokota et al. (1995) for euchromatin in interphase. They observed good agreement with a random walk model for genomic separations s less than 2 megabases (Mb). Specifically, 〈r²〉 ≡ Na² = [(1.9 μm²/Mb)s], where s is in Mb units and N is the number of segments of size a comprising s. The authors also estimated that their preparation caused a dilation by a factor of 4/3; so for in vivo conditions, we have to multiply all physical lengths by 3/4. Their measurements then agree with the assignment of 1 kb of DNA to each a = 30-nm segment [i.e., (3/4)² × 1.9 μm²/Mb ∼ 30² nm²/10³ bp]. The slope of 〈r²〉 versus s is not sufficient to fix both a and the number of base pairs per monomer. Hahnfeldt et al. (1993) used the curvature of this plot to infer >10 kb of DNA/monomer, but the theory they used to fit is at variance with the interpretation of the new data in Yokota et al. (1995). The open chromatin model reviewed by Woodcock and Horowitz (1995) corresponds to a length reduction of 10 (1 kb 30 nm), less than the factor of ∼30 often assumed for 30-nm fiber, which is predicated on a tightly wound helix of 10-nm fiber. We will assume a range of 1–2 kb of DNA per monomer in what follows; the larger value would allow for some degradation of solvent quality between interphase and meiotic prophase. The assumption of good solvent conditions makes interphase a not implausible reference point for meiotic prophase. The alternative of determining a directly from fits to meiotic chromosome data is problematical, because it is mixed in with other parameters.

The remaining parameters needed to define the brush model are the number of monomers per bristle N and their axial spacing λ. For chromosomal applications based on chromatin pressure, we will count one loop as slightly less than two bristles, because under good solvent conditions, the loops are open self-avoiding structures and the two bristles it defines are joined only at their ends. The best estimates of N are from preparations that comb out the DNA loops. If the nucleosomes are stripped off, then the measured bristle (1/2 loop) length divided by 1–2 kb will give N; if nucleosomes remain, then we assume that the measured radius is directly just Na.

The axial spacing of bristles is calculated from the genome size, the total axial length of all the chromosomes, the number of bp per bristle, and the copy number (e.g., two for mitotic chromosomes with undifferentiated sister chromatid arms and four for meiotic pachytene). Because we are mostly concerned with the bristles and their mutual interactions, the actual structure of the synaptonemal complex (SC) will not play a role in our discussions (the SC lateral dimensions are considerably less than the brush radius [Dobson et al., 1994]).

Table 1 lists three systems that have been studied in sufficient detail so that we can determine our parameters with some confidence.

Table 1.

Observed polymer brush parameters for three experimental systems

System	N	λ (nm)	R (μm)
Transcription loops (a)	10	40
Bombyx pachytene (b)	20	10	0.2
Mouse pachytene (c)	150	8	1–2

N, number of monomeric units per bristle; λ, axial spacing of bristles. 

Newt Lampbrushes.

These chromosomes display a brush morphology on two scales: an individual transcription loop is a (tapered) brush with RNP bristles and a DNA axis, and at the next level, these loops are the bristles of a larger brush, making up the entire chromosome. The pertinent parameters are most accessible for single transcription loops and we focus on this level only. When the extraction is done at physiological levels of salt, the RNP bristles on Triturus consist of a string of ≈30-nm particles (Figure 30 in Callan, 1981). Thus we continue to use this number for a and assume it corresponds to 1–2 kb of RNA, though the evidence for this choice is far weaker than for interphase chromatin. The original Miller spreads were performed on Newt lampbrushes, so the bristle length of the bare RNA can be measured directly or inferred from the size of the gene being transcribed, e.g., a fraction of 10 kb for the tandem RNA genes (Miller and Beatty, 1969; Macgregor, 1980, page 20); we estimate N = 10. The axial spacing of the transcripts varies a lot, and we use for numerical estimates λ = 40 nm, a value half the maximum reported (see Chapter 4 in Callan, 1986).

Moth Meiotic Prophase.

Meiotic prophase chromosomes of Bombyx mori have been studied by (Rattner et al., 1980, 1981). The haploid genome is 0.5 10⁹ bp, and Miller spreads indicate a maximum loop arc length of 25 μm, which we translate to 10 μm of bare DNA for a typical bristle length or N = 20. There are then roughly 60,000 bristles per pachytene chromosome, if all the DNA is in loops. The total axial chromosome length was measured to be 260 μm, indicating one bristle per λ = 4 nm (the loop spacing is of course twice that). (The authors’ value for the axial loop spacing in pachytene was taken as the ratio of 260 μm to the ∼7000 haploid loops. No evidence for the pairing of the four homologous loops was presented; however pairing has been seen in mouse pachytene chromosomes [Heng et al., 1994].) However, the authors also show data from early prophase where the loop spacing is 200 nm (Figure 1 in Rattner et al., 1981); the preparation may well have significantly elongated the axis in this case. We adopt a compromise value of λ = 10 nm. A bristle spacing of less than the segment size a is of course nonsensical along a very thin axis, but because the SC itself has a radius around 0.1 μm, there is no contradiction.

As a measure of the size of the chromatin halo in vivo, we use the authors minimally dispersed figures that give a radius ∼0.2 μm well into pachytene (figure 5 in Rattner et al., 1981). (However, ostensibly the same preparation, early in prophase [figure 5 in Rattner et al., 1980], gave radii in the range 0.5–1 μm, which is equivalent to the fully stretched bristle lengths of 10 μn noted above for bristles with histones removed.) For another species of moth, Moens and Pearlman (1988) have measured a bristle length of 2 μm with nucleosomes attached. Similar data is available in Weith and Traut (1980).

Mouse Meiotic Prophase.

Meiotic prophase in the mouse has become a model system for studying principles of chromosome organization. There are antibodies available to several of the SC proteins (Dobson et al., 1994), and the determinants of loop size have been the subject of several investigations (Heng et al., 1994, 1996). The haploid genome size is 2.5 × 10⁹ bp. Figure 2 of Comings and Okada (1970) shows a water-spread preparation in which enough of the fibers are visible so that one can crudely estimate their arc length to be 1.5 to 2 times larger than the nominal halo radius of 2–3 μm, e.g., N ∼ 100 − 200. Moens and Pearlman (1988) quote similar values for the mouse and rat.

A similar value can be inferred from figure 2b of Heng et al. (1994). A 40-copy λ DNA repeat (1.8 Mb) was inserted into the mouse genome and by using fluorescence in situ hybridization was seen to be attached only by flanking sequences to the SC. It appears as a mushroom, with a 4- to 5-μm stalk. We infer that the stalk length is set by the repulsion of the unanchored λ loop from the brush by the other (shorter) bristles, which were combed out by the preparation. The native mouse DNA is organized into a chromatin halo in optical pictures of stained low salt spread chromosomes of radius 2 μm (Moens and Pearlman, 1989; Heng et al. 1994, 1996), which Moens and Pearlman (1989) take as more indicative of the radius in vivo.

To determine λ in Table 1, we need the total chromosome length. From a variety of SC antibody and 4,6-diamidino-2-phenylindole-stained surface spreads, we found a value for the total SC length in pachytene of 200 μm (Heng et al., 1996; Moens, personal communication). This implies, assuming 10¹⁰ bp of DNA per cell in pachytene and 200 kb of DNA per bristle, that λ = 4 nm. However, some pairing of homologous regions was observed in Heng et al. (1994), so we use λ = 8 nm in Table 1. Heng et al. (1996) quote the radius of a rat pachytene nucleus in vivo to be ∼5 μm: therefore, the chromosomes fill the nucleus and perhaps interpenetrate. The much more compact (relative to the nuclear volume) human pachytene chromosomes in Figure 1 of Comings and Okada (1970) is probably due to the ethanol/acetic acid fixation that tends to collapse the chromatin more than does formaldehyde.

Other Data.

Several other meiotic systems should be noted. There is good quantitative data on meiotic chromosomes in maize (Dawe et al., 1994), which appear more condensed than their genome size (7.5 × 10⁹ bp, haploid) would suggest. Direct evidence for an open brush structure in humans is provided by Comings and Okada (1971). They show both an optical image of an intact but hypotonically swelled nucleus and electron microscope spreads that permit the bristle length to be measured. There is only a contraction of a factor of 2 to 3 occurring in vivo. For both maize and humans, these references suggest that the chromosomes occupy no more than one-fourth of the nuclear volume.

Physical Properties of Meiotic Chromosomes and Comparison with Experiment

Scale of Intracellular Forces.

The observed brush parameters (Table 1) permit us to evaluate (Table 2) the physical parameters derived in the previous section. To put the force numbers in some context, note that a radial force of 1 pN/μm acting on a rod with a length-to-diameter ratio of 10–100 will drag it through water at a velocity of 0.1 mm/sec normal to its long axis. Second, an axial force of T/a ∼ 0.1 pN will stretch chromatin fiber to about half its contour length of aN [which otherwise would be a random coil of radius ∼ aN]. Forces in the range of 2 pN will cause the release of bound histone octamers from DNA because they are comparable to the binding energy of the nucleosome divided by the length of the wrapped DNA (Marko and Siggia, 1997). Even larger forces of 50–100 pN are capable of modifying DNA or protein secondary structure (Cluzel et al., 1996; Smith et al., 1996). These numbers are all much less than the force that the mitotic spindle is capable of exerting on a chromosome of ∼700 pN (Nicklas, 1983).

Table 2.

Predictions for in vivo radius R, radial repulsive force per length F_r, the axial force F_a, and the thermal persistence length ρ_th for the three systems (a–c) defined in Table 1

System	R (μm)	Fr (pN/μ)	Fa (pN)	ρth (μm)
a	0.1	1.3	0.16	0.2
b	0.28	6.4	1.8	10
c	1.3	5.1	6.8	1100

The defining equations were Eq. 2a and Eqs. 4–6, respectively. 

Lampbrush Transcription Loops.

There are many observations reviewed in Callan (1986) and Scheer et al. (1984) that show that releasing RNA polymerase from the transcription loops or digesting the RNP fibrils leads to loop retraction. When the drugs were removed and transcription was resumed, the normal loop structure was restored. Although Scheer et al. (1984) were seeking to involve actin filaments in the loop structure, their actin antibody did lower the transcription of genes other than for rRNA. An alternative explanation of these observations is simply that the axial force produced by the RNP transcripts straightens out the loops. Its magnitude (Table 2) compared with the 0.1 pN required to elongate by half a chromatin bristle is certainly large enough. Scheer et al. (1984) also note a decrease in the axis of the lampbrush chromosome itself by a factor of 6 when the loops are retracted, indicating that entropic repulsion between the loops is also extending the chromosome axis.

It is rather difficult to estimate the forces induced by the chromatin pressure for the lampbrush chromosome as a whole, because the monomer size of the bristles is highly variable due to varying levels of transcription.

Diplotene Morphology.

Diplotene bivalents are oval-shaped. Between chiasmata, the two replicated homologous chromosomes bulge out to a distance comparable to the diameter of an individual half bivalent (Macgregor, 1993). This is no accident, according to our conclusion that a strong radial repulsive force is produced when two brushes overlap. The same free energy cost of bristle overlap is responsible for the thermal persistence length (or equivalently the bending modulus) of the brush as a whole. Because the ovals in question are rather elongated, most of the bristle compression is due to the overlap of the half bivalents, rather than the bending of an individual bivalent, so it is the former that is minimized. To minimize brush overlap at the chiasmata itself, the planes defined by successive ovals (or bivalents) should be perpendicular. That this is indeed seen (figure 453–4 in Wilson, 1937) and is a strong argument against ties between the bristles.

With isolated chromosomes, our interpretation could be tested by collapsing the loops (e.g., using high magnesium) and seeing the oval flatten. Such an observation would be direct proof that good solvent conditions are applicable because it would show that the native bristles are not packed at maximum density.

Mammalian Systems.

The radial force produced by bristle overlap also defines the free energy cost of assembling the SC from pairs of homologous chromosomes, because to do so pairs of brushes must be brought together. Interesting pictures of the leptotene–zygotene transition (i.e., the zipper-like progression of homologue pairing) are shown in Figure 4 of Dobson et al. (1994). The free energy per length involved is nothing but F_a of Table 2 in energy/length units, e.g., 1.2 T/nm for the mouse data (for reference, this is 10–20% the free energy binding the strands of double-stranded DNA together under normal conditions). These considerations also suggest why pairing begins at or near the telomeres; the loops are shortest there and the interbrush repulsion is least. The molecular mechanisms responsible for gluing together the homologues have yet to be elucidated.

The other surprising feature of pachytene brushes that emerges from Table 2 is that their rigidity is not due to the protein core, but rather to the brush itself. The thermal persistence length is a convenient way to characterize the elastic bending energy: e.g., the energy necessary to impose a radius of curvature of R on a segment of length R is Tρ_th/R. A persistence length longer than the chromosome itself merely means that they will be straight if free in solution with no forces acting (note that usual spreads generate capillary forces that can be much larger than thermal). In Figure 3 of Pearlman et al. (1992), there are electron micrographs of pachytene chromosomes treated with DNase to remove most of the bristles. The remaining SCs appear much more bent than the spread preparations. This suggests a more flexible structure, but differences in preparation conditions could be responsible: a controlled measurement is needed.

Heng et al. (1996) prepared transgenic mice in which the sections of the genome were interchanged between the middle and ends of the chromosome. The goal was to see whether the shorter loops characteristic of the chromosome ends were due to sequence or position. However, for purely geometrical reasons, bristles on the end of a brush will be stretched a factor of ∼2 less than in the middle because the bristle density is lower. Larger changes in bristle length as a function of position were noted by Heng et al. (1996), so their conclusions stand.

Other Experimental Comparisons.

The predicted radii in Table 2 are within a factor of two of experiment, which is reasonable considering the uncertainties on both sides. It would be interesting to verify the 3/4 power of N in Eq. 2a by comparing data between species. More data on the native radii are needed to compare with the known bristle lengths which range from 0.1 μm in yeast to 7 μm in grasshopper Moens and Pearlman (1988). Whether the solvent quality can also be assumed constant between species is open to debate, and the cells have to be properly phased because there is a gradual contraction from leptotene into pachytene. Comparative data for a variety of amphibians is presented in Scheer and Sommerville (1982).

We finally note an indirect consequence of the repulsive forces between chromatin loops that explains the well known hypotonic swelling of the nuclei of permeabilized cells. Although the swelling is taking place in low salt buffers, it cannot be attributed to the excess osmotic pressure of salt ions inside versus outside the nucleus, because this will equalize rapidly under the experimental conditions (and probably though nuclear pores in the native cell). Instead, hypotonic treatment is more likely loosening whatever shell confines the chromatin or, perhaps, further swelling the chromatin or the nuclear matrix itself.

Preliminary evidence for chromatin pressure as the source of hypotonic swelling was provided by Moens (personal communication) who compared two hypotonic buffers with the same osmolarity but different amounts of magnesium. With 10 mM divalent cations, the nucleus contracted. Previously, Widom (1986; personal communication) had observed that nuclei swelled under buffer conditions that favored unfolding and loosening of 30-nm fiber.

Mitotic Chromosomes

Experimental Basis for a Physio-Chemical Model of Condensation.

The chromatin organization within a mitotic chromosome is more difficult to infer from experiment than was the case for meiosis. Evidence for a radial loop model is surveyed by Paulson (1988) and refinements that relate it to banding patterns are presented in Saitoh and Laemmli (1994). This latter work proposes that each chromatid contains a helically wound thin fiber, which echoes a series of microscopy studies arguing in favor of such a coiled or perhaps folded structure (Ohnuki, 1968; Sedat and Manuelidis, 1978; Boy de la Tour and Laemmli, 1988). In any case, the chromatin must be somehow fastened to itself by the action of scaffold proteins (Paulson, 1988). The most prevalent nonhistone protein in the metaphase chromosome is topo II. Although required for chromosome resolution and condensation, recent work argues against topo II having an essential scaffold function (Hirano and Mitchison, 1993; Swedlow et al., 1993).

Recently the structural maintenance of chromosome (SMC) [in Xenopus chromosome-associated protein (XCAP)] family of proteins has been shown to be required for normal chromosome condensation and for maintenance of mitotic chromosome structure in both cell extracts and in vivo (Gasser, 1995; Hirano, 1995; Hirano et al., 1995; Koshland and Strunnikov, 1996). Antibody fluorescence studies of condensed chromosomes show that the SMCs are embedded within the chromatin and occupy a substantial part of the chromosomal cross-section. (Hirano et al. [1995] suggest the possibility of a helical SMC track.) It is intriguing that the SMCs are rod-like proteins, but how that affects the chromosome shape remains an open question.

Compelling evidence that chromatin can be considered as a flexible polymer in good or theta solvent has been provided by experiments of Hirano and Mitchison (1994, especially in Figure 5), who assembled metaphase-like chromosomes from Xenopus egg extracts and sperm and then immunodepleted the SMC proteins. After a few minutes, puffs of chromatin were seen to erupt from the chromosome, and eventually, the entire chromosome was seen to turn into a cloud of chromatin. Thus the SMCs act as a chromatin glue, and in their absence chromatin will disperse. If the chromatin had been in bad solvent conditions, removal of the SMCs should have resulted in either no change (i.e., if other structural proteins were able to maintain the chromosome shape) or the formation of a spherical globule of dense chromatin.

The cell systematically modifies a host of other chromatin-associated proteins during mitotis; e.g., histones are phosphorylated or acetylated and the level of H1 is varied (Bradbury, 1992; Roth and Allis, 1992). The variety of these changes and the degree of redundancy in the system (e.g., removing H1 does not block condensation; Ohsumi et al., 1993) indirectly support physically based models. All chemical parameters influencing solvent quality enter the theory through the χ parameter, and a similar variable will parameterize the association of the SMC glue and the chromatin. Hence the cell could merely ramp the concentrations of various condensing agents and sense the degree of chromatin compaction. The critical concentrations of the various factors does not need to be known in advance.

Our minimalist model for mitotic condensation will thus be to put the chromatin-buffer system under good solvent conditions and to assume that the SMCs have a higher affinity for chromatin than for buffer, leading to a dense chromatin–SMC phase. The strength of these interactions will be modulated in time to facilitate the resolution of entanglements.

Implications of Model.

Given our physio-chemical model (re-expressible in more formal terms as a phase diagram of the chromatin-buffer-SMC system), we can rationalize the following classical results: 1) chromosomes condense separately and are rod like in vivo, 2) sister chromatid arms separate in mitotically arrested cells without motors (see for instance Shamu and Murray, 1992, page 933; Miyazaki and Orr-Weaver, 1994; Bickel and Orr-Weaver, 1996) and are held together only by their centromeres, and 3) chromosomes thicken and shorten from prophase to metaphase. As well, we will reinterpret a number of more recent experiments.

Morphology.

If there is an excess of chromatin over SMCs, then the latter will occupy the center of the chromosome and there will be a halo of loose chromatin on the outside. This halo will tend to drive the overall shape of the chromosome into a rod, so as to disperse the chromatin as much as possible (due to good solvent conditions). This will also keep neighboring chromosomes and sister chromatid arms from adhering to one another, following the brush arguments of the previous section. Finally, because the chromosome is a continuous fiber, the halo is guaranteed to be organized into apparent radial loops: the chromatin pressure of these packed loops is essential to defining the shape of the condensing chromosome. The balance between the negative surface tension of the chromatin buffer interface (favoring a string) and the positive surface tension of the dense SMC containing phase (favoring a sphere) determines the aspect ratio of the chromosome.

On the basis of their length and a putative ATPase domain inferred from sequence homology (Hirano, 1995), a motor function was attributed to the SMCs that would actively compact chromatin (Peterson, 1994; Gasser, 1995) by cycling between an open and folded state. We argue that compaction per se does not require such an elaborate machine; however, the pure glue and motor points of view can be blended by noting that thermodynamically any system that switches between a sticky (mitotic) and nonsticky (interphase) state in response to ATP hydrolysis constitutes a motor (major conformational change in the protein is not required). With regard to this question, it would be interesting to see whether XCAP (Xenopus SMC homologue) fragments that have recently been cloned (Hirano, personal communication) are as effective in promoting condensation in vivo as the full protein (recent work of Hirano et al. [1997] indicates that XCAPs condense chromatin only when present in a large condensin complex).

Entanglement Resolution as an Annealing Process.

Entanglements ultimately are removed by topo II, which passes one double-stranded DNA through another. Topo II is required for condensation from interphase chromatin or the remodeling of sperm when introduced into an interphase extract (Figure 3 in Hirano and Mitchison, 1993). In both these cases, an external force is needed to bias strand passage toward unlinking: by itself, topo II cannot sense whether a given strand passage is increasing or decreasing the degree of entanglement.

Condensation is often thought to provide that directionality but will function as such only if it is energetically favorable for chromatin to be dispersed and if some work is done to compress it against that entropic force. Sperm introduced into a mitotic extract first expands by a factor of ∼10 in volume and only then collapses into compact chromosomes (Hirano and Mitchison, 1993). Of course, the protein profile is also altered during the expansion, but the fact remains that individual chromosomes only appear after expansion has occurred.

A well-characterized and almost natural process in which entanglement resolution accompanies condensation is the spontaneous separation of the sister chromatid arms in cells arrested in mitotis. It is challenging to deduce in a way consistent with basic physics and chemistry how this occurs in the requisite time. We enumerate a number of qualitative arguments herein as to how our model accounts for the separation (see APPENDIX for a semiquantitative calculation of the unlinking time).

At a growing condensation tip, the preponderance of the chromatin will be from the same fiber just by physical continuity of the chromatin, and in this way, condensation tests for continuity. There will be loops from the other chromatid incorporated in the growing tip, but they will be under more tension than the correct cis one (Figure 3). The ultimate source of this tension is the tendency for the buffer to wet and disperse chromatin.

Figure 3.

Two sister chromatids undergoing condensation and resolution. Interdigitated interchromatid loops will be under slightly more tension than the intrachromatid loops defining the arm. Bars represent condensing (possibly SMC) proteins.

There has to be an approximate balance between the strength of the SMC-chromatin interactions and the tendency for the chromatin to dissolve and disperse in the buffer. Simply introducing very strong glue into a tangle of chromatin will create a gel with no possibility of using the molecular continuity to delineate a single condensed entity. Instead if one begins with a weak glue, thermal fluctuations will sample a variety of linkages and allow a slight bias in the energy between interdigitated loops of the same and different molecules to direct their separation. A weak glue will only work if solvent quality is not so high as to disfavor even intramolecular associations. A stronger protein glue matched with better solvent conditions (greater chromatin–chromatin repulsion) later in metaphase or anaphase would serve to put more strain on loops between chromosomes and force their resolution.

Circumstantial evidence that chromatin entering mitotis is close to theta-solvent conditions is the sensitivity of structure to buffer and preparations conditions that bedevils in vitro experiments. The density of chromatin packing as a function of multivalent cations has been investigated in a titration experiment by Belmont et al. (1989).

The length of the SMCs is considerable, ≥ 0.1 μm, based on inferences from the primary sequence, and this feature could influence our hypothesized kinetics. At a growing tip, the SMCs extend far enough out to capture another sticky site on the chromatin if they are somewhat rare. In very early prophase, we expect condensation to begin at many loci at once. The subsequent organization of all these segments into a rod would be facilitated by sticky sites extending beyond the immediate chromatin halo.

This perspective suggests an alternative interpretation of several recent experiments. Strick and Laemmli (1995) have synthesized proteins with a high affinity for A+T-rich DNA (the so called scaffold associating regions) that depending on concentration, block the expansion and subsequent condensation of sperm in Xenopus egg extracts. We interpret their synthetic proteins to be such strong DNA binders that they block the resolution of entanglements by chromatin pressure. They are a sort of super glue.

A number of hypotheses, revolving around a specific chemical signal, were explored by Shamu and Murray (1992, pages 932–933) to explain the separation of the sister chromatid arms while the centromeres remained intact. However, under their assays, the activity of topo II did not change at the onset of anaphase, nor could evidence be found for a specific intersister glue that could be switched off. They did not consider the mechanism advanced herein, i.e., that there is no discrete switch for decatenation and that the process is regulated only in a generic way by the chromatin–solvent interfacial tension, which serves to bias the action of topo II toward unlinking rather than relinking. Any factors that tended to decondense chromatin would increase the tension in linkages between the sisters and thus promote their resolution.

Bulk Elasticity of Mitotic Chromosomes.

There have been only a few experiments that measure the elastic properties of mitotic chromosomes, yet they do convey significant information about the how the chromatin is internally organized and rule out certain models. It has been noted that human metaphase chromosomes display rather impressive elasticity, returning to their native length after being stretched by a factor of 10 in length (Claussen et al., 1994). For anaphase grasshopper chromosomes, Nicklas (1983) has estimated an elastic modulus of about 500 Pa (1 Pa = 1 N/m²). This is very weak elasticity compared with that of a DNA molecule (5 × 10⁸ Pa) or some other chemically bonded structure. Recent work of Houchmandzadeh et al. (1997) on mitotic newt lung cells found an elastic modulus of 5000 Pa at the end of prophase and 1000 Pa at metaphase; the chromosomes were found to return to their native lengths after being stretched up to 10 times.

If we consider a chromosome to just be a gel (e.g., with SMC cross-links) then we can infer a volume per cross-link from E = 500 Pa, as v = T/E = 8000 nm³, or a cube 20 nm on a side. This is a cross-link density approaching one per chromatin monomer and is, therefore, inconsistent with a weakly cross-linked gel that would be capable of a 10-fold extension.

An alternative is for the elasticity to originate from the deformation of a rigid internal structure or, perhaps, the breaking and remaking of chromatin cross-links. The possibility that chromatids have an extensible internal structure is supported by observations of coiling (Ohnuki, 1968; Boy de la Tour and Laemmli, 1988; Hirano et al., 1995) and also by the observation that after being stretched by more than 30 times, metaphase chromosomes are converted to a thin fiber with helical kinks along its length (Houchmandzadeh et al., 1997).

Another option consistent with the data is a native fiber with embedded rod shaped molecules (i.e., SMCs) with random orientations. Stretching will orient them and, on that basis alone, will entail a free energy change of T per molecule. Detecting optical activity in a stretched chromosome would be evidence of this scenario.

Other than by pulling on chromosomes with a needle or micropipette, their elastic properties (technically a bulk modulus) could be probed by observing a volume change after addition of polyethylene glycol to the buffer. This polymer, if of high enough molecular weight, will not penetrate into the chromatin and, instead, exert a concentration-dependent and known osmotic pressure (Parsegian et al., 1995). We would interpret the observations by Rasania and Swanson (1995) of reversible changes in nuclear volume induced by polyethelene glycol or dextran as osmotic compression.

Banding of Mitotic Chromosomes.

There are suggestions that the contrast in the A+T:G+C ratio that is picked up by the dyes used for chromosome banding is larger than would be expected by merely laying down the genome sequentially in the chromosome (Saitoh and Laemmli, 1994). This plus the appearance of bands within bands is indicative of thermodynamic phase separation. However, the parameters entering Eq. 9 are too poorly known to assess whether this is a realistic possibility. One can, however, reliably scale the kinetics from one set of parameters (e.g., overall DNA density, and A+T:G+C ratio contrast) to others, as well as predict how domain size grows in time.

Experiments to check these predictions and determine parameters might be possible by mixing defined-length samples of bacterial DNA that have very different A+T:G+C ratios, e.g., Clostridium perfingene ∼28% G+C versus Lysodeikticus ∼70% G+C or by looking for separation in concentrated solutions of partially digested eukaryotic chromatin. Comparison of pure DNA with chromatin would indicate whether the contrast in polarizabilities responsible for the separation resided on the proteins and only indirectly correlated with base composition.

TIME REQUIRED FOR UNLINKING OF SISTER CHROMATID ARMS

We will work in units of the time for topo II to preform one double-strand exchange ∼1 s. We assume, and justify later, that physical separation will occur rapidly once the chromosomes are unlinked. If p is the probability that two linked fibers under an opposing tension f are unlinked by topo II, then thermodynamics dictates that p/(1 − p) = exp(fa_∥/T), where a_∥ ∼ 5–10 nm is the distance over which the enzyme has taken hold of the two fibers during their interchange.

To appreciate how linkage can give rise to forces of entropic origin that can then bias the action of topos, we recall the simpler problem of separating two concatenated circular DNAs such as those resulting from plasmid replication in prokaryotes (Levene et al., 1995). The catenation is a constraint on both molecules that lowers their entropy (increases their free energy) and thus biases the action of topo IV (the prokaryote version of topo II) in the absence of any other forces. This free energy expressed per linkage will exceed T (and, therefore, rapidly drive resolution) provided the linking number exceeds (very roughly) one every few persistence lengths. Further resolution has been argued to be driven by supercoiling because gyrase has been implicated as essential for full decatenation (Zechiedrich and Cozzarelli, 1995).

Applying the same reasoning to chromatin loops with their 1- to 2-kb segment size indicates that there will be a rapid chromatin pressure-driven decatenation between loops on either the same or sister chromatid arms until there is one link per 5–10 segments or per 5–10 kb. Most of these reactions can proceed in parallel, because the result of one does not influence the others and the bias provided by the catenation is independent from loop to loop. Then, for a 10⁷- to 10⁸-bp chromosome arm, there will remain l ∼ 10³ to 10⁴ linkages to be resolved. We assume throughout that sufficient topo II is present that its diffusion to sites where fibers cross is not rate-limiting.

To see that tension is important, consider what would happen without it. Disentanglement would have to occur by random strand passages. The number of possible strand arrangements with l linkages is ∼2^l; continual action of topo II at all those linkage sites will require a time t* ≈ 2^l/l to find an unlinked state. Even if one waited this astronomical time, it is unclear how chromosome resolution would occur without tension before reentanglement occurred.

If there is appreciable tension, we can put an upper bound on the time to unlink by noting there exists a set of critical linkages that have to be broken in a specified order to separate the chromatids. The linkages and the order are determined by designating at each point in time the most tensed linkage as the next one to be resolved. Once broken, we assume the two strands move far enough apart that relinkage is improbable.

The critical linkages have to be resolved serially, so that one may describe this model as a stochastic zipper. There is no implication that successive links have any spatial relation to each other, and so the time to separate is given by the probability distribution for a one-dimensional biased random walk to first reach some extreme value.

The probability that topo II will correctly resolve all the linkages in a time t ≥ l follows the binomial distribution for the probability that after time t, (t + l)/2 correct steps and (t − l)/2 incorrect steps have been made:

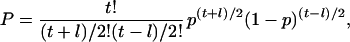10a

or for t >> l,

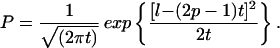10b

Delinkage will occur the first time topo II has performed a net of l passages in the correct direction; the characteristic time t* for this to occur follows from solving 1/t ∼ P(t) (this is merely an estimate of the time scale for the so called first-passage time problem; the kinetics are not exponential). If p ≥ 1/2 then,

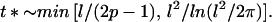11

For the strands to unlink during the experimentally observed condensation/segregation time of an hour, 2p − 1 should be of order unity, so tension is required. Chromatin pressure is implicated as the source of this tension.

The time to physically separate two unlinked chromatids (and also smaller regions once a critical linkage breaks) is of order the time to diffuse a similar-sized object through its longest dimension and, thus, is never rate limiting in this problem.