Shifts in the Population Response in the Middle Temporal Visual Area Parallel Perceptual and Motor Illusions Produced by Apparent Motion

Abstract

We recorded behavioral, perceptual, and neural responses to targets that provided apparent visual motion consisting of a sequence of stationary flashes. Increasing the flash separation degrades the quality of motion, but for some separations evoked larger smooth pursuit responses from both humans and monkeys than did smooth motion. The same flash separations also produced an increase in perceived speed in humans. Recordings from single neurons in the middle temporal visual area (MT) of awake monkeys revealed a potential basis for the illusion in the population response. Apparent motion produced diminished neural responses relative to smooth motion. However, neurons with slow preferred speeds were more affected than were those with fast preferred speeds. Increasing the flash separation thus caused the population response to become diminished in amplitude and to shift so that the most active neurons had higher preferred speeds. The entire constellation of effects of apparent motion on the magnitude and latency of the initial pursuit response was accounted for if the MT population response was decoded by (1) creating an opponent motion signal for each neuron by treating its preferred and opposite direction responses as those of a pair of oppositely tuned neurons and (2) computing the vector average of these opponent motion signals. Other ways of decoding the population response recorded in MT failed to account for one or more aspects of behavior. We conclude that the effects of apparent motion on both pursuit and perception can be accounted for if target speed is estimated from the MT population response by a neural computation that implements a vector average based on opponent motion.

It is often said that the brain represents a given sensory quantity via a “population code.” Such a statement usually pertains when individual neurons are “tuned” so that they respond maximally to a particular value of a sensory quantity. Submaximal responses can occur if the sensory quantity is either smaller or larger than preferred or if the stimulus is suboptimal in some other dimension. As a result, monitoring a single neuron may indicate little about the value of the sensory quantity. Thus, the hallmark of population coding is that decoding necessitates observation of more than one neuron (for review, see Lewis, 1999;Sparks et al., 1997).

For many visual areas, neural tuning properties appear to necessitate population-based decoding, as does the nature of many visual illusions (Gilbert and Wiesel, 1990; Tootell et al., 1995; Schrater and Simoncelli, 1998). Theoretical work suggests multiple methods for estimating a sensory quantity from a population response (Salinas and Abbott, 1994; Pouget et al., 1998), and physiological studies have provided support for some of them (Salzman et al., 1992; Groh et al., 1997; Lee et al., 1988; Lewis and Kristan, 1998; Lewis and Maler, 2001). However, very few studies have linked measurements of a cortical sensory population code to behavior in a direct and quantifiable way (although see, Takemura et al. 2001).

In the present paper, we compare population responses recorded from the middle temporal visual area (MT) with two behaviors that depend on visual motion: ocular smooth pursuit and perceptual speed discrimination. Anatomical (Glickstein et al., 1980; Tusa and Ungerleider, 1988), lesion (Newsome et al., 1985; Dursteler and Wurtz, 1988), and microstimulation (Komatsu and Wurtz, 1989;Born et al., 2000) studies demonstrate that MT supplies the pursuit system with visual motion signals. Recording and microstimulation studies also link MT with direction discrimination in monkeys (Newsome et al., 1989; Salzman et al., 1990; Britten et al., 1992, 1996;Shadlen et al., 1996). Our strategy was to parametrically degrade visual motion and find decoding computations that could account for the parallel changes in (1) the MT population response, (2) pursuit eye movements, and (3) the perception of target speed.

To degrade visual motion, we used “apparent motion”, consisting of sequential flashes that create the impression of motion, the quality of which depends on the time and distance between the flashes. Larger flash separations degrade the directional tuning of MT neurons (Mikami et al., 1986a,b) and create a number of changes in pursuit (Churchland and Lisberger, 2000). These changes include an unexpected increase in the strength of pursuit initiation, as though the pursuit system thought the target was moving faster than it actually was. We now show that apparent motion produces a perceptual illusion of increased speed and that this illusion is latent in the MT population response. Analysis of possible decoding computations reveals that a vector-average computation, based on the recorded neural responses, can account quantitatively for virtually all effects of apparent motion on both the magnitude and latency of smooth pursuit initiation, including the illusion of increased target speed. However, this was true only if the vector average was performed after an opponent motion computation. A standard vector average and a number of other methods failed to account for the pursuit evoked by apparent motion.

MATERIALS AND METHODS

Eye movement and neural recordings were obtained from two adult male rhesus monkeys (Macaca mulatta) that were trained to fixate and pursue visual targets for fluid reward. Monkeys were implanted with head restraints and scleral search coils as described in previous publications (Churchland and Lisberger 2000). After initial training, monkeys were implanted with a stainless steel cylinder (Crist Instruments, Hagerstown, MD) placed over a 20 mm diameter circular hole cut in the skull to allow access to MT for neural recordings. For each experimental session, the monkey voluntarily exited his home cage and sat in a custom constructed primate chair. During the experimental session, the monkey's head was restrained by connecting the implant to the ceiling of the primate chair, and the monkey was rewarded with juice or water for accurate tracking. After each experiment (which lasted 2–4 hr) the animal was returned to his home cage. Methods had been approved in advance by the Institutional Animal Care and Use Committee at the University of California, San Francisco.

Eye movements and perceptual judgments were measured using five human subjects who were unaware of the purpose of the experiments. Subjects sat with their heads immobilized via a chin support, two forehead supports, and an elastic strap. Eye movements were monitored using a Fourward Technologies Dual Purkinje Image Tracker (Generation 6.1). The auto stage and focus servos were disabled to avoid introducing head position artifacts into the eye position signal. Methods had been approved in advance by the Committee on Human Research at the University of California, San Francisco.

Stimulus presentation. For experiments using monkeys, visual stimuli were presented on a 12 inch diagonal analog oscilloscope. The display was positioned 30 cm from the monkey and subtended horizontal and vertical visual angles of 50° and 40°. For experiments using humans, a 19 inch oscilloscope was placed at a distance of 50 cm, so that it subtended 42° by 34°. For all experiments, the stimuli were square patches of moving dots. Patches contained on average 24 randomly spaced dots, bounded by an 8° square aperture, which was not itself visible. Individual dots were ∼0.2° across, and their luminance was 1.6 cd/m². For pursuit experiments, the dots and their bounding aperture moved together across the screen. For psychophysical and recording experiments, the dots moved behind the stationary aperture: dots disappeared upon reaching the far edge, while new dots appeared on the near edge. The control signals for the oscilloscopes were provided by the digital-to-analog converters of a digital signal processing board that ran in a Pentium computer. All stimuli provided apparent motion. Each dot in a stimulus was flashed sequentially at different locations, with a spatial and temporal separation between locations that varied according to the desired stimulus parameters. We refer to the spatial and temporal separation as Δx and Δt, with apparent speed defined as Δx/Δt. When Δt and Δx were small (<20 msec and 0.25°), stimulus motion appeared smooth. For larger flash separations, the motion became noticeably un-smooth. To maintain a constant mean luminance of the target, the luminance of each dot flash was varied linearly with Δt (e.g., if Δt was doubled, so was the luminance of each flash). Each individual flash was brief (160–2560 μsec, depending on luminance). All dots within the patch were updated at virtually the same time; i.e., presentation of dots during a flash was essentially synchronous (with no dots being present until the next flash). The specifications of the display oscilloscopes indicate that the phosphor decayed to 10% of its maximal level in 10 μsec to 1 msec.

Visual stimuli were presented in “trials”, in which each trial provided target motion at a given speed and Δt. Each experiment consisted of a list of trials, each of which lasted a few seconds. The presentation order of the list was shuffled randomly, and each trial was presented once. After completion of all trials, the list was reshuffled and presented again. Monkey subjects were required to satisfy fixation constraints. In rare instances in which these requirements were not met, the trial was aborted and placed at the end of the list, to be completed before the list was shuffled and repeated.

Human psychophysics. Each trial began with the appearance of a stationary point in the center of the display. Subjects were asked to fixate this point visually throughout the entire trial, and eye movements were recorded at the beginning of each experimental session to verify fixation. After 800 msec of fixation, a patch of moving dots was presented centered 4.5° above the fixation point for a random duration of 300–450 msec. No stimulus was present for the next 300 msec, after which a second patch appeared 4.5° below the fixation point, also for 300–450 msec. Subjects were then given 1400 msec to press one of two buttons, indicating whether the first or second patch appeared to move faster. One of the two patches, termed the “standard” patch, always moved at 16°/sec. One of two values of Δt was used for the standard: 4 msec and a larger separation selected specifically for each subject based on their pursuit performance. The other patch, termed the “comparator” patch, always had a Δt of 4 msec but had a speed that was chosen randomly from values ranging from 11–24°/sec. On half the trials (chosen randomly) the standard was the first patch, and the comparator the second. For the other half, the order was reversed. Subjects' responses were analyzed by calculating the percentage of trials for which the standard was judged to be faster than the comparator.

Human pursuit. Each pursuit trial began with the appearance of a fixation spot for a randomized interval of 700–1100 msec. The fixation point was then extinguished, and the target, a rightward-moving patch of dots, appeared centered 1–1.5° to the left of fixation. The offset situated the center of the patch eccentrically on the retina, although part of the patch still overlapped the fovea. The size of the offset was customized for each subject, to minimize the occurrence of early saccades. All targets moved for 1000 msec before being extinguished, except for targets moving at 24 and 32°/sec, which were extinguished after 800 and 600 msec when they neared the edge of the display. Subjects were instructed to visually track the target as it moved across the display.

Monkey pursuit. The trials were similar to those used for human subjects. Each trial began with a fixation point, which was then extinguished and replaced by a rightward-moving patch of dots that was initially centered 6.4° (monkey Mo) or 5.2° (monkey Q) to the left of fixation. These eccentricities were the average receptive-field eccentricity of neurons recorded in each of the two monkeys. Monkeys were required to keep eye position within 3° of the fixation point and within 6° of the center of the pursuit target. If these requirements were met, they received a reward at the end of the trial. We used the larger than usual 6° fixation window because of the 8° size of the tracking stimulus and because large values of Δt produced poor pursuit for faster stimuli. In our well trained monkeys larger fixation windows did not decrease the quality of tracking.

Neural recordings. Extracellular potentials were recorded from single neurons in area MT of the two awake monkeys used for the pursuit experiment. Recordings were made using sharp, 1–3 MΩ, tungsten microelectrodes (Frederick Haer Co., Bowdoinham, ME). The electrode location was determined by a guide tube inserted in a plastic grid (Crist), which was placed in the implanted cylinder each day. The guide tube was sharp and was pressed by hand through the dura after application of local anesthetic (1% lidocaine). The voltage recorded by the electrode was amplified conventionally (Dagan, Minneapolis, MN), bandpass filtered from 100 Hz to 10 kHz, and viewed on an analog oscilloscope.

A trigger was applied to the incoming voltage, and all waveforms that exceeded the trigger were displayed on an oscilloscope. The spikes from an individual neuron were discriminated by two time–amplitude windows (BAK Electronics Inc., Germantown, MD; DDIS-1) that triggered a logic pulse. Accepted waveforms were stored on a storage oscilloscope to verify that only one waveform was present and that there was the expected refractory period between spikes. This latter criterion allows us to insure that two similar waveforms are not mistaken for a single unit.

These criteria made us confident that a single unit was ideally isolated in ∼50% of our recordings. In the remaining recordings, we estimate that as many as 2% of the spikes we accepted may have come from other neurons or that a similar percentage of the spikes of the unit under study may have failed to trigger the discriminator.

Area MT was located based on (1) the well described response properties of MT neurons (Maunsell and Van Essen, 1983), (2) the described response properties of neurons in surrounding areas V4 and middle superior temporal area (MST) (Newsome et al., 1988; McAdams and Maunsell, 2000), and (3) the progression of white matter, gray matter, and lumen encountered before reaching MT. A successful penetration typically encountered the large-receptive-field directionally-selective neurons of area MST, then encountered lumen, and finally emerged into MT. We wished to record from MT neurons with receptive fields near the fovea, at the lateral extent of MT. For monkey Q, the expected topography described above was not found when we moved to the lateral extent of MT. Instead, the central representation in MT was located directly below an area with 4–8° receptive fields and directionally nonselective neurons that we presume to be V4. The transition from this area to MT was distinguished not by lumen, but by a shift in receptive field location toward the fovea and the sudden appearance of strong and consistent direction-selective responses. Although we think it unlikely, it is possible that some of the neurons we recorded from monkey Q were direction-selective V4 neurons near the V4/MT border.

Each trial began with the appearance of a fixation point. A patch of dots appeared 800 msec later, moved at a constant speed for 500 msec, and then was extinguished. The fixation point was extinguished 300 msec later, and the animal was rewarded with a drop of juice if he had fixated throughout the trial with an accuracy of 4–5°. Actual fixation was typically much more accurate, with the exception that fast stimuli presented near the fovea evoked a small response that the monkey was unable to entirely suppress. We searched for MT and for neurons within MT using large patches of moving dots. After receptive field locations were localized for the part of MT surveyed on a given day, we typically searched using 8° square patches of moving dots. Because we usually used search stimuli moving between 5 and 40°/sec (most frequently 16°/sec), our sampling of preferred speeds was probably biased and may have excluded neurons with very fast or slow preferred speeds. The bias is acceptable given the analyses we perform, which would not be affected by the exclusion of neurons that do not respond to apparent motion at 16 or 32°/sec.

After isolating a neuron, we first estimated its preferred direction using a set of eight trials, each of which presented motion in a different direction. Dot motion was presented within an 8° square window if the receptive field of the neuron was known roughly, or within a larger window if it was not. The preferred direction was estimated subjectively from histograms of the responses to these eight directions. We next estimated the receptive field of the neuron, either by using a list of trials that presented patches of dots at different spatial locations or by manually moving a patch to find the receptive field edges. For monkey Mo, receptive field eccentricity (measured as the distance from the fixation point to the center of the receptive field) varied from 5 to 8.9°, with a mean of 6.4° and a SD of 1.1°. For monkey Q, eccentricity varied from 2.7 to 7.9°, with a mean of 5.2° and a SD of 1.2°. Receptive fields sizes were of the same order as the 8° square patch stimulus. Finally, we studied the response of each neuron to apparent motion using a list of 52 trials. Apparent motion was presented at 16°/sec (Δt = 12, 16, 20, 24, 32, 44, and 64 msec) and 32°/sec (Δt = 12, 16, 24, 32, and 44 msec). Trials were also included to assess the speed tuning of the neuron. For these Δt was always 4 msec, and the stimulus speed was varied from 0 to 128°/sec. All trial types were presented in both the preferred direction of the neuron, and in the opposite, “null”, direction. The list of trials was repeated until the accumulated histograms showed a reasonable signal to noise ratio, judged subjectively. This typically took 15–30 min.

Data acquisition and analysis. Experiments were controlled by computer programs running on a UNIX workstation, and data were acquired by a Pentium computer running a real-time extension to Windows NT (RTX, VentureCom). An eye velocity signal was provided by analog differentiation of the eye position signal with a passband of DC to 25 Hz. Eye position and eye velocity were sampled a rate of 1 kHz on each channel. The times of the logic pulses produced by the hardware spike discriminator were recorded to the nearest 10 μsec.

Before analysis of the pursuit responses, the smooth component of eye velocity was isolated by removing saccades from the eye velocity traces. The start and end of each saccade were identified by eye, and the saccade was replaced with a straight line segment that interpolated velocity. We intentionally used target eccentricities that rarely produce saccades during the initial accelerating phase of pursuit, and trials in which a saccade did occur during initiation were excluded from analysis. Our analysis is therefore primarily an analysis of presaccadic pursuit, and the myriad interpretive complications introduced by saccades are avoided. An exception was made for responses to some targets with large flash separations. Such targets could produce very delayed pursuit and weak initial eye acceleration, making saccades inevitable during initial eye acceleration. Responses to such targets were included in the analysis after interpolation of the saccades. Because acceleration was so sluggish for these responses, linear interpolation provides a reasonable estimate of the underlying pursuit velocity.

Examples of pursuit responses (Fig.1B) were created by aligning responses to a given trial type on the onset of target motion and computing, for each time point, average eye velocity across responses. Because of variability in the latency of pursuit, averages of eye velocity slightly underestimate the magnitude of initial eye acceleration. We therefore performed a quantitative analysis of eye acceleration based on filtered individual trial responses. For each trial, we measured peak eye acceleration during pursuit initiation, and the “acceleration latency”, defined as the latency to reach 80% of the peak acceleration (Churchland and Lisberger, 2000).

Fig. 1.

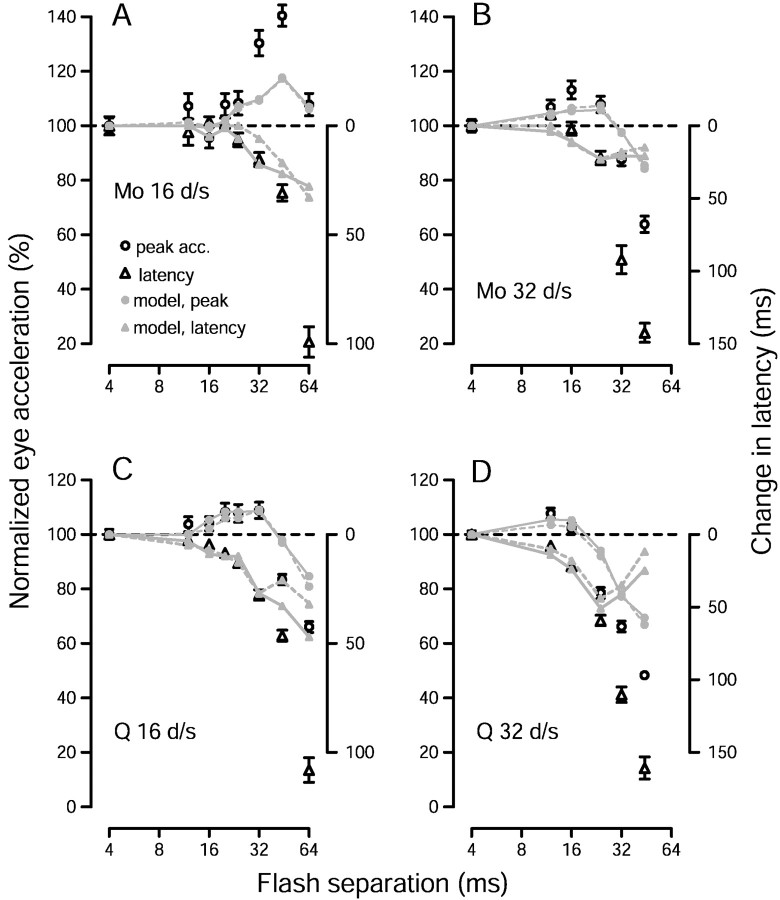
Evidence for an illusion of increased target speed in monkey pursuit. A, Illustration of the pursuit task. The two rectangles show the temporal sequence of the task. The monkey first fixated a small point (cross), and then pursued a patch of dots that appeared to the left of the extinguished fixation point and immediately moved rightward. The starting position of the center of the dot patch relative to the fixation point was set to equal the average receptive field eccentricity of the MT neurons recorded in that monkey (6.4° and 5.2° left of fixation for Mo and Q, respectively).B, Pursuit responses of monkey Mo to a 16°/sec target with different values of Δt. The tracesplot average eye velocity and acceleration as a function of time. Traces begin at the time the patch target appeared and began to move. Different line types plot responses for different values of Δt, as indicated in the key. C, The average peak eye acceleration evoked by a 16°/sec target (circles) and the average acceleration latency (triangles) are plotted as a function of Δt. Peak eye acceleration is plotted as a percentage of that when Δt was 4 msec. Latency is plotted as the change from the latency when Δt was 4 msec. Longer latencies are plotted downward. Thus, for both peak acceleration and the acceleration latency, symbols below thedashed line indicate deficits relative to the pursuit evoked when Δt was 4 msec. Measurements of peak acceleration and latency were made for each individual trial and averaged. Error bars indicate SEM.

Single neuron responses were initially characterized by constructing histograms of spike count (32 msec bin width) aligned on the onset of target motion. We also calculated the mean and SE of the spike rate over a 600 msec interval that began with the onset of the stimulus and ended 100 msec after the offset of the stimulus. The mean spike rate during this period was calculated separately for motion in the preferred and null directions of each neuron. For a given stimulus, we define the “directional response” as the difference in the mean spike rate evoked by the two directions. For each neuron, we also abstracted two scalar quantities: the limit of directionality and the preferred speed. The limit of directionality was estimated by plotting the directional response versus Δt and fitting with a sigmoid (as in Fig. 3). The limit of directionality was defined to be the Δt at the point of half-decline of the sigmoid. The preferred speed was estimated from the directional responses to stimulus speeds from 0.5–128°/sec when Δt was 4 msec. The directional response was plotted versus speed, and the data were fit with:

$$G(s)=R_{max}\left(e^{-{\left[\frac{log\left(\frac{s}{{\mu }_s}\right)}{{\varsigma }_s+\zeta log\left(\frac{s}{{\mu }_s}\right)}\right]}^2}-e^{{}^{-\left(1\frac{1}{{\zeta }^2}\right))}},\right.$$ Equation 1

where R_max is the maximal firing rate, μ_s is the preferred speed (the peak of the function), s is the speed of the stimulus, ς_s is the tuning width, andζ is the skew, after the background firing rate has been subtracted. R_max,μ_s,ς_s, and ζ were varied to achieve an optimal least squared fit to the data. For most neurons, the preferred speed measured from the directional responses was very similar to the preferred speed measured from preferred direction responses in the conventional manner. This is unsurprising, because most MT neurons show little response to the null direction for smooth motion. However, a minority of neurons with slow preferred speeds responded robustly both to stationary stimuli and to slow motion in their null direction. The preferred speed of such neurons was higher (although still slow) when measured using the directional response.

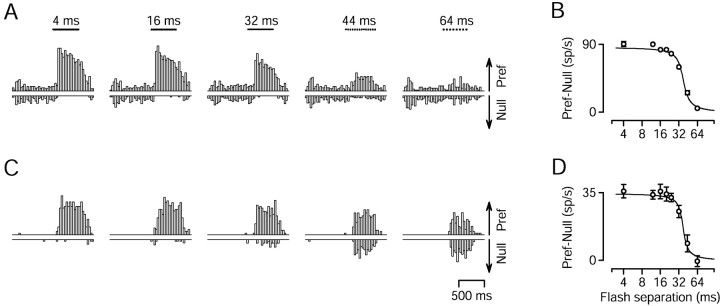
Fig. 3.

Effect of changing Δt on the responses of two MT neurons to apparent motion at 16°/sec.A, C, Histograms showing firing rate as a function of time for two MT neurons, with preferred speeds of 13.1°/sec (A) and 8.2°/sec (C). Bin width was 32 msec. Upward and downward histograms show the response to stimulus motion in the preferred and null directions of the neurons. The length of the arrowsat the right of the last histogram provides a scale, and indicates a firing rate of 100 spikes/sec in A and 50 spikes/sec in C. Stimulus duration was 500 msec and is indicated by the sequence of dots above each histogram. The locations of the dots indicate the timing of the flashes. The label above each pair of histograms inA indicates the value of Δt.B, D, The directional response of the neurons in A and C, plotted as a function of flash separation. The directional response is the mean firing rate evoked by motion in the preferred direction, minus that evoked by motion in the null direction. Error bars indicate SEM and are suppressed when smaller than the symbol size. The fits are sigmoidal least squares fits.

RESULTS

An illusory increase in apparent speed for pursuit

Figure 1A illustrates the pursuit task we used to test the effect of apparent motion on pursuit initiation. Monkey and human subjects fixated a stationary target (cross) and then pursued a patch of dots that moved at a constant apparent speed, and had a particular flash separation. For convenience, we describe the flash separation in terms of Δt; for a given speed Δt and Δx increase together. Figure1B shows pursuit responses of monkey Mo and illustrates the effects of increasing Δt on the initiation of pursuit. As Δt increased from 4 msec, which produces effectively smooth motion (Churchland and Lisberger, 2000), to 20, 32, and 44 msec, the rising phase of eye velocity was slightly delayed, but the initial response reached gradually higher speeds. The eye acceleration traces in the bottom of Figure 1Bdemonstrate that peak eye acceleration increased as a function of Δt, while the latency to the peak also increased.

Quantitative analysis (Fig. 1C) confirmed these impressions. The average peak eye acceleration (Fig. 1C, circles) was computed using measurements derived from individual trials and is plotted as a percentage of that when Δt was 4 msec. Peak eye acceleration was mostly unchanged as Δt increased from 4 to 24 msec, was elevated when Δt was 32 and 44 msec, and returned to control levels when Δt was 64 msec. Acceleration latency, defined as the latency to reach 80% of the peak eye acceleration, (Fig. 1C, triangles) showed little change until Δt reached 24 msec and then increased steadily. Increasing latencies are plotted downward, so that deficits in either latency or eye acceleration plot below the horizontal dashed line. The results of experiments using a dot speed of 32°/sec and of experiments using monkey Q are shown later in Figures 7 and 11. Comparison of the data for the two target speeds reveals that the increase in eye acceleration appeared for values of Δtfrom 20–44 msec for a stimulus speed of 16°/sec and from 12–24 msec for a stimulus speed of 32°/sec. These disparate ranges of Δt correspond to similar ranges of Δx: from 0.32 to 0.7° for apparent motion at 16°/sec and from 0.38 to 0.77° for 32°/sec. Thus, it appears that the acceleration increase is more closely tied to the distance between the flashes than to the time between the flashes. The pattern of results in the present paper is very similar to that reported in Churchland and Lisberger (2000), which used single dot stimuli.

Fig. 7.

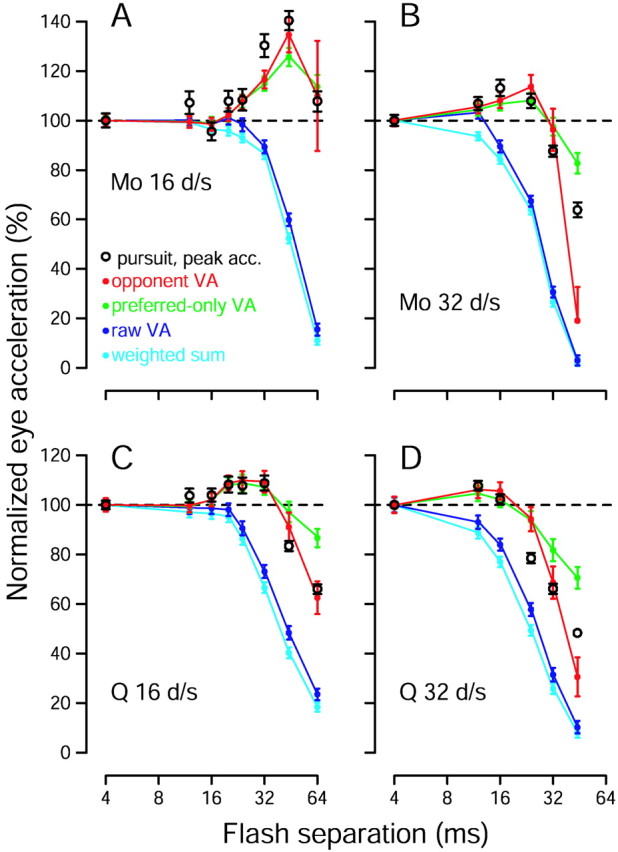
Comparison of pursuit responses with estimates of target speed extracted from the population response using a variety of computations. All quantities are plotted as a function of Δt. Open black symbols show mean peak pursuit eye acceleration, calculated and normalized as for Figure 1. Error bars indicate SEM. Colored traces show estimates of target speed extracted via four methods: three versions of the vector average (VA) and a weighted sum, as indicated in the key. These computations were applied to the recorded population response of the relevant monkey for each speed and value of Δt. For comparison with pursuit data, estimates of target speed are shown as a percentage of the estimated speed when Δt was 4 msec. Error bars indicate the SE of the estimates, computed based on the SE of the firing rate of the neurons providing the input to the estimation. A, Data for monkey Mo and a target speed of 16°/sec. Peak eye acceleration was significantly increased when Δt was 32 and 44 msec (p < 10⁻⁷ for each).B, Data for monkey Mo and a target speed of 32°/sec. Eye acceleration was significantly increased when Δtwas 16 and 24 msec (p < 0.03 for each) and was decreased for larger values of Δt(p < 10⁻⁴ for each).C, Data for monkey Q and a target speed of 16°/sec. Eye acceleration was significantly increased when Δtwas 20, 24, and 32 msec (p < 0.05 for each) and was decreased for larger values of Δt(p < 10⁻⁹ for each).D, Data for monkey Q and a target speed of 32°/sec. Eye acceleration was significantly increased when Δtwas 12 msec (p < 0.005) and was decreased for values of Δt that were ≥24 msec (p < 10⁻⁷ for each).

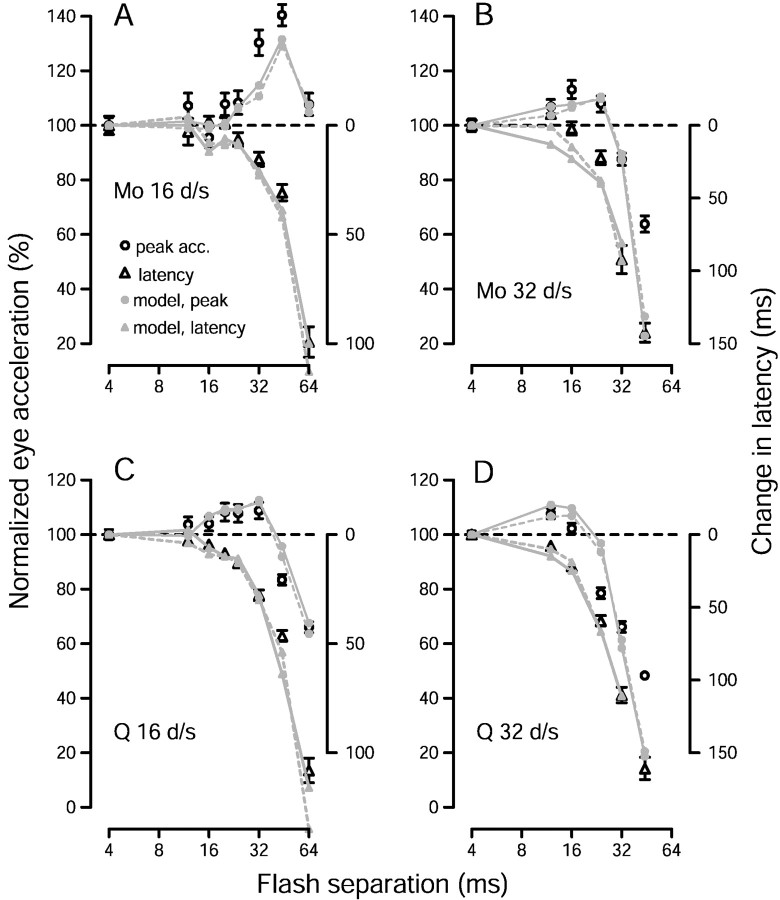
Fig. 11.

Comparison of pursuit with estimates of speed produced by the time-based version of the opponent vector average, applied to the recorded population response. Open symbols plot pursuit performance. Circles andtriangles plot, respectively, average peak acceleration and acceleration latency for each value of Δt, computed as in Figure 1. The small gray symbols andtraces plot measurements made from the estimate of speed. The estimate of speed for each stimulus was obtained by applying the opponent vector average to the time-varying population response recorded for that stimulus, resulting in traces such as those in Figure10, E and F. Small gray circles plot the peak estimate of speed (plotted against the left vertical axis), and small gray triangles plot the latency of the estimate of speed (plotted against the right vertical axis). Gray symbols connected by continuous lines show the results obtained when all neural responses were shifted to have a latency of 100 msec. Gray symbolsconnected by dashed lines show the results when the latency of each neuron was left at its natural value. All data are plotted relative to their values when Δt was 4 msec. Each graph shows results for a different monkey and target speed, as indicated.

An illusory increase in apparent speed for perception

The nearly linear relationship between initial pursuit eye acceleration and target speed (Lisberger and Westbrook, 1985; Krauzlis and Lisberger, 1994) suggests that the increase in eye acceleration produced by apparent motion may be attributable to an illusion of increased target speed present in the visual inputs driving pursuit. If so, then similar changes might be manifested perceptually. To assess this, we used the task illustrated in Figure2A and asked human subjects to make a two-alternative forced-choice perceptual judgment based on speed (see Materials and Methods). In Figure2B, the black symbols and curves show data for smooth motion (Δt = 4 msec) and plot the percentage of responses in which the standard stimulus was judged to be moving faster than the comparator. Subjects made the perceptual judgment well. When the comparator moved at 11 or 14°/sec, the 16°/sec standard was judged to be faster 97 and 82% of the time, averaged across subjects. When the comparator moved at 19 or 24°/sec, the standard was judged to be faster only 12 and 0.4% of the time. Identical comparator and standard stimuli (16°/sec; Δt = 4 msec) were not delivered.

Fig. 2.

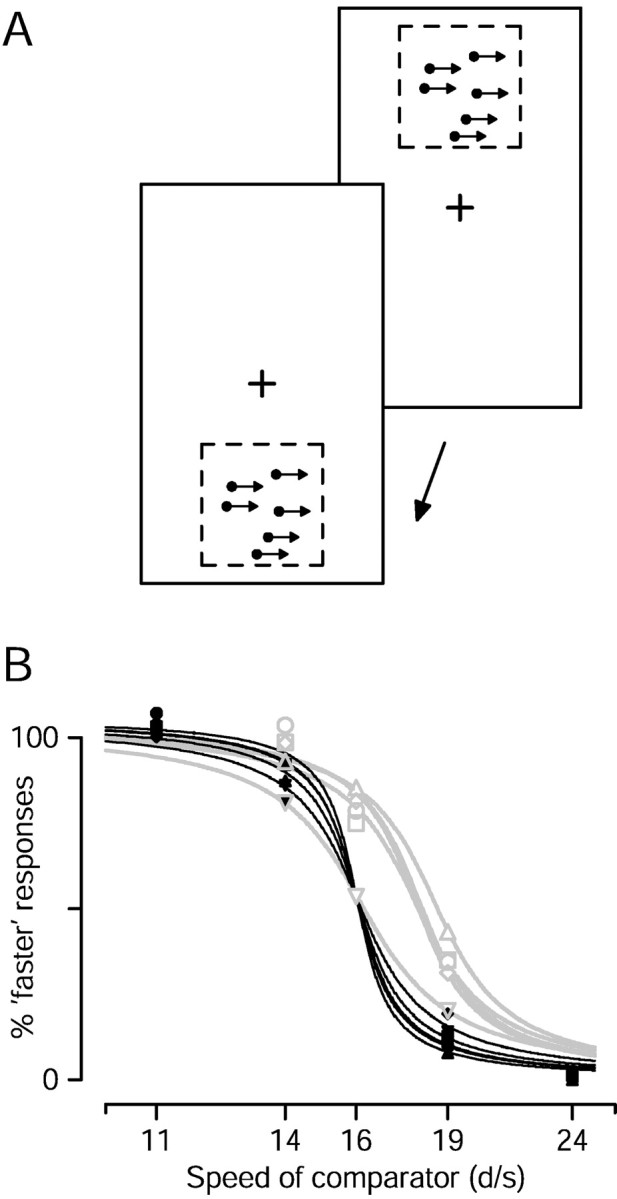
Human judgment of the speed of apparent motion.A, Illustration of the task. Subjects fixated a central spot (cross) throughout each trial. A patch of moving dots appeared briefly above fixation (top panel). A second patch then appeared briefly below fixation (bottom panel). Subjects pressed one of two buttons to indicate which patch was moving faster. B, Symbols plot the proportion of responses in which the 16°/sec standard patch was judged faster, as a function of the speed of the comparator patch.Filled symbols plot, for each of five subjects, responses when the two patches both had a Δt of 4, and differed only in speed. Open gray symbols plot responses when the comparator patch had a Δt of 4 msec and the standard patch had a Δt of 32–64 msec. The exact value of Δt used depended on the subject (see Results). The black and gray lines show sigmoidal least-square fits.

The gray symbols and lines in Figure 2B show data for apparent motion of the standard stimulus, at a single larger Δt, in each of five subjects. The value of Δtranged from 32 to 64 msec and depended on the subject (see below). The comparator always had a Δt of 4 msec. For four of the five subjects, the larger value of Δt for the standard caused the psychometric function to shift to the right: the standard was more often judged to be faster. This is most easily appreciated when both the standard and comparator moved at 16°/sec. The standard was judged to be faster by four of the five subjects (73, 80, 70, and 76% of the time). These values were significantly different from 50% (p < 0.01 for each subject). The fifth subject showed no evidence of an illusion of increased speed and judged the standard to be faster only 50% of the time, consistent with the perception that the standard and comparator moved at the same speed. The presence of a perceptual illusion implies that the increase in initial pursuit acceleration, seen for similar values of Δt, probably arises because the speed of the apparently moving target is overestimated.

The value of Δt used to create the perceptual illusion was different for each subject, and was chosen based on recordings of pursuit eye movements made immediately before the perceptual task. We chose a value of Δt in the range that had produced increased initial eye acceleration during pursuit of a 16°/sec patch of dots. Such an approach was necessary; as the number of trials subjects could perform in a given session was limited, it was not practical to test perception for many values of Δt. As that the exact value of Δt is critical for demonstrating the illusion, the one subject who failed to show the perceptual illusion might have shown it for a better choice of Δt. This subject also failed to show a discernable increase in initial eye acceleration for the values of Δt we used; we chose 32 msec for the perceptual task because it had worked for other subjects.

MT neurons lose directionality as flash separation is increased

The histograms in Figure3A show the responses of a representative MT neuron to apparent motion at 16°/sec. For a Δt of 4 msec, the neuron was strongly directional and showed a large response to preferred-direction motion (histogram with upward bars) and a suppression of baseline activity for null-direction motion (histogram with downward bars). As Δt was increased, the response to preferred-direction motion decreased, and the suppression of firing for null-direction motion was lost. At the largest value of Δt (64 msec), the neuron completely lost the ability to signal the direction of motion. Figure 3Cshows a similar set of histograms for a different neuron. This neuron continued to respond to preferred-direction motion even when Δt was 64 msec, but the response to null-direction motion increased as a function of Δt. Thus, like the neuron inA, the neuron in Figure 3C lost the ability to signal the direction of motion when Δt was 64 msec.

To quantify the loss of direction selectivity, Figure 3, Band D, plots the directional response of each neuron as a function of Δt. The directional response is defined as the difference between the mean response to the preferred and null directions (see Materials and Methods). The directional responses of both neurons remained near normal up to a Δt of 20–24 msec (Δx: 0.32–0.38°), fell sharply around 32 msec (Δx: 0.51°), and were near zero by 64 msec (Δx: 1.0°). We define the “directional limit” of each neuron to be the Δt that corresponds to the half-decline point of the sigmoidal fit to the directional responses. Both neurons in Figure 2 had a directional limit of 37 msec, corresponding to a Δx of 0.59°. However, these two neurons represent opposite ends of the distribution in terms of how directionality was lost.

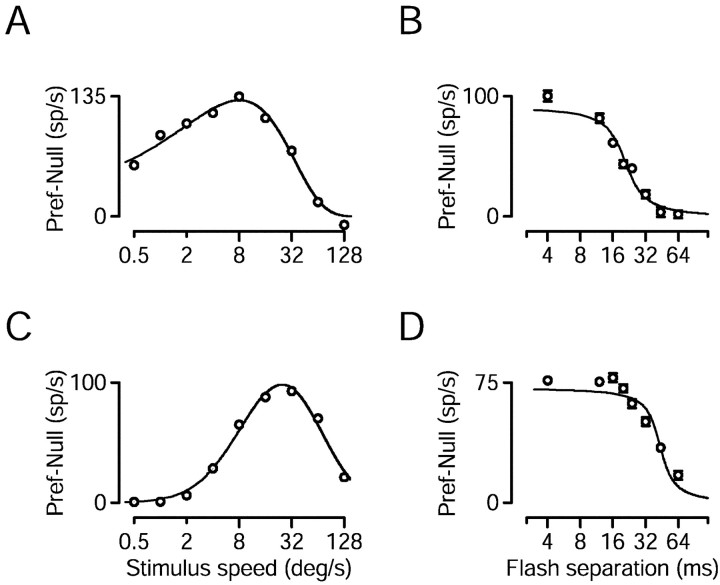
Directional limits were correlated with preferred speed. Speed tuning was assessed by recording responses to multiple speeds, using a Δt of 4 msec. Figure 4,A and C, shows the directional response of two MT neurons as a function of stimulus speed. We estimated the preferred speed of a neuron by taking the peak of the fit to such data (see Materials and Methods). The neurons in A and Chad preferred speeds of 8.0 and 24°/sec. Figure 4, B andD, shows that, for a 16°/sec stimulus, both neurons exhibited the expected decline in directional response as Δt was increased. However, the response of the neuron whose preferred speed was 8.0°/sec dropped off more swiftly than did that of the neuron whose preferred speed was 24°/sec. The limit of directionality was 20 msec (0.32°) for the former and 42 msec (0.67°) for the latter.

Fig. 4.

Responses of two MT neurons to smooth motion at different speeds and to apparent motion at 16°/sec. A,C, Speed tuning. The directional response to effectively smooth motion (Δt = 4 msec) is plotted as a function of stimulus speed. Fits are least squared fits as described in Materials and Methods. The peak of the fit is at 8.0°/sec inA and 24°/sec in C. B,D, The directional response of the neurons inA and C to 16°/sec stimulus motion, plotted as a function of Δt. The inflection point of the sigmoidal fits is at 20 msec in B and 42 msec inD. Error bars in B and Dindicate SEM and are suppressed when smaller than the symbol size.

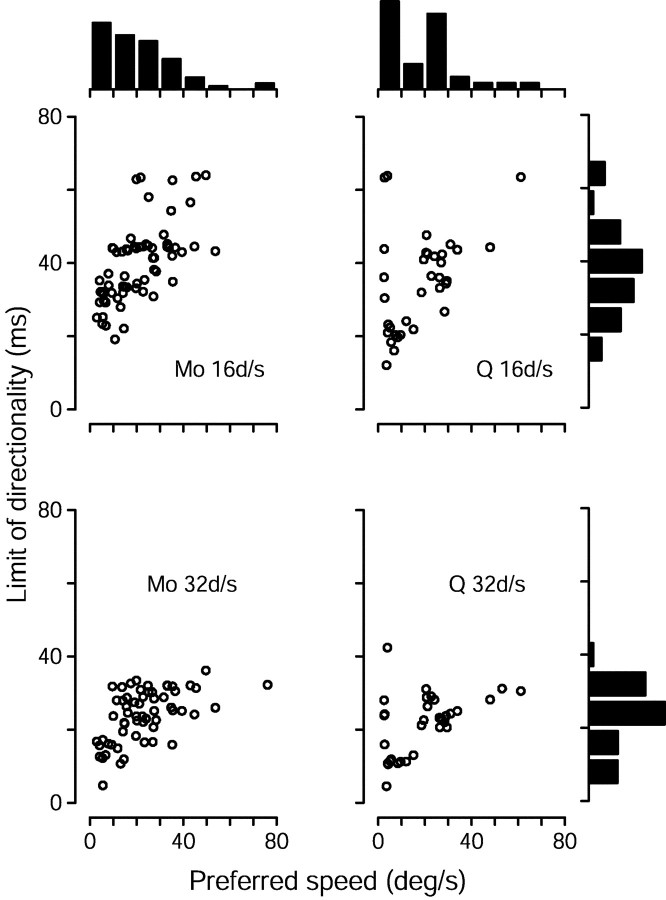
For both monkeys and both stimulus speeds tested, there was a strong tendency for neurons with higher preferred speeds to have larger limits of directionality, as illustrated by the scatter plots in Figure5. For a stimulus speed of 16°/sec, regression analysis yielded slopes of 0.54 and 0.43 msec/(°/sec) for monkeys Mo and Q (r² = 0.41 and 0.21; p < 10⁻⁷ and 10⁻², respectively). For a stimulus speed of 32°/sec, the directional limits, expressed in terms of Δt, were approximately half as large, and the resulting slopes approximately half as steep: 0.27 and 0.26 msec/(°/sec) (r² = 0.29 and 0.23; p < 10⁻⁵and 10⁻² for the two monkeys). The directional limits for the two stimulus speeds are more similar when expressed in spatial terms than when expressed in temporal terms. As shown in the histograms on the right of Figure 5, the directional limits were about twice as large, in terms of Δt, for target motion at 16 versus 32°/sec. For monkey Mo, the mean limits were 40 msec and 24 msec for the two speeds, corresponding to values of Δx of 0.64° and 0.77°, respectively. For monkey Q, the mean limits were 35 msec for 16°/sec and 22 msec for 32°/sec, corresponding to values of Δx of 0.59° and 0.69°. Thus, our data agree with the conclusion of Mikami et al. (1986a,b) that MT neurons lose directionality primarily because the distance between the flashes becomes too large, at least for the stimulus speeds we used.

Fig. 5.

Scatterplots showing the relationship between preferred speed and the limit of directionality. Each symbol corresponds to one cell. The limit of directionality was calculated as the inflection point of sigmoidal fits such as that in Figure4B. Data are shown separately for monkey Mo (left column) and monkey Q (right column) and for stimulus speeds of 16°/sec (top row) and 32°/sec (bottom row). The histogram at thetop of each column shows the distribution of preferred speeds recorded from each monkey. The histograms on theright show distributions of the limit of directionality for each of the two stimulus speeds, collapsed across both monkeys (for whom they were similar but not identical). A small number of neurons, with high or low preferred speeds, had such weak directional responses to stimulus speeds of 16 and/or 32°/sec that their limit of directionality could not be calculated with any confidence. For the relevant stimulus speed, such neurons were excluded from the analysis shown in this figure, but are included in subsequent analyses.

Population responses

Traditional data presentation, such as that shown in Figures 3-5, describes the responses of each neuron to a collection of stimuli whose parameters are varied systematically. These figures show that responses of a single MT neuron do not reveal an obvious basis for the illusion of increased speed produced by apparent motion. Neurons simply became less responsive and less directional as Δt was increased. It therefore seems likely that the illusion is attributable to changes manifested at the level of the population. To document the population response, it is necessary to adopt the alternate experimental design of recording (sequentially) from multiple neurons, using the same stimuli for each. When testing the effect of apparent motion, we therefore did not customize target speed to the preferred speed of each neuron, but rather recorded the response of each neuron to the same two speeds, and the same values of Δt. This allowed us to plot, for a given stimulus, the response of each neuron in our sample population.

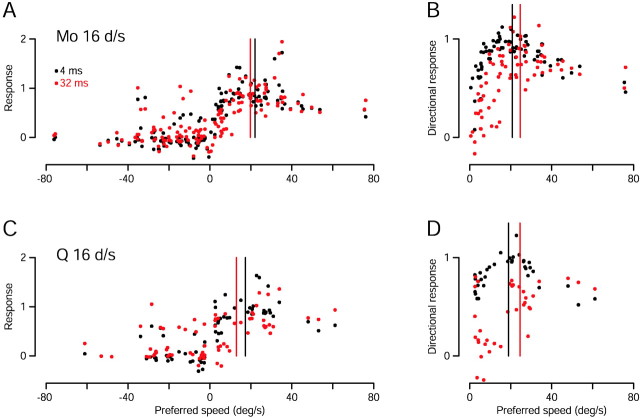
Figure 6 illustrates population responses for target motion at an apparent speed of 16°/sec for two values of Δt. Consider first the data from monkey Mo (Fig.6A). Each black symbol shows the response of one of 73 neurons to a 16°/sec stimulus with a Δt of 4 msec. The vertical position of the symbol indicates the strength of the neuron's response, whereas the horizontal position is set to the preferred speed of the neuron. The strength of the neuron's response was computed as the average firing rate over the interval starting at the stimulus onset and ending 100 msec after its offset, and was normalized so that the directional response to the preferred speed (calculated as in Eq. 1) was one when Δtwas 4 msec. Responses greater than one are thus possible if there was some positive response to motion in the null direction. Baseline activity levels were subtracted, so that responses less than zero indicate suppression of baseline firing. Two points are plotted for each neuron, one at a positive preferred speed for its response to motion in the preferred direction, and one at a negative preferred speed for its response to the null direction.

Fig. 6.

Effect of apparent motion on the population response of MT neurons to stimulus motion at 16°/sec. Each point corresponds to one neuron and plots its response to a 16°/sec stimulus against its preferred speed. Red andblack symbols show responses to motion with values of Δt of 32 and 4 msec. The top andbottom graphs show data for monkey Mo (73 neurons) and Q (34 neurons), respectively. A, C, The “raw population response.” The response of each neuron to motion in its preferred direction is plotted on the right-hand side (positive preferred speeds), while its response to motion in its null direction is plotted on the left-hand side(negative preferred speeds). Each neuron thus contributes two data points for each value of Δt. B,D, The “opponent population response.” Each point plots the directional response of that neuron, computed as the difference between the responses to stimulus motion in the preferred and null directions. For all panels, the response of each cell has been normalized by the peak of the fit to the speed tuning data, so that its directional response to its preferred speed is one when Δt is 4 msec. Vertical black andred lines show the centers of mass of the population when Δt was 4 and 32 msec, respectively.

Figure 6 is meant to indicate the population response for a given direction of motion (e.g., rightward) and to include the activity not only of neurons that prefer the direction of motion, but also of neurons that prefer the opposite direction. This was accomplished by recording the response of each neuron to both its preferred and null directions. Our approach treats every neuron's response to its preferred direction as if it were the response to rightward motion of a neuron that prefers rightward motion. Conversely, the response to the null direction is treated as if it were the response to rightward motion of a neuron that prefers leftwards motion. This approach is much more efficient than the alternate method of recording the response of every neuron to rightward motion and then sorting based on preferred direction. The approach is justified by the finding that there was no noticeable or statistically significant interaction between the preferred direction of a neuron and its response to apparent motion (data not shown).

As expected, for effectively smooth motion at 16°/sec (Fig.6A, black symbols) most neurons showed some response to the preferred direction, and little response, or even suppression, for motion in the null direction. For the preferred direction, neurons with preferred speeds near 16°/sec responded most robustly, but most neurons with higher and lower preferred speeds also responded above baseline. The same sample of 73 neurons showed a subtly different population response to a 16°/sec stimulus when Δt was increased to 32 msec (Fig. 6A, red symbols). For motion in the preferred direction, the majority of red symbols plot slightly below the black symbols, whereas for the null direction, the majority of red symbols plot slightly above the black symbols. The exception to this general trend occurs for neurons with preferred speeds >40°/sec, whose responses were little changed by the increase in Δt. The centers of mass of the two population responses are shown by the vertical black and red lines. For a Δt of 32 msec, the center of mass shifted to the left, toward smaller speeds. The leftward shift is caused by both the weaker responses to preferred-direction motion and the larger responses to null-direction motion. Figure 6C shows the same analysis for 34 neurons recorded from monkey Q. Again, an increase in flash separation from 4 to 32 msec shifted the center of mass toward slower speeds.

The center of mass computation used above is equivalent to taking the vector average of the population response. For a standard vector average, the response of every neuron is multiplied by a vector pointing in its preferred direction and of length proportional to its preferred speed. All such vectors are summed and then normalized by the total activity. Our population response considers only neurons with preferred directions oriented with or opposite to the direction of stimulus motion. The vector average thus yields a single scalar that gives an estimate of the speed of the stimulus. The analysis in Figure6, A and C, indicates that an illusion of increased speed is not to be expected if the MT population response is decoded using a standard vector average.

A number of authors have suggested that neural estimates of motion may depend on an opponent computation (Levinson and Sekuler, 1975; Adelson and Bergen, 1985; Heeger et al., 1999). Figure 6, Band D, show “opponent” population responses based on the directional responses of the neurons we recorded. This approach re-represents the population response as the difference between the response of neurons that prefer the direction of motion, and the response of neurons that prefer the opposite direction. Comparison of the opponent population response when Δt was 4 msec (black symbols) and 32 msec (red symbols) reveals a shift in the peak of the population response. The directional response of most neurons was reduced for the larger flash separation, but not all neurons showed the same reduction. Consistent with the data in Figure 5, neurons that prefer slow speeds showed a large reduction in directional firing, whereas neurons that prefer fast speeds responded almost as well to a Δt of 32 msec as to a Δt of 4 msec. As a result, the center of mass of the opponent population was located at a faster speed when Δtwas 32 msec (red vertical line) than when Δtwas 4 msec (black vertical line).

Neural computations to estimate speed from the population response

The data in Figure 6 suggest that changes in the MT population response underlie the increase in pursuit initiation produced by apparent motion. However, it appears that this increase can be accounted for by only some methods for estimating speed from the population. We tested different methods for estimating speed to see which, if any, could account for the full constellation of changes in pursuit initiation induced by apparent motion. All methods tested were based on the well known vector average:

$$\text{speed}=\frac{{\mathrm{\Sigma }}_i s_i{R}_i}{{\mathrm{\Sigma }}_i R_i},$$ Equation 2

where R_i is the response of thei^th neuron, ands_i is its preferred speed, which is positive or negative depending on whether the preferred direction is aligned with or against the direction of stimulus motion. For a well behaved population, the vector average is close to an optimal linear estimator of stimulus speed (Salinas and Abbott, 1994). As long as the population response is symmetric, the vector average is also equivalent to other methods that estimate the preferred speed of the most active neurons.

As Figure 6 illustrates, the result of any method for estimating the center of mass of the population will depend on how one expresses the population. The three equations below describe the vector average based on three ways to express the population.

The raw (or standard) vector average:

$$\text{speed}=\frac{{\mathrm{\Sigma }}_i s_i{R}_i^{\text{pref}}+(-s_i)R_i^{\text{null}}}{\varepsilon +{\mathrm{\Sigma }}_i(R_i^{\text{pref}}+R_i^{\text{null}})}.$$ Equation 3

The opponent vector average:

$$\text{speed}=\frac{{\mathrm{\Sigma }}_i s_i(R_i^{\text{pref}}-R_i^{\text{null}})}{\varepsilon +{\mathrm{\Sigma }}_i(R_i^{\text{pref}}-R_i^{\text{null}})}.$$ Equation 4

The preferred-only vector average:

$$\text{speed}=\frac{{\mathrm{\Sigma }}_i s_i{R}_i^{\text{pref}}}{\varepsilon +{\mathrm{\Sigma }}_i R_i^{\text{pref}}},$$ Equation 5

where s_i is the preferred speed of the i^th neuron, andR_i^pref andR_i^null are the responses of the i^th neuron in its preferred and null directions. The inclusion of ɛ makes the equation less sensitive to noise by preventing the denominator from nearing zero when responses are small. Each pair of responses (R_i^pref andR_i^null) can be thought of as belonging to two neurons of an opponent-pair, with similar preferred speeds but opposite preferred directions. We approximated this situation by recording the response of each neuron to both directions of motion. With this in mind, Equations 3-5 differ in how the population is configured. Equation 3 adds up the firing of all neurons weighted by their preferred speed and normalizes by the sum of all the activity. Equation 4 adds up the opponent firing of all neuron pairs, weighted by their preferred speed, and normalizes by the sum of the opponent signals. Note that Equations 3 and 4 are formally identical except for their denominator. Equation 5 assumes that the nervous system first estimates direction, and then estimates speed using only those neurons tuned for the preferred direction.

When simulating Equations 3-5, the values ofR_i^pref andR_i^null were the mean spike rate over a 600 msec interval starting at the onset of the stimulus. Baseline firing rates were subtracted. Because neurons had different maximum firing rates, the responses of each neuron were normalized by the peak of the fit to the speed tuning data, computed asR_max in Equation 1. Preferred speeds were calculated as previously described.

Current models of pursuit assume that an internal estimate of the retinal speed of the target is converted into a command for eye acceleration (Ringach, 1995; Churchland and Lisberger, 2001), and initial pursuit eye acceleration is indeed approximately proportional to retinal speed (Lisberger and Westbrook, 1985). We therefore wish to know if any of the vector-average methods described above can transform the measured population response into an estimate of target speed that accounts for the measured changes in pursuit eye acceleration. The four graphs in Figure 7plot data for two stimulus speeds and for both monkeys. Each graph superimposes the measured eye acceleration (black circles) and the target speed decoded by Equations 3 (dark blue), 4 (red), and 5 (green). Also shown (light blue) is the result of decoding by a pure weighted sum:

$$\text{speed}={\mathrm{\Sigma }}_i s_i{R}_i^{\text{pref}}+(-s_i)R_i^{\text{null}}.$$ Equation 6

As was done for pursuit, the estimates of speed produced by each method were normalized by their value when Δt was 4 msec. Increases and decreases in estimated speed thus plot above and below the dashed line at 100%.

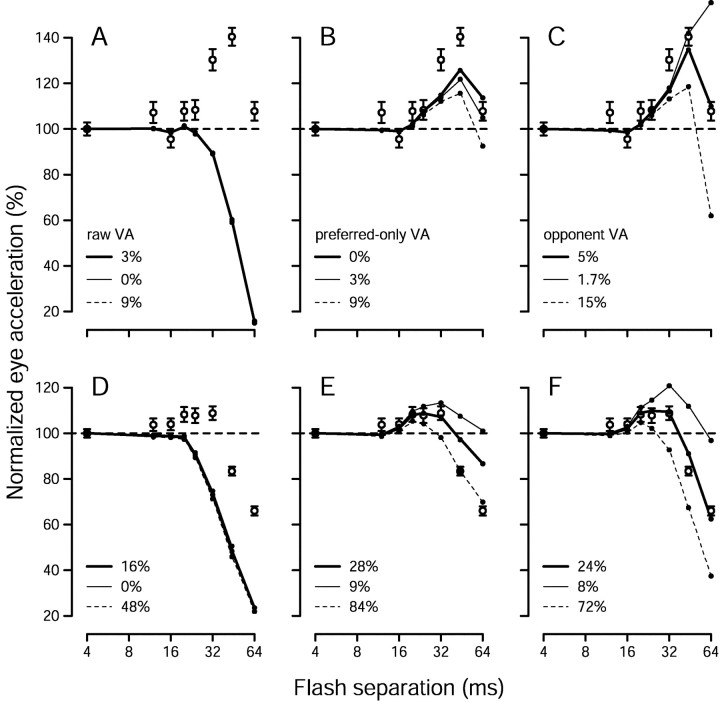
Neither the raw vector average (dark blue, Eq. 3) nor the weighted sum (light blue, Eq. 6) showed an increase in estimated speed for any Δt; both showed monotonic declines as Δt increased. The opponent vector average (red, Eq. 4) and the preferred-only vector average (green, Eq. 5) were more successful. Both produced an increase in estimated speed for moderate flash separations and a decrease in estimated speed for larger flash separations. Of the two, the opponent vector average appears to best match the magnitude of the changes in eye acceleration. However, because our sample of recorded neurons does not have a flat distribution of preferred speeds (Fig. 5), the estimate of speed produced by each method is not linearly related to the actual speed of the target. It is difficult to know how to correct for this, because it is difficult to know how and to what degree the nervous system does so. Thus, more than a relative comparison of magnitude is unwarranted. The important quantitative observation is that both the opponent and preferred-only vector averages produced increased estimates of speed for the same flash separations that produced increased eye acceleration at the initiation of pursuit. Conversely, the two methods produced diminished estimates for the flash separations that produced decreased acceleration.

For each point in Figure 7, the estimate of speed was based on the neural responses recorded from that monkey for that stimulus. The only free parameter used to fit the data was the value of ɛ, which was adjusted by hand until the fits appeared best. Our goal in fitting the data was that the estimate of speed be increased or decreased appropriately given the pursuit data. Sometimes we deemed it more crucial to capture the presence of a small effect (e.g., the increases in acceleration in Fig. 7C) than to capture the exact magnitude of a large effect (e.g., the decrease in acceleration for a Δt of 44 msec in that same panel). Because there was only one free parameter, fitting by hand was an easier way of achieving this goal than was creating an error function that captured our idea of an ideal fit. It is very unlikely that we missed a better fit because, as we show below, the impact of ɛ on the estimate of speed is easily understood.

Figure 8 demonstrates the influence of the parameter ɛ on the estimate of speed produced by the different vector average computations. The open symbols replot the pursuit acceleration data for a target speed of 16°/sec, for monkey Mo (A–C) and monkey Q (D–F). The solid lines replot from Figure 7, A and C, the estimates of speed produced using the value of ɛ that we considered ideal. The values of ɛ we used are indicated in the key, and are expressed as the percentage of the denominator thatɛ contributes when Δt is 4 msec. For example, if the sum of firing rates in the denominator was 200, and the value ofɛ was 10, then we express ɛ as 5%. Our general strategy was to test the prediction of each estimation method for values of ɛ that were 1/3 and 3 times the value providing the best fit to the data, although we deviated from this strategy if the optimal value of ɛ was close to zero. For the raw vector-average model (Fig. 8A,D), the value of ɛ had little impact on the decoding. For the opponent and preferred-only vector-average models (Fig. 8B,C,E,F), larger values of ɛ reduced the estimate of speed, especially for larger values of Δt.

Fig. 8.

The influence of the parameter ɛon the behavior of the three vector average methods for estimating speed. All graphs plot pursuit data (open circles) and estimates of target speed (filled symbolsconnected by lines) for a stimulus speed of 16°/sec, derived and plotted as described in Figure 7. The three sets offilled symbols in each panel show estimates of speed created using different values of ɛ, as indicated by the keys. The top panels (A–C) each show data for monkey Mo (with the same pursuit data reproduced in each), and the bottom panels(D–F) show data for monkey Q. A,D, Estimates of speed were produced by the raw vector average. B, E, Estimates of speed were produced by preferred-only vector average. C,F, Estimates of speed were produced by opponent vector average.

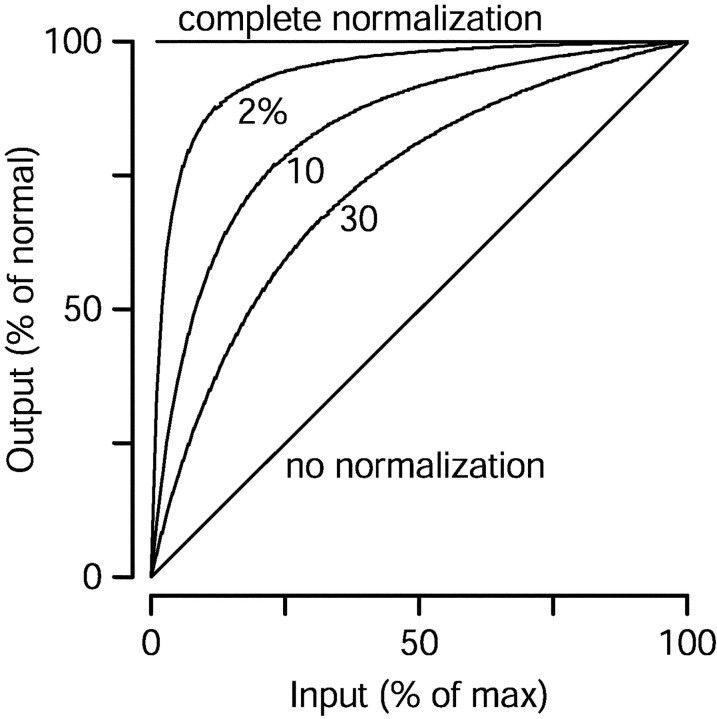
Equations 3-5 rely on divisive normalization. Figure9 illustrates the relationship between the parameter ɛ and the degree of normalization provided by Equations3-5. The traces show how a vector-average changes when its input is scaled but retains the same center of mass. They plot output as a function of input for the equation:

$$\text{output}=\frac{\text{input}}{\text{input}+\varepsilon }.$$ Equation 7

When ɛ is zero, normalization is complete: the output is independent of the input for all nonzero values. For larger values of ɛ, normalization is less complete. There is still a range over which the output stays relatively constant regardless of the scaling of the inputs, but for small inputs the output falls sharply. If there were no normalization, then the output would be linearly related to the size of the input (line of slope one, labeled “no normalization”). From a practical standpoint, normalization makes the vector-average method immune to changes in the overall level of input, whereas ɛ gives some noise immunity so that the output falls to near zero when the signal becomes smaller than the noise.

Fig. 9.

Illustration of the impact of the parameterɛ on the normalization provided by the vector average methods. The three curved traces show, for different values of ɛ, how the output of the vector average computations changes with the strength of the input, assuming the center of mass of the input is constant. The diagonal line shows the outcome if there were no normalization, and thehorizontal line shows the perfect normalization that results when ɛ is zero. The value of ɛ is expressed as a percentage of the denominator of the vector average when the input is at 100%.

Understanding the role of ɛ in creating incomplete normalization allows us to understand why the estimates of speed shown in Figure 7 and 8 change as they do. Consider the opponent vector average. As Δt is increased, there is a steady decrease in the overall magnitude of the population response and a rightward shift in the center of mass. For moderate values of Δt, the rightward shift dominates the vector average, but as the overall directional response falls, the vector average eventually does as well. Thus, the value of ɛ determines how large the increase in estimated speed can grow before it is counteracted by the falling responsiveness of the population.

The optimal values of ɛ were different for the two monkeys. Consider the opponent vector average. For a target speed of 16°/sec, the optimal value of ɛ was 4.8 times larger for monkey Q than for monkey Mo. This may be because the actual physiological normalization during readout of MT is less complete for monkey Q. Consistent with this interpretation, the pursuit data of monkey Q could be fit reasonably well (data not shown) using the neural data of monkey Mo, if ɛ was increased fivefold from the ideal value for monkey Mo. Similarly, the pursuit of monkey Mo could be fit reasonably well (data not shown) using the neural data of monkey Q if the value ofɛ was reduced by a factor of 6 from the ideal value for monkey Q. Nevertheless, the fits were not as good as when each monkey's pursuit data were fit using his own neural data. For example, the increase in eye acceleration was present for smaller values of Δt in monkey Q than in monkey Mo, and this could not be corrected by changing the value of ɛ.

The values of ɛ we used were slightly different when fitting the pursuit responses to the two stimulus speeds. For 16 and 32°/sec stimulus speeds, the values used for the opponent vector average were 5 and 12% (Mo) and 24 and 26% (Q). For the preferred-only vector average, the values of ɛ were 0 and 9% (Mo) and 28 and 30% (Q). The actual decoding algorithm applied by the nervous system is presumably the same for each speed, and it might therefore appear that ɛ should be set to be the same for the two speeds. However, as discussed above, the distribution of preferred speeds in our sample population and the actual distribution sampled by the nervous system may not be identical. Any discrepancy will create different ideal values of ɛ for the two speeds. For example, if we have undersampled the contribution of fast-tuned neurons (which seems possible given the distributions in Fig. 5), then ɛ will have to be larger when estimating speed for faster velocities (which it was). We therefore allowed different values of ɛ to be used for the two speeds. Nevertheless, fits were still reasonable if ɛ was constrained to be the same, particularly for the opponent vector average (data not shown).

Time-based estimates of speed

The estimates of target speed produced by the different methods in the previous section are static, because they are based on firing rates that were averaged over the 600 msec interval beginning at the onset of the stimulus and ending 100 msec after its offset. However, the pursuit system responds to the stimulus within 100 msec and continually updates its response based on the speed of the target image, presumably estimated from the time-varying responses of MT neurons. We therefore modified the opponent and preferred-only computations to estimate target speed on a millisecond time scale. We asked whether the time-based estimates of speed would still capture the effect of apparent motion on peak eye acceleration and whether they would also capture the effects on acceleration latency.

For each stimulus, the firing rate of each neuron was averaged across trials by accumulating spike counts in 1 msec time bins. Baseline firing, defined as the mean response for a stationary target, was subtracted. As before, average responses were normalized by the peak of the fit to the speed-tuning data for that neuron. Responses were filtered with an exponential filter of time constant 30 msec, chosen to be long enough to provide sufficient smoothing, but to be shorter than or equal to the estimated time constant of pursuit (Krauzlis and Lisberger, 1994; Churchland and Lisberger, 2001). A handful of neurons (four from monkey Mo, and zero from monkey Q) were excluded from this and subsequent analyses, because too few trials were collected to provide a low-noise estimate of their firing rate as a function of time. For each millisecond, we then used Equations 4 and 5 to compute estimates of speed from the averaged and filtered responses of all the neurons.

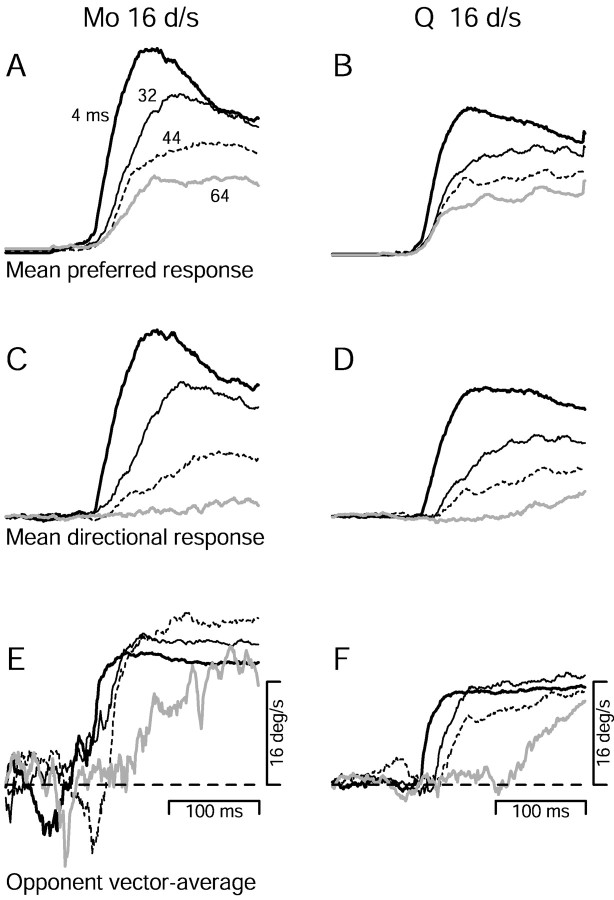
Figure 10, A andB, shows the time course of neural responses, averaged across all neurons from each monkey. Responses are for stimuli moving at 16°/sec in the preferred direction and are shown for four values of Δt. Larger values of Δt evoked smaller average firing rates that peaked slightly later. Responses were considerably above baseline even for the largest Δt. Figure 10, C and D, shows average directional responses for the same stimuli and neurons. For the larger values of Δt, directional firing rates were dramatically reduced and peaked much later than they did for small values of Δt. Figure 10, E and F, shows, again for the same stimuli and neurons, estimates of stimulus speed created by the opponent vector average. Consider first the data for monkey Mo inE. Before the beginning of the neural response (A, C) the estimate of stimulus speed inE fluctuated around zero. After the onset of the neural response, the estimate of speed increased and became more stable. When Δt was 4 msec (bold continuous traces), the peak estimate of speed was ∼18°/sec and was reached quickly. When Δt was 32 and 44 msec (fine black anddashed traces), the peak estimate of target speed was higher, but was reached later. When Δt was 64 msec (solid gray trace), the peak estimate was lower than for 44 msec, and was reached quite slowly. The overall pattern of effects is qualitatively similar in monkey Q (Fig. 10F), although the increase in the estimate of speed was smaller.

Fig. 10.

Time-varying estimates of target speed based on the time-varying population responses in area MT. Neural responses and estimates of speed are shown as a function of time for monkey Mo (left column) and Q (right column). Different trace types correspond to different values of Δt, as indicated by the numbers inA. A, B, Average responses of MT neurons to preferred direction motion at 16°/sec. Averages were made separately for each monkey, by summing the activity of all recorded neurons for a given stimulus, after normalization and filtering as described in Results. C,D, Average directional responses (the response to the preferred direction minus the response to the null direction) for the same stimuli as in A and B.E, F, Time-varying estimates of speed produced by the opponent vector average. Estimates were made by applying Equation 4 to the same neural responses that produced the averages in the above panels. All example traces in Figure 10 were computed after artificially shifting in time the responses of all MT neurons so that each had a latency of 100 msec for target motion of the preferred speed and direction.

On the premise that the neural estimate of target speed provides a command that determines smooth eye acceleration, we extracted two quantitative measures from curves like those in Figure 10, Eand F. For comparison with the magnitude of peak initial eye acceleration, we measured the peak estimate of target speed during the first 150 msec after the normal onset of the response (normal onset measured when Δt was 4 msec). For comparison with the “acceleration latency” of initial pursuit, we measured the time the estimate of speed reached 80% of its peak. As with pursuit, these measures are expressed relative to their values when Δtwas 4 msec. The peak estimate of speed is expressed as a percentage of that when Δt was 4 msec, and the latency of the estimate is expressed as the change (in milliseconds) from the latency when Δt was 4 msec.

Figure 11 shows that an estimate of target speed based on the opponent vector average undergoes changes in magnitude and latency that parallel those of pursuit eye acceleration. The values of Δt that produced increased peak eye acceleration (open circles) also produced increased peak estimates of speed (gray filled circles). For larger values of Δt, both peak eye acceleration and the peak estimate of speed declined. Pursuit and the estimate of speed also show similar latency increases as Δt is increased. The results for a 32°/sec stimulus with a Δt of 44 msec provide an exception to the generally good agreement. For both monkeys, peak pursuit acceleration was reduced by only 40–50% (relative to a Δt of 4 msec), whereas the peak estimate of speed was reduced by ∼80%. Furthermore, the estimate of speed was so small and noisy that no reliable measure of latency could be extracted. It is not surprising that the estimate of speed should be so degraded, because the MT neurons showed an almost complete lack of directional response to this stimulus (data not shown, but see the weighted sum in Fig.7B,D). It is surprising that pursuit should fare so well in the absence of reliable MT responses. The likely explanation is that pursuit is no longer operating in open loop for these very long latency responses. Small initial eye accelerations reduce the speed of the stimulus on the retina, reducing the retinal Δx, and aiding subsequent pursuit. It is really only proper to compare our recorded neural data with pursuit when changes in the acceleration latency are less than the open loop interval plus any change in the absolute latency, or ∼100–120 msec for our data.

As was the case for the static version of the model, the effect of Δt of the magnitude of the estimate of speed depended somewhat on the value of ɛ. In contrast, the latency measurement was affected very little by the value of ɛ. In Figure 11A–D, the values of ɛ were 9 and 13% for 16 and 32°/sec target motion for monkey Mo and 29 and 40% for monkey Q (the same value was used for both the peak and latency measurements). These values are similar to those used for the static version of the model. Fits were nearly as good if the same value of ɛ was used for both speeds, but much worse if the same value was used for both monkeys.

Figure 12 shows the magnitude and latency measures for the estimate of speed produced by the preferred-only vector average. Changes in the peak estimate of speed largely parallel the changes in peak eye acceleration. However, the preferred-only vector average captures poorly the changes in acceleration latency. For the largest values of Δt, the change in the latency of pursuit is underestimated by 50–100 msec. As with the opponent vector average, the value of ɛ had little effect on the latency measure. The values of ɛ used were 5 and 5% for stimulus speeds of 16 and 32°/sec in monkey Mo, and 39 and 40% for the two speeds in monkey Q.

Fig. 12.

Comparison of pursuit with estimates of speed produced by the time-based version of the preferred-only vector average, applied to the recorded population response. Open symbols plot pursuit performance, as in Figure 11. Thesmall gray symbols and traces plot measurements made from the estimate of speed. The estimate of speed for each stimulus was obtained by applying the preferred-only vector average to the time-varying population response recorded for that stimulus. Small gray circles plot the peak estimate of speed (plotted against the left vertical axis), and small gray triangles plot the latency of the estimate of speed (plotted against the right vertical axis). Gray symbols connected by continuous lines show the results obtained when all neural responses were shifted to have a latency of 100 msec.Gray symbols connected by dashed linesshow the results when the latency of each neuron was left at its natural value. All data are plotted relative to their values when Δt was 4 msec. Each graph shows results for a different monkey and target speed, as indicated.

The directional responses of different MT neurons can have very different latencies: in our data, the range was 58–120 msec for monkey Mo and 50–105 msec for monkey Q. Given the 20 msec latency of the pursuit response to microstimulation of MT (Komatsu and Wurtz, 1989), only a small proportion of MT neurons have latencies short enough to account for earliest part of pursuit. Monkey Mo had a pursuit latency of 85 msec, but only 17% of the neurons we recorded from monkey Mo had latencies <65 msec. Monkey Q had a pursuit latency of 80 msec, but only 44% of the neurons we recorded from Q had latencies <60 msec. In decoding target speed from the populations of neurons we recorded, we faced three choices. We could include (1) only those neurons with latencies short enough to account for the pursuit latency, (2) all neurons regardless of latency, or (3) all neurons, but with the responses artificially aligned so that each has the same short latency for target motion at its preferred speed. The first approach is impractical, as a minority of the neurons we recorded had latencies short enough. The second possibility appears the most natural. The third creates a population of neurons that all begin responding at the same time, which may mimic reality if pursuit is driven only by short-latency neurons. In practice, estimates of speed based on the second and third methods provided very similar results, illustrated by the gray circles connected by dashed and solid lines in Figures 11 and12. The absolute latencies of the estimate of speed differed slightly between the two methods (data not shown), but the changes in latency produced by changing Δt were very similar.

Eye movements during fixation

During neural recordings, monkeys fixated a small spot while the moving dot patch was presented in the receptive field of the neuron. The fixation window that surrounded the spot insured that the monkey did not saccade away from the desired fixation and that the dot patch remained in the receptive field. However, the fixation window did not punish slow smooth eye movements that were sometimes evoked by the motion of the dot patch. These smooth movements produced very small positional excursions (<1°) that were usually corrected by a saccade if they became significant. When they were present, the smooth movements were in the direction of the patch motion, began 100 msec after the patch began to move, reached their peak ∼20 msec later, and then usually declined to near zero velocity by 100–200 msec later. It is thus our impression that the monkeys were actively trying to suppress such smooth movements, but were not entirely successful.

The smooth eye movements evoked by our stimuli are a concern, even with the monkey fixating a stationary spot, because they change the retinal stimulus. For example, if the eye moves smoothly at 1°/sec for a 16°/sec stimulus, then the recorded MT neurons are really responding to15°/sec image motion. If different values of Δt elicit different degrees of smooth eye movement, then this would introduce an artifact into our recorded population responses. Specifically, if larger values of Δt evoked smaller eye movements, then neurons would be responding to a faster retinal stimulus, the population response would be shifted to toward higher target speeds, and a vector average computation would reflect this shift. Four facts argue that involuntary smooth eye movements were not the basis of the shifts in the population response that are reported and analyzed above. (1) We observed the same shift in the population responses for the same apparent motion stimuli in anesthetized and paralyzed monkeys (data not shown). (2) The actual eye velocities seen during neural recording were small (Table 1). For a 16°/sec stimulus in monkey Mo, average smooth eye velocity during the stimulus was 0.15°/sec and 0.01°/sec when Δt was 4 and 44 msec. Between these two values of Δt, the resulting image motion would shift the population response in MT by 0.14°/sec, or <1% of the 16°/sec target speed. In comparison, the opponent vector average produced an estimate of speed that was 34% higher for a Δt of 44 msec than for a Δt of 4 msec. The potential artifact can account for 3% of the effect of interest. Small potential artifacts were found for all relevant values of Δt in both monkeys and are summarized by the numbers in parentheses in Table 1. For monkey Mo, the potential artifacts were very small and unreliable in their direction. For monkey Q the potential artifacts were larger and more consistent, but could still account for an average of only 11% of the relevant changes in the estimate of speed. (3) Any image motion produced by smooth eye movements should cause a pure shift in the population response, whereas we found a decrease in the directional responses of neurons that prefer slow speeds without an increase in the response of neurons that prefer fast speeds. (4) The population response shows the shifts of interest even within the first 100 msec of the neuronal responses (Fig.10E,F), before eye movements could have changed the retinal stimulus driving the neurons. Thus, we are certain that the observed shifts in the MT population response, and the subsequent increases in estimated speed, result from the neural response to apparent motion, and are not artifacts related to imperfectly suppressed smooth eye movements.

Table 1.

Mean smooth eye velocities evoked despite fixation during neural recordings

Δt (msec)	Monkey M		Monkey Q
	16°/sec target	32°/sec target	16°/sec target	32°/sec target
4	0.15°/sec	0.10°/sec	0.55°/sec	0.63°/sec
12	0.10°/sec	0.14°/sec	0.61°/sec	0.55°/sec (4%)
16	0.16°/sec	0.22°/sec (−5%)	0.55°/sec	0.40°/sec
20	0.11°/sec		0.45°/sec (7%)
24	0.14°/sec	0.12°/sec (−5%)	0.36°/sec (12%)	0.19°/sec
32	0.13°/sec (1%)	0.09°/sec	0.22°/sec (22%)	0.07°/sec
44	0.01°/sec (3%)	−0.02°/sec	0.13°/sec	−0.01°/sec
64	−0.02°/sec		0.03°/sec

Means were calculated as the average smooth eye velocity in the direction of the stimulus, over the 500 msec time the stimulus was present, after excision of saccades. Means are shown for both monkeys, two target velocities, and the full range of values of Δt. For those values of Δt that evoked statistically significant increases in pursuit eye acceleration, parentheses show the percentage of the increase in estimated speed (calculated using the static version of the opponent vector-average) that could be accounted for by the change in smooth eye velocity from when Δt was 4 msec. Negative percentages indicate that the artifact introduced by smooth eye movements would actually produce a decrease in estimated speed.

DISCUSSION

Neural basis of an illusion of increased speed

Apparent motion can appear faster than smooth motion. This illusion is reflected in both pursuit eye movements and perception. The illusion seems paradoxical: why should degraded motion cause an increase in perceived speed? Neural recordings from area MT reveal a plausible explanation: as the flash separation is increased for a given target speed, neurons with slower preferred speeds show the largest reduction in directional response. Consequently, the balance between slow-preferring neurons and fast-preferring neurons is shifted toward the latter. Our results agree with the finding of Mikami et al. (1986a,b) that fast-preferring MT neurons respond directionally for larger spatial flash separations than do slow-preferring MT neurons.

Available evidence implies that MT provides inputs that guide both the initiation of pursuit and perceptual decisions based on motion, supporting our assumption that the population response in MT is responsible for the behavioral effects we report. However, directionally selective neurons in many visual areas probably have similar spatiotemporal limits to those of MT and could show the same correlation between preferred speed and maximum Δx. Thus, while we believe that the population shifts we report provide the explanation for the illusory increase in speed, we cannot be certain that shifts in the MT population are the only factor in creating the illusion. Similar population shifts in other areas may also be important.

Neural computations for estimating target speed

Given the effects of apparent motion on the MT population response, only some methods for estimating stimulus speed were able to account for the observed changes in pursuit. The opponent vector average accounted well for all three basic features of the behavioral data: (1) increases in initial pursuit eye acceleration for a mid-range of values of Δt, (2) decreases in eye acceleration for larger values of Δt, and (3) a progressive increase in pursuit latency as a function of Δt. The other computations tested each failed to account for at least one aspect of pursuit behavior, in each case for reasons that can be understood intuitively. The weighted sum never produced an increase in estimated speed because total neural activity drops steadily with increasing Δt, regardless of any changes in the center of mass. The standard or “raw” vector average showed the same failing but for a different reason. For the relevant values of Δt, neurons responded even when motion was in their null direction, pulling the center of mass toward zero.

The preferred-only vector average produced an appropriate increase in estimated speed, but failed to account for the large changes in pursuit latency seen at larger values of Δt. For large values of Δt, many MT neurons showed an initial short-latency response that was similar for preferred and null directions of motion. The preferred-only vector average is influenced by these early nondirectional responses, and thus underestimates the latency of pursuit. In general, its inability to discriminate directional from nondirectional responses makes the preferred-only vector average a suboptimal method for estimating speed. Indeed, it provides a robust estimate of target speed even when there is very little directional response (e.g., for 32°/sec and a Δt of 44 msec). Nonetheless, we cannot rule out the possibility that a preferred-only vector average is used by the nervous system, but is gated by another computation that is sensitive to directional responses.

Other explanations for the illusory increase in speed

The recorded MT response provides one explanation for the illusory increase in the estimate of target speed. An alternate explanation is that each dot may appear to be stationary from the moment it is flashed until the moment the next flash appears, at which point it could appear to move briefly at a very high speed. This explanation assumes temporal resolution beyond that of the visual system: for values of Δt from 12–32 msec, it is implausible that the stimulus is resolved into intervals of stationary and very high speed. Even if such resolution were possible, average speed would be unchanged. Furthermore, it is not clear how to account for the particular range of flash separations over which the illusion is obtained, or for the how this range changes with stimulus speed.

Another explanation is offered by Castet (1995). He also found that apparent motion can appear perceptually faster than smooth motion, and suggested an explanation based on an analysis of apparent motion in the frequency domain. Plotted in the spatiotemporal frequency domain, apparent motion produces “replicas” or “aliases” of the original frequency content that could excite motion sensors tuned to speeds both faster and slower than stimulus speed. Given certain assumptions, the excitation of fast-tuned sensors could dominate for slow stimulus speeds, consistent with the report of Castet (1995) that the illusion disappeared above 8°/sec. However, we observed an illusion of increased speed for target speeds up to 32°/sec, the highest tested. Furthermore, Castet's explanation proposes that aliasing increases the firing of fast-tuned neurons, whereas our neural data show that the reverse is true: shifts in the population response are attributable to a decrease in the response of slow-tuned neurons. Of course, the illusion reported by Castet may be different from ours; it was much larger in magnitude and appeared only at slower speeds. His explanation may be correct for his illusion.

The explanation we offer can also, of course, be conceived in the frequency domain. If speed tuning is largely determined by spatial frequency tuning, then aliasing will first impact neurons with high spatial frequency tuning and slow speed tuning. However, there is nothing “inevitable” about the illusion given the frequency representation. Depending on how the speed tuning of neural motion sensors is created, and on how the activity of those sensors is interpreted, apparent motion in the relevant range could increase, decrease, or leave unchanged the estimate of speed.

Computational principles driving approaches for decoding the population response

Our analysis suggests that speed is estimated from the MT population response by a computation that estimates the preferred speed of the most active neurons, following an opponent motion computation. The use of an opponent motion computation may have advantages for motion perception in the real world. For example, even smooth motion causes nondirectional “on” responses in some MT neurons. Less ideal or noisy stimuli may produce small to moderate nondirectional responses in many MT neurons. An opponent calculation would extract the directional component of the response, which could then be used to obtain a reliable estimate of target speed. Figure13 shows three population responses to illustrate the virtues of opponent motion computations graphically. A standard vector average based directly on the population responses in Figure 13 would estimate progressively smaller target speeds as the size of the nondirectional component of firing increased from zero (A, bold trace), to modest (B, thin trace), to as large as the directional component (C, dashed trace). In contrast, a vector average based on opponent motion responses would ignore the nondirectional response and would correctly estimate the same speed for the three population responses. A direct comparison between pairs of neurons with similar response properties but opposite preferred directions (Eq. 4) is conceptually helpful but formally unnecessary, because of the commutative nature of addition. The opponent vector average can also be conceived as (1) estimating the nondirectional component of the population response as the average response in the null direction, (2) subtracting this baseline from the response of every neuron, and (3) using a standard vector average.

Fig. 13.

Illustration of three hypothetical MT population responses. Neural response is plotted as a function of preferred speed, with rightward preferences on the right and leftward preferences on the left. The solid trace(A) shows an ideal population response with no baseline firing or nondirectional component. The thin trace (B) shows a population response with a small amount of baseline firing that contributes a nondirectional component. The dashed trace(C) shows a population response with a large nondirectional response component.

The vector average is a simple biologically reasonable method that has received empirical support (Lee et al., 1988; Groh et al., 1997). However, there other plausible methods for estimating speed from a population, some of which might account for our data. The optimal linear estimator (Baldi and Heiligenberg, 1988; Salinas and Abbott, 1994; Pouget et al., 1998) would likely account for our results, provided it was based on opponent responses and normalized appropriately. Pouget et al. (1998) have proposed a decoding method that might account for our results, although probably only if opponent motion emerged from the recurrent connections they used to generate a second population response with more desirable properties. Winner-take-all methods, which depend only on the responses of the most active neurons, might produce an increase in estimated speed even without an opponent motion computation. However, the behavior of a winner-take-all method is uncertain under some circumstances. We found values of Δt for which many neurons respond weakly but directionally, while others respond robustly but not directionally. Pursuit eye acceleration could be nearly normal for such values of Δt. In such a situation it is not clear to us how a winner take all method would extract a sensible estimate of speed without the aid of an opponent computation. It is also unclear how it would account for the decreases in eye acceleration observed for larger values of Δt.

Our data and analysis support our previous conclusion that the neural estimate of speed guiding pursuit is estimated by a computation that is based on the speed tuning of MT neurons (Priebe et al., 2001). The parallel effects of apparent motion on pursuit and perception argue that the perception of speed is similarly based on the speed tuning of motion sensitive neurons, perhaps in area MT. We argued previously (Churchland and Lisberger, 2000) that the changes in pursuit initiation produced by apparent motion are due to changes in the visually derived drive of eye acceleration. Our success in predicting these pursuit data, based on the population response in area MT, provides strong support for this interpretation and suggests that speed is estimated by a neural computation functionally similar to the opponent vector average used here.