Age-related changes in wavelength discrimination

Abstract

Wavelength discrimination functions (420 to 620–650 nm) were measured for four younger (mean 30.9 years) and four older (mean 72.5 years) observers. Stimuli consisted of individually determined isoluminant monochromatic lights (10 Td) presented in each half of a 2° circular bipartite field with use of a Maxwellian-view optical system. A spatial two-alternative forced-choice method was used in combination with a staircase procedure to determine discrimination thresholds across the spectrum. Small but consistent elevations in discrimination thresholds were found for older compared with younger observers. Because the retinal illuminance of the stimuli was equated across all observers, these age-related losses in discrimination are attributable to neural changes. Analyses of these data reveal a significant change in Weber fraction across adulthood for a chromatically opponent pathway receiving primarily antagonistic signals from middle-wavelength-sensitive and long-wavelength-sensitive cones but not for a short-wavelength-sensitive cone pathway.

1. INTRODUCTION

Results from tests involving color matching^1–3 and hue discrimination^4–6 have consistently shown age-related declines in color vision. Decreases in retinal illuminance caused by senescent changes in the crystalline lens and pupil lead to tritanlike behavior as measured by the Moreland color-match equation⁷ and the FM-100 hue test.⁶ However, more recent work has demonstrated that neuronal changes may also contribute to some of these observed losses in chromatic discrimination. For example, work by Schefrin et al.⁸ suggests that elevations in discrimination thresholds along individually determined tritan axes in older individuals can be ascribed either to increased rates of neural noise or to the relative inability of photoreceptors to capture quanta effectively. The question remains whether these types of neural changes, or others, can help to explain similar age-related losses in chromatic discrimination in portions of the spectrum subserved by opponent pathways that receive antagonistic inputs dominated by M and L cones.

A second goal of this study was to measure wavelength discrimination functions across the spectrum in a classical manner to permit comparisons with other data on wavelength discrimination that have not taken account of observer age. Thus wavelength discrimination functions were measured across the spectrum with criterion-free methods and individually determined isoluminant monochromatic lights. The results show small but consistent elevations in thresholds for older compared with younger observers.

2. METHODS

A. Observers

Wavelength discrimination functions were determined for four younger (mean 30.9 years) and four older (mean 72.5 years) observers ranging from 22 to 78 years of age. Two of the authors were included in the younger group; their data are consistent with those of na¿ve observers. They were aware of the purpose of the experiments but were provided no feedback about their results during testing. All observers reported a negative history of ocular and systemic disease, and none of them were taking medications known to interfere with ocular or neurological functioning. An optometrist evaluated the status of the retina and ocular media of all subjects by using direct ophthalmoscopy. These evaluations failed to show any evidence of retinal disease, and only a few scattered lenticular opacities were noted in two of the older subjects. All subjects were normal trichromats, according to results obtained with the Farnsworth Panel D-15 test, the F-2 plate, and the American Optical Corporation Hardy–Rand–Rittler pseudoisochromatic plates. All observers except CB possessed a best-corrected Snellen acuity of 20/25 or better in the tested eye. The best-corrected Snellen acuity for subject CB was equivalent to 20/27.

B. Apparatus

Stimuli were presented in Maxwellian view, using a conventional five-channel system. The optical system used two sources (300-W and 1000-W xenon lamps) powered by regulated dc power supplies. Water baths filtered infrared radiation. Optical elements of this system included front-surfaced mirrors and doublet achromat lenses. Lights from various channels were combined by beam splitters or by a rotating sectored mirror that produced square-wave flicker for the heterochromatic flicker photometry (HFP) measurements. Electromechanical shutters were placed in the paths of the combined light channels at various focal points. The radiance of each channel was controlled by placing neutral density filters and wedges in collimated portions and at focal points of the light beam, respectively. Wedges were under either manual or computer control. Their positions were monitored by potentiometers and a linear readout system connected to a computer through an analog/digital circuit board. The final combined beam was passed through an individually determined spherical corrective lens and an air-spaced achromatizing lens. The diameter of the final Maxwellian image was 2 mm at the plane of the pupil. A bite bar and forehead rest assembly with movements in three orthogonal directions was used to align subjects with this final Maxwellian image. Adjustments of the subject’s position relative to the achromatizing lens were made so that colored fringes could no longer be perceived around the borders of the stimulus. In addition, the position of the observer’s pupil could be monitored through an auxiliary optical channel.

The spectral compositions of the stimuli were shaped by holographic grating monochromators (Instruments S-A, model H-20), which had entrance and exit slits adjusted to produce bandwidths < 5 nm at half-power. Motor assemblies (Instruments S-A, model 73000019A) under computer control were used to position the gratings that produced the monochromatic lights. The wavelengths of the stimuli were in all cases within 0.25 nm of the intended nominal wavelength.

C. Calibrations

Radiometric measurements of spectral lights and calibrations of neutral density wedges and filters were made with a P-I-N 10 silicon photodiode and linear readout system (United Detector Technology, Optometer 81) previously calibrated against a standard traceable to the National Institute of Standards and Technology. Photometric calibrations at 570 nm were made with a Minolta luminance meter (LS-100) and barium sulfate plate and were subsequently converted into units of retinal illuminance, trolands (Td), with Westheimer’s method.⁹ Troland levels at other wavelengths were based on individually measured HFP functions.

Wavelength calibrations of the monochromaters were confirmed by using a He–Ne laser and a series of Mercury line interference filters. A spectroradiometer/photometer (Photo Research, Model PR703-A) was used to measure the chromaticity coordinates of monochromatic and mixtures of spectral lights.

D. Procedures

1. Measurement of Luminous Efficiency

In separate sessions, individual luminous-efficiency functions were measured for each subject in order to equate the monochromatic stimuli in terms of their retinal illuminance. The luminosities of test wavelengths relative to a 2°, 10-Td, 570-nm light standard were determined with HFP. The standard and the variable test lights were presented in alternating square-wave fashion at 15 Hz. Following 15 min dark adaptation, observers adjusted the radiance of the foveally viewed test lights until the perceived flicker associated with the paired lights was minimized. The isoluminant point for each test light was based on the geometric mean of four settings. The relative luminous efficiencies of the monochromatic test lights were measured in 10-nm steps from 420 to 480 nm and in 20-nm steps from 500 to 680 nm. Test lights were presented in a randomized order.

A smooth luminous-efficiency function was fitted to each subject’s HFP data on the basis of a least-squares minimization obtained by varying parameter values for the ratio of M to L cones and the densities of the lens and the macular pigment as tabulated by Vos.¹⁰ In the main experiment, these individual functions were used to calculate the radiance necessary to equate all monochromatic test lights in terms of their retinal illuminance to the 10-Td, 570-nm standard. On the basis of the previous work of Werner¹¹ and Norren and Vos,¹² we calculated the difference in optical density of the ocular media at 570 nm between modeled observers of 31 and 72 years, the respective mean ages of our younger and older subjects, to be only 0.03 log unit. Thus we assumed that the retinal illuminance of the stimuli was approximately equated across all observers.

2. Wavelength Discrimination

Wavelength discrimination thresholds were measured with a spatial, two-alternative forced-choice method combined with a two-down, one-up staircase procedure. Threshold was defined by the geometric mean of the last four of six reversals and corresponded to the 71% correct point of the psychometric function. The stimulus consisted of a circular 2° bipartite field vertically divided by a dark, 10 arc-min gap.

Before each test session, observers dark adapted for 10 min. Discrimination thresholds associated with multiple test wavelengths were measured one at a time within a single session. During a test trial for a particular wavelength, the subject initially viewed two isomeric hemi-fields for 4.5 s. Then the wavelength of one of the two hemifields was increased at a constant rate for a period of at least 4.5 s and held steady for 1 s. The rate of change in wavelength depended on the step size predetermined by the computer. To offset variations in retinal illuminance that accompanied increases in wavelength, the setting of a neutral density wedge, located in the appropriate test channel, was continually updated every 0.25 s. Following the offset of the stimulus, the subject depressed one of two buttons to indicate which hemifield changed in hue. Presentations of the stimulus were separated by at least 8 s. With this method, it should be pointed out that even though changes in wavelength were accomplished at near isoluminance, the two hemifields did not appear equally bright when threshold measurements required large changes in wavelength (e.g., at the spectral extremes). However, since luminance was held essentially constant, any brightness change must be based primarily on variations in chromatic signals.^13,14

Wavelength discrimination thresholds were measured in two sessions, approximately 2 h in length, held on different days. In order to provide well-defined wavelength discrimination functions, approximately 18 measurements were made for each younger observer. However, because of the relatively arduous nature of this task, only 9–12 measurements were collected from each older observer. For older observers, data were initially collected at six spectral loci (410, 440, 480, 510, 550, and 580 nm) that approximated local maxima and minima of published wavelength discrimination functions^15–22 and at 610 nm. On the basis of this preliminary data set, we measured discrimination thresholds at additional wavelengths that we thought would help define the shape of the older subjects’ wavelength discrimination functions.

3. RESULTS

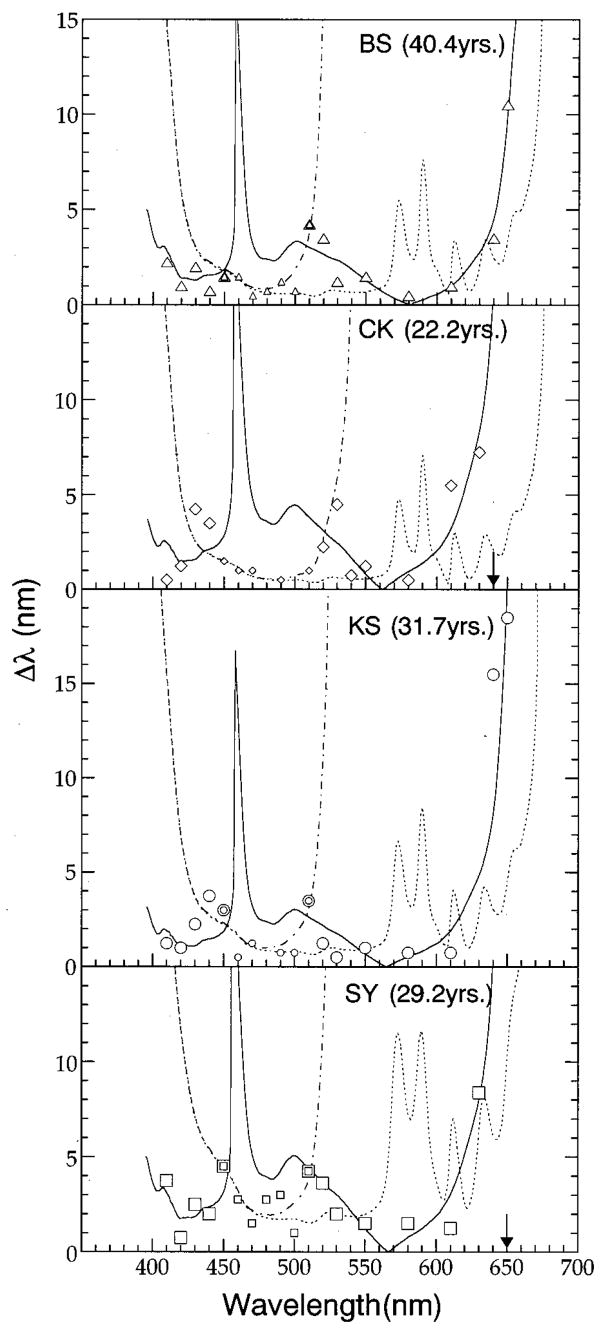
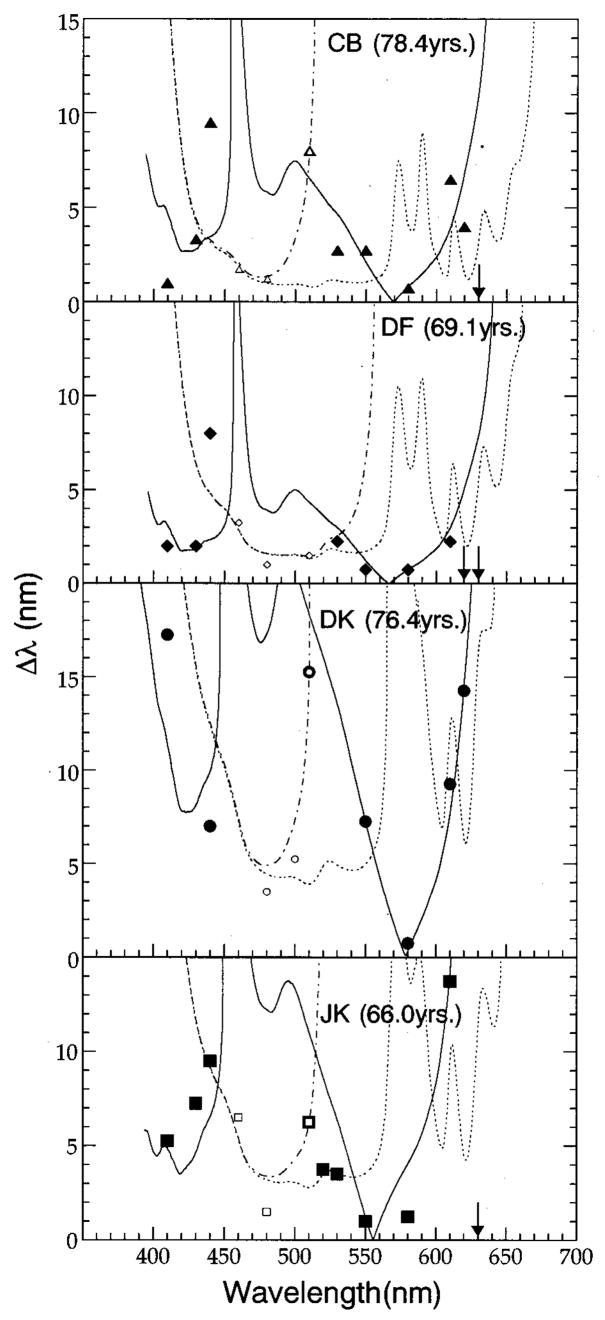
Each panel in Figs. 1 and 2 shows a wavelength discrimination function for an individual observer (younger in Fig. 1, older in Fig. 2). Discrimination thresholds, represented by the various symbols, were defined as the average difference, in nanometers, between the standard wavelength shown on the abscissa and the wavelength at which a subject could first detect a change in appearance between the two halves of the bipartite field. Within each panel, smaller and larger symbols represent discrimination thresholds that are assumed to be mediated by a short-wavelength-sensitive- (S-) cone pathway and a pathway that receives antagonistic inputs primarily from middle-wavelength sensitive (M) and long-wavelength sensitive (L) cones, respectively. Arrows correspond to wavelengths at which we were unable to determine thresholds. Although small differences in brightness between the two halves of the stimulus may have had a minor influence on the subject’s threshold settings, the Δλ versus λ functions obtained from the younger observers are consistent with wavelength discrimination functions previously reported in the literature.^15–22 An examination of Figs. 1 and 2 reveals that all subjects demonstrated local minima between 460 and 500 nm and between 550 and 610 nm. In addition, with the exception of subject DK, these observers exhibited a third distinct minimum at or below 420 nm. The curves in each panel of these figures are fits to each set of data based on a modified version of Boynton and Kambe’s²³ model of chromatic discrimination that incorporates the outputs from chromatic mechanisms dominated by S cones (dotted and dashed–dotted curves) and M and L cones (solid curves). The qualitative and quantitative aspects of this model and how the model was applied to the data are described in Section 4.

Fig. 1.

Wavelength discrimination thresholds (Δλ) plotted as a function of wavelength for four younger subjects. Smaller and larger symbols represent thresholds assumed to be mediated by an S-cone pathway and an L/M chromatically opponent pathway, respectively. Dashed–dotted and dotted curves represent thresholds calculated with Eq. (1) that incorporate or exclude, respectively, a noise parameter within an S-cone pathway. The solid curves represent thresholds calculated for the modeled L/M-cone pathway with Eqs. (3) and (4). Arrows correspond to standard wavelengths at which thresholds could not be determined.

Fig. 2.

Wavelength discrimination thresholds for four older subjects. All other details are the same as in Fig. 1.

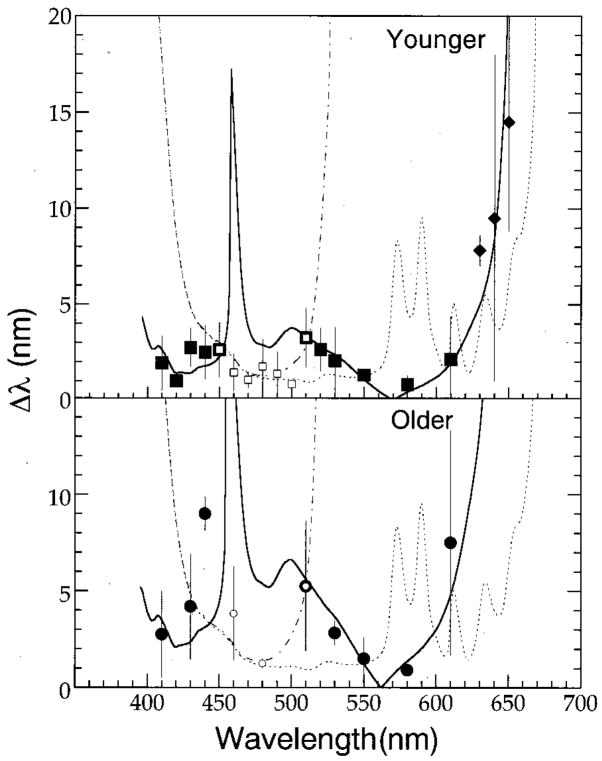
Mean wavelength discrimination functions for the two groups of observers are shown in separate panels in Fig. 3. Because wavelength discrimination thresholds were not measured at all wavelengths for all observers, the squares and diamonds in the upper panel represent mean thresholds for at least three and two of the younger observers, respectively. In the lower panel, the symbols represent mean thresholds for the older observers. Because subject DK’s data were so different from the other three cohorts, his results were excluded in calculating mean thresholds for the older observers. In each panel, error bars denote ±1 standard deviation of the mean. The functions passing through the mean data represent thresholds predicted by a model described in Section 4.

Fig. 3.

Mean wavelength discrimination thresholds for four younger and three older individuals shown in Figs. 1 and 2. Older observer DK is excluded for the mean. Error bars denote ±1 standard deviation. Diamonds in the top panel represent mean thresholds obtained from two of four observers. Smaller open symbols denote mean thresholds for an S-cone mechanism. Dashed–dotted and dotted curves represent thresholds calculated with Eq. (1) that incorporate or exclude, respectively, a noise parameter within an S-cone pathway. When the model was applied to the mean thresholds, the Weber fraction equaled 0.096 and the values for parameter CS_n for younger and older observers were 1.4 and 2.7, respectively. Larger symbols and solid curves denote mean thresholds and calculated thresholds [Eqs. (3) and (4)] for an L/M-cone chromatically opponent pathway. (See text and Tables 2 and 3 for details).

As can be seen in Fig. 3, there was a small but consistent difference in Δλ between the younger and older groups of observers. These differences in discrimination thresholds between younger and older observers appear to be smaller around the aforementioned minima and tend to increase at wavelengths higher and lower than these spectral locations. For example, at or near local minima of 420, 490, and 580 nm the average difference between younger and older observers was approximately 0.6 nm, whereas at local maxima at or near 440 and 610 nm the average difference between younger and older observers was approximately 5.9 nm. These latter differences in discrimination are statistically significant [unpaired t-test; p(one-tail) < 0.05].

4. DISCUSSION AND MODELING

We interpret the demonstrated age-related losses in wavelength discrimination as being due to receptoral and/or neural changes, because age-related changes in ocular media densities were compensated by equating the stimuli individually in terms of retinal illuminance. This conclusion is consistent with our previous work⁸ in which we investigated chromatic discriminations along individually determined tritan axes. However, these results are somewhat different from earlier findings by Ruddock,²⁴ who suggested that there were no age-related changes in wavelength discrimination when subjects were tested by a spatial forced-choice procedure. Perhaps this discrepancy between the two studies may be due to the small number of subjects tested with a forced-choice procedure in both studies along with individual variations in performance as can be seen in our data.

While quantitative models of wavelength discrimination differ in their description of how cone signals are antagonistically combined at more proximal sites in the visual system, it is generally assumed that at least two chromatically opponent pathways^25,26 mediate discrimination thresholds. Furthermore, on theoretical grounds,^25,27 wavelength discrimination functions obtained from presumed congenital tritanopes^28,29 and under experimental conditions that promote small field tritanopia,¹⁸ it appears that the differential stimulation of an S-cone pathway mediates discrimination thresholds over a narrow band of the spectrum from approximately 450 to 510 nm. Thresholds within other portions of the spectrum are thought to be mediated by a chromatic pathway that receives antagonistic inputs from M and L cones along with, perhaps, some minor input from S cones.^30,31 In the modeling that follows, M, and L represent the normalized cone fundamentals of Smith and Pokorny.³² The relative heights of the L- and M-cone sensitivity functions were adjusted so that their sum approximates Judd’s modified V(λ) function. The height of the S-cone sensitivity function, S, was normalized at 498 nm such that L + M = S.^23,33

A. Model of Contributions of an S-Cone Mechanism to Wavelength Discrimination

Previously we were able to interpret chromatic discriminations mediated by an S-cone mechanism within the context of a model put forward by Boynton and Kambe²³ in which the relation between discrimination thresholds, ΔS, and the amount of S-cone stimulation, S, is described as

$$\mathrm{\Delta }S/{(S+C{S}_n)}^a=W,$$ (1)

or, equivalently (in the case of a = 1),

$$(1/C)\mathrm{\Delta }S=W[(1/C)S+S_n]$$ (2)

Here S_n represents the amount of spontaneous noise occurring before sites of light adaptation within an S-cone pathway, and W is the limiting Weber fraction. The exponent a is a slope scalar of the function in logarithmic coordinates, and C is a parameter that scales either the amount of spontaneous noise within the S-cone pathway [Eq. (1)] or the extent of light adaptive gain changes that take place in the same visual pathway [Eq. (2)].⁸ These equations were used for descriptive purposes to fit the wavelength discrimination functions in Figs. 1–3.

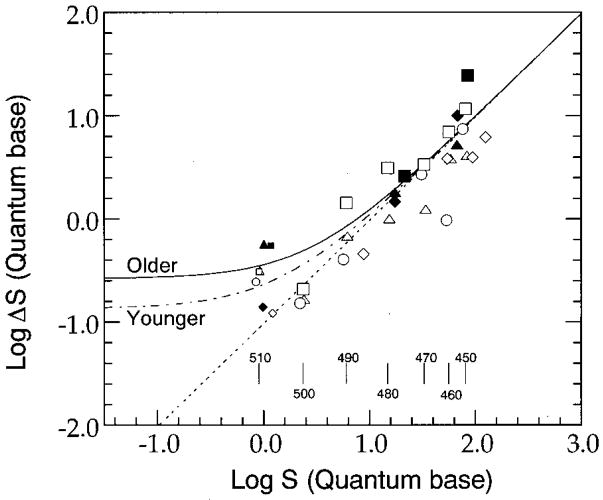
In order to determine the Weber fraction associated with an S-cone pathway that we presume mediates wavelength discrimination thresholds between 450 and 510 nm, we present data from Fig. 3 in Fig. 4 for individual observers plotted in terms of S-cone stimulation.³⁴ Open and solid symbols represent thresholds for individual older and younger observers, respectively. Symbol shapes in Fig. 4 denote individual observers corresponding to those in Figs. 1 and 2. S-cone stimulation is based on the number of quanta incident on the retina after adjustment for the densities of the ocular media and macular pigment. Larger symbols denote thresholds in terms of S-cone excitation measured between 450 and 500 nm, and smaller symbols denote those measured at 510 nm. The dotted line passing through the data sets represents a linear-regression fit to the data collected between 450 and 500 nm only, from both the older and the younger observers. Descriptive statistics for the samples and parameters for the least-squares linear-regression equations are summarized in Table 1. The slopes associated with each function suggest that both groups of subjects approximate Weber-like behavior under our experimental conditions. In addition, multiple regression analyses indicated that there was no significant interaction between age and the independent variable, S-cone stimulation. These results imply that there is no significant difference in the Weber fraction of an S-cone mechanism for younger (mean 0.076) and older (mean 0.12) observers. Therefore we performed a linear regression on the combined data between 450 and 500 nm and determined the Weber fraction to be 0.096. The fits with the common Weber fraction, 0.096, are denoted by dotted curves in both panels in Fig. 3.

Fig. 4.

Differential excitation of S cones at threshold as a function of S-cone simulation. Open and solid symbols represent thresholds from younger and older observers (except observer DK), respectively. Thresholds from individual observers are represented by the same-shaped symbols as in Figs. 1 and 2. Larger symbols and smaller symbols denote thresholds between 450 and 500 nm and thresholds at 510 nm, respectively. The dotted line represents a linear-regression fit to data between 450 and 500 nm obtained from both older and younger observers. Dashed–dotted and solid curves denote the fits obtained by the model with the common Weber fraction, 0.096, and the values for parameter CS_n for younger and older observers, 1.4 and 2.7, respectively. Vertical bars at the bottom of the figure denote the amount of S-cone stimulation at each standard wavelength calculated with the averaged luminous-efficiency function.

Table 1.

Descriptive Statistics and Parameters of Linear Regression As a Function of Pathway Stimulation for Discrimination Thresholds

Condition	Slope	Intercept	r	F	n
S cone, younger	0.89	−0.97	0.90	83.42a	21
S cone, older	1.34	−1.44	0.93	24.84a	6
L/M, younger	0.88	−1.36	0.66	33.22a	47
L/M, older	1.00	−1.02	0.69	20.96a	25

^aP < 0.05.

These results are consistent with those of our previous study⁸ in terms of the relatively large variation (approximately 0.03–0.43) and no significant relation to age in the Weber fractions for threshold discriminations measured along individually determined tritan lines. The Weber fraction, 0.096, determined in this study is reasonably close to the value of 0.17 and falls within the range of individual values determined for this parameter in our previous work.⁸ In addition, the Weber fraction found in this study falls between values previously reported by Boynton and Kambe²³ (18%) and Yeh et al.³⁴ (3%). These results thus support data from previous studies that show that increases in S-cone stimulation lead to elevations in discrimination thresholds mediated by an S-cone pathway.^35,36 Finally, thresholds for the two groups of observers appear to be approximately the same over a 0.7-log-unit range of S-cone excitation. This result is similar to findings previously collected in this laboratory that demonstrated a decline in age-related differences in chromatic discriminations along individually determined tritan axes as the level of S-cone stimulation was increased.⁸

Using Eq. (1), we performed a second analysis in an effort to estimate the possible contributions of spontaneous noise present within the tested S-cone channel. Initially we fitted a linear version of Eq. (1) to a subgroup of each individual data set shown in Figs. 1 and 2, represented by the smaller symbols, assuming no noise in an S-cone pathway. We obtained individual Weber fractions without a noise term for the best fit, applying a least-squared-error criterion to the individual data between 450 and 500 nm in wavelength coordinates. The calculated thresholds for this model are represented by the dotted curve in each panel, and the resultant Weber fractions are presented in Table 2. In our previous study,⁸ we found that the noise term associated with an S-cone pathway was approximately five times greater for older than for younger groups of observers. In an effort to determine the amounts of noise present in an S-cone pathway for subjects in this experiment, we applied a second version of Eq. (1) to a slightly expanded data set that included wavelengths from 450 to 510 nm. (Because wavelengths beyond 500 nm stimulate S cones to a lesser extent, the influence of noise should be greater on thresholds at those wavelengths than at shorter wavelengths contained in this data set.) In this modeling we maintained the values of the Weber fractions shown in Table 2 and included the parameter for noise given in the equation. The predicted thresholds for the latter model are represented by the dashed–dotted curve in each panel of Figs. 1 and 2, and the values for the noise parameter are given in Table 2. As shown in the table, there is little difference in the magnitudes of modeled noise between these two groups of observers. Two explanations that possibly underlie the discrepancy between our two studies are (1) the lack of clarity at these relatively longer wavelengths regarding which chromatic mechanism or combination of mechanisms mediates threshold discriminations and (2) the fewer number of subjects that were tested in the present study.

Table 2.

Parameter Values for Model Fits of Eq. (1) to Data in Figs. 1–3

Observers	Weber Fraction (W)	Noise (CSn)
Younger Observers
BS	0.059	4.0
CK	0.050	1.2
KS	0.074	2.1
SY	0.14	1.0
Mean	0.082 (SDa 0.037)	2.0 (SDa 1.2)
Average Younger Observers
With W for younger observers	0.076b	2.2
With common Weber	(0.096)c	1.4
Older Observers
CB	0.085	5.7
DF	0.13	0.072
JK	0.24	1.1
DK	0.32	0.93
Meand	0.15 (SDa 0.066)	2.3 (SDa 2.4)
Average Older Observers
With W for older observers	0.12b	2.0
With common Weber fraction	(0.096)c	2.7
All Observers
All observers	0.096b	—e

^aStandard deviation.

^bThis value is obtained from the fit in the log S versus log ΔS coordinates (Fig. 4). (See text for details).

^cThis value is the mean of all observers. (See text for details.)

^dThe data of observer DK were not included in the calculation of the mean values. (See text for details.)

^eThe value is not calculated.

To analyze the averaged data set for each group of observers in Fig. 3, we used the common Weber fraction, 0.096, obtained in S-cone excitation coordinates³⁴ between 450 and 500 nm. As with the fits for the individual data, the noise term is introduced in Eq. (1) and with the same Weber fraction obtained for the data expanded to 510 nm of each observer group, specified in wavelength coordinates. The values of the noise are presented in Table 2. The solid and the dashed–dotted curves in Fig. 4 denote the fits obtained by the model with the common Weber and the noise terms. As shown in Fig. 4, the amount of noise in Eq. (1) in one data set is determined by only one threshold datum at 510 nm, so this is not necessarily the best method in terms of determining the individual noise level, compared with the direct measurement on the tritan axis in our previous study.⁸

B. L- and M-cone Mechanisms with Small S-Cone Contributions

In Fig. 5, discriminations mediated by a chromatically opponent pathway that receives input primarily from M and L cones are plotted in terms of a modeled response function F. Quantitative predictions associated with this model are given by Eqs. (3) and (4):

$$F=\lfloor \alpha M-L\rfloor +\lfloor L-\alpha M\rfloor ,$$ (3)

$$\mathrm{\Delta }F/(F+C_F)=W.$$ (4)

Fig. 5.

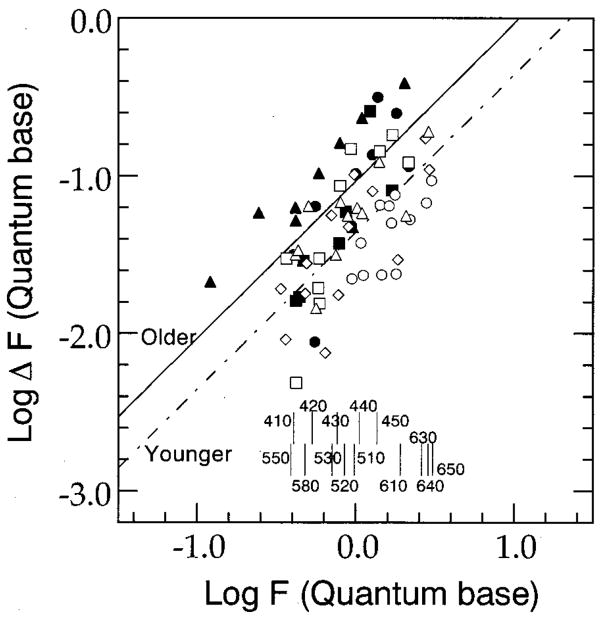
Differential response of function F [Eq. (3)] at threshold as a function of F. Open and solid symbols represent thresholds below 450 and above approximately 500–510 nm from younger and older observers (except observer DK), respectively. Thresholds from individual observers are represented by the same-shaped symbols as in Figs. 1 and 2. The dashed–dotted line and the solid line represent linear-regression fits to data obtained from older and younger observers with the Weber fraction, 0.044 and 0.093, respectively. Vertical bars at the bottom of the figure denote the response of function F at each standard wavelength calculated with the averaged luminous-efficiency function and averaged α, 1.9.

Here W represents the Weber fraction and C_F is a parameter that depends on the amount of S-cone stimulation and luminance of the stimulus. (See Appendix A for details.) The brackets in Eq. (3) indicate that the opponent responses undergo half-wave rectification. Thus over the entire visible spectrum it will never be the case that the two chromatically opponent terms will simultaneously contribute to the value of F. In this respect, the rectification of the opponent responses is similar to an approach taken by Thornton and Pugh³⁷ to model detection thresholds mediated by a red/green opponent channel.

The solid and the dashed–dotted lines in Fig. 5 represent linear-regression fits to the data, collected below 450 and above 500 (or 510) nm denoted by larger symbols in Figs. 1 and 2, from the older and the younger observers, respectively. The parameters associated with these fits are shown in Table 3. As can be seen from the slopes of the regression lines, both groups of subjects exhibit Weber-like behavior. However, a multiple regression analysis revealed that when we controlled for channel activity, log F, there was a significant difference between age groups (F_(1,69) =18.48; p < 0.0001). This analysis indicates that there is an age-related increase in the Weber fraction associated with these two groups of observers. (This effect is represented by the vertical separation between the two sets of data.) Thus, solid curves in Fig. 3 are determined by Eqs. (3) and (4) with these different Weber fractions. In addition, based on the linear regressions, the Weber fraction for the four younger observers is approximately 4% and is comparable to the Weber fraction (a concurrent 1% change in opposite directions for Land M-cone stimulation) determined by Boynton and Kambe.²³

Table 3.

Parameter Values for Model Fits of Eqs. (3) and (4) to Data in Figs. 1–3

Observers	Weber Fraction (W)	Balance Factor (a)
Younger Observers
BS	0.031	2.4
CK	0.063	1.8
KS	0.040	1.9
SY	0.064	1.9
Mean	0.050 (SDa 0.015)	2.0 (SDa 0.25)
Average Younger Observers
With W for younger observers	0.044b	(2.0)c
Older Observers
CB	0.088	2.0
DF	0.063	1.9
JK	0.22	1.7
DK	0.20	2.3
Meand	0.12 (SDa 0.069)	1.8 (SDa 0.22)
Average Older Observers
With W for older observers	0.093b	(1.8)c

^aStandard deviation.

^bThis value is obtained from the fit in the log F versus log ΔF coordinates (Fig. 5). (See text for details.)

^cThis value is the means of each observer group. (See text for details.)

^dThe data of observer DK were not included in the calculation of the mean values. (See text for details.)

The model defined by Eqs. (3) and (4) was best fitted by using a least-squared-error criterion to the individual and the mean sets of data collected below 450 nm and above approximately 500–510 nm in wavelength coordinates. The solid curves in Figs. 1 and 2 represent the modeled thresholds based on this procedure. In these fitting procedures the parameters α and W were allowed to vary, whereas the parameter C_F equaled zero. The values for the free-fitting parameters are shown in Table 3. An examination of these values indicates that the mean Weber fraction taken from the individual fittings is 2.4 times greater for the older observers than for the younger observers. Thus, two different analyses of discrimination thresholds presumed to be mediated by a chromatically opponent L/M-cone pathway are consistent in showing an increase in the Weber fraction associated with the older observers.

C. Brightness of Stimuli

The stimuli in this experiment were equiluminant, so it might be argued that changes in brightness rather than hue mediated perceived changes in wavelength. However, we believe that this possibility is unlikely for two reasons. First, there was no consistent change in the direction of brightness associated with the test field. That is, depending on the spectral locus of the standard wavelength, increases in the wavelength of the test field may result in the test field appearing either brighter or dimmer. In addition, Le Grand^38,39 noted that over small changes in wavelength, as was the case for most of the wavelengths tested in this experiment, the shape of the brightness function measured by the step-by-step method closely resembles the shape of the luminous-efficiency function.

5. CONCLUSION

Wavelength discrimination functions were measured for small groups of younger and older observers in a manner that controlled for age-related changes in retinal illuminance and criterion. Statistical analyses reveal a significant difference between young and old in the Weber fraction for an L/M-cone but not for an S-cone mechanism. Also, within the older group of observers, it appears that the Weber fraction is approximately the same for the two chromatic channels for discrimination of spectral lights.

APPENDIX A: RATIONALE FOR INSTANTIATION OF THE MODEL

This appendix summarizes how Eqs. (3) and (4) were obtained from the original Boynton–Kambe model. The original equation²³ is

$$\mathrm{\Delta }L/[(L+M)+0.8\mid L-2M\mid +\beta S]=W.$$ (A1)

Here W represents the Weber fraction and ΔL is the change in L-cone response necessary to discriminate between two stimuli. In our modified model, we substituted the fitting parameters α and k for the constants 2 and 0.8, respectively. By simple transformations, we obtained

$$[(\mathrm{\Delta }L-\alpha \mathrm{\Delta }M)+\alpha \mathrm{\Delta }I]/[\mid L-\alpha M\mid +(1/k)I+(\beta /k)S]=k(1+\alpha )W.$$ (A2)

Here, I is response of a luminance channel (=L +M). In our experimental procedure, I remained constant and ΔI was zero. If we assume that the contribution of S cones to the modeled chromatically opponent channel is much smaller than L- and M-cone signals,³⁵,³⁶ Eq. (A2) becomes

$$(\mathrm{\Delta }L-\alpha \mathrm{\Delta }M)/[\mid L-\alpha M\mid +C]=W_2.$$ (A3)

Here C =(1/k)I + (β/k)S_0, and W₂ is k(1 + α)W. Unlike the model of an S-cone pathway in which discriminations are mediated by the simulation of a single cone type, Eq. (A3) suggests that discriminations mediated by an L/M-cone pathway depend on the opponent interaction of two cone types. See Ref. 40 for details of the model of chromatic and achromatic responses and Ref. 41 for the quadratic equation used to calculate threshold in terms of wavelength. We determined parameters in the quadratic equation in 1-nm steps over a range of 20 nm. For example, the parameters for the model calculation of the threshold at 543 nm are determined to give the best fits to sensitivities for each cone type between 543 and 563 nm. Thus the quadratic equation is reasonably accurate for translating the wavelength data to cone excitations and vice versa.