Building trophic modules into a persistent food web

Abstract

Understanding what maintains species and perpetuates their coexistence in a network of feeding relationships (the food web) is of great importance for biodiversity conservation. A food web can be viewed as consisting of a number of simple subunits called trophic modules. Intraguild predation (IGP), in which a prey and its predator compete for the same resource, is one of the best-studied trophic modules. According to theory, there are two ways to yield a large persistent system from such modules: (i) to use persistent subunits as building blocks or (ii) to arrange the subunits in a way that externally supports the nonpersistent subunits. Here, I show that the complex food web of the Caribbean marine ecosystem is constructed in both ways. I show that IGP modules, which convey internal persistence because of the fact that prey are superior competitors for the resources, are overrepresented in the Caribbean ecosystem. The other modules, consisting of competitively inferior prey, are not persistent in isolation. However, competitively inferior prey in these modules tend to receive more advantage from extra-module interactions, which allows persistence of the IGP module. In addition, those exterior interactions tend to be provided by intrinsically persistent IGP modules to prevent cascading extinction of interacting IGP modules. The food web can be viewed as a set of interacting modules, nonrandomly arranged to enhance the maintenance of biodiversity.

The maintenance mechanisms of interacting species in nature have been a central issue in ecology (1–3). Theory has related the coexistence of interacting species to the network structure of species interactions (3), based on analyses of isolated and simple ‘modules’ (4) often consisting of only three or four species (5–7). However, there are no isolated modules in real nature. Trophic modules are embedded and interact with a larger community (8–10), and thus, their dynamics should be continuously influenced by the extra-module interactions. The gap between the module-based approach and real, complex food web leaves unanswered the question of how relevant module-based theory is to actual food webs (9, 11).

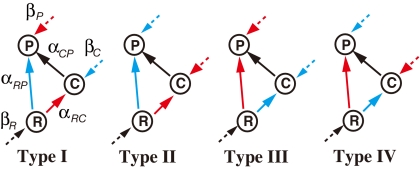
Here, through an analysis of trophic modules embedded in a real, complex food web, I present evidence that both the structure of individual modules and how they are combined contribute to species coexistence in a complex food web. An intraguild predation (IGP) module (12–19) is the best-studied trophic module, in which a prey (IGPrey; C) and its predator (IGPredator; P) compete for the same resource (R) (Fig. 1). Theory states that IGP modules will collapse unless the prey can outcompete the predator for the resource (13). However, this is true only if the module is isolated. If embedded in a larger community, an intrinsically nonpersistent module may persist with the support of exterior forces such as those supplied by an extra-module resource (17–19). Thus, an IGP module can be maintained via two distinct mechanisms (17, 18): one via the internal structure (competitive superiority of IGPrey) and one via extra-module forces provided by the surrounding communities.

Fig. 1.

The four types of IGP modules. An IGP module consists of a shared resource (R), an IGPrey (C), and an IGPredator (P), each of which may interact with the surrounding communities. IGP modules are classified into the four groups (Types I–IV) according to the internal structure (solid arrows) and the exterior structures (dotted arrows). Type I modules are only intrinsically persistent; Type II modules are intrinsically and externally persistent; Type III modules are intrinsically and externally nonpersistent; and Type IV modules are only externally persistent. The more and less advantageous interactions are in red and blue, respectively.

Combining a theoretical approach based on a dynamic model of IGP modules and a null model analysis (20–22) applied to the large Caribbean food web (20, 23) (see Materials and Methods), I show (i) that IGP modules with an internal structure that promotes persistence are overrepresented; (ii) that IGP modules with an internal structure that could not persist in isolation are allowed to persist by virtue of exterior interactions with the surrounding community; and (iii) that the external interactions are provided by intrinsically persistent IGP modules to prevent the cascading breakdown of the IGP modules. This study provides the basis to understanding a complex food web as a set of interacting simple modules, nonrandomly arranged to enhance the maintenance of biodiversity.

Results and Discussion

Classification of IGP Module Based on Their Maintenance Mechanisms.

A necessary condition for the existence of equilibrium with all species present in an IGP module (termed hereafter “feasibility condition”) is given by:

where T_i is the mass-specific respiration rate of species i (i = R, C, P); α_ji, the functional response of predator i to prey j; β_i, the net effect of trophic interactions with the species other than R, C, and P on species i; and asterisks indicate values at equilibrium (see Materials and Methods). This condition does not necessarily assume that the community is maintained at the equilibrium. Feasibility is necessary for persistence of IGP modules even when species coexist in unstable conditions (16, 24). T_i/α_Ri* is the minimum resource level required for species i to persist, equivalent to the R* concept (25). A smaller R* indicates competitive superiority (13, 25). β_i*/α_Ri* is the net effect of exterior interactions on species i measured in terms of resource biomass. Note that the classical prediction that IGP modules do not persist with competitively inferior prey (T_P/α_RP* > T_C/α_RC*) (13) is given as a condition for the special case that β_i = 0.

Inequality 1 allows IGP modules to be classified into four groups (Type I–IV) (Fig. 1). The feasibility condition holds when the IGPrey is superior in resource competition (T_P/α_RP* > T_C/α_RC*) and receives more advantage from exterior interactions (β_P*/α_RP* < β_C*/α_RC*) than the IGPredator (Type II). When the prey is neither superior in resource competition nor does it benefit from exterior interactions (Type III), the IGP module is inevitably nonpersistent. When only one of the aspects is satisfied (Type I or Type IV), the feasibility condition may hold, but this depends on the magnitude of the internal and external interactions. Several authors have reached similar predictions on the complementary role of internal and external interactions in IGP module maintenance (17, 18).

IGP Modules in the Caribbean Food Web.

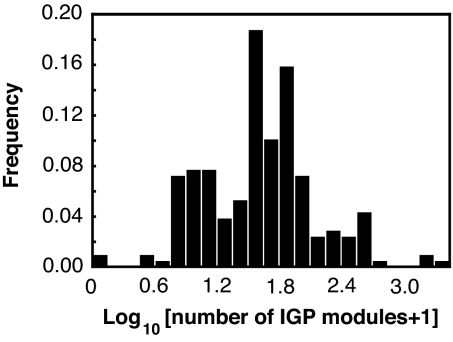
There are 4969 IGP modules distributed amongst the Caribbean food web with all except two teleost fish species, Opistognathus whitehurstii and Centropyge argi, belonging to at least one IGP module (Fig. 2). This implies that the persistence of IGP modules is actually relevant to the functioning of the entire system. The three species that belong to the largest number of IGP modules were sharks (Carcharhinus perezi, Galeocerdo cuvieri, and Carcharhinus falciformis belonging to 1503, 1339, and 1197 modules, respectively), which were IGPredators in most modules (1156, 1339, and 1011 modules). I conducted two analyses (Analyses I and II), in which the mass-specific respiration rates were estimated in different ways (see Materials and Methods for more details). The feasibility conditions for 980 and 4885 IGP modules were determined in Analysis I and II, respectively.

Fig. 2.

A species belongs to a number of IGP modules. The frequency distribution of the number of IGP modules to which a species belongs as either a resource, IGPrey, or IGPredator in the Caribbean food web (n = 208). The value ranges from 0 to 1503 (median = 28).

The IGP modules embedded in the Caribbean food web are classified into four module types (Type I-IV). This classification was based on the assumption that the Caribbean community represents, or is sufficiently close to, equilibrium and, thus, could be affected by temporal fluctuations inherent in natural populations. However, as the data (α_ji and β_i) of the Caribbean food web (20, 23) are quite unlikely to be biased in a way that systematically reverses the relative magnitude of T_i/α_Ri* or β_i*/α_Ri* for i = P or C in eqn. 1, the classification of IGP modules in the Caribbean food web would be adequate enough to serve for detection of the nonrandom patterns in food-web configuration.

Theory predicts that the Type III module, where an IGPredator is competitively superior and receives more advantage via external interactions, is inevitably nonpersistent. Thus, if there is a dynamic constraint in food-web configuration, the Type III module should be under-represented in the Caribbean food web. Indeed, null model analysis (Analyses I and II; see Materials and Methods) showed that the Type III module was less frequent than expected by chance (Table 1), suggesting that the representation of the module types may be constrained by their dynamics characteristics (26, 27).

Table 1.

Structural pattern in the Caribbean food web

Module type and ratio	Analysis 1 (86 fish species)			Analysis II (202 fish species)
	Observation	Randomized model		Observation	Randomized model
		Mean (SD)	P		Mean (SD)	P
Type I	691***	433 (30)	<0.0001	2940***	2097 (144)	<0.0001
Type II	78**	33 (19)	0.018	351	187 (121)	0.057
Type III	92***	246 (53)	0.9994	727***	1223 (156)	0.9992
Type IV	119**	268 (50)	0.9988	867***	1373 (148)	0.9997
Intrinsically persistent modules [Type I + II]	769***	466 (26)	<0.0001	3291***	2289 (68)	<0.0001
Extrinsically persistent modules [Type II + IV]	197*	301 (56)	0.9676	1218**	1562 (201)	0.9823
The level of compensation by exterior forces	2.81***	1.70 (0.13)	<0.0001	2.18***	1.66 (0.11)	<0.0001

P is the probability that a random replicate has larger values than the real food web The results are consistent between the two analyses, I and II.

*, P < 0.05 or P > 0.95;

**, P < 0.03 or P > 0.97;

***, P < 0.01 or P > 0.99.

Relative Roles of Internal and External Forces in Module Maintenance.

The structure of IGP modules was analyzed to estimate the relative roles of within- and extra-module forces in module maintenance. The numbers of modules with IGPrey competitive superiority (the intrinsically persistent module; Type I + II) and that of modules with IGPrey advantage via exterior interactions (modules made persistent through external interactions; Type II + IV) were counted and compared with those in the randomized model. Null model analysis showed that intrinsically persistent modules were over-represented, whereas modules that were persistent through external forces were under-represented in the Caribbean food web (Table 1). This implies that the IGP modules in the Caribbean food web tend to be made feasible by their internal structure, rather than by external forces.

The dominance of intrinsic persistence is explained on the basis of two well-documented constraints: bioenergetic-allometric theory (28) and feeding relationships (29, 30). Because mass-specific food consumption [(Q/B)_i] and respiration rate (T_i) follow similar allometric relationships with body mass [see supporting information (SI) Fig. S1], the minimum resource requirement, T_i/α_Ri (= T_iB_R/[(Q/B)_i(DC)_Ri]), should be independent of body mass and inversely proportional to the mass proportion of R in the diet, (DC)_Ri. On the other hand, an IGPredator tends to have more potential prey species and, thus, lower average values of (DC)_Ri than an IGPrey (Fig. S2), as predicted by the empirically derived food web model (29, 30). The abovementioned two constraints taken together can result in the observed competitive superiority of IGPrey (T_P/α_RP* > T_C/α_RC*). Actually, the prey number of an IGPredator is larger than that of an IGPrey in 92.9% of the intrinsically persistent modules, and (DC)_RC is larger than (DC)_RP in 97.7% of the intrinsically persistent modules. The prediction that the intrinsic persistence is attributable not to prey-predator metabolic difference but to their difference in (DC)_Ri is in contrast to the recent finding that the prey-predator metabolic difference plays a critical role in maintenance of trophic module (31) or whole food webs (32).

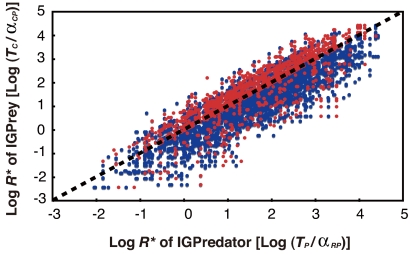
However, the under-representation of exterior interactions that allow modules to persist in the whole web does not mean that these forces are unimportant in module maintenance. The model predicts that if an IGP module is intrinsically nonpersistent (T_P/α_RP* < T_C/α_RC*), it is necessary for IGP module maintenance that the exterior interactions render more advantage to the IGPrey (β_P*/α_RP* < β_C*/α_RC*). This implies that the internal nonpersistent modules should be “favored” by external forces leading to module maintenance. To test this, I compared the fraction of modules with external persistence given internal nonpersistence of a module ([Type IV]/[Type III + IV]) with the fraction of modules with external persistence in the whole web ([Type II + IV]/[total]). This analysis shows that the intrinsically nonpersistent modules (Type III + IV) were 2.2–2.8 times more frequently accompanied by exterior interactions that provide more advantage to IGPrey, a force for external persistence, than in comparison to the average from overall IGP modules (Table 1 and Fig. 3). This level of interior–exterior structural association is unlikely to occur by chance, suggesting that the extra-module interactions are nonrandomly structured to compensate for internal nonpersistence.

Fig. 3.

Compensation of intrinsic nonpersistence by extra-module forces. Log R* of IGPredator is plotted against log R* of IGPrey. The broken line represents the equality that [log R* of IGPredator] = [log R* of IGPrey], the dots below which are intrinsically persistent because the prey is competitively superior. The red and blue dots are for modules where extrinsic forces promote persistence or not, respectively.

Nonrandom Combinations Between IGP Modules.

I then considered how the IGP modules, varying in their maintenance mechanisms, are combined to produce a complex food web. A Type IV module is intrinsically nonpersistent, but can persist by relying on the interactions of IGPrey and IGPredator with external communities. Therefore, if the extra-module force (β_R and β_C) that makes persistent the Type IV module is provided by other “neighboring” IGP modules, then a collapse of the neighboring modules may alter the strength of external force and, thus, lead to a cascading breakdown of the Type IV module, and consequently the food web. For long-term persistence of the system, the extra-module interactions should be provided by members of intrinsically persistent IGP modules to ensure more stable external forces. To test this pattern I analyzed the inter-module connection in the food web.

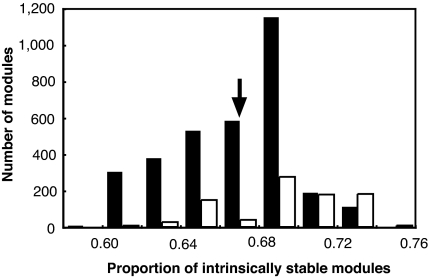
The proportion of intrinsically persistent modules in the modules that provide extra-module forces to each Type IV module ([Type I + II]/[all of the donor modules]) was compared with the proportion of intrinsically persistent modules ([Type I + Type II]/[total]) in the whole food web. Analysis using the 202-species data showed that 76.0% of the Type IV modules received extra-module forces from intrinsically persistent modules more than their global proportion, while such a bias occurred with only 54.4% of the intrinsically persistent modules (Fig. 4). This level of structural bias was unlikely to occur if interaction strengths were randomly assigned to trophic links (P = 0.0042; mean = 0.422, s.d. = 0.130). This indicates that the between module structure is also nonrandomly organized to prevent cascading breakdown of the IGP modules.

Fig. 4.

Proportion of exterior interactions provided by intrinsically persistent IGP modules. Presented is the frequency distribution of proportions of intrinsically persistent IGP modules in the modules that provide extra-module forces to intrinsically persistent modules (Type I + Type II; black bars) and Type IV (white bars) IGP modules in the Caribbean food web. The arrow indicates the proportion of intrinsically persistent modules in the whole food web.

Recent studies have shown that a food web, or more generally, a complex network can be viewed as a collection of simple modules with a characteristic frequency profile (8–10). Although the present study follows this idea, it is different from previous ones in three important ways. My study constitutes an attempt to analyze explicitly not only the structural forces within a module, but also the forces external to, and between modules (33) in a real complex network. Second, this study looked at a more quantitative aspect (i.e., interaction strength) of trophic module structure when evaluating the persistence of the community (but see 20). Third, these structural insights combined with the dynamic module-based theory lead to a finding that within- and extra-module structures maintain the entire system in concert, clearly suggesting that a complex food web is more than just a collection of individual modules. Given that intraguild predation is widespread among ecosystems (particularly marine and freshwater; 12), this conclusion would be widely relevant to many ecosystems. Understanding what maintains biodiversity in nature is not only a major goal of ecology, but also key to predicting the consequences of human-induced ecosystem changes. Given the complementary roles of the dynamical properties of the individual modules, and their combination, in biodiversity maintenance, this goal would not be achieved solely by understanding the modules in isolation or calculating their frequencies in the entire system. We need to know how dynamic modules are combined to produce the complex food webs that we see in nature.

Materials and Methods

The Model and Its Analysis.

The analysis of the Caribbean food web was conducted based on a simple dynamic model of the IGP module embedded in a larger community:

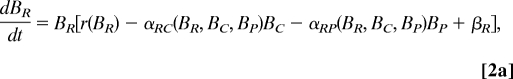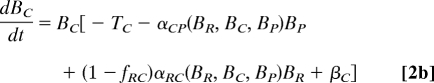and

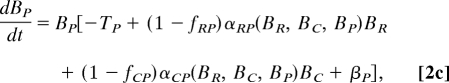where B_i is the biomass of species i; r(B_R), the mass-specific, net production rate of resource; T_i, the mass-specific respiration rate; α_ji, the functional response of predator i to prey j; f_ji, the fraction of loss as feces or urine when predator i consumes prey j, set to a constant (f = 0.15) (28); and β_i, the net effect of trophic interactions with the species other than R, C and P on species i, i.e., [biomass gains] − [biomass losses] = Σ_{sp. j∈sp. i's resources except P,C,R}(1 − f_ji)α_jiB_j − Σ_{sp. j∈sp. i's predator except P,C,R}α_ijB_j.

If the system in Eq. 2 has equilibrium with all of the species present (B_P*, B_C*, B_R* > 0), it should hold that: r(B_R*) − α_RC*B_C* − α_RP*B_P* + β_R* = 0, −T_C − α_CP*B_P* + (1 − f_RC)α_RC*B_R* + β_C* = 0, and −T_P + (1 − f_RP)α_RP*B_R* + (1 − f_CP)α_CP*B_C* + β_P* = 0. The latter two equations taken together lead to B_R* = (T_C + α_CP*B_P* − β_C*)/{(1 − f_RC)α_RC*} = {T_P − (1 − f_CP)α_CP*B_C* − β_P*}/{(1 − f_RP)α_RP*}, and thus, (T_C − β_C*)/{(1 − f_RC)α_RC*} < B_R* < (T_P − β_P*)/{(1 − f_RP)α_RP*}. Hence, by assuming that f_RC = f_RP (= f), inequality 1 follows without assuming any specific forms of r or αji.

The Food Web.

The published data of the Caribbean marine food web (20, 23) were analyzed. These data comprised both the benthic and the pelagic communities including 208 fish species, several invertebrate taxa, sea turtles, and sea birds. I focused on the IGP modules containing fish only, as they had been identified at species level. The data covered a wide range of biological parameters such as average body mass (m_i), biomass (B_i), and per capita interaction strength (α_ji), which allowed the present analysis.

The per capita interaction strength of predator i on prey j is estimated as the proportion of prey j biomass consumed by predator i per year (20), i.e., (Q/B)_i(DC)_ji/B_j, where (Q/B)_i is the total food consumption per unit biomass of species i, estimated based on empirical studies (34), and (DC)_ji is the mass proportion of species j in the diet of species i.

The annual mass-specific respiration rate is estimated by assuming the mass–balance relationship (23), [loss by respiration] = [gain by food consumption] − [loss by natural mortality]. Note that natural mortality was either cited from published literatures or estimated by means of an empirical model based on environmental temperature, body size, and growth coefficient (p. 27 in ref. 23), and its estimation was thus independent of predation mortality (Σ_{sp. j ∈ sp. i's predatorαijBj}). This allowed estimation of respiration rates of 86 fish species, for which (Q/B)_i and natural mortality data were available. Thus, the respiration rate estimated via the mass–balance relationship is independent of predation mortality, calculated based on trophic interactions, Σ_{j∈sp. i's predator}α_ijB_j).

The respiration rates of these species follows the scaling law, ln[T_i] = a · ln[m_i] + b (a = −0.161, b = 1.28, r² = 0.47), with the slope slightly more than the predicted value of −0.25 (28, 35) (see Fig. S1). The annual respiration rates of the other 116 fish species, for which the average body masses are available, were estimated using this allometric relationship resulting in respiration data for 202 species in total.

The annual mass-specific respiration rate (T_i) of 86 fish species, estimated based on the mass–balance relationship (23), was used in the analysis (Analysis I). As this consists of only 41.4% of all of the fish species, I performed a second analysis (Analysis II) using respiration rates from the remaining 116 fish species, estimated from a bioenergetic-allometric relationship (28, 35) (see Fig. S1), giving 202 fish species in total.

Null Model Analysis.

To determine the patterns in food-web configuration arising from the nonrandom arrangement of trophic links, (i) the observed numbers of each module type (Types I–IV, [Type I + II], [Type II + IV]) and (ii) the observed number of times the IGP modules with IGPredator competitive superiority is accompanied by exterior interaction advantageous to the IGPrey is more often than the overall average (the level of compensation by external forces; {[Type IV]/[Type III + IV]}/{[Type II + IV]/[total]}) in the Caribbean food web were compared with those in 10,000 replicates of a randomized model. In the randomized model, the topology of the food web was retained, but the interaction strengths between species were varied by random permutation of all of the interactions in the web. Thus, the prey-predator pairs and the frequency distribution of interaction strength in the original food web are preserved in the randomized model. The randomized model allowed evaluation of the probability that a pattern observed in the original web arises by chance (20–22). The probability that a random replicate has larger values than the real food web (P) was calculated for each value. If P < 0.05, the observed value is significantly higher than expected by chance; if P > 0.95, the observed value is significantly lower than expected by chance.