Theoretical Evidence for the Stronger Ability of Thymine to Disperse SWCNT than Cytosine and Adenine: self-stacking of DNA bases vs their cross-stacking with SWCNT

Abstract

Self-stacking of four DNA bases, adenine (A), cytosine (C), guanine (G) and thymine (T), and their cross-stacking with (5,5) as well as (10,0) single walled carbon nanotubes (SWCNTs) were extensively investigated with a novel hybrid DFT method, MPWB1K/cc-pVDZ. The binding energies were further corrected with MP2/6-311++G(d,p) method in both gas phase and aqueous solution, where the solvent effects were included with conductor-like polarized continuum model (CPCM) model and UAHF radii. The strongest self-stacking of G and A takes displaced anti-parallel configuration, but un-displaced or “eclipsed” anti-parallel configuration is the most stable for C and T. In gas phase the self-stacking of nucleobases decreases in the sequence G>A>C>T, while because of quite different solvent effects their self-stacking in aqueous solution exhibits a distinct sequence A>G>T>C. For a given base, cross-stacking is stronger than self-stacking in both gas phase and aqueous solution. Binding energy for cross-stacking in gas phase varies as G>A>T>C for both (10,0) and (5,5) SWCNTs, and the binding of four nucleobases to (10,0) is slightly stronger than to (5,5) SWCNT by a range of 0.1–0.5 kcal/mol. The cross-stacking in aqueous solution varies differently from that gas phase: A>G>T>C for (10,0) SWCNT and G>A>T>C for (5,5) SWCNT. It is suggested that the ability of nucleobases to disperse SWCNT depends on relative strength $(\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}})$ of self-stacking and cross-stacking with SWCNT in aqueous solution. Of the four investigated nucleobases thymine (T) exhibits the highest $(\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}})$ which can well explain the experimental finding that T more efficiently functionalizes SWCNT than C and A.

Introduction

Applications of carbon nanotubes (CNTs) into biotechnology have recently emerged, raising a great potential in such a few areas as biosensors, DNA and protein transporters for therapy purpose.^1–7 CNTs themselves have a very low solubility in aqueous solutions as well as in organic solvents, which had been a major barrier for a variety of potential applications. Strategic approaches toward solubilization of CNTs have been developed mainly through their surface functionalization of either covalent or non-covalent attachments to the sidewalls of CNTs.^{2, 8–13} The covalent modification involving chemical reactions between CNTs and molecules somewhat impairs the structural and peculiar electronic properties of CNTs. Therefore, noncovalent functionalization of CNT has attracted increasing attention. Noncovalent functionalization could not only enhance solubility of CNTs but also maintain their attractive geometric, electronic and mechanical properties. Among numerous functional species for solublizing CNTs, biological and bioactive materials are of special importance. The fundamental components in living systems, such as carbohydrates, proteins and nucleic acids, as well as their precursors have been explored to non-covalently functionalize CNTs towards the delivery of therapeutic agents. Several recent review papers deal with the functionalization of single-walled CNTs (SWCNT) with biomolecules and their biomedical applications.^{2, 3, 14}

Zheng et al. have reported that poly T (thymine) ssDNA could more efficiently disperse SWCNTs in water than poly A (adenine) and poly C (cytosine), and they attributed this difference to stronger self-stacking of the latter two poly-bases in aqueous solution.¹⁵ Their further molecular dynamics simulation demonstrated that poly (T) ssDNA wraps around (10,0) SWCNT mainly via π-π stacking between nucleobases and SWCNT, while the hydrophilic sugar-phosphate backbones point to water media to achieve solubility in water. To well understand different functionalization ability, it is necessary to extensively investigate self-stacking of DNA bases and their cross-stacking with SWCNT. The direct comparison between self-stacking and cross-stacking with SWCNT can illustrate the reason why ploy-T could better functionalize SWCNT than poly-C and poly-A. In order to either discuss interaction nature, strength or test novel theoretic methods for weak interactions, numerous studies have been done on the π⋯π stacking of nucleobases, which are represented by Hobza et al.’s systematic work.^16–20 Yet, optimizations were usually done with a constraint of rigid monomer, and geometric structures were not reported in detail. Especially, in spite of a few publications dealing with nucleobase stacking in aqueous solution with force fields, ^{19, 21} to the best of my knowledge there is lack of ab initio quantum mechanics treatment on this issue. Additionally, to be line with the current cross-stacking investigation between nucleobases and SWCNT in terms of theoretical methods and relevant corrections such as basis set superposition error (BSSE) and deformation energy, self-stacking of four different nucleobases will therefore also be investigated in both gas phase and aqueous solution.

Adsorptions through π ⋯ π stacking of adenine on (6,6) and thymine on (8,0) have been investigated by Shtogun et al with local density (LDA) method,²² yet it is well known that LDA usually overestimates dispersive force, a primary factor of stabilizing π stacked systems. Using HF/6-31G** together with force field calculations, Das et al very recently reported the binding energies of guanine (G), adenine (A), thymine (T) and cytosine (C) with (5,5) SWCNT.²³ HF method hardly deals with dispersion because of completely ignoring electron correlations effects. The strongest binding of A to (6,6) predicted by Shtogun et al is 0.354eV,²² while that of A to (5,5) from Das²³ is 0.54eV. The difference may be due to deficiency of employed theoretical methods. In the current work, a relatively suitable DFT method for π stacking, MPWB1K,²⁴ will be employed to fully optimize adsorption of the four nucleobases (G,A,C and T) on (5,5) and (10,0) SWCNTs, and then binding energy will be calculated in both gas phase and in aqueous solution at MP2 level. A comment will be finally made on the ability of the different bases to functionalize SWCNT by comparing binding energies of self-stacking of bases with those of their cross-stacking with SWCNT.

2. Models and Theoretical Calculations

All of the calculations were performed using the G03 program, revision D02.²⁵ Accurate description for noncovalent weak interaction systems like the current π stacked systems is still a challenge for density functional theory (DFT), a promising quantum mechanics method to large systems, although considerable improvements have been achieved over LDA and such conventional hybrid DFT as B3LYP in the recent years.^{26, 27} Recently, the novel exchange density functional modified from PW91 exchange functional together with a meta correlation, MPWB1K, provides relatively reasonable results for π⋯π stacking systems.²⁴ The MPWB1K/cc-pVDZ has also been applied to the binding of cytosine to SWCNTs via π⋯π stacking and NH/CH⋯π interactions, and provided relatively reasonable geometries for further electron correlation treatment with MP2/6-3++G(d,p) as compared with the geometries optimized with MP2/cc-pVDZ.²⁸ Even so, the MPWB1K method will be further validated for π⋯π stacking interaction in the present study. To discuss electron transfer induced by the interaction between nucleobases and SWCNT, atomic net charges will be calculated using the Mulliken and CHELPG ²⁹ schemes.

In order to explore a dependence of cross-stacking between nucleobases and SWCNT on the diameter of SWCNT, the fragments of C₂₄H₁₂ are adapted from an armchair (5,5) and a zigzag (10,0) SWCNTs. The geometries of the fragments were frozen as they are in the corresponding SWCNTs with C-C distance of 1.41Å and C-C-C angle of approximately 119.0°, yet the peripheral carbons are saturated with H-atoms. The MPWB1K/cc-pVDZ will be employed to fully optimize the adsorptions of nucleobases on SWCNTs via π⋯π stacking, and the binding energies are then corrected with MP2/6-311++G(d,p).

In aqueous solution nucleobases have a strong tendency to solvate, thereby resulting in nucleobases apart. Thus, it is necessary to take into account solvent effects on the self-stacking of nucleobases and their cross-stacking with SWCNTs. Since the conductor-like polarizable continuum model (CPCM)³⁰ could give more consistent errors on nuclear and electronic total polarization as compared with the dielectric PCM, the bulk solvent effects will be estimated for the interested systems at CPCM-MP2/6-311++G(d,p)//MPWB1K/cc-pVDZ level together with a UAHF radius. The effect of chosen radii on solvation will be discussed in the result section. In the CPCM model, the variation of the free energy when going from vacuum to solution is composed of the work required to build a cavity in the solvent (cavitation energy) together with the electrostatic and nonelectrostatic work(dispersion and repulsion energy).³¹ The solvation free energies (ΔG^sol) at MP2 level are calculated by comparing the results of two separate calculations performed in gas-phase and in solvent,

$$\mathrm{\Delta }{G}^{\text{sol}}=E^{\text{CPCM-MP2}}-E^{\text{MP2}}$$ (1)

where E^CPCM-MP2 and E^MP2 represent energies predicted by MP2/-6311++G(d,p)//MPWB1K/cc-pVDZ in gas and in solvent, respectively. The strength of the dimers via self- and cross-stacking will be illustrated by binding energies, ΔE_bin with corrections of basis set superposition error (BSSE) and deformation energy (ΔE_def). In gas phase

$$\mathrm{\Delta }{E}_{\text{bin}}=E{(\mathrm{A}\mathrm{B},r_{\mathrm{c}})}^{\mathrm{a}\mathrm{b}}-E{(\mathrm{A},r_{\mathrm{e}})}^{\mathrm{a}}-E{(\mathrm{B},r_{\mathrm{e}})}^{\mathrm{b}}+\mathrm{B}\mathrm{S}\mathrm{S}\mathrm{E}$$ (2)

$$\mathrm{B}\mathrm{S}\mathrm{S}\mathrm{E}=[E{(\mathrm{A},{\mathrm{r}}_{\mathrm{c}})}^{\mathrm{a}}-E{(\mathrm{A},{\mathrm{r}}_{\mathrm{c}})}^{\mathrm{a}\mathrm{b}}]+[\mathrm{E}{(\mathrm{B},{\mathrm{r}}_{\mathrm{c}})}^{\mathrm{b}}-\mathrm{E}{(\mathrm{B},{\mathrm{r}}_{\mathrm{c}})}^{\mathrm{a}\mathrm{b}}]$$ (3)

In Eq. (2) the superscripts ab, a and b indicate that the dimer (AB) at its optimized complex structure and the separate components at their equilibrium structures (A and B) are calculated in the basis sets ab, a and b. The BSSE was estimated with counterpoise method.³² In aqueous solution,

$$\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}=\mathrm{\Delta }{E}_{\mathit{\text{bin}}}+\mathrm{\Delta }\mathrm{\Delta }{G}^{\mathit{\text{sol}}}$$ (4)

$$\mathrm{\Delta }\mathrm{\Delta }{G}^{\mathit{\text{sol}}}=\mathrm{\Delta }{G}^{\mathit{\text{sol}}}(AB,r_c)-\mathrm{\Delta }{G}^{\mathit{\text{sol}}}(AB,r=12)$$ (5)

In Eq. (5) ΔG^sol(AB,r_c), ΔG^sol(AB,r = 12) are solvation free energies predicted by CPCM-MP2 for the optimized dimer and two monomers separated at a distance of 12Å, respectively.

3. Results and Discussions

3.1 Geometries and Binding Energies for the Self-Stacking of DNA Bases

Parallel face-to-back (ftb) as well as face-to-face (ftf) dimers via π-stacking have been carefully searched for the four nucleobases by varying relative locations of five- and six-membered rings. The geometries are fully optimized with MPWB1K/cc-pVDZ method. In spite of one dozen of located dimers, only a few typical ones are illustrated in Figure 1. A1, A2 and A3 are displaced parallel, antiparallel and rotated ftb dimers of adenine, respectively; while A4 and A5 represent the ftf dimers where one adenine monomer was flipped from ftb dimer. To carefully validate MPWB1K//cc-pVDZ method for optimizing π⋯π stacking structures, a variety of characteristic parameters of dimers A1–A5, predicted with MPWB1K/cc-pVDZ as well as MP2/cc-pVDZ are summarized in Table 1. The vertical separations (r) of two adenine molecules from MPWB1K/cc-pVDZ are approximately 0.2Å further than those optimized with MP2/cc-pVDZ, and binding from the former method are systematically weaker than those from the latter method. However, it is interesting to note that the corrected binding energies with MP2/6-311++G(d,p) for the geometries from the two distinct methods MP2/cc-pVDZ and MPWB1K/cc-pVDZ agree very well within ±1.0 kcal/mol, and both MP2/6-311++G(d,p)//MPBWB1K/cc-pVDZ and MP2/6-311++G(d,p)//MP2/cc-pVDZ predict that the displaced anti-parallel dimer (A2) is the most stable one among the located dimers. As a result, MPWB1K//cc-pVDZ can result in relatively reasonable geometries for π⋯ π stacking complexes.

Figure 1.

The selected top-view configurations for self-stacking dimers of four different nucleobases (A, G, C and T), predicted with MPWB1K/cc-pVDZ. Side-view only for the most stable configurations. The numbers in parentheses are binding energies in gas phase. A red ball stands for oxygen atom, blue for nitrogen, gray for carbon and white for hydrogen atoms.

Table 1.

Verticalseparation (r/Å), dipole moment (D/debye), and binding energies (ΔE_int/kcal/mol) of adenine dimers predicted by MPWB1K/cc-pVDZ and MP2/cc-pVDZ, and the binding energies for the dimers corrected with MP2/6-311++G(d,p).

Dimers	MPWB1K/cc-PVDZ			MP2/cc-PVDZ			MP2/6-311++G(d,p)//	MP2/6-311++G(d,p)
							MPWB1K/cc-PVDZ	// MP2/cc-PVDZ
	r	D	ΔEint*	r	D	ΔEint	ΔEint	ΔEint
A1: ftb, displaced parallel	3.2	4.6	−5.9	3.0	5.1	−5.6	−7.7	−7.9
A2: ftb, displaced antiparallel	3.3	0.1	−7.3	3.1	0.0	−8.9	−10.7	−11.6
A3: ftb, rotated	3.2	3.7	−6.9	3.1	4.1	−6.4	−9.1	−9
A4: ftf	3.2	4.5	−7.1	3.0	4.5	−5.8	−9.5	−8.7
A5: ftf	3.3	4.1	−5.3	3.1	4.2	−4.8	−7.1	−7.1

^*without BSSE

It is also true for guanine stacking dimers that the ftb displaced antiparallel configuration (G3) is the most stable one with a vertical separation of 3.1Å. This agrees with Hobza’s result employing MP2-adjusted empirical force field and rigid monomer with an interplane separation of 3.1Å.¹⁶ The ftb rotated dimer (G1) is less stable than G3 by approximately 1.8 kcal/mol, while the ftb displaced parallel dimer (G4) is quite unstable with a binding energy of only −5.7 kcal/mol. The ftf dimer G5 rather deviates from a parallel configuration with a short O and H distance of 2.67Å, which shows that its strong stability not only attributes to π⋯ π stacking also to a clear electrostatic interaction between electropositive H and electronegative O. In all of other dimers, the shortest distances of O and H are greater than 3.2 Å.

Cytosine may be the most widely studied DNA base for its dimerization via π⋯π stacking as well as hydrogen bonding.^{16, 17, 24} The ftf dimer (C4) has a similar structure to the ftf guanine dimer G5, i.e., one monomer significantly tilting from parallel orientation. As a result of two pairs of short N-H distance of 2.82Å, the expected strong electrostatic force is responsible for its strong stability. However, it will be revealed by solvent effect that the ftf dimers, G5 and C4, will not be the most stable dimers in aqueous solution as in gas phase. Opposite to adenine and guanine, ftb undisplaced antiparallel dimer (C1) is more stable than the displaced antiparallel dimers (C2 and C3), which is in line with Hobza‘s finding.¹⁷ Similar to cytosine, among the located thymine dimers ftb undisplaced antiparallel thymine dimer (T1) is also found to be the strongest configuration with a binding energy of −7.3 kcal/mol. Other two closely followed dimers are ftb displaced antiparallel (T2) and bridge (T4) configurations with respective binding energies of −7.2 and −7.1 kcal/mol. Dimer T3 and the ftf dimer T5 are relatively weak (ΔE_int = −6.6 and −5.7 kcal/mol). It is interesting to find that, similar to benzene the most stable configurations for G and A dimers via π stacking are displaced ones, where van der Waals interaction could be maximized. However, opposite to benzene stacking dimers un-displaced or “eclipsed” configurations are the most stable for C and T. This opposite pattern is resulted from different contributions of the major interaction components, such as electrostatic forces, dispersion and exchange-repulsion forces, into self-stacking of four different nucleobases.

The strongest stacking in the gas phase for the four DNA bases changes in the sequence: G(ΔE_int:−13.1 kcal/mol)>A (−10.7)>C (−10.0) >T (−7.3). Using MP2/6-31G(0.25)*// BH&H /6-311++G(d,p), the binding energies obtained by Waller et al ²⁰ for ftf stacked dimers follows the sequence: G(−12.5 kcal/mol)>C(−8.4)>A(−8.1)>T(−6.9). The opposite stacking binding for C and A dimers may lie on the different configurations. The present calculations deal with both ftb and ftf, while it is most likely that only ftf configurations were considered in Waller’s work.²⁰ If a comparison is made only for ftf configurations in Table 2, a consistent bind sequence with Waller’s result is reached: G (ΔE_int:−13.1 kcal/mol)>C(−10.0)>A(−9.4)>T(−5.7).

Table 2.

Vertical separation (r/Å), dipole moment (D/Debye) and binding energy (ΔE_int/kcal/mol) of nucleobases dimers via π⋯π stacking with MPWB1K/cc-pVDZ, and binding energy corrected by MP2/6-311++G(d,p)//MPWB1K/cc-pVDZ.

	MPWB1K/cc-pVDZ			MP2/6-311++G**/MPWB1K/cc-pVDZ
Dimer	r	D	ΔEinta	ΔEint (HF)b	ΔEintc	$\mathrm{\Delta }{E}_{\mathit{\text{int}}}^{\mathit{\text{sol}}}$c
A1: ftb, displaced parallel	3.2	4.6	−5.9	9.3	−7.7	−5.2
A2: ftb displaced antiparallel	3.3	0.1	−7.3	1.4	−10.7	−6.7
A3: ftb rotated	3.2	3.7	−6.9	3.4	−9.1	−6.7
A4: ftf	3.2	4.5	−7.1	4.6	−9.4	−6.9
A5: ftf	3.3	4.1	−5.3	3.4	−7.1	−5.5
G1: ftb rotated	3.1	10.2	−8.6	5.3	−9.2	−5.9
G2: ftb displaced antiparallel	3.2	0.0	−8.5	0.8	−10.5	−6.5
G3: ftb displaced antiparallel	3.1	2.8	−9.0	1.4	−11.0	−6.2
G4: ftb displaced parallel	3.3	11.4	−4.3	6.5	−5.7	−4.8
G5: ftf	3.3	7.1	−10.7	0.7	−13.1	−6.0
C1: ftb undisplaced antiparallel	3.4	0.1	−7.9	−3.0	−9.6	−3.3
C2: ftb slightly displaced antiparallel	3.2	0.0	−8.5	−0.7	−9.4	−2.3
C3: ftb displaced antiparallel	3.1	0.0	−8.5	−1.0	−8.8	−1.9
C4: ftf	3.2	3.8	−9.5	−0.3	−10.0	−2.5
T1: ftb undisplaced antiparallel	3.4	0	−7.2	0.8	−7.3	−3.6
T2: ftb displaced antiparallel	3.2	0	−8.1	2.1	−7.2	−3.2
T3: ftb displaced antiparallel	3.3	0	−8.1	2.5	−6.6	−3.1
T4: ftb bridge	3.4	0	−6.5	1.6	−7.1	−3.4
T5: ftf	3.3	7.1	−6.1	4.3	−5.7	−2.1

^abinding energy without BSSE;

^bbinding energy at HF/6−311++G(d,p)//MPWB1K/cc-pVDZ;

^cΔE_int and $\mathrm{\Delta }{E}_{\mathit{\text{int}}}^{\mathit{\text{sol}}}$ are the binding energies in gas phase and aqueous solution

3.2 Geometries and Binding Energies for the Cross-Stacking of DNA Bases with (5,5) and (10,0) SWCNT

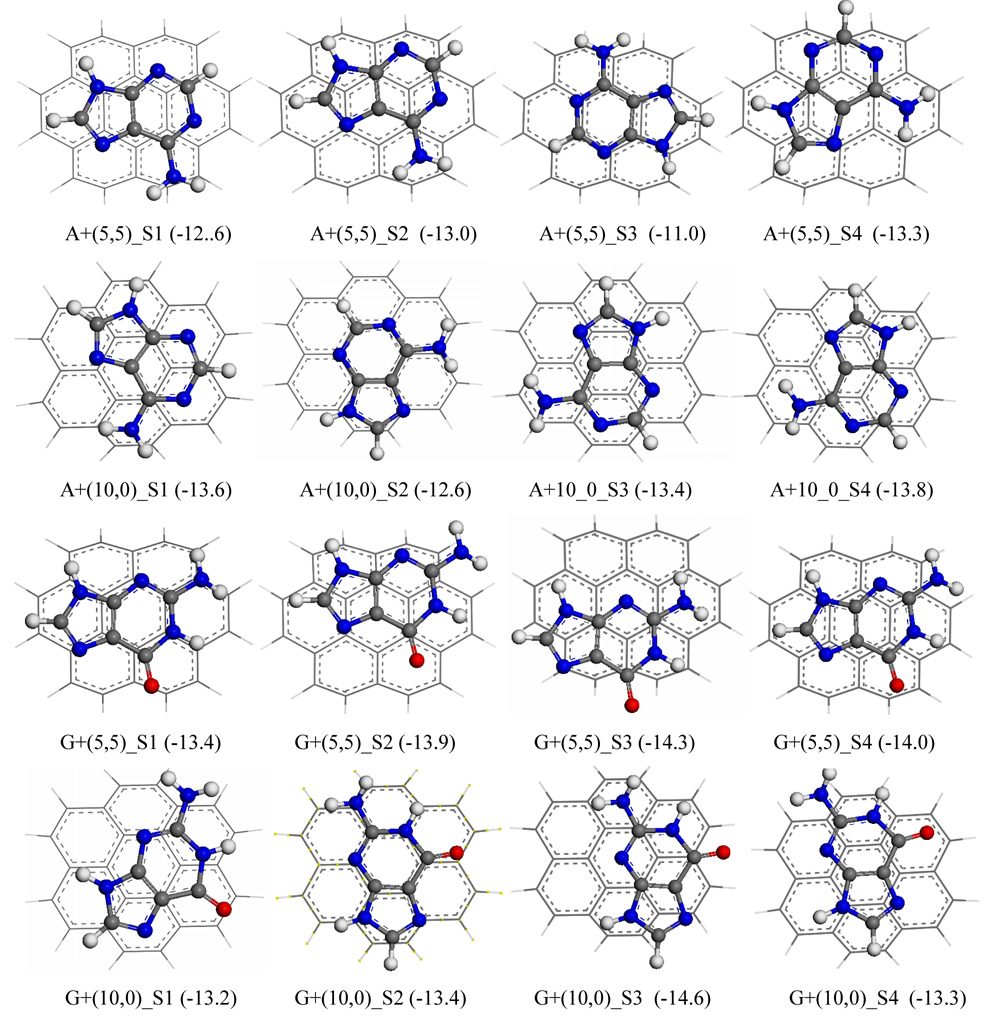
Starting with undisplaced or “eclipsed” configuration, where the hexagonal ring of adenine is just vertically separated from the central hexagonal ring of SWCNT by approximately 3.5Å, the different adsorption configurations were carefully searched by shifting adenine molecule from left to right as well as from top to bottom. The located configurations are generally classified into three categories: undisplaced, bridge, and displaced. The displaced configurations are very similar to AB type graphite layers with either C or N or both coordinated with six central carbons of SWCNT, denoted as C-η⁶ or N-η⁶ coordination, respectively. According to Table 3 and Figure 2, among these three sorts of configurations for the π stacking of adenine and (5,5) SWCNT the configuration, A+ (5,5)_S4, with C-η⁶ and 2N-η⁶ coordination is the most stable one with a binding energy of −13.3 kcal/mol, followed by A+(5,5)_S2 with C-η⁶ and N-η⁶ coordination (binding energy ΔE_int = −13.0kcal/mol), the bridge adsorption (A+(5,5)_S1, ΔE_int = −12.6 kcal/mol) and undisplaced configuration (A+(5_5)_S3, ΔE_int= −11.1 kcal/mol). The strongest binding of adenine to (6,6) SWCNT predicted by Shtogun et al. ²² with DFT-LDA plane-wave expansion, −8.2 kcal/mol, is much weaker than the current result. However, it is noted that the binding energy of adenine to (5,5) from Das et al ²³ by adding HF and van der Waals, −12.5 kcal/mol, is only 0.8 kcal/mol weaker than the present one.

Table 3.

Vertical separation (r/Å), dipole moment (D/Debye) and binding energy (ΔE_int/kcal/mol) of the stacking complex of nucleobases with (5,5) and (10,0) SWCNTs predicted by MPWB1K/cc-pVDZ, and binding energy corrected by MP2/6-311++G(d,p)//MPWB1K/cc-pVDZ. The symbol A+(5,5)_S1 represents the stacking configuration S1 of A with (5,5), and so on.

	MPBB1K/cc-pVDZ			MP2/6-311++G**/MPWB1K/cc-pVDZ)
Stacking complex	r	D	ΔEinta	ΔEint (HF)	ΔEint	$\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}$	qb
A+(5,5)_S1:C=C bridge	3.3	2.4	−5.4	8.1	−12.6	−10.6	−0.14
A+(5,5)_S2: C-η6, N-η6	3.3	3.0	−5.6	8.5	−13.0	−11.1	−0.12
A+(5,5)_S3: undisplaced	3.4	2.7	−1.1	7.3	−11.1	−9.8	−0.12
A+(5,5)_S4: C-η6, 2N-η6	3.4	3.9	−6.6	6.1	−13.3	−10.7	−0.14
A+(10,0)_S1: C-η6	3.2	3.1	−5.8	7.9	−13.6	−10.9	−0.12
A+(10,0)_S2: undisplaced	3.4	3.5	−4.7	6.5	−12.6	−9.9	−0.11
A+(10,0)_S3: C=C bridge	3.2	3.3	−5.3	6.9	−13.4	−10.5	−0.12
A+(10,0)_S4: C-η6	3.2	3.4	−6.3	6.9	−13.8	−10.7	−0.13
G+(5,5)_S1: undisplaced	3.4	6.4	−7.4	5.0	−13.4	−9.8	−0.14
G+(5,5)_S2: C-η6	3.2	6.1	−8.6	8.3	−13.9	−11.3	−0.13
G+(5,5)_S3: 3 N-η6	3.3	7.1	−10.0	5.5	−14.3	−9.5	−0.17
G+(5,5)_S4: C=C bridge	3.3	6.3	−8.9	7.3	−14.0	−11.0	−0.13
G+(10,0)_S1: C- η6	3.4	5.6	-5.1	8.0	−13.2	−10.1	−0.14
G+(10,0)_S2: undisplaced	3.3	5.4	−4.8	7.4	−13.4	−9.2	−0.14
G+(10,0)_S3: N- η6	3.2	5.6	−7.9	5.5	−14.6	−10.0	−0.14
G+(10,0)_S4: C=C bridge	3.3	5.4	−5.8	5.5	−13.3	−9.4	−0.13
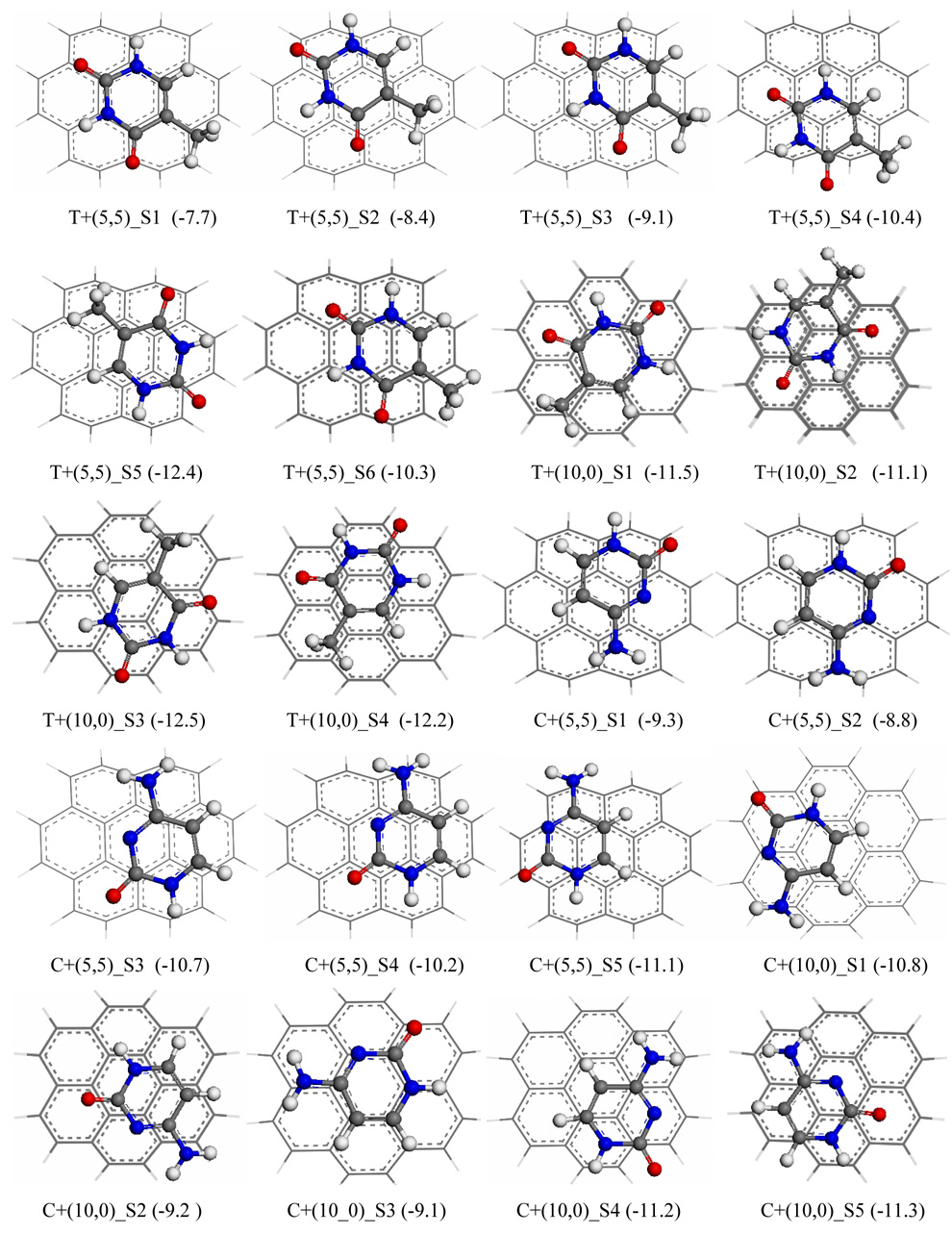
T+(5,5)_S1: undisplaced	3.7	4.7	−2.4	0.7	−7.7		−0.14
T+(5,5)_S2: slightly displaced	3.7	4.4	−2.9	1.1	−8.4	−6.8	−0.15
T+(5,5)_S3: N- η6	3.5	4.0	−3.2	4.4	−9.1	−7.5	−0.13
T+(5,5)_S4: N- η6	3.3	4.4	−5.6	4.0	−10.4	−7.6	−0.17
T+(5,5)_S5: C=C bridge, N- η6	3.3	4.4	−6.9	5.2	−12.4	−9.9	−0.17
T+(5,5)_S6: C-N and C=C bridge	3.3	4.1	−4.5	6.6	−10.3	−8.6	−0.14
T+(10,0)_S1: undisplaced	3.3	3.8	−5.3	6.0	−11.5	−8.7	−0.15
T+(10,0)_S2: N- η6	3.2	3.9	−5.3	6.3	−11.1	−8.6	−0.14
T+(10,0)_S3: C- η6	3.3	3.9	−7.1	3.4	−12.5	−9.5	−0.15
T+(10,0)_S4: C=C bridge	3.3	3.8	−6.3	4.3	−12.2	−9.3	−0.15
C+(5,5)_S1: C-C bridge	3.6	5.9	−6.4	0.5	−9.3	−6.0	−0.12
C+(5,5)_S2: undisplaced	3.5	5.6	−5.9	0.1	−8.8	−5.5	−0.12
C+(5,5)_S3: N- η6	3.3	5.2	−7.1	5.9	−10.7	−7.1	−0.12
C+(5,5)_S4: C-N and C=C bridge	3.2	5.4	−6.8	6.4	−10.2	−6.9	−0.12
C+(5,5)_S5: 2 C- η6	3.3	5.8	−7.7	5.3	−11.1	−7.0	−0.12
C+(10,0)_S1: C=C bridge	3.4	6.1	−6.2	2.1	−10.8	−8.5	−0.12
C+(10,0)_S2: C-N bridge	3.4	5.2	−4.1	5.6	−9.2	−6.3	−0.12
C+(10,0)_S3: undisplaced	3.4	5.6	−3.4	4.2	−9.1		−0.11
C+(10,0)_S4: C- η6	3.3	5.9	−6.0	3.3	−11.2	−7.5	−0.12
C+(10,0)_S5: N- η6	3.2	5.1	−6.2	5.3	−11.3	−7.2	−0.12

^abinding energy without BSSE

^bq, charge (e) carried by nucleobases

Figure 2.

The selected top-view configurations for cross-stacking dimers of adenine (A) and guanine (G) with (5,5) and (10,0), predicted with MPWB1K/cc-pVDZ. A+(5,5)_S1 represents the stacking configuration S1 of A with (5,5), and so on. The numbers in parentheses are binding energies in gas phase. A red ball stands for oxygen atom, blue for nitrogen, gray for carbon and white for hydrogen atoms.

The binding pattern between adenine and (10,0) SWCNT generally follows its binding to (5,5) SWCNT. The strongest and weakest bindings for instance are also η⁶-coordinated (A+(10,0)_S1 and A+(10,0)_S4; ΔE_int = −13.6 and −13.8 kcal/mol) and undisplaced (A+(10,0)_S2; ΔE_int = −12.6 kcal/mol) configurations respectively, and the bridge adsorption (A+(10,0)_S3; ΔE_int = −13.4kcal/mol ) lies in between. In line with the previous finding for the diameter dependence of π stacking between cytosine and SWCNT, ²⁸ the corresponding binding for adenine to (10,0) SWCNT is stronger than to (5,5) SWCNT. That again shows that flat aromatic ring is favorable to π⋯π stacking. For example, the strongest binding are −13.8 (A+(10,0)_S4) and −13.3 (A+(5,5)_S4) kcal/mol, respectively. In the case of undisplaced configurations (A+(10,0)_S2 and A+(5,5)_S3), the binding energy difference is more significant (ΔE_int: −12.6 vs. −11.1 kcal/mol).

The adsorption configuration of guanine, G+(5,5)_S2 with C-η⁶ coordination, is more stable than its resemblance of adenine, A+(5,5)_S2 (ΔEint: −13.9 vs −13.0 kcal/mol). Comparing other corresponding configurations, the interaction between guanine and (5,5) is generally stronger than that between adenine and (5,5) in a range of 1–2 kcal/mol. Since both adenine and guanine have a pentagonal imidazole ring and a hexagonal ring, the electronegative oxygen of carbonyl group in guanine molecules is probably responsible for the stronger interaction. The strongest interaction (G+(5,5)_S3: −14.3kcal/mol) is approximately 1.0 kcal/mol more negative than predicted by Das et al. ²³

For the adsorptions of guanine on (10,0) SWCNT, the respective binding energies are −13.2, −14.6, −13.3, and −13.4 kcal/mol for C-η⁶ (G+(10,0)_S1), N-η⁶ (G+(10,0)_S3), bridge (G+(10,0)_S4) and undisplaced (G+(10,0)_S2) configurations. Similar to adenine, it is also exhibited that the adsorption of guanine on (10,0) is stronger than on (5,5) SWCNT, evidenced by higher negative binding energy on (10,0) for the most favorable configuration (ΔE_int = −14.6 kcal/mol for G+(10,0)_S3 vs −14.3kcal/mol for G+(5,5)_S3).

As shown in Table 3 and Figure 3, among the six presented configurations for adsorptions of thymine on the (5,5) SWCNT configuration, T+(5,5)_S5 with a C=C bridge and N-η⁶ adsorptions, is the most stable one with a binding energy of −12.4 kcal/mol. Another two approximately 2.0 kcal/mol less stable configurations are T+(5,5)_S4 with N-η⁶ (ΔE_int: −10.4kcal/mol) and T+(5,5)_S6 with C-N and C=C bridge (ΔE_int:−10.3 kcal/mol). The binding energies for other three configurations are considerably less negative: undisplaced configuration (T+(5,5)_S1, ΔE_int=−7.7 kcal/mol), a slightly displaced configuration (T+(5,5)_S2, ΔE_int =−8.4 kcal/mol), and the displaced configuration T+(5,5)_S3 with N-η⁶ coordination (ΔE_int =−9.1 kcal/mol). The binding energy (−12.4 kcal/mol) for the most stable configuration, T+(5,5)_S5, is close to that of −11.3 kcal/mol reported by Das et al ²³. The most stable adsorption of thymine on (10,0), T+(10,0)_S3 with C-η⁶ coordination (ΔE_int =−12.5kcal/mol), shows slightly stronger than on (5,5), T+(5,5)_S5 (ΔE_int = −12.4kcal/mol).

Figure 3.

The selected top-view configurations for cross-stacking dimers of thymine (T) and cytosine (C) with (5,5) and (10,0), predicted with MPWB1K/cc-pVDZ. C+(5,5)_S1 represents the stacking configuration S1 of C with (5,5), and so on. The numbers in parentheses are binding energies in gas phase. A red ball stands for oxygen atom, blue for nitrogen, gray for carbon and white for hydrogen atoms.

Of the located configurations for cytosine adsorption on SWCNT (5,5) in Figure 3, the configuration C+(5,5)_S5 via two C-η⁶ coordination is the most stable one with a binding energy of −11.1 kcal/mol, which is closely followed by the configuration, C+(5,5)_S3 via N-η⁶ and C=C bridge adsorption (ΔE_int:−10.7 kcal/mol). The bridge configuration, C+(5,5)_S4 is also quite stable (ΔE_int:−10.2 kcal/mol). The binding energies for the two less stable configurations, the bridge adsorption (C+(5,5)_S1) and the undisplaced adsorption (C+(5,5)_S2), are −9.3 and −8.8 kca/mol, respectively. Once again the interaction between cytosine with (10,0) is stronger than with (5,5). For example, the respective binding energies for the undisplaced configurations C+(10,0)_S3 and C+(5,5)_S2 are −9.1 and −8.8 kcal/mol, and the binding of the most stable adsorption on (10,0) SWCNT (C+(10,0)_S5; ΔE_int = −11.3 kcal/mol) is stronger by 0.2 kcal/mol than the most stable one on (5,5) SWCNT (C+(5,5)_S5; BE=−11.1 kcal/mol).

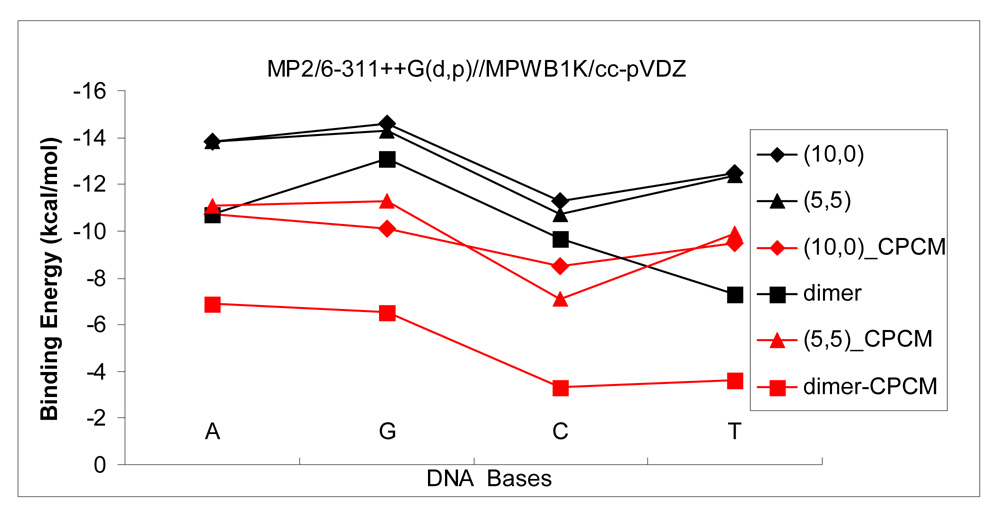
The binding energies for the strongest interactions are summarized in Table 4 for the four DNA bases with (5,5) and (10,0) SWCNT. Because the five-memberred imidazole ring is absent in thymine and cytosine molecules, the π stacking interactions between T/C with the given SWCNT are weaker than A and G. Although the self-stacking of T is weaker than C, its cross-stacking with the SWCNTs are stronger than C by approximately 1 kcal/mol. For the given SWCNT, the binding of the four DNA bases with SWCNT increase in the sequence: C < T < A <G (ΔE_int to (10,0) SWCNT: −11.3, −12.5, −13.8 and −14.6 kcal/mol; ΔE_int to (5,5): −11.1, −12.4, −13.3 and −14.3 kcal/mol). This sequence agrees with that of Das et al ²³.

Table 4.

The strongest binding energies in gas phase ( ΔE_bin, kcal/mol) and in aqueous solution ($(\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}},\text{kcal}/\text{mol})$, for the self stacking of nucleobases (A, G, C and T) and their cross stacking with (5,5) and (10,0) SWCNT

System	Binding energy	Methods	A	G	C	T
dimer	ΔEbin	MP2/6-311++G(d,p)	−10.7	−13.1	−9.7	−7.3
		MP2/aug-cc-pVDZa		−13.2	−10.2
		MP2/6-31G(0.25)b	−8.1	−12.5	−8.4	−6.9
	$\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}$	MP2-CPCM	−6.9	−6.5	−3.3	−3.6
Base+(10,0)	ΔEbin	MP2	−13.8	−14.6	−11.3	−12.5
		LDAd				−7.3
	$\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}$	MP2-CPCM	−10.7	−10.1	−8.5	−9.5
Base+(5,5)	ΔEbin	MP2	−13.3	−14.3	−11.1	−12.4
		HF+vdwe	−12.5	−13.4	−10.6	−11.3
		LDAc	−8.2
	$\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}$	MP2-CPCM	−11.1	−11.3	−7.1	−9.9

^aRef ¹⁶

^bRef. ²⁰

^cRef ²² for A on (6,6)

^dRef ²² for T on (8,0)

^eRef.²³

3.3 Solvent Effects on the Self-Stacking and Cross-Stacking of DNA Bases

To validate a cavity model for solvent effects with CPCM, a number of radii such as UAO, UAKS, UAHF, BONDI and PAULING were applied to the adenine dimer (A2). According to Table 5, the solvation energies (ΔG^sol) as well as binding energies in aqueous solution $(\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}})$ with MP2/6-311++G(d,p)//MPWB1K/cc-pVDZ considerably change with the radii. In spite of quite different solvation energy (ΔG^sol) as high as 4.0 kcal/mol, the three United Atom Topological Models (UA0, UAKS and UAHF) give a similar binding energy $(\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}})$ in aqueous solution, which lies between those expected with BONDI and PAULING. UAHF radii therefore will be applied to DNA bases stacking and their cross stacking with SWCNT.

Table 5.

Solvation free energy (ΔG^sol, kcal/mol) and binding energy ($\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}},\text{kcal}/\text{mol})$ in aqueous solutions of adenine dimer (dimer A2) predicted with MP2/6-311++G(d,p)//MPWB1K/cc-pVDZ using CPCM model with a variety of atomic radii

	UA0	UAKS	UAHF	BONDI	PAULING
a ΔGsol	−29.5	−30.1	−26.1	−32.3	−34.7
b $\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}$	−6.0	−6.4	−6.7	−8.6	−4.9

^aΔG^sol=E^CPCM-MP2−E^MP2

^b$\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}=\mathrm{\Delta }{E}_{\mathit{\text{bin}}}+\mathrm{\Delta }\mathrm{\Delta }{G}^{\text{sol}},$ ΔΔG^sol = ΔG^sol (AB,r_c)−ΔG^sol (AB,r = 12)

The MP2-CPCM predicted binding energies $(\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}})$ for the dimers via self- and cross-stacking are listed in Table 2 and Table 3. The bindings in aqueous solution are significantly weakened by approximately 2–7 kcal/mol. Solvation energies change with self and cross-stacking configurations because of geometries and dipole moments. For the given system the sequence of binding energies after taking into account solvent effects is not consistent with that in gas phase. For example, for the adenine dimers the strength of binding in vacuum decreases in the sequence A2>A4>A1>A3>A5, while the binding sequence in aqueous changes to A4>A1~A2>A5>A3.

The solvation of nucleobases will decrease their self-stacking to some extent, which depends on the degree of solvation. Because of different polarity of nucleobases, evidenced by the dipole moments of G (6.5 Debye) > C(6.3) >T(4.1)>A(2.4) at MPWB1K/cc-pvdz level, it can be expected that G and C are more strongly solvated than T and A. As a result of different solvent effects the self-stacking of DNA bases changes from the sequence G>A>C>T in gas phase to A>G>T>C in aqueous solutions with respective binding energy of −6.9, −6.5, −3.6 and −3.3 kcal/mol. The relatively strong solvation of G and C hinders their self-stacking so that self-stacking strength of G and C is weaker than A and T, respectively.

Similarly, the cross-stacking of nucleobases with SWCNT in aqueous solution also exhibits a different order than in gas phase. The binding of T to (10,0) as well as (5,5) in aqueous solution is the same as in gas phase, still stronger than C and weaker than G and A. For (5,5) SWCNT, in aqueous solution G remains more strongly interacts with the SWCNT than A $(\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}:-11.3\text{vs}.-11.1\text{kcal}/)$ although the binding energy difference is smaller than in gas phase (ΔE_bin: −14.3 vs. −13.3 kcal/mol). However, it is exhibited that in aqueous solution A more strongly binds to (10,0) than G ($\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}:-10.7\text{vs}.-10.1\text{kcal}/\text{mol}$), which is opposite to the trend in gas phase (E_bin: −13.8 vs. −14.6 kcal/mol). Thus, the binding of nucleobases to (10,0) SWCNT follows the sequence, A>G>T>C with respective binding energy of −10.7, −10.1, −9.5 and −8.5 kcal/mol, while the binding to (5,5) SWCNT decreases in the order G>A>T>C with a binding energy of −11.3, −11.1, −9.9 and −7.1 kcal/mol respectively.

3.4 Electron correlation effects and electron transfer

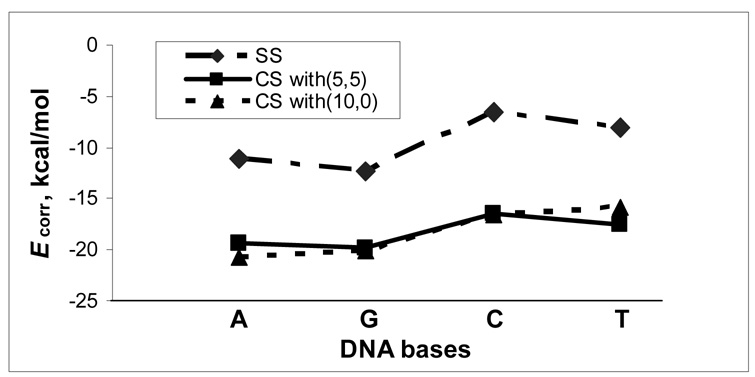
It is well established that dispersion plays the primarily binding role in π stacked systems like the current self-stacking of nucleobases and their cross-stacking with SWCNT. ^{20, 33, 34} Dispersion is a result of electron correlation effects, therefore to further understand the contribution of electron correlation to the π stacking the binding energy at HF/6-311++G(d,p)//MPWB1K/cc-pVDZ is also listed in Table 2 and Table 3. Table 2 shows that only for self-stacking of cytosine HF predicts bound states with negative binding energies from −0.3 to −3.0 kcal/mol, and HF fails to yield bound state for the self-stacking of G, A, and T. According to Table 3, for all of the located cross-stacking configurations HF binding energies are positive, i.e., non-bound state. Das et al ²³ employed HF/6-31G** to optimize the cross-stacking dimers of the four bases and (5,5), and obtained the bound states with rather small binding energies of −1.61, −0.92, −0.69 and −0.46 kcal/mol for C, G, A and T, respectively. The difference from the present work at HF is due to different optimization level. It is important that both the present work and Das’s result indicate that electron correlation effects are indeed dominant factors for stabilizing dimers of nucleobases self-stacking and their cross-stacking with SWCNTs.

The vertical contribution of electron correlation to the binding energy, E_corr, is defined as the difference between the binding energies predicted by MP2/6-311G(d,p)//MPWB1K/cc-pVDZ and HF/6-311G(d,p)//MPWB1K/cc-pVDZ. E_corr for the most stable self- and cross-stacking configurations is plotted in Figure 5 for the four DNA bases, A, G, C and T. Figure 5 shows that the cross-stacking for the given base with (5,5) and (10,0) SWCNTs has rather similar E_corr, yet the contribution to the cross-stacking of A and G is more important than that of C and T. The latter fact is also true for the self-stacking of the four bases. Additionally, for the given base E_corr of self-stacking is less than that of cross-stacking. It is not difficult to understand this scenario from the nature of base and SWCNT. Because of hydrophilic property of bases, besides considerable dispersion force they may also interact with each other via electrostatic interaction, which could be well covered by HF method. However, in the case of the cross-stacking between hydrophobic SWCNT and hydrophilic bases the electrostatic interaction becomes less important than the self-stacking, and the correlation interaction energy E_corr is relatively more significant.

Figure 5.

Electron correlation contribution, E_corr to binding energy in gas phase for the most stable configurations from self-stacking (SS) and crosee-stacking (CS) of the four DNA bases. E_corr, the difference between the binding energies predicted by MP2/6-311G(d,p)//MPWB1K/ccpVDZ and HF/6-311G(d,p)//MPWB1K/cc-pVDZ.

For the bio-nano systems, it is also interesting to get insight into charge transfer. Table 3 indicates that in all of the cross-stacking cases charge is transferred from SWCNT to nucleobases in a range of 0.11 to 0.17e. The small amount of charge carried by nucleobases implies that short range charge-transfer interaction may not play important role on the stability of the current π-stacked complexes.

3.5 On the different ability of nucleobases to disperse SWCNT

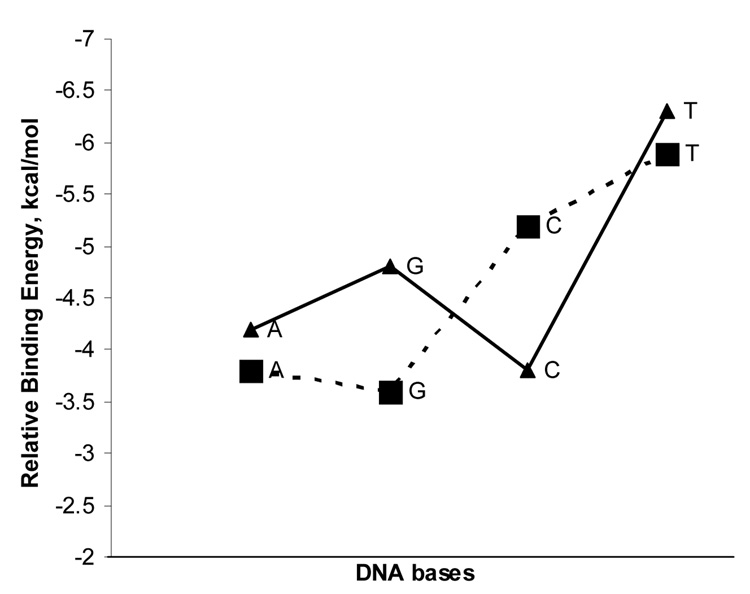
In practical experimental situations, nucleobases solvated by solvent molecules not only interact with like molecules via self-stacking, also interact with SWCNTs via cross-stacking. Therefore, the ability of nucleobases to disperse SWCNT depends on the competition of self stacking and cross-stacking, and it can be well reflected by the binding energy difference of the two stacking in aqueous solution. Therefore,

$$\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}=\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\text{sol}}(\text{crossing}-\text{satcking})-\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}(\text{self}-\text{stacking})$$

for the strongest stacking is plotted in Figure 6. The higher negative $\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}$, the higher ability the nucleobase has to disperse SWCNT via π stacking after overcoming its self-stacking. Although the binding of T to SWCNT is weaker than G and A, evidenced by lower negative $\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}$, Figure 6 indicates that for both (10,0) and (5,5) SWCNTs T has the highest negative $\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}$ This result fundamentally supports the experimental finding that poly T (thymine) ssDNA could more efficiently disperse SWCNTs in water than poly A (adenine) and poly C (cytosine).

Figure 6.

The relative binding energies ($\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}=\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\text{sol}}(\text{crossing}-\text{stacking})-\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}(\text{self}-\text{stacking})$) in aqueous solution of self- and cross-stacking of four different nucleobases (G, A, C and T). The solid line with triangle and dashed line with square stand for the cross-stacking with (5,5) and (10,0) SWCNTs, respectively.

4. Conclusions

Using MPWB1K/cc-pVDZ, the conformers from self-stacking of four DNA bases, adenine (A), cytosine (C), guanine (G) and thymine (T), and their cross-stacking with (5,5) as well as (10,0) SWCNTs were extensively and fully optimized. The binding energies were further corrected with MP2/6-311++G(d,p) method in both gas phase and aqueous solution. In gas phase the self-stacking of nucleobase decreases in the sequence G>A>C>T, while the binding in aqueous solution exhibit a distinct sequence of A>G>T>C. Regarding the cross-stacking between nucleobases with SWCNTs, it turns out that the binding sequence in gas phase varies as G>A>T>C for both (10,0) and (5,5) SWCNTs, and that the cross-stacking shows a weak dependence on the diameter of SWCNT, namely the binding of four nucleobases to (10,0) is slightly stronger than to (5,5) SWCNT by a range of 0.1–0.5 kcal/mol. For a given base, in both gas and aqueous solution cross-stacking is stronger than self-stacking. The relative strength $(\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}})$ of self-stacking and cross-stacking with SWCNT in aqueous solution indicates that thymine (T) exhibits the highest $\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}}$ of the four investigated nucleobases, which can well explain the experimental finding that T more efficiently functionalizes SWCNT than C and A.

Figure 4.

The binding energy for self- and cross-stacking in gas phase and in aqueous solution with MP2/6-311++G(d,p)//MPWB1K/cc-pVDZ. The black and red lines represent stacking in gas phase (ΔE_bin) and in aqueous solution $(\mathrm{\Delta }\mathrm{\Delta }{E}_{\mathit{\text{bin}}}^{\mathit{\text{sol}}})$, respectively.